1 Introduction

The second-order quantum master equation (QME) is a fundamental tool for studying the dynamics of open quantum systems and finds wide-ranging applications in diverse fields, including quantum optics, condensed matter physics, condensed phase chemistry, and biology [1,2,3,4,5,6]. However, employing the QME in regimes with strong non-Markovian behavior, characterized by slow environmental evolution and significant retardation effects on the subsystem, presents substantial challenges. These challenges become even more pronounced in low-temperature conditions and structured environments, where non-Markovian effects are amplified. A notable example is the unconventional impact of sub-Ohmic noise at zero temperature [7,8,9,10,11].

To address the limitations of the QME in handling pronounced non-Markovian retardation effects, incorporating higher order corrections that account for system-bath correlations becomes essential [12,13,14]. However, direct calculations involving these terms require computing high-dimensional time integrals, which is a daunting task [15, 16]. To the best of our knowledge, analytical calculations of high-order perturbations or kernels have only been achieved up to the sixth order [17, 18]. Previous work has employed numerical techniques such as hierarchical equations of motion (HEOM) to compute higher order effects [13, 14]. However, these approaches have been primarily limited to elevated-temperature regimes due to the exponential increase in the number of auxiliary density operators (ADOs) involved, a challenge commonly referred to as the curse of dimensionality. This challenge becomes even more severe as the temperature approaches zero, making the analysis of memory kernels’ properties and high-order perturbative master equations increasingly demanding.

To investigate the effects of high-order kernels in unconventional environments, we address key challenges such as zero-temperature calculations employing the widely used HEOM method [11, 13, 19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. The HEOM approach utilizes a set of ADOs to unravel system-bath correlations within an extended state space [26, 32, 33, 41, 45]. Conventionally, these ADOs are constructed as high-dimensional arrays based on a series of exponential functions derived from the decomposition of the bath correlation function. The extended space, expanded by ADOs, grows exponentially with the number of modes, posing significant challenges in scenarios involving low temperatures and structured bath spectra. This is particularly relevant as standard analytical Matsubara frequencies (i.e., \(\nu _k = 2k\pi /\beta\)) shift toward a continuum strip as temperatures decrease (\(\beta = 1/T\)). Therefore, developing an efficient method for obtaining a limited number of well-behaved modes becomes crucial for successfully implementing HEOM in the study of quantum master equations.

Several decomposition schemes [11, 43, 46] have been developed to address the limitations of HEOM in low-temperature and general spectral density scenarios, such as the frequency-domain barycentric spectrum decomposition (BSD) [11]. The effectiveness of these decomposition schemes has been demonstrated by their ability to reproduce phenomena like the Kondo resonance peak in Fermi baths [46] and the Shiba relation in sub-Ohmic boson baths [11]. Notably, by optimizing the properties of auxiliary modes under specific constraints, these schemes allow for the integration of a minimal number of modes (poles) into various versions of HEOM and other methods, such as the pseudomode approach [47], the hierarchy of pure states (HOPS) [48], and the nonequilibrium dynamical mean-field theory (DMFT) [49], even in unconventional environments.

In this work, we employ the Free-Poles HEOM (FP-HEOM) [11], which combines the optimized BSD and a hierarchical structure, to showcase the performance of higher order master equations in addressing unconventional environments. We also compare it with the well-established Non-Interacting-Blip Approximation (NIBA), a powerful but approximate scheme for non-perturbative treatment of the system-bath coupling in spin systems. The remainder of this paper is organized as follows: In Sections II and III, we provide a brief overview of the hierarchical equations of motion and discuss their limitations in simulating dynamics of open quantum systems. In Section IV, we present numerical simulation results to demonstrate the efficiency and accuracy of our proposed method. Finally, we summarize our findings and discuss potential avenues for future research in the concluding section.

2 Model Hamiltonian

The spin-boson model, which describes a two-state system interacting bilinearly with a harmonic bath, has been extensively studied in open quantum system dynamics [7]. In this work, we employ this model as a prototypical example to benchmark our method, while generalizations to more complex models are straightforward.

We consider a spin-boson model with the Hamiltonian

$$\begin{aligned} \begin{aligned} H_T&= \epsilon \sigma _z + \Delta \sigma _x + \sum _ic_ix_i\sigma _z \\&\quad + \sum _i{\frac{p_i^2}{2m_i} + \frac{1}{2}m_i\omega _i^2x_i^2} + \frac{1}{2}\mu \sigma _z^2 \;, \end{aligned} \end{aligned}$$
(1)

where the system degrees of freedom (DoF) are represented by dimensionless Pauli matrices \(\sigma _x\) and \(\sigma _z\). \(\Delta\) and \(2\epsilon\) denote the tunneling energy and energy bias between the two eigenstates of \(\sigma _z\), i.e., \(|\pm \rangle\). The ith harmonic modes of the reservoir is characterized by its mass, coordinate, momentum, and frequency, i.e., \(m_i\), \(x_i\), \(p_i\), and \(\omega _i\), respectively. The coupling between the system and the ith bath mode is denoted by \(c_i\) with \([m\omega ^2x]\) dimension.

The effective impact of the bath on the system is fully described by the coupling-weighted spectral density

$$\begin{aligned} J(\omega ) = \frac{\pi }{2} \sum _{i} \frac{c_i^2}{m_i\omega _i} \delta (\omega -\omega _i) \;\;. \end{aligned}$$
(2)

In the following, we assume a generic spectral density [50] of the form

$$\begin{aligned} J(\omega ) = \frac{\pi }{2}\,\alpha \, \omega _c^{1-s}\,\omega ^{s}\, \textrm{e}^{-\omega /\omega _c} \;, \end{aligned}$$
(3)

where \(\alpha\) is the dimensionless Kondo parameter characterizing the system-bath dissipation strength and \(\omega _c\) is the characteristic frequency of the bath. For \(s=1\), this spectral distribution describes an ohmic reservoir and it is called sub-ohmic for \(s<1\). In the latter situation, the interplay of the relatively large portion of low-frequency modes with the internal two-level dynamics makes this model extremely challenging to simulate, particularly in the long time limit and close to or at \(T = 0\).

3 Hierarchical equations of motion

We briefly describe the essence of the HEOM approach and refer to the literature for further details. The derivation assumes a factorized initial states of the total density at time zero, i.e., \(W(0) = \rho _s(0)\otimes e^{-\beta H_b}/{\textrm{Tr}}\, e^{-\beta H_b}\). The generalization to correlated initial states can be found in Refs. [51, 52].

In path integral representation [53], a formally exact expression for the reduced density is obtained by integrating over the bath degrees of freedom. The effective impact of the bath onto the system dynamics is captured by the Feynman–Vernon influence functional [53] which reads

$$\begin{aligned} {\mathcal {F}}[q^{+},q^{-}]&= -\int _{0}^{t}ds\int _0^sd\tau [q^{+}(s)-q^{-}(s)] \nonumber \\&\quad \times \left[ C(s-\tau )q^{+}(\tau ) - C^{*}(s-\tau )q^{-}(\tau ) \right] \;\; . \end{aligned}$$
(4)

In the expression above, the forward and backward paths of the subsystem, denoted by \(q^{\pm }(\tau )\), are defined through the relation

$$\begin{aligned} q^{\pm }(\tau ) = \langle q^\pm (\tau ^+) |\sigma _z|q^\pm (\tau )\rangle \;, \end{aligned}$$
(5)

where \(|q^\pm \rangle\) represent the eigenstates of \(\sigma _z\), and \(\tau ^+\) signifies the moment immediately following the time slice \(\tau\). The influence functional describes arbitrary long-ranged self-interactions in time of the system paths determined by the bath auto-correlation \(C(t)=\langle \xi (t) \xi (0)\rangle\) with the collective degree of freedom \(\xi =\sum _i c_i x_i\). Particularly at low temperatures, correlation functions are known to decay algebraically, so that direct simulations of the path integral, e.g., via path integral Monte Carlo (PIMC) [10, 54], are plagued by a degrading signal-to-noise ratio.

The hierarchical equations of motion (HEOM) approach deals with this problem by converting the time-non-local path integral into a set of time-local differential equations through the introduction of auxiliary density operators (ADOs). The basic ingredient is a decomposition of C(t) in a series of K exponential modes, where K has to be sufficiently bounded for the nested hierarchy to be practically solvable. To formulate a minimal set of modes is thus the prerequisite to access low temperatures and long times. As a matter of fact, this problem has been solved by us only recently [11] by implementing the barycentric representation of rational functions for the spectral noise power \(S_\beta (\omega )\), i.e., the Fourier transform of C(t)

$$\begin{aligned} \begin{aligned} C(t)&= \frac{1}{\pi } \int _{-\infty }^{+\infty } d\omega \, S_{\beta }(\omega ) \,\textrm{e}^{-i\omega t} \\&\quad = \sum _{k=1}^{K} \, d_k\, \textrm{e} ^{-z_k\,t} + \delta C(t) ~~ t \ge 0 \;\; \end{aligned} \end{aligned}$$
(6)

with complex-valued amplitudes \(d_k\) and frequencies \(z_k = \gamma _k + i\omega _k\), \(\gamma _k > 0\). Here, \(S_\beta (-\omega\) and \(S_\beta (\omega )\) are related by the fluctuation dissipation theorem which can be cast into the form \(S_\beta (\omega ) = 2[n_\beta (\omega ) +1 ] J(\omega )\) with the Bose distribution \(n_\beta (\omega ) = 1/[\exp (\beta \omega ) -1]\). The barycentric representation constructs a function \({\tilde{S}}_\beta (z)\) in the complex plane, such that it is along the real axis an approximant of \(S_\beta (\omega )\) (AAA algorithm, see [55]). The poles and the residues of \({\tilde{S}}_\beta\) appear as \(\{d_k\}\) and \(\{z_k\}\) in (6). For details of this Free-Pole HEOM, see [11, 56]. One can show that the FP-HEOM thus operates with a minimal set of K modes with the correction \(\delta C(t)\) below a chosen threshold.

The exponential function’s self-derivative property in (6) then allows to ‘unravel’ the time non-locality of the original Feynman–Vernon path integral by introducing ADOs \(\rho _{\textbf{m,n}}(t)\) with multi-indices \({\textbf{n}}=(n_1, \ldots , n_K)\) and \({\textbf{m}}=(m_1, \ldots , m_K)\). This then leads to a nested hierarchy of time-local evolution equations for the ADOs, that is

$$\begin{aligned} \dot{\hat{\rho }}_{\textbf{m,n}}= & {} -\left(i{\mathcal {L}}_s +\sum _{k=1}^{K} m_{k} z_{k} + \sum _{k=1}^{K} n_{k} z_{k}^{*} \right) {\hat{\rho }}_{\textbf{m,n}}\nonumber \\{} & {} -i\sum _{k=1}^{K} \sqrt{(m_k+1)\, d_k} \left[ {\hat{q}},{\hat{\rho }}_{\textbf{m}_k^{+},\textbf{n}} \right] \nonumber \\{} & {} -i\sum _{k=1}^{K} \sqrt{(n_k+1)\, d_k^*}\left[ {\hat{q}},{\hat{\rho }}_{\textbf{m,n}_k^{+}} \right] \nonumber \\{} & {} -i\sum _{k=1}^{K} \sqrt{m_k\, d_k}\;{\hat{q}}\;{\hat{\rho }}_{\textbf{m}_k^{-},\textbf{n}}\nonumber \\{} & {} +i\sum _{k=1}^{K} \sqrt{n_k\, d_k^*}\;{\hat{\rho }}_{\textbf{m,n}_k^{-}}{\hat{q}} \;. \end{aligned}$$
(7)

The subscript \(\varvec{m}_k^{\pm }\) and \(\varvec{n}_k^{\pm }\) denote \(\{m_1,\ldots ,m_k\pm 1,\ldots \,m_K\}\) and \(\{n_1,\ldots ,n_k\pm 1,\ldots ,n_K\}\), respectively. The bare system evolution is propagated by \({\mathcal {L}}_s\rho = [H_s,\rho ]\). Eventually, the physical reduced density matrix \({\hat{\rho }}_s\) corresponds to the multi-index \(\varvec{m}=\varvec{n}=0\). To boost the numerical efficiency of the FP-HEOM (7), matrix product state (MPS) representations can be conveniently implemented which allows to tackle also asymptotic times down to temperature zero [11].

Note that truncating the nested hierarchy of ADOs after the \(L^{\text {th}}\) tier, as given by

$$\begin{aligned} \sum _k (n_k+m_k)\le L\,, \end{aligned}$$
(8)

implies the inclusion of system-bath coupling strengths up to the order of \(\alpha ^{2\,L}\) [57]. Indeed, as demonstrated in previous works [58,59,60], truncating at \(L=1\) yields a generalized Redfield equation.

4 Numerical results

In this section, we employ the non-perturbative Free-Pole Hierarchical Equations of Motion (FP-HEOM) method to study the dynamics of a two-level quantum system coupled to a sub-Ohmic bosonic bath. We consider bath temperatures ranging from \(T = 0\) to finite \(T \ne 0\), with a spectral density \(J(\omega )\propto \omega ^s\) where \(0\le s\le 1\). Our analysis focuses on three key aspects: (i) The convergence properties of higher order master equations concerning the system-bath coupling strength \(\alpha\) and spectral exponent s. (ii) The accuracy of the Redfield-plus equation (12) across diverse temperature and bias regimes. (iii) The role of non-perturbative memory kernels as effective generators for system dynamics.

To ensure the accuracy of our results, we employed a barycentric decomposition with a stringent tolerance threshold defined by \(\delta C(t) \le 10^{-6}\), where \(\delta C(t)\) represents the time-dependent deviation of the computed correlation function. The FP-HEOM equations were propagated using the Time-Dependent Variational Principle (TDVP) [61], represented using Matrix Product States (MPS) [27]. It is noteworthy that the bond dimension, \(\chi\) of MPS exhibits an inverse relationship with the parameter \(s\). Through meticulous optimization tests, we ascertained that for \(s=0\), a bond dimension of \(\chi = 50\) is optimal, whereas \(s=1\) is best represented with \(\chi = 2\). All simulations were executed on a single core of an Intel Xeon Gold 6252 CPU clocked at 2.1 GHz. The computational durations varied, spanning from mere minutes to several hours, contingent on the specific scenario being analyzed.

4.1 Performance of truncated time-evolution equations within FP-HEOM

A variety of approximate methods for open quantum dynamics have been proposed, with the most notable ones considering the system-reservoir coupling up to the second order. When there is a clear separation in time scales between the rapid decay of reservoir correlations and the relaxation dynamics of the reduced density operator, these methods yield the Redfield master equation [62]. As highlighted earlier, an extended version of the Redfield equation, termed “Redfield-plus”, emerges naturally when the FP-HEIOM is restricted to ADOs satisfying \(\sum _k (n_k+m_k) \le 1\). Specifically, in the interaction picture, the ADOs of the zeroth tier (reduced density matrix) are given by

$$\begin{aligned} \dot{{\hat{\rho }}}^{I}(t)&= -i\sum _k[{\hat{q}}^{I}(t),\sqrt{d_k} \rho _{\textbf{0}_k^{+}, \textbf{0}}^{I}(t) + \sqrt{d_k^*} \rho _{\textbf{0},\textbf{0}_k^{+}}^{I}(t)] \, \end{aligned}$$
(9)

with the first-tier ADOs determined via

$$\begin{aligned} \frac{{\text {d}}}{{\text {d}}t}{\hat{\rho }}_{\textbf{0}_k^{+},\textbf{0}}^{I}(t)&= -z_k\rho _{\textbf{0}_k^{+},\textbf{0}}^{I}(t) -i\sqrt{d_k} {\hat{q}}^I(t) {\hat{\rho }}_{\textbf{0,0}}^I(t) \;\;; \end{aligned}$$
(10a)
$$\begin{aligned} \frac{{\text {d}}}{{\text {d}}t}{\hat{\rho }}_{\textbf{0,0}_k^{+}}^{I}(t)&= -z_k^*\rho _{\textbf{0},\textbf{0}_k^{+}}^{I}(t) -i\sqrt{d_k^*} {\hat{\rho }}_{\textbf{0,0}}^I(t) {\hat{q}}^I(t) \;\;. \end{aligned}$$
(10b)

Here, the index I indicates the interaction picture. It is worth noting that the structure of Eqs. (9) and (10) resembles the one known from generalized Floquet theory for driven systems [63,64,65]. The factorized initial state gives a boundary condition with \({\hat{\rho }}_{\textbf{0,0}}(0) = {\hat{\rho }}(0)\) and all ADOs with \(L>0\) are set to zero.

The inhomogeneous differential equations in Eqs. (10) can be formally solved

$$\begin{aligned} {\hat{\rho }}_{\varvec{0}_k^+,\varvec{0}}^I(t)&= -i\sqrt{d_k} \int _0^t {\text {d}}\tau \, \textrm{e}^{-z_k (t-\tau )} {\hat{q}}^I(\tau ) {\hat{\rho }}_{\textbf{0,0}}^I(\tau ) \;\;; \end{aligned}$$
(11a)
$$\begin{aligned} {\hat{\rho }}_{\varvec{0},\varvec{0}_k^+}^I(t)&= -i\sqrt{d_k^*} \int _0^t\, {\text {d}}\tau \textrm{e}^{-z_k^*(t-\tau )} {\hat{\rho }}_{\textbf{0,0}}^I(\tau ) {\hat{q}}^I(\tau ) \;\;. \end{aligned}$$
(11b)

and then plugged in into Eq. (9). Summation over the reservoir modes as in Eq. (6) then leads to the following time-evolution equation in Born approximation:

$$\begin{aligned} \frac{{\text {d}}}{{\text {d}}t}{\hat{\rho }}^{I}(t)&=-\int _{0}^{t}{\text {d}}\tau \, [{\hat{q}}^{I}(t),C(t-\tau ) {\hat{q}}^{I}(\tau )\rho ^{I}(\tau ) ] \nonumber \\&\quad -[{\hat{q}}^I(t), C^{*}(t-\tau )\rho ^I(\tau ){\hat{q}}^I(\tau )] \;\;. \end{aligned}$$
(12)

Note that no Markovian coarse-graining in time is done here, not even on the level of the reduced density so that the reservoir induced retardation is fully taken into account in this order of system-bath coupling. One regains the conventional Redfield equation by setting \(\rho ^I(\tau )\rightarrow \rho ^I(t)\), thus leading to a time-local evolution equation with time-dependent rates. Hence, we name the above integro-differential equation (12) Redfield-plus.

The FP-HEOM can be interpreted as an infinite-order extension of the Redfield-plus/Redfield approximation [57, 66]. Truncating at tier L results in a time-evolution equation of order \(\alpha ^{2L}\) that’s non-local in time. This approach offers a systematic way to analyze the influence of higher order system-reservoir correlations, which can be intricate within a perturbative framework.

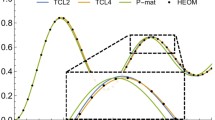
As illustrated in Fig. 1 for a coupling strength of \(\alpha = 0.1\), numerically converged “exact” results are attainable when truncating at tier \(L = 12\). However, the spin dynamics can be reasonably approximated at the 6th order (\(L = 3\)). The Redfield-plus approximation (\(L=1\)) tends to diverge over extended time intervals. It is worth noting that while the FP-HEOM can handle strong system-bath couplings, in this context, we have selected a relatively weak parameter \(\alpha\) to align with the perturbation series concept.

Fig. 1
figure 1

Comparison of high-order perturbative time-evolution equations at tier \(L\) of FP-HEOM with fully converged simulations. The population dynamics of a sub-Ohmic spin-boson model are shown. Simulation parameters: \(\epsilon = 0\), \(\Delta = 1\), \(\omega _c = 20\), \(T = 0\), \(\alpha = 0.1\), and \(s = 0.5\)

Full size image

4.2 Redfield-plus: influence of low-frequency modes

Environment engineering in open quantum systems [67] focuses on the deliberate design and manipulation of a quantum system’s environment to induce specific dynamics, ranging from Markovian to non-Markovian or from delocalization to localization. Such strategies are invaluable for counteracting the adverse effects of decoherence and noise, two persistent challenges in quantum systems. In this section, we investigate the consequences of modulating the environmental spectrum through the parameter \(s\) on the dynamics of the subsystem.

Fig. 2
figure 2

Comparison of Redfield-plus (dashed line) with exact simulations (solid line) across varying spectral exponents \(s\) for a sub-ohmic spin-boson model. The depicted population dynamics utilize the following simulation parameters: \(\epsilon = 0\), \(\Delta = 1\), \(\omega _c = 20\), \(T = 0\), and \(\alpha = 0.05\)

Full size image

For a sub-ohmic bosonic bath, the mode distribution, characterized by the spectral exponent \(s\), is instrumental in gauging the efficacy of the Redfield-plus perturbative expansion. With a fixed coupling strength of \(\alpha = 0.05\), Fig. 2 showcases that the Redfield-plus approximation closely mirrors the exact dynamics when the spectral exponents \(s\) are at least 0.5. However, as \(s\) diminishes, thereby accentuating the low-frequency modes, the precision of the second-order approximation wanes over incrementally shorter time intervals.

A decline in \(s\) within the sub-ohmic spectral density augments the spectral prominence of the low-frequency modes. This heightened influence of low-frequency modes undermines coherence by instigating extended temporal correlations, culminating in reservoir-dressed equilibrium states. Such dynamics have been previously observed, for example, in imaginary time path integral Monte Carlo simulations [9]. This intricate behavior underscores the limitations of a purely perturbative approach [7].

4.3 Redfield-plus: accuracy with respect to temperature and bias

In the high-temperature regime, the behavior of the effective noise spectral density at low frequencies becomes especially relevant. As the inverse temperature \(\beta\) (with \(\beta = 1/(kT)\), where \(k\) is the Boltzmann constant, \(T\) is the temperature) approaches zero, and the noise spectral density \(S_{\beta }(\omega )\) converges to

$$\begin{aligned} \lim _{\beta \rightarrow 0} S_{\beta }(\omega )& = \lim _{\beta \rightarrow 0} \frac{\frac{\pi }{2}\, \alpha \, \omega _c^{1-s} \, \omega ^s \, \textrm{e}^{-\omega /\omega _c}}{1-\textrm{e}^{-\beta \omega }}\nonumber \\{} & = \frac{\pi \alpha }{2\beta }\, \omega _c^{1-s}\, \omega ^{s-1}\, \textrm{e}^{-\omega /\omega _c} \;. \end{aligned}$$
(13)

This limit implies an increase in the effective system-bath coupling as the temperature rises. This is a regime where the Redfield-plus approximation may fail, as illustrated in Fig. 3.

Fig. 3
figure 3

Comparison of Redfield-plus (dashed line) and exact simulations (solid line) for a sub-ohmic spin-boson model at finite temperature. The simulation parameters are set as follows: \(\epsilon = 0\), \(\Delta = 1\), \(\omega _c = 20\), and \(\alpha = 0.05\)

Full size image

Figure 4 investigates the impact of bias on subsystem dynamics. As the bias escalates, the system transitions from a coherent to a decoherent state. Remarkably, under these conditions, the Redfield-plus approximation provides a reasonably accurate representation of the dynamics, as depicted in Fig. 4.

Fig. 4
figure 4

Comparison of Redfield-plus (dashed line) and exact simulations (solid line) for a sub-ohmic biased spin-boson model at finite temperature. The simulation parameters are set as follows: \(\Delta = 1\), \(\omega _c = 20\), \(\alpha = 0.05\), and \(\beta = 1\)

Full size image

4.4 Time-dependent memory kernel for populations: NIBA versus FP-HEOM

For a spin system with no bias, i.e., \(\epsilon =0\), immersed in a bosonic bath, the expectation is that the steady-state population is uniformly distributed between the two spin states, i.e., \(P(t\rightarrow \infty ) = \langle \sigma _z(t\rightarrow \infty ) \rangle \rightarrow 0\). However, it is well known that at zero temperature, a symmetry breaking can take place corresponding to a quantum phase transition from a delocalized to localized asymptotic state [10, 11]. Consequently, depending on the initial condition and reservoir parameters, \(P(t) \ne 0\) over long timescales, which is a purely quantum phenomenon due to the absence of thermal fluctuations at zero temperature.

Fig. 5
figure 5

Comparison of NIBA (dashed line) and exact simulations (solid line) for a sub-ohmic spin-boson model, illustrating the impact of varying the spectral exponent s on the memory kernel. Parameters: \(\epsilon = 0\), \(\Delta = 1\), \(\omega _c = 20\), \(\alpha = 0.05\), and \(T = 0\)

Full size image

This behavior can be conveniently analyzed using the time-dependent memory kernel K(t) which determines the spin dynamics according to

$$\begin{aligned} {\dot{P}}_{\sigma }(t) = -\sum _{\sigma ' = \pm }\int _0^t {\text {d}}\tau K_{\sigma ,\sigma '}(t-\tau ) P_{\sigma '}(\tau ) \;. \end{aligned}$$
(14)

We mention here that a powerful perturbative treatment to derive the kernel is the so-called Non-interacting Blip Approximation (NIBA) [7, 68] and its extensions. There, kernels in powers of the tunnel splitting \(\Delta\) are obtained with the NIBA kernel being of second order in the tunnel splitting \(\Delta ^2\). Accordingly, the NIBA is not based on a series expansion in \(\alpha\) and thus accounts also for strong spin-bath coupling. It neglects long-range quantum coherences though and does not predict the correct equilibrium state for \(\epsilon \ne 0\). In Fig. 5 results for the NIBA memory kernel are depicted. From these data, one would conclude a change in the dynamical behavior (monotonous decay versus oscillatory decay) to occur for values around \(s=0.5\). For smaller exponents, strong oscillations emerge with decreasing s.

In contrast, exact FP-HEOM data extracted from the exact dynamics [14] are shown in Fig. 5. For the chosen coupling strength, it is also observed that for \(s>0.5\), the memory decays clearly monotonous over time and remains always positive as also predicted by NIBA. However, quantitatively the exact decay appears to be much faster than within NIBA. For values of s below this threshold oscillatory pattern are seen as well for the FP-HEOM results, but with much smoother and with less oscillations as the NIBA prediction. We can thus conclude that while the NIBA provides qualitatively the correct physics, it is quantitatively in this regime of parameter space not reliable.

Physically, the changeover in dynamical behavior in K(t) can be attributed to a freezing of the population, since the total weight of the kernel tends toward zero when integrated over a time span where \(P_\sigma (t)\) does not change considerably. More specifically, in this regime of sufficiently small s, one may write for long times with \(P_\sigma (\tau )\approx P_\sigma (t)\) in Eq. (14) that

$$\begin{aligned} \lim _{t\rightarrow \infty } {\dot{P}}_{\sigma }(t) \approx -\sum _{\sigma ' = \pm } k_{\sigma ,\sigma '} P_{\sigma '}(t) \; \end{aligned}$$
(15)

with rates

$$\begin{aligned} k_{\sigma , \sigma '}= \int _0^\infty {\text {d}}\tau \ K_{\sigma ,\sigma '}(\tau )\,. \end{aligned}$$
(16)

Estimations from Fig. 5 allow to see that rates \(k_{\sigma ,\sigma '}\) tend indeed to zero corresponding to a slowing down of the relaxation dynamics up to the regime, where \(k_{\sigma , \sigma '}=0\), so that the spin requires an infinitely long time to reach a Gibbs equilibrium state and instead displays localization. This property aligns with the fact that hybridization between spin and reservoir induced by slow modes occurs, thus freezing the spin dynamics.

5 Conclusion

Since conventional second-order master equations fail in accurately capturing non-Markovian dynamics, this limitation becomes markedly significant for unconventional baths, particularly in conditions such as zero-temperature structured environments. One approach to circumvent this is to incorporate high-order corrections. However, the numerical computation of high-dimensional integrals in time poses considerable challenge as the accuracy of calculations become extremely sensitive to numerical errors.

In this work, we have employed the Hierarchical Equations of Motion (HEOM) approach to effectively address these challenges. This methodology enables the systematic unraveling of higher order master equations, balancing numerical efficiency with high precision. Consequently, our investigation has concentrated on the zero-temperature sub-Ohmic regimes, providing relevant computations to underscore our approach.

Furthermore, it is significant to note that the exact memory kernels in the quantum master equation can be extracted from the FP-HEOM approach and then be compared with those from perturbative schemes such as the NIBA. The extraction further offers a useful tool for the analysis of quantum phase transition dynamics, establishing a comprehensive and reliable platform for further explorations into open quantum system dynamics.