Nano-electronic Simulation Software (NESS): a flexible nano-device simulation platform

Abstract

The aim of this paper is to present a flexible and open-source multi-scale simulation software which has been developed by the Device Modelling Group at the University of Glasgow to study the charge transport in contemporary ultra-scaled Nano-CMOS devices. The name of this new simulation environment is Nano-electronic Simulation Software (NESS). Overall NESS is designed to be flexible, easy to use and extendable. Its main two modules are the structure generator and the numerical solvers module. The structure generator creates the geometry of the devices, defines the materials in each region of the simulation domain and includes eventually sources of statistical variability. The charge transport models and corresponding equations are implemented within the numerical solvers module and solved self-consistently with Poisson equation. Currently, NESS contains a drift–diffusion, Kubo–Greenwood, and non-equilibrium Green’s function (NEGF) solvers. The NEGF solver is the most important transport solver in the current version of NESS. Therefore, this paper is primarily focused on the description of the NEGF methodology and theory. It also provides comparison with the rest of the transport solvers implemented in NESS. The NEGF module in NESS can solve transport problems in the ballistic limit or including electron–phonon scattering. It also contains the Flietner model to compute the band-to-band tunneling current in heterostructures with a direct band gap. Both the structure generator and solvers are linked in NESS to supporting modules such as effective mass extractor and materials database. Simulation results are outputted in text or vtk format in order to be easily visualized and analyzed using 2D and 3D plots. The ultimate goal is for NESS to become open-source, flexible and easy to use TCAD simulation environment which can be used by researchers in both academia and industry and will facilitate collaborative software development.

1 Introduction

Further down-scaling of Complementary Metal-Oxide Semiconductor (CMOS) circuits has become increasingly complex and the fundamental challenges that the semiconductor industry faces at the device level will deeply affect the design of the next-generation integrated circuits and systems [1, 2]. Silicon technology has reached the nano-CMOS era with 10 and 7 nm Fin Field-Effect Transistors (FinFETs) CMOS technologies [3,4,5,6,7] in mass production and 5 nm and 3 nm Gate-All-Around (GAA) NanoWire Field Effect Transistors (NWFETs) in development stage [8]. It is widely recognized that charge transport in such nanometer-scale device dimensions could be dominated by quantum mechanical effects. Moreover, nano-scaled devices are more sensitive to systematic and statistical variability, which can result in significant differences between devices on the same chip [9]. Hence, variability and quantum mechanical effects are among the main challenges which should be addressed in order to keep Moore’s law alive.

In order to meet the challenges of the future nano-CMOS technology above, the most-time efficient and cost-effective method is to utilize numerical simulations based on relevant theories and physical models to screen material and device architecture options and to optimize the promising solution. It is also important for such tools to be user-friendly and to be published as an open-source software to allow collaboration and co-development by both industry and academia all over the world. This will allow a collaborative effort of the electron device community to find the solutions for tomorrow CMOS circuit designs.

The main aim of this paper is to introduce the concepts and the inner working of a new nanoelectronic device computational framework—Nano-electronic Simulation Software (NESS), which is currently under development at University of Glasgow. This paper is organized as follows. Section 2 presents a general overview of NESS and the link between its different components and features. Section 3 describes the structure generator module that was developed in order to create the simulated device structures and to introduce sources of statistical variability. Section 4 is dedicated to the effective mass extractor module which was developed in order to provide the parameters to the models and the corresponding solvers implemented in the transport module, described in Sect. 5. Each subsection in Sect. 5 is dedicated to a specific functional NESS solver. Finally, conclusions are drawn in Sect. 6.

2 Overview of NESS

Fig. 1

Flowchart of NESS detailing its modular structure

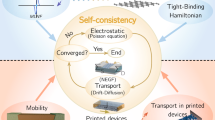
In this section, we provide an overview of NESS and its modular structure which is summarized in Fig. 1. There are two main modules in NESS: the structure generator and the transport solvers. The structure generator module provides flexible means to create the simulated device structures such as nanowire, FinFETs or bulk CMOS transistors considering different semiconductor materials such as Si, Ge or III–Vs materials. Furthermore, the structure generator is used to introduce the doping profile and generate the meshing of the simulation domain. It can also introduce the major sources of statistical variability such as Random Discrete Dopants (RDD), Line Edge Roughness (LER) and Metal Gate Granularity (MGG). Details of the implementation of the NESS structure generator are presented in Sect. 3.

The second main module in NESS contains the charge transport models and the corresponding solvers which can simulate using different approximations the mobility, the charge density and the current in nano-CMOS devices. The non-equilibrium Green’s function (NEGF) solver is the main transport solver in NESS. It is a quantum transport module capturing quantum mechanical effects such as quantum confinement and subsequent threshold voltage shift, coherent transport and impact of scattering, and the leakage and Band-To-Band Tunneling (BTBT) currents. A detailed description of the NEGF approach implemented in NESS is given in Sect. 5.2.

The NESS computational framework has two additional modules to support the work of the structure generator and numerical solvers. The first module is the Effective Mass (EM) extractor from atomistic simulations such as Density Functional Theory (DFT) or from semi-empirical models such as Tight-Binding (TB). The EM extractor is described in detail in Sect. 4. The other key module is material database which contains for each material all parameters relevant for the different simulation techniques and corresponding modules, e.g., dielectric constants, mobility model parameters, the parameters used in different scattering models etc. Those parameters serve as input information for the solvers.

3 Structure generator

The starting point for all NESS simulations is the creation of the simulation domain with the corresponding material regions and their parameters used by the different transport solvers. The NESS structure generator is very flexible and allows the user to create devices with various architectures, cross sections, doping profiles and variability sources. An example of a circular NWFET with LER, RDD and MGG variability sources is shown Fig. 2a, b. The methodology to generate the aforementioned sources of variability is described below:

Fig. 2

a Circular and b stacked NWFETs with all variability sources that can be generated by NESS

Random Discrete Dopants In order to introduce random discrete dopants in the structure, we have adopted a rejection technique which is based on the atomic arrangement in the crystal lattice of the corresponding material [10]. The probability of finding a RDD at the ith atom site is expressed as follows:

$$\begin{aligned} P_i=V_i \cdot N_i \end{aligned}$$

(1)

where $V_i$ and $N_i$ are the volume and the doping concentration of the ith atom. If the generated random number between 0 and 1 is smaller than $P_i$, the atom is replaced by the dopant. Therefore, dopants are randomly distributed based on the doping density, and the total number of dopants follows a Poisson distribution. Herein, the dopant has an elemental positive (for n-type) or negative (for p-type) charge assuming that all dopants are activated. The dopant charge is assigned to the eight surrounding nodes of the discretization grid using the cloud-in-a-cell approach.

Line edge roughness LER is generated at the interface between the channel material and the gate oxide using the same approach described in Ref. [11]. LER is thus characterized in NESS by an exponential auto-correlation function as follows:

$$\begin{aligned} C(r)= {\langle {\varDelta \left( r' \right) \varDelta \left( r'+r \right) }\rangle } = \varDelta _m^2{\hbox {e}}^{\sqrt{2}r/L_m} \end{aligned}$$

(2)

where $\varDelta _m$ is the root-mean-square (rms) fluctuation of the rough edge, $L_m$ is the correlation length, r is the distance $\Vert \vec {r} \Vert$, and $\varDelta \left( r\right)$ is the amplitude of LER at position $\vec {r}$.

Metal gate granularity In order to investigate the impact of MGG, grains in the metal gate have been generated by the Voronoi algorithm [12]. The work-function of each grain is assigned using a probability density specified by the user. For example, it is assumed that TiN has two grain orientations with two different values of work-function projected at the metal-insulator interface (4.4 and 4.6 eV) with a probability of 40% and 60%. The average work-function can be calculated as follows:

$$\begin{aligned} W_{{\mathrm{avg}}}=\sum _{i}W_{i} \cdot \hat{P}_i \end{aligned}$$

(3)

where $W_i$ is the ith work function value and $\hat{P}_i$ is its probability. $W_{{\mathrm{avg}}}$ is the typical work function for the corresponding metal material and $\sum _{i}\hat{P}_i$ must be equal to one.

4 Effective mass extraction module

Currently in NESS we use the parabolic Effective Mass (EM) approximation for both electrons and holes when solving transport equations. Currently, NESS supports only diagonal effective mass tensor. The confinement effective masses (e.g., $m_y$ and $m_z$ in the 1-D structure) play a critical role in the device simulations as they directly impact the subband energy levels and thus the electrostatics. In NESS, the confinement effective masses $m_{y,\nu }$ and $m_{z,\nu }$ are extracted in way to match the subband minima for the lowest two subbands of each dominant valley $\nu$ obtained using empirical TB or DFT. The confinement effective masses are obtained by solving the following set of equations for each valley using Newton-Raphson method:

$$\begin{aligned} E_{i,\nu }^{\mathrm{EM}}(m_y, m_z)-(E_{i,\nu }^{\mathrm{TB}}-E_{C,\nu }^{\mathrm{B}}) = 0, \quad i=1,2 \end{aligned}$$

(4)

where $\nu$ is the valley index and, $E_{i,\nu }^{\mathrm{EM}}$ and $E_{i,\nu }^{\mathrm{TB}}$ are the ith subband minima obtained from the parabolic EM approximation and TB methods, respectively, and $E_{\mathrm{C}}^{\mathrm{B}}$ is the bulk conduction band edge. The transport effective masses ($m_x$) are obtained from the curvature of the $E{-}k$ dispersion at the minima as follows

$$\begin{aligned} m_x = \hbar ^2 \left( \frac{\partial ^2 E}{\partial k_x^2} \right) ^{-1} \end{aligned}$$

(5)

Figure 3 compares the parabolic EM dispersion with the TB band structure, which is calculated using Synopsys QuantumATK with the Boykin parameter set [13, 14]. The first two subbands of both models are in good agreement for each $\varDelta$ valley especially at low energies, which are more relevant for transport. It is thus clear that at such a good agreement between the two band structure, the EM approximation can provide good estimate for the devices figures of merit at a much lower computational cost compared to the TB framework. More details about this module can be found in Ref. [15].

Fig. 3

Comparison of the parabolic EMA and TB band structures for a circular GAA nanowire (diameter = 5 nm). The inset shows the arrangement of silicon atoms in a cross section of the nanowire

5 Numerical solvers

5.1 Drift diffusion solver

NESS includes a 3D drift–diffusion (DD) transport solver based on the self-consistent solution of the Poisson’s equation and the current continuity equation. The equations being solved are:

(a) Poisson’s equation:

$$\begin{aligned} \nabla \cdot (\epsilon \nabla \psi ) = - q(p - n + N_{\mathrm{D}}^+ - N_{\mathrm{A}}^-) \end{aligned}$$

(6)

where $\epsilon$ is permittivity, $\psi$ is potential, q is the electron charge, n and p are the electron and hole concentrations, and $N_{\mathrm{D}}^+$ and $N_{\mathrm{A}}^-$ are the ionized donor and acceptor impurity concentrations, respectively.

(b) Continuity equation for electrons (assuming no carrier generation or recombination):

$$\begin{aligned} \nabla \cdot \mathbf {J}_\mathbf{n } = 0 \end{aligned}$$

(7)

where $\mathbf {J}_\mathbf{n }$ is the electrons current density vector given by

$$\begin{aligned} \mathbf {J}_\mathbf{n } = -qn\mu \nabla \psi + qD_n\nabla n \end{aligned}$$

(8)

where $\mu$ is carrier mobility and $D_n = k_{\mathrm{B}} T/q$ is the diffusion coefficient. The Scharfetter–Gummel approach has been used for the discretization of the drift–diffusion equations using the Bernoulli functions [16, 17]. The current density flowing from node 1 to node 2 is given by

$$\begin{aligned} J_{n12} = \frac{qD_{12}}{h_{12}}\left[ B\left( \frac{\psi _1 - \psi _2}{k_{\mathrm{B}}T/q}\right) n_1 - B\left( \frac{\psi _2 - \psi _1}{k_{\mathrm{B}}T/q}\right) n_2 \right] \end{aligned}$$

(9)

where $D_{12}$ and $\mu _{12}$ are, respectively, the diffusion coefficient and mobility at the middle of the two nodes, $n_1(n_2)$ is the electron concentration in node 1(node 2), $\psi _1(\psi _2$) is the potential at node 1(node 2), $k_{\mathrm{B}}$ is the Boltzmann constant, $h_{12}$ is the distance between the two nodes, and B(x) is the Bernoulli function defined as:

$$\begin{aligned} B(x) = \frac{x}{{\hbox {e}}^x - 1} \end{aligned}$$

(10)

Currently we have implemented four different models for the carrier mobility in this solver. Firstly, we have a constant mobility model that defines an isotropic low-field mobility value which is kept constant during the simulation. In addition, there are three other models to account for mobility reduction due to the impact of doping and electric fields. The Masetti model [18] has been included to capture the doping concentration dependence of mobility. This model defines a local low-field mobility dependent on the net local doping concentration N within the simulation domain. It follows the analytic function that fits empirical electron and hole mobilities as a function of the doping material and the temperature in bulk semiconductor material [18]:

$$\begin{aligned} \mu _{\mathrm{MM}}&= \mu _0{\hbox {e}}^{-p_c/N} + \frac{\mu _{\mathrm{max}}\left( \frac{T}{300}\right) ^{-\gamma }-\mu _1}{1+(N/C_r)^\alpha } \nonumber \\&\quad -\, \frac{\mu _2}{1+(C_s/N)^\beta } \end{aligned}$$

(11)

Here, the parameter $\mu _0$ refers to maximum mobility; $\mu _{\mathrm{max}}$ is the phonon limited maximum mobility with $\gamma$ defining its power law temperature dependence [19]; $\mu _1 = \mu _0$ for electrons and $\mu _1 =0$ for holes; $\mu _2$ is a mobility parameter; N is the net doping concentration; $C_r$ and $C_s$ are reference concentrations; $\alpha$, $\beta$ and $\gamma$ are fitting parameters; and $p_c = 0$ for electrons and positive for holes. Typical values for the parameters can be found in [18].

An interface mobility correction algorithm is applied after the Masetti model evaluation. This correction results in a further reduction of the mobility as the distance from the semiconductor/insulator interface increases. It is only evaluated at the nodes where the material is a semiconductor and which are located in the channel. The corrected mobility is calculated as:

$$\begin{aligned} \mu _{\mathrm{IC}} = \mu _{\mathrm{MM}} \cdot {\hbox {sFactor}} \cdot {\hbox {e}}^{\frac{-(\varDelta y + \varDelta z)}{l_{\mathrm{Decay}}}} \end{aligned}$$

(12)

where $\mu _{\mathrm{IC}}$ is the mobility after including the interface mobility correction, $\mu _{\mathrm{MM}}$ is pre-correction mobility from the Masetti model, sFactor is the surface mobility correction factor, $\varDelta y$ and $\varDelta z$ are the distances from the interface in the confinement directions (y and z, respectively), and $l_{\mathrm{Decay}}$ is the exponential decay factor.

The impact of the transverse electric field is captured using the well known Yamaguchi [20] model:

$$\begin{aligned} \mu _{\mathrm{YM}} = \frac{\mu _0}{\sqrt{1 + \left( \frac{|E_Z|}{Ec_{\mathrm{YM}}} \right) ^ {\alpha _{\mathrm{YM}}}}} \end{aligned}$$

(13)

where $\mu _0$ is either the output of the Masetti mobility model with interface correction (if used) or simply the low-field mobility, and $E_Z$ is the electric field in the direction normal to the transport. $Ec_{\mathrm{YM}}$ (critical field) and $\alpha _{\mathrm{YM}}$ are fitting parameters for this model.

Finally, the impact of the longitudinal electric field (along the transport direction), $E_X$ has been taken into account using the Caughey–Thomas model [21]:

$$\begin{aligned} \mu _{\mathrm{CTM}} = \frac{\mu _{\mathrm{YM}}}{\left[ 1 + \left( \frac{\mu _{\mathrm{YM}}|E_X|}{v_{\mathrm{sat}}} \right) ^\beta \right] ^ {1 / \beta }} \end{aligned}$$

(14)

Here $\mu _{\mathrm{YM}}$ is the transverse field dependent mobility calculated using the Yamaguchi model (Eq. 13), and $v_{\mathrm{sat}}$ and $\beta$ are temperature dependent fitting parameters.

As an example, Fig. 4 shows the transfer characteristics obtained using the constant mobility model with the bulk mobility value of 1400 cm$^2$/Vs as well as the cumulative impact of the three mobility degradation models for a NWFET with a square cross section of $3 \times 3\,{\hbox {nm}}^2$. When the mobility degradation models are switched on, the corresponding degradation of the carrier mobility is reflected in the device characteristics by a reduction of the current.

Currently, the main use of the DD module in NESS is to provide the trial potential for NEGF simulations. We provide in Sect. 5.3.3 a comparison of NEGF results to the ones obtained using DD with KG mobilities. Quantum corrections are being added to the DD solver to make it suitable for modeling devices that exhibit quantum confinement. The DD model is also useful for variability simulations after calibration to more physical models such as NEGF in the case of NESS.

Fig. 4

Transfer characteristics of a NWFET $(W = H = 3\,{\hbox {nm}}$, $L_{\mathrm{G}} = 20\,{\hbox {nm}})$ obtained from the classical DD module showing the impact of different mobility models. $V_{\mathrm{DS}} = 0.05\,{\hbox {V}}$

5.2 Non-equilibrium Green’s function solver

This solver is the main transport solver of NESS. It allows a quantum treatment of charge transport to capture phenomena such as tunnelling, coherence and particle interactions that strongly impact the performance of nano-scaled devices. The electrons are described in this solver by an effective mass Hamiltonian. By solving self-consistently Poisson and NEGF transport equations in coupled mode-space representation, we obtain the charge density, the potential profile and the corresponding current that flows in the device. We can either include the electron–phonon (e–ph) interactions or neglect them to study the transport in the ballistic limit [22]. It is also possible to consider other types of scattering explicitly such as RDD, LER or MGG.

5.2.1 Computation of the charge and the current

NEGF is a powerful quantum field theory tool that allows the computation of the time dependent quantum average of observables [23, 24]. When the system is in a steady state, one has to solve first at each energy E for the relevant components of the retarded $G^{\mathrm{R}}$, the advanced $G^{\mathrm{A}}$ and the lesser Green’s function $G^<$ using the following system of equations [25]:

$$\begin{aligned} G^{\mathrm{R}} \left( E\right)&= \frac{1}{\left( E+\text {i}.\eta \right) \cdot I-h-\varSigma ^{\mathrm{R}}\left( E\right) }, \end{aligned}$$

(15)

$$\begin{aligned} G^{\mathrm{A}}\left( E\right)&= \left[ G^{\mathrm{R}}\left( E\right) \right] ^\dagger , \end{aligned}$$

(16)

$$\begin{aligned} G^{\lessgtr } \left( E\right)&= G^{\mathrm{R}}\left( E\right) \cdot \varSigma ^{\lessgtr }\left( E\right) \cdot G^{\mathrm{A}}\left( E\right) , \end{aligned}$$

(17)

where h is the one-particle Hamiltonian, I is the identity matrix of the same dimension as h, $\eta$ is an infinitesimal positive real number, and $\varSigma ^{\mathrm{R}}$ and $\varSigma ^<$ are the retarded and lesser self-energies, respectively. These self-energies take into account electrons scattering and their interaction with the contacts. The contact self-energies stem from the embedding of the contacts degrees of freedom in the active region [24]. The interaction self-energies arise from the truncation of the Martin–Schwinger hierarchy [26] to the first equation, in which a conserving approximation to the two-particle Green’s function is introduced [27]. The charge at position r and the current in layer l are then obtained using the following equations [28, 29] :

$$\begin{aligned} n(r)&= -\frac{{i}}{2\pi }\int {\hbox {d}}E \, G^<\left( r,r;E\right) , \end{aligned}$$

(18)

$$\begin{aligned} j(l)&= \frac{2\cdot |q|}{\hbar }\int \frac{{\hbox {d}}E}{2\pi } {{\,\mathrm{Tr}\,}}\left[ 2{{\,\mathrm{Re}\,}}\left\{ h_{l+1,l} \cdot G^<_{l,l+1} \right\} \right] , \end{aligned}$$

(19)

where $h_{l+1,l}$ are the matrix elements of the Hamiltonian between the basis states in layer $l+1$ and layer l while $G^<_{l,l+1}$ are the matrix elements of $G^<$ between the basis states of layer l and layer $l+1$. For tri-diagonal Hamiltonians and under the assumption of local scattering mechanisms in real space, one needs to compute only the upper-diagonal, the lower-diagonal and the diagonal Blocks of the lesser Green’s function [22, 25]. Therefore, an efficient recursive algorithm has been proposed to solve only for these blocks [28].

5.2.2 Inclusion of the contacts as boundary conditions

The Hamiltonian representing the non interacting electron gas in the active region reads in real space:

$$\begin{aligned} \hat{H}=\int {\hbox {d}}r\,{\hbox {d}}r^\prime \; \hat{\varPsi }^\dagger \left( r\right) \; h\left( r,r^\prime \right) \; \hat{\varPsi }\left( r^\prime \right) \; \end{aligned}$$

(20)

where $\hat{\varPsi }^\dagger \left( r\right)$ ($\hat{\varPsi }\left( r^\prime \right)$) is the creation (annihilation) operator described in [23, 24]. In most models, one can represent the one-particle Hamiltonian h as a succession of layers coupled to their nearest neighbors. This is true for the discretized EM Hamiltonian implemented in NESS and one obtains a tridiagonal representation when finite difference approximation is used to discretize it:

$$\begin{aligned} h\left( r,r^\prime \right) \equiv \begin{pmatrix} &{}h_{1,1} &{}\quad h_{1,2} &{}\quad 0 &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad 0 \\ &{}h_{2,1} &{}\quad h_{2,2} &{}\quad h_{2,3} &{}0 &{}\quad \cdots &{}\quad \cdots &{}\quad 0 \\ &{}0 &{}\quad h_{3,2} &{}\quad h_{3,3} &{}\quad h_{3,4} &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ &{}\vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ &{}0 &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad 0 &{}\quad h_{N,N-1} &{}\quad h_{N,N} \end{pmatrix} \end{aligned}$$

(21)

where N is the number of layers in the active region. This matrix represents only the restriction of the EM Hamiltonian to the active region. The impact of the electron exchange with the contacts is taken via the contact self-energies $\varSigma _C$. This is possible because the contacts are assumed to be invariant under a unit cell translation and in equilibrium. Therefore, it is possible to compute exactly the so-called $g^{\mathrm{R}}\left( C,C\right)$, the retarded Green’s function of the contact at the interface with the device [30] and obtain the corresponding retarded self-energies for the electrons present in the device:

$$\begin{aligned} \varSigma ^{\mathrm{R}}_C= H_{D,C} \cdot g^{\mathrm{R}}\left( C,C\right) \cdot H_{C,D}, \end{aligned}$$

(22)

where $H_{D,C}$ is the matrix representing the Hamiltonian elements between the device states and the contact states and $H_{C,D}$ is its Hermitian conjugate. Thanks to the equilibrium property, the rate operator $\varGamma$ and the lesser component of contact induced self-energy $\varSigma ^<_C$ can be obtained from the retarded one in Eq. 22 using the fluctuation-dissipation theorem for the self-energies [24]:

$$\begin{aligned} \varGamma \left( E\right) = \;&\text {i} \left[ \varSigma ^{\mathrm{R}}\left( E\right) - \varSigma ^{\mathrm{A}}\left( E\right) \right] , \end{aligned}$$

(23)

$$\begin{aligned} \varSigma ^<_C = \;&\text {i} \cdot f\left( E-\mu _C\right) \varGamma \left( E\right) , \end{aligned}$$

(24)

where f is the Fermi distribution function and $\mu _C$ is the Fermi level of the contact. We use in NESS a fast iterative scheme to compute the contact self-energy [31].

5.2.3 The coupled-mode space approximation for effective mass Hamiltonian

The expression of the single particle Hamiltonian $h\left( x\right)$ in the EM approximation is:

$$\begin{aligned} h\left( r\right) = \underbrace{\left[ -\frac{\hbar ^2}{2m^*_{y,z}} \varDelta _{y,z} +V\left( r\right) \right] }_{h_T} \underbrace{-\frac{\hbar ^2}{2m^*_{y,z}} \frac{\partial ^2}{\partial x^2}}_{h_L}. \end{aligned}$$

(25)

where $\varDelta _{y,z}$ is Laplace operator in the (YZ) cross-sectional plane. Therefore, h(r) is the sum of a transverse part $h_T$ describing the layers and a longitudinal part $h_L$ describing their coupling. When Eq. 25 is discretized using a finite difference method, the Hamiltonian has the same representation as in Eq. 21 where $h_T$ contributes to the diagonal blocks $h_{n,n}$ and $h_L$ contributes to both diagonal and off-diagonal blocks $h_{n,n+1}$. The Coupled-Mode Space (CMS) representation is obtained by projecting each diagonal bock $h_{n,n}$ of the transverse part $h_T$ of EM Hamiltonian on a subspace spanned by some chosen eigenmodes $\phi _i\left( y,z;n\right)$ of $h_{n,n}$. The corresponding projector is obtained by forming for each layer n a matrix $U_{n,n}$, whose columns are chosen eigenvectors of $h_{n,n}$ , and performing the following transformations of the non-zero blocks of the RS Hamiltonian [32]:

$$\begin{aligned} \tilde{h}_{n,n}=\;&U^\dagger _{n,n} h_{n,n} U_{n,n} , \end{aligned}$$

(26)

$$\begin{aligned} \tilde{h}_{n,n+1}=\;&U^\dagger _{n,n} h_{n,n} U_{n+1,n+1}. \end{aligned}$$

(27)

The global transformation U is a block-diagonal matrix $U=\delta _{i,j}U_{i,j}$. The transformation U is not a unitary transformation since the transformed Hamiltonian is usually of a lower dimension than the real space one. It is unitary only in the limit where all the transverse modes are chosen and in this case the CMS Hamiltonian is simply a change of representation and is exactly equivalent to the real space Hamiltonian. However, the CMS Hamiltonian with few chosen modes reproduces by construction the exact selected EM subbands and their wavefunctions. It is therefore equal to the full rank EM Hamiltonian on the chosen subspace. Therefore, CMS offers the possibility to reproduce the effect of roughness or ionized impurities if one chooses a sufficient number of modes. The Green’s functions in CMS $\tilde{G}^{{\mathrm{R}},\lessgtr }$ and in real space are related by the same transformation in Eqs. 26, 27 [32]. For instance, the matrix element between the modes i and j both located on either of the layers l and $l^\prime =l, l\pm 1$ is given by:

$$\begin{aligned} \tilde{G}^{{\mathrm{R}},{\lessgtr }}\left( l,i;l^\prime ,j;E\right)& = \sum _{y,z}\sum _{y^\prime ,z^\prime }\phi ^*_i\left( y,z;l\right) \nonumber \\ &\quad \cdot G^{{\mathrm{R}},{\lessgtr }}\left( l,y,z;l^\prime ,y^\prime ,z^\prime ;E\right) \cdot \phi _j\left( y^\prime ,z^\prime ;l^\prime \right) \end{aligned}$$

(28)

Fig. 5

Simulation time and speed-up for a $5\times 5 \,{\hbox {nm}}^2$ square NWFETs with $L_{\mathrm{S}}=L_{\mathrm{D}}=10\,{\hbox {nm}}$ and $L_{\mathrm{G}} = 20\,{\hbox {nm}}$

5.2.4 Inclusion of electron–phonon interactions

The interaction of the electrons with the acoustic and optical phonons is accounted for in NESS by introducing the self-energies $\varSigma _{\mathrm{ac}}$ and $\varSigma _{\mathrm{op}}$ that read in real space representation under the local approximation [33, 34]:

$$\begin{aligned} \varSigma _{{\hbox {ac}}, \nu }^{<}(r; E)&=M_{\mathrm{ac}} G_{\nu }^{<}(r; E), \end{aligned}$$

(29)

$$\begin{aligned} \varSigma _{\mathrm{op},\nu }^{<}(r; E)&= \sum _{q,\nu ^{\prime }} \left| M_{q}^{\nu ,\nu ^{\prime }}\right| ^{2}\left[ n_{B,q} \cdot G_{\nu ^{\prime }}^{<}\left( r; E - \hbar \omega _{q}\right) \right. \nonumber \\&\quad +\,\left. \left( n_{B,q}+1 \right) \cdot G_{\nu ^{\prime }}^{<}\left( r; E + \hbar \omega _{q}\right) \right] \end{aligned}$$

(30)

$$\begin{aligned} \varSigma _{\mathrm{op},\nu }^{>}(r; E)&= \sum _{q,\nu ^{\prime }} \left| M_{q}^{\nu ,\nu ^{\prime }}\right| ^{2}\left[ n_{B,q} \cdot G_{\nu ^{\prime }}^{>}\left( r; E + \hbar \omega _{q}\right) \right. \nonumber \\&\quad +\,\left. \left( n_{B,q}+1\right) \cdot G_{\nu ^{\prime }}^{>}\left( r; E - \hbar \omega _{q}\right) \right] \end{aligned}$$

(31)

where $M_{\mathrm{ac}}$ is the coupling constant to the acoustic phonons, $\nu$ is the electronic valley index and q refers to the optical phonon with energy $\hbar \omega _q$. $M_{q}^{\nu ,\nu ^{\prime }}$ is the coupling strength of the electron–phonon interaction due to the phonons of frequency $\omega _q$ in the valley $\nu ^\prime$, whose density is given by Bose–Einstein occupation number $n_{B,q}$. We use the coupling constants obtained from the deformation potential theory [35]:

$$\begin{aligned} M_{\mathrm{ac}}&= \frac{\varXi ^{2} k_{\mathrm {B}} T}{2 \rho u_{\mathrm{s}}^{2}}, \end{aligned}$$

(32)

$$\begin{aligned} M^{\nu ,\nu ^\prime }_q&= \frac{\hbar \left( D_tK_q\right) ^2}{2\rho \omega _q}, \end{aligned}$$

(33)

where $\varXi$ is the acoustic deformation potential, $u_{{\mathrm{s}}}$ is the sound velocity in the material, $\rho$ its density and $\left( D_tK_q\right)$ the optical deformation potential corresponding to the coupling to the phonons of the valley $\nu ^\prime$. The retarded component of the self-energy due to the e–ph interaction is given by:

$$\begin{aligned} \varSigma ^{\mathrm{R}}(r; E)=\frac{1}{2}\left[ \varSigma ^>(r; E) - \varSigma ^<(r; E) \right] \end{aligned}$$

(34)

Using the same notations as in Eq. 28, the self-energies due to e–ph interaction read in CMS representation [36]:

$$\begin{aligned} \tilde{\varSigma }_{\mathrm{ac}}^{<}&\left( x,i;x,j;E\right) = M_{\mathrm{ac}}\sum _{k,l} F^{i,j}_{k,l}(x) \; \tilde{G}^{<}\left( x,k;x,l;E\right) \end{aligned}$$

(35)

$$\begin{aligned} \tilde{\varSigma }_{\mathrm{\mathrm{op}},\nu }^{<}&\left( x,i;x,j;E\right) = \sum _{k,l} F^{i,j}_{k,l}(x)\sum _{q,\nu ^{\prime }} \left| M_{q}^{\nu ,\nu ^{\prime }}\right| ^{2} \nonumber \\&\left[ \left( n_{B,q}+\frac{1}{2} \pm \frac{1}{2} \right) \tilde{G}_{\nu ^{\prime }}^{<}\left( x,k;x,l;E \pm \hbar \omega _{q}\right) \right] , \end{aligned}$$

(36)

$$\begin{aligned} \tilde{\varSigma }_{{\mathrm{op}},\nu }^{>}&\left( x,i;x,j;E\right) = \sum _{k,l} F^{i,j}_{k,l}(x)\sum _{q,\nu ^{\prime }} \left| M_{q}^{\nu ,\nu ^{\prime }}\right| ^{2} \nonumber \\&\left[ \left( n_{B,q}+\frac{1}{2} \pm \frac{1}{2} \right) \tilde{G}_{\nu ^{\prime }}^{>}\left( x,k;x,l;E \mp \hbar \omega _{q}\right) \right] , \end{aligned}$$

(37)

where F represents the form factors given by:

$$\begin{aligned} F_{kl}^{ij}(x)&=\int {\hbox {d}}y{\hbox {d}}z \, \phi ^*_i\left( y,z;x\right) \phi _j\left( y,z;x\right) \nonumber \\&\quad \phi _k\left( y,z;x\right) \phi ^*_l\left( y,z;x\right) \end{aligned}$$

(38)

The e–ph retarded self-energy in CMS is also given by Eq. 34 where the real space self energies are replaced by the CMS ones. It is important to note that these formulae are based on an important simplification assuming that the self-energies are local in both space and time. This is a consequence of assuming that acoustic phonons are elastic and that the optical ones are dispersionless, i.e., having a well-defined energies. Despite these simplifications, this treatment of the electron–phonon interaction captures fairly accurately the impact of this scattering mechanism on the operation of real nano devices. Moreover, the deformation potentials can be tuned to get a good quantitative with experimental phonon-limited mobilities [37]. After defining the total retarded and lesser self-energies as follows:

$$\begin{aligned} \varSigma ^{\mathrm{R}}&= \varSigma ^{\mathrm{R}}_C + \varSigma ^{\mathrm{R}}_{\mathrm{Scat}} \end{aligned}$$

(39)

$$\begin{aligned} \varSigma ^<&= \varSigma ^<_C + \varSigma ^<_{\mathrm{Scat}} \end{aligned}$$

(40)

It is clear that Eqs. 15–17 and 34–38 form a non-linear system that needs to be solved self-consistently for a given potential profile. This system is solved in NESS using the Self-Consistent Born Approximation (SCBA) [22, 25].

Fig. 6

The current spectra of a $3 \times 3\,{\hbox {nm}}^2$ NWFET with $L_{\mathrm{G}} = 10\,{\hbox {nm}}$ in a the OFF-sate in the ballistic limit, b the ON-State with e–ph scattering. The reference in energy is taken at the Source Fermi level ($E_{\mathrm{FS}} = 0\, {\hbox {eV}}$) and $V_{\mathrm{DS}} = 0.6\,{\hbox {V}}$

Fig. 7

$I_{\mathrm{D}}{-}V_{\mathrm{GS}}$ characteristic for $3\times 3\,{\hbox {nm}}^2$ square nanowire with and without phonons for different gate lengths

Fig. 8

a Drain induced barrier lowering and b Sub-threshold slope for 3 different gate lengths for a circular NWFET with 3 nm diameter and square ones with $3\times 3$ and $5\times 5\,{\hbox {nm}}^2$ cross sections

Fig. 9

$I_{\mathrm{D}}{-}V_{\mathrm{GS}}$ characteristic for 3 nm diameter circular NWFET and $3\times 3\, {\hbox {nm}}^{2}$ and $5\times 5 \, {\hbox {nm}}^2$ square NWFETs for $L_{\mathrm{G}} = 15\,{\hbox {nm}}$

5.2.5 Parallelization of the NEGF solver

The NEGF solver is written in C++ and is parallelized using Message Passing Interface (MPI) for C language. The main two sections of this solver which are parallelized are the diagonalization of the transverse part of the Hamiltonian in Eq. 25 and the solution of NEGF Eqs. 15–17. Therefore, the 2D Schrodinger equations for the device layers are distributed over all available cores and solved using ARPACK++ library [38], then each core communicates its results to all others before CMS NEGF calculations are started. NEGF calculation are parallelized over energy. The points in the energy grid are distributed evenly on available processors and both the Green function computation and storage is distributed over available cores. One obtains besides the calculation speed up an important decrease in the memory usage per core when the number of cores is increased. All matrix problems—except the eigenvalue problems—are solved using gmm++ library [39]. Point-to-point non-blocking communications using MPI_Issend and MPI_Irecv are used to transfer Green’s function data between relevant cores. When electron–phonon interactions are considered, each core needs virtual energy points to receive unavailable $G^{{\mathrm{R}},{\lessgtr }}\left( E \pm E_{\mathrm{ph}}\right)$ matrix elements that are needed for self-energy calculations and that are stored on other cores. Assuming dE is the energy discretization step and $E_{\mathrm{ph}}^M$ is the highest phonon energy, the ratio of the virtual nodes $N_{\mathrm{ph}}=E_{\mathrm{ph}}^M/{\hbox {d}}E$ to the sum of energy points stored on “neighboring” cores will determine the communication network topology. Based on this information, a matrix $T_{ij}$ is defined where row “i” contains the tags to be used in the MPI_Issend calls by core “i” to send to cores “j”. Conversely, core “j” uses tags in the column “j” in its MPI_Irecv calls to match all the MPI_Issend to it. This approach makes sure that deadlocks due to unmatched MPI_Issend/MPI_Irecv calls never happen.

The speed up obtained by this parallelization scheme is reported in Fig. 5 for $3\times 3$ and $5\times 5$ NWFETs with $L_{\mathrm{S}}=L_{\mathrm{D}}=10\,{\hbox {nm}}$ and $L_{\mathrm{G}}=20\,{\hbox {nm}}$. We used 1300 energy points for both devices and 6 subbands for the former and 10 subbands for the latter. The CPU used for this benchmark is an “Intel(R) Xeon(R) E5-2620 v4 @ 2.10 GHz” with 16 physical cores. For both examples a good speed up exceeding 12 is obtained for a parallel run with 16 cores. We have previously ran NESS NEGF calculations on hundreds of cores. However, the obtained speed up wasn’t as good as the one reported here because the nodes in the used cluster were heterogeneous and connected with an Ethernet network. We believe that a good speed up can be obtained with hundreds of cores on a cluster having equivalent nodes that are connected with an infiniband network.

5.2.6 Impact of electron–phonon interaction on charge transport

The OFF-state current spectrum in the ballistic limit for a square NWFET having a $3\times 3\,{\hbox {nm}}^2$ cross section and a 10 nm gate length is presented in Fig. 6a. It shows the pseudo-particles propagation without dissipation and current conservation for each energy along the device. Moreover, one can see on the figure that a non-negligible fraction of the carriers injected from the source with energies below the top of the barrier can reach drain. This highlights the importance of considering a quantum formalism to account for the source-to-drain tunneling which is important in transistors with sub-20 nm gate lengths. The ON-state current spectrum for the same device in the presence of e–ph interaction is shown in Fig. 6b. It shows an overall current damping due to acoustic phonons and an energy relaxation of carriers as they approach the drain due to optical phonons emission. However, $J\left( x\right)$, which is obtained by integrating the current spectrum over the energy and the transverse coordinates, is still a flat function of x, the position along the channel. Figure 7 shows a comparison of the $I_{\mathrm{D}}{-}V_{\mathrm{GS}}$ curves for the same $3\times 3\,{\hbox {nm}}^2$ square NWFET with and without e–ph interactions considering different gate lengths. It shows a progressive reduction of the current as the gate bias increased when e–ph interactions are taken into account, reaching 48% for $L_{\mathrm{G}}=10\,{\hbox {nm}}$ at $V_{\mathrm{DS}}=0.6\,{\hbox {V}}$ and nearly 65% for $L_{\mathrm{G}}=20\,{\hbox {nm}}$. It is also noticeable that both types of currents have higher values for $L_{\mathrm{G}}=10\,{\hbox {nm}}$ compared to their $L_{\mathrm{G}}=20\,{\hbox {nm}}$ counterparts. These observations are consistent with results previously reported in literature [22, 33].

5.2.7 Assessing of confinement and short channel effects

Shrinking the channel length to few decanonometers leads to a degradation of the electrostatic control of the gate over the electron transport in the channel [40]. The use of gate-all-around (GAA) architecture with appropriate NW cross section reduces significantly these short channel effects (SCE) [41]. However, this effect cannot be fully suppressed for sub-20 nm gate length devices because of the impact of direct source-to-drain tunneling occurring at such short channel lengths. Moreover, the effective mass of carriers in ultra-confined NW depends strongly on the NW cross section shape and size [42]. Therefore, the design rules must be established using a quantum simulator such as the NEGF solver of NESS, which can capture accurately these effects.

We have extracted in Fig. 8a, b the Drain Induced Barrier Lowering (DIBL) and Subthreshold slope ($S_{\mathrm{th}}$), respectively, for different nanowire shapes at different gate lengths. The effective masses were calibrated using TB band structure to take into account their dependence on the confinement [42]. As expected, the best electrostatic control is obtained for the NWFET with the narrowest Si cross section, i.e., the circular NWFET with 3 nm diameter, followed by the square ones with 3 nm$^2$ and 5 nm$^2$ cross sections, respectively.

Moreover, all three NWFETs show rapid degradation of both the DIBL and $S_{\mathrm{th}}$ when the gate length is shrunk below 10 nm. However, the $I_{\mathrm{D}}{-}V_{\mathrm{G}}$ in Fig. 9 shows that improving the electrostatic control by reducing the NW cross section decreases the drive current. The use of stacked nanowires is a contemplated solution to this problem [41], and simulation tools like NESS could help the designers to co-optimize the gate length, the cross section and the number of stacked NW they need to meet their performance targets.

5.2.8 Direct band-to-band tunneling model

In this section, we briefly summarize the novel procedure implemented in NESS to compute the direct band-to-band tunneling in nano-devices [43]. It is based on the coupled mode-space NEGF scheme within the EM approximation and the Flietner model of the imaginary dispersion [44, 45]. The results obtained by the BTBT model in NESS [46] show an excellent agreement with results obtained from the atomistic simulation tool OMEN [47]. The valence and conduction band edges are connected using the two-band model of the imaginary dispersion proposed by Flietner in Ref. [44]. For quantum transport simulations, the Flietner model can be rewritten as [45]:

$$\begin{aligned} \frac{\hbar ^2 k^2}{2m_0}&= \frac{E_{{\mathrm {g}}}(E-E_{\mathrm {c}})(E-E_{\mathrm {v}})}{\left[ \sqrt{\frac{m_0}{m_{\mathrm {c}}} }(E-E_{\mathrm {c}}) -\sqrt{\frac{m_0}{m_{\mathrm {v}}}} (E-E_{\mathrm {v}})\right] ^2} \end{aligned}$$

(41)

where $E_{{\mathrm {g}}}$, $E_{{\mathrm {c}}({\mathrm {v}})}$, and $m_{{\mathrm {c}}({\mathrm {v}})}$ are the band gap energy, the conduction (valence) band edge, and the conduction (valence) effective mass, respectively. The rest of the parameters take their usual meaning. Both the real conduction and valence bands in the vicinity of their extrema are correctly reproduced, and the parabolic effective mass approximation of the band-structure can be straightforwardly obtained.

Moreover, Eq. 41 allows the inclusion of an external potential $V({\mathbf {r}})$ in the bands dispersion straightforwardly:

$$\begin{aligned} E \approx E_{{\mathrm {c}}({\mathrm {v}})} + V({\mathbf {r}}) \pm \frac{\hbar ^2 k^2}{2m_{{\mathrm {c}}({\mathrm {v}})}} + \cdots . \end{aligned}$$

(42)

This sets up the appropriate envelope equation for low-dimensional semiconductors that incorporates both real and imaginary branches of the whole band structure.

The quantum transport problem for electrons and holes is then solved independently within the EM approximation using the NEGF technique in CMS representation and coupled self-consistently with the Poisson equation. Once the convergence is reached, the Valence Band (VB) and Conduction Bands (CB) are bridged through the two-band model of the imaginary dispersion proposed by Flietner and the BTBT current is computed by solving the following envelope equation:

$$\begin{aligned} -\frac{\hbar ^2}{2m_0}\frac{\partial ^2 \chi }{\partial x^2}&= \frac{E_{{\mathrm {g}}}(E-V_{\mathrm {c}})(E-U_{\mathrm {v}})}{\left[ \sqrt{\frac{m_0}{m_{\mathrm {c}}} }(E-V_{\mathrm {c}}) -\sqrt{\frac{m_0}{m_{\mathrm {v}}}} (E-V_{\mathrm {v}})\right] ^2} \chi \nonumber \\&= F(E, U_{\mathrm {c}}, V_{\mathrm {v}})\chi , \end{aligned}$$

(43)

with open boundary conditions. In the latter, $U_{{\mathrm {c}}({\mathrm {v}})}$ corresponds to the lowest conduction (highest valence) subband energy, and the coordinate x has been omitted for brevity. Finally, by defining a two-band Hamiltonian as:

$$\begin{aligned} H&=-\frac{\hbar ^2}{2m_0}\frac{\partial ^2}{\partial x^2} - F(E, U_{\mathrm {c}}, U_{\mathrm {v}}) + E, \end{aligned}$$

(44)

Equation 43 can be solved to calculate the BTBT current in nanowire transistors by means of a NEGF scheme. Figure 10b shows the current spectrum of the Tunnel Field Effect Transistors (TFET) depicted in Fig. 10a. The dashed lines represent the lowest and highest subbands of CB and VB, respectively. One can see clearly that the current flows from the VB of Si to the CB of the InAs. A detailed study of this problem has been published in Ref. [43], in which band non-parabolicity has been included for the conduction band of InAs.

Fig. 10

a A schematic representation of the TFETs considered in this study, b the corresponding current spectrum in the ON-state in presence of random discrete dopants in the InAs section

5.2.9 Variability in quantum mechanical context

Variability is one of the main challenges facing the down-scaling of CMOS devices. It is induced either by the fabrication process which produces variability sources such as the LER, or by statistical variability introduced by the discreteness of charge or granularity of matter as exemplified by random dopant fluctuations. The impact of these variability sources must be assessed carefully to maximize the yield.

As shown in Sect. 3, NESS comes with a powerful structure generator that enables the generation of LER, RDD and MGG. Moreover, the NEGF solver of NESS is parallelized using the Message Passing Interface (MPI), thus enabling simulations on hundreds of processing cores. Also, the Poisson solver coupled to the NEGF solver is based on a robust finite volume discretization and an efficient implementation of the self-consistency using auxiliary quasi-Fermi levels and corresponding Gummel’s iteration.

All these optimizations enabled us to perform quantum mechanical variability studies employing large statistical samples. For instance, we studied the impact of dopant diffusion in the channel of Si-NWFET in Ref. [48] and we performed in Ref. [49] a simulation study of all variability sources in Si$_X$Ge$_{1-X}$ employing 10,000 samples. NESS can also help assessing the viability of novel transistor architectures for future nodes. For example, a study of RDD induced variability in JunctionLess Field Effect Transistors (JLFET) and TFETs confirmed that the yield would be too low for those devices to be considered for digital applications [43, 50].

5.3 The Kubo–Greenwood solver

5.3.1 Features of the KG solver

The Kubo–Greenwood (KG) solver has been implemented in NESS for the calculation of the low-field electron mobility [51, 52]. This semi-classical approach combines the quantum effects based on the 1D multi-subband scattering rates of the most relevant scattering mechanisms in NWFETs [53] and the semi-classical Boltzmann transport equation (BTE) by applying the Kubo–Greenwood formula within the relaxation time approximation [54, 55]. Moreover, it is possible to make use of the effective masses calculated by the NESS EM extractor (Sect. 4). As this solver is based on the long-channel approximation, the first step is to pre-calculate the required subband levels ($E_l$) and the corresponding wavefunctions ($\xi _l$) using a self-consistent Poisson–Schrödinger simulation in the presence of a low electric field in the transport direction. The second step is to use these quantities to compute the scattering rates whose equations are directly derived from the Fermi golden rule. The following scattering mechanisms have been implemented in NESS: (1) acoustic phonon scattering; (2) optical phonon scattering, including g-type and f-type transitions; and (3) surface roughness scattering.

In this paper, we performed a comparison of the KG mobility with the one computed by NEGF method considering acoustic phonon and g-type (intra-valley transitions) optical phonon scattering mechanisms. More details of the all the aforementioned mechanisms as well as their equations can be found in [53]. The scattering rate for the acoustic phonon mechanism has been considered to be elastic and within the short wave vector limit. Its equivalent equation from a initial subband l and a final subband $l'$ is:

$$\begin{aligned} \begin{aligned} \varGamma _{\mathrm{Ac}}(l,k)&= \frac{|D_{\mathrm{Ac}}|^2 k_{\mathrm{B}} T}{\rho \hbar u_s^2}\frac{m}{\hbar ^2} \sum _{l'}\left[ \int {\hbox {d}}{\mathbf {s}} |\xi _l({\mathbf {s}})|^2 |\xi _{l'}({\mathbf {s}})|^2 \right] \\&\quad \times \, \theta (\epsilon (k)+\varDelta E_{l'}) \left( \frac{1}{|q_1+k|} + \frac{1}{|q_2+k|} \right) , \end{aligned} \end{aligned}$$

(45)

where $\xi _l$ is the wavefunction of subband l, $q_{1/2} = - k \pm \sqrt{k^2+\frac{\varDelta E_{l'}2m}{\hbar ^2}}$, $D_{\mathrm{Ac}}$ is the acoustic deformation potential ($D_{\mathrm{Ac}}= 14.5\,{\hbox {eV}}$ in this section), m is the electron effective mass in the transport direction, ${\mathbf {s}}$ are vectors normal to the transport direction, $\theta$ represents the step function, and $\epsilon (k)$ is the kinetic energy for a wave vector magnitude k. The rest of the parameters have their usual meaning.

We have considered fixed energy and deformation potential for the optical phonon scattering mechanism. Accordingly, the scattering rate for the g-type transitions is expressed as:

$$\begin{aligned} \varGamma _{Op}(j,l,k) & = \frac{|D_{Op,j}|^2}{2\rho \omega _j} \sum _{l'}\left[ \int {\hbox {d}}{\mathbf {s}} |\xi _l({\mathbf {s}})|^2 |\xi _{l'}({\mathbf {s}})|^2\right] \nonumber \\ &\quad \times \left[ \frac{n_j \theta (\epsilon (k) + \varDelta E_{l'j}^+) m }{\hbar ^2} \left( \frac{1}{|q_1+k|} + \frac{1}{|q_2+k|} \right) \right. \nonumber \\ &\quad+\,\left. \frac{(n_j+1) \theta (\epsilon (k) + \varDelta E_{l'j}^-) m }{\hbar ^2} \left( \frac{1}{|q_3+k|} + \frac{1}{|q_4+k|} \right) \right] \end{aligned}$$

(46)

where $q_{1/2} = - k \pm \sqrt{k^2+\frac{\varDelta E_{l'j}^{+}2m}{\hbar ^2}}$, $q_{3/4} = - k \pm \sqrt{k^2+\frac{\varDelta E_{l'j}^{-}2m}{\hbar ^2}}$, $\varDelta E_{l'j}^{\pm }=E_l-E_{l'} \pm \hbar \omega _j$, $n_j$ is the equilibrium phonon number, j refers to the phonon mode, and $\omega _j$ is the phonon energy.

Then, we present two strategies to calculate the total mobility. In the first one, the mobility associated with each particular scattering mechanism is calculated using its rate in the KG formula. The total mobility is then calculated as a function of the individual mobilities associated with each scattering mechanism using the Matthiessen rule [56]. In the second alternative, the scattering rate of both mechanisms are directly added to avoid the Matthiessen rule and thereby the total mobility for each subband is computed using the KG formalism. In general, the advantage of both semi-classical alternatives in comparison to purely quantum transport simulations is that the rates are individually computed and then combined, hence reducing dramatically the computational cost.

5.3.2 Comparison of KG and NEGF mobilities

The NEGF mobilities have been extracted using the formula [57]:

$$\begin{aligned} \mu = \left( \frac{{\hbox {d}}R}{{\hbox {d}}L}\right) ^{-1}\frac{1}{|q|\rho _{1{\hbox {D}}}}, \end{aligned}$$

(47)

where q is the electron charge, $\rho _{1{\hbox {D}}}$ is the 1D charge density along the NW transport direction, L is its channel length, and R is its resistance which is extracted by calculating the voltage to the current ratio. For this approximation to be valid, one must apply a very small bias of only few mV (2 mV in this section) and consider long channels to compute the resistance in the diffusive regime. We used 45 and 50 nm channel lengths to compute ${\hbox {d}}R/{\hbox {d}}L$. The results of the comparison for a $3\times 3\,{\hbox {nm}}^2$ square NW are shown in Fig. 11a, b. Both figures show a good agreement between the NEGF and KG mobilities for both acoustic and g-type optical phonons. The f-type optical phonons have not been implemented yet in the NEGF module of NESS and will probably be included soon in a future release. It’s interesting to note from Fig. 11b that the correct phonon-limited mobility given by the curve with triangles cannot be obtained in this case by extracting the acoustic and optical phonon-limited mobility then using Matthiessen rule. This is an indication of the importance of the interference of the two scattering mechanisms considered here. It is important to highlight that in this case, KG formalism reproduces the NEGF mobility when the scattering rates are summed up rather than using Matthiessen rule. This might be an indication that even for confined devices, KG suffices to calibrate the long channel mobilities for drift–diffusion models rather that running the more expensive NEGF simulations.

Fig. 11

Comparison of the phonon-limited mobility for a $3\times 3\,{\hbox {nm}}^2$ NWFET computed using NEGF and KG solvers for a the g-type Optical phonons and b the acoustic and acoustic+g-type optical phonons

5.3.3 Comparison of NEGF and DD+KG results

We present in Fig. 12 the comparison of the $I_{\mathrm{D}}{-}V_{\mathrm{GS}}$ characteristic obtained using NEGF solver with the transfer characteristic obtained using DD solver for a $3\times 3\,{\hbox {nm}}^2$ square NWFET with $L_{\mathrm{G}} = 20\,{\hbox {nm}}$. We have used in DD a constant mobility value of $190\,{\hbox {cm}}^2/{\hbox {Vs}}$, which is the value extracted from Fig. 11b for the sheet densities corresponding to the applied gate bias Fig. 11b. In the OFF-state, the logarithmic plot shows a good agreement between the NEGF characteristic and the DD one with Caughey–Thomas model, and a negative $V_{\mathrm{th}}$ shift of DD curve with constant mobility with respect to both aforementioned curve. However, the sub-threshold slopes obtained for all models are very similar. In the ON-state, the linear plots $V_{\mathrm{th}}$ shows that the NEGF transfer characteristic is positioned between the DD one with constant mobility and the one with Caughey–Thomas mobility degradation model.

This discrepancy in the transfer characteristics stems from the lack of quantum corrections in our DD simulations, which are crucial in the operation of a device with such a narrow cross section. Indeed, while NEGF captures the volume inversion as shown in Fig. 13a—i.e., most of the charge is located at the center of the device, the charge from the DD solution shown in Fig. 13b is mainly located at the edges and corner of the silicon body of the NWFET. This is an important shortcoming of DD that leads to inaccurate electrostatics for ultra-scaled NWFET and translates in a wrong estimate of the current. However, if quantum corrections are used in combination with mobility models to calibrate DD then a good match to NEGF results can be obtained [58]. The DD with constant mobility model and the NEGF self-consistent potential profiles in the center of the same device are shown in Fig. 14. Both types of potentials are quite similar, especially in the OFF-state where the NEGF simulation is usually started. Therefore, DD potential profiles are good trial potentials for NEGF self-consistent simulations despite the discrepancy in the transfer characteristics, and this can speed up considerably the NEGF solution for the first bias point.

Fig. 12

$I_{\mathrm{D}}{-}V_{\mathrm{GS}}$ characteristics for a $3\times 3\, {\hbox {nm}}^2$ square NWFET with $L_{\mathrm{G}} = 20\,{\hbox {nm}}$ obtained using NEGF with acoustic g-type e–ph interactions and classical DD with constant mobility and Caughey–Thomas model. The reference value of the mobility was obtained using the KG module. We used $V_{\mathrm{DS}} = 0.6\,{\hbox {V}}$

Fig. 13

Electron density profile (${\hbox {cm}}^{-3}$) across a transverse cross section of a $3\,{\hbox {nm}}\times 3\,{\hbox {nm}}$ square NWFET at the center of its 20 nm long channel from a NEGF, and b classical DD solvers at $V_{\mathrm{GS}} = 0.4\,{\hbox {V}}$ and $V_{\mathrm{DS}} = 0.6\,{\hbox {V}}$

Fig. 14

Comparison of the potential profiles along the transport direction obtained from DD and NEGF self-consistent simulations at different gate biases for a $3 \times 3\, {\hbox {nm}}^2$ square NWFET with $L_{\mathrm{G}} = 20\,{\hbox {nm}}$ at $V_{\mathrm{DS}} = 0.6\,{\hbox {V}}$. The potential was sampled at the center of each cross section.

6 Conclusion

In this paper we have presented NESS, a flexible nano-electronic device simulator under development in the Device Modeling Group of Glasgow university, and have described in details its main two modules. The first module is its structure generator that enables the generation of semiconducting devices with different architectures and can introduce the relevant sources of statistical variability in the corresponding solution domains. The second module contains the transport solvers that have been implemented so far: Drift–Diffusion, Kubo–Greenwood and non-equilibrium Green’s function. All these solvers share the same simulation domain, making NESS one of the few nanodevice simulation tools that offers the possibility to compare different models for the same device and to assess their strengths and shortcomings when simulating device characteristics and extracting particular figures of merit. The results reported herein and in other cited references show that at low applied biases the NEGF and KG solvers of NESS are in good agreement with all the main results reported in the literature for NWFETs. Moreover, the MPI optimizations for the NEGF solver and the robustness of our finite volume non-linear Poisson solver enabled quantum statistical variability studies employing large statistical samples. Additionally, NESS is modular and easily extensible. NESS will be released in the summer of 2020 as an open-source software which makes it very interesting for both academia and industry in helping to address the challenges subsequent to the further down-scaling of CMOS components.