Predators in the market: implications of market interaction on optimal resource management

Abstract

A two-species bioeconomic model is analyzed, but in contrast to most similar models, there is no biological interaction between the species, only economic. The interaction takes place in the market where the quantity of either species may affect the price of the other. The effects of cross-price elasticities on the optimal steady state and on the optimal paths in the sole-owner case are investigated both analytically (steady states) and numerically (optimal paths). First, it is shown that if the harvest of one species has impact on the price of another species, then this has a positive effect on its steady-state stock. The effect increases with the stock-elasticity in the cost function. Further, in the case of linear demand functions, the steady state outcome depends solely on the sum of the cross-price parameters and not their individual values. Secondly, in the investigation of optimal paths, it is shown that if the harvest of one species has impact on the price of the other, optimal trajectories reach steady state faster for itself and slower for the other species. Further, when cross-price elasticities are sufficiently high, the paths go from being monotonic to feature over- or undershooting.

1 Introduction

Analysis of multi-species and ecosystem models has been common in the bioeconomic literature at least since the 70s, whether it has been for the purpose of studying open access, maximum yield or economic rent; see e.g. Anderson (1975), Silvert and Smith (1977) and May et al. (1979). More recent contributions include Kasperski (2015) and Wang and Ewald (2010). In these articles, however, the interaction between species has always been biological, ecological and sometimes technical, but rarely in the market. Most articles that take market-interactions into account, are empirical studies, and many, if not most of them, seem to deal with interaction between aquaculture and wild caught fish (Anderson 1985; Ye and Beddington 1996).

Analysis of substitutes and complements in demand is fundamental in economics and well known from basic textbooks as well as numerous empirical studies, e.g. Meng (2014) and Garcia and Raya (2011) to mention a couple of recent ones. This phenomenon also applies to natural resources such as fish products (Vignes and Etienne 2011). However, there are only a few studies that systematically investigate implications of cross-price effects on optimal management of renewable resources from a conceptual and theoretical angle, probably because such models have a tendency to become very messy. There are, however, some recent exceptions to this rule, and Quaas et al. (2013) is one such. Their results are based on the assumption that there are two stocks with identical regeneration functions. Using this assumption they investigate the effect on resilience of substitutability and complementarity. Quaas and Requate (2013) study the effects of preferences for diversity in a model with an arbitrary number of fish species. An older example is Ruseski (1999) who uses a two-stage, two-period model to analyze the behavior of two agents, one regulated and one unregulated, who harvest identical products from two separate stocks. He finds that trade in the presence of market power and divergent management regimes may produce unexpected results.

Related problems have also been srtudied in the literature on the interplay between international trade and renewable resources like, for example, Chichilnisky (1994), Brander and Taylor (1997) and Bulte and Barbier (2005) None of these, however, deal with the same problem as studied here.

In this article a continuous time two-species bioeconomic model is applied to investigate the effects of economic (market) interaction between species on optimal management from a sole-owner perspective. That is, the owner, or manager, of both species is one and the same who maximizes the combined revenue from the two stocks. This may seem far-fetched if the term sole-owner is taken literally. But here the more common interpretation of the term sole-owner is used, namely that it represents the managing authority of a nation who behave as a sole-owner on behalf of its inhabitants in order to maximize the aggregated resource rent. There may, for example, exist two stocks in different parts of the country’s EEZ, but with certain similar characteristics making them substitutes in the market. Such characteristics can be that both species are “white fish” or that they are used for fish-meal or fish-oil production. This sole-owner exploits a certain degree of direct and indirect market power, and the demand functions are assumed to be stationary over time.

The biological model is a surplus growth model, but the only interaction between the species is in the market where the quantity of each species may affect the price of the other. The aim of this study is to investigate implications of market interaction upon the optimal steady state and on the paths leading to the steady state. Revenue and costs for each species are separable, but the harvest of one species enters the inverse demand function for the other. There are several possibilities, for example that one species affects the price of the other, but not vice versa. The most realistic assumption is probably that they are true substitutes such that both species affect the other species’ price. Somewhat facetiously, we can say that they predate on each others price. No technical or biological interactions are considered, but the two stocks can have completely different growth functions. No artificial assumptions about symmetry are made.

The analysis is divided in two parts, first a steady state analysis and then a dynamic analysis. Each of these parts are again divided in two, based on whether the net revenue function depends on the state variable(s) or not. This is because the state variables turn out to play an important role for the results. In the steady state analysis, the results are derived analytically from the mathematical model. In the dynamic analysis, on the other hand, numerical methods are resorted to as it is beyond realistic expectations to hope for closed-form solutions of a highly non-linear system of four differential equations.

2 The generic model

The model is a continuous-time, bioeconomic model of the surplus-growth type, with two species, x and y, but with no biological interaction. The two species are assumed to be substitutes in the market implying that the cross-price elasticities are negative. In other words, the price of one species may depend on both own supply and the supply of the other species, and therefore there exist certain degrees of market power that are exploited. The generic inverse demand functions look as follows:

$$\begin{aligned} p_{x}= & {} p_{x}(h_{x},h_{y})\\ p_{y}= & {} p_{y}(h_{x},h_{y}) \end{aligned}$$

where $p{}_{i}$ is price of species i and $h{}_{i}$ is harvest of species i. Technically it is assumed that $\partial p_{i}/\partial h_{j}<0$ for $i,j\in (x,y)$. The net revenue function, in its most generic form, is then defined as

$$\begin{aligned} R(x,y,h_{x},h_{y})=p_{x}(h_{x},h_{y})h_{x}+p_{y}(h_{x},h_{y})h_{y}-\kappa _{x}(x,h_{x})-\kappa _{y}(y,h_{y}) \end{aligned}$$

(1)

where x and y denote the size of the respective stocks, and $\kappa {}_{x}$ and $\kappa _{y}$ are cost functions. The separability of the cost functions rule out technical interactions.

The net revenue function is the objective function to be maximized with respect to $h_{x}$ and $h_{y}$ as control variables, whereas x and y are the state variables. The state and control variables are all functions of time, t. In addition there are two separate biological surplus growth functions, one for each species: f(x) and g(y). The infinite horizon dynamic optimization problem resulting from this leads to the following discounted Hamiltonian:

$$\begin{aligned} H=e^{-\delta t}R(x,y,h_{x},h_{y})+\lambda [f(x)-h_{x}]+\gamma [g(y)-h_{y}] \end{aligned}$$

where $\lambda$ and $\gamma$ are costate variables, also functions of t, and $\delta$ is the discount rate. The first-order conditions for this general case are given by¹

$$\begin{aligned} \partial H/\partial h_{x}=\partial H/\partial h_{y}=0 \end{aligned}$$

(2)

and

$$\begin{aligned} d\lambda /dt=-\partial H/\partial x,~d\gamma /dt=- \partial H/\partial y \end{aligned}$$

together with the dynamic constraints

$$\begin{aligned} dx/dt= & {} f(x)-h_{x} \end{aligned}$$

(3)

$$\begin{aligned} dy/dt= & {} g(y)-h_{y} \end{aligned}$$

(4)

and initial conditions $x(0)=x_{0}$ and $y(0)=y_{0}$. Now let R with subscripts represent the first and second partial derivatives with respect to its respective arguments as defined in Eq. (1). For example $R_{1} \equiv \partial R/\partial x$ and $R_{12}\equiv \partial ^{2}R/\partial x\partial y$. From the general definition of R it is seen that

$$\begin{aligned} R_{12}=R_{14}=R_{21}=R_{23}=R_{32}=R_{41}=0. \end{aligned}$$

The first-order conditions solved with respect to the discount rate yield the following two criteria:

$$\begin{aligned} \delta= & {} f{^{\prime }}(x)+\frac{R_{31}}{R_{3}}\frac{dx}{dt}+\frac{R_{33}}{ R_{3}}\frac{dh_{x}}{dt}+\frac{R_{34}}{R_{3}}\frac{dh_{y}}{dt}+\frac{R_{1}}{ R{}_{3}} \end{aligned}$$

(5)

$$\begin{aligned} \delta= & {} g{^\prime }(y)+\frac{R_{42}}{R_{4}}\frac{dy}{dt}+\frac{R_{43}}{ R_{4}}\frac{dh_{x}}{dt}+\frac{R_{44}}{R_{4}}\frac{dh_{y}}{dt}+\frac{R_{2}}{ R_{4}}. \end{aligned}$$

(6)

The two equations in (2) can be used to find explicit solutions for the costate variables and hence their time derivatives. Taking the first-order conditions and solving for $dx/dt,dy/dt,dh_{x}/dt$ and $dh_{y}/dt$ by eliminating the costate variables and their time derivatives, yields the following system of non-linear first-order differential equations:

$$\begin{aligned} dh_{x}/dt= & {} \frac{R_{34}A-R_{44}B}{C}\\ dh_{y}/dt= & {} \frac{-R_{33}A+R_{43}B}{C} \end{aligned}$$

where²

$$\begin{aligned} A= & {} R_{4}(g{^{\prime }}-\delta )+R_{42}(g-h_{y})+R_{2}\\ B= & {} R_{3}(f{^{\prime }}-\delta )+R_{31}(f-h_{x})+R_{1}\\ C= & {} R_{33}R_{44}-R_{34}R_{43}. \end{aligned}$$

Together with the dynamic constraints (3) and (4), using $R_{32}=R_{41}=0$, this constitutes a system of four differential equations. In the following we assume decreasing marginal return on harvest, that is $R_{33}<0$ and $R_{44}<0$. If, in addition, we assume $C>0$, then R will be partially convex in the control variables. This is fulfilled if the direct price effect is stronger than the cross-price effect, which seems to be a reasonable assumption. Restricting the search for optimal steady states to the closed intervals $0\le h_{i}\le MSY_{i}$, and x and y to be between zero and the natural carrying capacity, will guarantee the existence of both a maximum and minimum in the control variables on this interval. In the following, focus will be on interior solutions when they exist.

Finding closed form solutions for the time paths x(t),  y(t),  $h_{x}(t)$ and $h_{y}(t)$ for this system is far too optimistic, even in the simplest case. In stead, in the section Dynamic Analysis the system will be solved numerically. But first we will look at steady states.

3 Steady state analysis

In this section the properties of steady states are analyzed, and it is all based on the fairly general formulation of the net revenue function found in (1). By setting all time derivatives equal to zero, it is seen that the criteria (5) and (6) simplify to the following in steady state:

$$\begin{aligned} \delta= & {} f{^{\prime }}(x)+\frac{R_{1}}{R_{3}} \end{aligned}$$

(7)

$$\begin{aligned} \delta= & {} g{^{\prime }}(y)+\frac{R_{2}}{R_{4}} \end{aligned}$$

(8)

These two equations together with $h_{x}=f(x)$ and $h_{y}=g(y)$ yield four equations to be solved for x, y, $h_{x}$ and $h_{y}$. The following analysis is divided in two parts, namely when the net revenue (in practice costs) depends on the state variables x and y, and when it does not. These two cases can be thought of as representing purse seine technology and trawl technology, respectively. With purse seine technology there is usually little or no relationship between total stock size and costs of harvest whereas for trawl technology it is believed to be a strong relationship between stock size and costs. In reality, stock-dependence of costs varies along a continuum for both technologies. This dependence has been studied empirically by a number of authors, for example Harley et al. (2001) and Sandberg (2006). In this article, I focus on the extreme cases where the stock-elasticity is either zero or one, in order to isolate the most interesting results.

3.1 State-independent net revenue

When costs do not depend on the stock size, all costs can technically be integrated in the demand function by defining the price as a price net of costs. Then an interesting conclusion can be made directly from observing the two simple expressions (7) and (8). This is stated in the following proposition:

Proposition 1

If there is no stock-dependece of any kind in the revenue function, the optimal steady state stock and harvest levels will not be affected by own- or cross-price parameters.

Proof

If the stock levels are not explicitly included in the revenue function, or the derivatives are zero, the last terms in (7) and ( 8) will disappear as $R_{1}=R_{2}=0.$ Then these two equations will be two independent equations in x and y, and the steady state will only depend on biological parameters and the discount rate $\square$

The implication of Proposition 1 is that without stock-dependence the Golden Rule, as stated, for example, in Grafton et al. (2004, p. 113) is exactly the same in a two-species model with market interactions as it would be with two single-species models, namely that the marginal biological productivity of each stock should equal the alternative rate of return represented by the discount rate. As such, this is a generalization of the same result from single-species models. Mathematically it may look simple, but thinking about it, this is a fairly strong and far from obvious observation. Let us put it this way: If the quantity of herring in the market affects the price of mackerel and vice versa, this will not affect the optimal standing stock levels of mackerel or herring, nor their corresponding harvest levels, as the technology in these two fisheries are purse seine technology. If, on the other hand, the quantity of haddock in the market affects the price of cod and vice versa, this will affect the optimal standing stock and corresponding harvest levels as the fisheries in question are characterized by bottom trawl technology where the size of the stock has strong impact on the cost of harvesting. The intuition behind this is much the same as in the single-species case with downward sloping demand.

But even in the case where the optimal steady state is not affected by the cross-price parameters, the paths towards the steady will typically be affected irrespective of technology, as we shall see later. In practice, the way stock levels affect net revenue is through the cost functions. More specifically, therefore, if the cost functions are stock independent, optimal steady states will be characterized by the condition that marginal biological growth should equal the discount rate. In the special case that the discount rate is zero, the optimal steady states will correspond to the maximum sustainable yield levels. One practical implication of this is that cross-price effects do not make any difference with respect to steady states in schooling (purse seine) fisheries whereas they may make a difference in demersal (trawl) fisheries.

3.2 State-dependent net revenue

With state-dependent net revenue, the last terms in Eqs. (7) and (8) come into play as $R_{1}$ and $R_{2}$ are no longer zero. The cross-price parameters enter the equations through the denominator of the last term, namely $R_{3}$ and $R_{4}$. From (1) it is seen that these are given as

$$\begin{aligned} R_{3}= & {} \frac{\partial p_{x}}{\partial h_{x}}h_{x}+p_{x}+\frac{\partial p_{y}}{ \partial h_{x}}h_{y}-\frac{\partial \kappa _{x}}{\partial h_{x}} \end{aligned}$$

(9)

$$\begin{aligned} R_{4}= & {} \frac{\partial p_{x}}{\partial h_{y}}h_{x}+p_{y}+\frac{\partial p_{y}}{ \partial h_{y}}h_{y}-\frac{\partial \kappa _{y}}{\partial h_{y}}. \end{aligned}$$

(10)

It is the cross-price parameters that are of interest here, and these are $\frac{\partial p_{y}}{\partial h_{x}}<0$ in (9) and $\frac{\partial p_{x}}{\partial h_{y}}<0$ in (10). Let us concentrate on $R_{4},$ as the analysis of $R_{3}$ is equivalent. As the two species are supposed to be substitutes, the cross-price elasticities are negative implying that $R_{4}$ is smaller when the cross-price effect is taken into account than if the species are economically independent, that is $\frac{\partial p_{x}}{ \partial h_{y}}=0$. This will unambiguously lead to a higher steady state stock and a more conservative harvest policy. This can be stated in the following proposition:

Proposition 2

Assuming strictly concave growth functions and net revenue that depends positively on the stock level for one of the stocks, then if the harvest of one species reduces the price of the other species, this implies a higher optimal steady state stock for the affecting stock.

Proof

Assume that the only cross-price effect present is from $h_{y}$ to $p_{x}$. Then it is seen from (10) that having such a cross-price effect compared to not having it, will reduce $R_{4}$ through the term $\frac{\partial p_{x}}{\partial h_{y}}<0$. As $R_{2}>0,$ reducing $R_{4}$ will make the fraction $R_{2}/R_{4}$ larger. From (8) it is seen that making $R_{2}/R_{4}$ larger has to be compensated by a smaller $g^{\prime }(y)$ for a given $\delta$. $R_{4}$ and $g^{\prime }(y)$ therefore goes in the same direction. As g is assumed to be concave, smaller $g^{\prime }(y)$ implies going to the right (higher stock). Exactly the same reasoning applies to (9). $\square$

Proposition 2 says that if the harvest of y affects the price of x negatively, then this will imply a higher optimal standing stock of y, and vice versa, compared to when there is no such effect. The intuition is that the downward pressure on revenue from the other species can be regarded as an addition to the marginal cost for the sole owner, and therefore we have the well-known phenomenon that higher costs have a conservative effect. The interesting thing is that this only comes into effect when net revenue also depends on the stock. In practice, it implies that for demersal fisheries, where we expect high stock dependence of costs, cross-price relationships play a conservative role whereas for schooling fish stock (typical pelagic fisheries) cross-price relationships have little or no effect. This is an important result as it adds to the well-known fact that schooling species are already most vulnerable and exposed to extinction and collapse due to the technology in the fishery, which usually is purse seine. Demersal species caught by trawl, on the other hand, is to large extent naturally protected by their behavior (uniform distribution in the ocean) which makes it extremely costly to harvest on very small stocks even under open access regimes.

Corollary

The steady state stock for one of the species, for example x, may depend on the harvest of the other, y, even if the opposite is not true. This happens when $R_{1}\ne 0$ but $R_{2}=0$ or vice versa.

Proof

This follows directly from (7) and (8) $\square$

Even though (7) and (8) are easy to relate to conceptually, closed-form solutions for the steady state levels are almost impossible to find except for the simplest specifications of demand and cost functions, and even in these cases the expressions tend to become too long and messy to be of any practical value.

In the case of linear demand functions, that is when

$$\begin{aligned} p_{x}(h_{x},h_{y})= & {} a_{x}-b_{x}h_{x}-c_{x}h_{y} \end{aligned}$$

(11)

$$\begin{aligned} p_{y}(h_{x},h_{y})= & {} a_{y}-b_{y}h_{y}-c_{y}h_{x} \end{aligned}$$

(12)

where $a_{i}$ is the constant term, $b_{i}$ is the sensitivity to own harvest and $c_{i}$ is the cross-price sensitivity, the following statement is proposed:

Proposition 3

If demand functions are linear, the steady-states are determined exclusively by the sum of the cross-price parameters.

Proof

It is seen from the analysis above and Eqs. (7) and (8) that the cross-price parameters only affect the steady state through the terms $R_{3}$ and $R_{4}$. In the linear case these terms can be written

$$\begin{aligned} R_{3}= & {} a_{x}-2b_{x}h_{x}-(c_{x}+c_{y})h_{y} \\ R_{4}= & {} a_{y}-2b_{y}h_{y}-(c_{x}+c_{y})h_{x}. \end{aligned}$$

Thus it is seen that the cross-price parameters enter the equations that determine the steady state in the form of the sum of the two parameters. $\square$

In other words, no matter how asymmetric the economic and biological submodels are with respect to demand, cost structure and surplus growth function, if the cross-price parameters change value such that their sum remains the same, the steady state will remain unchanged. In practice this means that the two fish stocks can be quite different regarding economic, biological and technological aspects, if we let the cross-price parameters change values such that for example $c_{x}=3$ and $c_{y}=7$ instead of the other way around, it will not change the steady state.

4 Dynamic analysis

Not only the steady state, but also the optimal paths leading to the steady state are of interest, and, in particular, how they are affected by the cross-price parameters. As in the previous section, the case with stock-independent net revenue, in practice stock-independent costs, will be analyzed first. Thereafter the case where net revenue depends on the stocks, is investigated.

4.1 State-independent net revenue

Here we let net revenue depend on harvest only and not on the stock size. This is representative of fisheries with purse seine technology targeting schooling fish, and only the extreme case is investigated, that is no trace of the stocks in the net revenue function whatsoever, which implies that, in addition to $R_{32}=R_{41}=0$, from earlier, we also have

$$\begin{aligned} R_{1}=R_{2}=R_{31}=R_{42}=0 \end{aligned}$$

just like in Sect. 3.1. The first-order conditions corresponding to (5) and (6) then simplifies to:

$$\begin{aligned} \delta= & {} f{^{\prime }}(x)+\frac{R_{33}}{R_{3}}\frac{dh_{x}}{dt}+\frac{R_{34} }{R_{3}}\frac{dh_{y}}{dt}\\ \delta= & {} g{^{\prime }}(y)+\frac{R_{43}}{R_{4}}\frac{dh_{x}}{dt}+\frac{R_{44} }{R_{4}}\frac{dh_{y}}{dt} \end{aligned}$$

This system can be solved for the time derivatives of the control variables yielding

$$\begin{aligned} dh_{x}/dt= & {} \frac{R_{4}R_{34}(g{^{\prime }}-\delta )-R_{3}R_{44}(f{^{\prime }}-\delta )}{C} \end{aligned}$$

(13)

$$\begin{aligned} dh_{y}/dt= & {} \frac{R_{4}R_{33}(g{^{\prime }}-\delta )-R_{3}R_{34}(f{^{\prime }}-\delta )}{C} \end{aligned}$$

(14)

and C denotes the determinant as earlier, assumed to be positive. It is immediately seen that in the case with stock independent net revenue, although the steady states are unaffected by the cross-price parameters, the optimal paths are affected.

Together with the dynamic constraints, (3) and (4), the equations (13) and (14) constitute a system of four non-linear first-order differential equations. In principle, this is a solvable system yielding the optimal time paths for $h_{x}(t),~h_{y}(t),~x(t)$ and y(t). Due to the non-linearities, meaningful closed-form solutions are beyond expectation. The only approach, therefore, is to solve the system numerically.

In order to perform numerical analysis, special functional forms must be determined. Here linear inverse demand functions will be applied where the price of each species depends on both own harvest and the harvest of the other species as specified by Eqs. (11) and (12). In addition it is assumed that the growth functions, f and g, are standard logistic surplus growth functions:

$$\begin{aligned} f(x)= & {} r_{x}x\left( 1-\frac{x}{K_{x}}\right) \\ g(y)= & {} r_{y}y\left( 1-\frac{y}{K_{y}}\right) \end{aligned}$$

where $r_{i}$ and $K_{i}$ have the conventional interpretations as intrinsic growth rate and carrying capacity for $i=(x,y)$, see Clark (2010). The numerical specification of the above equations is given in appendix. The numbers are not meant to represent any real fisheries, rather they are meant to describe completely hypothetical, but still possible, fisheries with meaningful characteristics; in other words fisheries that very well might have existed.

First, the optimal steady state is found:

x	60
y	332.5
$h_{x}$	9
$h_{y}$	74.8125

From Proposition 1 we know that in this case the steady state is independent of the cross-price parameters $c_{i}$. In a non-linear four-dimensional system, there are multiple possible solutions, but fortunately, for the cases considered here, there is only one possible solution within the feasible region $x\in [0,K_{x}],$ $y\in [0,K_{y}]$ and $h_{i}\in \left[ 0,\frac{r_{i}K_{i}}{4}\right]$. Remember that with the logistic model $\frac{rK}{4}$ represents maximum sustainable yield.

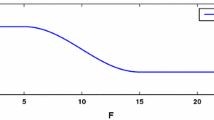
In order to investigate the effect of cross-price parameters on the optimal time paths, we start by looking at the development of x with ($c_{x}=0.08$ ) and without ($c_{x}=0$) cross-price effect in the case without stock-dependence. This is illustrated in Fig. 1.³

The stock is assumed to be overexploited initially (like so many fish stocks around the world), and it is seen that the approach to the steady state is asymptotic due to the non-linearity [as opposed to the bang-bang approach resulting from linear models, see Clark (2010)]. The boundary conditions applied here are $x_{0}=45$ and $h_{x}$ at $t=65$ equal to the optimal steady state harvest. It is reassuring to see that with these initial conditions the stock level approaches the independently calculated steady states even when they are not restricted to it. I take this as a confirmation that the paths are really optimal. It is seen that without cross-price effect both stock and harvest approach their steady state values monotonically. With cross price effect from the harvest of y on the price of x, on the other hand, the stock development of x goes down initially (undershooting) and reaches its steady state more slowly. The harvest is first higher than the steady state level, then goes below and then gradually approaches it. This is both an interesting, and very robust result.

The corresponding stock and harvest development for y is illustrated in Fig. 2. Here the initial stock is $y_{0}=300$.

Fig. 1

Stock and harvest development for species x with (x-c and hx-c) and without (x and hx) cross price effect when there is no stock-dependence. Harvest of y affects price of x

Fig. 2

Stock and harvest development for species y with (y-c and hy-c) and without (y and hy) cross price effect when there is no stock-dependence. Harvest of yaffects price of x

The most noticeable feature is that the effect on species x, whose price is affected by the other species, is more pronounced than for species y, which causes the effect. The stock of y approaches its steady state faster with cross-price effect than without.This is the opposite of the x-stock development which even goes down initially. In other words, the behavior of the x-stock is less bang-bang like and the y-stock more bang-bang like with cross-price effect from y on x.

4.2 State-dependent net revenue

In the section “Steady state analysis” there was significant difference between the cases with and without stock-dependent net revenue, in practice costs. It may therefore be interesting to investigate whether there is any noticeable difference in the dynamics case also. In this section the standard cost function derived from the Schaefer production is applied:

$$\begin{aligned} \kappa _{x}(h_{x},x)= & {} \frac{C_{x}h_{x}}{x}\\ \kappa _{y}(h_{y},y)= & {} \frac{C_{y}h_{y}}{y} \end{aligned}$$

where the values for the parameters $C_{x}$ and $C_{y}$ are given in Appendix.

First, the long-term optimum is calculated, and this is affected by the cross-price parameters as shown earlier. The steady state for the case without cross-price effects and for some combinations of parameter values are reported in Table 1.

Table 1 Results from the dynamic analysis and state-dependent costs

According to Proposition 2, x will increase when $c_{y}$ increases and vice versa, everything else equal. This is confirmed by the table. Typically the stock will also increase when the own price-parameter increases, but not necessarily so, as seen when $c_{y}$ increases from 0 to 0.01 for $c_{x}=0.08$. In this case the stock y decreases slightly.

Figures 3 and 4 illustrate the time-paths for x and y,  respectively, with and without cross-price effects, but this time with stock-dependent costs.

Fig. 3

Stock and harvest development for species x with (x-c and hx-c) and without (x and hx) cross price effect when there is stock-dependence in costs. Harvest of y affects price of x

Fig. 4

Stock and harvest development for species y with (y-c and hy-c) and without (y and hy) cross price effect when there is stock-dependence in costs. Harvest of y affects price of x

It is seen that the paths increase monotonically and approach the steady state asymptotically without any sign of over- or undershooting when there is no cross-price effect. And, just like in Figs. 1 and 2, it is seen that the introduction of market interaction leads to over- and undershooting for the species whose price is affected by the other species. The effect, however, is not very pronounced. It is further confirmed that the steady states themselves are affected by the stock-dependence, but this is almost negligible for the affecting stock.

Thus, it is seen that whether net revenue is stock-dependent or not does not have any significant impact on the shape of the optimal time paths although it has significant impact on the steady states. The shape of the time-paths are mainly affected by the cross-price parameters.

5 Summary and conclusions

This article is about a two-species bioeconomic model where the only interaction between the species is in the market. In other words, there is no technical or biological interaction between the species. This may be relevant for a social planner, for example the managing authorities in a country, who has to deal with several species around the coast. These species may be located in different geographical areas and therefore do not interact biologically, but their products are sold in the same market.

The article is structured in two parts, first steady-state analysis and then dynamic optimal path analysis. These parts again are divided in two sections, with and without state-dependent costs. Steady states are studied both analytically and numerically whereas optimal paths are studied numerically. The main result from the steady-state analysis is that if the harvest of one species has impact on the price of another species, then this has a positive effect on its stock. The effect increases with the stock-elasticity in the cost function. In other words, whether cross-price elasticities have impact on the steady state or not, depends on the technology in the respective fisheries. In fisheries where effort and costs are independent of the total stock size, cross-price elasticities have no such effect. This is typically relevant for fish species with schooling behavior, and therefore harvested using purse seine technology. For demersal species, which typically are caught using bottom trawl, the cross-price elasticities actually affect the optimal size of standing stocks and corresponding harvest. More precisely, the qualitative effect is such that the presence of cross-price elasticities have a conservative effect on the stocks. In other words, the presence of a substitute in the market reduces the price and thereby profitability, and hence has a conservational effect on the stock. This was shown analytically in the section Steady State Analysis. This is a generalization of the same result from single-species models. A novel result found here is that, in the case of linear demand functions, it is the sum and only the sum of the cross-price parameters that affect the steady states, and not their composition or individual values.

In the section Dynamic Analysis it is shown that optimal paths towards steady state are affected by cross-price elasticities whether costs depend on stock or not. If harvest of one species has impact on the price of another species, optimal trajectories reach steady state faster for itself and slower for the other species. Further, when the cross-price influence is sufficiently strong, the stock and harvest paths go from being monotonically increasing or decreasing to exhibit over- or undershooting. Overshooting is defined as the case where the stock is induced to increase initially even though the initial stock is above the target. Undershooting is defined as the case where the stock is induced to decrease although it already under the target steady state. In other words, over- and undershooting refer to regions where the variables make an initial departure from the target before they come “back on the track”. No trace of over- or undershooting have been found when the cross-price effects are removed. It is the indirect gain made by the cross-price effects that make over- and undershooting optimal.

The results presented here are fairly novel, and therefore there is scope for quite a bit of future research. This may include the combination of biological and market interaction, the combination of technological interaction and market interaction. And it may, of course, include other numerical examples, numerical analysis of other functional forms, and not least empirical investigation of particular cases.

Appendix

In this appendix the numerical specification applied in the analysis is summarized in the following table

$r_{x}$	$K_{x}$	$r_{y}$	$K_{y}$	$\delta$
0.25	150	0.4	760	0.05
$a_{x}$	$b_{x}$	$c_{x}$
10	0.1	0.08
$a_{y}$	$b_{y}$	$c_{y}$
15	0.02	0.01
$C_{x}$	$C_{y}$
200	1500