1 Introduction

We focus on a complex system and the question how to handle it. As a basis we use a well-known class of dynamical systems—predator–prey models—which is applied to a specific situation. Therefore, we give some theoretical background of predator–prey type models including economic interpretations of those models in the following section. In principle, our goal is to yield some findings in economic stabilisation, but, mainly for reasons of simplicity, the application at hand tackles the problem in the field of biology.

A biotope consisting of two populations should be brought to a stationary fixpoint level by means of two different instruments. The approach of Sect. 3 shows applications of predator–prey models for optimal harvesting and refers mainly to behavioural economics. Our aim consists mainly in collecting information how subjects handle such a complex system. Therefore, we create a decision support tool which should help us to understand human behaviour within complex systems in which the price of harvested objects plays an important role on one hand and the availability of the objects are important on the other side. With the help of an experimental setting in order to ascertain how successful human decision makers are in managing such a system we are able to demonstrate interesting results (Sect. 4).

Finally, we close with a summary where we have to admit that handling such a complex system can only give us some heuristic explanations with empirical evidence.

2 Theoretical background

2.1 Predator–prey type models

Independently of each other, Alfred Lotka and Vito Volterra (Lotka 1925; Volterra 1928) developed a system of nonlinear differential equations to model the simplest case of a predator–prey system. The corresponding mathematical formulation is a system of two nonlinear first-order differential equations:

$$ \begin{aligned} & dx/dt = \left( {a{-}by} \right)x \\ & dy/dt = \left( { - e + cx} \right)y \\ & with\;a,b,c,e > 0 \\ \end{aligned} $$
(1)

where x is the number of prey (for example small fish or rabbits); and y is the number of some predator (for example big fish or foxes); dx/dt and dy/dt represent instantaneous growth rates of the two populations; t represents time; a, b, c and e are positive real parameters describing the interaction of the two species.

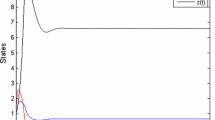
The underlying Lotka–Volterra system models an open, natural, discrete system. Two basic assumptions can be derived from the unconstrained system (1): First, the prey population grows logistically (there is no food restriction for the prey), and second, the predator population decreases exponentially (in case of lack of prey). A graphical representation of the formal system in a very general way is outlined in Fig. 1 as well for an economic as an ecologic system.

Fig. 1
figure 1

Fluctuations of two economic or biologic variables

Full size image

Variable x(t) represents a prey population (as prey fish) at time t that grows exponentially in the absence of predators [corresponding to the term ax(t)]. Variable y(t) represents a predator population (as predator fish) at time t with the prey as exclusive source of food. We are assuming a restricted territory as a biotope or a forest, which obviously limits the population of prey.

According to Goodwin (1951 and 1967), we also can apply the setting to business cycles with variables x as an intermediate product and variable y as the final product, created by one input only. Both products can be managed in optional quantities without any effect on market prices. Therefore, we can also use Goodwin’s economic interpretation for the two variables: in his model predator takes on the role of wage rate and prey takes on the role of employment rate.

Due to the linear dependence on food, the basic Lotka–Volterra system (1) is suitable for prey species that do not experience any capacity constraints. For other prey species with, e.g., intraspecific competition, ax(t) ≥ 0 has to be replaced by a logistic growth function. Additionally, a more refined representation of the ‘response’ of the predator population to prey supply could be substituted for bx(t) ≥ 0 and could thus include upper boundaries on consumption necessary per time unit, or whether or not ecological niches are occupied.

Therefore, different forms of predator–prey dynamics have been proposed [for a survey, see, e.g., Clark (1990) and Begon et al. (1996)]. In its most general form, the dynamics reads as:

$$ dx\left( t \right)/dt = g\left( {x\left( t \right)} \right) - f\left( {x\left( t \right)} \right)y\left( t \right)),\quad x\left( 0 \right) \ge 0 $$
(2a)
$$ dy\left( t \right)/dt = \left( {cf\left( {x\left( t \right)} \right) - d} \right)y\left( t \right),\quad y\left( 0 \right) \ge \, 0 $$
(2b)

with g(x(t)) ≥ 0 denoting the natural growth function of the prey population, and f(x(t)) ≥ 0 representing the ‘response’ of the predator population to prey supply.

As in (1), the parameter c > 0 measures predator’s efficiency of ‘converting’ prey caught into offsprings (i.e., its metabolic efficiency) and parameter d > 0 represents predator’s (natural) mortality rate.

The choice of different functional forms for g and f leads to different types of short-term and long-term system behaviour. For the basic Lotka–Volterra model, phase space is filled with infinitely many closed trajectories, i.e. wherever one starts [corresponding to initial conditions in terms of x(0) and y(0)] one undergoes recurrent behaviour for both species, except if one is located exactly at the non-hyperbolic (non-trivial) equilibrium.

In contrast, augmenting the Lotka–Volterra approach with logistic growth, i.e.

$$ g\left( {x\left( t \right)} \right) = ax\left( t \right)\left( {1 - x\left( t \right)/K} \right) $$

yields richer and considerably different system behaviour. The trivial and fatal equilibrium at the origin remains a saddle point as also observed for (1).

We find that in the long-term the extinction of the predator species happens if y’s efficiency is too low relative to its mortality rate, i.e. d > cbK, while for d < cbK the stable, i.e. non-recurrent, coexistence of both populations can be guaranteed. This result is driven by the constrained environment and by the resulting intra-species competition for prey population. Thus, if capacity for the prey population is sufficiently high, K > d/cb, the ecosystem remains intact and stabilizes without any additional intervention. Interestingly, the more efficiently predators can convert food into offsprings, reflected by an increasing parameter c, the higher is the degree of oscillation towards a stable state.

2.2 Economic interpretations of predator–prey models

While predator–prey models were originally developed for ecological problems at the population level, they have since been used in various other fields such as molecular biology, and also in a broad sense of economics including ecological problems of sustainability.

Multi-species modelling has a relatively short tradition in environmental and resource economics, with early applications found mostly for fisheries (e.g. Hannesson 1983), some on agriculture and forestry (Crépin 2003; Bulte and Horan 2003; Skonhoft and Solstad 1998), and more recent applications in environmental conservation (Bulte and van Kooten 1999; Hoekstra and van den Bergh 2005).

However, predator–prey models are not only applied to problems in environmental and resource economics, but also in other fields of economics. Goodwin’s theory of the business cycle (1967) addresses the problem of optimization and business fluctuations. Goodwin adopted the Lotka–Volterra system for population dynamics. In his model, employed workers have the role of predators, as their wage demands squeeze profits and hence investment, leading to an increase in unemployment. Another model, Goodwin’s Non-Linear Accelerator is also a model of endogenous cycles in economic activity; there the cycles do not rely on outside shocks or structurally unstable parameters. Business cycle models emphasize the importance of a lagged nonlinear accelerator in various disciplines.

Since Goodwin’s seminal work a huge number of solutions for nonlinear trade cycles models have been developed. Recently variations in the parameters and their effects have been explored. Moreover, the model has been applied to other economic problems such as pest control in agriculture (Christiaans et al. 2007), copyright piracy in the music industry (Vaquez and Watt 2011), China’s market miracle (Zhang 2012), and urban growth (Capello and Faggian 2002).

From the perspective of decision-makers, understanding current events is important; however more importantly they need to understand how such events can be controlled in order to achieve desired goals. Therefore, we need to analyse parameter sensitivity analysis of a descriptive model and utilize the methodology of optimal control theory: In particular Pontryagin’s Maximum Principle, helps in deriving strategic advice for intertemporal decision-problem sketched in Sect. 3.1. It is especially due to numerical analysis that applying optimal control theory has become a success story. Its applications are extremely diverse.

2.3 Applications of predator–prey models to optimal harvesting

Bednar-Friedl et al. (2017) seek to apply predator–prey modelling to illuminate the demanding task of efficient urban economic development (UED). According to a review of associated model variants by Capello and Faggian (2002), in an UED-context, prey can be understood as population density (measured, e.g., by residents per square kilometre of settlement area), and predators as urban rents (a proxy for negative localization factor, i.e., a centrifugal force). Bednar-Friedl et al. follow a related approach but focus on population density and environmental pollution as critical abundances for urban development. Moreover, they deviate from Capello and Faggian not only by seeking optimal state-dependent development plans but also by modelling population density as a prey-type variable, since even at zero-pollution, it would not exhibit more than logistic growth behaviour. Pollution is regarded as being a predator-type variable, since it would disappear in the absence of people driving cars and/or needing housing facilities; pollution increases with demand for mobility and/or residential property as can be seen in Fig. 2.

Fig. 2
figure 2

Illustration of cycles for pollution-population dynamics (Bednar-Friedl et al. 2017)

Full size image

In this paper by Bednar-Friedl et al. (2017), recycling has been modelled where recycling also generates income that is fully devoted to capital accumulation. They study qualitative properties of the resulting optimal control problem, notably in terms of optimal asymptotic states, stability and transition. They work out numerical examples and calculate some intriguing economic results relating to the seminal framework of Stokey (2016), both in terms of optimal pace of recycling and relationship between income and pollution.

In particular, the role played by recycling as an income generator is crucial in the sense that it gives rise to a contraction of both consumption and capital stock in the long run after an expansion phase. Polluting waste is predominantly due to production or consumption, and when recycling generates additional income, greater consumption and lower capital stock are obtained in the end compared with the situation when recycling does not create additional income. Meanwhile recycling generates additional income and greater recycling effort and lower stock of waste are achieved in the long run.

The paper by Behrens et al. (2018) reports a predator–prey model, which has helped to demonstrate effects between the variable of pollution on the one hand, and quality of life, respectively public health, on the other hand. The authors have created three different sets of parameter constellations, yielding three different scenarios with respect to residential lifestyle and pollution control. They illustrate the insight generated regarding interdependency of market-based and technological pollution controls. Analysis shows that setting additional measures to support evacuation and reduction of pollutants will be most effective after pollution has built up. They suggest an indicator assessing the cost of delayed interventions.

3 Behavioural economics

3.1 Laboratory experiments

Experimental economics has become a well-established tool for economists in general. The initial impetus originates from microeconomic research of individual choice behaviour. Theories depending on individual preferences rarely correspond or even match observations made in natural environments. Therefore, a new branch has been created to compare laboratory results with theoretical assumptions made about individual behaviour: experimental economics.

Experimental economists explore human behaviour mainly in laboratories. Laboratory experiments may have some drawbacks but in real environments, information sets of decision-makers cannot be controlled: their decisions can be observed but which information they use remains unclear. When we speak about laboratory experiments, we assume that the economic environment is completely controlled by experimenters.

Murphy et al. (1988) has shown that addictive consumer behaviour is consistent with intertemporal utility maximization. In a follow-up paper, Dockner and Feichtinger (1993) have demonstrated that addiction may lead to persistent oscillations of consumption rates. Since then scores of experiments have been designed to explore further systematic violations of utility theory. Much of the work on choice behaviour is surveyed in Camerer (2002).

The goal of labour experiments is to reveal the fascinating interplay between theory and experiment. Self-interest is not the only driving force shaping behaviour in such games. Experimental results suggest that considerations of fairness often play important roles: subjects are willing to forgo some monetary gains in order to avoid unfair treatment. For various experiments and models of fairness, see Fehr and Schmidt (1999), Becker and Leopold-Wildburger (1996), Becker et al. (2002) and Bednar-Friedl et al. (2017), as well as Behrens et al. (2018). Surveys of experiments concerning coordination and bargaining can be found in Kagel and Roth (1997).

Experiments offer the possibility of isolating specific effects of the rules of the game by which markets are determined. Chamberlin (1948) introduced a design, now widely used by experimenters, to create markets for artificial commodities in which experimenters can control reservation prices of buyers and sellers. Chamberlin’s design permits experiments to compare different rules of market organization can be compared while keeping all other parameters constant.

Experiments have increasingly been used as engineering tools to help test new market designs (see e.g. Roth 2002). A general overview of experimental economics, including details of its early history, can be found in Roth (1991). Experiments that deal indirectly with the problem of optimization and business fluctuation refer to Goodwin’s business cycle theory from 1951. Next, in 1967 Goodwin adopted the Lotka–Volterra system. Since subsequently a large number of solutions for nonlinear models of business cycles have been developed, including recent parameter variations and the exploration of their effects. These models emphasize the importance of a lagged nonlinear accelerator in various disciplines.

Another nonlinear dynamic system, that has been successfully used in experimental economics, was presented by Becker and Murphy (1988). They have shown that addictive consumer behaviour is consistent with intertemporal utility maximization. A subsequent paper, Dockner and Feichtinger (1993) has demonstrated that addiction may lead to persistent oscillations of consumption rates. Fehr and Schmidt (1999) report an experiment with addictive preferences in which addicts systematically consume too much compared to optimal consumption decisions.

Behrens and Neck (2015) present an algorithm developed to iteratively approximate equilibrium solutions of so-called tracking games, i.e. discrete-time nonzero-sum dynamic games with a finite number of players who face quadratic objective functions. Such a tracking game describes the behaviour of decision-makers by repeated applications who act in nonlinear discrete-time dynamical systems, and who aim at minimizing deviations from individually desirable paths of multiple states over a joint finite planning horizon.

Experiments scheduled within the framework at hand try to cast light on the economic and ecologic stabilization of a particular system, and address the same phenomena pertaining to typical behaviour of subjects. Participants of the experiment are tasked to decide in a situation aiming to guarantee long-term sustainable business success. For decision-makers who are not aware of the precise relationship as formalized by system (1) and the exact parameters chosen, the complexity of the decision stems from the interdependences of the size of the populations that are increasing or decreasing given the size of effects in a certain time-period. The goal is to keep both instruments/parameters at such a level that a stationary fixed-point level is reached and in future periods will be possible. This clearly relates to concepts of sustainability in business and economics respectively.

3.2 The predator–prey simulation

There are numerous contributions to the literature on the subject of experimental markets (see Sunder 1995; Kagel and Roth 1997). However, the framework of economic stabilization with the pursue of sustainability within a predator–prey ecology has hardly been used in a laboratory so far. Complementing results of dynamic optimal control, we aim to examine the behaviour of subjects experimentally in a simulation environment based on a Lotka–Volterra system. The main idea of the experiment at hand has been inspired by Becker and Leopold-Wildburger (1996) and Becker et al. (2002). In experimental approaches, subjects (participants) act as decision-makers. Their objective is to manage an environment such that environmental quality and population levels are optimal. In a first version of this simulation. To conduct the experiment, we reuse the EXPOSIM simulation software developed by Fritsch and Siegelmann (2006) which was applied by Grabner et al. (2008) to model one specific treatment combined with a questionnaire on personality treats.

Our goal is to provide a simulation model capable of handling a complex system as given in real world situations and consequently to provide managers with appropriate skills. Our aim is to support decision-making, to enable decision-makers to find judgments using experimental experience with the aim to learn to improve decision-making by repeated applications. With our simulation experiment we intend to analyse a problem in a biological domain, mainly with the aim to analyse a sustainable environment with diametrical goals to harvest as much as possible while allowing optimal population growth. In summary, the theoretical analysis is based on the following elements:

  • predator–prey system with carrying capacity,

  • numerical integration using the Euler method and

  • the fourth order Runge–Kutta method.

The following research questions will be tested in the experimental setting:

  1. (1)

    Will the participants of the experiment find out optimal strategies?

  2. (2)

    Does the number of possibilities for optimal strategies influence the results?

  3. (3)

    Will participants of the experiment more likely harvest prey population rather than the predator population?

  4. (4)

    Will prices of the harvested objects influence their behaviour?

  5. (5)

    Will the availability factor [in the sense of Kahneman and Tversky (1973)] play a more significant role than the prices of the objects? Will participants of the experiment consider that obviously, prey populations are far more available than predator populations while ignoring the price structure? Or with other words: Will prices/revenues play a less important role than availability?

4 Simulation experiment

4.1 The setup of the experiment

We use experiments for our study because they allow subjects to play repetitive games and give us the opportunity to analyse subjects’ behaviour in respect to tasks they were asked to handle the system in a way described below. We have used simulation software to manage a complex dynamic system in a sustainable environment. It models a Lotka–Volterra system with two populations, predator and prey, which should be harvested on an optimal orbit: this should allow maximal harvest at a maximal level of sustainability giving the possibility to harvest both populations at the same time. The fundamental assumptions of this model are:

  • isolated habitat,

  • prey population grows logistically, predator–prey population decreases exponentially,

  • mutual influences are due to predator–prey relationship,

  • prey population is diminished by predation,

  • predation boosts predator population.

Subjects are put into positions of decision makers and they are enabled to manage harvesting as well as the environment, both in an optimal way to avoid unsustainable caught.

We run the experiment with the possibility for the participants of direct intervention by taking/harvesting/fishing small and big fish. Obviously small fish take the role of prey x = x(t) and big fish like sharks the role of predator y = y(t). Both populations form a biotope for which Fig. 1 shows the typical behaviour of small and large fish over time in absence of interventions. We observe that the number of small fish and the number of large fish—which feed upon the small fish—fluctuate periodically, however out of phase. After predator have become a too large population and feed too many small fish, the large fish population begins to shrink due to the shortage of their food. By this development, the small fish get again a chance to recover. This, in turn, allows the large fish population to recover step by step and finally the process starts over again.

In the simulation, a short description of the simulated environment and of the task (i.e. the decision about the fishing quantities of both species) is presented to the participants of the study at the beginning of the simulation. They were put into the position of a decision maker and had to simultaneously harvest both fish species for T = 42 periods, such that the revenues from catching small fishes qx(1) + ··· + qx(T) and large fish qy(1) + ··· +qy(T) are maximized, while keeping the respective stocks of fish sufficiently large. The price of fish is exogenously given to each fisherman/participant of the experiment. Prices for small and large fish are denoted by p(prey) = px and p(pred) = py.

After each period, the remaining stocks were disclosed to the participants. To point out the importance of maintaining the ecosystem in the long run, we integrated the market value of the of the final stocks of both species of the terminal period into the current value of the fisherman’s revenue function. The subjects’ task is to maximize the harvested quantities qy respectively qx according to given prices to maximise the total sales Π for all 42 periods. Total sales account to cumulative harvest and final stocks of both species.

The calculation of total sales Π is presented as follows:

$$ {{\Pi}} = \sum\limits_{t = 1}^{42} {{p}_{{y}} {q}_{{y}} \left( {t} \right) \, + {p}_{{x}} {q}_{{x}} \left( {t} \right) + {p}_{{y}} \,{finalstock}_{{y}} \left( {T} \right) + {p}_{{x}} \,{finalstock}_{{x}} \left({T} \right),} \quad T = 42, $$
(3)

with x(t) and y(t) determined by system (1). The revenue function was displayed on the screen from the beginning of the experiment and remained throughout all 42 periods.

The optimal harvesting trajectory results from solving the finite maximisation problem (3) subject to system (1) and depends on the market prices paid for the two species. We run 5 different treatments varying the price of each species. Table 1 gives the 5 different treatments with the following prices for predator and prey:

Table 1 Treatments with different price structures
Full size table

Obviously, the different price combinations yield different optimal solutions respectively different optimal revenues.

4.2 Optimal solutions

From now on we use system (1) calculating optimal interventions applying values of the constants as follows: a = 0.6; b = 0.002; c = 0.001 and e = 0.4.

The analysis shows that there are two main phases: a starting phase at the beginning (starting periods t = 1,…,5) followed by a phase in which the system is at a stationary level in terms of optimal fishing quantities (from t = 6,…,42). During the latter optimal harvesting can be performed at optimally high levels of regeneration. We will call this the sustainability phase.

The optimal strategy derived from the Bellmann method (Bellman 1957) is unique and given for all treatments below by Tables 2 and 3. The level of harvesting during the sustainability phase should be kept constant to guarantee that as many predators and prey as possible can be harvested.

Table 2 Optimal solution for treatment 1 and treatment 2
Full size table
Table 3 Optimal solution for treatment 4 and treatment 5
Full size table

  • Treatment 1 and 2 have identical optimal solutions and can be pooled as treatments 4/2 and 5/2.

  • Treatment 4 and 5 have identical optimal solutions and can be pooled as treatments 4/1 and 5/1.

  • Treatment 3 can be best achieved by all possible optimal harvesting strategies.

Depending on prices of predators and prey, different equilibria strategies yield different outcomes. Depending on total sales revenue of such a strategy, optimal solutions are caused by different strategies.

Tables 2 and 3 give the optimal solutions for the treatments:

Optimal harvesting strategies are identical for pricing 4/2 and 5/2 (treatment 1 and treatment 2). The optimal harvest can be reached by catching each time 6 predator fish and 10 prey fish during all periods of the sustainability phase.

Also, for pricing 4/1 and 5/1 (treatment 4 and treatment 5), the optimal harvesting strategy is identical with each other. The optimal harvest can be reached by catching each time 9 predator fish and 1 prey fish during all periods of the sustainability phase.

In our analysis, we also used the pricing 3/1 (treatment 3) where four different equilibrium-strategies in the stability phase yield same optimal revenues.

Table 4 summarizes the strategies in the sustainability phase (from t6 to t42) with regard to the optimal revenue depending on the treatment and, respectively, different prices/treatments of the system.

Table 4 Optimal strategies and optimal revenues during sustainability phase
Full size table

A graphical representation of system (1) showing the development of an optimal intervention is given by Fig. 3 with the values of the constants in the following way: a = 0.6; b = 0.002; c = 0.001 and e = 0.4.

Fig. 3
figure 3

Graphical representation of the optimal strategies for the development of both species for all treatments

Full size image

We want to find out whether different prices for small fish and big fish might cause different participant behaviour in the simulation game at hand.

4.3 Results

Results of the empirical analyses of the experiments performed at the Karl Franzens University of Graz/Austria, are based on 247 subjects. Each subject played the simulation game 10 times over all 42 periods. Each participant was given a financial reward depending on his/her success.

We observed that the goal to harvest with high revenues and keeping the final stocks as high as possible was fulfilled by nearly all participants of the experiment within all treatments. The participants of the experiment managed avoiding unsustainable fishing and prevented seafood stocks from collapsing while harvesting as much as possible.

For our analysis, we consider the best game of each subject. It can be shown that the order of subjects with respect to their success is fairly stable. We compare results of best-games with the mean of three-best-games results. The results perform perfectly well. The correlation is ρ = 0.965 at a significance level of 0.01.

Table 5 shows the number of participants and their revenues in percentage of the theoretical optima. Results indicate that the participants in all 5 treatments perform in quite a reasonable way by searching actively for the optimal orbit (Result 1).

Table 5 Results for all treatments with number of participants n, mean and median in percentage of the revenue optimum
Full size table

Participants performed best in treatment 3, where four equilibrium strategies yield an optimal outcome. For treatment 3 with py/px = 3/1 the optimal behaviour was significantly more often reached than for the other treatments: participants reached on average 77.6% of the optimal revenues. So, the number of more chances for success yields indeed higher revenues. Obviously, the number of possibilities for optimal strategies influences the results (Result 2).

It can be seen easily that subjects in treatments 1 and 2 (using optimal harvesting of 6 predator fish and 10 prey fish during the sustainability phase) performed significantly better than subjects in treatment 4 and 5, where the optimal harvesting in the sustainability phase means 9 predator fish and 1 prey fish. According to Table 5, the difference between pooled treatments characterized by py/px = 4/2 and 5/2 and pooled treatments characterized by py/px = 4/1 and 5/1 is significant according to a t test on mean equivalence.

Inspecting the data reveals that the significant lower outcome for pooled treatments 4/1 and 5/1 results from selecting sub-optimal interventions: in the experimental setting, harvesting prey (fishing small fish) was significantly more often used than optimal (Result 3).

When taking this result into account we have to regard that it is valid when the price of this species is rather low (as in treatment 4 and 5) in relation to the price of the predator (large fish).

It appears that subjects are more likely to fail in finding the optimal solution when predators are worth more compared to the price of prey. Cheap prey population was systematically overharvested, while more expensive predators were under-harvested.

Comparing revenues of games with predator focus with revenues of games with prey focus shows a significant difference between the two groups at a level of 0.03. Therefore, we can state the most interesting result that participants prefer to harvest prey population rather than predator population independently of the revenue. We are able to point out that subjects tend to value quantity (prey) more than price (predators) in terms of revenues (Result 4).

Therefore, we finally can conclude that participants more likely harvest cheaper prey populations rather than more valuable predator populations which might be caused by the availability factor. We can conclude that prices/revenues of harvested objects do not primarily influence participants’ behaviour and play a less important role than availability of the objects (Result 5).

5 Summary

First of all, we want to point out that the complexity of handling the system by the participants of the experiment was not only to manage a simulated environment with increasing and decreasing population numbers. We have to remember that the two harvesting instruments qx(t) and qy(t) for t = 1,…, T, were interdependent and each intervention did have an impact on the targeted population, but also on the other population and vice versa.

We have analysed the results of an experimental study of human decision-making behaviour in a simulation environment build upon a predator–prey ecology (Grabner et al. 2008). The revenues for games with high predator prices (compared to the price of the other species) yield lower revenues, whereas games with lower predator prices (compared to the price of the other species) yield significantly higher revenues. Keeping track of the fact that prey population is obviously far better available than predator population. We could call the results a fallacy of big and small fish. Availability seems to be an important factor when revenues are considered.

Literature on fallacies in general is growing fast (see e.g. Fintan and Costello 2009a, b; Rakow and Newell 2010), laboratory studies, however, are rarely used. Here, we have the impression that the availability fallacy might have to do with risk. The reason for this so-called big-and-small-fish fallacy could be the probability of excessive periods without any catches. In general cases, it may be a more general fear of the unknown. This could deliver an explanation for the fact why predators are systematically under harvested in spite of the growing intensity of the price signal provided.

Finally, we are able to state that in our simulation model, prices play a less important role than availability. The idea is that a risk aversion in this general sense psychologically induces people to attach greater weight to short-term considerations.

Moreover, utilizing a predator–prey approach allows going beyond comparative statics and shifts the research focus from analysis of the long-run equilibrium state towards analysis of transients. This is particularly important as any control intervention initiated by a decision-maker kicks a system away from reaching what was the system’s equilibrium state before the intervention. Hence, we take account of the fact that being in (or close to) an equilibrium state is rather the exception than the rule.

The results of the present study show for the first time that we are making systematic errors in corresponding economic situations, in our case clearly preferring quantity to quality. The control of a predator population is more difficult than the control of a prey population. In an economic context, we could transfer this outcome to the assumption that wage rates are harder to be controlled than employment rates. This misjudgement of the value of the objects can be interpreted as a fallacy of significant overestimation of available amounts.

The experimental setting of the predator–prey-simulation could provide insights to manage similar systems. The most recent U.N. climate report signals threat to oceans and points out that fishery managers will need to crack down on unsustainable fishing practices to prevent seafood stocks from collapsing (UN Climate Report 2019)