Abstract
We give a definition of finitary type theories that subsumes many examples of dependent type theories, such as variants of Martin–Löf type theory, simple type theories, first-order and higher-order logics, and homotopy type theory. We prove several general meta-theorems about finitary type theories: weakening, admissibility of substitution and instantiation of metavariables, derivability of presuppositions, uniqueness of typing, and inversion principles. We then give a second formulation of finitary type theories in which there are no explicit contexts. Instead, free variables are explicitly annotated with their types. We provide translations between finitary type theories with and without contexts, thereby showing that they have the same expressive power. The context-free type theory is implemented in the nucleus of the Andromeda 2 proof assistant.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We present a general definition of a class of dependent type theories which we call finitary type theories. In fact, we provide two variants of such type theories, with and without typing contexts, and show that they are equally expressive by providing translations between them. Our definition broadly follows the development of general type theories [6], but is specialized to serve as a formalism for implementation of a proof assistant. Indeed, the present paper is the theoretical foundation of the Andromeda 2 proof assistant, in which type theories are entirely defined by the user.
To be quite precise, we shall study syntactic presentations of type theories, in the sense that theories are seen as syntactic constructions, and the meta-theorems conquered by a frontal assault on abstract syntax. Even though this may not be the most fashionable approach to type theory, we were lead to it by our determination to understand precisely what we were implementing in Andromeda 2. We certainly expect that the syntactic presentations will match nicely with some of the modern semantic accounts of type theories, and that the usefulness of finitary type theories will transcend mere theoretical support for proof assistants.
We thus present our development of type theories in an elementary style, preferring concrete to abstract definitions and constructions, without compromising generality. In particular, this means that we first define “raw” terms, judgements, rules, and the like, and then proceed in stages to carve out the well-behaved fragment via predicates. Our motivations for this choice are fourfold. First, in practice type systems are defined in this fashion. Second, an elementary definition requires only very modest meta-mathematical foundations and lends itself to interpretation in various foundational systems. Third, by eschewing intermediate surrogates such as logical frameworks [23, 38] or quotient inductive-inductive types [2], the semantics of finitary type theories may be addressed directly, without recourse to the interpretation of such intermediates. And in any case, even the intermediates must eventually be syntactically presented if they are to be used at all. Fourth, the programming languages available to us are not sufficiently expressive to isolate the well-formed fragment of type theory in one fell swoop. They enable and insist on a more traditional approach, in which the input strings are converted to syntactic trees, and the type theoretic entities presented in their “raw” form, as values of inductively defined datatypes. The concrete nature of our constructions and meta-theorems then makes it possible to transcribe them to code in a straightforward fashion. Further discussion of alternative approaches is postponed to Sect. 7.
Our definition captures dependent type theories of Martin–Löf style, i.e. theories that strictly separate terms and types, have four judgement forms (for terms, types, type equations, and typed term equations), and hypothetical judgements standing in intuitionistic contexts. Among examples are the intensional and extensional Martin–Löf type theory, possibly with Tarski-style universes, homotopy type theory, Church’s simple type theory, simply typed \(\uplambda \)-calculi, and many others. A detailed presentation of first-order logic and Martin–Löf type theory as finitary type theories is available in [30, Appendix A], and [24, Appendix B] presents a finitary type theory for Harper’s Equational LF [21], and encodes Gödel’s System T in the logical framework. Counter-examples can be found just as easily: in cubical type theory the interval type is special, cohesive and linear type theories have non-intuitionistic contexts, polymorphic \(\uplambda \)-calculi quantify over all types, pure type systems organize the judgement forms in their own way, and so on.
1.1 Contributions
In Sect. 2 we give an account of dependent type theories that is close to how they are traditionally presented. A type theory should verify certain meta-theoretical properties: the constituent parts of any derivable judgement should be well-formed, substitution rules should be admissible, and each term should have a unique type. The definition of finitary type theories proceeds in stages. Each of the stages refines the notion of rule and type theory by specifying conditions of well-formedness. We start with the raw syntax (Sect. 2.1) of expressions and formal metavariables, out of which contexts, substitutions, and judgements are formed. Next we define raw rules (Sect. 2.3), a formal notion of what is commonly called “schematic inference rule”. We introduce the structural rules (Figs. 4, 5, 6) that are shared by all type theories, and define congruence rules (Definition 2.17). These rules are then collected into raw type theories (Definition 2.21). The definition of raw rules ensures the well-typedness of each constituent part of a raw rule, by requiring the derivability of the presuppositions of a rule. Next, we introduce finitary rules and finitary type theories (Sect. 2.4), whose rules form a well-founded order under which each rule is well-typed with respect to its predecessors. This way we rule out circularities in the derivations of well-typedness of rules, while the well-founded order provides an induction principle for finitary type theories. Finally, standard type theories are introduced (Definition 2.25) to enforce that each symbol is associated to a unique rule.
We prove the following meta-theorems about raw (Sect. 3.1), finitary (Sect. 3.2), and standard type theories (Sect. 3.3): admissibility of substitution and equality substitution (Theorem 3.8), admissibility of instantiation of metavariables (Theorem 3.13) and equality instantiation (Theorem 3.17), derivability of presuppositions (Theorem 3.18), admissibility of “economic” rules (Propositions 3.19, 3.20 and 3.22), inversion principles (Theorem 3.24), uniqueness of typing (Theorem 3.26).
The goal of Sect. 4 is the development of a context-free presentation of finitary type theories that can serve as foundation of the implementation of a proof assistant. The definition of finitary type theories in Sect. 2 is well-suited for the metatheoretic study of type theory, but does not directly lend itself to implementation. For instance, in keeping with traditional accounts of type theory, contexts are explicitly represented as lists.
In context-free type theories, the syntax of expressions (Sect. 4.1) is modified so that each free variable is annotated with its type \({\textsf{a}}^{A}\) rather than being assigned a type by a context. As the variables occurring in the type annotation A are also annotated, the dependency between variables is recorded. Judgements in context-free type theories thus do not carry an explicit context. Metavariables are treated analogously. To account for the possibility of proof-irrelevant rules like equality reflection, where not all of the variables used to derive the premises are recorded in the conclusion, we augment type and term equality judgements with assumption sets (Sect. 4.1.5). Intuitively, in a judgement \(\vdash A \equiv B \;{\textsf{by}}\;\alpha \), the assumption set \(\alpha \) contains the (annotated) variables that were used in the derivation of the equation but may not be amongst the free variables of A and B. The conversion rule of type theory allows the use of a judgemental equality to construct a term judgement. To ensure that assumption sets on equations are not lost as a result of conversion, we include conversion terms (Fig. 9).
Following the development of finitary type theories, we introduce raw context-free rules and type theories (Sect. 4.2). We proceed to define context-free finitary rules and type theories whose well-formedness is derivable with respect to a well-founded order (Definition 4.13), and standard theories (Definition 4.14).
Subsequently, we prove meta-theorems about context-free raw (Sect. 5.1), finitary (Sect. 5.2), and standard type theories (Sect. 5.3). The meta-theorems in this section are similar to those obtained for finitary type theories, with the exception of the meta-theorems specific to context-free type theories (Sect. 5.4). In particular, and contrary to finitary type theories, context-free raw type theories satisfy strengthening (Theorem 5.16). We further prove that conversion terms do not “get in the way” when working in context-free type theory (Theorem 5.17). The constructions underlying these meta-theorems are defined on judgements rather than derivations, and can thus be implemented effectively in a proof assistant for context-free type theories without storing derivation trees.
In Sect. 6, we establish a correspondence between type theories with and without contexts by constructing translations back and forth (Theorems 6.5 and 6.10).
2 Finitary Type Theories
Our treatment of type theories follows in essence the definition of general type theories carried out in [6], but is tailored to support algorithmic derivation checking in three respects: we limit ourselves to finitary symbols and rules, construe metavariables as a separate syntactic class rather than extensions of symbol signatures by fresh symbols, and take binding of variables to be a primitive operation on its own.
2.1 Raw Syntax
In this section we describe the raw syntax of fintary type theories, also known as pre-syntax. We operate at the level of abstract binding trees, i.e. we construe syntactic entities as syntax trees generated by grammatical rules in inductive fashion, and with all bound variables well-scoped. Of course, we still display such trees concretely as string of symbols, a custom that should not detract from the abstract view.
Raw expressions are formed without any typing discipline, but they have to be syntactically well-formed in the sense that free and bound variables must be well-scoped and that all symbols must be applied in accordance with the given signature. We shall explain the details of these conditions after a short word on notation.
We write \([X_1, \ldots , X_n]\) for a finite sequence and \(f = \langle X_1 {\mapsto }Y_1, \ldots , X_n {\mapsto }Y_n \rangle \) for a sequence of pairs \((X_i, Y_i)\) that represents a map taking each \(X_i\) to \(Y_i\). An alternative notation is \(\langle X_1 {:}Y_1, \ldots , X_n {:}Y_n \rangle \), and we may elide the parentheses \([{\cdots }]\) and \(\langle {\cdots } \rangle \). The domain of such f is the set \(\textsf {f} = \{X_1, \ldots , X_n\}\), and it is understood that all \(X_i\) are different from one another. Given \(X \not \in \textsf {f}\), the extension \(\langle f, X {\mapsto } Y \rangle \) of f by \(X \mapsto Y\) is the map
Given a list \(\ell = [\ell _1, \ldots , \ell _n]\), we write \(\ell _{(i)} = [\ell _1, \ldots , \ell _{i-1}]\) for its i-th initial segment. We use the same notation in other situations, for example \(f_{(i)} = \langle X_1 \mapsto Y_1, \ldots , X_{i-1} \mapsto Y_{i-1} \rangle \) for f as above.
2.1.1 Variables and Substitution
We distinguish notationally between the disjoint sets of free variables \({\textsf{a}}, {\textsf{b}}, {\textsf{c}}, \ldots \) and bound variables \(x, y, z, \ldots \), each of which are presumed to be available in unlimited supply. The free variables are scoped by variable contexts, while the bound ones are always captured by abstractions.
The strict separation of free and bound variables is fashioned after locally nameless syntax [14, 28], a common implementation technique of variable binding in which free variables are represented as names and the bound ones as de Bruijn indices [17]. In Sect. 4 the separation between free and bound variables will be even more pronounced, as only the former ones are annotated with types.
We write e[s/x] for the substitution of an expression s for a bound variable x in expression e and \(e[\vec {s}/\vec {x}]\) for the (parallel) substitution of \(s_1, \ldots , s_n\) for \(x_1, \ldots , x_n\), with the usual proviso about avoiding the capture of bound variables. In Sect. 3.1, when we prove admissibility of substitution, we shall also substitute expressions for free variables, which of course is written as \(e[s/{\textsf{a}}]\). Elsewhere we avoid such substitutions and only ever replace free variables by bound ones, in which case we write \(e[x/{\textsf{a}}]\). This typically happens when an expression with a free variable is used as part of a binder, such as the codomain of a \(\Pi \)-type or the body of a lambda. We take care to always keep bound variables well-scoped under binders.
2.1.2 Arities and Signatures
The raw expressions of a finitary type theory are formed using symbols and metavariables, which constitute two separate syntactic classes. Each symbol and metavariable has an associated arity, as follows.
The symbol arity \((c, [(c_1, n_1), \ldots , (c_k, n_k)])\) of a symbol \({\textsf{S}}\) tells us that
-
1.
the syntactic class of \({\textsf{S}}\) is \(c \in \{{\textsf{Ty}}, {\textsf{Tm}}\}\),
-
2.
\({\textsf{S}}\) accepts k arguments,
-
3.
the i-th argument must have syntactic class \(c_i \in \{{\textsf{Ty}}, {\textsf{Tm}}, {\textsf{EqTy}}, {\textsf{EqTm}}\}\) and binds \(n_i\) variables.
The syntactic classes \({\textsf{Ty}}\) and \({\textsf{Tm}}\) stand for type and term expressions, and \({\textsf{EqTy}}\) and \({\textsf{EqTm}}\) for type and term equations, respectively. For the time being the latter two are mere formalities, as the only expression of these syntactic classes are the dummy values \({\star }_{\textsf{Ty}}\) and \({\star }_{\textsf{Tm}}\). However, in Sect. 4 we will introduce genuine expressions of syntactic classes \({\textsf{EqTy}}\) and \({\textsf{EqTm}}\).
Example 2.1
The arity of a type constant such as \({\textsf{bool}}\) is \(({\textsf{Ty}}, [])\), the arity of a binary term operation such as \(+\) is \(({\textsf{Tm}}, [({\textsf{Tm}}, 0), ({\textsf{Tm}}, 0)])\). The arity of a quantifier such as the dependent product \(\Uppi \) is \(({\textsf{Ty}}, [({\textsf{Ty}}, 0), ({\textsf{Ty}}, 1)])\) because it is a type former taking two type arguments, with the second one binding one variable, and the arity of a dependent function \(\uplambda \) is \(({\textsf{Tm}}, [({\textsf{Ty}}, 0), ({\textsf{Ty}}, 1), ({\textsf{Tm}}, 1)])\).
The metavariable arity associated to a metavariable \({\textsf{M}}\) is a pair (c, n), where the syntactic class \(c \in \{{\textsf{Ty}}, {\textsf{Tm}}, {\textsf{EqTy}}, {\textsf{EqTm}}\}\) indicates whether \({\textsf{M}}\) is respectively a type, term, type equality, or term equality metavariable, and n is the number of term arguments it accepts. The metavariables of syntactic classes \({\textsf{Ty}}\) and \({\textsf{Tm}}\) are the object metavariables, and can be used to form expressions. The metavariables of syntactic classes \({\textsf{EqTy}}\) and \({\textsf{EqTm}}\) are the equality metavariables, and do not participate in formation of expressions. We introduce them to streamline several definitions, and to have a way of referring to equational premises in Sect. 4. The information about metavariable arities is collected in a metavariable context, cf. Sect. 2.1.4.
A metavariable \({\textsf{M}}\) of arity (c, n) could be construed as a symbol of arity
This approach is taken in [6], but we keep metavariables and symbols separate because they play different roles, especially in context-free type theories in Sect. 4.
The information about symbol and metavariable arities is respectively collected in a symbol signature and a metavariable signature, which map symbols and metavariables to their arities. When discussing syntax, it is understood that such signature have been given, even if we do not mention them explicitly. In particular, whenever expressions are formed in a given metavariable context, as described below, it is assumed that the metavariable signature is the one induced by the context.
2.1.3 Raw Expressions
The raw syntactic constituents of a finitary type theory, with respect to given symbol and metavariable signatures, are outlined in Fig. 1. In this section we discuss the top part of the figure, which involves the syntax of term and type expressions, and arguments.
A type expression, or just a type, is formed by an application \({\textsf{S}}(e_1, \ldots , e_n)\) of a type symbol to arguments, or an application \({\textsf{M}}(t_1, \ldots , t_n)\) of a type metavariable to term expressions. A term expression, or just a term, is a free variable \({\textsf{a}}\), a bound variable x, an application \({\textsf{S}}(e_1, \ldots , e_n)\) of a term symbol to arguments, or an application \({\textsf{M}}(t_1, \ldots , t_n)\) of a term metavariable to term expressions.
An argument is a type or a term expression, the dummy argument \({\star }_{\textsf{Ty}}\) of syntactic class \({\textsf{EqTy}}\), or the dummy argument \({\star }_{\textsf{Tm}}\) of syntactic class \({\textsf{EqTm}}\). We write just \({\star }\) when it is clear which of the two should be used. Another kind of argument is an abstraction \(\{x\} e\), which binds x in e. An iterated abstraction \(\{x_1\} \{x_2\} \cdots \{x_n\} e\) is abbreviated as \(\{\vec {x}\} e\). Note that abstraction is a primitive syntactic operation, and that it provides no typing information about x.
Example 2.2
In our notation a dependent product is written as \(\Uppi (A, \{x\} B)\), and a fully annotated function as \(\uplambda (A, \{x\} B, \{x\} e)\). The fact that x ranges over A is not part of the raw syntax and will be specified later by an inference rule.
In all cases, in order for an expression to be well-formed, the arities of symbols and metavariables must be respected. If \({\textsf{S}}\) has arity \((c, [(c_1, n_1), \ldots , (c_k, n_k)])\), then it must be applied to k arguments \(e_1, \ldots , e_k\), where each \(e_i\) is of the form \(\{x_1\} \cdots \{x_{n_i}\} e_i'\) with \(e_i'\) a non-abstracted argument of syntactic class \(c_i\). Similarly, a metavariable \({\textsf{M}}\) of arity (c, n) must be applied to n term expressions. When a symbol \({\textsf{S}}\) takes no arguments, we write the corresponding expression as \({\textsf{S}}\) rather than \({\textsf{S}}()\), and similarly for metavariables.
As is usual, expressions which differ only in the choice of names of bound variables are considered syntactically equal, e.g., \(\{x\} {\textsf{S}}({\textsf{a}}, x)\) and \(\{y\} {\textsf{S}}({\textsf{a}}, y)\) are syntactically equal and we may write \((\{x\} {\textsf{S}}({\textsf{a}}, x)) = (\{y\} {\textsf{S}}({\textsf{a}}, y))\).
For future reference we define in Fig. 2 the sets of free variable, bound variable, and metavariable occurrences, where we write set comprehension as \(\{\hspace{-2.37pt}\vert \cdots \vert \hspace{-2.37pt}\}\) in order to distinguish it from abstraction. A syntactic entity is said to be closed if no free variables occur in it.
2.1.4 Judgements and Boundaries
The bottom part of Fig. 1 displays the syntax of judgements and boundaries, which we discuss next.
There are four judgement forms: “\(A\;{\textsf{type}}\)” asserts that A is a type; “t : A” that t is a term of type A; “\(A \equiv B \;{\textsf{by}}\;{\star }_{\textsf{Ty}}\)” that types A and B are equal; and “\(s \equiv t: A \;{\textsf{by}}\;{\star }_{\textsf{Tm}}\)” that terms s and t of type A are equal. We may shorten the equational forms to “\(A \equiv B\)” and “\(s \equiv t: A\)” in this section, as the only possible choice for \(\;{\textsf{by}}\;\) is \({\star }\).
Less familiar, but equally fundamental, is the notion of a boundary. Whereas a judgement is an assertion, a boundary is a question to be answered, a promise to be fulfilled, or a goal to be accomplished: “\(\Box \;{\textsf{type}}\)” asks that a type be constructed; “\(\Box : A\)” that the type A be inhabited; and “\(A \equiv B \;{\textsf{by}}\;\Box \)” and “\(s \equiv t: A \;{\textsf{by}}\;\Box \)” that equations be proved.
An abstracted judgement has the form  , where A is a type expression and
, where A is a type expression and  is a (possibly abstracted) judgement. The variable x is bound in
is a (possibly abstracted) judgement. The variable x is bound in  but not in A. Thus in general an abstracted judgement has the form
but not in A. Thus in general an abstracted judgement has the form

where  is a judgement thesis, i.e. an expression taking one of the four (non-abstracted) judgement forms. We may abbreviate such an abstraction as
is a judgement thesis, i.e. an expression taking one of the four (non-abstracted) judgement forms. We may abbreviate such an abstraction as  . Analogously, an abstracted boundary has the form
. Analogously, an abstracted boundary has the form

where  is a boundary thesis, i.e. it takes one of the four (non-abstracted) boundary forms. The reason for introducing abstracted judgements and boundaries will be explained shortly.
is a boundary thesis, i.e. it takes one of the four (non-abstracted) boundary forms. The reason for introducing abstracted judgements and boundaries will be explained shortly.
An abstracted boundary has the associated metavariable arity

where \(c \in \{{\textsf{Ty}}, {\textsf{Tm}}, {\textsf{EqTy}}, {\textsf{EqTm}}\}\) is the syntactic class of  . Similarly, the associated metavariable arity of an argument is
. Similarly, the associated metavariable arity of an argument is
where \(c \in \{{\textsf{Ty}}, {\textsf{Tm}}\}\) is the syntactic class of the (non-abstracted) expression e.
The placeholder \(\Box \) in a boundary  may be filled with an argument e, called the head, to give a judgement
may be filled with an argument e, called the head, to give a judgement  , provided that the arities of
, provided that the arities of  and e match. Because equations are proof irrelevant, their placeholders can be filled uniquely with (suitably abstracted) dummy value \({\star }\). Filling is summarized in Fig. 3, where we also include notation for filling an object boundary with an equation that results in the corresponding equation. The figure rigorously explicates the dummy values, but we usually omit them. Filling may be inverted: given an abstracted judgement
and e match. Because equations are proof irrelevant, their placeholders can be filled uniquely with (suitably abstracted) dummy value \({\star }\). Filling is summarized in Fig. 3, where we also include notation for filling an object boundary with an equation that results in the corresponding equation. The figure rigorously explicates the dummy values, but we usually omit them. Filling may be inverted: given an abstracted judgement  there is a unique abstracted boundary
there is a unique abstracted boundary  and a unique argument e such that
and a unique argument e such that  .
.
Example 2.3
If the symbols \({\textsf{A}}\) and \({\textsf{Id}}\) have arities
respectively, then the boundaries
may be filled with heads \(\{x\} \{y\} x\) and \(\{x\} \{y\} {\star }\) to yield abstracted judgements
Names of bound variables are immaterial, we would still get the same judgement if we filled the left-hand boundary with \(\{u\} \{v\} u\) or \(\{y\} \{x\} y\), but not with \(\{x\} \{y\} y\).
Information about available metavariables is collected by a metavariable context, which is a finite list  , also construed as a map, assigning to each metavariable \({\textsf{M}}_i\) a boundary
, also construed as a map, assigning to each metavariable \({\textsf{M}}_i\) a boundary  . In Sect. 2.3, the assigned boundaries will assign the typing of metavariable, while at the level of raw syntax they determine metavariable arities. That is, \(\Theta \) assigns the metavariable arity
. In Sect. 2.3, the assigned boundaries will assign the typing of metavariable, while at the level of raw syntax they determine metavariable arities. That is, \(\Theta \) assigns the metavariable arity  to \({\textsf{M}}_i\).
to \({\textsf{M}}_i\).
A metavariable context  may be restricted to a metavariable context
may be restricted to a metavariable context  .
.
The metavariable context \(\Theta \) is syntactically well formed when each  is a syntactically well-formed boundary over \(\Sigma \) and the metavariable signature induced by \(\Theta _{(i)}\). In addition each
is a syntactically well-formed boundary over \(\Sigma \) and the metavariable signature induced by \(\Theta _{(i)}\). In addition each  must be closed, i.e. contain no free variables.
must be closed, i.e. contain no free variables.
A variable context \(\Gamma = [{\textsf{a}}_1 {:}A_1, \ldots , {\textsf{a}}_n {:}A_n]\) over a metavariable context \(\Theta \) is a finite list of pairs written as \({\textsf{a}}_i {:}A_i\). It is considered syntactically valid when the variables \({\textsf{a}}_1, \ldots , {\textsf{a}}_n\) are all distinct, and for each i the type expression \(A_i\) is valid with respect to the signature and the metavariable arities assigned by \(\Theta \), and the free variables occurring in \(A_i\) are among \({\textsf{a}}_1, \ldots , {\textsf{a}}_{i-1}\). A variable context \(\Gamma \) yields a finite map, also denoted \(\Gamma \), defined by \(\Gamma ({\textsf{a}}_i) = A_i\).
A context is a pair \(\Theta ; \Gamma \) consisting of a metavariable context \(\Theta \) and a variable context \(\Gamma \) over \(\Theta \). A syntactic entity is considered syntactically valid over a signature and a context \(\Theta ; \Gamma \) when all symbol and metavariable applications respect the assigned arities, the free variables are among \(\vert \Gamma \vert \), and all bound variables are properly abstracted. It goes without saying that we always require all syntactic entities to be valid in this sense.
A (hypothetical) judgement has the form

It differs from traditional notion of a judgement in a non-essential way, which nevertheless requires an explanation. First, the context of a hypothetical judgement

provides information about metavariables, not just the free variables. Second, the variables are split between the context \({\textsf{a}}_1 {:}A_1, \ldots , {\textsf{a}}_n {:}A_n\) on the left of \(\vdash \), and the abstraction \(\{x_1 {:}B_1\} \cdots \{x_m {:}B_m\}\) on the right. It is useful to think of the former as the global hypotheses that interact with other judgements, and the latter as local to the judgement. We could of course delegate the metavariable context to be part of the signature as is done in [6], and revert to the more familiar form

by joining the variable context and the abstraction, but we would still have to carry the metavariable information in the signature, and would lose the ability to explicitly mark the split between the global and the local parts. The split will be especially important in Sect. 4, where the context will be removed, but the abstraction kept.
Hypothetical boundaries are formed in the same fashion, as

The intended meaning is that  is a well-typed boundary in context \(\Theta ; \Gamma \).
is a well-typed boundary in context \(\Theta ; \Gamma \).
2.1.5 Metavariable Instantiations
Metavariables are slots that can be instantiated with arguments. Suppose  is a metavariable context over a symbol signature \(\Sigma \). An instantiation of \(\Theta \) over a context \(\Xi ; \Gamma \) is a seqence \(I = \langle {\textsf{M}}_1 {\mapsto }e_1, \ldots , {\textsf{M}}_k {\mapsto }e_k \rangle \), representing a map that takes each \({\textsf{M}}_i\) to an argument \(e_i\) over \(\Xi ; \Gamma \) such that
is a metavariable context over a symbol signature \(\Sigma \). An instantiation of \(\Theta \) over a context \(\Xi ; \Gamma \) is a seqence \(I = \langle {\textsf{M}}_1 {\mapsto }e_1, \ldots , {\textsf{M}}_k {\mapsto }e_k \rangle \), representing a map that takes each \({\textsf{M}}_i\) to an argument \(e_i\) over \(\Xi ; \Gamma \) such that  .
.
An instantiation \(I = \langle {\textsf{M}}_1 {\mapsto }e_1, \ldots , {\textsf{M}}_k {\mapsto }e_k \rangle \) of \(\Theta \) may be restricted to an instantiation \(I_{(i)} = \langle {\textsf{M}}_1 {\mapsto }e_1, \ldots , {\textsf{M}}_{i-1} {\mapsto }e_{i-1} \rangle \) of \(\Theta _{(i)}\).
An instantiation I of \(\Theta \) over \(\Xi ; \Gamma \) acts on a term- or type-expression u over \(\Theta ; \Delta \) to give an expression \(I_{*} u\) in which the metavariables are replaced by expressions, as follows:
Here, the symbol \({\textsf{S}}\) and metavariable \({\textsf{M}}_i\) take n and \(n_i\) arguments respectively. The instantiated expression \(I_{*} u\) is valid for \(\Xi ; \Gamma , I_{*} \Delta \). Abstracted judgements and boundaries may be instantiated too:

and by imagining that \(I_{*} \Box = \Box \), the reader can tell how to instantiate a boundary. Finally, a hypothetical judgement  may be instantiated to
may be instantiated to  , and similarly for a hypothetical boundary.
, and similarly for a hypothetical boundary.
2.2 Deductive Systems
We briefly recall the notions of a deductive system, derivability, and a derivation tree; see for example [1, 37] for background material. A (finitary) closure rule on a set S is a pair \(([p_1, \ldots , p_n], q)\), also displayed as

where \(\{p_1, \ldots , p_n\} \subseteq S\) are the premises and \(q \in S\) is the conclusion. Let \({\textsf{Clos}}(S)\) be the set of all closure rules on S.
A deductive system (also called a closure system) on a set S is a family of closure rules \(C: R \rightarrow {\textsf{Clos}}(S)\), indexed by a set R of rule names. A set \(D \subseteq S\) is said to be deductively closed for C when, for all \(i \in R\), if \(C_i = ([p_1, \ldots , p_n], q)\) and \(\{p_1, \ldots , p_n\} \subseteq D\), then \(q \in D\). The associated closure operator is the map  which takes \(D \subseteq S\) to the least deductively closed supserset \(\overline{D}\) of D, which exists by Tarski’s fixed-point theorem [36]. We say that \(q \in S\) is derivable from hypotheses \(H \subseteq S\) when \(q \in \overline{H}\), and that it is derivable in C when \(q \in \overline{\emptyset }\).
which takes \(D \subseteq S\) to the least deductively closed supserset \(\overline{D}\) of D, which exists by Tarski’s fixed-point theorem [36]. We say that \(q \in S\) is derivable from hypotheses \(H \subseteq S\) when \(q \in \overline{H}\), and that it is derivable in C when \(q \in \overline{\emptyset }\).
A closure rule \(([p_1, \ldots , p_n], q)\) is admissible for C when \(\{p_1, \ldots , p_k\} \subseteq \overline{\emptyset }\) implies \(q \in \overline{\emptyset }\). Note that adjoining an admissible closure rule to a closure system may change its associated closure operator. In contrast, nothing changes if we adjoin a derivable closure rule, which is a rule \(([p_1, \ldots , p_n], q)\) such that \(q \in \overline{\{p_1, \ldots , p_n\}}\).
Derivability is witnessed by well-founded trees, which are constructed as follows. For each \(q \in S\) let \({\textsf{Der}}_{C}(q)\) be generated inductively by the clause:
-
for every \(i \in R\), if \(C_i = ([p_1, \ldots , p_n], q)\) and \(t_j \in {\textsf{Der}}_{C}(p_j)\) for all \(j = 1, \ldots , n\), then \({\textsf{der}}_i(t_1, \ldots , t_n) \in {\textsf{Der}}_{C}(q)\), where \({\textsf{der}}\) is a formal tag (a “constructor”).
The elements of \({\textsf{Der}}_{C}(q)\) are derivation trees with conclusion q. Indeed, we may view \({\textsf{der}}_i(t_1, \ldots , t_n)\) as a tree with the root labeled by i and the subtrees \(t_1, \ldots , t_n\). A leaf is a tree of the form \({\textsf{der}}_j()\), which arises when the corresponding closure rule \(C_j\) has no premises.
Proposition 2.4
Given a closure system C on S, an element \(q \in S\) is derivable in C if, and only if, there exists a derivation tree over C whose conclusion is q.
Proof
The claim is that \(T = \{q \in S \mid \exists t \in {\textsf{Der}}_{C}(q) \,.\, \top \}\) coincides with \(\overline{C}\). The inclusion \(\overline{C} \subseteq T\) holds because T is deductively closed. The reverse inclusion \(T \subseteq \overline{C}\) is established by induction on derivation trees. \(\square \)
We remark that allowing infinitary closure rules brings with it the need for the axiom of choice, for it is unclear how to prove that T is deductively closed without the aid of choice.
It is evident that derivability and derivation trees are monotone in all arguments: if \(S \subseteq S'\), \(R \subseteq R'\), and the closure system \(C': R' \rightarrow {\textsf{Clos}}(S')\) restricts to \(C: R \rightarrow {\textsf{Clos}}(S)\), then any \(q \in S\) derivable in C is also derivable in \(C'\) as an element of \(S'\). Moreover, any derivation tree in \({\textsf{Der}}_{C}(q)\) may be construed as a derivation tree in \({\textsf{Der}}_{C'}(q)\).
Henceforth we shall consider solely deductive systems on the set of hypothetical judgements and boundaries. Because we shall vary the deductive system, it is useful to write  when
when  , and similarly for
, and similarly for  .
.
2.3 Raw Rules and Type Theories
A type theory in its basic form is a collection of closure rules. Some closure rules are specified directly, but many are presented by inference rules—templates whose instantiations yield the closure rules. We deal with the raw syntactic structure of such rules first.
Definition 2.5
A raw rule over a symbol signature \(\Sigma \) is a hypothetical judgement over \(\Sigma \) of the form  . We notate such a raw rule as
. We notate such a raw rule as

The elements of \(\Theta \) are the premises and  is the conclusion. We say that the rule is an object rule when
is the conclusion. We say that the rule is an object rule when  is a type or a term judgement, and an equality rule when
is a type or a term judgement, and an equality rule when  is an equality judgement.
is an equality judgement.
Defining inference rules as hypothetical judgements with empty contexts and empty abstractions permits in many situations uniform treatment of rules and judgements. Note that the premises and the conclusion may not contain any free variables, and that the conclusion must be non-abstracted. Neither condition impedes expressivity of raw rules, because free variables and abstractions may be promoted to premises.
Example 2.6
To help the readers’ intuition, let us see how Definition 2.5 captures a traditional inference rule, such as product formation

The use of \({\textsf{A}}\) and \({\textsf{B}}\) in the premises reveals that their arities are \(({\textsf{Ty}}, 0)\), and \(({\textsf{Ty}}, 1)\), respectively. In fact, the premises assign boundaries to metavariables: each premise is a boundary filled with a particular head, namely a generically applied metavariable. If we pull out the metavariables from the heads of premises, the assignment becomes explicit:

This is just a different way of writing the raw rule
Example 2.7
We may translate raw rules back to their traditional form by filling the heads with metavariables applied to the variables they abstracts over. For example, the reader may readily verify that the raw rule
corresponds to the lambda introduction rule of dependent type theory that is traditionally written as

Metavariables occurring as arguments to symbols, such as \(\{x\} {\textsf{B}} (x)\) in the conclusion of the previous example, are often abstracted and immediately applied. We record this pattern in the following definition.
Definition 2.8
The generic application \(\widehat{{\textsf{M}}}\) of the metavariable \({\textsf{M}}\) with associated boundary  is defined as:
is defined as:
-
1.
\(\widehat{M} = \{x_1\} \cdots \{x_k\}\, {\textsf{M}}(x_1, \ldots , x_k)\) if
 and \(c \in \{{\textsf{Ty}}, {\textsf{Tm}}\}\),
and \(c \in \{{\textsf{Ty}}, {\textsf{Tm}}\}\), -
2.
\(\widehat{M} = \{x_1\} \cdots \{x_k\}\, {\star }\) if
 and \(c \in \{{\textsf{EqTy}}, {\textsf{EqTm}}\}\).
and \(c \in \{{\textsf{EqTy}}, {\textsf{EqTm}}\}\).
Using generic metavariable applications, we can write the conclusion of Tm-\(\uplambda \) more concisely as \(\vdash {\uplambda (\widehat{{\textsf{A}}}, \widehat{{\textsf{B}}}, \widehat{{\textsf{b}}})}: \Uppi (\widehat{{\textsf{A}}}, \widehat{{\textsf{B}}})\), where we note that \(\widehat{{\textsf{A}}} = {\textsf{A}}\).
Example 2.9
An informal presentation of type theory might specify the result type of applying \({\textsf{f}}\) to \({\textsf{a}}\) as “\({\textsf{B}}\) with \({\textsf{a}}\) substituted for x”, i.e. \({\textsf{B}}[{\textsf{a}}/x]\). Since substitution is not part of the syntax of raw type theories but defined as a meta-operation, such a formulation would be nonsensical in our setting. The raw rule for application with full typing annotations on \({\textsf{app}}\) can be written as follows.

Instead of using substitution, we define the type of the application as the metavariable application \({\textsf{B}}({\textsf{a}})\), which is syntactically well-formed since \({\textsf{ar}}({\textsf{B}}) = ({\textsf{Ty}}, 1)\) in the above rule.
Example 2.10
Raw rules can also describe how to derive equality judgements. For instance, the raw rule
corresponds to the equality reflection rule of extensional type theory that is traditionally written as

For everyone’s benefit, we shall display raw rules in traditional form, but use Definition 2.5 when formalities demand so.
Example 2.11
A rule that combines several aspects of the previous examples is \(\beta \)-reduction.

Just like in Tm-app, we use metavariable application \({\textsf{b}}({\textsf{a}})\) to describe the result of the \(\beta \)-reduction. Once the raw rule is instantiated into a closure rule, this application will be “activated” into a substitution.
It may be mystifying that there is no variable context \(\Gamma \) in a raw rule, for is it not the case that rules may be applied in arbitrary contexts? Indeed, closure rules have contexts, but raw rules do not because they are just templates. The context appears once we instantiate the template, as follows.
Definition 2.12
An instantiation of a raw rule  over context \(\Theta ; \Gamma \) is an instantiation \(I = \langle {\textsf{M}}_1 {\mapsto }e_1, \ldots , {\textsf{M}}_n {\mapsto }e_n \rangle \) of its premises over \(\Theta ; \Gamma \). The associated closure rule \(I_{*} R\) is \(([p_1, \ldots , p_n, q], r)\) where \(p_i\) is
over context \(\Theta ; \Gamma \) is an instantiation \(I = \langle {\textsf{M}}_1 {\mapsto }e_1, \ldots , {\textsf{M}}_n {\mapsto }e_n \rangle \) of its premises over \(\Theta ; \Gamma \). The associated closure rule \(I_{*} R\) is \(([p_1, \ldots , p_n, q], r)\) where \(p_i\) is  , q is
, q is  , and r is
, and r is  .
.
We included among the premises the well-formedness of the instantiated boundary  , so that the conclusion is well-formed. We need the premise as an induction hypothesis in the proof of Theorem 3.18. In Sect. 3.2 we shall formulate well-formedness conditions that allow us to drop the boundary premise.
, so that the conclusion is well-formed. We need the premise as an induction hypothesis in the proof of Theorem 3.18. In Sect. 3.2 we shall formulate well-formedness conditions that allow us to drop the boundary premise.
Of special interest are the rules that give type-theoretic meaning to primitive symbols. To define them, we need the boundary analogue of raw rules.
Definition 2.13
A raw rule-boundary over a symbol signature \(\Sigma \) is a hypothetical boundary over \(\Sigma \) of the form  . We notate such a raw rule-boundary as
. We notate such a raw rule-boundary as

The elements of \(\Theta \) are the premises and  is the conclusion boundary. We say that the rule-boundary is an object rule-boundary when
is the conclusion boundary. We say that the rule-boundary is an object rule-boundary when  is a type or a term boundary, and an equality rule-boundary when
is a type or a term boundary, and an equality rule-boundary when  is an equality boundary.
is an equality boundary.
Here is how a rule-boundary generates a rule associated to a symbol.
Definition 2.14
Given a raw object rule-boundary

over \(\Sigma \), the associated symbol arity is  , where \(c \in \{{\textsf{Ty}}, {\textsf{Tm}}\}\) is the syntactic class of
, where \(c \in \{{\textsf{Ty}}, {\textsf{Tm}}\}\) is the syntactic class of  . The associated symbol rule for \({\textsf{S}}\not \in \vert \Sigma \vert \) is the raw rule
. The associated symbol rule for \({\textsf{S}}\not \in \vert \Sigma \vert \) is the raw rule

over the extended signature  , where \(\widehat{{\textsf{M}}}_i\) is the generic application of the metavariable \({\textsf{M}}_i\) with associated boundary
, where \(\widehat{{\textsf{M}}}_i\) is the generic application of the metavariable \({\textsf{M}}_i\) with associated boundary  . A raw rule is said to be a symbol rule if it is the associated symbol rule for some symbol \({\textsf{S}}\).
. A raw rule is said to be a symbol rule if it is the associated symbol rule for some symbol \({\textsf{S}}\).
The above definition is motivated by the observation that the head of the conclusion of a symbol rule has a particular shape, which can be calculated from its rule-boundary. The definition thus only requires the specification of the necessary data. Instead of describing how to construct a symbol rule given a rule boundary and symbol, we could have defined them directly as raw rules with conclusion heads of a particular form, but that would be less economical, since we would have to write out the conclusion in full, and we would still have to verify that the supplied head is the expected one. In examples we shall continue to display symbol rules in their traditional form.
Example 2.15
According to Definition 2.14, the symbol rule for \(\Uppi \) is generated by the rule-boundary

Indeed, the associated symbol rule for \(\Uppi \) is

We allow equational premises in object rules. For example,

is a valid symbol rule, assuming \({\textsf{Id}}\) and \({\textsf{refl}}\) have their usual arities.
We also record the analogous construction of an equality rule from a given equality rule-boundary.
Definition 2.16
Given an equality rule-boundary

the associated equality rule is

We next formulate the rules that all type theories share, starting with the most nitty-gritty ones, the congruence rules.
Definition 2.17
The congruence rules associated with a raw object rule R

are closure rules, for any
of the form

In case of a term equation at type B, the congruence rule has the additional premise \(\Theta ; \Gamma \vdash I_{*} B \equiv J_{*} B\), which ensures that the right-hand side of the conclusion \(J_{*} e\) has type \(I_{*} B\). Having the equation available as a premise allows us to use it in the inductive proof of Theorem 3.18. In Sect. 3.2 we show that the rule without the premises is derivable under suitable conditions.
Example 2.18
The congruence rule associated with the product formation rule from Example 2.6 is

Next we have formation and congruence rules for the metavariables. As metavariables are like symbols whose arguments are terms, it is not suprising that their rules are quite similar to symbol rules.
Definition 2.19
Given a context \(\Theta ; \Gamma \) over \(\Sigma \) with  , and
, and  , the metavariable rules for \({\textsf{M}}_k\) are the closure rules of the form
, the metavariable rules for \({\textsf{M}}_k\) are the closure rules of the form

where \(\vec {x} = (x_1, \ldots , x_m)\) and \(\vec {t} = (t_1, \ldots , t_m)\). Recall that \(\vec {t}_{(j)}\) stands for \([t_1, \ldots , t_{j-1}]\). In the second line of premises, we thus substitute the preceding term arguments \(t_1, \ldots , t_{j-1}\) for the bound variables \(x_1, \ldots , x_{j-1}\) in each type \(A_j\). The last premise ensures the well-formedness of the boundary of the conclusion, just like the definition of the closure rule associated to a raw rule (Def. 2.12).
Furthermore, if  is an object boundary, then the metavariable congruence rules for \({\textsf{M}}_k\) are the closure rules of the form
is an object boundary, then the metavariable congruence rules for \({\textsf{M}}_k\) are the closure rules of the form

where \(\vec {s} = (s_1, \ldots , s_m)\) and \(\vec {t} = (t_1, \ldots , t_m)\).
Example 2.20
If we collect the metavariables \({\textsf{A}}\) and \({\textsf{B}}\) introduced by the premises of the product formation rule from Example 2.6 into a metavariable context \(\Theta = [{\textsf{A}} \,{:}\, \Box \;{\textsf{type}}, {\textsf{B}} \,{:}\, \{x {:}{\textsf{A}}\}\; \Box \;{\textsf{type}}]\), we can apply the metavariable rule TT-Meta to derive that \({\textsf{B}}({\textsf{a}})\) is a well-formed type under the context \(\Theta ; {\textsf{a}} \,{:}\, {\textsf{A}}\).

We are finally ready to give a definition of type theory which is sufficient for explaining derivability.
Definition 2.21
A raw type theory T over a signature \(\Sigma \) is a family of raw rules over \(\Sigma \), called the specific rules of T. The associated deductive system of T consists of:
-
1.
the structural rules over \(\Sigma \):
-
2.
the instantiations of the specific rules of T (Definition 2.12);
-
3.
for each specific object rule of T, the instantiations of the associated congruence rule (Definition 2.17).
We write  when
when  is derivable with respect to the deductive system associated to T, and similarly for
is derivable with respect to the deductive system associated to T, and similarly for  .
.
Several remarks are in order regarding the above definition and the rules in Figs. 4, 5 and 6:
-
1.
It is assumed throughout that all the entities involved are syntactically valid, i.e. that arities are respected and variables are well-scoped.
-
2.
The metavariable rules TT-Meta and TT-Meta-Congr are exactly as in Definition 2.19.
-
3.
The rules TT-Var, TT-Meta, and TT-Abstr contain side-conditions, such as \({\textsf{a}} \in \vert \Gamma \vert \) and
 . For purely aesthetic reasons, these are written where premises ought to stand. For example, the correct way to read TT-Abstr is: “For all \(\Theta \), \(\Gamma \), A, \({\textsf{a}}\),
. For purely aesthetic reasons, these are written where premises ought to stand. For example, the correct way to read TT-Abstr is: “For all \(\Theta \), \(\Gamma \), A, \({\textsf{a}}\),  , if \({\textsf{a}} \not \in \vert \Gamma \vert \), then there is a closure rule with premises \(\Theta ; \Gamma \vdash A\;{\textsf{type}}\) and
, if \({\textsf{a}} \not \in \vert \Gamma \vert \), then there is a closure rule with premises \(\Theta ; \Gamma \vdash A\;{\textsf{type}}\) and  , and the conclusion
, and the conclusion  .”
.” -
4.
The structural rules impose no well-typedness conditions on contexts. Instead, Fig. 7 provides two auxiliary judgement forms, “\(\vdash \Theta \;{\textsf{mctx}}\)” and “\(\Theta \vdash \Gamma \;{\textsf{vctx}}\)”, stating that \(\Theta \) is a well-typed metavariable context, and \(\Gamma \) a well-typed variable context over \(\Theta \), respectively. These will be used as necessary. Note that imposing the additional premise \(\Theta ; \Gamma \vdash \Gamma ({\textsf{a}})\;{\textsf{type}}\) in TT-Var (where \(\Gamma ({\textsf{a}})\) is the type assigned to \({\textsf{a}}\) by \(\Gamma \)) would not ensure well-formednes of \(\Gamma \), as not all variables need be accessed in a derivation. Requiring that TT-Meta check the boundary of the metavariable is similarly ineffective.
-
5.
We shall show in Sect. 3.1 that substitution rules (Fig. 8) are admissible.
This may be a good moment to record the difference between derivability and admissibility.
Definition 2.22
Consider a raw theory T and a raw rule R, both over a symbol signature \(\Sigma \):
-
1.
R is derivable in T when R qua judgement has a derivation in T.
-
2.
R is admissible in T when, for every instantiation I of R, if the premises of \(I_{*} R\) are derivable in T then so is its conclusion.
2.4 Finitary Rules and Type Theories
Raw rules are syntactically well-behaved: the premises and the conclusion are syntactically well-formed entities, and all metavariables, free variable and bound variables well-scoped. Nevertheless, a raw rule may be ill-formed for type-theoretic reasons, a deficiency rectified by the next definition.
Recall that a well-founded order on a set I is an irreflexive and transitive relation \(\prec \) satisfying, for each \(S \subseteq I\),
The logical reading of the above condition is an induction principle: in order to show \(\forall x \in I \,.\, \phi (x)\) one has to prove, for any \(i \in I\), that \(\phi (i)\) holds assuming that \(\phi (j)\) does for all \(j \prec i\).
Definition 2.23
Given a raw theory T over a symbol signature \(\Sigma \), a raw rule  over \(\Sigma \) is finitary over T when \(\vdash _T \Theta \;{\textsf{mctx}}\) and
over \(\Sigma \) is finitary over T when \(\vdash _T \Theta \;{\textsf{mctx}}\) and  . Similarly, a raw rule-boundary
. Similarly, a raw rule-boundary  is finitary when \(\vdash _T \Theta \;{\textsf{mctx}}\) and
is finitary when \(\vdash _T \Theta \;{\textsf{mctx}}\) and  .
.
A finitary type theory is a raw type theory \((R_i)_{i \in I}\) for which there exists a well-founded order \((I, {\prec })\) such that each \(R_i\) is finitary over \((R_j)_{j \prec i}\).
The type theories with context in this paper correspond loosely to the fragment of general type theories [6] where the arities of symbols and rules are restricted to be finite, while general type theories allow the premises to be families of arbitrary size. While raw type theories are already subject to this restriction, we reserve the name finitary for the “good” rules and theories, that are well-formed according to the above definition.
Examples of rules that exhibit problematic circularities which are ruled out by the finitary requirements can be found in the section on “Acceptable type theories” in [6]; see also Sect. 6 of loc. cit. for a thorough discussion of the merits of well-founded presentations of type theories.
Example 2.24
We take stock by considering several examples of rules. The rule

is not raw because it introduces the metavariable \({\textsf{t}}\) twice, and hence gives rise to a syntactically ill-formed metavariable context. Assuming \(\Uppi \) has arity \(({\textsf{Ty}}, [({\textsf{Ty}},0), ({\textsf{Ty}},1)])\), consider the rules

The rule Ty-\(\Uppi \)-Short is not raw because it fails to introduce the metavariable \({\textsf{A}}\), while Ty-\(\Uppi \)-Long is finitary over any theory. The rule

is raw when the symbols \({\textsf{bool}}\), \({\textsf{nat}}\), and \({\textsf{succ}}\) respectively have arities \(({\textsf{Ty}}, [])\), \(({\textsf{Ty}}, [])\), and \(({\textsf{Tm}}, [({\textsf{Tm}},0)])\). Whether it is also finitary depends on a theory. For instance, given the raw rules

the rule Succ-Congr-Typo is not finitary over the first three rules, but is finitary over all four of them. As a last example, given the symbol \({\textsf{Id}}\) with arity \(({\textsf{Ty}}, [({\textsf{Ty}},0), ({\textsf{Tm}},0), ({\textsf{Tm}},0)])\), the rules

are all raw, both Ty-Id and Ty-Id-Typo are finitary over an empty theory, while Eq-Reflect is finitary over a theory containing Ty-Id. The rule Ty-Id is a symbol rule, but Ty-Id-Typo is not.
Could we have folded Definition 2.5 of raw rules and Definition 2.23 of finitary rules into a single definition? Not easily, as that would generate a loop: finitary rules refer to theories and derivability, which refer to closure rules, which are generated from raw rules. Without a doubt something is to be learned by transforming the cyclic dependency to an inductive definition, but we do not attempt to do so here.
A finitary type theory is fairly well behaved from a type-theoretic point of view, but can still suffer from unusual finitary rules, such as Ty-Id-Typo from Example 2.24, which looks like a spelling mistake. We thus impose a further restriction by requiring that every rule be either a symbol rule or an equality rule.
Definition 2.25
A finitary type theory is standard if its specific object rules are symbol rules, and each symbol has precisely one associated rule.
A standard type theory and its symbol signature may be built iteratively as follows:
-
1.
The empty theory is standard over the empty signature.
-
2.
Given a standard type theory T over \(\Sigma \), and a rule-boundary

finitary for T:
-
If
 is an object boundary, and \({\textsf{S}}\not \in \vert \Sigma \vert \), then T extended with the associated symbol rule
is an object boundary, and \({\textsf{S}}\not \in \vert \Sigma \vert \), then T extended with the associated symbol rule 
is standard over the extended signature \(\langle \Sigma , {\textsf{S}}{\mapsto }\alpha \rangle \), where \(\alpha \) is the symbol arity associated with the rule-boundary.
-
If
 is an equation boundary, then T extended with the equality rule
is an equation boundary, then T extended with the equality rule 
is standard over \(\Sigma \).
-
A more elaborate well-founded induction may be employed when a theory features infinitely many rules, such as an infinite succession of universes.
3 Meta-theorems
We put our definitions to the test by proving meta-theorems which stipulate desirable structural properties of type theories. The theorems are all rather standard and expected. Nevertheless, we prove them to verify that our definition of type theories is sensible, and to provide general-purpose meta-theorems that apply in a wide range of situations.
Making the statements precise in full generality has not always been trivial. We therefore include them here, together with statements of auxiliary lemmas, to give the reader an overview of the technique, but mostly relegate the rather lengthy induction proofs to the appendix. We shall continue to do so in subsequent sections.
3.1 Meta-theorems About Raw Theories
A renaming of an expression u is an injective map \(\rho \) with domain \({\textsf{mv}}(u) \cup {\textsf{fv}}(u)\) that takes metavariables to metavariables and free variables to free variables. The renaming acts on u to yield an expression \(\rho _{*} u\) by replacing each occurrence of a metavariable \({\textsf{M}}\) and a free variable \({\textsf{a}}\) with \(\rho ({\textsf{M}})\) and \(\rho ({\textsf{a}})\), respectively. We similarly define renamings of contexts, judgements, and boundaries.
Proposition 3.1
(Renaming) If a raw type theory derives a judgement or a boundary, then it also derives its renamings.
Proof
Let \(\rho \) be a renaming of a derivable judgement  . We show that
. We show that  is derivable by induction on the derivation. The case of boundaries is similar.
is derivable by induction on the derivation. The case of boundaries is similar.
Most cases only require a direct application of the induction hypotheses to the premises. The only somewhat interesting case is TT-Abstr,

As \({\textsf{a}} \not \in \vert \Gamma \vert \), and thus \({\textsf{a}} \not \in \vert \rho \vert \), we may extend \(\rho \) to a renaming \(\rho ' = \langle \rho , {\textsf{a}} {\mapsto } {\textsf{b}} \rangle \), where \({\textsf{b}}\) is such that \({\textsf{b}} \not \in \vert \rho _{*} \Gamma \vert \). By induction hypothesis for the first premise, \(\rho _{*} \Theta ; \rho _{*} \Gamma \vdash \rho _{*} A\;{\textsf{type}}\) is derivable. We apply the induction hypothesis for the second premise to \(\rho '\) and obtain  , which equals
, which equals  . Thus, we may conclude by TT-Abstr,
. Thus, we may conclude by TT-Abstr,

\(\square \)
Proposition 3.2
(Weakening) For a raw type theory:
-
1.
If
 and \({\textsf{a}} \not \in \vert \Gamma _1, \Gamma _2\vert \) then
and \({\textsf{a}} \not \in \vert \Gamma _1, \Gamma _2\vert \) then  .
. -
2.
If
 and \({\textsf{M}}\not \in \vert \Theta _1, \Theta _2\vert \) then
and \({\textsf{M}}\not \in \vert \Theta _1, \Theta _2\vert \) then  .
.
An analogous statement holds for boundaries.
Proof
Once again we proceed by induction on the derivation of the judgement in a straightforward manner, where the case TT-Abstr relies on renaming (Proposition 3.1) to ensure that \({\textsf{a}}\) remains fresh in the subderivations. \(\square \)
In several places we shall require well-formedness of contexts, a useful consequence of which we record first.
Proposition 3.3
If a raw type theory derives \(\vdash \Theta \;{\textsf{mctx}}\) then it derives \(\Theta ; [\,]\vdash \Theta ({\textsf{M}})\) for every \({\textsf{M}}\in \vert \Theta \vert \); and if it derives \(\Theta \vdash \Gamma \;{\textsf{vctx}}\), then it derives \(\Theta ; \Gamma \vdash \Gamma ({\textsf{a}})\;{\textsf{type}}\) for every \({\textsf{a}} \in \vert \Gamma \vert \).
Proof
By induction on the derivation of \(\vdash \Theta \;{\textsf{mctx}}\) and \(\Theta \vdash \Gamma \;{\textsf{vctx}}\), respectively, followed by weakening. \(\square \)
3.1.1 Admissibility of Substitution
In this section we prove that in a raw type theory substitution rules are derivable closure rules in the sense of Sect. 2.2, and that substitution preserves judgemental equality.
Lemma 3.4
If a raw type theory derives  and \(\Theta ; \Gamma \vdash t: A\) then it derives
and \(\Theta ; \Gamma \vdash t: A\) then it derives  .
.
Proof
See the proof on Page 64. \(\square \)
Lemma 3.5
If a raw type theory derives  and \(\Theta ; \Gamma \vdash t: A\) then it derives
and \(\Theta ; \Gamma \vdash t: A\) then it derives  .
.
Proof
The base cases immediately reduce to the previous lemma. The case of TT-Bdry-Abstr is similar to the case of TT-Abstr in the previous lemma. \(\square \)
Lemma 3.6
In a raw type theory the following closure rules are admissible:

Proof
See the proof on Page 66. \(\square \)
The next lemma claims that substitution preserves equality, but is a bit finicky to state. Given terms s and t, and an object judgement  , define
, define  by
by

That is,  descends into abstractions by substituting s for \({\textsf{a}}\) in the types, and distributes types and terms over the equation \(s \equiv t\).
descends into abstractions by substituting s for \({\textsf{a}}\) in the types, and distributes types and terms over the equation \(s \equiv t\).
Lemma 3.7
If a raw type theory derives
then it derives
-
1.
 ,
, -
2.
 , and
, and -
3.
 if
if  is an object judgement.
is an object judgement.
Proof
See the proof on Page 66. \(\square \)
Theorem 3.8
(Admissibility of substitution) In a raw type theory, the closure rules from Fig. 8 are admissible.
Proof
We already established admissibility of TT-Subst, TT-Bdry-Subst, and TT-Conv-Abstr in Lemma 3.6. Both TT-Subst-EqTy and TT-Subst-EqTm are seen to be admissible the same way: invert the abstraction and apply Lemma 3.7 to derive the desired conclusion. \(\square \)
We provide two more lemmas that allow us to combine substitutions and judegmental equalities more flexibly.
Lemma 3.9
Suppose a raw type theory derives
-
1.
If it derives
$$\begin{aligned} \Theta ; \Gamma \vdash \{x {:}A\} \{\vec {y} {:}\vec {B}\} \; C \equiv D \quad \text {and}\quad \Theta ; \Gamma \vdash \{x {:}A\} \{\vec {y} {:}\vec {B}\} \; D\;{\textsf{type}} \end{aligned}$$then it derives \( \Theta ; \Gamma \vdash \{\vec {y} {:}\vec {B}[s/x]\} \; C[s/x] \equiv D[t/x]. \)
-
2.
If it derives
$$\begin{aligned} \Theta ; \Gamma \vdash \{x {:}A\} \{\vec {y} {:}\vec {B}\} \; u \equiv v: C \quad \text {and}\quad \Theta ; \Gamma \vdash \{x {:}A\} \{\vec {y} {:}\vec {B}\} \; v: C \end{aligned}$$then it derives \( \Theta ; \Gamma \vdash \{\vec {y} {:}\vec {B}[s/x]\} \; u[s/x] \equiv v[t/x]: C[s/x] \).
Proof
See the proof on Page 69. \(\square \)
Lemma 3.10
Suppose a raw type theory derives, for \(i = 1, \ldots , n\),
If it derives an object judgement  then it derives
then it derives

Proof
See the proof on Page 69. \(\square \)
3.1.2 Admissibility of Instantiations
We next turn to admissibility of instantiations, i.e. preservation of derivability under instantiation of metavariables by heads of derivable judgements.
Definition 3.11
An instantiation \(I = \langle {\textsf{M}}_1 {\mapsto }e_1, \ldots , {\textsf{M}}_n {\mapsto }e_n \rangle \) of a metavariable context  over \(\Theta ; \Gamma \) is derivable when
over \(\Theta ; \Gamma \) is derivable when  is derivable for \(k = 1, \ldots , n\).
is derivable for \(k = 1, \ldots , n\).
Lemma 3.12
In a raw type theory, let I be a derivable instantiation of \(\Xi \) over context \(\Theta ; \Gamma \). If  is derivable then so is
is derivable then so is  , and similarly for boundaries.
, and similarly for boundaries.
Proof
See the proof on Page 70. \(\square \)
Theorem 3.13
(Admissibility of instantiation) In a raw type theory, let I be a derivable instantiation of \(\Xi \) over context \(\Theta ; \Gamma \). If  is derivable then so is
is derivable then so is  , and similarly for boundaries.
, and similarly for boundaries.
Proof
Apply Lemma 3.12 with empty \(\Delta \). \(\square \)
We next show that, under favorable conditions, instantiating by judgementally equal instantiations leads to judgemental equality. To make the claim precise, define the notation  by
by

and say that instantiations
of  over \(\Theta ; \Gamma \) are judgementally equal when, for \(k = 1, \ldots , n\), if
over \(\Theta ; \Gamma \) are judgementally equal when, for \(k = 1, \ldots , n\), if  is an object boundary then
is an object boundary then  is derivable.
is derivable.
Lemma 3.14
In a raw type theory, consider derivable instantiations I and J of  over \(\Theta ; \Gamma \) which are judgementally equal. Suppose that \(\vdash \Xi \;{\textsf{mctx}}\) and \(\Theta \vdash \Gamma \;{\textsf{vctx}}\), and that
over \(\Theta ; \Gamma \) which are judgementally equal. Suppose that \(\vdash \Xi \;{\textsf{mctx}}\) and \(\Theta \vdash \Gamma \;{\textsf{vctx}}\), and that  is derivable for \(i = 1, \ldots , n\), and additionally that, for all \({\textsf{a}} \in \vert \Delta \vert \) with \(\Delta ({\textsf{a}}) = A\), so are
is derivable for \(i = 1, \ldots , n\), and additionally that, for all \({\textsf{a}} \in \vert \Delta \vert \) with \(\Delta ({\textsf{a}}) = A\), so are
If  is derivable then so are
is derivable then so are



Proof
See the proof on Page 71. \(\square \)
Lemma 3.14 imposes conditions on the instantiations and the context which can be reduced to the more familiar assumption of well-typedness of the context, using Lemma 3.14 itself, as follows.
Lemma 3.15
In a raw type theory, consider  such that \(\vdash \Xi \;{\textsf{mctx}}\), and derivable instantiations
such that \(\vdash \Xi \;{\textsf{mctx}}\), and derivable instantiations
of \(\Xi \) over \(\Theta ; \Gamma \) which are judgementally equal. Suppose further that \(\Theta \vdash \Gamma \;{\textsf{vctx}}\) and  for \(i = 1, \ldots , n\). If \(\Theta \vdash (\Gamma , \Delta )\;{\textsf{vctx}}\), then for all \({\textsf{a}} \in \vert \Delta \vert \) with \(\Delta ({\textsf{a}}) = A\):
for \(i = 1, \ldots , n\). If \(\Theta \vdash (\Gamma , \Delta )\;{\textsf{vctx}}\), then for all \({\textsf{a}} \in \vert \Delta \vert \) with \(\Delta ({\textsf{a}}) = A\):
Proof
See the proof on Page 74. \(\square \)
Lemma 3.16
In a raw type theory, consider  such that \(\vdash \Xi \;{\textsf{mctx}}\), and derivable instantiations
such that \(\vdash \Xi \;{\textsf{mctx}}\), and derivable instantiations
of \(\Xi \) over \(\Theta ; \Gamma \) which are judgementally equal. Suppose that \(\Theta \vdash \Gamma \;{\textsf{vctx}}\). Then  is derivable for \(i = 1, \ldots , n\).
is derivable for \(i = 1, \ldots , n\).
Proof
See the proof on Page 75. \(\square \)
Finally, the lemmas can be assembled into an admissibility theorem about judgementally equal derivable instantiations.
Theorem 3.17
(Admissibility of instantiation equality) In a raw type theory, consider derivable instantiations I and J of \(\Xi \) over \(\Theta ; \Gamma \) which are judgementally equal. Suppose that \(\vdash \Xi \;{\textsf{mctx}}\) and \(\Theta \vdash \Gamma \;{\textsf{vctx}}\). If an object judgement  is derivable then so is
is derivable then so is  .
.
Proof
Lemma 3.14 applies with empty \(\Delta \) because the additional precondition for I and J is guaranteed by Lemma 3.16. \(\square \)
Our last meta-theorem about raw type theories shows that whenever a judgement is derivable, so are its presuppositions, i.e., its boundary is well-formed.
Theorem 3.18
(Presuppositivity) If a raw type theory derives \(\vdash \Theta \;{\textsf{mctx}}\), \(\Theta \vdash \Gamma \;{\textsf{vctx}}\), and  then it derives
then it derives  .
.
Proof
See the proof on Page 76. \(\square \)
3.2 Meta-theorems About Finitary Type Theories
Several closure rules contain premises which at first sight seem extraneous, in particular the boundary premises in rule instantiations (Definition 2.12) and the object premises in a congruence rule (Definition 2.17). While these are needed for raw rules, they ought to be removable for finitary rules, which already have well-formed boundaries. We show that this is indeed the case by providing economic versions of the rules, which are admissible in finitary type theories. We also show that the metavariable rules (Definition 2.19) have economic versions that are valid in well-formed metavariable contexts, such as the metavariable contexts of finitary rules. Finitary type theories thus allow us to relegate the verification of boundary premises to the definition of the rules, when finitary conditions are checked once and for all, instead of deriving boundary premises for each instance.
Proposition 3.19
(Economic version of Definition 2.12) Let R be the raw rule  with
with  such that
such that  is derivable, in particular R may be finitary. Then for any instantiation \(I = [{\textsf{M}}_1 {\mapsto }e_1, \ldots , {\textsf{M}}_n {\mapsto }e_n]\) over \(\Theta ; \Gamma \), the following closure rule is admissible:
is derivable, in particular R may be finitary. Then for any instantiation \(I = [{\textsf{M}}_1 {\mapsto }e_1, \ldots , {\textsf{M}}_n {\mapsto }e_n]\) over \(\Theta ; \Gamma \), the following closure rule is admissible:

Proof
To apply \(I_{*} R\), derive the missing premise  via Theorem 3.13. \(\square \)
via Theorem 3.13. \(\square \)
Proposition 3.20
(Economic version of Definition 2.19) If a raw type theory derives \(\vdash \Theta \;{\textsf{mctx}}\) and \(\Theta \vdash \Gamma \;{\textsf{vctx}}\) with  , the following closure rules are admissible:
, the following closure rules are admissible:

Proof
See the proof on Page 77. \(\square \)
Lemma 3.21
In a raw type theory, suppose  , and consider judgementally equal derivable instantiations I, J of \(\Xi \) over \(\Theta ; \Gamma \). If
, and consider judgementally equal derivable instantiations I, J of \(\Xi \) over \(\Theta ; \Gamma \). If  is derivable then so is
is derivable then so is  .
.
Proof
See the proof on Page 78. \(\square \)
Proposition 3.22
(Economic version of Definition 2.17) In a finitary type theory, consider one of its object rules R

Given instantiations of its premises,
over \(\Theta ; \Gamma \) such that \(\vdash \Theta \;{\textsf{mctx}}\) and \(\Theta \vdash \Gamma \;{\textsf{vctx}}\), the following closure rule is admissible:

Proof
See the proof on Page 78. \(\square \)
3.3 Meta-theorems About Standard Type Theories
We next investigate to what extent a derivation of a derivable judgement can be reconstructed from the judgement itself. Firstly, a term expression holds enough information to recover a candidate for its type, since a standard type theory associates a unique rule, and thus a unique (type) boundary, to each (term) symbol.
Definition 3.23
Let T be a standard type theory. The natural type \(\tau _{\Theta ; \Gamma }(t)\) of a term expression t with respect to a context \(\Theta ; \Gamma \) is defined by:

We prove an inversion principle that recovers the “stump” of a derivation of a derivable object judgement.
Theorem 3.24
(Inversion) If a standard type theory derives an object judgement then there is a derivation of this judgement which concludes with precisely one of the following rules:
-
1.
the variable rule TT-Var,
-
2.
the metavariable rule TT-Meta,
-
3.
an instantiation of a symbol rule,
-
4.
the abstraction rule TT-Abstr,
-
5.
the term conversion rule TT-Conv-Tm of the form

where \(\tau _{\Theta ;\Gamma }(t) \ne A\).
Proof
See the proof on Page 79. \(\square \)
We may keep applying the theorem to all the object premises of a stump to recover the proof-relevant part of the derivation. The remaining proof-irrelevant parts are the equational premises. The inversion theorem yields further desirable meta-theoretic properties of standard type theories.
Corollary 3.25
If a standard type theory derives \(\Theta ; \Gamma \vdash t: A\) then it derives \(\Theta ; \Gamma \vdash \tau _{\Theta ; \Gamma }(t) \equiv A\).
Proof
By inversion, \(\tau _{\Theta ; \Gamma }(t) = A\) or we obtain a derivation of \(\vdash \tau _{\Theta ; \Gamma }(t) \equiv A\). \(\square \)
Theorem 3.26
(Uniqueness of typing) For a standard type theory:
-
1.
If \(\Theta ; \Gamma \vdash t: A\) and \(\Theta ; \Gamma \vdash t: B\) then \(\Theta ; \Gamma \vdash A \equiv B\).
-
2.
If \(\vdash \Theta \;{\textsf{mctx}}\) and \(\Theta \vdash \Gamma \;{\textsf{vctx}}\) and \(\Theta ; \Gamma \vdash s \equiv t: A\) and \(\Theta ; \Gamma \vdash s \equiv t: B\) then \(\Theta ; \Gamma \vdash A \equiv B\).
Proof
The first statement holds because A and B are both judegmentally equal to the natural type of t by Corollary 3.25. The second statement reduces to the first one because the presuppositions \(\Theta ; \Gamma \vdash t: A\) and \(\Theta ; \Gamma \vdash t: B\) are derivable by Theorem 3.18. \(\square \)
4 Context-Free Finitary Type Theories
In the forward-chaining style, characteristic of LCF-style theorem provers, which Andromeda 2 is designed to be, a judgement is not construed by reducing a goal to subgoals, but as a value of an abstract datatype, and built by applying an abstract datatype constructor to previously derived judgements. What should such a constructor do when its arguments have mismatching variable contexts? It can try to combine them if possible, or require that the user make sure ahead of time that they match. As was already noted by Geuvers et al. in the context of pure type systems [19], it is best to sidestep the whole issue by dispensing with contexts altogether. In the present section we give a second account of finitary type theories, this time without context and with free variables explicitly annotated with their types. These are actually implemented in the Andromeda 2 trusted nucleus.
Our formulation of context-free finitary type theories is akin to the \(\Gamma _\infty \) formalism for pure type systems [19]. We would like to replace judgements of the form “ ” with just “
” with just “ ”. In traditional accounts of logic, as well as in \(\Gamma _\infty \), this is accomplished by explicit type annotations of free variables: rather than having \({\textsf{a}}: A\) in the variable context, each occurrence of \({\textsf{a}}\) is annotated with its type as \({\textsf{a}}^{A}\).
”. In traditional accounts of logic, as well as in \(\Gamma _\infty \), this is accomplished by explicit type annotations of free variables: rather than having \({\textsf{a}}: A\) in the variable context, each occurrence of \({\textsf{a}}\) is annotated with its type as \({\textsf{a}}^{A}\).
We use the same idea, although we have to overcome several technical complications, of which the most challenging one is the lack of strengthening, which is the principle stating that if  is derivable and \({\textsf{a}}\) does not appear in \(\Delta \) and
is derivable and \({\textsf{a}}\) does not appear in \(\Delta \) and  , then
, then  is derivable. An example of a rule that breaks strengthening for finitary type theories is equality reflection from Example 2.10,
is derivable. An example of a rule that breaks strengthening for finitary type theories is equality reflection from Example 2.10,

Because the conclusion elides the metavariable \({\textsf{p}}\), it will not record the fact that a variable may have been used in the derivation of the fourth premise. Consequently, we cannot tell what variables ought to occur in the context just by looking at the judgement thesis. As it turns out, variables elided by derivations of equations are the only culprit, and the situation can be rectified by modifying equality judgements so that they carry additional information about usage of variables. In the present section we show how this is accomplished by revisiting the definition of type theories from Sect. 2 and making the appropriate modifications.
4.1 Raw Syntax of Context-Free Type Theories
Apart from removing the variable context and annotating free variables with type expressions, we make three further modifications to the raw syntax: we remove metavariable contexts, and instead annotate metavariables with boundaries; we introduce assumption sets that keep track of variables used in equality derivations; and we introduce explicit conversions.
4.1.1 Free and Bound Variables
The bound variables \(x, y, z, \ldots \) are as before, for example they could be de Bruijn indices, whereas the free variables are annotated explicitly with type expressions. More precisely, given a set of names \({\textsf{a}}, {\textsf{b}}, {\textsf{c}}, \ldots \) a free variable takes the form \({\textsf{a}}^{A}\) where A is a type expression, cf. Sect. 4.1.3. Two such variables \({\textsf{a}}^{A}\) and \({\textsf{b}}^B\) are considered syntactically equal when the symbols \({\textsf{a}}\) and \({\textsf{b}}\) are the same and the type expressions A and B are syntactically equal. Thus it is quite possible to have variables \({\textsf{a}}^{A}\) and \({\textsf{a}}^{B}\) which are different even though A and B are judegmentally equal. In an implementation it may be a good idea to prevent such extravaganza by generating fresh symbols so that each one receives precisely one annotation.
Similarly, metavariables are tagged with boundaries, where again  and
and  are considered equal when both the symbols \({\textsf{M}}\) and \({\textsf{N}}\) are equal and the boundaries
are considered equal when both the symbols \({\textsf{M}}\) and \({\textsf{N}}\) are equal and the boundaries  and
and  are syntactically identical.
are syntactically identical.
4.1.2 Arities and Signatures
Arities of symbols and metavariables are as in Sect. 2.1.2. We keep symbol signatures but eliminate metavariable signature, as their arities are induced by annotations.
4.1.3 Raw Expressions
The raw expressions of a context-free type theory are built over a symbol signature, as summarized in the top part of Fig. 9.
A type expression is either a type symbol \({\textsf{S}}\) applied to arguments \(e_1, \ldots , e_n\), or a metavariable  applied to term expressions \(t_1, \ldots , t_n\) where
applied to term expressions \(t_1, \ldots , t_n\) where  .
.
The syntax of term expressions differs from the one in Fig. 1 in two ways. First, we annotate free variables with type expressions and metavariables with boundaries, as was already discussed, where it should be noted that in an annotation A of \({\textsf{a}}^{A}\) or  of
of  there may be further free and metavariables, which are also annotated, and so on. We require that a boundary annotation
there may be further free and metavariables, which are also annotated, and so on. We require that a boundary annotation  be closed with respect to free variables (metavariables may occur). Furthermore, a type annotation A must not contain any “exposed” bound variables, i.e. A should be syntactically valid on its own, without having to appear under an abstraction. Second, we introduce the conversion terms “\(\upkappa (t, \alpha )\)”, which will serve to record the variables used to derive the equality along which t has been converted. The context-free conversion rules CF-Conv-Tm and CF-Conv-EqTm in Sect. 4.2 keep track of the assumptions occurring in derivations of type equalities (along which we convert), by recording them as conversion terms.
be closed with respect to free variables (metavariables may occur). Furthermore, a type annotation A must not contain any “exposed” bound variables, i.e. A should be syntactically valid on its own, without having to appear under an abstraction. Second, we introduce the conversion terms “\(\upkappa (t, \alpha )\)”, which will serve to record the variables used to derive the equality along which t has been converted. The context-free conversion rules CF-Conv-Tm and CF-Conv-EqTm in Sect. 4.2 keep track of the assumptions occurring in derivations of type equalities (along which we convert), by recording them as conversion terms.
The expressions of syntactic classes \({\textsf{EqTy}}\) and \({\textsf{EqTm}}\) are the assumption sets, which are finite sets of free and bound variables, and metavariables. As we are already using the curly braces for abstraction, we write finite set comprehension as \(\{\hspace{-2.37pt}\vert \cdots \vert \hspace{-2.37pt}\}\). Assumption sets record the variables and metavariables that are used in a derivation of an equality judgement but may not appear in the boundary of the conclusion.
We ought to be a bit careful about occurrences of variables, since the free variables may occur in variable annotations, and the metavariables in boundary annotations. Figure 10, the context-free analogue of Fig. 2, shows the definitions of free, bound and metavariable occurrences. Note the difference between \({\textsf{fv}}_0(e)\), which collects only the free variable occurrences not appearing in a type annotation, and \({\textsf{fv}}(e)\) which collects them all. Exposed bound variables need not be collected from annotations, as they cannot appear there.
The collection of all free, bound and metavariables occurring in an expression is its assumption set \({\textsf{asm}}(e)\). Sometimes we write \({\textsf{asm}}(e_1, \ldots , e_n)\) for the union \(\bigcup _i {\textsf{asm}}(e_i)\).
4.1.4 Substitution and Syntactic Equality
We must review substitution and syntactic equality, because they are affected by annotations, assumption sets, and conversion terms.
There are two kinds of substitutions. An abstraction \(e[x/{\textsf{a}}^{A}]\) transforms the free variable \({\textsf{a}}^{A}\) in e to a bound variable x, whereas a substitution e[s/x] replaces the bound variable x with the term s. These are shown in Fig. 11. Note that an abstraction \(e[x/{\textsf{a}}^{A}]\) is only valid when \({\textsf{a}}^{A}\) does not appear in any type annotation in e, \({\textsf{a}}^{A} \notin {\textsf{fvt}}(e)\), because type annotations cannot refer to bound variables. Consequently, abstraction of several variables must be carried out in the reverse order of their dependencies. We abbreviate a series of abstractions \(((e[x_1/{\textsf{a}}_{1}^{A_1}]) \cdots ) [x_n/{\textsf{a}}_{n}^{A_n}]\) as \(e[x_1/{\textsf{a}}_{1}^{A_1}, \ldots , x_n/{\textsf{a}}_{n}^{A_n}]\) or just \(e[\vec {x}/\vec {{\textsf{a}}}_n^{A_n}]\). Similarly, a series of substitutions \(((e[s_1/x_1]) \cdots )[s_n/x_n]\) is written \(e[s_1/x_1, \ldots , s_n/x_n]\) or just \(e[\vec {s}/\vec {x}]\).
Syntactic equality is treated in a standard way, we only have to keep in mind the fact that symbols are considered syntactically equal if the bare symbols are equal and their annotations are equal. More interestingly, since conversion terms and assumption sets carry proof-irrelevant information, they should be ignored in certain situations. For this purpose, define the erasure \(\lfloor e \rfloor \) to be the raw expression e with the assumption sets and conversion terms removed:

The mapping \(e \mapsto \lfloor e \rfloor \) takes the context-free raw syntax of Fig. 9 to the type-theoretic raw syntax of Fig. 1 where the variables \({\textsf{a}}^{A}\) and the metavariables  are construed as atomic symbols, i.e. their annotations are part of the symbol name.
are construed as atomic symbols, i.e. their annotations are part of the symbol name.
4.1.5 Judgements and Boundaries
The lower part of Fig. 9 summarizes the syntax of context-free judgements and boundaries. Apart from not having contexts, type judgements “\(A\;{\textsf{type}}\)” and term judgements “t : A” are as before. Equality judgements are modified to carry assumption sets: a type equality takes the form “\(A \equiv B \;{\textsf{by}}\;\alpha \)” and a term equality “\(s \equiv t: A \;{\textsf{by}}\;\alpha \)”.
Boundaries do not change, except of course that they have no contexts. The head of a boundary is filled like before, except that assumption sets are used instead of dummy values, see Fig. 12.
Free-variable occurrences in judgements are defined as follows, with  defined analogously to \({\textsf{fvt}}(e)\) in Fig. 12:
defined analogously to \({\textsf{fvt}}(e)\) in Fig. 12:

We trust the reader can emulate the above definition to define the set  of metavariable occurrences in a judgement
of metavariable occurrences in a judgement  , as well as occurrences of free and metavariables in boundaries.
, as well as occurrences of free and metavariables in boundaries.
4.1.6 Metavariable Instantiations
Next, let us rethink how metavariable instantiations work in the presence of the newly introduced syntactic constructs. As before an instantiation is a sequence, representing a map,

such that  and
and  , for each \(i = 1, \ldots , n\). As in Sect. 2.1.5, I acts on an expression u, provided that \({\textsf{mv}}(u) \subseteq \vert {}I\vert \), by replacing metavariables with the corresponding expressions, see Fig. 13. Note that the action of I on a free variable changes the identity of the variable by acting on its typing annotation.
, for each \(i = 1, \ldots , n\). As in Sect. 2.1.5, I acts on an expression u, provided that \({\textsf{mv}}(u) \subseteq \vert {}I\vert \), by replacing metavariables with the corresponding expressions, see Fig. 13. Note that the action of I on a free variable changes the identity of the variable by acting on its typing annotation.
4.2 Context-Free Rules and Type Theories
In this section we adapt the notions of raw and finitary rules and type theories to the context-free setting. We shall be rather telegraphic about it, as the changes are straightforward and require little discussion.
Definition 4.1
A context-free raw rule R over a symbol signature \(\Sigma \) has the form

where the premises  and the conclusion
and the conclusion  are closed and syntactically valid over \(\Sigma \),
are closed and syntactically valid over \(\Sigma \),  for every \(i = 1, \ldots , n\), and
for every \(i = 1, \ldots , n\), and  . We say that R is an object rule when
. We say that R is an object rule when  is a type or a term judgement, and an equality rule when
is a type or a term judgement, and an equality rule when  is an equality judgement.
is an equality judgement.
The condition  ensures that the conclusion of an instantiation of a raw rule records all uses of variables. We shall need it in the proof of Theorem 6.5.
ensures that the conclusion of an instantiation of a raw rule records all uses of variables. We shall need it in the proof of Theorem 6.5.
Example 4.2
The context-free version of equality reflection from Example 2.10 is
which is quite unreadable. We indulge in eliding annotations on any variable that is already typed by a premise or a hypothesis, and write just

As there are no contexts, we could remove \(\vdash \) too, but we leave it there out of habit. Note how the assumption set in the conclusion must record dependence on \({\textsf{p}}\), or else it would violate the assumption set condition of Definition 4.1.
When formulating equality closure rules we face a choice of assumption sets. For example, what should \(\gamma \) be in the transitivity rule

Its intended purpose is to record any assumptions used in the premises but not already recorded by A and C, which suggests the requirement
If we replace \(\subseteq \) with \(=\) we also avoid any extraneous asumptions, which leads to the following definition.
Definition 4.3
In a closure rule  whose conclusion is an equality judgement, \(\alpha \) is suitable when
whose conclusion is an equality judgement, \(\alpha \) is suitable when  .
.
Provided that  , we may always take the minimal suitable assumption set
, we may always take the minimal suitable assumption set  . We do not insist on minimality, even though an implementation might make an effort to keep the assumption sets small, because minimality is not preserved by instantiations, whereas suitability is. We shall indicate the suitability requirement in an equality closure rule by stating it as the side condition “\(\alpha \text { suitable}\)”.
. We do not insist on minimality, even though an implementation might make an effort to keep the assumption sets small, because minimality is not preserved by instantiations, whereas suitability is. We shall indicate the suitability requirement in an equality closure rule by stating it as the side condition “\(\alpha \text { suitable}\)”.
Definition 4.4
A context-free raw rule-boundary over a symbol signature \(\Sigma \) has the form

where the boundaries  and
and  are closed and syntactically valid over \(\Sigma \),
are closed and syntactically valid over \(\Sigma \),  for every \(i = 1, \ldots , n\), and
for every \(i = 1, \ldots , n\), and  . We say that R is an object rule-boundary when
. We say that R is an object rule-boundary when  is an object boundary, and an equality rule-boundary when
is an object boundary, and an equality rule-boundary when  is an equality boundary.
is an equality boundary.
Definition 4.5
Given an object rule-boundary

over \(\Sigma \), the associated symbol arity is  , where \(c \in \{{\textsf{Ty}}, {\textsf{Tm}}\}\) is the syntactic class of
, where \(c \in \{{\textsf{Ty}}, {\textsf{Tm}}\}\) is the syntactic class of  . The associated symbol rule for \({\textsf{S}}\not \in \vert \Sigma \vert \) is the raw rule
. The associated symbol rule for \({\textsf{S}}\not \in \vert \Sigma \vert \) is the raw rule

over the extended signature  , where
, where  is the generic application of the metavariable
is the generic application of the metavariable  , defined as:
, defined as:
-
1.
 if
if  and \(c \in \{{\textsf{Ty}}, {\textsf{Tm}}\}\),
and \(c \in \{{\textsf{Ty}}, {\textsf{Tm}}\}\), -
2.
 if
if  and \(c \in \{{\textsf{EqTy}}, {\textsf{EqTm}}\}\).
and \(c \in \{{\textsf{EqTy}}, {\textsf{EqTm}}\}\).
Definition 4.6
Given an equality rule-boundary

the associated equality rule is

Definition 4.7
An instantiation of a raw rule

over a symbol signature \(\Sigma \) is an instantiation  of the metavariables of R. The closure rule \(I_{*} R\) associated with I and R is \(([p_1, \ldots , p_n, q], r)\) where \(p_i\) is
of the metavariables of R. The closure rule \(I_{*} R\) associated with I and R is \(([p_1, \ldots , p_n, q], r)\) where \(p_i\) is  , q is
, q is  , and r is
, and r is  .
.
A minor complication arises when congruence rules (Definition 2.17) are adapted to the context-free setting, because conversions must be inserted. Consider the congruence rule (2.1) for \(\Uppi \) from Example 2.18. The premise \(A_1 \equiv A_2\) ensures that the premise \( \{x {:}A_1\} \; B_1(x) \equiv B_2(x) \) is well-formed by conversion of x on the right-hand side from \(A_1\) to \(A_2\), thus in the context-free version of the rule we should allow for the possibility of an explicit conversion. However, we should not enforce an unnecessary conversion in case \(A_1 = A_2\), nor should we require particular conversions, as there may be many ways to convert a term. We therefore formulate flexible congruence rules as follows: if an occurrence of a term t possibly requires conversion, we allow in its place a term \(t'\) such that \(\lfloor t \rfloor = \lfloor t' \rfloor \).
Definition 4.8
The context-free congruence rules associated with a context-free raw type rule

are closure rules, where

of the following form:

Similarly, the congruence rule associated with a raw term rule

are closure rules of the form

Example 4.9
The context-free congruence rules for \(\Uppi \) from Example 2.18 take the form

where the minimal suitable \(\beta \) is
The type expressions \(A'_2\) and \(B_2'\) may be chosen in such a way that the equations \(\vdash A_1 \equiv A'_2 \;{\textsf{by}}\;\alpha _1\) and \(\vdash \{x {:}A_1\} \; B_1 \equiv B'_2 \;{\textsf{by}}\;\alpha _2\) are well-typed, so long as they match \(A_2\) and \(B_2\) up to erasure. In this case, we expect to be able to directly use \(A_2\) for \(A'_2\). The equation \(\vdash \{x {:}A_1\} \; B_1 \equiv B_2 \;{\textsf{by}}\;\alpha _2\) where we use \(B_2\) instead of \(B_2'\) is not obviously well-typed, as \(B_2\) is a family over \(A_2\) rather than \(A_1\). Intuitively, \(B_2'\) should thus be \(B_2\) where uses of x have to first convert along the equation \(A_1 \equiv A_2 \;{\textsf{by}}\;\alpha _1\).
The context-free metavariable closure rules are in direct analogy with the usual ones from Definition 2.19:
Definition 4.10
The context-free metavariable rules associated with the metavariable  where
where  are the closure rules
are the closure rules

where \(\vec {x} = (x_1, \ldots , x_n)\), \(\vec {t} = (t_1, \ldots , t_n)\). Furthermore, if  is an object boundary, then the metavariable congruence rules for
is an object boundary, then the metavariable congruence rules for  are the closure rules CF-Meta-Congr-Ty and CF-Meta-Congr-Tm displayed in Fig. 14.
are the closure rules CF-Meta-Congr-Ty and CF-Meta-Congr-Tm displayed in Fig. 14.
The following definition of context-free raw type theories is analogous to Definition 2.21, except that we have to use the context-free versions of structural rules.
Definition 4.11
A context-free raw type theory T over a symbol signature \(\Sigma \) is a family of context-free raw rules, called the specific rules of T. The associated deductive system of T consists of:
-
1.
the structural rules over \(\Sigma \):
-
2.
the instantiations of the specific rules of T (Definition 4.7);
-
3.
for each specific object rule of T, the instantiations of the associated congruence rule (Definition 4.8).
We write  when
when  is derivable with respect to the deductive system associated to T, and similarly for
is derivable with respect to the deductive system associated to T, and similarly for  .
.
The formulations of the abstraction rules CF-Abstr and CF-Bdry-Abstr are suitable for the backward-chaining style of proof, because their conclusions take a general form. For forward-chaining, we may derive abstraction rules with premises in general form as follows:

The side condition  ensures that
ensures that  , hence CF-Abstr-Fwd can be derived as the instance of CF-Abstr
, hence CF-Abstr-Fwd can be derived as the instance of CF-Abstr

and similarly for boundary abstractions.
The context-free analogues of the auxiliary judgements \(\vdash \Theta \;{\textsf{mctx}}\) and \(\Theta \vdash \Gamma \;{\textsf{vctx}}\) are as follows. For simplicity we define a single notion that encompasses the well-formedness of all annotations.
Definition 4.12
An expression u has well-typed annotations when  for every
for every  and \(\vdash A\;{\textsf{type}}\) for every \({\textsf{a}}^{A} \in {\textsf{asm}}(u)\). The notion evidently extends to judgements and boundaries.
and \(\vdash A\;{\textsf{type}}\) for every \({\textsf{a}}^{A} \in {\textsf{asm}}(u)\). The notion evidently extends to judgements and boundaries.
The context-free version of finitary rules and type theories is quite similar to the original one.
Definition 4.13
Given a raw theory T over a symbol signature \(\Sigma \), a context-free raw rule  over \(\Sigma \) is finitary over T when
over \(\Sigma \) is finitary over T when  for \(k = 1, \ldots , n\), and
for \(k = 1, \ldots , n\), and  , Similarly, a raw rule-boundary
, Similarly, a raw rule-boundary  is finitary over T when
is finitary over T when  for \(k = 1, \ldots , n\), and
for \(k = 1, \ldots , n\), and  .
.
A context-free finitary type theory is a context-free raw type theory \((R_i)_{i \in I}\) for which there exists a well-founded order \((I, \prec )\) such that each \(R_i\) is finitary over \((R_j)_{j \prec i}\).
Definition 4.14
A context-free finitary type theory is standard if its specific object rules are symbol rules, and each symbol has precisely one associated rule.
5 Meta-theorems About Context-Free Theories
The meta-theorems from Sect. 3 carry over to the context-free setting. Unfortunately, there seems to be no wholesale method for transferring the proofs, and one simply has to adapt them manually to the context-free setting. The process is quite straightforward, so we indulge in omitting the details.
5.1 Meta-theorems About Context-Free Raw Theories
In the context-free setting, a renaming is still an injective map \(\rho \) taking unannotated symbols to unannotated symbols. Its action \(\rho _{*} e\) on an expression e recursively descends into e, including into variable annotations, i.e. \(\rho _{*} ({\textsf{a}}^{A}) = \rho ({\textsf{a}})^{\rho _{*} A}\) and  . The action is extended to judgements and boundaries in a straightforward manner. Renaming preserves the size of an expression, as long as all symbols are deemed to have the same size.
. The action is extended to judgements and boundaries in a straightforward manner. Renaming preserves the size of an expression, as long as all symbols are deemed to have the same size.
Proposition 5.1
(Context-free renaming) If a context-free raw type theory derives a judgement or a boundary, then it also derives its renamings.
Proof
Straightforward induction on the derivation. \(\square \)
Weakening (Proposition 3.2) is not applicable, as there is no context that could be weakened, and no variable ever occurs in the conclusion of a judgement without it being used in the derivation.
We next prove that substitution rules are admissible closure rules in the sense of Sect. 2.2. We take a slightly different route than in Sect. 3.1 in order to avoid substituting a term for a free variable, as that changes type annotations and therefore the identity of variables. Lemmas 5.2 and 5.3 are proved by mutual structural induction, with a further structural induction within each lemma.
Lemma 5.2
If a context-free raw type theory derives

then it derives  .
.
Proof
See the proof on Page 80. \(\square \)
Lemma 5.3
If a context-free raw type theory derives

then it derives  .
.
Proof
We proceed as in the proof of Lemma 5.2, where CF-Bdry-Abstr is treated like CF-Abstr, and the remaining ones invert to Lemma 5.2. \(\square \)
Theorem 5.4
(Context-free admissibility of substitution) In a context-free raw type theory, the following substitution rules are admissible closure rules:

Proof
The admissibility of CF-Subst and CF-Bdry-Subst corresponds to the case \(n = 1\) of Lemmas 5.2 and 5.3, respectively. \(\square \)
Before addressing the context-free versions of TT-Subst-EqTy and TT-Subst-EqTm, we prove the context-free presuppositivity theorem.
Of course, presuppositivity holds in the context-free setting as well.
Theorem 5.5
(Context-free presuppositivity)
If a context-free raw type theory derives  and
and  has well-typed annotations, then it derives
has well-typed annotations, then it derives  .
.
Proof
See the proof on Page 81. \(\square \)
Let us now turn to meta-theorems stating that equal substitutions act equally. Once again we need to account for insertion of conversions. In congruence rules such conversions appeared in premises: equations associated to object premises of the shape  referred to a primed version of \(g_i\) to allow the use of conversions in \(g_i\). In the following lemma, conversions appear in the result of a substitution. Therefore, rather than being permissive about insertions of conversions, we are faced with showing that it is possible to insert them. Similarly to Lemma 3.7, we prove that equal terms can be substituted into a judgement to yield equal results, but the right hand side of these results is only prescribed up to erasure, namely as \(C'\) and \(u'\).
referred to a primed version of \(g_i\) to allow the use of conversions in \(g_i\). In the following lemma, conversions appear in the result of a substitution. Therefore, rather than being permissive about insertions of conversions, we are faced with showing that it is possible to insert them. Similarly to Lemma 3.7, we prove that equal terms can be substituted into a judgement to yield equal results, but the right hand side of these results is only prescribed up to erasure, namely as \(C'\) and \(u'\).
Lemma 5.6
If a context-free raw type theory derives

where \(\{\vec {x} {:}\vec {A}\} \, {\mathcal {J}}\) has well-typed annotations, and for \(i = 1, \ldots , n\)

then:
-
1.
if
 then there are \(\gamma \) and \(C'\) such that \(\lfloor C[\vec {t}/\vec {x}] \rfloor = \lfloor C' \rfloor \), $$\begin{aligned} \vdash \{\vec {y} {:}\vec {B}[\vec {s}/\vec {x}]\} \; C[\vec {s}/\vec {x}] \equiv C' \;{\textsf{by}}\;\gamma , \end{aligned}$$
then there are \(\gamma \) and \(C'\) such that \(\lfloor C[\vec {t}/\vec {x}] \rfloor = \lfloor C' \rfloor \), $$\begin{aligned} \vdash \{\vec {y} {:}\vec {B}[\vec {s}/\vec {x}]\} \; C[\vec {s}/\vec {x}] \equiv C' \;{\textsf{by}}\;\gamma , \end{aligned}$$ -
2.
if
 then there are \(\delta \) and \(u'\) such that \(\lfloor u[\vec {t}/\vec {x}] \rfloor = \lfloor u' \rfloor \) and $$\begin{aligned} \vdash \{\vec {y} {:}\vec {B}[\vec {s}/\vec {x}]\} \; u[\vec {s}/\vec {x}] \equiv u': C[\vec {s}/\vec {x}] \;{\textsf{by}}\;\delta . \end{aligned}$$
then there are \(\delta \) and \(u'\) such that \(\lfloor u[\vec {t}/\vec {x}] \rfloor = \lfloor u' \rfloor \) and $$\begin{aligned} \vdash \{\vec {y} {:}\vec {B}[\vec {s}/\vec {x}]\} \; u[\vec {s}/\vec {x}] \equiv u': C[\vec {s}/\vec {x}] \;{\textsf{by}}\;\delta . \end{aligned}$$
Furthermore, no extraneous assumptions are introduced by \(\gamma \), \(C'\), \(\delta \) and \(u'\):

Proof
See the proof on Page 83. \(\square \)
Theorem 5.7
In a context-free raw type theory, the following closure rules are admissible:

Proof
See the proof on Page 86. \(\square \)
Lastly, we prove the context-free counterpart of instantiation admissibility Theorem 3.13. The notion of a derivable instantiation carries over easily to the context-free setting:  is derivable when
is derivable when  for every \(i = 1, \ldots , n\).
for every \(i = 1, \ldots , n\).
Theorem 5.8
(Context-free admissibility of instantiation) In a raw type theory, if  is derivable, it has well-typed annotations, and I is a derivable instantiation such that
is derivable, it has well-typed annotations, and I is a derivable instantiation such that  , then
, then  is derivable, and similarly for boundaries.
is derivable, and similarly for boundaries.
Proof
See the proof on Page 87. \(\square \)
5.2 Meta-theorems About Context-Free Finitary Theories
The context-free economic rules for finitary theories carry over to the context-free setting. The proofs are analogous to those of Sect. 3.2 so we omit them.
Proposition 5.9
(Economic version of Definition 4.7) Let R be the context-free raw rule  with
with  such that
such that  is derivable, in particular R may be finitary. Then for any instantiation
is derivable, in particular R may be finitary. Then for any instantiation  , the following closure rule is admissible:
, the following closure rule is admissible:

Proposition 5.10
(Economic version of Definition 4.10) In a context-free raw type theory, if  and
and  , and \(\vec {t}\) have well-typed annotations, then the following closure rule is admissible:
, and \(\vec {t}\) have well-typed annotations, then the following closure rule is admissible:

If, furthermore, \(\vec {s}\) has well-typed annotations, then there exists v, such that  and the following closure rule is admissible:
and the following closure rule is admissible:

5.3 Meta-theorems About Context-Free Standard Theories
Inversion and uniqueness of typing (Theorems 3.24, 3.26) carry over to context-free finitary theories. First, the notion of natural type is simpler, as it does not depend on the context anymore.
Definition 5.11
Let T be a finitary type theory. The natural type \(\tau _{}(t)\) of a term expression t is defined by:

Next, we define an operation which peels conversions off a term, and another one that collects the peeled assumption sets. We shall use these in the formulation of the context-free inversion theorem.
Definition 5.12
The conversion-stripping  of a term expression t is defined by:
of a term expression t is defined by:

The conversion-residue  is defined by
is defined by

Note that  and that
and that  .
.
Lemma 5.13
If a context-free standard type theory derives \(\vdash t: A\) then
-
1.
it derives
 by an application of CF-Var, CF-Meta, or an instantiation of a term symbol rule, and
by an application of CF-Var, CF-Meta, or an instantiation of a term symbol rule, and -
2.
it derives
 .
.
Proof
See the proof on Page 88. \(\square \)
Theorem 5.14
(Context-free inversion) If a context-free standard type theory derives \(\vdash t: A\), then:
-
if \(A = \tau _{}(t)\), it derives
 by a derivation which concludes with CF-Var, CF-Meta, or an instantiation of a term symbol rule;
by a derivation which concludes with CF-Var, CF-Meta, or an instantiation of a term symbol rule; -
if \(A \ne \tau _{}(t)\), it derives
 by CF-Conv-Tm.
by CF-Conv-Tm.
Proof
Apply Lemma 5.13 and, depending on whether \(A = \tau _{}(t)\), either use  so obtained directly or convert it along
so obtained directly or convert it along  , observing that the side condition
, observing that the side condition  holds because
holds because  . \(\square \)
. \(\square \)
Theorem 5.15
(Context-free uniqueness of typing) For a context-free standard type theory:
-
1.
If \(\vdash t: A\) and \(\vdash t: B\), then \(\vdash A \equiv B \;{\textsf{by}}\;\alpha \) for some assumption set \(\alpha \).
-
2.
If \(\vdash s \equiv t: A \;{\textsf{by}}\;\beta _1\) and \(\vdash s \equiv t: B \;{\textsf{by}}\;\beta _2\), with well-typed variables, then \(\vdash A \equiv B \;{\textsf{by}}\;\alpha \) for some assumption set \(\alpha \).
In both cases, \(\alpha \subseteq {\textsf{asm}}(t)\) can be computed from the judgements involved, without recourse to their derivations.
Proof
The first statement holds because A and B are both judegmentally equal to the natural type of t by Lemma 5.13. The second statement reduces to the first one because the presuppositions \(\vdash t: A\) and \(\vdash t: B\) are derivable by Theorem 5.5. \(\square \)
5.4 Special Meta-theorems About Context-Free Theories
We prove several meta-theorems which are specific to context-free type theories. The example of the equality reflection rule in the beginning of Sect. 4 showcased that finitary type theories do not enjoy strengthening. Context-free type theories, however, do satisfy this meta-property.
Theorem 5.16
(Strengthening) If a context-free raw type theory derives

and  then it also derives
then it also derives  .
.
Proof
We proceed by induction on the derivation of  . The only case to consider is CF-Abstr. If the outer abstraction is empty, then the derivation ends with the abstraction
. The only case to consider is CF-Abstr. If the outer abstraction is empty, then the derivation ends with the abstraction

Because  , it follows that
, it follows that  and that
and that  , which is the second premise, hence derivable. The other possibility is that the derivation ends with
, which is the second premise, hence derivable. The other possibility is that the derivation ends with

From  it follows that
it follows that  , hence we may apply the induction hypothesis to the second premise and conclude by abstracting \({\textsf{c}}^{C}\). \(\square \)
, hence we may apply the induction hypothesis to the second premise and conclude by abstracting \({\textsf{c}}^{C}\). \(\square \)
Why can we not adapt the above proof to type theories with contexts? In the derivation (5.2), the second premise turns out to be precisely the desired conclusion, whereas TT-Abstr would yield  where
where  is needed. Indeed, strengthening is not generally valid for type theories with contexts.
is needed. Indeed, strengthening is not generally valid for type theories with contexts.
The next lemma can be used to modify the head of a judgement so that it fits another boundary, as long as there is agreement up to erasure.
Theorem 5.17
(Boundary conversion) In a context-free raw theory, if  ,
,  ,
,  and
and  then there is \(e_2\) such that
then there is \(e_2\) such that  ,
,  and \(\lfloor e_1 \rfloor = \lfloor e_2 \rfloor \).
and \(\lfloor e_1 \rfloor = \lfloor e_2 \rfloor \).
Proof
See the proof on Page 88. \(\square \)
6 A Correspondence Between Theories With and Without Contexts
We now establish a correpondence between finitary type theories with and without contexts. We use the prefixes “tt“ (for “traditional types“) and “cf“ (for “context-free“) to disambiguate between the two versions of type theory. Thus the raw tt-syntax is the one from Fig. 1, and the raw cf-syntax the one from Fig. 9.
To ease the translation between the two versions of type theory, we shall use annotated free variables \({\textsf{a}}^{A}\) and annotated metavariables  in both version of raw syntax, where the annotations A and
in both version of raw syntax, where the annotations A and  are those of the cf-syntax. In the tt-syntax these annotations are considered part of the symbol names, and do not carry any type-theoretic significance.
are those of the cf-syntax. In the tt-syntax these annotations are considered part of the symbol names, and do not carry any type-theoretic significance.
6.1 Translation from cf-Theories to tt-Theories
We first show how to translate constituents of cf-theories to corresponding constituents of tt-theories. The plan is simple enough: move the annotations to contexts, elide the conversion terms, and replace the assumption sets with the dummy value.
The first step towards the translation was taken in Sect. 4.1.4, where we defined the erasure operation taking a cf-expression e to a tt-expression \(\lfloor e \rfloor \) by removing conversions and replacing assumption sets with the dummy value. Note that erasure and substitution commute, \(\lfloor e[t/x] \rfloor = \lfloor e \rfloor [\lfloor t \rfloor /x]\), by an induction on the syntactic structure of e.
Next, in order to translate cf-judgements to tt-judgements, we need to specify when a context correctly encodes the information provided by cf-annotations.
Definition 6.1
We say that \(\Theta \) is a suitable metavariable context for a set of cf-metavariables S when \(S \subseteq \vert {}\Theta \vert {}\) and  for all
for all  . Similarly, \(\Gamma \) is a suitable variable context for a set of free cf-variables V when \(V \subseteq \vert {}\Gamma \vert {}\) and \(\Gamma ({\textsf{a}}^{A}) = \lfloor A \rfloor \) for all \({\textsf{a}}^{A} \in V\). We say that \(\Theta ; \Gamma \) is a suitable context for S and V when \(\Theta \) is suitable for S an \(\Gamma \) for V.
. Similarly, \(\Gamma \) is a suitable variable context for a set of free cf-variables V when \(V \subseteq \vert {}\Gamma \vert {}\) and \(\Gamma ({\textsf{a}}^{A}) = \lfloor A \rfloor \) for all \({\textsf{a}}^{A} \in V\). We say that \(\Theta ; \Gamma \) is a suitable context for S and V when \(\Theta \) is suitable for S an \(\Gamma \) for V.
As a shorthand, we say that \(\Theta ; \Gamma \) is suitable for a syntactic entity e when it is suitable for \({\textsf{mv}}(e)\) and \({\textsf{fv}}(e)\). As suitability only depends on the assumption set, it follows from suitability of \(\Theta ; \Gamma \) for e and \({\textsf{asm}}(e') \subseteq {\textsf{asm}}(e)\) that \(\Theta ; \Gamma \) is also suitable for \(e'\).
Next, say that a free cf-variable \({\textsf{a}}^{A}\) depends on a free cf-variable \({\textsf{b}}^{B}\), written \({\textsf{b}}^{B} \prec {\textsf{a}}^{A}\), when \({\textsf{b}}^{B} \in {\textsf{fv}}(A)\), and that a set S of free cf-variables is closed under dependence when \({\textsf{b}}^{B} \prec {\textsf{a}}^{A} \in S\) implies \({\textsf{b}}^{B} \in S\). Every set S of cf-variables is contained in the least closed set, which is \(\bigcup \{\hspace{-2.37pt}\vert {\textsf{fv}}({\textsf{a}}^{A}) \mid {\textsf{a}}^{A} \in S \vert \hspace{-2.37pt}\}\). We similarly define dependence for cf-metavariables.
The following lemma shows how to construct suitable contexts.
Lemma 6.2
For every finite set of cf-metavariables S there exists a suitable metavariable context \(\Theta \), such that \(\vert {}\Theta \vert {}\) is the closure of S with respect to dependence. For every finite set of free cf-variables V there exists a suitable variable context \(\Gamma \), such that \(\vert {}\Gamma \vert {}\) is the closure of V with respect to dependence.
Proof
Given a finite set of free cf-variables S, the well-founded order \(\prec \) on \(\bigcup \{\hspace{-2.37pt}\vert {\textsf{fv}}({\textsf{a}}^{A}) \mid {\textsf{a}}^{A} \in S \vert \hspace{-2.37pt}\}\) may be extended to a total one, say \({\textsf{a}}_1^{A_1}, \ldots , {\textsf{a}}_n^{A_n}\). Now take \(\Gamma \) to be the variable context \({\textsf{a}}_1^{A_1}: \lfloor A_1 \rfloor , \ldots , {\textsf{a}}_n^{A_n}: \lfloor A_n \rfloor \). The argument for metavariables is analogous. \(\square \)
A totally ordered extension of \(\prec \) can be given explicitly, so the preceding proof yields an explicit construction of a suitable contexts. Notice that the construction does not introduce any spurious assumptions, in the sense that for a variable context \(\Gamma \) the constructed suitable set V contains only the variables appearing in \(\Gamma \) and the annotations of types appearing in \(\Gamma \).
Proposition 6.3
If \(\Theta ; \Gamma \) is suitable for a cf-judgement  then
then  is a syntactically valid tt-judgement, and similarly for boundaries.
is a syntactically valid tt-judgement, and similarly for boundaries.
Proof
A straightforward induction on the structure of the judgement  . \(\square \)
. \(\square \)
Next we translate rules, theories, and derivations.
Proposition 6.4
A cf-rule and a cf-rule-boundary

respectively translate to the raw tt-rule and the tt-rule-boundary

and

A raw-cf theory \(T = \langle R_i \rangle _{i \in I}\) over a symbol signature \(\Sigma \) is thus translated rule-wise to the raw tt-theory \({T}_{\textrm{tt}} = \langle {(R_i)}_{\textrm{tt}} \rangle _{i \in I}\) over the same signature.
Proof
The conditions in Definition 4.1 guarantee that  is a metavariable context and that it is suitable for
is a metavariable context and that it is suitable for  and
and  . \(\square \)
. \(\square \)
Theorem 6.5
(Translation from finitary cf- to tt-theories)
-
1.
The translation of a finitary cf-theory is finitary.
-
2.
Suppose T is a finitary cf-theory whose translation \({T}_{\textrm{tt}}\) is also finitary. Let \(\Theta ; \Gamma \) be tt-context such that \(\vdash _{{T}_{\textrm{tt}}} \Theta \;{\textsf{mctx}}\) and \(\Theta \vdash _{{T}_{\textrm{tt}}} \Gamma \;{\textsf{vctx}}\). If
 and \(\Theta ; \Gamma \) is suitable for
and \(\Theta ; \Gamma \) is suitable for  , then
, then  .
. -
3.
With T, \(\Theta ; \Gamma \) as in (2), if
 and \(\Theta ; \Gamma \) is suitable for
and \(\Theta ; \Gamma \) is suitable for  then
then  .
.
Proof
See the proof on Page 89. \(\square \)
With the theorem in hand, the loose ends are easily tied up.
Corollary 6.6
The translation of a standard cf-theory is a standard tt-theory.
Proof
The translation takes symbol rules to symbol rules, and equality rules to equality rules. \(\square \)
Corollary 6.7
If a finitary cf-theory T derives  and
and  has well-typed annotations then there exists a context \(\Theta ; \Gamma \) which is suitable for
has well-typed annotations then there exists a context \(\Theta ; \Gamma \) which is suitable for  such that \(\vdash _{{T}_{\textrm{tt}}} \Theta \;{\textsf{mctx}}\) and \(\Theta \vdash _{{T}_{\textrm{tt}}} \Gamma \;{\textsf{vctx}}\).
such that \(\vdash _{{T}_{\textrm{tt}}} \Theta \;{\textsf{mctx}}\) and \(\Theta \vdash _{{T}_{\textrm{tt}}} \Gamma \;{\textsf{vctx}}\).
Proof
We may use the suitable context \(\Theta ; \Gamma \) with \(\Theta \) and \(\Gamma \) constructed respectively from  and
and  as in Lemma 6.2. \(\square \)
as in Lemma 6.2. \(\square \)
6.2 Translation from tt-Theories to cf-Theories
Transformation from tt-theories to cf-theories requires annotation of variables with typing information, insertion of conversions, and reconstruction of assumption sets. Unlike in the previous section, we cannot directly translate judgements, but must look at derivations in order to tell where conversions should be inserted and what assumption sets used. We begin by defining auxiliary notions that help organize the translation.
Given a cf-expression e, let \(\lfloor \!\!\lfloor e \rfloor \!\!\rfloor \) be the double erasure of e, which is like erasure \(\lfloor e \rfloor \), except that we also remove annotations:  and \(\lfloor \!\!\lfloor {\textsf{a}}^{A} \rfloor \!\!\rfloor = {\textsf{a}}\). The following definition specifies when an assignment of annotations to variables, which we call a labeling, meets the syntactic criteria that makes it eligible for a translation.
and \(\lfloor \!\!\lfloor {\textsf{a}}^{A} \rfloor \!\!\rfloor = {\textsf{a}}\). The following definition specifies when an assignment of annotations to variables, which we call a labeling, meets the syntactic criteria that makes it eligible for a translation.
Definition 6.8
-
1.
Consider a metavariable context

An eligible labeling for \(\Theta \) is a map

which assigns to each \({\textsf{M}}_i\) a cf-boundary
 such that
such that  , and if
, and if  then
then  .
. -
2.
With \(\Theta \) and \(\theta \) as above, consider a variable context
$$\begin{aligned} \Gamma = [{\textsf{a}}_1 {:}A_1, \ldots , {\textsf{a}}_n {:}A_n], \end{aligned}$$over \(\Theta \). An eligible labeling for \(\Gamma \) with respect to \(\theta \) is a map
$$\begin{aligned} \gamma = \langle {\textsf{a}}_1 {\mapsto }A'_1, \ldots , {\textsf{a}}_n {\mapsto }A'_n \rangle \end{aligned}$$which assigns to each \({\textsf{a}}_i\) a cf-type \(A'_i\) such that \(\lfloor \!\!\lfloor A'_i \rfloor \!\!\rfloor = A_i\), if
 then
then  , and if \({\textsf{a}}_k^A \in {\textsf{fv}}(A_i)\) then \(A = \gamma ({\textsf{a}}_k)\).
, and if \({\textsf{a}}_k^A \in {\textsf{fv}}(A_i)\) then \(A = \gamma ({\textsf{a}}_k)\). -
3.
A pair \((\theta , \gamma )\) is an eligible labeling for \(\Gamma ; \Theta \) when \(\theta \) is eligible for \(\Theta \) and \(\gamma \) is eligible for \(\Gamma \) with respect to \(\theta \).
-
4.
With \((\theta , \gamma )\) eligible for \(\Theta ; \Gamma \), an eligible cf-judgement
 for a tt-judgement
for a tt-judgement  over \(\Theta ; \Gamma \) is one that satisfies
over \(\Theta ; \Gamma \) is one that satisfies  , if
, if  then
then  , and if
, and if  then \(A = \gamma ({\textsf{a}}_k)\).
then \(A = \gamma ({\textsf{a}}_k)\). -
5.
With \((\theta , \gamma )\) eligible for \(\Theta ; \Gamma \), an eligible cf-boundary
 for a tt-boundary
for a tt-boundary  over \(\Theta ; \Gamma \) is one that satisfies
over \(\Theta ; \Gamma \) is one that satisfies  , if
, if  then
then  , and if
, and if  then \(A = \gamma ({\textsf{a}}_k)\).
then \(A = \gamma ({\textsf{a}}_k)\).
We also postulate eligibility requirements for raw rules and theories.
Definition 6.9
Consider a raw tt-rule

An eligible raw cf-rule for R is a raw cf-rule

such that  is eligible for
is eligible for  , and
, and  is eligible for
is eligible for  with respect to \(\theta \) (and the empty labeling for \([\,]\)).
with respect to \(\theta \) (and the empty labeling for \([\,]\)).
Let \(T = \langle R_i \rangle _{i \in I}\) be a raw tt-theory over \(\Sigma \). An eligible raw cf-theory for T is a raw cf-theory \(T' = \langle R'_i \rangle _{i \in I}\) over \(\Sigma \) such that each \(R'_i\) is eligible for \(R_i\).
Theorem 6.10
(Translation of standard tt- to cf-theories)
-
1.
For any standard tt-theory T there exists a standard cf-theory \(T'\) eligible for T.
-
2.
For any T, \(T'\) as above, if \(\vdash _T \Theta \;{\textsf{mctx}}\) then there exists an eligible labeling \(\theta \) for \(\Theta \) such that \(\vdash _{T'} \theta ({\textsf{M}})\) for every \({\textsf{M}}\in \vert {}\Theta \vert {}\).
-
3.
For any T, \(T'\), \(\Theta \), \(\theta \) as above, if \(\Theta ; [\,]\vdash _T \Gamma \;{\textsf{vctx}}\) then there exists an eligible labeling \(\gamma \) for \(\Gamma \) with respect to \(\theta \) such that \(\vdash _{T'} \gamma ({\textsf{a}})\;{\textsf{type}}\) for every \({\textsf{a}} \in \vert {}\Gamma \vert {}\).
-
4.
For any T, \(T'\), \(\Theta \), \(\theta \), \(\Gamma \), \(\gamma \) as above, if
 then there exists an eligible cf-boundary
then there exists an eligible cf-boundary  for
for  with respect to \(\theta \), \(\gamma \) such that
with respect to \(\theta \), \(\gamma \) such that  .
. -
5.
For any T, \(T'\), \(\Theta \), \(\theta \), \(\Gamma \), \(\gamma \), as above, if
 then there exists an eligible cf-judgement
then there exists an eligible cf-judgement  for
for  with respect to \(\theta \), \(\gamma \) such that
with respect to \(\theta \), \(\gamma \) such that  .
.
Proof
See the proof on Page 93. \(\square \)
6.3 Transporting Meta-theorems Across the Correspondence
In Sect. 5 we proved enough meta-theorems about cf-theories to secure the translations between cf- and tt-theories. We may now take advantage of the translations by transporting meta-theorems about tt-theories to their cf-counterparts. We illustrate the technique by proving the cf-counterpart of Theorem 3.17, which states that judgementally equal derivations act equally on judgements, and by formulating the economic congruence cf-rules.
Proposition 6.11
In a standard cf-theory, consider derivable instantiations

such that  for each \(i = 1, \ldots , n\), as well as
for each \(i = 1, \ldots , n\), as well as

If an object cf-judgement  has well-typed annotations and is derivable then there is a derivable equality
has well-typed annotations and is derivable then there is a derivable equality  such that
such that  ,
,  , \(\lfloor e_I \rfloor = \lfloor I_{*} e \rfloor \) and \(\lfloor e_J \rfloor = \lfloor J_{*} e \rfloor \).
, \(\lfloor e_I \rfloor = \lfloor I_{*} e \rfloor \) and \(\lfloor e_J \rfloor = \lfloor J_{*} e \rfloor \).
Proof
Let \(\Theta ; \Gamma \) be a context which is suitable for both (6.1) and  , and is minimal in the sense that any variable appearing in it also appears in (6.1) or
, and is minimal in the sense that any variable appearing in it also appears in (6.1) or  . Let
. Let  . By Theorem 6.10, erasure yields judgementally equal derivable tt-instaniations \(\lfloor I \rfloor \) and \(\lfloor J \rfloor \) of \(\Xi \) over \(\Theta ; \Gamma \), and a derivable judgement
. By Theorem 6.10, erasure yields judgementally equal derivable tt-instaniations \(\lfloor I \rfloor \) and \(\lfloor J \rfloor \) of \(\Xi \) over \(\Theta ; \Gamma \), and a derivable judgement  . By Theorem 3.17, the tt-equality
. By Theorem 3.17, the tt-equality

is derivable. We apply the renaming  and \({\textsf{a}}^{A_i}_i {\mapsto }{\textsf{a}}_i\) to it and obtain
and \({\textsf{a}}^{A_i}_i {\mapsto }{\textsf{a}}_i\) to it and obtain

Next, we apply Theorem 6.10 to the above equation with labelings  and \(\gamma ({\textsf{a}}_i) = A_i\), which results in a derivable cf-equality
and \(\gamma ({\textsf{a}}_i) = A_i\), which results in a derivable cf-equality

such that  , \(\lfloor e_I \rfloor = \lfloor I_{*} e \rfloor \) and \(\lfloor e_J \rfloor = \lfloor J_{*} e \rfloor \). Because we required \(\Theta ; \Gamma \) to be minimal, \(\beta \) satisfies the desired constraint. \(\square \)
, \(\lfloor e_I \rfloor = \lfloor I_{*} e \rfloor \) and \(\lfloor e_J \rfloor = \lfloor J_{*} e \rfloor \). Because we required \(\Theta ; \Gamma \) to be minimal, \(\beta \) satisfies the desired constraint. \(\square \)
The previous proposition gives us a forward-chaining style of congruence rule, because the conclusion is calculated from the premises via the translation theorems. There is also a backward-chaining version in which we proceed from a given (well-formed) cf-equality that we wish to establish.
Corollary 6.12
In a standard cf-theory, consider derivable instantiation

such that  for each \(i = 1, \ldots , n\), as well as
for each \(i = 1, \ldots , n\), as well as

Suppose  is derivable, where
is derivable, where  , \(\lfloor e_I \rfloor = \lfloor I_{*} e \rfloor \) and \(\lfloor e_J \rfloor = \lfloor J_{*} e \rfloor \). Then there is
, \(\lfloor e_I \rfloor = \lfloor I_{*} e \rfloor \) and \(\lfloor e_J \rfloor = \lfloor J_{*} e \rfloor \). Then there is  such that
such that  is derivable.
is derivable.
Proof
By Proposition 6.11 there is a derivable judgement

such that  , \(\lfloor e'_I \rfloor = \lfloor I_{*} e \rfloor \), \(\lfloor e'_J \rfloor = \lfloor J_{*} e \rfloor \), and \(\beta \) satisfies that required condition. Apply Theorem 5.17 to rectify the boundary to the given one. \(\square \)
, \(\lfloor e'_I \rfloor = \lfloor I_{*} e \rfloor \), \(\lfloor e'_J \rfloor = \lfloor J_{*} e \rfloor \), and \(\beta \) satisfies that required condition. Apply Theorem 5.17 to rectify the boundary to the given one. \(\square \)
The method works on other meta-theorems, too. For example, the backward-chaining cf-variant of economic congruence tt-rules (Proposition 3.22) goes as follows.
Proposition 6.13
In a standard cf-theory, consider a derivable finitary object rule

and instantiations of its premises

Suppose the following are derivable:
-
1.
 for each equality boundary
for each equality boundary  ,
, -
2.
 with \(\lfloor g'_i \rfloor = \lfloor g_i \rfloor \) for each object boundary
with \(\lfloor g'_i \rfloor = \lfloor g_i \rfloor \) for each object boundary  .
.
Suppose  is derivable, where
is derivable, where  , \(\lfloor e_I \rfloor = \lfloor I_{*} e \rfloor \), \(\lfloor e_j \rfloor = \lfloor J_{*} e \rfloor \). Then there is
, \(\lfloor e_I \rfloor = \lfloor I_{*} e \rfloor \), \(\lfloor e_j \rfloor = \lfloor J_{*} e \rfloor \). Then there is  such that
such that  is derivable.
is derivable.
Proof
We proceed much as in the proof of Proposition 6.11 and Corollary 6.12, except that we apply Proposition 3.22 on the tt- side. \(\square \)
7 Related and Future Work
Our investigation into a general metatheory for type theory has lead us to present and study two languages. In Sect. 2, we gave a general definition of a broad class of finitary type theories and proved that it satisfies the expected desirable type theoretic meta-theorems. In Sect. 4, we introduced a context-free formulation of type theories and demonstrated that this definition satisfies further meta-theorems, notably strengthening and a context-free inversion principle. Context-free type theories serve as the theoretical foundation of Andromeda 2, as the annotation discipline for variables and metavariables turned out to be better suited for an effectful meta-language [24]. See in particular [24, Chapter 4] for a discussion of the implementation of context-free type theories in Andromeda 2. The generality of finitary type theories has been put to work in [7], where a general equality checking algorithm is shown to be sound for all standard type theories.
Our work was developed concurrently with several other general frameworks for type theory. There are different approaches to the study of formal systems such as logics and type theories, ranging from syntactic [11, 23] to semantic [9, 10, 18, 25] characterisations. To reasonably delimit the scope of this discussion we shall focus on those that (i) are sufficiently expressive to faithfully represent a wide family of dependent type theories, but (ii) are sufficiently restrictive to prove general meta-theorems that are comparable to ours.
7.1 General Dependent Type Theories
The closest relative are general dependent type theories [6], which we proposed together with Lumsdaine. Finitary and general dependent type theories (GDTTs) have more in common than divides them. FTTs can be seen as a bridge from GDTTs to context-free type theories (CFTTs). As context-free type theories in turn are intended as the theoretical underpinning of Andromeda 2, the choice was made to restrict arities of rules and symbols to be finite, which allows for a direct representation as concrete syntax. This restriction is somewhat coincidental, and we expect that it should be possible to generalise much of the treatment of FTTs and possibly CFTTs to arbitrary arities.
The treatment of variables and metavariables in FTTs differs from that of GDTTs in an inessential way: the former uses a locally-nameless discipline and metavariable contexts, while the latter uses shape systems and metavariables as theory extensions. Once again the difference is motivated by implementation details and the rôle metavariables play in proof assistants.
Finally, the levels of well-formedness of the two formalisms differs slighly. GDTTs places fewer restrictions on the rules of raw type theories, while raw FTTs already satisfies presuppositivity.
We expect that translations between the finitary fragment of GDTTs and FTTs can be defined under mild assumptions, and leave their formal comparison as future work.
7.1.1 Logical Frameworks
Perhaps the most prominent family of systems for representing logics are logical frameworks [23, 32]. Logical frameworks have spawned a remarkably fruitful line of work [13, 16, 40] and several implementations exist [31, 33]. In concurrent work to the development of GDTTs and FTTs, Uemura [38] and Harper [21] recently proposed frameworks with the purpose of representing type theories.
Both Uemura’s LF (ULF for short), and Harper’s Equational LF (henceforth EqLF) extend previous frameworks by the addition of an equality type satisfying reflection to judgemental equality at the framework level, and Uemura includes a substantial development of a general categorical semantics. Harper’s Equational LF almost forms a standard finitary type theory. In fact, only inessential modifications are needed to put it in standard form, as is confirmed by a formalisation of EqLF in Andromeda 2 [24]. We compare both accounts of type theory to FTTs along several axes. As they are quite similar, we focus on Uemura’s variant.
In one way, ULF is more expressive than FTTs. While FTTs allow only one judgement form for types, terms, and their equalities, ULF can also capture theories with other judgement forms, such as the fibrancy judgement of the homotopy type system or two-level type theory [4, 39], or the face formulas of cubical type theory [15]. While it may be possible to reconstruct some type theories expressible in ULF via the use of universes in FTTs, a careful analysis would be required to show that the account is faithful, for instance by showing that it is sound and complete for derivability. Conversely, every standard finitary type theory is expressible in ULF. The translation is straightforward, and we take this as a sign that both ULF and FTTs achieve their goal of giving a “natural” account of type theory.
Finitary type theories on the other hand are not directly expressible in ULF or in EqLF. Frequently, accounts of type theory present rules that are not standard, most often because a symbol does not record all of the metavariables introduced by its premises as arguments. But it is also standard practice to have only one notation for say dependent products which may occur at more than one sort, as is done in [21, 27], or give a general cumulativity rule allowing the silent inclusion of types from one sort into another [26, 38]. One may of course take the view that such presentations are not really type theories and should be read with full annotations inserted. It is usually understood that such an annotated presentation can be given, and by including the right set of equations the original calculus can be recovered [22]. Proofs that an unannotated theory is equivalent to a fully annotated one are hard labour [35, Theorem 4.13]. Finitary type theories can thus serve to study the elaboration of such unannotated to a standard FTT or ULF presentation. One such useful general result can already be found in [6], where it is shown that every raw type theory, possibly containing cyclic dependencies between rules, is equivalent to a well-founded one. The assumption of well-founded stratification is hardwired in ULF through the definition of a signature and in EqLF through the inductive construction of a context serving as signature, so that such a theorem could not even be stated in ULF or EqLF. In ongoing research, Petković Komel is employing finitary type theories to investigate a general elaboration theorem, stating that all finitary type theories can be elaborated to standard ones [29].
It would be useful to prove a general adequacy theorem of Uemura’s or Harper’s [21] logical framework for finitary type theories. Conversely, the extension of finitary and context-free type theories to other judgement forms in the style of Uemura’s LF seems within reach and would allow the expression of exciting new type theories such as those based on cubical sets [3, 12, 15]. Another active domain of current research are modal type theories [8, 34]. Multimodal type theory does not readily fit into our setup or the framework of Uemura [20], and the development of modal finitary type theories is an exciting possibility for further work.
7.1.2 Context-Free Type Theories
Geuvers et al. [19] investigated the \(\Gamma _\infty \) system, a context-free formulation of pure type systems. They prove similar meta-theorems, including translations from and to traditional pure type systems. Pure type systems disallow proof-irrelevant rules such as equality reflection. Consequently, the results of [19] are obtained more straightforwardly and without complications arising from the use of conversion terms and assumption sets. Like the authors of [19], our motivation for avoiding explicit contexts came from implementation considerations. A previous version of Andromeda implemented a form of extensional type theory with assumption sets [5]. The results of [19] have been formalised in the Coq proof assistant. A formalisation of context-free type theories could serve as trusted nucleus of a future version of Andromeda. Generalisations of finitary type theories to more general judgement forms in the style of [38] should be mirrored by the development of the corresponding context-free notions and eventually implemented in Andromeda.
References
Aczel, P.: An introduction to inductive definitions. Stud. Logic Found. Math. 90, 739–782 (1977)
Altenkirch, T., Kaposi, A.: Type theory in type theory using quotient inductive types. ACM SIGPLAN Notices 51(1), 18–29 (2016)
Angiuli, C., Hou (Favonia), K.-B., Harper, R.: Cartesian cubical computational type theory: constructive reasoning with paths and equalities. In: Ghica, D., Jung, A. (eds.) CSL 2018 (2018). https://doi.org/10.4230/LIPIcs.CSL.2018.6
Annenkov, D., Capriotti, P., Kraus, N., Sattler, C.: Two-level type theory and applications. arXiv:1705.03307 (2019)
Bauer, A., Gilbert, G., Haselwarter, P.G., Pretnar, M., Stone, C.A.: Design and implementation of the andromeda proof assistant. In: TYPES’16 (2018). https://doi.org/10.4230/lipics.types.2016.5
Bauer, A., Haselwarter, P.G., Lumsdaine, P.L.: A general definition of dependent type theories. arXiv:2009.05539 (2020)
Bauer, A., Petković Komel, A.: An extensible equality checking algorithm for dependent type theories. arXiv:2103.07397 (2021)
Birkedal, L., Nuyts, A., Kavvos, G.A., Gratzer, D.: Multimodal dependent type theory. In: Logical Methods in Computer Science (2021). https://doi.org/10.46298/lmcs-17(3:11)2021
Bocquet, R., Kaposi, A., Sattler, C.: Relative induction principles for type theories. arxiv:2102.11649 (2021)
Capriotti, P.: Models of type theory with strict equality. PhD thesis, University of Nottingham (2016). arxiv:1702.04912
Cartmell, J.W.: Generalised algebraic theories and contextual categories. PhD thesis, University of Oxford (1978)
Cavallo, E., Mörtberg, A., Swan, A.W.: Unifying cubical models of univalent type theory. In: CSL 2020 (2020). https://doi.org/10.4230/LIPIcs.CSL.2020.14
Cervesato, I., Pfenning, F.: A linear logical framework. Inf. Comput. 179(1), 19–75 (2002). https://doi.org/10.1006/inco.2001.2951
Charguéraud, A.: The locally nameless representation. J. Autom. Reason. 49, 363–408 (2012)
Cohen, C., Coquand, T., Huber, S., Mörtberg, A.: Cubical type theory: a constructive interpretation of the univalence axiom. arXiv:1611.02108 (2016)
Cousineau, D., Dowek, G.: Embedding pure type systems in the Lambda-Pi-calculus modulo. In: Della Rocca, S.R. (ed.) Typed Lambda Calculi and Applications. Lecture Notes in Computer Science, pp. 102–117 (2007). https://doi.org/10.1007/978-3-540-73228-0_9
de Bruijn, N.G.: Lambda calculus notation with nameless dummies, a tool for automatic formula manipulation with application to the Church-Rosser theorem. Indag. Math. 75(5), 381–392 (1972)
Fiore, M., Mahmoud, O.: Functorial semantics of second-order algebraic theories. arxiv:1401.4697 (2014)
Geuvers, H., Krebbers, R., McKinna, J., Wiedijk, F.: Pure type systems without explicit contexts. Electron. Proc. Theoret. Comput. Sci. 34, 53–67 (2010). https://doi.org/10.4204/EPTCS.34.6
Gratzer, D.: Normalization for multimodal type theory. arXiv:2106.01414 (2021)
Harper, R.: An equational logical framework for type theories. arXiv:2106.01484 (2021)
Harper, R., Pollack, R.: Type checking with universes. Theoret. Comput. Sci. 89(1), 107–136 (1991)
Harper, R., Honsell, F., Plotkin, G.: A framework for defining logics. J. ACM 40(1), 143–184 (1993)
Haselwarter, P.G.: Effective metatheory of type theory. PhD thesis, University of Ljubljana. https://repozitorij.uni-lj.si/IzpisGradiva.php?id=134439 &lang=eng (2021)
Isaev, V.: Algebraic presentations of dependent type theories. arxiv:1602.08504 (2016)
Luo, Z.: An extended calculus of constructions. PhD thesis, University of Edinburgh (1990)
Martin-Löf, P.: Constructive mathematics and computer programming. In: Studies in Logic and the Foundations of Mathematics, vol. 104, pp. 153–175 (1982)
McKinna, J., Pollack, R.: Pure type systems formalized. In: TLCA, vol. 664 (1993)
Petković Komel, A.: Towards an Elaboration Theorem. HoTT/UF, Invited Talk (2021)
Petković Komel, A.: Meta-analysis of type theories with an application to the design of formal proofs. PhD thesis, University of Ljubljana. https://repozitorij.uni-lj.si/IzpisGradiva.php?id=134058 &lang=eng (2021)
Pfenning, F., Schürmann, C.: System description: Twelf—a meta-logical framework for deductive systems. In: Ganzinger, H. (ed.) Automated Deduction—CADE-16. Lecture Notes in Computer Science, pp. 202–206 (1999). https://doi.org/10.1007/3-540-48660-7_14
Pfenning, F.: Logical frameworks. In: Robinson, J.A., Voronkov, A. (eds.) Handbook of Automated Reasoning, vol. 2, pp. 1063–1147 (2001)
Pientka, B., Dunfield, J.: Beluga: a framework for programming and reasoning with deductive systems (system description). In: International Joint Conference on Automated Reasoning, pp. 15–21 (2010)
Schreiber, U., Shulman, M.: Quantum gauge field theory in cohesive Homotopy type theory. Electron. Proc. Theoret. Comput. Sci. 158, 109–126 (2014). https://doi.org/10.4204/EPTCS.158.8
Streicher, T.: Semantics of Type Theory. Progress in Theoretical Computer Science. Birkhaauser, Basel (1991)
Tarski, A.: A lattice-theoretical fixpoint theorem and its applications. Pac. J. Math. 5(2), 285–309 (1955)
Troelstra, A.S., Schwichtenberg, H.: Basic Proof Theory, vol. 43, 2nd edn. Cambridge Tracts in Theoretical Computer Science, Cambridge University Press, Cambridge (2000)
Uemura, T.: A general framework for the semantics of type theory. arXiv:1904.04097 (2019)
Voevodsky, V.: HTS—a simple type system with two identity types (2013)
Watkins, K., Cervesato, I., Pfenning, F., Walker, D.: A Concurrent Logical Framework I: Judgments and Properties. Technical report, Carnegie Mellon University (2003)
Acknowledgements
The present work draws its inspiration from our joint work with Peter LeFanu Lumsdaine on general type theories [6]. We thank Peter for spearheading the development of general type theories, which inspired us to implement user-definable dependent type theories in Andromeda 2. We also thank Anja Petković Komel for numerous fruitful discussions, and for pushing through even the most horrid technicalities with us. The theorems about admissibility of substitutions and instantiations are to be considered joint work with Anja. We are grateful to Robert Harper and Matija Pretnar for valuable comments on an earlier version of this material as included in [24]. Finally, we are also grateful to the anonymous reviewers of the Journal of Automated Reasoning for their detailed and helpful feedback.
Funding
This material is based upon work supported by the Air Force Office of Scientific Research under Award numbers FA9550-14-1-0096 and FA9550-21-1-0024.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Proofs of Statements
Appendix A: Proofs of Statements
We provide here without further comment the rather technical detailed proofs that were elided in the main text.
1.1 Proofs of Meta-theorems About Type Theories
This section provides missing proofs from Sect. 3.
Lemma 3.4
If a raw type theory derives  and \(\Theta ; \Gamma \vdash t: A\) then it derives
and \(\Theta ; \Gamma \vdash t: A\) then it derives  .
.
Proof
We proceed by induction on the derivation of the judgement. The induction is mutual with the corresponding statement for boundaries, Lemma 3.5.
Case TT-Var: If the derivation ends with the variable rule for \({\textsf{a}}\) then we apply weakening to \(\Theta ; \Gamma \vdash t: A\) to get \(\Theta ; \Gamma , \Delta [t/{\textsf{a}}] \vdash t: A\). For other variables, we apply the variable rule for the same variable.
Case TT-Abstr: Consider a derivation which ends with an abstraction

The induction hypotheses for the premises yield

Note that  , because x does not occur in t, and \({\textsf{a}} \not = {\textsf{b}}\). Hence abstracting \({\textsf{b}}\) in the second premise yields
, because x does not occur in t, and \({\textsf{a}} \not = {\textsf{b}}\). Hence abstracting \({\textsf{b}}\) in the second premise yields

as desired.
Case TT-Meta and TT-Meta-Congr: We only consider the congruence rules, as the metavariable rule is treated similarly. Consider a derivation which ends with the congruence rule for a metavariable \({\textsf{M}}\) whose boundary is  :
:

We apply the induction hypotheses to the premises, and conclude by TT-Meta-Congr for \({\textsf{M}}\), applied to \(\vec {s}[{\textsf{a}}/x]\) and \(\vec {t}[{\textsf{a}}/x]\), taking into account that in general \((e[u/x])[v/{\textsf{a}}] = (e[v/{\textsf{a}}])[u[v/{\textsf{a}}]/x]\).
Case of a specific rule: Consider a derivation ending with the application of a raw rule  with
with  , instantiated by \(I = \langle {\textsf{M}}_1 {\mapsto }e_1, \ldots , {\textsf{M}}_n {\mapsto }e_n \rangle \),
, instantiated by \(I = \langle {\textsf{M}}_1 {\mapsto }e_1, \ldots , {\textsf{M}}_n {\mapsto }e_n \rangle \),

The induction hypotheses for the premises yield, for \(i = 1, \ldots , n\),

which equals

By Lemma 3.5, we further obtain  . Now apply R instantiated at \(I[t/a] = \langle {\textsf{M}}_1 {\mapsto }e_1[t/{\textsf{a}}], \ldots , {\textsf{M}}_n {\mapsto }e_n[t/{\textsf{a}}] \rangle \) to derive
. Now apply R instantiated at \(I[t/a] = \langle {\textsf{M}}_1 {\mapsto }e_1[t/{\textsf{a}}], \ldots , {\textsf{M}}_n {\mapsto }e_n[t/{\textsf{a}}] \rangle \) to derive  , which equals
, which equals  .
.
Case of a congruence rule: Apply the induction hypotheses to the premises and conclude by the same rule.
Cases TT-EqTy-Refl, TT-EqTy-Sym, TT-EqTy-Trans, TT-EqTm-Refl, TT-EqTm-Sym, TT-EqTm-Trans, TT-Conv-Tm, TT-Conv-EqTm: These cases are dispensed with, once again, by straightforward applications of the induction hypotheses. \(\square \)
Lemma 3.6
In a raw type theory the following closure rules are admissible:

Proof
Suppose the premises of TT-Subst are derivable. By inversion the first premise is derived by an application of TT-Abstr, therefore for some \({\textsf{a}} \not \in \vert {}\Gamma \vert {}\), we can derive  . Lemma 3.4 yields
. Lemma 3.4 yields  , which is equal to the conclusion of TT-Subst.
, which is equal to the conclusion of TT-Subst.
The rule TT-Bdry-Subst follows from Lemma 3.5.
Next, assuming the premises of TT-Conv-Abstr are derivable, its conclusion is derived as

\(\square \)
Lemma 3.7
If a raw type theory derives
then it derives
-
1.
 ,
, -
2.
 , and
, and -
3.
 if
if  is an object judgement.
is an object judgement.
Proof
We proceed by induction on the derivation of (3.4).
Case TT-Var: For a variable \({\textsf{b}} \in \vert {}\Gamma \vert {}\), (1) and (2) follow by the same variable rule, while (3) follows by reflexivity for \({\textsf{b}}\) and the same variable rule.
For the variable \({\textsf{a}}\), the desired judgements are precisely the assumptions (3.1), (3.2), and (3.3) weakened to \(\Gamma , \Delta [s/{\textsf{a}}]\).
For a variable \({\textsf{b}} \in \vert {}\Delta \vert {}\) with \(B = \Delta ({\textsf{b}})\), the same variable rule derives \(\Theta ; \Delta [s/{\textsf{a}}] \vdash {\textsf{b}}: B[s/{\textsf{a}}]\) to satisfy (1), while (2) requires an additional conversion along
which is just (3.5). To show (3), namely \(\Theta ; \Gamma , \Delta [s/{\textsf{a}}] \vdash {\textsf{b}} \equiv {\textsf{b}}: B[s/{\textsf{a}}]\), we use TT-EqTm-Refl and the variable rule.
Case TT-Abstr: Consider a derivation ending with an abstraction

The induction hypothesis (1) applied to the first premise yields
Equation (A3) ensures that the extended variable context \(\Delta , {\textsf{b}} {:}B\) satisfies (3.5), hence we may use the induction hypothesis (1) for the last premise to show

which equals

We can thus use the abstraction rule with (A2) and (A4) to derive  , as required.
, as required.
The derivation of  is more interesting. We first apply induction hypothesis (2) to the last premise and get
is more interesting. We first apply induction hypothesis (2) to the last premise and get

Abstraction now gets us to  , after which we apply TT-Conv-Abstr from Lemma 3.6 to replace \(B[s/{\textsf{a}}]\) with \(B[t/{\textsf{a}}]\) using (A3).
, after which we apply TT-Conv-Abstr from Lemma 3.6 to replace \(B[s/{\textsf{a}}]\) with \(B[t/{\textsf{a}}]\) using (A3).
Lastly, we use the induction hypothesis (3) for the last premise to derive

which equals

We may thus apply abstraction to (A2) and (A5) to derive

as desired.
Case TT-Meta: Suppose (3.4) concludes with the metavariable rule for \({\textsf{M}}\), where  :
:

Judgements (1) and (2) are derived by the metavariable rule for \({\textsf{M}}\), applied to the corresponding induction hypotheses for the premises of (A6). We address (3) in case  , and leave the simpler case
, and leave the simpler case  to the reader. We thus seek a derivation of
to the reader. We thus seek a derivation of
which equals
This is just the conclusion of the congruence rule TT-Meta-Congr for \({\textsf{M}}\), suitably applied so that its term and term equation premises are precisely the induction hypotheses (1,2,3) for the term premises of (A6), and its type equation premise is obtained by application of the induction hypothesis (3) to the last premise of (A6).
Case TT-Meta-Congr: If (3.4) ends with a congruence rule for an object metavariable \({\textsf{M}}\) then both (1) and (2) follow by the same congruence rule, applied to the respective induction hypotheses for the premises.
Case of a specific rule: Suppose (3.4) ends with an application of the raw rule  instantiated with \(I = \langle {\textsf{M}}_1 {\mapsto }e_1, \ldots , {\textsf{M}}_n {\mapsto }e_n \rangle \):
instantiated with \(I = \langle {\textsf{M}}_1 {\mapsto }e_1, \ldots , {\textsf{M}}_n {\mapsto }e_n \rangle \):

We would like to derive


and in case  is an object judgement, also
is an object judgement, also
We derive (A8) by \((I[s/{\textsf{a}}])_{*} R\) where \(I[s/{\textsf{a}}] = \langle {\textsf{M}}_1 {\mapsto }e_1[s/{\textsf{a}}], \ldots , {\textsf{M}}_n {\mapsto }e_n[s/{\textsf{a}}] \rangle \), as its premises are induction hypotheses. Similarly, (A9) is derived by \((I[t/{\textsf{a}}])_{*} R\). We consider (A10) in case  and leave the simpler case
and leave the simpler case  to the reader. We thus need to derive
to the reader. We thus need to derive
which we do by applying the congruence rule, where \(J = I [s/{\textsf{a}}]\) and \(K = I [t/{\textsf{a}}]\),

The first three rows of premises are just the induction hypotheses for the first row of premises of (A7), and the last one is (3) for the last premise of (A7).
Case of a congruence rule: Both (1) and (2) are derived by applying the induction hypotheses to the premises and using the congruence rule.
Case TT-Conv-Tm: Consider a derivation ending with a conversion

The judgements \(\Theta ; \Gamma , \Delta [s/{\textsf{a}}] \vdash u[s/{\textsf{a}}]: C[s/{\textsf{a}}]\) and \(\Theta ; \Gamma , \Delta [s/{\textsf{a}}] \vdash u[t/{\textsf{a}}]: C[t/{\textsf{a}}]\) immediately follow from the induction hypothesis and conversion. To derive \(\Theta ; \Gamma , \Delta [s/{\textsf{a}}] \vdash (u: C)[(s \equiv t)/{\textsf{a}}]\), note that the induction hypothesis (3) for the first premise yields
and (1) applied to the second premise
Thus by equality conversion we conclude \(\Theta ; \Gamma , \Delta [s/{\textsf{a}}] \vdash u[s/{\textsf{a}}] \equiv u[t/{\textsf{a}}]: C[s/{\textsf{a}}]\).
Cases TT-EqTy-Refl, TT-EqTy-Sym, TT-EqTy-Trans, TT-EqTm-Refl, TT-EqTm-Sym, TT-EqTm-Trans, TT-Conv-EqTm: These cases are dispensed with by straightforward applications of the induction hypotheses. \(\square \)
Lemma 3.9
Suppose a raw type theory derives
-
1.
If it derives
$$\begin{aligned} \Theta ; \Gamma \vdash \{x {:}A\} \{\vec {y} {:}\vec {B}\} \; C \equiv D \quad \text {and}\quad \Theta ; \Gamma \vdash \{x {:}A\} \{\vec {y} {:}\vec {B}\} \; D\;{\textsf{type}} \end{aligned}$$then it derives \( \Theta ; \Gamma \vdash \{\vec {y} {:}\vec {B}[s/x]\} \; C[s/x] \equiv D[t/x]. \)
-
2.
If it derives
$$\begin{aligned} \Theta ; \Gamma \vdash \{x {:}A\} \{\vec {y} {:}\vec {B}\} \; u \equiv v: C \quad \text {and}\quad \Theta ; \Gamma \vdash \{x {:}A\} \{\vec {y} {:}\vec {B}\} \; v: C \end{aligned}$$then it derives \( \Theta ; \Gamma \vdash \{\vec {y} {:}\vec {B}[s/x]\} \; u[s/x] \equiv v[t/x]: C[s/x] \).
Proof
We spell out the proof of the first claim only. By substituting s for x in the first assumption we obtain
and by applying TT-Subst-EqTy to the second assumption
These two may be combined to give the desired judgement by unpacking the abstraction, applying transitivity, and packing up the abstraction. \(\square \)
Lemma 3.10
Suppose a raw type theory derives, for \(i = 1, \ldots , n\),
If it derives an object judgement  then it derives
then it derives

Proof
First, by inversion on the derivation of  we see that, for \(i = 1, \ldots , n\),
we see that, for \(i = 1, \ldots , n\),
Next, we claim that, for all \(j = 1, \ldots , i-1\),
Indeed, when \(j = 1\) the statement reduces to reflexivity, while an application of Lemma 3.9 lets us pass from j to \(j+1\). When \(j = i\) we obtain
and this can be used to show by conversion that \( \Theta ; \Gamma \vdash t_i: A_i[\vec {s}_{(i)}/\vec {x}_{(i)}] \). Now the goal can be derived by repeated applications of Lemma 3.9. \(\square \)
Lemma 3.12
In a raw type theory, let I be a derivable instantiation of \(\Xi \) over context \(\Theta ; \Gamma \). If  is derivable then so is
is derivable then so is  , and similarly for boundaries.
, and similarly for boundaries.
Proof
We proceed by structural induction on the derivation of  , only devoting attention to the metavariable and abstraction rules, as all the other cases are straightforward.
, only devoting attention to the metavariable and abstraction rules, as all the other cases are straightforward.
Case TT-Meta: Consider an application of a metavariable rule for \({\textsf{M}}\) with  and \(I({\textsf{M}}) = \{\vec {x}\} e\):
and \(I({\textsf{M}}) = \{\vec {x}\} e\):

We need to derive

By induction hypothesis, for each \(j = 1, \ldots , m\),
while derivability of I at \({\textsf{M}}\) and weakening by \(I_{*} \Delta \) yield

We now derive (A12) by repeatedly using TT-Subst to substitute \(I_{*} t_i\)’s for \(x_i\)’s in (A13).
Case TT-Meta-Congr: Consider an application of a metavariable congruence rule for \({\textsf{M}}\) with  and \(I({\textsf{M}}) = \{\vec {x}\} e\):
and \(I({\textsf{M}}) = \{\vec {x}\} e\):

We need to derive

Derivability of I yields

We may apply Lemma 3.10 to (A14) with terms \(I_{*} \vec {s}\) and \(I_{*} \vec {t}\). The preconditions of the lemma are met by the induction hypotheses for the premises.
Case TT-Abstr: Suppose the derivation ends with an abstraction

The induction hypotheses for the premises state

Because  we may abstract \({\textsf{a}}\) to derive
we may abstract \({\textsf{a}}\) to derive

\(\square \)
Lemma 3.14
In a raw type theory, consider derivable instantiations I and J of  over \(\Theta ; \Gamma \) which are judgementally equal. Suppose that \(\vdash \Xi \;{\textsf{mctx}}\) and \(\Theta \vdash \Gamma \;{\textsf{vctx}}\), and that
over \(\Theta ; \Gamma \) which are judgementally equal. Suppose that \(\vdash \Xi \;{\textsf{mctx}}\) and \(\Theta \vdash \Gamma \;{\textsf{vctx}}\), and that  is derivable for \(i = 1, \ldots , n\), and additionally that, for all \({\textsf{a}} \in \vert \Delta \vert \) with \(\Delta ({\textsf{a}}) = A\), so are
is derivable for \(i = 1, \ldots , n\), and additionally that, for all \({\textsf{a}} \in \vert \Delta \vert \) with \(\Delta ({\textsf{a}}) = A\), so are
If  is derivable then so are
is derivable then so are



Proof
Note that (3.6) already follows from Theorem 3.13, so we do not bother to reprove it, but we include the statement because we use it repeatedly. We proceed by structural induction on the derivations of \(\vdash \Xi \;{\textsf{mctx}}\) and  .
.
Case TT-Var: Consider a derivation ending with the variable rule

We derive (3.7) by the variable rule, and when \({\textsf{a}}_i \in \vert {}\Delta \vert {}\) a subsequent conversion along \(\Theta ; \Gamma , I_{*} \Delta \vdash I_{*} A_i \equiv J_{*} A_i\). The judgement (3.8) holds by TT-EqTm-Refl.
Case TT-Abstr: Consider a derivation ending with an abstraction

The induction hypothesis for the first premise yields
The extended variable context \(\Gamma , \Delta , {\textsf{b}} {:}B\) satisfies the preconditions of the induction hypotheses for the second premise, therefore



where (A20) is present only when  is an object judgement. Now (3.8) follows by abstraction from (A15) and (A20). To derive (3.7), we first abstract (A19) to get
is an object judgement. Now (3.8) follows by abstraction from (A15) and (A20). To derive (3.7), we first abstract (A19) to get

and then apply TT-Conv-Abstr to convert it along (A17) to derive the desired

Case of a specific rule: Consider a specific rule

and an instantiation \(K = \langle {\textsf{N}}_1 {\mapsto }g_1, \ldots , {\textsf{N}}_m {\mapsto }g_m \rangle \). Suppose the derivation ends with the instantiation \(K_{*} R\):

We derive (3.7) by \((J_{*} K)_{*} R\) where \(J_{*}K = \langle {\textsf{N}}_1 {\mapsto }J_{*}g_1, \ldots , {\textsf{N}}_m {\mapsto }J_{*}g_m \rangle \). The resulting premises for \(i = 1, \ldots , m\) are precisely the induction hypotheses (3.7) for the premises of (A21). The last premise,  , follows by case analysis of
, follows by case analysis of  and the same induction hypothesis (3.7). To establish (3.8), we must derive
and the same induction hypothesis (3.7). To establish (3.8), we must derive

We do so by an application of the congruence rule associated with R, instantiated with \(I_{*} K\) and \(J_{*} K\). The resulting closure rule has four sets of premises, all of which are derivable:
-
both copies of premises of R are derivable because they are the induction hypotheses (3.6) and (3.7) for the premises of (A21),
-
the additional equational premises are derivable because they are the induction hypotheses (3.8) for the premises of (A21).
Case of a congruence rule: Similar to the case of a specific rule. Given a congruence rule with instantiations L and K, (3.7) follows from the same congruence rule with instantiations \(J_{*} L\) and \(J_{*} K\). The premises hold by induction hypothesis (3.7).
Case TT-Meta: Consider a derivation ending with an application of the metavariable rule for \({\textsf{M}}_i\), where \(\vec {x} = (x_1, \ldots , x_m)\), \(\vec {t} = (t_1, \ldots , t_m)\), \(J({\textsf{M}}_i) = \{\vec {x}\} e\), and  ,
,

Because J is derivable we know that  . For (3.7), we derive
. For (3.7), we derive

by substituting \(J_{*} \vec {t}\) for \(\vec {x}\) by repeated applications of TT-Subst, which generate premises, for \(j = 1, \ldots , m\),
These are precisely the induction hypotheses for the premises of (A22). It remains to show (3.8). Writing \(I({\textsf{M}}_i)\) as \(\{x\} e'\), we must establish

Because I and J are judgementally equal, we know that

By substituting \(I_{*} {\vec {t}}\) for \(\vec {x}\) by repeated use of TT-Subst, we derive

where the substitutions generate obligations, for \(j = 1, \ldots , m\),
These are precisely the induction hypotheses for the term premises of (A22). By transitivity it suffices to derive

The induction hypotheses for the premises of (A22) for \(j = 1, \ldots , m\) are
We would like to apply Lemma 3.10 to these judgements to derive (A24), but the type of the terms \(J_{*} t_j\) in (A26) does not match the type of the corresponding terms \(I_{*} t_j\). We rectify the situation by successively deriving the equality of the types involved and converting, as follows.
By assumption \(\vdash \Xi \;{\textsf{mctx}}\) holds and hence \(\Xi _{(i)}; [\,]\vdash \{x_1 {:}A_1\} \cdots \{x_{j-1} {:}A_{j-1}\}\; A_j\;{\textsf{type}}\) for \(j = 1, \ldots , m\). Note that the preceding judgement is derivable in a smaller metavariable context, and we can thus appeal to the induction hypothesis to derive
We apply Lemma 3.10 together with (A25,A26,A27) to obtain
We now appeal to TT-Conv-Tm to derive
Finally we derive (A24) by applying Lemma 3.10 to (A25,A28,A27) and to the judgement  , which equals
, which equals  and so is derivable by assumption.
and so is derivable by assumption.
Case TT-Meta-Congr: Consider a derivation ending with an application of the congruence rule for \({\textsf{M}}_i\), where \(\vec {x} = (x_1, \ldots , x_m)\), \(\vec {s} = (s_1, \ldots , s_m)\), \(\vec {t} = (t_1, \ldots , t_m)\), \(J({\textsf{M}}_i) = \{\vec {x}\} e\), and  ,
,

Because J is derivable we know that  , therefore by weakening also
, therefore by weakening also

The desired judgement

may be derived by repeated applications of TT-Subst-EqTm, provided that, for \(j = 1, \ldots , m\),
These are precisely induction hypotheses for (A29).
Cases TT-EqTy-Refl, TT-EqTy-Sym, TT-EqTy-Trans, TT-EqTm-Refl, TT-EqTm-Sym, TT-EqTm-Trans, TT-Conv-Tm, and TT-Conv-EqTm : The remaining cases are all equality rules. Each is established by an appeal to the induction hypotheses for the premises, followed by an application of the same rule. \(\square \)
Lemma 3.15
In a raw type theory, consider  such that \(\vdash \Xi \;{\textsf{mctx}}\), and derivable instantiations
such that \(\vdash \Xi \;{\textsf{mctx}}\), and derivable instantiations
of \(\Xi \) over \(\Theta ; \Gamma \) which are judgementally equal. Suppose further that \(\Theta \vdash \Gamma \;{\textsf{vctx}}\) and  for \(i = 1, \ldots , n\). If \(\Theta \vdash (\Gamma , \Delta )\;{\textsf{vctx}}\), then for all \({\textsf{a}} \in \vert \Delta \vert \) with \(\Delta ({\textsf{a}}) = A\):
for \(i = 1, \ldots , n\). If \(\Theta \vdash (\Gamma , \Delta )\;{\textsf{vctx}}\), then for all \({\textsf{a}} \in \vert \Delta \vert \) with \(\Delta ({\textsf{a}}) = A\):
Proof
We proceed by induction on the length of \(\Delta \). The base case is trivial. For the induction step, suppose \(\Theta \vdash (\Gamma , \Delta , {\textsf{b}} {:}B)\;{\textsf{vctx}}\). For \({\textsf{a}} \in \vert {}\Delta \vert {}\) we apply the induction hypothesis to \(\Delta \) and weaken by \({\textsf{b}} {:}I_{*} B\). To deal with \({\textsf{b}}\), we apply Lemma 3.14 to \(\Theta ; \Gamma , \Delta \vdash B\;{\textsf{type}}\), which holds by inversion, and weaken by \({\textsf{b}} {:}I_{*} B\) to derive the desired
\(\square \)
Lemma 3.16
In a raw type theory, consider  such that \(\vdash \Xi \;{\textsf{mctx}}\), and derivable instantiations
such that \(\vdash \Xi \;{\textsf{mctx}}\), and derivable instantiations
of \(\Xi \) over \(\Theta ; \Gamma \) which are judgementally equal. Suppose that \(\Theta \vdash \Gamma \;{\textsf{vctx}}\). Then  is derivable for \(i = 1, \ldots , n\).
is derivable for \(i = 1, \ldots , n\).
Proof
We proceed by induction on n. The base case is trivial. To prove the induction step for \(n > 0\), suppose the statement holds for \(\Xi _{(n)}\), \(I_{(n)}\) and \(J_{(n)}\), and that  . By inversion on \(\vdash \Xi \;{\textsf{mctx}}\) and weakening we derive
. By inversion on \(\vdash \Xi \;{\textsf{mctx}}\) and weakening we derive  . Then by inverting the abstractions of
. Then by inverting the abstractions of  we obtain variables \(\vec {a} = ({\textsf{a}}_1, \ldots , {\textsf{a}}_m)\) such that, with \(A'_i = A_i[\vec {a}_{(i)}/\vec {x}_{(i)}]\) and \(\Delta = [{\textsf{a}}_1 {:}A'_1, \ldots , {\textsf{a}}_m {:}A'_m]\),
we obtain variables \(\vec {a} = ({\textsf{a}}_1, \ldots , {\textsf{a}}_m)\) such that, with \(A'_i = A_i[\vec {a}_{(i)}/\vec {x}_{(i)}]\) and \(\Delta = [{\textsf{a}}_1 {:}A'_1, \ldots , {\textsf{a}}_m {:}A'_m]\),

We apply Lemma 3.15 to \(\Xi _{(n)}\), \(I_{(n)}\), \(J_{(n)}\), and \(\Delta \) to derive, for \(i = 1, \ldots , m\),
where (A30) follows by conversion from the judgement above it. Next, we use (A30) to substitute \({\textsf{a}}_i\) for \(x_i\) in  , which results in
, which results in

If we can reduce (A31) to

we will be able to derive the desired judgement

by abstracting \({\textsf{a}}_1, \ldots , {\textsf{a}}_n\) in (A32). There are four cases, depending on what  is.
is.
Case  : (A31) and (A32) are the same.
: (A31) and (A32) are the same.
Case  : We convert (A31) along
: We convert (A31) along
which holds by Lemma 3.14 applied to \(\Xi _{(n)}; \Gamma , \Delta \vdash B[\vec {a}/\vec {x}]\;{\textsf{type}}\) with \(\Xi _{(n)}\), \(I_{(n)}\), and \(J_{(n)}\).
Case  : Here (A31) and (A32) are respectively
: Here (A31) and (A32) are respectively
The latter follows from the former if we can also derive
We invert \(\Xi _{(n)}; \Gamma , \Delta \vdash B \equiv C \;{\textsf{by}}\;\Box \) to derive
When we apply Lemma 3.14 to (A34) it gives us (A33).
Case  : Here (A31) and (A32) are respecetively
: Here (A31) and (A32) are respecetively
The latter follows from the former if we can also derive
We invert \(\Xi _{(n)}; \Gamma , \Delta \vdash s \equiv t: B \;{\textsf{by}}\;\Box \) to derive
When we apply Lemma 3.14 to (A36) it gives us (A35). \(\square \)
Theorem 3.18
(Presuppositivity) If a raw type theory derives \(\vdash \Theta \;{\textsf{mctx}}\), \(\Theta \vdash \Gamma \;{\textsf{vctx}}\), and  then it derives
then it derives  .
.
Proof
We proceed by induction on the derivation of  .
.
Case TT-Var: By Proposition 3.3.
Case TT-Meta: The presupposition  is available as premise.
is available as premise.
Case TT-Meta-Congr: Consider a derivation ending with an application of the congruence rule for \({\textsf{M}}\) whose boundary is  :
:

If  , the presupposition \(\Theta ; \Gamma \vdash {\textsf{M}}(\vec {s}) \equiv {\textsf{M}}(\vec {t}) \;{\textsf{by}}\;\Box \) follows directly by TT-Bdry-EqTy and two uses of TT-Meta. If
, the presupposition \(\Theta ; \Gamma \vdash {\textsf{M}}(\vec {s}) \equiv {\textsf{M}}(\vec {t}) \;{\textsf{by}}\;\Box \) follows directly by TT-Bdry-EqTy and two uses of TT-Meta. If  , the presuppositions of \(\vdash {\textsf{M}}(\vec {s}) \equiv {\textsf{M}}(\vec {t}): C[\vec {s}/\vec {x}] \;{\textsf{by}}\;\Box \) follow by TT-Bdry-EqTm:
, the presuppositions of \(\vdash {\textsf{M}}(\vec {s}) \equiv {\textsf{M}}(\vec {t}): C[\vec {s}/\vec {x}] \;{\textsf{by}}\;\Box \) follow by TT-Bdry-EqTm:
-
1.
\(\Theta ; \Gamma \vdash C[\vec {s}/\vec {x}]\;{\textsf{type}}\) holds by substitution of \(\vec {s}\) for \(\vec {x}\) in \(\Theta ; \Gamma \vdash \{\vec {x} {:}\vec {A}\} \; C\;{\textsf{type}}\) much like in the previous case,
-
2.
\(\Theta ; \Gamma \vdash {\textsf{M}}(\vec {s}): C[\vec {s}/\vec {x}]\) holds by TT-Meta,
-
3.
\(\Theta ; \Gamma \vdash {\textsf{M}}(\vec {t}): C[\vec {s}/\vec {x}]\) is derived from \(\Theta ; \Gamma \vdash {\textsf{M}}(\vec {t}): C[\vec {t}/\vec {x}]\) by conversion along \(\Theta ; \Gamma \vdash C[\vec {t}/\vec {x}] \equiv C[\vec {s}/\vec {x}]\), which holds by the last premise.
When applying TT-Meta above, the premise  is required, and likewise for \(\vec {t}\). We may derive it by applying Proposition 3.3 to \(\vdash \Theta \;{\textsf{mctx}}\) and substituting \(\vec {s}\) for \(\vec {x}\) with the help of TT-Subst, and analogously for \(\vec {t}\).
is required, and likewise for \(\vec {t}\). We may derive it by applying Proposition 3.3 to \(\vdash \Theta \;{\textsf{mctx}}\) and substituting \(\vec {s}\) for \(\vec {x}\) with the help of TT-Subst, and analogously for \(\vec {t}\).
Case TT-Abstr: Consider an abstraction

By induction hypothesis on the last premise, we obtain  after which we apply TT-Bdry-Abstr.
after which we apply TT-Bdry-Abstr.
Case of a specific rule: The presupposition is available as premise.
Case of a congruence rule: Consider a congruence rule associated with an object rule R and instantiated with I and J, as in Definition 2.17.
If R concludes with \(\vdash A\;{\textsf{type}}\), the presuppositions are \(\Theta ; \Gamma \vdash I_{*} A\;{\textsf{type}}\) and \(\Theta ; \Gamma \vdash J_{*} A\;{\textsf{type}}\), which are derivable by \(I_{*} R\) and \(J_{*} R\), respectively.
If R concludes with \(\vdash t: A\), the presuppositions are \(\Theta ; \Gamma \vdash I_{*} A\;{\textsf{type}}\), \(\Theta ; \Gamma \vdash I_{*} t: I_{*} A\), and \(\Theta ; \Gamma \vdash J_{*} t: I_{*} A\). We derive the first one by applying the induction hypothesis to the premise \(\Theta ; \Gamma \vdash I_{*} B \equiv J_{*} B\), the second one by \(I_{*} R\), and the third one by converting the second one along the aforementioned premise.
Cases TT-EqTy-Refl, TT-EqTy-Sym, TT-EqTy-Trans, TT-EqTm-Refl, TT-EqTm-Sym, TT-EqTm-Trans: These are all dispensed with by straightforward appeals to the induction hypotheses.
Case TT-Conv-Tm: Consider a term conversion

Then \(\Theta ; \Gamma \vdash B\;{\textsf{type}}\) holds by the induction hypothesis for the second premise.
Case TT-Conv-EqTm: Consider a term equality conversion

As in the previous case, the induction hypothesis for the second premise provides \(\Theta ; \Gamma \vdash B\;{\textsf{type}}\). The induction hypothesis for the first premise yields
We may convert these to \(\Theta ; \Gamma \vdash s: B\) and \(\Theta ; \Gamma \vdash t: B\) using the second premise. \(\square \)
Proposition 3.20
(Economic version of Definition 2.19) If a raw type theory derives \(\vdash \Theta \;{\textsf{mctx}}\) and \(\Theta \vdash \Gamma \;{\textsf{vctx}}\) with  , the following closure rules are admissible:
, the following closure rules are admissible:

Proof
To prove admissibility of TT-Meta-Eco, note that by Proposition 3.3 we have  so we may derive
so we may derive  by substituting \(\vec {t}\) for \(\vec {x}\) by repeated applications of TT-Bdry-Subst to the premises of TT-Meta-Eco. We can now apply TT-Meta.
by substituting \(\vec {t}\) for \(\vec {x}\) by repeated applications of TT-Bdry-Subst to the premises of TT-Meta-Eco. We can now apply TT-Meta.
Next, we address admissibility of TT-Meta-Congr-Eco by deriving its conclusion with the aid of TT-Meta-Congr. For this purpose we need to derive

The first group follows by Theorem 3.18. The second is established by induction on j: by Proposition 3.3,  holds, and thus \(\Theta \vdash \{\vec {x}_{(j)} {:}\vec {A}_{(j)}\} \; A_j\;{\textsf{type}}\) by inversion of TT-Bdry-Abstr. By applying Lemma 3.10, we obtain \(\Theta ; \Gamma \vdash A_j[\vec {s}_{(j)}/\vec {x}_{(j)}] \equiv A_j[\vec {t}_{(j)}/\vec {x}_{(j)}]\) and we can convert \(\Theta ; \Gamma \vdash t_j: A_j[\vec {s}_{(j)}/\vec {x}_{(j)}]\) which holds again by Theorem 3.18. Finally, the last premise holds again by Lemma 3.10, this time applied to \(\Theta \vdash \{\vec {x} {:}\vec {A}\} \; C\;{\textsf{type}}\). \(\square \)
holds, and thus \(\Theta \vdash \{\vec {x}_{(j)} {:}\vec {A}_{(j)}\} \; A_j\;{\textsf{type}}\) by inversion of TT-Bdry-Abstr. By applying Lemma 3.10, we obtain \(\Theta ; \Gamma \vdash A_j[\vec {s}_{(j)}/\vec {x}_{(j)}] \equiv A_j[\vec {t}_{(j)}/\vec {x}_{(j)}]\) and we can convert \(\Theta ; \Gamma \vdash t_j: A_j[\vec {s}_{(j)}/\vec {x}_{(j)}]\) which holds again by Theorem 3.18. Finally, the last premise holds again by Lemma 3.10, this time applied to \(\Theta \vdash \{\vec {x} {:}\vec {A}\} \; C\;{\textsf{type}}\). \(\square \)
Lemma 3.21
In a raw type theory, suppose  , and consider judgementally equal derivable instantiations I, J of \(\Xi \) over \(\Theta ; \Gamma \). If
, and consider judgementally equal derivable instantiations I, J of \(\Xi \) over \(\Theta ; \Gamma \). If  is derivable then so is
is derivable then so is  .
.
Proof
We proceed by induction on the derivation of  .
.
Case TT-Bdry-Ty: We have  , the statement is trivial.
, the statement is trivial.
Case TT-Bdry-Tm: We have  . From \(\Xi ; \Gamma \vdash A\;{\textsf{type}}\) we obtain \(\Theta ; \Gamma \vdash I_{*} A \equiv J_{*} A\) using Theorem 3.17, and convert \(\Theta ; \Gamma \vdash e: I_{*} A\) to \(\Theta ; \Gamma \vdash e: J_{*} A\).
. From \(\Xi ; \Gamma \vdash A\;{\textsf{type}}\) we obtain \(\Theta ; \Gamma \vdash I_{*} A \equiv J_{*} A\) using Theorem 3.17, and convert \(\Theta ; \Gamma \vdash e: I_{*} A\) to \(\Theta ; \Gamma \vdash e: J_{*} A\).
Case TT-Bdry-EqTy: We have  . From Theorem 3.18 we get \(\Xi ; \Gamma \vdash A\;{\textsf{type}}\), hence \(\Theta ; \Gamma \vdash I_{*} A \equiv J_{*} A\) by Theorem 3.17. It follows similarly that \(\Theta ; \Gamma \vdash I_{*} B \equiv J_{*} B\). We may combine these with \(\Theta ; \Gamma \vdash I_{*} A \equiv I_{*} B\) using transitivity to derive \(\Theta ; \Gamma \vdash J_{*} A \equiv J_{*} B\).
. From Theorem 3.18 we get \(\Xi ; \Gamma \vdash A\;{\textsf{type}}\), hence \(\Theta ; \Gamma \vdash I_{*} A \equiv J_{*} A\) by Theorem 3.17. It follows similarly that \(\Theta ; \Gamma \vdash I_{*} B \equiv J_{*} B\). We may combine these with \(\Theta ; \Gamma \vdash I_{*} A \equiv I_{*} B\) using transitivity to derive \(\Theta ; \Gamma \vdash J_{*} A \equiv J_{*} B\).
Case TT-Bdry-EqTm: We have  . From Theorem 3.18 we get
. From Theorem 3.18 we get
and from Theorem 3.17
Together with \(\Xi ; \Gamma \vdash I_{*} s \equiv I_{*} t: I_{*} A\) this is sufficient to derive \(\Xi ; \Gamma \vdash J_{*} s \equiv J_{*} t: J_{*} A\) using transitivity and conversions.
Case TT-Bdry-Abstr: We have  and
and  . We use induction hypothesis and abstraction to derive
. We use induction hypothesis and abstraction to derive  and then convert the abstracion to \(J_{*} A\) using TT-Conv-Abstr. \(\square \)
and then convert the abstracion to \(J_{*} A\) using TT-Conv-Abstr. \(\square \)
Proposition 3.22
(Economic version of Definition 2.17) In a finitary type theory, consider one of its object rules R

Given instantiations of its premises,
over \(\Theta ; \Gamma \) such that \(\vdash \Theta \;{\textsf{mctx}}\) and \(\Theta \vdash \Gamma \;{\textsf{vctx}}\), the following closure rule is admissible:

Proof
We appeal to the congruence rule for R,

whose premises are derived as follows.
The equational premises of the first row are given, while the object premises follow from the corresponding equational premises in TT-Congr-Eco by Theorem 3.18.
The second row of premises is more challenging. First, for each object premise, applying Theorem 3.18 to the corresponding equational premise in TT-Congr-Eco yields  which is then converted to
which is then converted to  with the aid of Lemma 3.21. For an equational premise, we again use Lemma 3.21, except that we apply it to the corresponding equational premise in the first row, noting that in this case \(f_i\) and \(g_i\) are the same.
with the aid of Lemma 3.21. For an equational premise, we again use Lemma 3.21, except that we apply it to the corresponding equational premise in the first row, noting that in this case \(f_i\) and \(g_i\) are the same.
The third row of premises is given. The last premise, when present, follows by Theorem 3.17 from the fact that R is finitary. \(\square \)
Theorem 3.24
(Inversion) If a standard type theory derives an object judgement then there is a derivation of this judgement which concludes with precisely one of the following rules:
-
1.
the variable rule TT-Var,
-
2.
the metavariable rule TT-Meta,
-
3.
an instantiation of a symbol rule,
-
4.
the abstraction rule TT-Abstr,
-
5.
the term conversion rule TT-Conv-Tm of the form

where \(\tau _{\Theta ;\Gamma }(t) \ne A\).
Proof
We proceed by induction on the derivation  . If the derivation concludes with TT-Var, TT-Meta, a symbol rule, or TT-Abstr, then it already has the desired form. The remaining case is a derivation D ending with a term conversion rule
. If the derivation concludes with TT-Var, TT-Meta, a symbol rule, or TT-Abstr, then it already has the desired form. The remaining case is a derivation D ending with a term conversion rule

By induction hypothesis we may invert \(D_1\) and obtain a derivation \(D'\) of \(\Theta ; \Gamma \vdash t: A\) as in the statement of the theorem:
-
1.
If \(D'\) ends with TT-Var, TT-Meta or a term symbol rule then \(A = \tau _{\Theta ; \Gamma }(t)\). Either \(\tau _{\Theta ; \Gamma }(t) = B\) and we use \(D'\), or \(\tau _{\Theta ; \Gamma }(t) \ne B\) and we use D.
-
2.
If \(D'\) concludes with a term conversion

there are again two cases. If \(\tau _{\Theta ; \Gamma }(t) = B\) we use \(D'_1\), otherwise we combine \(\tau _{\Theta ; \Gamma }(t) \equiv A\) and \(A \equiv B\) by transitivity and conversion:

\(\square \)
1.2 Proofs of Meta-theorems About Context-Free Type Theories
This section provides missing proofs from Sect. 5.
Lemma 5.2
If a context-free raw type theory derives

then it derives  .
.
Proof
We may invert the derivation of  to obtain a series of applications of CF-Abstr, yielding types \(A'_1, \ldots , A'_n\) and (suitably fresh) free variables \({\textsf{a}}_{1}^{A'_1}, \ldots , {\textsf{a}}_{n}^{A'_n}\) where, for \(i = 1, \ldots , n\),
to obtain a series of applications of CF-Abstr, yielding types \(A'_1, \ldots , A'_n\) and (suitably fresh) free variables \({\textsf{a}}_{1}^{A'_1}, \ldots , {\textsf{a}}_{n}^{A'_n}\) where, for \(i = 1, \ldots , n\),
At the top of the abstractions sits a derivation D of the judgement

The proof proceeds by induction on the derivation D, i.e. we only ever apply the induction hypotheses to derivations that have a series of abstractions, and on the top a derivation that is structurally smaller than D. Let us write
Case CF-Var: Suppose the derivation ends with the variable rule

If \({\textsf{b}}^{B}\) is one of \({\textsf{a}}_{i}^{A'_i}\) then  , hence
, hence  , which is derivable by assumption. If \({\textsf{b}}^{B}\) is none of \({\textsf{a}}_{i}^{A_i}\)’s then \({\textsf{a}}_{i}^{A_i} \notin {\textsf{fv}}(B)\) by freshness, hence
, which is derivable by assumption. If \({\textsf{b}}^{B}\) is none of \({\textsf{a}}_{i}^{A_i}\)’s then \({\textsf{a}}_{i}^{A_i} \notin {\textsf{fv}}(B)\) by freshness, hence  , so we may reuse the same variable rule.
, so we may reuse the same variable rule.
Case CF-Abstr: Suppose the derivation ends with an abstraction

We extend the substitution by \(t_{n+1} = {\textsf{a}}_{n+1}^{A_{n+1} \tau }\) and apply the induction hypothesis to the abstracted derivation of the right-hand premise, whose conclusion is  , to obtain
, to obtain  . We may abstract \({\textsf{a}}_{n+1}^{A_{n+1} \tau }\) to get the desired judgement
. We may abstract \({\textsf{a}}_{n+1}^{A_{n+1} \tau }\) to get the desired judgement  .
.
All other cases The remaining cases all follow the same pattern: abstract the premises, apply the induction hypotheses to them, and conclude with the same rule. We demonstrate how this works in case of D ending with an instance of a specific rule  instantiated with
instantiated with  :
:

Define the instantiation J of the premises of R by \(J({\textsf{M}}_i) = e'_i = (e_i \zeta ) \tau \). Note that  equals
equals  , therefore we may derive it by \(J_{*} R\). The last premise of \(J_{*} R\) is
, therefore we may derive it by \(J_{*} R\). The last premise of \(J_{*} R\) is  , and it follows by Lemma 5.3 applied to the last premise of \(I_{*} R\). For \(i = 1, \ldots , n\), abstract
, and it follows by Lemma 5.3 applied to the last premise of \(I_{*} R\). For \(i = 1, \ldots , n\), abstract  to
to

and apply the induction hypothesis to derive  , which equals
, which equals  and because
and because  does not contain any free variables, also to
does not contain any free variables, also to  \(\square \)
\(\square \)
Theorem 5.5
(Context-free presuppositivity) If a context-free raw type theory derives  and
and  has well-typed annotations, then it derives
has well-typed annotations, then it derives  .
.
Proof
The proof proceeds by induction on the number of metavariables appearing in the judgement and the derivation of  . That is, each appeal to the induction hypothesis reduces the number of metavariables, or is applied to a subderivation.
. That is, each appeal to the induction hypothesis reduces the number of metavariables, or is applied to a subderivation.
Case CF-Var: Immediate, by the well-typedness of annotations.
Case CF-Meta: Immedate as the desired judgement is a premise of the rule.
Case CF-Meta-Congr-Tm: Suppose  and consider a derivation ending with the metavariable congruence rule
and consider a derivation ending with the metavariable congruence rule

The presuppositions are derived as follows:
-
\(\vdash B[\vec {s}/\vec {x}]\;{\textsf{type}}\) follows by CF-Subst from \(\vdash {\vec {x} {:}\vec {A}} \; B\;{\textsf{type}}\), which in turn follows by inversion on
 .
. -
 follows by CF-Meta.
follows by CF-Meta. -
\(v: B[\vec {s}/\vec {x}]\) is a premise.
Case CF-Abstr: Consider an abstraction

By induction hypothesis on the last premise, we obtain  after which we apply CF-Bdry-Abstr.
after which we apply CF-Bdry-Abstr.
Case of a specific rule: Immediate, as the well-formedness of the boundary is a premise.
Case of a congruence rule: Consider a congruence rulles associated with an object rule R and instantiated with I and J, as in Definition 4.8.
If R concludes with \(\vdash A\;{\textsf{type}}\), the presuppositions are \(\vdash I_{*} A\;{\textsf{type}}\) and \(\vdash J_{*} A\;{\textsf{type}}\), which are derivable by \(I_{*} R\) and \(J_{*} R\), respectively.
If R concludes with \(\vdash t: A\), the presuppositions are \(\vdash I_{*} A\;{\textsf{type}}\), \(\vdash I_{*} t: I_{*} A\), and \(\vdash t': I_{*} A\). We derive the first one by applying the induction hypothesis to the premise \(\vdash t': I_{*} A\), the second one by \(I_{*} R\), while the third one is a premise.
CasesCF-EqTy-Refl, CF-EqTy-Sym, CF-EqTy-Trans, CF-EqTm-Refl, CF-EqTm-Sym, CF-EqTm-Trans: These are all dispensed with straightforward appeals to the induction hypotheses.
Case CF-Conv-Tm: Consider a term conversion

By induction hypothesis for the second premise, \(\vdash B\;{\textsf{type}}\).
Case CF-Conv-EqTm: Consider a term equality conversion

As in the previous case, the induction hypothesis for the second premise provides \(\vdash B\;{\textsf{type}}\). The induction hypothesis for the first premise yields
We may convert these to \(\vdash \upkappa (s, \gamma ): B\) and \(\vdash \upkappa (t, \delta ): B\) using the second premise. \(\square \)
Lemma 5.6
If a context-free raw type theory derives

where  has well-typed annotations, and for \(i = 1, \ldots , n\)
has well-typed annotations, and for \(i = 1, \ldots , n\)
then:
-
1.
if
 then there are \(\gamma \) and \(C'\) such that \(\lfloor C[\vec {t}/\vec {x}] \rfloor = \lfloor C' \rfloor \), $$\begin{aligned} \vdash \{\vec {y} {:}\vec {B}[\vec {s}/\vec {x}]\} \; C[\vec {s}/\vec {x}] \equiv C' \;{\textsf{by}}\;\gamma , \end{aligned}$$
then there are \(\gamma \) and \(C'\) such that \(\lfloor C[\vec {t}/\vec {x}] \rfloor = \lfloor C' \rfloor \), $$\begin{aligned} \vdash \{\vec {y} {:}\vec {B}[\vec {s}/\vec {x}]\} \; C[\vec {s}/\vec {x}] \equiv C' \;{\textsf{by}}\;\gamma , \end{aligned}$$ -
2.
if
 then there are \(\delta \) and \(u'\) such that \(\lfloor u[\vec {t}/\vec {x}] \rfloor = \lfloor u' \rfloor \) and $$\begin{aligned} \vdash \{\vec {y} {:}\vec {B}[\vec {s}/\vec {x}]\} \; u[\vec {s}/\vec {x}] \equiv u': C[\vec {s}/\vec {x}] \;{\textsf{by}}\;\delta . \end{aligned}$$
then there are \(\delta \) and \(u'\) such that \(\lfloor u[\vec {t}/\vec {x}] \rfloor = \lfloor u' \rfloor \) and $$\begin{aligned} \vdash \{\vec {y} {:}\vec {B}[\vec {s}/\vec {x}]\} \; u[\vec {s}/\vec {x}] \equiv u': C[\vec {s}/\vec {x}] \;{\textsf{by}}\;\delta . \end{aligned}$$
Furthermore, no extraneous assumptions are introduced by \(\gamma \), \(C'\), \(\delta \) and \(u'\):

Proof
. As in the proof of Lemma 5.2, we invert the derivation of  to obtain types \(A'_1, \ldots , A'_n\) and (suitably fresh) free variables \({\textsf{a}}_{1}^{A'_1}, \ldots , {\textsf{a}}_{n}^{A'_n}\) where, for \(i = 1, \ldots , n\),
to obtain types \(A'_1, \ldots , A'_n\) and (suitably fresh) free variables \({\textsf{a}}_{1}^{A'_1}, \ldots , {\textsf{a}}_{n}^{A'_n}\) where, for \(i = 1, \ldots , n\),
and a derivation D of the judgement

The proof proceeds by induction on the well-founded ordering of the rules, the number of metavariables, with a subsidiary induction on the derivation D. That is, each appeal to the induction hypotheses either decreases the number of metavariables appearing in the judgement, or descends to a subderivation of D. Let us write
Case CF-Var: Suppose the derivation ends with the variable rule

If \({\textsf{b}}^{B}\) is one of \({\textsf{a}}_{i}^{A'_i}\) then  , hence (2) is satisfied by (5.1). If \({\textsf{b}}^{B}\) is none of \({\textsf{a}}_{i}^{A_i}\)’s then \({\textsf{a}}_{i}^{A_i} \notin {\textsf{fv}}(B)\) by freshness, hence (2) is satisfied by \(\vdash {\textsf{b}}^{B} \equiv {\textsf{b}}^{B}: B \;{\textsf{by}}\;\{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\}\), which holds by CF-EqTm-Refl.
, hence (2) is satisfied by (5.1). If \({\textsf{b}}^{B}\) is none of \({\textsf{a}}_{i}^{A_i}\)’s then \({\textsf{a}}_{i}^{A_i} \notin {\textsf{fv}}(B)\) by freshness, hence (2) is satisfied by \(\vdash {\textsf{b}}^{B} \equiv {\textsf{b}}^{B}: B \;{\textsf{by}}\;\{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\}\), which holds by CF-EqTm-Refl.
Case CF-Abstr: Suppose the derivation ends with an abstraction

We may abstract the first premise to \(\vdash \{\vec {x} {:}\vec {A}\} \; A_{n+1}\;{\textsf{type}}\), apply Lemma 5.2 to derive \(\vdash A_{n+1} \tau \;{\textsf{type}}\), and the induction hypothesis to obtain \(\beta _{n+1}\) and \(A'\) such that \(\lfloor A_{n+1} \tau \rfloor = \lfloor A' \rfloor \),
By CF-EqTy-Trans and CF-EqTy-Refl it follows that for some \(\gamma _{n+1}\)
Let \({\textsf{a}}_{n+1}^{A_{n+1} \sigma }\) be fresh, and define
We may abstract the last premise of (A37) to

apply the induction hypothesis with the given \(s_{n+1}\), \(t_{n+1}\) and \(t'_{n+1}\) to derive either (1) or (2), and abstract \({\textsf{a}}_{n+1}^{A_{n+1} \sigma }\) to get the desired judgements.
Case CF-Meta: We consider the case of an object metavariable, and leave the easier case of a type metavariable to the reader. Let  , and suppose the derivation ends with an application of the metavariable rule,
, and suppose the derivation ends with an application of the metavariable rule,

For each \(j = 1, \ldots , m\) we may abstract the premise of (A38) to
and apply Lemma 5.2, once with \(\vec {s}\) and once with \(\vec {t}\), to derive
where we took into account the fact that \(B_j\) does not contain any bound variables. Also, by induction hypothesis there are \(\delta _j\) and \(u'_j\) such that \(\lfloor u_j \tau \rfloor = \lfloor u'_j \rfloor \) and
Next, we invert the last premise of (A38) and abstract it to \( \vdash \{\vec {x} {:}\vec {A}\} \; C[\vec {u}/\vec {y}]\;{\textsf{type}} \). By induction hypothesis we obtain \(\delta '\) and \(C'\) such that \(\lfloor C' \rfloor = \lfloor C[\vec {u} \tau /\vec {y}] \rfloor \) and \(\vdash C[\vec {u} \sigma /\vec {y}] \equiv C' \;{\textsf{by}}\;\delta '\), hence \(\vdash C[\vec {u} \sigma /\vec {y}] \equiv C[\vec {u} \tau /\vec {y}] \;{\textsf{by}}\;\delta ''\) for some \(\delta ''\). Now (2) is satisfied, for some \(\delta '''\)

where the last judgement follows by the congruence rule for  .
.
Case of a specific term rule: Suppose the derivation ends with a specific rule  instantiated with
instantiated with  :
:

Let \(\zeta = [x_n/{\textsf{a}}_{n}^{A'_n}, \ldots , x_1/{\textsf{a}}_{1}^{A'_1}]\) be the abstraction that undoes \(\theta \). Define \(e_j = e'_j \zeta \) and \(I = I' \zeta \), so that \(e'_j = e_j \theta \) and \(I' = I \theta \), which allows us to write the above judgement as

We invert the last premise, abstract to \( \vdash \{\vec {x} {:}\vec {A}\} \; I_{*} B\;{\textsf{type}} \), and apply Lemma 5.2 to derive \(\vdash (I_{*} B) \sigma \;{\textsf{type}}\). Next, the induction hypothesis provides \(\beta \) and \(B'\) such that \(\lfloor B' \rfloor = \lfloor (I_{*} B) \tau \rfloor \) and \(\vdash (I_{*} B) \sigma \equiv B' \;{\textsf{by}}\;\beta \). Therefore, we have \(\beta '\) such that
It suffices to show
for a suitable \(\delta \). This is precisely the conclusion of the congruence rule for R, so we derive its premises. For any \(j = 1, \ldots , m\) we may abstract the j-th premise to

and apply Lemma 5.2, once with \(\vec {s}\) and once with \(\vec {t}\), to derive

For each object premise with boundary  , the remaining premises are provided precisely by the induction hypotheses.
, the remaining premises are provided precisely by the induction hypotheses.
Case of a specific type rule: Suppose the derivation ends with a specific rule  instantiated with
instantiated with  :
:

With \(\zeta \) and I as in the previous case, we may write the above as

where we elided the trivial boundary premise. It suffices to find a suitable \(\gamma \) such that \( \vdash (I_{*} B) \sigma \equiv (I_{*} B) \tau \;{\textsf{by}}\;\gamma \), which is precisely the conclusion of the congruence rule for R, whose premises are derived as in the previous case.
Case CF-Conv-Tm: Suppose the derivation ends with an application of the conversion rule

We abstract the first premise to \(\vdash \{\vec {x} {:}\vec {A}\} \; u: B\) and apply the induction hypothesis to obtain \(\delta \) and \(u'\) such that \(\lfloor u' \rfloor = \lfloor u \tau \rfloor \) and
We abstract the second premise to \(\vdash \{\vec {x} {:}\vec {A}\} \; B \equiv C \;{\textsf{by}}\;\beta \), apply Lemma 5.2 to derive \( \vdash B \sigma \equiv C \sigma \;{\textsf{by}}\;\beta \sigma \), and use CF-Conv-EqTm to conclude, for suitable \(\gamma \) and \(\gamma '\),
\(\square \)
Theorem 5.7
In a context-free raw type theory, the following closure rules are admissible:

Proof
Lemma 5.6 applied to the premises of CF-Subst-EqTy provides \(\gamma \) and \(C'\) such that \(\lfloor C[\vec {t}/\vec {x}] \rfloor = \lfloor C' \rfloor \) and
We would like to replace \(C'\) in the right-hand side with \(C[\vec {t}/\vec {x}]\), which we can so long as
The first judgement holds by Theorem 5.5 applied to (A40) under the abstraction, while the second one is a substitution instance of the first premise. This establishes derivability of CF-Subst-EqTy.
In case of CF-Subst-EqTm the same lemma yields \(\delta \) and \(u'\) such that \(\lfloor u[\vec {t}/\vec {x}] \rfloor = \lfloor u' \rfloor \) and
We would like to replace \(u'\) with a converted \(u[\vec {t}/\vec {x}]\), which we can by an argument similar to the one above. \(\square \)
Theorem 5.8
(Context-free admissibility of instantiation) In a raw type theory, if  is derivable, it has well-typed annotations, and I is a derivable instantiation such that \({\textsf{mv}}({\mathcal {J}}) \subseteq |I|\), then
is derivable, it has well-typed annotations, and I is a derivable instantiation such that \({\textsf{mv}}({\mathcal {J}}) \subseteq |I|\), then  is derivable, and similarly for boundaries.
is derivable, and similarly for boundaries.
Proof
. We proceed by induction on the derivation of  . We only devote attention to the metavariable and abstraction rules, as all the other cases are straightforward. Suppose
. We only devote attention to the metavariable and abstraction rules, as all the other cases are straightforward. Suppose  .
.
Case CF-Meta: Consider an application of the metavariable rule for  with
with  and \(e_i = \{\vec {x}\} e\):
and \(e_i = \{\vec {x}\} e\):

Because  we need to derive
we need to derive

Because I is derivable, we know that  . By induction hypothesis \( \vdash I_{(i){*}} t_j: (I_{(i){*}} A_j)[I_{(i){*}} \vec {t}_{(j)}/\vec {x}_{(j)}]) \) for each \(j = 1, \ldots , m\), so by Lemma 5.2 we derive
. By induction hypothesis \( \vdash I_{(i){*}} t_j: (I_{(i){*}} A_j)[I_{(i){*}} \vec {t}_{(j)}/\vec {x}_{(j)}]) \) for each \(j = 1, \ldots , m\), so by Lemma 5.2 we derive  , which coincides with (A41).
, which coincides with (A41).
Case CF-Meta-Congr-Ty: We consider the congruence rule for types only. Suppose the derivation ends with an application of the congruence rule for  with
with  and \(e_i = \{\vec {x}\} B\):
and \(e_i = \{\vec {x}\} B\):

Because I is derivable, we know that \( \vdash \{\vec {x} {:}I_{(i){*}} \vec {A}\} \; B\;{\textsf{type}} \), hence Lemma 5.6 applies.
Case CF-Abstr: Suppose the derivation ends with an abstraction

Without loss of generality we may assume that  . (If not, rename \({\textsf{a}}\) to a fresh symbol.) We may apply the induction hypotheses to both premises and get
. (If not, rename \({\textsf{a}}\) to a fresh symbol.) We may apply the induction hypotheses to both premises and get

and derive the desired judgement  by abstracting \({\textsf{a}}^{I_{*} A}\) in the right-hand judgement. \(\square \)
by abstracting \({\textsf{a}}^{I_{*} A}\) in the right-hand judgement. \(\square \)
Lemma 5.13
If a context-free standard type theory derives \(\vdash t: A\) then
-
1.
it derives
 by an application of CF-Var, CF-Meta, or an instantiation of a term symbol rule, and
by an application of CF-Var, CF-Meta, or an instantiation of a term symbol rule, and -
2.
it derives
 .
.
Proof
We proceed by induction on the derivation of \(\vdash t: A\).
CasesCF-Var, CF-Meta, and symbol rule: In these cases  and \(\tau _{}(t) = A\), so we already have
and \(\tau _{}(t) = A\), so we already have  , while \(\vdash \tau _{}(t) \equiv A \;{\textsf{by}}\;\{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\}\) holds by reflexivity.
, while \(\vdash \tau _{}(t) \equiv A \;{\textsf{by}}\;\{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\}\) holds by reflexivity.
Case CF-Conv-Tm: Consider a derivation ending with a conversion

where \({\textsf{asm}}(t, B, A, \beta ) = {\textsf{asm}}(t, A, \alpha )\). By induction hypothesis for the first premise we obtain  and
and  , derived by one of the desired rules. Because
, derived by one of the desired rules. Because  and \(\tau _{}(t) = \tau _{}(\upkappa (t, \alpha ))\), the first claim is established. For the second one, we apply CF-EqTy-Trans like this:
and \(\tau _{}(t) = \tau _{}(\upkappa (t, \alpha ))\), the first claim is established. For the second one, we apply CF-EqTy-Trans like this:

Suitability of  is implied by
is implied by  :
:

\(\square \)
Theorem 5.17
(Boundary conversion) In a context-free raw theory, if  ,
,  ,
,  and
and  then there is \(e_2\) such that
then there is \(e_2\) such that  ,
,  and \(\lfloor e_1 \rfloor = \lfloor e_2 \rfloor \).
and \(\lfloor e_1 \rfloor = \lfloor e_2 \rfloor \).
Proof
We proceed by induction on the derivation of  .
.
Case CF-Bdry-Ty: If  then
then  and we may take \(e_2 = e_1\).
and we may take \(e_2 = e_1\).
Case CF-Bdry-Tm: If  then
then  and \(\lfloor A_1 \rfloor = \lfloor A_2 \rfloor \), therefore \(\vdash A_1 \equiv A_2 \;{\textsf{by}}\;\{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\}\) by CF-EqTy-Refl. We may take \(e_2 = \upkappa (e_1, {\textsf{asm}}(A_1) {\setminus } {\textsf{asm}}(A_2))\) and derive \(\vdash e_2: A_2\) by CF-Conv-Tm.
and \(\lfloor A_1 \rfloor = \lfloor A_2 \rfloor \), therefore \(\vdash A_1 \equiv A_2 \;{\textsf{by}}\;\{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\}\) by CF-EqTy-Refl. We may take \(e_2 = \upkappa (e_1, {\textsf{asm}}(A_1) {\setminus } {\textsf{asm}}(A_2))\) and derive \(\vdash e_2: A_2\) by CF-Conv-Tm.
Case CF-Bdry-EqTy: If  then
then  , \(\lfloor A_1 \rfloor = \lfloor A_2 \rfloor \) and \(\lfloor B_1 \rfloor = \lfloor B_2 \rfloor \). By CF-EqTy-Refl we obtain \(\vdash A_2 \equiv A_1 \;{\textsf{by}}\;\{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\}\) and \(\vdash B_1 \equiv B_2 \;{\textsf{by}}\;\{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\}\). We take \(e_2 = (e_1 \cup {\textsf{asm}}(A_1) \cup {\textsf{asm}}(B_1)) {\setminus } ({\textsf{asm}}(A_2) \cup {\textsf{asm}}(B_2))\) and derive \(\vdash A_2 \equiv B_2 \;{\textsf{by}}\;e_2\) by two applications of CF-EqTy-Trans.
, \(\lfloor A_1 \rfloor = \lfloor A_2 \rfloor \) and \(\lfloor B_1 \rfloor = \lfloor B_2 \rfloor \). By CF-EqTy-Refl we obtain \(\vdash A_2 \equiv A_1 \;{\textsf{by}}\;\{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\}\) and \(\vdash B_1 \equiv B_2 \;{\textsf{by}}\;\{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\}\). We take \(e_2 = (e_1 \cup {\textsf{asm}}(A_1) \cup {\textsf{asm}}(B_1)) {\setminus } ({\textsf{asm}}(A_2) \cup {\textsf{asm}}(B_2))\) and derive \(\vdash A_2 \equiv B_2 \;{\textsf{by}}\;e_2\) by two applications of CF-EqTy-Trans.
Case CF-Bdry-EqTm: If  then
then  , \(\lfloor s_1 \rfloor = \lfloor s_2 \rfloor \), \(\lfloor t_1 \rfloor = \lfloor t_2 \rfloor \) and \(\lfloor A_1 \rfloor = \lfloor A_2 \rfloor \). By CF-EqTy-Refl we obtain \(\vdash A_1 \equiv A_2 \;{\textsf{by}}\;\{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\}\), then by CF-Conv-EqTm
, \(\lfloor s_1 \rfloor = \lfloor s_2 \rfloor \), \(\lfloor t_1 \rfloor = \lfloor t_2 \rfloor \) and \(\lfloor A_1 \rfloor = \lfloor A_2 \rfloor \). By CF-EqTy-Refl we obtain \(\vdash A_1 \equiv A_2 \;{\textsf{by}}\;\{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\}\), then by CF-Conv-EqTm
where \(\gamma = {\textsf{asm}}(A_1) {\setminus } {\textsf{asm}}(s_1, A_2)\) and \(\delta = {\textsf{asm}}(A_1) {\setminus } {\textsf{asm}}(t_1, A_2)\). Next, by reflexivity
We may chain these together by transitivity to derive
where \(e_2 = {\textsf{asm}}(e_1, s_1, t_1, A_1) {\setminus } {\textsf{asm}}(s_2, t_2, A_2)\).
Case CF-Bdry-Abstr: If  then \(e_1 = \{x\} e'_1\),
then \(e_1 = \{x\} e'_1\),  , \(\lfloor A_1 \rfloor = \lfloor A_2 \rfloor \), and
, \(\lfloor A_1 \rfloor = \lfloor A_2 \rfloor \), and  . There is
. There is  such that
such that  . We may apply Lemma 5.2 to
. We may apply Lemma 5.2 to  and \(\vdash \upkappa ({\textsf{a}}^{A_2}, \{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\}): A_1\) to derive
and \(\vdash \upkappa ({\textsf{a}}^{A_2}, \{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\}): A_1\) to derive

By CF-Bdry-Subst we have  , hence we may apply the induction hypothesis to obtain \(e''_2\) such that \(\lfloor e''_2 \rfloor = \lfloor e_1'[\upkappa ({\textsf{a}}^{A_2}, \{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\})/x] \rfloor \),
, hence we may apply the induction hypothesis to obtain \(e''_2\) such that \(\lfloor e''_2 \rfloor = \lfloor e_1'[\upkappa ({\textsf{a}}^{A_2}, \{\hspace{-2.37pt}\vert \vert \hspace{-2.37pt}\})/x] \rfloor \),  , and
, and  . Set \(e'_2 = e''_2[x/{\textsf{a}}^{A_2}]\) and apply CF-Bdry-Abstr to derive
. Set \(e'_2 = e''_2[x/{\textsf{a}}^{A_2}]\) and apply CF-Bdry-Abstr to derive  . Thus we may take \(e_2 = \{x\} e'_2\). \(\square \)
. Thus we may take \(e_2 = \{x\} e'_2\). \(\square \)
1.3 Proofs of Theorems About Translation Betweeen tt- and cf-Type Theories
This section provides missing proofs from Sect. 6.
Theorem 6.5
(Translation from finitary cf- to tt-theories)
-
1.
The translation of a finitary cf-theory is finitary.
-
2.
Suppose T is a finitary cf-theory whose translation \({T}_{\textrm{tt}}\) is also finitary. Let \(\Theta ; \Gamma \) be tt-context such that \(\vdash _{{T}_{\textrm{tt}}} \Theta \;{\textsf{mctx}}\) and \(\Theta \vdash _{{T}_{\textrm{tt}}} \Gamma \;{\textsf{vctx}}\). If
 and \(\Theta ; \Gamma \) is suitable for
and \(\Theta ; \Gamma \) is suitable for  , then
, then  .
. -
3.
With T, \(\Theta ; \Gamma \) as in (2), if
 and \(\Theta ; \Gamma \) is suitable for
and \(\Theta ; \Gamma \) is suitable for  then
then  .
.
Proof
We proceed by mutual structural induction on all three statements. To prove statement (1), consider a finitary cf-theory \(T = (R_i)_{i \in I}\), and let \((I, {\prec })\) be a well-founded order witnessing the finitary character of T (Definition 4.13). We prove that \({T}_{\textrm{tt}}\) is finitary with respect to \((I, {\prec })\) by a well-founded induction on the order. Given any \(i \in I\), with

let  . We verifty that
. We verifty that  is finitary in \(T' = {((R_j)_{j \prec i})}_{\textrm{tt}}\) as follows:
is finitary in \(T' = {((R_j)_{j \prec i})}_{\textrm{tt}}\) as follows:
-
\(\vdash _{T'} \Theta \;{\textsf{mctx}}\) holds by induction on \(k = 1, \ldots , n\): assuming \(\vdash _{T'} \Theta _{(k)}\;{\textsf{mctx}}\) has been established, apply (2) to a cf-derivation of
 and the suitable context \(\Theta _{(k)}; [\,]\).
and the suitable context \(\Theta _{(k)}; [\,]\). -
 holds by application of (2) to a cf-derivation of
holds by application of (2) to a cf-derivation of  and the suitable context \(\Theta ; [\,]\).
and the suitable context \(\Theta ; [\,]\).
We next address statement (2), which we prove by structural induction on the derivation of  .
.
Case CF-Var: A cf-derivation ending with the variable rule

is translated to an application of TT-Var

By suitability of \(\Gamma \) the side-condition \({\textsf{a}}^{A} \in \vert {}\Gamma \vert {}\) is satisfied, and \(\Gamma ({\textsf{a}}^{A}) = \lfloor A \rfloor \).
Case CF-Meta: Consider a cf-derivation ending in

Because erasure commutes with substitution we have

Applying TT-Meta to the translation of the premises obtained by the induction hypothesis thus yields the desired result. Suitability of \(\Theta ; \Gamma \) is ensured because all premises are recorded in the conclusion.
Cases CF-Meta-Congr-Ty and CF-Meta-Congr-Tm: We spell out the translation of the latter rule, where  :
:

The context \(\Theta ; \Gamma \) is suitable for the premises because \(\beta \) is suitable. We apply TT-Meta-Congr as follows:

The first two rows of premises are secured by the induction hypotheses for the corresponding rows in (A42), and the premises in the third row are derivable by the side conditions in the third row and induction hypotheses for the fourth row. The last premise follows by Theorem 3.8 applied to \(\Theta ; \Gamma \vdash _{{T}_{\textrm{tt}}} \lfloor B \rfloor \;{\textsf{type}}\), which holds because we assumed \(\vdash _{{T}_{\textrm{tt}}} \Theta \;{\textsf{mctx}}\).
Case CF-Abstr: A cf-derivation ending with an abstraction

is translated to a tt-derivation ending with TT-Abstr

The premises get their derivations from induction hypotheses, where \({\textsf{b}}^{A} \not \in \vert {}\Gamma \vert {}\) ensures that \(\Gamma , {\textsf{b}}^{A} {:}\lfloor A \rfloor \) is suitable for  .
.
Case of a specific rule: Consider a derivation ending with an instantiation  of a raw cf-rule
of a raw cf-rule  :
:

Let  . Because erasure commutes with instantiation we have
. Because erasure commutes with instantiation we have

and  . Thus we may appeal to the induction hypotheses for the premises and conclude by \({R}_{\textrm{tt}}\), so long as we remember to check that \(\Theta ; \Gamma \) is suitable for the premises, which it is because Definition 4.1 of raw cf-rules requires
. Thus we may appeal to the induction hypotheses for the premises and conclude by \({R}_{\textrm{tt}}\), so long as we remember to check that \(\Theta ; \Gamma \) is suitable for the premises, which it is because Definition 4.1 of raw cf-rules requires  .
.
Case of a congruence rule: Consider an application of the congruence rule associated with a cf-rule

as in Definition 4.8:

The context \(\Theta ; \Gamma \) is suitable for the premises because \(\beta \) is suitable. We apply the corresponding congruence for \({R}_{\textrm{tt}}\) (Definition 2.17):

The first and the second row of premises are derivable by induction hypotheses for the corresponding rows in (A43), while the third row is derivable because of the side conditions on the third row and induction hypotheses for the fourth row. The last premise follows by Theorem 3.17 applied to \(\Theta ; \Gamma \vdash _{{T}_{\textrm{tt}}} A\;{\textsf{type}}\), which in turn follows by induction hypothesis applied to a derivation of \(\vdash _T A\;{\textsf{type}}\) witnessing the finitary character of R.
Case CF-Conv-Tm: Consider a term conversion

The side condition \({\textsf{asm}}(t, A, B, \alpha ) = {\textsf{asm}}(t, B, \beta )\) ensures that \(\Theta ; \Gamma \) is suitable for both premises, hence we may apply the induction hypotheses to the premisess and conclude by TT-Conv-Tm.
Case CF-Conv-EqTm: Consider an equality conversion

The side conditions
ensure that \(\Theta ; \Gamma \) is suitable for both premises, hence we may apply the induction hypotheses to the premises and conclude by TT-Conv-EqTm. As in the preceding case all assumptions in the premises already appear in the conclusion, and suitability is preserved.
Cases CF-EqTy-Refl, CF-EqTy-Sym, CF-EqTy-Trans, CF-EqTm-Refl, CF-EqTm-Sym, CF-EqTm-Trans: These all proceed by application of induction hypotheses to the premises, followed by the corresponding tt-rule, where crucially we rely on recording metavariables in the assumption sets to make sure that \(\Theta \) and \(\Gamma \) are suitable for the premises.
Finally, we address statement (2), which is proved by structural induction on  . The base cases CF-Bdry-Ty, CF-Bdry-Tm, CF-Bdry-EqTy, CF-Bdry-EqTm reduce to translation of term and type judgements, while the induction step CF-Bdry-Abstr is similar to the case CF-Abstr above. \(\square \)
. The base cases CF-Bdry-Ty, CF-Bdry-Tm, CF-Bdry-EqTy, CF-Bdry-EqTm reduce to translation of term and type judgements, while the induction step CF-Bdry-Abstr is similar to the case CF-Abstr above. \(\square \)
Theorem 6.10
(Translation of standard tt- to cf-theories)
-
1.
For any standard tt-theory T there exists a standard cf-theory \(T'\) eligible for T.
-
2.
For any T, \(T'\) as above, if \(\vdash _T \Theta \;{\textsf{mctx}}\) then there exists an eligible labeling \(\theta \) for \(\Theta \) such that \(\vdash _{T'} \theta ({\textsf{M}})\) for every \({\textsf{M}}\in \vert {}\Theta \vert {}\).
-
3.
For any T, \(T'\), \(\Theta \), \(\theta \) as above, if \(\Theta ; [\,]\vdash _T \Gamma \;{\textsf{vctx}}\) then there exists an eligible labeling \(\gamma \) for \(\Gamma \) with respect to \(\theta \) such that \(\vdash _{T'} \gamma ({\textsf{a}})\;{\textsf{type}}\) for every \({\textsf{a}} \in \vert {}\Gamma \vert {}\).
-
4.
For any T, \(T'\), \(\Theta \), \(\theta \), \(\Gamma \), \(\gamma \) as above, if
 then there exists an eligible cf-boundary
then there exists an eligible cf-boundary  for
for  with respect to \(\theta \), \(\gamma \) such that
with respect to \(\theta \), \(\gamma \) such that  .
. -
5.
For any T, \(T'\), \(\Theta \), \(\theta \), \(\Gamma \), \(\gamma \), as above, if
 then there exists an eligible cf-judgement
then there exists an eligible cf-judgement  for
for  with respect to \(\theta \), \(\gamma \) such that
with respect to \(\theta \), \(\gamma \) such that  .
.
Proof
We prove the above existence statements by explicit constructions, e.g., we prove (1) by constructing a specific \(T'\) which meets the criteria, and similarly for the remaining parts. We proceed by simultaneous structural induction on all the parts.
Proof of part (1): We proceed by induction on a well-founded order \((I, {\prec })\) witnessing the finitary character of \(T = (R_i)_{i \in I}\). Consider any \(i \in I\), with the corresponding specific rule

and let \(T_i = (R_j)_{j \prec i}\). By induction hypothesis the tt-theory \(T'_i\) eligible for \(T_i\) has been constructred. Because \(\vdash _{T_i} \Theta \;{\textsf{mctx}}\), by (2) there is an eligible labeling  for \(\Theta \) such that
for \(\Theta \) such that  for each \(k = 1, \ldots , n\). The empty map \(\gamma = \langle \rangle \) is an eligible labeling for the empty context \([\,]\). Because
for each \(k = 1, \ldots , n\). The empty map \(\gamma = \langle \rangle \) is an eligible labeling for the empty context \([\,]\). Because  , by (4) there is an eligible cf-boundary
, by (4) there is an eligible cf-boundary  for
for  with respect to \(\theta , \gamma \) such that
with respect to \(\theta , \gamma \) such that  . We now are in possession of the cf-rule-boundary
. We now are in possession of the cf-rule-boundary

eligible for the tt-rule-boundary  . Let
. Let

be the symbol or equality cf-rule induced by (A44), as in Definitions 4.5 and 4.6. Comparison with Definitions 2.14 and 2.16 shows that \(\lfloor \!\!\lfloor e' \rfloor \!\!\rfloor = e\), as required.
Proof of part (2): We proceed by induction on the derivation of \(\vdash _T \Theta \;{\textsf{mctx}}\). The empty map is an eligible labeling for the empty metavariable context. If  then by inversion \(\vdash _T \Theta \;{\textsf{mctx}}\) and
then by inversion \(\vdash _T \Theta \;{\textsf{mctx}}\) and  . By induction hypothesis there exists an eligible labeling \(\theta \) for \(\Theta \), and by (4) applied to T, \(T'\), \(\Theta \), \(\theta \), \([\,]\), \(\langle \rangle \) a cf-boundary
. By induction hypothesis there exists an eligible labeling \(\theta \) for \(\Theta \), and by (4) applied to T, \(T'\), \(\Theta \), \(\theta \), \([\,]\), \(\langle \rangle \) a cf-boundary  eligible for
eligible for  such that
such that  . The map
. The map  is eligible for
is eligible for  , and moreover \(\vdash _{T'} \theta '({\textsf{M}}')\) for every \({\textsf{M}}' \in \vert {}\theta '\vert {}\).
, and moreover \(\vdash _{T'} \theta '({\textsf{M}}')\) for every \({\textsf{M}}' \in \vert {}\theta '\vert {}\).
Proof of part (3) is analogous to part (2).
Proof of part (4): The non-abstracted boundaries reduce to instances of (5) by inversion, while the case of TT-Bdry-Abstr is analogous to the case TT-Abstr below.
Part (5): Let T, \(T'\), \(\Theta \), \(\theta \), \(\Gamma \), \(\gamma \) be as in (5) with

We have the further assumption that each \({\textsf{M}}_i\) has a cf-derivation \(D_{{\textsf{M}}_i}\) of  , and each \({\textsf{a}}_j\) a cf-derivation \(D_{{\textsf{a}}_j}\) of \(\vdash _{T'} A'_j\;{\textsf{type}}\). We proceed by structural induction on the derivation of
, and each \({\textsf{a}}_j\) a cf-derivation \(D_{{\textsf{a}}_j}\) of \(\vdash _{T'} A'_j\;{\textsf{type}}\). We proceed by structural induction on the derivation of  . In each case we construct a cf-derivation concluding with
. In each case we construct a cf-derivation concluding with  such that
such that  is eligible for
is eligible for  .
.
Case TT-Var: Consider a tt-derivation ending with the variable rule

The corresponding cf-derivation is the application of CF-Var

Case TT-Meta: Consider a tt-derivation ending with the metavariable rule, where  and
and  :
:

The correspond cf-derivation ends with and application of CF-Meta,

where the cf-terms \(\vec {t}' = (t'_1, \ldots , t'_m)\) are constructed inductively as follows. Assuming we already have \(\vec {t}'_{(j)}\), we apply the induction hypothesis to the j-th premise and obtain its eligible counterpart \( \vdash _{T'} t''_j: B''_j \), so that \(\lfloor \!\!\lfloor t''_j \rfloor \!\!\rfloor = t_j\) and \(\lfloor \!\!\lfloor B''_j \rfloor \!\!\rfloor = B_j[\vec {t}_{(j)}/\vec {x}_{(j)}]\). It follows that \(\lfloor B''_j \rfloor = \lfloor B'_j[\vec {t}'_{(j)}/\vec {x}_{(j)}] \rfloor \), therefore we may use Theorem 5.17 to modify \(t''_j\) to a term \(t'_j\) which fills \(B'_j[\vec {t}'_{(j)}/\vec {x}_{(j)}]\).
Case TT-Meta-Congr: We consider a tt-derivation ending with a metavariable term congruence rule, where  and
and  :
:

The corresponding cf-derivation ends with CF-Meta-Congr-Tm

where suitable \(\vec {s}'\), \(\vec {t}'\), \(\vec {t}''\), \(\vec {\alpha }\), v, and \(\beta \) remain to be constructed. The terms \(\vec {s}'\) and \(\vec {t}'\) are obtained as in the previous case, using the first two rows of premises of (A45). The induction hypotheses for the third row give us judgements, for \(j = 1, \ldots , m\),
such that \(\lfloor B''_j \rfloor = \lfloor B_j[\vec {s}'_{(j)}/\vec {x}_{(j)}] \rfloor \). We convert the above equality along \(\vdash _{T'} B''_j \equiv B_j[\vec {s}'_{(j)}/\vec {x}_{(j)}]\) to derive
and since \(\lfloor s'''_j \rfloor = \lfloor s'_j \rfloor \) by reflexivity and transitivity
It remains to construct v and \(\beta \). For the former, we apply CF-Subst-EqTy to \(\vdash _{T'} \{\vec {x}: \vec {B}'\} \; C'\;{\textsf{type}}\) to derive
ands use it to convert \(\vdash _{T'} {\textsf{M}}_k(\vec {t}'): C'[\vec {t}'/\vec {x}]\) to \(\vdash _{T'} \upkappa ({\textsf{M}}_k(\vec {t}'), \epsilon ): C'[\vec {s}'/\vec {x}]\) for a suitable \(\epsilon \). We take \(v = \upkappa ({\textsf{M}}_k(\vec {t}'), \epsilon )\) and the minimal suitable \(\beta \).
Case TT-Abstr: Consider a tt-derivation ending with an abstraction

By induction hypothesis we obtain a derivation of \(\vdash _{T'} A'\;{\textsf{type}}\) which is eligible for the first premise. The extended map \(\langle \gamma , {\textsf{a}} {\mapsto }A' \rangle \) is eligible for \(\Gamma , {\textsf{a}} {:}A\), and so by induction hypothesis we obtain a derivble  which is eligible for the second premise with respect to \((\theta , \langle \gamma , {\textsf{a}} {\mapsto }A' \rangle )\). We form the desired abstraction by CF-Abstr,
which is eligible for the second premise with respect to \((\theta , \langle \gamma , {\textsf{a}} {\mapsto }A' \rangle )\). We form the desired abstraction by CF-Abstr,

Case of a specific rule: Consider a specific tt-rule

and the corresponding cf-rule

Consider a tt-derivation ending with \(I_{*} R\) where \(I = \langle {\textsf{N}}_1 {\mapsto }e_1, \ldots , {\textsf{N}}_m \rightarrow e_m \rangle \):

The corresponding cf-derivation is obtained by an application of \(R'\) instantiated with

which is constructed inductively as follows. Suppose \(\vec {e'}_{(j)}\) have already been constructed in such a way that \(\lfloor \!\!\lfloor e'_k \rfloor \!\!\rfloor = e_k\) and  for all \(k < j\). The induction hypothesis for the j-th premise of (A47) yields
for all \(k < j\). The induction hypothesis for the j-th premise of (A47) yields  such that
such that  . We apply Theorem 5.17 to modify \(e''_j\) to \(e'_j\) such that
. We apply Theorem 5.17 to modify \(e''_j\) to \(e'_j\) such that  and \(\lfloor \!\!\lfloor e'_j \rfloor \!\!\rfloor = \lfloor e''_j \rfloor \). Lastly, the premise
and \(\lfloor \!\!\lfloor e'_j \rfloor \!\!\rfloor = \lfloor e''_j \rfloor \). Lastly, the premise  is derivable because \(R'\) is finitary.
is derivable because \(R'\) is finitary.
Case of a congruence rule: Consider a term tt-rule

and the corresponding cf-rule

Given instantiations
suppose the tt-derivation ends with the congruence rule for R:

The corresponding cf-derivation ends with the congruence rule for \(R'\),

where

It remains to determine \(\vec {f}'\), \(\vec {g}'\), \(\vec {g}''\), and \(t''\).
The terms \(\vec {f}'\) and \(\vec {g}'\) are constructed from the first two rows of premises of the tt-derivation in the same way as \(\vec {e}'\) in the previous case. The third row of premises yields equations, which after an application of Theorem 5.17, take the form

As \(\lfloor f'_i \rfloor = \lfloor f''_i \rfloor \), these can be rectified by reflexivity and transitivity to the desired form

Finally, we construct \(t''\) by converting \(\vdash _{T'} J_{*} t': J_{*} C\) along \( \vdash _{T'} J'_{*} C' \equiv I'_{*} C' \;{\textsf{by}}\;\gamma \), which is derived as follows. The induction hypothesis for the last premise of (A48) gives
such that \(\lfloor C_1 \rfloor = \lfloor I'_{*} C' \rfloor \) and \(\lfloor C_2 \rfloor = \lfloor J'_{*} C' \rfloor \). Because \(\vdash _{T'} I'_{*} C'\;{\textsf{type}}\) and \(\vdash _{T'} J'_{*} C'\;{\textsf{type}}\), as well as \(\vdash _{T'} C_1\;{\textsf{type}}\) and \(\vdash _{T'} C_2\;{\textsf{type}}\) by Theorem 5.5, we may adjust the above equation to
which is only a symmetry away from the desired one.
The case of a type specific rule is simpler and dealt with in a similar fashion.
Cases TT-EqTy-Refl, TT-EqTy-Sym, TT-EqTm-Refl, TT-EqTm-Sym: each of these is taken care of by applying the induction hypotheses to the premises, followed by application of the corresponding cf-rule.
Cases TT-EqTy-Trans and TT-EqTm-Trans: Consider a derivation ending with term transitivity

The induction hypotheses for the premises produce eligible judgements
Because \(\lfloor A' \rfloor = \lfloor A'' \rfloor \) and \(\lfloor t' \rfloor = \lfloor t'' \rfloor \), we may convert the second judgement to \(A'\), and rectify the left-hand side, which results in
Now CF-EqTm-Trans applies. The case of transitivity of type equality similar and easier.
Case TT-Conv-Tm: Consider a conversion

The induction hypotheses for the premises produce eligible judgements
Because \(\lfloor A' \rfloor = \lfloor A'' \rfloor \), we obtain \(A' \equiv B' \;{\textsf{by}}\;\beta \), after which CF-Conv-Tm can be used to convert \(\vdash _{T'} t'': A'\) to a judgement \(\vdash _{T'} t': B' \;{\textsf{by}}\;\beta \) which is eligible for the conclusion.
Case TT-Conv-EqTm: This case follows the same pattern as the previous one. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Haselwarter, P.G., Bauer, A. Finitary Type Theories With and Without Contexts. J Autom Reasoning 67, 36 (2023). https://doi.org/10.1007/s10817-023-09678-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10817-023-09678-y


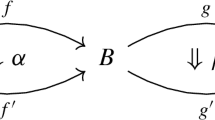





 and
and  and
and 


 . For purely aesthetic reasons, these are written where premises ought to stand. For example, the correct way to read
. For purely aesthetic reasons, these are written where premises ought to stand. For example, the correct way to read  , if
, if  , and the conclusion
, and the conclusion  .”
.”


 is an object boundary, and
is an object boundary, and 
 is an equation boundary, then T extended with the equality rule
is an equation boundary, then T extended with the equality rule 
 and
and  .
. and
and  .
. ,
, , and
, and if
if  is an object judgement.
is an object judgement.





 if
if  and
and  if
if  and
and 


 then there are
then there are  then there are
then there are  by an application of
by an application of  .
. by a derivation which concludes with
by a derivation which concludes with  by
by  and
and  , then
, then  .
. and
and  then
then  .
.

 such that
such that  , and if
, and if  then
then  .
. then
then  , and if
, and if  for a tt-judgement
for a tt-judgement  over
over  , if
, if  then
then  , and if
, and if  then
then  for a tt-boundary
for a tt-boundary  over
over  , if
, if  then
then  , and if
, and if  then
then  then there exists an eligible cf-boundary
then there exists an eligible cf-boundary  for
for  with respect to
with respect to  .
. then there exists an eligible cf-judgement
then there exists an eligible cf-judgement  for
for  with respect to
with respect to  .
. for each equality boundary
for each equality boundary  ,
, with
with  .
. ,
, , and
, and if
if  is an object judgement.
is an object judgement.


 .
. follows by
follows by  then there are
then there are  then there are
then there are  by an application of
by an application of  .
. and
and  , then
, then  .
. and
and  then
then  .
. and the suitable context
and the suitable context  holds by application of (2) to a cf-derivation of
holds by application of (2) to a cf-derivation of  and the suitable context
and the suitable context  then there exists an eligible cf-boundary
then there exists an eligible cf-boundary  for
for  with respect to
with respect to  .
. then there exists an eligible cf-judgement
then there exists an eligible cf-judgement  for
for  with respect to
with respect to  .
.