Intersection bodies of polytopes: translations and convexity

Abstract

We continue the study of intersection bodies of polytopes, focusing on the behavior of IP under translations of P. We introduce an affine hyperplane arrangement and show that the polynomials describing the boundary of $I(P+t)$ can be extended to polynomials in variables $t\in \mathbb {R}^d$ within each region of the arrangement. In dimension 2, we give a full characterization of those polygons such that their intersection body is convex. We give a partial characterization for general dimensions.

1 Introduction

In the field of convex geometry, intersection bodies have been widely studied from an analytical viewpoint, and mainly in the context of volume inequalities. Originally introduced by Lutwak [18], they have played a significant role in solving the Busemann–Petty problem, which asks to compare the volume of two convex bodies based on the volumes of their linear sections [11,12,13, 16, 23]. The goal of this article is to investigate the behavior of intersection bodies of polytopes under translations, and to determine under which translations the intersection body is convex.

Unlike its more famous counterparts, the projection body, the intersection body IK of a star body K is not invariant under affine translation, and it may be convex or non-convex. Convexity is certified by Busemann’s theorem [7], which states that IK is convex if K is a convex body centered at the origin (i.e., K is centrally symmetric, where the center of symmetry is the origin), and this statement has been generalized to $L_p$-intersection bodies [3]. On the other hand, given a convex body $K\subseteq \mathbb {R}^d$, there always exists some $t\in \mathbb {R}^d$ such that $I(K+t)$ is not convex [10, Thm. 8.1.8]. For more negative results, see [8].

The occurrence of non-convex intersection bodies has motivated considerations of various measures for capturing the magnitude of their non-convexity, leading to the study of p-convexity of intersection bodies both over the complex numbers and over the reals [15, 17]. Another direction of research concerns an adaptation of the construction of intersection bodies in order to get convexity, which resolves in convex intersection bodies [21, 22]. A different relative of intersection bodies is the cross section body [19, 20]; however, this star-shaped set turned out to be non-convex as well, in the general case [4]. Summarizing, many of the positive results toward convexity in all these works concern intersection bodies of centrally symmetric star bodies. In contrast, we focus on affine translates, and consider objects which are not necessarily centrally symmetric.

In our previous work [2], we exhibit rich semialgebraic structures of intersection bodies of polytopes. However, in general, the intersection body IP of a polytope P is not a basic semialgebraic set, and there exists a central hyperplane arrangement which describes the regions in which the topological boundary of IP is defined by a fixed polynomial. Taking advantage of these combinatorial and semialgebraic structures opens up new possibilities to study the question of convexity in the present work. In particular, exploiting this semialgebraicity, we are able to characterize convexity by using elementary geometric arguments.

In this article, we introduce an affine hyperplane arrangement associated to a fixed polytope P. We prove that for translation vectors $t \in \mathbb {R}^d$ within a region of this arrangement, the polynomials defining the boundary of $I(P+t)$ can be extended to polynomials in $t_1,\dots ,t_d$ (Theorem 3.5). In dimension 2, we give a full characterization of those polygons with a convex intersection body. We give a partial characterization for general dimension.

Results

Let P be a full-dimensional polytope in $\mathbb {R}^d$.

• (i) If $d=2$ then IP is convex if and only if $P=-P$.

• (ii) If $P\subset \mathbb {R}^d$ is a cuboid, then IP is convex if and only if $P=-P$.

A full classification of the 2-dimensional case is given in Theorem 4.4, and the remaining statements can be found in Proposition 5.4 and Remark 5.5. The above results may suggest that intersection bodies of polytopes are either non-convex or polyhedral. However, an example of a strictly convex intersection body is given in Example 5.6.

1.1 Overview

The article is structured as follows. In Sect. 2, we review the main concepts and notation from [2]. In Sect. 3, we introduce an affine hyperplane arrangement and describe how it governs the behavior of IP under translation of P. We then turn to the characterization of convexity, where Sect. 4 concerns the 2-dimensional case, and Sect. 5 the case of general dimensions.

2 Preliminaries

We will rely on methods and results which were developed in [2]. In this section, we review the most important concepts and results we are going to make use of.

Let $P \subseteq \mathbb {R}^d$ be a convex polytope. The intersection body IP of P is the star-shaped set

$$\begin{aligned} IP = \left\{ x \in \mathbb {R}^d \ \Big \vert \ \rho _{IP}(x) \ge 1 \right\} , \end{aligned}$$

where the radial function $\rho _{IP}:\mathbb {R}^d\rightarrow \mathbb {R}$ of IP is

$$\begin{aligned} \rho _{IP}(x) = \frac{1}{\Vert x \Vert } {{\,\textrm{vol}\,}}_{d-1}(P \cap x^\perp ). \end{aligned}$$

Here, ${{\,\textrm{vol}\,}}_{d-1}$ denotes the $(d-1)$-dimensional Euclidean volume, and $x^\perp \subseteq \mathbb {R}^d$ denotes the linear hyperplane which is orthogonal to $x \in \mathbb {R}^d$, namely the set $x^\perp = \{y\in \mathbb {R}^d \,|\, \langle x, y \rangle = 0\}$. To obtain meaningful results, we may thus assume that $P \subseteq \mathbb {R}^d$ is a d-dimensional polytope throughout this article. The topological boundary of the intersection body IP is defined by the equation $\partial IP = \{ x \in \mathbb {R}^d \mid \rho _{IP}(x) = 1 \}$. Since the radial function satisfies $\rho _{IP}(\lambda x) = \frac{1}{\lambda } \rho _{IP}(x)$ for every $\lambda >0$, it is completely determined by its restriction to the unit sphere.

The intersection body IP of a polytope is governed by the central hyperplane arrangement

$$\begin{aligned} \mathcal {H}(P)= \bigcup _{\begin{array}{c} v\ne \textbf{0}\text { is a } \\ \text {vertex of } P \end{array}} v^\perp . \end{aligned}$$

We denote the set of vertices of P by ${{\,\textrm{vert}\,}}(P)$, and the origin is denoted by $\textbf{0}\in \mathbb {R}^d$. An open chamber C of $\mathcal {H}(P)$ is a connected component of $\mathbb {R}^d \setminus \mathcal {H}(P)$. Given such a chamber C, all hyperplanes $x^\perp$ for $x \in C$ intersect P in the interiors of a fixed set of edges. The radial function restricted to such a chamber is a quotient of polynomials

$$\begin{aligned} \rho _{IP}|_C = \frac{p_C}{\Vert x \Vert ^2 q_C}, \end{aligned}$$

(1)

where $p_C$ is divisible by $\Vert x\Vert ^2$. Therefore, the topological boundary $\partial IP \cap C$ is the zero-set of the (irreducible) polynomial $\frac{p_C}{\Vert x \Vert ^2} - q_C$. We repeat a key argument in the proof of (1). Let $x \in C$ and $Q = P \cap x^\perp$. The value $\rho _{IP}(x)$ is by definition the volume of Q. This computation is done by considering a triangulation $\mathcal {T}$ of the boundary of Q. We extend this to a covering of $\text {conv}(Q,\textbf{0})$ by considering the set $\text {conv}(\Delta ,\textbf{0})$ for every simplex $\Delta \in \mathcal {T}$ such that $\textbf{0}\not \in \Delta$. Note that if $\textbf{0}\in P$, then this induces a central triangulation of Q. Denoting $v_1, \dots , v_d$ the vertices of a simplex $\Delta \in \mathcal {T}$, the volume of $\text {conv}(\Delta ,\textbf{0}) = \text {conv}(v_1, \dots , v_d, \textbf{0})$ is, up to a constant scaling factor, given by the determinant of the matrix

$$\begin{aligned} M_{\Delta }(x) = \begin{bmatrix} \frac{\langle b_{i_1}, x \rangle a_{i_1} - \langle a_{i_1}, x \rangle b_{i_1}}{\langle b_{i_1}-a_{i_1}, x \rangle } \\ \vdots \\ \frac{\langle b_{i_{d-1}}, x \rangle a_{i_{d-1}} - \langle a_{i_{d-1}}, x \rangle b_{i_{d-1}}}{\langle b_{i_{d-1}}-a_{i_{d-1}}, x \rangle } \\ x \end{bmatrix}, \end{aligned}$$

where the vertices $v_i$ arise as intersection of $x^\perp$ with edges of P, i.e., $v_i = \text {conv}(a_i,b_i) \cap x^\perp$ for $a_i, b_i \in {{\,\textrm{vert}\,}}(P)$. Assigning ${{\,\textrm{sgn}\,}}(\Delta ) \in \{-1,1\}$ to each simplex, this gives

$$\begin{aligned} \rho _{IP}(x) = {{\,\textrm{vol}\,}}_{d-1}(Q) = \frac{1}{\Vert x\Vert ^2 (d-1)!} \sum _{\Delta \in \mathcal {T}} {{\,\textrm{sgn}\,}}(\Delta ) \det (M_\Delta (x)). \end{aligned}$$

3 Translations and affine hyperplane arrangements

Let $P \subseteq \mathbb {R}^d$ be a polytope. In this section, we consider how the intersection body of $P+t$ transforms under variation of $t \in \mathbb {R}^d$. Recall from Sect. 2 that the combinatorial structure of the boundary of $I(P+t)$ is described by the central hyperplane arrangement $\mathcal {H}(P+t)$. We thus begin by studying the behavior of this hyperplane arrangement under translation of P. For this, we introduce a new affine hyperplane arrangement ${\mathscr {L}}(P)$, which captures the essence of $\mathcal {H}(P+t)$ under variation of t. We show that within a region R of ${\mathscr {L}}(P)$, the polynomials describing the boundary of $I(P+t)$, for $t \in R$, can be extended to polynomials in the variables $t_1,\dots ,t_d$.

Let $P \subseteq \mathbb {R}^d$ be a polytope and let ${{\,\textrm{vert}\,}}(P)$ be the set of its vertices. Denote by $H_v = v^\perp \subseteq \mathbb {R}^d$ the hyperplane through the origin that is orthogonal to a vertex $v\in {{\,\textrm{vert}\,}}(P)$. As described in the previous section, the collection of all such hyperplanes forms a central hyperplane arrangement $\mathcal {H}(P)$ in $\mathbb {R}^d$. For each such hyperplane, we define its positive and negative side as

$$\begin{aligned} H_v^+ = \left\{ x \in \mathbb {R}^d \mid \langle x,v \rangle > 0 \right\} \text { and } H_v^- = \left\{ x \in \mathbb {R}^d \mid \langle x,v \rangle < 0 \right\} . \end{aligned}$$

We now choose a translation vector $t \in \mathbb {R}^d$ and consider the vertices $\left\{ v+t \ \Big \vert \ v \in {{\,\textrm{vert}\,}}(P) \right\}$ of the translated polytope $P+t$. The hyperplane arrangement $\mathcal {H}(P+t)$ is given by the hyperplanes $(v+t)^\perp$, where v ranges over the vertices of P. The hyperplane $H_{v+t}$ can be obtained from $H_v$ by a rotation $r_{v,t}: \mathbb {R}^d \rightarrow \mathbb {R}^d$ such that $r_{v,t}\left( \tfrac{v}{||v||}\right) = \tfrac{v+t}{||v+t||}$, and thus $r_{v,t}(H_v) = H_{v+t}$, $r_{v,t}(H^+_v) = H^+_{v+t}$ and $r_{v,t}(H^-_v) = H^-_{v+t}$.

We label each maximal chamber C of $\mathcal {H}(P+t)$ with a sign vector $s(C)_{} \in \{+,-\}^{{{\,\textrm{vert}\,}}(P+t)}$ indexed by the vertices $w=v+t$ of $P+t$, where

$$\begin{aligned} s(C)_{w}&= + \quad \hbox { if } C \subseteq H^+_w, \\ s(C)_{w}&= - \quad \hbox { if } C \subseteq H^-_w. \end{aligned}$$

The set $\left\{ s(C)_{} \mid C \hbox { maximal chamber of } \mathcal {H}(P+t) \right\}$ describes the chirotope or signed cocircuits of the underlying oriented matroid of the hyperplane arrangement [14, Chapter 6.2.3].

Fig. 1

The hyperplane arrangements of $P+t$ from Example 3.1

Example 3.1

Let $P = \text {conv}\left( v_1, v_2, v_3 \right)$ be the triangle with vertices

$$\begin{aligned} v_1 = \begin{pmatrix}0 \\ 1 \end{pmatrix}, \qquad v_2 = \begin{pmatrix}-1 \\ -1 \end{pmatrix}, \qquad v_3 = \begin{pmatrix}1 \\ -1 \end{pmatrix}. \end{aligned}$$

Figure 1 shows the hyperplane arrangements $\mathcal {H}(P+t)$ for $t_0 = \textbf{0}$, $t_1 = (0,2)$, and $t_2 = (0,-2)$. Note that the underlying oriented matroids of $\mathcal {H}(P+t)$ for $t = t_1$ and $t = t_2$ are the same. We continue with this in Example 3.3.

We begin by showing that the signed cocircuit s(C) of a chamber C fully determines the set of edges of P which are intersected by $x^\perp$ for any $x \in C$.

Lemma 3.2

Let $P \subseteq \mathbb {R}^d$ be a polytope and let $t \in \mathbb {R}^d$. Let C be a maximal open chamber of $\mathcal {H}(P)$, and $C_t$ be a maximal open chamber of $\mathcal {H}(P+t)$ such that $s(C)_{} = s(C_t)_{}$, i.e., their signed cocircuits agree. Given $x \in C, \ x_t \in C_t$ consider

$$\begin{aligned} \mathcal {E}&= \{ e\subseteq P \mid e\text { is an edge of } P,\ x^\perp \cap e\ne \emptyset \}, \\ \mathcal {E}_t&= \{ e_t \subseteq P+t \mid e_t \text { is an edge of } P+t,\ x_t^\perp \cap e_t \ne \emptyset \}. \end{aligned}$$

Then, $\mathcal {E}_t = \{e + t \mid e \in \mathcal {E}\}$.

Proof

Let $e= \text {conv}\left( v_1, v_2 \right) \in \mathcal {E}$ be an edge of P. Since $x^\perp \cap e\ne \emptyset$, we have that $v_1,v_2$ lie on different sides of $x^\perp$. Equivalently, we have $s(C)_{v_1} = -s(C)_{v_2}$, and without loss of generality $s(C)_{v_1} = +$. Thus, $x \in H^+_{v_1} \cap H^{-}_{v_2}$. Since $\mathcal {H}(P+t)$ is obtained from $\mathcal {H}(P)$ by rotating the hyperplanes individually, and $s(C)_{} = s(C_t)_{}$, it follows that $x_t \in H^+_{v_1+t} \cap H^{-}_{v_2+t}$. Since $e+t$ is an edge of $P+t$ if and only if $e$ is an edge of P, the claim follows.$\square$

We consider the affine hyperplane arrangement

$$\begin{aligned} {\mathscr {L}}(P) = \{ {{\,\textrm{aff}\,}}(-v_1,\dots ,-v_d) \mid v_1,\dots ,v_d \text { are affinely independent vertices of } P \}, \end{aligned}$$

where ${{\,\textrm{aff}\,}}(-v_1,\dots ,-v_d)$ denotes the unique affine hyperplane containing the points $-v_1,$ $\dots ,$ $-v_d$. An open region R of ${\mathscr {L}}(P)$ is a connected component of $\mathbb {R}^d \setminus {\mathscr {L}}(P)$. We emphasize that there are two hyperplane arrangements in $\mathbb {R}^d$ which we consider simultaneously. We have the central hyperplane arrangement $\mathcal {H}(P+t)$, which depends on the choice of t, and subdivides $\mathbb {R}^d$ into open d-dimensional cones, which we call chambers of $\mathcal {H}(P+t)$. On the other hand, we have the affine hyperplane arrangement ${\mathscr {L}}(P)$, which subdivides $\mathbb {R}^d$ into open d-dimensional components, which we call regions of ${\mathscr {L}}(P)$. Note that ${\mathscr {L}}(P+t) = {\mathscr {L}}(P) - t$ by construction.

Example 3.3

Let P be the triangle from Example 3.1. The affine line arrangement ${\mathscr {L}}(P)$ is shown in Fig. 2. Note that the translation vectors $t = t_0,t_1,t_2$ all lie in different regions of the arrangement, despite the fact that the signed cocircuits of $\mathcal {H}(P+t_1)$ and $\mathcal {H}(P+t_2)$ agree, as displayed in Fig. 1.

Fig. 2

The arrangement ${\mathscr {L}}(P)$ of the triangle from Examples 3.1 and 3.3

In the following, we show that ${\mathscr {L}}(P)$ captures the characteristics of $\mathcal {H}(P+t)$ under variation of t. More precisely, we show that within a region R of ${\mathscr {L}}(P)$ the polynomials describing the boundary of $I(P+t)$, for $t \in R$, can be extended to polynomials in $t_1,\dots ,t_d$.

Proposition 3.4

Let $P \subseteq \mathbb {R}^d$ be a polytope and R be an open region of ${\mathscr {L}}(P)$. Then, the set of signed cocircuits of $\mathcal {H}(P+t)$ is fixed for all $t \in R$.

Proof

Let $v_1,\dots ,v_d$ be affinely independent vertices of P. By construction of ${\mathscr {L}}(P)$, R does not intersect $\mathcal {A} = {{\,\textrm{aff}\,}}(-v_1,\dots ,-v_d)$, i.e., R is strictly contained in one side of this hyperplane. Without loss of generality, we assume $R \subseteq \mathcal {A}^+$. The points $w_k = v_k + t$, for $k=1,\ldots ,d$, are linearly independent vertices of $P+t$ for all $t \in \mathbb {R}^d \setminus \mathcal {A}$. Hence, the subarrangement of $\mathcal {H}(P+t)$ consisting of hyperplanes $w_1^\perp ,\dots ,w_d^\perp$ is a simplicial arrangement which dissects $\mathbb {R}^d$ into $2^d$ open chambers, where each chamber is the image of an orthant of $\mathbb {R}^d$ under the linear map f defined by $e_i \mapsto w_i$ for all $i = 1,\ldots ,d$. Note that the signed cocircuits are fixed for every $t \in \mathcal {A}^+$. We now consider $\mathcal {H}(P+t)$ as common refinement of all subarrangements formed by d hyperplanes with linearly independent normals. The signed cocircuit of a chamber of $\mathcal {H}(P+t)$ is uniquely determined by the signed cocircuits of all subarrangements, and the cocircuits of the subarrangements are fixed for all $t \in R$. Thus, the cocircuits of $\mathcal {H}(P+t)$ are fixed for all $t \in R$.$\square$

Based on the above statement, we can prove the main result of the paper. This can be interpreted as a generalization of [9, Thm. 6], where P is the standard simplex with centroid at the origin and the hyperplane sections are linear.

Theorem 3.5

Let R be an open region of ${\mathscr {L}}(P)$, $t \in R$, and let $C_t$ be an open chamber of $\mathcal {H}(P+t)$. Then, the radial function $\rho _{I(P+t)}|_{C_t}$ of $I(P+t)$ restricted to the chamber $C_t$ and for $t\in R$ is a polynomial in the variables $t_1,\ldots ,t_d$ of degree at most $d-1$.

Proof

By Proposition 3.4, for a fixed region R the set of signed cocircuits of $\mathcal {H}(P+t)$ is fixed. Lemma 3.2 then implies that given a region R, $t \in R$, and a chamber $C_t$ of $\mathcal {H}(P+t)$, for any vector $x \in C_t$ the set of edges of $P+t$ which intersect $x^\perp$ is fixed. Let $Q = P \cap x^\perp$, for a certain $x \in C_t$, and let $\mathcal {T}$ be a triangulation of $\partial Q$, as explained in Sect. 2. Let $\Delta \in \mathcal {T}$ be a maximal simplex with vertices $v_1, \dots , v_{d-1}$ such that $\textbf{0}\not \in \Delta$ and, for each $i = 1,\ldots ,d-1$, let $a_i,b_i \in {{\,\textrm{vert}\,}}(P)$ such that $v_i = \text {conv}(a_i +t, b_i +t) \cap x^\perp$. The volume of the d-dimensional simplex $\text {conv}(\Delta ,\textbf{0})$ is, up to a multiplicative factor of $\frac{\pm 1}{\Vert x\Vert (d-1)!}$, the determinant of the matrix

$$\begin{aligned} M_{\Delta }(x,t) = \!\begin{bmatrix} \frac{\langle b_{1}+t, x \rangle (a_{1}+t) - \langle a_{1}+t, x \rangle (b_{1}+t)}{\langle b_{1}-a_{1}, x \rangle } \\ \vdots \\ \frac{\langle b_{d-1}+t, x \rangle (a_{d-1}+t) - \langle a_{d-1}+t, x \rangle (b_{d-1}+t)}{\langle b_{d-1}-a_{d-1}, x \rangle } \\ x \end{bmatrix} = M_{\Delta }(x,\textbf{0}) +\! \begin{bmatrix} \frac{\langle t, x \rangle (a_{1}-b_1)}{\langle b_{1}-a_{1}, x \rangle } + t \\ \vdots \\ \frac{\langle t, x \rangle (a_{d-1}-b_{d-1}) }{\langle b_{d-1}-a_{d-1}, x \rangle } + t \\ \textbf{0}\end{bmatrix}. \end{aligned}$$

The determinant of this matrix is a polynomial in the variables $t_1,\dots ,t_d$ of degree at most $d-1$. Since the volume of Q can be computed as

$$\begin{aligned} {{\,\textrm{vol}\,}}(Q) = \frac{1}{\Vert x\Vert (d-1)!} \sum _{\Delta \in \mathcal {T}} {{\,\textrm{sgn}\,}}(\Delta ) \det (M_\Delta (x,t)), \end{aligned}$$

the claim follows.$\square$

Remark 3.6

The result by Filliman [9, Thm. 6] uses a slightly different language, since it deals with linear sections of any dimension of simplices. In this setting, the natural ambient space is therefore the Grassmannian, and the volume function is shown to be piecewise rational in the Plücker coordinates. A generalization of this statement for any polytope is expected to hold true, and it is left for future research.

Example 3.7

Figure 3 shows the continuous deformation of the intersection body $I(P+t)$ of the unit square $P = [-1,1]^2$ under translation by $t\in \mathbb {R}^2$ within each bounded region of the affine line arrangement ${\mathscr {L}}(P)$. The figure shows the 6 lines of the affine line arrangement in black. For choices of translation vectors $t \in \mathbb {R}^2$ from the interior of a maximal region, the corresponding intersection body $I(P+t)$ is drawn in red at the position t in the picture. Whenever t is chosen from a point on a line of the arrangement, then $I(P+t)$ is drawn next to the line with a gray arrow indicating the position of t.

Fig. 3

The arrangement ${\mathscr {L}}(P)$ of affine lines for $P = [-1,1]^2$, in black, together with $I(P+t)$ for different choices of t, in red, as in Example 3.7

4 Convexity in dimension 2

For each fixed region R of the affine line arrangement ${\mathscr {L}}(P)$, Theorem 3.5 implies that, as we move $t \in R$ continuously, the intersection body $I(P+t)$ deforms continuously as well. We now characterize under which circumstances the intersection body of a polygon is convex. Note that IP cannot be convex if the origin lies outside of P or is a vertex of P (the argument for general dimensions will be given in Remark 5.1). We thus consider the distinct cases of when the origin lies in the interior of P, and when the origin lies in the interior of an edge. Figure 3 indicates that in the case of the square, the intersection body of $P+t$ is convex (up to Euclidean closure, see Remark 4.5) for precisely 5 translation vectors: the center of symmetry and the midpoints of the four edges. In Theorem 4.4, we show that the number of such translation vectors is always finite, and that parallelograms maximize this number.

The goal of this section is to give a characterization of polygons whose intersection bodies are convex. In the following Propositions 4.1 and 4.2, we consider polygons with the origin in the interior, and characterize the geometry of the boundary of IP. More precisely, we will see that the chambers in which IP is convex correspond to pairs of parallel edges of P, and that the polynomials defining the boundary of IP are linear in this case.

Proposition 4.1

Let $P \subseteq \mathbb {R}^2$ be a polygon. Let C be a chamber of $\mathcal {H}(P)$, and consider $x\in C$. We denote by $v_1(x), v_2(x)$ the points of intersection $x^\perp \cap \partial P = \left\{ v_1(x), v_2(x) \right\}$. Let $\text {conv}\left( a_1,b_1 \right) , \text {conv}\left( a_2,b_2 \right)$ be edges of P such that $v_1(x)\in \text {conv}\left( a_1,b_1 \right)$ and $v_2(x)\in \text {conv}\left( a_2,b_2 \right)$. Then, the polynomial defining $\partial IP$ in the chamber C is linear if and only if the segments $\text {conv}\left( a_1,b_1 \right)$ and $\text {conv}\left( a_2,b_2 \right)$ are parallel.

Proof

We want to prove that $\{x\in C \mid \ \rho _{IP}|_C(x)=1\}$ is a line segment if and only if the two edges $\text {conv}\left( a_i,b_i \right)$ are parallel. Assume that $v_1(x) = \lambda a_1 + (1-\lambda ) b_1$ and $v_2(x) = \mu a_2 + (1-\mu ) b_2$ for some $\lambda ,\mu \in (0,1)$. Since $v_1(x), v_2(x) \in x^\perp$, we have

$$\begin{aligned} \lambda = \frac{ \langle b_1, x \rangle }{ \langle b_1-a_1, x \rangle }, \qquad \mu = \frac{ \langle b_2, x \rangle }{ \langle b_2-a_2, x \rangle }. \end{aligned}$$

We compute the length of $\text {conv}(v_1(x),v_2(x))$, or equivalently of $\text {conv}(\textbf{0}, v_1(x) - v_2(x))$. We do this via the area of the triangle with vertices $\textbf{0}, v_1(x) - v_2(x)$ and $\tfrac{x}{\Vert x \Vert ^2}$. Hence, the radial function can be computed by the determinantal expression

$$\begin{aligned} \rho _{IP}|_C(x) = \frac{1}{\Vert x\Vert ^2} \left| \det \begin{bmatrix} v_1(x)-v_2(x) \\ x \end{bmatrix} \right| . \end{aligned}$$

We compute the radial function explicitly. First,

$$\begin{aligned}{} & {} v_1(x)-v_2(x) \\{} & {} \quad = \frac{ \left( \langle b_2-a_2, x \rangle \left( \langle b_1,x \rangle a_1 - \langle a_1,x \rangle b_1\right) - \langle b_1-a_1, x \rangle \left( \langle b_2,x \rangle a_2 - \langle a_2,x \rangle b_2 \right) \right) }{ \langle b_1-a_1, x \rangle \langle b_2-a_2, x \rangle }. \end{aligned}$$

The boundary $\partial P \cap C$ is given by the set of points $x \in C$ such that $\rho _{IP}|_C(x)=1$, i.e., the points which satisfy

$$\begin{aligned} \frac{1}{\Vert x\Vert ^2} \det \begin{bmatrix} \langle b_2-a_2, x \rangle \left( \langle b_1,x \rangle a_1 - \langle a_1,x \rangle b_1\right) - \langle b_1-a_1, x \rangle \left( \langle b_2,x \rangle a_2 - \langle a_2,x \rangle b_2 \right) \\ x \end{bmatrix} \nonumber \\ \qquad = \; \langle b_1-a_1, x \rangle \langle b_2-a_2, x \rangle , \end{aligned}$$

(2)

assuming that the determinant in the left hand side is positive in C (otherwise it gets multiplied by $-1$). This determinant is a cubic polynomial in x, which by [2, Prop. 5.5] is divisible by $\Vert x\Vert ^2$. Hence, the left hand side of (2) is a homogeneous linear polynomial in x. It divides the right hand side if and only if $(b_2-a_2) = \kappa (b_1-a_1)$ for some $\kappa \in \mathbb {R}$, i.e., if the two edges $\text {conv}\left( a_i,b_i \right)$ are parallel. In this case, (2) is a linear equation, and hence, the curve defined by (2) is a line; otherwise, it is a conic, passing through the origin.$\square$

Proposition 4.2

Let $P\subseteq \mathbb {R}^2$ be a polygon with the origin in its interior. If there exists a line through the origin which intersects $\partial P$ in two non-parallel edges, then IP is not convex.

Proof

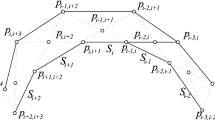
Let C be a chamber of $\mathcal {H}(P)$ such that $x^\perp$ intersects two non-parallel edges $\ell _1, \ell _2$ of P. Consider $u_a,u_b\in C\cap S^1$. As shown in Fig. 4, we denote

$$\begin{aligned}&\qquad u_a^\perp \cap \ell _1 = a = \left( {\begin{matrix}a_1 \\ a_2 \end{matrix}}\right) ,{} & {} u_b^\perp \cap \ell _1 = b = \left( {\begin{matrix}b_1 \\ b_2\end{matrix}}\right) , \qquad \\&\qquad u_a^\perp \cap \ell _2 = -\alpha a,{} & {} u_b^\perp \cap \ell _2 = -\beta b, \qquad \end{aligned}$$

for some positive real numbers $\alpha , \beta > 0$. Since $\ell _1$ and $\ell _2$ are not parallel, we have $\alpha \ne \beta$. We can choose a, b such that $u_a = \frac{1}{\Vert a\Vert } \left( {\begin{matrix}a_2 \\ -a_1 \end{matrix}}\right)$ and $u_b = \frac{1}{\Vert b\Vert } \left( {\begin{matrix}b_2 \\ -b_1 \end{matrix}}\right)$. The lengths of the line segments $u_a^\perp \cap P = \text {conv}\left( a, -\alpha a \right)$ and $u_b^\perp \cap P = \text {conv}\left( b, -\beta b \right)$ are

$$\begin{aligned} \Vert u_a^\perp \cap P \Vert = \Vert a - ( - \alpha a) \Vert = (1+\alpha ) \Vert a \Vert , \\ \Vert u_b^\perp \cap P \Vert = \Vert b - ( - \beta b) \Vert = (1+\beta ) \Vert b \Vert . \end{aligned}$$

Thus, the boundary points of IP in directions $u_a,u_b$ are

$$\begin{aligned} p_a&:= \rho _{IP} (u_a) \, u_a = (1 + \alpha ) \Vert a\Vert \, u_a = (1 + \alpha ) \, \begin{pmatrix}a_2 \\ -a_1 \end{pmatrix}, \\ p_b&:= \rho _{IP} (u_b) \, u_b = (1 + \beta ) \Vert b\Vert \, u_b = (1 + \beta ) \, \begin{pmatrix}b_2 \\ -b_1\end{pmatrix}, \end{aligned}$$

respectively. Consider the midpoint $\frac{a+b}{2}\in \ell _1$ and let $u_{a+b}$ be the unit vector in C orthogonal to $a+b$ (and thus also to $\frac{a+b}{2}$). Then, $u_{a+b} = \tfrac{1}{\Vert a+b\Vert } \left( {\begin{matrix}a_2 + b_2 \\ -a_1 - b_1\end{matrix}}\right)$, $u_{a+b}^\perp \cap \ell _2 = -\frac{\alpha \beta }{\alpha + \beta } (a+b)$ and the boundary point of IP in direction $u_{a+b}$ is

$$\begin{aligned} p_{a+b} = \rho _{IP} (u_{a+b}) \, u_{a+b} = \left( \frac{1}{2} + \frac{\alpha \beta }{\alpha + \beta } \right) \Vert a+b\Vert \, u_{a+b} = \left( \frac{1}{2} + \frac{\alpha \beta }{\alpha + \beta } \right) \, \begin{pmatrix}a_2 + b_2 \\ -a_1 - b_1 \end{pmatrix}. \end{aligned}$$

Let $q = \text {conv}\left( p_a,p_b \right) \cap {{\,\textrm{cone}\,}}\left( u_{a+b} \right)$, as in Fig. 4. We want to prove that $IP\cap C$ is not convex, by showing that $\Vert q\Vert > \Vert p_{a+b}\Vert$. Indeed, we can compute that

$$\begin{aligned} q = \frac{(1+\alpha )(1+\beta )}{2+\alpha +\beta } (a_2 + b_2,-a_1 - b_1), \end{aligned}$$

and therefore

$$\begin{aligned} \Vert q\Vert - \Vert p_{a+b}\Vert&= \frac{(1+\alpha )(1+\beta )}{2+\alpha +\beta } \Vert a+b\Vert - \left( \frac{1}{2} + \frac{\alpha \beta }{\alpha + \beta } \right) \Vert a+b\Vert \\&= \frac{(\alpha -\beta )^2}{2(2+\alpha +\beta )(\alpha +\beta )} \Vert a+b\Vert . \end{aligned}$$

Since $\alpha \ne \beta$, this expression is strictly positive, and so $q\not \in IP$. This proves that $p_a,p_b \in IP$, but the segment $\text {conv}\left( p_a,p_b \right)$ is not contained in IP. Hence, IP is not convex.

Fig. 4

The proof of Propositions 4.2 in a picture. Left: the lines orthogonal to $u_a,u_b, u_{a+b}$ and their intersections with the edges $\ell _1, \ell _2$ of P. Right: the points $p_a,p_b,p_{a+b}\in \partial IP$, and the point $q\in \text {conv}\left( p_a,p_b \right)$, but $q\not \in IP$

$\square$

We are now ready to move toward a full classification of convexity of intersection bodies of polygons for any translation. Note that if P is centrally symmetric, then the convexity of P and the description of IP follow from the following classical statement.

Theorem 4.3

[10, Theorem 8.1.4] Let $K \subseteq \mathbb {R}^2$ be a centrally symmetric convex body centered at the origin. Then, $IK = r_{\frac{\pi }{2}}(2K)$, where $r_{\frac{\pi }{2}}$ is a counter-clockwise rotation by $\frac{\pi }{2}$.

Our goal is to classify also the cases in which P is not centrally symmetric and centered at the origin. We now prove the main result of this section.

Theorem 4.4

Let $P \subseteq \mathbb {R}^2$ be a polygon. Then, IP is a convex body if and only if $P=-P$.

Proof

As noted in Remark 5.1, IP is not convex if the origin lies in $\mathbb {R}^2\setminus P$, or if the origin is a vertex of P. We are left to analyze the cases in which the origin lies in the interior of P or in the interior of an edge of P.

We first consider the case in which the origin lies in the interior of P and show that IP is convex if and only if $P = -P$. If $P=-P$, then Theorem 4.3 implies that IP is convex. Assume now that IP is convex, and the origin lies in the interior of P. Then, $C\cap IP$ is convex for every chamber C of $\mathcal {H}(P)$. In particular, by Propositions 4.2, every line $u^\perp$, $u \in S^1$, which does not intersect a vertex of P intersects $\partial P$ in the interior of two parallel edges. Hence, the edges of P come in pairs of parallel edges. We rotate $u \in S^1$ continuously. Whenever $u^\perp$ crosses a vertex of one edge, it must also cross a vertex in the parallel edge, since otherwise this results in a pair of non-parallel edges. This implies that for every vertex v of P, there exists a vertex w of P such that $w = -\lambda v$ for some $\lambda >0$. Since all edges are pairwise parallel, this positive scalar $\lambda$ is the same for all vertices. Therefore, we also get that $v = -\lambda w$, which implies that $\lambda =1$. Hence, $P=-P$.

Consider now the case in which the origin lies in the interior of an edge of P with normal vector $e \in \mathbb {R}^2$. Thus, $\rho _{IP}(x) = \tfrac{1}{2} \rho _{ I(P \cup -P)}(x)$ for all $x \in \mathbb {R}^2 \setminus \mathbb {R}e$ and $\rho _{IP}(e) > \tfrac{1}{2} \rho _{I(P \cup -P)}(e)$. Here, $\mathbb {R}e$ denotes the line spanned by e. Since the origin lies in the interior of the star body $P \cup -P$, its radial function is continuous, which implies that also $\tfrac{1}{2}\rho _{ I(P \cup -P)}$ is continuous. Hence, $\rho _{IP}$ is discontinuous, and therefore, IP is not convex. $\square$

Remark 4.5

The last case of the proof of Theorem 4.4 can be made more precise. Using the notion of chordal symmetral from [10, Chapter 5.1], we deduce that

$$\begin{aligned} \frac{1}{2} I(P\cup -P) = P \cup -P. \end{aligned}$$

Therefore, $I(P\cup -P)$ is convex if and only if $P \cup -P$ is convex. This is the case if and only if the origin is the midpoint of an edge and the sum of the angles adjacent to this edge is at most $\pi$. Using elementary properties of the sums of interior and exterior angles of polygons, it can be shown that a polygon admits at most 4 such edges, and equality is realized exactly when P is a parallelogram. Figure 5 shows a collection of examples of polygons, together with the possible positions of the origin on such edges. In this case, the argument from the proof of Theorem 4.4 implies that the Euclidean closure of $IP \setminus \mathbb {R}e$ is convex. Here, $\mathbb {R}e$ denotes the line spanned by e.

Fig. 5

Examples of positions of the origin (orange bullet) in which IP is almost convex, as described in Remark 4.5. From left to right: a parallelogram, an acute triangle, a diamond shape, a panettone shape, and a centrally symmetric polygon (which has no admissible positions)

We close this section by pointing out that many arguments made in this section do not generalize to higher dimensions: In contrast to Propositions 4.1 and 4.2, in higher dimensions there exist convex pieces $IP \cap C$ which are not linear. Furthermore, the identification with the chordal symmetral body, as in Remark 4.5, does not hold in general. However, these insights in the 2-dimensional case will turn out to be essential for arguments on the general case in the following section.

5 Convexity in higher dimensions

We devote this section to discuss the convexity of intersection bodies of polytopes of dimension $d >2$. We make use of the results obtained in section 4 to show that, similar to the 2-dimensional case, the intersection body of a d-dimensional cuboid is convex if and only if the origin is its center of symmetry. Notice that this result was partially proven in [8], when the origin lies in the interior of the polytope. Our results complete the analysis for boundary points. Moreover, we provide computational evidence that there exist intersection bodies of polytopes that are strictly convex.

Remark 5.1

To obtain an intersection body IP which is convex, the origin must lie in the interior of P. If the origin lies in the interior of a facet, the argument from Theorem 4.4 applies analogously, i.e., $\rho _{IP}(x) = \tfrac{1}{2} \rho _{ I(P \cup -P)}(x)$ for all $x \in \mathbb {R}^2$ except for the two normals of the facet, for which a strict inequality holds. Hence, $\rho _{IP}$ is discontinuous, and therefore IP is not convex. If the origin lies on a lower-dimensional face F, there exists a hyperplane $x^\perp$ such that $P \cap x^\perp = F$ and thus the radial function of IP in direction x has value 0. The set of such x is a cone $V = C \cup -C$, where $C\subset \mathbb {R}^d$ is a convex pointed cone. Then, given $x\in C$, there exist $x_1,x_2 \in \mathbb {R}^d \setminus V$ such that x is a convex combination of $x_1$ and $x_2$. Since $\rho _{IP}(x) = 0$, the segment with extrema $\rho _{IP}(x_1) \, x_1$ and $\rho _{IP}(x_2) \, x_2$ is not entirely contained in the intersection body IP, but its extrema are.

The next result connects the intersection body of a convex body to the intersection body of a prism over the given convex body.

Proposition 5.2

Let $L \subseteq \mathbb {R}^{d-1}$ be a convex body and $K = L \times [a,b] \subseteq \mathbb {R}^{d-1} \times \mathbb {R}\cong \mathbb {R}^d$ be a prism over L. Then, the intersection of IK with the hyperplane $H = \{x \in \mathbb {R}^d \mid x_d=0\}$ is the $(b-a)$th dilate of IL, i.e.,

$$\begin{aligned} IK \cap H = (b-a) \ IL. \end{aligned}$$

Proof

Let $u = (\widetilde{u},0) \in H$ and consider its orthogonal complement $u^\perp \subseteq \mathbb {R}^{d}$, which in this case can be interpreted as $\widetilde{u}^\perp \times \mathbb {R}\subseteq \mathbb {R}^{d-1}\times \mathbb {R}$. Then

$$\begin{aligned} K \cap u^\perp = (L \times [a,b]) \cap (\widetilde{u}^\perp \times \mathbb {R}) = (L\cap \widetilde{u}^\perp ) \times [a,b]. \end{aligned}$$

We can therefore compute the radial function of IK as

$$\begin{aligned} \rho _{IK}(u) = {{\,\textrm{vol}\,}}_{d-1} (K \cap u^\perp ) = {{\,\textrm{vol}\,}}_{d-1} \big ( (L\cap \widetilde{u}^\perp ) \times [a,b] \big ) = (b-a) \cdot \rho _{IL}(\widetilde{u}) \end{aligned}$$

for $u\in H$. Equivalently, $IK \cap H = (b-a) \ IL$.$\square$

It follows that if IL is non-convex, then so is IK. This behavior can be observed in the following example.

Example 5.3

Consider the unit cube $P = [-1,1]^3$, which is a prism over a square. With the translation $t = (1,1,1)$, we obtain the cube $P+t = [0,2]^3$, and $I(P+t)$ is displayed in Fig. 6, from two different points of view. Proposition 5.2 implies that $I(P+t) \cap (0,0,1)^\perp$ is the second dilation of the intersection body of the square $[0,2]^2$, which is also displayed at the bottom left of Fig. 3 in red. Figure 6 originally appeared as [2, Figure 3].

Fig. 6

The intersection body of the 3-dimensional cube $P=[0,2]^3$ (blue) and the intersection body of the square $Q = [0,2]^2$ (red)

We can now use Propositions 5.2 to describe the convexity of intersection body of a cuboid in any dimension.

Proposition 5.4

Let $P = [a_1,b_1]\times [a_2,b_2] \times \dots \times [a_d,b_d]$ be a d-dimensional cuboid. Then, IP is convex if and only if $P=-P$.

Proof

If $P=-P$ then IP is convex by Busemann’s Theorem [7]. Conversely, let $P \ne -P$. We prove that IP is not convex by induction on d. The base case of $d = 2$ follows from Theorem 4.4. Let now $P = [a_1,b_1]\times [a_2,b_2] \times \dots \times [a_d,b_d]$. By Remark 5.1, we assume that the origin lies in the interior of P, and thus $a_i< 0 < b_i$ for all $i \in 1,\dots ,d$. Without loss of generality, $P \ne -P$ implies that $a_1 \ne -b_1$. Let $Q = P \cap H$, where $H = \{x \in \mathbb {R}^d \mid x_d = 0 \}$. Notice that $P = Q \times [a_d,b_d]$. Thus, Q is a cuboid of dimension $(d-1)$ such that $Q \ne -Q$. By induction, this implies that IQ is not convex. Propositions 5.2 implies that $IP \cap H = (b_d - a_d) IQ$. As a consequence, $IP \cap H$ is not convex, and therefore IP is not convex.$\square$

Remark 5.5

We note that whenever the intersection body is strictly convex, then there is an open ball around the origin of translation vectors such that the intersection body is still convex. Indeed, this holds in more generality for the intersection body IK of any star body $K \subseteq \mathbb {R}^d$, with $\textbf{0}$ in its interior, and follows directly from the continuity of the volume function, and therefore of the radial function, with respect to t. Let $x,y\in \mathbb {R}^d$ and $p_{\star } \!=\! \rho _{I(K+t)}(\star ) \cdot \star$ for $\star \in \{x, y, x+y\}$, so that $p_{\star } \in \partial I(K+t)$. Denote by $q_{x+y}$ the point of the segment $\text {conv}\left( p_x,p_y \right)$ which is a multiple of $x+y$, namely $q_{x+y} = \frac{\rho _{I(P+t)}(x)\, \rho _{I(K+t)}(y)}{\rho _{I(K+t)}(x) + \rho _{I(K+t)}(y)} (x+y)$. Then, $I(K+t)$ is strictly convex if and only if

$$\begin{aligned} \frac{\rho _{I(P+t)}(x)\, \rho _{I(K+t)}(y)}{\rho _{I(K+t)}(x) + \rho _{I(K+t)}(y)} = \frac{\Vert q_{x+y}\Vert }{\Vert x+y\Vert } < \frac{\Vert p_{x+y}\Vert }{\Vert x+y\Vert } = \rho _{I(K+t)}(x+y). \end{aligned}$$

(3)

This gives a quadratic condition in $\rho _{I(K+t)}$, which is continuous in t. Therefore, if (3) holds for IK, it holds also for $I(K+t)$ with $t\in B_\varepsilon (\textbf{0})$, for some $\varepsilon >0$.

The next example shows that strictly convex intersection bodies of polytopes as in Propositions 5.5 do indeed exist.

Example 5.6

The intersection body of the 3-dimensional centrally symmetric icosahedron P is strictly convex. Indeed, using HomotopyContinuation.jl [6] one obtains numerical evidence that the algebraic varieties that define the boundary of IP do not contain lines (this is reasonable, since the generic quintic and sextic surfaces in 3-dimensional space do not contain lines). Moreover, because of the central symmetry, the intersection body is convex. Hence, it is strictly convex. This intersection body is displayed Fig. 7 (which originally appeared in [2, Figure 1], and our computations can be verified using the code on MathRepo [1].

Fig. 7

The intersection body of the icosahedron from Example 5.6

To summarize, we have studied the admissible positions of the origin with respect to a full-dimensional polytope P, such that IP is convex. For $d=2$, we have shown that the set of admissible positions is precisely the center of symmetry (if it exists). In higher dimensions, it is sometimes infinite, as for the icosahedron, but other times only a single point, as for a cube. We note that proving non-convexity is a much easier task then proving convexity, as the first can be achieved by showing the non-convexity of a small curve on the boundary, while convexity is a global condition. A possible approach to tackle this problem in the case of polytopes might be studying the curvature of the algebraic hypersurfaces defining the boundary of the intersection body, as in [5].

Another interesting direction of research concerns the topology of the set of admissible positions. We collect here some open questions.

• 1. If the set of admissible positions of P is finite, what is its cardinality?

• 2. If the set of admissible positions of P is infinite, how many connected components does it have? What is the dimension of these connected components?

• 3. If IP is convex but not strictly convex, does this imply $P = -P$?

• 4. What are the conditions on P that make IP strictly convex?