Abstract
We provide an explicit construction of finite 4-regular graphs \((\Gamma _k)_{k\in {\mathbb {N}}}\) with \(\text {girth}\, \Gamma _k\rightarrow \infty \) as \(k\rightarrow \infty \) and \(\frac{\text {diam}\,\Gamma _k}{\text {girth}\,\Gamma _k}\leqslant D\) for some \(D>0\) and all \(k\in {\mathbb {N}}\). For each fixed dimension \(n\geqslant 2,\) we find a pair of matrices in \(SL_{n}({\mathbb {Z}})\) such that (i) they generate a free subgroup, (ii) their reductions \(\bmod \, p\) generate \(SL_{n}({\mathbb {F}}_{p})\) for all sufficiently large primes p, (iii) the corresponding Cayley graphs of \(SL_{n}({\mathbb {F}}_{p})\) have girth at least \(c_n\log p\) for some \(c_n>0\). Relying on growth results (with no use of expansion properties of the involved graphs), we observe that the diameter of those Cayley graphs is at most \(O(\log p)\). This gives infinite sequences of finite 4-regular Cayley graphs of \(SL_n({\mathbb {F}}_p)\) as \(p\rightarrow \infty \) with large girth and bounded diameter-by-girth ratio. These are the first explicit examples in all dimensions \(n\geqslant 2\) (all prior examples were in \(n=2\)). Moreover, they happen to be expanders. Together with Margulis’ and Lubotzky–Phillips–Sarnak’s classical constructions, these new graphs are the only known explicit logarithmic girth Cayley graph expanders.
Similar content being viewed by others
Data availibility
Not applicable as the results presented in this manuscript rely on no external sources of data or code.
Notes
For \(n\geqslant 3\), \(G=SL_n({\mathbb {Z}})\) has Kazhdan’s property (T), hence any generating set S and a nested family of finite index normal subgroups
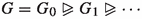 with \(\bigcap _{n=0}^{\infty }G_n=\{1\}\) naturally provide an infinite expander \(\bigsqcup _{n=0}^{\infty } Cay(G/G_n, S_n),\) where \(S_n\) is the canonical image of S. Such expanders are neither of large girth, nor dg-bounded.
with \(\bigcap _{n=0}^{\infty }G_n=\{1\}\) naturally provide an infinite expander \(\bigsqcup _{n=0}^{\infty } Cay(G/G_n, S_n),\) where \(S_n\) is the canonical image of S. Such expanders are neither of large girth, nor dg-bounded.For elements g, h in a group G, the commutator [g, h] is equal to \(g^{-1}h^{-1}gh\).
A map between graphs is regular if it is Lipschitz and pre-images of vertices have uniformly bounded cardinality. Two graphs are regularily equivalent if there exist two regular maps: from one graph to the other, and back.
References
Arzhantseva, G., Delzant, T.: Examples of random groups, available on the authors’ websites (2008)
Arzhantseva, G., Guentner, E., Špakula, J.: Coarse non-amenability and coarse embeddings. Geom. Funct. Anal. 22(1), 22–36 (2012)
Arzhantseva, G., Tessera, R.: Admitting a coarse embedding is not preserved under group extensions. Int. Math. Res. Not. IMRN 20, 6480–6498 (2019)
Biggs, N.: Constructions for cubic graphs with large girth. Electron. J. Combin. 5, Article 1 (1998)
Bourgain, J., Gamburd, A.: Uniform expansion bounds for Cayley graphs of \({\rm SL}_2({\mathbb{F}}_p)\). Ann. Math. (2) 167(2), 625–642 (2008)
Bourgain, J., Varjú, P.P.: Expansion in \(SL_d({\bf Z}/q{\bf Z}),\, q\) arbitrary. Invent. Math. 188(1), 151–173 (2012)
Breuillard, E.: Approximate subgroups and super-strong approximation. In: Groups St Andrews 2013: London Mathematical Society Lecture Note Series, vol. 422, pp. 1–50. Cambridge University Press, Cambridge (2015)
Breuillard, E., Green, B., Tao, T.: Approximate subgroups of linear groups. Geom. Funct. Anal. 21(4), 774–819 (2011)
Brooks, R.: The spectral geometry of a tower of coverings. J. Differ. Geom. 23, 97–107 (1986)
Burger, M.: Petites valeurs propres du Laplacien et topologie de Fell, doctoral thesis, Econom Druck AG (Basel) (1986)
Davidoff, G., Sarnak, P., Valette, A.: Elementary Number Theory, Group Theory, and Ramanujan Graphs, London Mathematical Society Student Texts, vol. 55. Cambridge University Press, Cambridge (2003)
Erdős, P., Sachs, H.: Reguläre Graphen gegebener Taillenweite mit minimaler Knotenzahlare Graphen gegebener Taillenweite mit minimaler Knotenzahl. Wiss. Z. Martin-Luther-Univ. Halle-Wittenberg Math.-Natur. Reihe 12, 251–257 (1963)
Golsefidy, A.S., Varjú, P.P.: Expansion in perfect groups. Geom. Funct. Anal. 22(6), 1832–1891 (2012)
Gow, R., Tamburini, M.C.: Generation of \({\rm SL}(n, {\bf Z})\) by a Jordan unipotent matrix and its transpose. Linear Algebra Appl. 181, 63–71 (1993)
Gowers, W.T.: Quasirandom groups. Combin. Probab. Comput. 17(3), 363–387 (2008)
Gromov, M.: Random walk in random groups. Geom. Funct. Anal. 13(1), 73–146 (2003)
Helfgott, H.A.: Growth and generation in \({\rm SL}_2({\mathbb{Z}}/p{\mathbb{Z}})\). Ann. Math. (2) 167(2), 601–623 (2008)
Higson, N., Lafforgue, V., Skandalis, G.: Counterexamples to the Baum–Connes conjecture. Geom. Funct. Anal. 12(2), 330–354 (2002)
Hume, D.: A continuum of expanders. Fund. Math. 238(2), 143–152 (2017)
Kasparov, G., Yu, G.: The coarse geometric Novikov conjecture and uniform convexity. Adv. Math. 206, 1–56 (2006)
Kontorovich, A., Long, D.D., Lubotzky, A., Reid, A.W.: What is \(\dots \) a thin group? Notices Amer. Math. Soc. 66(6), 905–910 (2019)
Kun, G.: On sofic approximations of property (T) groups (2016), arxiv:1606.04471
Lafforgue, V.: Un renforcement de la propriété (T). Duke Math. J. 143(3), 559–602 (2008)
Lafforgue, V.: Propriété (T) renforcée Banachique et transformation de Fourier rapide. J. Topol. Anal. 1(3), 191–206 (2009)
Landesman, A., Swaminathan, A., Tao, J., Xu, Y.: Lifting subgroups of symplectic groups over \({\mathbb{Z}}/\ell {\mathbb{Z}}\). Res. Number Theory 3, Art. 14 (2017)
Larsen, M.: Navigating the Cayley graph of \(SL_2({\mathbb{F}}_p)\). Int. Math. Res. Not. 27, 1465–1471 (2003)
Lubotzky, A.: One for almost all: generation of \({\rm SL}(n, p)\) by subsets of \({\rm SL}(n, {\bf Z})\), Algebra, \(K\)-theory, groups, and education (New York, 1997), Contemporary Mathematics, vol. 243. American Mathematical Society, Providence, RI 1999, 125–128 (1999)
Lubotzky, A., Phillips, R., Sarnak, P.: Ramanujan graphs. Combinatorica 8(3), 261–277 (1988)
Lubotzky, A., Venkataramana, T.N.: The congruence topology, Grothendieck duality and thin groups. Algebra Number Theory 13(6), 1281–1298 (2019)
Lucas, E.: Theorie des Fonctions Numeriques Simplement Periodiques. Amer. J. Math. 1(2), 184–196 (1878)
Lyndon, R.C., Schupp, P.E.: Combinatorial Group Theory, Classics in Mathematics. Springer, Berlin. Reprint of the 1977 edition (2001)
Margulis, G.A.: Explicit constructions of graphs without short cycles and low density codes. Combinatorica 2(1), 71–78 (1982)
Matthews, C.R., Vaserstein, L.N., Weisfeiler, B.: Congruence properties of Zariski-dense subgroups. I. Proc. London Math. Soc. (3) 48(3), 514–532 (1984)
Mendel, M., Naor, A.: Nonlinear spectral calculus and super-expanders. Publ. Math. Inst. Hautes Études Sci. 119, 1–95 (2014)
Mendel, M., Naor, A.: Expanders with respect to Hadamard spaces and random graphs. Duke Math. J. 164(8), 1471–1548 (2015)
Naor, A., Silberman, L.: Poincaré inequalities, embeddings, and wild groups. Compos. Math. 147(5), 1546–1572 (2011)
Nikolov, N., Pyber, L.: Product decompositions of Quasirandom groups and a Jordan type theorem. J. Eur. Math. Soc. (JEMS) 13(4), 1063–1077 (2011)
Nori, M.V.: On subgroups of \(GL_n ({\mathbb{F}}_p)\). Invent. Math. 88, 257–275 (1987)
Nowak, P., Sawicki, D.: Warped cones and spectral gaps. Proc. Amer. Math. Soc. 145(2), 817–823 (2017)
Ostrovskii, M.I.: Low-distortion embeddings of graphs with large girth. J. Funct. Anal. 262(8), 3548–3555 (2012)
Pyber, L., Szabó, E.: Growth in finite simple groups of Lie type. J. Amer. Math. Soc. 29(1), 95–146 (2016)
Sachs, H.: Regular graphs with given girth and restricted circuits. J. London Math. Soc. 38, 423–429 (1963)
Sarnak, P.: Notes on thin matrix groups, Thin groups and superstrong approximation, 343–362, Math. Sci. Res. Inst. Publ., 61. Cambridge University Press, Cambridge (2014)
Selberg, A.: On the estimation of Fourier coefficients of modular forms. In: Proceedings of Symposia in Pure Mathematics, Vol. 8, pp. 1–15. American Mathematical Society, Providence (1965)
Weigel, T.: On the profinite completion of arithmetic groups of split type, Lois d’algèbres et variétés algébriques (Colmar, 1991), pp. 79–101. Travaux en Cours, 50, Hermann, Paris (1996)
Acknowledgements
We thank Peter Sarnak for indicating that free subgroups from our Main Theorem are thin matrix groups, see Sect. 6, Alex Lubotzky for pointing out that our result also yields r-regular logarithmic girth Cayley expander graphs, for all even integer \(r\geqslant 4\), see Corollaries 6.1 and 6.2 and Nikolay Nikolov for attracting our attention to Nori’s result [38]. We are grateful to the anonymous referees for detailed comments and useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was partially supported by the European Research Council (ERC) Grant of Goulnara Arzhantseva, “ANALYTIC” Grant Agreement No. 259527.
Appendix
Appendix
For an interested reader, we give a detailed proof of Theorem 5.3.
Proof of Theorem 5.3
Fix \((n-1) = k\in {\mathbb {N}}\) and consider the matrix \(A^{lr_{i}}B^{ls_{i}}\) with \(l \geqslant 3k\) and \(r_{i},s_{i}\in {\mathbb {Z}}\backslash \lbrace 0\rbrace \). Let \(a,b\in {\mathbb {N}}\) with \(a,b\geqslant 2\). Suppose
where the polynomials \(P_{uv}(a,b), 1\leqslant u,v\leqslant n\) satisfy
-
\(P_{11}(a,b) = {lr_{i} \atopwithdelims ()k}{ls_{i} \atopwithdelims ()k}a^{k}b^{k} + {lr_{i} \atopwithdelims ()k-1}{ls_{i} \atopwithdelims ()k-1}a^{k-1}b^{k-1}+ \cdots + {lr_{i} \atopwithdelims ()3}{ls_{i} \atopwithdelims ()3}a^{3}b^{3} + {lr_{i} \atopwithdelims ()2}{ls_{i} \atopwithdelims ()2}a^{2}b^{2} + {lr_{i} \atopwithdelims ()1}{ls_{i} \atopwithdelims ()1}ab~+~1\)
-
\(P_{12}(a,b) = {lr_{i} \atopwithdelims ()k}{ls_{i} \atopwithdelims ()k-1}a^{k}b^{k-1} + {lr_{i} \atopwithdelims ()k-1}{ls_{i} \atopwithdelims ()k-2}a^{k-1}b^{k-2}+ \cdots + {lr_{i} \atopwithdelims ()3}{ls_{i} \atopwithdelims ()2}a^{3}b^{2} + {lr_{i} \atopwithdelims ()2}{ls_{i} \atopwithdelims ()1}a^{2}b^{1} + {lr_{i} \atopwithdelims ()1}a \)
...
and in general
-
\(P_{uv}(a,b) = \Sigma _{u'=u,v'=v}^{u'=k+2-v,v'=k+1}{lr_{i} \atopwithdelims ()k-u'+1}{ls_{i} \atopwithdelims ()k-v'+1}a^{k-u'+1}b^{k-v'+1} \) with \(u\leqslant v\)
-
\(P_{uv}(a,b) = \Sigma _{u'=u,v'=v}^{u'=k+1, v' = k+2-u}{lr_{i} \atopwithdelims ()k-u+1}{ls_{i} \atopwithdelims ()k-v+1}a^{k-u'+1}b^{k-v'+1}\) with \(u > v\)
...
-
\(P_{nn}(a,b) = 1\)
Then, we have the following inequalities for \(l\geqslant 3k\).
-
(1)
\(1 - \frac{1}{15}\leqslant \frac{P_{11}(a,b)}{{lr_{i} \atopwithdelims ()k}{ls_{i} \atopwithdelims ()k}a^{k}b^{k}} \leqslant 1 + \frac{1}{15}\).
-
(2)
\( |\frac{P_{12}(a,b)}{{lr_{i} \atopwithdelims ()k}{ls_{i} \atopwithdelims ()k}a^{k}b^{k}}| \leqslant \frac{1}{4}(1+\frac{1}{4^{2}}+ \frac{1}{4^{4}}+\cdots +\frac{1}{4^{2k-2}}) < \frac{1}{4}.\frac{16}{15} .\)
...
and in general
-
(3)
\( |\frac{P_{uv}(a,b)}{{lr_{i} \atopwithdelims ()k}{ls_{i} \atopwithdelims ()k}a^{k}b^{k}}| \leqslant \frac{1}{4^{u+v-2}} \cdot \frac{16}{15}\,\, \forall uv > 1.\)
We proceed as in the \(n=4\) case and consider
We shall show, by induction, that \(|z_{11}| > |z_{12}| + \cdots + |z_{1n}| + 1\), where the \(z_{ij}, 1\leqslant i,j\leqslant n\) denote the elements of the matrix Z.
From the above inequalities, it is clear that \(\Sigma _{v=2}^{n} |\frac{P_{1v}(a,b)}{{lr_{i} \atopwithdelims ()k}{ls_{i} \atopwithdelims ()k}a^{k}b^{k}}|<\frac{1}{2}\) which gives
and in turn implies that the inductive assumption (basis of induction) holds.
For the main step of the induction, suppose we are already given
with \(|z_{11}| > |z_{12}| + \cdots + |z_{1n}| + 1 \).
Let
Expand the first row of \(Z'\), i.e., \(z'_{1j}, 1\leqslant j \leqslant n\) in terms of the first row of Z, \(z_{1j}, 1\leqslant j\leqslant n\) and the elements of the matrix \( A^{lr_{t+1}}B^{ls_{t+1}}\). Then, we can conclude by considering the inductive assumption \(|z_{11}| > |z_{12}| + \cdots + |z_{1n}| + 1 \) and the above inequalities for the matrix \(A^{lr_{t+1}}B^{ls_{t+1}}\) that
\(\square \)
Rights and permissions
About this article
Cite this article
Arzhantseva, G., Biswas, A. Logarithmic girth expander graphs of \(SL_n({\mathbb {F}}_p)\). J Algebr Comb 56, 691–723 (2022). https://doi.org/10.1007/s10801-022-01128-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10801-022-01128-z



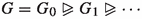 with
with