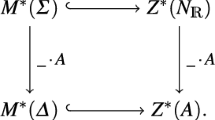Embedding the Picard group inside the class group: the case of $\mathbb {Q}$-factorial complete toric varieties

Abstract

Let X be a $\mathbb {Q}$-factorial complete toric variety over an algebraic closed field of characteristic 0. There is a canonical injection of the Picard group $\mathrm{Pic}(X)$ in the group $\mathrm{Cl}(X)$ of classes of Weil divisors. These two groups are finitely generated abelian groups; while the first one is a free group, the second one may have torsion. We investigate algebraic and geometrical conditions under which the image of $\mathrm{Pic}(X)$ in $\mathrm{Cl}(X)$ is contained in a free part of the latter group.

1 Introduction

Let X be an irreducible and normal algebraic variety over an algebraic closed field k of characteristic 0. Then, the group $H^0(X,\mathcal {K}^*/\mathcal {O}^*)$ of Cartier divisors of X can be represented as the subgroup of locally principal divisors of the group ${{\,\mathrm{Div}\,}}(X)$ of Weil divisors [5, Rem. II.6.11.2]. Quotienting both these groups by their subgroup of principal divisors one realizes the group ${{\,\mathrm{CaCl}\,}}(X)$ of classes of Cartier divisors as a subgroup of the group ${{\,\mathrm{Cl}\,}}(X)$ of classes of Weil divisors. In addition it turns out a canonical isomorphism between ${{\,\mathrm{CaCl}\,}}(X)$ and the Picard group ${{\,\mathrm{Pic}\,}}(X)$ of classes of isomorphic line bundles on X [5, Propositions II.6.13,15], so giving a canonical injection

(1)

For this reason, in this paper we will not distinguish between linear equivalence classes of Cartier divisors and isomorphism classes of line bundles, so identifying ${{\,\mathrm{CaCl}\,}}(X)={{\,\mathrm{Pic}\,}}(X)$.

Assume now that ${{\,\mathrm{Cl}\,}}(X)$ is finitely generated. It is well known that a finitely generated abelian group decomposes (noncanonically) in a direct sum of a free part and its torsion subgroup. Both ${{\,\mathrm{Pic}\,}}(X)$ and ${{\,\mathrm{Cl}\,}}(X)$ may have nontrivial torsion, and clearly, (1) induces an injection ${{\,\mathrm{Tors}\,}}({{\,\mathrm{Pic}\,}}(X))\hookrightarrow {{\,\mathrm{Tors}\,}}({{\,\mathrm{Cl}\,}}(X))$. Then, the following natural question arises:

(*):

under which conditions on X there exist free parts $F_C$ and $F_W$ of ${{\,\mathrm{Pic}\,}}(X)$ and ${{\,\mathrm{Cl}\,}}(X)$, respectively (see Definition 1), such that the injection (1) induces an injection

(2)

One should expect some geometric condition on X answering to question (*), but we could not find anything, in the current literature. Motivated by algebraic considerations (see Proposition 2) we call pure a normal, irreducible algebraic variety X such that ${{\,\mathrm{Cl}\,}}(X)$ is finitely generated and there exist free parts $F_C$ and $F_W$ positively answering problem (*) (see Definition 3). On the contrary if for each choice of free parts $F_C$ and $F_W$ the injection (1) does not induce any injection (2), then X is called impure. Obvious examples of pure varieties are given by those varieties X whose class group ${{\,\mathrm{Cl}\,}}(X)$ is finitely generated and free, and by smooth varieties admitting a finitely generated class group. Examples of impure varieties are in general more involved: Some of them are given in Sect. 3.3.

In the present paper we will consider the easier case of a $\mathbb {Q}$-factorial complete toric variety X, essentially for three reasons:

• (a) ${{\,\mathrm{Cl}\,}}(X)$ is a finitely generated abelian group (see, e.g., [2, Thm. 4.1.3])

• (b) ${{\,\mathrm{Pic}\,}}(X)$ is free, i.e., ${{\,\mathrm{Tors}\,}}({{\,\mathrm{Pic}\,}}(X))=0$ (see, e.g., [2, Prop. 4.2.5])

• (c) locally principal divisors can be easily described by means of principal divisors on affine open subsets of $X(\Sigma )$ associated with maximal cones of the fan $\Sigma$.

Conditions (a) and (b) translate problem (*) in the following

(**):

under which conditions on X there exists a free part F of ${{\,\mathrm{Cl}\,}}(X)$ such that (1) induces an injection ${{\,\mathrm{Pic}\,}}(X)\hookrightarrow F$ ?

The main result of the present paper is a sufficient condition for a $\mathbb {Q}$-factorial complete toric variety to be a pure variety. This is given by Theorem 2 and can be geometrically summarized as follows:

Theorem 1

Let $X(\Sigma )$ be a $\mathbb {Q}$-factorial complete toric variety of dimension n. Then, it admits a canonical covering $Y({\widehat{\Sigma }})\twoheadrightarrow X(\Sigma )$, unramified in codimension 1, such that the class group ${{\,\mathrm{Cl}\,}}(Y)$ is free (this follows by [8, Thm. 2.2]). Both X and Y are orbifolds [2, Thm. 3.1.19 (b)]; let

$$\begin{aligned} \{U_{{\widehat{\sigma }}}\}_{{\widehat{\sigma }}\in {\widehat{\Sigma }}(n)} \end{aligned}$$

be the collection of affine charts given by the maximal cones and covering Y. Calling ${{\,\mathrm{mult}\,}}({\widehat{\sigma }})$ the maximum order of a quotient singularity in the affine chart $U_{{\widehat{\sigma }}}$ (i.e., the multiplicity of the cone ${\widehat{\sigma }}\in {\widehat{\Sigma }}(n)$, see Definition 4), X is a pure variety if $m_\Sigma :=\gcd \{{{\,\mathrm{mult}\,}}({\widehat{\sigma }})\,|\,{\widehat{\sigma }}\in {\widehat{\Sigma }}(n)\}$ is coprime with the order of the Galois group of the covering $Y\rightarrow X$.

This is not a necessary condition: Example 2 gives a counterexample.

Section 3.3 is entirely devoted to give nontrivial examples of pure and impure varieties. A big class of nontrivial examples of pure varieties is exhibited in Sect. 3.4: Namely, it is given by

• all $\mathbb {Q}$-factorial complete toric varieties whose small $\mathbb {Q}$-factorial modifications (s$\mathbb {Q}$m) are actually isomorphisms.

Here s$\mathbb {Q}$m of X means a birational map $f:X\dashrightarrow Y$ such that f is an isomorphism in codimension 1 and Y is still a complete $\mathbb {Q}$-factorial toric variety. By the combinatorial point of view the previous geometric property translates in requiring that there is a unique simplicial and complete fan $\Sigma$ admitting 1-skeleton given by $\Sigma (1)$. Our proof that those varieties are pure (see Proposition 5) passes through showing that every maximal simplicial cone generated by rays in $\Sigma (1)$ and not containing any further element of $\Sigma (1)$ other than its generators (we call minimal such a maximal simplicial cone) is actually a cone of a complete and simplicial fan. This fact produces a completion procedure of fans looking to be of some interest by itself (see Lemma 4 and Sect. 3.4.1), when compared with standard completion procedures [3, Thm. III.2.8], [4, 6].

Further results of the present paper are given by:

• algebraic considerations given in Sect. 2; apart from the definition of a pure submodule given in Definition 2 and some consequences appearing in Proposition 2, the rest of this section consists of original considerations, as far as we know;

• a characterization of ${{\,\mathrm{Pic}\,}}(X)$ as a subgroup of ${{\,\mathrm{Cl}\,}}(X)$, when X is a pure, $\mathbb {Q}$-factorial, complete, toric variety: In [7, Thm. 2.9.2] we gave a similar characterization in the case of a poly weighted space (PWS: see Notation 3.1), that is, when ${{\,\mathrm{Cl}\,}}(X)$ is free; a first generalization was given in [9, Thm. 3.2 (3)] which is here improved in Sect. 4 and in particular by Theorem 3;

• an example of a four-dimensional simplicial fan whose completions necessarily require the addition of some new rays (see Example 3): Ewald, in his book [3], already announced the existence of examples of this kind (see the Appendix to Chapter III in [3]), but we were not able to recover it. We then believe that Example 3 may fill up a lack in the literature on these topics.

This paper is structured as follows: The first section gives all needed algebraic ingredients. Section 3 is devoted to state and prove the main result, given by Theorem 2, and produce examples of pure and impure varieties in the toric setup (see Sects. 3.3 and 3.4). Section 4 gives the above-mentioned characterization of ${{\,\mathrm{Pic}\,}}(X)$ as a subgroup of ${{\,\mathrm{Cl}\,}}(X)$ when X is a pure, $\mathbb {Q}$-factorial, complete, toric variety.

2 Algebraic considerations

Let A be a PID, $\mathcal {M}$ be a finitely generated A-module of rank r, and $T={{\,\mathrm{Tors}\,}}_A(\mathcal {M})$.

Definition 1

A free part of $\mathcal {M}$ is a free submodule $L\subseteq \mathcal {M}$ such that $\mathcal {M}=L\oplus T$.

It is well known that a free part of $\mathcal {M}$ always exists.

Let $H\subseteq \mathcal {M}$ be a free submodule of rank h. In general it is not true that H is contained in a free part of $\mathcal {M}$. For example, let $A=\mathbb {Z}$, $\mathcal {M}=\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$ and let $H=\langle (2,1)\rangle$.

Proposition 1

There exist elements $a_1,\ldots , a_h\in A$ such that $a_1|a_2 |\ldots |a_h$ satisfying the following property: every free part L of $\mathcal {M}$ has a basis $\mathbf {f}_1,\ldots , \mathbf {f}_r$ such that $a_1\mathbf {f}_1+t_1, \ldots , a_h\mathbf {f}_h+t_h$ is a basis of H for suitable $t_1,\ldots , t_h\in T$.

Proof

Let $\pi :\mathcal {M}\rightarrow \mathcal {M}/T$ the quotient map. The group $\mathcal {M}/T$ is free of rank r. The restriction of $\pi$ to H is injective, since H is free and $\ker (\pi )=T$. Therefore, $\pi (H)$ is a subgroup of rank h of the free group $\mathcal {M}/T$. By the elementary divisor theorem, there exist a basis ${\tilde{\mathbf {f}}}_1,\ldots , {\tilde{\mathbf {f}}}_r$ and element $a_1,\ldots , a_h\in A$ such that $a_1|a_2 |\ldots |a_h$ and $a_1{\tilde{\mathbf {f}}}_1,\ldots , a_h{\tilde{\mathbf {f}}}_h$ is a basis of $\pi (H)$. Let $\mathbf {h}_1,\ldots , \mathbf {h}_h$ be the basis of H such that $\pi (\mathbf {h}_i)=a_i{\tilde{\mathbf {f}}}_i$.

Now let L be a free part of $\mathcal {M}$. The decomposition $\mathcal {M}=L\oplus T$ gives rise to a section $s:\mathcal {M}/T \rightarrow L$, i.e., $\pi \circ s= id$. By putting $\mathbf {f}_i=s({\tilde{\mathbf {f}}}_i)$ we get a basis $\mathbf {f}_1,\ldots , \mathbf {f}_r$ of L such that $a_1\mathbf {f}_1,\ldots , a_h\mathbf { f}_h$ is a basis of $s(\pi (H))$. For $i=1,\ldots , h$ put $t_i=\mathbf {h}_i-a_i\mathbf {f}_i$. Then, $t_i\in \ker (\pi )=T$, so that the claim is proved. $\square$

Remark 1

When $A=\mathbb {Z}$, the objects whose existence is established by Proposition 1 are effectively computable. In fact, assume that $\mathcal {M}= \mathbb {Z}^r\oplus T$, where T is a finite group, and that $\mathbf {g}_1+s_1,\ldots , \mathbf {g}_h+s_h$ is a basis of H, with $\mathbf {g}_1,...,\mathbf {g}_h\in \mathbb {Z}^r$ and $s_1,\ldots , s_h\in T$. Let G be the $h\times r$ matrix having rows $\mathbf {g}_1,...,\mathbf {g}_h$. It is possible to compute the Smith normal form S of G and matrices $U\in {\text {GL}}_h(\mathbb {Z})$, $V\in {\text {GL}}_r(\mathbb {Z})$ such that $UGV=S$. Then, the rows of $V^{-1}$ give the basis $\mathbf {f}_1,\ldots , \mathbf {f}_r$, the diagonal entries of S give $a_1,\ldots , a_h\in \mathbb {Z}$. Moreover, we recover the elements $t_1,\ldots , t_h$ by putting (with the obvious notation)

$$\begin{aligned} \begin{pmatrix} t_1\\ \vdots \\ t_h \end{pmatrix} = U \begin{pmatrix} s_1\\ \vdots \\ s_h \end{pmatrix}. \end{aligned}$$

The following definition is standard (see, for example, [10, Ex. B-3.6]):

Definition 2

Let $\mathcal {M}$ be an A-module. A submodule $\mathcal {M}'\subseteq \mathcal {M}$ is said pure if the following property is satisfied:

$$\begin{aligned} \text {if}\, am\in \mathcal {M}'\, \text {for some}\, a\in A,m\in \mathcal {M},\, \text {then there is}\, m'\in \mathcal {M}'\, \text {such that}\, am'=am. \end{aligned}$$

Proposition 2

The following are equivalent:

• (a) H is contained in a free part of $\mathcal {M}$.

• (b) The image of T in $\mathcal {M}/H$ is a free summand.

• (c) The image of T in $\mathcal {M}/H$ is a pure submodule.

• (d) Let L be a free part of $\mathcal {M}$ and $\mathbf {f}_1,\ldots , \mathbf {f}_r$ be a basis of L as in Proposition 1; then, for $i=1,\ldots , h$ the element $t_i$ is divisible by $a_i$ in T, that is, there exists $u_i\in T$ such that $t_i=a_iu_i$;

Proof

a) $\Rightarrow$ b): Let L be a free part of $\mathcal {M}$ such that $H\subseteq L$. Then, $\mathcal {M}/H = (L\oplus T)/H \cong (L/H)\oplus T$.

The equivalence of (b) and (c) is a the well-known fact that, for modules finitely generated over a PID, pure submodules and direct summands coincide (see, for example, [10, Ex. B-3.7 (ii)]).

c) $\Rightarrow$ d): Since $a_i\mathbf {f}_i+t_i\in H$, the image of $a_i\mathbf {f}_i$ in $\mathcal {M}/H$ belongs to the image of T, for $i=1,\ldots , r$. By purity, there exists $u_i\in T$ such that the images of $a_i\mathbf {f}_i$ and $-a_iu_i$ coincide in $\mathcal {M}/H$, that is $a_i\mathbf {f}_i +a_iu_i$ in H. But then $t_i-a_iu_i\in H\cap T=\{0\}$, because H is free.

c) $\Rightarrow$ d): Let $L'$ be the submodule of $\mathcal {M}$ generated by $\mathbf {f}_1+u_1,\ldots ,\mathbf {f}_h+u_h, \mathbf {f}_{h+1},\ldots , \mathbf {f}_r.$ Then, $L'$ is a free part of $\mathcal {M}$ containing H. $\square$

Notice that since H is free, $H\cap T=\{0\}$, so that the image of T in $\mathcal {M}/H$ is isomorphic to T.

For every prime element p of A, we denote by $A_{(p)}$ the localization of A at the prime ideal (p). If $\mathcal {M}$ is an A-module, $\mathcal {M}_{(p)}$ is the localized $A_{(p)}$-module.

The localization of T at (p) coincide with the p-torsion of T, and $T=\bigoplus _p T_{(p)}$.

If L is a free part of $\mathcal {M}$ and $\mathcal {M}=L\oplus T$ is the corresponding decomposition, then $L_{(p)}$ is a free part of $\mathcal {M}_{(p)}$, that is, there is a decomposition $\mathcal {M}_{(p)}=L_{(p)}\oplus T_{(p)}$. The natural map $\mathcal {M}\rightarrow \mathcal {M}_{(p)}$ is the sum of the injection $L\rightarrow L_{(p)}$ and the surjection $T\rightarrow T_{(p)}$.

Proposition 3

H is contained in a free part of $\mathcal {M}$ if and only if $H_{(p)}$ is contained in a free part of $\mathcal {M}_{(p)}$ for every prime element $p\in A$.

The proof of Proposition 3 is based on the next two lemmas:

Lemma 1

Let A be a commutative ring with unity, $\mathcal {M}$ be an A-module and $N\subseteq \mathcal {M}$ be a submodule. Then, N is a direct summand of $\mathcal {M}$ if and only if there exists a map $\varphi : \mathcal {M}\rightarrow N$ such that $\varphi |_N=id_N$.

Proof

Assume that a map $\varphi : \mathcal {M}\rightarrow N$ as in the statement of the Lemma exists, and set $K=\ker (\varphi )$. Then, $K\cap N=\{0\}$, so that the map $\theta : N\oplus K\rightarrow \mathcal {M}$ given by the sum of the inclusions is injective. If $m\in \mathcal {M}$, put $n=\varphi (m)=\varphi (n)$; then, $m-n\in K$ and $m=n+(m-n)$, and this shows that $\theta$ is surjective. The converse is obvious.$\square$

Lemma 2

Let A be a commutative ring with unity, $\mathcal {M}$ be an A-module and $N,K\subseteq \mathcal {M}$ be direct summands of $\mathcal {M}$. Assume that the two ideals $Ann_A(N)$, $Ann_A(K)$ are coprime. Then, $N\oplus K$ is a direct summand of $\mathcal {M}$.

Proof

Firstly notice that by hypothesis there exist $a\in Ann_A(N), b\in Ann_A(K)$ such that $a+b=1$. This shows that $N\cap K=\{0\}$: If $x\in N\cap K$, then $x=ax+bx=0$. Write $\mathcal {M}=N\oplus N'$; let $k\in K$ and write $k=k_1+k_2$, with $k_1\in N$ and $k_2\in N'$. Then, from $bk=0$ we deduce

$$\begin{aligned} 0=bk_1=(1-a)k_1=k_1, \end{aligned}$$

so that $K\subseteq N'$. The composition

$$\begin{aligned} N'\hookrightarrow K\oplus K'\twoheadrightarrow K \end{aligned}$$

is the identity when restricted to K so that K is a direct summand of $N'$. $\square$

Proof of Proposition 3. Since localization is an exact functor, we have

$$\begin{aligned} \mathcal {M}_{(p)}/H_{(p)}\simeq \left( \mathcal {M}/H\right) _{(p)}. \end{aligned}$$

Let $T_{(p)}$ be the p-torsion of T; it coincides with the localization at (p) of T and it is a direct summand of T. Moreover, the natural maps from $T_{(p)}$ in $\mathcal {M}/H$ and in $\mathcal {M}_{(p)}/H_{(p)}$ are injective, so that we can regard $T_{(p)}$ as a submodule of $\mathcal {M}/H$ and of $\mathcal {M}_{(p)}/H_{(p)}$.

Now assume that H is contained in a free part of $\mathcal {M}$. Then, T is a direct summand of $\mathcal {M}/H$, by Proposition 2, so that there is a map $\mathcal {M}/H\rightarrow T$ which is the identity over T. Let p be a prime element in A; by localizing at (p) we find a map $\mathcal {M}_{(p)}/H_{(p)}\rightarrow T_{(p)}$ which is the identity over $T_{(p)}$, so that $T_{(p)}$ results to be a direct summand of $\mathcal {M}_{(p)}/H_{(p)}$; therefore, $H_{(p)}$ is contained in a free part of $\mathcal {M}_{(p)}$.

Conversely, assume that $H_{(p)}$ is contained in a free part of $\mathcal {M}_{(p)}$, for every prime element p of A. Then, $T_{(p)}$ is a direct summand of $\mathcal {M}_{(p)}/H_{(p)}$, so that there is a map $\left( \mathcal {M}/H\right) _{(p)}\simeq M_{(p)}/H_{(p)}\rightarrow T_{(p)}$ which is the identity when restricted to $T_{(p)}$. If we compose with the natural map $\mathcal {M}/H\rightarrow \left( \mathcal {M}/H\right) _{(p)}$ we get a map $\mathcal {M}/H\rightarrow T_{(p)}$ which is the identity over $T_{(p)}$. Then, $T_{(p)}$ is a direct summand of $\mathcal {M}/H$ for every prime p. By Lemma 2, $T=\prod _p T_{(p)}$ is a direct summand of $\mathcal {M}/H$, so that H is contained in a free part of $\mathcal {M}$, again by Proposition 2. (Notice that the product above is in fact a finite product since by hypothesis $\mathcal {M}$ and hence T, are finitely generated modules.)

3 Application to toric varieties

As already mentioned in the Introduction, we put the following

Definition 3

Let X be an irreducible and normal algebraic variety such that ${{\,\mathrm{Cl}\,}}(X)$ is finitely generated. Then, X is called pure if there exist free parts $F_C$ and $F_W$ of ${{\,\mathrm{Pic}\,}}(X)$ and ${{\,\mathrm{Cl}\,}}(X)$, respectively, such that the canonical injection ${{\,\mathrm{Pic}\,}}(X)\hookrightarrow {{\,\mathrm{Cl}\,}}(X)$ descends to give the following commutative diagram

In particular, if $X=X(\Sigma )$ is a n-dimensional toric variety whose n-skeleton $\Sigma (n)$ is not empty (see the following Sect. 3.1 for notation), then ${{\,\mathrm{Pic}\,}}(X)$ is free (see, e.g., [2, Prop. 4.2.5]), meaning that X is pure if and only if ${{\,\mathrm{Pic}\,}}(X)$ is contained in a free part of ${{\,\mathrm{Cl}\,}}(X)$.

If X is not pure, it is called impure.

Of course, if ${{\,\mathrm{Cl}\,}}(X)$ is free, then X is pure; moreover if X is smooth and ${{\,\mathrm{Cl}\,}}(X)$ is finitely generated, then it is pure, because the injection ${{\,\mathrm{Pic}\,}}(X)\hookrightarrow {{\,\mathrm{Cl}\,}}(X)$ is an isomorphism.

Conversely, producing examples of impure varieties is definitely more complicated (see Example 1).

3.1 Notation on toric varieties

Let $X=X(\Sigma )$ be a n-dimensional toric variety associated with a fan $\Sigma$. Calling $\mathbb {T}\cong (k^*)^n$ the torus acting on X, we use the standard notation M, for the characters group of $\mathbb {T}$, and $N:={{\,\mathrm{Hom}\,}}(M,\mathbb {Z})$. Then, $\Sigma$ is a collection of cones in $N_{\mathbb {R}}:=N\otimes {\mathbb {R}}\cong {\mathbb {R}}^n$. $\Sigma (i)$ denotes the i-skeleton of $\Sigma$, that is, the collection of i-dimensional cones in the fan $\Sigma$. We shall use the notation $\tau \preceq \sigma$ to indicate that the cone $\tau$ is a face of $\sigma$.

Given a toric variety $X(\Sigma )$ we will denote by $\mathcal {W}_{T}(X)\subseteq {{\,\mathrm{Div}\,}}(X)$ the subgroup of torus invariant Weil divisors and by $\mathcal {C}_{T}(X)\subseteq \mathcal {W}_{T}(X)$ the subgroup of Cartier torus invariant divisors. It is well known that

$$\begin{aligned} \mathcal {W}_{T}(X)=\bigoplus _{\rho \in \Sigma (1)}\mathbb {Z}\cdot D_\rho \quad \text {where}\quad D_\rho :=\overline{\mathbb {T}\cdot x_\rho } \end{aligned}$$

the latter being the closure of the torus orbit of the distinguished point $x_\rho$ of the ray $\rho$ [2, § 3.2, § 4.1]. In particular the homomorphism $D\mapsto [D]$, sending a Weil divisor to its linear equivalence class, when restricted to torus invariant divisors still gives a epimorphism $d_X:\mathcal {W}_{T}(X)\twoheadrightarrow {{\,\mathrm{Cl}\,}}(X)$ [2, Thm. 4.1.3].

In [7, Def. 2.7] we introduced the notion of a poly weighted space (PWS), which is a $\mathbb {Q}$-factorial complete toric variety Y whose class group ${{\,\mathrm{Cl}\,}}(Y)$ is free. This is equivalent to say that Y is connected in codimension 1 (1-connected); when $k=\mathbb {C}$ this means that the regular locus $Y_\text {reg}$ of Y is simply connected, as Y is a normal variety: Recall that $\pi _1(Y_\text {reg})\cong {{\,\mathrm{Tors}\,}}({{\,\mathrm{Cl}\,}}(Y))=0$ [8, Cor. 1.8, Thm. 2.1]. As proved in [8, Thm. 2.2], every $\mathbb {Q}$-factorial complete toric variety $X(\Sigma )$ is a finite quotient of a unique PWS $Y({\widehat{\Sigma }})$, which is its universal covering unramified in codimension 1 (1-covering). The Galois group of the torus equivariant covering $Y\twoheadrightarrow X$ is precisely the dual group $\mu (X)={{\,\mathrm{Hom}\,}}({{\,\mathrm{Tors}\,}}({{\,\mathrm{Cl}\,}}(X)),k^*)$. At lattice level, the equivariant surjection $Y\twoheadrightarrow X$ induces an injective automorphism $\beta : N\hookrightarrow N$ whose ${\mathbb {R}}$-linear extension $\beta _{\mathbb {R}}:N_{\mathbb {R}}\hookrightarrow N_{\mathbb {R}}$ identifies the associated fans, that is $\beta _{\mathbb {R}}({\widehat{\Sigma }})=\Sigma$. Recall that one has the following commutative diagram (see diagram (5) in [9])

(3)

where

• $T={{\,\mathrm{Tors}\,}}({{\,\mathrm{Cl}\,}}(X))$ ;

• $\mathrm{div}_X,\mathrm{div}_Y$ are the morphisms sending a character in M to the associated principal divisor in $\mathcal {W}_{T}(X),\mathcal {W}_{T}(Y)$, respectively;

• $d_X,d_Y$ are the morphisms sending a torus invariant divisor in $\mathcal {W}_{T}(X),\mathcal {W}_{T}(Y)$, respectively, to its class in ${{\,\mathrm{Cl}\,}}(X),{{\,\mathrm{Cl}\,}}(Y)$, respectively;

• $\alpha$ is the identification $\mathcal {W}_{T}(X)\cong \mathcal {W}_{T}(Y)$ induced by inverse images of rays by $\beta _{\mathbb {R}}$, that is,

  $$\begin{aligned} \alpha \left( \sum _{\rho \in \Sigma (1)} a_\rho D_{\rho }\right) = \sum _{\beta _{\mathbb {R}}^{-1}(\rho )\in {\widehat{\Sigma }}(1)} a_\rho D_{\beta _{\mathbb {R}}^{-1}(\rho )}\,; \end{aligned}$$

• ${\overline{\alpha }}$ is what induced by $\alpha$ on classes groups;

• $V,\widehat{V}$ are matrices whose transposed represent $div_X,div_Y$, respectively, w.r.t. a chosen a basis of M and standard bases of torus orbits of rays of $\mathcal {W}_{T}(X)$ and $\mathcal {W}_{T}(Y)$, respectively; since $|\Sigma (1)|=|{\widehat{\Sigma }}(1)|=n+r$, where

  $$\begin{aligned} r={{\,\mathrm{rk}\,}}({{\,\mathrm{Cl}\,}}(Y))={{\,\mathrm{rk}\,}}({{\,\mathrm{Cl}\,}}(X)) \end{aligned}$$

  both V and $\widehat{V}$ are $n\times (n+r)$ integer matrices called fan matrices of X and Y, respectively; they turn out to be F-matrices, in the sense of [7, Def. 3.10], and $\widehat{V}$ is also a CF-matrix; notice that, still calling $\beta$ the representative matrix of the homonymous morphism $\beta :N\hookrightarrow N$ w.r.t. the basis dual to that chosen in M, there is the relation

  $$\begin{aligned} V=\beta \cdot \widehat{V} \end{aligned}$$

  (see [7, Prop. 3.1 (3)] and [8, Rem. 2.4]); concretely, both V and $\widehat{V}$ can be obtained as matrices whose columns represent primitive generators of rays in $\Sigma (1)$ and ${\widehat{\Sigma }}(1)$, respectively, w.r.t. the dual basis, i.e.,

  $$\begin{aligned} V=\left( \begin{array}{ccc} \mathbf {v}_1 &{} \cdots &{} \mathbf {v}_{n+r} \\ \end{array} \right) \ ,\quad \widehat{V}=\left( \begin{array}{ccc} {\widehat{\mathbf {v}}}_1 &{} \cdots &{} {\widehat{\mathbf {v}}}_{n+r} \\ \end{array} \right) \end{aligned}$$

  where $\Sigma (1)=\{\langle \mathbf {v}_1\rangle , \ldots ,\langle \mathbf {v}_{n+r}\rangle \}$, ${\widehat{\Sigma }}(1)=\{\langle {\widehat{\mathbf {v}}}_1\rangle , \ldots , \langle {\widehat{\mathbf {v}}}_{n+r}\rangle \}$, being $\langle \mathbf {v}\rangle$ the ray generated by $\mathbf {v}$ in ${\mathbb {R}}^n\cong N_{\mathbb {R}}$ ;

• Q is a matrix representing $d_Y$ w.r.t. a chosen basis of ${{\,\mathrm{Cl}\,}}(Y)$; it is a $r\times (n+r)$ integer matrix which turns out to be a Gale dual matrix of both V and $\widehat{V}$, in the sense of [7, § 3.1] and a W-matrix, in the sense of [7, Def. 3.9]; it is called a weight matrix of both X and Y;

• the choice of a basis of ${{\,\mathrm{Cl}\,}}(Y)$ as above determines a basis of a free part of ${{\,\mathrm{Cl}\,}}(X)$; complete such a basis with a set of generators of the torsion subgroup $T\subseteq {{\,\mathrm{Cl}\,}}(X)$; then, $d_X$ decomposes as $d_X=f_X\oplus \tau _X$ where

  

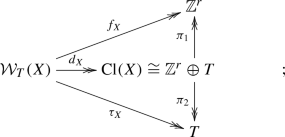
  with respect to these choices, the weight matrix Q turns out to be a representative matrix of $f_X$, too, while morphism $\tau _X$ is represented by a torsion matrix $\Gamma$ [9, Thm. 3.2 (6)].

3.1.1 Some further notation

Let $A\in \mathbf {M}(d,m;\mathbb {Z})$ be a $d\times m$ integer matrix, then

$$\begin{aligned}&\mathcal {L}_r(A)\subseteq \mathbb {Z}^m \text {denotes the sublattice spanned by the rows of}\, A; \\&\mathcal {L}_c(A)\subseteq \mathbb {Z}^d \text {denotes the sublattice spanned by the columns of}\, A; \\&\quad A_I,\,A^I \text { for any }\,I\subseteq \{1,\ldots ,m\}, \text {the former is the submatrix of}\, A\, \text {given by}\\&\quad \text {the columns indexed by}\, \text {I and the latter is the submatrix of}\\&\quad A\, \text {whose columns are indexed by the complementary }\\&\quad \text {subset}\, \{1,\ldots ,m\}\backslash I; \end{aligned}$$

Given a fan matrix $V=(\mathbf {v}_1,\ldots ,\mathbf {v}_{n+r})\in \mathbf {M}(n,n+r;\mathbb {Z})$ then

$$\begin{aligned}&\langle V\rangle =\langle \mathbf {v}_1,\ldots ,\mathbf {v}_{n+r}\rangle \subseteq N_{{\mathbb {R}}} \,\text {denotes the cone generated by the columns of } V; \\&\quad \mathcal {SF}(V)=\mathcal {SF}(\mathbf {v}_1,\ldots ,\mathbf {v}_{n+r}) \,\text {is the set of all rational simplicial and complete}\\&\quad \text { fans}\, \Sigma \text { such that}\,\Sigma (1)=\{\langle \mathbf {v}_1\rangle ,\ldots ,\langle \mathbf {v}_{n+r}\rangle \}\subset N_{{\mathbb {R}}}\\&\quad (\text {see [7, Def. 1.3]}). \end{aligned}$$

Given a fan $\Sigma \in \mathcal {SF}(V)$ we put

$$\begin{aligned} \mathcal {I}^{\Sigma }= & {} \{I\subseteq \{1,\ldots ,n+r\}:\left\langle V^I\right\rangle \in \Sigma (n)\}. \end{aligned}$$

3.2 A sufficient condition

This section is aimed to give a sufficient condition for a $\mathbb {Q}$-factorial complete toric variety to be a pure variety. Let us, first of all, outline some equivalent facts.

Proposition 4

Let $X(\Sigma )$ be a $\mathbb {Q}$-factorial complete toric variety, $Y({\widehat{\Sigma }})\twoheadrightarrow X(\Sigma )$ be its universal 1-covering, V and $\widehat{V}$ be fan matrices of X and Y, respectively. Assuming notation as in diagram (3), the following are equivalent:

• (a) X is a pure variety;

• (b) there is a decomposition $\mathcal {W}_{T}(X)=\mathcal {L}_r({\widehat{V}})\oplus F$ such that $\mathcal {C}_{T}(X)\subseteq \mathcal {L}_r(V)\oplus F$;

• (c) for every prime p there exists a $\mathbb {Z}_{(p)}$-module $F_p$ and a decomposition

  $$\begin{aligned} \mathcal {W}_{T}(X)_{(p)}=\mathcal {L}_r(\widehat{V})_{(p)}\oplus F_p \end{aligned}$$

  such that $\mathcal {C}_{T}(X)_{(p)}\subseteq \mathcal {L}_r(V)_{(p)}\oplus F_p$.

Proof

• a) $\Rightarrow$ b): If X is a pure variety, let ${{\,\mathrm{Cl}\,}}(X)=L\oplus T$ be a decomposition such that L is a free part and ${{\,\mathrm{Pic}\,}}(X)\subseteq L$. We can identify L with $\mathbb {Z}^r$ in the first row of diagram (3). Let $s:L\rightarrow \mathcal {W}_{T}(X)$ be any section (i.e., $Q\circ s=id_L$ ) and put $F=s(L)$. If $x\in \mathcal {W}_{T}(X)$, write $d_X(x)=a+b$, with $a\in L$ and $b\in T$. Then, $Q(x-s(a))=0$ so that $x-s(a)\in \mathcal {L}_r({\widehat{V}})$; this proves that $\mathcal {W}_{T}(X)=\mathcal {L}_r({\widehat{V}})\oplus F$. If $x\in \mathcal {C}_{T}(X)$, then write $x=a+b$ with $a\in \mathcal {L}_r({\widehat{V}})$ and $b\in F$; since $d_X(x)\in L$, we have $\Gamma \cdot x=\Gamma \cdot a=0$, so that $a\in \mathcal {L}_r(V)$.

• b) $\Rightarrow$ c) is obvious.

• c) $\Rightarrow$ a): Let p be a prime and put $F'_p=F_p\cap \mathcal {C}_{T}(X)_{(p)}$. We have

  $$\begin{aligned} \mathcal {C}_{T}(X)_{(p)}=\mathcal {L}_r(V)_{(p)}\oplus F'_p \end{aligned}$$

  so that

  $$\begin{aligned} {{\,\mathrm{Cl}\,}}(X)_{(p)}/{{\,\mathrm{Pic}\,}}(X)_{(p)}=\mathcal {W}_{T}(X)_{(p)}/\mathcal {C}_{T}(X)_{(p)}\cong & {} \left( \mathcal {L}_r({\widehat{V}})_{(p)}/\mathcal {L}_r(V)_{(p)}\right) \oplus \left( F_p/F'_p\right) \\\cong & {} T_{(p)}\oplus \left( F_p/F'_p\right) \end{aligned}$$

  Then, we see that the image of $T_{(p)}$ is a direct summand in ${{\,\mathrm{Cl}\,}}(X)_{(p)}/{{\,\mathrm{Pic}\,}}(X)_{(p)}$, so that ${{\,\mathrm{Pic}\,}}(X)_{(p)}$ is contained in a free part of ${{\,\mathrm{Cl}\,}}(X)_{(p)}$ by Proposition 2 b). Since this holds for every p we can apply Proposition 3 and deduce that ${{\,\mathrm{Pic}\,}}(X)$ is contained in a free part of ${{\,\mathrm{Cl}\,}}(X)$, so that X is pure.

$\square$

Definition 4

Let $\Sigma$ be a fan in ${\mathbb {R}}^n$. For every simplicial cone $\sigma \in \Sigma$, let $\mathbf {w}_1,\ldots , \mathbf {w}_k\in \mathbb {Z}^n$ be the set of minimal generators of $\sigma$. Let $\mathcal {V}$ be the subspace of ${\mathbb {R}}^n$ generated by $\sigma$, and $L=\mathcal {V}\cap \mathbb {Z}^n$. The multiplicity of $\sigma$ is the index

$$\begin{aligned} {{\,\mathrm{mult}\,}}(\sigma )=[L: \mathbb {Z}\mathbf {w}_1\oplus \ldots \oplus \mathbb {Z}\mathbf {w}_k]. \end{aligned}$$

If $\Sigma$ is a simplicial fan we put

$$\begin{aligned} m_\Sigma =\gcd \{{{\,\mathrm{mult}\,}}(\sigma )\ |\ \sigma \hbox { is a maximal cone in } \Sigma \}. \end{aligned}$$

Set, once for all, the following notation:

$$\begin{aligned} \forall \,I\subseteq \{1,\ldots ,n+r\}\quad E_I:=\{\mathbf {x}=(x_1,\ldots , x_{n+r})\in \mathbb {Z}^{n+r}\ |\ x_i=0, \forall i\not \in I\}. \end{aligned}$$

(4)

We are now in a position to state and prove the main result of the present paper.

Theorem 2

Let $X=X(\Sigma )$ be a complete $\mathbb {Q}$-factorial toric variety and $Y=Y({\widehat{\Sigma }})$ be its universal 1-covering; let $\widehat{V}$ be a fan matrix associated with Y, and $V=\beta \cdot \widehat{V}$ be a fan matrix associated with X. Suppose that $(\det (\beta ), m_{{\widehat{\Sigma }}})=1$. Then, X is a pure variety.

Proof

By Proposition 4, it suffices to show that for every prime p there exists a $\mathbb {Z}_{(p)}$-module $F_p$ and a decomposition $\mathcal {W}_{T}(X)_{(p)}=\mathcal {L}_r(\widehat{V})_{(p)}\oplus F_p$ such that $\mathcal {C}_{T}(X)_{(p)}\subseteq \mathcal {L}_r(V)_{(p)}\oplus F_p$. If $p\not | \det (\beta )$, then $\mathcal {L}_r(V)_{(p)}=\mathcal {L}_r(\widehat{V})_{(p)}$ and we are done. Assume that $p|\det (\beta )$; by hypothesis there exists a maximal cone ${\widehat{\sigma }}={\widehat{\sigma }}^I\in {\widehat{\Sigma }}$ such that $p\not |{{\,\mathrm{mult}\,}}({\widehat{\sigma }})=\det (Q_I)$. Put $F_p=E_{I,{(p)}}$, where $E_I$ is defined in (4). By definition $\mathcal {C}_{T}(X)\subseteq \mathcal {L}_r(V)\oplus E_I$, so that $\mathcal {C}_{T}(X)_{(p)}\subseteq \mathcal {L}_r(V)_{(p)}\oplus F_p$. We claim that $\mathbb {Z}_{(p)}^{n+r}=\mathcal {L}_r(\widehat{V})_{(p)}\oplus F_p$. The inclusion $\supseteq$ being obvious, assume that $\mathbf {x}\in \mathbb {Z}_{(p)}^{n+r}$. Since $\det (Q_I)$ is invertible in $\mathbb {Z}_{(p)}$, there exists $\mathbf {y}\in E_I$ such that $Q\mathbf {x}=Q\mathbf {y}$, that is, $\mathbf {x}-\mathbf {y}\in \ker (Q)=\mathcal {L}_r(\widehat{V})$. $\square$

Corollary 1

Let $Y=Y({\widehat{\Sigma }})$ be a poly weighted projective space such that $m_{{\widehat{\Sigma }}}=1.$ Then, every $\mathbb {Q}$-factorial complete toric variety having Y as universal 1-covering is pure.

Remark 2

Geometrically the previous Theorem 2 translates precisely in Theorem 1 stated in the introduction. In fact a $\mathbb {Q}$-factorial complete toric variety is an orbifold (see [2, Thm. 3.1.19 (b)]) whose n-skeleton parameterizes a covering by affine charts. In particular Y has only finite quotient singularities whose order is necessarily a divisor of some multiplicity ${{\,\mathrm{mult}\,}}({\widehat{\sigma }})$, for ${\widehat{\sigma }}\in {\widehat{\Sigma }}(n)$. Moreover, the affine chart $U_{{\widehat{\sigma }}}$ has always a quotient singularity of maximum order ${{\,\mathrm{mult}\,}}({\widehat{\sigma }})$. Hence Theorem 1 follows.

In particular the previous Corollary 1 gives the following

Corollary 2

Let Y be a n-dimensional, $\mathbb {Q}$-factorial, complete toric variety admitting a torus invariant, Zariski open subset $U\subseteq Y$, biregular to $\mathbb {C}^n$. Then, Y is a PWS and every $\mathbb {Q}$-factorial complete toric variety having Y as universal 1-covering is pure.

3.3 Examples

The present section is devoted to give some examples of pure and impure $\mathbb {Q}$-factorial complete toric varieties.

Example 1

Consider the fan matrix

$$\begin{aligned} \widehat{V}=\begin{pmatrix} 1 &{}\quad -1&{}\quad 2&{}\quad -3&{}\quad -1\\ 1&{}\quad -1&{} \quad -1&{}\quad 2&{}\quad -1\\ 1&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad -5\end{pmatrix} \end{aligned}$$

The corresponding weight matrix is

$$\begin{aligned} Q=\begin{pmatrix} 3&{}\quad 1&{}\quad 10&{}\quad 6&{}\quad 4\\ 3&{}\quad 2&{}\quad 0&{}\quad 0&{}\quad 1\end{pmatrix}. \end{aligned}$$

One can check that $|\mathcal {SF}(\widehat{V})|=2$. These two fans are given by taking all the faces of the following lists of maximal cones:

$$\begin{aligned}&{\widehat{\Sigma }}_1=\{\langle 1, 2, 3\rangle ,\langle 1, 2, 4\rangle , \langle 2, 4, 5\rangle , \langle 1, 4, 5\rangle , \langle 2, 3, 5\rangle , \langle 1, 3, 5\rangle \}\\&{\widehat{\Sigma }}_2=\{ \langle 1, 3, 4\rangle , \langle 2, 3, 4\rangle ,\langle 2, 4, 5\rangle , \langle 1, 4, 5\rangle , \langle 2, 3, 5\rangle , \langle 1, 3, 5\rangle \} \end{aligned}$$

We denote by $\langle i,j,k\rangle$ the cone generated by the columns $\mathbf {v}_i,\mathbf {v}_j,\mathbf {v}_k$ of the matrix $\widehat{V}$. The list of multiplicities of maximal cones for the two fans is, respectively,

$$\begin{aligned} 6,10 ,30, 20,18,12 \hbox { and } 7,9, 30, 20,18,12, \end{aligned}$$

so that

$$\begin{aligned} m_{{\widehat{\Sigma }}_1}=2,\quad \quad m_{{\widehat{\Sigma }}_2}=1. \end{aligned}$$

Define

$$\begin{aligned} \beta :=\begin{pmatrix} 1 &{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0 \\ 0&{}\quad 0&{}\quad 2\end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} V:=\beta \cdot \widehat{V}=\begin{pmatrix} 1 &{}\quad -1&{}\quad 2&{}\quad -3&{}\quad -1\\ 1&{}\quad -1&{}\quad -1&{}\quad 2&{}\quad -1\\ 2&{}\quad 2&{}\quad 2&{}\quad 2&{}\quad -10\end{pmatrix}. \end{aligned}$$

A torsion matrix $\varGamma$ with entries in $\mathbb {Z}/2\mathbb {Z}$ such that $Q\oplus \varGamma$ represents the morphism assigning to each divisor its class, as in the previous diagram (3), is given by

$$\begin{aligned} \varGamma =\left( \begin{array}{ccccc} 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 0 \\ \end{array} \right) . \end{aligned}$$

Let $\Sigma _1$ be the fan in $\mathcal {SF}(V)$ corresponding to ${\widehat{\Sigma }}_1$. We show that $X(\Sigma _1)$ is an impure variety. Using methods explained in [9, Thm. 3.2 (2)], we obtain that a basis of $\mathcal {C}_{T}(X)$ is given by the rows of the following matrix

$$\begin{aligned} C_X=\begin{pmatrix} 40 &{}\quad 0 &{}\quad 0&{}\quad 0&{}\quad 0\\ 0 &{}\quad 60&{}\quad 0&{}\quad 0&{}\quad \quad 0\\ 0&{}\quad 0&{}\quad 3&{}\quad 0&{}\quad 0\\ -24 &{}\quad -24&{}\quad 0&{}\quad 1&{}\quad 0\\ -9 &{}\quad -47&{}\quad -2&{}\quad 0&{}\quad 1 \end{pmatrix}. \end{aligned}$$

Then,

$$\begin{aligned} Q\cdot C_X^\mathrm{T} =\begin{pmatrix} 120 &{}\quad 60&{}\quad 30&{}\quad -90&{}\quad -90\\ 120 &{}\quad 120&{}\quad 0&{}\quad -120&{}\quad -120 \end{pmatrix},\quad \quad \varGamma \cdot C_X^T = \begin{pmatrix} 0&\quad 0&\quad 1&\quad 1&\quad 1 \end{pmatrix} \end{aligned}$$

Then, we see that ${{\,\mathrm{Pic}\,}}(X)$ is generated in ${{\,\mathrm{Cl}\,}}(X)\cong \mathbb {Z}^2\oplus \mathbb {Z}/2\mathbb {Z}$ by elements

$$\begin{aligned} (120,120), (60,120), (30,0)+[1]_2,(90,120)+[1]_2. \end{aligned}$$

the first and the last of them are obviously generated by the remaining two elements, so that ${{\,\mathrm{Pic}\,}}(X)$ is generated by (60, 120) and $(30,0)+[1]_2$. Every free part of ${{\,\mathrm{Cl}\,}}(X)$ contains an element z of the form $(15,0)+[a]_2$ for some $a\in \{0,1\}$; therefore, it must contain $2z=(30,0)$; then, $(30,0)+[1]_2$ cannot belong to any free part, meaning that $X(\Sigma _1)$ is impure.

Notice that purity is a property depending on the fan choice. In fact $\Sigma _2$ satisfies hypothesis of Theorem 2, as $m_{\Sigma _2}=1$. Then, $X(\Sigma _2)$ is pure.

The following is a counterexample showing that a converse of Theorem 2 cannot hold.

Example 2

Let $\widehat{V}$ be the fan matrix of Example 1. Consider the matrix

$$\begin{aligned} \beta '=\begin{pmatrix} 1 &{}\quad 0&{}\quad 0\\ 0&{}\quad 2&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1\end{pmatrix} \end{aligned}$$

and put

$$\begin{aligned} V':=\beta '\cdot \widehat{V}=\begin{pmatrix} 1 &{}\quad -1&{}\quad 2&{}\quad -3&{}\quad -1\\ 2&{}\quad -2&{}\quad -2&{}\quad 4&{}\quad -2\\ 1&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad -5\end{pmatrix}. \end{aligned}$$

A torsion matrix $\varGamma '$ with entries in $\mathbb {Z}/2\mathbb {Z}$ such that $Q\oplus \varGamma '$ represents the morphism assigning to each divisor its class is given by

$$\begin{aligned} \varGamma '=\left( \begin{array}{ccccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 \\ \end{array} \right) .\end{aligned}$$

(5)

Let $\Sigma '_1$ be the fan in $\mathcal {SF}(V)$ corresponding to ${\widehat{\Sigma }}_1$ and $X'=X(\Sigma '_1)$. In this case $X'$ is a pure variety. In fact, a basis of $\mathcal {C}_{T}(X')$ is given by the rows of the following matrix

$$\begin{aligned} C_{X'}=\begin{pmatrix} 40 &{}\quad 0 &{}\quad 0&{}\quad 0&{}\quad 0\\ 0 &{}\quad 60&{}\quad 0&{}\quad 0&{}\quad 0\\ -20 &{}\quad -30 &{}\quad 3&{}\quad 0&{}\quad 0\\ -8 &{}\quad -48&{}\quad 0&{}\quad 2&{}\quad 0\\ 15 &{}\quad 37 &{}\quad -2&{}\quad -1&{}\quad 1 \end{pmatrix}. \end{aligned}$$

Then,

$$\begin{aligned} Q\cdot C_{X'}^T =\begin{pmatrix} 120 &{}\quad 60&{}\quad -60&{}\quad -60&{}\quad 60\\ 120 &{}\quad 120&{}\quad -120 &{}\quad -120&{}\quad 120 \end{pmatrix},\quad \quad \varGamma '\cdot C_{X'}^T = \begin{pmatrix} 0&\quad 0&\quad 0&\quad 0&\quad 0 \end{pmatrix} \end{aligned}$$

Then, we see that ${{\,\mathrm{Pic}\,}}(X')$ is generated in ${{\,\mathrm{Cl}\,}}(X')\cong \mathbb {Z}^2\oplus \mathbb {Z}/2\mathbb {Z}$ by the elements

$$\begin{aligned} (120,120), (60,120) \end{aligned}$$

so that $X'$ is pure. On the other hand $m_{{\widehat{\Sigma }}_1}=2=\det (\beta ')$, so proving that a converse of Theorem 2 cannot hold.

3.4 The case $|\mathcal {SF}(V)|=1$

The aim of this section is to exhibit a large class of pure toric varieties, by establishing the purity of every $\mathbb {Q}$-factorial complete toric variety $X=X(\Sigma )$ whose fan matrix V admits a unique simplicial and complete fan given by $\Sigma$ itself. Geometrically, this property means that a small $\mathbb {Q}$-factorial modification of X is necessarily an isomorphism, as explained in the Introduction.

We need a few preliminary lemmas. If V is an F-matrix we put

$$\begin{aligned} \mathcal {I}_{V,\mathrm{tot}}= & {} \{I\subseteq \{1,\ldots , n+r\}\ |\ |I|=r \hbox { and } \det (V^I)\not =0 \}\\ \mathcal {I}_{V,\mathrm{min}}= & {} \{I\in \mathcal {I}_{V,\mathrm{tot}}\ |\ \langle V^I\rangle \hbox { does not contain any column of}\, V\\&\text {apart from its generators }\}. \end{aligned}$$

Lemma 3

Put

$$\begin{aligned} m_{V,\mathrm{tot}}= & {} \gcd \{\det (V^I)\ |\ I\in \mathcal {I}_{V,\mathrm{tot}}\}\\ m_{V,\mathrm{min}}= & {} \gcd \{\det (V^I)\ |\ I\in \mathcal {I}_{V,\mathrm{min}}\}; \end{aligned}$$

then $m_{V,\mathrm{min}}=m_{V,\mathrm{tot}}$.

Proof

Since $\mathcal {I}_{V,\mathrm{min}}\subseteq \mathcal {I}_{V,\mathrm{tot}}$ we have $m_{V,\mathrm{tot}}|m_{V,\mathrm{min}}$ We firstly show that the assertion is true when $m_{V,\mathrm{tot}}=1$. Otherwise, there would exist a prime number p dividing $\det (V^I)$ for every $I\in \mathcal {I}_{V,\mathrm{min}}$; and there would exist $I_0\in \mathcal {I}_\mathrm{tot}$ such that $p\not | \det (I_0)$. We choose such an $I_0$ with the property that the number $n_0$ of columns of V belonging to $\langle V^{I_0}\rangle$ is minimum. Let $\mathbf {v}_1,\ldots , \mathbf {v}_n$ be the columns of $V^{I_0}$ and let $\mathbf {v}^*\in \langle V^{I_0}\rangle$ be a column of V different from $\mathbf {v}_i$ for every i; then, we can write $\mathbf {v}^*=\sum _{i=1}^n \frac{a_i}{b} \mathbf {v}_i$ with $a_i,b\in \mathbb {Z}$ and $(a_1,\ldots , a_n,b)=1$. For $i=1,\ldots , n$ let $\sigma _i=\langle \mathbf {v}_1,\ldots , \mathbf {v}_{i-1},\mathbf {v}^*,\mathbf {v}_{i+1},\ldots , \mathbf {v}_n\rangle$. Then, $|\det (\sigma _i) |=\left( \frac{a_i}{b}\right) ^n |\det (V^{I_0})|$ and p divides $\det (\sigma _i)$ by the minimality hypothesis on $I_0$. It follows that p divides $a_i$ for $i=1,\ldots , n$; therefore, $\mathbf {v}^*\in p\mathbb {Z}^n$ and this is a contradiction because V is a fan matrix, hence reduced (see [7, Def. 3.13]).

Suppose now that $m_{V,\mathrm{tot}}\not =1$. Then, by [7, Prop. 3.1 (3)] there exist a CF-matrix ${\widehat{V}}$ such that $V=\beta \widehat{V}$ for some $\beta \in \mathbf {M}_n(\mathbb {Z})\cap {\text {GL}}_n(\mathbb {Q})$; and $m_{\widehat{V},\mathrm{tot}}=1$ by [7, Prop. 2.6], so that we can apply the first part of the proof to $\widehat{V}$ and deduce that $m_{\widehat{V},\mathrm{min}}=1$. Notice that $\mathcal {I}_{V,\mathrm{tot}}=\mathcal {I}_{\widehat{V},\mathrm{tot}}$, $\mathcal {I}_{V,\mathrm{min}}=\mathcal {I}_{\widehat{V},\mathrm{min}}$ and $\det (V^I)=\det (\beta )\det (\widehat{V}^I)$ for every $I\in \mathcal {I}_{V,\mathrm{tot}}$, so that $m_{V,\mathrm{min}}=\det (\beta )m_{\widehat{V},\mathrm{min}}$ and $m_{V,\mathrm{tot}}=\det (\beta )m_{\widehat{V},\mathrm{tot}}$. It follows that $m_{V,\mathrm{min}}=m_{V,\mathrm{tot}}=\det (\beta )$. $\square$

Lemma 4

Let $\Sigma _0$ be a simplicial fan in $\mathbb {R}^n$ such that $\sigma =|\Sigma _0|$ is a full dimensional convex cone. Let $\mathbf {w}_1,\ldots , \mathbf {w}_k\in \mathbb {R}^n$ be such that $\mathbf {w}_i\not \in \sigma$ for $i=1,\ldots , k$. There exists a simplicial fan $\Sigma$ in ${\mathbb {R}}^n$ such that

• (a) $|\Sigma |= \sigma +\langle \mathbf {w}_1,\ldots , \mathbf {w}_k\rangle$;

• (b) $\Sigma (1)= \Sigma _0(1)\cup \{\langle \mathbf {w}_1\rangle ,\ldots , \langle \mathbf {w}_k\rangle \}$;

• (c) $\Sigma _0 \subseteq \Sigma$.

Proof

By induction on k. For the case $k=0$, we take $\Sigma =\Sigma _0$. Assume that the result holds true for $k-1$. Let $\mathcal {W'}= \sigma +\langle \mathbf {w}_1,\ldots , \mathbf {w}_{k-1}\rangle$, $\mathcal {W}=\sigma +\langle \mathbf {w}_1,\ldots , \mathbf {w}_{k}\rangle$. By inductive hypothesis there exists a simplicial fan $\Sigma '$ such that $|\Sigma '|=\mathcal {W'}$, $\Sigma '(1)= \Sigma _0(1)\cup \{ \langle \mathbf {w}_1\rangle ,\ldots , \langle \mathbf {w}_{k-1}\rangle \}$ and $\Sigma _0\subseteq \Sigma '$. We distinguish two cases:

• Case 1: $\mathbf {w}_{k}\in \mathcal {W'}$, so that $\mathcal {W}=\mathcal {W}'$; let $\tau$ be the minimal cone in $\Sigma '$ containing $\mathbf {w}_{k}$. We take $\Sigma =s(\mathbf {w}_k,\tau )\Sigma '$, the stellar subdivision of $\Sigma '$ in direction $\mathbf {w}_k$ (see [3, Def. III.2.1]). Concretely, every m-dimensional cone $\mu =\langle \mathbf {x}_1,\ldots , \mathbf {x}_m\rangle \in \Sigma$ containing $\mathbf {w}_k$ is replaced by the set of the m-dimensional cones of the form $\langle \mathbf {x}_1,\ldots , \mathbf {x}_{i-1}, \mathbf {w}_k,\mathbf {x}_{i+1},\ldots , \mathbf {x}_m\rangle$. Conditions a) and b) are immediately verified. For condition c) notice that, since $\mathbf {w}_{k}\not \in \sigma$, $\tau$ is not a face of any cone in $\Sigma _0$; therefore, $\Sigma _0\subseteq \Sigma$.

• Case 2: $\mathbf {w}_{k}\not \in \mathcal {W'}$, so that $\mathcal {W'}\subsetneq \mathcal {W}$. Let $\mathcal {F}$ be the set of facets f in $\Sigma '(n-1)$ which are cut out by an hyperplane strictly separating $\mathcal {W}'$ and $\mathbf {w}_k$; that is $f\subseteq \partial \mathcal {W}'$, $f\not \subseteq \partial \mathcal {W}$ and the cone $\tau _f=\langle f, \mathbf {w}_{k}\rangle$ is n dimensional. Notice that $\mathcal {F}\not = \emptyset$: In fact $\mathcal {W}'$ is a convex polyhedral cone and $\mathbf {w}_k\not \in \mathcal {W}'$; then, there is an hyperplane H cutting a facet $\varphi$ of $\mathcal {W}'$ and strictly separating $\mathcal {W}'$ and $\mathbf {w}_k$; let f be a facet of $\Sigma '$ contained in $\varphi$; then, $f\in \mathcal {F}$.

Consider the set of simplicial cones

$$\begin{aligned} \Sigma =\Sigma '\cup \{\tau \ |\ \tau \preceq \tau _{f}\ \text {for some}\ f\in \mathcal {F} \}. \end{aligned}$$

We claim that $\Sigma$ is a fan. By construction it is closed by faces, so that it suffices to show that $\tau _1\cap \tau _2$ is a face of both $\tau _1$ and $\tau _2$, whenever $\tau _1,\tau _2\in \Sigma$. Let $\tau _1,\tau _2\in \Sigma$. If they are both in $\Sigma '$, then $\tau _1\cap \tau _2$ is a face of $\tau _1,\tau _2$ because $\Sigma '$ is a fan. Assume that $\tau _1\in \Sigma '$ and $\tau _2\not \in \Sigma '$; then, $\tau _2=\langle \tau , \mathbf {w}_k\rangle$, where $\tau$ is a face of some $f\in \mathcal {F}$. Let H be the hyperplane cutting f; then, $\mathbf {w}_k$ lies on the other side of H with respect to $\mathcal {W'}$, so that $\tau _1\cap \tau _2\subseteq f$. Therefore, $\tau _1\cap \tau _2=\tau _1\cap \tau \in \Sigma '$, so that it is a face of both $\tau _1$ and $\tau$ by induction hypothesis; but $\tau \preceq \tau _1$ so that $\tau _1\cap \tau _2\preceq \tau _2$. Finally, assume that both $\tau _1$ and $\tau _2$ are not in $\Sigma '$. This means that there are facets $f_1,f_2$ in $\mathcal {F}$ and faces $\mu _1\preceq f_1,\mu _2\preceq f_2$ such that $\tau _1=\langle \mu _1,\mathbf {w}_k\rangle$ and $\tau _2=\langle \mu _2,\mathbf {w}_k\rangle$. We show that $\tau _1\cap \tau _2=\langle \mu _1\cap \mu _2,\mathbf {w}_k \rangle \in \Sigma$. Let $\mathbf {x}\in \tau _1\cap \tau _2$: Then, we can write $\mathbf {x}=\mathbf {y}_1+\lambda _1\mathbf {w}_k=\mathbf {y}_2+\lambda _2\mathbf {w}_k$, where $\mathbf {y}_1\in \mu _1, \mathbf {y}_2\in \mu _2$ and $\lambda _1, \lambda _2 \ge 0$. Without loss of generality we can assume $\lambda _1\ge \lambda _2$; put $\lambda =\lambda _1-\lambda _2$; then, $\mathbf {y}_1+\lambda \mathbf {w}_k=\mathbf {y}_2$. Let H be the hyperplane cutting $f_1$; since $f_1\in \mathcal {F}$, $\mathbf {w}_k\not \in H$, so that there exists a vector $\mathbf {n}$ be a normal to H such that $\mathbf {n}\cdot \mathbf {x}\le 0$ for every $\mathbf {x}\in \mathcal {W}'$ and $\mathbf {n}\cdot \mathbf {w}_k>0$. Then, $\mathbf {n}\cdot \ \mathbf {y}_2\le 0$ and $\mathbf {n}\cdot (\mathbf {y}_1+\lambda \mathbf {w}_k)=\mathbf {n}\cdot \lambda \mathbf {w}_k\ge 0$, so that $\lambda =0$; this implies $\mathbf {y}_1=\mathbf {y}_2\in \mu _1\cap \mu _2$ and $\mathbf {x}\in \langle \mu _1\cap \mu _2,\mathbf {w}_k\rangle$.

Now we show that condition a) holds for $\Sigma$. By construction $|\Sigma |=|\Sigma '|\cup \bigcup _{f\in \mathcal {F}} \tau _f\subseteq \mathcal {W'}+\langle \mathbf {w}_k\rangle =\mathcal {W}$; conversely, let $\mathbf {x}\in \mathcal {W}$; if $\mathbf {x}\in \mathcal {W}'$, then $\mathbf {x}\in |\Sigma '|\subseteq |\Sigma |$; if $\mathbf {x}\not \in \mathcal {W}'$, then $\mathbf {x}=\mathbf {y}+\lambda \mathbf {w}_k$ for some $\mathbf {y}\in \mathcal {W}'$ and $\lambda >0$; up to replacing $\mathbf {y}$ by $\mathbf {y}+\mu \mathbf {w}_k$ for some $0\le \mu <\lambda$ we can assume that $\mathbf {y}+\epsilon \mathbf {w}_k\not \in \mathcal {W}'$ if $\epsilon >0$. Then, for every $\epsilon$ there exists an hyperplane $H_\epsilon$ cutting a facet $\varphi _\epsilon$ of $\mathcal {W}'$ which separates $\mathcal {W}'$ and $\mathbf {y}+\epsilon \mathbf {w}_k$; since the facets of $\mathcal {W}'$ are finitely many, by the pigeonhole principle $H_\epsilon ,\varphi _\epsilon$ do not depend on $\epsilon$ for $\epsilon \rightarrow 0$; call them $H,\varphi$, respectively. Let $\mathbf {n}$ be a normal vector to H such that $\mathbf {n}\cdot \mathbf {y}\le 0$ and $\mathbf {n}\cdot (\mathbf {y}+\epsilon \mathbf {w}_k)>0$ for $\epsilon \rightarrow 0$; the existence of such $\mathbf {n}$ implies $\mathbf {n}\cdot \mathbf {y}=0$ and $\mathbf {n}\cdot \mathbf {w}_k>0$, so that $\mathbf {y}\in \varphi$ and $\mathbf {w}_k\not \in H$. Then, there is a facet $f\in \mathcal {F}$ such that $\mathbf {y}\in f$; therefore, $\mathbf {x}\in \tau _f$, and a) is proved. We showed that $\Sigma {\setminus }\Sigma '\not =\emptyset$; and every cone in $\Sigma {\setminus } \Sigma '$ has $\mathbf {w}_k$ as a vertex and all other vertices in $\Sigma '(1)$. Then, condition b) is verified. Condition c) is obvious since $\Sigma _0\subseteq \Sigma '\subseteq \Sigma$. $\square$

Corollary 3

Let V be a fan matrix. Then, for every $I\in \mathcal {I}_{V,\mathrm{min}}$ the cone $\langle V^I\rangle$ belongs to a fan in $\mathcal {SF}(V)$.

Proof

It suffices to apply Lemma 4 in the case $\Sigma _0=\{\tau \ |\ \tau \preceq \langle V^I\rangle \}$ and $\mathbf {w}_1,\ldots , \mathbf {w}_k$ are the columns of $V_I$. $\square$

Corollary 3 has the following immediate consequence:

Corollary 4

Let V be a fan matrix such that $\mathcal {SF}(V)$ contains a unique fan $\Sigma$. Then, for every $I\in \mathcal {I}_{V,\mathrm{min}}$ the cone $\langle V^I\rangle$ belongs to $\Sigma$.

We are now in position to prove our purity condition:

Proposition 5

Let X be a $\mathbb {Q}$-factorial complete toric variety and let V be a fan matrix of X. Assume that $\mathcal {SF}(V)$ contains a unique fan. Then, X is pure.

Proof

Let $Y=Y({\widehat{\Sigma }})$ be the universal 1-covering of X and let $\widehat{V}$ be a fan matrix associated with Y. Then, $\widehat{V}$ is a CF-matrix, so that $m_{\widehat{V},\mathrm{tot}}=1$ by [7, Prop. 2.6 and Def. 2.7]. By Corollary 4, $\mathcal {I}^{\Sigma }= \mathcal {I}^{{\widehat{\Sigma }}}=\mathcal {I}_{\widehat{V},\mathrm{min}}$ so that $m_{{\widehat{\Sigma }}}=m_{\widehat{V},\mathrm{min}}$ and, by Lemma 3, the latter is equal to $m_{\widehat{V},\mathrm{tot}}=1$. Then, X is pure by Corollary 1. $\square$

Remark 3

Proposition 5 implies that the following toric varieties are pure:

• two-dimensional $\mathbb {Q}$-factorial complete toric varieties

• toric varieties whose universal 1-covering is a product of weighted projective spaces.

Remark 4

In the case $|\mathcal {SF}(V)|=1$ the unique complete and $\mathbb {Q}$-factorial toric variety X whose fan matrix is V is necessarily projective. This is a consequence of the fact that $\mathrm {Nef}(X)=\mathrm {\overline{Mov}}(X)$, recalling that the latter is a full dimensional cone, by [1, Thm. 2.2.2.6].

3.4.1 An application to completions of fans

Lemma 4 can be applied to give a complete refinement $\Sigma$ of a given fan $\Sigma _0$ satisfying the further additional hypothesis:

(*):

assume that $|\Sigma |=\Sigma _0 + \langle \mathbf {w}_1,\ldots , \mathbf {w}_k\rangle ={\mathbb {R}}^n$.

In particular, if we consider the fan $\Sigma '=\Sigma _0\cup \{\langle \mathbf {w}_1\rangle \,\ldots ,\langle \mathbf {w}_k\rangle \}$, then Lemma 4gives a completion $\Sigma$ of $\Sigma '$ without adding any new ray.

The latter seems to us an original result. In fact, it is actually well known that every fan $\Sigma '$ can be refined to a complete fan $\Sigma$ (see [3, Thm. III.2.8], [4] and the more recent [6]). Anyway, in general the known completion procedures need the addition of some new ray, so giving $\Sigma '(1)\subsetneq \Sigma (1)$. As observed in the Remark following the proof of [3, Thm. III.2.8], just for $n=3$ “completion without additional 1-cones can be found,” but this fact does no more hold for $n\ge 4$: At this purpose, Ewald refers the reader to the Appendix to section III, where he is further referred to a number of references. Unfortunately we were not able to recover, from those references and, more generally, from the current literature, as far as we know, an explicit example of a four-dimensional fan which cannot be completed without adding some new ray. For this reason, we believe that the following example may fill up a lack in the literature on these topics.

Example 3

Consider the fan matrix

$$\begin{aligned} V= \left( \begin{array}{ccccccc} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -1&{}\quad 1 \\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad -1&{}\quad -1&{}\quad 2 \\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad -1&{}\quad 0&{}\quad 1 \\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad -1&{}\quad -1&{}\quad 1 \\ \end{array} \right) \end{aligned}$$

and consider the fan $\Sigma$ given by taking all the faces of the following three maximal cones generated by columns of V

$$\begin{aligned} \Sigma (4)=\left\{ \langle 2,3,4,6\rangle ,\langle 2,4,5,7\rangle ,\langle 1,4,5,6\rangle \right\} \end{aligned}$$

The fact that $\Sigma$ is a fan follows immediately by easily checking that

$$\begin{aligned} \langle 2,3,4,6\rangle \cap \langle 2,4,5,7\rangle= & {} \langle 2,4\rangle \\ \langle 2,3,4,6\rangle \cap \langle 1,4,5,6\rangle= & {} \langle 4,6\rangle \\ \langle 1,4,5,6\rangle \cap \langle 2,4,5,7\rangle= & {} \langle 4,5\rangle . \end{aligned}$$

Notice that $\Sigma$ is not a complete fan since, e.g., the three-dimensional cone

$$\begin{aligned} \langle 2,3,6\rangle =\left\langle \begin{array}{ccc} 0 &{}\quad 0 &{}\quad -1 \\ 1 &{}\quad 0 &{}\quad -1 \\ 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -1 \end{array} \right\rangle \end{aligned}$$

is a facet of the unique cone

$$\begin{aligned} \langle 2,3,4,6\rangle =\left\langle \begin{array}{cccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad -1 \\ 1 &{}\quad 0 &{}\quad 0 &{}\quad -1 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad -1 \end{array}\right\rangle \in \Sigma (4). \end{aligned}$$

Moreover, it cannot be completed since every further maximal cone admitting $\langle 2,3,6\rangle$ as a facet does not intersect correctly the remaining cones in $\Sigma (4)$. In fact

• $\langle 1,2,3,6\rangle \cap \langle 2,4,5,7\rangle \supsetneq \langle 2\rangle$ : Consider, e.g.,

  $$\begin{aligned} \mathbf {v}=\left( \begin{array}{cccc} 1&{}\quad 1&{}\quad 0&{}\quad 0 \\ \end{array} \right) ^T\in \langle 1,2\rangle \cap \langle 5,7\rangle \end{aligned}$$

• $\langle 2,3,5,6\rangle \cap \langle 1,4,5,6\rangle \supsetneq \langle 5,6\rangle$ : Consider, e.g.,

  $$\begin{aligned} \mathbf {w}=\left( \begin{array}{cccc} 0 &{}\quad -2 &{}\quad -1 &{}\quad -2 \\ \end{array} \right) ^T\in \langle 3,5\rangle \cap \langle 1,5,6\rangle \quad \text {but}\quad \mathbf {w}\not \in \langle 5,6\rangle \end{aligned}$$

• $\langle 2,3,6,7\rangle$ is not a maximal cone.

4 A characterization of ${{\,\mathrm{Pic}\,}}(X)$ for some pure toric variety

Let $X=X(\Sigma )$ be a complete $\mathbb {Q}$-factorial toric variety having V as a fan matrix; let Y be its universal 1-covering, ${\widehat{V}}$ be a fan matrix associated with Y and $V=\beta \widehat{V}$. Recall that a Weil divisor $L=\sum _{j=1}^{n+r}a_jD_j$ is a Cartier divisor if it is locally principal, that is,

$$\begin{aligned} \forall I\in \mathcal {I}^\Sigma \ \exists \mathbf {m}_I\in M \hbox { such that } \mathbf {m}_I\cdot \mathbf {v}_j=a_j, \forall j\not \in I. \end{aligned}$$

Let $\mathcal {C}_{T}(X)$ be the group of torus invariant Cartier divisors of X. Then,

$$\begin{aligned} \mathcal {C}_{T}(X)=\bigcap _{I\in \mathcal {I}^\Sigma }\mathcal {L}_r(V^I)=\bigcap _{I\in \mathcal {I}^\Sigma }(\mathcal {L}_r(V)\oplus E_I) \end{aligned}$$

recalling notation (4). The Picard group ${{\,\mathrm{Pic}\,}}(X)$ of X is the image of $\mathcal {C}_{T}(X)$ in ${{\,\mathrm{Cl}\,}}(X)$, via morphism $d_X$ (recall here and in the following, notation introduced in diagram (3)).

In [7, Thm. 2.9.2] we showed that if Y is a PWS, then we can identify

$$\begin{aligned} {{\,\mathrm{Pic}\,}}(Y)=\bigcap _{I\in \mathcal {I}^\Sigma } \mathcal {L}_c(Q_I)\subseteq \mathbb {Z}^r.\end{aligned}$$

(6)

Let $\mathbf {x}\in {{\,\mathrm{Pic}\,}}(Y)$. For $I\in \mathcal {I}^\Sigma$ we can write $\mathbf {x}=Q\cdot \mathbf {a}_I$ where $\mathbf {a}_{I}\in E_I$. If $I,J\in \mathcal {I}^\Sigma$ put

$$\begin{aligned} \mathbf {u}_{IJ}=\mathbf {a}_I-\mathbf {a}_J\in \ker (Q)=\mathcal {L}_r(\widehat{V}). \end{aligned}$$

(7)

Let $\mathbf {z}\in \mathcal {C}_{T}(Y)$ such that $Q\cdot \mathbf {z}=\mathbf {x}$. By definition, for every $I\in \mathcal {I}^\Sigma$ there is a unique decomposition $\mathbf {z}=\mathbf {t}(I)+\mathbf {a}_I$ with $\mathbf {t}(I)\in \mathcal {L}_r(\widehat{V})$. Moreover,

$$\begin{aligned} \mathbf {z}\in \mathcal {C}_{T}(X)\Leftrightarrow \mathbf {t}(I)\in \mathcal {L}_r(V), \forall I\in \mathcal {I}^\Sigma . \end{aligned}$$

(8)

Proposition 6

$\mathbf {x}\in {\overline{\alpha }}({{\,\mathrm{Pic}\,}}(X))$ if and only if $\mathbf {x}\in {{\,\mathrm{Pic}\,}}(Y)$ and $\mathbf {u}_{IJ}\in \mathcal {L}_r(V)$, for every $I,J\in \mathcal {I}^\Sigma$, where $\mathbf {u}_{IJ}$ is defined by (7).

Proof

Suppose that $\mathbf {x}\in {\overline{\alpha }}({{\,\mathrm{Pic}\,}}(X))$. Then, there exists $\mathbf {z}\in \mathcal {C}_{T}(X)$ such that $Q\cdot \mathbf {z}=\mathbf {x}$. For every $I\in \mathcal {I}^\Sigma$ consider the decomposition $\mathbf {z}=\mathbf {t}(I)+\mathbf {a}_I$ with $\mathbf {t}(I)\in \mathcal {L}_r(V)$. Then, $\mathbf {u}_{IJ}=\mathbf {a}_I-\mathbf {a}_J= \mathbf {t}(J)-\mathbf {t}(I)\in \mathcal {L}_r(V)$ for every $I,J\in I^\Sigma$. Conversely, suppose that $\mathbf {u}_ {IJ}\in \mathcal {L}_r(V)$ for every $I,J\in \mathcal {I}^\Sigma$. Let $\mathbf {z}'\in \mathcal {C}_{T}(Y)$ be such that $Q\cdot \mathbf {z}'=\mathbf {x}$. For every $I\in \mathcal {I}^\Sigma$ there is a decomposition $\mathbf {z}'=\mathbf {t}'(I)+\mathbf {a}_I$ with $\mathbf {t}'(I)\in \mathcal {L}_r({\widehat{V}})$. Fix $I_0\in \mathcal {I}^\Sigma$ and put $\mathbf {z}=\mathbf {z}'-\mathbf {t}'(I_0)$. We claim that $\mathbf {z}\in \mathcal {C}_{T}(X)$. Indeed, let $I\in \mathcal {I}^\Sigma$ and decompose $\mathbf {z}=\mathbf {t}(I)+\mathbf {a}_I$ with $\mathbf {t}(I)\in \mathcal {L}_r({\widehat{V}})$ and $\mathbf {t}(I_0)=\mathbf {0}$. It follows that for every $I\in \mathcal {I}^\Sigma$

$$\begin{aligned} \mathbf {t}(I)=\mathbf {t}(I)-\mathbf {t}(I_0)=\mathbf {a}_{I_0}-\mathbf {a}_I=\mathbf {u}_{I_0I}\in \mathcal {L}_r(V). \end{aligned}$$

$\square$

Theorem 3

Let X be a pure $\mathbb {Q}$-factorial complete toric variety and choose an isomorphism ${{\,\mathrm{Cl}\,}}(X)\cong \mathbb {Z}^r\oplus T$ such that ${{\,\mathrm{Pic}\,}}(X)$ is mapped in $\mathbb {Z}^r$. Then, the following characterization of ${{\,\mathrm{Pic}\,}}(X)$ holds:

$$\begin{aligned} \mathbf {x}\in {{\,\mathrm{Pic}\,}}(X)\,\Leftrightarrow \,\forall \,I,J\in \mathcal {I}^\Sigma \quad \mathbf {x}\in \bigcap _{I\in \mathcal {I}^\Sigma } \mathcal {L}_c(Q_I)\ \text {and}\ \mathbf {u}_{IJ}\in \mathcal {L}_r(V) \end{aligned}$$

where $\mathbf {u}_{IJ}$ is defined by (7).

Proof

Define $s:\mathbb {Z}^r\rightarrow \mathbb {Z}^r\oplus T$ by $s(a)=(a,0)$. Then, ${\overline{\alpha }}\circ s=id_{\mathbb {Z}_r}$ and $s\circ {\overline{\alpha }}|_{{{\,\mathrm{Pic}\,}}(X)}=id_{{{\,\mathrm{Pic}\,}}(X)}$. Then, we have for every $\mathbf {x}\in \mathbb {Z}^r$

$$\begin{aligned} \mathbf {x}\in {\overline{\alpha }}({{\,\mathrm{Pic}\,}}(X))\Leftrightarrow s(\mathbf {x})\in {{\,\mathrm{Pic}\,}}(X). \end{aligned}$$

The result follows from Proposition 6 by identifying $\mathbf {x}$ and $s(\mathbf {x})$. $\square$

Example 4

Let $\Sigma '_1$ be the fan defined in Example 2. Then,

$$\begin{aligned} \mathcal {I}^{\Sigma '_1}=\mathcal {I}^{{\widehat{\Sigma }}_1}=\{\{1,3\},\{2,3\}, \{3,5\},\{1,4\}, \{2,4\},\{4,5\}\}. \end{aligned}$$

so that

$$\begin{aligned} \bigcap _{I\in \mathcal {I}^{\Sigma '_1}} \mathcal {L}_c(Q_I)=\mathbb {Z}(30,0)\oplus \mathbb {Z}(0,60). \end{aligned}$$

Let $\mathbf {x}=(30x, 60y)\in \bigcap _{I\in \mathcal {I}^{\Sigma '_1}} \mathcal {L}_c(Q_I)$, with $x,y\in \mathbb {Z}$. For $I\in \mathcal {I}^{\Sigma '_1}$ we can write $\mathbf {x}=Q\cdot \mathbf {a}_I$ where $\mathbf {a}_{I}\in E_I$. The $\mathbf {a}_I$’s are easily calculated:

$$\begin{aligned} \begin{array}{lllcccccl} \mathbf {a}_{\{1,3\}}&{}=&{}(&{}20y &{}0 &{}3x-6y &{} 0 &{} 0&{})\\ \mathbf {a}_{\{2,3\}}&{}=&{} (&{}0 &{}30y &{}3x-3y &{} 0 &{} 0&{} )\\ \mathbf {a}_{\{3,5\}}&{}=&{} (&{}0 &{}0 &{}3x-24y &{} 0 &{} 60y&{} )\\ \mathbf {a}_{\{1,4\}}&{}=&{} (&{}20y &{}0 &{}0 &{} 5x-10y &{} 0&{} )\\ \mathbf {a}_{\{2,4\}}&{}=&{} (&{}0 &{}30y &{}0 &{} 5x-5y &{} 0&{} )\\ \mathbf {a}_{\{4,5\}}&{}=&{} (&{}0 &{}0 &{}0 &{} 5x-40y &{} 60y&{} ) \end{array} \end{aligned}$$

Notice that, with the notation of (7), $\mathbf {u}_{IJ}=\mathbf {u}_{IK}-\mathbf {u}_{KJ}$; then, in order to calculate $\mathbf {u}_{IJ}$ for every $I,J\in \mathcal {I}^{\Sigma '_1}$ it suffices to compute $\mathbf {u}_{I_jI_{j+1}}$ for a sequence $I_1,\ldots , I_s$ such that $\langle Q_{I_j}\rangle$ and $\langle Q_{I_{j+1}}\rangle$ have a common facet and $\mathcal {I}^{\Sigma '_1}=\{I_1,\ldots , I_s\}$; in this way, we obtain vectors having at most $r+1=3$ nonzero components:

$$\begin{aligned} \begin{array}{lllcccccl} \mathbf {u}_{\{1,3\}\{2,3\}}&{}=&{} (&{} 20y&{}-30y&{}-3y&{}0&{}0&{} )\\ \mathbf {u}_{\{2,3\}\{3,5\}} &{} =&{} (&{} 0&{} 30y&{}21y&{}0&{}-60y&{})\\ \mathbf {u}_{\{3,5\}\{4,5\}} &{}=&{} (&{} 0&{}0&{}3x-24y&{}-5x+40y&{} 0&{} )\\ \mathbf {u}_{\{4,5\}\{1,4\}}&{}=&{} (&{} -20y&{}0&{}0&{}-30y&{}60y&{})\\ \mathbf {u}_{\{1,4\}\{2,4\}}&{}=&{} (&{} 20y&{}-30y&{}0&{}-5y&{}0 &{}) \end{array} \end{aligned}$$

Multiplying by the matrix $\Gamma '$ found in (5) we obtain

$$\begin{aligned}&\Gamma '\cdot \mathbf {u}_{\{1,3\}\{2,3\}}^T=0;\quad \Gamma '\cdot \mathbf {u}_{\{2,3\}\{3,5\}}^T=-60y;\quad \Gamma '\cdot \mathbf {u}_{\{3,5\}\{4,5\}}^T=-5x+40y;\\&\Gamma '\cdot \mathbf {u}_{\{4,5\}\{1,4\}}^T=30y;\quad \quad \Gamma '\cdot \mathbf {u}_{\{1,4\}\{2,4\}}^T=-5y. \end{aligned}$$

Recall that $\varGamma '$ takes values in $\mathbb {Z}/2\mathbb {Z}$ and that for every $\mathbf {u}\in \mathcal {L}_r({\widehat{V}})$

$$\begin{aligned} \Gamma '\cdot \mathbf {u}^T=0\hbox { if and only if } \mathbf {u}\in \mathcal {L}_r(V'); \end{aligned}$$

then, we see that $\mathbf {u}_{IJ}\in \ker (\Gamma ')$ for every $I,J\in \mathcal {I}^{\Sigma '_1}$ if and only if $x,y\in 2\mathbb {Z}$, that is, if and only if $\mathbf {x}\in \mathbb {Z}(60,0)\oplus \mathbb {Z}(0,120)$. By Theorem 3, ${{\,\mathrm{Pic}\,}}(X')$ can be identified with the subgroup $\mathbb {Z}(60,0)\oplus \mathbb {Z}(0,120)$ in ${{\,\mathrm{Cl}\,}}(X')\simeq \mathbb {Z}^2\oplus \mathbb {Z}/2\mathbb {Z}$, according to what we established in Example 2.