Abstract
We conjecture an explicit positive combinatorial formula for the expansion of unicellular LLT polynomials in the elementary symmetric basis. This is an analogue of the Shareshian–Wachs conjecture previously studied by Panova and the author in 2018. We show that the conjecture for unicellular LLT polynomials implies a similar formula for vertical-strip LLT polynomials. We prove positivity in the elementary symmetric basis for the class of graphs called “melting lollipops” previously considered by Huh, Nam and Yoo. This is done by proving a curious relationship between a generalization of charge and orientations of unit-interval graphs. We also provide short bijective proofs of Lee’s three-term recurrences for unicellular LLT polynomials, and we show that these recurrences are enough to generate all unicellular LLT polynomials associated with abelian area sequences.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background on LLT polynomials
LLT polynomials were introduced by Lascoux, Leclerc and Thibon in [24] and are q-deformations of products of skew Schur functions. An alternative combinatorial model for the LLT polynomials was later introduced in [16] while studying Macdonald polynomials. In their paper, LLT polynomials are indexed by a k-tuple of skew shapes. In the case each such skew shape is a single box, the LLT polynomial is said to be unicellular LLT polynomial. Such unicellular LLT polynomials are the main topic of this paper.
1.2 Background on chromatic symmetric functions
In [7] Carlsson and Mellit introduced a more convenient combinatorial model for unicellular LLT polynomials, indexed by (area sequences of) Dyck paths. They also highlighted an important relationship using plethysm between unicellular LLT polynomials and the chromatic quasisymmetric functions introduced by Shareshian and Wachs in [30].
The chromatic quasisymmetric functions refine the chromatic symmetric functions introduced by Stanley in [28]. The Stanley–Stembridge conjecture [27] states that such chromatic symmetric functions associated with unit-interval graphs, and more generally, incomparability graphs of \(3+1\)-free posets are positive in the elementary symmetric basis, or \(\mathrm {e}\)-positive for short. Their conjecture was refined with the introduction of an additional parameter q in [30]. The class of graphs for which this conjecture is believed to hold was later extended to the class of circular unit-interval graphs in [11, 12] where it is conjectured that the chromatic quasisymmetric functions expanded in the \(\mathrm {e}\)-basis have coefficients in \({\mathbb {N}}[q]\), see Conjecture 13. To this date, there is still not even a conjectured combinatorial formula for the \(\mathrm {e}\)-expansion of the chromatic symmetric functions.
The idea of studying LLT polynomials in parallel with chromatic quasisymmetric functions originated in [7], although the connection is perhaps in hindsight apparent in the techniques used in [16]. We also mention an interesting paper by Haglund and Wilson [21] explores the connection between the integral-form Macdonald polynomials and the chromatic quasisymmetric functions.
1.3 Main results
In [1], we stated an analogue of the Shareshian–Wachs conjecture regarding \(\mathrm {e}\)-positivity of unicellular LLT polynomials, \(\mathrm {G}_{\mathbf {a}}({\mathbf {x}};q+1)\) and proved the conjecture in a few cases. We also provided many similarities between unicellular LLT polynomials and chromatic quasisymmetric functions associated with unit-interval graphs. The problem of \(\mathrm {e}\)-positivity of unicellular LLT polynomials is the main topic of this article.
The main results are:
-
We present a precise conjectured combinatorial formula for the \(\mathrm {e}\)-expansion of \(\mathrm {G}_{\mathbf {a}}({\mathbf {x}};q+1)\). Our conjecture states that the unicellular LLT polynomial \(\mathrm {G}_{{\mathbf {a}}}({\mathbf {x}};q)\) is given as
$$\begin{aligned} \mathrm {G}_{{\mathbf {a}}}({\mathbf {x}};q+1) {:}{=}\sum _{\theta \in O({\mathbf {a}})} q^{{{\,\mathrm{asc}\,}}(\theta )}\mathrm {e}_{{{\overline{\pi }}}(\theta )}({\mathbf {x}}). \end{aligned}$$(1)where \(O({\mathbf {a}})\) is the set of orientations of the unit-interval graph with area sequence \({\mathbf {a}}\), and \({{\overline{\pi }}}(\theta )\) is an explicit partition-valued statistic on such orientation. This formula can be extended to vertical-strip LLT polynomials and has been verified on the computer for all unit-interval graphs up to 10 vertices. This formula is surprising, as there is still no analogous conjectured formula for chromatic symmetric functions.
A possible application of (1) is to find a positive combinatorial formula for the Schur-expansion of \(\mathrm {G}_{{\mathbf {a}}}({\mathbf {x}};q)\).
-
We prove in Corollary 32 that the conjectured formula (1) implies a generalized formula for the so-called vertical-strip LLT polynomials. Furthermore, we prove that (1) holds for the family of complete graphs and line graphs.
-
Analogous recursions for the unicellular LLT polynomials are given by Lee in [23]. We give short bijective proofs of these recurrences and show that all graphs associated with abelian Hessenberg varieties can be computed recursively via Lee’s recurrences, starting from unicellular LLT polynomials associated with the complete graphs.
-
In Sect. 5, we prove that the transformed Hall–Littlewood polynomials \(\mathrm {H}_\lambda ({\mathbf {x}};q+1)\) are positive in the complete homogeneous basis. This implies that a corresponding family of vertical-strip LLT polynomials are \(\mathrm {e}\)-positive.
Note that vertical-strip LLT polynomials appear in diagonal harmonics, see for example [5, Section 4] and [4, 17]. Consequently, (1) provides support for some of the conjectures regarding \(\mathrm {e}\)-positive in these references. We note that the authors of a recent preprint [14] also independently found the conjecture in (1). The \(\mathrm {e}\)-positivity part of the conjecture has since been proved by M. D’Adderio in [8]. We remark that \(\mathrm {e}\)-positivity is very rare in reality, see [26] for details.
-
In Sect. 6, we prove a curious identity between a generalization of charge, denoted \({{\,\mathrm{wt}\,}}_{\mathbf {a}}(T)\), and the set of orientations, \(O({\mathbf {a}})\), of a unit-interval graph \(\varGamma _{\mathbf {a}}\). It states that
$$\begin{aligned} \sum _{\lambda \vdash n} \sum _{T \in \mathrm {SYT}(\lambda )} (q+1)^{{{\,\mathrm{wt}\,}}_{\mathbf {a}}(T)} \mathrm {s}_\lambda ({\mathbf {x}}) = \sum _{\theta \in O({\mathbf {a}})} q^{{{\,\mathrm{asc}\,}}(\theta )} \mathrm {e}_{\sigma (\theta )}({\mathbf {x}}), \end{aligned}$$(2)where \({{\,\mathrm{asc}\,}}(\cdot )\) and \(\sigma (\cdot )\) are certain combinatorial statistics on orientations. This version of charge was considered in [19] in order to prove Schur positivity for unicellular LLT polynomials in the melting lollipop graph case.
As a consequence, we get an explicit positive \(\mathrm {e}\)-expansion the case of melting lollipop graphs which has previously been considered in [19]. The corresponding family of chromatic quasisymmetric functions was considered in [10] where they were proved to be \(\mathrm {e}\)-positive. Note, however, that the statistic \({{\overline{\pi }}}(\theta )\) in (1) and \(\sigma (\theta )\) in (2) are different.
The paper is organized as follows. We first introduce the family of unicellular- and vertical-strip LLT polynomials and some of their basic properties. In Sect. 3, we prove several recursive identities for such LLT polynomials. In particular, we show that the recursions by Lee [23] can be used to construct unicellular LLT polynomials indexed by any abelian area sequence.
Some vertical-strip LLT polynomials are closely related to the transformed Hall–Littlewood polynomials. In Sect. 5, we show that the transformed Hall–Littlewood polynomials \(\mathrm {H}_\lambda ({\mathbf {x}};q+1)\) are \(\mathrm {h}\)-positive, which gives further support for the main conjecture.
In Sect. 6, we study the relationship between a type of generalized cocharge introduced in [19] and \(\mathrm {e}\)-positivity. This provides a proof that unicellular LLT polynomials given by melting lollipop graphs are \(\mathrm {e}\)-positive.
Finally in Sect. 7, we describe a possible approach to prove (1) by a comparison in the power-sum symmetric basis.
2 Preliminaries
We use the same notation and terminology as in [1]. The reader is assumed to have a basic background on symmetric functions and related combinatorial objects, see [25, 29]. All Young diagrams and tableaux are presented in the English convention.
2.1 Dyck paths and unit-interval graphs
An area sequence is an integer vector \({\mathbf {a}}=(a_1,\dotsc ,a_n)\) which satisfies
-
\(0 \le a_i \le i-1 \) for \(1 \le i \le n\) and
-
\(a_{i+1} \le a_{i} + 1\) for \(1 \le i < n\).
The number of such area sequences of size n is given by the Catalan numbers. Note that [19] uses a reversed indexing of entries in area sequences.
Definition 1
For every area sequence of length n, we define a unit-interval graph \(\varGamma _{\mathbf {a}}\) with vertex set [n] and the directed edges
for all \(i = 1,\dotsc ,n\). We say that (u, v) with \(u<v\) is an outer corner of \(\varGamma _{\mathbf {a}}\) if (u, v) is not an edge of \(\varGamma _{\mathbf {a}}\), and either
-
\(u+1=v\) or
-
\((u+1,v)\) and \((u,v-1)\) are edges of \(\varGamma _{\mathbf {a}}\).
Example 2
We can illustrate area sequences and their corresponding unit-interval graphs as Dyck diagrams, as is done in [1, 15]. For example, (0, 1, 2, 3, 2, 2) corresponds to the diagram

where the area sequence specify the number of white squares in each row, bottom to top. The squares on the main diagonal are the vertices of \(\varGamma _{\mathbf {a}}\), and each white square corresponds to a directed edge of \(\varGamma _{\mathbf {a}}\). In the second figure we see this correspondence where edge (i, j) is marked as ij. The outer corners of \(\varGamma _{\mathbf {a}}\) are (2, 5) and (3, 6).
Caution We do not really distinguish the terms area sequence, Dyck diagram and unit-interval graph, as they all relate to the same objects. What term is used depends on context and what features we wish to emphasize.
Let \(\varGamma _{\mathbf {a}}\) be an unit-interval graph with n vertices. We let \({\mathbf {a}}^{\mathrm{T}}\) denote the area sequence of \(\varGamma _{\mathbf {a}}\) where all edges have been reversed, and every vertex \(j \in [n]\) has been relabeled with \(n+1-j\). This operation corresponds to simply transposing the Dyck diagram.
Lemma 3
(See [1]) The entries in an area sequence \({\mathbf {a}}\) is a rearrangement of the entries in \({\mathbf {a}}^{\mathrm{T}}\).
Most results in this paper concern a few special classes of area sequences.
Definition 4
An area sequence of length n is called rectangular if either \({\mathbf {a}}= (0,1,2,\dotsc ,n-1)\) or there is some \(k \in [n]\) such that
This condition is equivalent with all non-edges forming a \(k \times (n-k)\)-rectangle in the Dyck diagram. Furthermore, an area sequence \({\mathbf {a}}'\) is called abelian whenever \(a'_i \ge a_i\) for some rectangular sequence \({\mathbf {a}}\). For example, the area sequence in (4) is abelian.
The terminology is motivated by [20], where abelian area sequences are associated with abelian Hessenberg varieties.
We will also consider the following families of area sequences:
-
The complete graphs, \((0,1,2,\dotsc ,n-1)\).
-
The line graphs \((0,1,1,\dotsc ,1)\).
-
Lollipop graphs, where
$$\begin{aligned} a_i = {\left\{ \begin{array}{ll} i-1 &{}\quad \text {for } i=1,\dotsc ,m \\ 1&{}\quad \text {for } i=m+1,\dotsc ,m+n \end{array}\right. } \end{aligned}$$for some \(m,n\ge 1\).
-
Melting complete graph,
$$\begin{aligned} a_i = {\left\{ \begin{array}{ll} i-1&{}\quad \text {for } i=1,2,\dotsc ,n-1 \\ n-k-1 &{}\quad \text {for } i=n \end{array}\right. } \end{aligned}$$where \(0\le k \le n-1\).
-
Melting lollipop graphs, defined as
$$\begin{aligned} a_i = {\left\{ \begin{array}{ll} i-1&{}\quad \text {for } i=1,\dotsc ,m-1 \\ m-1-k &{}\quad \text {for } i=m \\ 1&{}\quad \text {for } i=m+1,\dotsc ,m+n \end{array}\right. } \end{aligned}$$for \(m,n\ge 1\) and \(0\le k \le m-1\).
2.2 Vertical-strip diagrams
A vertical-strip diagram is a Dyck diagram where some of the outer corners have been marked with \(\rightarrow \). We call such an outer corner a strict edge. These markings correspond to some extra oriented edges of \(\varGamma _{\mathbf {a}}\). We use the notation \(\varGamma _{{\mathbf {a}},{\mathbf {s}}}\) to denote a directed graph with some additional strict edges \({\mathbf {s}}\) and refer to the graph \(\varGamma _{{\mathbf {a}},{\mathbf {s}}}\) as a vertical-strip diagram as well.
Example 5
Below is an example of a vertical-strip diagram.

The edges (1, 4) and (3, 6) are strict of \(\varGamma _{{\mathbf {a}},{\mathbf {s}}}\), and the directed edges of \(\varGamma _{{\mathbf {a}}}\) (which are also edges of \(\varGamma _{{\mathbf {a}},{\mathbf {s}}}\)) are
Note that this is another example of a diagram with an abelian area sequence.
2.3 Vertical-strip LLT polynomials
Let \(\varGamma _{{\mathbf {a}},{\mathbf {s}}}\) be a vertical-strip diagram. A valid coloring \(\kappa :V(\varGamma _{{\mathbf {a}},{\mathbf {s}}}) \rightarrow {\mathbb {N}}\) is a vertex coloring of \(\varGamma _{{\mathbf {a}},{\mathbf {s}}}\) such that \(\kappa (u)<\kappa (v)\) whenever (u, v) is a strict edge in \({\mathbf {s}}\). Given a coloring \(\kappa \), an ascent of \(\kappa \) is a (directed) edge (u, v) in \(\varGamma _{{\mathbf {a}},{\mathbf {s}}}\) such that \(\kappa (u)<\kappa (v)\). Note that strict edges do not count as ascents. Let \({{\,\mathrm{asc}\,}}(\kappa )\) denote the number of ascents of \(\kappa \).
Definition 6
Let \(\varGamma _{{\mathbf {a}},{\mathbf {s}}}\) be a vertical-strip diagram. The vertical-strip LLT polynomial \(\mathrm {G}_{{\mathbf {a}},{\mathbf {s}}}({\mathbf {x}};q)\) is defined as
where the sum is over valid colorings of \(\varGamma _{{\mathbf {a}},{\mathbf {s}}}\). Whenever \({\mathbf {s}}= \emptyset \), we simply write \(\mathrm {G}_{{\mathbf {a}}}({\mathbf {x}};q)\) and refer to this as a unicellular LLT polynomial.
As an example, here is \(\mathrm {G}_{0012}({\mathbf {x}};q)\) expanded in the Schur basis:
The polynomials \(\mathrm {G}_{{\mathbf {a}},{\mathbf {s}}}({\mathbf {x}};q)\) are known to be symmetric, and correspond to classical LLT polynomials indexed by k-tuples of skew shapes as in [16]. In fact, the unicellular LLT polynomials correspond to the case when all shapes in the k-tuple are single cells, and the vertical-strip case corresponds to k-tuples of single columns. This correspondence is proved in [1] and is also done implicitly in [7]. There is a close connection with the \(\zeta \) map used by Haglund and Loehr, see [15, 18].
Example 7
In the following vertical-strip diagram, we illustrate a valid coloring \(\kappa \) where we have written \(\kappa (i)\) on vertex i. That is, \(\kappa (1)=1\), \(\kappa (2)=3\), \(\kappa (3)=2\), etc.

The strict edges and edges contributing to \({{\,\mathrm{asc}\,}}(\kappa )\) have been marked with \(\rightarrow \). Hence, \(\kappa \) contributes with \(q^{5}x_1^2 x_2 x_3^2 x_4\) to the sum in (5).
2.4 A conjectured formula
Definition 8
Let \({\mathbf {a}}\) be an area sequence of length n and \({\mathbf {s}}\) be some strict edges of \(\varGamma _{\mathbf {a}}\). Let \(O({\mathbf {a}},{\mathbf {s}})\) denote the set of orientations of the graph \(\varGamma _{\mathbf {a}}\) (seen as an undirected graph) together with the extra directed edges in \({\mathbf {s}}\). Thus, the cardinality of \(O({\mathbf {a}},{\mathbf {s}})\) is simply \(2^{a_1+\cdots +a_n}\). If \({\mathbf {s}}=\emptyset \), we simply write \(O({\mathbf {a}})\) for the set of orientations of \(\varGamma _{\mathbf {a}}\). Given \(\theta \in O({\mathbf {a}},{\mathbf {s}})\), an edge (u, v) is an ascending edge in \(\theta \) if it is oriented in the same manner as in \(\varGamma _{\mathbf {a}}\). Let \({{\,\mathrm{asc}\,}}(\theta )\) denote the number of ascending edges in \(\theta \). Note that edges in \({\mathbf {s}}\) are not considered to be ascending!
We now define the highest reachable vertex, \({{\,\mathrm{hrv}\,}}_\theta (u)\) for \(u\in [n]\) as the maximal v such that there is a path from u to v in \(\theta \) using only strict and ascending edges. Note that \({{\,\mathrm{hrv}\,}}_\theta (u)\ge u\) for all u. The orientation \(\theta \) defines a set partition \({\pi }(\theta )\) of the vertices of \(\varGamma _{\mathbf {a}}\), where two vertices are in the same part if and only if they have the same highest reachable vertex. Let \({{\overline{\pi }}}(\theta )\) denote the partition given by the sizes of the sets in \({\pi }(\theta )\).
Let \({\mathbf {a}}\) be an area sequence and \({\mathbf {s}}\) be some strict edges of \(\varGamma _{\mathbf {a}}\). Define the symmetric function \(\hat{\mathrm {G}}_{{\mathbf {a}},{\mathbf {s}}}({\mathbf {x}};q)\) via the relation
Example 9
Below, we illustrate an orientation \(\theta \in O({\mathbf {a}},{\mathbf {s}})\), where \({\mathbf {a}}= (0,1,2,2,2,2)\) and \({\mathbf {s}}= \{ (1,4), (2,5) \}\). As before, strict edges and edges contributing to \({{\,\mathrm{asc}\,}}(\theta )\) are marked with \(\rightarrow \).

We have that \({{\,\mathrm{hrv}\,}}_\theta (2)={{\,\mathrm{hrv}\,}}_\theta (5)={{\,\mathrm{hrv}\,}}_\theta (6)=6\) and \({{\,\mathrm{hrv}\,}}_\theta (1)={{\,\mathrm{hrv}\,}}_\theta (3)={{\,\mathrm{hrv}\,}}_\theta (4)=4\). Thus \({\pi }(\theta ) = \{652,431\}\) and the orientation \(\theta \) contributes with \(q^{5}\mathrm {e}_{33}({\mathbf {x}})\) in (6). The full polynomial \(\hat{\mathrm {G}}_{{\mathbf {a}},{\mathbf {s}}}({\mathbf {x}};q+1)\) is
Conjecture 10
(Main conjecture) For any vertical-strip LLT polynomial \(\mathrm {G}_{{\mathbf {a}},{\mathbf {s}}}({\mathbf {x}};q)\), we have that \(\mathrm {G}_{{\mathbf {a}},{\mathbf {s}}}({\mathbf {x}};q) = \hat{\mathrm {G}}_{{\mathbf {a}},{\mathbf {s}}}({\mathbf {x}};q)\).
Note that this conjecture implies that \(\mathrm {G}_{{\mathbf {a}},{\mathbf {s}}}({\mathbf {x}};q+1)\) is \(\mathrm {e}\)-positive, with the expansion given as a sum over all orientations of \(\varGamma _{\mathbf {a}}\). Such a conjecture was first stated in [1] but without a precise definition of \({{\overline{\pi }}}(\theta )\). Conjecture 10 is a natural analogue of the Shareshian–Wachs conjecture, [30, 31], and therefore is also closely related to the Stanley–Stembridge conjecture [27, 28]. There is also a natural generalization of Eq. (6) that predicts the \(\mathrm {e}\)-expansion of the LLT polynomials indexed by circular area sequences considered in [1].
2.5 Properties of LLT polynomials
We use standard notation and let \(\omega \) be the involution on symmetric functions that sends the complete homogeneous symmetric function \(\mathrm {h}_\lambda \) to the elementary symmetric function \(\mathrm {e}_\lambda \) or, equivalently, sends \(\mathrm {s}_\lambda \) to \(\mathrm {s}_{\lambda '}\).
Proposition 11
(See [1]) For any area sequence \({\mathbf {a}}\) of length n,
where \({\mathbf {a}}^{\mathrm{T}}\) denotes the transpose of the Dyck diagram.
In [1], we gave a proof that \(\omega \mathrm {G}_{{\mathbf {a}},{\mathbf {s}}}({\mathbf {x}};q+1)\) is positive in the power-sum basis. It also follows from a much more general result given in [2]. Note that if \(f({\mathbf {x}})\) is \(\mathrm {e}\)-positive, then \(\omega f({\mathbf {x}})\) is positive in the power-sum basis. Later in Proposition 49, the power-sum expansion of \(\omega \mathrm {G}_{{\mathbf {a}},{\mathbf {s}}}({\mathbf {x}};q+1)\) is stated explicitly.
The following lemma connects the LLT polynomials with the chromatic quasisymmetric functions \(\mathrm {X}_{\mathbf {a}}({\mathbf {x}};q)\) introduced in [30]. The function \(\mathrm {X}_{\mathbf {a}}({\mathbf {x}};q)\) is defined exactly as \(\mathrm {G}_{\mathbf {a}}({\mathbf {x}};q)\), but the sum in Eq. (5) is taken only over proper colorings of \(\varGamma _{\mathbf {a}}\), so that no monochromatic edges are allowed.
Lemma 12
(Adaptation of [7, Prop. 3.5]. See also [16, Sec. 5.1]) Let \({\mathbf {a}}\) be a Dyck diagram of length n. Then
where the bracket denotes a substitution using plethysm.
From this formula, together with Conjecture 10, we have a novel conjectured formula for the chromatic quasisymmetric functions:
Perhaps it is possible to do some sign-reversing involution together with plethysm manipulations to obtain the \(\mathrm {e}\)-expansion of \(\mathrm {X}_{\mathbf {a}}({\mathbf {x}};q)\) and thus find a candidate formula for the Shareshian–Wachs conjecture.
Conjecture 13
(Shareshian–Wachs [30, 31]) There is some partition-valued statistic \(\rho \) on acyclic orientations of \(\varGamma _{\mathbf {a}}\), such that
Here \(AO({\mathbf {a}})\) denotes the set of acyclic orientations of \(\varGamma _{\mathbf {a}}\).
Note that the original Stanley–Stembridge conjecture is closely related to the \(q=1\) case, which was stated for the incomparability graphs of \(3+1\)-avoiding posets.
Problem 14
Prove that the family \(\hat{\mathrm {G}}_{\mathbf {a}}({\mathbf {x}};q)\) defined in (6) fulfills the involution identity (7).
3 Recursive properties of LLT polynomials
We shall now cover several recursive relations for the vertical-strip LLT polynomials. Our proofs are bijective and directly use the combinatorial definition as a weighted sum over vertex colorings. We illustrate these bijections with Dyck diagrams where only the relevant vertices and edges are shown.
The reader thus is encouraged to interpret a diagram as a weighted sum over colorings, where decorations of the diagrams indicate restrictions of the colorings, or how the colorings contribute to \({{\,\mathrm{asc}\,}}(\cdot )\). For example, given an edge \(\epsilon \) of \(\varGamma _{{\mathbf {a}},{\mathbf {s}}}\), there are two possible cases. Either \(\epsilon \) contributes to the number of ascents, or it does not. We can illustrate this simply as

where the white box is the edge \(\epsilon \) and \(\downarrow \) indicates an edge that cannot be an ascent. Note that the vertices shown do not need to have consecutive labels—the intermediate vertices (and edges) are simply not shown. Shaded boxes are not edges of \(\varGamma _{\mathbf {a}}\) and therefore do not contribute to ascents of the coloring. To conclude, the class of diagrams considered here may be described as follows:
-
The white boxes are determined by some area sequence \({\mathbf {a}}\), so that each white box is an edge in \(\varGamma _{\mathbf {a}}\).
-
Every edge (box) is either white or shaded.
-
Only white boxes contribute to the ascent statistic.
-
A box (white or shaded) may contain an arrow, a \(\rightarrow \) or \(\downarrow \), imposing a strict or weak inequality requirement, respectively, on the colorings. In particular, a white box containing a \(\rightarrow \) is thus a sum over colorings where this particular edge must be an ascent.
Note that this is a slightly broader class of diagrams than the class of vertical-strip diagrams, as the additional arrows impose more restrictions on the colorings.
The following recursive relationship allows us to express vertical-strip LLT polynomials as linear combinations of unicellular LLT polynomials. Later in Proposition 31, we prove that the polynomials in Eq. (6) satisfy the same recursion. We use the notation \({\mathbf {a}}\cup \{\epsilon \}\) to describe the area sequence of the unit-interval graph where the edge \(\epsilon \) has been added to the edges of \(\varGamma _{\mathbf {a}}\). The notation \({\mathbf {s}}\cup \{\epsilon \}\) for strict edges is interpreted in a similar manner.
Proposition 15
If \(\varGamma _{{\mathbf {a}},{\mathbf {s}}}\) is a vertical-strip diagram, and \(\epsilon \) is a non-strict outer corner of \(\varGamma _{{\mathbf {a}},{\mathbf {s}}}\), then
Proof
By shifting the variable q, the identity can be restated as
which in (as sum over colorings) diagram form can be expressed as follows. The two vertices shown are the vertices of \(\epsilon \).

The first and last diagram can be expanded into subcases,

and here it is evident that both sides agree. \(\square \)
The above recursion seems to relate to certain recursions on Catalan symmetric functions, see [6, Prop. 5.6]. Catalan symmetric functions are very similar in nature to LLT polynomials.
3.1 Lee’s recursion
In Proposition 18, we prove a recursion on certain LLT polynomials. We then show that this relation is equivalent to Lee’s recursion, given in [23, Thm 3.4].
Definition 16
Let \({\mathbf {a}}\) be an area sequence of length \(n\ge 3\). An edge \((i,j) \in E(\varGamma _{\mathbf {a}})\), \(3\le j \le n\), is said to be admissible if the following four conditions hold:
-
\(i = j-a_j\)
-
\(j=n\) or \(a_j \ge a_{j+1} +1\)
-
\(a_j \ge 2\),
-
\(a_i+1 = a_{i+1}\).
The last condition is automatically satisfied if the first three are true and \({\mathbf {a}}\) is abelian. Note that if (i, j) is admissible, then for all \(k<i\) or \(k>i+1\) we have
These properties are crucial in later proofs.
Example 17
For the following diagram \({\mathbf {a}}\), the edge (2, 5) is admissible.

Let \({\mathbf {e}}_j\) denote the \(j{\text {th}}\) unit vector.
Proposition 18
Suppose (i, j) is an admissible edge of the area sequence \({\mathbf {a}}\), set \({\mathbf {a}}^1 {:}{=}{\mathbf {a}}-{\mathbf {e}}_j\) and \({\mathbf {a}}^2 {:}{=}{\mathbf {a}}-2{\mathbf {e}}_j\) and \({\mathbf {s}}^1 {:}{=}\{(i,j)\}\), \({\mathbf {s}}^2 {:}{=}\{(i+1,j)\}\). Then
Proof
We use the diagram-type proof as before, now only showing the vertices i, \(i+1\) and j. The identity we wish to show is then presented as

Both sides are considered as a weighted sum over colorings with restrictions indicated by \(\rightarrow \). Subdividing these sums into subcases by forcing additional inequalities gives

Two terms cancel and additional inequalities follows by transitivity. It therefore suffices to prove the following.

Note that the additional q in the left-hand side appears due to the ascent \((i,i+1)\).
There is now a simple q-weight-preserving bijection between colorings on the diagram on the left-hand side, and colorings of the diagram on the right-hand side. For a coloring \(\kappa \) in the left-hand side, we have \(\kappa (i) < \kappa (j)\le \kappa (i+1)\), while on the right-hand side, we have \(\kappa (i+1) < \kappa (j) \le \kappa (i)\). Hence, vertex i and vertex \(i+1\) are never assigned the same color.
The bijection is to simply swap the colors of the adjacent vertices i and \(i+1\). The property in Eq. (12) ensures that the number of ascending edges are preserved under this swap. \(\square \)
The following example illustrates the color swapping argument used to prove the identity in (14).
Example 19
In the following figures, we have the vertices \(x{:}{=}i\), \(y{:}{=}i+1\) and \(z{:}{=}j\). Suppose that we have a vertex coloring in the left-hand side, with \(\kappa (x)<\kappa (y)\). By swapping the colors of x and y, every ascending edge marked with a \(\bullet \) in the left-hand side corresponds to an ascending edge marked with a \(\bullet \) in the right-hand side. The same argument holds for edges marked with \(\circ \)—the two sets of edges marked \(\bullet \) and \(\circ \) with possible ascents are simply swapped.

A similar argument is carried out for the two sets of edges marked \(*\) and \(\star \), where now the ascending edges are swapped between columns.
Corollary 20
(Local linear relation [23, Thm 3.4]) Let \({\mathbf {a}}\) be an area sequence for which (i, j) is admissible, and let \({\mathbf {a}}^0 {:}{=}{\mathbf {a}}\), \({\mathbf {a}}^1 {:}{=}{\mathbf {a}}-{\mathbf {e}}_j\) and \({\mathbf {a}}^2 {:}{=}{\mathbf {a}}-2{\mathbf {e}}_j\). Then
Proof
We see that the left-hand side of (16) can be rewritten in diagram form using Eq. (10):

The right-hand side is treated in a similar manner:

The identity in (13) now implies that \(\text {LHS}=\text {RHS}\). \(\square \)
Example 21
As an illustration of Corollary 20, we have \((i,j)=(2,5)\) and the following three Dyck diagrams.

3.2 The dual Lee recursion
There is a “dual” version of Corollary 20, obtained by applying \(\omega \) to both sides of (16), and then apply the relation in (7). We shall now state this in more detail.
Definition 22
Let \({\mathbf {a}}\) be an area sequence of length \(n\ge 3\). An edge (i, j) is said to be dual-admissible if the edge \((n+1-j,n+1-i)\) is admissible for \({\mathbf {a}}^{\mathrm{T}}\).
We can then formulate the dual versions of Proposition 18 and Corollary 20.
Proposition 23
(The dual Lee recursion) Let \({\mathbf {a}}\) be an area sequence for which (i, j) is dual-admissible and let \({\mathbf {a}}^0 {:}{=}{\mathbf {a}}\), \({\mathbf {a}}^1 {:}{=}{\mathbf {a}}-{\mathbf {e}}_j\) and \({\mathbf {a}}^2 {:}{=}{\mathbf {a}}-{\mathbf {e}}_j-{\mathbf {e}}_{j-1}\). Then
and
where \({\mathbf {s}}^1 {:}{=}\{(i,j)\}\) and \({\mathbf {s}}^2 {:}{=}\{(i,j-1)\}\).
Proof sketch
We can either prove these identities by applying \(\omega \) as outlined above, or bijectively using diagrams. We leave out the details. \(\square \)
Example 24
Proposition 18 applies in the following generic situation. Here, the edge (x, z) is an admissible edge. The crucial condition in (12) states that the area of the rows with vertices x and y in the diagram differs by exactly one.

Similarly, the dual recursion in Eq. (17) applies in the following situation, where (x, z) is a dual-admissible edge:

3.3 Recursion in the complete graph case
We end this section by recalling a recursion for LLT polynomials in the complete graph case.
Proposition 25
([1, Prop.5.8]) Let \(\mathrm {G}_{K_n}({\mathbf {x}};q)\) denote the LLT polynomial for the complete graph, where the area sequence is \((0,1,2,\dotsc ,n-1)\). Then
Lemma 26
If \({\mathbf {a}}\) is rectangular and the non-edges form a \(k\times (n-k)\)-rectangle in the Dyck diagram, then \(\mathrm {G}_{{\mathbf {a}}}({\mathbf {x}};q) = \mathrm {G}_{K_k}({\mathbf {x}};q)\mathrm {G}_{K_{n-k}}({\mathbf {x}};q)\).
Proof
The unit-interval graph \(\varGamma _{\mathbf {a}}\) is a disjoint union of two smaller complete graphs, so this now follows immediately from the definition of unicellular LLT polynomials. \(\square \)
For the remaining of this section, it will be more convenient to use the notation in [23], and index unicellular LLT polynomials of degree n with partitions \(\lambda \) that fit inside the staircase \((n-1,n-2,\dotsc ,2,1,0)\). We fix n and let the area sequence \({\mathbf {a}}\) correspond to the partition \(\lambda \) where \(\lambda _i = n-i - a_{n+1-i}\). Hence, \(\lambda \) is exactly the shape of the (shaded) non-edges in the Dyck diagram. By definition, \(\lambda \) is abelian if it fits inside some \(k \times (n-k)\)-rectangle.
Lemma 27
(Follows from [19, Thm. 3.4]) Let \(\lambda \) be abelian with \(\ell \ge 2\) parts such that \(\lambda _\ell <\lambda _{\ell -1}\). Let
Then there are rational functions c(q) and d(q) such that \(\mathrm {G}_\lambda ({\mathbf {x}};q) = c(q)\mathrm {G}_\mu ({\mathbf {x}};q) + d(q)\mathrm {G}_\nu ({\mathbf {x}};q)\).
Proof
Use Corollary 20 repeatedly on row \(\ell \) of \(\mu \). \(\square \)
Example 28
To illustrate Lemma 27, we have the following three partitions:

Proposition 29
Every \(\mathrm {G}_{\lambda }({\mathbf {x}};q)\), where \(\lambda \) is abelian, can be expressed recursively via Lee’s recurrences, as a linear combination of some \(\mathrm {G}_{\mu ^j}({\mathbf {x}};q)\) where the \(\mu ^j\) are rectangular.
Proof
Let \(\lambda \) be abelian partition with exactly \(\ell \) parts, so that it fits in a \(\ell \times (n-\ell )\)-rectangle. We shall do a proof by induction over \(\lambda \), and in particular its number of parts.
-
(1)
Case \(\lambda =\emptyset \). This is rectangular by definition.
-
(2)
Case \(\lambda =(n-1)\). This is rectangular.
-
(3)
Case \(\ell =1\). Use Lemma 27 to reduce to Case (1) and Case (2).
-
(4)
Case \(\ell >1\) and \(\lambda _i \le \ell -i\) for some \(i \in [\ell ]\). The conditions imply that it is possible to remove a \(2\times 1\) or a \(1 \times 2\)-domino from \(\lambda \) and obtain a new partition. Hence we can use Lee’s recursion to express \(\mathrm {G}_{\lambda }({\mathbf {x}};q)\) using polynomials indexed by two smaller partitions. For example, this case applies in the following situation:
 (22)
(22) -
(5)
Case \(\ell >1\) and \(\lambda _i > \ell -i\) for all \(i \in [\ell ]\). Three things can happen here, and it is easy to see that this list is exhaustive.
-
\(\lambda \) is rectangular and we are done.
-
We can add a \(2\times 1\) or \(1 \times 2\)-domino to \(\lambda \) without increasing \(\ell \) and still obtain a partition. Similar to Case (4), we can therefore reduce to cases where \(|\lambda |\) has increased by 1 and 2.
-
Lemma 27 can be applied, thus reducing \(\lambda \) to a case where \(\ell \) has strictly been decreased, and a case where \(\lambda \) has increased by one box.
-
Notice that Case (4) reduces only back to Case (4), or a case where \(\ell \) is decreased, and the same goes for Case (5). There are therefore no circular dependencies among these cases and the induction is valid. \(\square \)
4 Recursions for the conjectured formula
In this section, we prove that \(\hat{\mathrm {G}}({\mathbf {x}};q)\) also fulfills the recursion in Proposition 15. We use similar bijective technique as in Sect. 3, but diagrams now represent weighted sums over orientations as in Eq. (6). Note that we now also consider the shifted polynomial \(\hat{\mathrm {G}}_{{\mathbf {a}},{\mathbf {s}}}({\mathbf {x}};q+1)\).
Each diagram now represents a weighted sum over orientations, where the weight of a single orientation \(\theta \) is \(q^{{{\,\mathrm{asc}\,}}(\theta )}\mathrm {e}_{{\pi }(\theta )}\). The class of diagrams we now consider is as follows.
-
The white boxes are determined by some area sequence.
-
Every edge (box) is either white or shaded.
-
Only white boxes contribute to the ascent statistic.
-
A box (white or shaded) may contain an arrow, a \(\rightarrow \) or \(\downarrow \), imposing a restriction on the orientations being summed over. In particular, a white box containing a \(\rightarrow \) is thus a sum over orientations where this particular edge must be an ascent.
Hence, each diagram represents a sum over \(2^W\) orientations, where W is the number of white boxes not containing any arrow.
Example 30
Suppose the following diagram illustrates the entire graph. The diagram represents the weighted sum over all orientations of the non-specified edges (x, y) and (y, z). The edge (x, z) is strict, and (z, w) is forced to be ascending. Remember that each ascending edge contributes with a q-factor.

There are four orientations in total,

which according to (6) give the sum \(q\mathrm {e}_{31} + q^2\mathrm {e}_{31} + q^2\mathrm {e}_{4} + q^3\mathrm {e}_{4}\).
In the diagrams below, only relevant vertices of the graphs are included.
Proposition 31
If \(\varGamma _{{\mathbf {a}},{\mathbf {s}}}\) is a vertical-strip graph, with \(\epsilon \) being a non-strict outer corner, then
Proof
In diagram form, this amounts to showing that orientations of the diagram in the left-hand side can be put in q-weight-preserving bijection with the disjoint sets of orientations in the right-hand side, while also preserving the \({\pi }(\cdot )\)-statistic. Thus we wish to proveFootnote 1 that

Consider an orientation in the left-hand side. There are two cases to consider:
-
The edge (x, y) is ascending. We map the orientation to an orientation of the first diagram in the right-hand side, by preserving the orientation of all other edges.
-
The edge (x, y) is non-ascending. We map this to the second diagram, by preserving the orientation of all other edges.
In both cases above, note that both the q-weight and \({\pi }(\cdot )\) are preserved under this map. \(\square \)
Corollary 32
If Conjecture 10 holds in the unit-interval case, it holds in the vertical-strip case.
Proof
We can use Propositions 31 and 15 to recursively remove all strict edges. Since both families satisfy the same recursion, we have that the unicellular case of Conjecture 10 implies the vertical-strip case. \(\square \)
4.1 The complete graph recursion and line graphs
Analogous to Proposition 25, we have a recursion for the corresponding \(\hat{\mathrm {G}}_{K_n}({\mathbf {x}};q)\), where we again consider the complete graph case. Here, \(\left( {\begin{array}{c}[n]\\ k\end{array}}\right) \) denotes the set of k-subsets of \(\{1,\dotsc ,n\}\).
Lemma 33
The polynomial \(\hat{\mathrm {G}}_{K_n}({\mathbf {x}};q)\) satisfies \(\hat{\mathrm {G}}_{K_0}({\mathbf {x}};q) {:}{=}1\) and \(\hat{\mathrm {G}}_{K_n}({\mathbf {x}};q+1)\) is equal to
Proof
We first give an argument for the recursion in (24). Given an orientation \(\theta \) of \(K_i\), we can construct a new orientation \(\theta '\) of \(K_n\) by inserting a new part of size \(n-i\) in the vertex partition where vertex n is a member. Choose an i-subset in \([n-1]\) and let \(\theta \) define the orientation of the edges in \(\theta '\) on these vertices.
The remaining set \(S = \{s_1,\dotsc ,s_{n-i-1}\}\) of \((n-i-1)\) vertices will be in the new part. Let us index them such that \(n>s_1>s_2> \cdots > s_{n-i-1} \ge 1\). We wish to extend \(\theta \) such that the following holds:
-
For all pairs of vertices, t, \(s_j\) with \(t \notin S\) and \(s_j \in S\), (i) the edge \((t,s_j)\) is not ascending, and (ii) the edge \((s_j,t)\) may or may not be ascending.
-
Each \(s_j \in S\) has at least one ascending edge to one of the vertices in the set \(\{n,s_1,\dotsc ,s_{j-1}\}\).
The first condition ensures that the highest reachable vertex for vertices not in S remains the same in \(\theta '\). The last condition ensures that all vertices in S has n as the highest reachable vertex in \(\theta '\). It then follows that for such a subset S, there are
\({{\,\mathrm{asc}\,}}(\cdot )\)-weighted ways of choosing such subsets of ascending edges in \(\theta '\). Hence,
is the \({{\,\mathrm{asc}\,}}(\cdot )\)-weighted count of the number of orientations of \(K_n\), where the part of the vertex partition containing n has exactly \(n-i\) members. Finally, by sending each \(s_i\) to \(n-s_i\), which is an involution on \(\left( {\begin{array}{c}[n-1]\\ n-1-i\end{array}}\right) \), we get the desired formula. \(\square \)
We shall now prove that \(\hat{\mathrm {G}}_{K_n}({\mathbf {x}};q) = \mathrm {G}_{K_n}({\mathbf {x}};q)\). By using Lemma 33 and Proposition 25, this follows from the following lemma.
Lemma 34
For all n and \(1\le i \le n-1\), we have that
Proof
We first apply the substitution \(i {:}{=}(n-i-1)\). This gives
After dividing both sides by \(\prod _{j=1}^{i} [ q^j - 1 ]\), we recognize the left-hand side as the q-binomial coefficient \(\genfrac[]{0.0pt}{}{n-1}{i}_q\) and we arrive (after setting \(n {:}{=}n+1\)) at the fairly standard identity
which can be found in [22, Eq. (6.5)]. \(\square \)
The case of line graphs follows immediately from [1, Prop. 5.18].
Proposition 35
Let \({\mathbf {a}}= (0,1,1,\dotsc ,1)\) be a line graph. Then \(\hat{\mathrm {G}}_{{\mathbf {a}}}({\mathbf {x}};q) = \mathrm {G}_{{\mathbf {a}}}({\mathbf {x}};q)\).
4.2 On Lee’s recursion for orientations
We would also like to prove that the \(\hat{\mathrm {G}}({\mathbf {x}};q)\) fulfill Lee’s recursions. However, this is a surprisingly challenging and we are unable to show this at the present time. A proof that Lee’s recursions hold for \(\hat{\mathrm {G}}({\mathbf {x}};q)\) would imply that \(\mathrm {G}_{\mathbf {a}}({\mathbf {x}};q) = \hat{\mathrm {G}}_{\mathbf {a}}({\mathbf {x}};q)\) at least for all abelian area sequences \({\mathbf {a}}\). Computer experiment with \(n\le 7\) confirms that the polynomials \(\hat{\mathrm {G}}_{\mathbf {a}}({\mathbf {x}};q)\) indeed do satisfy these recurrences.
The class of melting lollipop graphs can be constructed recursively from the complete graphs and the line graphs by just using the recursion in Corollary 20. This is in fact done in [19], so we simply sketch a proof of this statement. Recall that a melting lollipop graph \({\mathbf {a}}\) is given by
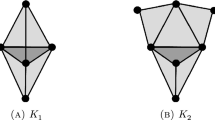
for some \(m,n\ge 1\) and \(0\le k \le m-1\). Melting lollipop graphs for various parameters are shown below.

We can use the recursion in Corollary 20 repeatedly to express LLT polynomials by adding one and removing one shaded box in row m. For example, C can be expressed in terms of B and D. Similarly, B can be expressed in terms of A and C, and we get a system of linear equations expressing B, C and D in terms of only A and E.
When \(k=m-1\) (as for E above), the graph \(\varGamma _{\mathbf {a}}\) is a disjoint union of a complete graph and a line graph, which is a base case. Furthermore, when \(k=0\), (as for A above) we obtain a melting lollipop graph with the new parameters \(m'=m+1\), \(k'=m-2\) and \(n'=n-1\), which are dealt with by induction over n.
5 The Hall–Littlewood case
In [16], the modified Macdonald polynomials \({\tilde{\mathrm {H}}}_\lambda ({\mathbf {x}};q,t)\) are expressed as a positive sum of certain LLT polynomials. The modified Macdonald polynomials specialize to modified Hall–Littlewood polynomials at \(q=0\), which in turn are closely related to the transformed Hall–Littlewood polynomials.
Definition 36
(See [9, 32] for a background) Let \(\lambda \) be a partition. The transformed Hall–Littlewood polynomials are defined as
where \(K_{\lambda \mu }(q)\) are the Kostka–Foulkes polynomials.
The \(\mathrm {H}_\lambda \) is sometimes denoted \(Q'_\lambda \) and is the adjoint basis to the Hall–Littlewood P polynomials for the standard Hall scalar product, see [9]. A more convenient definition of the transformed Hall–Littlewood polynomials is the following. For \(\lambda \vdash n\) we have
where \(R_{ij}\) are raising operators acting on the partitions (or compositions) indexing the complete homogeneous symmetric functions as
Note that \(\mathrm {s}_\lambda ({\mathbf {x}}) = \mathrm {H}_\lambda ({\mathbf {x}};0)\), and (26) gives \( \mathrm {s}_\lambda ({\mathbf {x}}) = \prod _{i<j} (1 - R_{ij})\mathrm {h}_{\lambda }({\mathbf {x}}) \) which is just the Jacobi–Trudi identity for Schur functions in disguise. Furthermore, note that (26) immediately implies that
where \(\vartriangleright \) denotes the dominance order, since the raising operators \(R_{ij}\) can only make partitions larger in dominance order.
We now connect the transformed Hall–Littlewood polynomials with certain vertical-strip LLT polynomials.
Definition 37
Given a partition \(\mu \vdash n\), let \(s_i\) be defined as \(s_i {:}{=}\mu _1+\cdots +\mu _i\), with \(s_0 {:}{=}1\). From \(\mu \), we construct a vertical-strip diagram \(\varGamma _{\mu }\) on n vertices with the following edges:
-
(a)
For each \(j=1,\dotsc ,{{\,\mathrm{\ell }\,}}(\mu )\), let the vertices \(\{s_{j-1},\dotsc ,s_{j}\}\) constitute a complete subgraph of \(\varGamma _{\mu }\),
-
(b)
For each \(j=2,\dotsc ,{{\,\mathrm{\ell }\,}}(\mu )\), we also have the \(\left( {\begin{array}{c}\mu _j\\ 2\end{array}}\right) \) edges
$$\begin{aligned} \{ s_{j-1}-i \rightarrow s_{j-1}+k+1 \text { whenever } 0\le i,k \text { and } i + k \le \mu _j-1\}. \end{aligned}$$
Thus, for each \(j\ge 2\) in item (b), we obtain a triangular shape of boxes with edges, as marked in (28), where \(\mu _j=5\).

Furthermore, all outer corners are taken as strict edges, see Example 39. As before, let \(O(\varGamma _\mu )\) denote the set of orientations of the edges of \(\varGamma _\mu \).
Proposition 38
Let \(\mu \) be a partition and let \(\varGamma _\mu \) be the vertical-strip diagram constructed from \(\mu \) and let \(\mathrm {G}_{\mu }({\mathbf {x}};q)\) be the corresponding LLT polynomial. Then
Brief proof sketch
We use [15, A.59] which states that for any partition \(\lambda \), the coefficient of \(t^{n(\lambda )}\) in the modified Macdonald polynomial \({\tilde{\mathrm {H}}}_{\lambda }({\mathbf {x}};q,t)\) is almost a transformed Hall–Littlewood polynomial:
The \({\tilde{\mathrm {H}}}_{\lambda }({\mathbf {x}};q,t)\) is a sum over certain LLT polynomials and in particular, the coefficient of \(t^{n(\lambda )}\) is a single vertical-strip LLT polynomial, multiplied with \(q^{-A}\), where A is the sum of arm lengths in the diagram \(\lambda \). Unraveling the definitions in [15, A.14], we arrive at the identityFootnote 2 in (29). \(\square \)
Example 39
The Hall–Littlewood polynomial \(\mathrm {H}_{3321}({\mathbf {x}};q)\) is related to the vertical-strip diagram \(\varGamma _{432}\) in (29).

The edges marked with a dot are the edges in item (b). There are \(\sum _{i\ge 2} \left( {\begin{array}{c}\mu _i\\ 2\end{array}}\right) \) such edges. Notice that the vertex partition of this orientation is \(\{974,863,52,1\}\). Furthermore, it is fairly straightforward to see that for any orientation \(\theta \) of \(\varGamma _{\mu }\), we must have that the partition \({{\overline{\pi }}}(\theta )\) dominates \(\mu '\).
We can now easily give some strong support for Conjecture 10.
Corollary 40
For any partition \(\mu \), the vertical-strip LLT polynomial \(\mathrm {G}_{\mu }({\mathbf {x}};q+1)\) is \(\mathrm {e}\)-positive.
Proof
Using (29), it suffices to prove that \(\mathrm {H}_{\lambda '}({\mathbf {x}};q+1)\) is \(\mathrm {h}\)-positive. From (26), we have that
This proves positivity. \(\square \)
Problem 41
Find a bijective proof that \(\hat{\mathrm {G}}_\mu ({\mathbf {x}};q+1)\) is equal to \(\mathrm {G}_\mu ({\mathbf {x}};q+1)\), by interpreting each term in Eq. (34), and combine with (29).
It is tempting to believe that summing over the orientations of \(\varGamma _\mu \) in Definition 37 where all edges in condition (b) are oriented in a non-descending manner would give exactly \(\omega \mathrm {H}_{\mu '}({\mathbf {x}};q+1)\). However, this fails for \(\mu =222\).
6 Generalized cocharge and \(\mathrm {e}\)-positivity
In [19], the authors consider a certain classes of unicellular LLT polynomials that can be expressed in a particularly nice way. These are polynomials indexed by complete graphs, line graphs and a few other families. In this section, we prove that the corresponding LLT polynomials are positive in the elementary basis. In fact, we do this by giving a rather surprising relationship between a type of cocharge and orientations.
For a semi-standard Young tableau T, the reading word is formed by reading the boxes of \(\lambda \) row by row from bottom to top, and from left to right within each row. The descent set of a standard Young tableau T is defined as
Given a Dyck diagram \({\mathbf {a}}\), we define the weight as
The weight here is also known as cocharge whenever \({\mathbf {a}}\) is the complete graph \((0,1,2,\dotsc ,n-1)\), see for example [15]. If we let \(T'\) denote the transposed tableau, then for any T and \({\mathbf {a}}\), we have
It will be convenient to define
Example 42
Let \({\mathbf {a}}=(0,1,2,3,3,2,2,3)\) and

The reading word of T is 75268134, \(\mathrm {Des}(T) = \{1,4,6\}\) so \({{\,\mathrm{wt}\,}}_{\mathbf {a}}(T) = a_8 + a_5+a_3 = 7\) and \({{\,\mathrm{{\widetilde{wt}}}\,}}_{\mathbf {a}}(T) = 9\).
Definition 43
Given an area sequence \({\mathbf {a}}\) of length n, we define the polynomial
From this definition, it follows that
The following proposition is a collection of results in [19].
Proposition 44
We have that \(\tilde{\mathrm {G}}_{\mathbf {a}}({\mathbf {x}};q) = \mathrm {G}_{\mathbf {a}}({\mathbf {x}};q)\) for the the families of graphs listed in Sect. 2.1: the complete graphs, line graphs, lollipop graphs, melting complete graphs and melting lollipop graphs.
Given a composition \(\gamma \), let
Lemma 45
Let \(\lambda \vdash n\) and let \(\gamma \) be a composition of n with \(\ell \) parts. Then the standardization map
is a bijection.
Proof
This is straightforward from the definition of standardization and descents, see for example [15, p. 5]. \(\square \)
We shall now introduce a different statistic on orientations. Given \(\theta \in O(\varGamma _{\mathbf {a}})\), we say that a vertex v is a bottom of \(\theta \) if there is no \(u<v\) such that (u, v) is ascending in \(\theta \). Let \(s_1,\dotsc ,s_k\) be the bottoms ordered decreasingly and let \(s_0 {:}{=}n+1\). By definition, vertex 1 is always a bottom. Let \(\sigma (\theta )\) be defined as the composition of n with the parts given by \(\{ s_{i-1}-s_{i} : i=1,\dotsc ,k \}\) and note that \(D(\sigma (\theta )) = \{n+1-s_i : i=1,2,\dotsc ,k-1\}\).
Example 46
The orientation \(\theta \) in (39) has vertices 1, 3 and 6 as bottoms. Furthermore, \(\sigma (\theta )=(1,3,2)\) and \(D(\sigma (\theta )) = \{1,4\}\).

Note that \({{\overline{\pi }}}(\theta )=(5,1)\) so \(\sigma \) and \({{\overline{\pi }}}\) are indeed very different.
The following theorem was proved for the complete graph and the line graph in [1]. We can now generalize it to all unit-interval graphs.
Theorem 47
Let \({\mathbf {a}}\) be an area sequence of length n. Then
Proof
We apply \(\omega \) on both sides of Eq. (40), so it suffices to prove that
Recall, in, e.g., [25], the standard expansion
where \(K_{\lambda ,\nu } = |\mathrm {SSYT}(\lambda ,\nu )|\) are the Kostka coefficients. Thus, comparing both sides of (41) in the Schur basis, it suffices to show that for every partition \(\lambda \),
Using Lemma 45 in the right-hand side and unraveling the definition in the left-hand side, it is enough to prove that
It then suffices to prove that for a fixed \(T \in \mathrm {SYT}(\lambda )\) we have
Both sides may now be interpreted as a weighted sum over all orientations of \(\varGamma _{\mathbf {a}}\) where no ascending edges end in \(\{i : n+1-i \in \mathrm {Des}(T) \}\). \(\square \)
Corollary 48
All families of unicellular LLT polynomials \(\mathrm {G}_{\mathbf {a}}({\mathbf {x}};q+1)\) indexed by complete graphs, line graphs, lollipop graphs and melting lollipop graphs are \(\mathrm {e}\)-positive.
Notice that the formula in (40) is different from the conjectured formula in Conjecture 10, since \({{\overline{\pi }}}(\theta )\) and \(\sigma (\theta )\) are different. This is not surprising as \(\mathrm {G}_{\mathbf {a}}({\mathbf {x}};q)\) and \(\tilde{\mathrm {G}}_{\mathbf {a}}({\mathbf {x}};q)\) are not equal for general \({\mathbf {a}}\). However, it is rather remarkable that Conjecture 10 implies that (40) and Eq. (6) agree whenever \(\mathrm {G}_{\mathbf {a}}({\mathbf {x}};q) = \tilde{\mathrm {G}}_{\mathbf {a}}({\mathbf {x}};q)\).
7 A possible approach to settle the main conjecture
In [1] and later in [2] (with a different approach) we gave formulas for the power-sum expansion of all vertical-strip LLT polynomials. The unicellular case is a straightforward consequence of Lemma 12 (see [1, 21]) together with the power-sum expansion formula for the chromatic symmetric functions. We note that the formula in the chromatic case was first conjectured by Shareshian–Wachs and later proved by Athanasiadis [3].
It is straightforward to expand (6) in the power-sum basis, so to settle Conjecture 10, it suffices to show that \(\omega \mathrm {G}_{\mathbf {a}}({\mathbf {x}};q+1) = \omega \hat{\mathrm {G}}_{\mathbf {a}}({\mathbf {x}};q+1)\) for all \({\mathbf {a}}\) by comparing coefficients of \(\mathrm {p}_\lambda /z_\lambda \). We shall now introduce the necessary terminology from [2] to state Conjecture 10 in this form.
For any subset \(S \subseteq E(\varGamma _{\mathbf {a}})\), let P(S) denote the poset given by the transitive closure of the edges in S. Given a poset P on n elements, let \({\mathcal {O}}(P)\) be the set of order-preserving surjections \(f: P\rightarrow [k]\) for some k. The type of a surjection f is defined as
and this is a composition of n with k parts. Let \({\mathcal {O}}_\alpha (P) \subseteq {\mathcal {O}}(P)\) be the set of surjections of type \(\alpha \). Finally, let \({\mathcal {O}}^*_\alpha (P) \subseteq {\mathcal {O}}_\alpha (P)\) be the set of surjections \(f \in {\mathcal {O}}_\alpha (P)\) such that for each \(j \in [k]\), \(f^{-1}(j)\) is a subposet of P with a unique minimal element.
Proposition 49
(See [2, Thm. 5.6, Thm. 7.10]) The power-sum expansion of \(\omega \mathrm {G}_{{\mathbf {a}}}({\mathbf {x}};q+1)\) is given as
where \(P(\theta )\) is the poset on [n] and edges given by the transitive closure of the ascending edges in \(\theta \).
The family of functions \(\hat{\mathrm {G}}_{{\mathbf {a}}}({\mathbf {x}};q+1)\) has a similar expansion in terms of the power-sum symmetric functions.
Lemma 50
The power-sum expansion of \(\omega \hat{\mathrm {G}}_{{\mathbf {a}}}({\mathbf {x}};q+1)\) is given as
where \(B(\theta )\) is the poset consisting of a disjoint union of chains with lengths given by \({{\overline{\pi }}}(\theta )\).
Proof
This follows easily from the definition of \(\hat{\mathrm {G}}_{{\mathbf {a}}}({\mathbf {x}};q+1)\) and the expansion of the elementary symmetric functions into power-sum symmetric functions, see [13] and [2, Section 7]. \(\square \)
Conjecture 51
(Equivalent with Conjecture 10) For any area sequence \({\mathbf {a}}\) of length n and partition \(\lambda \vdash n\),
References
Alexandersson, P., Panova, G.: LLT polynomials, chromatic quasisymmetric functions and graphs with cycles. Discrete Math. 341(12), 3453–3482 (2018)
Alexandersson, P., Sulzgruber, R.: P-partitions and p-positivity. Int. Math. Res. Not. (2019). https://doi.org/10.1093/imrn/rnz130
Athanasiadis, C.A.: Power sum expansion of chromatic quasisymmetric functions. Electron. J. Combin. 22(2), 1–9 (2015)
Bergeron, F.: Multivariate diagonal coinvariant spaces for complex reflection groups. Adv. Math. 239, 97–108 (2013)
Bergeron, F.: Open questions for operators related to rectangular Catalan combinatorics. J. Combin. 8(4), 673–703 (2017)
Blasiak, J., Morse, J., Pun, A., Summers, D.: \(k\)-Schur expansions of Catalan functions. arXiv e-prints (2018). arXiv:1811.02490
Carlsson, E., Mellit, A.: A proof of the shuffle conjecture. J. Amer. Math. Soc. 31(3), 661–697 (2017)
D’Adderio, M.: e-positivity of vertical strip LLT polynomials. J. Combin. Theory Ser. A 172, 105212 (2020). https://doi.org/10.1016/j.jcta.2020.105212
Désarménien, J., Leclerc, B., Thibon, J.-Y.: Hall-Littlewood functions and Kostka-Foulkes polynomials in representation theory. Séminaire Lotharingien de Combinatoire 32, 38 (1994)
Dahlberg, S., van Willigenburg, S.: Lollipop and lariat symmetric functions. SIAM J. Discrete Math. 32(2), 1029–1039 (2018)
Ellzey, B.: Chromatic quasisymmetric functions of directed graphs. In: 29th International Conference on Formal Power Series and Algebraic Combinatorics, vol. 78B. Séminaire Lotharingien de Combinatoire (2017)
Ellzey, B.: A directed graph generalization of chromatic quasisymmetric functions. arXiv e-prints (2017). arXiv:1709.00454
Eğecioğlu, Ö., Remmel, J.B.: Brick tabloids and the connection matrices between bases of symmetric functions. Discrete Appl. Math. 34(1–3), 107–120 (1991)
Garsia, A.M., Haglund, J., Qiu, D., Romero, M.: \(e\)-positivity results and conjectures. arXiv e-prints (2019). arXiv:1904.07912
Haglund, J.: The \(q\),\(t\)-Catalan numbers and the space of diagonal harmonics, vol. 41. University Lecture Series. American Mathematical Society, Providence, RI (2008)
Haglund, J., Haiman, M., Loehr, N.A.: A combinatorial formula for Macdonald polynomials. J. Amer. Math. Soc. 18(03), 735–762 (2005)
Haglund, J., Haiman, M., Loehr, N.A., Remmel, J.B., Ulyanov, A.: A combinatorial formula for the character of the diagonal coinvariants. Duke Math. J. 126(2), 195–232 (2005)
Haglund, J., Loehr, N.: A conjectured combinatorial formula for the Hilbert series for diagonal harmonics. Discrete Math. 298(1–3), 189–204 (2005)
Huh, J., Nam, S.-Y., Yoo, M.: Melting lollipop chromatic quasisymmetric functions and Schur expansion of unicellular LLT polynomials. Discrete Math. 343(3), 111728 (2020). https://doi.org/10.1016/j.disc.2019.111728
Harada, M., Precup, M.: The cohomology of abelian Hessenberg varieties and the Stanley-Stembridge conjecture. Sém. Lothar. Combin. 80B, 49 (2018)
Haglund, J., Wilson, A.T.: Macdonald polynomials and chromatic quasisymmetric functions. arXiv e-prints (2017). arXiv:1701.05622
Kac, V., Cheung, P.: Quantum Calculus (Universitext). Springer, Berlin (2001)
Lee, S.J.: Linear relations on LLT polynomials and their \(k\)-Schur positivity for \(k=2\). arXiv e-prints (2018). arXiv:1807.03951
Lascoux, A., Leclerc, B., Thibon, J.-Y.: Ribbon tableaux, Hall–Littlewood functions, quantum affine algebras and unipotent varieties. J. Math. Phys. 38, 1041–1068 (1997)
Macdonald, I.G.: Symmetric Functions and Hall polynomials, 2nd edn. Oxford University Press, New York (1995). With contributions by A. Zelevinsky, Oxford Science Publications
Patrias, R., van Willigenburg, S.: The probability of positivity in symmetric and quasisymmetric functions. arXiv e-prints (2018). arXiv:1810.11038
Stanley, R.P., Stembridge, J.R.: On immanants of Jacobi-Trudi matrices and permutations with restricted position. J. Combin. Theory Ser. A 62(2), 261–279 (1993)
Stanley, R.P.: A symmetric function generalization of the chromatic polynomial of a graph. Adv. Math. 111(1), 166–194 (1995)
Stanley, R.P.: Enumerative Combinatorics: vol. 2, 1st edn. Cambridge University Press (2001)
Shareshian, J., Wachs, M.L.: Chromatic quasisymmetric functions and Hessenberg varieties. In: Configuration Spaces, pp 433–460. Scuola Normale Superiore (2012)
Shareshian, J., Wachs, M.L.: Chromatic quasisymmetric functions. Adv. Math. 295(4), 497–551 (2016)
Tudose, G., Zabrocki, M.: A \(q\)-analog of Schur’s Q-functions. In: Jing, N. (ed.) Algebraic Combinatorics and Quantum Groups, pp. 135–161. World Scientific, River Edge, NJ (2003)
Acknowledgements
Open access funding provided by Stockholm University. The author would like to thank Qiaoli Alexandersson, François Bergeron, Svante Linusson, Greta Panova, Robin Sulzgruber and Michelle Wachs for helpful discussions and suggestions. The author also appreciates the comments by the anonymous referees which improved the paper. This research has been funded by the Knut and Alice Wallenberg Foundation (2013.03.07).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alexandersson, P. LLT polynomials, elementary symmetric functions and melting lollipops. J Algebr Comb 53, 299–325 (2021). https://doi.org/10.1007/s10801-019-00929-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10801-019-00929-z