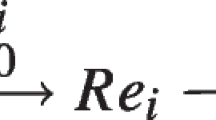On the Gauss algebra of toric algebras

Abstract

Let A be a K-subalgebra of the polynomial ring $S=K[x_1,\ldots ,x_d]$ of dimension d, generated by finitely many monomials of degree r. Then, the Gauss algebra ${\mathbb {G}}(A)$ of A is generated by monomials of degree $(r-1)d$ in S. We describe the generators and the structure of ${\mathbb {G}}(A)$, when A is a Borel fixed algebra, a squarefree Veronese algebra, generated in degree 2, or the edge ring of a bipartite graph with at least one loop. For a bipartite graph G with one loop, the embedding dimension of ${\mathbb {G}}(A)$ is bounded by the complexity of the graph G.

1 Introduction

Let $V\subseteq {\mathbb P}_K^{n-1}$ be a projective variety of dimension $d-1$ over an algebraically closed field K of characteristic zero. Denote by $V_{\mathrm{sm}}$ the set of non-singular points of V and by ${\mathbb G}({d-1},n-1)$ the Grassmannian of $d-1$-planes in ${{\mathbb P}_K^{n-1}}$. The Gauss map of V is the morphism

$$\begin{aligned} \gamma : V_{\mathrm{sm}}\longrightarrow {\mathbb G}({d-1},n-1), \end{aligned}$$

which sends each point $p\in V_{\mathrm{sm}}$ to the embedded tangent space ${\text {T}}_{p}V$ of V at the point p. The closure of the image of $\gamma$ in ${\mathbb G}({d-1},n-1)$ is called the Gauss image of V, or the variety of tangent planes, and is denoted by $\gamma (V)$. The homogeneous coordinate ring of $\gamma (V)$ in the Plücker embedding of the Grassmannian ${\mathbb {G}}({d-1},n-1)$ of ${(d-1)}$-planes is called the Gauss algebra of V. The Gauss map is a classical subject in algebraic geometry and has been studied by many authors. For example, it is known that the Gauss map of a smooth projective variety is finite [4, 13]; in particular, a smooth variety and its Gauss image have the same dimension with the obvious exception of a linear space. Zak [13, Corollary 2.8] showed that, provided V is not a linear subvariety of ${\mathbb P}_K^n$, the dimension of the Gauss image satisfies the inequality $\dim V-\dim {\text {Sing}}(V)-1\le \dim \gamma (V)\le \dim V$, where ${\text {Sing}}(V)$ denotes the singular locus of V. For an algebraic proof of Zak’s inequality, see [11].

We take up the situation where $V\subset {\mathbb P}_K^{n-1}$ is a unirational variety. To elaborate on the algebraic side of the picture, consider the polynomial ring $S=K[x_1,\ldots ,x_d]$. Let $\mathbf{g}=g_1,\ldots ,g_n$ be a sequence of non-constant homogeneous polynomials of the same degree in S generating the K-subalgebra $A=K[\mathbf{g}]\subseteq S$ of dimension d. Then, the Jacobian matrix $\Theta (\mathbf{g})$ of $\mathbf{g}$ has rank d [10, Proposition 1.1]. In this situation, we define the Gauss algebra associated with $\mathbf{g}$ as the K-subalgebra generated by the set of $d\times d$ minors of $\Theta (\mathbf{g})$ [1, Definition 2.1]. Since the definition does not depend on the choice of the homogeneous generators of A, we simply denote the Gauss algebra associated with $\mathbf{g}$, by ${\mathbb G}(A)$, and call it the Gauss algebra of A. The Gauss algebra ${\mathbb {G}}(A)$ is isomorphic to the coordinate ring of the Gauss image of the projective variety defined parametrically by $\mathbf{g}$ in the Plücker embedding of the Grassmannian ${\mathbb {G}}({d-1},n-1)$ of $d-1$-planes. Moreover, there is an injective homomorphism of K-algebras ${\mathbb G}(A)\hookrightarrow A$ inducing the rational map from $\mathrm{Proj}\, (A)$ to its Gauss image [1, Lemma 2.3].

In this paper, we study the Gauss algebra of toric algebras. If $A\subset S$ is a toric algebra with monomial generators $\mathbf{g}=g_1,\ldots ,g_n$ of the same degree, then all minors of $\Theta (\mathbf{g})$ are monomials. In particular, the Gauss algebra is a toric algebra. For example, it has been shown that the Gauss algebra of a Veronese algebra is again Veronese [1, Proposition 3.2]. Veronese algebras are special cases of a more general class of algebras, namely the class of Borel fixed algebras. As a generalization of the above mentioned result, we show that the Gauss algebra of any Borel fixed algebra is again Borel fixed, see Theorem 2.2. This approach provides a simple proof for [1, Proposition 3.2]. Veronese algebras are actually principal Borel fixed algebras, that is, the Borel set defining the algebra admits precisely one Borel generator. In general the number of Borel generators of the Borel fixed algebra A and that of ${\mathbb G}(A)$ may be different. However, in Theorem 2.4 we show that the Gauss algebra of a principal Borel fixed algebra is again principal. This has the nice consequence that the Gauss algebra of a principal Borel fixed algebra is a normal Cohen–Macaulay domain, and its defining ideal is generated by quadrics. Note that in general the property of A being normal does not imply that ${\mathbb G}(A)$ is normal, and vice versa (Example 1.2 and Theorem 3.2(d)).

The Gauss algebra of a squarefree Veronese algebra is much harder to understand. We can give a full description of ${\mathbb G}(A)$, when A is a squarefree Veronese algebra generated in degree 2. In Theorem 3.2 we show that ${\mathbb G}(A)$ is defined by all monomials u of degree d and $|{\text {supp}}(u)|\ge 3$, provided $d\ge 5$. Algebras of this type may be viewed as the base ring of a polymatroid. In particular, ${\mathbb G}(A)$ is normal and Cohen–Macaulay. However, ${\mathbb G}(A)$ is not normal for $d=4$. Yet for any d, the Gauss map $\gamma : \mathrm{Proj}\, (A)\dashrightarrow \mathrm{Proj}\, ({\mathbb G}(A))$ is birational.

In the last section of this paper we study the Gauss algebra of the edge ring of a finite graph. Let G be a loop-less connected graph with d vertices. It is well known that the dimension of the edge ring $A=K[G]$ of G is d, if G is not bipartite, and is $d-1$ if G is bipartite. In our setting, ${\mathbb G}(A)$ is defined under the assumption that $\dim A=d$. By using a well-known theorem [5] of graph theory, the generators of ${\mathbb G}(A)$, when G is not bipartite, correspond to d-sets E of edges of G, satisfying the property that the subgraph with edges E has an odd cycle in each of its connected components. In the bipartite case we form the graph $G^L$, where L is a non-empty subset of the vertex set of G, by adding a loop to G for each vertex in L. Then, $A=K[G^L]$ has dimension d, and there is bijective map from the set of pairs (V, T) to the set of monomial generators of ${\mathbb G}(A)$, where V is a non-empty subset of L and T is a set of edges which form a spanning forest G(T) of G with the property that each connected component of G(T) contains exactly one vertex of V. From this description it follows that if $|L|=1$, then the embedding dimension of the Gauss algebra is bounded by the complexity of the graph, which by definition, is the number of spanning trees of the graph. This is an important graph invariant. The number of spanning trees provides a measure for the global reliability of a network. For a complete bipartite graph $K_{m;n}$ the embedding dimension of the Gauss algebra is $\left( {\begin{array}{c}n+m-2\\ n-1\end{array}}\right) \left( {\begin{array}{c}n+m-2\\ m-1\end{array}}\right)$, see Example 4.7, while the number of spanning tress is $m^{n-1}n^{m-1}$, see for instance [6, Theorem 1]. In general, the defining ideal of the Gauss algebra admits many binomial generators. Thus, it is not surprising that the Gauss algebra is rarely a hypersurface ring. This is, for example, the case, when G is a cycle with one loop or a path graph with two loops attached. The Gauss algebra of an odd (resp. even) cycle of length d with one loop attached is a hypersurface ring of dimension d (resp. $d-1$). More generally, we expect that if G is a bipartite graph on [d], $L=\{i\}$ and A is the edge ring of $G^L$, then ${\mathbb G}(A)$ is a hypersurface ring of dimension $d-1$, if and only if G is an even cycle.

2 Toric algebras

In this section, we collect some basic fact s about the Gauss algebra of a toric algebra. Let $S=K[x_1,\ldots ,x_d]$ be a polynomial ring over K, where K is a field of characteristic zero. Let $\mathbf{g}=g_1,\ldots ,g_n$ be a sequence of monomials with $g_i= {x_1^{a_{1i}}\cdots x_d^{a_{di}}}$ for $i=1,\ldots ,n$. We associate with the sequence $\mathbf{g}$ two matrices, namely $\Theta (\mathbf{g})$ and ${\text {Log}}(\mathbf{g})$, where $\Theta (\mathbf{g})$ is the Jacobian matrix of $\mathbf{g}$ and ${\text {Log}}(\mathbf{g})=(a_{ij})$ is the exponent matrix (or log-matrix ) of $\mathbf{g}$, whose columns are the exponent vectors of the monomials in $\mathbf{g}$. We denote the r-minor

$$\begin{aligned} \det \begin{bmatrix} \frac{\partial g_{i_1}}{\partial x_{j_1}}&\quad \cdots&\quad \frac{\partial g_{i_1}}{\partial x_{j_r}} \\ \vdots&\quad \ddots&\quad \vdots \\ \frac{\partial g_{i_r}}{\partial x_{j_1}}&\quad \cdots&\quad \frac{\partial g_{i_r}}{\partial x_{j_r}}\\ \end{bmatrix}= \det \begin{bmatrix} a_{i_1j_1}\frac{g_{i_1}}{x_{j_1}}&\quad \cdots&\quad a_{i_1j_r}\frac{g_{i_1}}{x_{j_r}} \\ \vdots&\quad \ddots&\quad \vdots \\ a_{i_rj_1}\frac{g_{i_r}}{x_{j_1}}&\quad \cdots&\quad a_{i_rj_r}\frac{g_{i_r}}{x_{j_r}} \\ \end{bmatrix} \end{aligned}$$

by $[i_1,\ldots ,i_r\ | \ j_1,\ldots ,j_r ]_{\Theta (\mathbf{g})}$.

The multi-linearity property of the determinant implies that

$$\begin{aligned} x_{j_1}\ldots x_{j_r} [i_1,\ldots ,i_r\ | \ j_1,\ldots ,j_r ]_{\Theta (\mathbf{g})}=g_{i_1}\ldots g_{i_r}[i_1,\ldots ,i_r\ | \ j_1,\ldots ,j_r ], \end{aligned}$$

where $[i_1,\ldots ,i_r\ | \ j_1,\ldots ,j_r ]$ is the r-minor corresponding to the rows $i_1,\ldots ,i_r$ and columns $j_1,\ldots ,j_r$ of the transpose of ${\text {Log}}(\mathbf{g})$. Therefore, r-minors of $\Theta (\mathbf{g})$ are monomials of the form

$$\begin{aligned}{}[i_1,\ldots ,i_r\ | \ j_1,\ldots ,j_r ]\cdot \frac{g_{i_1}\ldots g_{i_r}}{x_{j_1}\ldots x_{j_r}}. \end{aligned}$$

(1)

By relation (1), the Jacobian matrix and the log-matrix of $\mathbf{g}$ have the same rank (see also [9, Proposition 1.2]).

Let $A=K[\mathbf{g}]$ be the toric K-algebra with generators $\mathbf{g}=g_1,\ldots ,g_n$. It is well known that the dimension of A is the rank of the matrix ${\text {Log}}(\mathbf{g})$. Thus, if all monomials of $\mathbf{g}$ are of degree r and the rank of ${\text {Log}}({\mathbf{g}})$ is d, then the Gauss algebra ${\mathbb G}(A)$ of A is a toric algebra generated by monomials of degree $(r-1)d$. Then, (1) implies that

$$\begin{aligned} {\mathbb G}(A)=K[(g_{i_1}\cdots g_{i_d})/(x_1\cdots x_d) :\ \ \det ({\text {Log}}(g_{i_1},\ldots , g_{i_d}))\ne 0]. \end{aligned}$$

The injective K-algebra homomorphism ${\mathbb G}(A)\hookrightarrow A$ is defined by multiplying each generator of ${\mathbb G}(A)$ by $x_1\cdots x_d$. Therefore,

$$\begin{aligned} {\mathbb G}(A)\simeq K[g_{i_1}\cdots g_{i_d} :\ \det ({\text {Log}}(g_{i_1},\ldots , g_{i_d}))\ne 0]\subseteq A. \end{aligned}$$

The morphism ${\mathbb G}(A)\hookrightarrow A$ induces the rational Gauss map

$$\begin{aligned} \gamma : \mathrm{Proj}\, (A)\dashrightarrow \mathrm{Proj}\, ({\mathbb G}(A)). \end{aligned}$$

Remark 1.1

Let $A=K[g_1,\ldots , g_n]$ be a standard graded K-subalgebra of $K[x_1,\ldots ,x_d]$, up to degree renormalization, and $X=\mathrm{Proj}\, (A)$. Since

$$\begin{aligned} X=\bigcup _{i=1}^n {\text {Spec}}(K[g_1/g_i,\ldots ,g_n/g_i]), \end{aligned}$$

it follows that the field K(X) of rational functions of X is equal to the field of fractions of any of the algebras $K[g_1/g_i,\ldots ,g_n/g_i]$.

Let $B\subset A$ be an extension of homogeneous standard graded algebras, and $X=\mathrm{Proj}\, (A)$ and $Y=\mathrm{Proj}\, (B)$. Let A be a domain. Then, the corresponding dominant rational map $X \dashrightarrow Y$ is birational if and only if $K(X)=K(Y)$.

Therefore, if $A=K[g_1,\ldots ,g_n]$ is the toric algebra as above, then the morphism $\gamma :\mathrm{Proj}\, (A) \dashrightarrow \mathrm{Proj}\, ({\mathbb G}(A))$ is birational if and only if for all $i<j$, the fractions $g_i/g_j$ can be expressed as a product of fractions of the form $(g_{i_1}\cdots g_{i_d})/(g_{j_1}\cdots g_{j_d})$ with $\det ({\text {Log}}(g_{i_1},\ldots , g_{i_d}))\ne 0$ and $\det ({\text {Log}}(g_{j_1},\ldots , g_{j_d}))\ne 0$.

For example, $\gamma : \mathrm{Proj}\, (A) \dashrightarrow \mathrm{Proj}\, ({\mathbb G}(A))$ is birational, when $A\subseteq k[s,t]$ is the coordinate ring of the projective monomial curve parametrized by the generators of A [1, Proposition 3.8].

In general, normality, Cohen–Macaulayness or other homological or algebraic properties are not preserved when passing from A to ${\mathbb G}(A)$. For example, the squarefree r-Veronese algebra $A=K[V_{r,d}]$ is normal Cohen–Macaulay, while for $r=2$ the Gauss algebra ${\mathbb G}(A)$ is normal and Cohen–Macaulay if and only if $d\ge 5$, see Theorem 2.3.

The following example shows that the Gauss algebra of a non-normal toric algebra may be normal.

Example 1.2

Let $A=K[s^6, s^5t, s^4t^2,s^3t^3, t^6]\subset K[s,t]$ be the homogeneous coordinate ring of the projective monomial curve embedded in ${\mathbb P}_K^4$. By [1, Lemma 3.7], the K-algebra A is not an isolated singularity and hence is not normal. However, the Gauss algebra ${\mathbb G}(A)$ is the 8-Veronese algebra in k[t, s], which is normal, Cohen–Macaulay and an isolated singularity.

3 Borel fixed algebras

We start with the following lemma which is crucial for the kind of algebras studied in this section.

Lemma 2.1

Let $g_1,\ldots ,g_d\in S = K[x_1,\ldots ,x_d]$ be homogeneous polynomials, and let $\varphi : S\rightarrow S$ be a linear automorphism. Then,

$$\begin{aligned} \det (\Theta (\varphi (g_1),\ldots , \varphi (g_d)) {)}=\det (\varphi )\cdot \varphi (\det (\Theta (g_1,\ldots ,g_d)) {)}. \end{aligned}$$

Proof

Consider the linear transformation $\varphi (x_i)=\sum _{j=1}^{d}a_{ji}x_j$, $i=1,\ldots ,d$. For polynomial $g\in K[x_1,\ldots ,x_d]$, a direct computation with derivatives shows that

$$\begin{aligned} \dfrac{\partial \varphi (g)}{\partial x_i}=a_{i1} \varphi \left( \dfrac{\partial g}{\partial x_1}\right) +\cdots + a_{id} \varphi \left( \dfrac{\partial g}{\partial x_d}\right) . \end{aligned}$$

We have

$$\begin{aligned} \det (\Theta (\varphi (g_1), \ldots , \varphi (g_{ {d}})))= & {} \det \left( \begin{bmatrix} a_{11}&\quad \cdots&\quad a_{1d}\\ \vdots&\quad \ddots&\quad \vdots \\ a_{d1}&\quad \cdots&\quad a_{dd} \end{bmatrix} \begin{bmatrix} \varphi \left( \dfrac{\partial g_1}{\partial x_1}\right)&\quad \cdots&\quad \varphi (\dfrac{\partial g_d}{\partial x_1})\\ \vdots&\quad \ddots&\quad \vdots \\ \varphi \left( \dfrac{\partial g_1}{\partial x_d}\right)&\quad \cdots&\quad \varphi \left( \dfrac{\partial g_d}{\partial x_d}\right) \end{bmatrix}\right) \\ \\= & {} \det (\varphi ).\det (\varphi (\Theta (g_1,\ldots ,g_d)))\\= & {} \det (\varphi ).\varphi (\det ((\Theta (g_1,\ldots ,g_d)))). \end{aligned}$$

$\square$

Recall that a set $G=\{g_1,\ldots ,g_n\}$ of monomials of the same degree in $K[x_1,\ldots ,x_d]$ is called Borel set, if the monomial ideal generated by G is fixed under the action of all linear automorphisms $\varphi : S\rightarrow S$ defined by non-singular upper triangular matrices. The ideal generated by a Borel set is called a Borel fixed ideal.

If ${\text {char}}(K)=0$, as we always assume in this paper, the Borel fixed ideals are just the strongly stable monomial ideals, that is, the monomial ideals I with the property that $x_i(u/x_j)\in I$ for the all monomial generators u of I, and all integers $i<j$ such that $x_j$ divides u. Let $B\subseteq G$. Then, the elements of B are called Borel generators of G, if G is the smallest Borel set containing B. In this case, if $B=\{u_1,\ldots ,u_t\}$, we write $G=\langle u_1,\ldots ,u_t\rangle$. For instance, the Borel set generated by $\{x_1x_3, x_2x_4\}$ is $\langle x_1x_3, x_2x_4\rangle =\{x_1^2,x_1x_2,x_1x_3,x_1x_4,x_2^2,x_2x_3,x_2x_4\}$. A Borel set G is called principal if there exists $u\in G$ such that $G=\langle u\rangle$.

Let G be a Borel set of monomials of degree r. The Borel generators of G are characterized by the property that they are maximal among the monomials of G with respect to the following partial order on the monomials: Let $u= x_{i_1}x_{i_2}\ldots x_{i_r}$ and $v=x_{j_1}x_{j_2}\ldots x_{j_r}$ with $i_1\le i_2\le \cdots \le i_r$ and $j_1\le j_2\le \cdots \le j_r$. Then, we set $u\prec v$, if $i_k\le j_k$ for $k=1,\ldots ,r$. In particular, if $v=x_{i_1}^{c_1}\cdots x_{i_r}^{c_r}$ with $c_i>0$, and $u=x_1^{a_1}\cdots x_d^{a_d}$. Then, $u\npreceq v$ if and only if there exists j, such that

$$\begin{aligned} a_{i_j+1}+\cdots +a_d\ge c_{j+1}+\cdots +c_r+1. \end{aligned}$$

(2)

Let $G=\{g_1,\ldots ,g_n\}\subset K[x_1,\ldots ,x_d]$ be a Borel set. Then, we call $A=K[g_1,\ldots ,g_n]$, a Borel fixed algebra, if $\dim (A)=d$. Note that $\dim (A)=d$, if and only if there exists j such that $x_d|g_j$. Indeed, since G is a Borel set, the condition implies that $\{x_1^r,x_1^{r-1}x_2,\ldots ,x_1^{r-1}x_d\}\subseteq G$, where r is the degree of the monomials in G. The log-matrix of these elements is upper triangular and so has rank d. This shows that $\dim (A)=d$. Indeed, A is isomorphic to the polynomial ring $K[x_1,\ldots ,x_d]$ by multiplication by $1/x^{r-1}$.

Theorem 2.2

The Gauss algebra of a Borel fixed algebra is a Borel fixed algebra.

Proof

Let A be a Borel fixed algebra with monomial generators $G=\{g_1,\ldots ,g_n\}$. Let $G'$ be the set of the corresponding monomial generators of ${\mathbb G}(A)$. We want to show that $G'$ is a Borel set. For this, it is enough to show that the ideal $I'$ generated by $G'$ is a Borel fixed ideal. Let g be a monomial generator in $I'$. Then, $g=\det (\Theta (g_{i_1},\ldots ,g_{i_d}))$. Let I be the monomial ideal generated by G. By Lemma 2.1, for any upper triangular automorphism $\varphi :\; S\rightarrow S$, one has

$$\begin{aligned} \varphi (g)=\varphi (\det (\Theta (g_{i_1},\ldots ,g_{i_d})))=\det (\varphi )^{-1}(\det \Theta (\varphi (g_{i_1}),\ldots ,\varphi (g_{i_d}))). \end{aligned}$$

Since I is a Borel fixed ideal, each $\varphi (g_i)$ is a K-linear combination of elements of G. By using the fact that $\Theta (-)$ is a multilinear function, we get $\varphi (g)\in I'$. This shows that ${\mathbb G}(A)$ is Borel fixed. $\square$

Corollary 2.3

([1], Proposition 3.2) The Gauss algebra of an r-Veronese algebra is an $(r-1)d$-Veronese algebra.

Proof

Consider the monomials $g_1= x_1x_d^{r-1},\ldots , g_{d-1}=x_{d-1}x_d^{r-1}, g_d=x_d^r$. As the log-matrix of $\mathbf{g}$ is non-singular, the monomial $g_1\cdots g_d/x_1\cdots x_d= x_d^{(r-1)d}$ belongs to the Gauss algebra. Since the r-Veronese is a Borel fixed ideal, the assertion follows from Theorem 2.2. $\square$

In general, the number of Borel generators of the Borel fixed algebra A and that of ${\mathbb G}(A)$ may be different. In fact, let $\{x_2x_3, x_1x_4\}$ be the set of Borel generators of A. Then, $A=K[x_1^2,x_1x_2,x_2^2,x_1x_3,x_2x_3,x_1x_4]$ and the log-matrix of the generators of A is

$$\begin{aligned} \begin{bmatrix} 2&\quad 1&\quad 0&\quad 1&\quad 0&\quad 1\\ 0&\quad 1&\quad 2&\quad 0&\quad 1&\quad 0\\ 0&\quad 0&\quad 0&\quad 1&\quad 1&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 1 \end{bmatrix}. \end{aligned}$$

Therefore, ${\mathbb G}(A)=K[x_1^4,x_1^3x_2,x_1^2x_2^2,x_1x_2^3,x_1^3x_3,x_1^2x_2x_3,x_1x_2^2x_3]$, and $x_1x_2^2x_3$ is the single Borel generator of ${\mathbb G}(A)$.

However if A is principal Borel, then ${\mathbb G}(A)$ is principal Borel as well. More precisely, we have the following.

Theorem 2.4

Let A be a principal Borel fixed algebra with Borel generator $m=x_{i_1}^{a_{i_1}}\cdots x_{i_r}^{a_{i_r}}$ with $a_{i_j}>0$, for $j=1,\ldots ,r$. Then, ${\mathbb {G}}(A)$ is a principal Borel fixed algebra with Borel generator

$$\begin{aligned} m'=\frac{m^{i_r}}{x_{i_1}^{i_1-1}x_{i_2}^{i_2-i_1}\cdots x_{i_{r-1}}^{i_{r-1}-i_{r-2}}x_{i_r}^{i_r-i_{r-1}+1}}. \end{aligned}$$

Proof

We first show that $m'\in {\mathbb G}(A)$. Let $g_{k,l}=x_l(m/x_{i_k})$, $k=1,\ldots ,r$, $l=i_{k-1},\ldots ,i_k-1$ for all k, where $i_0=1$. Then, the $g_{k,l}$ belong to $\langle m\rangle$, and

$$\begin{aligned} m'=\left( \prod _{k=1}^{r}\prod _{l=i_{k-1}}^{i_k-1}g_{k,l}\right) /x_1x_2\cdots x_d. \end{aligned}$$

We order the monomials $g_{k,l}$ lexicographically and consider the corresponding log-matrix A. The $i\hbox {th}$ row with $i\notin \{i_1,\ldots ,i_r\}$ has only one nonzero entry which is 1. So in order to compute the determinant of the log-matrix, we reduce to the computation of the cofactor of that nonzero entry; indeed, we skip the $i\hbox {th}$ row and the column corresponding to the nonzero entry. This can be done for all $i\notin \{i_1,\ldots ,i_r\}$. Then, we obtain the log-matrix M of the following sequence of monomials

$$\begin{aligned} m, x_{i_1}\frac{m}{x_{i_2}},\ldots , x_{i_{r-1}}\frac{m}{x_{i_r}} \end{aligned}$$

with respect to $x_{i_1},\ldots , x_{i_r}$. Subtracting the first column of M from the other columns of M, we obtain the following matrix

$$\begin{aligned} \begin{bmatrix} a_{i_1}&\quad 1&\quad 0&\quad \cdots&\quad \cdots&\quad \cdots&\quad 0\\ a_{i_2}&\quad -1&\quad 1&\quad 0&\quad \cdots&\quad \cdots&\quad 0\\ a_{i_3}&\quad 0&\quad -1&\quad 1&\quad 0&\quad \cdots&\quad 0\\ \vdots&\quad \vdots&\quad \ddots&\quad \ddots&\quad \ddots&\quad {\ddots }&\quad \vdots \\ \vdots&\quad \vdots&\quad&\quad \ddots&\quad \ddots&\quad 1&\quad 0\\ a_{i_{r-1}}&\quad 0&\quad \cdots&\quad \cdots&\quad 0&\quad -1&\quad 1\\ a_{i_r}&\quad 0&\quad \cdots&\quad \cdots&\quad \cdots&\quad 0&\quad -1\\ \end{bmatrix} \end{aligned}$$

Now for each $i>1$, we add the $i\hbox {th}$ row to the first row. The result is a lower triangular matrix with nonzero entries on the diagonal. This shows that A is non-singular, and proves that $m'$ is a generator of the Borel fixed algebra ${\mathbb G}(A)$.

Since ${\mathbb G}(A)$ is a Borel fixed ideal, by Theorem 2.2, it is enough to prove that for any monomial g in ${\mathbb G}(A)$, one has $g\preceq m'$. Let $m=x^{a_{i_1}}_{i_1}\cdots x^{a_{i_r}}_{i_r}$, $m'=x^{a'_{i_1}}_{i_1}\cdots x^{a'_{i_r}}_{i_r}$. By definition of $m'$, we have $a'_{i_j}=i_ra_{i_{j+1}}-i_{j+1}+i_j$ for $j=2,\ldots ,r-1$, and $a'_{i_r}=i_r(a_{i_r}-1)+i_{r-1}-1$. Let

$$\begin{aligned} g=\left( \prod ^{i_r}_{i=1}g_i\right) /x_1x_2\cdots x_{i_r}, \end{aligned}$$

where $g_1,\ldots ,g_{i_r}$ belong to the minimal monomial generating set of A, the latter having a non-singular log-matrix. If $g\npreceq m'$, then by Borel order property (2), there exists $1\le j\le r-1$, such that $\prod ^{i_r}_{j=1}g_j$ is divisible by $w=x_{i_j}^{b_{i_j}}\cdots x_{i_r}^{b_{i_r}}$, and

$$\begin{aligned} \sum ^{i_r}_{l=i_j+1}b_l-(i_r-i_j)\ge & {} 1+\sum ^{i_r}_{l=i_{j+1}}a'_{i_l}\\= & {} \sum _{k=j}^{r-2}(i_ra_{i_{k+1}}-i_{k+1}+i_k)+i_r(a_{i_{r}}-1)+i_{r-1}\\= & {} \left( \sum ^r_{l=j+1}a_{i_l}-1\right) i_r+i_j. \end{aligned}$$

Therefore,

$$\begin{aligned} \sum ^r_{l=i_j+1}b_{i_l}\ge \left( \sum ^r_{l=j+1}a_{i_l}\right) i_r. \end{aligned}$$

(3)

We may write $g_s$ as a product of monomials $g_s=f_{s}h_{s}$ with ${\text {supp}}(f_{s})\subseteq \{i_1,\ldots ,i_j\}$ and ${\text {supp}}(h_{s})\subseteq \{i_{j+1},\ldots ,i_r\}$. As $g_s\preceq x^{a_{i_1}}_{i_1}\cdots x^{a_{i_r}}_{i_r}$, we have $\deg (h_{s})\le \sum ^r_{l=j+1}a_{i_j}$ and, since w divides $g_1\cdots g_{i_r}$, we get

$$\begin{aligned} \sum ^{i_r}_{l=i_j+1}b_{i_l}\le \sum ^d_{s=1}\deg (h_s)\le d\sum ^r_{l=j+1}a_{i_l}. \end{aligned}$$

Together with (3), it follows that $\sum ^{i_r}_{s=1}\deg (h_s)=i_r\sum ^r_{l=j+1}a_{i_l}$, and this implies $\deg (h_s)=\sum ^r_{l=j+1}a_{i_l}$.

Let L be the log-matrix of $g_1,\ldots ,g_{i_r}$. Then, the summation of the last $i_r-i_j$ entries of each column of L is equal to $\sum ^r_{l=j+1}a_{i_l}$, and so the summation of the first j entries of each column is equal to $i_r-\sum ^r_{l=j+1}a_{i_l}$. This implies that L is singular, a contradiction. $\square$

Corollary 2.5

Let A be a principal Borel fixed algebra. Then, ${\mathbb G}(A)$ is normal and for suitable monomial order its defining ideal has a quadratic Gröbner basis.

Proof

By the above theorem, ${\mathbb G}(A)$ is a principal Borel fixed algebra. A principal Borel set is a polymatroid. Therefore, ${\mathbb G}(A)$ is normal, see [7, Corollary 6.2]. In [3] it is shown that the principal Borel fixed sets are sortable, and so ${\mathbb G}(A)$ has quadratic Gröbner basis. $\square$

Corollary 2.6

Let A be a Borel fixed algebra such that $\dim A=\dim {\mathbb G}(A)=d$. Then, the Gauss map $\gamma : \mathrm{Proj}\, (A)\dashrightarrow \mathrm{Proj}\, ({\mathbb G}(A))$ is birational.

Proof

By the hypothesis on the dimension of ${\mathbb G}(A)$, there exists a generator u of ${\mathbb G}(A)$ such that $x_d|u$. For $1\le i<j\le d$, we have

$$\begin{aligned} \frac{x_i}{x_j}=\frac{x_i(u/x_d)}{x_j(u/x_d)}, \end{aligned}$$

which implies that $\gamma$ is birational, since any quotient of monomials in A is the product of some of the $x_i/x_j$, see Remark 1.1. $\square$

4 Squarefree Veronese algebras

Let $V_{r,d}$ be the set of all squarefree monomials of degree r in $S=K[x_1,\ldots ,x_d]$. The K-subalgebra $A=K[V_{r,d}]$ of S is called the squarefreer-Veronese algebra. By Proposition 2.3, the Gauss algebra associated with a Veronese algebra is again a Veronese algebra. The situation for squarefree Veronese algebra is more complicated.

Denote by ${\text {Mon}}_S(t,r)$ the set of all monomials u of degree r in S, such that $|{\text {supp}}(u)|\ge t$, where ${\text {supp}}(u)=\{i \ : \ x_i|u\}$.

Proposition 3.1

The monomial ideal generated by ${\text {Mon}}_S(t,r)$ is polymatroidal. In particular, the K-algebra $K[{\text {Mon}}_S(t,r)]$ is normal and Cohen–Macaulay.

Proof

The normality of the K-algebra $K[{\text {Mon}}_S(t,r)]$ follows from [7, Theorem 6.1], once we have shown that the ideal generated by ${\text {Mon}}_S(t,r)$ is polymatroidal. Let $u=x_1^{a_1}\cdots x_d^{a_d},v=x_1^{b_1}\cdots x_d^{b_d}\in {\text {Mon}}_S(t,r)$. By symmetry, we may assume that $a_1>b_1$. Suppose $a_1>1$, then $x_iu/x_1\in {\text {Mon}}_S(t,r)$ for any $i\ne 1$, and so the exchange property holds. Next suppose that $a_1=1$, then $b_1=0$. If ${\text {supp}}(u)$ has more than t elements, we may replace $x_1$ by any variable $x_i\in {\text {supp}}(v)$. Finally, suppose that ${\text {supp}}(u)$ has exactly t elements. Since $x_1\notin {\text {supp}}(v)$, there exists $x_j\in {\text {supp}}(v){\setminus }{\text {supp}}(u)$. Replacing $x_1$ by $x_j$, the exchange property is satisfied. $\square$

In the following result, we describe the structure of the Gauss algebra of the squarefree 2-Veronese algebra $K[V_{2,d}]$. Note that for $d\le 3$, the Gauss algebra is isomorphic to a polynomial ring.

Theorem 3.2

Let $A=K[V_{2,d}]$, with $d\ge 4$. Then,

• (a) ${\mathbb G}(A)=K[{\text {Mon}}_S(3,4){\setminus }\{x_1x_2x_3x_4\}]$, if$d=4$;

• (b) ${\mathbb G}(A)=K[{\text {Mon}}_S(3,d)]$, if$d\ge 5$;

• (c) the embedding dimension of ${\mathbb G}(A)$ is

  $$\begin{aligned} {\text {edim}} {\mathbb G}(k[A])=\left\{ \begin{array}{ll} e-1, &{}\quad {\mathrm{if}}\; {d=4,} \\ e, &{}\quad {\mathrm{if}} \; {d=5,} \end{array} \right. \end{aligned}$$

  where $e=\left( {\begin{array}{c}2d-1\\ d\end{array}}\right) -(d-1)\left( {\begin{array}{c}d\\ 2\end{array}}\right) -d$;

• (d) the Gauss algebra is a normal Cohen–Macaulay domain, if and only if $d\ge 5$;

• (e) the Gauss map $\gamma : \mathrm{Proj}\, (A)\dashrightarrow \mathrm{Proj}\, ({\mathbb G}(A)))$ is birational.

For the proof of the theorem, we need the following

Lemma 3.3

([5, Theorem 2.1]) Let G be a loop-less connected graph with the same number of vertices and edges. Then, the log-matrix of the edge ideal of G is non-singular if and only if G contains an odd cycle.

Proof of Theorem 3.2

First, we show that any monomial of the form $m=g/x_1\cdots x_d$ belongs to ${\text {Mon}}_S(3,d)$, where $g=g_{i_1}\cdots g_{i_d}$ is a product of pairwise distinct elements of $V_{2,d}$. This then yields the inclusion ${\mathbb G}(A)\subseteq K[{\text {Mon}}_S(3,d)]$. Suppose that the number of elements in the support of m is less than 3. Then, at least $d-2$ variables have degree 1 in g. Hence, g can be written as a product of at most $d-1$ monomials in A, which is a contradiction.

Now, to prove (a) and (b), let m be an element of ${\text {Mon}}_S(3,d)$. For $d=4$ and $d=5$, the assertions can be shown by direct computations. Let $d>5$, and first assume that $m=x_1\cdots x_d$. If d is odd, then let

$$\begin{aligned} g_1=x_1x_2, g_2=x_2x_3,\ldots , g_{d-1}=(x_{d-1}x_d), g_d=(x_dx_1). \end{aligned}$$

Then, the log-matrix of $g_1,\ldots ,g_d$ is non-singular by Lemma 3.3. If d is even, then let

$$\begin{aligned}&g_1=x_1x_2, g_2=x_2x_3,g_3=x_3x_1,g_4=x_4x_5,g_5=x_5x_6,\ldots ,\\&\quad g_{d-1}=(x_{d-1}x_d), g_d=(x_dx_4). \end{aligned}$$

Now, the log-matrix is

$$\begin{aligned} \begin{bmatrix} A&\quad 0\\ 0&\quad B\\ \end{bmatrix}, \end{aligned}$$

where A and B are incidence matrices of odd cycles, and so it is non-singular.

Next assume that $m\ne x_1\cdots x_d$. Without loss of generality, we may assume that $m=x_1^{r_1}\cdots x_{d-1}^{r_{d-1}}$. Since $\deg (m)=d$, there exists i such that $r_i>1$. Let $u=m/x_i$. Then, $u\in {\text {Mon}}_{S'}(3,d-1)$, where $S'=K[x_1,\ldots ,x_{d-1}]$. By induction, $(x_1\cdots x_{d-1})u=g_1\cdots g_{d-1}$ with $g_i\in A$ and $L(g_1,\ldots , g_{d-1})$ non-singular. Let $g_d=x_ix_d$. Then, $(x_1\dots x_d)m=g_1\cdots g_{d-1}g_d$. Since all the entries of the last row of ${\text {Log}}(g_1,\ldots ,g_d)$ are zero, except the last one, which is equal to 1, we see that ${\text {Log}}(g_1,\ldots ,g_d)$ is non-singular.

(c) follows from (b) by a simple counting argument.

(d): If $d\ge 5$, it follows from (b) and Proposition 3.1 that ${\mathbb G}(A)$ is normal, and Cohen–Macaulay by Hochster [8]. On the other hand, a calculation with Singular [2] shows that for $d=4$, the h-vector of ${\mathbb G}(A)$ has a negative component. Therefore, in this case ${\mathbb G}(A)$ is not Cohen–Macaulay.

(e): By Remark 1.1, it is suffices to show that for every $1\le i<j\le n$,

$$\begin{aligned} K\left[ \dfrac{x_ix_j}{x_rx_s} \ | \ 1\le r<s\le n\right] \subset K\left[ \frac{u}{v}\ | \ u,v\in {\text {Mon}}(3,d) \right] . \end{aligned}$$

For $1\le i<j\le d$, one has

$$\begin{aligned} \dfrac{x_i}{x_j}=\dfrac{x_k x_l^{d-2}x_i}{x_k x_l^{d-2}x_j}, \end{aligned}$$

(4)

with i, j, k, l pairwise distinct. Hence, $(x_ix_j)/(x_rx_s)$ has an expression as in (4), if $\{i,j\}\cap \{r,s\}\ne \emptyset$. Otherwise,

$$\begin{aligned} \frac{x_ix_j}{x_rx_s}=\frac{(x_jx_s^{d-2}x_i)(x_ix_r^{d-2}x_j)}{(x_jx_s^{d-2}x_r)(x_ix_r^{d-2}x_s)}. \end{aligned}$$

$\square$

Remark 3.4

(a) Let $A=K[V_{r,d}]$. We may assume that $d\ge r+2$; otherwise, ${\mathbb G}(A)$ is a polynomial ring. Then,

$$\begin{aligned} {\mathbb G}(A)\subseteq \{x_1^{a_1}\cdots x_d^{a_d}\in {\text {Mon}}_{S}(r+1,(r-1)d)\ : \ a_i\le d-2 \quad \text {for}\quad 1\le i\le d\}. \end{aligned}$$

For $r=2$, the equality holds if and only if $d\ge 5$. It would be interesting to know for which $r>2$ and d the equality holds.

(b) According to White’s conjecture [12], the base ring of a polymatroid is generated by the so-called exchange relations, which are quadratic binomials. Since ${\text {Mon}}_{S}(3,d)$ is polymatroidal, we expect that the Gauss algebra of $K[V_{2,d}]$ has quadratic relations.

5 Edge rings

Let G be a simple graph on the vertex set $V(G)=[d]$ and edge set $E(G)=\{e_1,\ldots ,e_m\}$. For given subset $V\subseteq [d]$, we set $x_V=\prod _{i\in V}x_i$. In the case that V is an edge $e=\{i,j\}$, we simply write e instead of $x_V=x_ix_j$. The edge ideal I(G), of G, is the ideal generated by the monomials $e\in E(G)$. Note that the log-matrix of E(G) is the incidence matrix of G.

Let $V\subseteq V(G)$ and $E\subseteq E(G)$ with $| V|=| E|$. We denote by $\Delta _{V,E}$ the minor of the log-matrix ${\text {Log}}(E(G))$, with rows V and columns E.

Lemma 4.1

Let $V\subseteq V(G)$ and $E\subseteq E(G)$ with $|V|=|E|=r$, and let $\Delta _{V,E}$ be the minor of the log-matrix ${\text {Log}}(E(G))$, with rows V and columns E. Suppose the edges in E can be labeled as $e_1,\ldots ,e_r$, such that

$$\begin{aligned} | V\cap (e_1\cup \cdots \cup e_i)| =i \quad \text {for} \quad i=1,\ldots ,r. \end{aligned}$$

(5)

Then, $\Delta _{V,E}\ne 0$. The converse holds if G is a bipartite graph.

Proof

Suppose condition (5) holds. Let M be the matrix with rows V and columns E. Let $V\cap e_1=\{v\}$. Then, the first column of M has only one nonzero entry, corresponding to vertex v. Let $V'=V{\setminus }\{v\}$, and then

$$\begin{aligned} |V'\cap \{e_2,\ldots ,e_i\}|=i-1 \quad \text {for}\quad i=2,\ldots ,r. \end{aligned}$$

Now, by the induction hypothesis the matrix $M'$ whose rows are $V'$ and whose columns are $e_2,\ldots ,e_r$ is non-singular. It follows that M is non-singular.

Conversely, assume that $\Delta _{V,E}\ne 0$. Then, we claim that there exists a column $e_1$ in E such that $| V\cap e_1|=1$. Indeed, if $| V\cap e_i|>1$, for $i=1,\ldots ,r$, then M is the incidence matrix of a bipartite graph. Now, Lemma 3.3 implies $\Delta _{V,E}=0$, contradiction. Let $V'=V{\setminus }\{v_1\}$, where $V\cap e_1=\{v_1\}$. Then, the matrix $M'$ whose rows are $V'$ and whose columns are $e_2,\ldots ,e_r$, is non-singular. Now, $|V'\cap \{e_2,\ldots ,e_i\}|=i-1$ for $i=2,\ldots ,r$, by induction. This implies that $| V'\cap \{e_1,\ldots ,e_i\}|=i$ for $i=2,\ldots ,r$. $\square$

Corollary 4.2

Let G be a graph with c connected components, and $V\subset V(G)$, with $| V|\le d-c$. Then, there exists $E\subseteq E(G)$ with $| E|=|V|$ such that $\Delta _{V,E}\ne 0$.

Proof

Let $| V|=r$. Since $r\le d-c$, we can choose a set E of r edges such that $e\cap V\ne \emptyset$ for each $e\in E$. Now, the matrix M with rows V and columns E is not the incidence matrix of a forest, since for a forest the number of vertices is strictly bigger than the number of edges. Hence, there exists an edge $e_1$ in E such that $e_1\cap V=\{v\}$. Removing the edge $e_1$ from G, the number of connected components $c'$ of $G{\setminus }\{e_1\}$ is at most $c+1$. Let $V'=V{\setminus }\{v\}$. Then, $|V'|\le d-c'$. By induction, there exist edges $e_2,\ldots ,e_r$ such that $|V'\cap e_2\cup \cdots \cup e_i|=i-1$ for $i=2,\ldots ,r$. It follows that $e_1,\ldots ,e_r$ satisfies condition (5). Therefore, the desired result follows from Lemma 4.1. $\square$

Let G be a simple bipartite graph. Let L be a non-empty subset of [d], and let $G^L$ be the graph which is obtained from G by attaching a loop to G at each vertex belonging to L. For given set $T\subseteq E(G)$, let G(T) denote the graph with $V(G(T))=V(G)$ and $E(G(T))=T$.

Theorem 4.3

Let G be a bipartite graph with r components and L be a subset of [d]. Let A be the edge ring of $G^L$. Then, the following statements hold.

• (a) A has dimension d if and only if L contains at least one vertex of each component of G.

• (b) If condition (a) is satisfied, then the Gauss algebra ${\mathbb G}(A)$ is generated by the monomials

  $$\begin{aligned} g_{V,T}= x_{V}\frac{e_{T}}{x_{V^c}}, \end{aligned}$$

  where V is a non-empty subset of L, $V^c=[d]{\setminus } V$, and $e_T=\prod _{e\in T}e$ where $T\subseteq E(G)$ satisfies

  • (i) G(T) is a forest , which may have isolated vertices as some of its connected components;

  • (ii) each connected component of G(T) contains exactly one vertex of V.

  In particular, when $|V|=1$, the cardinality of the minimal set of generators of ${\mathbb G}(A)$ is bounded by the number of spanning trees of G. Moreover, $g_{V,T}=g_{V,T'}$ if and only if each vertex of G has the same degree in T and $T'$.

Proof

(a) As G is a bipartite graph, the log-matrix of G is singular by Lemma 3.3. We show that the log-matrix of $G^L$ has a non-singular maximal minor, if and only if L contains at least one vertex of each component of G. Let $L_i=G_i\cap L$, then $G_1^{L_1},\ldots ,G_r^{L_r}$ are the connected components of $G^L$, and the log-matrix of $G^L$ has maximal rank if and only if the log-matrix of each $G_i^{L_i}$ has maximal rank. Therefore, it is enough to show that the log-matrix of a connected graph G, with at least one loop, is non-singular. Assume that there is a loop at vertex 1. Then, the first column has only one nonzero entry at 1st row. Let A denote the log-matrix of G and $|V(G)|=n$. In order to compute the rank of A, we may skip the first row and the first column, obtaining a new matrix $A_1$, which has maximal rank $n-1$, by Corollary 4.2. Therefore, the rank of A is equal to n.

(b) We first show that conditions (i) and (ii) are equivalent to

($\alpha$):

$|T|=|V^c|$;

($\beta$):

the elements of T can be labeled as $e_1,\ldots ,e_m$ such that

$$\begin{aligned} |V^c\cap (e_1\cup \cdots \cup e_i)|=i \quad \text {for} \quad i=1,\ldots ,m. \end{aligned}$$

Suppose that (i) and (ii) are satisfied. If $T=\emptyset$, then the equivalence of (i),(ii) with $\alpha ,\beta$ is trivial. Now, assume that $T\ne \emptyset$, and let $G(T)_1,\ldots ,G(T)_t$ be the connected components of G(T) with $|V(G(T)_i)|\ge 2$ and $v_i$ be the vertex of V belonging to $G(T)_i$. Since $G(T)_i$ is a tree, we may label the edges of $G(T)_i$ as $e_{i_1},\ldots ,e_{i_{s_i}}$ such that $v_i\in e_{i_1}$ and $|e_{i_j}\cap (e_{i_1}\cup \cdots \cup e_{i_{j-1}})|=1$ for all $j=1,\ldots ,s_i$. Then, the sequence of edges

$$\begin{aligned} e_{1_1},\ldots ,e_{1_{s_1}},e_{2_1},\ldots ,e_{2_{s_2}},e_{3_1},\ldots \end{aligned}$$

satisfies conditions ($\alpha$),($\beta$).

Conversely, condition $(\beta )$ guarantees that G(T) does not contain any cycle, and so it is a forest, which by $(\alpha )$ has $d-|V|$ edges. Therefore, |V| is equal to the number of connected components of G(T). Let $G(T)_1,\ldots ,G(T)_t$ be the connected components of G(T) with $|V(G(T)_i)|\ge 2$, and let $e_{i_j}$ be the first edge, with respect to the labeling in ($\beta$), such that $e_{i_j}\cap G(T)_j\ne \emptyset$. Then, $|e_{i_j}\cap V|=1$, so each connected component of G(T) contains at least one vertex in V. Since G(T) has |V| number of components, each component should contain exactly one element of V.

Let g belong to the minimal set of generators of ${\mathbb G}(A)$. Then, $g=\frac{g_1\cdots g_d}{x_1\cdots x_d}$, where $g_i$ is a monomial generator of A and the log-matrix of $g_1,\ldots ,g_d$ is non-singular. Since the incidence matrix of a bipartite graph is singular by Lemma 3.3, at least one $g_i$ corresponds to a loop. After relabeling, we may assume that $\{g_1,\ldots ,g_d\}=\{x_1^2,\ldots ,x_s^2,e_1,\ldots ,e_{d-s}\}$ and

$$\begin{aligned} \ {\text {Log}}\left( x_1^2\cdots x_s^2e_{1}\cdots e_{{d-s}}\right) = \begin{bmatrix} 2&\quad 0&\quad \cdots&\quad 0&\quad a_{1,1}&\quad \cdots&\quad a_{1,d-s}\\ 0&\quad 2&\quad&\quad 0&\quad a_{2,1}&\quad \cdots&\quad a_{2,d-s}\\ \vdots&\quad&\quad \ddots&\quad \vdots&\quad \vdots&\quad \vdots \\ 0&\quad 0&\quad \cdots&\quad 2&\quad a_{s,1}&\quad \cdots&\quad a_{s,d-s}\\ 0&\quad 0&\quad \cdots&\quad 0&\quad a_{s+1,1}&\quad \cdots&\quad a_{s+1,d-s}\\ \vdots&\quad \vdots&\quad \vdots&\quad \vdots&\quad \vdots&\quad \vdots&\quad \vdots \\ 0&\quad 0&\quad 0&\quad 0&\quad a_{d,1}&\quad \cdots&\quad a_{d,d-s} \end{bmatrix}, \end{aligned}$$

where $A=[a_{r,t}]$ is the log-matrix of $e_{1}\cdots e_{{d-s}}$. Let $V=\{1,\ldots ,s\}$ and $T=\{e_1,\ldots ,e_{d-s}\}$. Then,

$$\begin{aligned} g=g_{V,T}=\frac{x_1^2\cdots x_s^2e_{1}\cdots e_{{d-s}}}{x_1\cdots x_d}=x_1\cdots x_s\frac{e_{1}\cdots e_{{d-s}}}{x_{s+1}\cdots x_{d}}, \end{aligned}$$

and the log-matrix is non-singular if and only if the submatrix $A'$ with rows $s+1,\ldots ,d$ and columns $s+1,\ldots , d$, is non-singular, and by Lemma 4.1, $A'$ is non-singular if and only if condition ($\beta$) is satisfied. $\square$

Example 4.4

Let G be a path graph with d vertices, and edges $\{1,2\},\{2,3\},\ldots ,\{d-1,d\}$. Let $L\subseteq [d]$ and A be the edge ring of $G^L$. The induced subgraph by any set $T\subset E(G)$ can be considered as a disjoint union of intervals. Since G is a path graph, G(T) is a forest. By Theorem 4.3, the product of edges in T should be divisible by all vertices in $[d]{\setminus } V$. Therefore, G(T), covers [d]. In other words, the generators of ${\mathbb G}(A)$ correspond to interval partitions of [d] with the property that each interval contains exactly one element of V. Let $[d]=\cup ^r_{i=1}[a_i,b_i]$ with $[a_i,b_i]\cap [a_j,b_j]=\emptyset$ for all $i\ne j$, and with $|V\cap [a_i,b_i]|=1$ for $i=1,\ldots ,r$. The corresponding generator of ${\mathbb G}(A)$ is

$$\begin{aligned} \left( \prod ^r_{i=1}\prod _{j\in ]a_i,b_i[ }x_j\right) \prod _{j\in L}x_j^{c_j}, \end{aligned}$$

(6)

where $c_j=2$, if j belongs to a proper interval, and is $c_j=1$, otherwise. Here $[a_i,b_i]$ is said to be proper if $b_i-a_i>0$.

The above discussions show that if $L=[d]$, then the number of generators of ${\mathbb G}(A)$ is the number

$$\begin{aligned} \lambda _d=\sum ^{d}_{r=1}\sum _{a\in P_r}\prod _{i=1}^r(a_{i+1}-a_i), \end{aligned}$$

where $P_r=\{a=(a_0,\ldots ,a_r) : 0=a_0<a_1< a_2<\cdots <a_r=d)\}$, for $r=1,\ldots ,d$. The sequence $(\lambda _d)_{d\ge 1}$ begins as follows

$$\begin{aligned} 1,3,8,21,55,144,377,\ldots . \end{aligned}$$

The recursive formula $\lambda _d=3\lambda _{d-1}-\lambda _{d-2}$ describes the beginning of the sequence. This seems to be the rule for the whole sequence $(\lambda _d)_{d\ge 1}$.

In the case that $L=\{i<j\}$, ${\mathbb G}(A)$ is generated by $j-i+2$ monomials

$$\begin{aligned} x^2_ix_2\cdots x_{d-1},\ x_j^2x_2\cdots x_{d-1}, \ \left( x_i^2x_j^2x_2\cdots x_{d-1}\right) /x_{k}x_{k+1} \quad \text {for} \quad i\le k\le j-1. \end{aligned}$$

An easy calculation shows that the log-matrix of ${\mathbb G}(A)$ has rank $j-i+1$. In particular, ${\mathbb G}(A)$ is a hypersurface ring. It can be shown that the multiplicity of ${\mathbb G}(A)$ is $j-i$. When $i=1,j=d$, the defining equation of ${\mathbb G}(A)$ is

$$\begin{aligned} f=\left\{ \begin{array}{ll} {\mathop {\prod }\nolimits ^{d/2}_{i=1}}y^2_{2i}-y_1y_{d+1}{\mathop {\prod }\nolimits _{i=1}^{d/2-1}}y^2_{2i+1}, &{} \text { if } d \text { is even; }\\ \\ y_1{\mathop {\prod }\nolimits ^{(d-1)/2}_{i=1}}y^2_{2i+1}-y_{d+1}{\mathop {\prod }\nolimits _{i=1}^{(d-1)/2}}y^2_{2i+1}, &{} \text { if } d \text { is odd, }\end{array} \right. \end{aligned}$$

and if $j=i+1$, then the defining equation is quadratic. By computing the singular locus, we see that ${\mathbb G}(A)$ is normal if and only if $d=2$.

Example 4.5

Let G be a cycle with d vertices, and edges $\{1,2\},\{2,3\},\ldots ,\{d-1,d\},\{1,d\}$. Let $L=\{1\}$ and A be the edge ring of $G^L$. When d is even, the spanning trees of G correspond to the generators of ${\mathbb G}(A)$. Each spanning tree of G is obtained by removing one edge from G, and so the generators of ${\mathbb G}(A)$ are

$$\begin{aligned} x_1^2\prod ^d_{i=3}x_i, \ x_1^2\prod ^{d-1}_{i=2}x_i, \ x_1^3\frac{\prod ^d_{i=2}x_i}{x_jx_{j+1}} \quad \text {for} \quad j=2,\ldots ,d-1. \end{aligned}$$

(7)

When d is odd, in addition to the monomials in (7), ${\mathbb G}(A)$ has one more generator, namely $x_1\cdots x_d$. For even d, $\dim ({\mathbb G}(A))=d-1$, and for odd d, $\dim ({\mathbb G}(A))=d$. Hence in both cases ${\mathbb G}(A)$ is a hypersurface ring with defining equation

$$\begin{aligned} f=\left\{ \begin{array}{ll} y_{d-1}\prod \nolimits ^{d/2-1}_{i=1}y_{2i}-y_{d}\prod \nolimits _{i=1}^{d/2-1}y_{2i-1}, &{} \text { if } d \text { is even; }\\ \\ y_d\prod \nolimits ^{(d-1)/2}_{i=1}y_{2i}-y_{d+1}\prod \nolimits _{i=1}^{(d-1)/2}y_{2i-1}, &{} \text { if } d \text { is odd. }\end{array} \right. \end{aligned}$$

The initial monomial of f (with respect to any monomial order) is squarefree. Therefore, ${\mathbb G}(A)$ is normal.

Remark 4.6

Let G be a bipartite graph on [d], $L=\{i\}$ and A be the edge ring of $G^L$. The above examples and computational evidence indicate that ${\mathbb G}(A)$ is a hypersurface ring of dimension $d-1$ if and only if G is an even cycle.

Example 4.7

Let $G=K_{n,m}$ be a complete bipartite graph with partition sets $X=\{x_1,\ldots ,x_n\}$ and $Y=\{y_1,\ldots ,y_m\}$. Let A be the edge ring of G with one loop at vertex $x_1$. Then,

$$\begin{aligned} {\mathbb G}(A)=K\left[ x_1^2(x_1,\ldots ,x_n)^{m-1}(y_1,\ldots ,y_m)^{n-1}\right] . \end{aligned}$$

Indeed, any generator of ${\mathbb G}(A)$ can be written as $x_1^2(e_1\cdots e_{n+m})/x_1\cdots x_ny_1\cdots y_m$, where $e_j$ is an edge of G, which follows ${\mathbb G}(A)\subseteq K[x_1^2(x_1,\ldots ,x_n)^{m-1}(y_1,\ldots ,y_m)^{n-1}]$.

Let f be a monomial in the generating set of $(x_1,\ldots ,x_n)^{m-1}(y_1,\ldots ,y_m)^{n-1}$. Then, $f=x_{i_1}\cdots x_{i_{m-1}}y_{j_1}\cdots y_{j_{n-1}}$, for some $1\le i_1\le \cdots \le i_{m-1}\le n$ and $1\le j_1\le \cdots \le j_{n-1}\le m$. Now, let T be the subgraph of G with $V(T)=V(G)$ and E(T) equal to

$$\begin{aligned}&\{e_1=x_1y_{j_1},\ldots , e_{n-1}=x_{n-1}y_{j_{n-1}},e_{n}=y_1x_{i_1},\ldots ,e_{n+m-2}\\&\quad =y_{m-1}x_{i_{m-1}}, e_{n+m-1}=x_ny_n\}. \end{aligned}$$

Then, T is a spanning tree of G, which implies that

$$\begin{aligned} x_1^2f=x_1^2e_1\cdots e_{n+m-1}/x_1\cdots x_ny_1\cdots y_m \end{aligned}$$

is a generator of ${\mathbb G}(A)$.

As a consequence, the embedding dimension of ${\mathbb G}(A)$ is $\left( {\begin{array}{c}m+n-2\\ n-1\end{array}}\right) \left( {\begin{array}{c}m+n-2\\ m-1\end{array}}\right)$. However, the number of spanning tress of G is $n^{m-1}m^{n-1}$, see [6, Theorem 1]. Therefore, among the spanning trees of G, many of them correspond to the same generator in ${\mathbb G}(A)$.