1 Introduction

A homogeneous polynomial \(h(\mathbf {x}) \in \mathbb {R}[x_1, \ldots , x_n]\) is hyperbolic with respect to a vector \(\mathbf {e}\in \mathbb {R}^n\) if \(h(\mathbf {e}) \ne 0\), and if for all \(\mathbf {x}\in \mathbb {R}^n\) the univariate polynomial \(t \mapsto h(t\mathbf {e}-\mathbf {x})\) has only real zeros. Note that if h is a hyperbolic polynomial of degree d, then we may write

$$\begin{aligned} \displaystyle h(t{\mathbf {e}} - {\mathbf {x}}) = h({\mathbf {e}}) \prod _{j=1}^d (t - \lambda _j({\mathbf {x}})), \end{aligned}$$

where

$$\begin{aligned} \lambda _\mathrm{max}(\mathbf {x})=\lambda _1({\mathbf {x}}) \ge \cdots \ge \lambda _d({\mathbf {x}})=\lambda _\mathrm{min}(\mathbf {x}) \end{aligned}$$

are called the eigenvalues of \({\mathbf {x}}\) with respect to \({\mathbf {e}}\). The (hyperbolic) rank of \({\mathbf {x}} \in {\mathbb {R}}^n\) with respect to \({\mathbf {e}}\) is defined as \(\text {rk}({\mathbf {x}}) = \#\{ \lambda _i({\mathbf {x}}) \ne 0 \}\). The hyperbolicity cone of h with respect to \({\mathbf {e}}\) is the set \(\varLambda _{+}(h, {\mathbf {e}}) = \{ {\mathbf {x}} \in {\mathbb {R}}^n : \lambda _\mathrm{min}({\mathbf {x}}) \ge 0 \}\). If \(\mathbf {v}\in \varLambda _{+}(h, \mathbf {e})\), then h is hyperbolic with respect to \(\mathbf {v}\) and \(\varLambda _{+}(h,\mathbf {v}) = \varLambda _{+}(h, \mathbf {e})\). For this reason, we usually abbreviate and write \(\varLambda _{+}(h)\) if there is no risk for confusion. We denote by \(\varLambda _{++}(h)\) the interior of \(\varLambda _{+}(h)\). The cone \(\varLambda _{++}(h)\) is convex and can be characterized as the connected component of the set \(\{\mathbf {x}\in \mathbb {R}^n :h(\mathbf {x}) \ne 0 \}\) containing \(\mathbf {e}\). These are all facts due to Gårding [14].

Example 1.1

An important example of a hyperbolic polynomial is \(\det (X)\), where \(X = (x_{ij})_{i,j =1}^n\) is a matrix of variables where we impose \(x_{ij} = x_{ji}\). Note that \(t \mapsto \det (tI - X)\) where \(I = \text {diag}(1,\dots , 1)\), is the characteristic polynomial of a symmetric matrix so it has only real zeros. Hence, \(\det (X)\) is a hyperbolic polynomial with respect to I, and its hyperbolicity cone is the cone of positive semidefinite matrices. Note that the hyperbolic rank of a symmetric matrix X with respect to I coincides with the usual notion of rank for matrices.

Denote the directional derivative of \(h(\mathbf {x}) \in \mathbb {R}[x_1, \dots , x_n]\) with respect to \(\mathbf {v}= (v_1, \dots , v_n)^\mathrm{T} \in \mathbb {R}^n\) by

$$\begin{aligned} \displaystyle D_{\mathbf {v}}h(\mathbf {x}) = \sum _{k=1}^n v_k \frac{\partial h}{\partial x_k} (\mathbf {x}). \end{aligned}$$

The following lemma is well known and essentially follows from the identity \(D_{\mathbf {v}}h(t) = \frac{\mathrm{d}}{\mathrm{d}t}h(t \mathbf {v}+ \mathbf {x}) |_{t=0}\) together with Rolle’s theorem (see [14, 30]).

Lemma 1.2

Let h be a hyperbolic polynomial, and let \(\mathbf {v}\in \varLambda _+\) be such that \(D_{\mathbf {v}}h \not \equiv 0\). Then, \(D_{\mathbf {v}} h\) is hyperbolic with \(\varLambda _{+}(h, \mathbf {v}) \subseteq \varLambda _{+}(D_{\mathbf {v}} h, \mathbf {v})\).

A class of polynomials which is intimately connected to hyperbolic polynomials is the class of stable polynomials. A polynomial \(P(\mathbf {x}) \in {\mathbb {C}}[x_1, \dots , x_n]\) is stable if \(P(z_1,\ldots ,z_n) \ne 0\) whenever \(\mathrm{Im}(z_j)>0\) for all \(1\le j \le n\). A stable polynomial \(P(\mathbf {x}) \in {\mathbb {R}}[x_1, \dots , x_n]\) is said to be real stable. Hyperbolic and stable polynomials are related as follows, see [3, Prop. 1.1].

Lemma 1.3

Let \(P \in {\mathbb {R}}[x_1, \dots , x_n]\) be a homogenous polynomial. Then, P is stable if and only if P is hyperbolic with \({\mathbb {R}}_+^n \subseteq \varLambda _+(P)\).

The next theorem which follows (see [22]) from a theorem of Helton and Vinnikov [18] proved the Lax conjecture (after Lax [20]).

Theorem 1.4

(Helton–Vinnikov [18]) Suppose that h(x, y, z) is of degree d and hyperbolic with respect to \(e = (e_1,e_2,e_3)^\mathrm{T}\). Suppose further that h is normalized such that \(h(e) = 1\). Then, there are symmetric \(d \times d\) matrices A, B, C such that \(e_1A+e_2B+ e_3C = I\) and

$$\begin{aligned} \displaystyle h(x,y,z) = \det (xA + yB + zC). \end{aligned}$$

Remark 1.5

The exact analogue of Theorem 1.4 fails for \(n>3\) variables. This may be seen by comparing dimensions. The set of polynomials on \({\mathbb {R}}^n\) of the form \(\det (x_1A_1 + \cdots x_nA_n)\) with \(A_i\) a \(d\times d\) symmetric matrix for \(1 \le i \le n\), has dimension at most \(n \left( {\begin{array}{c}d+1\\ 2\end{array}}\right) \) (as an algebraic image \((A_1,\dots , A_n) \mapsto \det (x_1A_1 + \cdots x_nA_n)\) of a vector space of the same dimension), whereas the set of hyperbolic polynomials of degree d on \({\mathbb {R}}^n\) has non-empty interior in the space of homogeneous polynomials of degree d in n variables (see [29]) and therefore has the same dimension \(\left( {\begin{array}{c}n+d-1\\ d\end{array}}\right) \).

A convex cone in \(\mathbb {R}^n\) is spectrahedral if it is of the form

$$\begin{aligned} \displaystyle \left\{ {\mathbf {x}} \in {\mathbb {R}}^n : \sum _{i = 1}^n x_i A_i \,\, \text { is positive semidefinite} \right\} \end{aligned}$$

where \(A_i\), \(i = 1, \dots , n\) are symmetric matrices such that there exists a vector \((y_1, \dots , y_n) \in {\mathbb {R}}^n\) with \(\sum _{i=1}^n y_i A_i\) positive definite. It is easy to see that spectrahedral cones are hyperbolicity cones. A major open question asks if the converse is true.

Conjecture 1.6

(Generalized Lax conjecture [18, 32]) All hyperbolicity cones are spectrahedral.

Remark 1.7

An important consequence of Conjecture 1.6 in the field of optimization is that hyperbolic programming [30] is the same as semidefinite programming.

We may reformulate Conjecture 1.6 as follows, see [18, 32]. The hyperbolicity cone of \(h({\mathbf {x}})\) with respect to \({\mathbf {e}} = (e_1, \dots ,e_n)\) is spectrahedral if there is a homogeneous polynomial \(q({\mathbf {x}})\) and real symmetric matrices \(A_1, \ldots , A_n\) of the same size such that

$$\begin{aligned} \displaystyle q({\mathbf {x}})h({\mathbf {x}}) = \det \left( \sum _{i = 1}^n x_i A_i \right) \end{aligned}$$
(1)

where \(\varLambda _{++}(h, {\mathbf {e}}) \subseteq \varLambda _{++}(q, {\mathbf {e}})\) and \(\sum _{i=1}^n e_iA_i\) is positive definite. If we can choose \(q(\mathbf {x}) \equiv 1\), then we say that \(h(\mathbf {x})\) admits a definite determinantal representation.

  • Conjecture 1.6 is true for \(n=3\) by Theorem 1.4,

  • Conjecture 1.6 is true for homogeneous cones [7], i.e. cones for which the automorphism group acts transitively on its interior,

  • Conjecture 1.6 is true for quadratic polynomials, see, e.g. [28],

  • Conjecture 1.6 is true for elementary symmetric polynomials, see [5],

  • Weaker versions of Conjecture 1.6 are true for smooth hyperbolic polynomials, see [19, 27].

  • Stronger algebraic versions of Conjecture 1.6 are false, see [1, 4].

The paper is organized as follows. In Sect. 2, we prove Conjecture 1.6 for a multivariate generalization of the matching polynomial (Theorem 2.16). We also show that this implies Conjecture 1.6 for elementary symmetric polynomials (Theorem 2.19). Our result may therefore be viewed as a generalization of [5]. In Sect. 3, we generalize further to a multivariate version of the independence polynomial using a recent divisibility relation of Leake and Ryder [21] (Theorem 3.9). The variables of the homogenized independence polynomial do not fully correspond combinatorially (under the line graph operation) to the more refined homogeneous matching polynomial. The restriction of Theorem 3.9 to line graphs is therefore weaker than Theorem 2.16. Finally, in Sect. 4 we consider a hyperbolic convolution of determinant polynomials generalizing an identity of Godsil and Gutman [12] which asserts that the expected characteristic polynomial of a random signing of the adjacency matrix of a graph is equal to its matching polynomial.

Unless stated otherwise, \(G = (V(G),E(G))\) denotes a simple undirected graph. We shall adopt the following notational conventions.

  • \(\text {Sym}(S)\) denotes the symmetric group on the set S. Write \(\mathfrak {S}_n = \text {Sym}([n])\).

  • \(N_G(u) = \{ v \in V(G) : (u,v) \in E(G) \}\) (resp. \(N_G[u]= N_G(u) \cup \{u\}\)) denotes the open (resp. closed) neighbourhood of \(u \in V(G)\).

  • If \(S \subseteq V(G)\), then G[S] denotes the subgraph of G induced by S.

  • \(G \sqcup H\) denotes the disjoint union of the graphs G and H.

  • \(\mathbb {R}^S = \{ (a_s)_{s \in S} : a_s \in \mathbb {R}\} \cong \mathbb {R}^{|S|}\).

  • \(\mathbb {R}^G = \mathbb {R}^{V(G)} \times \mathbb {R}^{E(G)}\).

2 Hyperbolicity cones of multivariate matching polynomials

A k-matching in G is a subset \(M \subseteq E(G)\) of k edges, no two of which have a vertex in common. Let \({\mathcal {M}}(G)\) denote the set of all matchings in G, and let m(G, k) denote the number of k-matchings in G. By convention \(m(G,0) = 1\). We denote by V(M) the set of vertices contained in the matching M. If \(|V(M)| = |V(G)|\), then we call M a perfect matching. The (univariate) matching polynomial is defined by

$$\begin{aligned} \displaystyle \mu (G, t)= \sum _{k \ge 0} (-1)^k m(G,k) t^{|V(G)|-2k}. \end{aligned}$$

Note that this is indeed a polynomial since \(m(G,k) = 0\) for \(k > \frac{|V(G)|}{2}\). Heilmann and Lieb [17] studied the following multivariate version of the matching polynomial with variables \({\mathbf {x}} = (x_i)_{i \in V}\) and non-negative weights \(\varvec{\lambda } = (\lambda _e)_{e \in E}\),

$$\begin{aligned} \displaystyle \mu _{\varvec{\lambda }}(G, {\mathbf {x}}) = \sum _{M \in {\mathcal {M}}(G)} (-1)^{|M|} \prod _{ij \in M} \lambda _{ij} x_i x_j. \end{aligned}$$

Remark 2.1

Note that \(\displaystyle t^{|V(G)|} \mu _{{\mathbf {1}}}(G, t^{-1} {\mathbf {1}}) = \mu (G,t)\), where \({\mathbf {1}} = (1, \dots , 1)\).

Theorem 2.2

(Heilmann–Lieb [17]) If \(\varvec{\lambda } = (\lambda _e)_{e \in E}\) is a sequence of non-negative edge weights, then \(\mu _{\varvec{\lambda }}(G, {\mathbf {x}})\) is stable.

Remark 2.3

A quick way to see Theorem 2.2 is to observe that

$$\begin{aligned} \displaystyle \text {MAP} \left( \prod _{e = (i,j) \in E(G)} (1- \lambda _{e} x_i x_j) \right) = \mu _{\varvec{\lambda }}(G, {\mathbf {x}}) \end{aligned}$$

where \(\text {MAP}: {\mathbb {C}}[z_1, \dots , z_n] \rightarrow {\mathbb {C}}[z_1, \dots , z_n]\) is the stability preserving linear map taking a multivariate polynomial to its multiaffine part (see [2]). Since real stable univariate polynomials are real-rooted the Heilmann–Lieb theorem (together with Remark 2.1) implies the real-rootedness of \(\mu (G, t)\).

We will consider the following homogeneous multivariate version of the matching polynomial.

Definition 2.4

Let \({\mathbf {x}} = (x_v)_{v \in V}\) and \({\mathbf {w}} = (w_e)_{e \in E}\) be indeterminates. Define the homogeneous multivariate matching polynomial\(\mu (G, {\mathbf {x}} \oplus {\mathbf {w}} ) \in {\mathbb {R}}[{\mathbf {x}}, {\mathbf {w}}]\) by

$$\begin{aligned} \displaystyle \mu (G, {\mathbf {x}} \oplus {\mathbf {w}} ) = \sum _{M \in {\mathcal {M}}(G)} (-1)^{|M|} \prod _{v \not \in V(M)} x_v \prod _{e \in M} w_e^2. \end{aligned}$$
Fig. 1
figure 1

A labelled graph G

Full size image

Example 2.5

The homogeneous multivariate matching polynomial of the graph G in Fig. 1 is given by

$$\begin{aligned}&\mu (G, \mathbf {x}\oplus \mathbf {w}) = x_1x_2x_3x_4 - x_3x_4w_a^2 - x_1x_4w_b^2 - x_2x_4w_c^2 - x_1x_2w_d^2\\&\qquad \qquad \qquad \qquad - x_2x_3w_e^2 + w_a^2w_d^2 + w_b^2w_e^2. \end{aligned}$$

Remark 2.6

Note that \(\displaystyle \mu (G, t {\mathbf {1}} \oplus {\mathbf {1}}) = \mu (G, t)\) and that \(\mu (G, {\mathbf {0}} \oplus {\mathbf {w}})\) is the multivariate matching polynomial restricted to perfect matchings.

In this section, we prove Conjecture 1.6 in the affirmative for the polynomials \(\mu (G, {\mathbf {x}} \oplus {\mathbf {w}} )\). We first assert that \(\mu (G, {\mathbf {x}} \oplus {\mathbf {w}} )\) is indeed a hyperbolic polynomial.

Lemma 2.7

The polynomial \(\mu (G, {\mathbf {x}} \oplus {\mathbf {w}} )\) is hyperbolic with respect to \({\mathbf {e}} = {\mathbf {1}} \oplus {\mathbf {0}}\).

Proof

Clearly, \(\mu (G, {\mathbf {1}} \oplus {\mathbf {0}} ) = 1 \ne 0\). Let \({\mathbf {x}} \oplus {\mathbf {w}} \in \mathbb {R}^G\) and \(\lambda _e = w_{e}^2\) for all \(e \in E(G)\). Then,

$$\begin{aligned} \displaystyle \mu (G, t {\mathbf {e}} - {\mathbf {x}} \oplus {\mathbf {w}} ) = \left( \prod _{v \in V} (t - x_v) \right) \mu _{\varvec{\lambda }}(G, (t{\mathbf {1}} - {\mathbf {x}})^{-1}). \end{aligned}$$

Since \(\mu _{\varvec{\lambda }}(G, {\mathbf {x}})\) is real stable by Heilmann–Lieb theorem it follows that the right hand side is real-rooted. Hence, \(\mu (G, {\mathbf {x}} \oplus {\mathbf {w}} )\) is hyperbolic with respect to \({\mathbf {e}} = {\mathbf {1}} \oplus {\mathbf {0}}\). \(\square \)

Analogues of the standard recursions for the univariate matching polynomial (see [11, Thm 1.1]) also hold for \(\mu (G, {\mathbf {x}} \oplus {\mathbf {w}} )\). In particular, the following recursion is used frequently so we give details.

Lemma 2.8

Let \(u \in V(G)\). Then, the homogeneous multivariate matching polynomial satisfies the recursion

$$\begin{aligned} \displaystyle \mu (G, {\mathbf {x}} \oplus {\mathbf {w}} ) = x_u \mu (G {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}} ) - \sum _{v \in N(u)} w_{uv}^2 \mu ((G {\setminus } u) {\setminus } v, {\mathbf {x}} \oplus {\mathbf {w}} ). \end{aligned}$$

Proof

The identity follows by partitioning the matchings \(M \in {\mathcal {M}}(G)\) into two parts depending on whether \(u \in V(M)\) or \(u \not \in V(M)\). Let \(f_G(M) = \prod _{v \not \in V(M)} x_v \prod _{e \in M} w_e^2\). Then,

$$\begin{aligned} \displaystyle \mu (G, {\mathbf {x}} \oplus {\mathbf {w}})&= \sum _{M \in {\mathcal {M}}(G)} (-1)^{|M|} f_G(M) \\&= \sum _{\begin{array}{c} M \in {\mathcal {M}}(G) \\ u \not \in V(M) \end{array}} (-1)^{|M|} f_{G}(M) + \sum _{\begin{array}{c} M \in {\mathcal {M}}(G) \\ u \in V(M) \end{array} } (-1)^{|M|} f_G(M) \\&= x_u \sum _{M \in M(G {\setminus } u)} (-1)^{|M|} f_{G {\setminus } u}(M) + \sum _{v \in N(u)} \sum _{\begin{array}{c} M \in {\mathcal {M}}(G) \\ uv \in M \end{array}} (-1)^{|M|} f_G(M) \\&= x_u \mu (G {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}} ) - \sum _{v \in N(u)} w_{uv}^2 \sum _{M \in M( (G {\setminus } u) {\setminus } v)} (-1)^{|M|} f_{(G {\setminus } u){\setminus } v}(M) \\&= x_u \mu (G {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}} ) - \sum _{v \in N(u)} w_{uv}^2 \mu ((G {\setminus } u) {\setminus } v, {\mathbf {x}} \oplus {\mathbf {w}}). \end{aligned}$$

\(\square \)

Let G be a graph and \(u \in V(G)\). The path treeT(G, u) is the tree with vertices labelled by simple paths in G (i.e. paths with no repeated vertices) starting at u and where two vertices are joined by an edge if one vertex is labelled by a maximal subpath of the other.

Example 2.9

figure a

Definition 2.10

Let G be a graph and \(u \in V(G)\). Let \(\phi : {\mathbb {R}}^{T(G,u)} \rightarrow {\mathbb {R}}^{G}\) denote the linear change of variables defined by

$$\begin{aligned} \displaystyle x_{p}&\mapsto x_{i_k}, \\ w_{pp'}&\mapsto w_{i_k i_{k+1}}, \end{aligned}$$

where \(p = i_1 \cdots i_k\) and \(p' = i_1 \cdots i_k i_{k+1}\) are adjacent vertices in T(G, u). For every subforest \(T \subseteq T(G,u)\), define the polynomial

$$\begin{aligned} \eta (T, \mathbf {x}\oplus \mathbf {w}) = \mu (T, \phi (\mathbf {x}' \oplus \mathbf {w}')) \end{aligned}$$

where \(\mathbf {x}' = (x_p)_{p \in V(T)}\) and \(\mathbf {w}' = (w_e)_{e \in E(T)}\).

Remark 2.11

Note that \(\eta (T, \mathbf {x}\oplus \mathbf {w})\) is a polynomial in variables \(\mathbf {x}= (x_v)_{v \in V(G)}\) and \(\mathbf {w}= (w_e)_{e \in E(G)}\).

For the univariate matching polynomial, we have the following rather unexpected divisibility relation due to Godsil [10],

$$\begin{aligned} \frac{\mu (G {\setminus } u, t)}{\mu (G, t)} = \frac{\mu (T(G,u) {\setminus } u, t)}{\mu (T(G,u), t)}. \end{aligned}$$

Below we prove a multivariate analogue of this fact. A similar multivariate analogue was also noted independently by Leake and Ryder [21]. In fact, they were able to find a further generalization to independence polynomials of simplicial graphs. We will revisit their results in Sect. 3. The arguments all closely resemble Godsil’s proof for the univariate matching polynomial. For the convenience of the reader, we provide the details in our setting.

Lemma 2.12

Let \(u \in V(G)\). Then,

$$\begin{aligned} \displaystyle \frac{\mu (G {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}} )}{ \mu (G, {\mathbf {x}} \oplus {\mathbf {w}})} = \frac{\eta (T(G,u) {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}})}{ \eta (T(G,u), {\mathbf {x}} \oplus {\mathbf {w}})}. \end{aligned}$$

Proof

If G is a tree, then \(\mu (G, \mathbf {x}\oplus \mathbf {w}) = \eta (T(G,u), \mathbf {x}\oplus \mathbf {w})\) and \(\mu (G {\setminus } u, \mathbf {x}\oplus \mathbf {w}) = \eta (T(G,u) {\setminus } u, \mathbf {x}\oplus \mathbf {w})\) so the lemma holds. In particular, the lemma holds for all graphs with at most two vertices. We now argue by induction on the number of vertices of G. We first claim that

$$\begin{aligned} \frac{\eta (T(G,u){\setminus } \{ u, uv \}, \mathbf {x}\oplus \mathbf {w})}{\eta (T(G,u) {\setminus } u, \mathbf {x}\oplus \mathbf {w})} = \frac{\eta (T(G {\setminus } u, v){\setminus } v, \mathbf {x}\oplus \mathbf {w}) }{\eta (T(G {\setminus } u, v), \mathbf {x}\oplus \mathbf {w})}. \end{aligned}$$

Let \(v \in N(u)\). By examining the path tree T(G, u), we note the following isomorphisms

$$\begin{aligned} T(G, u) {\setminus } u&\cong \bigsqcup _{n \in N(u)} T(G {\setminus } u, n), \\ T(G, u) {\setminus } \{ u,uv \}&\cong \left( \bigsqcup _{\begin{array}{c} n \in N(u) \\ n \ne v \end{array}} T(G {\setminus } u, n) \right) \sqcup T(G {\setminus } u,v) {\setminus } v, \end{aligned}$$

following from the fact that \(T(G{\setminus } u, n)\) is isomorphic to the connected component of \(T(G,u){\setminus } u\) which contains the path un in G. By the definition of \(\phi \) and the general multiplicative identity

$$\begin{aligned} \displaystyle \mu (G \sqcup H, {\mathbf {x}} \oplus {\mathbf {w}}) = \mu (G, {\mathbf {x}} \oplus {\mathbf {w}})\mu (H, {\mathbf {x}} \oplus {\mathbf {w}}), \end{aligned}$$

the above isomorphisms translate to the following identities

$$\begin{aligned} \displaystyle \eta (T(G, u) {\setminus } u, \mathbf {x}\oplus \mathbf {w})&= \prod _{n \in N(u)} \eta (T(G {\setminus } u, n), \mathbf {x}\oplus \mathbf {w}), \\ \eta (T(G,u) {\setminus } \{u,uv\}, \mathbf {x}\oplus \mathbf {w})&= \eta (T(G{\setminus } u,v) {\setminus } v, \mathbf {x}\oplus \mathbf {w}) \prod _{\begin{array}{c} n \in N(u) \\ n \ne v \end{array}} \eta (T(G {\setminus } u, n), \mathbf {x}\oplus \mathbf {w}), \end{aligned}$$

from which the claim follows. By Lemma 2.8, induction, above claim and the definition of \(\phi \), we finally get

$$\begin{aligned} \displaystyle \frac{\mu (G, \mathbf {x}\oplus \mathbf {w})}{\mu (G {\setminus } u, \mathbf {x}\oplus \mathbf {w})}&= \frac{x_u \mu (G{\setminus } u, \mathbf {x}\oplus \mathbf {w}) - \sum _{v \in N(u)}w_{uv}^2 \mu (G {\setminus } \{u,v \}, \mathbf {x}\oplus \mathbf {w}) }{\mu (G {\setminus } u, \mathbf {x}\oplus \mathbf {w})} \\&= x_u - \sum _{v \in N(u)}w_{uv}^2 \frac{\mu ((G {\setminus } u) {\setminus } v, \mathbf {x}\oplus \mathbf {w})}{\mu (G {\setminus } u, \mathbf {x}\oplus \mathbf {w})} \\&= x_u - \sum _{v \in N(u)} w_{uv}^2 \frac{\eta (T(G {\setminus } u, v) {\setminus } v, \mathbf {x}\oplus \mathbf {w})}{\eta (T(G {\setminus } u, v), \mathbf {x}\oplus \mathbf {w})} \\&= x_u - \sum _{v \in N(u)} w_{uv}^2 \frac{\eta (T(G,u){\setminus } \{ u, uv \}, \mathbf {x}\oplus \mathbf {w})}{\eta (T(G,u) {\setminus } u, \mathbf {x}\oplus \mathbf {w})} \\&= \frac{\eta (T(G,u), \mathbf {x}\oplus \mathbf {w})}{\eta (T(G,u) {\setminus } u, \mathbf {x}\oplus \mathbf {w})} \end{aligned}$$

which is the reciprocal of the desired identity. \(\square \)

Lemma 2.13

Let \(u \in V(G)\). Then, \(\mu (G, \mathbf {x}\oplus \mathbf {w})\) divides \(\eta (T(G,u), \mathbf {x}\oplus \mathbf {w})\).

Proof

The argument is by induction on the number of vertices of G. Deleting the root u of T(G, u), we get a forest with |N(u)| disjoint components isomorphic to \(T(G {\setminus } u, v)\), respectively, for \(v \in N(u)\). This gives

$$\begin{aligned} \displaystyle \eta (T(G,u) {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}}) = \prod _{v \in N(u)} \eta (T(G {\setminus } u,v), {\mathbf {x}} \oplus {\mathbf {w}}). \end{aligned}$$
(2)

Therefore, \(\eta (T(G {\setminus } u,v), {\mathbf {x}} \oplus {\mathbf {w}})\) divides \(\eta (T(G,u) {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}})\) for all \(v \in N(u)\). By induction \(\mu (G {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}})\) divides \(\eta (T(G {\setminus } u,v), {\mathbf {x}} \oplus {\mathbf {w}})\) for all \(v \in N(u)\). Hence, \(\mu (G {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}})\) divides \(\eta (T(G,u) {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}})\), so by Lemma 2.12, \(\mu (G, {\mathbf {x}} \oplus {\mathbf {w}})\) divides \(\eta (T(G,u), {\mathbf {x}} \oplus {\mathbf {w}})\). \(\square \)

In [12], Godsil and Gutman proved the following relationship between the univariate matching polynomial \(\mu (G,t)\) of a graph G and the characteristic polynomial \(\chi (A,t)\) of its adjacency matrix A

$$\begin{aligned} \displaystyle \chi (A,t) = \sum _{C} (-2)^{\text {comp}(C)} \mu (G {\setminus } C, t), \end{aligned}$$

where the sum ranges over all subgraphs C (including \(C = \emptyset \)) in which each component is a cycle of degree 2 and \(\text {comp}(C)\) is the number of connected components of C. In particular, if T is a tree, then the only such subgraph is \(C = \emptyset \), and therefore

$$\begin{aligned} \displaystyle \chi (A,t) = \mu (T,t). \end{aligned}$$

Next, we will derive a multivariate analogue of this relationship for trees.

Lemma 2.14

Let \(T = (V,E)\) be a tree. Then, \(\mu (T, {\mathbf {x}} \oplus {\mathbf {w}})\) has a definite determinantal representation.

Proof

Let \(X = \text {diag}({\mathbf {x}})\) and \(A = (A_{ij})\) be the matrix

$$\begin{aligned} A_{ij} = {\left\{ \begin{array}{ll} w_{ij} &{} \text { if }\quad ij \in E(T) \\ 0 &{} \text { otherwise} \end{array}\right. } \end{aligned}$$

for all \(i,j \in V(T)\). If \(\sigma \in \text {Sym}(V(T))\) is an involution (i.e \(\sigma ^2 = id\)), then clearly \(A_{j \sigma (j)} = w_{j\sigma (j)} = A_{\sigma (j) \sigma ^2(j)}\) since A is symmetric. Hence by acyclicity of trees, we have that

$$\begin{aligned} \displaystyle \det (X + A)&= \sum _{\sigma \in \text {Sym}(V(T))} \text {sgn}(\sigma ) \prod _{i \in V(T)} (X_{i \sigma (i)} + A_{i \sigma (i)}) \\&= \sum _{S \subseteq V(T)} \prod _{i \in V(T) {\setminus } S} x_i \sum _{\begin{array}{c} \sigma \in \text {Sym}(S) \\ \sigma (j) \ne j \forall j \in S \\ \sigma ^2 = \text {id} \end{array}} \text {sgn}(\sigma ) \prod _{j \in S} A_{j \sigma (j)} \\&= \sum _{S \subseteq V(T)} \prod _{i \in V(T) {\setminus } S} x_i \sum _{\begin{array}{c} M \in {\mathcal {M}}(T[S])\\ M \text { perfect} \end{array}}(-1)^{|M|} \prod _{jk \in M} w_{jk}^2 \\&= \sum _{M \in {\mathcal {M}}(T)} (-1)^{|M|} \prod _{i \not \in V(M)} x_i \prod _{jk \in M} w_{jk}^2&\\&= \mu (T, {\mathbf {x}} \oplus {\mathbf {w}}). \end{aligned}$$

Write

$$\begin{aligned} \displaystyle X + A = \sum _{i \in V(T)} x_i E_{ii} + \sum _{ij \in E(T)} w_{ij} (E_{ij} + E_{ji}), \end{aligned}$$

where \(\{E_{ij} : i,j \in V(T)\}\) denotes the standard basis for the vector space of all real \(|V(T)| \times |V(T)|\) matrices. Evaluated at \(\mathbf {e}= {\mathbf {1}} \oplus {\mathbf {0}}\), we obtain the identity matrix I which is positive definite. \(\square \)

Remark 2.15

The proof of Lemma 2.14 is not dependent on T being connected so the statement remains valid for arbitrary undirected acyclic graphs (i.e. forests).

We now have all the ingredients to prove our main theorem.

Theorem 2.16

The hyperbolicity cone of \(\mu (G, {\mathbf {x}} \oplus {\mathbf {w}})\) is spectrahedral.

Proof

The proof is by induction on the number of vertices of G. For the base case we have \(\mu (G, \mathbf {x}\oplus \mathbf {w}) = x_v\), so \(\varLambda _{+} = \{ x \in \mathbb {R}: x \ge 0 \}\) which is clearly spectrahedral. Assume G contains more than one vertex. If \(G = G_1 \sqcup G_2\) for some non-empty graphs \(G_1,G_2\), then \(\varLambda _{++}(\mu (G_i, \mathbf {x}\oplus \mathbf {w}))\) is spectrahedral by induction for \(i = 1,2\). Therefore,

$$\begin{aligned} \displaystyle \varLambda _{++}(\mu (G, \mathbf {x}\oplus \mathbf {w}))&= \varLambda _{++}(\mu (G_1 \sqcup G_2, \mathbf {x}\oplus \mathbf {w})) \\ {}&= \varLambda _{++} \left( \mu (G_1, \mathbf {x}\oplus \mathbf {w})\mu (G_1, \mathbf {x}\oplus \mathbf {w}) \right) \\&= \varLambda _{++}(\mu (G_1, \mathbf {x}\oplus \mathbf {w})) \cap \varLambda _{++}(\mu (G_2, \mathbf {x}\oplus \mathbf {w})) \end{aligned}$$

showing that \(\varLambda _{++}(\mu (G, \mathbf {x}\oplus \mathbf {w}))\) is spectrahedral. We may therefore assume G is connected. Let \(u \in V(G)\). Since G is connected and has size greater than one, \(N(u) \ne \emptyset \). By Lemma 2.13, we may define the polynomial

$$\begin{aligned} q_{G,u}(\mathbf {x}\oplus \mathbf {w}) = \frac{\eta (T(G,u), \mathbf {x}\oplus \mathbf {w})}{\mu (G, \mathbf {x}\oplus \mathbf {w})} \end{aligned}$$

for each graph G and \(u \in V(G)\). We want to show that

$$\begin{aligned} \varLambda _{++}(\mu (G, \mathbf {x}\oplus \mathbf {w})) \subseteq \varLambda _{++}(q_{G,u}(\mathbf {x}\oplus \mathbf {w})). \end{aligned}$$

By Lemma 2.12, we have that

$$\begin{aligned} \displaystyle q_{G,u}({\mathbf {x}} \oplus {\mathbf {w}}) \mu (G {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}} ) = \eta (T(G,u) {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}}). \end{aligned}$$

Fixing \(v \in N(u)\) it follows using (2) that

$$\begin{aligned} \displaystyle \frac{q_{G,u}({\mathbf {x}} \oplus {\mathbf {w}}) }{q_{G {\setminus } u,v}({\mathbf {x}} \oplus {\mathbf {w}})}&= \frac{q_{G,u}({\mathbf {x}} \oplus {\mathbf {w}}) \mu (G {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}}) }{q_{G {\setminus } u,v}({\mathbf {x}} \oplus {\mathbf {w}}) \mu (G {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}})} \\&= \frac{\eta (T(G,u) {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}} )}{ \eta (T(G {\setminus } u, v), {\mathbf {x}} \oplus {\mathbf {w}})} \\&= \prod _{w \in N(u) {\setminus } v} \eta (T(G {\setminus } u, w), {\mathbf {x}} \oplus {\mathbf {w}}) \\&= \prod _{w \in N(u) {\setminus } v} q_{G {\setminus } u,w}({\mathbf {x}} \oplus {\mathbf {w}}) \mu (G {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}}). \end{aligned}$$

Note that

$$\begin{aligned} \frac{\partial }{\partial x_u} \mu (G, {\mathbf {x}} \oplus {\mathbf {w}}) = \mu (G {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}}). \end{aligned}$$

Therefore by Lemma 1.2,

$$\begin{aligned} \displaystyle \varLambda _{++}(\mu (G, {\mathbf {x}} \oplus {\mathbf {w}})) \subseteq \varLambda _{++}(\mu (G {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}})) \subseteq \varLambda _{++}(q_{G {\setminus } u,w}({\mathbf {x}} \oplus {\mathbf {w}})) \end{aligned}$$

for all \(w \in N(u)\) where the last inclusion follows by inductive hypothesis. Hence,

$$\begin{aligned} \displaystyle \varLambda _{++}(\mu (G, {\mathbf {x}} \oplus {\mathbf {w}}))&\subseteq \bigcap _{w \in N(u)} \varLambda _{++} (q_{G {\setminus } u,w}(\mathbf {x}\oplus \mathbf {w})) \cap \varLambda _{++} \left( \mu (G {\setminus } u, \mathbf {x}\oplus \mathbf {w}\right) ) \\&= \varLambda _{++} \left( q_{G {\setminus } u, v}({\mathbf {x}} \oplus {\mathbf {w}}) \prod _{w \in N(u) {\setminus } v} q_{G {\setminus } u,w}({\mathbf {x}} \oplus {\mathbf {w}}) \mu (G {\setminus } u, {\mathbf {x}} \oplus {\mathbf {w}}) \right) \\&= \varLambda _{++}(q_{G,u}(\mathbf {x}\oplus \mathbf {w})). \end{aligned}$$

Finally by Lemma 2.14, \(\eta (T(G,u), {\mathbf {x}} \oplus {\mathbf {w}})\) has a definite determinantal representation. Hence, the theorem follows by induction. \(\square \)

Remark 2.17

To show that a hyperbolic polynomial h has a spectrahedral hyperbolicity cone it is by Theorem 2.16 sufficient to show that h can be realized as a factor of a matching polynomial \(\mu (G, {\mathbf {x}} \oplus {\mathbf {w}})\) with \(\varLambda _{++}(h, {\mathbf {e}}) \subseteq \varLambda _{++} \left( \frac{\mu (G, {\mathbf {x}} \oplus {\mathbf {w}})}{h}, {\mathbf {e}} \right) \) (possibly after a linear change of variables).

Fig. 2
figure 2

The star graph \(S_n\) labelled by vertex and edge variables

Full size image

The elementary symmetric polynomial\(e_d(\mathbf {x}) \in \mathbb {R}[x_1, \dots , x_n]\) of degree d in n variables is defined by

$$\begin{aligned} e_d(\mathbf {x}) = \sum _{\begin{array}{c} S \subseteq [n] \\ |S| = d \end{array}} \prod _{i \in S} x_i. \end{aligned}$$

The polynomials \(e_d(\mathbf {x})\) are hyperbolic (in fact stable) as a consequence of e.g Grace–Walsh–Szegő theorem (see [26, Thm 15.4]).

Example 2.18

The star graph, denoted \(S_n\), is given by the complete bipartite graph \(K_{1,n}\) with \(n+1\) vertices. As an application of Theorem 2.16, we show that several well-known instances of hyperbolic polynomials have spectrahedral hyperbolicity cones by realizing them as factors of the multivariate matching polynomial of \(S_n\) under some linear change of variables. With notation as in Fig. 2, using the recursion in Lemma 2.8, the multivariate matching polynomial of \(S_n\) is given by

$$\begin{aligned} \displaystyle \mu (S_n, {\mathbf {x}} \oplus {\mathbf {w}}) = \prod _{i = 1}^{n+1} x_i - \sum _{i=1}^n w_i^2 \prod _{\begin{array}{c} j = 1 \\ j \ne i \end{array}}^{n} x_j. \end{aligned}$$
  1. 1.

    For \(h({\mathbf {x}}) = e_{n-1}({\mathbf {x}})\) consider the linear change of variables \(x_n \mapsto -x_n\) and \(w_i \mapsto x_n\) for \(i = 1, \dots , n-1\). Then, \(\mu (S_{n-1}, {\mathbf {x}} \oplus {\mathbf {w}}) \mapsto -x_n e_{n-1}({\mathbf {x}})\). Clearly, \(\varLambda _{++}(e_{n-1}({\mathbf {x}}), {\mathbf {1}}) \subseteq \varLambda _{++}(x_n, {\mathbf {1}})\). The spectrahedrality of \(\varLambda _{++}(e_{n-1}(\mathbf {x}), {\mathbf {1}})\) was first proved by Sanyal in [31].

  2. 2.

    For \(h({\mathbf {x}}) = e_{2}({\mathbf {x}})\) consider the linear change of variables \(x_i \mapsto e_1(x_1,\dots , x_n)\) and \(w_i \mapsto x_i\) for \(i = 1, \dots , n+1\). Then, \(\mu (S_{n}, {\mathbf {x}} \oplus {\mathbf {w}}) \mapsto 2e_1({\mathbf {x}})^{n-1}e_{2}({\mathbf {x}})\). Since \(D_{{\mathbf {1}}} e_2(\mathbf {x}) = (n-1)e_1(\mathbf {x})\), Lemma 1.2 implies that \(\varLambda _{++}(e_2(\mathbf {x}), {\mathbf {1}}) \subseteq \varLambda _{++}(e_1(\mathbf {x}), {\mathbf {1}})\). Hence, \(\varLambda _{++}(e_2(\mathbf {x}), {\mathbf {1}})\) is spectrahedral.

  3. 3.

    Let \(h({\mathbf {x}}) = x_n^2 - x_{n-1}^2 - \cdots - x_{1}^2\). Recall that \(\varLambda _{++}(h, {\mathbf {e}})\) is the Lorentz cone where \({\mathbf {e}} = (0, \dots , 0,1)\). Consider the linear change of variables \(x_i \mapsto x_n\) and \(w_i \mapsto x_{i}\) for \(i = 1, \dots , n\). Then, \(\mu (S_{n-1}, {\mathbf {x}} \oplus {\mathbf {w}}) \mapsto x_n^n - \sum _{i = 1}^{n-1} x_{i}^2 x_n^{n-2} = x_n^{n-2}h({\mathbf {x}})\). Clearly, \(\varLambda _{++}(h, {\mathbf {e}}) \subseteq \varLambda _{++}(x_n^{n-2}, {\mathbf {e}})\). Hence, the Lorentz cone is spectrahedral. Of course this (and the preceding example) also follow from the fact that all quadratic hyperbolic polynomials have spectrahedral hyperbolicity cone [28].

Hyperbolicity cones of elementary symmetric polynomials have been studied by Zinchenko [34], Sanyal [31] and Brändén [5]. Brändén proved that all hyperbolicity cones of elementary symmetric polynomials are spectrahedral. As an application of Theorem 2.16, we give a new proof of this fact using matching polynomials.

Fig. 3
figure 3

The length k-truncated path tree \(T_{n,k}\) of \(K_n\) labelled by linear change of variables

Full size image

Theorem 2.19

Hyperbolicity cones of elementary symmetric polynomials are spectrahedral.

Proof

For a subset \(S \subseteq [n]\), we shall use the notation

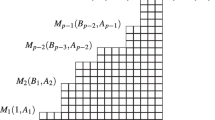
$$\begin{aligned} \displaystyle e_k(S) = \sum _{\begin{array}{c} T \subseteq S \\ |T| = k \end{array}} \prod _{j \in T} x_j. \end{aligned}$$

We show that \(e_k({\mathbf {x}}) = e_k([n])\) divides the multivariate matching polynomial of the length k-truncated path tree \(T_{n,k}\) of the complete graph \(K_n\) rooted at a vertex v after a linear change of variables. Let \((C_k)_{k \ge 0}\) denote the real sequence defined by

$$\begin{aligned} \displaystyle C_{0} = 1, \,\, C_{1} = 1, \,\, C_k = \prod _{j = 0}^{\lfloor k/2 \rfloor - 1} \frac{k - 2j}{k - 2j-1} \text { for } k \ge 2, \end{aligned}$$

so that

$$\begin{aligned} \displaystyle C_{k}C_{k-1} = k \text { for all } k \ge 1. \end{aligned}$$

Consider the family

$$\begin{aligned} \displaystyle M_{S,k,i} = \mu (T_{|S|, k}, \phi _{S,k,i}({\mathbf {x}} \oplus {\mathbf {w}})) \end{aligned}$$

of multivariate matching polynomials where \(i \in S, k \in {\mathbb {N}}\) and \(\phi _{S,k,i}\) is the linear change of variables defined recursively (see Fig. 3) via

  1. 1.

    \(\phi _{S,0,i}\) is the map \(x_v \mapsto e_1(S)\) for all \(S \subseteq [n]\) and \(i \in S\).

  2. 2.

    \(x_{v} \mapsto L_{S,k,i}\) if \(k \ge 1\) where

    $$\begin{aligned} L_{S,k,i} = \frac{1}{C_{k-1}}e_1(S {\setminus } i) + C_k x_i \end{aligned}$$

    and \(x_v\) is the variable corresponding to the root of \(T_{n,k}\).

  3. 3.

    \(w_{e_j} \mapsto x_j\) for \(j \in S {\setminus } i\) where \(w_{e_j}\) are the variables corresponding to the edges \(e_j\) incident to the root of \(T_{n,k}\).

  4. 4.

    For each \(j \in S {\setminus } i\) make recursively the linear substitutions \(\phi _{S {\setminus } i, k-1, j}\), respectively, to the variables corresponding to the j-indexed copies of the subtrees of \(T_{n,k}\) isomorphic to \(T_{n-1,k-1}\).

We claim

$$\begin{aligned} \displaystyle M_{S,0,i}&= e_1(S), \\ M_{S,k,i}&= \frac{C_k e_k(S)}{e_{k-1}(S {\setminus } \{i\})} \prod _{j \in S {\setminus } \{i\}} M_{S {\setminus } i, k-1, j} \end{aligned}$$

for all \(S \subseteq [n], i \in S\) and \(k \in {\mathbb {N}}\) by induction on k. Clearly, \(M_{S,0,i} = e_1(S)\) since \(\mu (T_{n,0}, {\mathbf {x}} \oplus {\mathbf {w}}) = x_v\). By Lemma 2.8 and induction, we have

$$\begin{aligned} \displaystyle&M_{S,k,i} \\&= L_{S,k,i} \prod _{s \in S {\setminus } \{i \}} M_{S {\setminus } i, k - 1, s} - \sum _{j \in S {\setminus } i} x_j^2 \prod _{s \in S {\setminus } \{i,j\}} M_{S {\setminus } i, k - 1, s} M_{S {\setminus } \{i,j \}, k - 2, s}\\&= \left( \frac{1}{C_{k-1}}e_1(S {\setminus } i) + C_kx_i - \sum _{j \in S {\setminus } \{i\}} x_j^2 \frac{e_{k-2}(S {\setminus } \{i,j \})}{C_{k-1}e_{k-1}(S {\setminus } i)} \right) \prod _{s \in S {\setminus } \{i\}} M_{S {\setminus } i, k-1, s} \\&=\frac{1}{e_{k-1}(S {\setminus } i)} \left( \left( \frac{1}{C_{k-1}}e_1(S {\setminus } i) + C_k x_i \right) e_{k-1}(S {\setminus } i) - \frac{1}{C_{k-1}}\sum _{j \in S {\setminus } i} x_j^2 e_{k-2}(S {\setminus } \{i,j \}) \right) \\&\quad \times \prod _{s \in S {\setminus } \{i\}} M_{S {\setminus } i, k-1, s} \\&= \frac{1}{e_{k-1}(S {\setminus } i)} \left( \frac{k}{C_{k-1}} e_{k}(S {\setminus } i) + C_kx_i e_{k-1}(S {\setminus } i) \right) \prod _{s \in S {\setminus } \{i\}} M_{S {\setminus } i, k-1, s} \\&= \frac{C_k e_k(S)}{e_{k-1}(S {\setminus } i)} \prod _{s \in S {\setminus } \{i\}} M_{S {\setminus } i, k-1, s}. \end{aligned}$$

Unwinding the above recursion, it follows that \(M_{S,k,i}\) is of the form

$$\begin{aligned} \displaystyle M_{S,k,i} = C e_k(S) \prod _{\begin{array}{c} T \subseteq S {\setminus } i \\ |T| > |S| - k \end{array}} e_{k + |T| - |S|}(T)^{\alpha _T} \end{aligned}$$

for some constant C and exponents \(\alpha _T \in {\mathbb {N}}\) . Taking \(S = [n]\), we thus see that \(e_k({\mathbf {x}})\) is a factor of the multivariate matching polynomial \(M_{[n], k, n}\). It remains to show that

$$\begin{aligned} \displaystyle \varLambda _{++}(e_k({\mathbf {x}}), {\mathbf {1}}) \subseteq \varLambda _{++} \left( \frac{M_{[n],k,n}}{e_k({\mathbf {x}})}, {\mathbf {1}} \right) . \end{aligned}$$

for all \(k \le n\). By Lemma 1.2 above inclusion follows from the fact that

$$\begin{aligned} \displaystyle \varLambda _{++}(e_k(S), {\mathbf {1}}) \subseteq \varLambda _{++}(e_{k-1}(S), {\mathbf {1}}) \end{aligned}$$

for all \(k \ge 1\) since \(D_{{\mathbf {1}}} e_{k}(S) = (|S|-k)e_{k-1}(S)\), and from the fact that

$$\begin{aligned} \displaystyle \varLambda _{++}(e_k(S), {\mathbf {1}}) \subseteq \varLambda _{++} \left( e_k(T), {\mathbf {1}} \right) \end{aligned}$$

for all \(T \subseteq S\) since \(e_k(T) = \left( \prod _{i \in S {\setminus } T} \frac{\partial }{\partial x_i} \right) e_k(S)\). Hence \(\varLambda _{++}(e_k({\mathbf {x}}), {\mathbf {1}})\) is spectrahedral by Theorem 2.16. \(\square \)

3 Hyperbolicity cones of multivariate independence polynomials

A subset \(I \subseteq V(G)\) is independent if no two vertices of I are adjacent in G. Let \({\mathcal {I}}(G)\) denote the set of all independent sets in G, and let i(G, k) denote the number of independent sets in G of size k. By convention, \(i(G,0) = 1\). The (univariate) independence polynomial is defined by

$$\begin{aligned} I(G,t) = \sum _{k \ge 0} i(G,k) t^k. \end{aligned}$$

The line graphL(G) of G is the graph having vertex set E(G) and where two vertices in L(G) are adjacent if and only if the corresponding edges in G are incident. It follows that \(\mu (G,t) = t^{|V(G)|}I(L(G),-t^{-2})\). Therefore, the independence polynomial can be viewed as a generalization of the matching polynomial. In contrast to the matching polynomial, the independence polynomial of a graph is not real-rooted in general. However, Chudnovsky and Seymour [8] proved that I(G, t) is real-rooted if G is claw free, that is, if G has no induced subgraph isomorphic to the complete bipartite graph \(K_{1,3}\). The theorem was later generalized by Engström to graphs with weighted vertices.

Theorem 3.1

(Engström [9]) Let G be a claw-free graph and \(\varvec{\lambda } = (\lambda _v)_{v \in V(G)}\) a sequence of non-negative vertex weights. Then, the polynomial

$$\begin{aligned} I_{\varvec{\lambda }}(G,t) = \sum _{I \in {\mathcal {I}}(G)} \left( \prod _{v \in I} \lambda _v \right) t^{|I|} \end{aligned}$$

is real-rooted.

A full characterization of the graphs for which I(G, t) is real-rooted remains an open problem.

A natural multivariate analogue of the independence polynomial is given by

$$\begin{aligned} I(G, \mathbf {x}) = \sum _{I \in {\mathcal {I}}(G)} \prod _{v \in I} x_v. \end{aligned}$$

Leake and Ryder [21] define a strictly weaker notion of stability which they call same-phase stability. A polynomial \(p(\mathbf {z}) \in \mathbb {R}[z_1, \dots , z_n]\) is (real) same-phase stable if for every \(\mathbf {x}\in \mathbb {R}_+^n\), the univariate polynomial \(p(t \mathbf {x})\) is real-rooted. The authors prove that \(I(G, \mathbf {x})\) is same-phase stable if and only if G is claw free. In fact, the same-phase stability of \(I(G, \mathbf {x})\) is an immediate consequence of Theorem 3.1.

The added variables in a homogeneous multivariate independence polynomial should preferably have labels carrying combinatorial meaning in the graph. For line graphs, it is additionally desirable to maintain a natural correspondence with the homogeneous multivariate matching polynomial \(\mu (G, \mathbf {x}\oplus \mathbf {w})\). Unfortunately, we have not found a hyperbolic definition that satisfies both of the above properties. We have thus settled for the following definition.

Definition 3.2

Let \(\mathbf {x}= (x_v)_{v \in V}\) and t be indeterminates. Define the homogeneous multivariate independence polynomial\(I(G,\mathbf {x}\oplus t) \in \mathbb {R}[\mathbf {x},t]\) by

$$\begin{aligned} I(G,\mathbf {x}\oplus t) = \sum _{I \in {\mathcal {I}}(G)} (-1)^{|I|} \left( \prod _{v \in I} x_v^2 \right) t^{2|V(G)| -2 |I|}. \end{aligned}$$

Lemma 3.3

If G is a claw-free graph, then \(I(G, \mathbf {x}\oplus t)\) is a hyperbolic polynomial with respect to \(\mathbf {e}= (0, \dots , 0,1) \in \mathbb {R}^{V(G)} \times \mathbb {R}\).

Proof

First note that \(I(G, \mathbf {e}) = 1 \ne 0\). Let \(\mathbf {x}\oplus t \in \mathbb {R}^{V(G)} \times \mathbb {R}\) and \(\lambda _v = x_v^2\) for all \(v \in V(G)\). Then

$$\begin{aligned} I(G, s\mathbf {e}- \mathbf {x}\oplus t) = (s-t)^{2|V(G)|} I_{\varvec{\lambda }}(G, -(s-t)^{-2}). \end{aligned}$$

By Theorem 3.1 the polynomial \(I_{\varvec{\lambda }}(G, s)\) is real-rooted. Clearly, all roots are negative which implies \(I_{\varvec{\lambda }}(G, -s^{-2})\) is real-rooted. Hence, the univariate polynomial \(s \mapsto I(G, s\mathbf {e}- \mathbf {x}\oplus t)\) is real-rooted which shows that \(I(G, \mathbf {x}\oplus t)\) is hyperbolic with respect to \(\mathbf {e}\). \(\square \)

An induced clique K in G is called a simplicial clique if for all \(u \in K\) the induced subgraph \(N[u] \cap (G {\setminus } K)\) of \(G {\setminus } K\) is a clique. In other words, the neighbourhood of each \(u \in K\) is a disjoint union of two induced cliques in G. Furthermore, a graph G is said to be simplicial if G is claw free and contains a simplicial clique.

In this section, we prove Conjecture 1.6 for the polynomial \(I(G, \mathbf {x}\oplus t)\) when G is simplicial. The proof unfolds in a parallel manner to Theorem 2.16 by considering a different kind of path tree. Before the results can be stated, we must outline the necessary definitions from [21].

A connected graph G is a block graph if each 2-connected component is a clique. Given a simplicial graph G with a simplicial clique K, we recursively define a block graph \(T^{\boxtimes }(G,K)\) called the clique tree associated to G and rooted at K (see Fig. 4).

We begin by adding K to \(T^{\boxtimes }(G,K)\). Let \(K_u = N[u] {\setminus } K\) for each \(u \in K\). Attach the disjoint union \(\bigsqcup _{u \in K} K_u\) of cliques to \(T^{\boxtimes }(G,K)\) by connecting \(u \in K\) to every \(v \in K_u\). Finally, recursively attach \(T^{\boxtimes }(G{\setminus } K,K_u)\) to the clique \(K_u\) in \(T^{\boxtimes }(G,K)\) for every \(u \in K\). Note that the recursion is made well-defined by the following lemma.

Lemma 3.4

(Chudnovsky–Seymour [8]) Let G be a claw-free graph, and let K be a simplicial clique in G. Then, \(N[u] {\setminus } K\) is a simplicial clique in \(G {\setminus } K\) for all \(u \in K\).

Fig. 4
figure 4

A simplicial graph G and its associated relabelled clique tree \(T^{\boxtimes }(G,K)\) rooted at \(K = \{a,b,c \}\)

Full size image

It is well known that a graph is the line graph of a tree if and only if it is a claw-free block graph [16, Thm 8.5]. In [21], it was demonstrated that the block graph \(T^{\boxtimes }(G,K)\) is the line graph of a certain induced path tree\(T^{\angle }(G,K)\). Its precise definition is not important to us, but we remark that it is a subtree of the usual path tree defined in Sect. 2 that avoids traversed neighbours. This enables us to find a definite determinantal representation of \(I(T^{\boxtimes }(G,K), \mathbf {x}\oplus t)\) via Lemma 2.14. The second important fact is that \(I(G, \mathbf {x})\) divides \(I(T^{\boxtimes }(G,K), \mathbf {x})\) where \(T^{\boxtimes }(G,K)\) is relabelled according to the natural graph homomorphism \(\phi _K: T^{\boxtimes }(G,K) \rightarrow G\). Hence using the recursion provided by the simplicial structure of G, we have almost all the ingredients to finish the proof of Conjecture 1.6 for \(I(G, \mathbf {x}\oplus t)\).

Lemma 3.5

(Leake–Ryder [21]) For any simplicial graph G, and any simplicial clique \(K \le G\), we have

$$\begin{aligned} L(T^{\angle }(G,K)) \cong T^{\boxtimes }(G,K). \end{aligned}$$

The following theorem is a generalization of Godsil’s divisibility theorem for matching polynomials. It can be proved in a similar manner by induction using the recursive structure of simplicial graphs and removing cliques instead of vertices. For the proof to go through in the homogeneous setting, we must replace the usual recursion by

$$\begin{aligned} I(G, \mathbf {x}\oplus t) = t^{2|K|} I(G {\setminus } K, \mathbf {x}\oplus t) - \sum _{v \in K} t^{2|N(v)|} x_v^2 I(G {\setminus } N[v], \mathbf {x}\oplus t). \end{aligned}$$

Theorem 3.6

(Leake–Ryder [21]) Let K be a simplicial clique of the simplicial graph G. Then,

$$\begin{aligned} \frac{I(G, \mathbf {x}\oplus t)}{I(G {\setminus } K, \mathbf {x}\oplus t)} = \frac{I(T^{\boxtimes }(G,K), \mathbf {x}\oplus t)}{I(T^{\boxtimes }(G,K) {\setminus } K, \mathbf {x}\oplus t)}, \end{aligned}$$

where \(T^{\boxtimes }(G,K)\) is relabelled according to the natural graph homomorphism \(\phi _K: T^{\boxtimes }(G,K) \rightarrow G\). Moreover, \(I(G, \mathbf {x}\oplus t)\) divides \(I(T^{\boxtimes }(G,K), \mathbf {x}\oplus t)\).

The following lemma ensures the hyperbolicity cones behave well under vertex deletion.

Lemma 3.7

Let \(v \in V(G)\). Then, \(\varLambda _{++}(I(G, \mathbf {x}\oplus t)) \subseteq \varLambda _{++}(I(G {\setminus } v, \mathbf {x}\oplus t))\).

Proof

Let \(\mathbf {x}\oplus t \in \mathbb {R}^{V(G)} \times \mathbb {R}\) and \(\mathbf {e}= (0, \dots , 0,1)\). By Lemma 3.3 the polynomials \(s\mapsto I(G, s\mathbf {e}- \mathbf {x}\oplus t)\) and \(s \mapsto I(G{\setminus } v, s\mathbf {e}- \mathbf {x}\oplus t)\) are both real-rooted. Denote their roots by \(\alpha _1, \dots , \alpha _{2n}\) and \(\beta _1, \dots , \beta _{2n-2}\), respectively, where \(n = |V(G)|\). We claim that

$$\begin{aligned} \min _i \alpha _i \le \min _{i} \beta _i \le \max _{i} \beta _i \le \max _i \alpha _i \end{aligned}$$

by induction on the number of vertices of G. Indeed, the claim is vacuously true if \(|V(G)| = 1\). Suppose therefore \(|V(G)| > 1\). If G is not connected, then \(G = G_1 \sqcup G_2\) for some non-empty graphs \(G_1,G_2\). Without loss assume \(v \in G_1\). Then, \(G {\setminus } v = (G_1{\setminus } v) \sqcup G_2\). By induction, the claim holds for the pair \(G_1\) and \(G_1 {\setminus } v\). This implies the claim for G and \(G {\setminus } v\) since \(I(G, \mathbf {x}\oplus t)\) is multiplicative with respect to disjoint union. We may therefore assume G is connected. Thus, \(G {\setminus } N[v]\) is of strictly smaller size than \(G {\setminus } v\). We have

$$\begin{aligned} \displaystyle I(G, \mathbf {x}\oplus t) = t^2 I(G {\setminus } v, \mathbf {x}\oplus t) - x_v^2 t^{2|N(v)|} I(G {\setminus } N[v], \mathbf {x}\oplus t). \end{aligned}$$
(3)

By induction, the maximal root \(\gamma \) of \(I(G {\setminus } N[v], s\mathbf {e}- \mathbf {x}\oplus t)\) is less than the maximal root \(\beta \) of \(I(G {\setminus } v, s\mathbf {e}- \mathbf {x}\oplus t)\). Since \(I(G {\setminus } N[v], s\mathbf {e}- \mathbf {x}\oplus t)\) is an even degree polynomial with positive leading coefficient we have that \(I(G {\setminus } N[v], s \mathbf {e}- \mathbf {x}\oplus t) \ge 0\) for all \(s \ge \gamma \). By (3), this implies that \(I(G, \beta \mathbf {e}- \mathbf {x}\oplus t) \le 0\). Hence, \(\max _{i} \beta _i \le \max _{i} \alpha _i\) since \(I(G, s \mathbf {e}- \mathbf {x}\oplus t) \rightarrow \infty \) as \(s \rightarrow \infty \). Since each of the terms involved in the polynomials \(I(G, s \mathbf {e}- \mathbf {x}\oplus t)\) and \(I(G {\setminus } v, s \mathbf {e}- \mathbf {x}\oplus t)\) has even degree in \(s-t\), their respective roots are symmetric about \(s = t\). Hence, \(\min _i \alpha _i \le \min _i \beta _i\) proving the claim. Finally, if \(\mathbf {x}_0 \oplus t_0 \in \varLambda _{++}(I(G, \mathbf {x}\oplus t))\), then \(\min _i \alpha _i > 0\) so by the claim \(\min _i \beta _i > 0\) showing that \(\mathbf {x}_0 \oplus t_0 \in \varLambda _{++}(I(G {\setminus } v, \mathbf {x}\oplus t))\). This proves the lemma. \(\square \)

Remark 3.8

Since

$$\begin{aligned} I(G, \mathbf {x}\oplus t) \biggr |_{x_v = 0} = t^{2} I(G{\setminus } v, \mathbf {x}\oplus t), \end{aligned}$$

we see by Lemma 3.7 that setting vertex variables equal to zero relaxes the hyperbolicity cone.

Theorem 3.9

If G is a simplicial graph, then the hyperbolicity cone of \(I(G, \mathbf {x}\oplus t)\) is spectrahedral.

Proof

Let K be a simplicial clique of G. Arguing by induction as in Theorem 2.16, using the clique tree \(T^{\boxtimes }(G,K)\) instead of the path tree T(G, u), and invoking Theorem 3.6 we get a factorization

$$\begin{aligned} \displaystyle q_{G,K}(\mathbf {x}\oplus t) = q_{G {\setminus } K, K_v}(\mathbf {x}\oplus t) \prod _{w \in K {\setminus } v} q_{G{\setminus } K, K_w}(\mathbf {x}\oplus t) I(G {\setminus } K, \mathbf {x}\oplus t), \end{aligned}$$
(4)

where \(v \in K\) is fixed, \(K_w = N[w]{\setminus } K\) and

$$\begin{aligned} q_{G, K}(\mathbf {x}\oplus t)I(G, \mathbf {x}\oplus t)&= I(T^{\boxtimes }(G,K), \mathbf {x}\oplus t), \\ q_{G {\setminus } K, K_w}(\mathbf {x}\oplus t) I(G {\setminus } K, \mathbf {x}\oplus t)&= I(T^{\boxtimes }(G {\setminus } K,K_w), \mathbf {x}\oplus t) \end{aligned}$$

for \(w \in K\). Repeated application of Lemma 3.7 gives

$$\begin{aligned} \varLambda _{++}(I(G, \mathbf {x}\oplus t)) \subseteq \varLambda _{++}(I(G {\setminus } K, \mathbf {x}\oplus t)). \end{aligned}$$

By factorization (4) and induction, we hence get the desired cone inclusion

$$\begin{aligned} \varLambda _{++}(I(G, \mathbf {x}\oplus t)) \subseteq \varLambda _{++}(q_{G,K}(\mathbf {x}\oplus t)). \end{aligned}$$

Since \(L(T^{\angle }(G,K)) \cong T^{\boxtimes }(G,K)\) by Lemma 3.5 we see that

$$\begin{aligned} I(T^{\boxtimes }(G,K), \mathbf {x}\oplus t) = \mu (T^{\angle }(G,K), t{\mathbf {1}} \oplus \mathbf {x}). \end{aligned}$$

Hence, \(I(T^{\boxtimes }(G,K), \mathbf {x}\oplus t)\) has a definite determinantal representation by Lemma 2.14 proving the theorem. \(\square \)

4 Convolutions

If G is a simple undirected graph with adjacency matrix \(A = (a_{ij})\), then we may associate a signing \(\mathbf {s}= (s_{ij}) \in \{\pm 1 \}^{E(G)}\) to its edges. The symmetric adjacency matrix \(A^{\mathbf {s}} = (a_{ij}^s)\) of the resulting graph is given by \(a_{ij}^{\mathbf {s}} = s_{ij} a_{ij}\) for \(ij \in E(G)\) and \(a_{ij}^{\mathbf {s}} = 0\) otherwise. Godsil and Gutman [13] proved that

$$\begin{aligned} \mathop {{\mathbb {E}}}_{\mathbf {s}\in \{ \pm 1 \}^{E(G)}} \det \left( tI - A^{\mathbf {s}} \right) = \mu (G,t). \end{aligned}$$
(5)

In other words, the expected characteristic polynomial of an independent random signing of the adjacency matrix of a graph is equal to its matching polynomial. Therefore, the expected characteristic polynomial is real-rooted. This was one of the facts used by Marcus, Spielman and Srivastava [23] in proving that there exist infinite families of regular bipartite Ramanujan graphs. Since then, several other families of characteristic polynomials have been identified with real-rooted expectation (see, e.g. [15, 25]). Such families are called interlacing families, based on the fact that there exists a common root interlacing polynomial if and only if every convex combination of the family is real-rooted. The method of interlacing families has been successfully applied to other contexts, in particular to the affirmative resolution of the Kadison–Singer problem [24].

In this section, we define a convolution of multivariate determinant polynomials and show that it is hyperbolic as a direct consequence of a more general theorem by Brändén [6]. In particular, this convolution can be viewed as a generalization of the fact that the expectation in (5) is real-rooted. Namely, we show that the expected characteristic polynomial over any finite set of independent random edge weightings is real-rooted barring certain adjustments to the weights of the loop edges.

Recall that every symmetric matrix may be identified with the adjacency matrix of an undirected weighted graph (with loops).

Definition 4.1

Let \(W \subseteq \mathbb {R}\) be a finite set. Given a real symmetric matrix A and a vector \({\mathbf {w}} \in W^{\left( {\begin{array}{c}n\\ 2\end{array}}\right) }\), define a weighting of A to be a symmetric matrix \(A^{{\mathbf {w}}} = (a_{ij}^{{\mathbf {w}}})\) given by

$$\begin{aligned} a_{ij}^{\mathbf {w}} = {\left\{ \begin{array}{ll} w_{ij} a_{ij} &{} \text { if }\quad i < j \\ \sum _{k = 1}^i a_{ik} + \sum _{k = i+1}^n w_{ik}^2 a_{ik} &{} \text { if }\quad i = j \end{array}\right. }. \end{aligned}$$

Definition 4.2

Let \(X = (x_{ij})_{i,j=1}^n\) and \(Y = (y_{ij})_{i,j=1}^n\) be symmetric matrices in variables \(\mathbf {x}= (x_{ij})_{i \le j}\) and \(\mathbf {y}= (y_{ij})_{i \le j}\), respectively. Let \(W \subseteq \mathbb {R}\) be a finite set. We define the convolution

$$\begin{aligned} \displaystyle \det (X) {{\mathrm{*}}}_{W} \det (Y) = \mathop {{\mathbb {E}}}_{\mathbf {w}_1, \mathbf {w}_2 \in W^{\left( {\begin{array}{c}n\\ 2\end{array}}\right) }} \det ( X^{\mathbf {w}_1} + Y^{\mathbf {w}_2}) \in {\mathbb {R}}[\mathbf {x}, \mathbf {y}]. \end{aligned}$$

We have the following general fact about hyperbolic polynomials.

Theorem 4.3

(Brändén [6]) Let \(h(\mathbf {x})\) be a hyperbolic polynomial with respect to \(\mathbf {e}\in {\mathbb {R}}^n\); let \(V_1, \dots , V_m\) be finite sets of vectors of rank at most one in \(\varLambda _+\). For \({\mathbf {V}} = (\mathbf {v}_1, \dots , \mathbf {v}_m) \in V_1 \times \cdots \times V_m\), let

$$\begin{aligned} \displaystyle g({\mathbf {V}};t) = h(t\mathbf {e}+ \mathbf {u}-\alpha _1 \mathbf {v}_1 - \cdots - \alpha _m \mathbf {v}_m) \end{aligned}$$

where \(\mathbf {u}\in {\mathbb {R}}^n\) and \((\alpha _1, \dots , \alpha _m) \in {\mathbb {R}}^{m}\). Then, \(\displaystyle \mathop {{\mathbb {E}}}_{{\mathbf {V}} \in V_1 \times \cdots \times V_m} g({\mathbf {V}};t)\) is real-rooted.

Proposition 4.4

Let \(W \subseteq {\mathbb {R}}\) be a finite subset. Then, \(\det (X) {{\mathrm{*}}}_W \det (Y)\) is hyperbolic with respect to \(\mathbf {e}= I \oplus {\mathbf {0}}\) where I denotes the identity matrix.

Proof

Let \(h(X \oplus Y) = \det (X) {{\mathrm{*}}}_{W} \det (Y)\). We note that \(h(\mathbf {e}) = 1 \ne 0\). Let \(\delta _1, \dots , \delta _n\) denote the standard basis of \({\mathbb {R}}^n\). Put

$$\begin{aligned} V_{ij} = \{ \mathbf {v}_{ijw} : w \in W \} \end{aligned}$$

where \(\mathbf {v}_{ijw} = (\delta _{i} + w \delta _j) (\delta _{i} + w \delta _j)^{\mathrm{T}}\) for \(i < j\) and \(w \in W\). Note that \(\mathbf {v}_{ijw}\) is a rank one matrix belonging to the hyperbolicity cone of positive semidefinite matrices (with nonzero eigenvalue \(w^2+1\)). Letting \(\mathbf {u}= {\mathbf {0}}\) and \(\alpha _{ij}^X = x_{ij}, \alpha _{ij}^Y = y_{ij}\) for \(i < j\), we see that

$$\begin{aligned} \displaystyle h(t \mathbf {e}- X \oplus Y)&= \mathop {{\mathbb {E}}}_{\mathbf {w}_1, \mathbf {w}_2} \det (tI - X^{\mathbf {w}_1} - Y^{\mathbf {w}_2}) \\&= \mathop {{\mathbb {E}}}_{\begin{array}{c} \mathbf {v}_{ijw_1}, \mathbf {v}_{ijw_2} \in V_{ij} \\ i< j \end{array}} \det \left( tI + \mathbf {u}- \sum _{i < j} (\alpha _{ij}^X \mathbf {v}_{ijw_1} + \alpha _{ij}^Y \mathbf {v}_{ijw_2}) \right) , \end{aligned}$$

where the right hand side is a real-rooted polynomial in t by Theorem 4.3. Hence, \(\det (X) {{\mathrm{*}}}_W \det (Y)\) is hyperbolic with respect to \(\mathbf {e}\). \(\square \)

Remark 4.5

Taking \(W = \{ \pm 1 \}\) we see that \(a_{ii}^{{\mathbf {w}}} = \sum _{k=1}^n a_{ik}\) for all \({\mathbf {w}} \in W\) and \(i=1,\dots , n\). Therefore, setting \(\mathbf {u}= \text {diag}(d_1, \dots , d_n)\) where \(d_i = \sum _{j \ne i} (x_{ij} + y_{ij})\) in the proof of Proposition 4.4, we get that

$$\begin{aligned} \displaystyle \mathop {{\mathbb {E}}}_{\mathbf {s}_1, \mathbf {s}_2} \det (X^{\mathbf {s}_1} + Y^{\mathbf {s}_2}) \end{aligned}$$
(6)

is hyperbolic, where the expectation is taken over independent random signings of the matrices X and Y as in (5) without weighting the diagonal. This shows in particular that the expectation in (5) is real-rooted.

Corollary 4.6

Let \(W \subseteq \mathbb {R}\) be a finite subset and A a real symmetric \(n \times n\) matrix. Then,

$$\begin{aligned} \displaystyle \mathop {{\mathbb {E}}}_{\mathbf {w}\in W^{\left( {\begin{array}{c}n\\ 2\end{array}}\right) }} \det (tI - A^{\mathbf {w}}) \end{aligned}$$

is real-rooted.

Proof

By Corollary 4.4, the polynomial \(\det (Y) {{\mathrm{*}}}_W \det (X)\) is hyperbolic, so in particular \(\displaystyle t \mapsto \mathop {{\mathbb {E}}}_{\mathbf {w}} \det (tI - A^{\mathbf {w}})\) is real-rooted with \(X = {\mathbf {0}}\) and \(Y = A\). \(\square \)

Next, we see that convolution (6) over independent random signings can be realized as a convolution of multivariate matching polynomials. The proof is similar to that of the univariate identity (5) (cf [13]). Let \(G_X\) and \(G_Y\) denote the weighted graphs corresponding to the symmetric matrices X and Y.

Proposition 4.7

Let \(X = (x_{ij})_{i,j = 1}^n\) and \(Y = (y_{ij})_{i,j = 1}^n\) be symmetric matrices in variables \(\mathbf {x}= (x_{ij})_{i \le j}\) and \(\mathbf {y}= (y_{ij})_{i \le j}\). Then

$$\begin{aligned} \displaystyle&\mathop {{\mathbb {E}}}_{\mathbf {s}^{(1)}, \mathbf {s}^{(2)}} \det (X^{\mathbf {s}^{(1)}} + Y^{\mathbf {s}^{(2)}}) \\&= \sum _{S \subseteq [n]} (-1)^{|S|/2} \prod _{i \not \in S} (x_{ii} + y_{ii}) \sum _{S_1 \sqcup S_2 = S} \mu (G_X[S_1], {\mathbf {0}} \oplus {\mathbf {x}}) \mu (G_Y[S_2], {\mathbf {0}} \oplus {\mathbf {y}}) \end{aligned}$$

where the expectation is taken over independent random signings as in (5).

Proof

Expanding the convolution from the definition of the determinant, we have

$$\begin{aligned} \displaystyle&\mathop {{\mathbb {E}}}_{\mathbf {s}^{(1)}, \mathbf {s}^{(2)}} \det ( X^{\mathbf {s}^{(1)}} + Y^{\mathbf {s}^{(2)}}) \\&= \mathop {{\mathbb {E}}}_{\mathbf {s}^{(1)}, \mathbf {s}^{(2)}} \sum _{\sigma \in \mathfrak {S}_{n}} \text {sgn}(\sigma ) \prod _{i = 1}^{n} \left( X^{\mathbf {s}^{(1)}} + Y^{\mathbf {s}^{(2)}} \right) _{i \sigma (i)} \\&= \mathop {{\mathbb {E}}}_{\mathbf {s}^{(1)}, \mathbf {s}^{(2)}} \sum _{S \subseteq [n]} \prod _{i \not \in S} (x_{ii} + y_{ii}) \sum _{\begin{array}{c} \sigma \in \text {Sym}(S) \\ \sigma (j) \ne j \,\, \forall j \in S \end{array}} \text {sgn}(\sigma ) \prod _{j \in S} \left( s_{j \sigma (j)}^{(1)} x_{j \sigma (j)} + s_{j \sigma (j)}^{(2)} y_{j \sigma (j)} \right) \\&= \sum _{S \subseteq [n]} \prod _{i \not \in S} (x_{ii} + y_{ii}) \sum _{\begin{array}{c} \sigma \in \text {Sym}(S) \\ \sigma (j) \ne j \,\, \forall j \in S \end{array}} \text {sgn}(\sigma ) \sum _{S_1 \sqcup S_2 = S} \mathop {{\mathbb {E}}}_{\mathbf {s}^{(1)}} \prod _{j \in S_1} s_{j \sigma (j)}^{(1)} x_{j \sigma (j)} \mathop {{\mathbb {E}}}_{\mathbf {s}^{(2)}} \prod _{j \in S_2} s_{j \sigma (j) }^{(2)} y_{j \sigma (j)} \end{aligned}$$

Note the following regarding the random variables \(s_{ij}^{(k)}\), \(k = 1,2\):

  1. 1.

    \(s_{ij}^{(k)}\) appears with power at most two in each of the products.

  2. 2.

    The random variables \(s_{ij}^{(k)}\) are independent.

  3. 3.

    \(\mathop {{\mathbb {E}}} s_{ij}^{(k)} = 0\).

  4. 4.

    \(\mathop {{\mathbb {E}}} (s_{ij}^{(k)})^2 = 1\).

As a consequence, permutations with the following characteristics may be eliminated since they produce factors \(s_{ij}^{(k)}\) of power one making the term vanish:

  1. 1.

    \(\sigma \in \mathfrak {S}_n\) having no factorization \(\sigma = \sigma _1 \sigma _2\) for \(\sigma _i \in \text {Sym}(S_i)\), \(i = 1,2\).

  2. 2.

    \(\sigma \in \mathfrak {S}_n\) such that \(\sigma \) is not a complete product of disjoint transpositions.

This leaves us with products of fixed-point-free involutions in \(\text {Sym}(S_1)\) and \(\text {Sym}(S_2)\). Thus, the non-vanishing terms are those corresponding to perfect matchings on \(G_X[S_1]\) and \(G_Y[S_2]\). Hence,

$$\begin{aligned} \displaystyle \mathop {{\mathbb {E}}}_{\mathbf {s}^{(1)}, \mathbf {s}^{(2)}} \det \left( X^{\mathbf {s}^{(1)}} + Y^{\mathbf {s}^{(2)}}\right) = \sum _{S \subseteq [n]} \prod _{i \not \in S} (x_{ii} + y_{ii}) \sum _{S_1 \sqcup S_2 = S} P_1(\mathbf {x}) P_2(\mathbf {y}) \end{aligned}$$

where

$$\begin{aligned} \displaystyle P_1(\mathbf {x})&= \sum _{\begin{array}{c} \sigma _1 \in \text {Sym}(S_1) \\ \sigma _1(j) \ne j \,\, \forall j \in S_1 \end{array}} \text {sgn}(\sigma _1) \mathop {{\mathbb {E}}}_{\mathbf {s}^{(1)}} \prod _{i \in S_1} s_{i \sigma _1(i) }^{(1)} x_{i \sigma _1(i)} \\&= \sum _{ \begin{array}{c} M \in {\mathcal {M}}(G_X[S_1]) \\ M \text { perfect } \end{array}} (-1)^{|S_1|/2} \prod _{ij \in M} \mathop {{\mathbb {E}}}_{\mathbf {s}^{(1)}} (s_{ i j }^{(1)})^2 x_{i j}^2 \\&= (-1)^{|S_1|/2} \sum _{\begin{array}{c} M \in {\mathcal {M}}(G_X[S_1]) \\ M \text { perfect } \end{array}} \prod _{ij \in M} x_{ij}^2 \\&= (-1)^{|S_1|/2} \mu (G_X[S_1], {\mathbf {0}} \oplus {\mathbf {x}}) \end{aligned}$$

and similarly for \(P_2(\mathbf {y})\). \(\square \)

Remark 4.8

The expression in Proposition 4.7 may also be written

$$\begin{aligned} \displaystyle \displaystyle \mathop {{\mathbb {E}}}_{\mathbf {s}^{(1)}, \mathbf {s}^{(2)}} \det \left( X^{\mathbf {s}^{(1)}} + Y^{\mathbf {s}^{(2)}}\right) = \sum _{M \in {\mathcal {M}}(K_n)} (-1)^{|M|} \prod _{i \not \in V(M)} (x_{ii} + y_{ii}) \prod _{jk \in M} \left( x_{jk}^2 + y_{jk}^2\right) . \end{aligned}$$

Example 4.9

  1. 1.

    Let A be the adjacency matrix of a simple undirected graph G. Under the specialization \(X = tI\) and \(Y = -A\) in Proposition 4.7, we recover identity (5) of Godsil and Gutman.

  2. 2.

    Let A and B both be adjacency matrices of the complete graph \(K_n\). It is well known (see, e.g. [11]) that the number of perfect matchings in \(K_n\) is given by \((n-1)!!\) if n is even and 0 otherwise, where \((n)!! = n(n-2)(n-4)\cdots \). By Proposition 4.7 and a simple calculation it follows that

    $$\begin{aligned} \displaystyle \mathop {{\mathbb {E}}}_{\mathbf {s}^{(1)}, \mathbf {s}^{(2)}} \det ( tI + A^{\mathbf {s}^{(1)}} + B^{\mathbf {s}^{(2)}})&= \sum _{k = 0}^{\lfloor n/2 \rfloor } t^{n-2k} (-1)^k \left( {\begin{array}{c}n\\ 2k\end{array}}\right) \sum _{i+j = k} \left( {\begin{array}{c}2k\\ 2i\end{array}}\right) (2i-1)!!(2j-1)!! \\&= \sum _{k = 0}^{\lfloor n/2 \rfloor } t^{n-2k} (-1)^k \left( {\begin{array}{c}n\\ 2k\end{array}}\right) (2k-1)!! \left( \frac{3}{2} \right) ^k \\&= t^n \mu _{\frac{3}{2} {\mathbf {1}}}(K_n, t^{-1}{\mathbf {1}}). \end{aligned}$$

5 Concluding remarks

In Theorem 3.9, we proved Conjecture 1.6 for \(I(G, \mathbf {x}\oplus t)\) whenever G is a simplicial graph. An extension of the divisibility relation in Theorem 3.6 to all claw-free graphs would immediately extend Theorem 3.9 to all claw-free graphs.

An interesting extension of this work would be to study a family of stable graph polynomials introduced by Wagner [33] in a general effort to prove Heilmann–Lieb type theorems. Let \(G = (V,E)\) be a graph. For \(H \subseteq E\), let \(\deg _H: V \rightarrow {\mathbb {N}}\) denote the degree function of the subgraph (V, H). Furthermore, let

$$\begin{aligned} \displaystyle \mathbf {u}^{(v)} = \left( u_0^{(v)}, u_1^{(v)}, \dots , u_d^{(v)}\right) \end{aligned}$$

denote a sequence of activities at each vertex \(v \in V\) where \(d = \deg _G(v)\). Define the polynomial

$$\begin{aligned} \displaystyle Z(G, \varvec{\lambda }, \mathbf {u}; \mathbf {x}) = \sum _{H \subseteq E} (-1)^{|H|} \varvec{\lambda }^H \mathbf {u}_{\deg _H} \mathbf {x}^{\deg _H} \end{aligned}$$

where \(\varvec{\lambda }= \{\lambda _e\}_{e \in E}\) are edge weights and

$$\begin{aligned} \displaystyle \varvec{\lambda }^H = \prod _{e \in H} \lambda _e, \mathbf {u}_{\deg _H} = \prod _{v \in V} u_{\deg _H(v)}^{(v)}, \mathbf {x}^{\deg _H} = \prod _{v \in .V} x_v^{\deg _H(v)}. \end{aligned}$$

Wagner proves that \(Z(G, \varvec{\lambda }, \mathbf {u}, \mathbf {x})\) is stable whenever \(\lambda _e \ge 0\) for all \(e \in E\) and the univariate key-polynomial\(K_v(z) = \sum _{j=0}^d \left( {\begin{array}{c}d\\ j\end{array}}\right) u_j^{(v)} z^j\) is real-rooted for all \(v \in V\) (cf [33, Thm 3.2]). We note in particular that if \(u_0^{(v)} = u_1^{(v)} = 1\), \(u_k^{(v)} = 0\) for all \(k > 1\) and \(\,\, v \in V\), then \(Z(G, \varvec{\lambda }, \mathbf {u}; \mathbf {x}) = \mu _{\varvec{\lambda }}(G,\mathbf {x})\) where \(\mu _{\varvec{\lambda }}(G,\mathbf {x})\) is the weighted multivariate matching polynomial studied by Heilmann and Lieb [17]. An appropriate homogenization of \(Z(G, \varvec{\lambda }, \mathbf {u}; \mathbf {x})\) could be defined as

$$\begin{aligned} W(G, {\mathbf {u}}; \mathbf {x}\oplus \mathbf {w}) = \sum _{H \subseteq E} (-1)^{|H|} \mathbf {u}_{\deg _H} \mathbf {w}^{2H} \mathbf {x}^{\deg _G - \deg _H}. \end{aligned}$$

Since \(W(G, {\mathbf {u}}; \mathbf {x}\oplus \mathbf {w}) = \mathbf {x}^{\deg _G} Z(G, \mathbf {w}^2, \mathbf {u}; \mathbf {x}^{-1} )\) we see that \(W(G, {\mathbf {u}}; \mathbf {x}\oplus \mathbf {w})\) is hyperbolic with respect to \(\mathbf {e}= {\mathbf {1}} \oplus {\mathbf {0}}\) whenever \(K_v(z)\) is real-rooted for all \(v \in V\). We also note the following edge and node recurrences for \(e \in E\) and \(v \in V\),

$$\begin{aligned}&W(G, \mathbf {u}; \mathbf {x}\oplus \mathbf {w}) \\&= \mathbf {x}^e W(G {\setminus } e, \mathbf {u}; \mathbf {x}\oplus \mathbf {w}) - \mathbf {w}^{2e} W(G {\setminus } e, \mathbf {u}\ll e; \mathbf {x}\oplus \mathbf {w}) \\&= \sum _{S \subseteq N(v)} (-1)^{|S|} u_{|S|}^{(v)} \mathbf {w}^{2E(S,v)} x_v^{\deg _G(v) - |S|}\mathbf {x}^{N(v) {\setminus } S}W(G {\setminus } v,\mathbf {u}\ll S; \mathbf {x}\oplus \mathbf {w}) \end{aligned}$$

where \(E(S,v) = \{ sv \in E : s \in S \}\) and \(\displaystyle (\mathbf {u}\ll S)^{(v)} = {\left\{ \begin{array}{ll} (u_1^{(v)}, \dots , u_d^{(v)}), &{} v \in S \\ \mathbf {u}^{(v)}, &{} v \not \in S \end{array}\right. }\)

Although it is not clear in general how to find a definite determinantal representation of \(W(G, {\mathbf {u}}; \mathbf {x}\oplus \mathbf {w})\), it may be possible to consider special form activity vectors and obtain a reduction by constructing divisibility relations in the spirit of Lemma 2.12 and Theorem 3.6. This may also be of independent interest for studying root bounds of their univariate specializations.