Truncated Quillen complexes of $p$-groups

Abstract

Let $p$ be an odd prime and let $P$ be a $p$-group. We examine the order complex of the poset of elementary abelian subgroups of $P$ having order at least $p^2$. Bouc and Thévenaz showed that this complex has the homotopy type of a wedge of spheres. We show that, for each nonnegative integer $l$, the number of spheres of dimension $l$ in this wedge is controlled by the number of extraspecial subgroups $X$ of $P$ having order $p^{2l+3}$ and satisfying $\Omega _1(C_P(X))=Z(X)$. We go on to provide a negative answer to a question raised by Bouc and Thévenaz concerning restrictions on the homology groups of the given complex.

1 Introduction

Since the appearance of the seminal papers [5, 6] by Brown and [15] by Quillen, group theorists, topologists, and combinatorialists have studied connections between the algebraic structure of a group $G$ and the topology of the order complexes of various posets of $p$-subgroups of $G$. An excellent and extensive description of such activity appears in the book [16]. The complex that has received the most attention is the Quillen complex $\Delta {\mathcal A}_p(G)$, whose faces are chains of nontrivial elementary abelian subgroups of $G$. (Relevant terms used in this introduction will be defined in Sect. 2).

When $P$ is a finite $p$-group, $\Delta {\mathcal A}_p(P)$ is contractible. So, one cannot learn much about $P$ from the topology of $\Delta {\mathcal A}_p(P)$. However, Bouc and Thévenaz observed in [4] that if one removes from ${\mathcal A}_p(P)$ all subgroups of $P$ having order $p$, things become more interesting.

Definition 1.1

Let $p$ be a prime and let $P$ be a finite $p$-group. We define ${\mathcal A}_{\ge 2}(P)$ to be the set of elementary abelian subgroups of $P$ having order at least $p^2$, ordered by inclusion.

The main result in [4] is as follows

Theorem 1.2

Let $p$ be a prime and let $P$ be a finite $p$-group. The order complex $\Delta {\mathcal A}_{\ge 2}(P)$ has the homotopy type of a wedge of spheres.

It is natural to ask how many spheres of each dimension appear in the wedge described in Theorem 1.2. Equivalently, one can ask for the rank of each homology group of $\Delta {\mathcal A}_{\ge 2}(P)$. Bouc and Thévenaz observed that if $P$ is a $3$-group of order at most $3^6$ then, $\Delta {\mathcal A}_{\ge 2}(P)$ has at most one nontrivial reduced homology group. They observed also that if $P$ s a $2$-group of order at most $2^9$ then, $\Delta {\mathcal A}_{\ge 2}(P)$ has at most two nontrivial reduced homology groups, and if ${\widetilde{H}}_i(\Delta {\mathcal A}_{\ge 2}(P))$ and ${\widetilde{H}}_j(\Delta {\mathcal A}_{\ge 2}(P))$ are nontrivial then $|i-j| \le 1$. They asked whether the phenomena just described persist for larger $p$-groups. A partial positive answer to their question was given by Bornand in [3].

Theorem 1.3

([3], Corollary 4.12) Let $p$ be a prime and let $P$ be a finite $p$-group. Assume $[P,P]$ is cyclic. If $p$ is odd then $\Delta {\mathcal A}_{\ge 2}(P)$ has at most one nontrivial reduced homology group. If $p=2$ then $\Delta {\mathcal A}_{\ge 2}(P)$ has at most two nontrivial reduced homology groups, and if $\Delta {\mathcal A}_{\ge 2}(P)$ has two nontrivial reduced homology groups then these groups appear in consecutive dimensions.

Our main results are Theorem 1.4 and Corollaries 1.6, 1.7, and 1.8 below. The point of Corollary 1.6 is that determining the homotopy type of $\Delta {\mathcal A}_{\ge 2}(P)$ is the same as enumerating certain subgroups of $P$. Corollaries 1.7 and 1.8 provide negative answers to the question of Bouc and Thévenaz.

Theorem 1.4

Let $p$ be an odd prime and let $P$ be a noncyclic finite $p$-group. Let ${\mathcal E}(P)$ be the set of subgroups $X \le P$ such that

• $X$ is extraspecial of exponent $p$, and

• $\Omega _1(C_P(X))=Z(X)$.

Then

$$\begin{aligned} \Delta {\mathcal A}_{\ge 2}(P) \simeq \bigvee _{X \in {\mathcal E}(P)}\Delta {\mathcal A}_{\ge 2}(X). \end{aligned}$$

We prove Theorem 1.4 in Sect. 3.

When $X$ is extraspecial of exponent $p$, the homotopy type of $\Delta {\mathcal A}_{\ge 2}(X)$ is known.

Proposition 1.5

(See [3], Proposition 4.7) Let $p$ be an odd prime and let $X$ be an extraspecial group of exponent $p$ and order $p^{2n+1}$. Then, $\Delta {\mathcal A}_{\ge 2}(X)$ has the homotopy type of a wedge of $p^{n^2}$ spheres of dimension $n-1$.

Note that when $P$ is a cyclic $p$-group, $\Delta {\mathcal A}_{\ge 2}(P)=\{\emptyset \}$. By convention, (the geometric realization of) $\Delta {\mathcal A}_{\ge 2}(P)$ is thus the $(-1)$-sphere $S^{-1}$. Combining this fact with Theorem 1.4 and Proposition 1.5, we get a new proof of Theorem 1.2, when $p$ is odd. In addition, we get the following result.

Corollary 1.6

Let $p$ be an odd prime and let $P$ be a finite $p$-group. For each positive integer $n$, let $a_n(P)$ be the number of subgroups $X \le P$ such that

• $X$ is extraspecial of exponent $p$ and order $p^{2n+1}$, and

• $\Omega _1(C_P(X))=Z(X)$.

Then, for each nonnegative integer $l$,

$$\begin{aligned} {\widetilde{H}}_l(\Delta {\mathcal A}_{\ge 2}(P)) \cong {\mathbb Z}^{a_{l+1}(P)p^{(l+1)^2}}. \end{aligned}$$

Applying Theorem 1.4 to certain split extensions of extraspecial $p$-groups by automorphisms of order $p$, we prove the following result in Sect. 4.

Corollary 1.7

Let $t$ be nonnegative integer and let $k$ be a positive integer. For each prime $p>2k+3$ there exists a group $P$ of order $p^{2(t+k+2)}$ such that the only nontrivial homology groups of $\Delta {\mathcal A}_{\ge 2}(P)$ are ${\widetilde{H}}_t(\Delta {\mathcal A}_{\ge 2}(P))$ and ${\widetilde{H}}_{k+t}(\Delta {\mathcal A}_{\ge 2}(P))$.

Further constructions using central products, also found in Sect. 4, yield the following result.

Corollary 1.8

Let $\Omega$ be the smallest collection of subsets of the set ${\mathbb N}_0$ of nonnegative integers satisfying

• (1) if $I \subseteq {\mathbb N}_0$ and $|I| \le 2$, then $I \in \Omega$, and

• (2) if $I,J \in \Omega$, then

  $$\begin{aligned} 1+I+J:=\{1+i+j:i \in I,j \in J\} \in \Omega . \end{aligned}$$

For each $I \in \Omega$, there exists an integer $N(I)$ such that for every prime $p>N(I)$, there exists a $p$-group $P$ of exponent $p$ satisfying

$$\begin{aligned} {\widetilde{H}}_i(\Delta {\mathcal A}_{\ge 2}(P)) \ne 0 \text{ if } \text{ and } \text{ only } \text{ if } i \in I. \end{aligned}$$

Applying condition (2) of Corollary 1.8 repeatedly to the set $\{0,1\}$, we see that, for each $n \in {\mathbb N}_0$, the set $\{n,n+1,\ldots ,2n,2n+1\}$ lies in $\Omega$. It follows that for each $m \in {\mathbb N}_0$, there exist some odd prime $p$ and some $p$-group $P$ such that $\Delta {\mathcal A}_{\ge 2}(P)$ has exactly $m$ nontrivial reduced homology groups. It remains to be seen whether, for each finite subset $I$ of ${\mathbb N}_0$, there exist a prime $p$ and a $p$-group $P$ such that ${\widetilde{H}}_i(\Delta {\mathcal A}_{\ge 2}(P))$ is nontrivial if and only if $i \in I$. Also of interest is whether the restriction $p>N(I)$ can be removed from Corollary 1.8 or from any stronger result of a similar nature.

2 Definitions, notation, and preliminary results

2.1 Topology

The objects and ideas from topology that we will use are well known. Each is discussed in at least one of [2, 13] and [18].

For a partially ordered set ${\mathcal P}$, the order complex $\Delta {\mathcal P}$ is the abstract simplicial complex whose $k$-dimensional faces are all chains $x_0<\cdots <x_k$ of length $k$ from ${\mathcal P}$. We make no distinction between an abstract simplicial complex $\Delta$ and an arbitrary geometric realization of $\Delta$, as all such realizations have the same homeomorphism type.

We write $X \simeq Y$ to indicate that topological spaces $X,Y$ have the same homotopy type.

Let $X_1,\ldots ,X_k$ be nonempty, pairwise disjoint topological spaces, and pick $x_i \in X_i$ for each $i \in [k]:=\{1,\ldots ,k\}$. The wedge $\bigvee _{i=1}^{k}(X_i,x_i)$ is obtained from the (disjoint) union $\bigcup _{i=1}^{k}X_i$ by identifying all the $x_i$. That is, $\bigvee _{i=1}^{k}(X_i,x_i)$ is the quotient space $\bigcup _{i=1}^{k}X_i/\sim$, where $\sim$ is the equivalence relation whose elements are $(x_i,x_j)$ for all $1 \le i<j \le k$.

If, for each $i \in [k]$, the connected components of $X_i$ are pairwise homotopy equivalent, then the homotopy type of $\bigvee _{i=1}^{k}(X_i,x_i)$ does not depend on the choice of the $x_i$ and we write $\bigvee _{i=1}^{k}X_i$ for any wedge of the $X_i$. In particular, if each $X_i$ is a sphere then, the wedge of spheres $\bigvee _{i=1}^{k}X_i$ is well defined. For each $l \ge 0$, there is an isomorphism of reduced homology groups

$$\begin{aligned} {\widetilde{H}}_l(\bigvee _{i=1}^kX_i) \cong \bigoplus _{i=1}^k {\widetilde{H}}_l(X_i). \end{aligned}$$

In particular, if each $X_i$ is a sphere then, the homotopy type of $\bigvee _{i=1}^{k}X_i$ is uniquely determined by its reduced homology, as asserted implicitly in the introduction.

If $\Delta$ is a simplicial complex and $\Gamma$ is a contractible subcomplex of $\Delta$, then $\Delta$ is homotopy equivalent to the quotient space $\Delta /\Gamma$. Therefore, if $\Delta _1,\Delta _2$ are simplicial complexes such that $\Delta _1 \cap \Delta _2$ is contractible then, $\Delta _1 \cup \Delta _2$ is homotopy equivalent with a wedge $\Delta _1 \vee \Delta _2$. In particular, if $\Delta _1$ and $\Delta _2$ are simplicial complexes such that $\Delta _1$, $\Delta _2$ and $\Delta _1 \cap \Delta _2$ are contractible, then $\Delta _1 \cup \Delta _2$ is also contractible. It follows by induction on $k$ that if $\Delta _1,\ldots ,\Delta _k$ are simplicial complexes such that $\bigcap _{i \in I}\Delta _i$ is contractible for each nonempty $I \subseteq [k]$ then $\bigcup _{i=1}^{k}\Delta _i$ is contractible. Now we can derive the following lemma, which is key in our proof of Theorem 1.4. A result that is essentially the same as this lemma was proved earlier by Kratzer and Thévenaz (see [14, Lemma 2.8]).

Lemma 2.1

Say $\Delta _1,\ldots ,\Delta _k$ are simplicial complexes such that $\bigcap _{i \in I}\Delta _i$ is contractible for each $I \subseteq [k]$ satisfying $|I| \ge 2$. Then, there exist $x_1,\ldots ,x_k$ such that $x_i \in \Delta _i$ for each $i \in [k]$ and

$$\begin{aligned} \bigcup _{i=1}^{k}\Delta _i \simeq \bigvee _{i=1}^{k}(\Delta _i,x_i). \end{aligned}$$

Proof

Set $\Delta :=\bigcup _{i=1}^{k} \Delta _i$ and $\Gamma :=\bigcup _{1 \le i<j\le k}(\Delta _i \cap \Delta _j)$. Then, $\Gamma$ is contractible. Therefore, $\Delta \simeq \Delta /\Gamma$. For each $i \in [k]$, set $\Gamma _i:=\bigcup _{j \ne i}(\Delta _i \cap \Delta _j)$. Then $\Gamma _i$ is contractible. Therefore, $\Delta _i \simeq \Delta _i/\Gamma _i$. Each $\Delta _i/\Gamma _i$ can be realized as a CW-complex with one $0$-cell $y_i$ corresponding to the subcomplex $\Gamma _i$ along with one $d$-cell for each $d$-dimensional face in $\Delta _i {\setminus }\Gamma _i$. By construction, $\Delta /\Gamma =\bigvee _{i=1}^{k}(\Delta _i/\Gamma _i,y_i)$. To get the wedge described in the lemma, we can take $x_i$ to be any point in $\Gamma _i$.$\square$

By convention, the wedge of an empty collection of spaces is a point.

2.2 Group theory

We use standard group theoretic notation as can be found in [1, 7, 17]. All groups are assumed to be finite. For a group $G$ and $x,y \in G$, we write $[x,y]$ for the commutator $x^{-1}y^{-1}xy$. For $A,B \subseteq G$, we write $[A,B]$ for the subgroup of $G$ generated by all commutators $[a,b]$ with $a \in A$ and $b \in B$. For $x,y \in G$, we write $x^y$ for $y^{-1}xy$. We record here the following well-known commutator formulas

$$\begin{aligned}{}[uv,w]&= [u,w]^v[v,w], \end{aligned}$$

(1)

$$\begin{aligned}{}[u,vw]&= [u,w][u,v]^w \end{aligned}$$

(2)

for all $u,v,w \in G$.

Let $p$ be a prime and let $P$ be a $p$-group. We say that $P$ has exponent $p$ if every $g \in P$ satisfies $g^p=1$. A nontrivial group $P$ is elementary abelian if $P$ is abelian of exponent $p$, in which case $P$ admits a vector space structure over the field ${\mathbb F}_p$ of order $p$. The group $P$ is extraspecial if its center $Z(P)$ has order $p$ and $P/Z(P)$ is elementary abelian. An extraspecial $p$-group has order $p^{2n+1}$ for some positive integer $n$ (see for example [1, (23.10)]). The subgroup $\Omega _1(P) \le P$ is, by definition, generated by all elements of order $p$ in $P$. As is standard, we define the terms of the lower central series of $P$ as $\gamma _1(P)=P$ and $\gamma _n(P)=[P,\gamma _{n-1}(P)]$ for each positive integer $n$. The nilpotence class of $P$ is the smallest $n$ such that $\gamma _{n+1}(P)=1$. Finally, $P$ is a central product of subgroups $Q,R$ if $P=QR$ and $[Q,R]=1$. Given groups $Q,R$ with subgroups $S \le Z(Q),T \le Z(R)$ and an isomorphism $\phi :S \rightarrow T$, one constructs a central product of $Q$ and $R$ as $(Q \times R)/\{(s^{-1},\phi (s)):s \in S\}$.

We will use the following results, the first of which is well known and appears as [1, (23.8)] and the second of which is due to Hall (see [10, Sect. 4], [11, Introduction], both of these papers can be found in [12]).

Lemma 2.2

Say $X \le P$ is extraspecial and $[P,X] \le Z(X)$. Then $P=XC_P(X)$

Theorem 2.3

(P. Hall) Let $p$ be a prime and let $P$ be a $p$-group. If the nilpotence class of $P$ is less than $p$ and $P=\Omega _1(P)$, then $P$ has exponent $p$.

3 The proof of Theorem 1.4

Throughout this section, $p$ is an odd prime and $P$ is a $p$-group.

3.1 Some useful elementary abelian sections

Let $Z \le \Omega _1(Z(P))$. (While we begin our discussion with no other condition on $Z$, soon we will turn to the case where $|Z|=p$.) Define

$$\begin{aligned} {\mathcal M}_Z(P):=\{X \le P:Z<X=\Omega _1(X) \text{ and } [X,X] \le Z\}. \end{aligned}$$

Note that if $Z \ne \Omega _1(P)$ then ${\mathcal M}_Z(P)$ is nonempty, since $\langle Z,x \rangle \in {\mathcal M}_Z(P)$ for each $x$ of order $p$ in $P{\setminus }Z$. We consider ${\mathcal M}_Z(P)$ to be partially ordered by inclusion and define

$$\begin{aligned} {\mathcal M}^*_Z(P):=\{X \in {\mathcal M}_Z(P):X \text{ is } \text{ maximal } \text{ in } {\mathcal M}_Z(P)\}. \end{aligned}$$

Each $X \in {\mathcal M}_Z(P)$ has nilpotence class at most two. By Lemma 2.3, each $X \in {\mathcal M}_Z(P)$ has exponent $p$.

The following technical lemma will be used both in the proof of Theorem 1.4 and in the construction of examples proving Corollaries 1.7 and 1.8 in Sect. 4.

Lemma 3.1

Assume $P$ is a central product of proper subgroups $P_1,P_2$ such that at least one $P_i$ has exponent $p$.

Set $Z=P_1 \cap P_2$. Then

$$\begin{aligned} {\mathcal M}^*_Z(P)=\{X_1X_2:X_i \in {\mathcal M}^*_Z(P_i) \text{ for } i=1,2\}. \end{aligned}$$

Proof

We show first that if $X_i \in {\mathcal M}_Z(P_i)$ for $i=1,2$ then $X:=X_1X_2 \in {\mathcal M}_Z(P)$. It follows from commutator identities (1) and (2) that if $g_i,h_i \in P_i$ for $i=1,2$ then

$$\begin{aligned}{}[g_1g_2,h_1h_2]=[g_1,h_1][g_2,h_2]. \end{aligned}$$

(3)

Therefore,

$$\begin{aligned}{}[X,X]=[X_1,X_1][X_2,X_2] \le Z. \end{aligned}$$

Also, $X=\Omega _1(X)$, since $X_i=\Omega _1(X_i)$ for $i=1,2$. Note also that each $X_i$ lies in ${\mathcal M}_Z(P)$.

Next let $T \in {\mathcal M}_Z(P)$. There are surjective homomorphisms

• $\phi :P_1 \times P_2 \rightarrow P$, $\phi ((p_1,p_2))=p_1p_2$,

• $\pi _1:P_1 \times P_2 \rightarrow P_1$, $\pi _1((p_1,p_2))=p_1$, and

• $\pi _2:P_1 \times P_2 \rightarrow P_2$, $\pi _2((p_1,p_2))=p_2$.

For $i=1,2$, set

$$\begin{aligned} T^i:=\pi _i(\phi ^{-1}(T)). \end{aligned}$$

We claim that, for $i=1,2$, either $T^i \in {\mathcal M}_Z(P_i)$ or $T^i=Z$. The truth of this claim implies the truth of the Lemma. Indeed, assuming the claim, $T \le T^1T^2 \in {\mathcal M}_Z(P)$. It follows that every element of ${\mathcal M}^*_Z(P)$ is of the form $X_1X_2$ with $X_i \in {\mathcal M}^*_Z(P_i)$. On the other hand, say $X=X_1X_2$ with each $X_i \in {\mathcal M}^*_Z(P_i)$. If $X \le T \in {\mathcal M}_Z(P)$, then $X_i \le T^i \in {\mathcal M}_Z(P_i)$ for $i=1,2$. Therefore, each $T^i=X_i$ and $T=X$.

Now we prove our claim. We assume without loss of generality that $i=1$. Note that $Z \le T^1$, since $(z,1) \in \phi ^{-1}(Z)$ for each $z \in Z$. Let $g_1,h_1 \in T^1$. There exist $g_2,h_2 \in P_2$ such that $g_1g_2$ and $h_1h_2$ are in $T$. Now

$$\begin{aligned}{}[g_1g_2,h_1h_2] \in Z \le P_2, \end{aligned}$$

since $[T,T] \le Z$. It follows from (3) that $[g_1,h_1] \in P_2$, since both $[g_1g_2,h_1h_2]$ and $[g_2,h_2]$ are in $P_2$. Therefore, $[g_1,h_1] \in P_1 \cap P_2=Z$ and $[T^1,T^1] \le Z$.

It remains to show that $T^1=\Omega _1(T^1)$. Assume for contradiction that $T^1$ has an element $g_1$ of order $p^2$. There is some $g_2 \in T^2$ such that $g_1g_2 \in T$. By Lemma 2.3, $(g_1g_2)^p=1$. As $P_1$ does not have exponent $p$, it must be the case that $g_2^p=1$. It follows now from $[P_1,P_2]=1$ that

$$\begin{aligned} 1=(g_1g_2)^p=g_1^pg_2^p=g_1^p, \end{aligned}$$

which gives the desired contradiction and completes our proof.$\square$

3.2 Proof of Theorem 1.4

Let us recall a basic assumption under which we are working.

Hypothesis 3.2

The $p$-group $P$ (of odd order) is not cyclic.

Our goal is to show that $P$ is not a counterexample to Theorem 1.4.

Assume first that the center $Z(P)$ is not cyclic. As shown in [4] by applying the Quillen fiber lemma to the map $A \mapsto A\Omega _1(Z(P))$ on ${\mathcal A}_{\ge 2}(P)$, $\Delta {\mathcal A}_{\ge 2}(P)$ is contractible. (This is a key technique in the study of subgroup complexes that is used first, to our knowledge, in [15] and described also in [16, Definition 3.3.1 and Lemma 3.3.3].) Let $X \le P$ be extraspecial. Then $\Omega _1(C_P(X)) \ne Z(X)$, since $Z(X)$ is cyclic. So, Theorem 1.4 holds when $Z(P)$ is not cyclic. We proceed under the following assumption.

Hypothesis 3.3

$Z(P)$ is cyclic.

Let $Z=\Omega _1(Z(P))$. Then, $Z$ is cyclic of order $p$. We define

$$\begin{aligned} {\mathcal A}_{>Z}(P):=\{H \in {\mathcal A}_{\ge 2}(P):Z<H\}. \end{aligned}$$

As shown in [4] by applying the Quillen fiber lemma to the map $A \mapsto AZ$ on ${\mathcal A}_{\ge 2}(P)$,

$$\begin{aligned} \Delta {\mathcal A}_{>Z}(P) \simeq \Delta {\mathcal A}_{\ge 2}(P). \end{aligned}$$

(4)

(Again, this is a basic and key technique that is used in [15] and appears in [16, Proposition 3.1.12(2)]). So, we work from now on with ${\mathcal A}_{>Z}(P)$ in place of ${\mathcal A}_{\ge 2}(P)$.

Lemma 3.4

Let $X \in {\mathcal M}_Z(P)$. If $X$ is not extraspecial, then $\Delta {\mathcal A}_{>Z}(X)$ is contractible.

Proof

Note that first $X$ is extraspecial if and only if $Z(X)=Z$. If $Z(X) \ne Z$, then $\Omega _1(Z(X) \in {\mathcal A}_{\ge 2}(X)$. Now we get that $\Delta {\mathcal A}_{>Z}(X)$ is contractible by applying the Quillen fiber lemma to the map $A \mapsto AZ(X)$ on ${\mathcal A}_{>Z}(X)$, as discussed above.$\square$

Note that it follows from Proposition 1.5 and Lemma 3.4 that the wedge $\bigvee _{X \in {\mathcal M}^*_Z(P)}\Delta {\mathcal A}_{>Z}(X)$ is well defined.

Lemma 3.5

Assume $X \in {\mathcal M}_Z(P)$ is extraspecial. Then, $X \in {\mathcal M}^*_Z(P)$ if and only if $\Omega _1(C_P(X))=Z$.

Proof

Say $\Omega _1(C_P(X)) \ne Z$. Pick $Y<\Omega _1(C_P(X))$ such that $|Y|=p$ and $Y \ne Z$. Then $X<XY \in {\mathcal M}_Z(P)$, since $XY \cong X \times Y$. Therefore, $X \not \in {\mathcal M}^*_Z(P)$. Conversely, say $X \not \in {\mathcal M}^*_Z(P)$. There is some $T$ such that $X<T \in {\mathcal M}_Z(P)$. Then $X \lhd T$ and $[T,X] \le Z=Z(X)$, since $[T,T]=Z<X$. By Lemma 2.2, $T=XC_T(X)$. There is some $g \in C_T(X){\setminus }Z$ with $|g|=p$, since $T$ has exponent $p$ and $T \ne X$. Now $g \in \Omega _1(C_P(X)){\setminus }Z$. $\square$

Each $A \in {\mathcal A}_{>Z}(P)$ lies in ${\mathcal M}_Z(P)$. The argument used to obtain (4) above applies to $X \in {\mathcal M}^*_Z(P)$, as well as to $P$. Therefore,

$$\begin{aligned} \Delta {\mathcal A}_{>Z}(P)=\bigcup _{X \in {\mathcal M}^*_Z(P)}\Delta {\mathcal A}_{>Z}(X). \end{aligned}$$

Moreover, if an extraspecial $p$-group $X$ does not have exponent $p$, then $X \ne \Omega _1(X)$. It follows now from Lemma 3.5 that ${\mathcal E}(P)$ consists of those members of ${\mathcal M}^*_Z(P)$ that are extraspecial. With Lemmas 3.4 and 3.5 in hand, we can invoke Lemma 2.1 to prove Theorem 1.4 once we show that the intersection of two or more members of ${\mathcal M}^*_Z(P)$ lies in ${\mathcal M}_Z(P)$ and is not extraspecial. Lemma 3.7 below says that this condition on intersections does indeed hold, and thus completes the proof of Theorem 1.4.

Lemma 3.6

$P$ has a normal elementary abelian subgroup $N$ of order $p^2$. Each $S \in {\mathcal M}^*_Z(P)$ contains $N$.

Proof

The existence of $N$ is [8, Lemma 10.11]. Now $[P,N] \lhd P$. Moreover, $1<[P,N]<N$, since $Z(P)$ is cyclic and $N$ is not and $P$ is nilpotent. Therefore, $[P,N]=Z$, since $[P,N] \cap Z(P) \ne 1$. Let $S \in {\mathcal M}^*_Z(P)$. Then $[S,N] \le Z$. It follows from (1),(2) that $[SN,SN] \le Z$. Therefore, $SN/Z$ is abelian. Moreover, $SN=\Omega _1(SN)$, since $S=\Omega _1(S)$ and $N=\Omega _1(N)$. It follows that $SN \in {\mathcal M}_Z(P)$. Therefore, $N \le S$, since $S \in {\mathcal M}^*_Z(P)$.$\square$

Lemma 3.7

Let ${\mathcal S}\subseteq {\mathcal M}^*_Z(P)$ with $|{\mathcal S}| \ge 2$. Then, $\bigcap _{S \in {\mathcal S}}S$ lies in ${\mathcal M}_Z(P)$ and is not extraspecial.

Proof

Let $Y= \bigcap _{S \in {\mathcal S}}S$. Then $Z \le Y$ and, for any $S \in {\mathcal S}$, $[Y,Y] \le [S,S] \le Z$. Moreover, $Y=\Omega _1(Y)$, since each $S \in {\mathcal S}$ has exponent $p$. By Lemma 3.6, $Y$ has a subgroup of order $p^2$, so $Z<Y$. Therefore, $Y \in {\mathcal M}_Z(P)$.

Assume for contradiction that $Y$ is extraspecial. Set $Q:=\langle \{S:S \in {\mathcal S}\} \rangle$. Now $[Y,Y]=Z=Z(Y)$ and it follows that $[S,Y]=Z$ for each $S \in {\mathcal S}$, since $[S,S] \le Z$. By commutator formulas (1) and (2), $[Q,Y]=Z$. By Lemma 2.2, $Q=YC_Q(Y)$. Note that $Y \cap C_Q(Y)=Z$.

Now

$$\begin{aligned} Q=\Omega _1(Q)=Y\Omega _1(C_Q(Y)). \end{aligned}$$

Indeed, the first equality holds, since $S=\Omega _1(S)$ for each $S \in {\mathcal S}$. To prove the second equality, we assume $x \in Q$ has order $p$ and write $x=yh$ with $y \in Y$ and $h \in C_Q(Y)$. Then

$$\begin{aligned} 1=x^p=(yh)^p=y^ph^p=h^p, \end{aligned}$$

since $Y$ has exponent $p$ and $[Y,h]=1$. Therefore, $h \in \Omega _1(C_Q(Y))$ and $x \in Y\Omega _1(C_Q(Y))$ as claimed.

We claim that $C_Q(Y)$ is not cyclic. Indeed,

$$\begin{aligned} C_Q(Y)&= C_Q(Y) \cap Y \Omega _1(C_Q(Y)) \\&= \Omega _1(C_Q(Y))(Y \cap C_Q(Y)) \\&= \Omega _1(C_Q(Y))Z \\&= \Omega _1(C_Q(Y)), \end{aligned}$$

the second equality following from the Dedekind modular law (see for example [1, (1.14)]). Therefore, if $C_Q(Y)$ is cyclic then $C_Q(Y)=Z$ and $Q=Y$. However, as $|{\mathcal S}| \ge 2$, we know that $Y \not \in {\mathcal S}$ and it follows that $Q \ne Y$.

Assume now that $Z(C_Q(Y))$ is cyclic. We may apply Lemma 3.6 to $C_Q(Y)$. Every normal subgroup of $C_Q(Y)$ is centralized by $Y$, and therefore normal in $Q$. Thus, there is some $N \lhd Q$ such that

• $N$ is elementary abelian of order $p^2$,

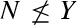• (as $[Y,N]=1$ and $|Z(Y)|=p$), and

• every $\tilde{S} \in {\mathcal M}^*_Z(C_Q(Y))$ contains $N$.

By Lemma 3.1, each $S \in {\mathcal M}^*_Z(Q)$ satisfies $S=Y\tilde{S}$ for some $\tilde{S} \in {\mathcal M}^*_Z(C_Q(Y))$. The contradiction

$$\begin{aligned} Y<YN \le \bigcap _{S \in {\mathcal S}}S=Y \end{aligned}$$

now follows, as ${\mathcal S}\subseteq {\mathcal M}^*_Z(Q)$.

Finally, assume $Z(C_Q(Y))$ is not cyclic. Let $N=\Omega _1(Z(C_Q(Y))$. Then, $Z<N$ and . Moreover, $N \le Z(Q)$. Let $S \in {\mathcal S}$. Then $[S,N]=1$. By commutator formulas (1) and (2), $[SN,SN]=Z$. Moreover, $SN=\Omega _1(SN)$. It follows that $SN \in {\mathcal M}_Z(P)$. Therefore, $N \le S$, as $S \in {\mathcal M}^*_Z(P)$. Again we get the contradiction

$$\begin{aligned} Y<YN\le \bigcap _{S \in {\mathcal S}}S=Y. \end{aligned}$$

$\square$

4 Examples

Here we prove Corollaries 1.7 and 1.8. Our first step is to produce, for every positive integer $m$ and every prime $p>2m+1$, a $p$-group $P$ of order $p^{2m+2}$ and exponent $p$ such that

$$\begin{aligned} \{i:{\widetilde{H}}_i(\Delta {\mathcal A}_{\ge 2}(P)) \ne 0\}=\{0,m-1\}. \end{aligned}$$

(5)

Recall that in Sect. 3 we observed that when $Z(P)$ is cyclic, ${\mathcal E}(P)$ consists of those $X \in {\mathcal M}^*_Z(P)$ thst are extraspecial. Thus by Theorem 1.4 and Proposition 1.5 (or by Corollary 1.6), if $Z(P)$ is cyclic then the set of all $i>0$ such that ${\widetilde{H}}_{i-1}$ is nontrival is the set of all $i>0$ such that ${\mathcal M}^*_Z(P)$ contains an extraspecial $p$-group of order $p^{2i+1}$. So, for our purposes, it is necessary and sufficient to produce $P$ of the desired order $p^{2m+2}$ and exponent $p$ such that

• $Z:=Z(P)$ is cyclic, and

• ${\mathcal M}^*_Z(P)$ contains extraspecial groups of orders $p^3$ and $p^{2m+1}$ and no extraspecial groups of other orders.

Let $X$ be an extraspecial group of exponent $p$ and order $p^{2m+1}$. Let $Z=Z(X)$ and let $z$ generate $Z$. There exist generators $x_1,\ldots ,x_m,y_1,\ldots ,y_m$ for $X$ such that

$$\begin{aligned}{}[x_i,x_j]=[y_i,y_j]=1 \end{aligned}$$

for all $i,j \in [m]$ and

$$\begin{aligned}{}[x_i,y_j]=\left\{ \begin{array}{ll} z &{} i=j, \\ 1 &{} i \ne j. \end{array} \right. \end{aligned}$$

Identifying $Z$ with ${\mathbb F}_p$, one gets a nondegenerate, alternating bilinear form $\langle \cdot ,\cdot \rangle$ on $X/Z$, defined by

$$\begin{aligned} \langle Zx,Zy \rangle :=[x,y] \end{aligned}$$

(see for example [1, (23.10)]).

Set

$$\begin{aligned} B:=\{g \in Aut(X):z^g=z\}. \end{aligned}$$

The action of any $g \in B$ on $X$ induces a linear transformation on the ${\mathbb F}_p$-vector space $X/Z$. This transformation preserves the form $\langle \cdot ,\cdot \rangle$. Thus, we have a homomorphism $\Phi$ from $B$ to the group $Sp(X/Z)$ of linear transformations preserving this form. As shown by D. L. Winter in [19], $\Phi$ is surjective and the kernel of $\Phi$ is the group $Inn(X)$ of inner automorphisms of $X$. Thus we have a short exact sequence

$$\begin{aligned} 1 \rightarrow Inn(X) \rightarrow B \rightarrow Sp(X/Z) \rightarrow 1 \end{aligned}$$

(6)

of groups. As noted by Griess in the introduction of [9], the sequence (6) splits.

Assume for the moment that there is some $\phi \in Sp(X/Z)$ such that

• $\phi$ has order $p$ and

• the unique eigenspace $C_{X/Z}(\phi )$ for $\phi$ is generated by $Zy_1$.

(We will see shortly that such a $\phi$ exists whenever $p>2m$.) There is some $g \in B$ such that $|g|=p$ and $\Phi (g)=\phi$, since (6) splits.

We form the semidirect product $P:=\langle g \rangle X$. The group $P$ has order $p^{2m+2}$. So, the nilpotence class of $P$ is at most $2m+1$. Assuming $p>2m+1$, we see that $P$ has exponent $p$ by Theorem 2.3, as $P=\Omega _1(P)$.

The group $P/Z$ is not abelian, since $C_{X/Z}(\phi ) \ne X/Z$. Therefore, $X \in {\mathcal M}^*_Z(P)$, as $X$ is maximal in $P$.

There is some integer $j$ with $0 \le j <p$ such that $[g,y_1]=z^j$, since $Zy_1 \in C_{X/Z}(\phi )$. By (1), $[x_1^{1-j},y_1]=z^{1-j}$ and $[gx_1^{1-j},y_1]=z$. Therefore, the subgroup $S:=\langle gx_1^{1-j},y_1 \rangle \le P$ is nonabelian of order $p^3$. It follows that $S$ is extraspecial and lies in ${\mathcal M}_Z(P)$. We claim that $S \in {\mathcal M}^*_Z(P)$. Indeed, say $S \le T \in {\mathcal M}_Z(P)$. Then, $T/Z$ is contained in $C_{P/Z}(S/Z)$. It follows that $T/Z \cap X/Z=\langle Zy_1 \rangle$, since $\Phi (gx_1^{1-j})=\phi$. Now $|T/Z| \le p^2$, since $[P/Z:X/Z]=p$. It follows that $|T| \le p^3=|S|$ and $T=S$ as claimed.

Let $T \in {\mathcal M}_Z(P)$. We claim that either $T \le X$ or $|T| \le p^3$. Indeed, assume . Then $T$ contains some $gh$, with $h \in X$, and $T/Z$ centralizes $Zgh$. Now $C_{X/Z}(Zgh)=\langle Zy_1 \rangle$, since $\Phi (gh)=\phi$. Therefore, $|T/Z| \le p^2$ and $|T| \le p^3$ as claimed.

We see now that every extraspecial group in ${\mathcal M}^*_Z(P)$ other than $X$ has order $p^3$, since no extraspecial group has order $p^2$. Next, we produce the desired linear transformation $\phi$, thereby proving the existence of groups $P$ satisfying (5).

Let $V=X/Z$. We use additive notation for our group operation on $V$ and write $\bar{x}$ for $Zx \in V$. Now $V$ has basis $\bar{x}_1,\ldots ,\bar{x}_m,\bar{y}_1,\ldots ,\bar{y}_m$ and our alternating form $\langle \cdot ,\cdot \rangle$ is given by

$$\begin{aligned} \langle \bar{x}_i,\bar{x}_j \rangle =\langle \bar{y}_i,\bar{y}_j\rangle =0 \end{aligned}$$

for all $i,j$, and

$$\begin{aligned} \langle \bar{x}_i,\bar{y}_j \rangle =-\langle \bar{y}_j,\bar{x}_i \rangle =\left\{ \begin{array}{ll} 1 &{} i=j, \\ 0 &{} i \ne j. \end{array} \right. \end{aligned}$$

Define the linear transformation $\phi$ by

$$\begin{aligned} x^*_i:=\bar{x}_i\phi :=(-1)^{m+1-i}\bar{y}_m+\sum _{j=i}^{m}(-1)^{j-i}\bar{x}_j \end{aligned}$$

for all $i$,

$$\begin{aligned} y^*_i:=\bar{y}_i\phi :=\bar{y}_i+\bar{y}_{i-1} \end{aligned}$$

for $2 \le i \le m$, and

$$\begin{aligned} y^*_1:=\bar{y}_1\phi :=\bar{y}_1. \end{aligned}$$

To show that $\langle v\phi ,w\phi \rangle =\langle v,w \rangle$ for all $v,w \in V$, it suffices to examine the cases where $v,w$ lie in our basis. Certainly

$$\begin{aligned} \langle y^*_k,y^*_l \rangle =0=\langle \bar{y}_k,\bar{y}_l \rangle \end{aligned}$$

for all $k,l$. Also,

$$\begin{aligned} \langle x^*_k,x^*_l \rangle&= \left\langle (-1)^{m+1-k}\bar{y}_m+\sum _{s=k}^{m}(-1)^{s-k}\bar{x}_s,(-1)^{m+1-l}\bar{y}_m+\sum _{t=l}^{m}(-1)^{t-l}\bar{x}_t \right\rangle \\&= \langle (-1)^{m-k}(\bar{x}_m-\bar{y}_m),(-1)^{m-l}(\bar{x}_m-\bar{y}_m) \rangle \\&= 0 \\&= \langle \bar{x}_k,\bar{x}_l \rangle . \end{aligned}$$

For arbitrary $k$ and $1<l \le m$,

$$\begin{aligned} \langle x^*_k,y^*_l \rangle&= \sum _{s=k}^{m}(-1)^{s-k}\langle \bar{x}_s,\bar{y}_l \rangle +\sum _{t=k}^{m}(-1)^{t-k}\langle \bar{x}_t,\bar{y}_{l-1} \rangle \\&= \left\{ \begin{array}{l@{\quad }l} 0+0 &{} k>l \\ 1+0 &{} k=l \\ (-1)^{l-k}+(-1)^{l-1-k} &{} k<l \end{array} \right. \\&= \langle \bar{x}_k,\bar{y}_l \rangle . \end{aligned}$$

Finally,

$$\begin{aligned} \langle x^*_k,y^*_1 \rangle&= \sum _{s=k}^{m}(-1)^{s-k}\langle \bar{x}_s,\bar{y}_1 \rangle \\&= \left\{ \begin{array}{l@{\quad }l} 1 &{} k=1 \\ 0 &{} k>1 \end{array} \right. \\&= \langle \bar{x}_k,\bar{y}_1 \rangle . \end{aligned}$$

With respect to the ordering $x_1,\ldots ,x_m,y_m,\ldots ,y_1$ of our basis (note the $y_i$ appear in reverse order), the matrix of $\phi$ is upper triangular with $1$ on the diagonal. Therefore, $(\phi -1)^{2m}=0$. So, if $p>2m$ then

$$\begin{aligned} 0=(\phi -1)^p=\phi ^p-1 \end{aligned}$$

(the second equality following from the binomial theorem) and $\phi$ has order $p$.

Now we compute $C_V(\phi )$, the unique eigenspace of $\phi$. Pick

$$\begin{aligned} v=\sum _{i=1}^m\alpha _i \bar{x}_i+\sum _{j=1}^{m}\beta _j \bar{y}_j, \end{aligned}$$

an arbitrary element of $V$. Write

$$\begin{aligned} v\phi =\sum _{i=1}^{m}\gamma _i\bar{x}_i+\sum _{j=1}^{m}\delta _j\bar{y}_j. \end{aligned}$$

Then, $v \in C_V(\phi )$ if and only if $\alpha _i=\gamma _i$ and $\beta _j=\delta _j$ for all $i,j$. We calculate

$$\begin{aligned} \gamma _i=\sum _{s=1}^{i}(-1)^{i-s}\alpha _s \end{aligned}$$

(7)

for $1 \le i \le m$,

$$\begin{aligned} \delta _j=\beta _j+\beta _{j+1} \end{aligned}$$

(8)

for $1 \le j<m$, and

$$\begin{aligned} \delta _m=\beta _m+\sum _{s=1}^{m}(-1)^{m+1-s}\alpha _s. \end{aligned}$$

(9)

Say $v \in C_V(\phi )$. From (7) we conclude that $\alpha _i=0$ for $1 \le i \le m-1$. With this conclusion in hand, we obtain from (9) that $\alpha _m=0$. From (8) we conclude that $\beta _j=0$ for $2 \le j \le m$. Certainly $\bar{y}_1 \in C_V(\phi )$. We see now that

$$\begin{aligned} C_V(\phi )=\langle \bar{y}_1\rangle \end{aligned}$$

as desired.

We observe now that, with $P$ a central product of $P_1$ and $P_2$ as in Lemma 3.1 and $X_i \in {\mathcal M}^*_Z(P_i)$ for each $i$, the product $X_1X_2$ is extraspecial if and only if both $X_i$ are extraspecial. Moreover, if each $X_i$ is extraspecial of order $p^{2m_i+1}$ (and therefore, $\Delta {\mathcal A}_{\ge 2}(X_i)$ has reduced homology concentrated in degree $m_i-1$) then $X_1X_2$ has order $p^{2(m_1+m_2)+1}$ (and $\Delta {\mathcal A}_{\ge 2}(X_1X_2)$ has reduced homology concentrated in degree $m_1+m_2-1$). Corollary 1.7 is obtained from Lemma 3.1 by taking $P_1$ be a group of exponent $p$ and order $p^{2k+4}$ with nontrivial reduced homology concentrated in degrees $0$ and $k$, as constructed above (with $k=m+1$) and taking $P_2$ to be extraspecial of order $p^{2t+1}$ and exponent $p$. Corollary 1.8 follows from Lemma 3.1, Proposition 1.5 and Corollaries 1.6 and 1.7. Indeed, Proposition 1.5 and Corollary 1.7 show that $I \in \Omega$ in the cases $|I|=1$ and $|I|=2$, respectively. Moreover, $\emptyset \in \Omega$, since ${\mathcal A}_{\ge 2}(P)$ is contractible if $P$ is elementary abelian of order at least $p^2$. Now assume that $P_1$ and $P_2$ both have cyclic center and exponent $p$ and that the set of orders of elements of ${\mathcal M}^*_Z(P_i)$ is $\{2j+1:j \in I_i\}$ for $i=1,2$. Let $P$ be a central product of $P_1$ and $P_2$. Then, by Lemma 3.1, the set of orders of elements of ${\mathcal M}^*_Z(P)$ is $\{2(i_1+i_2)+1:i_1 \in I_1,i_2 \in I_2\}$. Part (2) of Corollary 1.8 now follows from Corollary 1.6.