Skip to main content
SpringerLink
Log in

Vibrations of a corrugated orthotropic cylindrical shell with free edges

  • Published:
International Applied Mechanics Aims and scope

Abstract

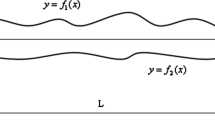
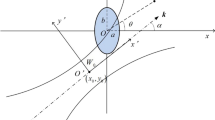
The natural vibrations of a corrugated elastic orthotropic cylindrical shell with a directrix perpendicular to its edges that are free are examined

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. A. Abramov, “On transfer of boundary conditions for systems of linear ordinary differential equations (a modification of the sweep method),” Zh. Vych. Mat. Mat. Fiz., 1, No. 3, 542–545 (1961).

    MathSciNet  Google Scholar 

  2. S. A. Ambartsumyan, General Theory of Anisotropic Shells [in Russian], Nauka, Moscow (1974).

    Google Scholar 

  3. S. A. Ambartsumyan and M. V. Belubekyan, “On bending waves localized along the edge of a plate,” Int. Appl. Mech., 30, No. 2, 135–140 (1994).

    Article  MATH  MathSciNet  Google Scholar 

  4. A. G. Aslanyan, “Relationship between the moment and momentless problems in the theory of vibrations of thin elastic shells,” Izv. AN SSSR, Mekh. Tverd. Tela, No. 5, 118–124 (1977).

  5. R. A. Bagdasaryan, M. V. Belubekyan, and K. B. Kazaryan, “Rayleigh waves in a semi-infinite closed cylindrical shell,” in: Wave Problems in Mechanics [in Russian], Nizhni Novgorod (1992), pp. 87–93.

  6. M. V. Belubekyan and I.A. Engibaryan, “Waves localized along the free edge of a plate with cubic symmetry,” Izv. RAN, Mekh. Tverd. Tela, No. 6, 139–143 (1996).

  7. I. A. Viktorov, Acoustic Surface Waves in Solids [in Russian], Nauka, Moscow (1981).

    Google Scholar 

  8. A. L. Gol’denveizer, V. B. Lidskii, and P. E. Tovstik, Free Vibrations of Thin Elastic Shells [in Russian], Nauka, Moscow (1979).

    Google Scholar 

  9. Ya. M. Grigorenko, E. I. Bespalova, A. B. Kitaigorodskii, and A. I. Shinkar’, Free Vibrations of Elements of Shell Structures [in Russian], Naukova Dumka, Kyiv (1986).

    Google Scholar 

  10. G. R. Gulgazaryan, “A formula for the distribution of the frequencies of a cylindrical shell with an arbitrary directrix,” Izv. AN SSSR, Mekh. Tverd. Tela, No. 2, 161–163 (1979).

  11. G. R. Gulgazaryan, “Rayleigh waves in a semi-infinite corrugated plate,” Izv. NAN Armenii, Mekh., 52, No. 3, 17–22 (1999).

    Google Scholar 

  12. G. R. Gulgazaryan, “Rayleigh waves in a semi-infinite corrugated orthotropic momentless cylindrical shell,” in: Mathematical Analysis and Its Applications [in Russian], Issue 1, Yerevan (2000), pp. 74–88.

  13. G. R. Gulgazaryan, “Waves localized near the generatrix of a semi-infinite corrugated orthotropic thin elastic cylindrical shell,” Vest. NNGU, Ser. Mekh., Issue 1(5), Izd. Nizhn. Novg. Gos. Univ, Nizhni Novgorod (2003), pp. 23–31.

    Google Scholar 

  14. G. R. Gulgazaryan, “Natural vibrations localized at the free end of a semi-infinite closed circular cylindrical shell,” Izv. RAN, Mekh. Tverd. Tela, No. 1, 180–192 (2003).

  15. G. R. Gulgazaryan, “Vibrations of a semiinfinite, orthotropic, cylindrical shell of open profile,” Int. Appl. Mech., 40, No. 2, 199–212 (2004).

    Article  Google Scholar 

  16. G. R. Gulgazaryan and L. G. Gulgazaryan, “Vibrations localized at the free edge of a semi-infinite open momentless cylindrical shell,” Akust. Visn. AN Ukrainy, 2, No. 4, 42–48 (1999).

    MATH  Google Scholar 

  17. G. R. Gulgazaryan and L. G. Gulgazaryan, “Rayleigh waves in a semi-infinite corrugated cylindrical shell,” Izv. RAN, Mekh. Tverd. Tela, No. 3, 151–158 (2001).

  18. G. R. Gulgazaryan and L. G. Gulgazaryan, “Vibrations of a cantilever corrugated orthotropic momentless cylindrical shell,” in: College-Level Mathematics [in Russian], Issue 3(9), Izd. Yerevan. Gos. Ped. Univ., Yerevan (2004), pp. 46–66.

    Google Scholar 

  19. G. R. Gulgazaryan, V. B. Lidskii, and G. I. Éskin, “Spectrum of a momentless system—a thin shell of arbitrary profile,” Sibir. Mat. Zh., 4, No. 5, 978–986 (1973).

    Google Scholar 

  20. G. R. Gulgazaryan and V. B. Lidskii, “Frequency density of the free vibrations of a thin anisotropic shell composed of anisotropic layers,” Izv. AN SSSR, Mekh. Tverd. Tela, No. 3, 171–174 (1982).

  21. A. Yu. Ishlinskii, “A case of passing to the limit in the theory of stability of elastic rectangular plates,” Dokl. AN SSSR, 95, No. 3, 477–479 (1954).

    Google Scholar 

  22. Yu. K. Konenkov, “On a flexural Rayleigh-type wave,” Akust. Zh., 6, No. 1, 124–126 (1960).

    MathSciNet  Google Scholar 

  23. L. V. Kantorovich and V. I. Krylov, Approximate Methods of Higher Analysis [in Russian], Gostekhizdat, Leningrad (1952).

    Google Scholar 

  24. V. P. Kostromin and V. I. Myachenkov, “Vibrations of open cylindrical shells of variable curvature,” Int. Appl. Mech., 8, No. 8, 912–914 (1972).

    Google Scholar 

  25. F. Riesz and B. Szökefalvi-Nagy, Functional Analysis, Ungar, New York (1955).

    Google Scholar 

  26. V. A. Solonnikov, “General boundary-value problems for Douglis-Nirenberg elliptic systems,” Izv. AN SSSR, Mat., 28, 665–706 (1964), Tr. Mat. Inst. AN SSSR, 110, No. 6, 233–297 (1970).

    MATH  MathSciNet  Google Scholar 

  27. G. M. Fikhtengol’ts, A Course of Differential and Integral Calculus [in Russian], Vol. 3, Nauka, Moscow (1969).

    Google Scholar 

  28. J. W. Rayleigh, “On waves propagated along the plane surface of an elastic solid,” Proc. Lond. Math. Soc., No. 253, 4–11 (1885/1986).

  29. Ya. M. Grigorenko and L. S. Rozhok, “Solving the stress problem for hollow cylinders with corrugated elliptical cross section,” Int. Appl. Mech., 40, No. 2, 169–175 (2004).

    Article  Google Scholar 

  30. Ya. M. Grigorenko and L. S. Rozhok, “Stress solution for transversely isotropic corrugated hollow cylinders,” Int. Appl. Mech., 41, No. 3, 277–282 (2005).

    Article  Google Scholar 

  31. Ya. M. Grigorenko and S. N. Yaremchenko, “Influence of variable thickness on displacements and stresses in nonthin cylindrical orthotropic shells with elliptic cross-section,” Int. Appl. Mech., 40, No. 8, 900–907 (2004).

    Article  Google Scholar 

  32. N. P. Semenyuk, I. Yu. Babich, and N. B. Zhukova, “Natural vibrations of corrugated cylindrical shells,” Int. Appl. Mech., 41, No. 5, 512–519 (2005).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Mechanics, National Academy of Sciences of Armenia, Yerevan

    G. R. Gulgazaryan & L. G. Gulgazaryan

Authors
  1. G. R. Gulgazaryan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. L. G. Gulgazaryan
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

__________

Translated from Prikladnaya Mekhanika, Vol. 42, No. 12, pp. 97–114, December, 2006.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gulgazaryan, G.R., Gulgazaryan, L.G. Vibrations of a corrugated orthotropic cylindrical shell with free edges. Int Appl Mech 42, 1398–1413 (2006). https://doi.org/10.1007/s10778-006-0210-0

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10778-006-0210-0

Keywords

Search

Navigation