A CS-Based Grant-Free Media Access Scheme for NOMA-Based Industrial IoTs with Location Awareness

Abstract

Grant-free media access is vital for applications in Industrial IoTs (IIoTs), where stringent delays are required. Recently, due to the capability of supporting parallel receptions, Non-Orthogonal Multiple Access (NOMA) has gained research interests in IIoTs. Obviously, combining them organically is beneficial for enhancing the delay performances. In this paper, for a typical convergecast wireless network where its data sink is NOMA-based, we propose a grant-free MAC (Media Access Contention) scheme based on Compressive Sensing in Busy Tone Channel (CSiBTC), by exploiting the transmission sparsity in IIoTs. First, a to-be transmitter acquires the identities of active transmitters with the proposed CSiBTC scheme completely by itself. Two construction methods for CSiBTC are proposed for two distinct application scenarios respectively. Then, given the locations of all wireless sensors and the data sink in the network, the to-be transmitter can find out if it is eligible for starting its transmission without impairing the on-going transmissions. The scheme is grant-free and makes the most use of the parallel reception capability of NOMA, and therefore both the delay performance and throughput performance can be improved with respect to the general CS-based MAC. Performance evaluations also strongly support the above conclusions.

In Industrial Internet of Things (IIoTs), various wireless sensors are usually installed for sensing environment or events, and one or more sinks are also installed for collecting information sensed by wireless sensors for professional analysis. For many industrial applications, such as the well-logging applications in oil and gas drilling, real-time analysis is compulsive to ensure industrial safety [1]. Therefore, the delay performance is the focus of these applications.

Transmission delay is one of the key factors which influence the delay performances. However, to achieve low-delay transmissions is not an easy task for wireless networks due to the wireless collisions. Recently, with the continuous development of Internet technology, the diversification of access technologies and the reduction of the cost of access equipment, the parallel multi-connection technology is used widely to transmit data between the two communication ends [2]. Obviously, transmission delay could be reduced by parallel accesses because more wireless accesses are provided. In one word, wireless parallel access technology is necessary for real-time IIoTs.

Relative to the ordinary broad-band parallel access technologies, such as Code-Division Multiple Access (CDMA), Frequency-Division Multiple Access (FDMA), power domain Non-Orthogonal Multiple Access (NOMA) can provide massive connections even with narrow bandwidth, and therefore it is more suitable for IIoTs.

The basic principle of power-domain NOMA is depicted in Fig. 1, where the toy network consists of two wireless sensors, $User_1$ and $User_2$, and one sink, BS. The received powers of $User_1$ and $User_2$ at BS are $rp_1$ and $rp_2$, respectively. If $rp_{1} \>rp_{2}$ and the Signal-to-Interference-plus-Noise Ratio (SINR) of $UE_1$ is no less than $\gamma$, i.e. ${SINR}_{1} \ge \gamma$, where $\gamma$ is the decoding threshold, signal from $User_1$ can be decoded successfully. Then, it is removed from the aggregate received signal, thus ${SINR}_{2}={rp}_{2}/{n}_{0}$, where $n_0$ is the ambient noise. If ${SINR}_{2} \ge \gamma$ holds, the signal from $User_2$ can also be successfully decoded. Obviously, compared with the traditional TDMA (Time-Division Multiple Access), the channel access time based on power-domain NOMA is reduced by half in this example.

Fig. 1

Power-domain NOMA in uplink transmissions

Despite of the parallel access capability provided by power-domain NOMA, the traditional Media Access Control (MAC) protocols, e.g., Carrier Sensing Multiple Access (CSMA/CA), cannot exploit it effectively. On the other hand, although some existing MACs for NOMA, such as [3], can take full advantage of the capability of parallel reception, they are grant-based and centralized in essence, and therefore, the delay of request-grant process cannot be exempted and may even grow rapidly with the increasing number of wireless sensors [4]. In one word, for achieving low delay, grant-free MAC schemes exploiting NOMA so as to support massive connections are urgently expected in IIoTs.

In this paper, given the necessary locations information, we introduce a new MAC scheme for exploiting the capability of NOMA without centralized control as follows. Illustrated in Fig. 2, based on the radio signal attenuation model, an inactive transmitter can find whether the active transmissions will be impaired by its to-be transmission, and whether its to-be transmission can be decoded correctly, by estimating the total interference at the data sink [5]. Only if both answers are yes, the inactive transmitter is eligible for turning active and then starts its transmission. Note that the wireless sensors and data sinks are generally not mobile in IIoTs, their locations are known after deployment. Thus, the assumption of known locations is indeed practical in IIoTs.

Obviously, to distributedly find the identities of active transmissions is the key problem, which is the so-called Blind Multi-User Detection (BMUD) problem. We solve it by exploiting the characteristic of transmission sparsity in IIoTs, which means that only a small portion of wireless sensors transmit simultaneously [6]. According to the statistics in [7], transmission sparsity is indeed realistic in many applications in IIoTs. Naturally, the characteristic of transmission sparsity inspires us to formulate BMUD under the Compressive Sensing (CS) framework [8]. In this paper, we then present a Compressive Sensing in Busy Tone Channel (CSiBTC) scheme which outputs the identities of active transmitters. The scheme lays the foundation for low access latency.

Fig. 2

Network topology of NOMA-based IIoTs

The novelities of this paper are as follows. We accomplish an accurate BMUD based on busy-tone channel instead of the regular scheme based on RSS (Received Signal Strength) of data packets, which not only greatly simplifies the system design of wireless sensors, but also refrains from the fluctuation of RSS due to varing data content. Besides, two construction methods for BMUD are proposed for two opposite application scenarios, i.e., the power-tolerate and the low-power IIoTs. Last but not the least, by fully utilizing the immobility in IIoTs, the BMUD is effectively combined with NOMA to enhance delay performance.

The remainder of this paper is organized as follows. Related works are presented in Sects. 2, and 3 elaborates the system model. The grant-free MAC scheme is introduced in Sect. 4, which includes the CSiBTC method for BMUD, estimating the channel gains to the data sink, and the criterion to be an active transmitter. Performance evaluation is carried out in Sect. 5, and the last section gives conclusions.

1 Related Works

The problem of MUD for grant-free NOMA has been discussed in many articles. At present, in the grant-free NOMA systems, MUD assumes that receivers fully know the user activity information, which is indeed very challenging, since a large number of users can randomly enter or leave the system. In other words, due to the uncertainty of user activity information during transmissions in IIoTs, active device detection is a critical step where BS needs to identify d active users from n total users in a specific time slot.

It has been found that CS can use a small number of random measurements to reconstruct the inherent high-dimension inherent sparse signal [9]. In current wireless systems, the number of active users is usually much smaller than the total users in the system, even during busy times [10]. This discovery indicates that perhaps CS can be used to detect active user information during the transmission process due to the inherent sparsity of user activities, and also provide new ideas for random accesses in wireless sensor networks. CS-MUD is considered as a promising candidate to enable grant-free NOMA for mMTC.

Literature [11], which is inspired by the theory of CS and random channel access, proposes a distributed energy-efficient random access scheme, which guarantees that a small number of packages are randomly selected from different wireless sensors and reconstructed accurately with high probability. In this paper, the analytical expression of the minimum bandwidth required to support RACS and the limit of its energy consumption are presented. [12] proposes the combination of CS and the Message Passing Algorithm (MPA) to design the CS-MPA detector, in order to realize the user activity and data detection for grant-free NOMA. Similarly, by observing a structured sparsity of user activity in mMTC, [13] proposes a low-complexity access scheme based on structured CS for NOMA MUD to further improve the signal detection performance.

As the sparsity of active users varies from time to time, a low complexity dynamic CS-based MUD is proposed in [14]. This is based on the idea that while users can access/leave the network systems at random, some users usually transmit their information at a high probability in adjacent time slots. In [15], a CS-based multi-user interference cancellation (CS-IC) method is proposed to detect the active users and activity information of the grant-feee NOMA system. The method utilizes the temporal correlation of active subscriber sets to enable active users and data detection in the uplink NOMA system within multiple contiguous time slots. Furthermore, the CS-IC detection method can get better Block Error Ratio (BLER) performance than the MMSE-IC detection algorithm when the active users are sparse. By exploiting this temporal correlation, the estimated active user set in a particular time slot is used as the initial set to estimate the transmitted signal in the next time slot in the dynamic CS-based MUD.

2 System Model

We consider a single-hop wireless network consisting of n single-antenna wireless sensors $u_1, u_2, \ldots , u_n$, and a single-antenna data sink $u_0$. The coordinate of wireless sensor $u_i$ is $(x_i, y_i)$ for all $i \in [1,n]$, and that of the data sink is (0, 0).¹ The sink is equipped with one SIC-based receiver which can decode multiple signals simultaneously, provided that SINR of every signal after interference cancellation is larger than the decoding threshold $\gamma$, which is greater than 1 in general. There are one data channel and a busy tone channel across the network, and every wireless sensor can sense the received power of the busy tone.

For transmissions from $u_i$, if its transmit power at the busy tone channel is $tp_i$, the corresponding reception power at $u_j$ is ${rp}_{{ij}}={g}_{{ij}} {tp}_{{i}}$, for ${i} \in [1, {n}], {j} \in [1, {n}]$, where $g_{ij}$ is the channel gain of $u_i$ w.r.t. $u_j$. In general, $g_{ij}$ has great relation with $d_{ij}$, where ${d}_{{ij}}=\sqrt{\left( {x}_{{i}}-{x}_{{j}}\right) ^{2}+\left( {y}_{{i}}-{y}_{{j}}\right) ^{2}}$ is the Euler distance from $u_i$ to $u_j$, and we assume that $g_{i j}=\frac{d_{i j}^{\alpha }}{d_{l k}^{\alpha }} g_{l k}+n_{0}$ for any $i, j, l, {k} \in [1, {n}]$ , where $\alpha$ is the propagation coefficient, and ${n}_{0} \sim \mathcal {N}\left( 0, \sigma ^{2}\right)$ is the stochastic noise. We assume that $g_{ij}$ keeps unchanged during a frame time.

We only consider perfect interference cancellation, i.e., the residual error is zero, which has been widely adopted in NOMA related researches [16].

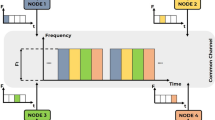
The busy tone channel is synchronized across the network, and time is divided into frames. Specifically, one frame consists of $h(h\le n)$ slots², just as illustrated in Fig. 3.

The busy tone channel and data channel are synchronized across the network. The CSiBTC method that we proposed is conducted in the busy tone channel, and user’s listening activity is allowed only at the beginning of the frame. We also assume that the transmit power of the busy tone channel is tunable, while that of data channel is fixed as P³.

Fig. 3

Frame structure of busy tone channel

3 CS-Based Media Access Scheme

This section includes three subsections. In the first subsection, CSiBTC for finding the active transmitters is presented. The next subsection introduces how to estimate the channel gain w.r.t. the data sink provided that locations are given. Based on the above two steps, an inactive transmitter can determine whether it is suitable for turning active, which is introduced in the third subsection. An estimator for network sparsity is introduced in the last subsection, so as to break the assumption of the known transmission sparsity.

3.1 Identifying Active Transmitters

Definition 1

Users Activity Status Vectors (UASV) is a vector $\left( s_{1}, s_{2}, \dots , s_{n}\right) ^{{T}}$, where $s_{i}=\left\{ \begin{array}{ll}{1,} &{}\quad {u_{i} \text{ is } \text{ an } \text{ active } \text{ transmitter } } \\ {0,} &{}\quad {u_{i} \text{ is } \text{ not } \text{ an } \text{ active } \text{ transmitter } }\end{array}\right.$.

For the slot j in a frame, an active transmitter, e.g., $u_i$, sends busy tone at busy tone channel with power $tp_{ji}$. Therefore, for an inactive transmitter, e.g., $u_k$, its receiving powers during the frame which includes h slots are

$$\begin{aligned} \begin{aligned} \left[ \begin{array}{c}{{r} {p}_{{1}}} \\ {{r} {p}_{2}} \\ {\vdots } \\ {{r} {p}_{{h}}}\end{array}\right] =\left[ \begin{array}{cccc}{{t} {p}_{{1} 1}} &{} {{t} {p}_{12}} &{} {\ldots } &{} {{t} {p}_{1 n}} \\ {{t} {p}_{21}} &{} {{t} {p}_{22}} &{} {\ldots } &{} {{t} {p}_{2 n}} \\ {\vdots } &{} {\vdots } &{} {\ddots } &{} {\vdots } \\ {{t} {p}_{{h} 1}} &{} {{t} p_{{h} 2}} &{} {\cdots } &{} {{t} {p}_{{\text {hn}}}}\end{array}\right] \left[ \begin{array}{c}{{g}_{{1 k}} {s}_{1}} \\ {{g}_{2 {k}} {s}_{2}} \\ {\vdots } \\ {{g}_{n {k}} {s}_{{n}}}\end{array}\right] \end{aligned}, \end{aligned}$$

(1)

where $rp_j$ is the received power at the slot j in the frame. For convenience, the above equality group is briefly notated as $R_p=T_pG{S^*}$, where $R_p$ is termed as the observation vector, $T_p$ is the power pattern matrix, and $GS^*$ is the product of channel gain vector of $u_k$ with UASV. Now, our task, i.e., BMUD, is to infer UASV based on the knowledge of $R_p$, provided that h and $T_p$ are known in advance.

Definition 2

d-sparsity of UASV. A UASV is d-sparsity if the number of non-zero element in the UASV is no larger than d.

Theorem 1

If S is d-sparsity, to get a unique solution to (1), any 2d columns of $T_p$ should be linearly independent.

Proof

Please refer to Theorem 1 in [17]. □

Note that Theorem 1 reveals that $h\ge 2d$ must hold, i.e., 2d is the minimum value for h.

If $p_1\ne \ p_2\ne \ldots \ne p_n$, since any 2d columns of the following Vandermonde matrix $\left[ \begin{array}{cccc}{1} &{} {1} &{} {\ldots } &{} {1} \\ {p_1} &{} {p_2} &{} {\cdots } &{} {p_n} \\ {\vdots } &{} {\vdots } &{} {\ddots } &{} {\vdots } \\ {p_1^{2d-1}} &{} {p_2^{2d-1}} &{} {\cdots } &{} {p_n^{2d-1}}\end{array}\right]$ are linearly independent, the minimum access delay can be achieved if the above Vandermonde matrix is used as the power pattern matrix. There are n columns in the Vandermonde matrix, and every column is assigned uniquely to a wireless sensor aforehand. For example, $p_{i}^{j}$, i.e., $p_{i}$ to the power of j, is the transmitting power of $u_i$ at slot j, where $i \in [1, n], j \in [0, h-1]$.

Once $u_k$ knows its channel gain vector G, we can get UASV as follows; $s_{i}=\left\{ \begin{array}{cc}{1,} &{} { \text{ if } g_{i k} s_{i}>\epsilon } \\ {0,} &{} { \text{ if } g_{i k} s_{i}\le \epsilon }\end{array},\quad i=1,2, \ldots , n\right.$, where $\epsilon$ is a pre-determined noise level of the system⁴. Furthermore, $u_k$ can also gets $g_{ik}$, which is its channel gain of $u_i$ w.r.t. $u_k$. The information will be used later by $u_k$ to precisely estimate the channel gain of $u_i$ w.r.t. the data sink, whatever the noise item $n_0$ in the channel gain model is.

The values of ${p_1}, {p_2}, \ldots , {p_n}$ in the Vandermonde matrix are closely related with the usable power levels of transmitters. Obviously, $p_{i}^{j}$ should be usable power level. For example, if the usable power set is $\left\{ 2^{0}, 2^{1}, \ldots , 2^{{q}}\right\}$⁵, then a feasbile power setting is that$\quad {p}_{{i}}=2^{(i-1)}, \forall {i} \in [2, {n}]$. In that case, $q\ge {n}(2{d}-1)$ must be held so as to provide enough transmiting power levels.

A shortcoming of the above transmit power matrix based on Vandemonde matrix is that the dynamic range of the transmiting power is too wide, which brings great challenges for power amplifiers. Obviously, the construction method is only fit for the power-tolerate application scenarios. For the low-power application, another construction method is proposed based on the following theorem.

Theorem 2

Let $T_p$ be an $h\times n$ Gaussian random matrix, i.e., every element of ${T_p}\sim N\left( 0, \frac{1}{{h}}\right)$, then there exists a small positive real e, which is related with h/n, such that equality group (1) can have at most one d-sparsity solution with overwhelming probability,⁶ provided $h \ge edlog(n/d)$.

Proof

Please refer to Chap. 9 in [18]. □

In that case, DMUD designed based on Theorem 2 is effective only if the power level is a stoachastic Gaussian variable, and the design is obviously suitable for low-power applications in IIoTs. Of course, the extra cost of the method is the possibility of failure in BMUD.

3.2 Estimating Channel Gains of Active Transmitters w.r.t. Data Sink

Obviously, to keep from impairing on-going transmissions, any inactive wireless sensor has to find whether it is suitable for starting a new transmission. Since the SIC-based data sink is for parallel data collection, a to-be transmitter has to estimate the residual decoding capability of the data sink. To achieve it, the channel gains of all active transmitters w.r.t. the data sink have to be derived.

W.l.o.g., assume that the active wireless sensors set estimated by $u_k$ is $\left\{ {u}_{{a}_{1}}, {u}_{{a}_{2}}, \ldots , {u}_{{a}_{{m}}}\right\}$ where $m\le k$, and their channel gains w.r.t. $u_k$ are ${g}_{{a_{1}k}}, {g}_{{a_{2}k}}, \ldots , {g}_{{a_{m}k}}$, respectively. Based on the signal attenuation model, since ${g}_{{{a_j}k}}=\frac{{d}_{ {a}_{{j}}0}^{\alpha }}{{d}_{{{a_j}k}}^{\alpha }} {g}_{ {a}_{{j}}0}+{n}_{{aj}}$ , $\forall {j} \in [1, {m}],$ where ${n}_{{a_j}} \sim {N}\left( 0, \sigma _{{a_j}}^{2}\right)$, and ${g}_{{a_j}0}$ is the channel gain of $u_{a_j}$ w.r.t. the data sink, the channel gains of all active transmitters w.r.t. the data sink estimated by $u_k$ can be estimated using the criterion of achieving the minimum mean square error as follows:

$$\begin{aligned}&{\mathop {argmin}\limits _{\widehat{{g}_{a {0}}}}} \left( \left\| {g}_{a {0}}-\widehat{{g}_{a {0}}}\right\| ^{2}\right) \end{aligned}$$

(2)

$$\begin{aligned}&s.t. \quad {g}_{{ak}}=H\times g_{a {0}}+{n}_{{a}} \end{aligned}$$

(3)

where,

$$\begin{aligned}&{g}_{{ak}}=\left( {g}_{{a}_{1}k}, {g}_{{a}_{2}k}, \ldots , {g}_{{a}_{{m}}k}\right) ^{{T}}, {n}_{{a}}=\left( {n}_{{a}_{{1}}}, {n}_{{a}_{2}}, \ldots , {n}_{{a}_{{m}}}\right) ^{{T}},\\&{H}=\left[ \begin{array}{cccc}{\frac{{d}_{ {a}_{1}0}^{\alpha }}{{d}_{{a}_{1}k}^{\alpha }}} &{} {0} &{} {\cdots } &{} {0} \\ {0} &{} {\frac{{d}_{{a}_{2}0}^{\alpha }}{{d}_{{a}_{2}k}^{\alpha }}} &{} {\cdots } &{} {0} \\ {\vdots } &{} {\vdots } &{} {\ddots }&{} {\vdots } \\ {0} &{} {0} &{} {\cdots } &{} {\frac{{d}_{{a}_{m}0}^{\alpha }}{{d}_{{a}_{m}k}^{\alpha }}}\end{array}\right] , \end{aligned}$$

and $\widehat{g_{a0}}=\left( \frac{d_{ a_{1}k}^{\alpha }}{d_{a_{1}0}^{\alpha }} g_{a_{1}k}, \frac{d_{a_{2}k}^{\alpha }}{d_{a_{2}0}^{\alpha }} g_{ a_{2}k}, \dots , \frac{d_{{{a}_m} k}^{\alpha }}{d_{ a_{m}0}^{\alpha }} g_{a_{m}k}\right)$.

${g}_{{a0}}$ can thus be estimated using the following theorem.

Theorem 3

$\widehat{g_{a0}}$ is the solution to the optimization problem (2) and (3).

Proof

Based on $(3), \quad g_{a_{j}0}=\frac{g_{ a_{j}k}-n_{a_{j}}}{H_{\text{ jj } }}, j=$ $1,2,\ldots ,m$. Since $n_{a_{j}} \sim \mathcal {N}\left( 0, \sigma _{a_{j}}^{2}\right) , g_{ a_{j}0} \sim \mathcal {N}\left( \frac{g_{{a}_{j}k}}{H_{{jj}}},\left( \frac{\sigma _{a_{{j}}}}{H_{{jj}}}\right) ^{2}\right)$ and therefore $\left( {g}_{{a}_{{j}}0}-\widehat{{g}_{ {a}_{{j}}0}}\right) \sim \mathcal {N}\left( \frac{{g}_{{a}_{{j}}k}}{{H}_{{jj}}}-\widehat{{g}_{ {a}_{{j}}0}},\left( \frac{{\sigma }_{{a}_{{j}}}}{{H}_{{jj}}}\right) ^{2}\right)$. Since ${E}\left( \left( {g}_{{a}_{{j}}0}-\widehat{{g}_{ {a}_{{j}}0}}\right) ^{2}\right) =$ $\left( \frac{{g}_{a_{{j}}k}}{{H}_{{jj}}}-\widehat{{g}_{ {a}_{{j}}0}}\right) ^{2}+\left( \frac{{\sigma }_{{a}_{{j}}}}{{H}_{{jj}}}\right) ^{2}, \quad \min \limits _{\widehat{{g}_{{a}_{{j}}0}}} {E}\left( \left( {g}_{ {a}_{{j}}0}-\widehat{{g}_{{a}_{j}0}}\right) ^{2}\right) =$ $\min \limits _{\widehat{{g}_{ {a}_{j}0}}}\left( \left( \frac{{g}_{ {a}_{j}k}}{{H}_{{jj}}}-\widehat{{g}_{ {a}_{j}0}}\right) ^{2}+\left( \frac{\sigma _{a_{j}}}{{H}_{{jj}}}\right) ^{2}\right)$. Therefore, the optimal $\widehat{{g}_{ a_{j}0}}=\frac{{g}_{{a}_{j}k}}{{H}_{{jj}}}=\frac{{d}_{{a_j}k}^{\alpha }}{{d}_{{a}_{j}0}^{\alpha }} {g}_{{a}_{j}k}, {j}=1,2, \ldots , {m}. \min \limits _{\widehat{{g}_{ {a}0}}} {E}\left( \Vert {g}_{a 0}-\widehat{{g}_{a 0}} \Vert ^{2}\right) =\min \limits _{\widehat{{g}_{a 0}}} \left( \sum _{{j=1}}^{{m}} {E}\left( \left( {g}_{{a}_{{j}}0}-\right. \right. \right.$ $\left. \left. \widehat{{g}_{ {a}_{j}0}})^{2}\right) \right) =\sum _{j=1}^{{m}} \min \limits _{\widehat{{g}_{{a}_{j}0} }} {E}\left( \left( {g}_{{a}_{{j}}0}-\widehat{{g}_{ {a}_{{j}}0}}\right) ^{2}\right)$. Therefore, the optimal ${\widehat{{g}_{{a0}}}}$ estimated at $u_k$ is $\left( \frac{{d}_{{a}_{1}k}^{{\alpha }}}{{d}_{{a}_{1}0}^{{\alpha }}} {g}_{{a}_{1}k}, \frac{{d}_{{a}_{2}k}^{\alpha }}{{d}_{{a}_{2}0}^{\alpha }} {g}_{{a}_{2}k}, \ldots , \frac{{d}_{{a}_{{m}}k }^{\alpha }}{{d}_{{a}_{{m}}0}^{\alpha }} {g}_{{a}_{{m}}k}\right)$. □

3.3 The Criterion to be Active Transmitter

Definition 3

Decodable Sequence. $\left\langle {u}_{{m}}, {u}_{{m}-1}, \dots , {u}_{{1}}\right\rangle$ is a decodable sequence if and only if ${SINR}_{{i}}=\frac{{g}_{{i}0} {P}}{\sum _{{j}=1}^{{i}-1} {g}_{{j}0} {P}+{n}_{0}} \ge \gamma , {i}\in [1,m]$, where P is the transmiting power in data channel, and $g_{i0}$ is the channel gain of $u_i$ w.r.t. $u_0$.

Obviously, since $\gamma >1$, if $\left\langle {u}_{{m}}, {u}_{{m}-1}, \dots , {u}_{{1}}\right\rangle$ is a decodable sequence, ${g}_{{m}0}>{g}_{ {m0}-1}>\cdots >{g}_{10}$.

Theorem 4

Given active wireless sensors set $\left\{ {u}_{1}, {u}_{2}, \dots , {u}_{{m}}\right\}$, w.l.o.g., assume that $\left\langle {u}_{{m}}, {u}_{{m}-1}, \dots , {u}_{{1}}\right\rangle$ is a decodable sequence. An inactive transmitter $u_k$ can turn active, if and only if any of the following three cases holds.

• (1) There is a ${j} \in [1, {m}-1],$ such that ${g}_{ {j0}}<{g}_{{k0}}<$ ${g}_{({j}+1)0},\left\langle {u}_{{m}}, \ldots , {u}_{{j}+1}, {u}_{{k}}, {u}_{{j}}, \ldots , {u}_{1}\right\rangle$ is a decodable sequence.

• (2) ${g}_{{k0}}>{g}_{ {m0}}$ and $\left\langle {u}_{{k}},{u}_{{m}}, {u}_{{m}-1}, \dots , {u}_{{1}}\right\rangle$ is a decodable sequence.

• (3) ${g}_{{k0}}<{g}_{{10}}$ and $\left\langle {u}_{{m}}, {u}_{{m}-1}, \dots , {u}_{1},{u}_{{k}}\right\rangle$ is a decodable sequence.

Proof

Since $\gamma >1$, for any an active wireless sensor set, there is at most one decodable sequence, i.e., the wireless sensors sequence which is sorted by the decreasing order of their channel gains. □

For any inactive transmitter, after it finished estimating the channel gain of the active wireless sensors, according to the channel gain of itself, it judges whether one of the above three cases are held and the corresponding ordered sequence is decodable. If the answer is yes, it can turn active, and in all other cases, it must keep inactive.

3.4 Estimating Sparsity

The above theory is based on the assumption that the transmission sparsity is known in prior, which is impractical indeed, and therefore, we have to estimate it.

In [19], it presents an unbiased estimator $\widehat{{x}}=\frac{\widehat{\Vert {x}\Vert _{1}}^{2}}{\widehat{\Vert {x}\Vert _{2}}^{2}}$ for the sparsity of vector x, where $\widehat{\Vert {x}\Vert _{p}}$ is an estimator for the p-norm of vector x. Combined with CSiBTC scheme, the estimator is executed as follows.

• (1) Generate a Cauchy random matrix $[a_{ij}]$ of dimension $\lfloor n/2\rfloor \times n$, where every element obeys $C(0,\gamma )$ and $\gamma >0$ is the decoding threshold of SIC decoder. Then, modify $a_{i j}$ as $a_{i j} / g_{j0}$ for all $i \in [1, \lfloor n/2\rfloor ], j \in [1, n]$.

• (2) Using CSiBTC with the modified Cauchy matrix, the sink computes the statistic $\widehat{\Vert {x}\Vert _{1}}=\frac{1}{\gamma } {median}\left( \left| {rp}_{1}\right| ,\left| {rp}_{2}\right| , \ldots ,\left| {rp}_{\lfloor n/2\rfloor }\right| \right)$, where median(x) is for the median value of array x.

• (3) Generate a Gaussian random matrix $[a_{ij}]$ of dimension $\lceil n/2\rceil \times n$, where exery element obeys $N(0,\gamma ^2)$, and modify $a_{i j}$ as $a_{i j} / g_{ j0}$ for all $i \in [1, \lceil n/2\rceil ], j \in [1, n]$.

• (4) Using CSiBTC with the modified Gaussian matrix, the sink compute the statistic $\widehat{\Vert {x}\Vert _{2}}^2$= $\frac{1}{\gamma ^{2}\lceil n / 2\rceil }\left( {r p}_{1}^{2}+{r p}_{2}^{2}+\cdots +{r p}_{\lceil n / 2\rceil }^{2}\right)$.

• (5) Estimated sparsity is thus $\frac{\widehat{\Vert {x}\Vert _{1}}^{2}}{\widehat{\Vert {x}\Vert _{2}}^{2}}$. Sparsity estimation can be executed periodically, in case that wireless sensors are dynamically added or removed.

4 Performance Evaluations

We consider a wireless network consisting of 30 sensor nodes and an SIC-based data sink. In the network, these sensor nodes randomly distributed in a circular area with a diameter of 120 meters, and the sink is located at the center of the circle area.

In all the following simulation experiments, unless otherwise indicated, the network parameters are sets as follows: decoding threshold $\gamma$ of SIC receiver is 2, channel attenuation factor $\alpha$ is 2.5, and environmental noise power $n_0$ is $-116dBm/Hz$, and the bandwidth of busy tone channel is 30kHz. The transmission power of data band of all wireless sensors is 0dBm.

In this section, we will analyze the system’s Bit Error Rate (BER)⁷ performance and real-time⁸ performance when the data sink is equipped with a k-SIC receiver where $k=1,2,3$,⁹ respectively. Real-time performance is denoted by the average delay of data packets, while system BER reveals the occurrence rate of wireless collisions. Obviously, the smaller is the system BER, less wireless collisions take place, which shows that our algorithm is more effective.

Fig. 4

The meaning of boxplot

We repeat every experiment a thousand times and plot the results using boxplot as shown above in Fig. 4.¹⁰ The experimental results of system BER are illustrated in Figs. 5 and 6, while that of average delay is in Fig. 7. The x-axis is for $R_{packet}$, which is the packet generation rate of users. In any frame time, each user has the same generation rate. We assume that the length of single data packet is 100–200 bits and that one data packet cannot be sent completely in a frame. So, multiple frames will be combined to form a complete data packet. That is to say, the transmission of a single data packet may span 2–3 frame times.

4.1 System BER of the Proposed Distributed Media Access

Fig. 5

System BER with packet generation rate

The BER performance is shown in Fig. 5 where the value of $R_{packet}$ varies from 0.01 to 0.1. The y-axis is $pack_{fail}/pack_{sum}$, i.e., the system BER. First, we aim to reveal how the system BER is influenced by generation rate of packet with various SIC receivers. As shown in the Fig. 5, for the three cases of 1-SIC, 2-SIC and 3-SIC, although their system BER always increases with increasing $R_{packet}$, their increasing rates are distinct. For the case of 1-SIC, the system BER increases rapidly when $R_{packet}\le 0.04$. When $R_{packet}>0.04$, the system BER is close to 1.0 and keeps stable, which means that all packets collide and cannot be decoded correctly. For the case of 2-SIC, the peak system BER occurs when $R_{packet}=0.06$. For 3-SIC, the BER basically stabilizes and approaches 1.0 when $R_{packet}$ varies from 0.08 and 0.09. The above results in Fig. 5 show that, the system BER of 3-SIC is always smaller than that of 2-SIC and far less than that of 1-SIC, as long as $R_{packet} < 0.1$, which is obviously consistent with our intuitions.

Fig. 6

System BER with packet generation rate

When $R_{packet}$ is greater than 0.1, the experimental result of the system BER is shown in Fig. 6, of which x-axis is from 0.1 to 1. It can be known that in any slot, there are at least 3 users who want to send packet if $R_{packet} > 0.1$. Obviously, the number of data packets they send is far more than the decoding capability of the SIC receiver, and thus collisions will occur with a high probability. As shown in Fig. 6, whatever the receiver is, the system BER is greater than 0.9, which shows that almost all of the data packets have failed. The above phenomenon shows that our algorithm which is built on the prerequisite of transmission sparsity is not effective for the scenarioes of high network loads.

4.2 Real-time Performance of the Proposed Distributed Media Access

The simulation result of the system real-time performances is shown in Fig. 7. The range of x-axis is intentionally limited from 0.01 to 0.1, since system BER approaches 1.0 if $R_{packet} > 0.1$. The y-axis represents the average delay, which is the total delay of the data packets divided by the number of data packets. Obviously, the delay performance of the case of 3-SIC is much better than these of 2-SIC and 1-SIC, which is certainly since 3-SIC decoders have stronger decoding capability.

As can be seen from Fig. 7, for the case of 1-SIC, the delay continues to increase until $R_{packet}=0.04$, and then it keeps stable. The reason is as follows: when $R_{packet}$ is less than 0.04, as the number of data packets increases, the to-be transmitter will have to postpone its transmissions once it detects a busy channel, so the system delay will increase accordingly. However, when $R_{packet}$ is greater than 0.04, basically every to-be transmitter has packets to transmit. Due to the deadlock of detecting busy-tone channel, all transmitters turn active. So the transmission delay keeps stable, and the system BER is close to 1.0 at that time.

Fig. 7

Real-time performance with packet generation rate

The same is true for the cases of 2-SIC and 3-SIC. From the experimental graph of the system BER and the average delay, we can find that the value of $R_{packet}$ when BER is 1.0 is exactly same to that when the average delay reaches its peak.

5 Conclusions

For IIoTs, delay performance may be one of the most important metrics in wireless communication protocols. The technique of power-domain NOMA has great potentions in enhancing delay performance for IIoTs. In this paper, a grant-free real-time MAC based on compressive sensing is proposed, and the MAC is optimized for both the power-tolerate and the low-power scenarioes. The MAC scheme is not only grant-free but also low-latency, which lays solid foundations for applications of large-scale IIoTs.