Skip to main content
SpringerLink
Log in

Sharing Genuine Entanglement of Generalized Tripartite States by Multiple Sequential Observers

  • Research
  • Published:
International Journal of Theoretical Physics Aims and scope Submit manuscript

Abstract

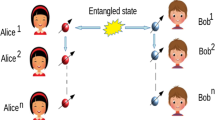
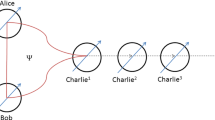
Genuine entanglement serves as a valuable resource for multipartite quantum information processing. Recently, the ability to share the genuine entanglement among a long sequence of independent observers has gained considerable attention, especially when the state preparation faces significant limitations. Firstly, this paper focuses on investigating the sharing ability of genuine tripartite entanglement under unilateral sequential measurements. We propose a measurement strategy for generalized tripartite Greenberger-Horne-Zeilinger (GHZ) states to enable arbitrarily long sequence of independent observers to detect the genuine entanglement using entanglement witnesses. Moreover, when the sharpness parameters of each sequential observer’s measurement settings are equal, we give the correlation between the controllable angle of generalized GHZ state and the maximum number of sequential observers capable of detecting genuine entanglement. In particular, we identify the controllable angle range within which the same number of such observers can be achieved for generalized GHZ states as with the maximally entangled GHZ state. We also determine the controllable angle range for generalized tripartite \(\varvec{W}\) states, where the number of sequential observers can be same as that with maximally entangled \(\varvec{W}\) state. Furthermore, we design a measurement strategy for the trilateral sequential scenario, demonstrating that the genuine tripartite entanglement of any generalized GHZ state can be shared by arbitrarily many groups of observers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Pironio, S., Acín, A., Massar, S., et al.: Random numbers certified by Bell’s theorem. Nature 464, 1021 (2010)

    Article  ADS  CAS  PubMed  Google Scholar 

  2. Ekert, A.K.: Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661 (1991)

    Article  ADS  MathSciNet  CAS  PubMed  Google Scholar 

  3. Barrett, J., Hardy, L., Kent, A.: No signaling and quantum key distribution. Phys. Rev. Lett. 95, 010503 (2005)

    Article  ADS  PubMed  Google Scholar 

  4. Gühne, O., Tóth, G.: Entanglement detection. Phys. Rep. 474, 1 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  5. Guhne, O., Seevinck, M.: Separability criteria for genuine multiparticle entanglement. New J. Phys. 12, 053002 (2010)

  6. Scarani, V., Gisin, N.: Quantum communication between \(N\) partners and Bell’s inequalities. Phys. Rev. Lett. 87, 17901 (2001)

  7. Murao, M., Jonathan, D., Plenio, M.B., Vedral, V.: Quantum telecloning and multiparticle entanglement. Phys. Rev. A 59, 156 (1999)

    Article  ADS  CAS  Google Scholar 

  8. Hyllus, P., Laskowski, W., Krischek, R., Schwemmer, C., et al.: Fisher information and multiparticle entanglement. Phys. Rev. A 85, 022321 (2012)

  9. Chruściński, D., Sarbicki, G.: Entanglement witnesses: construction, analysis and classification. J. Phys. A 47, 483001 (2014)

    Article  MathSciNet  Google Scholar 

  10. Horodecki, R., Horodecki, P., Horodecki, M., et al.: Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  11. Gühne, O., Hyllus, P.: Investigating three qubit entanglement with local measurements. Int. J. Theor. Phys. 42, 1001 (2003)

    Article  MathSciNet  Google Scholar 

  12. Uffink, J.: Quadratic Bell inequalities as tests for multipartite entanglement. Phys. Rev. Lett. 88, 230406 (2002)

    Article  ADS  MathSciNet  PubMed  Google Scholar 

  13. Mermin, N.D.: Extreme quantum entanglement in a superposition of macroscopically distinct states. Phys. Rev. Lett. 65, 1838 (1990)

    Article  ADS  MathSciNet  CAS  PubMed  Google Scholar 

  14. Brunner, N., Cavalcanti, D., Pironio, S., et al.: Bell nonlocality. Rev. Mod. Phys. 86, 419 (2014)

    Article  ADS  Google Scholar 

  15. Clauser, J.F., Horne, M.A., Shimony, A., et al.: Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880 (1969)

    Article  ADS  Google Scholar 

  16. Aharonov, Y., Albert, D.Z., Vaidman, L.: How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 60, 1351 (1988)

    Article  ADS  CAS  PubMed  Google Scholar 

  17. Brown, P.J., Colbeck, R.: Arbitrarily many independent observers can share the nonlocality of a single maximally entangled qubit pair. Phys. Rev. Lett. 125, 090401 (2020)

    Article  ADS  MathSciNet  CAS  PubMed  Google Scholar 

  18. Xiao, Y., Guo, F., Dong, H., et al.: Expanding the sharpness parameter area based on sequential \(3\rightarrow 1\) parity-oblivious quantum random access code. Quantum Inf. Process. 22, 195 (2023)

    Article  ADS  Google Scholar 

  19. Das, D., Ghosal, A., Sasmal, S., et al.: Facets of bipartite nonlocality sharing by multiple observers via sequential measurements. Phys. Rev. A 99, 022305 (2019)

    Article  ADS  CAS  Google Scholar 

  20. Gupta, S., Maity, A.G., Das, D., et al.: Genuine Einstein-Podolsky-Rosen steering of three-qubit states by multiple sequential observers. Phys. Rev. A 103, 022421 (2021)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  21. Jebaratnam, C., Das, D., A, Roy., et al.: Tripartite-entanglement detection through tripartite quantum steering in one-sided and two-sided device-independent scenarios, Phys. Rev. A 98, 022101 (2018)

  22. Silva, R., Gisin, N., Guryanova, Y., et al.: Multiple observers can share the nonlocality of half of an entangled pair by using optimal weak measurements. Phys. Rev. Lett. 114, 250401 (2015)

    Article  ADS  PubMed  Google Scholar 

  23. Zhang, T., Fei, S.M.: Sharing quantum nonlocality and genuine nonlocality with independent observables. Phys. Rev. A 103, 032216 (2021)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  24. Cheng, S., Liu, L., Baker, T.J., et al.: Limitations on sharing Bell nonlocality between sequential pairs of observers. Phys. Rev. A 104, L060201 (2021)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  25. Zhu, J., Hu, M.J., Li, C.F., et al.: Einstein-Podolsky-Rosen steering in two-sided sequential measurements with one entangled pair. Phys. Rev. A 105, 032211 (2022)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  26. Ren, C., Liu, X., Hou, W., et al.: Nonlocality sharing for a three-qubit system via multilateral sequential measurements. Phys. Rev. A 105, 052221 (2022)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  27. Saha, S., Das, D., Sasmal, S., et al.: Sharing of tripartite nonlocality by multiple observers measuring sequentially at one side. Quantum Inf. Process. 18, 42 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  28. Curchod, F.J., Johansson, M., Augusiak, R., et al.: Unbounded randomness certification using sequences of measurements. Phys. Rev. A 95, 020102 (2017)

    Article  ADS  Google Scholar 

  29. Mohan, K., Tavakoli, A., Brunner, N.: Sequential random access codes and self-testing of quantum measurement instruments. New J. Phys. 21, 083034 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  30. Tavakoli, A., Cabello, A.: Quantum predictions for an unmeasured system cannot be simulated with a finite-memory classical system. Phys. Rev. A 97, 032131 (2018)

    Article  ADS  CAS  Google Scholar 

  31. Srivastava, C., Pandit, M., Sen, U.: Entanglement witnessing by arbitrarily many independent observers recycling a local quantum shared state. Phys. Rev. A 105, 062413 (2022)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  32. Bera, A., Mal, S., Sen(De), A., et al.: Witnessing bipartite entanglement sequentially by multiple observers. Phys. Rev. A 98, 062304 (2018)

  33. Pandit, M., Srivastava, C., Sen, U.: Recycled entanglement detection by arbitrarily many sequential and independent pairs of observers. Phys. Rev. A 106, 032419 (2022)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  34. Maity, A.G., Das, D., Ghosal, A., et al.: Detection of genuine tripartite entanglement by multiple sequential observers. Phys. Rev. A 101, 042340 (2020)

    Article  ADS  CAS  Google Scholar 

  35. Xi, Y., Li, M.S., Fu, L., et al.: Sharing tripartite nonlocality sequentially by arbitrarily many independent observers. Phys. Rev. A 107, 062419 (2023)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  36. Nieto-Silleras, O., Pironio, S., Silman, J.: Using complete measurement statistics for optimal device-independent randomness evaluation. New J. Phys. 16, 013035 (2014)

    Article  ADS  Google Scholar 

  37. Busch, P.: Unsharp reality and joint measurements for spin observables. Phys. Rev. D 33, 2253 (1986)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  38. Wath, Y., Hariprasad, M., Shah, F., et al.: Eavesdropping a quantum key distribution network using sequential quantum unsharp measurement attacks. Eur. Phys. J. Plus 138, 54 (2023)

    Article  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant Nos. 62171056, 61973021) and Henan Key Laboratory of Network Cryptography Technology (LNCT2022-A03).

Author information

Authors and Affiliations

  1. School of Science, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Yao Xiao & Fenzhuo Guo

  2. Henan Key Laboratory of Network Cryptography Technology, Zhengzhou, 450001, China

    Yao Xiao & Fenzhuo Guo

  3. State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Yao Xiao, Fenzhuo Guo & Qiaoyan Wen

  4. School of Instrumentation Science and Opto-Electronics Engineering, Beihang University, Beijing, 100191, China

    Haifeng Dong

Authors
  1. Yao Xiao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fenzhuo Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Haifeng Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Qiaoyan Wen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fenzhuo Guo.

Ethics declarations

Conflicts of interest

The authors declare no conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The entanglement witness operator \(\mathcal {W}_{\textsf{GHZ}}\) given by (3) can be decomposed as [4]

$$\begin{aligned} \mathcal {W}_{\textsf{GHZ}}= & {} \dfrac{1}{8}\bigg [3\mathbb {I}\otimes \mathbb {I}\otimes \mathbb {I}-\mathbb {I}\otimes \sigma _z\otimes \sigma _z-\sigma _z\otimes \mathbb {I}\otimes \sigma _z-\sigma _z\otimes \sigma _z\otimes \mathbb {I}\nonumber \\{} & {} -2\sigma _x^{\otimes 3}+\sqrt{2}\left( \dfrac{\sigma _x+\sigma _y}{\sqrt{2}}\right) ^{\otimes 3}+\sqrt{2}\left( \dfrac{\sigma _x-\sigma _y}{\sqrt{2}}\right) ^{\otimes 3}\bigg ], \end{aligned}$$
(44)

with four correlations \(\sigma _z^{\otimes 3}\), \(\sigma _x^{\otimes 3}\), \(((\sigma _x+\sigma _y)/\sqrt{2})^{\otimes 3}\) and \(((\sigma _x-\sigma _y)/\sqrt{2})^{\otimes 3}\), where \(\sigma _x\), \(\sigma _y\), \(\sigma _z\) are the Pauli matrices.

The decomposition of entanglement witness operator \(\mathcal {W}_{W}\) given by (4) can be written as

$$\begin{aligned} \mathcal {W}_{W}= & {} \dfrac{1}{24}\Bigg [13\mathbb {I}\otimes \mathbb {I}\otimes \mathbb {I}+3\sigma _z\otimes \mathbb {I}\otimes \mathbb {I}+3\mathbb {I}\otimes \sigma _z\otimes \mathbb {I}+3\mathbb {I}\otimes \mathbb {I}\otimes \sigma _z+5\mathbb {I}\otimes \sigma _z\otimes \sigma _z\nonumber \\{} & {} +5\sigma _z\otimes \mathbb {I}\otimes \sigma _z+5\sigma _z\otimes \sigma _z\otimes \mathbb {I}+7\sigma _z\otimes \sigma _z\otimes \sigma _z-\sqrt{2}\Bigg (\mathbb {I}\otimes \mathbb {I}\otimes \left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \nonumber \\{} & {} +\mathbb {I}\otimes \left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}+\left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \mathbb {I}+\mathbb {I}\otimes \mathbb {I}\otimes \left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \nonumber \\{} & {} +\mathbb {I}\otimes \left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}+\left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \mathbb {I}+\mathbb {I}\otimes \mathbb {I}\otimes \left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \nonumber \\{} & {} +\mathbb {I}\otimes \left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}+\left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \mathbb {I}+\mathbb {I}\otimes \mathbb {I}\otimes \left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \nonumber \\{} & {} +\mathbb {I}\otimes \left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}+\left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \mathbb {I}\Bigg )-2\sqrt{2}\Bigg (\left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) ^{\otimes 3}\nonumber \\{} & {} +\left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) ^{\otimes 3}+\left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) ^{\otimes 3}+\left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) ^{\otimes 3}\Bigg )\nonumber \\{} & {} -2\Bigg (\mathbb {I}\otimes \left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \otimes \left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) +\left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \nonumber \\{} & {} +\left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \otimes \left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}+\mathbb {I}\otimes \left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \otimes \left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \nonumber \\{} & {} +\left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) +\left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \otimes \left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}\nonumber \\{} & {} +\mathbb {I}\otimes \left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \otimes \left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) +\left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \nonumber \\{} & {} +\left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \otimes \left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}+\mathbb {I}\otimes \left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \otimes \left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \nonumber \\{} & {} +\left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) +\left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \otimes \left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}\Bigg )\Bigg ], \end{aligned}$$
(45)

with five correlations \(\sigma _z^{\otimes 3}\), \(((\sigma _z+\sigma _x)/\sqrt{2})^{\otimes 3}\), \(((\sigma _z-\sigma _x)/\sqrt{2})^{\otimes 3}\), \(((\sigma _z+\sigma _y)/\sqrt{2})^{\otimes 3}\) and \(((\sigma _z-\sigma _y)/\sqrt{2})^{\otimes 3}\).

The decomposition of witness operator \(\mathcal {W}_{W}\) in the case of the scenario in Section 3.2 becomes

$$\begin{aligned} \mathcal {W}_{W}^{\lambda _{{k}}}= & {} \dfrac{1}{24}\Bigg [13\mathbb {I}\otimes \mathbb {I}\otimes \mathbb {I}+3\sigma _z\otimes \mathbb {I}\otimes \mathbb {I}+3\mathbb {I}\otimes \sigma _z\otimes \mathbb {I}+3\mathbb {I}\otimes \mathbb {I}\otimes \lambda _{{k}}\sigma _z+5\mathbb {I}\otimes \sigma _z\otimes \lambda _{{k}}\sigma _z\nonumber \\{} & {} +5\sigma _z\otimes \mathbb {I}\otimes \lambda _{{k}}\sigma _z+5\sigma _z\otimes \sigma _z\otimes \mathbb {I}+7\sigma _z\otimes \sigma _z\otimes \lambda _{{k}}\sigma _z\nonumber \\{} & {} -\sqrt{2}\Bigg (\mathbb {I}\otimes \mathbb {I}\otimes \lambda _{{k}}\left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) +\mathbb {I}\otimes \left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}+\left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \mathbb {I}\nonumber \\{} & {} +\mathbb {I}\otimes \mathbb {I}\otimes \lambda _{{k}}\left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) +\mathbb {I}\otimes \left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}+\left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \mathbb {I}\nonumber \\{} & {} +\mathbb {I}\otimes \mathbb {I}\otimes \lambda _{{k}}\left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) +\mathbb {I}\otimes \left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}+\left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \mathbb {I}\nonumber \\{} & {} +\mathbb {I}\otimes \mathbb {I}\otimes \lambda _{{k}}\left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) +\mathbb {I}\otimes \left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}+\left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \mathbb {I}\Bigg )\nonumber \\{} & {} -2\sqrt{2}\lambda _{{k}}\Bigg (\left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) ^{\otimes 3}+\left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) ^{\otimes 3}+\left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) ^{\otimes 3}+\left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) ^{\otimes 3}\Bigg )\nonumber \\{} & {} -2\Bigg (\mathbb {I}\otimes \left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \otimes \lambda _{{k}}\left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) +\left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \lambda _{{k}}\left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \nonumber \\{} & {} +\left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \otimes \left( \dfrac{\sigma _z+\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}+\mathbb {I}\otimes \left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \otimes \lambda _{{k}}\left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \nonumber \\{} & {} +\left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \lambda _{{k}}\left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) +\left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \otimes \left( \dfrac{\sigma _z-\sigma _x}{\sqrt{2}}\right) \otimes \mathbb {I}\nonumber \\{} & {} +\mathbb {I}\otimes \left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \otimes \lambda _{{k}}\left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) +\left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \lambda _{{k}}\left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \nonumber \\{} & {} +\left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \otimes \left( \dfrac{\sigma _z+\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}+\mathbb {I}\otimes \left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \otimes \lambda _{{k}}\left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \nonumber \\{} & {} +\left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}\otimes \lambda _{{k}}\left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) +\left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \otimes \left( \dfrac{\sigma _z-\sigma _y}{\sqrt{2}}\right) \otimes \mathbb {I}\Bigg )\Bigg ], \end{aligned}$$
(46)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xiao, Y., Guo, F., Dong, H. et al. Sharing Genuine Entanglement of Generalized Tripartite States by Multiple Sequential Observers. Int J Theor Phys 63, 21 (2024). https://doi.org/10.1007/s10773-023-05539-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10773-023-05539-x

Keywords

Search

Navigation