1 Introduction

In the study of quantum phase and phase transition, and quantum computations are paradigmatic.In quantum spin systems, lower energy state for a nuclear spin in an external field is spin (+ 1/2) while the higher energy corresponds to spin (− 1/2). The quantum spin chains in a magnetic field was studied in [1], by using Bethe-ansatz solutions which arise from string solutions that continuously connect the mode of the lowest-energy excitation. In [2], It was reported that antiferromagnetic HSCs, in a 1D trap, are stabilized by strong repulsive interactions between the two spin components in the absence of an external potential. A scheme for conditional state transfer in a HSC, produced in a transistor, was proposed and analyzed in [3, 4]. Exact solutions of the generalized HSCS were found and the thermodynamic features were studied on the basis of the exact solutions [5]. Analytical and numerical studies of spin transport in a 1D Heisenberg model, in linear-response regime, were carried [6]. In [8], the integrability of 1D classical continuum inhomogeneous biquadratic HSC and the effect of nonlinear inhomogeneity on the soliton of completely integrable spin model are studied.The integrability aspects of a classical one-dimensional continuum isotropic biquadratic HSC in its continuum limit was studied. This was achieved via a differential geometric approach, the dynamical equation for the spin chain is expressed in the form of a higher-order NLSE [7]. The conserved quantities are expressed in terms of a sum over simple polynomials in spin variables. Very recently, It was shown that for a NLSE, whatever its formulation, is integrable (or compeletly integrable) when the real and imaginary parts are linearly dependent [9,10,11,12]. A direct construction of explicit expressions for all the quantum integrals of motion for the isotropic Heisenberg s = 1/2 spin chain was presented [13]. Although the 1D Heisenberg ferromagnetic spin chain (HFSC) was rarely studied in the literature, the (2 + 1) dimensional HFSC was remarkably considered. This may be argued to that in the first case the model equation (ME) is taken a NLSE with biquadratic dispersion and fifth degree nonlinearity. While in the second case, the ME is taken a NLSE with quadratic dispersion and Kerr nonlinearituy but in (2 + 1) dimensions. In [14], the (2 + 1)-dimensional HFSC that describes the nonlinear dynamics of magnet was studied. Two mathematical approaches for showing dark, bright, kink-type and singular soliton solutions to the HFSCS were presented. The NLSE in (2 + 1) dimensions, with beta derivative evolution, was considered to study nonlinear coherent structures for HFSC with magnetic exchanges [15]. In [16], the NLSE in (2 + 1)-dimensions for the HFSC, with anisotropic and bilinear interactions in the semi classical limit,. where two integrating schemes were used, was studied. The (2 + 1)-dimensions HFSCS was considered for the objective of finding the exact solutions via a specific transformation and adopting a modified version of the Jacobi elliptic expansion method [17]. An ansatz method,to solve The HFSC equation was used to get bright and dark 1-soliton solutions.Some conditions of integrability were given which guarantee the existence of solitons [18]. In [19], constructio0n of further exact soliton solutions of the (2 + 1)-dimensional HFSCE and investigating the nonlinear dynamics of magnets and explains their ordering in ferromagnetic materials were carried.. The collision dynamics of soliton in discrete classical ferromagnetic spin chain with Dzyaloshinskii-Moriya (DM) interaction in the classical limit are analyzed [20]. In [21], The conformable fractional derivative HFSC was considered via the complete discrimination system for polynomial method. The rational combined multi-wave solutions were obtained for HFSCE by using the logarithmic transformation and symbolic computation with ansatz functions [22]. The NLSE that describes the spin dynamics of (2 + 1)-dimensional inhomogeneous IHFSC with bilinear and anisotropic interactions in the semi classical limit was investigated [23]. n [24], Hirota bilinear method with appropriate polynomial functions in bilinear forms, the one-order rogue waves solution and its existence condition were obtained. Different methods and techniques were used to solve nonlinear evolution equations; Tanh and Exp-function [25, 26], \(\frac {G^{\prime }}{G}\) expansion [27], Darboux transformation [28], Kyrdiashov method, [29], Hirota-bilinear transformation [30], Lie symmetries of NLPDEs [31].Very recently different methods and techniques were introduced, among them, the first integral method, the improved q- homotopy perturbation method and the unified algebraic and auxiliary equation expansion methods [32,33,34,35,36,37,38,39,40,41]. Here, the unified method (UM) [42,43,44,45,46,47] is used in this paper.

The method used here is compared with the known methods, known in the in the literature.

Indeed, the UM [36] prevails the all known methods such as, the tanh, modified, and extended versions, the F-expansion, the exponential, the G’/G expansion method, the Kerdyashov methods, as it is of low time cost in symbolic computation.Further, It provides solutions which cannot be obtained by the other methods.

The outlines of the paper is in what follows. Section 2 is devoted to mathematical equations and outlines of the UM and GUM. the solutions in the polynomial form are presented in Section 3. While the solutions in the rational forms are carried in Section 4. Section 5 is devoted to modulation stability analysis. Conclusions are given in Section 6.

2 The Model equation and outlines of the UM

2.1 The Model equation

For the 1D classical HFSCS with biquadratic exchange and a bilinear exchange interaction, the Hamiltonian is,

$$ H=-J{\sum}_{n}(S_{n}..S_{n+1})-\alpha J{\sum}_{n}(S_{n}..S_{n+1})^{2},\quad Sn=({S_{n}^{x}},{S_{n}^{y}},{S_{n}^{z}}),{S_{n}^{2}}~=1,\quad(J>0), $$
(1)

where Sn := Sn(t) and α is the biquadratic exchange parameter, which is considered in a dominant parameter. By assuming that the lattice side, a, is small, in the continuum analog, we write x = na and \(S_{n+1}=S(x,t)+aS_{x}(x,t)+a^{2}\textit {S}_{xx}\)(x,t)/2!+... Up to the order of a4, the equation of motion takes the form,

$$ S_{t}=S\times[S_{xx}+\nu S_{xxx}+\beta((S..S_{xx})S_{x}+\frac{2~}{3}(S..S_{xxx})S_{x})], $$
(2)

whereν = a2/12 and β = αa2/(1 + 2α). The continuum model equation, based on (2) was constructed [47]

$$ \begin{array}{c} iw_{t}+w_{xx}+2w\mid w\mid^{2}+\nu w_{xxxx}-4\delta w_{xx}^{*}w^{2}-4\mid w\mid^{2}w_{xx}\\ -4\alpha\mid w\mid^{2}w_{xx}-4\nu_{0}w^{*}(w_{x})^{2}-24\sigma\mid w\mid^{4}w=0, \end{array} $$
(3)

where \(\alpha \text {:=}4\beta +9\nu ; \mu =2\beta +3\nu ; \nu _{0}\text {=}2\beta +\frac {7\mu }{2}, \sigma \text {=}\frac {\beta }{2}+\nu ; \delta \text {=}\beta +2\nu ,\) and w := w(x,t). Equation (1) is a NLSE with the highest biquadratic dispersion and highest nonlinearity of fifth degree.

The spectral characteristics are, here, introduced. To this issue, we write,

$$ w(x,t)=\mid w(x,t)\mid e^{i(Kx-{\Omega} t)}, $$
(4)

where K is the w2ave number and Ω is the frequency;

$$ K=\frac{\intop_{0}^{\infty}(\intop_{-\infty}^{\infty}\mid w_{x}(x,t)\mid dx)dt}{\intop_{0}^{\infty}(\intop_{-\infty}^{\infty}\mid w(x,t)\mid dx)dt},\quad{\Omega}=\frac{\intop_{0}^{\infty}(\intop_{-\infty}^{\infty}\mid w_{t}(x,t)\mid dx)dt}{\intop_{0}^{\infty}(\intop_{-\infty}^{\infty}\mid w(x,t)\mid dx)dt}, $$
(5)

and the spectrum content is,

$$ W(k_{0},t\}=\intop_{-\infty}^{\infty}e^{-i k_{0}x}w(x,t)dx. $$
(6)

For the objective of finding the solutions of (3), we introduce a transformation for w(x,t) with complex amplitude,

$$ w(x,t)=(u(x,t)+iv(x,t))e^{i(kx-\omega t)},\quad w(x,t)^{*}=(u(x,t)-iv(x,t))e^{-i(kx-\omega t)}. $$
(7)

This transformation allows to inspect the effect of soliton- periodic wave collision, which is elastic or inelastic depending on the waves solutions if they are smooth or not smooth. When inserting (7) into (3) gives rise, for the real and imaginary parts respectively, to,

$$ \begin{array}{l} -4\alpha k^{2}u^{3}+4\delta k^{2}u^{3}+4k^{2}\mu u^{3}+4k^{2}{\nu}\text{o}u^{3}+k^{4}\nu u-k^{2}u-24\sigma u^{5}+2u^{3}+u\omega\\ \\ -v_{t}-4\alpha k^{2}uv^{2}+4\delta k^{2}uv^{2}+4k^{2}\mu uv^{2}+4k^{2}{\nu}\text{o}uv^{2}-48\sigma u^{3}v^{2}++2uv^{2}\\ \\ -24\sigma\text{uv}^{4}-4k^{3}\nu v_{x}++8\alpha kuvu_{x}-16\delta kuvu_{x}-2kv_{x}-4\alpha u\left( u_{x}\right)^{2}-4{\nu}\text{o}u\left( u_{x}\right)^{2}\\ \\ -8\alpha ku^{2}v_{x}+8\delta ku^{2}v_{x}+8k\mu u^{2}v_{x}+8k{\nu}\text{o}u^{2}v_{x}-8\delta kv^{2}v_{x}+8k\mu v^{2}v_{x}^{)}\\ \\ -6k^{2}\nu u_{xx}++8k{\nu}\text{o}v^{2}v_{x}-4\delta u^{2}u_{xx}-4\mu u^{2}u_{xx}-8{\nu}\text{o}vu_{x}v_{x}+u_{xx}-4\alpha u\left( v_{x}\right)^{2}\\ \\ +4{\nu}\text{o}u\left( v_{x}\right)^{2}-4k\nu v_{xxx}+\nu u_{xxxx}++4\delta v^{2}u_{xx}-4\mu v^{2}u_{xx}-8\delta uvv_{xx}=0, \end{array} $$
(8)
$$ \begin{array}{l} -4\alpha k^{2}u^{2}v+4\delta k^{2}u^{2}v+4k^{2}\mu u^{2}v+4k^{2}{\nu}\text{o}u^{2}v+k^{4}\nu v-k^{2}v+2u^{2}v+v\omega\\ \\ 2ku_{x}+u_{t}-4\alpha k^{2}v^{3}+4\delta k^{2}v^{3}+4k^{2}\mu v^{3}+4k^{2}{\nu}\text{o}v^{3}-48\sigma u^{2}v^{3}-24\sigma u^{4}v-24\sigma v^{5}\\ \\ +2v^{3}+[-4k^{3}\nu+8\delta ku^{2}-8k\mu u^{2}-8k{\nu}\text{o}u^{2}+8\alpha kv^{2}-8\delta kv^{2}-8k\mu v^{2}-8k{\nu}\text{o}v^{2}]u_{x}\\ \\ -4\alpha v\left( u_{x}\right)^{2}+4{\nu}\text{o}v\left( u_{x}\right)^{2}-8\alpha kuvv_{x}+16\delta kuvv_{x}-8\ {\nu}\text{o}uu_{x}v_{x}-4\alpha v\left( v_{x}\right)^{2}\\ \\ -4{\nu}\text{o}v\left( v_{x}\right)^{2}-6k^{2}\nu v_{xx}+4k\nu u_{xxx}+4\delta v_{xx}u(x,t)^{2}-4\mu u^{2}v_{xx}-8\delta u\text{v}u_{xx}\\ -4\delta v^{2}v_{xx}-4\mu v^{2}v_{xx}+\nu v_{xxxx}+v_{xx}=0. \end{array} $$
(9)

We search for traveling waves solutions. To this end, we use the transformations u(x,t) = U(z),v(x,t) = V (z) and z = ax + bt. Under these transformations (8) and (9) become, respectively,

$$ \begin{array}{l} -V^{\prime}\left( 8a^{2}{\nu}\text{o}VU^{\prime}-4ak^{3}\nu+8akV^{2}(\delta-\mu-{\nu}\text{o})+2ak+b\right)+U^{3}\\ \\ \left( 4k^{2}(-\alpha+\delta+\mu+{\nu}\text{o})-48\sigma V^{2}+2\right)+4aU^{2}\left( a(\delta+\mu)U^{\prime\prime}+2kV^{\prime}(\alpha-\delta-\mu-{\nu}\text{o})\right)\\ \\ -24\sigma U^{5}+U\left( k^{4}\nu+V^{2}\left( 4k^{2}(-\alpha+\delta+\mu+{\nu}\text{o})+2\right)-k^{2}+\omega\right.\\ \\ -4a^{2}(\alpha+{\nu}\text{o})\left( U^{\prime}\right)^{2}-4a^{2}\alpha\left( V^{\prime}\right)^{2}+4a^{2}{\nu}\text{o}\left( V^{\prime}\right)^{2}-8aV\left( a\delta V^{\prime\prime}-k(\alpha-2\delta)U^{\prime}\right)\\ -24\sigma V^{4})+a^{2}\left( a\nu\left( aU^{(4)}-4kV^{(3)}\right)+U^{\prime\prime}\left( -6k^{2}\nu+4V^{2}(\delta-\mu)+1\right)\right)=0, \end{array} $$
(10)
$$ \begin{array}{l} V^{3}\left( 4k^{2}(-\alpha+\delta+\mu+{\nu}\text{o})-48\sigma U^{2}+2\right)-24\sigma V^{5}-k^{2}-24\sigma U^{4}+\omega\\ +U^{\prime}\left( -4ak^{3}\nu+2ak+b\right.\\ \left.+8akU^{2}(\delta-\mu-\nu\text{o})-8a^{2}\nu\text{o}UV^{\prime}\right)+V\left( k^{4}\nu\right.\\ +U^{2}\left( 4k^{2}(-\alpha+\delta+\mu+\nu\text{o})+2\right)\\ \left.+4a^{2}(\nu\text{o}-\alpha)\left( U^{\prime}\right)^{2}-4a^{2}\alpha\left( V^{\prime}\right)^{2}-4a^{2}\nu\text{o}\left( V^{\prime}\right)^{2}-8aU\left( a\delta U^{\prime\prime}+k(\alpha-2\delta)V^{\prime}\right)\right)\\ \\ a^{2}\left( a\nu\left( aV^{(4)}+4kU^{(3)}\right)+V^{\prime\prime}\left( -6k^{2}\nu+4U^{2}(\delta-\mu)+1\right)\right)\\ -4aV^{2}\left( a(\delta+\mu)V^{\prime\prime}+2kU^{\prime}(-\alpha+\delta+\mu+\nu\text{o})\right)==0. \end{array} $$
(11)

Here, the solutions of (10) and (11) are found by using the UM and GUM. The Um asserts that the solutions of NLPDEs (NLODEs) are formulated in polynomial and rational forms, in auxiliary functions that satisfy appropriate auxiliary equations AE).

2.2 Outlines of the UM

2.2.1 Polynomial forms

By considering (10) and (11), the polynomial forms are,

$$ U(z)={\sum}_{j=0}^{m_{1}}a_{j}g(z)^{j},\quad V(z)={\sum}_{j=0}^{m_{2}}b_{j}g(z)^{j},(g^{\prime}(z))^{p}={\sum}_{j=0}^{rp}c_{j}g(z)^{j},p=1,2. $$
(12)

To determine mi,i = 1,2 and r, we use the balance and compatibility conditions. First, we consider the case when p = 1.The balance condition is determined by balancing the highest order derivative and highest nonlinearity terms. In the present case, the balance condition reads m1 = m2 = r − 1. To determine the consistency condition, we require the following

(a) the number of equations that result from inserting (12) into (10) and (11) and by setting the coefficients of g(z)i.,i = 0,1,2,..., say h(k).

(b) the number of arbitrary parameters ai,bi,ci, say f(k). For integrable equations the condition is h(k) − f(k) ≤ s,where s is the highest order derivative (here s = 4). In the present case the consistency condition reads 1 ≤ r ≤ 3.

The case case when p = 2 can be analyzed by the same way. We mention that when p = 1, the solutions of the AE are elementary functions, while they are periodic or ellptic whenp = 2.

2.2.2 Rational forms

In the UM the rational solutions are written,

$$ \begin{array}{c} U(z)=\frac{a_{1}g(z)+a_{0}}{s_{1}g(z)+s_{0}},\quad V(z)=\frac{b_{1}g(z)+b_{0}}{s_{1}g(z)+s_{0}},\\ \\ (g^{\prime}(z))^{p}={\sum}_{j=0}^{rp}c_{j}g(z)^{j},p=1,2. \end{array} $$
(13)

3 Polynomial solutions of (10) and (11)

Here, we consider the following cases.

3.1 When p = 1and r = 2

In this case (12) reduces to

$$ U(z)=a_{1}g(z)+a_{0},\quad V(z)=b_{1}g(z)+b_{0}, g^{\prime}(z)=c_{2}g(z)^{2}+c_{1}g(z)+c_{0}. $$
(14)

When inserting (14) into (10) and (11), and by setting the coefficients of g(z)i = 0,i = 0,1,.., we have, (for linearity dependent solutions, b0 = a0b1/a1),

$$ \begin{array}{ll} &~~\nu=\frac{\left( {a_{1}^{2}}+{b_{1}^{2}}\right)\left( a^{2}{c_{2}^{2}}(\alpha+2\delta+2\mu+\nu\text{o})+6\sigma\left( {a_{1}^{2}}+{b_{1}^{2}}\right)\right)}{6a^{4}\text{c2}^{4}},c_{2}=-r^{2},\\ \\ &~\nu_{0} = \frac{6\sigma\left( {a_{1}^{2}}+{b_{1}^{2}}\right)}{a^{2}{c_{2}^{2}}}+\alpha+4\delta,\quad\delta\text{:=}\frac{1}{12c_{2}{a_{1}^{2}}k^{2}\left( {a_{1}^{2}}+{b_{1}^{2}}\right)}\left( 4{a_{0}^{2}}{b_{1}^{2}}\text{c2}\left( 12{b_{1}^{2}}\sigma - a^{2}\text{c2}^{2}(\alpha - 2\mu)\right)\right.\\ \\ &~~~~~~~-48{a_{1}^{6}}c_{0}\sigma+{a_{1}^{4}}\left( 4a^{2}c_{0}{c_{2}^{2}}(\alpha-2\mu)+c_{2}\left( 48{a_{0}^{2}}\sigma+6\alpha k^{2}-3\right)-96c_{0}{b_{1}^{2}}\sigma\right)\\ \\ &~~~~~~~\left.+{a_{1}^{2}}\left( {b_{1}^{2}}\text{c2}\left( 4a^{2}c_{2}c_{0}(\alpha-2\mu)+96{a_{0}^{2}}\sigma+6\alpha k^{2}-3\right)\right)\right)\\ &~~~~~~~+{a_{1}^{2}}(+a^{2}\text{c2}^{3}\left( -4{a_{0}^{2}}(\alpha-2\mu)-3\right)-48{b_{1}^{4}}\text{co}\sigma))\\ &~c_{1}=\frac{2a_{0}c_{2}}{a_{1}},b=\frac{P}{H}, P=2ak(-\left( \alpha\left( 12k^{2}\nu - 1\right)+2\mu - 3\nu\right)\\ \\ &~~~~~~~~~+3a^{4}\nu r^{8}\left( 4k^{2}\nu+1\right) a^{2}r^{4}\left( {a_{1}^{2}}+{b_{1}^{2}}\right), H=\left( {a_{1}^{2}}+{b_{1}^{2}}\right)\left( 12\sigma\left( {a_{1}^{2}}+{b_{1}^{2}}\right)-a^{2}r^{4}(\alpha-2\mu)\right),\\ \\ &~c_{0}=\frac{H_{1}}{H_{2},}, H_{1}=-a^{4}r^{8}\left( \text{a1}^{2}\left( 4\text{ao}^{2}(\alpha-2\mu)+12k^{2}\nu+3\right)+4{a_{0}^{2}}{b_{1}^{2}}(\alpha-2\mu)\right)\\ \\ &~~~~~~~~~+24\text{a1}^{2}k^{2}\sigma\left( {a_{1}^{2}}+{b_{1}^{2}}\right)^{2}+a^{2}r^{4}\left( {a_{1}^{2}}+{b_{1}^{2}}\right),\left( {a_{1}^{2}}\left( 48{a_{0}^{2}}\sigma+2k^{2}(5\alpha+2\mu)-3\right)+48{a_{0}^{2}}{b_{1}^{2}}\sigma\right)\\ &H_{2}=4a^{2}{a_{1}^{2}}r^{2}\left( {a_{1}^{2}}+{b_{1}^{2}}\right)\left( a^{2}r^{4}(\alpha-2\mu)-12\sigma\left( {a_{1}^{2}}+{b_{1}^{2}}\right)\right),\\ \\ &~~\omega=\frac{H_{3}}{H_{4}},\quad H_{3}=90a^{10}k^{2}\nu r^{20}(\alpha-2\mu)\left( 4k^{2}\nu+1\right)-432a^{2}k^{2}r^{4}\left( {a_{1}^{2}}+{b_{1}^{2}}\right)^{4}\sigma^{2}\left( 2k^{2}(\alpha+2\mu)-1\right)\\ \\ &~~~~~~~~-1728k^{4}\sigma^{3}\left( {a_{1}^{2}}+{b_{1}^{2}}\right)^{5}-3a^{8}\ {a_{1}^{2}}+{b_{1}^{2}}\ r^{16}\left( -8k^{2}\mu^{2}\left( 13k^{2}\nu+2\right)\right.\\ &~~~~~~~~+2\alpha^{2}k^{2}\left( 71k^{2}\nu+4\right)-\alpha\left( 232k^{4}\mu\nu+k^{2}(8\mu+42\nu)+3\right)\\ \\ &~~~~~~~~+\mu\left( 84k^{2}\nu+6\right)\left.9\sigma\left( 112k^{4}\nu^{2}+16k^{2}\nu-3\right)-\alpha\left( 232k^{4}\mu\nu+k^{2}(8\mu+42\nu)+3\right)\right)\\ \\ &~~~~~~~~+9a^{4}r^{8}\sigma\left( {a_{1}^{2}}+{b_{1}^{2}}\right)^{3}(4k^{4}\left( 5\alpha^{2}-28\alpha\mu-12\mu^{2}+168\nu\sigma\right)\\ &~~~~~~~~+4k^{2}(\alpha+10\mu+12\sigma)-3)\left.+\alpha\left( -144k^{4}\left( \mu^{2}-14\nu\sigma\right)+12k^{2}(8\mu-33\sigma)+9\right)\right),\\ \\ &H_{4}=6a^{4}r^{8}\left( {a_{1}^{2}}+{b_{1}^{2}}\right)\left( a^{2}r^{4}(\alpha-2\mu)-12\sigma\left( {a_{1}^{2}}+{b_{1}^{2}}\right)\right)^{2}. \end{array} $$
(15)

By solving the AE in (14), the solutions of (8) and (9) are,

$$ \begin{array}{c} u(x,t)=a_{1}\frac{K tanh (\frac{(z+A_{0})K}{K_{0}})}{K_{0}}\\ \\ K=\sqrt{3a^{4}r^{8}\left( 4k^{2}\nu+1\right)-(24k^{2}\sigma({a_{1}^{2}}+{b_{1}^{2}})+M}, \end{array} $$
$$ \begin{array}{l} M~=a^{2}r^{4}\left( 2k^{2}(5\alpha+2\mu)-3\right))\left( {a_{1}^{2}}+{b_{1}^{2}}\right)\\ K_{0}=2ar^{2}\sqrt{{a_{1}^{2}}+{b_{1}^{2}}}\sqrt{12\sigma\left( {a_{1}^{2}}+{b_{1}^{2}}\right)-a^{2}r^{4}(\alpha-2\mu)},\\ \\ v(x,t)=\frac{b_{1}}{a_{1}}u(x,t), z=ax+bt. \end{array} $$
(16)

The solutions in (16) are evaluated numerical and the results are used to display Rew in Fig. 1(i)-(v).

Fig. 1
figure 1

The 3D plot is displayed for Rew against x and t by varying the values of α and ν when r := 1.2,k = 1.5,a := 1.2,a1 = 0.7,b1 = 0.5,σ = 0.6,μ = 0.5,A0 = − 5. In (i) α = 1.5,ν = 0.3,(ii)α = 1.5,ν = 1.3 (iii) α = 2.5,ν = 0.3

Full size image

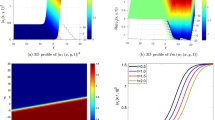
Figures 4 and 5. In (iv), the contour plots is displayed, while in (v) the variation of Rew against x for different values of t is done.

Figure 1(i) shows “continuum” soliton chain with trapping, while Fig. 1(ii) and (iii) show complex soliton chain. Fig. 1(iv) shows super lattices and Fig. 1(v) shows “continuum” solton chain.

The Spectral characteristics which are given in (5) and (6) are shown in Fig. 2(i)-(iii), for the wave number, the frequency and spectrum respectively.

Fig. 2
figure 2

The wave number, the frequency and the spectrum are shown for the same caption as in Fig. 1 (i)-(v), but in (iii)ν = 0.5

Full size image

Figure 2(i) shows the there a critical value of ν where it incre4ases and decreases abruptly. Figure 2(ii) shows that the frequency increases with ν. Figure 2(iii) shows soliton chain with small amplitude apart near x = 0.

3.2 When p = 2and r = 2

In this case consider the solution in (14), but the AE is,

$$ g^{\prime}(z)=g(z)\sqrt{c_{2}g(z)^{2}+c_{1}g(z)+c_{0}}. $$
(17)

By substituting from (14) and (17) into (10) and (11), by the same way as in Section 3.1, we get,

$$ \begin{array}{l} a_{1}=\frac{\sqrt{3a^{2}c_{2}\nu-{b_{1}^{2}}(-\delta+\mu+\nu\text{o})}}{\sqrt{-\delta+\mu+\nu\text{o}}}, a_{0}=\frac{c_{1}}{4c_{2}}a_{1,} c_{0}=\frac{3a^{3}{c_{1}^{2}}k\nu+ac_{1}\ k\left( 8k^{2}\nu-4\right)-2bc_{2}}{8a^{3}c_{2}k\nu},\\ \\ ~\sigma=\frac{(\alpha+4\delta-\nu\text{o})(\delta-\mu-\nu\text{o})}{18\nu}, b=\frac{2ak\left( 3\alpha\left( 4k^{2}\nu-1\right)+\delta\left( 4k^{2}\nu-7\right)-4k^{2}\mu\nu-4k^{2}\nu\nu\text{o}+\mu-3\nu+\nu\text{o}\right)}{3\alpha+8\delta-2(\mu+\nu\text{o})},\\ \\ c_{2}=-\frac{a^{2}\nu(3\alpha+8\delta-2(\mu+\nu\text{o})){}_{1}^{c2}}{4\left( -6\alpha k^{2}\nu+\delta\left( 12k^{2}\nu-1\right)+\mu+3\nu+\nu\text{o}\right)},\\ \\ ~\omega=\frac{3(\alpha+4\delta-\nu\text{o})\left( -\delta-6\alpha k^{2}\nu+12\delta k^{2}\nu+\mu+3\nu+\nu\text{o}\right)^{2}}{4\nu(\delta-\mu-\nu\text{o})(3\alpha+8\delta-2(\mu+\nu\text{o}))^{2}}+k^{4}(-\nu)+k^{2}\\ \\ ~~~~~~~~-\frac{3\left( 2k^{2}(-\alpha+\delta+\mu+\nu\text{o})+1\right)\left( -6\alpha k^{2}\nu+\delta\left( 12k^{2}\nu-1\right)+\mu+3\nu+\nu\text{o}\right)}{2(\delta-\mu-\nu\text{o})(3\alpha+8\delta-2(\mu+\nu\text{o}))}. \end{array} $$
(18)

Finally, the solutions of (8) and (9) are,.

$$ \begin{array}{l} u(x,t)=\frac{K_{1}}{K_{2}}, K_{1}=-6\alpha k^{2}\nu+\delta\left( 12k^{2}\nu-1\right)+\mu+3\nu\\ ~~~~~~~~~~~~~~+\nu\text{o}\left( \exp\left( (A_{0}+z)\left( 3\nu\left( 4\delta k^{2}+1\right)+\mu+\nu\text{o}\right)K\right)\right.\\ ~~~~~~~~~~~~~~+a^{2}c_{1}\ \exp\left( (\text{Ao}+z)\left( \delta+6\alpha k^{2}\nu\right)K\right)\nu(3\alpha+8\delta-2(\mu+\nu\text{o})))\\ \\ \sqrt{-\frac{3a^{4}{c_{1}^{2}}\nu^{2}(3\alpha+8\delta-2(\mu+\nu\text{o}))}{4\left( -6\alpha k^{2}\nu+\delta\left( 12k^{2}\nu-1\right)+\mu+3\nu+\nu\text{o}\right)}+{b_{1}^{2}}(\delta-\mu-\nu\text{o})},\\ \\ K_{2}=a^{2}c_{1}\ \nu\sqrt{-\delta+\mu+\nu\text{o}}3\alpha+8\delta-2(\mu+\nu\text{o})\\ ~~~~~~~~~\left( -\exp\left( (\ A_{0}+z)\left( 3\nu\left( 4\delta k^{2}+1\right)+\mu+\nu\text{o}\right)K\right)\right.\\ \left.~~~~~~~~+a^{2}\text{c1}\nu(3\alpha+8\delta-2(\mu+\nu\text{o}))\exp\left( (A_{0}+z)\left( \delta+6\alpha k^{2}\nu\right)K\right)\right),\\ \\ K=\sqrt{\frac{1}{a^{2}\nu(2(-4\delta+\mu+\nu\text{o})-3\alpha)\left( -6\alpha k^{2}\nu+\delta\left( 12k^{2}\nu-1\right)+\mu+3\nu+\nu\text{o}\right)}},\\ v(x,t)=\frac{b_{1}}{a_{1}}u(x,t),z=ax+\frac{2ak\left( 3\alpha\left( 4k^{2}\nu-1\right)+\delta\left( 4k^{2}\nu-7\right)-4k^{2}\mu\nu-4k^{2}\nu\nu\text{o}+\mu-3\nu+\nu\text{o}\right)}{3\alpha+8\delta-2(\mu+\nu\text{o})}t. \end{array} $$
(19)

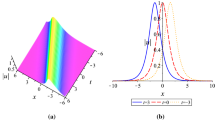
The solutions in (20) are used to display Rew in Fig. 3 (i)-(iii)

Fig. 3
figure 3

In Fig. 3(i) and , the 3D plot , contour plots are displayed for Rew, while the variation againstx for different values oft is displayed in Fig. 3(iii)

Full size image

When ν0 = 3.2,k := 1.5,a := 1.2,a1 = 0.7,b1 = 0.1,σ = ∖0.6,α = 0.5,μ := 2.5,ν = 1.3,A0 = − 5,δ = 0.1,c1 = 0.6. Theses figures show “continuum” soliton chain.

3.3 When p = 2 and r = 2

Here, we consider the AE,

$$ g^{\prime}(z)=\sqrt{c_{4}g(z)^{4}+c_{2}g(z)^{2}+c_{0}}. $$
(20)

By inserting (14) and (20) into (10) and (11), we have,

$$ \begin{array}{l} a_{1}=\frac{\sqrt{3a^{2}c_{4}\nu-{b_{1}^{2}}(-\delta+\mu+\nu\text{o})}}{\sqrt{-\delta+\mu+\nu\text{o}}}, a_{0}=0, b=-2ak\left( 2a^{2}c_{2}\nu-2k^{2}\nu+1\right),\\ \\ ~\sigma=\frac{(\alpha+4\delta-\nu\text{o})(\delta-\mu-\nu\text{o})}{18\nu}, k=\frac{\sqrt{-6\alpha a^{2}c_{2}\nu-\delta\left( 16a^{2}c_{2}\nu+1\right)+4a^{2}c_{2}\mu\nu+4a^{2}c_{2}\nu\nu\text{o}+\mu+3\nu+\nu\text{o}}}{\sqrt{6}\sqrt{\nu(\alpha-2\delta)}},\\ \\ ~\omega=a^{4}\nu\left( -{c_{2}^{2}}-\frac{12c_{4}\text{co}(\alpha+\delta-\mu)}{\delta-\mu-\nu\text{o}}\left)-\frac{\left( -6\alpha a^{2}\text{c2}\nu-16a^{2}\text{c2}\delta\nu+4a^{2}\text{c2}\mu\nu+4a^{2}\text{c2}\nu\nu\text{o}-\delta+\mu+3\nu+\nu\text{o}\right)^{2}}{36\nu(\alpha-2\delta)^{2}}\right.\right.\\ \\ ~~~~~~~~+\frac{a^{2}c_{c}\left( -\alpha\left( 6a^{2}c_{2}\nu+1\right)-16a^{2}c_{2}\delta\nu+4a^{2}c_{2}\mu\nu+4a^{2}c_{2}\nu\nu\text{o}+\delta+\mu+3\nu+\nu\text{o}\right)}{\alpha-2\delta}\\ \\ ~~~~~~~~+\frac{-6\alpha a^{2}c_{2}\nu-\delta\left( 16a^{2}c_{2}\nu+1\right)+4a^{2}c_{2}\mu\nu+4a^{2}c_{2}\nu\nu\text{o}+\mu+3\nu+\nu\text{o}}{6\nu(\alpha-2\delta)}, \\ c_{4}=m^{2}, c_{0}=r^{2}, c_{2}=-n^{2}, \end{array} $$
(21)

The solutions of (8) and (9) are,

$$ \begin{array}{c} u(x,t)=\frac{\sqrt{3a^{2}m^{2}\nu-{b_{1}^{2}}(-\delta+\mu+\nu\text{o})}}{\sqrt{-\delta+\mu+\nu\text{o}}}\\ \\ \frac{\sqrt{2}\left( n^{2}\sqrt{n^{4}-4m^{2}r^{2}}+2m^{2}r^{2}-n^{4}\right)\text{sn}\left( \sqrt{2}r\sqrt{\frac{m^{2}}{n^{2}-\sqrt{n^{4}-4m^{2}r^{2}}}}(\text{Ao}+z),|\frac{n^{2}-\sqrt{n^{4}-4m^{2}r^{2}}}{n^{2}+\sqrt{n^{4}-4m^{2}r^{2}}}\right)}{\left( n^{2}-\sqrt{n^{4}-4m^{2}r^{2}}\right)^{2}\sqrt{\frac{m^{2}}{n^{2}-\sqrt{n^{4}-4m^{2}r^{2}}}}}\\ v(x,t)=\frac{b_{1}}{a_{1}}u(x,t),z=ax-2ak\left( 2a^{2}c_{2}\nu-2k^{2}\nu+1\right)t. \end{array} $$
(22)

The solutions in (22) are used to display ∣w∣ in Fig. 4 (i)-(iii).

Fig. 4
figure 4

In Fig. 4(i) and , the 3D plot , contour plots are displayed for ∣w∣, while the variation againstx for different values of t is displayed in Fig. 4(iii)

Full size image

When ν0 = 3.2;k := 1.5,a = 1.2,a1 = 0.7;b1 = 0.1,σ = 0.6,α = 0.5,μ = 2.5,ν = 1.3,A0 = − 5,δ = 0.3,m := 0.6,r = 1.2,n = 3.

Figure 4(i) shows complex chirped waves, while Fig. 4(ii) shows super lattices. Figure 4(iii) shows dense “continuum” solion chain.

4 Rational solutions of (10) and (11)

We consider the solution in (13), together with AE,

$$ \begin{array}{@{}rcl@{}} g^{\prime}(z) & = & c_{1}g(z)+c_{0}. \end{array} $$
(23)

By using (13) and (23) into (10) and (11), we get,

$$ \begin{array}{l} \omega=\frac{1}{{s_{1}^{4}}}(2{b_{1}^{2}}{s_{1}^{2}}\left( 2k^{2}(\alpha-\delta-\mu-\nu\text{o})-1\right)+k^{2}{s_{1}^{4}}\left( 1-k^{2}\nu\right)\\ ~~~~~~~+24{a_{1}^{4}}\sigma+24{b_{1}^{4}}\sigma+{a_{1}^{2}}\left( {s_{1}^{2}}\left( 4k^{2}(\alpha-\delta-\mu-\nu\text{o})-2\right)\right)+48{b_{1}^{2}}\sigma)),\\ \\ ~b=\frac{1}{a_{1}c_{1}{s_{1}^{4}}}\left( a^{2}b_{1}{c_{1}^{2}}{s_{1}^{4}}\left( a^{2}{c_{1}^{2}}\nu-6k^{2}\nu+1\right)\right.-4{b_{1}^{3}}{s_{1}^{2}}\left( a^{2}{c_{1}^{2}}(\delta+\mu)\right.\\ ~~~~~~~\left.+2k^{2}(\alpha-\delta-\mu-\nu\text{o})-1\right)\\ ~~~~~~~-2aa_{1}c_{1}k{s_{1}^{2}}\left( {s_{1}^{2}}\left( 2a^{2}\text{c1}^{2}\nu-2k^{2}\nu+1\right)+4{b_{1}^{2}}(\delta-\mu-\nu\text{o})\right)\\ ~~~~~~~+8a{a_{1}^{3}}c_{1}k{s_{1}^{2}}(-\delta+\mu+\nu\text{o})-96{a_{1}^{4}}b_{1}\sigma-96{b_{1}^{5}}\sigma\\ ~~~~~~~\left.-4a_{^{2}1}\left( b_{1}\ {s_{1}^{2}}\left( a^{2}{c_{1}^{2}}(\delta+\mu)+2k^{2}(\alpha-\delta-\mu-\nu\text{o})-1\right)+48{b_{1}^{3}}\sigma\right)\right),\\ \\ c_{0}=-\frac{3c_{1}s_{0}}{2s_{1}}, \mu=\frac{P_{1}}{Q}, P_{1}=-5a^{5}{b_{1}^{2}}{c_{1}^{5}}\nu {s_{1}^{2}}+242a^{4}a_{1}b_{1}{c_{1}^{4}}k\nu {s_{1}^{2}}\\ ~~~~~~~+4a_{1}b_{1}k\left( {a_{1}^{2}}\left( 11-38\alpha k^{2}\right)\right.\left.+{b_{1}^{2}}\left( 11-38\alpha k^{2}\right)+3k^{2}{s_{1}^{2}}\left( 6k^{2}\nu-1\right)\right)\\ ~~~~~~~+a^{3}{c_{1}^{2}}{s_{1}^{2}}\left( 456{a_{1}^{2}}k^{2}\nu+{b_{1}^{2}}\left( 99k^{2}\nu+1\right)\right)+2a^{2}\ a_{1}b_{1}{c_{1}^{2}}k\left( -4\alpha\left( {a_{1}^{2}}+{b_{1}^{2}}\right)\right.\\ ~~~~~~~\left.+{s_{1}^{2}}\left( 114k^{2}\nu+13\right)\right)+a_{1}c_{1}\left( {b_{1}^{4}}\left( 4-16\alpha k^{2}\right)+3{b_{1}^{2}}k^{2}\text{s1}^{2}\left( 1-6k^{2}\nu\right)\right.\\ ~~~~~~~-4{a_{1}^{2}}\left( {b_{1}^{2}}\left( 4\alpha k^{2}-1\right)+12k^{4}\nu {s_{1}^{2}}\right)),\quad Q=16a_{1}b_{1}k\left( {a_{1}^{2}}+{b_{1}^{2}}\right)\left( 3k^{2}-a^{2}\text{c1}^{2}\right),\\ \\ ~\delta=\frac{P_{2}}{Q},\quad P_{2}=-102a^{4}a_{1}b_{1}{c_{1}^{4}}k\nu {s_{1}^{2}}+5a^{5}{b_{1}^{2}}{c_{1}^{5}}\nu\text{s1}^{2}\\ ~~~~~~~+12a_{1}b_{1}k\left( {a_{1}^{2}}+{b_{1}^{2}}\right)\left( 2\alpha k^{2}-1\right)\\ ~~~~~~~+ab_{1}{c_{1}^{2}}\left( 4{a_{1}^{2}}\left( 4\alpha k^{2}-1\right)+4{b_{1}^{2}}\left( 4\alpha k^{2}-1\right)+3k^{2}\text{s1}^{2}\left( 6k^{2}\nu-1\right)\right)\\ ~~~~~~~+2a^{2}a_{1}b_{1}{c_{1}^{2}}k\left( 4\alpha\left( {a_{1}^{2}}+{b_{1}^{2}}\right)-3{s_{1}^{2}}\text{s1}^{2}\left( 8k^{2}\nu+1\right)\right)\\ ~~~~~~~-a^{3}{c_{1}^{2}}{s_{1}^{2}}\left( 120{a_{1}^{2}}k^{2}\nu+{b_{1}^{2}}\left( 99k^{2}\nu+1\right)\right), a\text{=}\frac{k}{\sqrt{2}c_{1}}, k\text{=}\frac{1}{2\sqrt{\alpha}},\\ b_{1}=\frac{1}{4}\sqrt{\frac{\sqrt{\frac{2}{15}}{s_{1}^{2}}\sqrt{\sigma(8\alpha-17\nu)}}{\alpha\sigma}-16{a_{1}^{2}}}, a_{0}\text{=}-\frac{4a_{1}s_{0}}{s_{1}}.\\ \end{array} $$
(24)

The solutions of (8) and (9) are,

$$ \begin{array}{l} u(x,t)=\frac{2A_{0}a_{1}s_{1}e^{c_{1}z}-5a_{1}s_{0}}{2A_{0}{s_{1}^{2}}e^{c_{1}z}+5a_{1}s_{0}},\quad v(x,t)=\text{=}\frac{1}{4}\sqrt{\text{s1}^{2}\frac{\sqrt{\frac{2}{15}}\sqrt{\sigma(8\alpha-17\nu)}}{\alpha\sigma}-16{a_{1}^{2}}}u(x,t),\\ ~~~~~~~~~z=\frac{H_{3}}{H_{4}},\quad H_{3}=-3\sigma {s_{1}^{4}}t\left( 448\alpha^{2}-8384\alpha\nu+15793\nu^{2}\right)\\ ~~~~~~~~~~~~~~~+24\ a_{1}\alpha\sigma {s_{1}^{2}}\sqrt{\sigma(8\alpha-17\nu)}\left( \sqrt{30}\ a_{1}t(56\alpha-449\nu)\right.\\ ~~~~~~~~~~~~~~~\left.+4\left( -6\alpha t+99\nu t+10\alpha^{3/2}x\right)\sqrt{\frac{\text{s1}^{2}\sqrt{30}\sqrt{\sigma(8\alpha-17\nu)}-240\alpha\text{a1}^{2}\sigma}{\alpha\sigma}}\right)\\ ~~~~~~~~~~~~~~~+8\ \text{s1}^{2}\ t(8\alpha-17\nu)(\alpha+{\nu}\text{o})\left( {s_{1}^{2}}\sqrt{30}\sqrt{\sigma(8\alpha-17\nu)}-240\alpha {a_{1}^{2}}\sigma\right.\\ ~~~~~~~~~~~~~~~\left.+2\sqrt{30}\alpha\text{a1}\sigma\sqrt{\frac{{s_{1}^{2}}\sqrt{30}\sqrt{\sigma(8\alpha-17\nu)}-240\alpha\text{a1}^{2}\sigma}{\alpha\sigma}}\right),\\ \\ H_{4}=1920\sqrt{2}\alpha^{3}\text{a1}\text{c1}\sigma {s_{1}^{2}}\sqrt{\sigma(8\alpha-17\nu)}\sqrt{\frac{{s_{1}^{2}}\sqrt{30}\sqrt{\sigma(8\alpha-17\nu)}-240\alpha\text{a1}^{2}\sigma}{\alpha\sigma}}. \end{array} $$
(25)

The results in (25) are used to display Rew in Fig. 5 (i)-(iii).

Fig. 5
figure 5

When a1 = 0.5,ν0 = 3.2,k = 1.5,a := 1.2,σ= 0.6,α= 1.5,μ:= 2.5,ν= 0.5,A0 = 5,s1 = 3,s0 = 1.5,c1 = 2.5

Full size image

In Fig. 5(i) and (ii0, the 3D and contour plots of Rew are displayed, while the variation of Rew against x fo0r different values of t is displayed.

Figure 5(i) shows “—continuum” soliton chain with trap, while )ii) shows mixed lattice- solitons.

5 Modulation stability analysis

To study the modulation instability of a system, it should exhibit a normal mode. That is a periodic standing waves. Here, (3) has a solution of the form.

$$ w_{m}(x,t)\text{=}Qe^{i(rx-qt)},\quad w_{m}(x,t)^{*}\text{=}Qe^{-i(rx-qt)}. $$
(26)

By inserting (24) into (3), we get

$$ q\text{=}4\alpha Q^{2}r^{2}-4\delta Q^{2}r^{2}-4\mu Q^{2}r^{2}-4\nu\text{o}Q^{2}r^{2}+24Q^{4}\sigma-2Q^{2}-\nu r^{4}+r^{2}. $$
(27)

We write the solution expansion near wm,

$$ \begin{array}{c} w(x,t)\text{=}Qe^{i(rx-qt)}\left( 1+\varepsilon_{1}e^{\lambda t}(U(x)+iV(x))+O(\varepsilon^{2})\right)\\ w(x,t)^{*}\text{=}Qe^{-i(rx-qt)}\left( 1+{\epsilon}\text{2}e^{\lambda t}(U(x)-iV(x))+O(\varepsilon^{2})\right), \end{array} $$
(28)

in (3) and Calculations give rise to,

$$ \begin{array}{l} H\left( \begin{array}{c} \varepsilon_{1}\\ \varepsilon_{2} \end{array}\right)=0, H=\left( \begin{array}{cc} h_{11} & h_{12}\\ h_{21} & h_{22} \end{array}\right),\\ \\ h_{11}=U\left( q+Q^{2}\left( 8r^{2}(-\alpha+\delta+\mu+\nu\text{o})+4\right)-72Q^{4}\sigma+r^{2}\left( \nu r^{2}-1\right)\right)\\ ~~~~~~~~~~+2rV^{\prime}\left( Q^{2}(4(\mu+\nu\text{o})-2\alpha)+2\nu r^{2}-1\right)-4\mu Q^{2}U^{\prime\prime}-6\nu r^{2}U^{\prime\prime}\\ ~~~~~~~~~~-4\nu rV^{(3)}+\nu U^{(4)}+U^{\prime\prime},\\ h_{21}=V\left( q+Q^{2}\left( 8r^{2}(-\alpha+\delta+\mu+\nu\text{o})+4\right)-72Q^{4}\sigma+r^{2}\left( \nu r^{2}-1\right)\right)'\\ ~~~~~~~~~~+4\alpha Q^{2}rU-8\mu Q^{2}rU^{\prime}-8\nu\text{o}Q^{2}rU^{\prime}-4\mu Q^{2}V^{\prime\prime}-4\nu r^{3}U^{\prime}\\ ~~~~~~~~~~-6\nu r^{2}V^{\prime\prime}+4\nu rU^{(3)}+2rU^{\prime}+\lambda U+\nu V^{(4)}+V^{\prime\prime},\\ h_{12}=2Q^{2}U\left( -24Q^{2}\sigma+2r^{2}(-\alpha+\delta+\mu+\nu\text{o})+1\right)\\ ~~~~~~~~~~-4Q^{2}\left( r(\alpha-2\delta)V^{\prime}+\delta U^{\prime\prime}\right),\\ h_{22}=2Q^{2}\left( V\left( 24Q^{2}\sigma+2r^{2}(\alpha-\delta-\mu-\nu\text{o})-1\right)-2r(\alpha-2\delta)U^{\prime}+2\delta V^{\prime\prime}\right). \end{array} $$
(29)

The solution of (26) is detH = 0, which yields,

$$ \begin{array}{l} \left( V\left( 24Q^{2}\sigma+2r^{2}(\alpha-\delta-\mu-\nu\text{o})-1\right)-2r(\alpha-2\delta)U^{\prime}+2\delta V^{\prime\prime}\right.\\ \left( U\left( q+Q^{2}\left( 8r^{2}(-\alpha+\delta+\mu+\nu\text{o})+4\right)-72Q^{4}\sigma+r^{2}\left( \nu r^{2}-1\right)\right)+2rV^{\prime}\right.\\ \left.\left( Q^{2}(4(\mu+\nu\text{o})-2\alpha)+2\nu r^{2}-1\right)-4\mu Q^{2}U^{\prime\prime}-6\nu r^{2}U^{\prime\prime}-4\nu rV^{(3)}+\nu U^{(4)}+U^{\prime\prime}\right)\\ -\left( U\left( -24Q^{2}\sigma+2r^{2}(-\alpha+\delta+\mu+\nu\text{o})+1\right)-2\left( r(\alpha-2\delta)V^{\prime}+\delta U^{\prime\prime}\right)\right)\\ \left( V\left( q+Q^{2}\left( 8r^{2}(-\alpha+\delta+\mu+\nu\text{o})+4\right)-72Q^{4}\sigma+r^{2}\left( \nu r^{2}-1\right)\right)+\lambda U\right.'\\ +4\alpha Q^{2}rU-8\mu Q^{2}rU^{\prime}-8\nu\text{o}Q^{2}rU^{\prime}-4\mu Q^{2}V^{\prime\prime}\\ \left.\left.-4\nu r^{3}U^{\prime}-6\nu r^{2}V^{\prime\prime}+4\nu rU^{(3)}++2rU^{\prime}+\nu V^{(4)}+V^{\prime\prime}\right)\right)=0.\\ \end{array} $$
(30)

We solve the eigenvalue problem in (27) subjected to the boundary conditions \(\mid U(\pm \infty )\mid \leq U_{0}\) and \(\mid V(\pm \infty )\mid \leq V_{0}\). Thus the eigenfunctions take the form.

$$ U(x)\text{=}\text{U0}e^{i(hx)},\quad V(x)\text{=}\text{V0}e^{i(hx)}. $$
(31)

By substituting from (28) into (27), we have,

$$ \begin{array}{l} \lambda=\frac{1}{Q}2V_{0}\left( 2\delta h^{6}\nu+2Q^{2}\left( 24Q^{2}\sigma+2r^{2}(\alpha-\delta-\mu-\nu\text{o})-1\right)^{2}\right.\\ ~~~~~~~+h^{4}\left( \nu+\delta\left( 8\mu Q^{2}+30\nu r^{2}-2\right)\left.+2\nu r^{2}(-5\alpha+\mu+\nu\text{o})-24\nu Q^{2}\sigma\right)\right.\\ ~~~~~~~+h^{2}\left( -\left( 4Q^{2}(\delta+\mu)-1\right)-4\nu r^{4}(5\alpha-7\delta-3(\mu+\nu\text{o}))\right.\\ ~~~~~~~~(24Q^{2}\sigma-1)+2r^{2}\left( -\mu+3\nu-\nu\text{o}+(4\alpha^{2}+4\delta^{2}+4\mu^{2}+4\mu\nu\text{o})Q^{2}\right.\\ \\ ~~~~~~\left.\left.\left.+\alpha\left( 3-4Q^{2}(3\delta+3\mu+2\nu\text{o})\right)+\delta\left( 4Q^{2}(6\mu+5\nu\text{o})-5\right)-72\nu Q^{2}\sigma\right)\right)\right),\\ \end{array} $$
(32)
$$ Q\text{:=}\frac{\sqrt{{U_{0}^{2}}-{V_{0}^{2}}}\sqrt{2h^{2}\nu+2\nu r^{2}-1}}{2\sqrt{{U_{0}^{2}}(\alpha-\delta-\mu-\nu\text{o})+\text{Vo}^{2}(-\delta+\mu+\nu\text{o})}}, $$
(33)

together with as lengthy equation for σ, which will not produced here. The eigenvalue λ given in (29) is displayed against the dominant parameters ν,α and ν0in Fig. 6 (i)-(iii)

Fig. 6
figure 6

When r= 1.2,k:= 1.5,δ = 0.2,h= 0.5,μ= 0.5,U0 = 5,V0 = 3.In (i) α= 2.5,ν0 = 2.3,(ii) ,α= 2.5,ν= 1.3

Full size image

and (iii);α= 2.5,ν= 1.7,ν0 = 2.3.

Figure 6(i) shows that modulation stability holds against ν. While, in Fig. 6(ii) and (iii) there are the critical values νocr = 1.25 and αcr = 1.4,where below these values instability hols otherwise stability occurs.

6 Conclusions

The 1D Heisenberg spin chain system is considered. In continuum analog a o equation wad derived in the literature. Which is a nonlinear Schrodinger equation with bi-quadratic dispersion and fifth degree nonlinearity. Here, this equation is studied for the objectives of finding the exact solutions and investigating the relevant phenomena vis-a-vis with spin chain.The exact solutions are obtained by using the unified method in polynomial and rational forms. A transformation that enables us to inspect the effects of soliton- periodic wave collision is proposed.The collision can be elastic or inelastic according to the waves solutions are smooth or not smooth. Numerical evaluation of the solutions are carried and displayed in figures. It is found that the solutions exhibit “continuum” soliton chain, while the contour plots show super lattices or lattices with trapping. It is remarked the the solutions are bounded by − 1/4 and 1/4 which may be relevant with the spin − 1/2 and 1/2.The modulation stability analysis is carried and it is shown that there is a critical value of the dominant parameters that separates stability and instability. It is worth noticing that the waves solutions found here are smooth, so waves collision is elastic.