1 Introduction

Entanglement has become one of the most fascinating subjects of various topics and fields , because entanglement is the key to the distinguishing feature of quantum mechanics setting that separates it from classical physics.This concept which is related to the superposition of two different multi-particle states,was introduced for the first time by Schrodinger in 1935 [1] . A quantum state of a composite system, consisting of two or more subsystems, is entangled if it can not be factorized into direct product of the states of the subsystems . The notion of entanglement is also referred to the inseparability characteristic of the wave function of a multi-particle system versus the multiplication of wave functions of the subsystems. Thus, the entanglement is used as the main basis for quantum information processing [2,3,4].Further more, entangled states have many applications in quantum information processing such as quantum teleportation [5], quantum key distribution [6] and superdense coding [7]. Studying quantum information theory using entangled coherent states has recently received much attention [8,9,10].In a related context the entangled coherent states of the SU(2) and the SU(1, 1) algebras were studied [11].In the last two decades, various types of entangled quantum states such as entangled cat states [12, 13], entangled coherent states [8,9,10, 14, 15] and entangled squeezed states [16] have been introduced and discussed. Following these states, photon-added and photon-subtracted entangled states have been respectively introduced by exciting and depleting entangled states and studied their nonclassical properties [17, 18].

On the other hand, a nontrivial semi coherent state(Semi CS) was introduced in [19], which is a normalized superposition of two distinct CSs |α〉 and |β〉 of the form

$$ |\alpha\perp\beta \rangle =\frac{|\alpha \rangle -|\beta \rangle \langle \beta|\alpha \rangle }{[1-|\langle \beta|\alpha \rangle|^{2}]^{\frac{1}{2}}} $$

The state |α ⊥ β〉 refers to the projection of a coherent state |α〉 orthogonal to another coherent state |β〉 so that 〈β|α ⊥ β〉 = 0

The purpose of the present work is to study entangled states as to incorporate systems with quantum algebraic symmetries [20, 21].In this article ,we concentrate on the entanglement of the semi coherent state belonging to SU(1,1) algebra.The article is organized as follows: in the next section,we introduce the semi SU(1,1) coherent state(SU(1,1) Semi CS). Next, we consider a special form of the maximally entangled SU(1,1) Semi CS in Section 3. We study the entanglement characteristics of these entangled states in Section 4 by using the concurrence. Followed by a study of the probability distribution function in Section 5. We consider some of their nonclassical features in Section 6 by investigating the second order correlation function and the quadrature squeezing. The Q-function is presented in Section 7. The paper is concluded in Section 8.

2 SU(1,1) Semi Coherent States(SU(1,1) Semi CS)

For the SU(1,1) algebra [22,23,24], the three generators , K0,K−,K+ satisfy the commutation relations

$$ [K_{0}, K_{\pm}] = \pm K_{\pm}\qquad,\qquad [K_{-}, K_{+}] = 2K_{0} $$

Also, there exists the Casimir operator

$$ K^{2} = {K_{0}^{2}} -\frac{1}{2}(K_{+}K_{-} + K_{-}K_{+}) $$

For a positive discrete series representation, k > 0, the basis is denoted by {|m,k〉}, where m = 0,1,2,..... and the actions of the SU(1,1) generators on these states are given by:-

$$ \begin{array}{@{}rcl@{}} K^{2}|m, k \rangle&=&k(k-1)|m, k \rangle\\ K_{0}|m, k \rangle&=&(m+k)|m, k \rangle \\ K_{+}|m, k \rangle&=&\sqrt{(m+1)(m+2k)}|m+1, k \rangle \\ K_{-}|m, k \rangle&=&\sqrt{m(m+2k-1)}|m-1, k \rangle \end{array} $$
(2.1)

where k denotes the Bargmann index .It is apparent that K0 and K2 are diagonal in this representation.

2.1 Realization of the SU(1,1) Lie Algebra

One-mode realization

We know the radiation field can be described by bosonic operators a and a‡. If we form the quadratic combination

$$K_{+} =\frac{1}{2}(a^{\dagger})^{2}, \quad K_{-}=\frac{1}{2} a^{2}, \quad K_{0}=\frac{1}{4}(aa^{\dagger}+a^{\dagger}a)$$

In this case the Casimir operator reduces identically t

$$K^{2}=k(k-1)=-\frac{3}{16} $$

which corresponds to \(k =\frac {1}{4}\) or \(k =\frac {3}{4}\).

Two-mode realization

It is also possible to introduce a two-mode realization of the algebra su(1,1). This is done by defining the generators

$$ K_{+} =a^{\dagger}b^{\dagger}, \quad K_{-}= ab, \quad K_{0}=\frac{1}{2}(a^{\dagger}a+b^{\dagger}b+1) $$

In this case the Casimir operator is given by

$$K^{2}=k(k-1)=\frac{1}{4}(a^{\dagger}a-b^{\dagger}b)^{2}-\frac{1}{4} $$

then \(k=\frac {1}{2}(n+1)\), where n is the difference between two modes.

According to Barut-Girardello (BG),the SU(1,1) coherent state [25] is the eigenstate of the operator K−,such that

$$ \begin{array}{@{}rcl@{}} K_{-}|\alpha,k \rangle =\alpha |\alpha,k \rangle \end{array} $$

Its decomposition in the basis {|m,k〉},takes the form

$$ \begin{array}{@{}rcl@{}} |\alpha,k \rangle =N(\alpha,k)\sum\limits_{m=0}^{\infty}\frac{\alpha^{m}}{\sqrt{m!{\Gamma}(m+2k)}} |m,k \rangle \end{array} $$
(2.2)

with the normalization constant

$$ \begin{array}{@{}rcl@{}} N_(\alpha,k)=\sqrt{\frac{\alpha^{2k-1}}{I_{2k-1} (2|\alpha|) }} \end{array} $$

where Iν(x) is the modified Bessel function of the first kind of order ν given by,

$$ I_{\nu}(x)=\sum\limits_{m=0}^{\infty}\frac{1}{m! {\Gamma}(\nu+m+1)}\left( \frac{x}{2}\right)^{(2m+\nu)} $$

and Γ(x) is Euler’s Gamma function. The SU(1,1) Semi CS are defined as follows:-

$$ (|\alpha\perp \beta,k \rangle =|\eta,k \rangle)=\frac{|\alpha ,k\rangle -| \beta ,k\rangle \langle k, \beta|\alpha ,k\rangle }{[1-|\langle k, \beta|\alpha ,k \rangle|^{2}]^{\frac{1}{2}}} $$
(2.3)

where |α,k〉,|β,k〉 are SU(1,1) coherent states (BG-CS), and |η,k〉 is a SU(1,1) Semi CS,where |η,k〉 represents the projection of the SU(1,1) coherent state |α,k〉 orthogonal to the SU(1,1) coherent state |β,k〉,which means that 〈k,β|η,k〉 = 0. A new family of semi coherent states, for a charged particle moving in a constant uniform magnetic field have been introduced [26]. Then SU(1,1) Semi CS is expressed in terms of the basis {|m,k〉} as follows:-

$$ \begin{array}{@{}rcl@{}} |\eta,k \rangle&=&N(\alpha,\beta,k)\sum\limits_{m=0}^{\infty}\frac{ N(\alpha,k)\alpha^{m}-N(\beta,k)\mu(\alpha,\beta,k) \beta^{m}}{\sqrt{m!{\Gamma}(m+2k)}} |m,k \rangle \end{array} $$
(2.4)
$$ \begin{array}{@{}rcl@{}} &&\mu(\alpha,\beta,k)=N(\alpha,k)N(\beta,k)\sum\limits_{m=0}^{\infty}\frac{(\beta^{\ast} \alpha)^{m} }{m!{\Gamma}(m+2k)} \end{array} $$
(2.5)

with

$$ \begin{array}{@{}rcl@{}} N(\alpha,\beta,k)=(1-|\mu(\alpha,\beta,k)|^{2})^{\frac{-1}{2}} \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} N(\gamma,k)=\sqrt{\frac{\gamma^{2k-1}}{I_{2k-1} (2|\gamma|) }} \quad ,\quad \gamma=\alpha , \beta \end{array} $$

the normalization factor given in (2.2). The SU(1,1) Semi CS (2.4) is considered as a superposition of two SU(1,1) coherent states (2.2).It will be used in the following section as the corner stone of the entangled state under condition α≠β.

3 Entangled SU(1,1) Semi CS

Now, we consider a special type of entangled SU(1,1) Semi CS based on SU(1,1) coherent states and SU(1,1) Semi CS. This state is defined by[27]:

$$ |\psi,k\rangle= W(\alpha,\beta,k)\Big[|\beta,k \rangle_{a} \otimes|\eta,k \rangle_{b}+e^{i \theta}|\eta,k \rangle_{a}\otimes |\beta,k \rangle_{b}\Big] $$
(3.6)

where |β,k〉 is the SU(1,1) (BG) coherent state , |η,k〉 of (2.4) is the SU(1,1) Semi CS, in which 〈k,β|η,k〉 = 0, W(α,β,k) is the normalization coefficient, whose form is:

$$ W(\alpha,\beta,k) =\Big[2+2 (\cos\theta) |\langle k,\beta| \eta,k \rangle|^{2}\Big]^{\frac{-1}{2}}=\frac{1}{\sqrt{2}} $$
(3.7)

and the subscripts a and b represent the first and second modes respectively. Then |ψ,k〉 has the expression,

$$ |\psi,k\rangle=W(\alpha,\beta,k)N(\alpha,\beta,k)N_{\beta}(\beta,k)\sum\limits_{n,m=0}^{\infty}G(\alpha,\beta,k,n,m)|n,k\rangle |m,k\rangle $$
(3.8)

where

$$ \begin{array}{@{}rcl@{}} G(\alpha,\beta,k,n,m)=\frac{\Delta}{\sqrt{n!m!{\Gamma}(n+2k){\Gamma}(m+2k)}} \end{array} $$
(3.9)

with

$$ \begin{array}{@{}rcl@{}} {\Delta}=\beta^{n}(N(\alpha,k)\alpha^{m}-N(\beta,k)\mu(\alpha,\beta,k) \beta^{m})\\+e^{i \theta}[\beta^{m}(N(\alpha,k)\alpha^{n}-N(\beta,k)\mu(\alpha,\beta,k) \beta^{n})] \end{array} $$

This state will be the main subject of the study in the sections that follows. In the next sections, we will study the degree of entanglement by using the concurrence measure for different values of α,β and k, followed by some quantum properties of the state under consideration . We set 𝜃 = 0 in the calculations that follow .

4 Degree of Entanglement

To study the entanglement property, we may choose one of several entanglement quantifiers such as concurrence [28, 29], linear entropy [30], negativity [31], relative entropy of entanglement [32], entanglement of distillation [33], entanglement of formation [34], and so on. Here, we evaluate the degree of entanglement of the introduced state by applying the concurrence measure.

4.1 Concurrence

The concurrence of the introduced state in Section 3 is to be calculated here .It is generally defined for discrete-variable entangled state as follows [30,31,32]:

$$ C=|\langle {\Psi}|\sigma_{y}\otimes\sigma_{y}{\Psi}^{\ast}\rangle | $$

where σy is the Pauli matrix and Ψ∗ is the complex conjugate of Ψ. The concurrence is 1 for a maximally entangled state. To study the concurrence for continuous-variable entangled states like the entangled SU(1,1) Semi CS (3.8), one can consider a general two-mode entangled state as follows:

$$ {\Psi}=M^{-1} (\nu|\delta \rangle\otimes|\lambda \rangle+\tau|\zeta \rangle\otimes|\gamma \rangle ) $$

where |δ〉and|ζ〉 (|λ〉 and |γ〉 ) are normalized states of the first (second) mode with ν and τ complex and M the normalization factor.By making use of the transformation of the continuous variables-type components to the discrete orthogonal basis and using the Schmidt decomposition, the concurrence for the above mentioned entangled state can be obtained in the following form [33, 34]:

$$ \begin{array}{@{}rcl@{}} C=\frac{2|\nu||\tau|}{M^{2}}\sqrt{(1-|P^{(1)}|^{2})(1-|P^{(2)}|^{2})} \end{array} $$
(4.10)
$$ \begin{array}{@{}rcl@{}} P^{(1)}=\langle\delta |\zeta \rangle \qquad,\qquad P^{(2)}=\langle\gamma |\lambda \rangle \end{array} $$
(4.11)

Therefore, the concurrence of the state (3.8) is given by the following expression :

$$ \begin{array}{@{}rcl@{}} C=2 [W(\alpha,\beta,k)]^{2}(1-|P(\alpha,\beta,k)|^{2})\\ P^{(1)}=P^{(2)}=P(\alpha,\beta,k)=\langle k,\beta |\eta ,k \rangle=0 \\ C=1 \end{array} $$
(4.12)

with \(W(\alpha ,\beta ,k)=\frac {1}{\sqrt {2}}\) as defined before.Which means that the class of the states defined in (3.8) is a class of maximally entangled states

5 Probability Distribution Function

For the density operator \( \hat {\rho }=|k,\psi \rangle \langle \psi ,k| \) the probability distribution function is given by

$$ \begin{array}{@{}rcl@{}} P(n,m,\alpha,\beta,k)&=&Tr\Big(\hat{\rho}|n,m\rangle \langle m,n|\Big) =\Big|\langle n,m|\psi ,k \rangle\Big|^{2}\qquad \end{array} $$
(5.13)
$$ \begin{array}{@{}rcl@{}} P(n,m,\alpha,\beta,k)&=&\Big|W(\alpha,\beta,k)N(\alpha,\beta,k)N(\beta,k)G(\alpha,\beta,k,n,m)\Big|^{2}\quad \end{array} $$
(5.14)

where W(α,β,k), N(α,β,k),N(β,k) and G(α,β,k,n,m) are defined before. The probability distribution function of the state (3.8) is plotted versus n and m for different values of α by fixing k = 10,β = 12 in Fig. 1 It is seen that at α = 3, the state exhibits two separated peaks squeezed in the bases near the (0,0) corner forming a crescent, can be clearly observed in Fig. 1a. As α increases to α = 5 we observe that , the two peaks start to merge and a third peak in the middle of the plane starts to appear , as shown in Fig. 1b .At α = 9,we note that there is a single peak shifted toward higher values of m with a crescent like bases and the peak in the middle gains further height as shown in Fig. 1c. At α = 11.9, the peak in the corner is almost Gaussian and the one in the middle plain is gaining further height as shown in Fig. 1d. But when we take (α = 10i,β = 10) ,the state exhibits a different type of distribution. One observes three peaks, a middle higher peak directed diagonally with squeezed bases, while the two side peaks have the same direct and lower higher with squeezed bases. Generally, with α ≪ β the distribution starts with two separated peaks with a joint bases forming a crescent near the (0,0) corner. But at α increases the two peaks start to marge and a Gaussian peak in the middle of the plane starts to grow . For α approaches β, the two peaks marge into an almost Gaussian peak near to (0,0) corner, and the middle peak gains further height. However when we take imaginary α and real β, the state shows a different type with a middle peak and two side lower peaks squeezed with bases and directed diagonally in the plane.

Fig. 1
figure 1

Three-diminution probability distribution function of the entangled SU(1,1) Semi CS versus n and m at fixed k = 10, (β = 12,α = 3)in (a), (β = 12,α = 5)in (b), (β = 12,α = 9)in (c) and (β = 12,α = 11.9)in (d) and (β = 10,α = 10i)in (e)

Full size image

6 Non-classical Properties

Now, we consider some nonclassical features related to the state (3.8).For this purpose, we study in this section , two of the important nonclassical phenomena,namely: the second-order correlation function and quadrature squeezing .

6.1 Correlation Function

We pay some attention to one of the nonclassical behaviors, namely the (sub- Poissonian behavior [35]).Thus we introduce the second-order correlation function g(2)(0) [36, 37],which leads to better understanding of the nonclassical behavior of the quantum states [38]. A state for which g(2)(0) < 1 has sub-Poissonian distribution (nonclassical state), while a state for which g(2)(0) > 1 has a super- Poissonian distribution (classical state), while the state is Poissonian when the function g(2)(0) = 1.If g(2)(0) = 2(> 2)it is called thermal (super-thermal) state. This function can be introduced for the SU(1,1) group generators [39] as follows

$$ g^{(2)}(0)=\frac{\langle K_{+}^{2}K_{-}^{2}\rangle}{\langle K_{+} K_{-}\rangle^{2}} \qquad $$
(6.15)

For the state (3.8), we may use \(K_{-}=K_{-}^{a}K_{-}^{b} \). While , \( K_{-}^{a}(K_{-}^{b}) \) is lowering generator for mode a(b). And superscripts a(b) refer to first (second) mode with bases |n,k〉(|m,k〉) , and \(K_{+}=K_{+}^{a}K_{+}^{b}=K_{-}^{\dagger } \) then

$$ \begin{array}{@{}rcl@{}} \langle K_{+}K_{-}\rangle=\Big|W(\alpha,\beta,k)N(\alpha,\beta,k)N(\beta,k)\Big|^{2} \\ \times \sum\limits_{n=0}^{\infty}\sum\limits_{m=0}^{\infty}|G(\alpha,\beta,k,n,m)|^{2}[nm(n+2k-1)(m+2k-1)] \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} \langle K_{+}^{2}K_{-}^{2}\rangle=\Big|W(\alpha,\beta,k)N(\alpha,\beta,k)N(\beta,k)\Big|^{2} \\ \times \sum\limits_{n=0}^{\infty}\sum\limits_{m=0}^{\infty}|G(\alpha,\beta,k,n,m)|^{2}[nm(n+2k-1)(m+2k-1)]\\ \times[(n-1)(m-1)(n+2k-2)(m+2k-2)] \end{array} $$

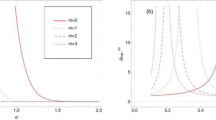
We plot the second-order correlation function g(2)(0)for the state (3.8) against β for different values of α and fixed k = 10 in Fig. 2a, and b. We note that for different values of α = (6.1,8,10), the state exhibits sub-Poissonian distribution in the ring β < 6.But for α = (8,9,10), the state exhibits super-Poissonian distribution for the ring β > 10.The plot of the second-order correlation function of the state (3.8) versus α for different values of β and fixed k = 10 in Fig. 2c, d, and e, we note that at small values of β = (0.5,2,3), the state exhibits sub-Poissonian distribution in the ring α < 12. But in the ring α < 8, the state comes from super-thermal distribution to super -Poissonian distribution for β = (8.1,9,10). But at ring α > 10, the state comes from super- Poissonian distribution to Poissonian distribution.On the other hand when α takes imaginary values such that (α = 4i,5i,6i ), the function g(2)(0) starts sub-Poissonian for β = 0 then it increases to become super-Poissonian until it settles to almost Poissonian for large values of β as shown in Fig. 2f. In contrast for β = 4i the g(2)(0) starts sub-Poissonian then it increases , while for β = 5i,6i the g(2)(0) starts super-Poissonian and drops down to almost Poissonian as shown in Fig. 2g.

Fig. 2
figure 2

second-order correlation function of the entangled SU(1,1) Semi CS: versusβ for different values of(α = 6.1,8,10)in (a), and versusβ for different values of(α = 8,9,10) in (b), and versus α for different values of (β = 0.5,2,3) in (c), and versus α for different values of (β = 8.1,9,10) in (d), and versus α for different values of (β = 8,9,10) in (e), and versus β for different values of (α = 4i,5i,6i) in (f), and versus α for different values of (β = 4i,5i,6i) in (g). At fixed k = 10

Full size image

6.2 Squeezing Effect

Squeezing of fluctuations is important in quantum measurement and communication theories [40]. In the SU(1,1) group [41],one can define two hermitian operators X and Y as follows:-

$$ X = \frac{ K_{-}+ K_{+}}{2} \qquad ,\qquad Y = \frac{ K_{-}- K_{+}}{2i} $$

They satisfy the commutation relation [X,Y ] = iZ.When we define \( K_{-}= K_{-}^{a} K_{-}^{b} = K_{+}^{\dagger }\) as before , then

$$ Z= {K_{0}^{a}}[({K_{0}^{b}})^{2}-(K^{b})^{2}]+ {K_{0}^{b}}[({K_{0}^{a}})^{2}-(K^{a})^{2}] $$

where a(b) refer to first (second) mode with base |n,k〉(|m,k〉). The uncertainty relation in the measurements for these operators takes the form

$$ {\Delta} X{\Delta} Y \geq \frac{1}{2} |\langle Z \rangle| $$

Fluctuations in the X (or Y ) component are squeezed if the following condition is satisfied

$$ ({\Delta} X)^{2} \textless \frac{1}{2} |\langle Z \rangle| \qquad or \qquad ({\Delta} Y)^{2} \textless \frac{1}{2} |\langle Z \rangle| $$

where (ΔX)2 = 〈X2〉−〈X〉2 and(ΔY )2 = 〈Y2〉−〈Y 〉2. To measure the degree of squeezing, we define the following squeezing parameters,

$$ \begin{array}{@{}rcl@{}} S_{X} = \frac{({\Delta} X)^{2}- 0.5 |\langle Z \rangle| }{ 0.5 |\langle Z \rangle|} \quad \text{ and} \quad S_{Y} = \frac{({\Delta} Y)^{2}- 0.5 |\langle Z \rangle| }{ 0.5 |\langle Z \rangle|} \end{array} $$

The squeezing condition can be expressed as

$$ S_{X}<0 \qquad \qquad or \qquad \qquad S_{Y}<0 $$

In Fig. 3a, we note that state (3.8) achieves squeezing phenomenon in SX. The factor SX is plotted for the range β > 0.3 for the values of α = (0.2,0.25,0.3).It is shown that the amount of squeezing is larger for the smaller values of α, and the squeezing exists for large range of β compared with the others values.However, when we plot SX against α for the ring α > 2 for the values of β = (0.5,1,2) we note that the squeezing exists for all values of β considered , and increases as α increases . However, with smaller values of β the squeezing starts earlier in the α axis as in Fig. 3b

Fig. 3
figure 3

SX for the entangled SU(1,1) Semi CS versus β for different values of α = (0.2,0.25,0.3) with origin (0.31, 0) in (a) and versus α for different values of β = (0.5,1,2) with origin (2.1, 0) in (b) at fixed k = 10

Full size image

7 Q-function

In the following we investigate one of the quasi-probability distribution functions, that is the Q-function [42,43,44,45]. The Q-function is a convenient tool to calculate expectation values of anti-normally ordered products of operators. It is well known that the Q-function can be defined in terms of basis diagonal elements of the density operator in the coherent state. Therefore, we use the density operator \( \hat {\rho }=|k,\psi \rangle \langle \psi ,k| \) for the state (3.8) to study its quasi-probability distribution. The Q-function in this case is given by

$$ Q(\delta,\gamma)=\frac{1}{\pi^{2}}\Big|\langle\delta,\gamma,k|\psi ,k \rangle\Big|^{2}, $$
(7.16)

where δ,γ ∈ C, the space of complex numbers ,|δ,γ,k〉 = |δ,k〉⊗|γ,k〉, |δ,k〉 and |γ,k〉 are the usual SU(1,1) coherent states (BG-CSS).Generally there are four variables associated with the real and imaginary parts of δ,γ. For visualization let us confine ourselves to a subspace determined by δ = x + iy = γ [46]. In that subspace the Q-function for the state (3.8) is calculated to be

$$ \begin{array}{@{}rcl@{}} Q(\delta,\gamma)&=&\frac{|W(\alpha,\beta,k)N(\alpha,\beta,k)N(\beta,k)N(\delta,k)N(\gamma,k)|^{2}}{\pi^{2}}\\ &\times&\bigg|\sum\limits_{n,m=0}^{\infty }\frac{\delta^{\ast n}\gamma^{\ast m} {\Delta}}{n!m!{\Gamma}(n+2k){\Gamma}(m+2k)} \bigg|^{2} \end{array} $$

where W(α,β,k), N(α,β,k),N(β,k), Δ, N(δ,k)andN(γ,k) are defined before.

To study Q-function for the state (3.8),we plot some figures, to display its behavior for different values of the parameters involved. Some details of the behavior can be seen if the function is plotted against x (Reδ) and y (Imδ) for some different values of α and β with fixed k = 10.This has been done in Fig. 4. When (α = 6,β = 1) , Q-function has a single peak with a crater and squeezed base symmetric around the y-axis with a slant irregular rim,as shown in Fig. 4a. When (α = 6,β = 3),we note that the crater is apparent but less than before with its slant rim rotating slightly anticlockwise,as shown in Fig. 4b. At (α = 6,β = 6.1) ,we note that the shape of the function is sensitive to change in β, where its shape now turns to a peak with a crater and irregular rim and it is symmetric around the center(5,0),as shown in Fig. 4c. For the case (α = 6,β = 9),the Q-function is similar to Fig. 4b, but its slant rim turned to the opposite side,as displayed in Fig. 4d. At (α = 6,β = 12),the shape of the function is further rotated anticlockwise as exhibited in Fig. 4e.

Fig. 4
figure 4

Q-function for entangled SU(1,1) Semi CS versus x (Reδ) and y (Imδ) at fixed k = 10, (β = 1,α = 6)in (a) and (β = 3,α = 6)in (b) and (β = 6.1,α = 6)in (c) and (β = 9,α = 6)in (d) ,and (β = 12,α = 6) in (e)

Full size image

8 Conclusions

Based on Barut-Girardello (BG) SU(1.1) coherent states we defined SU(1,1) Semi coherent states.Using these Semi CS a special type of entangled states is introduced. We calculated the entanglement degree of these entangled states by using the concurrence measure,which shows that the state has maximum degree of entanglement . Also,we considered some of their nonclassical features such as probability distribution function, which showed different shapes depending on the values of (α,β) and their type (real or imaginary). The second-order correlation function shows that the nonclassical behaviour exists for chosen values ofα and β.We considered the quadrature squeezing,which showed that quadrature squeezing occurs for different chosen values of α and β. Moreover,we plotted the Q-function in a sup space which showed that the shape of the function is very sensitive to changes of α and β.