The Correlated Two-Photon Transport in a One-Dimensional Waveguide Coupling to a Hybrid Atom-Optomechanical System

Abstract

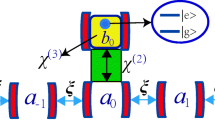
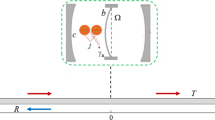
We investigate the two-photon transport properties inside one-dimensional waveguide side coupled to an atom-optomechanical system, aiming to control the two-photon transport by using the nonlinearity. By generalizing the scheme of Phys. Rev. A 90, 033832, we show that Kerr nonlinearity induced by the four-level atoms is remarkable and can make the photons antibunching, while the nonlinear interaction of optomechanical coupling participates in both the single photon and the two photon processes so that it can make the two photons exhibiting bunching and antibunching.

Appendix A: Two-Photon Scattering Eigenstate

In this Appendix, we provide a step to derive the scattering states for two incident photons in the right-going mode. Decomposing the right-going mode to the even and odd modes by $a_{R}^{\dag } (x)=[a_{e}^{\dag } (x)+a_{o}^{\dag } (x)]/\sqrt {2}$, the incoming state [(8)] can be written as

$$\begin{array}{@{}rcl@{}} |\psi_{i}\rangle &=&\sum\limits_{n}[\frac{1}{2}\int dx_{1}dx_{2}\phi_{k}(x_{1},x_{2})\frac{1}{\sqrt{2}}a_{e}^{\dag} (x_{1})a_{e}^{\dag} (x_{2})|0\rangle_{c}|\phi \rangle |n\rangle_{b} \\ &&+\frac{1}{2}\int dx_{1}dx_{2}\phi_{k}(x_{1},x_{2})\frac{1}{\sqrt{2}} a_{o}^{\dag} (x_{1})a_{o}^{\dag} (x_{2})|0\rangle_{c}|\phi \rangle |n\rangle_{b} \\ &&+\frac{1}{\sqrt{2}}\int dx_{1}dx_{2}\phi_{k}(x_{1},x_{2})\frac{1}{\sqrt{2} }a_{e}^{\dag} (x_{1})a_{o}^{\dag} (x_{2})|0\rangle_{c}|\phi \rangle |n\rangle_{b}] \end{array} $$

(A.1)

where |ϕ〉 is no photon in the waveguide. The general two-photon scattering state of the system in the spaces with even and odd modes can be written as (10) with

$$\begin{array}{@{}rcl@{}} \psi_{ee} &=& \sum\limits_{n}\int\int dx_{1} dx_{2}\phi_{ee}(x_{1},x_{2},n)\frac{1}{ \sqrt{2}}a^{\dag}_{e}(x_{1})a^{\dag}_{e}(x_{2})|0\rangle_{c}|\phi\rangle|n \rangle_{b}\\ &&+\sum\limits_{n}\int dx\phi_{ae}(x,n)a^{\dag}_{e}(x)a^{\dag}|0\rangle_{c}|\phi\rangle|\widetilde{n} (1)\rangle_{b} \\ &&+\sum\limits_{n}\phi_{aa}\frac{1}{\sqrt{2}} a^{\dag}a^{\dag}|0\rangle_{c}|\phi \rangle|\widetilde{n}(2)\rangle_{b} \end{array} $$

(A.2)

$$\begin{array}{@{}rcl@{}} \phi_{oe} &=& \sum\limits_{n}\int\int dx_{1} dx_{2}\phi_{oe}(x_{1},x_{2},n)a^{\dag}_{o}(x_{1})a^{\dag}_{e}(x_{2})|0 \rangle_{c}|\phi\rangle|n\rangle_{b}\\ && +\sum\limits_{n}\int dx\phi_{oa}(x,n)a^{\dag}_{o}(x)a^{\dag}|0\rangle_{c}|\phi\rangle|\widetilde{n} (1)\rangle_{b} \end{array} $$

(A.3)

$$\begin{array}{@{}rcl@{}} \phi_{eo} &=& \sum\limits_{n}\int\int dx_{1} dx_{2}\phi_{eo}(x_{1},x_{2},n)a^{\dag}_{o}(x_{1})a^{\dag}_{e}(x_{2})|0 \rangle_{c}|\phi\rangle|n\rangle_{b}\\ && +\sum\limits_{n}\int dx\phi_{ao}(x,n)a^{\dag}_{o}(x)a^{\dag}|0\rangle_{c}|\phi\rangle|\widetilde{n} (1)\rangle_{b} \end{array} $$

(A.4)

$$\begin{array}{@{}rcl@{}} \phi_{oo}&=&{\sum}_{n}\int \int dx_{1}dx_{2}\phi_{oo}(x_{1},x_{2},n)\frac{1}{ \sqrt{2}}a_{o}^{\dag} (x_{1})a_{o}^{\dag} (x_{2})|0\rangle_{c}|\phi \rangle |n\rangle_{b} \end{array} $$

(A.5)

where ϕ _{i j} (i,j = e,o,a) is the amplitude of the two photons with one photon in mode i and the other in mode j, subscript e(o) stands for the even (odd) mode and subscript a stands for the cavity mode. In order to satisfy the statistical property of photons, the amplitudes satisfy the relations ϕ _{e e} (x ₁, x ₂) = ϕ _{e e} (x ₂, x ₁), ϕ _{o o} (x ₁, x ₂) = ϕ _{o o} (x ₂, x ₁),ϕ _{e o} (x ₁, x ₂) = ϕ _{o e} (x ₂, x ₁), and ϕ _{o a} (x) = ϕ _{a o} (x). Under the two-photon transport of the frequency E = v _g (k ₁ + k ₂) + n ₀ ω _m , by solving Schr$\ddot {o}$dinger equation H|Ψ〉 = E|Ψ〉, we obtain the amplitudes for the two-photon scattering state

$$\begin{array}{@{}rcl@{}} \phi_{ee}(x_{1},x_{2},n) \!&\,=\,&\!\frac{1}{\sqrt{2}}[\phi_{e,k_{1}}(x_{1})\phi_{e,k_{2}}(x_{2})+\phi_{e,k_{1}}(x_{2})\phi_{e,k_{2}}(x_{1}) \\ &&+\{\theta (x_{2}-x_{1})\theta (x_{1})Be^{iE\frac{x_{c}}{v_{g}}} e^{\{i[E-2(\omega_{eff}-n\omega_{m}-\delta )]-(\kappa -{\Gamma} )\}\frac{x}{ 2v_{g}}}\,+\,(x_{2}\longleftrightarrow x_{1})\}\\ && \end{array} $$

(A.6)

$$\begin{array}{@{}rcl@{}} \phi_{oe}(x_{1},x_{2},n)=\frac{1}{\sqrt{2}}[\phi_{o,k_{1}}(x_{1})\phi _{e,k_{2}}(x_{2})+\phi_{e,k_{1}}(x_{2})\phi_{o,k_{2}}(x_{1})] \end{array} $$

(A.7)

$$\begin{array}{@{}rcl@{}} \phi_{oo}(x_{1},x_{2})=\frac{1}{\sqrt{2}}[\phi_{o,k_{1}}(x_{1})\phi _{o,k_{2}}(x_{2})+\phi_{o,k_{1}}(x_{2})\phi_{o,k_{2}}(x_{1})] \end{array} $$

(A.8)

$$\begin{array}{@{}rcl@{}} \phi_{oa}(x_{i},m)=\rho_{k_{1}}e^{ik_{1}x_{i}}+\rho_{k_{1}}e^{ik_{2}x_{i}} \end{array} $$

(A.9)

$$\begin{array}{@{}rcl@{}} \phi_{ae}(x_{i},m) &=&\theta (-x_{i})(\mu_{k_{1}}e^{ik_{1}x_{i}}+\mu_{k_{2}}e^{ik_{2}x_{i}})+ \\ &&\theta (x_{i})\{\eta_{k_{1}}e^{i[k_{1}+(n_{0}-m)\frac{\omega_{m}}{v_{g}} ]}x_{i}+\eta_{k_{2}}e^{i[k_{2}+(n_{0}-m)\frac{\omega_{m}}{v_{g}} ]})x_{i}+\xi (m)e^{\lambda (m)x_{i}}\}\\ \end{array} $$

(A.10)

$$\begin{array}{@{}rcl@{}} \phi_{aa}(m^{\prime} ) &=&-\sum\limits_{n}U_{n_{1}m_{2}^{\prime} }^{*}\frac{\sqrt{2} \overline{V}\phi_{ae}(0^{-},n)}{2U+2\omega_{eff}-i(\kappa+{\Gamma})+m^{\prime} \omega_{m}-E-4\delta} \end{array} $$

(A.11)

with

$$\begin{array}{@{}rcl@{}} \phi_{e,k_{i}}(x_{j},n) &=& \frac{1}{\sqrt{2\pi}}[\delta_{nn_{0}} \theta(-x_{j})+t_{k_{i}}\theta(x_{j})]e^{i[k_{i}+(n_{0}-n)\frac{\omega_{m}}{ v_{g}}]x_{j}} \end{array} $$

(A.12)

$$\begin{array}{@{}rcl@{}} \phi_{o,k_{i}}(x_{j},n) &=& \frac{\delta_{nn_{0}}}{\sqrt{2\pi}} e^{i[k_{i}+(n_{0}-n)\frac{\omega_{m}}{v_{g}}]x_{j}} \end{array} $$

(A.13)

where

$$\begin{array}{@{}rcl@{}} \mu_{k_{1}}(m) &=& \frac{\overline{V}U_{n_{0}m_{1}}^{*}}{2\pi}[\frac{1}{ -\omega_{eff}+i\frac{\kappa+{\Gamma}}{2}+v_{g}k_{2} +(n_{0}-m)\omega_{m}+\delta} ] \end{array} $$

(A.14)

$$\begin{array}{@{}rcl@{}} \mu_{k_{2}}(m) &=& \frac{\overline{V}U_{n_{0}m_{1}}^{*}}{2\pi}[\frac{1}{ -\omega_{eff}+i\frac{\kappa+{\Gamma}}{2}+v_{g}k_{1} +(n_{0}-m)\omega_{m}+\delta }] \end{array} $$

(A.15)

$$\begin{array}{@{}rcl@{}} t_{k_{1}}(n) &=& \sum\limits_{m}U_{nm_{1}}U_{n_{0}m_{1}}^{*}[\frac{-\omega_{eff}+i \frac{\kappa-{\Gamma}}{2}+v_{g}k_{2} +(n_{0}-m)\omega_{m}+\delta}{ -\omega_{eff}+i\frac{\kappa+{\Gamma}}{2}+v_{g}k_{2} +(n_{0}-m)\omega_{m}+\delta} ] \end{array} $$

(A.16)

$$\begin{array}{@{}rcl@{}} t_{k_{2}}(n) &=& \sum\limits_{m}U_{nm_{1}}U_{n_{0}m_{1}}^{*}[\frac{-\omega_{eff}+i \frac{\kappa-{\Gamma}}{2}+v_{g}k_{1} +(n_{0}-m)\omega_{m}+\delta}{ -\omega_{eff}+i\frac{\kappa+{\Gamma}}{2}+v_{g}k_{1} +(n_{0}-m)\omega_{m}+\delta} ] \end{array} $$

(A.17)

$$\begin{array}{@{}rcl@{}} \eta_{k_{1}}(m^{\prime} ) &=& \sum\limits_{n}U_{nm_{1}^{\prime} }^{*}\frac{ \overline{V}}{2\pi}\frac{t_{k_{1}}} {-\omega_{eff}+i\frac{\kappa-{\Gamma}}{2} +v_{g}k_{2}+(n-m^{\prime} )\omega_{m}+\delta} \end{array} $$

(A.18)

$$\begin{array}{@{}rcl@{}} \eta_{k_{2}}(m^{\prime} ) &=& \sum\limits_{n}U_{nm_{1}^{\prime} }^{*}\frac{ \overline{V}}{2\pi}\frac{t_{k_{2}}} {-\omega_{eff}+i\frac{\kappa-{\Gamma}}{2} +v_{g}k_{1}+(n-m^{\prime} )\omega_{m}+\delta} \end{array} $$

(A.19)

$$\begin{array}{@{}rcl@{}} \xi(n) &=& \sum\limits_{m}U_{nm_{1}}\frac{\sqrt{2}\overline{V}}{iv_{g}} \phi_{aa}(m)+\mu_{k_{1}}(n)+\mu_{k_{2}}(n)-\eta_{k_{1}}(n)-\eta_{k_{2}}(n) \end{array} $$

(A.20)

$$\begin{array}{@{}rcl@{}} B(n) &=& \sum\limits_{m^{\prime} }U_{nm_{1}^{\prime} }\frac{\overline{V}}{\sqrt{2} iv_{g}}\xi \end{array} $$

(A.21)

$$\begin{array}{@{}rcl@{}} \lambda(m^{\prime} ) &=& \frac{1}{iv_{g}}(\omega_{eff}-i\frac{\kappa+{\Gamma}}{ 2}+m^{\prime} \omega_{m}-E-\delta) \end{array} $$

(A.22)

and $\rho _{k_{i}}=\mu _{k_{i}}/\sqrt {2}$

$$\begin{array}{@{}rcl@{}} U_{nm_{1}} &=& \sum\limits_{l}e^{\frac{1}{2}(\frac{g_{0}}{\omega_{m}})^{2}}(-\frac{ g_{0}}{\omega_{m}})^{l+m-n}(-\frac{g_{0}}{\omega_{m}})^{l} \frac{(l+m)!}{ (l+m-n)!l!\sqrt{n!m!}} \end{array} $$

(A.23)