Abstract
Algorithms for answering the k nearest-neighbor (k-NN) query are widely used for queries in spatial databases and for distance classification of a group of query points against a reference dataset to derive the dominating feature class. GPU devices have significantly more processing cores than CPUs and faster device memory than the main memory accessed by CPUs, thus, providing higher computing power for processing demanding queries like the k-NN. However, since device and/or main memory may not be able to host an entire, rather big, reference and query datasets, storing these datasets in a fast secondary device, like a solid state disk (SSD), and partially retrieve the required, at each stage, partitions is, in many practical cases, a feasible solution. We propose and implement the first GPU-based algorithms for processing the k-NN query for big reference and query spatial data stored on SSDs. Based on 3d synthetic and real big spatial data, we experimentally compare these algorithms and highlight the most efficient algorithmic variation. This variation utilizes a CUDA feature known as Concurrent Kernel Execution, to further improve its performance.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Processing of big spatial data is demanding, and it is often assisted by parallel processing. GPU-based parallel processing has become very popular during last years [1]. In general, GPU devices have much larger numbers of processing cores than CPUs and device memory, which is faster than main memory accessed by CPUs, providing high-performance computing capabilities even to commodity computers.
GPU devices can be utilized for efficient parallel computation of demanding spatial queries, like the k nearest-neighbor (k-NN) query, which is widely used for spatial distance classification in many problems areas. We consider a set of query points and a set of reference points. For each query point, we need to compute the k-NNs of this point within the reference dataset. This permits us to derive the dominating class among these k-NNs (in case the class of each reference point is known).
Since GPU device memory is a rather scarce resource, it is very important to take advantage of this memory as much as possible to scale-up to larger datasets and avoid the need for distributed processing, which suffers from excessive network cost, sometimes outweighing the benefits of distributed parallel execution. However, since device and/or main memory may not be able to host an entire, rather big, reference dataset, storing this dataset in a fast secondary device, like a solid state disk (SSD) is, in many practical cases, a feasible solution.
In this paper,
-
We propose and implement (extending the DSPP algorithm [2]) the first GPU-based algorithms for processing the k-NN query not only on big reference, but also on big query spatial data stored on SSDs.
-
We exploit concurrent CUDA kernel execution to enable multiple concurrent CUDA stream k-NN calculations, resulting to better utilization of GPU resources and data transfers/computation overlap.
-
We utilize either an array-based, or a max-Heap based buffer for storing the distances of the current k nearest neighbors, which are combined with our new methods, deriving two algorithmic variations.
-
Based on 3d synthetic and real big spatial data, we present an extensive experimental comparison of these algorithmic variations, varying query dataset size, reference dataset size and k. These experiments highlight that the new methods, combined with either an array or a max-Heap buffer are performance winners, especially for very large reference and query spatial datasets and big k values.
The rest of this paper is organized as follows. In Sect. 2, we review related material and present the motivation for our work. Next, in Sect. 3, we introduce the new algorithm that we developed for the k-NN GPU-based processing on disk-residentFootnote 1 data and in Sect. 4, we present the experimental study that we performed for analyzing the performance of all our algorithms and for determining the performance winner among 10 (6 existing and 4 new) algorithmic variations tested on synthetic and real big reference and query data. Finally, in Sect. 5, we present the conclusions arising from our work and discuss our future plans.
2 Related Work and Motivation
A recent trend in the research for parallelization of nearest neighbor search is to use GPUs. Parallel k-NN algorithms on GPUs can be usually implemented by employing Brute-Force methods or by using Spatial Subdivision techniques. In this section, we review the most relevant contributions of these two approaches to design and implement k-NN algorithms on GPUs. Furthermore, concurrent kernel execution is an effective method to improve hardware utilization, and it can be used on GPUs to improve resource utilization and system performance, especially when kernels are running together. We review some interesting works where this mechanism has been applied to improve the performance on GPUs.
2.1 Brute-Force Techniques
Despite the great potential of GPU-accelerated k-NN algorithms, much of the literature focuses on optimizing Brute-Force approaches which emphasize the good performance in high-dimensional data spaces. k-NN on GPUs using a Brute-Force method applies a two-stage scheme: (1) the computation of distances and (2) the selection of the nearest neighbors by using sorting algorithms [3]. For the first stage, a distance matrix is built grouping the distance array to each query point. In the second stage, several selections are performed in parallel on the different rows of the matrix. In the literature, many Brute-Force approaches have been proposed and the most representative ones are briefly reviewed in the following.
One of the first implementations of a Brute-Force k-NN algorithm on GPUs is proposed in [4]. In this work the authors highlight two important characteristics: (1) each thread computes the distance between a given query point and a reference point, and (2) each thread sorts all the distances computed for a given query point. An important aspect of this work is the use of the insertion sort algorithm which only outputs the k smallest elements. Similarly, in [5], the distance matrix is split into blocks of rows and each matrix row is sorted using the radix sort method, obtaining performance more than 10\(\times\) faster than the sequential counterpart. Moreover, the authors used a segmentation method for pair-wise distance computations.
Following a slightly different approach as [4, 5] to compute the distance matrix, [6] proposes the CUKNN algorithm, a CUDA-based parallel implementation of k-NN. It computes, for the selection phase, a local k-NN for each block of threads, then merging and sorting them in order to obtain a global k-NN. Experimentally, CUKNN shows good scalability on data objects as well as up to 15x speedup in overall execution over large datasets.
In [7], an improved GPU-based approach by using the CUBLAS (CUDA Basic Linear Algebra Subroutines) API is proposed for a faster Brute-Force k-NN parallelization to efficiently calculate a distance matrix. A modified version of the insertion sort algorithm proposed in [4] is applied when each column of the distance matrix is sorted. The processing of the algorithm is separated into 8 parts, each of which is processed through a kernel. Furthermore, if the distance matrix is too large to be handled by GPU memory, the query points are split, processed separately, and the distances to the k-NNs are merged together on the CPU/host memory side.
Another two-step scheme to implement a Brute-Force k-NN algorithm on GPU is proposed in [8]. A GPU heap-based algorithm (called Batch Heap-Reduction) is presented, which achieves a better performance than the sorting-based GPU-Quicksort algorithms. The Batch Heap-Reduction algorithm uses a heap for each thread of a CUDA Block and performs a three-step algorithm to obtain the final k-NN. In the first step, the distance vector is evenly distributed across the CUDA block threads. Each thread determines its own partial k-NNs by the heap sort algorithm. The other two steps implement the reduction of the partial heaps. It is important to highlight that heap insertions usually imply warp divergences and lack of locality, thus increasing the number of GPU-memory read/write operations.
Another fast and scalable two-step Brute-Force k-NN implementation using GPUs, called GPU-FS-kNN algorithm, is presented in [9]. This exhaustive algorithm divides the computation of the distance matrix into smaller sub-matrices (squared chunks) in all dimensions, in order to parallelize distance calculations and k-NN search over these chunks. Each chunk is computed using a different kernel call, reusing the allocated GPU-memory. In the selection phase, each chunk is processed with a modified version of the insertion sort algorithm. An interesting feature of this method is the introduction of padded input matrix rows and columns so that the algorithm can work with any number of rows and columns.
A hybrid parallelization approach for Brute-Force computation of multiple k-NN queries on GPUs is proposed in [10]. For the matrix computation this method uses the general scheme of [5, 7], modifying the selection phase with multi-select algorithm based on quicksort. An additional optimization is also implemented, using voting functions available on the latest GPUs along with user-controlled cache. The warp voting function is used to partition the input without reading the input array twice and without executing the parallel-prefix sum.
Another efficient Brute-Force k-NN implementation is proposed in [11] by using a modified inner loop of the SGEMM kernel in the MAGMA library, a well-optimized open-source matrix multiplication kernel. Besides, the algorithm searches only the k smallest squared Euclidean distances for each query by using the merge-path function from the Modern GPU library and a truncated merge sort built on top of sorting and merging functions.
A new incremental neighborhood computation scheme that eliminates the dependencies between the dataset size and memory is presented in [12]. As a result, a new scalable and memory efficient design for a GPU-based k-NN rule, called GPU-SME-kNN, is proposed. It takes advantage of asynchronous memory transfers, making the data structures fit into the available memory while delivering high run-time performance independently of the dataset size. An experimental study of GPU-SME-kNN is also presented, showing a high performance, even in cases that other methods cannot address. Moreover, the GPU-SME-kNN algorithm has also been applied to k-NN-based lazy learning algorithms, reducing run-times in a significant way.
Novel GPU approaches to solving k-NN queries using Brute-Force algorithms based on the selection sort, quick sort and state-of-the-art heaps-based algorithms are proposed in [13]. Due to the fact that the best approach depends on the k value in the k-NN query, the authors also introduce a multi-core algorithm to be used as reference for the experiments and a hybrid algorithm which combines the proposed sorting algorithms with a state-of-the-art heaps-based method, in which the best performance is obtained with large k values. The authors also extend the proposed algorithms to be able to deal with large datasets that do not fit in GPU memory and whose performance does not deteriorate as dataset size increases.
Another parallel Brute-Force algorithm to solving k-NN queries on a multi-GPU platform is presented in [14]. The proposed method comprises two stages, the first being based on pivots using the value of k to reduce the search space, and the second one uses a set of heaps to return the final results. Through a wide-ranging set of experiments, this exhaustive algorithm outperformed previous state-of-the-art approaches.
Recently, a novel GPU-based Brute-Force algorithm to solve k-NN queries is proposed in [15], which is composed of two steps. The first step is based on pivots to reduce the range of search by using the k value, and the second one uses a set of heaps as auxiliary structures to return the final results. The authors also extend the exhaustive algorithm to be able to use a multi-GPU platform and a multi-node/multi-GPU platform. The proposed algorithm is experimentally compared with the state-of-the-art methods, reaching a speed-up of 389\(\times\) over 4 GPUs on a single node and up to 1840\(\times\) by using 20 GPUs over a multi-node/multi-GPU platform.
Some of these Brute-Force algorithms for solving k-NN queries (like the ones of [7] and their improved implementations of k-NNFootnote 2) consume a lot of device memory, since a Cartesian product matrix, containing the distances of reference points to the query points, is stored. In [16], two new algorithms based on GPUs to process k-NN queries on spatial data are proposed, using the Thrust library [1], that maximize device memory utilization. The first algorithm is based on Brute-Force scheme and the second one uses heuristics to minimize the reference points near a query point. In addition, the first GPU-based algorithms for parallel processing the k-NN query on large reference datasets stored on SSDs are proposed in [2]. These GPU-based algorithms utilize a Brute-Force schema and the plane-sweep technique. Such algorithms exploit the numerous GPU cores, use the device memory as much as possible and take advantage of the speed and storage capacity of SSDs, thus processing efficiently big reference datasets.
2.2 Spatial Subdivision Techniques
Spatial subdivision is a powerful technique to improve the overall manageability of large datasets in a variety of spatial applications. This spatial partitioning can also improve the spatial query performance mainly in two ways. First, partitioning the dataset into smaller units allows the processing of a spatial query in parallel, and thus improves its performance. Second, with a proper spatial partitioning schema, I/O can be significantly reduced by only scanning a few partitions that contain relevant data to answer the spatial query. There are many data structures that handle spatial subdivision efficiently [17] and, they can be used as GPU index-based data structures to perform efficiently k-NNQ. The most representative approaches of this category are briefly reviewed in the following.
kd-trees [18] have been successfully used for nearest neighbor searching for long time. For this reason, several variations of kd-trees have been implemented on GPUs. In [19], an algorithm for constructing kd-trees on GPUs is developed. The building process adopts a top-down, breadth-first search order, starting from the root bounding box. The k-NN implementation is based on a range search on the tree (with a given radius), and it continues to increase the size of the radius until k elements are retrieved. In [20], a buffer kd-tree for GPUs is presented. The buffer kd-tree algorithm avoids several drawbacks of the GPU’s architecture. In particular, the buffer refers to a query buffer located in every node of kd-tree, which is used to delay the execution of queries by waiting for sufficient work to be accumulated into a buffer before accessing leaf nodes. Each node in the buffer kd-tree corresponds to a set of reference patterns. Therefore, a lazy nearest neighbor search schema is applied. The algorithm also focuses on improving the fraction of coalesced memory accesses by having threads within a warp access either consecutive or nearby memory addresses.
In the context of spatial indexes, a grid structure is a regular tessellation of a manifold that divides the space into a series of contiguous cells, which can then be assigned unique identifiers and used for spatial indexing purposes. According to this subdivision of the space, a GPU grid-based data structure is appropriate for massively parallel nearest neighbor searches over dynamic point datasets. A key contribution is [21], where a grid-based indexing solution for 3-dimensional k-NN searches on the GPU is proposed. The k-NN algorithm works as follows: for a given query point, the algorithm expands the number of grid cells searched to ensure that at least k neighbors are found. That is, the algorithm uses a query-centric approach that expands the search radius when the number of found neighbors is less than k. The proposed k-NN algorithm minimizes the memory transfer between device and system memories, improving overall performance. Another GPU grid-based approach is the Adaptive Inverse Distance Weighting (AIDW) interpolation algorithm on GPU [22], where a fast k-NN search approach based on an even grid is used.
Efficient spatial indexing structures such as R-trees [23] are promising in speeding up such computing on GPUs; therefore, several contributions have been proposed for this purpose. One of the most significant one is [24], where parallel designs of bulk loading R-trees and several parallel query processing techniques (range query) on GPUs using R-trees are implemented. Moreover, in [25], a parallel bottom-up construction of SS-tree [26] on GPUs is proposed, along with the development of a data parallel tree traversal algorithm, called Parallel Scan and Backtrack (PSB), for k-NN query processing on the GPU. This algorithm traverses a SS-tree index while avoiding warp divergence problems. In order to take advantage of accessing contiguous memory blocks, the proposed PSB algorithm performs linear scanning of sibling leaf nodes, which increases the chance to optimize memory coalescing and locality.
Effective spatial data partitioning [27] is critical for task parallelization, load balancing, and directly affects system performance. A proper spatial partitioning schema is essential for optimal query performance and system efficiency for parallel spatial query processing. Keeping this in mind, in [28], a new algorithm for the k-NN query processing on GPUs is presented. It implements a new GPU-based partitioning algorithm based on a sort-tile partitioning method for the k-NN query (called Symmetric Progression Partitioning, SPP), using the CUDA runtime API, avoiding the calculation of distances for the whole dataset. Moreover, this k-NN query algorithm maximizes the utilization of device memory (using KNN-DLB buffer) and therefore permits larger reference datasets to take part in the processing of the query. Thus, by processing only the necessary parts of the reference dataset and by executing the whole process in the GPU device only, it minimizes execution speed. A thorough experimental evaluation proves that the proposed algorithm, not only works faster than existing methods, but also scales-up to much larger reference datasets.
2.3 Similarity Techniques
There are also other techniques like in [29] where the k-NN algorithm is extensively used. This paper describes a novel GPU similarity search algorithm, that can be applied in database systems handling complex data such as images or videos, which are typically represented by high-dimensional features and require specific indexing structures. The proposed methods can scale to billion-sized databases. Note that, unlike our work, the methods of this paper are not optimized for 2d and 3d spatial data and do not focus on computing NNs, but on the use of NNs for similarity search.
2.4 Concurrent Kernel Execution
Recent GPUs support concurrent kernel execution, that enables different kernels to run simultaneously on the same GPU, sharing the GPU hardware resources. Concurrent kernel execution can improve GPU hardware utilization and system performance. This feature of the current GPU programming models can be used in different scenarios to allow better utilization of GPU resources.
The impact of concurrent kernel execution on performance improvement by funneling all kernels of a multi-threaded host process into a single GPU context was firstly examined in [30]. In the same scenario, a kernel reordering technique is proposed in [31] to improve GPU performance by taking advantage of concurrent kernel execution focusing on the order in which GPU kernels are invoked on the host side.
In [32], the authors experimentally validate the benefits of using concurrent kernel execution to improve GPU energy-efficiency for computational kernels. For this purpose, they design power-performance models to carefully select the appropriate kernel combinations to be executed concurrently, the relative contributions of the kernels to the thread mix, along with the frequency choices for the cores and the memory to achieve high performance per watt metric.
Dai et al. [33] illustrates that compute-intensive kernels may be starved because other memory-intensive kernels block the memory pipeline on Simultaneous Multitasking (SMK) GPUs. To solve this problem, a dynamic memory instruction limiting method to mitigate the memory pipeline contention and accelerate concurrent kernel execution is proposed. The experimental results show that the proposed approach improves weighted speedup by 27.2% on average over SMK, with minor hardware cost.
In [34], the authors highlight that memory interference can significantly affect the throughput and fairness of concurrent kernel execution. They make a case that even the optimal Cooperative Thread Array (CTA) combination does not eliminate the negative memory interference impact. To address this problem effectively, a coordinated approach for CTA combination and bandwidth partitioning for GPU concurrent kernel execution is proposed. This approach effectively reduces the memory latency for the latency-sensitive kernels. In the meanwhile, the bandwidth utilization is also improved for the bandwidth-intensive kernels.
The performance of compute-intensive kernels is significantly reduced when memory-intensive kernels block memory pipeline and occupy most L1 data cache (L1D) resources, and it is highlighted in [35]. They propose a fair and cache blocking aware warp scheduling (FCBWS) approach for concurrent kernel execution on GPU to ameliorate the contention on data cache and improve system performance. FCBWS adopts kernel aware warp scheduling to provide equal chance of issuing instructions to each kernel. Moreover, for a ready memory instruction to be issued, if it is predicated that this instruction will block the data cache, FCBWS will select and issue another ready instruction of the same kernel; otherwise, this memory instruction will be issued to the memory pipeline. The experiment results indicate that FCBWS has important advantages over spatial multitasking and previous SMK works.
Another context to use concurrent kernel execution is to implement scheduling policies on GPUs. For example, a software scheduler for GPU applications, called FlexSched, has been recently presented in [36], that takes advantage of concurrent kernel execution to implement scheduling policies aimed at maximizing application execution performance, or meeting Quality of Service (QoS) application requirements such as maximum turnaround time. An important feature of FlexSched is the use of a productive on-line profiling, employing a heuristic that compares different co-execution configurations to find a suitable CTA allocation scheme that fulfills the scheduling requirements: throughput or QoS. In a real scheduling scenario, where new applications are launched as soon as GPU resources become available, FlexSched reduces the average overall execution time by a factor of 1.25\(\times\) with respect to the time obtained when proprietary hardware (HyperQ) is employed.
For interested readers, [37] is a recent survey on GPU multitasking methods, where concurrent kernel execution is studied as a feature of GPUs to support multitasking.
2.5 Motivation
Based on our literature research we concluded that there are no methods targeting big reference and query datasets (larger than the available device memory), neither are there methods that explore concurrent kernel execution, for the calculation of k-NN. Furthermore, our previous k-NN method implementations, address only big reference data; they can process only query datasets big enough to fit in device memory.
Based on these facts, there is no work so far that uses the advantages of concurrent kernel execution, to efficiently design and implement k-NN algorithms on GPUs. We will try to investigate and test how the invocation of this feature would increase k-NN calculation performance.
Moreover, we will try to extend our methods implementations, to aim also big query datasets. We will also leverage the trade-offs that arise from new algorithmic overheads and evaluate the effectiveness of our new methods.
3 kNN Disk Algorithms
A common practice to handle big data is data partitioning. In order to describe our new algorithms, we first present the mechanism of data partition transfers to device memory. This step is identical in all our methods. Each reference dataset is partitioned in N partitions containing an equal number of reference points. If the total reference points is not divided exactly by N, the Nth partition contains the remainder of the division. Initially the host (the computing machine hosting the GPU device) reads a partition from SSDFootnote 3 and loads it into the host memory. The host copies the in-memory partition data into the GPU device memory.Footnote 4
Another common approach in all our four methods is the GPU thread dispatching. Every query point is assigned to a GPU thread. The GPU device starts the k-NN calculation simultaneously for all threads in the kernel execution geometry. The thread dispatching consists of 4 main steps:
-
1.
The kernel is invoked with a grid of N threads.
-
2.
The requested N threads are assigned to N query points.
-
3.
Every thread carries out the calculation of reference point distances to its query point and updates the k-NN buffer holding the current (and eventually the final) nearest neighbors of this point.
-
4.
The final k-NN list produced by each kernel invocation is populated with the results of all the query points.
In the next sections we will describe our existing and new methods. These methods are based on three main algorithms, “Disk Brute-force”, “Disk Plane-sweep” and “Symmetric Progression Partitioning”. In all of them we have implemented two k-NN buffer variations resulting in a total of 6 existing and 4 new methods (algorithmic variations).
3.1 Disk Brute-Force Algorithm
The Disk Brute-force algorithm (denoted by DBF) [2] is a Brute-force algorithm enhanced with capability to read SSD-resident data. Brute-force algorithms are highly efficient when executed in parallel. The algorithm accepts as inputs a reference dataset R consisting of m reference points \(R=\{r_1,r_2,r_3,\ldots r_m\}\) in 3d space and a dataset Q of n query points \(Q=\{q_1,q_2,q_3,\ldots q_n\}\) also in 3d space. The host reads the query dataset and transfers it in the device memory. The reference dataset is transfered to the device memory and is partitioned into equally sized bins. For each partition, we apply the k-NN Brute-force computations for each of the threads.
For every reference point within the loaded partition, we calculate the Euclidean distance to the query point of the current thread. Every calculated distance is compared to the current thread maximum distance and if it is smaller, we add it to the k-NN list buffer. We will use and compare two alternative k-NN buffer implementations, presented in Sects. 3.6 and 3.7.
3.2 Disk Plane-Sweep Algorithm
An important improvement for join queries is the use of the Plane-sweep technique, which is commonly used for computing intersections [38]. The Plane-sweep technique is applied in [39] to find the closest pair in a set of points which resides in main memory. The basic idea, in the context of spatial databases, is to move a line, the so-called sweep-line, perpendicular to one of the axes, e.g., X-axis, from left to right, and process objects (points, in the context of this paper) as they are reached by this sweep-line. We can apply this technique for restricting all possible combinations of pairs of objects from the two datasets. The Disk Plane-sweep algorithm (denoted as DSP) incorporates this technique which is further enhanced with capability to read SSD-resident data.
Like DBF, DPS accepts as inputs a reference dataset R consisting of m reference points \(R=\{r_1,r_2,r_3,\ldots r_m\}\) in 3d space and a dataset Q of n query points \(Q=\{q_1,q_2,q_3,\ldots q_n\}\) also in 3d space. The host reads the query dataset and transfers it in the device memory. The reference dataset is partitioned in equally sized bins. Each bin is transferred to the device memory and sorted by the x-values of its reference points. (Algorithm 1). For each partition we apply the k-NN Plane-sweep technique (Fig. 1).
Starting from the leftmost reference point of the loaded partition, the sweep-line moves to the right. The sweep-line hops every time to the next reference point until it approaches the x-value of the query point (Fig. 1). Using the x-value of the query point, a virtual rectangle is created. This rectangle has a length of \(2*l\), where l is the currently largest k-NN distance in the k-NN buffer of the query point of the current thread.
For every reference point within this rectangle, we calculate the Euclidean distance (Algorithm 2) to this query point. The first k distances are added to its k-NN buffer. Every subsequent calculated distance is compared with the largest one in the k-NN buffer and if it is smaller, it replaces the largest one in the k-NN buffer.
In Fig. 1, we observe that all the reference points located on the right of the right rectangle limit are not even processed. The reference points located on left of the left rectangle limit are only processed for comparing their x-axis value. The costly Euclidean distance calculation is limited within the rectangle.


3.3 Disk Symmetric Progression Partitioning
A more efficient method than the previous ones is the “Disk Symmetric Progression Partitioning” [40], denoted as DSPP. DSPP is enhanced with the capability to read SSD-resident big data. The DSPP algorithm is using partitioning in both the host and the GPU device. The first level partitioning is taking place in the host, when reading data from the SSD-resident datasets, as we discussed in Sect. 3. The second level partitioning takes place in the device memory and is essential for the DSPP execution. We will document in detail the usage of the two distinct levels of partitioning later in this section.
Like DBF and DPS, DSPP accepts as inputs a reference dataset R consisting of m reference points \(R=\{r_1,r_2,r_3,\ldots r_m\}\) in 3d space and a dataset Q of n query points \(Q=\{q_1,q_2,q_3,\ldots q_n\}\) also in 3d space. The host reads the whole query dataset and transfers it in the device memory. The reference dataset is partitioned in equally sized bins (first level partition). Each partition is transferred to device memory and sorted by the x-values of its reference points (Algorithm 3). The host fetches back the sorted partition from the device in order to further partition it, into smaller sub-partitions (second level partition), and prepare the sub-partition index data for the SPP execution. This second partitioning will be taking place in the device memory and further accelerates the k-NN process, as we have proven in previous work [40, 41]. The host process, as a last step, executes the GPU kernel.

From the device perspective, every query point is assigned to a GPU thread. The GPU starts the k-NN calculation simultaneously for all threads, in kernel execution geometry.
The in-device-memory partitioning technique we are using, partitions the dataset in equally sized sub-partitions across the X-axis. DSPP searches for k-NN, traversing the partition index (Algorithm 4), that the host provided, and checks if its bounding box contains the query point (sub-partition number 5, in our example, Fig. 2). If k-NN are not found the thread searches for k-NN in the next closest sub-partition (sub-partition 6). Similarly, the process continues until all reference points are processed. In Fig. 2 we search for 20 nearest neighbors. We processed 7 out of 10 partitions and found the k-NN. Sub-partitions 1, 9 and 10 were excluded because the 20 nearest neighbors were already found.

DSPP sub-partition example, query point represented by + symbol, reference points represented by \(\times\) symbols (k-NN points), analyzed points represented by empty circles, non-analyzed points represented by filled circles, \(k = 20\) [28]
The host algorithm continuous to read partitions from the reference dataset, process them and execute the GPU kernel, until the reference dataset is fully read. Every kernel execution, merges into the k-NN buffer list the calculated distances that are shorter than the maximum current ones and produces the final k-NNs upon read reference data completion.
We will use and compare two alternative k-NN buffer implementations, presented in Sects. 3.6 and 3.7, thus resulting to two DSPP method variations.
3.4 Improved Disk Symmetric Progression Partitioning
One disadvantage of the DSPP method is that it can only process query datasets that fit in device memory. Surely modern GPUs are equipped with abundant memory, however modern big data query datasets can easily surpass GPU memory capacity. To fill this gap we designed and implemented an improved DSPP method, denoted by DSPP+. In our first new method, we incorporated an extra step of query dataset partitioning, just before the device k-NN calculation (Fig. 3). This means that the query dataset will be fully read, partition by partition, every time we need to process the next reference partition (Algorithm 5). If we partition the reference dataset in N partitions, then the query dataset will be read N times. Taking this under consideration, we expect an execution performance decrease, unless we manage to overlap those transfers with useful computation (which we address in Sect. 3.5). We must outline that this approach has some extra advantages, apart from processing big query datasets. One advantage is that when we initiate kernel processes the scheduled CUDA blocks query smaller volumes or points resulting in better L2 cache locality. Furthermore, the device data processed are close to each other and the method benefits from coalesced memory transaction, when consecutive threads access consecutive memory addresses.
Like our previous methods, DSPP+ accepts as inputs a reference dataset R consisting of m reference points \(R=\{r_1,r_2,r_3,\ldots r_m\}\) in 3d space and a dataset Q of n query points \(Q=\{q_1,q_2,q_3,\ldots q_n\}\) also in 3d space. We partition the reference dataset PR consisting of pm reference partitions \(PR=\{pr_1,pr_2,pr_3,\ldots pr_{pm}\}\). In analogy, we partition the query dataset QR consisting of qn query partitions \(QR=\{qr_1,qr_2,qr_3,\ldots qr_{qn}\}\). For each PR[i] partition, we traverse sequentially all QR[j] partitions and merge the resulting k-NNs to our k-NN buffer (Fig. 3).
Like our previous methods, we will use and compare two alternative k-NN buffer implementations, presented in Sects. 3.6 and 3.7, thus resulting to two DSPP+ method variations.


3.5 Improved Disk Symmetric Progression Partitioning with Pinned Memory
The second new method we are presenting, exploits a significant CUDA feature. CUDA streams, which aim to hide the latency of memory copy and kernel launch from different independent operations [42], are widely used in computational tasks to increase performance [43].
When CUDA Streams are used, together with pinned memory supporting asynchronous data transfers, we can overlap data transfers with kernel execution, thus effectively hiding data transfer latency. This improves GPU utilization and reduces execution time.
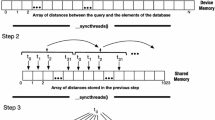
This new method is the Improved Disk Symmetric Progression Partitioning with pinned memory (denoted by DSPP+P).
The DSPP+ algorithm partitions the query dataset and calculates the k-NN for each one. In this second new algorithm, we process every query partition in a new stream. The CUDA kernel executes concurrently and the k-NNs are written to the output buffer (Fig. 4).
Like DSPP+, DSPP+P accepts as inputs a reference dataset R consisting of m reference points \(R=\{r_1,r_2,r_3,\ldots r_m\}\) in 3d space and a dataset Q of n query points \(Q=\{q_1,q_2,q_3,\ldots q_n\}\) also in 3d space. We partition the reference dataset PR consisting of pm reference partitions \(PR=\{pr_1,pr_2,pr_3,\ldots pr_{pm}\}\). Analogously we partition the query dataset QR consisting of qn query partitions \(QR=\{qr_1,qr_2,qr_3,\ldots qr_{qn}\}\). For each PR[i] partition, we traverse in a parallel and fully asynchronous way, all QR[j] partitions and merge the resulting k-NNs to our k-NN buffer (Fig. 4).
Like our previous methods, we will use and compare two alternative k-NN buffer implementations, presented in Sects. 3.6 and 3.7, thus resulting to two DSPP+P method variations.


3.6 k-NN Distance List Buffer
In our methods we implemented two different k-NN list buffers. The first one is the k-NN Distance List Buffer (denoted by KNN-DLB). KNN-DLB is an array where all calculated distances are stored (Table 1, distance values in bold are the ones inserted in the buffer). KNN-DLB array size is k per thread, resulting in minimal device memory utilization. When the buffer is not full, we append the calculated distances. When the buffer is full, we compare every newly calculated distance with the largest one stored in KNN-DLB. If it is smaller, we simply replace the largest distance with the new one. Therefore, we use sorting. The resulting buffer contains the correct k-NNs, but not in an ascending order. The usage of KNN-DLB buffer performs better than sorting a large distance array [28].
3.7 k-NN Max-Heap Distance List Buffer
The second list buffer that we implemented is based on a max-Heap (a priority queue represented by a complete binary tree which is implemented using an array, Fig. 5). max-Heap array size is \(k+1\) per thread, because the first array element is occupied by a sentinel. The sentinel value is the largest value for double numbers (for C++ language, used in this work, it is the constant DBL_MAX). KNN-DLB is adequate for smaller k values, but when k value increases performance deteriorates, primarily due to KNN-DLB O(n) insertion complexity. On the other hand, max-Heap insertion complexity is O(log(n)) and for large enough k max-Heap implementations are expected to outperform KNN-DLB ones.
4 Experimental Study
We run a large set of experiments to quantify the performance of our proposed algorithms. All experiments query a variety of dataset volumes of synthetic and real data. We are using double precision accuracy for the points representation in 3D space (Algorithm 9) to be able to discriminate among small distance differences.

All experiments were performed on a Dell G5 15 laptop, running Ubuntu 20.04, equipped with a six core (12-thread) Intel I7 CPU, 16 GB of main memory, a 1TB SSD disk used and a NVIDIA Geforce 2070 (Mobile Max-Q) GPU with 8 GB of device memory (as a representative setup for everyday computing). CUDA version 11.2 was used.
We run experiments to compare the performance of k-NN queries regarding execution time, as well as memory utilization. We tested a total of ten algorithms.
-
1.
DBF, Disk Brute-force using KNN-DLB buffer
-
2.
DBF Heap, Disk Brute-force using max-Heap buffer
-
3.
DPS, Disk Plane-sweep using KNN-DLB buffer
-
4.
DPS Heap, Disk Plane-sweep using max-Heap buffer
-
5.
DSPP, Disk Symmetric Progression Partitioning using KNN-DLB buffer
-
6.
DSPP Heap, Disk Symmetric Progression Partitioning using max-Heap buffer
-
7.
DSPP+, Improved Disk Symmetric Progression Partitioning using KNN-DLB buffer
-
8.
DSPP+ Heap, Improved Disk Symmetric Progression Partitioning using max-Heap buffer
-
9.
DSPP+P, Improved Disk Symmetric Progression Partitioning with pinned memory using KNN-DLB buffer
-
10.
DSPP+P Heap, Improved Disk Symmetric Progression Partitioning with pinned memory using max-Heap buffer
To the best of our knowledge, these are the first methods to address the k-NN query on SSD-resident data, that can process big reference and query datasets.
The experimental study is divided in two main subsection. The first one is based on synthetic data and the second one on real data.
4.1 Synthetic Data Experiments
In this section we will evaluate the performance of our methods, based only on synthetic data. All the datasets were created using the SpiderWeb [44] generator. This generator allows users to choose from a wide range of spatial data distributions and configure the size of the dataset and its distribution parameters. This generator has been successfully used in research work to evaluate index construction, query processing, spatial partitioning, and cost model verification [45].
Table 2 lists all the generated datasets. For the reference dataset, we created five datasets using the “Bit” distribution (Fig. 6 right), with file sizes ranging from 32 to 160 MB. The reference points dataset size ranges from 1 points to 5 M points. For the query points dataset we created five “Uniform" datasets (Fig. 6, left) ranging from 100 to 500 K points.
Three different sets of experiments on synthetic data were conducted. In the first one, we scaled the reference dataset size, in the second one we scaled the query dataset size and in the third one we scaled the number of the nearest neighbors, k. We also evaluated the performance of the two alternative list buffers to clarify the pros and cons of using KNN-DLB and max-Heap buffer.
4.1.1 Reference Dataset Scaling
In our first series of tests, we used the “Bit” distribution synthetic datasets for the reference points. The size of the reference point dataset ranged from 1 M points to 5 M points. Furthermore, we used a fixed query dataset of 100 K points, with “Uniform” distribution and a k value of 20, in order to focus only on the reference dataset scaling.
In Fig. 7, we can see the experiment results chart. In these results, we notice that the execution time of the Brute-force methods is larger than the rest of the methods. Apart from the Brute-force methods, all other methods have quite similar executions times, for each reference dataset size. For example, for the 1 M dataset the execution times range from 6.81 s for DBF Heap (slowest) to 2.20 s for the DSPP (fastest). The execution times increase proportionally to the reference dataset size. As expected, we get the slowest execution times for the 5 M dataset, ranging from 34.41 s for DBF Heap to 9.08 for the DSPP Heap method.
In order to compare the performance of our methods in Table 3, we present the execution speedup gain, using the slowest method (DFB) as the baseline. Every number in this table represents the method gain relative to the base method DBF (how many times faster than DBF). As expected, the DBF Heap method gain is close to 1, meaning that the DBF and DBF Heap are performing equally in all reference datasets. The execution speedup gain of the other methods ranges from 2.08 (times faster) in DPS for the 1 M reference dataset, to 3.69 (times faster) in DSPP for the 5 M reference dataset. We should notice that the method DSPP+P, is the second fastest method, performing slightly worse than DSPP, and achieved a speedup of 3.56 for the 4 M reference dataset.
The reference dataset scaling experiments reveal that the Brute-force methods did not perform well. This behaviour is expected because of the naive Brute-force algorithm of these methods. The DSPP method is faster than the DPS one, confirming our results from our previous publications [2, 28]. The interesting part of this experiment is that our new methods DSPP+ and DSPP+P performed about equally to DSPP, despite their query partitioning algorithm adding an overall overhead by repeatedly reading the query dataset. Especially DSPP+P performance is equivalent to DSPP. As we experimentally validate, this overhead was leveraged by the concurrent kernel execution invocation of DSPP+P. Furthermore, we can observe that the two k-NN distance list buffers, KNN-DLB and max-Heap, perform equally in all reference datasets. The value of \(k=20\) is explicitly selected to be small enough so that the buffer usage does not affect the experimental results. The difference between the two buffers will be quantified in the k scaling experiment later on.
4.1.2 Query Dataset Scaling
In our second set of experiments, we also used the “Uniform” distribution synthetic datasets for the query points. The size of the query point dataset ranged from 100 K points to 500 K points. Furthermore, we used a fixed reference dataset of 1 M points, with “Bit" distribution and a k value of 20, in order to focus only on the query dataset scaling.
In Fig. 8, we can see the experiment results chart. In these results, we see similar results as in our previous experiment. The execution time of the Brute-force methods is higher than the rest of our methods. All the other methods have comparable executions times, for each reference dataset size. For example, for the 200 K query dataset the execution times range from 13.72 s for DBF Heap (slowest) to 4.28 s for DSPP (fastest). The execution times increase proportionally to the query dataset size. We get the highest execution times for the 500 K dataset, ranging from 35.87 s for DBF Heap to 11.54 for the DSPP method.
To compare the performance of our methods, in Table 4 we present the speedup, using the slowest method (DFB) as the baseline. Similarly to the previous experiment, the two Brute-force methods are again performing identically for all query datasets. The speedup of the other methods ranges from 2.07 (times faster) in DPS for the 200 K dataset, to 3.06 (times faster) in DSPP for the 400 K query dataset. As was also the case for our reference scale experiment, we notice that the method DSPP+P, is the second fastest method, performing slightly worse than DSPP, and achieved a speedup gain of 2.96 for the 100 K query dataset.
The query dataset scaling experiment revealed once again that the Brute-force methods did not perform well for the same reasons as in our first experiment. The DSPP method is faster than the DPS one, confirming our results from our previous publications. Our new methods DSPP+ and DSPP+P performed about equally to DSPP, even if their query partitioning algorithm is adding an overall overhead by repeatedly reading the query dataset. Especially DSPP+P performance is equivalent to DSPP. We confirm again in this experiment that this overhead was leveraged by the concurrent kernel execution invocation of DSPP+P.
4.1.3 k Scaling
The k scaling is our third experiment. In these tests we used k values of 20, 40, 60, 80 and 100. For the reference points we used the 1 M “Bit” distribution synthetic dataset and for the query dataset 100K points, with “Uniform” distribution.
In Fig. 9, we can see the experiment results chart. The results in this experiment are quite different than the previous experiments. The execution time of the Brute-force methods is higher than the rest of our methods and we can see that the execution time of all KNN-DLB methods (DBF, DPS, DSPP, DSPP+ and DSPP+P), tend to increase in exponential way for larger k values. On the other hand, the execution time of all heap methods are increasing in a linear way. For \(k=100\) the execution times range from 10.79 s for DBF (slowest) to 3.76 s for DSPP+P (fastest).
In Table 5, we compare the execution performance of our methods, we present the execution speed gain, based on our slowest method DFB. In contrary to our previous experiments the two Brute-force methods are not performing identically; the DBF Heap method is faster for larger k values. Generally all heap methods perform clearly faster for larger k values. The execution gain of our methods for \(k=100\), ranges from 1.25 (times faster) in DBF Heap, to 2.87 (times faster) in DSPP+P Heap. In this experiment the DSPP+P method is a clear winner. It is better than DSP in all k values except the smallest one, \(k=20\).
In the k scaling experiment the heap methods stand out. For larger k values the max-Heap buffer is a much faster algorithm, because of its O(log(n)) complexity. Another interesting result is that DSPP+P Heap is overtaking even the DSPP Heap method. When we increase the k value, the k-NN calculation is even more computationally bound. The use of CUDA streams and the associated data transfers/kernel execution overlap, further accelerates this GPU costly operation, resulting in lower execution times, even if the DSPP+P methods repeatedly read the query dataset and transfer it to device memory. We confirm again in this experiment that the read overhead was successfully leveraged by the concurrent kernel execution invocation of DSPP+P.
4.2 Real Data Experiments
In this section we will present three real data experiments, using the real datasets documented in Sect. 4. We used three big real datasets [46], which represent water resources of North America (Water Dataset) consisting of 5.8M line-segments and world parks or green areas (Parks Dataset) consisting of 11.5 M polygons and world buildings (Buildings Dataset) consisting of 114.7 M polygons (Table 6). To create sets of points, we used the centers of the line-segment MBRs from Water and the centroids of polygons from Park and Buildings. For all datasets the 3-dimensional data space is normalized to have unit length (values [0, 1] in each axis).
These experiments will evaluate our new methods performance when targeting real life data. The first of them queries only the smallest datasets, in order to compare our new methods performance with our previous ones. The second and third experiments query the larger real datasets, which our previous methods couldn’t target.
4.2.1 Real Experiment 1: Parks 11.5 M, Water 5.8 M
In Fig. 10, we can see the first real data experiment results chart. The results in this experiment are similar to the reference and query scaling experiments. The execution time of the Brute-force methods is much larger than the rest of our methods. The execution times range from 5117 s for DBF (slowest method) to just 93 s for DSPP+P Heap (fastest method). When data volumes increase, the streaming kernel execution implementation in the DSPP+P methods, clearly outperforms all other methods, even the DSPP ones. In Table 7 we observe that DSPP+P was 57.23 times faster than DBF. Even in comparison to the best existing method (DSPP), the proposed method (DSPP+P) is 3.36 times faster.
4.2.2 Real Experiment 2: Buildings 114.7 M, Water 5.8 M
The next real data experiment is presented in Fig. 11. In this experiment we evaluated only our new methods; our previous ones could not target a query dataset so large, because its footprint exceeds device memory capacity. The execution times range from 1500 s for DSPP+ (slowest method) to 807 s for DSPP+P Heap (fastest method). Once again, when data volumes increase, the streaming kernel execution implementation in the DSPP+P methods, clearly outperforms all other methods.
4.2.3 Real Experiment 3: Buildings 114.7 M, Parks 11.5 M
The last real data experiment is presented in Fig. 12. In this experiment we evaluated again only our new methods. The new methods successfully processed these large datasets, which were the largest in our experiments. The execution times range from 4010 s for DSPP+ (slowest method) to 1930 s for DSPP+P Heap (fastest method). Our results are once more validated, when data volumes increase, the streaming kernel execution implementation in the DSPP+P methods, is the performance winner.
5 Conclusions and Future Plans
In this paper, we introduced the first GPU-based algorithms for parallel processing the k-NN query on reference and query big spatial data stored on SSDs, utilizing the Symmetric Progression Partitioning technique. Our new algorithms exploit the manycore GPU architecture, the concurrent kernel execution feature of Nvidia GPUs, utilize the device memory efficiently, take advantage of the speed and storage capacity of SSDs and, thus, process efficiently big reference and query datasets. Through an extensive experimental evaluation on synthetic and real datasets, we highlighted that the DSPP+P algorithm and especially its Heap variation, when using large k values and/or larger dataset volumes, is a clear performance winner.
Our future work plans include:
Notes
We used an SSD and in the rest of the text “SSD” instead of “disk” is used.
Reading from SSD is accomplished by read operations of large sequences of consecutive pages, exploiting the internal parallelism of SSDs, although our experiments showed that reading from SSD does not contribute significantly to the performance cost of our algorithms.
The hardware we used does not support GPUDirect storage.
References
Barlas, G.: Multicore and GPU Programming: An Integrated Approach, 1st edn. Morgan Kaufmann, Los Altos (2014)
Velentzas, P., Vassilakopoulos, M., Corral, A.: GPU-based algorithms for processing the \(k\) nearest-neighbor query on disk-resident data. In: MEDI Conference, pp. 264–278 (2021). https://doi.org/10.1007/978-3-030-78428-7_21
Singh, D.P., Joshi, I., Choudhary, J.: Survey of GPU based sorting algorithms. Int. J. Parallel Prog. 46(6), 1017–1034 (2018). https://doi.org/10.1007/s10766-017-0502-5
Garcia, V., Debreuve, E., Barlaud, M.: Fast k nearest neighbor search using GPU. In: CVPR Workshops, pp. 1–6 (2008). https://doi.org/10.1109/CVPRW.2008.4563100
Kuang, Q., Zhao, L.: A practical GPU based kNN algorithm. In: SCSCT Conference, pp. 151–155 (2009)
Liang, S., Wang, C., Liu, Y., Jian, L.: CUKNN: a parallel implementation of k-nearest neighbor on CUDA-enabled GPU. In: YC-ICT Conference, pp. 415–418 (2009). https://doi.org/10.1109/YCICT.2009.5382329
Garcia, V., Debreuve, E., Nielsen, F., Barlaud, M.: K-nearest neighbor search: fast GPU-based implementations and application to high-dimensional feature matching. In: ICIP Conference, pp. 3757–3760 (2010). https://doi.org/10.1109/ICIP.2010.5654017
Barrientos, R.J., Gómez, J.I., Tenllado, C., Prieto-Matías, M., Marín, M.: kNN query processing in metric spaces using GPUs. In: Euro-Par Conference, pp. 380–392 (2011). https://doi.org/10.1007/978-3-642-23400-2_35
Arefin, A.S., Riveros, C., Berretta, R., Moscato, P.: GPU-FS-kNN: a software tool for fast and scalable kNN computation using GPUs. PLoS ONE 7(8), 1–13 (2012). https://doi.org/10.1371/journal.pone.0044000
Komarov, I., Dashti, A., D’Souza, R.M.: Fast k-NNG construction with GPU-based quick multi-select. PLoS ONE 9(5), 1–9 (2014). https://doi.org/10.1371/journal.pone.0092409
Li, S., Amenta, N.: Brute-force k-nearest neighbors search on the GPU. In: SISAP Conference, pp. 259–270 (2015). https://doi.org/10.1007/978-3-319-25087-8_25
Gutiérrez, P.D., Lastra, M., Bacardit, J., Benítez, J.M., Herrera, F.: GPU-SME-kNN: scalable and memory efficient kNN and lazy learning using GPUs. Inf. Sci. 373, 165–182 (2016). https://doi.org/10.1016/j.ins.2016.08.089
Barrientos, R.J., Millaguir, F., Sánchez, J.L., Arias, E.: GPU-based exhaustive algorithms processing kNN queries. J. Supercomput. 73(10), 4611–4634 (2017). https://doi.org/10.1007/s11227-017-2110-y
Riquelme, J.A., Barrientos, R.J., Hernández-García, R., Navarro, C.A.: An exhaustive algorithm based on GPU to process a kNN query. In: SCCC Conference, pp. 1–8 (2020). https://doi.org/10.1109/SCCC51225.2020.9281231
Barrientos, R.J., Riquelme, J.A., Navarro, R.H.-G.C.A., Soto-Silva, W.: Fast kNN query processing over a multi-node GPU environment. J. Supercomput. 78(2), 3045–3071 (2022). https://doi.org/10.1007/s11227-021-03975-2
Velentzas, P., Vassilakopoulos, M., Corral, A.: In-memory k nearest neighbor GPU-based query processing. In: GISTAM Conference, pp. 310–317 (2020). https://doi.org/10.5220/0009781903100317
Samet, H.: Foundations of Multidimensional and Metric Data Structures. Morgan Kaufmann Series in Data Management Systems, Academic Press, London (2006)
Bentley, J.L.: Multidimensional binary search trees used for associative searching. Commun. ACM 18(9), 509–517 (1975). https://doi.org/10.1145/361002.361007
Zhou, K., Hou, Q., Wang, R., Guo, B.: Real-time kd-tree construction on graphics hardware. ACM Trans. Graph. 27(5), 126 (2008). https://doi.org/10.1145/1409060.1409079
Gieseke, F., Heinermann, J., Oancea, C.E., Igel, C.: Buffer k-d trees: processing massive nearest neighbor queries on GPUs. In: ICML Conference, pp. 172–180 (2014)
Leite, P.J.S., Teixeira, J.M.X.N., Farias, T.S.M.C., Reis, B., Teichrieb, V., Kelner, J.: Nearest neighbor searches on the GPU—a massively parallel approach for dynamic point clouds. Int. J. Parallel Prog. 40(3), 313–330 (2012). https://doi.org/10.1007/s10766-011-0184-3
Mei, G., Xu, N., Xu, L.: Improving GPU-accelerated adaptive IDW interpolation algorithm using fast kNN search. Springerplus 5(1), 1389 (2016). https://doi.org/10.1186/s40064-016-3035-2
Guttman, A.: R-trees: a dynamic index structure for spatial searching. In: SIGMOD Conference, pp. 47–57 (1984). https://doi.org/10.1145/602259.602266
You, S., Zhang, J., Gruenwald, L.: Parallel spatial query processing on GPUs using r-trees. In: BigSpatial@SIGSPATIAL Workshop, pp. 23–31 (2013). https://doi.org/10.1145/2534921.2534949
Nam, M., Kim, J., Nam, B.: Parallel tree traversal for nearest neighbor query on the GPU. In: ICPP Conference, pp. 113–122 (2016). https://doi.org/10.1109/ICPP.2016.20
White, D.A., Jain, R.C.: Similarity indexing with the SS-tree. In: ICDE Conference, pp. 516–523 (1996). https://doi.org/10.1109/ICDE.1996.492202
Aji, A., Vo, H., Wang, F.: Effective spatial data partitioning for scalable query processing. CoRR 1–12 (2015). arXiv:1509.00910
Velentzas, P., Vassilakopoulos, M., Corral, A.: A partitioning GPU-based algorithm for processing the k nearest-neighbor query. In: MEDES Conference, pp. 2–9 (2020). https://doi.org/10.1145/3415958.3433071
Johnson, J., Douze, M., Jégou, H.: Billion-scale similarity search with GPUs. IEEE Trans. Big Data 7(3), 535–547 (2021). https://doi.org/10.1109/TBDATA.2019.2921572
Wang, L., Huang, M., El-Ghazawi, T.A.: Exploiting concurrent kernel execution on graphic processing units. In: HPCS Conference, pp. 24–32 (2011). https://doi.org/10.1109/HPCSim.2011.5999803
Wende, F., Cordes, F., Steinke, T.: On improving the performance of multi-threaded CUDA applications with concurrent kernel execution by kernel reordering. In: SAAHPC Conference, pp. 74–83 (2012). https://doi.org/10.1109/SAAHPC.2012.12
Jiao, Q., Lu, M., Huynh, H.P., Mitra, T.: Improving GPGPU energy-efficiency through concurrent kernel execution and DVFS. In: CGO Conference, pp. 1–11 (2015). https://doi.org/10.1109/CGO.2015.7054182
Dai, H., Lin, Z., Li, C., Zhao, C., Wang, F., Zheng, N., Zhou, H.: Accelerate GPU concurrent kernel execution by mitigating memory pipeline stalls. In: HPCA Conference, pp. 208–220 (2018). https://doi.org/10.1109/HPCA.2018.00027
Lin, Z., Dai, H., Mantor, M., Zhou, H.: Coordinated CTA combination and bandwidth partitioning for GPU concurrent kernel execution. ACM Trans. Archit. Code Optim. 16(3), 23–12327 (2019). https://doi.org/10.1145/3326124
Zhao, C., Gao, W., Nie, F., Wang, F., Zhou, H.: Fair and cache blocking aware warp scheduling for concurrent kernel execution on GPU. Futur. Gener. Comput. Syst. 112, 1093–1105 (2020). https://doi.org/10.1016/j.future.2020.05.023
López-Albelda, B., Castro, F.M., González-Linares, J.M., Guil, N.: Flexsched: efficient scheduling techniques for concurrent kernel execution on GPUs. J. Supercomput. 78(1), 43–71 (2022). https://doi.org/10.1007/s11227-021-03819-z
Zhao, C., Gao, W., Nie, F., Zhou, H.: A survey of GPU multitasking methods supported by hardware architecture. IEEE Trans. Parallel Distrib. Syst. 33(6), 1451–1463 (2022). https://doi.org/10.1109/TPDS.2021.3115630
Preparata, F.P., Shamos, M.I.: Computational Geometry—An Introduction. Texts and Monographs in Computer Science, Springer, Berlin (1985)
Hinrichs, K.H., Nievergelt, J., Schorn, P.: Plane-sweep solves the closest pair problem elegantly. Inf. Process. Lett. 26(5), 255–261 (1988). https://doi.org/10.1016/0020-0190(88)90150-0
Velentzas, P., Vassilakopoulos, M., Corral, A.: GPU-aided edge computing for processing the \({k}\) nearest-neighbor query on SSD-resident data. Internet of Things 15, 100428 (2021). https://doi.org/10.1016/j.iot.2021.100428
Velentzas, P., Moutafis, P., Mavrommatis, G.: An improved GPU-based algorithm for processing the k nearest neighbor query. In: PCI Conference, pp. 372–375 (2020). https://doi.org/10.1145/3437120.3437343
NVIDIA: CUDA 7 Streams Simplify Concurrency (2015). https://developer.nvidia.com/blog/gpu-pro-tip-cuda-7-streams-simplify-concurrency/ Accessed 11 Jan 2021
Zhou, H., Bateni, S., Liu, C.: \(\text{S}^{\text{3dnn }}\): Supervised streaming and scheduling for GPU-accelerated real-time DNN workloads. In: RTAS Conference, pp. 190–201 (2018). https://doi.org/10.1109/RTAS.2018.00028
Katiyar, P., Vu, T., Eldawy, A., Migliorini, S., Belussi, A.: Spiderweb: a spatial data generator on the web. In: SIGSPATIAL Conference, pp. 465–468 (2020). https://doi.org/10.1145/3397536.3422351
Vu, T., Migliorini, S., Eldawy, A., Belussi, A.: Spatial data generators. In: SpatialGems—SIGSPATIAL International Workshop on Spatial Gems, pp. 1–7 (2019). https://doi.org/10.1145/3391234.3421234
Eldawy, A., Mokbel, M.F.: Spatialhadoop: a mapreduce framework for spatial data. In: ICDE Conference, pp. 1352–1363 (2015). https://doi.org/10.1109/ICDE.2015.7113382
Roumelis, G., Velentzas, P., Vassilakopoulos, M., Corral, A., Fevgas, A., Manolopoulos, Y.: Parallel processing of spatial batch-queries using \(\text{ xbr}^+\)-trees in solid-state drives. Clust. Comput. 23(3), 1555–1575 (2020). https://doi.org/10.1007/s10586-019-03013-0
Corral, A., Manolopoulos, Y., Theodoridis, Y., Vassilakopoulos, M.: Closest pair queries in spatial databases. In: ACM SIGMOD Conference, pp. 189–200 (2000). https://doi.org/10.1145/342009.335414
Acknowledgements
The work of M. Vassilakopoulos and A. Corral was funded by the EU ERDF and the Andalusian Government (Spain) under the project UrbanITA (ref. PY20_00809) and the Spanish Ministry of Science and Innovation under the R &D project HERMES (ref. PID2021-124124OB-I00).
Funding
Open access funding provided by HEAL-Link Greece. The work of M. Vassilakopoulos and A. Corral was funded by the EU ERDF and the Andalusian Government (Spain) under the project UrbanITA (ref. PY20_00809) and the Spanish Ministry of Science and Innovation under the R &D project HERMES (ref. PID2021-124124OB-I00).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Velentzas, P., Vassilakopoulos, M., Corral, A. et al. GPU-Based Algorithms for Processing the k Nearest-Neighbor Query on Spatial Data Using Partitioning and Concurrent Kernel Execution. Int J Parallel Prog 51, 275–308 (2023). https://doi.org/10.1007/s10766-023-00755-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10766-023-00755-8