The Measurement of Soret and Thermodiffusion Coefficients in Binary and Ternary Liquid Mixtures

Abstract

This review provides an overview of the major, currently used techniques for investigating the Soret effect and measuring thermodiffusion and Soret coefficients, and in most cases also isothermal Fickian diffusion coefficients, in liquid mixtures. The methods are introduced with a focus on binary mixtures. The optical methods comprise optical beam deflection (OBD), optical digital interferometry (ODI) both on the ground and under microgravity conditions in the SODI-IVIDIL experiment for the study of the influence of vibrations onboard the International Space Station, which are all based on Soret cells. The transient holographic grating technique of thermal diffusion-forced Rayleigh scattering (TDFRS) employs light not only for detection of the concentration changes but also for optical volume heating. Thermogravitational columns (TGC) utilize the coupling between convection and thermodiffusion to create concentration changes inside a vertical column with a horizontal temperature gradient. While samples are analyzed after extraction from the column in a classical setup, the recently developed transparent microcolumn allows for interferometric in situ monitoring of the concentration field. The most recent technique relies on the measurement of giant non-equilibrium fluctuations (NEFs) by small-angle light scattering techniques. Research on ternary mixtures, both on the ground and in microgravity, has gained momentum in the context of the DCMIX microgravity project of ESA. Most techniques employed for binaries can be extended to ternaries by introducing a second detection color or by analyzing both refractive index and density of extracted TGC samples. The accuracy is limited by the unavoidable inversion of the so-called contrast factor matrix.

1 Introduction

Thermodiffusion (also known as thermal diffusion or the Soret effect) refers to a transport mechanism in which temperature gradients cause mass transfer in mixtures. The Soret effect has been observed in various fluid systems, including gases, liquids, colloidal suspensions, and even solids. The movement of particles dispersed in a continuous medium in response to a temperature gradient is called thermophoresis, but the distinction from the Soret effect is not as strict and it is sometimes also applied to molecular motion. Thermodiffusion plays a significant role in various natural and industrial processes, such as geothermal systems, separation techniques, combustion, crystal growth, biological processes, and microfluidics devices. The effect is quantified by the Soret coefficient, which is a measure of the ratio of thermodiffusion to the overall mass diffusion in a system.

There is a formal phenomenological description of thermodiffusion based on non-equilibrium thermodynamics; however, there is still no clear microscopic picture. Although molecular dynamics simulations have made significant progress in predicting the Soret coefficient, experimental studies remain indispensable.

In the last two decades, several reviews have been published presenting different aspects of the Soret effect. Among them, one should mention reviews considering the experiments, such as the review by Platten [1] presenting several experimental techniques with an accent on the Thermogravitational column (TGC), by Wiegand [2] on binary mixtures and polymers focusing on optical methods, a historical review with a brief overview of the experimental techniques by Eslamian and Saghir [3] and, the most recent one by Morozov and Köhler [4]. The latter one presented a general view on the research in liquid mixtures with Soret effect. All these reviews are not losing momentum, but other research trends are on the rise.

Our paper offers a review on modern experimental techniques, which may be applied equally for binary and ternary mixtures. The experimental techniques for the measurement of Soret coefficients in liquid binary mixtures are rather well established. During the past decade, however, the scientific focus moved towards ternary mixtures that expand the scope of the studies to more realistic real-world applications. The complexity increases significantly when going from binaries to ternaries. The simultaneous presence of three components, which can interact in complex ways, demands much more attention. Experimental techniques for measuring Soret coefficients in ternary mixtures are more challenging than those for binary mixtures, since they require careful selection of two-wavelength light sources, better control of temperature gradients, and rather complex signal processing.

The mathematical description of ternary mixtures is more complicated not only due to the increased number of components but also due to interactions involved. For example, the signs of the Soret and thermodiffusion coefficients may be different due to large cross-diffusion resulting in the emergence of instabilities preventing measurement of transport coefficients [5, 6]. The values of diffusion coefficients in ternary mixtures depend on the order of the components as well as on the frame of reference for which the diffusive fluxes are written [7]. Accordingly, the value of the sequential Soret coefficient ($S_{T,i}^{\prime }$, i = 1,2,3) is assigned to a specific component. We adopted a hydrodynamic approach to the numbering of components, which corresponds to a decreasing order of density.

Since this review includes experiments in both binary and ternary mixtures, the mathematical description is given for a ternary mixture. The first part of the review is devoted to the description of the underlying principles of modern experimental techniques using binary mixtures as an example. The second part of the review presents the adaptation of these experimental methods to ternary mixtures. This structure would allow readers to understand the foundational principles and techniques employed in binary mixtures and subsequently see how those methods can be adapted and applied to more complex ternary systems.

Our review covers the most important experimental techniques nowadays employed. It is, however, by no means complete, as we neither discuss less frequently used methods, such as thermal lensing [8], nor more specialized ones, like, e.g., thermal field flow fractionation [9].

2 Binary Mixtures

2.1 Optical Beam Deflection

Optical beam deflection (OBD) is based on a straightforward principle. A Soret cell contains a thin horizontal slab of the multicomponent sample liquid of refractive index n that is subjected to a vertical temperature gradient. The temperature gradient is created between two parallel metal plates (e.g., copper or aluminum) which are rapidly brought to different temperatures after an initial equilibration period. This can be achieved through various methods such as circulating thermostated water baths [10], applying constant electrical power to the hot plate [11], or using thermoelectric Peltier heat exchangers [12,13,14,15]. In the design shown in Fig. 1, the sample of length l and height h is laterally confined by a rectangular glass frame that allows for optical access. It is sealed against the two metal plates by 10 $\mu$m thick teflon gaskets. The temperature of the two plates is measured by means of thermistors that are inserted into thin holes close to the inner surfaces. Their measured resistance is fed into a control loop to stabilize the plate temperature and to maintain a well-defined temperature gradient.

Here, we will discuss the case of binary mixtures with a weight fraction w of the independent component. Once the temperature gradient $|\nabla T| = (T_2 - T_1)/h$ is switched on, heat diffuses very rapidly and a stationary temperature distribution is attained almost instantaneously. Thermodiffusion is much slower and leads to a gradual build-up of a superimposed concentration gradient $\nabla w$. Both gradients combine to form a resulting refractive index gradient:

$$\begin{aligned} \nabla n = \left( \frac{\partial n}{\partial T} \right) _{p,w} \nabla T + \left( \frac{\partial n}{\partial w} \right) _{p,T} \nabla w ~, \end{aligned}$$

(1)

which can be detected by observing the deflection of a laser beam that is sent through the sample. The laser needs to be aligned with its incoming optical axis in x-direction and at $z=0$ halfway between the metal plates.

Fig. 1

Sketch of a typical OBD setup. Typical numbers are $l=1$ cm, $l_c= 1$ m, $h=1.2$ mm, and $T_2 -T_1 \approx 1.0$ K

The beam deflection $\delta z$ is detected by, e.g., a line camera at a distance $l_c$ behind the sample. For the geometry sketched in Fig. 1 and under the approximations of negligible contributions from the two windows and small deflection angles, it is given by

$$\begin{aligned} \delta z = \frac{dn}{dz} \, l \left( \frac{l}{2 n} + \frac{l_c}{n_a} \right) ~. \end{aligned}$$

(2)

Here, $n_a$ is the refractive index of air.

It is convenient to normalize the total beam deflection to the practically instantaneous contribution $\delta z_T$ from the temperature gradient, which results in the OBD signal [16]

$$\begin{aligned} s_\textrm{OBD}^\textrm{norm}(t) = \frac{\delta z(t)}{\delta z_T} = 1 + M\, f_\textrm{OBD}(t)~. \end{aligned}$$

(3)

An analytical solution for the build-up of the concentration field in a plane-parallel cell geometry has been given in Ref. [17], from which the time evolution of the concentration gradient across the sample is obtained [18]. The finite width of the laser beam is accounted for by averaging the refractive index gradient over its Gaussian beam profile $I(z) \sim \exp (-2z^2/w^2)$ [12, 14, 16, 18], which eventually leads to

$$\begin{aligned} \begin{aligned}&f_{\textrm{OBD}}({t}) = \int _{-h/2}^{h/2} dz\, I(z) f(z,t) ~\left[ \int _0^h dz I(z)\right] ^{-1}\\&\mathrm with\\&f(z,t) = 1 + \frac{1}{2}\sum _{n=- N}^{N}(-1)^n \\&\left[ \textrm{erf} \left( \frac{2\tilde{z} - 2n -1}{4\sqrt{\tilde{t}}} \right) - \textrm{erf} \left( \frac{2\tilde{z} - 2n +1}{4\sqrt{\tilde{t}}} \right) \right] \\&+ \sum _{n=-N}^{N}(-1)^n \frac{1}{4\sqrt{\pi \tilde{t}}}\\&\left[ \exp \left( -\frac{(2\tilde{z} - 2n +1)^2}{16 \tilde{t}} \right) + \exp \left( -\frac{(2\tilde{z} - 2n -1)^2}{16 \tilde{t}} \right) \right] ~. \end{aligned} \end{aligned}$$

(4)

Here, $\tilde{z} = z/h$ is the dimensionless vertical position within the cell and $\tilde{t} = t / (h^2 / D)$ the reduced time. The fit of Eq. 3 yields the diffusion coefficient D and the solutal amplitude factor M, from which the Soret coefficient

$$\begin{aligned} S_T = \frac{M}{w(1-w)} \left( \frac{\partial n}{\partial T}\right) _{p,w} \left( \frac{\partial n}{\partial w}\right) _{p,T}^{-1} \end{aligned}$$

(5)

and the thermodiffusion coefficient $D_T = S_T D$ are obtained.

The analytic model above usually provides a very good description of the experimental OBD signal. An interesting alternative approach has been described in Ref. [14], where the coupled heat and mass diffusion equations are solved numerically with the measured temperatures of the copper plates as time-dependent boundary conditions (Fig. 2). This allows one to explicitly account even for tiny temperature fluctuations of the order of a few milli-Kelvin and for occasional overshooting that is difficult to avoid after a rapid temperature jump.

Fig. 2

OBD signals for an ethanol/water mixture with $w=0.15$ ethanol weight fraction [14]. The signals are shown for different temperature differences between the two plates. The insert shows an enlarged view of the signal together with a fit of a numerical model with the measured temperature fluctuations of the copper plates as time-dependent boundary conditions

Convective instabilities can pose problems if left unaddressed, but they can generally be prevented in binary mixtures with proper care. Typically, experiments are performed in the heated from above configuration. In systems with a negative separation ratio

$$\begin{aligned} \psi = - \frac{\beta }{\alpha } S_T w(1-w) \end{aligned}$$

(6)

and a density $\rho = \rho _0 [1-\alpha (T-T_0) - \beta (w-w_0)]$, the thermally stable stratification can, however, become unstable due to the migration of the denser component towards the hot boundary at the top. To prevent this, it is necessary to reverse the temperature gradient and heat from below, thereby ensuring that the critical Rayleigh number is not exceeded and thermal instability is avoided. The slower mass diffusion will then further stabilize the quiescent state of the mixture. While instability can almost always be avoided in binary mixtures, it is a much more severe problem in ternaries and may even require microgravity conditions.

OBD measurements for a system with negative separation ratio are shown in Fig. 3. All measurements with a Soret cell heated from above, corresponding to positive temperature differences, show instabilities, whereas all measurements with an inverted temperature gradient show clean unperturbed OBD signals. Since a certain time is needed for the development of the unstable concentration gradient, all normalized solutal signals coincide for short times before convection sets in.

Fig. 3

Normalized OBD signals for a eutectic succinonitrile/(d)camphor (SCN/DC, DC weight fraction $w=0.236$, $T=45$ K) mixture with a negative separation ration [16]. Oscillations indicate solutal instability for positive temperature differences (heated from above)

2.2 Optical Digital Interferometry (ODI)

The instrument for the ODI method consists of two principal parts: the Soret cell and an interferometer along with equipment for the digital recording and processing of the phase information. Unlike the thin Soret cell used in the OBD technique, the cell is higher in the vertical direction. In early experiments, the Soret cell had the shape of a cube [19], later on, a rectangular cuboid shape with a smaller aspect ratio was selected as more advantageous, for example, with horizontal cross section of the inner cavity of $l_x \times l_y = 18.0 \times 18.0$ mm$^2$, and height $h \approx 6$ mm [20]. The larger cell height highlights unique feature of the ODI method to trace the transient path of the system over the entire 2D cross section of the cell throughout the whole diffusion process. The entire view of the cell allows one to recognize the presence of residual convection or instability, if any. In addition, the axial symmetry of the cell enables the application of a tomography algorithm to reconstruct the refractive index/concentration distribution inside the cell in 3D [21]. The typical design of the ODI cell is shown in Fig. 4a.

Fig. 4

Sketch of typical ODI setup [23]. (a) Cross section of the cell. (b) Top view of the entire setup which is placed inside a thermally insulated box equipped with an air-to-air cooling/heating assembly

The temperature gradient between two parallel metal plates made of copper [19, 22] or brass [23] or nickel-plated blocks [20] is created by two independent Peltier modules which are brought to different temperatures [24]. The temperature of the back sides of the Peltier elements is kept constant by water heat exchangers connected to the circulating water bath. The Peltier modules and copper plates are essentially larger than the cell, which is formed by a rectangular glass frame clamped between the copper blocks with special seals of high thermal conductivity and thickness of either 0.08 mm (in the case of epoxy glue) or 0.15 mm (in case of rubber). Our observation showed that the stability of temperature maintained by the controllers is kept at the level of 0.01–0.02 K during the characteristic time of the experiment (1–2 days). The stable temperature gradient applied across the cell is usually $\sim$1 K·mm⁻¹. For the initial cell thermalization at the mean temperature, a waiting period of at least 10 h is needed.

Here, we discuss the case of a binary mixture with a weight fraction w of the denser component. The concentration variation within the liquid mixtures is observed by means of a Mach-Zehnder interferometer. The optical arrangement is sketched in Fig. 4b. The laser beam is expanded by a spatial filter, then passes through a collimating lens and at the exit its diameter covers the entire area of the cell. Next, the beam splitter divides the beam into two parts of equal intensity (reference and objective). The objective beam traverses the experimental cell, while the reference beam bypasses the cell in the open air. Then, beams are redirected by mirrors and merged at the second beam splitter, creating an interferometric pattern. One of the beams can be inclined with respect to the other in order to create a narrow fringe pattern. The resulting interferogram is recorded by a CCD camera and a sensor with a size of (1280 $\times$ 1024) pixels provides a resolution of the imaging system of about 50 pixels·mm⁻¹. An example of a raw interferogram is shown in Fig. 5a.

Fig. 5

(a) Typical interference pattern covering full cell width with insert of magnified fringe pattern in top left corner obtained for water isopropanol [19]. (b) Example of wrapped optical phase map $\Delta \varphi (x, z)$ corresponding to the concentration distribution at the end of the experiment and obtained by processing of the fringe pattern

Determination of the Soret and diffusion coefficients involves two main steps: processing of raw fringe patterns into optical phase/refractive index/concentration maps, and fitting the experimental data to a mathematical model. Extraction of the optical phase information $\phi (x,z)$ from the interferogram includes the following steps: 2D Fourier transform, quadrants exchange since the meaningful data are located in disjoint corner areas, bandpass filtering, carrier frequency removal, and inverse Fourier transform (see Refs. [19, 22] for details). The resulting raw optical phase map is wrapped within $[-\pi ;\pi )$ interval, since it is obtained using the arc-tangent function after the inverse Fourier transform, and then is subjected to 2D phase unwrapping, to end up with a smooth distribution of phase. An example of the wrapped phase map is shown in Fig. 5b.

The working interferogram is always processed relative to the reference one, which includes all phase shifts caused by purely optical and mechanical elements of the system. Usually, this reference image is selected at the beginning of the experiment after setting the temperature gradient. The resulting phase map $\Delta \varphi (x, z) = \varphi (x, z, t) - \varphi (x, z, t_{ref})$ provides an optical phase variation related to the property of interest (e.g., concentration). The change in the refractive index $\Delta n$ is determined from the unwrapped optical phase with subtracted reference as follows:

$$\begin{aligned} \Delta n'(x, z, t) = \frac{\lambda }{2 \pi l_y} \Delta \varphi (x, z, t) ~, \end{aligned}$$

(7)

where $l_y$ is the path length of the beam in the liquid and $\lambda$ is the wavelength. Due to the specifics of the unwrapping procedure, these $n'(x,z,t)$ maps are determined up to an arbitrary offset and need to be tied to some known value. Most straightforward is the subtraction of the mean value $n_0(T_0,w_0)$, which is equivalent to subtraction of the average $\langle \Delta n'(x, z) \rangle$, due to the natural symmetry of the temperature and concentration variations around their mean values $T_0$ and $w_0$,

$$\Delta n(x, z) = \Delta n'(x, z) - \langle \Delta n'(x, z) \rangle .$$

For a given wavelength $\lambda$, the spatial variation of the refractive index n(x, z) includes temperature and concentration contributions, see Eq. 1. However, in liquid mixtures, the heat transfer by conduction occurs much faster than the mass transfer by diffusion. The common practice is to split contributions of temperature and concentration variations in time. This means that the linear temperature profile is assumed to be already established before the Soret separation starts, and that the thermodiffusion step occurs in a completely thermalized mixture. These assumptions are violated for small times, where the heat and mass transfer occur simultaneously. The loss of the Soret separation during this initial period can be taken into account in the fitting procedure by including an additional parameter in the model [21].

Another assumption used in the development of the mathematical model is that heat and mass transfer occurs only in the vertical direction, which is true in the absence of the temperature perturbations. The solution of 1D diffusion equation can be written in the form (where $w_0$ is the initial mass fraction and $\Delta w^{st} = - S_T^{\prime } \,\Delta T$)

$$\begin{aligned}{} & {} w(z,t)-w_0=\Delta w^{st} \cdot f(z,t,D), \qquad \text{ where } \end{aligned}$$

(8)

$$\begin{aligned}{} & {} \quad f=\frac{1}{2}-\frac{z}{h}-\frac{4}{\pi ^2}\sum _{k=0}^{\infty }\frac{1}{(2k +1)^2}\cos \left( \frac{(2k+1)\pi z}{h} \right) \exp \left( - \frac{(2k+1)^2 \, t}{t_r} \right) , \end{aligned}$$

(9)

where $t_r={h^2}/{\pi ^2 D}$ is the relaxation time. Under the assumption of constant temperature, the solution of the diffusion problem can be written via refractive index due to the direct relationship between w and n at constant temperature (see Eq. 1), then Eq. 8 takes the form

$$\begin{aligned} n(z,t)-n_0=\Delta n^{st} \cdot f(z,t,D), \quad \text{ and } \quad \Delta n^{st}= -S_T' \, {\Delta T} \,\left( \frac{\partial n}{\partial w}\right) _{p,T}. \end{aligned}$$

(10)

Accordingly, a fitting procedure is applied to the refractive index data. There are at least three different options for determining the Soret and diffusion coefficients using Eqs. 9–10

1. The use of the full-path solution that includes all available data points, both in time and in space, i.e., utilizing Eqs. 9–10 in a fitting procedure

2. The use of the refractive index (concentration) difference between top and bottom of the cell. In this case, function $f(z,t,D)=f(t,D)$ is simplified

$$\begin{aligned} \frac{\Delta n (t)}{\Delta n^{st}}= f(t,D)=1-\frac{8}{\pi ^2}\sum _{k=0}^{\infty }\frac{1}{(2k+1)^2}\, \exp \left( - \frac{(2k+1)^2 \,t}{t_r} \right) \end{aligned}$$

(11)

3. The use of the gradient solution (resembling the OBD approach) which utilizes the refractive index (concentration) gradient at mid-height of the cell, i.e., $z=h/2$

$$\begin{aligned} \frac{h}{\Delta n^{st}} \frac{\partial n}{\partial z}\Bigg |_{z=h/2}= 1-\frac{4}{\pi }\sum _{k=0}^{\infty }\frac{1}{(2k+1)} \sin \left( \frac{(2k+1)\pi }{2} \right) \exp \left( - \frac{(2k+1)^2 \,t}{t_r} \right). \end{aligned}$$

(12)

The application of the various options can lead to slightly different results since the amount of data involved in the extraction of the coefficients is essentially different. The refractive index difference (or $\Delta w$) between the top and bottom of the cell, the option #2, gives more weight to data points near horizontal walls, while the gradient approach #3 assigns more weight to data points located in the center of the cell. The gradient in the middle of the cell is less sensitive to thermal jitter, which affects regions along the hot/cold plates the most.

An example of an experimental optical signal along with the results of data fitting to two analytical solutions is shown in Fig. 6 for the TEG/water (0.1/0.9 composition in mass fractions) mixture according to (a) full-path solution after Eqs. 8–9 and (b) gradient solution after Eq. 12. The values of the Soret and diffusion coefficients written on the graphs indicate good agreement between the results of the two approaches. The details of fitting procedure can be found elsewhere, e.g., in Ref. [22].

Fig. 6

(a) Full refractive index profiles corresponding to Soret separation at different times; (b) the time evolution of the refractive index gradient in the middle of the cell. The experimental data obtained by the ODI for the TEG/water (0.1/0.9) mixture at T = 298.15 K in Ref. [23] are supplemented with the fit curves after Eqs. 8–9 and Eq. 12

2.3 SODI Instrument on the International Space Station (ISS)

The Selectable Optical Diagnostics Instrument (SODI) aboard the space station is a sophisticated instrument used for analyzing thermodiffusion in liquids. It has two modifications, the SODI-IVIDIL intended for binary mixtures and the SODI-DCMIX for ternary mixtures, among them each mission included one binary cell [25]. The optical design of both SODIs is based on the Mach-Zehnder interferometer concept, but has a different implementation. The interferometric pattern of SODI-IVIDIL (Influence of VIbration on DIffusion in Liquids) is similar to the ODI described above, while the SODI-DCMIX interferometer is designed to use the phase shift technique. Here, we briefly consider only SODI-IVIDIL and SODI-DCMIX will be discussed later.

SODI-IVIDIL has analyzed the effect of onboard g-jitter and control vibrations on diffusion processes in liquids [26]. The working liquid is placed in a cubic cell with an internal side length of 10.0 mm. The cell design allowed optical observations along two perpendicular directions. Interference patterns captured from the both views of the cell were treated in the same manner as ground experiments using the ODI technique. Two mixtures of water/IPA with mass fractions of 90/10 kg/kg and 50/50 kg/kg were investigated during the experiments. The former corresponds to a negative Soret effect, while the latter corresponds to a positive Soret effect.

Fig. 7

Results of IVIDIL experiment on the ISS. (a) Isosurfaces of the concentration after 12 h of the Soret separation in water–IPA mixture. The midsurface (green) corresponds to the initial concentration $w_0$= 0.9, and the following surfaces are separated by the step $\delta w=\pm 6 \cdot 10^{-4}$ [26]. (b) Soret coefficients $S_T$ for water/IPA from ground experiments [20] with two points from IVIDIL (Color figure online)

The IVIDIL was the first experiment inside the SODI and had confirmed that the daily onboard environment of the ISS does not perturb diffusion-controlled experiments. Figure 7a presents five isosurfaces of equal concentrations for the mixture with negative Soret effect at the end of the thermodiffusion step. This 3D concentration field reveals no significant disturbances due to onboard accelerations, except for small ripples on isosurfaces typical of most experiments. Panel (b) presents a quantitative comparison of the results obtained on the ISS and in ground laboratories using different techniques. This favorable agreement validates the several existing terrestrial techniques that are able to measure negative Soret coefficients and pave the way for research on ternary mixtures in the SODI demonstrating that g-jitter would not affect the results.

2.4 Thermal Diffusion Forced Rayleigh Scattering

The thermal diffusion-forced Rayleigh scattering (TDFRS) technique stands out from the other methods discussed in this paper as it utilizes light not only for detection of concentration changes but also for sample heating. The technique involves the absorption of a holographic interference grating to create a spatially periodic heating pattern throughout the volume of the liquid. With a grating period d of approximately 10 $\mu$m, the diffusion length scale is two to three orders of magnitude shorter than in most other experiments. Consequently, this reduces the characteristic diffusion times from hours down to milliseconds for small molecules and up to several seconds for slow polymeric or colloidal systems.

The TDFRS setup, illustrated in Fig. 8, utilizes an argon ion laser operating at a wavelength of $\lambda _w = 488$ nm or, alternatively, a solid state laser operating at 532 nm, to write the grating. The laser is divided into two beams, which intersect at the sample under an angle $\theta$. Phase modulation and adjustment of the phase of the grating are achieved by a Pockels cell and piezo mirrors. A HeNe laser with a wavelength of $\lambda _r = 633$ nm is employed to read the resulting phase grating, using a heterodyne detection scheme [27]. The reference wave is generated by a local oscillator, which can be as simple as a scratch on the cuvette. The diffracted beam and the reference wave are coherently superimposed and detected using a single-mode optical fiber connected to an avalanche photodiode module (APD) for photon counting. For increased stability, the critical parts of the split writing laser path are mounted on a separate breadboard. An inert dye, e.g., quinizarin, is added to the mixture in a very low concentration for optical absorption at the writing wavelength. Alternatively, an infrared laser can be used for direct absorption in aqueous systems [28]. First measurements of the Soret effect have been reported by Thyagaraijan and Lallemand for a CS$_2$-ethanol mixture [29] and by Pohl for a critical mixture of 2,6-lutidine and water [30]. Ref. [27] provides a detailed discussion of the operation of the instrument, particularly the heterodyne detection scheme and the separation of homodyne and background signal contributions.

Fig. 8

Sketch of a TDFRS setup for heterodyne detection. The CCD cameras serve for measurement of the grating period and facilitate alignment

It is sufficient to consider a one-dimensional mathematical description with the x-axis along the q-vector of the interference grating as indicated in Fig. 8. It is based on the heat equation:

$$\begin{aligned} \frac{\partial T(x,t)}{\partial t} = D_{th} \Delta T(x,t) + \frac{1}{\rho c_p} \dot{Q}(x,t) \end{aligned}$$

(13)

with an additional source term for the local heat production per unit volume $\dot{Q}(x,t)$, which accounts for the heating by the absorbed laser light. Neglecting a constant offset, the periodic part of the light intensity is $I(x,t) = I_q(t) \exp (iqx)$ with the grating vector $q = (4 \pi /\lambda _2) \sin (\theta /2)$, which leads to the source term $\dot{Q}(x,t)= \alpha I(x,t) = \alpha I_q(t) \exp (iqx)$. Here, $\rho$ and $c_p$ are the density and the specific heat of the sample and $\alpha$ is its optical absorption coefficient at the writing wavelength. The evolution of the concentration field is then obtained from the thermodiffusion equation:

$$\begin{aligned} \frac{\partial w(x,t)}{\partial t} = D \Delta w(x,t) + D_T w(1-w) \Delta T(x,t)~. \end{aligned}$$

(14)

Eqs. 13 and 14 yield spatially periodic solutions for both the temperature and the concentration with time-dependent amplitudes $T_q(t)$ and $w_q(t)$, respectively. In Ref. [31], a solution of both PDEs has been given using Green’s functions, which yield the time response to arbitrary excitations. The resulting refractive index grating then takes the form:

$$\begin{aligned} n(x,t)= & {} n_0 + n_q(t) \textrm{e}^{iqx}\nonumber \\= & {} n_0 + \left[ \left( \frac{\partial n}{\partial T} \right) _{w,p} T_q(t) + \left( \frac{\partial n}{\partial w} \right) _{T,p} w_q(t) \right] \exp (iqx)~. \end{aligned}$$

(15)

The heterodyne diffraction efficiency is linear in the refractive index modulation $n_q(t)$ of the phase grating. For a step-like excitation at $t=0$, the measured heterodyne TDFRS signal after normalization to the thermal contribution becomes

$$\begin{aligned} \zeta _{het}(t)= & {} 1 - \exp \left( -\frac{t}{\tau _{th}}\right) - \frac{M}{\tau - \tau _{th}} \times \nonumber \\{} & {} \left\{ \tau \left[ 1-\exp \left( -\frac{t}{\tau }\right) \right] -\tau _{th} \left[ 1-\exp \left( -\frac{t}{\tau _{th}}\right) \right] \right\} ~. \end{aligned}$$

(16)

A fit of Eq. 16 yields the thermal diffusivity $D_{th} = (\tau _{th} q^2)^{-1}$ and the diffusion coefficient $D = (\tau q^2)^{-1}$ from the two characteristic time constants, the Soret coefficient from the amplitude M according to Eq. 5, and the thermodiffusion coefficient $D_T = S_T D$.

Figure 9 presents the TDFRS measurement data with a fitting of Eq. 16, demonstrating excellent agreement between the model and the experimental results. Thanks to the fast electro-optic switching of the interference grating, which occurs on a microsecond time scale, TDFRS is capable of accurately measuring not only the solutal mode, but also the thermal diffusivity. This distinguishes TDFRS from other techniques that rely on wall heating.

Fig. 9

TDFRS measurement of a mixture of 1,2,3,4-tetrahydronaphthalene and dodecane ($w=0.5$, $T=308.5$ K) [31]. Top: normalized heterodyne diffraction efficiency with fit of Eq. 16. Bottom: residuals

The rapid diffusion time of milliseconds, as shown in Fig. 9, facilitates more than ten single shots per second, allowing for averaging over a significant number of excitations, ranging from $10^4$ to $10^5$ within just a few hours. Such a high level of averaging is imperative due to the relatively high noise level of individual measurements.

TDFRS has been used for the investigation of the isotopic [32,33,34] and pseudo-isotopic [35] Soret effect of small molecules, for the development of the thermophobicity concept [36, 37], for benchmark measurements [38], for the investigation of thermodiffusion of polymer solutions [39, 40] and blends [41], for cellulose solutions [42] and, with IR excitation for aqueous mixtures [28] and for the investigation of protein ligand systems [43], to name a few examples.

The extremely rapid electro-optic switching, with switching times significantly shorter than $\tau _{th}$, enables the use of alternative excitation schemes that go beyond a basic step excitation. For instance, stochastic excitation using pseudo-stochastic white noise has successfully been implemented [44], while frequency domain experiments that utilize lock-in techniques have also been demonstrated in our laboratory at the University of Bayreuth.

The experiment depicted in Fig. 10 employed a maximum-length random binary sequence featuring a flat power spectrum to drive the Pockels cell for the phase switching of the grating. The measured heterodyne diffraction efficiency shown below the pseudo-random excitation exhibits a noise-like appearance. By performing a Hadamard transform to deconvolute the system response and the pseudo-random excitation, the Green function of the solutal mode g(t) was obtained, as outlined in Ref. [44].

Fig. 10

TDFRS experiment with pseudo-stochastic random noise excitation. Linear response function g(t), random binary sequence for excitation (insert top), and system response (insert bottom) [44]. Polystyrene ($M \approx 250$ kg·mol⁻¹, $T \approx 298$ K)

2.5 The Thermogravitational Technique

The thermogravitational column (TGC) is one of the oldest techniques for separating liquid and gaseous mixtures. There are two configurations of thermogravitational columns: parallelepiped and cylindrical. The parallelepiped column consists of two vertical parallel plates separated by a distance forming a rectangular gap and the cylindrical column consists of two concentric tubes. The very first experiments in thermogravitational columns using the cylindrical configuration were performed by Clusius & Dickel with the aim of separating isotopes of gases [45]. In both configurations, the gap is very narrow in relation to the height, and opposite walls are maintained at different temperatures. Since the temperature gradient is horizontal, the Soret effect induces component separation in horizontal direction creating a mass flux $(J_{D_T})$. This concentration gradient, in turn, generates a diffusion flux $(J_D)$, which tends to mix again the constituents of the mixture. The convective flow created by buoyancy and temperature gradient transfers the components near the cold wall to the bottom and near the hot wall upwards, see Fig 11a. The combined effect of thermodiffusion and convection leads to an enhanced component separation between the vertical ends of the column, from which the thermodiffusion coefficient is calculated in the stationary [1] and the diffusion coefficient in the transient regimes [46].

The theory of thermogravitational column for a binary mixture was formulated by Furry, Jones, and Onsager (FJO theory) for gases [47], expanded to concentrated solutions by Majumdar [48] and extended to ternary mixtures by Marcou &Charrier-Mojtabi [49]. In these works, it was assumed that the contribution of compositional dependence of density to the buoyancy force is negligible (the “forgotten effect”). The working expression is written in the following form:

$$\begin{aligned} \Delta w_i = \frac{504L_z}{gL_x^4} \frac{\nu D_{Ti}}{\alpha }w_i\,(1-w_i) \end{aligned}.$$

(17)

Here $L_z$ and $L_x$ are the length and the gap of the column, $\alpha$ is the thermal expansion coefficient and $w_i$, is the mass fraction of one of the binary mixture components. According to the expression (17), the separation of the components in the steady state does not depend on the applied temperature gradient, as well as the sought thermodiffusion coefficient. On the contrary, the coefficient of molecular diffusion, D, determined by transient separation, depends on the temperature gradient. Omitting the forgotten effect, Madariaga et al. [50] proposed the following expression for the temporal evolution of the vertical separation in a thermogravitational column:

$$\begin{aligned} \Delta w(t) =\Delta w_{\infty } \left[ 1- \frac{a}{\pi ^2}\sum _{k=0}^{\infty } \frac{\exp (\frac{(2k+1)^2t}{\tau _r})}{(k+1)^2} \right], \end{aligned}$$

(18)

where $\Delta w_{\infty }$ is the separation in equilibrium, $a=\frac{4L_z}{\Delta z}\left( \cos (\frac{\pi z_1}{L_z}) - \cos (\frac{\pi z_2}{L_z}) \right)$ is the geometrical parameter of the thermogravitational column, and $\tau_r$ the relaxation time given by

$$\begin{aligned} \tau _r = \frac{9! L_z^2 \mu ^2 D}{(\pi \Delta T g \rho \alpha L_x^3)^2}, \end{aligned}$$

(19)

where $\mu$ is the dynamic viscosity, $\rho$ the density, $\alpha$ the thermal expansion coefficient, and D is the molecular diffusion coefficient.

Fig. 11

Presentation of the principle of TGC operation. (a) Internal fluxes inside TGC; (b) Sketch of TGC operation with five extraction points; (c) Variation of the density with column height in the steady state at 25$^{\circ }$C for the mixture of water–ethanol at 33.6% mass fraction of water. Results are obtained in TGC of a parallelepiped configuration

Equations 18–19 can be applied for flat and cylindrical columns. In both configurations, the thermodiffusion coefficients were measured in binary mixtures with positive Soret coefficients [51, 52], while experiments with negative Soret coefficients were only conducted in cylindrical columns [53, 54]. Over years, the thermogravitational method has been used to perform $D_T$ measurements at normal [55, 56] and high pressures [57], and D was measured in binary [58] and ternary [59] mixtures. The possibility to enhance the steady separation by an inclination of the parallelepiped column was considered [60].

In the parallelepiped configuration, a new approach based on optical system (Laser-Doppler Velocimetry) was developed to determine the Soret coefficient using the maximum velocity amplitude (overshoot effect) [61]. This approach using the overshoot effect was found to be valid only for mixtures with a large separation ratio [62].

There are two available methods for the analysis of the thermodiffusion phenomenon in TGCs. The conventional method is based on the sample extraction along the height of the column [63], while the novel optical method is based on the continuous monitoring of the concentration distribution by means of digital interferometry [64].

2.5.1 TGC: Conventional Method

Several parallelepiped columns with different aspect ratios ($L_z$= 500 mm and $L_z$= 980 mm) with a gap of $L_x$= 1 mm and a depth of $L_y$= 50 mm are currently used [65]. A taller column ($L_z$= 980 mm) makes it possible to achieve greater separation of the mixture between the vertical ends, which increases the sensitivity of determining the thermodiffusion coefficient in mixtures with a small separation ratio. The shorter column requires less liquid for the experiment, i.e., 30 cm$^3$ versus 55 cm$^3$.

The working principle is outlined in Fig. 11b. The temperature gradient is created by water from thermostatic baths circulating along the aluminum sidewalls with a temperature control of 0.1$^{\circ }$C by means of a Pt-100 probe. After the walls reach the required test temperature, the filling of the column begins, followed by the experiment. At the steady state, defined as five times the relaxation time of the mixture ($\tau _r$, see Eq. 19), the small sample quantities of 2 ml are extracted from five equidistant sampling points placed along the height of the column.

For the $D_T$ determination, it is sufficient to analyze either the density or the refractive index of the five extracted samples, in addition to the thermophysical properties. In the case of the density-based analysis, the thermodiffusion coefficient can be obtained as follows:

$$\begin{aligned} D_T = \frac{g L_x^4}{504} \frac{\alpha }{w_i\,(1-w_i)\,\beta _i\,\mu }\frac{\partial \rho }{\partial z}. \end{aligned}$$

(20)

An example of density variation in steady state with column height is shown in the Fig. 11c illustrating ideal linearity.

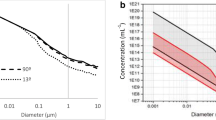
To study thermodiffusion at high pressures, a cylindrical thermogravitational column is used [67]; photo of its installation is shown in Fig. 12a. The inner and outer cylinders, 500 mm high, are made of stainless steel and separated by an annular gap of 1 mm. The high-pressure module consists of a hydraulic system and a pressure intensifier with a pressure ratio of 1 to 5. A hydraulic system compresses the fluid inside the column to the desired pressure using a control valve. The sample volume required to run this TGC varies from 230 cm$^3$ to 360 cm$^3$ depending on the given pressure. The samples for analysis are extracted at steady state through valves built into the outer tube of the column. These extraction points are hermetically sealed without confining any dead volume of liquid. The results obtained in the high-pressure TGC are presented in Fig. 12b for the dodecane–n-hexane system in a wide range of pressures.

Fig. 12

(a) Photo of the high-pressure TGC in cylindrical configuration; (b) Variation of the thermodiffusion coefficient with pressure for different concentrations of the dodecane–n-hexane mixture at 25$^{\circ }$C [66]

2.5.2 TGC: Optical Method

The described above TGCs have been traditionally used for $D_T$ determining from the samples extracted at steady state. In these TGCs, the required volume of a mixture per experiment is relatively high, and the experimental time is quite long. In order to overcome these problems, a new TGC has been developed, the so-called microcolumn $\mu$TGC, based on digital interferometry [68]. In the case of binary mixtures, the transient analysis of separation in the $\mu$TGC allows obtaining both the thermodiffusion and the molecular diffusion coefficients. In addition, the continuous tracking of concentration allows observing possible thermohydrodynamic instabilities that can occur in the mixture [6].

A schematic of the microcolumn is given in Fig. 13b. The microcolumn has a planar geometry with a height of $L_z$= 30 mm, a gap of $L_x$= 0.51 mm, and a depth $L_y$= 3 mm and requires a sample volume of less than 50 $\mu l$. The $\mu$TGC is equipped with two sapphire windows transparent in the visible range of light. The thermogravitational microcolumn with a contactless optical detection system operates on the principle of a Mach-Zehnder interferometer and is adopted for the use of one, two, or three lasers.

Fig. 13

(a) Schematic of Mach–Zehnder interferometer with two lasers; (b) sketch of microcolumn and (c) steady-state concentration profile in a binary mixture

Table 1 The results of experiments in the $\mu$TGC with the THN-Tol mixture at a mass fraction 60.04% in the transient regime at $T_{mean}$=25$^{\circ }$C: imposed temperature difference ($\Delta T$), the concentration gradient (dw/dz), the thermodiffusion coefficient ($D_T$), the relaxation time ($\tau _r$), the molecular diffusion coefficient (D ), and the Soret coefficient ($S_T$)

The principle scheme with two lasers is shown in Fig. 13a. The raw image processing is the same as described in as Optical Digital Interferometry (ODI) in previous section. The determination of the thermal diffusion coefficient can be divided into the following steps: image processing resulting to wrapped phase, phase unwrapping ($\Delta \varphi$), refractive index retrieving ($\Delta n$), and calculation of concentration ($\Delta w$). The last two steps in mathematical form are written as follows:

$$\begin{aligned} \Delta n(z,t)= \left( \frac{\lambda }{2 \pi L_x}\right) \Delta \varphi (z,t), \qquad \Delta w(z,t)= \left( \frac{\partial n}{\partial w}\right) ^{-1}_{p,T,\lambda } \Delta n(z,t), \end{aligned}$$

(21)

where $\lambda$ is the wavelength of the light and $({\partial n}/{\partial w})_{p,T,\lambda }$ is the solutal optical contrast factor for a given wavelength.

In the steady state, $D_T$ is determined according Eq. 17 from the concentration distribution along the height. In the transient regime, first, the relaxation time is sought from Eq. 18 and, next, the diffusion coefficient is determined from Eq. 19. Note that the relaxation time depends on the given temperature difference between the walls. To illustrate this, the results in the transient regime are given in Table 1 for the THN-Tol mixture at mass fraction 60.04%. The results show that all the coefficients $D_T,$ D and $S_T$ do not depend on the applied temperature difference, and the small variations are in the limit of the uncertainties.

2.6 Non-equilibrium Fluctuations

A liquid subjected to a temperature and/or concentration gradient exhibits giant non-equilibrium fluctuations (NEFs) [69]. The amplitudes of these long-ranged fluctuations, which are absent in equilibrium, grows proportional to $q^{-4}$. For small wave vectors q, they are cut-off by the influence of gravity, but in microgravity, they are only limited by the finite size of the container [70, 71].

The utilization of (NEFs) as a tool for the measurement of the Soret effect is relatively new and has only been employed for few systems. Segrè et al. employed heterodyne small-angle light scattering to determine the Soret coefficient of toluene/n-hexane mixtures [72]. Although the numerical values of their results could not be confirmed by subsequent TDFRS [73] and OBD [10] measurements, they demonstrated the principal suitability of NEFs as a new and alternative tool for the measurement of Soret coefficients.

More recent investigations of NEFs are typically performed by means of the shadowgraph technique [74,75,76,77,78,79,80]. A typical setup is sketched in Fig. 14 [79]. It is built around a horizontal Soret cell with two sapphire windows separated by a distance h and kept at different temperatures $T_1$ and $T_2$. The vertical temperature gradient is aligned parallel to the optical axis. The sample is illuminated by the collimated beam of a superluminescent diode. The interference of the scattered and the primary beams is detected on the sensor of a camera at a distance of approximately $Z \approx 0.2$ m behind the cell.

Fig. 14

Sketch of a shadowgraph setup with a Soret cell

In a binary or higher multicomponent mixture with a prescribed temperature gradient, the Soret effect leads to a concentration gradient with corresponding thermal and solutal NEFs, which are analyzed by means of the differential dynamic analysis (DDA) method [81, 82]. Here, we will closely follow the representation from Ref. [80].

In a first step, a series of evenly spaced images is recorded, from which the structure function of Fourier transformed images is computed in q-space:

$$\begin{aligned} C(q, \Delta t) = 2 \tilde{T}(q) S(q) [1-f(q,\Delta t)] + B(q) \end{aligned}.$$

(22)

Here, B(q) is a background term, $\tilde{T}(q) = 4 \sin ^2(q^2\,Z/(2k))$ the optical transfer function, $S(q) = S^T(q) + S^c(q)$ the static structure factor and

$$\begin{aligned} f(q,\Delta t) = \frac{S^T(q)}{S(q)}\exp \left( -\frac{\Delta t}{\tau ^T}\right) + \frac{S^c(q)}{S(q)}\exp \left( -\frac{\Delta t}{\tau ^c}\right) ~. \end{aligned}$$

(23)

the intermediate scattering function. The amplitudes of the thermal and the solutal static structure factors are given by

$$\begin{aligned} S^i(q) = \frac{I_0^i}{1 + (q/q^i_{ro})^4} ~~~~~~i=T,c ~. \end{aligned}$$

(24)

They diverge $\sim q^{-4}$ but gravity cuts them off below the respective roll-off wavevectors:

$$\begin{aligned} q^T_{ro} = \left( \frac{\beta _T g \nabla T }{\nu D_{th}}\right) ^{1/4} \textrm{and}~~~ q^c_{ro}= & {} \left( \frac{\beta _c g \nabla c }{\nu D}\right) ^{1/4} . \end{aligned}$$

(25)

Here, g is the gravitational acceleration, $\nu$ is the kinematic viscosity and $\beta _T$ and $\beta _c$ are the thermal and solutal expansion coefficients, respectively. The two time constants show diffusive behavior for high q values, but they are also dominated by the gravitational cut-off at small wavenumbers [83]:

$$\begin{aligned} \tau ^T(q)= & {} \frac{1}{D_{th} q^2 (1 + (q^T_{ro}/q)^4)} \end{aligned},$$

(26)

$$\begin{aligned} \tau ^c(q)= & {} \frac{1}{D q^2 (1 + (q^c_{ro}/q)^4)} ~. \end{aligned}.$$

(27)

Croccolo et al. have determined the Soret coefficient from the solutal roll-off wavevector and the diffusion coefficient, both of which are extracted from the shadowgraph experiment [76, 77]:

$$\begin{aligned} S_T = \frac{(q_{ro}^c)^4 \nu D h}{\beta _c g (T_2 - T_1) w(1-w)}. \end{aligned}$$

(28)

Zapf and Köhler have used an equivalent expression that is entirely based on information extracted from the NEFs and does not require the exact knowledge of the temperature gradient:

$$\begin{aligned} S_T = \frac{-1}{w(1-w)} \frac{\beta _T}{\beta _c} \frac{D}{D_{th}} \left( \frac{q_{ro}^c}{q_{ro}^T}\right) ^4 \end{aligned}.$$

(29)

Even though the determination of the Soret coefficient involves an optical technique, it is not necessary to know the optical contrast factors when using Eqs. 28 or 29. This is because these equations rely solely on the roll-off wavevectors, and not on the amplitudes of the structure functions. However, it is essential to measure the thermal and solutal expansion coefficients in addition. Eqs. 28 and 29 involve different signs, where the negative sign in Eq. 29 has been carried over from the thermodiffusion equation. It must be kept in mind, however that NEFs allow only the determination of the modulus of $S_T$ but not its sign. Information about the sign can, e.g., be obtained from an inversion of the temperature gradient and the search for solutal convective instabilities characteristic for a negative separation ratio [84].

Figure 15 shows measurements of the Soret coefficient of a dilute polymer solution by means of the shadowgraph technique for different temperature gradients [80, 85]. For small gradients, an excellent agreement with the literature value is found. For larger gradients, nonlinear effects begin to dominate and a linear treatment leads to an overestimation of the Soret coefficient. The figure also shows simulations of the experiment with the full nonlinear model, which agree very well with the measured values. As a rule of thumb, the linear model is applicable as long as the temperature difference between the cold and the hot side does not exceed $\Delta T = S_T^{-1}$.

Fig. 15

Soret coefficient of polystyrene (17.9 kg·mol⁻¹) in toluene, $w=0.01$, $T_0 = 298.15$ K as measured and simulated for different temperature differences $\Delta T$. The gray dots are simulations. Literature value from Refs. [40, 86]

2.7 Experimental Uncertainty

The determination of uncertainties in thermodiffusion experiments is an important challenge, just as it is for any other property measurements. This task is, however, not straightforward and easy, and differs depending on the technique. Most simply the uncertainty determination is done for the thermogravitational column technique, where the $D_T$ coefficient is determined at steady state as a simple function of several parameters independent of the applied temperature gradient (see Eq. 20), with some of them measured directly (dynamic viscosity $\mu$ and the slit width $L_x$), and others obtained by simple linear regression (thermal and mass expansion coefficients $\alpha$ and $\beta _i$, and the density or refractive index distribution over the column height, $\partial \rho /\partial z$ or $\partial n/\partial z$), and all the parameters have well-defined uncertainty estimates. Then, the relative uncertainty of $D_T$ is calculated as the square root of the sum of the squares of the relative uncertainties of all participating parameters. Claimed relative uncertainty of $D_T$ measurements by TGC technique is generally around 2.5%. As for the transient analysis, according to Eq. 19, the determination of uncertainties in diffusion experiments is up to 7.5%.

Other techniques, featuring non-invasive optical diagnostics, give more information, but the error estimation for them is less straightforward, as they rely on data extraction by use of multivariate optimization, and the errors can be only estimated by collecting sufficient statistics. In general, all optical techniques deliver two main parameters: the optical signal amplitude, directly related to the Soret coefficient, and the separation kinetics, determined by the diffusion coefficient. It can be seen by the separation curves in Figs. 3 and 6b, where the plateau of the curve corresponds to the optical signal amplitude, while the time for reaching the steady state is related to the diffusion coefficient.

It is recognized that the most serious source of random errors in the optical techniques utilizing Soret cell is the thermal jitter, which may have different nature and can vary from daily scale [19] to seconds scale [14]. Some of its sources can be effectively eliminated by adequate isolation of the setup, but the inherent instability of the active thermal regulation of the cell remains unavoidable. The thermal jitter of the cell regulation is translated into the noise of the optical signal (see insert in Fig. 2 as an example), and in principle can be accounted for, by the cost of essential computational complication of the fitting procedure [14]. It is, however, not an option for routine experiments, in which this noise is normally considered as random. Importantly, the signal-to-noise ratio (SNR) depends upon the mixture’s optical properties and the separation magnitude (see detailed consideration in [87]), and is not uniform even for different state points of the same mixture. The uncertainty of the Soret coefficient is inversely proportional to SNR and may drop well below 1% when SNR $>100-200$, but grows to several percent and more when SNR approaches 10.

The error of the diffusion coefficient is also affected by the strength of the optical signal, or SNR. It was explicitly demonstrated in the recent study of diffusion by ODI [88] that the uncertainty of the diffusion coefficient is linked to the characteristic refractive index difference and dramatically grows when $\Delta n < 1 \times 10^{-4}$ while staying below 2% if $\Delta n > 2 \times 10^{-4}$.

Some concerns may exist about possible technique-dependent systematic errors, which are difficult to identify if staying in the frame of the same technique. To eliminate these concerns, thermodiffusion studies are often implemented in a benchmark manner, when the results are provided as independent measurements done by different groups utilizing different techniques [20, 38, 89, 90]. The general good agreement indicates the absence of hidden sources of systematic errors in the most commonly used measurement techniques. In summary, it can be said that all techniques can reach accuracies of the order of one percent, but in most practical cases, this optimum is not reached for various reasons.

3 Ternary Mixtures

Historically, there has been a strong discrepancy between the almost exclusively investigated binary mixtures and the liquids occurring in nature and technology. The latter are frequently multicomponent and consist of significantly more than just two constituents, with crude oil containing literally thousands of components as a prominent example. Ternary mixtures are the logical next step after binaries and are of particular interest, since they show already characteristic properties of true multicomponent systems, e.g., cross-diffusion. Compared to mixtures with even more constituents, they are still manageable, which makes them ideal model systems for multicomponent mixtures.

Until approximately two decades ago, only sporadic works on thermodiffusion in ternary mixtures have been published [15, 91,92,93,94,95,96,97]. The situation changed with the DCMIX microgravity project of ESA during the second decade of this century. During the course of DCMIX, four microgravity campaigns aboard the International Space Station (ISS) were launched with the aim to investigate thermodiffusion in selected ternary model systems. In parallel, a strong effort was put into the investigation of ternary mixtures in the laboratories of the participating research groups from a number of different countries [89, 98,99,100,101,102,103,104]. A comparison result obtained by different techniques was not obvious. An approach was proposed for comparing thermodiffusion coefficients obtained by different techniques [105], which showed that the more accurate results can be achieved with the right combination of two techniques even with a one probing. As of today, most works about thermodiffusion in ternary systems have originated from the DCMIX project.

3.1 Theoretical Background

There are two independent concentrations $w_1$ and $w_2$ in a ternary mixture of density $\rho$, which relate to two independent mass fluxes:

$$\begin{aligned} \textbf{j}_{1}= & {} -\rho \left( D_{11} \nabla w_1 + D_{12} \nabla w_2 + D_{T,1}^\prime \nabla T \right) \end{aligned},$$

(30)

$$\begin{aligned} \textbf{j}_{2}= & {} -\rho \left( D_{21} \nabla w_1 + D_{22} \nabla w_2 + D_{T,2}^\prime \nabla T \right) \end{aligned}.$$

(31)

Here, $D_{T,i}^\prime$ are the so-called primed thermodiffusion coefficients, which are defined without the usual concentration prefactors known from the binaries, and $D_{ij}$ are the four entries of the diffusion matrix $\underline{\underline{\textbf{D}}}$. We have used the primed coefficients, as these are the ones that are most widely used in the current literature. Only recently, concentration prefactors for frame invariant coefficients (without prime) similar to the ones used for binary mixtures have been derived [106, 107]. The primed Soret coefficients are defined by the concentration gradients in the steady state:

$$\underline{{\nabla w}} = - \nabla T \underline{{S^{\prime}_{T} }}.$$

(32)

The notation $\underline {S'_T} = (S'_{T,1}, S'_{T,2})^T$ indicates a column vector in the concentration space with the two primed Soret coefficients, which are related to the diffusion and thermodiffusion coefficients by [108]

$$\begin{aligned} \underline {S'_T} = \underline{\underline{\textbf{D}}}^{-1} \underline {D'_T} \end{aligned}.$$

(33)

Combining Eqs. 30 and 31 with the continuity equation for mass conservation yields the thermodiffusion equation for the description of experiments:

$$\begin{aligned} \frac{\partial \underline {w}}{\partial t} = \underline{\underline{\textbf{D}}} (\nabla ^2 \underline {w}) + \underline {D_T^\prime } \nabla ^2 T \end{aligned}.$$

(34)

Since there are two independent concentrations, the measurement of a single quantity, like refractive index or density, is not sufficient for an unambiguous determination of the concentration changes. For purely optical experiments, it is necessary to measure the refractive index changes at two different detection wavelengths and to rely on the refractive index dispersions of the constituents of the ternary mixture. In order to compute the concentration changes from the measured refractive index changes $\delta n_i$ at wavelengths $\lambda _i$, the solutal contrast factor matrix $\underline{\underline{\mathbf {N_w}}}$ with entries $N_{w,ij} = (\partial n_i / \partial w_j)_{p,T} ~(i,j=1,2)$ needs to be inverted:

$$\begin{aligned} \underline {\delta w} = \underline{\underline{\mathbf {N_w}}}^{-1} \underline {\delta n} \end{aligned}.$$

(35)

For the majority of described techniques, this equation forms a basis for further calculation of Soret coefficients specific to a ternary mixture. It should be noted, however that if some other diagnostic is applied (say, density $\rho$ instead of the second wavelength, which is possible for the technique relying on sampling), Eq. 35 changes to

$$\begin{aligned} \underline {\delta w} = \begin{bmatrix} \partial n / \partial w_1 &{} \partial n / \partial w_2 \\ \partial \rho / \partial w_1 &{} \partial \rho / \partial w_1 \end{bmatrix}^{-1} \begin{pmatrix} \delta n \\ \delta \rho \end{pmatrix}= \underline{\underline{\mathbf {N_w}}}^{-1} \begin{pmatrix} \delta n \\ \delta \rho \end{pmatrix} \end{aligned}.$$

(36)

The derivatives of the measured properties with respect to concentration, the so-called contrast factors $(\partial n / \partial w),$ or $(\partial \rho / \partial w)$, are properties of the ternary mixture and can routinely be measured in advance [109,110,111]. Figure 16 illustrates the huge amount of preparatory work before starting a thermodiffusion experiment: measuring either the density and refractive index, or the refractive index at two wavelengths and calculating the condition number $\mathcal {K}$. The value of the condition number quantifies the influence of errors in the input on the result of a calculation: the smaller condition number, the less error amplification is expected. The $\mathcal {K}$ condition number map (panel c) shows that not all compositions can be measured using the optical approach, i.e., the red area corresponding to large $\mathcal {K}$, see Sect. 3.3.3 for details.

Fig. 16

An example of the preparatory measurements in a ternary mixture for thermodiffusion experiment (Triethylene–Glycol (TEG)–Water–Ethanol at equal mass fraction at 298.15 K; a) density, b) refractive index (c) map of condition number $\mathcal {K}$ (the magnitude of $\mathcal {K}$ increases from blue to red). The dots indicate points studied at the ISS [101] (Color figure online)

3.2 Instrumentation for Ternary Measurements

Adaptation of the measurement techniques to the ternary measurements can be done differently, depending on the particular technique, its instrument configuration, and its flexibility. In all optical techniques, it is normally implemented by adding a second light source with a different wavelength to the setup. Guiding the second beam and its directing to the cell requires adding the beam splitter/combiner and some effort for accurate alignment of both beams (see Fig. 13a as an example). In some cases, simple machinery may be needed for alternated interruption of the beams and synchronizing it with the acquisition camera. Such an arrangement permits measuring both properties/signals simultaneously in the same experiment. Alternatively, the measurement with the second wavelength can be performed not simultaneously but rather in a separate experiment. This is typically done in the ODI setup, which achieves a repeatability of the optical signal within approximately 0.2 percent.

The extension to ternary measurements is much simpler for the TGC technique based on sampling. The extracted liquid samples can be analyzed for an arbitrary selection of properties that allows the resolution of two independent concentrations. Most often, density and refractive index at some standard wavelength are employed.

3.3 Data Evaluation

In the following, we will focus on the evaluation of two-color optical measurements. The arguments can, however, easily be transferred to other detection schemes. Even if fitting is not always exactly performed as here described, all employed procedures are essentially equivalent. Various techniques, which differ by the signal kind and data evaluation approaches lead to slightly different mathematical descriptions. Below are the basic equations for the most commonly used OBD and ODI techniques.

3.3.1 OBD

As explained, the measurements are performed in refractive index space. The time-dependent solutal signals for the two detection colors can be written after normalization to the thermal signal amplitudes in the form:

$$\begin{aligned} \underline {\delta s(t)}= \begin{pmatrix} \delta s_1(t) \\ \delta s_2(t) \end{pmatrix}= 1 + \underline{\underline{\textbf{M}}} \begin{pmatrix} f(t,\hat{D}_1) \\ f(t,\hat{D}_2) \end{pmatrix}~, \end{aligned}$$

(37)

where $\underline{\underline{\textbf{M}}}$ is a $2 \times 2$ amplitude matrix and $f(t,\hat{D}_i)$ a normalized dimensionless function that describes the thermodiffusion dynamics for the mode corresponding to the diffusion eigenvalue $\hat{D}_i$ [18]. The form of $f(t,\hat{D}_i)$ depends on the actual experiment and the corresponding analytic solution (see Eqs. 4, 9, 11, and 12 as examples). Provided that the two diffusion eigenvalues are sufficiently different to resolve the two temporal modes, the fit of Eq. 37 yields six independent parameters: the four entries $M_{ij}$ of the amplitude matrix and the two diffusion eigenvalues $\hat{D}_i$. If the diffusion eigenvalues are very close and cannot be separated, the number of independent parameters that can safely be obtained reduces to three: a mean diffusion eigenvalue and the two steady-state amplitudes $M_{i1} + M_{i2}$ for the two wavelengths $\lambda _i$.

In order to obtain the thermodiffusive transport coefficients, it is necessary to transform the fit results from the refractive index to the concentration space, which finally leads to

$$\begin{aligned} \underline{\underline{\textbf{D}}}= & {} (\underline{\underline{\mathbf {N_w}}}^{-1} ~ \underline{\underline{\mathbf {N_T}}} ~ \underline{\underline{\textbf{M}}}) \,\, \hat{\underline{\underline{\textbf{D}}}} \,\, (\underline{\underline{\textbf{M}}}^{-1} ~ \underline{\underline{\mathbf {N_T}}}^{-1} ~ \underline{\underline{\mathbf {N_w}}}) \end{aligned},$$

(38)

$$\begin{aligned} \underline {D_T^\prime }= & {} - \underline{\underline{\mathbf {N_w}}}^{-1} ~ \underline{\underline{\mathbf {N_T}}} ~ \underline{\underline{\textbf{M}}} ~ \hat{\underline{\underline{\textbf{D}}}} ~ \underline {1} \end{aligned},$$

(39)

$$\begin{aligned} \underline {S_T^\prime }= & {} - \underline{\underline{\mathbf {N_w}}}^{-1} ~ \underline{\underline{\mathbf {N_T}}} ~ \underline{\underline{\textbf{M}}} ~ \underline {1} ~. \end{aligned}$$

(40)

Here, $N_{T,ij} = (\partial n_i / \partial T)_{c_1, c_2,p}\, \delta _{ij}$ is the diagonal thermal contrast factor matrix and $\underline {1} = (1, 1)^T$.

3.3.2 ODI

The ODI signals are not normalized to the thermal amplitudes and the $Q_{ij}$ are the amplitudes of concentration-dependent refractive index variations corresponding to wavelength $\lambda _i$ and eigenvalue $\hat{D}_j$ [102]

$$\begin{aligned} \begin{pmatrix} \delta n_1(z,t) \\ \delta n_2(z,t) \end{pmatrix} = \begin{bmatrix} Q_{11} &{} Q_{12} \\ Q_{21} &{} Q_{22} \end{bmatrix} \begin{pmatrix} f(z,t,\hat{D}_1) \\ f(z,t,\hat{D}_2) \end{pmatrix}. \end{aligned}$$

(41)

The non-dimensional functions $f(z,t,\hat{D}_i)$ describing the separation kinetics with the eigenvalue $\hat{D}_i$ are the same as in the OBD case, with Eqs. 9 and 12 used in the majority of ODI experiments.

Derivation of the transport coefficients is done similarly to the OBD case, with only minor differences, which account for the different matrix of the experimental amplitudes, $\underline{\underline{\textbf{Q}}}$, and for the absence of the thermal input in the ODI measured signal. The latter means that the matrix $\underline{\underline{\mathbf {N_T}}}$ can be omitted in Eqs. 38–40. Then, for example, the expression for Soret coefficient for the ODI method will take the form (cf. Eq. 40):

$$\begin{aligned} \underline {S_T^\prime } = - \underline{\underline{\mathbf {N_w}}}^{-1} ~ \underline{\underline{\textbf{Q}}} ~ \underline {1} ~. \end{aligned}$$

(42)

As in the OBD case, resolving the full diffusion matrix from a single thermodiffusion experiment is hardly possible because of the optimization convergence and robustness problems and $\underline{\underline{\textbf{D}}}$ should be measured independently [112, 113]. At the same time, the parameters $\underline{\underline{\textbf{Q}}}$ and $\underline {\hat{D}}$ can be reliably extracted for the mixtures with distinct $\hat{D}_i$. If, however, the diffusion matrix for the mixture is already known, little attention can be paid to the accuracy of $\underline {\hat{D}}$ and the individual elements of $Q_{ij}$. The only valuable information in this case is the total amplitude at each wavelength $\delta n^{st}_i = Q_{i1} + Q_{i2}$, which is typically determined with the highest possible accuracy and serves for deriving the Soret coefficients using Eqs. 35 and 32.

3.3.3 Soret Coefficient Measurement Errors in Ternary Mixtures

While the evaluation of two-color measurements on ternary mixtures in refractive index space is usually possible without major problems, the transformation to the concentration space is hampered by the necessary inversion of the frequently ill-condition solutal contrast factor matrix $\underline{\underline{\mathbf {N_w}}}$ [114] in Eqs. 38–40, 42. The consequence is a significant error amplification along a certain direction in the space of the independent concentrations. Figure 17 illustrates the error transformation when reconstructing the concentration from the optical signal $\underline {\delta n}$ with Gaussian noise. The result is inherently asymmetric in the concentration space.

Fig. 17

Visual representation of the error propagation in a thermodiffusion experiment in a ternary mixture. The Monte Carlo simulation illustrates that the uniform round noise distribution around $\underline {\delta n}$ turns into very elongated ellipsoid around $\underline {\delta w}$ [102]. Dashed blue and red lines correspond to isolines $\delta n_i = \text {const}$ (Color figure online)

The strength of asymmetry is characterized by the so-called condition number $\mathcal {K}$ of the matrix $\underline{\underline{\mathbf {N_w}}}$. When the condition number of the matrix grows, the error distribution cloud in the space $\underline {\delta w}$ turns into an ellipse, which becomes more and more squeezed and elongated; when $\mathcal {K}$ exceeds, say, one hundred, it practically stretches into a line.

The attempt to change the independent concentrations with the purpose to decrease the condition number does not bring a direct advantage. This is illustrated in the Gibbs triangle (Fig. 18) for the three Soret coefficients of a ternary mixture of water+ethanol+triethylene glycol at equal mass fractions [115]. The figure shows the results obtained by different experimental techniques together with the elongated error ellipsoids obtained from a Monte Carlo simulation with initially isotropically distributed errors in the experimental refractive index space. As can be seen from the projections of the error ellipsoid onto the axes, not all three Soret coefficients are affected by this problem to the same extent.

Fig. 18

Gibbs triangle for the three Soret coefficients of a mixture of water+ethanol+triethylene glycol at equal mass fractions. Measurements were performed by TGC, two-color OBD (2-OBD), and in microgravity as part of the DCMIX3 campaign aboard the ISS. The error ellipsoids were obtained by Monte Carlo simulation with Gaussian random noise on the measured signals. The error ellipsoid of the SODI-experiment is projected onto the axis to show the effect of the error amplification for the three Soret coefficients [115]. $T = 298.15$ K

4 Summary and Conclusion

We have discussed the most important experimental techniques that are nowadays used for the investigation of the Soret effect in binary and ternary liquid mixtures. Most of the employed methods use optical detection, which allows for in situ measurement of the concentration and temperature changes by monitoring the refractive index of the sample. The methods based on Soret cells, OBD, ODI, and SODI share many similarities and differ mainly by the dimensions of the cell and the detection and signal processing methods. Together with the NEFs, they all rely on a quiescent stratified liquid heated from the boundaries. The TDFRS method is somewhat different, as it relies on laser-induced transient gratings for volume heating with about two orders of magnitude shorter diffusion lengths. The powerful but time-consuming TGC technique in its traditional form is the only presently employed method that actively relies on convection in combination with sample extraction for external analysis. A recently developed micro-TGC column with transparent windows has brought also this method into the realm of optical techniques with in situ monitoring.

For binary mixtures, all discussed methods are capable of measuring thermodiffusion, Soret and Fickian diffusion coefficients—or a subset thereof—with an accuracy of the order of a few percent or better. The situation becomes, however, more complex for ternary mixtures. A single quantity, like the refractive index at a particular wavelength, is no longer sufficient to disentangle the combined signal of two independent concentration variables. Most of the research on ternary mixtures has been conducted in the context of the DCMIX microgravity project, where a second detection color has been introduced both in the space and in most laboratory experiments. Again, TGC plays a special role, as in these experiments, the second detection color was substituted by a density measurement.

While there has been significant progress, the limitations of these methods became also obvious. Due to the mandatory inversion of the frequently ill-conditioned contrast factor matrices, it is not possible to achieve a level of accuracy comparable to the binary case. For quaternary and even higher multicomponent mixtures, the complexity grows enormously [116] and a separation by multi-wavelength techniques is most likely not feasible. A possible route for future development and improvement might be to introduce new detection schemes, like in situ Raman spectroscopy [117]. Sample extraction, although it is always connected with a perturbation of the system, opens the route to a huge variety of commercially available analytical tools, e.g., NMR or gas chromatography. For systems with a large number of components, this might be the most promising and possibly only viable option.