High-Temperature Collision Integrals for m-6-8 and Hulburt–Hirschfelder Potentials

Abstract

This study is aimed to determine collision integrals for atoms interacting according to the m-6-8 and Hulburt–Hirschfelder potentials and analyze the differences between potentials. The precision of four significant digits was reached at all tested temperatures, and for high-temperature applications, six digits were calculated. The proposed method was tested on the Lennard-Jones potential and found to excellently agree with the recent high-quality data. In addition, the Hulburt–Hirschfelder potential was used for determining the collision integrals of the interaction of nitrogen atoms in the ground electronic state and compared with other known values. The calculations were performed using Mathematica computation system which can deal with singularities (so-called orbiting).

1 Introduction

The collision integrals are used evaluating the transport properties of gases (including diffusion coefficient and thermal transport coefficient) [1]. The most basic and commonly used collision integrals are the $\varOmega ^{(1,1)}$ and $\varOmega ^{(2,2)}$, which are called the diffusion collision integral and the viscosity collision integral, respectively. They are the first-order approximations in the Chapman-Enskog theory, while for higher-order approximations, other collision integrals are needed.

In recent studies, collision integrals have been used for analyzing diffusion [2] and the transport properties of equilibrium and non-equilibrium two-temperature plasmas [3,4,5,6,7] and of hypersonic flows [8,9,10], and also for modeling combustion [11, 12].

Accurate estimation of the collision integrals for colliding atoms is complex. Specialized methods have been developed [13, 14] by some authors, but their codes are not open. The older software of O’Hara and Smith [15] is available, in which authors have reached respectable five significant digits and this code is still in use. However, often the precision of collision integrals remains unknown [16].

The present study is mainly focused on higher temperatures (reduced temperature $T^{*}\ge 10$) for two reasons—they are appropriate for classical mechanics (quantum mechanical approach has been applied in some studies [17, 18]) and allow extending study to the interaction of not only atoms but also molecules (at high temperatures, molecular rotations are fast and, thus, enable to average over rotations and use effective potential energy curve (PEC) [17]; the most appropriate data for the interaction of molecules are, however, based on full potential energy surfaces [10]).

The most basic and the most widely used is the Lennard-Jones (12-6) potential energy function, for which high-accuracy data are available for comparison [14]. Due to its simplicity, scattering data based on this potential and its modification are still in commonly used [19, 20].

Other possible potential functions that can be considered to correctly describe interatomic interactions (or effective atom-molecule or molecule-molecule) and in particular successfully compared with the experiment, are the m-6-8 potential [21]. An advantage of the m-6-8 potential that it allows optimizing the collisions of particular atoms (or molecules) [22].

The third potential considered in the present study is the Hulburt–Hirschfelder potential (generalized Morse potential), which is commonly used to describe interatomic potential and the related collision integrals, notably for high-temperature applications such as hypersonic flows [13, 23,24,25]. Some PECs (can be described by the Hulburt–Hirschfelder functional form) may have multiple extrema [26], but in the studied cases, such features were not found and so they are not included in the scope of the present study.

This study aimed to determine collision integrals in reduced variables for m-6-8 and the Hulburt–Hirschfelder potentials with up to six-digit precision (with prior testing on the Lennard-Jones potential).

The calculations are made for potentials with parameters adjusted for describing argon dimer, but Mathematica notebooks allow changing the parameters of potential and generating collision integrals for the interaction of other atoms. The m-6-8 potential is appropriate for describing of rare gas dimers (especially it perfectly agrees with the ab initio curve of Ref. [27]), whereas the Hulburt–Hirschfelder potential is more appropriate for common molecules such as nitrogen or oxygen atoms.

The main purpose of this study is to demonstrate the usefulness of the method (hence, the Mathematica notebooks are made available) rather than the generation of data. However it has analyzed the interaction of nitrogen atoms, for which new values are calculated (and fitted to functional forms) and compared with those known so far.

2 Theory

The deflection angle of particles (refers here to atoms) interacting with the potential energy function V(r) is calculated in the scattering theory as follows [28]:

$$\begin{aligned} \chi (b,\gamma )=\pi -2b\int _{r_{c}}^{\infty } \frac{dr}{r^{2}\sqrt{1-\frac{b^2}{r^2}-\frac{V(r)}{kT\gamma ^2}}}, \end{aligned}$$

(1)

where b is the impact parameter, $r_{c}$ is the classical turning point (distance of the closest approach), and $\gamma ^2=\mu g^2/(2kT)$ ($\mu$ reduced mass, g relative velocity, k Boltzmann constant, and T temperature).

Collision integrals are defined in terms of deflection angle $\chi$ and collision cross section $Q^{(l)}$ [1]

$$\begin{aligned} Q^{(l)}(\gamma )=2\pi \int _{0}^{\infty }(1-\cos ^{l}\chi (b,\gamma ))bdb, \end{aligned}$$

(2)

by the formula

$$\begin{aligned} \varOmega ^{(l,s)}=\left( \frac{kT}{2\pi \mu }\right) ^{1/2} \int _{0}^{\infty }e^{-\gamma ^2}\gamma ^{2s+3}Q^{(l)}(\gamma )d\gamma . \end{aligned}$$

(3)

If the potential energy has the form $V(r)=\epsilon f(r/\sigma )$, it is customary to introduce reduced variables [1], namely $r^{*}=r/\sigma$ (with $\sigma$ defined by $V(\sigma )=0$), $b^{*}=b/\sigma$, $V^{*}=V/\epsilon$, $T^{*}=kT/\epsilon$, and $g^{*}=\mu g^2/(2\epsilon )$, and divide by the hard sphere expression; the resulting expression for collision integrals is

$$\begin{aligned} \varOmega ^{(l,s)*}(T^{*})= & {} \frac{4}{(s+1)!(1-\frac{1}{2}\frac{1+(-1)^l}{1+l}) T^{*s+2}}\int _{0}^{\infty }\int _{0}^{\infty }e^{g^{*2}/T^{*}} g^{*(2s+3)}\cdot\nonumber \\&\cdot(1-\cos ^{l}\chi ^{*})b^{*}db^{*}dg^{*}, \end{aligned}$$

(4)

with

$$\begin{aligned} \chi ^{*}(b^{*},g^{*})=\pi -2b^{*}\int _{r_{c}^{*}}^{\infty } \frac{dr^{*}}{r^{*2}\sqrt{1-\frac{b^{*2}}{r^{*2}}-\frac{V^{*}(r^{*})}{g^{*2}}}}. \end{aligned}$$

(5)

The Lennard-Jones (12-6) potential in the reduced coordinates is

$$\begin{aligned} V_{LJ}^{*}(r^{*})= 4(1/r^{*12}-1/r^{*6}). \end{aligned}$$

(6)

The m-6-8 potential is [29]

$$\begin{aligned} V_{m68}^{*}(r^{*})=\frac{6+2\gamma '}{(m-6)(r^{*}/d)^{m}} -\frac{m-\gamma '(m-8)}{(m-6)(r^{*}/d)^{6}}-\frac{\gamma '}{(r^{*}/d)^{8}}, \end{aligned}$$

(7)

with $\gamma '=3.0$, $m=11$, and $d=1.11 446$ which are the parameters for argon atom collisions [21, 30].

The Hulburt–Hirschfelder potential in the reduced form is written as follows:

$$\begin{aligned} V^{*}_{HH}(r^{*})= & {} \exp (-2\alpha (r^{*}/d-1))-2\exp (-\alpha (r^{*}/d-1))+\nonumber \\&+\beta (r^{*}/d-1)^3[1+\gamma (r^{*}/d-1)]\exp (-2\alpha (r^{*}/d-1)), \end{aligned}$$

(8)

with $\alpha =6.21 571$, $\beta =-13.8668$, $\gamma =-4.4466$, and $d=1.12 042$. Note that this potential has four free parameters (one more compared to the m-6-8 potential) which are related to spectroscopic constants.

For collision of the ground-state nitrogen atoms, the parameters of the Hulburt–Hirschfelder potential were taken from Ref. [31]. The missing values of $\sigma$ calculated from non-reduced PECs are $\sigma _{1}=1.581 369$ ($d=1.31 173$) for $X^{1}\Sigma _{g}^{+}$ state, $\sigma _{2}=1.93 955$ ($d=1.25 355$) for $A^{3}\Sigma _{u}^{+}$, $\sigma _{3}=2.75 276$ ($d=1.11 089$) for $A'^{5}\Sigma _{g}^{+}$, and $\sigma _{4}=6.19849$ ($d=1.13 254$) for $^{7}\Sigma _{u}^{+}$.

2.1 Computational Details

Multidimensional integration was performed in the Mathematica software [32] using the inbuilt NIntegrate function with $Method\rightarrow \{GlobalAdaptive, MaxErrorIncreases\rightarrow 100000,SymbolicProcessing\rightarrow 0,SingularityHandler\rightarrow None\}$ options (such options are suggested by the Mathematica community for complex numerical integration cases). The number of significant digits is fixed by the PrecisionGoal option. This approach was evaluated on high-quality collision integrals known for the Lennard-Jones potential. At higher temperatures ($T^{*}\ge 10$), six significant digits can be reached with a moderate computation time, whereas at lower temperatures, only four significant digits can be evaluated. Calculations with six-digit precision take more than 10 times longer time compared to those done with four-digit precision.

Although the calculations of collision integrals involved singularities, they are effectively dealt by the algorithm (also, setting $SingularityHandler\rightarrow Automatic$ gives the same results within the given precision).

As for accuracy, there are no analytical results available for the real potentials to make definite comparisons, but in case of the Lennard-Jones potential comparison is done with the results of specialized software.

At low temperatures, the Mathematica issues warnings. However, comparisons with the Lennard-Jones and m-6-8 potentials also show that the results are reliable (at least for those simple potentials). Since warnings are only seen at lower temperatures, it can be concluded that the present approach is reliable and capable of yielding many significant digits for high temperatures and PECs with one minimum and no maxima.

3 Results

3.1 Testing—Comparison with High-Precision Data for the Lennard-Jones Potential

The high-precision data for the Lennard-Jones potential were previously calculated by Kim and Monroe [14].

Prior to the comparison of the collision integrals themselves, the deflection angles were compared (Table 1). After appropriate round off, the values perfectly agreed. It should be noted that both Lennard-Jones values and Kim and Monroe values differ from the old Hirschfelder data [33], especially in the case small impact parameters but agree with the contemporary Sharipov and Bertoldo values [34].

Table 1 Comparison of the Lennard-Jones deflection angles $\chi (b,\sqrt{0.1})$ of the present method (Eq. 1) with Kim and Monroe (KM) values (given in Table 3 of Ref. [14])

The reduced collision integrals $\varOmega ^{(l,s)*}$ were compared with the Kim and Monroe data as shown in Tables 2 and 3.

Table 2 Comparison of the Lennard-Jones collision integrals $\varOmega ^{(l,s)*}$, results of the proposed method, and Kim and Monroe (KM) results

Table 3 Comparison of the Lennard-Jones collision integrals $\varOmega ^{(l,s)*}$, results of the proposed method, and Kim and Monroe (KM) results

It can be noted that all six or at least five significant digits are the same, which confirms the success of the proposed general, non-specialized approach.

Values at lower temperatures can also be calculated with the same precision but the calculation can take a significantly longer time. For example, for at $T^{*}=10$, the calculation times with precision of four, six, and eight significant digits can be related as 1:12:80 (calculation time with four digits is set to unity but of course the actual time depends on the machine used).

Also for lower temperatures calculation is longer, for example the calculation time (with the same precision) for the reduced temperature 50 is more than 4 times faster than for reduced temperature 10.

Table 4 Comparison of the 11-6-8 collision integrals $\varOmega ^{(l,s)*}$, results of the proposed method, and Hanley and Klein (HK) results

It is crucial to note that even though no specialized treatment of singularities was applied the method agrees well with high-accuracy data. The deflection angle of course had singularities (orbiting) in the integration interval, as indicated in Fig. 1.

Fig. 1

Deflection angle for the Lennard-Jones potential

3.2 The m-6-8 and Hulburt–Hirschfelder Potentials

To test the applicability to other potentials, the m-6-8 (with m = 11 here) and Hulburt–Hirschfelder potentials were chosen. The values obtained from the presented approach were compared with the Hanley and Klein data, as presented in Table 4 [1, 21]. The agreement comparison revealed that the method does not agree well with the m-6-8 potential compared to the Lennard-Jones potential but that the Hanley and Klein data are older than the highly accurate Kim and Monroe data.

The values noted for the m-6-8 potential are similar to the Lennard-Jones potential-based values, but it is known that it translates to significantly different transport properties [21], and therefore, highly accurate collision integrals are crucial.

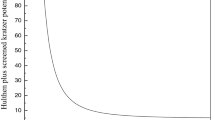
Finally, the Hulburt–Hirschfelder potential was used to compare with the previous data. Figure 2 shows the differences between all three potential functions, while Fig. 3 shows the differences between the respective $\varOmega ^{(1,1)*}$ collision integrals. Interestingly, the difference between collision integrals is smaller at higher temperatures than at lower ones, which is contrary to the case of thermodynamics where discrepancies between potentials increase with increase in temperature [35].

Fig. 2

Potential energy curves of the Lennard-Jones, m-6-8, and Hulburt–Hirschfelder potentials

Fig. 3

Collision integrals $\varOmega ^{(1,1)*}$ on the Lennard-Jones (LJ), m-6-8 (m-6-8), and Hulburt–Hirschfelder (HH) potential energy curves

3.3 Application of the Hulburt–Hirschfelder Potential to Collisions of Nitrogen Atoms

The PECs of nitrogen atoms interactions can be conveniently presented in the form of the Hulburt–Hirschfelder potential, and the data of, often needed, collision integrals can be generated and compared with other data.

The collision integral of atoms is defined as the weighted average (in units of squared Angstroms by change of units of $\sigma$’s)

$$\begin{aligned} \sigma ^{2}\varOmega ^{(1,1)*}:=\frac{\sigma _{1}^{2}\varOmega ^{(1,1)*}(X^{1} \Sigma _{g}^{+})+3\sigma _{2}^{2}\varOmega ^{(1,1)*}(A^{3}\Sigma _{u}^{+}) +5\sigma _{3}^{2}\varOmega ^{(1,1)*}(A'^{5}\Sigma _{g}^{+}) +7\sigma _{4}^{2}\varOmega ^{(1,1)*}(^{7}\Sigma _{u}^{+})}{1+3+5+7}, \end{aligned}$$

(9)

the statistical weights are determined form molecular term symbols (for each PEC) of the N$_{2}$ molecule electronic states given in brackets. The average is done because the N$_{2}$ molecule dissociates from those four electronic states and becomes the ground state nitrogen atoms, so that when the atoms collide they interact according to one of those curves with appropriate statistical weights (to determine the probability of the potential curve) and such weighted average is the proper description of the total process that reflected by macroscopic transport properties.

Some datasets are available for the ground-state nitrogen atoms, and they show certain disagreement. Those datasets are the values of Levin et al. [36] (Levin1990 in Table 5) calculated using the semiclassical approach on PECs based on ab initio data and experimental data; the values of Capitelli et al. from year 2000 [37] which are based on Lennard-Jones and Morse potential models (Capitelli2000 in Table 5), and the values of Capitelli et al. from year 2007 [38], in which the collision integrals were revisited using of Piriani PEC (Capitelli2007 in Table 5).

The differences may be due to the use of classical versus semiclassical approach (at lower temperatures) and differences other than the shapes of reduced potentials—potentials in reduced coordinates generate negligible differences at high temperatures (Fig. 3) so that the difference can be attributed to the depths of PECs (used to calculate reduced temperatures $T^{*}=k_{B}T/D_{e}$; it should be noted that they are different for each PEC) or the values of $\sigma$ (the choice for mostly repulsive $^{7}\Sigma$ potential can differ).

Because the reduced temperatures are often lower than unity (especially for the ground electronic state curve), the three significant digits were calculated. However, due to the differences between datasets, such precision is satisfactory.

Table 5 Collision integrals $\sigma ^{2}\varOmega ^{(1,1)*}$ for the interaction of ground-state nitrogen atoms

Fig. 4

Graphical comparison of collision integrals $\sigma ^{2}\varOmega ^{(1,1)*}$ given in Table 5

Graphical comparison in Fig. 4 shows that the present values at lower temperatures agree with Capitelli2000 [37] or Capitelli2007 data [38]. At higher temperatures, Capitteli2007 [38] data start to significantly diverge, whereas Levin1990 [36] and the present data are in much better agreement.

Other collision integrals are only given in the work of Levin et al. [36] and are compared in Table 6.

Table 6 Comparison of collision integrals $\sigma ^{2}\varOmega ^{(2,2)*}$ for the interaction of ground-state nitrogen atoms with Levin1990 [36]

The fits for $\varOmega ^{(1,1)*}$ and $\varOmega ^{(2,2)*}$ are the following (symbol f underlines that it is the fitting function and not the actual calculated value):

$$\begin{aligned} f_{\sigma ^2\varOmega ^{(1,1)*}}(T)= \,& {} 4.5727-1.9884\cdot 10^{-4}T+8.3134\cdot 10^{-9}T^2 - 2.0674\cdot 10^{-13}T^3+\nonumber \\&+2.155\cdot 10^{-18}T^4+3651.9/T-1.3798\cdot 10^6/T^2, \end{aligned}$$

(10)

and

$$\begin{aligned} f_{\sigma ^2\varOmega ^{(2,2)*}}(T)= \,& {} 4.8663-1.9083\cdot 10^{-4}T+8.7536\cdot 10^{-9}T^2 - 2.444\cdot 10^{-13}T^3+\nonumber \\&+2.7856\cdot 10^{-18}T^4+4273.8/T-1.6939\cdot 10^6/T^2, \end{aligned}$$

(11)

where $T\in [1000\text {K},30,000\text {K}]$.

4 Conclusions

The collision integrals $\varOmega ^{(l,s)*}$ were calculated by applying the general numerical integration method using the Mathematica software at higher and lower temperatures for the Lennard-Jones, m-6-8, and Hulburt–Hirschfelder potentials (the basic case of one minimum and no maxima was considered). The high precision of six digits was reached at higher reduced temperatures. The results observed for the Lennard-Jones potential agree very well with the previous high-precision calculations, which confirms not only good precision but also accuracy of the results. Moreover, there was no need to develop specialized software to deal with singularities.

The present results for the m-6-8 potential are not in such good agreement with other data which are older and most probably not so accurate as the recent Lennard-Jones results. The Hulburt–Hirschfelder potential-based collision integrals were calculated and compared with those based on other potential energies showing increased discrepancies with lowering temperature—collisions at low energies are more sensible to the structure of potential.

The Hulburt–Hirschfelder potential was also utilized to calculate collision integrals for ground electronic state nitrogen atoms (using four potential energy curves) and successfully compared with other known data. Those collision integrals were fitted to functional forms to facilitate their use.

The Mathematica notebooks for each potential are made freely available in order to facilitate the use of the proposed approach.