Abstract
A complete theoretical analysis of the fluid and solid dynamics of the torsional quartz crystal viscometer is presented which for the first time, establishes a firm theoretical basis for two working equations whereby the viscosity of a fluid may be determined from measurements of the resonant frequency of the crystal and the width of the resonance when immersed in the fluid. Modern instrumentation means that it is possible to achieve higher resolution in the measurement of these two quantities than hitherto and the new theory opens the way to securing a concomitant accuracy in the determination of viscosity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The use of quartz-crystal devices for the measurement of the viscosity of fluids has a long tradition. The systematic study of such devices was begun by Mason [1,2,3] in the 1940′s. He, and others [4,5,6,7] reported applications of a variety of devices to the task over a period of 20 years with both the theory and the instrumentation of the devices becoming increasingly sophisticated. Gradually, one device emerged as superior to others for measurements of the viscosity of a range of fluids and that was the torsional quartz-crystal viscometer which was adopted by those with an interest in the properties of fluids rather than those interested in the devices themselves or those seeking applications for quartz transducers. The advantages of the piezoelectric material quartz for these devices were its ready availability and the extensive expertise for its preparation as a viscosity sensor among those who sought applications for quartz crystals. Among the early adopters of the technique interested in the thermophysical properties of fluids were Collings and McLaughlin at Imperial College in London [8], the National Bureau of Standards in Boulder USA, specifically Diller [9] and then Haynes, Laesecke and their colleagues [10,11,12]. Other notable early users were De Bock and others [13], D’yachenko in the Soviet Union [14] and Barlow and his colleagues [15]. More recently the device has been employed by Meier and his colleagues for high-precision measurements on a series of fluids [16,17,18].
For reasons probably connected with its origins, the detailed mechanical and fluid dynamic theory of the device and the conditions within which its operation should be constrained were never fully explored. Rather, the device was treated as a generic oscillator that was loaded by a viscous fluid with non-zero density to produce a more highly damped oscillation whose bandwidth reflected a combination of these two properties. This led investigators to adopt a working equation for the viscometer based upon bandwidth measurements alone and empirically to study the conditions under which it could be employed successfully [8,9,10,11,12,13,14,15,16,17,18].
The precision with which it is now possible to measure the resonant frequency of oscillators means that there is interest in seeking to exploit additionally an equation based upon the effect of viscosity on the resonant frequency of the oscillator. On the one hand this gives another means of deriving the fluid viscosity from measurements on the same sensor and, on the other hand, it allows the opportunity for an examination of the premise that the device operates in accord with the theoretical description of it. This was not hitherto possible.
In this paper we present a rigorous analysis of solid and fluid dynamics for the torsional quartz-crystal viscometer and derive two working equations for its application. The conditions under which these working equations should be valid are established to guide design of the instrument. Subsequently, in Part II of this paper [19], we employ original experimental data acquired in several different viscometers of this type to examine the extent to which existing instruments conform to the theory.
2 Physical Model of the Viscometer
The torsional quartz-crystal viscometer consists of an X-cut right-circular cylinder of radius \(R\) and length \(L\) and of density \(\rho_{{\text{c}}}\), with elastic constants \(c_{11} ,c_{12} ,c_{13} ,c_{14} ,c_{33} {\text{ and }}c_{44}\) as well as piezoelectric constants \(d_{11} {\text{ and }}d_{14}\) and permittivities \(\varepsilon_{1} {\text{ and }}\varepsilon_{3}\). The crystal is forced to vibrate torsionally at a (radian) frequency ω with angular amplitude \(\varepsilon\). The crystal is suspended by a mechanism which exerts no force upon it other than to oppose gravity and is immersed in an incompressible Newtonian fluid of viscosity \(\mu\) and density \(\rho\).
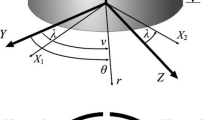
A diagram of the quartz crystal is contained in Fig. 1, which also illustrates the coordinate system that we shall employ and indicates the positions of the four electrodes used to excite motion. In order to build a mathematical model of the crystal oscillations we employ a right-handed coordinate system. For a quartz crystal, rectangular coordinates {X,Y,Z} are conventionally used such that the X-direction is aligned along the binary axis of the crystal and the Z-direction is aligned along its trigonal axis. An X-cut quartz cylinder is one such that the X-direction is aligned with the axis of the cylinder. It is also appropriate to use a system of cylindrical polar coordinates {r,θ,z} with its origin at the center of the one end of the cylinder and the z-direction aligned along its axis towards its other end. Thus z = X and it is convenient to let r = Y when θ = 0 so r = Z when \(\theta = \pi /2\).
The electric field that is applied to force torsional vibrations of the crystal has been contrived by a variety of mechanisms [8,9,10,11,12,13,14,15,16,17,18]. In one scheme, it is induced by four electrodes plated along the length of the surface of the crystal. The first electrode is in the quadrant \( \varPhi < \theta < \varPhi + \pi /2, \) the second in \( \varPhi + \pi /2 < \theta < \varPhi + \pi , \) the third in \( \varPhi + \pi < \theta < \varPhi + 3\pi /2, \) and the fourth in \( \varPhi + 3\pi /2 < \theta < \varPhi\,+\,2\pi.\) Here, \(\varPhi\) is the angle about the z-axis through which the crystal is twisted: \(\varPhi\) has the same sense as θ and is of the form
where \(i = \sqrt {\left( {{-}1} \right)}\) and t denotes time. Note that the quadrants spanned by the electrodes depend on \(\varPhi\) because the electrodes twist with the crystal. The first and third electrodes are at a potential \(+ V_{0} \exp \left( {i\omega t} \right)\) and the second & fourth at a potential \(- V_{0} \exp \left( {i\omega t} \right)\). Electrical connections are made to the electrodes by wires attached at the mid-plane \((z\,=\,L/2)\): these wires also serve to support the quartz crystal. Although other methods have been used to generate the forcing electric field the consequences for the analysis that follows are identical.
While in principle, the quartz crystal could be made in a variety of sizes it is typically 50–100 mm long and 5–10 mm in diameter. These dimensions together with the elastic constants of quartz constrain the magnitudes of some of the variables for the instrument and it is useful to summarize them and a variety of quantities that we introduce in the analysis early in the discussion. Thus, Table 1 lists the main quantities of interest and the values they have in a typical instrument. Each quantity is defined in the text. Table 2 lists of some of the dimensionless groups that are important in the analysis, their typical values for a representative instrument and for two fluids of the type that are studied in such instruments. We consider for these purposes an organic fluid with six carbon atoms (C6) and one with one carbon atom (C1) at two different pressures. We include values for the dimensionless groups that the theory developed here uses and the constraints that it places on them for its validity. The latter constraints are expressed as inequalities and the equation or table number that follows each in the column labeled “Desired Value” indicates where they arise in the analytic treatment that follows.
2.1 Fluid Mechanics
We consider the situation in which the crystal is driven into oscillation continuously so that any transients associated with the initiation of oscillation have decayed and it is surrounded by a Newtonian fluid of density \(\rho\) and viscosity \(\mu\). Then, provided the radial dimension of the region in which there are significant spatial variations of flow variables is much less than the axial dimension of the cylinder and provided the twist on the cylinder varies weakly with axial position, that is, provided \( \varepsilon R \ll L \), the flow is planar, so the velocity field \({\mathbf{u}}\) and the pressure field p do not vary significantly with axial position z, and u has no z-component. Together with axisymmetry, this implies that
where \({\mathbf{i}}_{\theta }\) is a unit vector in the θ-direction. The form of Eq. (2) automatically ensures that mass is conserved. Provided that the flow is laminar, which is assured if the Reynolds number \(Re = \rho \omega \varepsilon R^{2} /\mu \ll 1\;{\text{or}}\;{{\sim 1}} \) (the latter because the flow is nearly non-accelerating), the momentum conservation equation yields
so that \( p = p_{\infty}+\rho\int\limits_{\infty}^{r} {(u_{\theta }^{2}/r )} \,dr \) and
subject to the boundary conditions
We now introduce dimensionless variables so that
where
Equation (4) then becomes
with
and,
The solution of Eq. (8) is
where bern( ), bein( ), kern( ) and kein( ) are n-th order Kelvin functions. It follows from Eq. (9) that
The shear stress \(\sigma_{r\theta }\) in the fluid is given by
Using the properties of Kelvin functions [20] we find that on the cylinder surface, at r = R (σ = 1)
Using the values drawn from practical examples of the application of the technique given in Tables 1, 2\(\sqrt \varOmega > > 1\) which means physically that there is a very thin shear layer near the surface of the cylinder in which there are significant spatial velocity variations. We also note that \(\sqrt \varOmega > > 1\) implies that the flow is planar.
Again, from the properties of Kelvin functions [20]
Thus,
or since \(\sqrt \varOmega > > 1\)
If d is the thickness of the shear layer then, because \(\sigma_{r\theta } |_{R} \sim \mu \omega \varepsilon\,R/d\), and from Eq. (18) \(\sigma_{r\theta } |_{R} \sim \mu \omega \varepsilon\,\sqrt \varOmega\); it follows that \(d\sim R/\sqrt \varOmega\) which shows that the shear layer is indeed thin if \(\sqrt \varOmega > > 1\).
The force F' per unit length of cylinder exerted by the fluid on the cylinder is given by \(F^{\prime}{ = }{-}2\pi R\,\sigma_{r\theta } |_{R}\) so the moment, \(M^{\prime}\), per unit length of cylinder exerted by the fluid on the cylinder is given by
or
But \({-}\omega^{2}\,\varepsilon\,exp\left( {i\omega t} \right)\) is the angular acceleration, \({\partial^{2}} {\varPhi} /\partial t^{2}\), of the cylinder and \(i\omega\,\varepsilon\exp \left( {i\omega t} \right)\) is its angular velocity, ∂Φ/∂t so that we can write
where
For a cylinder of finite length L, as well as the stress on the cylindrical circular surface there is drag at each of its ends (z = 0 and z = L). To leading order, the velocity field u near the ends has no radial component or axial component and its angular component \(u_{\theta } \left( {r,z,t} \right)\) is determined by the solution of
assuming that velocity variations are confined to a thin shear layer so that gradients with respect to r are insignificant compared with those with respect to z. The boundary conditions after the initial transient on start-up of the flow has decayed are
If we consider just the end at \(z \, = \, L\) and write
then Eqs. (23) and (24) become
The solution of Eq. (26) subject to (27) is
so that the shear stress, \(\sigma_{z\theta } = \mu \frac{{\partial u_{\theta } }}{\partial z}\) can be shown to be
Thus, the shear stress \(\sigma_{z\theta } |_{L}\) exerted on the fluid by the end of the cylinder at z = L (ζ* = 0) is given by
and the moment \( M|_{L}\) exerted by the fluid on the end of the cylinder is
or
and by symmetry
2.2 Effects in the Fluid that Are Rendered Negligible
So far we have considered the major effects of the fluid on the oscillation of the quartz crystal but for completeness of the analysis we need to look at other fluid effects that may affect the operation of any instrument and its accuracy. First, we have so far assumed that the fluid is isothermal throughout and remains at an equilibrium temperature with the crystal. However, in principle, heat generation by viscous dissipation causes a local rise in temperature T in the fluid. This rise has a negligible effect on the viscosity of the fluid provided the Nahme number
where λ is the thermal conductivity of the fluid and \(\left| {\partial \mu /\partial T} \right|\) is evaluated at the ambient temperature of the fluid. Table 2 shows that in a typical realization of the instrument \(Na < 10^{ - 14}\) so that the condition for the neglect of viscous heating is easily fulfilled.
We have also assumed that the fluid is incompressible for our analysis of fluid flow. Compressibility effects vary as the square of the Mach number
where c is the speed of sound and so their neglect is justified so long as Ma « 1. For practical instruments, Table 2 shows that \(Ma < 5 \times 10^{ - 8}\) so that it is legitimate to treat the fluid as incompressible.
3 Solid Mechanics
We now consider the crystal itself and its response to the fluid behavior surrounding it. The crystal motion is driven by the converse piezoelectric effect which involves application of an electric field to produce a stress. If an electric field, E acts on the quartz crystal, the components of the resultant stress field, σ, are related to those of E and the strain e as follows
where
The strain components are defined in terms of displacements ξ, η and ζ in the X-, Y- and Z-directions, respectively, as follows
The electric field E is solenoidal (i.e. \({\varvec{\nabla}}\)·E = 0) and is given by the negative gradient of the potential V (E = – \({\varvec{\nabla}}\) V), so V is harmonic (i.e. it satisfies Laplace’s equation:\(\nabla^2 \) V = 0). If \(\varepsilon\,R \, \ll L\) then E is planar; it has no z-component and does not vary in the z-direction. Thus
For the disposition of electrodes discussed earlier the boundary conditions are
The solution of Eq. (44) subject to (45) is
or transforming to {X,Y,Z} coordinates
But cos \(\varPhi\) = 1 and sin \(\varPhi\) = 0 to leading order since є « 1 and so
Here we note that EX = – ∂V/∂X = 0 and EY = – ∂V/∂Y, while EZ = – ∂V/∂Z is irrelevant to the stress in the crystal. It then follows from Eqs. (36) to (41) inclusive that the direct effect of the electric field E occurs because its Y-component, EY induces shear strains \(e_{XZ} \;{\text{and }}e_{XY}\) and hence shear stresses \(\sigma_{XZ} \;{\text{and }}\sigma_{XY}\) We now assume there is no shear strain in a plane normal to the X-axis so that \(e_{YZ} = \, 0.\) Then, \(\sigma_{YZ} = 0\,{\text{ and }}\sigma_{XY} {\text{and }}\sigma_{XZ}\) are given by
The normal strain components \(e_{XX} , \, e_{YY} {\text{ and }}e_{ZZ}\) are not assumed to vanish and in general they do not do so. Thus, the normal stress components \(\sigma_{XX} , \, \sigma_{YY} {\text{and }}\sigma_{ZZ}\) do not vanish either. It follows that it is appropriate to transform from {X,Y,Z} coordinates to {X,X1,X2} coordinates where the X1- and X2-directions are aligned with the principal axes of the symmetric matrix \(\left( {\begin{array}{*{20}c} {c_{66} } & {c_{14} } \\ {c_{14} } & {c_{44} } \\ \end{array} } \right)\) the eigen-values of which are \(\nu_{1} {\text{ and }}\nu_{2}\). Then
where \(\nu {\text{ is }}\nu_{1} {\text{ or }}\nu_{2}\). It follows that
and so, arbitrarily assigning \(\nu_{1} {\text{ and }}\nu_{2}\) and hence the X1- and X2-directions
so that
If λ is the angle between the Y- and X1-directions, and hence also between the Z- and X2-directions, and λ has the same sense as θ then
The two diagonal components of Eq. (54) merely reproduce Eq. (53); the two off-diagonal components are the same and yield
For quartz, c14 ≈ –18 GPa, c66 ≈ 40 GPa and c44 ≈ 58 GPa [21] so λ ≈ + 0.55 rad.
If \(\xi , \, \xi_{1} {\text{ and }}\xi_{2}\) are the displacements in the X-, X1- and X2-directions, respectively, then for torsion through a small angle Φ (i.e. for є « 1)
where Φ is independent of X1 and X2, ∂Φ/∂X is the twist and \(\psi \left( {X_{1} ,X_{2} } \right)\) is the torsion function, which accounts for distortion of cross-sections that are planar and normal to the X-axis in the untwisted crystal. Thus
and
In the absence of the electric field, when \(E_{Y} = \, 0\) then Eqs. (49) yield
on transformation to {X,X1,X2} coordinates and so, using Eqs. (57) and (58)
If we now introduce the stress function \(\chi \left( {X_{1} ,X_{2} } \right)\) such that
then it follows that
and
At the surface of the crystal (r = R), no force is exerted in the X-direction if the crystal is in vacuo: an insignificant force is exerted in the X-direction if the crystal is immersed in a fluid provided \(\varepsilon\,R \, \ll \, L\). Thus, there is no force in the X-direction per unit area normal to the r-direction and hence \(\sigma_{Xr} = \, 0{\text{ at }}r \, = \, R\). Now putting
and transforming coordinates, we have
so that
Since \(\sigma_{Xr} = \, 0{\text{ at }}r \, = \, R\), it follows that χ is independent of γ and hence constant at r = R. Thus, to within an arbitrary integration constant,
The solution of Eq. (63) subject to Eq. (68) is
which is independent of γ. Thus \(\partial \chi /\partial \gamma \, = \, 0 \, {\text{for}}\, 0 \, \le \, r \, \le \, R\) and so \(\sigma_{Xr} = \, 0\) everywhere in the cylinder and not just on its surface. Provided \(\varepsilon\, \ll \, 1\), convective inertial effects are insignificant compared with transient inertial effects and the two transverse components of the momentum conservation equation yield
Substitution of Eq. (56), Eq. (64) and Eq. (69) into Eq. (70) yields
Since Φ is independent of \(X_{1} {\text{ and }}X_{2}\) and hence of \(r{\text{ and }}\gamma\), it follows that the equation of motion is
provided there is no resistance to twisting at the surface of the cylinder, i.e. provided the crystal is not surrounded by fluid. Here, the polar second moment of area \(I\) is given by
and the moment of compliance \(C_{{\text{m}}}\) is given by
so
It follows from Eqs. (66) and (69) that
which is independent of γ.
The internal moment on a cross-section of cylinder is given by
It follows from Eqs. (62) and (69) that
Hence,
and so, assuming without loss of generality, that there is no displacement in the X-direction of the axis \(\left( {X_{1} = \, 0 \, = \, X_{2} } \right)\) of the crystal
For quartz, c14 ≈ –18 GPa, c66 ≈ 40 GPa and c44 ≈ 58 GPa [21] so ψ ≈ + 0.41 X1X2.
Clearly, \(\psi \, > \, 0\) where the product \( X_{1} X_{2} > \,0\,\text {i.e.}\,\text{for}\,\pi/2 < \gamma < \pi \,\text{and}\,3\pi /2 < \gamma \, < 2\pi \) and \(\psi \, < \, 0\) where the product \( X_{1} X_{2} < \,0\,\text{i.e.}\,\text{for}\,\pi /2 < \gamma < \pi \,\text{and}\,3\pi /2 < \gamma \, < 2\pi \).
Because \(\psi \ne 0\) except where the product \(X_{1} X_{2} = \, 0\) (i.e. where \(X_{1} = \, 0\) and/or \(X_{2} = \, 0\)) and because \(\partial \varPhi /\partial X \, \ne \, 0{\text{ at }}X = 0{\text{ or }}X = L\), the distortion causes the ends of the crystal to ripple. Here we note that although Φ is a maximum with respect to X at \(X \, = \, 0{\text{ and }}X \, = \, L\), its gradient with respect to X does not generally vanish there because of the non-zero moments \(M\left| {_{0}\,{\text{and}}\,M}\right|_{L}\) exerted by the fluid on the ends of the cylinder and, as will be seen shortly in Eq. (90), an additional piezoelectric contribution to those moments. These ripples in the ends of the crystal induce pressure fluctuations in the fluid of order \(\rho \omega^{2} \varepsilon^{2} R^{2}\). It follows from Eqs. (18) and (30), however, that the shear stress components in the fluid are of order \( \mu \omega \varepsilon \sqrt \varOmega \; = \;\rho \omega ^{2} \varepsilon ^{2} R^{2} /\sqrt {\varepsilon {Re} } . \) Because Re « 1 or ~ 1 and є « 1, the effect of the ripples on the dynamics of the fluid is insignificant. Of course, for an isotropic solid where \(c_{14} = \, 0 \, , \, c_{44} = \, c_{66} = \, G\), where G is the shear modulus, \(\psi \, = \, 0\) and there is no distortion.
In the case where there is an electric field and \(E_{Y} \ne \, 0\) then Eqs. (49) yield
on transformation to \(\left\{ {X,X_{1} ,X_{2} } \right\}\) coordinates, where \(\tau_{1} {\text{ and }}\tau_{2}\) are directly proportional to \(E_{Y}\), linear functions of \(d_{11} {\text{ and }}d_{14}\) and non-linear functions of \(c_{14} , \, c_{44} {\text{ and }}c_{66}\): \(E_{Y}\) varies with position, i.e. with \(X_{1} {\text{ and }}X_{2}\). Thus Eq. (60) must be modified to yield
and so Eq. (61) becomes
Equations (62) and (63) are unchanged while Eq. (64) becomes
Transforming coordinates using Eq. (65) and putting
means that Eqs. (66) are unchanged while Eq. (67) becomes
It follows from the symmetry of the location of the electrodes that \(E_{Y}\) is anti-symmetric about the plane \(\theta \, = \, \varPhi + \pi/2 \pm \pi/2 \). Thus, at \(r \, = \, R\), the average value of \(E_{Y}\) is zero and so, again at \( r \, = \, R\) the average value of \(\tau_{r}\) is zero. Since \(\sigma_{Xr} = \, 0\) at \(r \, = \, R\), it follows that Eqs. (68) and hence Eq. (69) still hold in an average sense. The fact that they only hold in an average sense is consistent with the different functional dependence of \(\tau_{1} {\text{ and }}\tau_{2} {\text{ on }}X_{1} {\text{ and }}X_{2}\) from that of \(e_{{XX_{1} }} {\text{ and }}e_{{XX_{2} }}\): the electric field does not induce pure torsion in the crystal. Equation (70) is unchanged and so, because \(E_{Y}\) and hence \(\tau_{1} \, {\text{and}}\, \tau_{2}\) are independent of X, Eqs. (71) to (75) inclusive are unchanged though Eqs. (71) and (72) hold only in an average sense. Again, in an average sense, Eq. (76) becomes
Note that, in the same average sense, both \(\sigma_{X\gamma } {\text{ and }}\tau_{\gamma }\) are independent of γ. Thus, the first of Eqs. (77) is unchanged while the second becomes
where the actual dependence of \(\tau_{\gamma } {\text{ on }}r\) is acknowledged. Because \(\tau_{1} {\text{ and }}\tau_{2} \, \) are directly proportional to \(E_{Y}\) and hence to the applied potential V, it follows from Eq. (85) that \(\tau_{\gamma }\) is directly proportional to V. It is convenient, therefore, to introduce an effective moment piezoelectric constant \(D_{{\text{m}}}\) given by
so that
Now, the components of the electric displacement D are given by
The surface charge per unit area is given by the outward normal component \(D_{{\text{n}}} {\text{ of }}{{D}}\) at the surface of the crystal: thus \(D_{{\text{n}}} = - D_{X}\) at \(X = 0\), \(D_{{\text{n}}} = + D_{X}\) at \(X = L\) and \(D_{{\text{n}}} = + D_{r}\) at \(r = R\). It follows from Eqs. (36), (43), (46) and (56) that
where ψ is given by Eq. (80) and
But
so
since σXr|R = 0.
Substitution from Eq. (87) yields in an average sense
where \(\tau_{\gamma } |_{R,\theta - \lambda }\) implies that \(\tau_{\gamma }\) is to be evaluated at r = R and γ = θ – λ.
The total surface charge Q on the crystal is given by
It follows from Eqs. (94) and (95) that
Integration with respect to θ over the range 0 to 2π is the same as integration with respect to \(\gamma \, = \, \theta \, {-}\lambda\) over the range 0 to 2 π. Hence it follows from Eq. (80) that
since \(X_{1} = r\text{cos}\gamma\) and \(X_{2} = r\text{sin}\gamma\) and so
Thus, there is no net contribution to the total charge, Q, from the ends (z = 0 and z = L) of the cylinder. This is true despite the fact that Eq. (87) holds only in an average sense: symmetry means that, although there is rippling of the ends of the crystal, there is no net strain in either end, which in turn means that there is no net stress on either end and hence no net electric displacement at either end. It follows, therefore, that Eq. (100) yields, in an average sense
Thus, again in an average sense
It follows from Eqs. (57), (58) and (81) that \((\varPhi |_{L} {-} \, \varPhi |_{0} )\) is directly proportional to V, provided є « 1. Because τγ is also directly proportional to V, it follows that τγ is directly proportional to \((\varPhi |_{L} {-} \, \varPhi |_{0} )\). It is convenient, therefore, to introduce another effective moment piezoelectric constant Em given by
The capacitance C of the crystal is given by
or since є « 1
where \(E_{Y} = {-} \, \partial V/\partial Y\), \(E_{Z} = {-}\partial V/\partial Z\) and V is given by Eq. (48).
We can write Eq. (105) as
The moment of compliance, \(C_{{\text{m}}}\) and the effective piezoelectric constants \(D_{{\text{m}}} {\text{ and }}E_{{\text{m}}}\) are defined by Eqs. (75), (89) and (106), respectively. They can, therefore, be determined, in principle, from the fundamental elastic and piezoelectric constants of the crystal as well as its dimensions \(\left( {R{\text{ and }}L} \right).\) It is more convenient, however, to determine Cm, Dm and Em from the resonant and anti-resonant frequencies of the crystal in vacuo instead. The capacitance C is defined by Eq. (108) and can, therefore, be determined from the fundamental crystal constants (now also including \(\varepsilon_{1} {\text{ and }}\varepsilon_{3}\)) and the size of the crystal. It is more convenient, however, to determine C from the overall electrical properties of the crystal instead.
4 System Mechanics
For torsional motion of a cylinder in a fluid, Eq. (72) must be modified using Eq. (21) to yield
where M is given in Eq. (90).
Substitution of Eq. (1) into Eq. (110) yields
where
When the transient that occurs on start-up of the crystal has decayed, the solution of Eq. (111) is
where
so that
For practical viscometers, \(\left( {k{/}\rho_{{\text{c}}} I} \right) \, \ll \, 1\) so (\(b/\omega \, a) \, = \, \left( {k/\left( {\rho_{{\text{c}}} I{ + }k} \right)} \right) \, \ll \, 1\) and so
Now, at \(z \, = \, 0,\) Eqs. (1) and (113) yield
and Eq. (114) yields
Hence
and
The current, A, is given by \(A \, = {\text{ d}}Q/{\text{d}}t\) with Q given by Εquation (109) and so
Putting
using Eqs. (32) and (33). Then Eqs. (120) and (121) become
and
Thus, eliminating \({M|_{L}}\) and \({M|_{0}}\)
and so, eliminating \(\left( {\partial \varPhi /\partial t} \right)|_{L}\)
while
Thus, the general equation for the current, Eq. (122), becomes
4.1 Crystal in Vacuo
For a crystal in vacuo, k = 0 and a = ρc I Cm, b = 0.
Thus,
and
Hence Eq. (130) becomes
or
Thus \(\left| A \right| \, \to \, \infty\) and resonance occurs when \(\omega \, = \, \omega_{{0{\text{R}}}}\) where \( \omega_{{0{\text{R}}}}\) is given by
which can, of course, be used to determine Cm. Also \(\left| A \right| \, \to \, 0\) and anti-resonance occurs when \(\omega \, = \, \omega_{{0{\text{A}}}}\) where \(\omega_{{0{\text{A}}}}\) is given by the solution of
If we let
then
The use of trigonometric relationships leads to
In practice, \(\Delta \omega_{0} \ll \, \omega_{{0{\text{R}}}}\) so, since \(\tan \left( x \right) \, = \, x{\text{ for }}x \, \ll \, 1\)
thus, Eq. (136) yields
whence, because \(\Delta \omega_{0} \ll \omega_{{0{\text{R}}}}\)
which can be used to determine the product \(D_{{\text{m}}} E_{{\text{m}}}\). We note that, although \(D_{{\text{m}}} {\text{ and }}E_{{\text{m}}}\) are not determined separately, it is only their product that is of relevance. We also note that it follows from Eq. (142) that \(\Delta \omega_{0} > \, 0\) so that \(\omega_{{0{\text{A}}}} > \, \omega_{{0{\text{R}}}}\).
4.2 Cystal in a Fluid
If there is fluid around the crystal, substitution of Eq. (142) into Eq. (130) yields
Now we can assume that near resonance in the fluid, \(\omega \, \sim \, \omega_{{0{\text{R}}}}\) so that \(\varGamma_{{\text{r}}} \ll \varGamma_{{\text{i}}} \sim {\pi \mathord{\left/ {\vphantom {\pi L}} \right. \kern-\nulldelimiterspace} L}\). Expanding \(\tanh \left({\nicefrac{1}{2} \, \varGamma \, L} \right)\) yields
Since \(\varGamma_{{\text{r}}} \ll \varGamma_{{\text{i}}} \sim {\pi \mathord{\left/ {\vphantom {\pi L}} \right. \kern-\nulldelimiterspace} L}\) it follows that
But Eqs. (112), (117) and (135) yield
so, if
it follows that
Thus Eq. (145) yields
and, since \(\varGamma_{{\text{r}}} \ll \, \varGamma_{{\text{i}}} \sim \, \pi \, / \, L, \, \left| {\Delta \omega } \right|/\omega_{{0{\text{R}}}} \ll \, 1{\text{ and }}\left( {k/\rho_{{\text{c}}} I} \right) \, \ll \, 1\)
expanding \(\text{tanh}(\varGamma L)\)
since \(\tan \, \left( {\pi \, + \, x} \right) \, = \, \tan \left( x \right).\)
Now, because \(\varGamma_\text{r} \ll \, \varGamma_\text{i} \sim \, \pi /L, \, \left| {\Delta \omega } \right|/\omega_{0R} \ll \, 1{\text{ and }}\left( {k/\rho_{c} I} \right) \, \ll \, 1\)
and so, to leading order
Thus Eq. (143) becomes
where
It follows from Eq. (123) that
and from Eq. (146) that \(\varGamma_{{\text{r}}} \ll \, \varGamma_{{\text{i}}} \sim \, \omega {/}\left( {\omega_{0R} L} \right){\text{ so }}Z_{2} / \, Z_{1} \sim \, k\omega^{2} RC_{{\text{m}}} /\left( {\omega /\left( {\omega_{0R} /L} \right)} \right).\) But \(\omega \, \sim \, \omega_{{0{\text{R}}}}\) so, using Eq. (135), it follows that \(Z_{2} /Z_{1} \sim \, kR \, /\left( {\rho_{{\text{c}}} IL} \right).\) Hence, because \(k/\left( {\rho_{{\text{c}}} I} \right) \, \ll \, 1{\text{ and }}R/L \, \ll \, 1{\text{ or }}\sim \, 1\) in practice, it follows that \( \, Z_{2} /Z_{1} \ll \, 1.\) Thus, to leading order
and so
Put
where from Eq. (123)
Because \(Z_{1} = \, \varGamma_{{\text{i}}} {/}\left( {\omega C_{{\text{m}}} } \right){\text{ since }}\varGamma_{{\text{r}}} \ll \, \varGamma_{{\text{i}}} \sim \, \pi /L\), it follows that Z1 is real to leading order and hence
For an electrical circuit comprising a capacitance, C1, in parallel with a series combination of a resistance R2, an inductance, L2 and a capacitance C2, an applied potential \(V \, = \, V_{0} \exp \left( {i\omega t} \right)\) gives the total current A through the whole electrical circuit as
Comparison of Eqs. (153) and (160) with Eq. (161) reveals the following equivalences
If we let
then the impedance, \(Z\), is
and finally
If the crystal in the fluid is balanced in a bridge circuit by a variable resistance R* in parallel with a variable capacitance C* then an applied potential V gives a current V/R* in the resistance and a current V i ω C* in the capacitance. Thus, the impedance Z* is given by
If the bridge is balanced, then \(Z^* \, = { Z}\) and so Eqs. (167) and (168) yield
and
whence
Thus,
or
and
or
Note that the minimum value of the resistance, R*, with respect to frequency ω occurs when
and then
It follows from Eq. (165) that Σ vanishes at a frequency \(\omega \, = \, \tilde{\omega }\) given by
If \(\omega \, \ll \, \tilde{\omega }{\text{ or }}\omega \, \gg \, \tilde{\omega }{\text{ then }}\left| \varSigma \right| \, \gg \, R_{2}\) and it follows from Eqs. (173) and (175) that \(R^{*} \to \infty {\text{ and }}C^{*} = C_{1} {.}\)
When the crystal is immersed in a fluid, resonance is, in practice, defined to occur not when |A| is a maximum but when the balancing resistance \(R^{*}\) in the bridge circuit is a minimum. Using Eqs. (164), (165) and (175), it follows that resonance occurs when \( \, \omega \, = \, \omega_{{1{\text{R}}}} = \, \omega_{{0{\text{R}}}} + \, \Delta \omega_{1}\) where Δω1 is given by
or
which shows that \(\Delta \omega_{1} < 0\), so that \(\omega_{{1{\text{R}}}} < \omega_{{0{\text{R}}}}\). Also, since \(k/\left( {\rho_{{\text{c}}} I} \right) \, \ll \, 1{\text{ and }}\left( {R/L} \right) \, \ll \, 1{\text{ or }}\sim \, 1\) in practice, it follows that |Δω1| /ω0R \( \ll\) 1, as assumed originally, thus proving consistency. Substituting for k using Eq. (22) and for I using Eq. (73) yields
The term \(\left( {1 \, + \, \left( {R/L} \right)} \right)\) in Eq. (181) is a result of the two contributions to viscous drag on the crystal: the first from its curved surface at r = R and the second, a factor (R/L) of the size of the first, from its ends at \(z \, = \, 0{\text{ and }}z \, = \, L.\)
5 Working Equations for a Viscometer
In order to use the torsional quartz crystal as a viscometer it is necessary to explicitly relate the viscosity of the fluid surrounding the crystal to parameters of the resonance that can be measured with a small uncertainty and to the measurable physical characteristics of the crystal. When the idea of the viscometer was first proposed by electrical engineers, it was possible to attain the greatest relative precision in the measurement of the width of the resonant peak. However, we should also recognize that with modern instrumentation it is possible to achieve exceedingly high precision in the measurement of the resonant frequency itself so that we also consider first that quantity in devising a working equation for the viscometer. Subsequently we return to the bandwidth measurement to find a second working equation.
5.1 Working Equation for the Resonant Frequency with Only Viscous Losses
It follows from Eq. (181) and using Eq. (73) that the viscosity of the fluid, assuming that there are no losses in the system except viscous losses is given by
5.2 Working Equation for a Real Crystal
In a real crystal, there is bound to be non-viscous damping resulting from internal losses. In addition, there will inevitably be losses such as those arising from the crystal support.
As a result, Eq. (110) must be replaced by
where all non-viscous losses are accounted for in the damping coefficient, K, and all viscous losses are accounted for in k. The presence of non-viscous damping means that ω0R given by Eq. (135) is a theoretical quantity that cannot be measured directly and also cannot be determined from Eq. (135) since \(C_{{\text{m}}}\) is unknown. Thus \(\omega_{{0{\text{R}}}}\) is not the resonant frequency of the real crystal in vacuo: instead, resonance in vacuo must be defined to occur when the balancing resistance \(R^{*}\) in the bridge circuit is a minimum, just as it is for a crystal in a fluid. Henceforth, it is assumed that the crystal is a real one so that K ≠ 0 and, for clarity, all frequencies for the real system are denoted with a superscript *.
For the real crystal in vacuo then k = 0 and it follows by analogy with Eq. (180) that
where \(\omega_{0R}\) is given by Eq. (135) and it follows that
If the crystal is in a fluid, then k ≠ 0 and it follows by analogy with Eq. (180) that
where \(\omega_{{0{\text{R}}}}\) is again given by Eq. (135) and it follows that
Because any well-designed viscometer would ensure that \(K \, \ll {\text{ or }}\sim \, k\), it follows that \(K/\left( {\rho_{{\text{c}}} I} \right) \, \ll \, 1\) and so it follows from Eqs. (184) and (186) that \(\omega_{{0{\text{R}}}}^{*}\) is slightly lower than \(\omega_{{0{\text{R}}}}\) and that in turn, \(\omega_{{1{\text{R}}}}^{*}\) is slightly lower than \(\omega_{{0{\text{R}}}}^{*}\) It follows from Eqs. (185) and (187) that
from which it follows using Eqs. (22) and (73) that
This cannot be used as a working equation for the viscometer as it stands because it still contains \(\omega_{{0{\text{R}}}}\) which cannot be measured directly.
No electrical power is dissipated in the capacitance \(C^{*}\) in the bridge circuit provided it is a pure capacitance: the power, P, is dissipated only in the resistance \(R^{*}\) and is given in terms of the root-mean-square voltage \(V_\text{{{{rms}}}}\) and root-mean-square current \(A_{{{\text{rms}}}}\) by
and it follows from Eq. (45) that
At resonance, \(R^{*}\) is given by Eq (177) and so the electrical power at resonance when the crystal is in vacuo \(P_{{0{\text{R}}}}\) or in a fluid \(P_{{1{\text{R}}}}\) is given by
where the value of the resistance, R2 is, of course, different when the crystal is in vacuo from when it is in a fluid.
The bandwidth \(B_{0}^{*}\) for the crystal in vacuo is the difference between the two frequencies \(\omega_{{{0 + } }}^{*} \, \left( { > \, \omega_{{0{\text{R}}}}^{*} } \right){\text{ and }}\omega_{{{{0{-}}} }}^{*} \, \left( { < \, \omega_{{0{\text{R}}}}^{*} } \right)\) where the power is (arbitrarily but conventionally) \({{P_{{0{\text{R}}}} } \mathord{\left/ {\vphantom {{P_{{0{\text{R}}}} } 2}} \right. \kern-\nulldelimiterspace} 2}\): it is related to the quality factor \(Q_{0}^{*}\), where it is assumed that \(Q_{0}^{*} \gg 1\), by
Similarly, the bandwidth \(B_{1}^{*}\) for the crystal in a fluid is the difference between the two frequencies \(\omega_{1 + }^{*} \, \left( { > \, \omega_{{1{\text{R}}}}^{*} } \right){\text{ and }}\omega_{1 - }^{*} \, \left( { < \, \omega_{{1{\text{R}}}}^{*} } \right)\) where the power is \( P_{{1{\text{R}}}} /2\): it is related to the quality factor \(Q_{1}^{*} {,}\) where it is assumed that \(Q_{1}^{*} \gg 1\), by
Thus, if \(P \, = \, P_{0 \pm } = \, \nicefrac{1}{2} \, P_{{0{\text{R}}}}\) when \(\omega^{*} \, = \, \omega_{0 + }^{*} {\text{ or }}\omega^{*} = \, \omega_{0 - }^{*}\) and \(P \, = \, P_{1 \pm } = \, \nicefrac{1}{2} P_{{1{\text{R}}}}\) when \(\omega^{*} \, = \, \omega_{1 + }^{*} {\text{ or }}\omega_{{}}^{*} \, = \, \omega_{1 - }^{*}\)
and so
and the current \(A_{{{\text{rms}}}}\) is a factor of \(\left( {{1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-\nulldelimiterspace} {\sqrt 2 }}} \right)\) smaller than its value at resonance. Hence, using Eq. (173)
For notational convenience, let \(\omega_{0 \pm }^{*}\) denote \(\omega_{0 + }^{*} {\text{ or }}\omega_{0 - }^{*} \, \) and let \(\Delta \omega_{0 \pm }^{*}\) denote \(\Delta \omega_{0 + }^{*} {\text{ or }}\Delta \omega_{0 - }^{*}\) where
and
so that, combining Eqs. (198) and (199)
Then, using Eqs. (164) and (165) with k replaced by K because k = 0 when the crystal is in vacuo,
Using Eqs. (135) and (146) with k replaced by K and noting that \(\varGamma_{{\text{r}}} \ll \, \varGamma_{{\text{i}}}\), it follows from Eq. (155) that
so, using Eq. (73) and since \(K \, /\left( {\rho_{{\text{c}}} I} \right) \, \ll \, 1\)
Using Eqs. (112), (117) and (73) with k replaced by K
whence, using Eq. (135)
Thus, since \(\omega_{0 \pm }^{*} \, = \, \omega_{{0{\text{R}}}}^{*}\) to leading order
and
Thus Eq. (201) becomes, using Eq. (73)
whence
so \(\Delta \omega_{0 \pm }^{*} \, \le \, 0{\text{ and }}\left| {\Delta \omega_{0 \pm }^{*} } \right| \, /\omega_{{0{\text{R}}}}^{*} \, \ll \, 1\) since \(K/\left( {\rho_{{\text{c}}} I} \right) \, \sim \, K/\left( {\rho_{{\text{c}}} R^{4} } \right) \, \ll \, 1\) so \(\omega_{0 \pm }^{*} \, = \, \omega_{{0{\text{R}}}}^{*}\) to leading order (proving consistency). It follows that
which can be rearranged to give
which can be used to determine K. Note that it follows from Eq. (193) and Eq. (211) that \(Q_{0}^{*} \sim \, \rho_{{\text{c}}} R^{4} /K \, \gg \, 1\), as assumed (proving consistency).
If the crystal is immersed in a fluid, then K is replaced by (k + K), \(B_{0}^{*}\) is replaced by \(B_{1}^{*}\) and \(\omega_{{0{\text{R}}}}^{*}\) is replaced by \(\omega_{{1{\text{R}}}}^{*}\) in Eqs (210) and (211). Hence
and
whence, eliminating K using Eq. (211)
It follows from Eq. (214) using Eq. (22) that to leading order
Note that Eq. (215) is, like Eq. (182), similar in form to Eq. (189). However, unlike Eq. (182), Eq. (215) is a practical working equation for viscosity since it does not involve the experimentally inaccessible \(\omega_{{0{\text{R}}}}\): all parameters on the right-hand side of Eq. (215) can be measured directly. An alternative form of Eq. (215) can be obtained by noting that the mass of the crystal, \(M_{{\text{c}}}\), is given by
and the total surface area of the crystal (including its ends) \(S_{{\text{c}}}\) is given by
Thus, it follows from Eq. (215) that
Note that it follows from Eqs. (194) and (214) using Eq. (22) that \(Q_{1}^{*} \, \sim \, \rho_{{\text{c}}} R \, /\sqrt {\rho \, \mu \, /\omega_{{0{\text{R}}}}^{*} }\) so the fact that \({{\Delta \omega_{{0}} } \mathord{\left/ {\vphantom {{\Delta \omega_{{0}} } {\omega_{{{\text{0R}}}} }}} \right. \kern-\nulldelimiterspace} {\omega_{{{\text{0R}}}} }} \ll 1{\text{ and }}{{\Delta \omega_{1} } \mathord{\left/ {\vphantom {{\Delta \omega_{1} } {\omega_{{{\text{1R}}}} }}} \right. \kern-\nulldelimiterspace} {\omega_{{{\text{1R}}}} }} \ll 1 \, \) implies that the resonant frequencies of the crystal in vacuo and in a fluid are not very different and in turn that \(Q_{1}^{*} \gg \, 1,\) as assumed (proving consistency). Moreover, it is clear that \(Q_{0}^{*} \, > \, {Q_{1}^{*}}{\text{ so }}Q_{0}^{*} \, \gg \, 1\), as assumed (again proving consistency). As a result, it follows that the conditions under which Eq. (218) holds are precisely the same as those under which Eq. (189) holds. In addition, however, in order not to compromise the accuracy with which viscosity can be measured, it is necessary that:
Note that K can be eliminated between Eqs. (185) and (211) using Eq. (73) to yield
so ω0R can be eliminated from Eq. (189) to yield
or
This is a working equation for the viscosity in terms of resonant frequencies in which all terms on the right-hand side can be measured directly.
6 Effects of Departures from the Ideal Model of the Viscometer
We have already considered the major departure of the viscometer from the ideal model of it by allowing there to be losses in the crystal itself and its support. However, there are several other possible effects which we should consider in order either to be able to apply a correction to the working equations for the viscometer or to render them negligible by design.
6.1 Ellipticity
It is always possible that the quartz crystal departs from the exact cylindrical shape assumed. Thus, we suppose the quartz crystal is a right cylinder of (weakly) elliptical (as opposed to circular) cross-section with major (or respectively minor) radius A and minor (or respectively major) radius B (thus A = R = B if the crystal is of circular cross-section). In cylindrical polar coordinates {r,θ,z}, the surface of the crystal is defined by
where the radius A is oriented at an angle Θ to the Y-direction.
We define the ellipticity, e, as
where |e| « 1 and e = 0 corresponds to a crystal of circular cross-section. Now consider two identical crystals of (weakly) elliptical cross-section, the first with B < A and
so that
and the second (the same as the first but with the major and minor radii rotated by ± ½ π) with A < B and
so that
If the two crystals are surrounded by the same fluid with all conditions identical, other than the reciprocal orientations of the major and minor radii, then the two systems are entirely equivalent and have identical resonant frequencies \(\omega_{{0{\text{R}}}}^{*} {\text{ and }}\omega_{{1{\text{R}}}}^{*} .\) Since |e| « 1, we assume that \(\omega_{{\# {\text{R}}}}^{*}\) (where # = 0 or 1) can be expanded in a power series as follows
Clearly, \(\omega_{{0{\text{R0}}}} = \omega_{{0{\text{R}}}}\) and \(\omega_{{1{\text{R0}}}} = \omega_{{1{\text{R}}}}\) for a crystal of circular cross-section. Expanding \(\omega_{{\# {\text{R}}}}^{*}\) using Eq. (226) yields
and expanding \(\omega_{{\# {\text{R}}}}^{*}\) using Eq. (228) yields
whence, equating coefficients of like powers of \(e^{*}\), Eqs. (230) and (231) together yield
This implies that ellipticity (ie non-circularity) has no effect on the resonant frequencies to first order, i.e. O(e): the only effect of ellipticity is at higher order. Note that, conventionally, the eccentricity \(e^{{{\text{cc}}}}\) of an ellipse is defined as
where B < A to give a real value of ecc. Clearly, ecc is related to e as follows
but use of the ellipticity instead of the eccentricity greatly simplifies the reciprocity argument. It is generally possible to arrange that the ellipticity of a crystal is such that its effect can be rendered negligible.
6.2 Surface Roughness
Various causes, such as the crystal production or the way the electrodes are attached to the crystal, may mean that the surface of the crystal is not perfectly smooth. If the surface roughness is characterized by a linear dimension lr (where \(l_{{\text{r}}} \ll R\)) then, in order that roughness does not have a significant effect on the behavior of the crystal, it is necessary that the roughness is insignificant compared with the shear layer thickness d, i.e.
It is a matter of manufacture and design to ensure that this condition is met. Table 2 shows that if the roughness is at the level of optical wavelengths (\(0.5\mu {\text{m}}\)), then for typical crystals used and for the fluids usually studied to date \(l_{{\text{r}}} \sqrt {(\rho \omega_{0R} )/\mu } \sim 10^{ - 1} - 10^{ - 2}\).
6.3 Containing Vessel
The crystal is immersed in a fluid, the viscosity of which is to be determined and the fluid must be held within a vessel (perhaps pressurized). If \(L^{*}\) denotes the typical distance between the wall of the containing vessel and all surfaces of the crystal (\({\text{at }}r \, = \, R{\text{ and at }}z \, = \, 0{\text{ and at }}z \, = \, L\)) then the presence of the walls of the containing vessel does not significantly interfere with the behavior of the crystal if the thickness, d, of the shear layer is very small compared with \(L^{*}\) i.e. if \(d{ / }L^{*} \, \sim \, \left( {R/ \, L^{*} } \right)/\sqrt \varOmega \, \ll \, 1\) i.e.
since \(\sqrt \varOmega \, \gg \, 1\). This can readily be achieved by a suitable design.
6.4 Variable Fluid Properties
The viscosity, μ, and density, ρ, both vary with pressure, p, and temperature, T. As already noted, the flow induces pressure fluctuations in the fluid of order \( \rho {\omega^{2}} {\varepsilon^{2}}R^{2}\) so the effect of pressure variations on the measured viscosity, μ, is negligible provided
and the effect of pressure variations on the density is negligible provided that
and provided the Mach number Ma « 1, as already noted.
For an imposed (or adventitious) temperature difference ΔT* in the system, the effect of temperature variations on the viscosity is negligible provided that
and the effect of temperature variations on the density, ρ, is negligible provided that
Here, \(\left| {\partial \mu /\partial p} \right|, \, \left| {\partial \rho /\partial p} \right|, \, \left| {\partial \mu /\partial T} \right|{\text{ and }}\left| {\partial \rho /\partial T} \right|\) are all evaluated at the ambient temperature of the fluid. Table 2 shows these conditions are easily satisfied.
6.5 Decay of Initial Transient
In order for the transient that occurs on start-up of the flow to decay sufficiently for Eq. (5) to hold, a time t* must elapse that is much larger than the characteristic time, (d2 ρ/μ) for a shear wave to propagate through the shear layer of thickness d. Since \(d \, \sim \, R/\sqrt \varOmega\) where Ω is given by Eq. (10), the start-up transient has decayed sufficiently if
Again, this is a condition easily satisfied in practice as Table 2 shows.
6.6 Edges
The moments \(M\left| {_{L}\,{\text{and}}\,M} \right|_{0}\) exerted on the ends of the crystal by the fluid are given by Eqs. (32) and (33) respectively, assuming that rippling of the ends of the crystal at z = 0 or z = L has a negligible effect. An additional correction should, however, be made in the vicinity of what might be termed the edges of the cylinder where r = R and z = 0 or z = L. The shear stress exerted by the crystal on the fluid σrθ is given by Eq. (18) in the region where 0 ≤ z ≤ L and r = R. The shear stress exerted by the crystal on the fluid σzθ is given by Eq. (30) in the region where z =L and 0 ≤ r ≤ R. At the edge at z = L and r = R, Eqs. (18) and (30) can be combined to give
where n denotes the outer normal to the surface of the crystal. Clearly, Eq. (242) also holds at the other corner at z = 0 and r = R. Thus, the shear stress σnθ|R,L giving rise to the moment and hence the loading by the fluid on the cylinder is continuous over the entire the surface of the cylinder, though its gradient is discontinuous at the edges. Moreover, \(\sigma_{n\theta } |_{R,L} \sim \, \mu \omega \varepsilon \sqrt \varOmega\) so the thickness of the shear layer \(d \, \sim \, R/\sqrt \varOmega \, \ll \, 1\) everywhere on the crystal. Thus, although nothing has been deduced about the matching region that must exist in the vicinity of the edges, the extent of that matching region must be O(d) in both the r- and z-directions. Thus, the overall effect of the corners is negligible provided \(d \, \ll \, R{\text{ and }}d \ll \, L\) which is guaranteed if \( \, \sqrt \varOmega \, \gg 1\) and \(R/L \, \ll \, 1{\text{ or }}\sim \, 1\).
6.7 Standing Waves
Standing (acoustic) waves can arise if any of the overall dimensions of the system (\(2R,L{\text{ and }}L^{*}\)) is an integer multiple of half of the wavelength \(\lambda^{\prime}\) of the torsional oscillations of the crystal. Now \(\lambda^{\prime} = \, 2\pi \, c/\omega_{1R}\) (where c is the speed of sound) so, if \(L^{\prime}\) denotes \(2R,L{\text{ and }}L^{*}\), standing waves can be avoided if, for all integer n
But \(\omega_{{1{\text{R}}}} = \, \omega_{{0{\text{R}}}} + \, \Delta \omega_{1}\) so, substituting from Eq. (181) for Δω1, standing waves can be avoided if, for all integer n
Careful operation can secure this condition.
6.8 Viscous Dissipation
The power dissipated by viscous action Pv is given by the time-average over a cycle of oscillation of the integral over the total surface area of the crystal of the product of the real part, denoted \(R()\), of the speed uθ of the cylinder and the real part of the shear stress exerted by the fluid on the cylinder –σrθ on the curved surface of the cylinder or –σzθ on the two planar ends of the cylinder. Over the curved surface of the cylinder 0 ≤ z ≤ L and r = R, it follows from Eq. (18) that
and it follows from Eq. (24) that
Similarly, over the planar surface of the cylinder at 0 ≤ r ≤ R and z = 0 or z = L, it follows from Eq. (24) that
and it follows from Eq. (30) that
Thus, the time-varying power Pv(t) is given by
so the time averaged power is
The term \(\left[ {1 \, + \, \nicefrac{1}{2}\, \left( {R \, / \, L} \right)} \right]\) in Eq. (250) is a result of two contributions to the viscous dissipation at the surface of the crystal: the first from its curved surface at r = R and the second, a factor ½ (R/L) of the size of the first, from its ends at z = 0 and z = L. For typical crystals the total dissipation amounts to \(\sim 10^{ - 9} {\text{ W}}\).
To obtain an upper limit of the effect of this power it can be assumed that this amount is dissipated in the thin fluid shear layer of thickness d at the surface of the cylinder and nowhere else. In which case, the temperature rise of the fluid per unit time, \(\left( {{{{\text{d}}T} \mathord{\left/ {\vphantom {{{\text{d}}T} {{\text{d}}t}}} \right. \kern-\nulldelimiterspace} {{\text{d}}t}}} \right)_{{{\text{visc}}}}\) in that layer caused by this amount of heat is given approximately by
This amounts to approximately \(2 \times 10^{ - 7} {\text{K s}}^{ - 1}\) for liquid Hexane in a typical installation. For the dilute gas state of Methane, the equivalent calculation leads to a rate of temperature rise of \(3 \times 10^{ - 6} {\text{ K s}}^{ - 1}\). In neither case would such a rise lead to significant changes in the properties of the fluid being measured.
7 Conclusions
The rigorous analysis of the torsional quartz crystal viscometer presented here has enabled us to derive two working equations for the measurement of the viscosity of a fluid surrounding the crystal from parameters that can be determined with high precision using modern instrumentation. The first equation which uses measured bandwidths, \(B_{j}^{*}\) and resonant frequencies, \(\omega_{{j{\text{R}}}}\)
has often been employed [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,17]. The second equation, which uses resonant frequencies only, is
Both working equations are valid subject to a number of clear criteria which can be satisfied by appropriate and practical design of the instrument. In Part II of this work [19] we examine the two working equations with respect to the detailed and careful experimental work of three groups who have employed the torsional crystal oscillator for measurements of the viscosity of fluids in both gaseous and liquid states.
Availability of Data and Material
The paper contains no new data, and all material is freely available.
References
W.P. Mason, Trans. ASME 69, 359 (1947)
W.P. Mason, J. Coll. Sci. 3, 147 (1948)
W.P. Mason, W.O. Baker, H.J. McSkimin, J.H. Heiss, Phys. Rev. 75, 936 (1949)
B. Welber, S.I. Quimby, Phys. Rev. 107, 645 (1957)
P.E. Rouse, Jr., E.D. Bailey and J.A. Minkin,, Laboratories of the Franklin Institute Report 2048, presented to the Symp. Anal. Research, Am. Petroleum Institute, Cleveland, Ohio (1950)
R.W.H,. Webeler, PhD Thesis, University of Cincinatti, U.S.A (1961)
R.W.H. Webeler and D.C. Hammer NASA Technical Note TN-D-4381 (1968)
A.F. Collings, E.D. McLaughlin, Trans. Faraday Soc. 61, 340 (1971)
D.E. Diller, J. Chem. Phys. 42, 2089 (1965)
W.M. Haynes, Physica 67, 440 (1973)
D.E. Diller, N.V. Frederick, Int. J. Thermophys. 10, 145 (1989)
A. Laesecke, K. Meier, R.F. Hafer, J. Mol. Liq. 251, 128 (2018)
A. De Bock, W. Grevendonk, H. Awouters, Physica 34, 49 (1967)
B.P. D’yachenko, translated from Izmerit. Tekh. No. 8, 78 (1970)
A.J. Barlow, G. Harrison, J. Richter, H. Seguin, J. Lamb, Lab. Practice (London) 10, 786 (1961)
K. Meier, Observation and Modeling of Polar Fluid Behavior in a Torsionally Oscillating Crystal Viscometer Study Thesis (Universität Hannover, FRG, 1994).
B. Junker, K. Meier, J. Appl. Phys. 128, 044505 (2020)
B. Junker, K. Meier, (Private Communication) 2020
S.M. Richardson and W.A. Wakeham, Int. J. Thermophys. (To be published) 2021
M. Abramowitz and I.A. Stegun, Eds., Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables (Dover, 1965)
H. Kinizuka, S. Oguba, J. Li, Y. Shibutani, Phys Rev B 75, 054109 (2007)
Acknowledgements
The authors are grateful to Arno Laesecke, Carlos Castro, Fernando Santos, Dwain Diller, Karsten Meier and Clemens Junker for discussions over many years that have encouraged us to continue with this work and also to many of them for the provision of their experimental data.
Funding
This work was not funded by any external source.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
There are no known conflicts or competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wakeham, W.A., Richardson, S.M. The Torsional Quartz-Crystal Viscometer. Int J Thermophys 42, 120 (2021). https://doi.org/10.1007/s10765-021-02807-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10765-021-02807-y