1 Introduction

The diffraction-free propagation of surface acoustic waves around a spherical object, namely a steel ball bearing, was first generated and observed by the acousto-optical system [1] and analyzed [2] in the year 2000. Immediately after that, the ball SAW(surface acoustic wave) device by means of fabricating the interdigital transducers on a spherical solid was conceptualized and demonstrated [3, 4]. In the following years, a variety of gas sensors were developed by depositing various sensitive layers on the ball SAW device: a hydrogen gas sensor [5], an odor sensor [6], and a portable gas chromatograph [7]. Then it was accidentally found [8] that a very small amount of moisture in the ambient gas affected the acoustic properties of a SAW device made of a single-crystal quartz ball without any sensitive layers. It had been a mystery for a while how the surface of a single-crystal quartz was affected by the ambient moisture at room temperature, until a mechanism was eventually proposed that the surface of the particular quartz ball was damaged during the production process and a thin amorphous layer of silica was produced which captured water molecules resulting into the change of the acoustic properties. According to this hypothesis, a ball SAW device was fabricated by depositing a thin layer of amorphous silica using sol-gel method on a single-crystal quartz ball without a surface damage, and the detection of water molecules in the ambient \(\hbox {N}_{2}\) gas at densities far less that \(1~\upmu \hbox {mol}{\cdot } \hbox {mol}^{-1}\) was achieved [9]. Now it remains an unanswered question how the water molecules enter into the amorphous silica layer at room temperature.

2 Ball SAW Moisture Sensors

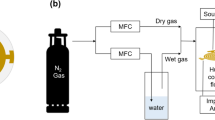
The design and fabrication of the ball SAW device for the moisture sensor is found in [9]. The water molecules in the ambient gas surrounding the ball SAW device somehow react with a thin layer of amorphous silica deposited on the spherical surface of the device. When the moisture density is low as \(1~\upmu \hbox {mol}{\cdot }\hbox {mol}^{-1}\), the phase velocity of the surface acoustic wave increases with the moisture density, which means that the amorphous silica film stiffens with moisture. When the moisture density further increases the phase velocity starts to decrease which can be explained by the standard model of mass loading effect on the surface acoustic waves [10]. In the following, we concentrate on the new phenomena, stiffening of the amorphous silica layer due to the ambient moisture in the low-density limit.

3 Thermodynamic Model

It is known [11] that the water molecules dissociate and the resultant \(\hbox {H}^{+}\) and \(\hbox {OH}^{-}\) chemically react with the network in silica glass at an elevated temperature as

$$\begin{aligned} (\hbox {bulk})\equiv \hbox {Si--O--Si}\equiv (\hbox {bulk})+\hbox {H}_{2}\hbox {O}< - > 2 \cdot (\hbox {bulk}) \equiv \hbox {Si-OH}\, . \end{aligned}$$
(1)

As an elementary process in the reaction described by Eq. 1, we start with a simple model of dissolving the “solutes” of \(\hbox {H}^{+}\) and \(\hbox {OH}^{-}\) into a “solvent” of amorphous silica and analyze the thermodynamics of the system. Let \(\hbox {H}_{2}\hbox {O}\) in the ambient gas and the dissociated \(\hbox {H}^{+}\) and \(\hbox {OH}^{-}\) dissolving in the matrix of silica are in the equilibrium as

$$\begin{aligned} \hbox {H}_{2}\hbox {O}< - >\hbox {H}^{+} +\hbox {OH}^{-} \end{aligned}$$
(2)

where the chemical potentials, \(\upmu \), for the constituents satisfy the equation

$$\begin{aligned} \upmu (\hbox {H}_{2}\hbox {O})=\upmu (\hbox {H}^{+})+\upmu (\hbox {OH}^{-})\, . \end{aligned}$$
(3)

Since we assume that the reaction is a simple dissociation, we propose that for each constituent

$$\begin{aligned} \upmu =\upmu _{0}{(T)}+k {T}\, \log ([\hbox {x}]), \end{aligned}$$
(4)

where T and [x] are the temperature and the density, respectively, of the constituent x, and k is the Boltzmann constant. T has the same value in all constituents in the equilibrium. By substituting Eq. 4 into Eq. 3, we have

$$\begin{aligned} \upmu _{0}(\hbox {H}_{2}\hbox {O})+k {T}\log ([\hbox {H}_{2}\hbox {O}])=\upmu _{0}(\hbox {H}^{+})+k {T}\log ([\hbox {H}^{+}])+\upmu _{0}(\hbox {OH}^{-})+k {T}\log ([\hbox {OH}^{-}]). \end{aligned}$$
(5)

Then

$$\begin{aligned}{}[\hbox {H}^{+}]{\cdot } [\hbox {OH}^{-}] / [\hbox {H}_{2}\hbox {O}]= \exp \{(\upmu _{0}(\hbox {H}_{2}\hbox {O})-\upmu _{0}(\hbox {H}^{+})-\upmu _{0}(\hbox {OH}^{-})) / k {T}\} . \end{aligned}$$
(6)

Assuming

$$\begin{aligned}{}[\hbox {H}^{+}]=[\hbox {OH}^{-}] \end{aligned}$$
(7)

Eq. 6 leads to following Eq. 8,

$$\begin{aligned}&\displaystyle [\hbox {H}^{+}]=[\hbox {H}_{2}\hbox {O}]^{1/2} {\cdot } \exp \{\Delta \upmu _{0}/2k {T}\}, \end{aligned}$$
(8)
$$\begin{aligned}&\displaystyle \hbox {where}\, \Delta \upmu _{0}=\upmu _{0}(\hbox {H}_{2}\hbox {O}) -\upmu _{0}(\hbox {H}^{+})-\upmu _{0}(\hbox {OH}^{-}) . \end{aligned}$$
(9)

4 Dependence on Moisture Density and Temperature

Let us look at the dependence on the moisture density. Maintaining the temperature at a constant value and changing the density of \(\hbox {H}_{2}\hbox {O}, [\hbox {H}_{2}\hbox {O}]\), in Eq. 8, the dependence of \([\hbox {H}^{+}]\) on \([\hbox {H}_{2}\hbox {O}]\) is

$$\begin{aligned} \log [\hbox {H}^{+}]~\sim ~(1/2) \log [\hbox {H}_{2}\hbox {O}]+\hbox {Const}. \end{aligned}$$
(10)

It seems reasonable to assume that the variation in the phase velocity of the surface acoustic wave is proportional to \([\hbox {H}^{+}]\) in its low-density limit; then the dependence of the phase velocity on the moisture \([\hbox {H}_{2}\hbox {O}]\) in the \(\hbox {N}_{2}\) carrier gas was measured to validate the model.

Fig. 1
figure 1

Delay time change versus trace moisture concentration at a constant temperature, \(21\,{^{\circ }}\hbox {C}\). The x and y coordinates are in logarithmic scale. The change in the delay time is linearly proportional to the trace moisture concentration in the logarithmic scale when it is small enough. The long-term fluctuation in the delay time measurement is \({\pm }0.05\) ppm, and a standard deviation of phase noise is 0.016 ppm as discussed in the text. The uncertainty in the trace moisture concentration is \({\pm }4\,\%\)

Full size image

4.1 Method of Measurements and its Uncertainty

The setup of experiment, the method of generating the trace moisture and its accuracy, and the procedure of the measurement were detailed in [12]. We generated the trace moisture in the \(\hbox {N}_{2}\) carrier gas by means of a diffusion tube method and measured the SAW delay time change which was negatively proportional to the phase velocity change of SAW. First, we consider the amount of uncertainty in the set values of trace moisture in the experiment. The amount of generated moisture was inversely proportional to the temperature of the diffusion tube [12]. The temperature of the diffusion tube was affected by the room temperature which fluctuated as large as \({\pm } 5\,{^{\circ }}\hbox {C}\). This led to an uncertainty of about \({\pm }2\,\%\). The generated humid \(\hbox {N}_{2}\) gas was mixed with a dry \(\hbox {N}_{2}\) gas by means of a mass flow controller to obtain a target humidity. The uncertainty due to the allowance of the mass flow rate was \({\pm }2\,\%\) according to the specification of the instrument. Hence, the accumulated uncertainty in the amount of generated moisture was estimated to be less than \({\pm }4\,\%\). Next, we consider the amount of uncertainty in the delay time measurement of SAW. The elasticity of single-crystal quartz depends on temperature. Thus, the amount of success in the temperature compensation was the most important factor affecting the uncertainty in the measurement of delay time change. Its procedure is described in depth in [12], and the uncertainty was estimated as low as \({\pm } 0.05\) ppm. Another factor affecting the delay time change was the presence of a jitter or a phase noise in the electronic circuitry. By observing the phase noise in the output signal from the instrument when the dry nitrogen gas was introduced into the sensor head, the standard deviation of the phase noise was estimated to be 0.016 ppm [12].

4.2 Result of the Measurement

Figure 1 shows the experimental dependence of delay time change on the trace moisture \([\hbox {H}_{2}\hbox {O}]\) in the \(\hbox {N}_{2}\) carrier gas. A detection limit is indicated in the plot which is three times the standard deviation of the phase noise: 0.016 ppm. Error bars in the plots are barely seen because the error due to the phase noise(0.016 ppm) was too small to be seen in the plot except for a few points where deviations due to the fluctuation in room temperature were not fully compensated. The experimental dependence was in good accordance with Eq. 10 at small values of \([\hbox {H}_{2}\hbox {O}]\). When \([\hbox {H}_{2}\hbox {O}]\) becomes larger, the experimental data deviate from the relationship in Eq. 10 and start to behave according to the familiar mass loading model [10]. This suggests that we are observing a new phenomenon of penetration of \(\hbox {H}^{+}\) and \(\hbox {OH}^{-}\) dissociated from water molecules into the amorphous silica layer at room temperature in the very low level of concentration, thanks to the very high sensitivity of ball SAW sensors.

Next, we examined the dependence on temperature. Maintaining the trace moisture density of \(\hbox {H}_{2}\hbox {O}, [\hbox {H}_{2}\hbox {O}]\) at a constant value, and changing the temperature, T, the dependence of \([\hbox {H}^{+}]\) on T is

$$\begin{aligned} \log [\hbox {H}^{+}]~\sim ~\Delta \upmu _{0}/2k {T}+\hbox {Const}. \end{aligned}$$
(11)

The absorption of gases by metals is described by Sievert’s law [13, 14]. Here we follow the line of thought and approximate the chemical potential for \(\hbox {H}_{2}\hbox {O}\) gas by that for the ideal gas,

$$\begin{aligned} \upmu _{0}(\hbox {H}_{2}\hbox {O})~\sim ~\varepsilon (\hbox {H}_{2}\hbox {O})+k {T} (\log \hbox {P} -5/2 \log {T}+\hbox {constant}), \end{aligned}$$
(12)

and the chemical potentials for the \(\hbox {H}^{+}\) and \(\hbox {OH}^{-}\) in the amorphous silica layer by

$$\begin{aligned}&\upmu _{0}(\hbox {H}^{+})~\sim ~\varepsilon (\hbox {H}^{+}),\end{aligned}$$
(13)
$$\begin{aligned}&\upmu _{0}(\hbox {OH}^{-})~\sim ~\varepsilon (\hbox {OH}^{-}). \end{aligned}$$
(14)

Substituting Eqs. 12–14 into Eq. 9, Eq. 8 results in

$$\begin{aligned}&\log [\hbox {H}^{+}]~\sim ~\Delta \varepsilon /2k {T} - 5/4 \log {T}+1/2 \log [\hbox {H}_{2}\hbox {O}]+\hbox {C},\end{aligned}$$
(15)
$$\begin{aligned}&\hbox {where}\, \Delta \varepsilon =\varepsilon (\hbox {H}_{2}\hbox {O}) -\varepsilon (\hbox {H}^{+})-\varepsilon (\hbox {OH}^{+}). \end{aligned}$$
(16)

Note that \(\Delta \varepsilon \) and C are independent of temperature and \(\hbox {H}_{2}\hbox {O}\) density. We obtained experimental data for this relationship; mean values of the measured delay time change at each set value of temperature for a constant trace moisture concentration, \(1~\upmu \hbox {mol}{\cdot } \hbox {mol}^{-1}\), are listed in Table 1. The standard deviation in the delay time change measurement was 0.016 ppm as already discussed above. The uncertainty in temperature was due to the limited accuracy of a Peltier device which controlled the temperature of the sensor unit [12]. The uncertainty in the temperature controlled by the Peltier device was \({\pm }0.1\,{^{\circ }}\hbox {C}\) according to the specification by the manufacturer. Figure. 2 shows the mean values with a fitted line according to the first term in the right-hand side of Eq. 15. It should be noticed that the experimental data in Fig. 2 are consistent with a positive value for \(\Delta \upmu _{0}\) in Eq. 11. This indicates that \(\hbox {H}^{+}\) and \(\hbox {OH}^{-}\) would like to be in the amorphous silica layer rather than in the ambient gas when the temperature goes down.

Table 1 Change in the delay time versus temperature at a constant trace moisture concentration, \(1~\upmu \hbox {mol}\,{\cdot }\,\hbox {mol}^{-1}\)
Full size table
Fig. 2
figure 2

Delay time change versus temperature at a constant trace moisture concentration, \(1~\upmu \hbox {mol}{\cdot } \hbox {mol}^{-1}\). The x coordinate is \({T}^{-1} [\hbox {K}^{-1}]\) and the y coordinate is logarithm of the delay time change in ppm. Each dot represents a mean value of the measured delay time change. The standard deviation of those measurements were 0.016 ppm, and the uncertainty in temperature was \({\pm }0.1\,{^{\circ }}\hbox {C}\)

Full size image

5 Discussion

It was shown that a simple model of dissociation of \(\hbox {H}_{2}\hbox {O}\) and dissolution of the resultant \(\hbox {H}^{+}\) and \(\hbox {OH}^{-}\) into the matrix of amorphous silica leads to a strikingly good agreement with experimental dependences on the moisture density as shown in Fig. 1 and on the temperature as shown in Fig. 2. Based on Eq. 8, we are developing a calibration method to compensate for the deviations in both temperature and materials characteristics of the ball SAW device during the ultrasensitive moisture measurement. The calibration method and its experimental validation will be reported in a separate paper.

The simple thermodynamic model presented in this paper is a phenomenological one where we have neglected the mechanism how the \(\hbox {H}^{+}\) and \(\hbox {OH}^{-}\) react with the network of amorphous silica which is an important process for the stiffening of the amorphous silica layer. It was suggested [11] that the water molecules dissociate and the resultant \(\hbox {H}^{+}\) and \(\hbox {OH}^{-}\) chemically react with the network in silica glass at an elevated temperature as in Eq. 1. Recently, it was pointed out by simulation [15] and experiments [16] that the chemical reaction described by Eq. 1 does occur at room temperature. The combination of these studies with our theoretical and experimental work will be an important step toward the understanding of the reaction of water molecules with the amorphous silica surface at room temperature in the very low water molecule density.

6 Conclusion

It was shown in this paper that a very small amount of moisture at less than \(1~\upmu \hbox {mol}{\cdot } \hbox {mol}^{-1}\) in the ambient \(\hbox {N}_{2}\) gas was measured by a ball SAW moisture sensor. The paper proposed a mechanism to understand how the water molecules in the ambient gas affected the surface of the sensor made of single-crystal quartz with a thin layer of amorphous silica. Experimental data were found in a good agreement with a thermodynamic consideration of the physical model of the measurement. But the model was empirical one, and a further study based on the atomistic model will be necessary for sufficient understanding of the phenomena. The adsorption and absorption of water molecules into silica glass have been a subject of materials research for decades, but most research focused on a substantial amount of water at an elevated temperature. Only recently, a few papers came to appear discovering and simulating the water molecules chemically bonding to the network of silicon and oxygen at the surface of silica glass at room temperature. The authors hope that the present paper paves a way to the research on the behavior of water molecules less than a monolayer thick on the surface of silica glass at room temperature.