Abstract
Modern studies of animal movement use the Global Positioning System (GPS) to estimate animals’ distance traveled. The temporal resolution of GPS fixes recorded should match those of the behavior of interest; otherwise estimates are likely to be inappropriate. Here, we investigate how different GPS sampling intervals affect estimated daily travel distances for wild chacma baboons (Papio ursinus). By subsampling GPS data collected at one fix per second for 143 daily travel distances (12 baboons over 11–12 days), we found that less frequent GPS fixes result in smaller estimated travel distances. Moving from a GPS frequency of one fix every second to one fix every 30 s resulted in a 33% reduction in estimated daily travel distance, while using hourly GPS fixes resulted in a 66% reduction. We then use the relationship we find between estimated travel distance and GPS sampling interval to recalculate published baboon daily travel distances and find that accounting for the predicted effect of sampling interval does not affect conclusions of previous comparative analyses. However, if short-interval or continuous GPS data—which are becoming more common in studies of primate movement ecology—are compared with historical (longer interval) GPS data in future work, controlling for sampling interval is necessary.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Understanding how animals interact with and move through their environment enables researchers to better understand animal behavior, physiology, and ecology (Getz and Saltz 2008; Nathan et al. 2008). Modern studies of animal movement use the Global Positioning System (GPS) to estimate animals’ travel distance over a given time period. Researchers record GPS fixes at intervals along the journey of a focal animal or group— either using a handheld GPS (Santhosh et al. 2015; Schreier and Grove 2010), or by attaching a GPS logger to a focal animal (Hampson et al. 2010a,b; Ren et al. 2008)—and sum the distances traveled between GPS fixes. More refined estimates of distance traveled are also possible; for example, modeling movement as a continuous-time stochastic process minimizes the effects of position and velocity autocorrelation that are inherent in such data (Calabrese et al. 2016).
Recording of GPS at intervals in time (rather than continuously) is common because it saves battery life and allows researchers to increase the time over which data are collected (Mitchell et al. 2019; Ryan et al. 2004; Sahraei et al. 2017). However, this practice underestimates travel distance (McGavin et al. 2018; Sennhenn-Reulen et al. 2017). For example, a study of Guinea baboons (Papio papio) (Sennhenn-Reulen et al. 2017) examined differences in travel distance estimates from 2-h periods by subsampling GPS data collected at one fix per second, finding that travel distances were significantly shorter if less frequent GPS fixes were used in calculations. Indeed, extensive theoretical and empirical work has shown that the temporal resolution of GPS fixes needs to match those of the behavior of interest; otherwise estimates are likely to be inappropriate (Borger et al. 2006; de Weerd et al. 2015; Ganskopp and Johnson 2007; Johnson and Ganskopp 2008; McGavin et al. 2018; Mills et al. 2006; Mitchell et al. 2019; Noonan et al. 2019; Postlethwaite and Dennis 2013; Rowcliffe et al. 2012; Sennhenn-Reulen et al. 2017; Swain et al. 2008; Tanferna et al. 2012).
Here, we estimate daily travel distances for chacma baboons (Papio ursinus) using GPS data collected at one fix per second synchronously for 12 adult individuals over 11–12 days. By sampling different temporal resolutions from this high-frequency GPS data set, we investigate the relationship between estimated travel distances and GPS sampling frequency (Sennhenn-Reulen et al. 2017). Then, we use the quantified relationship between estimated travel distance and GPS sampling interval to recalculate published baboon daily travel distances (e.g., Dunbar 1992; Johnson et al. 2015) and see how estimates alter when accounting for the relationship between estimated distance and GPS sampling interval found in our own data set.
Methods
Study System
We studied wild adult chacma baboons in the Da Gama group in Cape Town, South Africa (34.1617° S, 18.4054° E). The group’s home range includes urban areas comprising residential suburbs and natural areas that fall mostly within Table Mountain National Park which are dominated by indigenous fynbos vegetation with smaller patches of exotic vegetation (Hoffmann and O’Riain 2012). The Mediterranean climate of the Cape Peninsula is characterized by hot dry summers and mild winters with moderate–high rainfall (Hoffman and O’Riain 2012), and in this study we use GPS data collected during winter (August) of a field season lasting from July to November 2018. The Da Gama group comprised 2 adult males, 19 adult females, and ca. 30 subadults, juveniles, and infants.
Movement Data
During the field season, we recorded GPS data for 13 individuals (2 males, 11 females) for a mean ± SD of 42.77 ± 9.92 days, range = 21–54 days (Bracken et al. in press) using in-house assembled SHOALgroup collars (F2HKv3) containing GiPSy 5 GPS loggers (TechnoSmArt, Italy) recording GPS fixes at 1-s sampling intervals between 06:00:00 and 18:00:00 UTC (Bracken et al. in press). Here we use a subset of these GPS data that provide continuous data for 12 baboons (2 males, 10 females) for 11–12 days in August 2018, representing 143 daily travel distances.
Before calculating daily travel distances (below), we removed erroneous GPS fixes outside the study area, or successive GPS fixes between which it would have been impossible for the baboons to travel (Bracken et al. in press). These fixes represented a median 0.01% of GPS fixes per collar (range 0.00%–0.01%) and the remaining missing or removed fixes that lasted a time period of less than or equal to 10 s, were interpolated using the fixLocNA function in the swaRm package (Garnier 2016) following O'Bryan et al. (2019) and Bracken et al. (in press). This resulted in a median 0.01% of each baboon’s tracks being interpolated (range 0.00%–0.01%). Remaining missing fixes lasting >10 s represented a median 0.56% per collar (range 0.00%–1.61%).
Daily Travel Distances
To investigate the effect of GPS sampling interval on estimated daily travel distance, we subsampled the high-frequency GPS data and calculated travel distances for each baboon, for each day, using GPS fixes set at 1 s, 30 s, 60 s, 300 s, 1200 s, 3600 s, and 7200 s. We estimated daily distance by summing distances between GPS fixes and used fixed time intervals from the 1 s data set, since we wanted to simulate different programmed sampling intervals used by on-animal GPS loggers.
Because travel distance estimates made using short GPS sampling intervals will be more sensitive to measurement error than estimates made using longer GPS sampling intervals, we also calculated daily travel distances using 1 s smoothed data in an attempt to reduce high-frequency noise (Noonan et al. 2019). To smooth data, we used the function TrajSmoothSG from the trajr package in Rstudio (version 1.3.0), which uses a Savitzky–Golay ethod (McLean and Skowron Volponi 2018). We applied a filter order of 2 and a filter length of 7, which approximately corresponds to our maximum level of GPS error and was thus expected to reduce potential noise while retaining track characteristics (McLean and Skowron Volponi 2018). We performed ad hoc checks of the GPS data using known landmarks at the field site in South Africa, and in Swansea, UK and these indicated positional accuracy always to be within 5 m.
GPS Sampling Interval and Daily Travel Distances
We investigated how GPS sampling interval affected daily travel distance estimates by fitting a linear mixed-effect model in RStudio using the lme4 package (Bates et al. 2015). We fitted daily travel distances (N = 1144) as our response variable and sampling interval (1 s, 1 s [smoothed], 30 s, 60 s, 300 s, 1200 s, 3600 s, and 7200 s) as a fixed categorical effect. We fitted baboon identity as a random effect to control for potential interindividual differences in travel distance, checked model residuals, and used the emmeans package (version 1.4.8; Lenth 2020) for post hoc (Tukey method) tests for each combination of sampling interval.
Quantifying the Reduction in Daily Travel Distance
We compared estimated daily travel distance using one fix per second GPS data to different GPS sampling intervals to quantify the reduction in estimated distance when using less frequent sampling intervals and expressed this value as a proportion. We found the reduction in estimated distance traveled was proportional to GPS sampling interval and was best modeled by a logarithmic function. Using this model, we recalculated travel distances for 38 baboon groups (provided by Johnson et al. 2015) that provide information on GPS sampling intervals.
Ethical Note
To fit collars, a veterinarian anesthetized baboons using Ketamine (dose adjusted for body mass) after cage trapping conducted by service providers in accordance with local protocols (described by Fehlmann et al. 2017a). Collars were approved by Swansea University's Ethics Committee (IP-1314-5), weighed mean 2.2% baboon body mass (range 1.2%–2.6%), and were fitted with a drop-off mechanism (version CR-7, Telonics, Inc.) to avoid the need for recapture (ESM Fig. S1). The authors declare that there are no conflicts of interests.
Data Availability
The dataset generated and analyzed during is available in the Electronic Supplementary Material (ESM 3).
Results
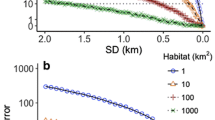
The mean estimated daily travel distance across all days and baboons was 10.86 km when calculated using a 1 fix per second sampling interval and 2.71 km when using a 7200 s sampling interval. The estimated daily travel distance becomes progressively shorter with less frequent GPS sampling because fewer GPS fixes do not properly capture the animal’s movement path (Fig. 1; ESM Video S1). As a result, less frequent GPS fixes result in a significant reduction in calculated daily travel distances (Fig. 2a; ESM Table S1; Video S1), and this reduction changes with GPS sampling interval according to a logarithmic function (proportion distance captured = 0.081ln(sampling interval) + 0.9682; r2 = 0.99; Fig. 2b and c).
Path traveled (black line) by one adult female chacma baboon between 06:18 and 18:00 UTC on August 4th, 2018 in Cape Town, South Africa, estimated using a GPS sampling interval of (a) 1 s, (b) 1 s smoothed, (c) 30 s, (d) 60 s, (e) 300 s, (f) 1200 s, (g) 3600 s, and (h) 7200 s. In (b)–(h) an additional green line representing the path estimated using 1-s sampling interval is shown for comparison.
(a) Kernel probability density of daily travel distances by 12 chacma baboons over 11–12 days, in Cape Town, South Africa, measured using GPS sampling intervals ranging one fix per second to one fix per 7200 s; smoothed 1-s data (1S) are also shown. (b) Comparison of the estimated distance calculated with one fix per second GPS compared to less frequent GPS sampling intervals, expressed as a proportion. (c) Comparison of the estimated distance calculated with one fix per second GPS compared to less frequent GPS sampling intervals (log scale). For (b) and (c) individual baboon data (N = 12) are modeled by colored lines, and the fitted logarithmic function across all data is given by the black line. The vertical axis in (b) and (c) is reversed to aid interpretation.
Applying our model to published baboon daily travel distances (Fig. 3a), we found travel distances were ≥50% farther when using one fix per second sampling interval (Fig. 3b). We found that the range of GPS sampling intervals used in the published work is small (300–3600 s; Fig. 3a), and the proportion of distance captured did not get larger or smaller for groups that travel farther (Fig. 3b and c).
(a) Comparison of the estimated distance calculated with one fix per second GPS (filled circle) compared to less frequent GPS sampling intervals, expressed as a proportion. The dashed box indicates the range of GPS sampling interval (300–3600 s) used in 38 published groups’ daily travel distances (Johnson et al. 2015). (b) Estimation of the proportion of distance captured for 38 published group daily travel distances (data points given by open circles inside the dashed box) based on their reported GPS sampling intervals, using the relationship modeled in (a). One fix per second GPS data used in the current study is shown by the filled circle data point. (c) Predicted daily distance traveled for 38 published groups (Johnson et al. 2015), based on the reported groups’ daily travel distances and their GPS sampling interval, using the model shown in (a). One fix per second GPS data (current study) is shown by the filled circle that falls on a 1:1 line.
Discussion
Using less frequent GPS sampling intervals to estimate chacma baboon daily travel distances reduces the opportunity to measure an animal’s deviation from a linear path, resulting in smaller estimated daily travel distances. The reduction in estimated travel distance seen with increasing GPS sampling interval (here, the difference between estimates at one fix per second and other intervals) can be modeled by a logarithmic function. Our findings therefore support empirical and theoretical work showing that the interval at which GPS fixes are taken can systematically change movement distances calculated (Borger et al. 2006; de Weerd et al. 2015; Ganskopp and Johnson 2007; Johnson and Ganskopp 2008; McGavin et al. 2018; Mills et al. 2006; Mitchell et al. 2019; Noonan et al. 2019; Postlethwaite and Dennis 2013; Rowcliffe et al. 2012; Sennhenn-Reulen et al. 2017; Swain et al. 2008; Tanferna et al. 2012) and affirm research with Guinea baboons reporting similar findings when estimating travel distances over a shorter time frame (2-h blocks) and with fewer baboons (N = 4) (Sennhenn-Reulen et al. 2017).
Miscalculation of travel distances can have important implications for studies of movement ecology (Hebblewhite and Haydon 2010; Patterson et al. 2008; Schick et al. 2008), disease dynamics (Dougherty et al. 2018; White et al. 2018) and designation of conservation spaces (Cristescu et al. 2013; Darnell et al. 2014; Douglas-Hamilton et al. 2005). For example, distances traveled calculated from GPS data have been used to estimate the energy cost coefficients of locomotion (e.g., Brosh et al. 2010) and these will alter substantially if the relationship between estimated distances and sampling interval that we report is typical across species and contexts. Indeed, our baboon case study suggests that moving from a GPS frequency of one fix every second to one fix every 30 s results in a 33% reduction in estimated daily travel distance, while using hourly GPS fixes results in a 66% reduction in estimated daily travel distance.
Future studies should consider the impact of GPS sampling intervals on distance estimates. Assuming that estimated distances change with GPS sampling interval according to a logarithmic function may be informative, but other factors will also need to be considered. In the context of baboon behavior, for example, 1) the tortuosity of the travel path and 2) the speed of travel will affect how much a path is underestimated (Sennhenn-Reulen et al. 2017), because while slower movement decreases travel distance, more tortuous movement increases travel distance (Johnson et al. 2015). Therefore, while the logarithmic relationship we describe could be a general phenomenon, the effect size (exponent) will change with a myriad of social and ecological factors (Dunbar 1992; Johnson et al. 2015). Where high-accuracy estimates of travel distance are needed, researchers should therefore consider continuous-time stochastic process models (Calabrese et al. 2016) to minimize confounding effects of position and velocity autocorrelation.
Comparative investigations of daily travel distances between species and populations rely on estimates of travel distances, typically from GPS data (Carbone et al. 2005; Dunbar 1992; Johnson et al. 2015). Given the significant differences in estimated distances according to GPS sampling interval, this could result in flawed comparisons. Using the relationship described for our data, we calculated daily travel distance for 38 baboon groups (Johnson et al. 2015) as if they had used a GPS sampling interval of one fix per second. Published travel distances captured a minimum 50% of the distance predicted if a 1-s sampling interval was used, but because the range of GPS sampling intervals used by baboon researchers to date is small (300–3600 s) the model predicted distances did not systematically vary across groups/sampling intervals. Previous comparisons of daily travel distances in baboons are therefore sound. However, if high-resolution GPS data (as used in the present study) were to be included in such comparisons in future, this would introduce pronounced differences in travel distance estimates. Estimated travel distances using high-frequency GPS data therefore cannot be compared to published distance estimates (that use less frequent sampling intervals) without properly controlling for differences in sampling regimes.
Our case study also highlights an understudied aspect of high-resolution GPS data in animal movement studies: positional accuracy. Because GPS positional error is Gaussian in nature, this error will not tend to systematically alter estimates of interindividual distances (Haddadi et al. 2011; King et al. 2012) or interaction with features of the environment (Fehlmann et al. 2017a; Strandburg-Peshkin et al. 2017), or conspecifics (Farine et al. 2016, 2017; Strandburg-Peshkin et al. 2015), and therefore does not normally need to be accounted for in such contexts. However, calculated distance traveled estimates are sensitive to positional measurement error (McGavin et al. 2018; Noonan et al. 2019), and these errors are pronounced at short GPS sampling intervals which will affect the estimated travel path. We therefore smoothed our 1-s GPS data in an attempt to reduce the impact of such high-frequency noise, and this resulted in significantly shorter distance estimates (ESM Table SI). Further work is now needed to explore if such smoothing is required because GPS loggers have on-board smoothing algorithms (which typically cannot be accessed by the end-user). These algorithms minimize “jitter” or “drift” when the logger is slow-moving or stationary (see ESM Fig. S2 for an example from our data) making it challenging to determine if post hoc smoothing removes “real movement,” “noise,” or both. Combining aerial video footage and GPS data of moving animals in the wild (e.g., on a beach where tracks are left) would be one way to investigate the relationship between true movement and GPS measured movement. Another would be to match GPS data to acceleration data to distinguish between active and nonactive time periods (Fehlmann et al. 2017b).
Finally, our findings highlight the need to choose an appropriate GPS sampling interval. The smaller the sampling interval, the higher the number of GPS fixes taken within a given time frame and the higher the accuracy of any subsequent distance estimate. But this comes at the cost of shorter battery life, and hence a shorter data collection period. This makes high-resolution GPS sampling less practical for longer-term studies in primate spatial ecology because collars need to increase in size and weight to accommodate larger batteries. However, this issue can be overcome if collars use solar cells with rechargeable batteries and dynamically switch between different sampling rates depending on the animal’s activity (e.g., Wilson et al. 2018). Given these tradeoffs, studies will likely continue to use different GPS sampling regimes, and so our case study provides useful rule-of-thumb for the magnitude of change expected when estimated travel distances with different GPS sampling intervals.
References
Bates, D., Machler, M., Bolker, B. M., & Walker, S. C. (2015). Fitting linear mixed-effects models using lme4. Journal of Statistical Software, 67(1), 1–48.
Borger, L., Franconi, N., De Michele, G., Gantz, A., Meschi, F., et al (2006). Effects of sampling regime on the mean and variance of home range size estimates. Journal of Animal Ecology, 75(6), 1393–1405.
Bracken, A. M., Christensen, C., O’Riain, M. J., Fehlmann, G., Holton, M. D., et al (in press). Socioecology explains individual variation in urban space-use in response to management in Cape chacma baboons (Papio ursinus). International Journal of Primatology.
Brosh, A., Henkin, Z., Ungar, E. D., Dolev, A., Shabtay, A., et al (2010). Energy cost of activities and locomotion of grazing cows: A repeated study in larger plots. Journal of Animal Science, 88(1), 315–323.
Calabrese, J. M., Fleming, C. H., & Gurarie, E. (2016). ctmm: an r package for analyzing animal relocation data as a continuous-time stochastic process. Methods Ecol Evol, 7, 1124–1132. https://doi.org/10.1111/2041-210X.12559.
Carbone, C., Cowlishaw, G., Isaac, N. J. B., & Rowcliffe, J. M. (2005). How far do animals go? Determinants of day range in mammals. American Naturalist, 165(2), 290–297.
Cristescu, B., Bernard, R. T. F., & Krause, J. (2013). Partitioning of space, habitat, and timing of activity by large felids in an enclosed South African system. Journal of Ethology, 31(3), 285–298.
Darnell, A. M., Graf, J. A., Somers, M. J., Slotow, R., & Gunther, M. S. (2014). Space use of african wild dogs in relation to other large carnivores. PLoS ONE, 9(6), e98846.
de Weerd, N., van Langevelde, F., van Oeveren, H., Nolet, B. A., Kolzsch, A., et al (2015). Deriving animal behaviour from high-frequency gps: Tracking cows in open and forested habitat. PLoS ONE, 10(6).
Dougherty, E. R., Seidel, D. P., Carlson, C. J., Spiegel, O., & Getz, W. M. (2018). Going through the motions: Incorporating movement analyses into disease research. Ecology Letters, 21(4), 588–604.
Douglas-Hamilton, I., Krink, T., & Vollrath, F. (2005). Movements and corridors of African elephants in relation to protected areas. Naturwissenschaften, 92(4), 158–163.
Dunbar, R. I. M. (1992). Time: A hidden constraint on the behavioural ecology of baboons. Behavioral Ecology and Sociobiology, 31(1), 35–49.
Farine, D. R., Strandburg-Peshkin, A., Berger-Wolf, T., Ziebart, B., Brugere, I., et al (2016). Both nearest neighbours and long-term affiliates predict individual locations during collective movement in wild baboons. Scientific Reports, 6, 27704.
Farine, D. R., Strandburg-Peshkin, A., Couzin, I. D., Berger-Wolf, T. Y., & Crofoot, M. C. (2017). Individual variation in local interaction rules can explain emergent patterns of spatial organization in wild baboons. Proceedings of the Royal Society B: Biological Sciences, 284(1853), 20162243.
Fehlmann, G., O’Riain, M. J., Kerr-Smith, C., Hailes, S., Luckman, A., et al (2017a). Extreme behavioural shifts by baboons exploiting risky, resource-rich, human-modified environments. Scientific Reports, 7(1), 15057.
Fehlmann, G., O’Riain, M. J., Hopkins, P. W., O’Sullivan, J., Holton, M. D., et al (2017b). Identification of behaviours from accelerometer data in a wild social primate. Animal Biotelemetry, 5(1), 6.
Ganskopp, D. C., & Johnson, D. D. (2007). GPS error in studies addressing animal movements and activities. Rangeland Ecology & Management, 60(4), 350–358.
Garnier, S. (2016). SwaRm. https://github.com/swarm-lab/swaRm.
Getz, W. M., & Saltz, D. (2008). A framework for generating and analyzing movement paths on ecological landscapes. Proceedings of the National Academy of Sciences of the USA, 105(49), 19066–19071.
Haddadi, H., King, A. J., Wills, A. P., Fay, D., Lowe, J., et al (2011). Determining association networks in social animals: Choosing spatial-temporal criteria and sampling rates. Behavioral Ecology and Sociobiology, 65(8), 1659–1668.
Hampson, B. A., de Laat, M. A., Mills, P. C., & Pollitt, C. C. (2010a). Distances travelled by feral horses in 'outback' Australia. Equine Veterinary Journal, 42, 582–586.
Hampson, B. A., Morton, J. M., Mills, P. C., Trotter, M. G., Lamb, D. W., & Pollitt, C. C. (2010b). Monitoring distances travelled by horses using GPS tracking collars. Australian Veterinary Journal, 88(5), 176–181.
Hebblewhite, M., & Haydon, D. T. (2010). Distinguishing technology from biology: A critical review of the use of GPS telemetry data in ecology. Philosophical Transactions of the Royal Society B: Biological Sciences, 365(1550), 2303–2312.
Hoffman, T. S., & O’Riain, M. J. (2012). Monkey management: Using spatial ecology to understand the extent and severity of human–baboon conflict in the Cape Peninsula, South Africa. Ecology and Society, 17(3), 13.
Johnson, C., Piel, A. K., Forman, D., Stewart, F. A., & King, A. J. (2015). The ecological determinants of baboon group movements at local and continental scales. Movement Ecology, 3, 14.
Johnson, D. D., & Ganskopp, D. C. (2008). GPS collar sampling frequency: Effects on measures of resource use. Rangeland Ecology & Management, 61(2), 226–231.
King, A. J., Wilson, A. M., Wilshin, S. D., Lowe, J., Haddadi, H., et al (2012). Selfish-herd behaviour of sheep under threat. Current Biology, 22(14), R561–R562.
Lenth, R. (2020). emmeans: Estimated marginal means, aka least-squares means. R package version 1.4.7. https://CRAN.R-project.org/package=emmeans
McGavin, S. L., Bishop-Hurley, G. J., Charmley, E., Greenwood, P. L., & Callaghan, M. J. (2018). Effect of GPS sample interval and paddock size on estimates of distance travelled by grazing cattle in rangeland, Australia. Rangeland Journal, 40(1), 55–64.
McLean, D. J., & Skowron Volponi, M. A. (2018). trajr: An R package for characterisation of animal trajectories. Ethology, 124(6), 440–448.
Mills, K. J., Patterson, B. R., & Murray, D. L. (2006). Effects of variable sampling frequencies on GPS transmitter efficiency and estimated wolf home range size and movement distance. Wildlife Society Bulletin, 34(5), 1463–1469.
Mitchell, L. J., White, P. C. L., & Arnold, K. E. (2019). The trade-off between fix rate and tracking duration on estimates of home range size and habitat selection for small vertebrates. PLoS ONE, 14(7), e0219357.
Nathan, R., Getz, W. M., Revilla, E., Holyoak, M., Kadmon, R., et al (2008). A movement ecology paradigm for unifying organismal movement research. Proceedings of the National Academy of Sciences of the USA, 105(49), 19052–19059.
Noonan, M. J., Fleming, C. H., Akre, T. S., Drescher-Lehman, J., Gurarie, E., et al (2019). Scale-insensitive estimation of speed and distance traveled from animal tracking data. Movement Ecology, 7(1), 35.
O’Bryan, L. R., Abaid, N., Nakayama, S., Dey, T., King, A. J., et al (2019). Contact calls facilitate group contraction in free-ranging goats (Capra aegagrus hircus). Frontiers in Ecology and Evolution, 7, 73.
Patterson, T. A., Thomas, L., Wilcox, C., Ovaskainen, O., & Matthiopoulos, J. (2008). State-space models of individual animal movement. Trends in Ecology & Evolution, 23(2), 87–94.
Postlethwaite, C. M., & Dennis, T. E. (2013). Effects of temporal resolution on an inferential model of animal movement. PLoS ONE, 8(5), e57640.
Ren, B. P., Li, M., Long, Y. C., Gruter, C. C., & Wei, F. W. (2008). Measuring daily ranging distances of Rhinopithecus bieti via a global positioning system collar at Jinsichang, China: A methodological consideration. International Journal of Primatology, 29(3), 783–794.
Rowcliffe, J. M., Carbone, C., Kays, R., Kranstauber, B., & Jansen, P. A. (2012). Bias in estimating animal travel distance: The effect of sampling frequency. Methods in Ecology and Evolution, 3(4), 653–662.
Ryan, P. G., Petersen, S. L., Peters, G., & Gremillet, D. (2004). GPS tracking a marine predator: The effects of precision, resolution and sampling rate on foraging tracks of African Penguins. Marine Biology, 145(2), 215–223.
Sahraei, N., Watson, S. M., Pennes, A., Peters, I. M., & Buonassisi, T. (2017). Design approach for solar cell and battery of a persistent solar powered GPS tracker. Japanese Journal of Applied Physics, 56(8), ME01.
Santhosh, K., Kumara, H. N., Velankar, A. D., & Sinha, A. (2015). Ranging behavior and resource use by lion-tailed macaques (Macaca silenus) in selectively logged forests. International Journal of Primatology, 36(2), 288–310.
Schick, R. S., Loarie, S. R., Colchero, F., Best, B. D., Boustany, A., et al (2008). Understanding movement data and movement processes: Current and emerging directions. Ecology Letters, 11(12), 1338–1350.
Schreier, A. L., & Grove, M. (2010). Ranging patterns of hamadryas baboons: Random walk analyses. Animal Behaviour, 80(1), 75–87.
Sennhenn-Reulen, H., Diedhiou, L., Klapproth, M., & Zinner, D. (2017). Estimation of baboon daily travel distances by means of point sampling: The magnitude of underestimation. Primate Biology, 4(2), 143–151.
Strandburg-Peshkin, A., Farine, D. R., Couzin, I. D., & Crofoot, M. C. (2015). Shared decision-making drives collective movement in wild baboons. Science, 348(6241), 1358–1361.
Strandburg-Peshkin, A., Farine, D. R., Crofoot, M. C., & Couzin, I. D. (2017). Habitat and social factors shape individual decisions and emergent group structure during baboon collective movement. Elife, 6, e19505.
Swain, D. L., Wark, T., & Bishop-Hurley, G. J. (2008). Using high fix rate GPS data to determine the relationships between fix rate, prediction errors and patch selection. Ecological Modelling, 212(3–4), 273–279.
Tanferna, A., Lopez-Jimenez, L., Blas, J., Hiraldo, F., & Sergio, F. (2012). Different location sampling frequencies by satellite tags yield different estimates of migration performance: Pooling data requires a common protocol. PLoS ONE, 7(11), e49659.
White, L. A., Forester, J. D., & Craft, M. E. (2018). Dynamic, spatial models of parasite transmission in wildlife: Their structure, applications and remaining challenges. Journal of Animal Ecology, 87(3), 559–580.
Wilson, A., Hubel, T., Wilshin, S., Lowe, J. C., Lorenc, M., et al (2018). Biomechanics of predator–prey arms race in lion, zebra, cheetah and impala. Nature, 554, 183–188.
Acknowledgments
Data were collected during fieldwork approved by the Baboon Technical Team (BTT) in the Cape Peninsula and by Research Agreement with South African National Parks (SANParks). Thanks to Human Wildlife Solutions and veterinarian Dorothy Breed for organizing baboon cage trapping, and to Justin O’Riain, Gary Buhrman, Esme Beamish, and Human Wildlife Solutions for their assistance. We thank Carlo Catoni (TechnoSmArt), Gwenda Kesans (Ride and Drive Equestrian), Gaelle Fehlmann, Mark Holton, and Phil Hopkins for assistance with collar design and build. AB thanks Alexis Malagnino for advice with GPS processing. AJK and IF thank Layla King for support. AB and CC were supported by College of Science/Swansea University PhD scholarships. Research was supported by grants from Swansea University’s College of Science and the Association for the Study of Animal Behaviour (ASAB). We are grateful to Editor-in-Chief Jo Setchell and two anonymous reviewers for excellent and constructive feedback during peer review.
Author information
Authors and Affiliations
Contributions
AJK and IF conceived the study. AB and CC constructed the tracking collars and collected data in the field. AB processed the data. RMcC analyzed the data and conducted statistical analyses with input from AJK, IF, and AB. RMcC wrote the first draft of the manuscript, which was revised by AJK with input from all authors, who read and approved the final manuscript.
Corresponding authors
Additional information
Handling Editor: Joanna Setchell.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
McCann, R., Bracken, A.M., Christensen, C. et al. The Relationship Between GPS Sampling Interval and Estimated Daily Travel Distances in Chacma Baboons (Papio ursinus). Int J Primatol 42, 589–599 (2021). https://doi.org/10.1007/s10764-021-00220-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10764-021-00220-8