Our enduring engagements with mathematics prospective teachers, in and out of class sessions, offered us numerous opportunities to reflect on ourselves, on the students, and on the many interactions that evolved. In one such case, we asked five students, who volunteered to be individually interviewed, whether they prefer to be interviewed about extrema points, inflection points, or asymptotes (three subjects that we intended to discuss in the methods course). All five chose “extrema points” because “it’s the easiest,” and “it’s relevant to high school students in all levels.” The findings were interesting and quite surprising. Here are our findings regarding the PTs’ conceptions of extrema points and of mathematical definitions in general.

Literature Review

Mathematical concepts and theorems, along with definitions and proofs are the essence of the mathematical realm (Halmos, 1980). Mathematical concepts are the product of human definitions, either when constructing new mathematical objects or when naming pre-existing ones (Morgan, 2005). Mathematical definitions are arbitrary, hierarchically constructed (Edwards & Ward, 2008), and agreed upon conventions (Jayakody & Zazkis, 2015) that are sensibly chosen (Werndl, 2009). According to Tall and Vinner (1981), a concept definition is the minimal set of necessary and sufficient critical attributes of the concept, which are acceptable by the mathematicians at a given time. Knowledge of concept definitions calls for formal knowledge regarding the nature of mathematical definitions in general (Fischbein, 1994) and specific knowledge regarding a particular concept such as infinity (Tirosh, 1991) and inflection point (Tsamir & Ovodenko, 2013). It has been found that although defining is a significant component of mathematical knowledge, it is still a major challenge for learners (Mariotti & Fischbein, 1997; Winicki-Landman & Leikin, 2000).

Studies have shown that definitions have little, if any influence on students’ conceptions (Fischbein & Nachlieli, 1998; Leikin & Zazkis, 2010; Vinner, 1991). What seems to be the most influential in the grasp of mathematical concepts are learners’ primary intuitions (Fischbein, 1987) that culminate in concept images (Tall & Vinner, 1981). Primary intuitions are immediate, self-evident, and confidently regarded as valid assertions, although they are not necessarily so, and concept images incorporate knowledge segments and intuitions. Concept images are built over the years through various, early mathematical, and daily experiences, changing as one meets different stimuli. The formation of concept images tallies with Fischbein’s notion of primacy effect, referring to peoples’ tendencies to consider early learnt substance, while ignoring later, updated information (Fischbein, 1987). Different parts of the concept image might be evoked under different circumstances. Mathematics education research has been often concerned with exploring tensions among the evoked concept images (Bingolbali & Monaghan, 2008; Kontorovich, 2018).

The definition of a mathematical concept determines two mutually exclusive sets–a set of examples and a set of nonexamples. Examples are mathematical objects that satisfy all the critical attributes listed in the definition of the concept, and nonexamples of the concept that do not satisfy at least one of the critical attributes. One’s concept images might cause confusion between examples and nonexamples. Studies that analyzed learners’ related difficulties distinguished between mis-in examples, that mistakenly grant nonexamples the status of examples and mis-out examples, that mistakenly regard examples as nonexamples (Tirosh & Tsamir, 2022; Tsamir & Tirosh, 2023). In the literature, mis-in and mis-out examples have been widely reported, commonly without characterizing them as such. For instance, regarding the concept “tangent” studies reported on students’ tendencies to draw more than one tangent at a certain point of a circle or a function, adding mis-in examples; other students claimed that a tangent cannot “touch” the graph more than once, and consequently mis-out examples (Biza & Zachariades, 2010; Çekmez & Baki, 2016; Vinner, 1982, 1991).

Examples and nonexamples are not only a product of a particular concept definition, but they also play a key role in the actual conceptualization, bearing the potential to serve as pointers to distinguishing between critical and non-critical attributes of the concept (Vinner, 2011; Zodik & Zaslavsky, 2008). The notions example-space, dimensions of possible variation, and range of permissible change were offered, pointing to learners’ (explicit or implicit) recognition of eligible example-variations that maintain examplehood (Fukawa-Connelly & Newton, 2014; Mason & Watson, 2008). Although learners’ recognition may not be immediate, their example spaces can still be enriched by guiding probes. However, the meaning of mathematical concepts often develops while occasionally encountering and adopting, seemingly, yet not necessarily, relevant examples (Goldenberg & Mason, 2008). In such cases, intuitive examples (examples that are easily identified as such) and intuitive nonexamples (nonexamples that are easily identified as such) attain a prototypical status that often hinders the comprehension of the concept (Tsamir et al., 2008). To get a better insight into learners’ grasp of connections between mathematical concepts, examples, and nonexamples, various example-based research tools were designed. For instance, “generate examples of…” (Alcock & Inglis, 2008; Zazkis & Leikin, 2007, 2008) or “evaluate – is this an example of…” (Tsamir et al., 2008; Tsamir & Tirosh, 2023). In this study, we investigated learners’ conceptions of extrema points by addressing both, their definitions and their exemplification of the concept.

Extrema points are frequently referred to in the investigations of functions in calculus lessons. However, several publications pointed to a number of related errors made by high school and even by university students. Students were found to believe that extrema cannot be discontinuity points (Shepherd, et al., 2012; Zaslavsky & Shir, 2005) that the derivative at extrema is necessarily zero (Zaslavsky & Shir, 2005) and that relative minimum and absolute minimum are the same (Shepherd et al., 2012). These publications report on studies that briefly address the extrema issue as one of many, wider issues. Our study focused on the investigation of secondary school mathematics prospective teachers’ (PTs) conceptions of extrema points, by examining their definitions, as well as their offerings of examples and nonexamples and their identifications of examples, with special attention to the domain. More specifically, the research questions are as follows:

  • (a) What in PTs’ view is an extreme point?

  • (b) What points on a function, in PTs’ view, are not extrema points?

The Study

The data was derived from interviews, conducted with PTs who enrolled in the Secondary Mathematics Teaching Certificate Program at Tel Aviv University.

Participants

Five PTs who had rich mathematical, post-secondary school credentials that included at least Calculus 1 and 2, participated in this study. In their Calculus 1 courses, they were offered a list of recommended textbooks, for instance, Thomas et al. (2004), Zorich (2004), which they admitted not to have used. They had weekly assignments and a final exam for which they went over summaries of the lectures and solved worked-out examples presented in Ayers and Mendelson (2008). The definitions of local extremum presented, for instance, in the students’ preferred textbook, Ayers and Mendelson (2008, p. 98) is as follows:

  • Definition A: …[A function] f is said to have a relative minimum at x0 if f (x0) ≤ f (x) for all x in some open interval containing x0 (and for which f (x) is defined). In other words, the value of f at x0 is less than or equal to all values of f at nearby points.

Also, in the textbooks and in the lectures, connections between extrema and f′ = 0 were presented in theorems. We limit ourselves here to local extrema, since these were the only ones that the participants referred to in this study.

The five PTs expressed high mathematical self-efficacy, and eagerness to acquire didactical tools for teaching. They volunteered to take part in the interviews, and during our conversations, each of them offered an opening to his/her lines of reasoning, hesitations, and dilemmas. The names listed ahead are pseudonyms.

Tools

The assignment given to the participants included the following four tasks:

  • Task 1

    • What is a minimum point? Define.

  • Task 2

    • Draw a graph of a function and mark on it a point that is a minimum point.

    • Draw another such drawing, and another one.

  • Task 3

    • Draw a graph of a function and mark on it a point that is not a minimum point.

    • Draw another such drawing, and another one.

  • Task 4

    • Sara, an 11th grader, solved the following task:

    • Given: the graph of f(x), f: (−11, 20) (that is, −11 < x < 20) → R

    • Mark all extreme points on the graph of f (x),

    • Indicate for each point whether it is a maximum or a minimum

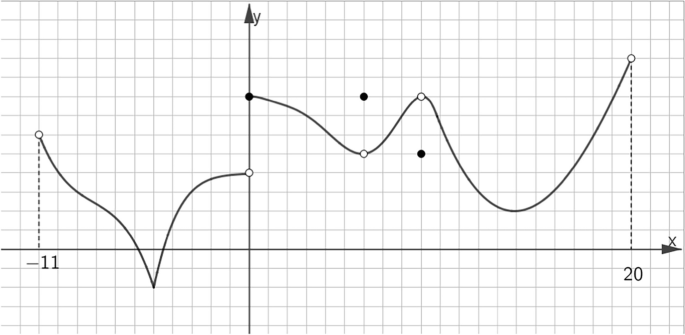
      figure a

    • Sara marked five points and wrote A—min, B—max, C—max, D—min, and E—min

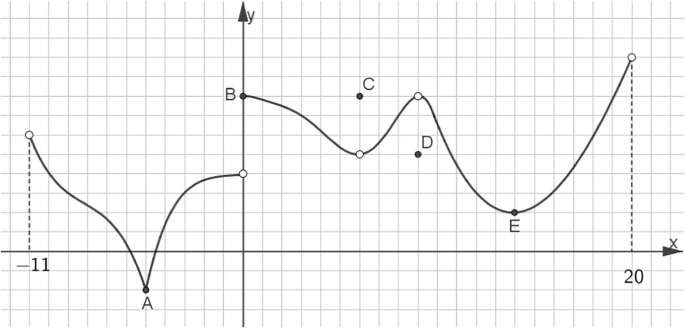
    figure b
  1. a.

    For each point that Sara marked, indicate correct/incorrect.

  2. b.

    If, in your opinion, any point/s are incorrectly marked, explain the error.

  3. c.

    If, in your opinion, any extrema point/s are missing. Specify max/min. Explain.

The succession of the tasks was designed to start with giving rise to PTs’ concept images of minima points, which served among other things, in examining their tendencies to refer to the domain, i.e., the fundamental set (Edwards & Ward, 2008; Zazkis & Leikin, 2008). In Tasks 2 and 3, we encouraged intuitive examples and intuitive nonexamples (Tsamir et al., 2008) which might grant a flavor of PTs’ basic example space and their most accessible examples of extrema points (Goldenberg & Mason, 2008). It is documented that storage of examples in mind differs from accessing it in a given context. An accessible example space is what appears in one’s thought first off (Watson & Mason, 2005). Deficiency in presentation of certain examples is not necessarily evidence that one is not familiar with these examples. It might just be that the specific setting did not cause these examples to spark. However, learners might benefit from explicit stimuli to reflect on the dimensions of possible variation and associated ranges of permissible change (Goldenberg & Mason, 2008; Zodik & Zaslavsky, 2008). For this purpose, we formulated Task 4. It is an “evaluate the solution” task, and it presents a range of permissible changes of function domains. We aimed to examine participants’ acceptance of extrema points placed in various function intervals, as well as their tendencies to rebuff certain examples and verbally explain what, in their view, is not an extreme point. We included in Task 4 a collection of an intuitive example (Point E) and non-intuitive examples (A, B, C, D) (Tsamir et al., 2008). Non-intuitive examples may assist in identifying the sensitivity of participants’ concept images to guises of nonexamples. This task also offered PTs an opportunity to mark additional points, mis-in examples, which they regarded as extrema points (Tirosh & Tsamir, 2022). The tasks called for verbal and graphic reference, as different representations may assist in evoking an assorted responsiveness to the concept (Goldin, 2002; Molina et al., 2017). The first and third authors designed the tasks, which were revised following the comments of the second author.

Procedure

The data arise from two sources gathered during individual meetings with each participant:

Written solutions to the assignment (presented in the “Tools” section) and follow-up interviews.

  1. Stage 1.

    At the beginning of each individual, interview session, about 10 min were dedicated to PTs’ involvement in writing solutions to the four tasks. When the PTs concluded their written solutions, we started the oral engagement.

  2. Stage 2.

    Each PT was interviewed once for about 40 min. The interviews were conducted by the first two authors, audio recorded, and transcribed. One of the authors led the session in a certain interview, and the other wrote notes in real-time, for instance, the student hesitates and giggles; then in the following session, the roles switched. The five interviews took place for one week.

During the entire interview session, the PT’s written solutions remained on the table, available for additional reference. The interviews were flexible, semi-structured, somewhat informal conversations, and all included questions that invited the PTs (a) to examine/revise their definitions in light of their different solutions and (b) to specify what points on a function are not extrema points.

The data was analyzed in three rounds: Round 1—Identifying what, in the PTs’ view, is an extreme point. Round 2—Identifying what, in the PTs’ view, is not an extreme point, Round 3—Identifying additional interesting findings. Each round included three major steps: (a) individual work for each author, separately analyzed the materials; (b) pair meetings (first and second author) to discuss the analysis of the data as suggested by each of us; and (c) finally, the third author went over the data and commented; if there was a need, we communicated and discussed the suggestions, and then, the analysis was finalized.

Findings

The PTs’ written solutions to the tasks offered a rainbow of opportunities to explore their conceptions of extrema points. While from Tasks 1 and 2, we could mostly get the feel of what points are intuitively viewed as extrema points; Tasks 3 and 4, shed light on the PTs’ justified rejections of such points. Since concept images are setting-dependent, we collected the puzzle pieces from the various tasks to get a wide-ranging picture regarding their conception of extrema points. In the following sections, we address our two research questions—What is an extreme point? and What is not an extreme point? as well as a peculiarity that surfaced during the analysis of the data—What is (surprisingly) not a must for an extreme point? In the following interview segments, capital letters indicate vocal emphasis, and authors’ comments are added in parenthesis.

What Is an Extreme Point?

The observations presented in this section primarily unfolded from the PTs’ straightforward, written definitions of minima points in Task 1 and from their explanations during the interviews. This information was enriched by the graphic examples (Task 2) and by some justified evaluations of Sara’s work (Task 4). It should be noted that all PTs drew correct examples of either smooth minima points or (one) cusp point (Task 2, Table 1). Also, reactions to Sara’s work uncovered a unanimous, correct acceptance of E as a minimum point (Table 2), expressing the view that the highest/lowest point, where the function changes its monotonicity and also f′ = 0 (or, a “peak point” that is placed in a differentiable interval), is an extremum. It seems that the PTs considered these conditions as sufficient for extrema points, it does not reveal, however, whether they regarded these conditions as necessary as well.

Table 1 Students’ graphic examples and nonexamples of minima points (Task 2, Task 3)
Full size table
Table 2 Students’ written definitions and reactions to Sara’s solution (Task 1, Task 4)
Full size table

The categorization offered in this section follows the PTs’ initial definitions of minimum point (Task 1); then, based on their other written and oral answers, we added to each category our interpretation of domains that PTs’ seemed to have in mind. Three concept images were identified in the written definitions (Table 3): The lowest point in the neighborhood, a point where the monotonicity changes, and a point that satisfies both, change in monotonicity and f ′ = 0. None of the definitions included reference to the related fundamental set (i.e., to the domain of the function, or more precisely, the domain of the functional interval). Still, as we demonstrate ahead, the declared definitions only partly revealed the complexity of the underlying concept images.

Table 3 Students’ written and orally revised definitions of minimum point (Task 1, interview)
Full size table

The Lowest/Highest Point in the Neighborhood

Mor, Anat, and Gad based their definition on this criterion, but their other, written and oral answers included reference to supplementary attributes (Table 3). It turned out that in addition to the “peak point” idea, these PTs cling to three different domain-related requisites.

The Domain Is Any Interval in R that Includes the Extreme Point

In Task 4, Mor seemed to correctly implement the “highest/lowest point” definition to the full range of real-function intervals (Table 2). Mor evaluated Sara’s solution as correct and complete, accepting all marked extrema points, and missing no others. Consequently, her concept image seemed to be the highest/lowest point included in any kind of real function interval. In her interview, she accentuated this point:

I1:What is the domain of the function… in the neighborhood of extrema points?

Mor2:There are NO RESTRICTIONS… Any interval of a function… OK, that THE POINT IS IN [the domain] [giggles].

I3:ANY function?

Mor4:SURE. Ehhh…. Perhaps not. Maybe there is a need to say A REAL function, ehhh… BUT… that’s the only kind of functions that THEY know at high school… Right?

I5:Ehhh…

Mor6:[interrupts] OK… OK… you asked to focus on the math… no high school… no teaching… So, perhaps I should add this [condition] to the definition.

I7:What would your definition be?

Mor8:Ehhh... a minimum point is THE LOWEST POINT in a certain interval of A REAL FUNCTION [hesitates]. But seriously, in high school it’s just a meaningless addition… What is the definition in their textbook? I have to look it up.

Mor’s concerns addressed pedagogical dilemmas.

The Domain Is a Continuous Interval

Anat accepted the smooth point E and the cusp extremum A in Task 4, rejecting all discontinuity points. Thus, Anat seemed to implement her definition to the domain of continuous functions. During her interview, she explained:

I1:Here [Task 4] you marked points B, C and D errors, right?

Anat2: [examines her solution] YES.

I3:But these points fulfill the conditions in your definition, right?

Anat4:Ehhh, but… NO… It’s discontinuous…

I5:The peak-point condition is in your definition, but the continuity not…

Anat6: [hesitates] I wrote the main… the most important, the characteristic that MAKES a point minimal… Should I also include this [condition] in the definition? It feels too obvious… I remember that minimum is the least of something… here it’s the lowest, like the least in height, the bottom… You declined to it, then evolve from it… But I don’t remember having continuity in the definition…. I’m not sure it’s needed … I have to check in high school textbooks… You mean that YOU WANT ME to change my definition?

I7:Would YOU like to?

Anant8: [hesitates] I don’t know… You mean that the definition should be… ehhh, a minimum point is the lowest point on a CONTINUOUS interval of the function. ehhh… I really don’t remember seeing this kind of definition. NEVER… but, maybe…

Anat revised her definition quite reluctantly, yet in accordance with her choices of examples in Task 4. She rightfully noted that she had no recollection of such a definition, since the definitions are not limited to the domain of continuous intervals. Later, in her interview, Anat further explained that discontinuity points cannot be extrema (the “Neither on Increasing/Decreasing Intervals, nor (Any) Discontinuity Point” section).

The Domain Is a Differential Interval and f' = 0

Gad evaluated only E (smooth extreme point) as correct (Task 4). In his interview, he explained:

I1: You only marked point E as correct.

Gad2:YES.

I3:Why? You defined a minimum point as ‘the lowest point’. There are other peak points here [points to Task 4].

Gad4:Yes. But only HERE [point E] it seems that the derivative is zero.

I5:It’s an additional condition?

Gad6:Ehhh… f'=0 is a NECESSARY condition… in calculus. I mean, it’s an extension from algebra to calculus. We first calculated extrema points of parabolas in algebra lessons.

I7:SO???

Gad8:In calculus we got familiar with derivatives… we investigated functions… actually, even in algebra the extremum of parabolas… f ' is zero, but we didn’t mention it. We didn’t KNOW about derivatives. In calculus it’s possible to have a COMPLETE definition. At extrema points f '=0. It’s common practice in the investigation of functions.

I9:If it’s a NECESSARY condition, how come you didn’t mention it in your definition?

Gad10:Gosh… I think that I gave the BASIC definition… like in algebra… It IS a necessary condition. I should have included it.

I11: Can you offer a full definition?

Gad12:Sure. Minimum point… where the function has its lowest value, and the derivative is zero… Something like that.

Gad willingly revised his definition to include the f′ = 0 attribute for extrema points.

A “Change in Monotonicity” Point

Ben wrote in Task 1 that a minimum point is a point where the graph changes from decreasing to increasing (Table 3), but in Task 4, he accepted as extrema, points A (cusp), E (smooth), and also, the jump discontinuity point B. It seemed that for Ben an extreme point is either embedded in a continuous interval or a jump-discontinuity point. Ben explained in his interview:

Ben1: An extremum has to be ON THE GRAPH, within an interval or at the edge… like the edge of a closed interval…

I2:Would you like to change your definition of a minimum point?

Ben3:A minimum point is a point ON THE GRAPH where the function turns from decreasing to increasing.

Later in his interview, Ben explained why removable discontinuity points differ from jump discontinuity points (the “Neither Increasing or Decreasing Intervals, nor (Only) Removable Discontinuity Points” section).

A “Change in Monotonicity” Point and f′ =0

Dan defined a minimum point as a point where f′ = 0 and the function turns from decreasing to increasing (Table 3). Still, in Task 4, he accepted point E, jump discontinuity point B, and semi-accepted the removable discontinuity points C and D (Table 2). His written justification regarding the removable-discontinuous points, expressed not only what, in his view is wrong with Sara’s solution, but also what attribute should have been enacted. He wrote, “point C is marked at a correct place, but there’s a minimum because the function changes there from decreasing to increasing.” For D, he wrote, “same explanation as C”. Dan seemed to hold a “change in monotonicity” concept image, overgeneralized to discontinuity points. In his interview, he shared with us his lines of reasoning:

Dan1:Here [points at the x of C] the derivative from both sides tends to zero. Both, the left-sided limit and the right sided limit… deleted limits… SO, the decreasing changes to increasing and f ' tends to zero…The same happens also at B… and D.

I2:Let’s look again at your definition, would you change it?

Dan3:[reads] NO… It’s actually OK. The condition f '=0 is practiced when looking for extrema points in the investigation of functions. The limit method, it’s… ehhh advanced. Surely irrelevant to high school students.

It seems that Dan’s concept image regarding the domain of extrema points was, an interval where f′ is zero or tends to zero. However, Dan refused to revise his definition according to his added criteria, referring to high school, curriculum issues.

What Is Not an Extreme Point?

The data in this section evolved from the PTs’ nonexamples of minima points in Task 3, from their justified rejections to Sara’s solutions in Task 4, and from their explanations in the interviews. During the interviews, each of them was asked to summarize, what points of a function are, in their view, not minima points.

All five PTs provided in Task 3 correct nonexamples of smooth minima points (Table 1). First, a maximum point of a “parabolic” graph, then, mostly points on an increasing or decreasing interval. The third nonexample of one PT was a point on the constant function y = 5.

There was a mismatch in the PTs’ evaluations of Sara’s work (Table 2). Still, every PT exhibited identical considerations when addressing the two removable-discontinuity points C and D. All in all, Sara’s solutions to points A, B, C, and D were regarded correct by some PTs yet rejected by the others. Rejections either completely disallowed the marked points, or banned Sara’s labeling points as minimum or maximum.

No Point on an Increasing/Decreasing or a Constant Interval

Mor who defined a minimum point “the lowest point in an interval of a function” (Task 1, Table 3) and fully accepted Sara’s solution (Task 4, Table 2), specified in her interview what points are not minima:

I9:Can you summarize what points of a function are NOT minima points?

Mor10:Well, it’s a bit trivial… surely A MAXIMUM is not a minimum… and where the function is NOT AT ITS PEAK. I mean, it has to be THE HIGHEST or THE LOWEST point in the interval, otherwise, it’s not an extremum… BY DEFINITION it’s not. So, also this [the point marked on y=5] is not, it’s the same height as the other points in its neighborhood…

Mor’s concept image amply corresponds with the definition of strict extrema points (see the “What Are the Main Lessons Learnt from This Study?” section ahead).

Neither on Increasing/Decreasing Intervals, nor (Any) Discontinuity Point

Anat who defined “a minimum point has the smallest value of f(x) in an interval of the function” (Task 1, Table 3), rejected in Task 4 all the discontinuous extrema points, briefly justifying “it’s discontinuous” (Table 2). In her interview, she summarized which points are not minima points:

Anat9:DISCONTINUITY POINTS can’t be extrema…

I10:Only…?

Anat11:Yes… No, also points that aren’t the HIGHEST or LOWEST.

I12:To summarize… points on a graph that are NOT minima points are…

Anat13: [looks at her pages]… on an interval where the function increases… decreases, maxima points… or ehhh… discontinuity points...

Neither Increasing/Decreasing Intervals, nor Cusp or (Any) Discontinuity Points

Gad defined “a minimum point is the lowest point in a specific neighborhood of the function,” and in Task 4 rejected all non-smooth extrema points, with meagre justifications: “it’s a cusp point” (for A), “it’s discontinuous” (for B, C, and D) (Table 2 and 3). In his interview, he summarized what points are not minima points:

Gad13:Let’s see… edgy points and discontinuity points can’t be extrema, there is no derivative there. [looks at his work] Also… points that are not the lowest… so, a maximum, and on an increasing or decreasing part…

Like Anat, Gad too tried to address a complement set to his set of examples as a set of nonexamples.

Neither Increasing or Decreasing Intervals, nor (Only) Removable Discontinuity Points

Ben’s written definition (Task 1) was based on “change in monotonicity” considerations, and in Task 4, he accepted all the points except for the removable-discontinuous extrema points C and D (Table 2 and 3). He provided no justification in writing, but in the interview, he explained:

Ben4:C is not an extremum… It’s actually NOT ON THE GRAPH… point D too... the same.

I5:What do you mean NOT ON THE GRAPH? It’s here (fingers C on the worksheet).

Ben6:It’s OUT… out of the graph…

I7:Do you mean that it’s a discontinuity point?

Ben8:THAT’S NOT IT. B is also a discontinuity point, but B is ON the edge of the interval of the graph. Those (C and D) are NOT.

I9:Can you summarize what points of a function are NOT minima points?

Ben10:Yes… a maximum, an increasing… or decreasing point [looking at his pages] and those that are not on the graph.

While initially it seemed reasonable to agree with Ben’s demand to have extrema points on the graph, his clarification that C and D are not on the on graph made it unacceptable.

Neither Increasing/Decreasing or Cusp Points, nor if f′ Is Not Zero/Does Not Tend to Zero

Dan’s written definition (Task 1, Table 3) entailed two critical attributes: “change in monotonicity” and “derivative equals zero.” In Task 4, Dan marked the cusp point A as the only “full” error (Table 2). In his interview, he explained that since the derivative, there tends to be zero from both sides, the discontinuity point B is OK, and points C and D are partly OK; they need to be re-labeled from minimum to maximum and vice versa. During our conversation, he added:

Dan4:Cusp points are NEVER extrema… because there is no derivative… and the limits of the derivative from both sides are NEVER equal… [looks at his work] also points on increasing or decreasing functions… can’t be.

I5:So, being a discontinuity-point, in itself, is NOT a problem…

Dan6:Not at all. I explained.

In his list, Dan missed out the “maximum point,” but it was a nonexamples that he drew in Task 3 (Table 1).

What Is (Surprisingly) Not a Must for an Extreme Point?

Dan’s reaction to the removable discontinuity points C and D (Task 4) felt like a vague semi-acceptance. With a sense that further clarification would help us understand his ideas, we asked him to elaborate on his explanation. Dan readily answered voicing two extraordinary ideas: Existence and uniqueness are not a must for extrema points.

Existence Is Optional

Dan was asked to read his written justification to point C and to explicate his reasoning.

Dan7:[reads] Yes, C is NOT AN EXTREMUM POINT. The place… THE X, where it’s marked is the X of the extremum, BUT C is not THE extremum point.

I8: What do you mean?

Dan9:The extremum is actually here [fingers the hole at the x of C]. The limit of the function is here… where both the derivative tends to zero, and the function tends to its minimum.

I10:The minimum is IN THE HOLE?

Dan11:Yes… a DELETED limit… It TENDS to this point [fingers the hole].

Dan’s explanation about points C and D guided us to correct our first impression that he regarded points C and D, as the extrema, which should only be labeled differently. It turned out that he did not consider those points. Not at all.

Uniqueness for a Given x Is Optional

Dan’s explanation regarding point C led us to re-discuss with him his evaluation of jump-discontinuity B.

I12:Let’s look again at point B. you marked that it IS a maximum point. Can you clarify?

Dan13:SURE. The derivative tends to zero, both… from right and left…

I14:About point C you said that the extremum is in the hole… the function tends to the hole… right?

Dan15:Yes.

I16:Look, here the function tends to B from the right, BUT, at the same x, it tends from the left to the hole beneath B…

Dan17: Wow [hesitates] Maybe I missed this maximum [fingers the hole beneath B]. Maybe, this is ALSO a maximum… the function does increase towards it and decreases afterwards…

I18:To be clear… Do you mean that BOTH, B and this point [the hole at the x of B, beneath B], BOTH are maximum points?

Dan19:Yes… I think so…

Dan holds a “change in monoticity” and “(tends to) zero-derivative” extremum concept image that seems to interfere even with his prior knowledge about the definition of “function.”

Discussion

What Are the Main Lessons Learnt from This Study?

This study offers some novel findings regarding PTs’ conceptions of extrema points and regarding their grasp of mathematical definitions in general. The data provides various explicit and oblique indications of an imperative role allotted by PTs to the non-critical attributes f′ = 0 and “change in monoticity” for extrema points. For instance, Gad who defined the minimum point as the lowest in an interval and added in his interview: “f′ = 0 is a necessary condition” (Gad6), and Dan included the condition f′ = 0 in his written definition right from the start (see also, Zaslavsky & Shir, 2005). Change in monotonicity considerations was presented in Ben’s and Dan’s written definitions, but also incidentally mentioned by Anat6 (“you decline to it, then evolve from it”). These characteristics seem to be etched in the PTs’ memory as concept identity-tags. Gad shared with us recollections of the sequence of instructional steps that familiarized him with the concept in middle school algebra and in high school calculus. We assumed that the two non-critical attributes were implicitly rooted also in the primacy effect of other participants’ early acquisition of the concept (Fischbein, 1987; Tall & Vinner, 1981). In secondary schools, definitions are widely accompanied by conventional example spaces of smooth extrema where, indeed, f′ = 0, and the function changes its monoticity. These examples are typically displayed in textbooks and used by teachers in mathematics engagements, thus playing a crucial role in learners’ concept formation (Morgan, 2005; Watson & Mason, 2005).

Many times, during early stages, primitive, lacking, definitions are taught, progressively advancing to more rigorous definitions at higher levels (Fischbein, 1987), and mathematical concepts that are included in more than one theoretical framework do not bear the same meaning and thus cause learners quite some difficulties (Kontorovitch, 2018). This is not the case here. Gad’s reference to the early definition as an unripe, primitive version that could only be shaped and finalized with derivatives, is wrong. Both, in algebra as well as in calculus, extrema points have identical definitions. The move from algebra to calculus offers, by means of theorems, derivatives as investigation tools in restricted differentiable domains. These theorems do not induce any modification of the domain of the definition of extrema (Leikin & Zazkis, 2010). For instance, there is no converse to the theorem (Ayers & Mendelson, 2008, p. 98):

If f has a relative extremum at a point x0 at which f′(x0) is defined, then f′(x0) = 0. That is, the statement: If at a point x0 at which f′(x0) is defined, f′(x0) = 0, then f has at x0 a relative extremum, is false. Still, students’ difficulties in differentiating the validity of a statement and of its converse, as well as students’ jumbling of definitions and theorems are well documented (Hoyles & Kuchemann, 2002; Nardi, 2008).

A question that comes to mind is the following: How did the PTs’ address critical attributes of extrema points? Our findings indicate the following: One of the critical attributes of local minima, which seems to be abandoned in all the PTs’ solutions, is “…the value of f at x0 is less than or equal to all values of f at nearby points” (definition A, the “Participants” section). An examination of the definitions in Zorich (2004, p. 212, quoted ahead), reveals that the five PTs seemed to hold a strict-extremum concept image:

  • Definition 1: A point x0 ε E ⊂ R is called a local maximum (resp. local minimum) and the value of a function f: E → R at that point a local maximum value (resp. local minimum value) if there exists a neighborhood UE of x0 in E such that at any point xε UE (x0) we have f (x) ≤ f (x0) (resp. f (x) ≥ f (x0)).

  • Definition 2: If the strict inequality f (x) < f (x0) (resp. f (x) > f (x0)) holds at every point x εUE (x0) / x0=ŮE(x0), the point is called strict local maximum (resp. strict local minimum) and the value of a function f: E → R a strict local maximum value (resp. strict local minimum value).

We arrived at this view from some written and some of the voiced solutions. Mor, Anat, and Gad wrote that a minimum point is “the lowest in an interval” and further stressed LOWEST in their interviews, insinuating an extreme, rock bottom point. Mor reinforced our assumption by stipulating a point on a y = 5 as a nonexample to minimum, while it is actually a (strange) example according to definition 1 (the “Participants” section). Also, Ben and Dan defined minimum points as points where the function shifts from decreasing to increasing, and Anat6 added in her interview “change in monotonicity” considerations (the “The Lowest/Highest Point in the Neighborhood” section), all implying strict extrema. This concept image might be rooted in common language expressions “the least of something… the lowest in height… the bottom” (Anat6) that convey the message of strict-bottom situations (see, Fischbein, 1987; Kasner & Newman, 1988; Pimm, 1990).

The critical attribute, that an extreme point be included in the related interval, i.e., “…open interval containing x0 (and for which f(x) is defined…” (definition A, the “Participants” section)) might seem self-evident and redundant. However, Dan’s unacceptable ideas regarding the “deleted derivative-limit, hole-extrema” proved this criterion to be, at least didactically essential. In their interviews, Mor, Ben, and Dan explicitly referred to this characteristic in different ways. Mor mentioned this attribute but addressed it as an unneeded supplement. Ben repeatedly highlighted that “an extremum has to be ON THE GRAPH” (the “A “Change in Monotonicity” Point” and “Neither Increasing/Decreasing Intervals, nor Cusp or (Any) Discontinuity Points” sections), but with an unacceptable interpretation that removable discontinuity points are “out.” Dan, however, completely omitted this critical attribute, allowing undefined points to be hole-extrema (the “Existence Is Optional” section).

Last but certainly not least is the issue of the fundamental set. As noted, only during the interviews, while re-examining their written, domain-less definitions and their solutions to the domain-sensitive Task 4, the issue of the domain riveted the participants’ attention. Subsequently, in one way or another, each of them cited a certain domain. Mor claimed, in line with the definition (the “Participants” section) that the domain is an interval in R. Anat, Gad, and Ben offered incomplete domains, thus missing out examples. Anat required continuous intervals, missing out discontinuity extrema; Ben only allowed extrema either within smooth intervals or at the edge of jump discontinuity points, missing out removable discontinuity extrema and Gad required differentiability, missing out cusp and discontinuity extrema; An overextended domain was offered by Dan, thus missing in examples. His domain included perforated intervals with non-existent, missing in holes or gaps where the function is not defined. Even more troubling than the absence of the domain were the justifications provided for the insufficient definitions and PTs’ reluctance to revise these definitions. The following motives surfaced in PTs’ justifications:

  1. a.

    It suffices to include in the definition only the most typical characteristics—Anat6 said: “I wrote the main… the most important, the characteristic that MAKES a point minimal”, and Gad10 suggested that he provided “the BASIC definition”. Furthermore, and in this spirit, PTs’ viewed obvious attributes as being redundant. Anat6 said: “Should I also include this [continuity condition] in the definition? [thinking]… It feels too obvious…”, and Mor2 giggled when mentioning that “THE POINT IS IN [the domain]”, then omitted it from her revised definition. This can be a result of the widespread, secondary school culture in Israel, where citation of partial definitions within mathematical solutions is regarded acceptable (see also, Nardi, 2008).

  2. b.

    Although they were asked to focus on the mathematics at hand (no didactics), PTs were reluctant to include the domain in their definitions due to high-school teaching–learning issues (Mor4, Mor8, Anat6, Dan3). The boundaries between mathematical and pedagogical matters are occasionally vague. Still, proficiency in both and an ability to differentiate between them is valuable (Ball & Bass, 2000; Dreher et al., 2018; Krauss et al., 2008). Consequently, Mor and Anat reluctantly revised their definitions and Dan3 refused to do it, explaining that his (erroneous) zero-derivative-limit ideas are “irrelevant to high school students”.

Where Can We Go from Here?

Having presented our findings, one may wonder: “So what”? What practical benefits can a teacher educator possibly gain from this study? Our answer is sharp and clear—the mathematics education community by and large could largely benefit from such studies. The mathematics education community includes teachers, teacher educators, researchers, curriculum developers, and instruction designers. For each of these members, knowing what is easy for learners and where difficulties might arise is regarded as fundamental knowledge (Ball et al., 2008; Carpenter et al., 1989; Fischbein, 1987). By taking into consideration research publications, the emphasis in teaching (for instance, allotted time, specific activities) would be professionally put on the challenging issues. In the following section, we offer research-based suggestions for some instructional measures.

Two possible, next-step avenues are the following: using the data in designing instruction and delineating some follow-up studies. Having secondary school mathematics PTs in mind, promoting their conceptions of extrema points can serve as an aim and as a means in widening the scope to general issues, like mathematical definitions, examples, nonexamples, and the relationships among them. In academic publications, the importance of clear definitions, both from a mathematical and a pedagogical point of view, is emphasized (De Villiers, 1998; Edwards & Ward, 2008; Vinner, 1991). For this sake, it is advisable for instance to assign PTs to write definitions for minimum point, and then, to encourage group discussions where each participant presents his/her definition, and the colleagues reflect on every suggestion (Borasi, 1996; Mason, 2004; Nardi, 2008; Pimm, 1990). It is also possible to ask the group to evaluate the definitions presented in related publications, such as our study (Borasi, 1996; Zaslavsky & Shir, 2005). We believe that specific attention should be paid to the hierarchical nature of mathematical definitions, and more specifically to related fundamental sets (in our case, the domain). PTs should also be trained to reflect on their own definitions, bearing in mind that “obviousness is always the enemy to correctness” (Russell, 1988/1956, p. 1553).

Growing appreciation to the role of examples in shaping learners’ grasp of mathematical concepts led to studies, recommending various ways of employing example activities (Borasi, 1996; Petty & Jansson, 1987), such as learner-generated examples (Leikin & Winicki-Landman, 2001; Watson & Mason, 2005). Asking PTs to construct routine, intuitive and also non-routine, unintuitive examples and nonexamples, is recommended, as a means to widen their example spaces and to discuss the related definitions (Mason, 2004; Nardi, 2008; Tsamir et al., 2008; Watson & Mason, 2005). For instance,

If possible, draw a graph of a function and mark on it

  1. a.

    A minimum point M1

  2. b.

    A minimum point M2 that is a cusp point

  3. c.

    A minimum point M3 that is a discontinuity point.

If in your opinion it is impossible, explain why.

It is also possible to present the PTs with a collection of options, like the ones in our study, or based on our findings, asking whether these are extrema points, and to discuss the mis-in and mis-out examples. In general, engagement with concepts in teacher education should include experiences going from examples to definitions and also from definitions to examples (Edwards & Ward, 2008).

Clearly, it is advisable that our novel findings be reexamined in a wider scale research, and that any experimental intervention be accompanied by well-designed studies for careful examination (Fischbein, 1987).