1 Introduction

What kind of content knowledge (CK) do secondary mathematics teachers need? How can a profession-specific mathematical CK be characterized? These questions are highly relevant for the design of mathematics teacher education programs as well as for investigating teachers’ professional knowledge. As the field of mathematics education encompasses different research traditions, such central questions can be considered from different perspectives. Bishop (1992) distinguished three different research traditions—pedagogue tradition, empirical scientist tradition, and scholastic philosopher tradition—which provide a means to structure different perspectives concerning these questions. In the pedagogue tradition, the goal of enquiry is the direct improvement of practice (e. g., Bishop 1992, p. 713). Regarding the issue of secondary mathematics teachers’ CK, this would mean that the design of specific teacher education programs and courses is paramount, which is the case for practice-oriented development projects such as “Mathematik neu denken” (Thinking mathematics in new ways) that restructured the teacher education program for the higher secondary level at the universities in Gießen and Siegen (e. g., Beutelspacher et al. 2011). However, in order to investigate systematically what kind of learning opportunities in teacher education are effective or whether there is an interrelation between secondary teachers’ CK and their instructional quality or student learning, it is necessary to have a corresponding model of teacher professional knowledge, a conceptualization of secondary mathematics teachers’ CK, and a corresponding operationalization. Such research, which has the aim of explaining educational reality by means of objective data, can be seen in the empirical scientist tradition (e. g., Bishop 1992, p. 713). Especially during the past 15 years, this kind of research on teachers’ professional knowledge has received a lot of attention among researchers in mathematics education. As a result, there is a broad base of research on how to conceptualize and capture the professional knowledge of mathematics teachers (e. g., Hill et al. 2004), on effects of professional knowledge on student learning outcomes (e. g., Baumert et al. 2010), and on the development of professional knowledge during the course of mathematics teacher education (e. g., Blömeke et al. 2014). Most of these studies are based on models for teachers’ professional knowledge which draw on the categories “content knowledge” and “pedagogical content knowledge” identified by Shulman (1986). However, since Shulman’s model is quite general, it is, for instance, not clear how to conceptualize and operationalize the construct of teachers’ professional CK. Consequently, existing studies show wide discrepancies regarding this construct, which is usually conceptualized based on school subject knowledge and refers to academic mathematics to a greater or lesser extent (e. g., Heinze et al. 2016). This problem indicates that the answer to the introductory questions by means of the third research tradition, the scholastic philosopher tradition (Bishop 1992), is not yet clear. The goal of inquiry from this perspective is to establish a theoretically argued position—in this case regarding the question as to what kind of profession-specific CK secondary teachers need, i. e., what is the idealized situation toward which educational reality should aim? Accordingly, as early as in the 1970s, Fletcher (1975, p. 206) pointed out the need to specify such a profession-specific mathematical knowledge:

The mathematics teacher requires a general knowledge of mathematics in order to be able to communicate with other mathematicians and also to establish his credentials; but he also requires special knowledge of certain areas of mathematics, in the way that an engineer or an astronomer requires special knowledge. […] It is part of our problem that the teacher’s special mathematical knowledge is inadequately defined and insufficiently esteemed.

Thus, although our main goal was to empirically investigate a construct of profession-specific CK of secondary mathematics teachers (e. g., Heinze et al. 2016), it is necessary to elaborate in detail on the theoretical foundation of such a construct. Hence, while Heinze et al. (2016) took mainly the stance of the empirical scientist tradition on conceptualizing discipline-specific teacher knowledge, the aim of this article is to outline the theoretical argumentation that leads to the proposed construct school-related content knowledge (SRCK) as a specific mathematical CK that secondary mathematics teachers need.

To this end, we begin with a consideration of the difference between academic and school mathematics that makes salient the issue that it is not clear what kind of mathematical CK secondary mathematics teachers need. Our approach to obtain insight into how such a profession-specific CK of secondary mathematics teachers should be characterized is to resume currently unconnected ideas to bridge the gap between academic and school mathematics. We will then integrate these ideas in order to introduce our conceptualization of SRCK that comprises knowledge concerning the non-trivial relations between academic and school mathematics. Subsequently, we illustrate an operationalization of SRCK by possible sample items, and its distinction from the well-known construct specialized content knowledge (e. g., Ball et al. 2008) will be discussed.

2 The Difference Between Academic and School Mathematics

Studying mathematics, one usually realizes that the kind of mathematics taught at university is apparently different from the kind of mathematics taught at school (e. g., Deng 2007; Klein 1932 [1908]; Schweiger 2006; Tall 1992). It is well known that already at the beginning of the twentieth century, Felix Klein emphasized that there is a discrepancy between the mathematics taught at schools and the mathematics taught at university (1932 [1908]). At that time in Germany, the gap between school mathematics and academic mathematics was understood mainly in terms of content, since at school, merely algebraic analysis was taught, whereas in university courses, the focus was exclusively on infinitesimal calculus (e. g., Allmendinger 2016). In this spirit, Klein (2016, p. 166 [1908]) criticized that “the teacher manages to get along still with the cumbersome algebraic analysis, in spite of its difficulties and imperfections, and avoids any smooth infinitesimal calculus” and that “the university frequently takes little trouble to make connection with what has been taught at schools, but builds up its own system”. However, Klein also saw differences between the mathematics taught at school and the mathematics taught at university that go beyond aspects of content. He characterized school mathematics as being “intuitive and genetic, i. e., the entire structure is gradually erected on the basis of familiar, concrete things, in marked contrast to the customary logical and systematic method in higher education” (Klein 2016, p. 9 [1908]). Hence, even though infinitesimal calculus has been—at least to a certain degree—included into upper secondary school mathematics in the meantime, differences between the kinds of mathematics taught at school and at university remain. These have been illustrated for instance by Wu (2011). One of his examples was the topic of fractions, which is central in lower secondary mathematics: When fractions are taught in university mathematics courses, usually ℚ is defined as a set of equivalence classes of ordered pairs of integers. Addition and multiplication on this set are subsequently defined such that the axioms of a ring are satisfied and it is routinely checked that these definitions are compatible with the equivalence relation. Hence, the rational numbers are introduced in an axiomatic-deductive way, which is typical for how academic mathematics is taught. This introduction is characterized by a high level of abstraction as well as a symbolic mathematical language and it illustrates what Klein called the “customary logical and systematic method in higher education” (Klein 2016, p. 9 [1908]). When fractions are taught in school mathematics, the introduction normally does not start with a definition, but with a context. In order to present fractions as parts of a whole, often “familiar and concrete things” (Klein 2016, p. 9 [1908]) like pizzas or chocolate bars are used. Since it is not defined what a “whole” is, the pizza is used as a prototypical “whole” (Wu 2011, p. 374). Also the way in which addition and multiplication of fractions works is justified in a different manner compared to the university course: If the learners are not just asked to learn the calculation rules without any reasoning, then, usually, contexts like pizza and chocolate bars are used to make sense of why the rules should work like this. However, at this point it is not enough to interpret a fraction as a part of a whole and students are thus asked to understand fractions as different things at the same time (e. g., an operator or a ratio). There is generally not much reasoning about why fractions can be all these things at the same time and sometimes it is even said that \(\frac{3}{4}\) is “3 divided by 4,” which is not mathematically coherent with the students’ understanding of division, as argued by Wu (2011, p. 374). In the context of the mathematics taught at university, however, Wu pointed out that given suitable definitions of “part of a whole” and of “\(m\div n\) for arbitrary integers \(m\) and \(n(n\neq 0)\)”, it is a provable theorem that, indeed, \(\frac{m}{n}=m\div n\). In particular, this illustrates that the kinds of mathematics taught at school and at university differ also in terms of rigor and in the necessity that is seen for justification.

To sum up, this and also further examples (e. g., Wu 2011) show that these two kinds of mathematics typically differ in the following aspects: Mathematics as the scientific discipline taught at university has an axiomatic-deductive structure and focuses on the rigorous establishment of theory in terms of definitions, theorems, and proofs. It usually deals with objects that are not bound to reality and it is often characterized by a high level of abstraction and a symbolic mathematical language (e. g., Bourbaki 1950; Tall 1992; Wu 2011).

Of course, it should be noted that mathematics as a scientific discipline does not always work in an axiomatic-deductive manner. Taking the example of fractions, it is obvious that fractions were introduced and used in mathematics before the discipline had its axiomatic structure. Also when new concepts are found in mathematical research, the concept formation does not usually happen deductively. However, when mathematical results are reported in journals or books, and when mathematics is taught to university students, it is usually presented in an axiomatic-deductive way. Since this is the kind of mathematics that prospective secondary mathematics teachers as well as future mathematicians are confronted with during the course of their university studies, this is the kind of mathematics we refer to throughout this article by using the term academic mathematics.

On the other hand, mathematics as a school subject usually places its main focus on applying mathematics as a tool for describing as well as understanding reality, and for facilitating everyday live (literacy concepts, e. g., Jablonka 2003). Consequently, mathematical objects are often introduced in an empirical manner and bound to a certain context. Concept formation in mathematics classrooms at school is, accordingly, often done in an inductive way by means of prototypes (e. g., Bromme 1994; Wu 2011). Mostly, intuitive and context-related reasoning is more in the focus than rigorous proofs. This is the kind of mathematics we refer to by the notion of school mathematics.

Discrepancies between a school subject and the related academic discipline do not only exist in the case of mathematics, but are a more general phenomenon, as Bromme (1994, p. 74) pointed out:

The contents of teaching are not simply the propaedeutical basics of the respective science. Just as the contents to be learned in German lessons are not simplified German studies, but represent a canon of knowledge of their own, the contents of learning mathematics are not just simplifications of mathematics as it is taught in universities. The school subjects have a “life of their own” with their own logic; that is, the meaning of the concepts taught cannot be explained simply from the logic of the respective scientific disciplines. […] Rather, goals about school (e. g., concepts of general education) are integrated into the meanings of the subject-specific concepts.

The insight that “purposes of schooling and the concept of development” are important factors for this discrepancy was also pointed out by Deng (2007, p. 510) in his discussion of what sets school subjects apart from academic disciplines. Moreover, he emphasized a position identified by Stengel (1997) that construes academic and school subjects as different but related in a dialectic fashion. Since Stengel (1997) argued that Dewey’s discussion of his well-known logical-psychological distinction epitomizes this position, Deng (2007) analyzed Dewey’s work from this perspective. Accordingly, for Dewey, the academic discipline “is developed with a primary reference to the end-product of academic inquiry” and the school subject on the other hand “is formulated in a way that takes into account the experience of the immature learner” (Deng 2007, p. 511). Hence, the structure of the school subject takes into account a psychological perspective. Connected with this psychological aspect of a school subject is the epistemological question of “How, out of the crude native experience which the child already has, the complex and systematic knowledge of the adult consciousness is gradually and systematically worked out” (Dewey 1972, p. 177). Furthermore, Dewey (1972) pointed out that there are also social aspects that shape the structure of school subjects, since a school subject has the task of preparing learners to meet the needs of the present society.

Taking a look back at the descriptions of academic mathematics and school mathematics given above, one recognizes in these explanations by Dewey the reasons for the major differences between these two kinds of mathematics. However, academic discipline and school subject are also dialectically related: “The former supplies the guidance and direction for the latter, and reveals the possibilities of growth inherent in the experience of the learners […]. The latter is considered as the means of leading the learner toward the realization of these possibilities” (Deng 2007, p. 513). Therefore, in a sense, academic mathematics precedes school mathematics, as it functions as a frame of reference for the structure of school mathematics. However, in another sense, school mathematics precedes academic mathematics, since it provides the path for getting to know academic mathematics.

3 What Mathematics Do Secondary Teachers Need to Know? An Old Question and Ongoing Discussion

In view of these major differences between academic and school mathematics, the question arises as to what kind of mathematics secondary school teachers need to know and what kind of mathematics prospective mathematics teachers should be taught. Is it school mathematics? Or academic mathematics? Or both? Or something else? Questions like these have already been raised by Otte in 1979: “How in particular is his [the mathematics teacher’s] knowledge related to the content of the mathematics school curriculum and to mathematics as a science?” (p. 119).

Since academic mathematics is different from what mathematics teachers teach at school, one could argue that CK in mathematics teacher education should mainly focus on school mathematics. There is, however, a broad consensus among scholars and researchers in mathematics education that mathematics teachers in general—and in particular those teaching at a secondary level—need to have insight into academic mathematics (e. g., Dörfler and McLone 1986; Ferrini-Mundy and Findell 2001; Fletcher 1975; Winsløw and Grønbæk 2014). Klein (1932, p. 192 [1908]) already pointed out that “the teacher’s knowledge should be far greater than that which he presents to his pupils. He must be familiar with the cliffs and the whirlpools in order to guide his pupils safely past them”. Consequently, in many countries, teacher education for secondary schools includes large parts of academic mathematics, especially if there is a focus on the upper secondary level (e. g., Blömeke et al. 2014; Speer et al. 2015). This often means that prospective mathematics teachers take largely the same courses as their fellows studying mathematics as a scientific discipline. This approach usually ensures that these prospective teachers know far more mathematics than their future students, but it does not guarantee that they can guide them safely past “the cliffs and the whirlpools” in the mathematics classroom. The gap between the academic mathematics taught at university and the school mathematics is often too wide, so that prospective mathematics teachers are not able to make connections. Based on the frequently cited quote of Felix Klein (1932, p. 1 [1908]), this problem is well known as “double discontinuity.” About 100 years after Klein, Wu (2011, p. 372) argued even more critically: Teaching secondary teachers the same advanced mathematics as prospective mathematics researchers and expecting “the Intellectual Trickle-Down-Theory to work overtime to give these teachers the mathematical content knowledge they need in the school classroom” is as ridiculous as teaching future French teachers Latin instead of French.

Hence, it appears to be neither sufficient to teach prospective (secondary) mathematics teachers school mathematics nor does academic mathematics alone ensure that pre-service teachers have the CK needed in the mathematics classroom (e. g., Buchholtz et al. 2013; Dörfler and McLone 1986). Against this background, Klein (e. g., 2016 [1908]) suggested that prospective (secondary) mathematics teachers should be taught elementary mathematics from a higher standpoint. In his corresponding lecture series for pre-service secondary teachers, which required knowledge of the main fields of academic mathematics as a prerequisite, he focused on relations between academic mathematics and school mathematics by taking an academic-mathematical perspective on school mathematics (e. g., Allmendinger 2016). However, what is a contemporary interpretation of his well-known notion? Understanding the non-trivial relationship between academic and school mathematics appears to be central to answering this question. Hence, analyzing this relationship as well as figuring out how the gap between these two kinds of mathematics may be bridged appears to be essential for characterizing the specific CK secondary mathematics teachers need.

4 Theoretical Approaches to Bridging the Gap

In the following, theoretical considerations of the relationship between academic and school mathematics as well as corresponding professional requirements for secondary mathematics teachers according to different scholars are reviewed. Subsequently, these approaches will be integrated in order to characterize a profession-specific mathematical CK for secondary mathematics teachers.

4.1 Curriculum Development and Fundamental Ideas

The first approach reviewed here addresses the gap between academic and school mathematics in terms of linking them by focusing on the curriculum. This was already an aspect of Klein’s lecture series, where curricular questions were addressed (e. g., Allmendinger 2016). Later, in the context of development of new curricula in the 1960s and 1970s, an intense discussion emerged about what CK teachers need. Fletcher (1975) pointed out, for instance, that curricula can only be implemented in the classrooms if teachers understand and accept them. Such curricular knowledge is not part of school mathematics itself, since the curricular structure is not usually a topic in the mathematics classroom. Hence, teachers should not only know school mathematics, but they should also know about its structure in the sense of meta-knowledge. This is, in the first instance, factual knowledge about the curricular order of contents and their interdependencies. However, in order to understand the structure of school mathematics, there is also knowledge needed about reasons for this curricular structure, which are at least partly rooted in the structure of academic mathematics. As pointed out above, it is part of the dialectical relation between the two kinds of mathematics that academic mathematics supplies guidance and direction for school mathematics. Hence, the structure of the academic discipline functions to a certain extent as a frame of reference for the curricular structure of school mathematics (e. g., Bruner 1960; Schwab 1964; Shulman 1986). Bruner (1960) suggested focusing on so-called fundamental ideas as a means to capture the structure of the discipline and thus to find answers to the question as to which mathematical contents should be part of a school curriculum. He described an idea as being fundamental if it has “wide as well as powerful applicability” (Bruner 1960, p. 18). Later, fundamental ideas of mathematics were characterized more precisely by four descriptive criteria (e. g., Schweiger 1984): Accordingly, these ideas (1) recur in the historical development of mathematics (time dimension), (2) recur in different areas of mathematics (horizontal dimension), (3) recur at different levels (vertical dimension), and are (4) anchored in everyday activities. Focusing on such fundamental ideas of mathematics (e. g., measuring, function, and symmetry) affords giving well-justified answers to the question as to which mathematical contents should be part of the curriculum and also facilitate bridging the gap between academic and school mathematics (e. g., Schweiger 2006). Hence, in order to understand the structure of school mathematics (i. e., the school curriculum), mathematics teachers should know about fundamental ideas of mathematics as a legitimation of this structure as well as of the selection and focus of contents.

However, such attempts to bridge the gap between academic mathematics and school mathematics on a global level cannot be entirely successful, since school mathematics can reflect the structure of academic mathematics to only a limited extent, even when mediated by fundamental ideas (e. g., Schweiger 2006). From the perspective of academic mathematics, school mathematics remains incomplete and even inconsistent, since by far not all the systematic reasoning of academic mathematics is possible in school mathematics (e. g., Freudenthal 1973; Klein 2016 [1908]). In order to deal with this, teachers should—in Klein’s (1932, p. 192 [1908]) words—“be familiar with the cliffs and the whirlpools in order to guide his pupils safely past them”. Accordingly, the teacher should know, for instance, that the fundamental laws of reckoning (e. g., the associative law) in school arithmetic cannot be shown in a purely logical way, but depend on intuition. Even if an axiomatic-deductive perspective in terms of academic mathematics is taken, the justification of the application of these axioms to actual conditions in the real world is not clear (e. g., Klein 2016 [1908], p. 17). This means that connections between academic and school mathematics must be made on the level of specific contents. This can be done in two different directions: top-down and bottom-up (i. e., with academic or school mathematics as a starting point, respectively). Ideas regarding both of these directions can be found already in early reflections on the profession of mathematics teachers and the relation between academic and school mathematics. Hence, corresponding approaches will be reviewed in the following.

4.2 Transforming Mathematical Contents for Teaching Purposes

Taking academic mathematics as a starting point (i. e., the top-down direction), the question as to how such mathematical contents can be transformed for teaching purposes has always been central for scholars and practitioners of mathematics education (e. g., Dörfler and McLone 1986; Fletcher 1975; Freudenthal 1973; Kirsch 2000 [1976]; Klafki 1995 [1958]). In the 1950s, Klafki (1995 [1958]) described, for instance, how contents of the academic discipline can be reduced for the school classroom by means of a so-called “didactical analysis,” which focuses on exemplifying in order to make fundamental ideas visible and graspable. Another well-known example is Chevallard’s (1985) theory of didactic transposition, which builds on Brousseau’s (1997) theory of didactic situations set up in the 1970s: The idea of didactic transposition is that “for certain knowledge to be taught at school transpositive work needs to be carried out so that something that was not made for school changes into something that may be reconstructed inside school” (Bosch and Gascón 2006, p. 53).

On the one hand, such transformations from academic to school mathematics encompass processes of reduction or trimming (e. g., McCrory et al. 2012), where detail is intentionally omitted or the level of rigor is lowered, while taking care that the contents are still taught in an “intellectually honest” way (Bruner 1960, p. 33) and that mathematical integrity is maintained (e. g., Ball and Bass 2000). On the other hand, decompressing or unpacking may be in the focus of the transformation (e. g., Ball and Bass 2000; Cohen 2004; McCrory et al. 2012). Ball and Bass (2000, p. 98) pointed out that “because teachers must be able to work with content for students in its growing, not finished, state, they must be able to do something perverse: work backward from mature and compressed understanding of the content to unpack its constituent elements”. The problem that lies behind the need for decompressing is what Sfard (1991, p. 20) called reification: In the course of learning mathematics, processes and actions are replaced by objects; “various representations of the concept become semantically unified by this abstract, purely imaginary construct”. Sfard (2008, p. 59) argued that for this reason: “we lose the ability to see as different what children cannot see as the same”. Hence, teachers need to actively deconstruct their own mathematical knowledge (academic mathematics) into the different representations and processes that are yet to be connected and integrated by the learners in the mathematics classroom.

We may thus conclude that secondary mathematics teachers need to know how to transform mathematical contents for teaching purposes in the sense of reducing and decompressing academic mathematics into school mathematics. To this end, they need to make connections between academic and school mathematics, and take care of both mathematical integrity and the specific character of school mathematics.

4.3 Mathematical Background Theories

Since teachers often have to deal with textbooks and learning environments that contain already transformed mathematical contents, they also have to be able to decide whether these contents have been transformed in an appropriate way. In this case, school mathematics can be seen as a starting point and therefore connections between school and academic mathematics have to be made in bottom-up direction. This encompasses, for example, checking whether a definition in a school textbook is usable by learners at a particular level and whether it is still also mathematically appropriate (e. g., Ball and Bass 2003). Also in the interaction with students, connections in bottom-up direction have to be made, for instance when evaluating creative questions and answers by students with respect to the mathematical contents and ideas involved (e. g., Ferrini-Mundy and Findell 2001).

Hence, teachers also have to know how the topics of school mathematics are rooted in the structures of the academic discipline. This means knowing which mathematical definitions, theorems, proofs, and ideas lie behind specific contents in the mathematics classroom. Such connections, made in bottom-up direction, were considered by scholars particularly in the course of subject-specific lesson planning. In the 1970s, for instance, the concept of “(heteronomous) mathematical background theories” (German: “(heteronome) Hintergrundtheorien”) was introduced (e. g., Becker 1977; Vollrath 1979, 1988). According to Vollrath (e. g., 1979, p. 8–9), this notion (in a broad sense) was used to describe the complex of mathematical concepts, statements, interrelations, methods, and representations that lie behind a sequence of teaching in the mathematics classroom. Such background theories were typically developed by scholars beginning with a pedagogical decision such as using a real-world situation as a starting point for a mathematical content domain (e. g., Vollrath 1979). Since the background theory of a teaching sequence intended by a school textbook is usually not published explicitly, teachers often have to make connections to such a mathematical background theory themselves (e. g., Vollrath 1979).

Of course, whether connections are made in top-down or bottom-up direction may not always be clearly distinguished: Considering the interplay between academic and school mathematics in practice, there is often no obvious starting point, but rather both of them have to apparently be looked at simultaneously. However, in order to avoid a one-sided perspective, both directions merit attention in making connections between academic and school mathematics.

Until recently, Klein’s (2016 [1908]) elementary mathematics from a higher standpoint was understood as taking into account merely top-down connections (e. g., Allmendinger 2016). For this reason, different scholars explicitly added a bottom-up component in the sense of higher mathematics from an elementary standpoint in order to complement Klein’s idea (e. g., Courant and Robbins 1962; Kirchgraber 2008). Indeed, in his lectures, Klein (2016 [1908]) focused mainly on making connections in top-down direction, starting from the academic mathematics that functioned as a prerequisite for the lectures. However, as Allmendinger (2016) pointed out, in fact both directions were addressed in Klein’s lectures. Instances where Klein took school mathematics as a starting point for making connections between the two kinds of mathematics can be seen when he developed a background theory in view of the introduction of the logarithm function common in school mathematics, as well as when he criticized the usual introduction of negative numbers in school mathematics against the background of academic mathematics.

5 Toward a Comprehensive Conceptualization of Secondary Teachers’ Mathematical Content Knowledge

Informed by these early reflections on the profession of mathematics teachers and the relation between academic and school mathematics, we argue that secondary mathematics teachers need a specific kind of mathematical CK to make connections between academic and school mathematics. In order to distinguish this mathematical CK from the academic mathematical CK that these teachers typically learn in the mathematics courses at university and that they have in common with research mathematicians, we call this specific mathematical CK school-related content knowledge (SRCK). We understand SRCK as a special kind of mathematical CK for teaching secondary mathematics. It is a conceptual mathematical CK about interrelations between academic and school mathematics, and thus this CK component comprises knowledge of elements of academic and school mathematics as well as of their relations. SRCK clearly differs from academic CK as well as from pedagogical content knowledge (PCK), and goes beyond school mathematics. In contrast to the academic CK that prospective secondary mathematics teachers share with future research mathematicians, SRCK necessarily includes knowledge about school mathematics and its non-trivial interrelations with academic mathematics. Contrary to PCK, SRCK is CK that is not blended with pedagogical knowledge—hence, there is, for instance, no knowledge on typical students’ misconceptions needed.

5.1 Three Facets of School-Related Content Knowledge

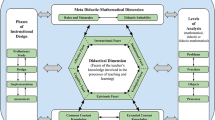
Corresponding to the three kinds of theoretical approaches reviewed in the previous section, SRCK was conceptualized to consist of three facets: (1) knowledge about the curricular structure and its legitimation in the sense of (meta-)mathematical reasons as well as knowledge about the interrelations between school mathematics and academic mathematics in (2) top-down and in (3) bottom-up directions. The model shown in Fig. 1 illustrates in a systematic way this conceptualization of SRCK, consisting of three components and the construct’s relation to CK of school mathematics and CK of academic mathematics.

Fig. 1
figure 1

Conceptualization of school-related content knowledge (SRCK)

Full size image

The facet of curricular knowledge about the structure of school mathematics and corresponding reasons encompasses knowledge concerning the following kinds of questions:

  • For what mathematical or meta-mathematical reasons are specific topics treated in school mathematics? This includes, for instance, knowledge about fundamental ideas of mathematics and the significance of certain topics regarding these ideas (e. g., Why has the topic of functions a prominent role in school mathematics? Why are fractions taught at school?). However, this facet does not include knowledge about non-mathematical reasons such as normative educational goals.

  • What are the mathematical ideas by which you can explain a mathematical concept to a student in a certain grade? This includes knowledge about the concepts and ideas that were taught in previous grades (see sample item in Table 1).

  • Which concepts and ideas will be picked up in further grades? This includes knowledge about which aspects of a concept need to be discussed since they are mathematical prerequisites for what will be learned later (e. g., What aspects of the real numbers should be treated when they are introduced in order to facilitate the concepts of analysis that will be treated later?).

Table 1 Sample item “structure of school mathematics”
Full size table

The facet of knowledge about interrelations between school mathematics and academic mathematics in top-down direction encompasses knowledge concerning the following kinds of questions:

  • How can a certain mathematical idea be reduced for teaching purposes in the school context? This includes knowledge about which definitions, approaches, examples, etc. maintain mathematical integrity and take into account the specific character of school mathematics (see sample item in Table 2).

  • How can a certain mathematical idea be decompressed? This includes knowledge about which different representations and processes were compressed to a specific mathematical concept (e. g., function, completeness) that are not yet integrated by the learners in the mathematics classroom.

  • With what kind of mathematical problem can learners discover a certain mathematical idea (e. g., density of rational numbers, infinity)? This includes knowledge about problems that are adequate in the school context and have the potential to give insight into a certain mathematical idea.

Table 2 Sample item “top-down direction,” solution indicated by crossed boxes
Full size table

The facet of knowledge about interrelations between school mathematics and academic mathematics in bottom-up direction encompasses knowledge concerning the following kinds of questions:

  • Which mathematical ideas might be reflected by a student’s remark in class? This includes knowledge about the definitions, theorems, and proofs that can be seen behind such a remark, as well as about its adequacy in the context of school mathematics and in terms of mathematical integrity.

  • Is the introduction of a mathematical concept, a definition, theorem, or proof given in a textbook or a certain learning environment “intellectually honest” (Bruner 1960, p. 33)? This includes knowledge about corresponding definitions, theorems, and proofs in academic mathematics (see sample item in Table 3).

  • Which reasons/proofs lie behind claims and assumptions that are often made implicitly in school mathematics? This includes knowledge about the cliffs and whirlpools past which students should be guided safely (Klein 1932 [1908]; e. g.,: In grade 6, the expression \(0.\overline{9}\) is introduced as a process. The fact that \(0.\overline{9}\)can be considered as a number is based on a limit process which remains implicit in grade 6).

Table 3 Sample item “bottom-up direction”
Full size table

5.2 An Operationalization of School-Related Content Knowledge

In the following, these facets will be illustrated by means of sample items that could be used for an operationalization of this construct.

As reasoned above, curricular knowledge in the sense of knowing about the curricular order of contents and their interdependencies is not school mathematical knowledge, but rather grasps the structure of school mathematics on a meta-level. Since the curricular structure of school mathematics is culture dependent to a certain extent, it should be noted that the example given in Table 1 refers to the German context. It could of course be adapted to other national or regional affordances.

School mathematics has a “life of its own” (Bromme 1994) and hence does not necessarily satisfy the scientific standards of academic mathematics. Regarding the example of the number π as the relation between the circumference and the diameter of a circle, this can be illustrated in a prototypical way. There are essentially two challenges: (1) Finding the relation between circumference and diameter of a specific circle in order to find the numerical value of π and (2) a justification for the fact that this relation is the same for all circles (usually done by the argument that all circles are similar). However, in some German states (e. g., Bavaria) the curricula locate the introduction of the number π not in grade 9 or 10 after the mathematical requirements have been treated, but already in grade 7, in the context of the topic “proportionality.” From the perspective of academic mathematics, this leads to problems that should be recognized by secondary teachers (and this affords SRCK). To this end, they need to know how school mathematics in grade 7 treats proportionality. The concept of proportionality is normally introduced inductively, by means of real-world examples where relations are considered, for instance, between number of items and price. This is also done with the relation between circumference and diameter by measuring with respect to a few circles. Bringing up the problem of measurement inaccuracy, a proportional relationship is then inductively accepted as being plausible. Such an approach is not unusual in school mathematics and thus expresses an essential difference to academic mathematics, as was outlined above. The item shown in Table 1 addresses the problem that within the scope of such an approach in grade 7, it cannot be justified that the number π is identical for all circles. For a correct answer it should be known that a mathematical requirement for this justification is usually the topic of similarity, and that this topic has not yet been treated in grade 7. Alternatively, it can also be justified that “limit processes” is a topic that is missing at this point.

As reasoned above, secondary mathematics teachers need a certain sensitivity for inconsistencies between academic and school mathematics at the level of specific contents. To this end, they need to make connections between elements of school mathematics and corresponding elements of academic mathematics, as well as vice versa. On the one hand, secondary mathematics teachers need knowledge to transform academic mathematics into mathematical contents that can be taught at school and, on the other hand, they need to know what academic mathematics lies behind the school mathematics they encounter in textbooks, learning materials, and in the classroom. The sample items shown in Tables 2 and 3 illustrate how such knowledge regarding corresponding interrelations in top-down and bottom-up directions may be operationalized.

In academic mathematics, the complete ordered field of real numbers is constructed from the field of rational numbers, such that the operations are preserved. There are different approaches, all of which are abstract and involve equivalence class formation. From a top-down perspective, the item given in Table 2 addresses the question as to how this topic can be treated in the mathematics classroom in a way that both mathematical integrity is maintained and the specific character of school mathematics is taken into account. Introducing the real numbers in the mathematics classroom does not merely aim at the existence of irrational numbers, but also at embedding the familiar field of rational numbers into the newly constructed field of real numbers (including the plausibility of the preservation of the operations). To this end, the fact that the rational numbers are dense in the real numbers is essential. In school mathematics this is illustrated by means of the decimal number representation of the rational numbers, since this—together with the localization on the number line as a geometric representation—has been the consistent element of number representation since the beginning of elementary school. Contrary to academic mathematics, school mathematics is essentially based on representations that facilitate an empirical inductive access using specific examples (e. g., Freudenthal 1973). Hence, the reduction of abstract procedures of academic mathematics for the mathematics classroom needs to provide a corresponding possibility to make them tangible. Considering the four options given in the sample item against this background suggests that not all of them should be chosen: The topological closure can only yield the set, but not the field of the real numbers. Furthermore, the reduced version (“filling in gaps on the number line”) does not indicate the density (“size” of the gaps is not clear) and does not yield any connection to the decimal number representation. The approach using Cauchy sequences is also not suitable for this purpose, as it is too abstract. The Dedekind cuts can easily be represented on the number line, but in a reduced form this approach also does not yield the density or any connection to the decimal number representation. To this end, in addition, a sequence representation similar to the one that is commonly used in the reduced form of nested intervals would be necessary. In this case, the Dedekind cuts would not have any added value compared to the nested intervals except from some abstract additional information (the two partitioning subsets) that is not relevant for dealing with real numbers in school mathematics.

According to the bottom-up facet of SRCK, the sample item given in Table 3 focuses on knowledge about connections between given elements of school mathematics and corresponding elements in academic mathematics. In this case, the folding operation as an element of school mathematics is central. This operation is usually introduced already in elementary school as an enactive representation of the reflection across a line, where the folding line represents the axis of reflection (even though the folding line is of finite length). In the sample item, double folding is used to introduce the relation of being perpendicular regarding lines in the plane. This approach fits the character of school mathematics in the sense that the introduction of concepts is often tied to the real-world experiences of the students and processes, which are subsequently abstracted (e. g., Freudenthal 1973; Sfard 2008). Hence, the mathematical definition of the reflection across a line (two lines g, h are called perpendicular, if g ≠ h and a reflection across h maps g onto itself) lies behind the folding activity described in the item.

6 Is School-Related Content Knowledge a New Construct?

During the past decades, many scholars and researchers have made suggestions of how to conceptualize and operationalize the CK of mathematics teachers (e. g., Krauss et al. 2008; Brese and Tatto 2012). Most of them did not emphasize a construct of profession-specific mathematics CK that is needed for teaching mathematics, but conceptualized CK of mathematics teachers basically as school mathematical knowledge with at most a few parts of academic mathematics (e. g., Buchholtz et al. 2013; Heinze et al. 2016). A well-known exception is the construct specialized content knowledge introduced by Deborah Loewenberg Ball, Hyman Bass, and their colleagues at the University of Michigan (e. g., Ball and Bass 2003), which is an explicit conceptualization of the profession-specific CK needed to teach mathematics. For this reason, we will outline in the following why specialized CK—as it was conceptualized by the Michigan group—is, from our perspective, less suitable than SRCK to characterize the profession-specific CK of secondary mathematics teachers.

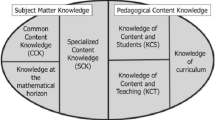
Driven by the question as to “what mathematical knowledge is entailed by the work of teaching mathematics” (Ball and Bass 2003, p. 5), the Michigan group pursued a bottom-up approach: Starting with a job analysis of elementary mathematics teachers, they aimed at uncovering “the mathematical work of teaching” for these teachers (Bass 2005, pp. 228–229). As a result of this analysis, they proposed a practice-based model of Mathematical Knowledge for Teaching (MKT) that focuses on the subject-specific core categories CK and PCK by Shulman (1986), and differentiates these further. The conceptualization of CK consists of three parts: common content knowledge (CCK), specialized content knowledge (SCK), and horizon content knowledge (HCK). SCK was introduced to designate a kind of mathematical CK that is specialized in the sense that it is “not needed or used in settings other than mathematics teaching” (Ball et al. 2008, p. 396). In contrast to SCK, CCK was defined as the mathematical knowledge “used in settings other than teaching” and described as referring to “questions that typically would be answerable by others who know mathematics” (Ball et al. 2008, p. 399). In order to illustrate what the construct of SCK consists of, Ball et al. (2008, p. 400) gave examples of what they see as profession-specific instances where such mathematical knowledge is used: “looking for patterns in student errors,” “sizing up whether a nonstandard approach would work in general,” or “understanding different interpretations of the operations in ways that students need not explicitly distinguish.” In general, it is difficult to distinguish between SCK and CCK, because both constructs are defined in an indirect way by the context in which the knowledge becomes relevant. In view of the examples cited previously, it may be asked whether the CCK a mathematician uses “in settings other than teaching” is also sufficient to solve the problems in the SCK examples.

Speer et al. (2015) discussed this issue when they investigated the question as to whether or not the MKT framework generalizes to the secondary work of teaching. Analyzing cases of secondary teachers’ classroom practices, they illustrated in particular the problems of distinguishing between CCK and SCK in this context. They argued that the assumption made in the elementary context that CCK is knowledge held or used by an average mathematically literate citizen is not sensible in the secondary context if CCK is to be contrasted with SCK as a specialized mathematical knowledge for teaching. Instead, according to Speer et al. (2015, p. 114), CCK should be considered as the mathematical CK of “the population of similarly situated mathematical knowers—those possessing at least an undergraduate mathematics major”. Then, however, Speer et al. (2015) pointed out further, aspects of mathematical knowledge that were considered part of SCK by the Michigan group can be seen as CCK for this group of reference.

The second question one may ask regarding the distinction between SCK and CCK by the Michigan group is whether the kind of CK described as SCK is really “not needed or used in settings other than mathematics teaching” (Ball et al. 2008, p. 396). Speer et al. (2015) argued that the central aspects of SCK as described by Ball et al. (2008) are also part of the day-to-day lives of mathematicians when they evaluate their peers’ work and provide feedback: “In both the teaching and research contexts, the mathematician needs to make sense of the mathematical ideas and reasoning presented by someone else and determine whether the reasoning is correct” (Speer et al. 2015, p. 116). Speer et al. (2015, p. 118) acknowledged, however, that a possible difference may be that giving a response to students instead of peers usually requires the responder to “transform his understanding of why a solution path is or is not valid into a description that would be accessible to the students given their assumed mathematical backgrounds”. In other words: While the research mathematician can evaluate the mathematical ideas of a peer and give feedback in terms of academic mathematics, the secondary teacher needs to evaluate the mathematical ideas of a student against the background of school mathematics and academic mathematics, and give feedback that is accessible to the student in the context of school mathematics, but which also retains the integrity of the mathematical ideas. Therefore, whereas the distinction between common and specialized CK as defined by Ball et al. (2008) may not be very useful in the context of secondary mathematics teaching (Speer et al. 2015), the distinction between academic and school mathematics can be seen as essential.

HKT, the third CK domain in the MKT framework, was described as “an awareness of how mathematical topics are related over the span of mathematics included in the curriculum” (Ball et al. 2008, p. 403). The explanations by Ball and Bass (2009, pp. 15–16) regarding this construct suggest that HCK can be framed either as knowledge about background theories of school mathematics or can be seen as knowledge about fundamental ideas: “We see that teaching requires a sense of how the mathematics at play now is related to larger mathematical ideas, structures, and principles”. Arguing that they “have known from the beginning that there is a kind of CK that is neither common nor specialized” (Ball and Bass 2009, p. 15), Ball and Bass indicated that HCK cannot be determined from the perspective of their distinction between common and specialized knowledge. This reinforces the impression that for grasping the specific CK that secondary mathematics teachers need, the MKT framework lacks a focus on a dimension that goes beyond the distinction between common and specialized—namely a focus on the non-trivial relation between academic and school mathematics.

One possibility to deal with this matter without introducing a new construct would be to redefine the construct SCK with respect to secondary school mathematics teachers. However, there are at least two problems this would cause: Firstly, the notion of SCK has been established in the community of mathematics education research for more than 20 years and thus a new meaning of this label would lead to confusion. Secondly, such a redefinition with a focus on secondary mathematics teachers would not only affect SCK, but also the related constructs of CCK and HCK as outlined above.

7 Conclusion and Outlook

In order to find an answer to the initial question of how a profession-specific mathematical CK for teaching secondary mathematics can be characterized, this theoretical contribution has integrated different ideas proposed by scholars over the past 100 years on how to bridge the gap between academic and school mathematics. All of these ideas refer to the identification of a profession-specific mathematical CK. As has been elaborated, some of these ideas are similar, but some are also complementary and have so far only partly been brought together in the literature. Hence, the integration of these ideas lies in the perspective of specific professional requirements. As a result, the construct SRCK was proposed as profession-specific CK of secondary mathematics teachers concerning interrelations between the two kinds of mathematics. This construct includes on the one hand knowledge about the curricular structure of school mathematics as well as the legitimation of this structure from a (meta-)mathematical perspective and, on the other hand, knowledge about interrelations between school and academic mathematics at the level of specific contents in both top-down and bottom-up directions. In view of these different facets, one could get the impression that what we call SRCK is not a coherent construct, but rather heterogeneous. However, all three facets encompass mathematical CK about interrelations between the two kinds of mathematics that build on the specific character and logic of school mathematics as well as on mathematical integrity in the sense of academic mathematics. Moreover, these facets often appear combined rather than being strictly separable. Ultimately, the construct can be seen as being homogeneous as a result of the property of being profession-specific CK for teaching secondary mathematics from a requirements perspective.

Since all three facets were, in principle, mentioned in Klein’s (2016 [1908]) lectures on elementary mathematics from a higher standpoint, the construct of SRCK can be seen as a central aspect of a contemporary interpretation of his well-known notion. Furthermore, ideas by other scholars that have been pointed out in different contexts over time were integrated in order to characterize a profession-specific CK of secondary mathematics teachers more explicitly and in view of today’s educational reality.

As was emphasized in the introduction, this contribution can be seen as a theoretical foundation for projects regarding profession-specific CK of secondary mathematics teachers, which—in Bishop’s (1992) terms—focus on the perspectives of the pedagogue or the empirical scientist tradition. Therefore, we think that the introduction of SRCK in addition to academic CK constitutes a promising step toward finding answers to the central questions as to what professional CK secondary mathematics teachers need and how such knowledge can be taught in teacher education programs. As was mentioned above, some elements of SRCK have already been implemented in different teacher education programs. In this context in Germany, the development project “Mathematik neu denken” (Thinking mathematics in new ways), for instance, is worth mentioning, which restructured the teacher education program for the higher secondary level at the universities in Gießen and Siegen: Mathematics courses specifically for teachers were introduced that bring to the fore interrelations between academic and school mathematics (e. g., Beutelspacher et al. 2011). Another example of a practice-oriented approach in mathematics teacher education addressing aspects of SRCK is the conception of so-called interface modules at the Philipps University of Marburg: In extra modules attached to the usual mathematics courses, future secondary mathematics teachers work on problems that focus explicitly on top-down and bottom-up connections between academic and school mathematics (e. g., Bauer 2013). In order to systematically investigate how the professional CK of prospective secondary mathematics teachers develops during the course of their teacher education and what kind of learning opportunities are effective, it is necessary to have a corresponding model that is suitable in theoretical as well as in empirical terms.

Empirical research on SRCK requires, in particular, that this CK component can be assessed. Following the theoretically derived SRCK framework presented in this article, we developed test items and conducted a first study to investigate an extended model of pre-service secondary teachers’ professional content-specific knowledge (e. g., Heinze et al. 2016). The findings of a quantitative study (N = 505) and an interview study (N = 18) showed that SRCK can be empirically separated from the related constructs academic CK and PCK, and that these three constructs can be measured in a valid and reliable way.

There is, however, more empirical research needed, not only to replicate these results but also in order to answer further questions regarding the construct. For instance, it remains an open question by which cognitive processes SRCK can be characterized, which calls for qualitative analyses to identify such processes. Further research should also focus on how this profession-specific knowledge can be acquired. It is not clear to what extent SRCK can be taught and acquired without academic CK as a basis. We assume that this is not possible, since SRCK does not have its own systematic structure and thus needs the structure of academic mathematics. Moreover, the model that was introduced may pave the way for finding answers to essential questions regarding the professional CK of in-service teachers, such as: Which role do different components of professional CK (and in particular SRCK) play for the teachers’ acting in the classroom, the quality of their instruction, and eventually for the learning outcomes of their students? Answers to these questions may then of course, in turn, inform the discussion about how professional mathematical CK should be taught in the course of teacher education programs.

By introducing the construct SRCK, we also hope to provide a new starting point to focus on a professional CK for teaching secondary mathematics that is on the one hand energized by a profound understanding of academic mathematics and on the other hand enables teachers to solve the evolving problems of teaching secondary school mathematics.