Measuring Pre-service Primary Teachers’ Shame in Mathematics—a Comprehensive Validation Study

Abstract

Emotions play an essential role in educational processes. Previous research has mainly dealt with achievement emotions which are experienced in specific situations such as exams or learning situations in mathematics (e.g. enjoyment or anxiety). Some achievement emotions are rather experienced in social contexts in mathematics and are closely related to the self. These emotions such as shame are assumed to be also relevant for mathematics achievement. However, a reliable and valid instrument is missing to measure shame in mathematics. Validity evidence for the newly developed Shame in Mathematics Questionnaire (SHAME-Q) was collected in three studies with pre-service primary teachers. Study 1 investigated the content validity by conducting a systematic expert panel study. Study 2 and study 3 examined with two different samples the factorial structure and relations to other constructs in terms of discriminant (enjoyment) and convergent (anxiety) validity as well as to pre-service teachers’ grade in school mathematics, their intention to teach mathematics at school, and gender. The data supported strongly the validity assumptions as well as reliability and parsimony of the instrument. Psychometric limitations of SHAME-Q and applicability of the questionnaire are discussed.

Introduction

Emotions play an essential role in educational settings (e.g. Laine et al., 2020; Martínez-Sierra et al., 2019). This applies particularly to so-called achievement emotions, such as shame, which develop in the context of learning processes and affect one’s achievement in general and in specific domains, for instance in mathematics (Pekrun & Perry, 2014). In educational research, emotions are conceptualized as a dimension of affect besides others, such as beliefs or attitudes (e.g. Hannula, 2019). They are understood as also consisting of cognitive, physiological, and motivational components (Pekrun et al., 2011). These components are revealed in emotional expressions (e.g. observable behavior, facial expressions) (see Scherer (2009) for details).

In addition, emotions can be described along different categories: According to Steyer et al. (1999) and Hannula (2012), each emotion can be conceptualized either as a stable disposition, which means independent of a specific situation (trait), or as an immediate reaction within a specific situation (state). Furthermore, emotions can be experienced as pleasant (positive valence; e.g. enjoyment) or as unpleasant (negative valence; e.g. anxiety or shame) and as activating or deactivating¹ (Feldman Barrett & Russell, 1998). The taxonomy of achievement emotions of Pekrun et al. (2018) also differentiates between emotions that are experienced prospectively (e.g. anxiety), during (e.g. enjoyment), or retrospectively (e.g. shame) to an achievement situation.

Furthermore, Lewis (2003) conceptualized so-called self-conscious emotions (e.g. pride or shame). In contrast to basic emotions such as enjoyment or anxiety, these are by definition closely related to representations of oneself and are linked to higher degrees of self-awareness. Also, they provide emotional information for an individual about the perceived overlap of their real self and ideal self. Self-conscious emotions are also referred to as social emotions, since the self develops in social contexts, for example, through social comparisons or social feedback (Lewis et al., 1989). In this respect, Tangney (1999, p. 543) states: “The self-conscious emotions are not only intimately connected to the self. They are also intimately connected to our relationships with others.” Thus, self-conscious emotions can be understood as psychosocial constructs.

Studies revealed that prospective teachers’ emotions affect the decision about their career choice (Scott, 2005), their learning trajectory during teacher education (Cooke, 2015; Jenßen et al., 2021), and the emotions they experience when they are teaching later at school (Eren, 2014; Marbán et al., 2020; Peker & Ertekin, 2011). However, it must be noted that research on pre-service teachers’ emotions so far almost exclusively has included emotions such as enjoyment or anxiety. Self-conscious emotions, especially shame, are only rarely considered which means that previous research has not sufficiently covered the self-reference and social context of pre-service teachers’ emotional experiences. Pre-service teachers tend to compare themselves with fellow students, particularly when presenting their achievements in front of a large plenum, for example, during presentations or lectures in seminars. These situations highly trigger social or self-conscious emotions. Only examining emotions such as enjoyment and anxiety would neglect the aforementioned dynamics to a large extent. In addition, emotions are assumed to form pre-service teachers’ identity (Hodgen & Askew, 2007; Lutovac & Kaasila, 2018; Zembylas, 2003). That is, self-conscious emotions influence the development of an individual’s identity enormously as they provide emotional information about one’s behavior and experiences in social contexts (Lewis, 2003).

An explanation for the limited body of research regarding pre-service teachers’ self-conscious emotions might be the lack of valid and reliable assessments needed for quantitative studies. The Teacher Emotions Scales assess only enjoyment, anger, and anxiety but not shame, and are limited to in-service teachers and not transferrable to pre-service teachers (Frenzel et al., 2016). Another option to assess emotions in achievement situations in general is the Achievement Emotion Questionnaire (AEQ) (Pekrun et al., 2011) that includes a shame subscale. However, studies revealed that achievement emotions are domain-specific with regard to frequency and intensity (Goetz et al., 2006). An adapted version of the AEQ to mathematics (AEQ-M; Pekrun et al., 2005) exists, but is restricted to students’ achievement emotions at school. Thus, the AEQ-M items specifically address the significance of the classroom teacher or other school-specific situations for experiencing shame, which limits the application of the AEQ-M beyond school, for example, to pre-service teachers.

To sum up, shame seems to be an important emotion when investigating pre-service primary teachers’ competence and identity development, but assessments covering pre-service primary teachers’ shame in mathematics are not available. Consequently, a valid and reliable questionnaire assessing pre-service teachers’ shame in mathematics would fill this gap.

Conceptual Framework of Shame in Achievement Situations

According to the taxonomy of achievement emotions, shame is classified as an unpleasant and activating achievement emotion that appears retrospectively to an achievement situation (Pekrun et al., 2018). Frequency and intensity of shame might differ across cultures, but shame experiences have been reported across all cultures (Bierbrauer, 1992; Sznycer et al., 2016).

The affective component of shame can be described by feelings of embarrassment, insufficiency, and humiliation (Oades-Sese et al., 2014). The feeling of shame typically includes global self-judgments (Lewis, 2003) such as “I’m a total loser in mathematics” (cognitive component). Such self-referential cognitions are mostly concerned with the discrepancy between one’s real self and the ideal self in a domain (Lewis, 2003). The physiological component of shame is experienced as tense and can trigger blushing (Velotti et al., 2017). The motivational component of shame appears as avoiding situations that may cause shame (Schmader & Lickel, 2006) or as overcompensating subjectively perceived shortcomings (e.g. perfectionism, aggression) (Tangney et al., 1992).

In contrast to basic emotions such as enjoyment and anxiety, shame can—similar to pride—be understood as a social emotion (Oades-Sese et al., 2014). This means that shame can only be experienced in a social context (the social context can also be imaginary) and occurs especially at high social exposure (Smith et al., 2002). Social comparisons can therefore be regarded as the motor of shame. The ability to experience shame is not innate but shaped by psychosocial processes and develops over the life span (Orth et al., 2010).

Shame can also be contrasted to other emotions such as anxiety and enjoyment, as shame is experienced only retrospectively to achievement situations, while anxiety is experienced prospectively and enjoyment prospectively, during, and retrospectively to such situations. The self in the context of others (e.g. avoiding others or the tendency to become invisible, social upward comparisons) is neither a characteristic of anxiety or enjoyment but of shame (Lewis, 2003). Nevertheless, as anxiety and shame are defined as unpleasant and activating emotions, there is a conceptual overlap which should be visible in strong positive correlations. In contrast, enjoyment is a pleasant activating emotion which should be visible in a strong negative correlation to shame. Anxiety and enjoyment can therefore be used to validate shame measurements.

According to the control-value theory of emotions in achievement situations (Pekrun & Perry, 2014), shame is experienced when controllability of the learning process is subjectively perceived as low (de Hooge et al., 2018), for example, because of a lack of knowledge. The value of a situation is perceived as negative because the person failed at a specific task while the specific domain, for example, mathematics, is highly valued.

Extending the perspective of control-value theory by integrating attribution theory (Weiner & Kukla, 1970), it becomes clear that the individual’s failure is closely linked to their lack of ability (Russell & McAuley, 1986; Tracy & Robins, 2006). Studies revealed that shame is especially experienced when an individual has failed at easy tasks, because the individual attributes this to their subjective shortcomings (Lewis et al., 1992). Regarding attributing failure, gender-specific effects were found already during childhood (Dickhäuser & Meyer, 2006). Girls attribute failure related to an easy task more often to themselves than boys and thus experience shame more often (Lewis et al., 1992). Overall, research findings underline that females report shame more often than males (Benetti-Mcquoid & Bursik, 2005).

Both theories, control-value theory and attribution theory, provide evidence for that shame is closely related to the knowledge and achievement of a person (Bibby, 1999; Tangney, 1992; Thompson et al., 2004). On average, low achievers report more shame. Pekrun et al. (2011), for example, revealed a negative moderate correlation between undergraduate students’ shame and their general grade point average at university.

Shame in Mathematics

Although shame can be experienced in all subjects (e.g. physical education: Ryall, 2019), mathematics shows domain-specific features that are associated with the experience of shame (Amidon et al., 2020; Bibby, 2002). First, commonly shared beliefs such as “Mathematics represents my general intelligence” may lead to experiences of shame. According to Goldin (2014, p. 295), “such beliefs, reflected in educational practice in many countries, may affect self-expectations and the expectations of others, influencing in turn success or failure emotions.” Second, misunderstanding central concepts has long-term consequences for one’s experience of competence due to the hierarchical nature of the mathematics curriculum (Goldin, 2014). Third, in the “traditional” mathematics classroom, teachers frequently evaluate student solutions in a right-or-wrong manner (Goldin, 2014), which implies that there is only success or failure for the students. This practice leads automatically to frequent shame experiences. After failure in a mathematics test, the individual might tend to attribute this to a lack of their own global ability in mathematics, which could be the starting point for a vicious cycle in the experience of shame (Heyd-Metzuyanim, 2015).

Instructional settings such as competitive games or social exposure in front of the class at the blackboard might also occur more frequently in the mathematics classroom than in other subjects, and might be associated with shameful experiences (Bibby, 2002). At the same time, mathematics is given high relevance for success on the labor market and in society as it is regarded as a decisive cultural asset (Goldin, 2014). The knowledgeable use of mathematics is sometimes even called a twenty-first century skill (ibid.). Such a positive overall evaluation of the relevance of mathematics in addition to a negative situation such as failing with mathematical tasks reinforces shame experiences. In line with the general state of research mentioned above, shame is experienced more often when individuals rate their own mathematics achievement as lower compared to other students (Holm et al., 2020b), or by students who receive special education support in mathematics being in classes with students who do not need such special help (Holm et al., 2020a).

Shame of Pre-service Primary Teachers

Primary teacher education focuses in many countries on training generalists who are supposed to teach a broad range of subjects later at primary school, including mathematics. The training as generalists means that only rarely extended opportunities to learn mathematics are offered (Cooke et al., 2019). Consequently, pre-service primary teachers’ knowledge of mathematics is often low and the potential for shame might be therefore high (Bibby, 2002). Studies revealed in addition that pedagogical motives are more crucial for choosing a career as a primary school teacher than subject-specific interests (Blömeke et al., 2012). Mathematical knowledge gained at school is therefore probably not very pronounced, either (ibid.).

Pre-service primary teachers experienced shame already throughout their educational history at school, especially in mathematics (Jenßen et al., 2022). They report to a large extent shame-inducing school situations (ibid.). In this sense, shame can potentially be regarded as a constituent component of a primary school mathematics teacher’s identity when they enter teacher education (Lutovac, 2020; Panagi, 2013). Jenßen (2021) revealed that pre-service primary teachers’ shame in mathematics develops through upward comparisons and is associated with low mathematics achievement and a low ability self-concept in mathematics and is more often reported by females than males.

Development of the Shame in Mathematics Questionnaire

Although studies and theoretical assumptions support the relevance of shame in mathematics for pre-service primary teachers, there is no reliable and valid instrument for a standardized assessment of this population. Existing instruments are restricted to measure students’ achievement emotions including shame at school and specifically address the role of their teachers or other school-specific situations for experiencing shame, which limits the application to other populations (Pekrun et al., 2011).

Our aim was therefore to develop a time-efficient, parsimonious, and functional self-report questionnaire, measuring pre-service primary teachers’ shame in mathematics according to the trait concept (Hannula, 2012; Steyer et al., 1999) across different situations (Bieg et al., 2013) and based on the control-value theory of achievement emotions (Pekrun & Perry, 2014). The Shame in Mathematics Questionnaire (SHAME-Q) was intended to capture the construct with a reasonable number of items to limit the response burden and reduce response bias due to fatigue or boredom in the context of empirical studies where such a scale typically would be included as one measure among many (DeVellis, 2012).

In line with the conceptual framework documented above, the items were supposed to reflect shame in mathematics as a unidimensional construct but nevertheless in its full breadth by covering the affective, cognitive, physiological, and motivational components as well as the importance of the self and others for experiencing shame. These components were therefore used as a heuristic for the development of the questionnaire without aiming at measuring them as distinct sub-dimensions at this moment. The latter would require several items for each sub-dimension resulting in a very long questionnaire.

The development of the questionnaire contained two phases: the item construction phase and the pilot study. An item pool including 24 items was constructed (in German), which covered characteristics of the construct description. We ensured face validity of the items during the construction phase as the term shame (or ashamed) was directly addressed in the wording of each item. According to Holden and Jackson (1979), this is an established strategy to enhance item validity. This strategy is also used in assessments which measure shame in other domains, for example, clinical settings (Garcia et al., 2017). It relies on the fact that a shared understanding of this term exists and enhances item clarity (Garcia et al., 2017). Furthermore, this ensures that the source of an unpleasant emotion is correctly addressed to shame but not to other emotions such as anxiety, for example (see McCord, 2021, for a similar approach).

Pre-service primary teachers were asked to provide feedback and comments on the different items using think-aloud techniques (Padilla & Leighton, 2017). In addition, they worked on the questionnaire (pre-testing), so that data on the practicability concerning comprehension and implementation of the items could be collected. On the basis of this information, confusing items have been eliminated from the item pool if the covered characteristic was assessed by another item. Otherwise, confusing items were revised with regard to wording or structure of the sentence.

After having revised the questionnaire, 15 items were piloted with n = 135 pre-service primary school teachers. Based on statistical parameters from classical test theory (e.g. item-inter-correlations, mean values of items, reliability) and theoretical considerations (in particular coverage of the different shame components), a systematic item reduction process was carried out. Finally, six items were identified that met common psychometric criteria (DeVellis, 2012) and ensured sufficient construct coverage.

Validating the Shame in Mathematics Questionnaire

The purpose of the present study is to provide evidence for the validity of the inferences that would be derived from the SHAME-Q score. The understanding of validity has changed over time and is now known as “an integrated evaluative judgement of the degree to which empirical evidence and theoretical rationales support the adequacy and appropriateness of interpretations and actions based on test scores” (Messick, 1992, p. 1487). Following the approach by Kane (2013), a conclusive statement regarding the validity of an assessment is based on different validity arguments related to several categories of evidence: content, response processes, factorial structure, relations to other variables, and consequences (AERA et al., 2014). The category relations to other variables includes strong positive relations with similar constructs (convergent validity), negative or no relations with constructs which strongly differ (discriminant validity), and relations to constructs in a nomological net. The latter one is often referred to by the term criterion validity (McCoach et al., 2013). Synthesizing the different validation approaches provides information on the quality of an assessment (Kane, 2013).

In this paper, we provide validity arguments with respect to content, factorial structure, and relations to other variables. Validity argument 1 stresses the content representation of SHAME-Q regarding the construct shame in mathematics (study 1). Validity argument 2 refers to the factorial structure of SHAME-Q representing a unidimensional understanding of shame in mathematics (study 2). Validity argument 3 refers to convergent and discriminant validity by providing evidence that shame in mathematics is positively related to another unpleasant achievement emotion but still can be differentiated from this one, namely mathematics anxiety, and that it is negatively related to enjoyment in mathematics as a pleasant achievement emotion (study 2). Validity argument 4 follows the assumption of shame in mathematics being related negatively to achievement in mathematics and being an activating emotion as it leads to an avoidance tendency concerning mathematics; furthermore, we expect that female pre-service teachers report more shame in mathematics than male teachers (study 3). With respect to the objective of the questionnaire, the validation procedure was performed with different samples of pre-service primary teachers.

Study 1: Validation with Regard to Content of SHAME-Q

Content validity refers to the fit of items and construct, and is usually ensured by expert panels. According to validity theory (Kane, 2013), test content can be under- or overrepresented which would harm the construct validity of an assessment. In contrast to other facets of validity, content validity cannot be directly estimated but evaluated through systematic expert panels (Popham, 1993). With our first study, we examine the following research question: Do the items adequately represent the construct shame in mathematics?

Participants

Five experts from both academia and the practice field were invited to evaluate the content representation of the items. The academic experts were all engaged in pedagogical-psychological research on emotions. Psychotherapists who also worked as supervisors of pre-service psychotherapists were chosen as practitioners because they deal extensively with the phenomenon of shame in their daily work. The expertise of the latter respondents is indicated by their professional experience: On average, the psychotherapists had been working in the profession for M = 13 years (SD = 6.2). The expertise of the academics is indicated by the number of publications related to emotions (M = 21.2, SD = 20.2) and shame in particular (M = 9.3, SD = 8.3). Both practitioners and academics stated that they had conducted seminars or workshops on the topic of shame.

Assessment and Analysis

Content validity of SHAME-Q was evaluated by an expert panel in a standardized way (Jenßen et al., 2015). A construct definition was given to the experts, which included all relevant information given in the description above (e.g. the four components of shame in the “Conceptual Framework of Shame in Achievement Situations” section). The experts rated the six items regarding the prompt “Does the content of the item represent the construct shame in mathematics?” on a 4-point scale (1=totally no, 2=rather no, 3=rather yes, 4=totally yes). The experts were encouraged to rate each item as a whole.

We analyzed the data by calculating the content validity index (CVI) on item level (I-CVI) as well as on scale level (S-CVI). According to Polit and Beck (2006), ratings of 3 or 4 on our 4-point scale indicate construct-relevant items and are coded as 1 while ratings of 1 or 2 indicate non-relevant items and are coded as 0. The I-CVI is calculated by the number of experts who rated the items as relevant divided by the number of all experts who took part in the rating (Polit & Beck, 2006; Yusoff, 2019). The calculation of the S-CVI is based on the I-CVI and represents the average of I-CVI scores across all items of the scale (Yusoff, 2019). Values lower than CVI = 1.00—meaning that one of the experts coded one of the items as not relevant for measuring the construct—are not regarded as acceptable according to Yusoff (2019). Additionally, the experts judged whether the six items together were an adequate construct representation on a continuous scale from 0 to 100%.

Results

The results of the expert panel are presented in Table 1. No expert provided an estimate lower than 3 (= rather yes), so I-CVI = 1.00 in all cases was indicating relevance of each item. Consequently, the CVI on scale level was S-CVI = 1.00 and indicated a good representation of the construct shame in mathematics as captured by each of the six items. The experts stated that the six items together represented the construct to 90% (Min = 80%, Max = 100%). According to the experts’ comments, an aspect that was not sufficiently represented (i.e. construct under-representation) was the physiological symptom of blushing.

Table 1 Experts’ ratings of each item

Study 2: Factorial, Discriminant, and Convergent Validity of SHAME-Q

In study 2, we analyzed further validity criteria of SHAME-Q. First, we examined the factorial structure. The research question was: Does the questionnaire provide scores that represent shame as a one-dimensional construct? Despite considering different components of shame, it was conceptualized as one latent trait which should be reflected empirically in a one-factorial structure.

Second, regarding discriminant and convergent relations, the research question was: Does the SHAME-Q score show theoretically assumed relations to other variables, derived from a nomological network? Relations to enjoyment in mathematics (discriminant) and mathematics anxiety (convergent) as two other achievement emotions were examined. Enjoyment is perceived as pleasant in contrast to shame (Feldman Barrett & Russell, 1998). Thus, we hypothesized a negative relation between enjoyment and shame.

In contrast, anxiety and shame are experienced both as unpleasant and activating. However, anxiety is directed prospectively towards the outcome, but shame tends to appear retrospectively after an achievement outcome (Pekrun et al., 2018). Nevertheless, shame of failure can grow into anxiety of failure (McGregor & Elliot, 2005), and one can also be ashamed of the perceived anxiety during achievement activities. Consequently, shame in mathematics should be strongly positively related to mathematics anxiety, but both should nevertheless differ sufficiently from each other. To examine whether SHAME-Q delivers test scores that can be distinguished from mathematics anxiety test scores, we tested a “one-emotion-factor model” against a model separating both emotions (see Ganley et al., 2019; Pekrun et al., 2011).

Participants

This validation study involved n = 397 pre-service primary school teachers from Germany. The average age of the participants was M = 27.6 years (SD = 8.30, Min = 17, Max = 53). The gender ratio was as expected (75% female, 25% male). The majority of students (69%) was in the first half of their bachelor’s degree which is the first step in a teacher education program in Germany. About 14% were in the second half of the bachelor’s program, and 17% were in the master’s program which is the second step of teacher education. Mathematics was only to a limited extent part of the program as the pre-service teachers were trained as generalists which means that they studied mathematics besides several other subjects (e.g. German, social sciences, and general pedagogy). The participants received no incentives for participating in the study. At any time, they were given the chance to terminate their participation.

Assessments

The six items of SHAME-Q had to be rated on a 5-point Likert scale from 0 (= does not apply at all) to 4 (= fully applies). Psychometric properties of this scale and the following scales are presented in the results section.

In order to measure mathematics anxiety in an economic and valid way, a scale included in the Programme for International Student Assessment Lee (2009) was used (Lee, 2009). The scale measures the anxiety of learners in mathematics on a 4-point scale and has been also applied to mathematics pre-service teachers (Jenßen et al., 2021). The four items (e.g. “I get very nervous doing mathematics problems”) are to be rated from 0 (= totally disagree) to 3 (= totally agree).

Enjoyment of mathematics was measured by a scale used in large-scale assessments of pre-service primary school teachers’ knowledge (Tatto et al., 2012). The scale has been validated in terms of its factorial structure and relationships to other variables and consists of three items (e.g. “I enjoy working on mathematical tasks.”). The items had also to be evaluated on a 4-point scale ranging from 0 (= totally disagree) to 3 (= totally agree).

Data Analyses

To investigate the factorial structure of SHAME-Q, dimensional analyses were carried out. First, an exploratory factor analysis was applied to check the dimensionality of the scale based on the data (e.g. Yang et al., 2021). A principal axis factor analysis was conducted on the six items with orthogonal rotation (varimax). The Kaiser-Meyer-Olkin measure was used to verify the sampling adequacy for the analysis and Kaiser’s criterion was used with respect to the eigenvalue. The variance explained and factor loadings were inspected as well.

In a second step, our hypothesis of a one-factorial structure was further validated by means of a confirmatory factor analysis (CFA) where all factor loadings were estimated freely. The combination of exploratory and confirmatory factor analyses reflects a common procedure to cross-validate the findings regarding dimensionality (e.g. Hemi & Maor, 2020; Yin, 2012).

Common criteria were used to evaluate the model fit. We decided to accept RMSEA values ≤.08 (Schermelleh-Engel et al., 2003) due to small degrees of freedom (Kenny et al., 2015). Reliability of the scale was estimated by calculating McDonald’s omega (ω). The hypothesized relationships to other variables were tested using structural equation modeling (SEM). We applied a robust maximum likelihood estimator (MLR) to ensure an adequate estimation of the standard errors due to non-normal distributions of the indicators (Rhemtulla et al., 2012). Exploratory factor analysis (EFA) was performed by using SPSS 25.0 (IBM Corp., 2017), and CFA and SEM were performed by using the software Mplus 8 (Muthén & Muthén, 2017).

Results with Regard to Factorial Structure

The Kaiser-Meyer-Olkin measure supported the sampling adequacy for an EFA, KMO = 0.90. Only one factor could be extracted. The factor had an eigenvalue above Kaiser’s criterion of 1 (4.02) and explained 67.07% of the variance. All factor loadings were substantial (> .60). In a second step, a CFA confirmed the factorial structure. Standardized factor loadings of each indicator are given in Table 2. All loadings were above acceptable thresholds. The model fitted the data well (𝝌²(9) = 27.076, p = .0014, RMSEA = .07 [.04;.10], CFI = .99, SRMR = .02). Reliability of the scale was very good (McDonald’s ω = .90) and did not increase if any item was deleted.

Table 2 Standardized factor loadings

Results with Regard to Discriminant and Convergent Relations

The descriptive results of the variables used are given in Table 3. In the sample, shame has been experienced at a low level on average. The distribution parameters indicate a left-sided distribution (Mo = 6.00, Md = 6.00, M = 6.67, SD = 4.96). About 17% of the participants revealed shame in mathematics above the theoretically expected scale mean of M = 12, indicating a neutral shame experience.

Table 3 Raw scores of study 2

The model for enjoyment had a very good fit to the data (𝝌²(2) = 5.719, p = .057, RMSEA = .06 [.00; .14], CFI = .99, SRMR = .01). The reliability in the sample was also very good (McDonald’s ω = .91). The model for anxiety showed a good model fit (𝝌²(2) = 9.26, p = .01, RMSEA = .08 [.04; .16], CFI = .99, SRMR = .02). The reliability was good (McDonald’s ω= .83). The full model with integrating shame also showed an acceptable model fit (𝝌²(74) = 153.61, p < .001, RMSEA = .05 [.04; .06], CFI = .97, SRMR=.04).

Enjoyment revealed negative correlations with both shame (r = −.55) and anxiety (r = −.54), in line with theory. Shame and anxiety correlated with r = .79, which indicated a strong positive correlation. This relationship was also in line with theoretically based assumptions.

In light of the strength of the correlation between shame and anxiety, we validated our assumption that both constructs are empirically distinguishable. First, we modeled anxiety items and shame items as indicators of one latent dimension (unpleasant emotion, “one-emotion-factor model”; see Pekrun et al., 2011). Second, we modeled shame items and anxiety items as indicators representing two distinct factors that are related to each other. The fit of the second model (𝝌²(34) = 87.932, p < .001, RMSEA = .06 [.04; .08], CFI = .97, SRMR = .03) was better than the fit of the first model (𝝌²(35) = 195.655, p < .001, RMSEA = .10 [.09; .12], CFI = .90, SRMR = .06). The lower AIC and BIC of the second model (AIC: 8450.80, BIC: 8574.23) compared to the first model (AIC: 8588.42, BIC: 8707.86) also indicated the better fit of the model with distinct factors of anxiety and shame.

Study 3: Criterion Validity of SHAME-Q

In study 3, empirical relations of SHAME-Q to three variables derived from a nomological net were examined, namely to pre-service primary teachers’ self-reported achievement (last grade in mathematics at school), their intention to teach mathematics later at school, and their gender. Based on expectancy-value theory (Eccles, 2005) and control-value theory (Pekrun & Perry, 2014), a complex mediation model was developed that included the intention to teach mathematics as the criterion, predicted by achievement and shame, again predicted by gender. With regard to expectancy-value theory (Eccles, 2005), emotions, achievement, and gender are relevant factors influencing career choices. Shame is an activating unpleasant achievement emotion, leading to a high avoidance tendency in other contexts (Schmader & Lickel, 2006). Therefore, we hypothesized that pre-service teachers with higher levels of shame are more likely to decide against teaching mathematics at school.

Besides emotions, achievement is also assumed to affect career choices by the expectancy-value theory (Eccles, 2005). According to control-value theory (Pekrun & Perry, 2014), the correlation between achievement (grades) and shame should be positive (as higher grades represent lower achievement in Germany) and of moderate size. This assumption is in line with findings from studies on shame with students at school where low achievers reported higher levels of shame than high achievers (Pekrun et al., 2011).

Finally, based on the expectancy-value theory (Eccles, 2005), gender is assumed to affect career choices, mediated by achievement and emotions (Eccles, 2005). As many studies revealed that females report higher levels of shame than males (e.g. Benetti-Mcquoid & Bursik, 2005), we included gender as a predictor of shame and hypothesized that the regressive relation between shame and gender indicates that female pre-service primary teachers report higher levels of shame in mathematics than male ones. Since evidence in addition points to lower mathematics achievement of females, we included gender as a predictor of self-reported school grades as well (Guo et al., 2015). Moreover, in accordance with expectancy-value theory (Eccles, 2005), we also tested whether gender had a direct effect on the intention to teach beyond a potential mediation effect (Guo et al., 2015; Watt et al., 2012).

Participants

The third validation study was conducted with a new sample comprising n = 198 pre-service primary school teachers from Germany. All participants were at the beginning of the first bachelor semester of their studies as prospective primary school teachers at university. The majority of the participants were female (77%). The average age of the participants was M = 25.86 years (SD = 8.31) with a minimum of 17 years and a maximum of 53 years. The participants received no incentives for participating in the study. At any time, they were given the opportunity to terminate their participation.

Assessments

To assess participants’ shame in mathematics, the SHAME-Q was used. Participants reported their last grade in mathematics at high school, ranging from 1 (= best) to 6 (= worst). The intention to later teach mathematics as a primary teacher in school was assessed with a single item to be rated on a 4-point scale ranging from 0 (= not at all) to 3 (= in any case) by the participants. Gender was assessed as dichotomous variable via self-report (male/female).

Data Analysis

We applied SEM to test the hypothesized relationships. Shame in mathematics was included as a latent variable while gender, the last grade in mathematics, and the intention to teach mathematics at school were included as manifest variables. Common fit indices as mentioned earlier were used to evaluate the model fit. We also applied MLR due to the non-normal distributions of the indicators and the small sample size. All analyses were done with Mplus 8 (Muthén & Muthén, 2017).

Results

The model for shame in mathematics revealed a very good fit to the data (𝝌²(9) = 12.630, p = .18, RMSEA = .04 [.00; .10], CFI = .99, SRMR = .02). Reliability was also very good ( ω = .89). Descriptive results are given in Table 4.

Table 4 Raw scores of study 3

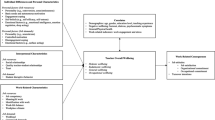
The model fit of the full model including all variables was very good (𝝌²(25) = 26.617, p = .32, RMSEA = .02 [.00; .06], CFI = 1.00, SRMR = .03). The results are shown in Fig. 1. Shame and the last grade in mathematics at school were positively related (p < .001), meaning that higher levels of shame were associated with worse grades in mathematics. The strength of the relationship was of medium size. Additionally, shame in mathematics showed a significant effect on the intention to teach mathematics at school (p < .001). The effect was large.

Fig. 1

Empirical model of shame in mathematics in relation to criterion variables school grades in mathematics, intention to teach, and gender (standardized parameters). si, ith indicator of the SHAME-Q scale

Gender showed a negative effect on shame, indicating that female participants reported higher levels on the SHAME-Q (p < .05). The effect was small. However, there was no effect from gender on the last grade in mathematics at school (β = .10, p = .20). Gender showed no direct effect on the intention to teach mathematics, but a small positive indirect effect via shame (β_ind = .10, p < .05), indicating that male participants reported higher willingness to teach mathematics later at primary school and that this willingness was mediated by shame. The last grade in mathematics at school showed no significant effect on the intention to teach mathematics as a teacher (β = −.10, p = .17).

Discussion

In the present paper, we report the results of a comprehensive validation procedure of a newly developed questionnaire assessing pre-service primary teachers’ shame in mathematics. The development of a new scale was necessary as existing instruments were limited to the assessment of students’ shame in mathematics at school (e.g. AEQ-M; Pekrun et al., 2005). We validated the SHAME-Q regarding different categories of evidence in three studies. First, we examined validity related to the content of the questionnaire. Second, we paid attention to factorial, discriminant, and convergent relations, and third, we explored the relations to other variables, following other validation studies on achievement emotions in mathematics (Lichtenfeld et al., 2012; Primi et al., 2014).

Regarding content validity, the construct representation can be considered high. SHAME-Q measures affective, cognitive, physiological, and motivational characteristics of shame. In line with Holden and Jackson (1979) and assessments covering shame in other domains (Garcia et al., 2017), we directly included the term shame (or ashamed) to enhance face validity of the items. According to Kane (2004), the representation of the items in relation to the target domain (in this application, shame in mathematics of pre-service primary teachers) is the essential basis for making valid inferences. One expert stated that blushing as one possible physiological symptom is not present as an indicator but that this symptom might be relevant for the expression of shame. Even though we agree with this observation, we argue that the physiological component is still represented sufficiently by the item covering tension in relation to the experience of shame. Scherer (2009) suggested a need to represent an expression component such as blushing when describing emotions but also pointed out that the experience of the expressive component might be unconscious (and thus, difficult to measure by self-reports). Consequently, we assume that by including tension we meet the requirement of construct representation with SHAME-Q.

The validation study with regard to the factorial structure supported our objective of creating a one-dimensional scale. This means that our questionnaire consisting of six items can be seen as a parsimonious instrument to measure shame without overburdening respondents. We assume that by increasing the number of items, differentiating shame into its sub-dimensions according to affective, cognitive, physiological, and motivational components might be possible. However, this would require a large number of items. Since our focus was on developing a scale that can be included as one measure among others in empirical studies, we were note interested in gathering more information about sub-dimensions of the construct.

With regard to discriminant and convergent relations to other variables, all findings are consistent with a priori developed theoretical assumptions regarding shame in mathematics. SHAME-Q shows a discriminant relation to enjoyment and can be sufficiently distinguished from mathematics anxiety. In studies with secondary school students in mathematics (grade 9), shame and anxiety were correlated to each other with r = .92 on a latent level and shame and enjoyment with r = −.36, as assessed by the AEQ-M (Pekrun et al., 2017). The latent correlation between anxiety and shame could in this case be evaluated as very high so that it was almost impossible to empirically distinguish both emotions, although they differ from a theoretical point of view. SHAME-Q revealed a lower latent correlation to anxiety with r = .79 but a stronger negative relation to enjoyment with r = −.55.

These results can be regarded as favorable from an empirical point of view. A latent correlation of r = .79 might appear as large, but it is in fact possible to distinguish between both constructs not only conceptually but also empirically (Pohl & Carstensen, 2013). Nevertheless, the correlation might reflect the closeness of both emotions as anxiety and shame are both understood as unpleasant and activating ones. With regard to theory, we provided evidence for that we did not conceptualize shame as an inherent part of mathematics anxiety (Wilson, 2017). Whether the deviating findings presented by Pekrun et al. (2017) for ninth graders are caused by measurement properties or differences in the developmental stage of the target populations is an important follow-up research question.

In the third study, we examined relations to other variables derived from a nomological net and especially the effect of SHAME-Q on the avoidance of mathematics as criterion. A small effect of gender on SHAME-Q was found. This effect is in line with theory that females often report higher levels of shame (e.g. Benetti-Mcquoid & Bursik, 2005). Study 3 also revealed that SHAME-Q and pre-service primary teachers’ school grades in mathematics were related to each other as it had been hypothesized based on the theoretical assumption of control-value theory (Pekrun & Perry, 2014). The strength of the association was comparable to those between achievement and other unpleasant emotions (e.g. mathematics anxiety: Ma, 1999). As hypothesized, shame in mathematics had predictive power on the intention to teach mathematics in school later, while the last grade in mathematics and gender did not affect this intention directly. Thus, SHAME-Q predicted an avoidance tendency of mathematics, comparable to other unpleasant emotions (Chipman et al., 1992; Huang et al., 2019).

According to Kane (2013), a statement regarding the validity of a measurement has to integrate the validity arguments based on empirical data. The first argument (content validity) is supported by the experts’ high ratings implying content validity for each item and the whole scale regarding the construct of shame in mathematics. The second argument of a one-dimensional structure, which was the focus of the development, can be empirically supported. The third argument (unpleasant emotion, different from mathematics anxiety, strong negative relations to enjoyment) can also be underlined by our dimensional analyses in study 2. The third argument (negative relation to achievement, prediction of avoidance of mathematics) is backed up by our findings in study 3. When integrating the empirical evidence, we are able to summarize that our instrument covers a construct that is a negative, activating emotion, negatively related to achievement in mathematics and referred to as shame in mathematics by persons who are experts in the field of emotions in educational contexts.

Limitations

The results of our study should be evaluated in light of several limitations, which we discuss in the following. Shame can be considered a fleeting emotion, which might be difficult to measure (Frenzel, 2014). In our study, measuring pre-service primary teachers’ shame in mathematics indeed proved to be difficult. The left-sided distribution of the sum score of SHAME-Q indicates that for most participants, there seemed to be no significant shame experience in mathematics. The low mean values of SHAME-Q in study 2 and study 3 reveal that for the majority of the participants the statements do not apply.

Another explanatory factor might be social desirability as individuals tend to avoid to inform others about their own experiences of shame (de Hooge et al., 2018). However, about 17% of the students reported shame to be present in mathematics. This group is particularly interesting for future research.

In addition, there is a limited representativeness of our samples as we were only able to examine pre-service teachers from one university (thus, we could only draw on convenience samples from one university). Additionally, our samples may represent a positively selected subsample of the population. Moreover, the sample size of study 3 might appear as small. However, as we were only interested in relations between variables but did not search for mean level differences, and as only shame was modeled as a latent variable, the sample size can be regarded as adequate for the purpose of this validation study (Wolf et al., 2013).

Another limiting point might be that we have treated categorical variables (last grade in mathematics, intention to teach mathematics at school) as continuous variables in our model. Although this is quite common in empirical research as the application of more complex techniques and models might be less feasible due to small sample sizes, this may lead to biased estimations of parameters. With respect to the last grade in mathematics, our analysis might be not problematic as this variable has five categories and a simulation study by Johnson and Creech (1983) showed that estimates will not be affected in such a case. In contrast, estimations with the variable concerning the intention to teach mathematics might be biased as this variable has only four categories. However, Li (2016) argues that the use of an MLR estimator in a study with a sample size of around 200 (which is nearly the case in this validation study) provides less biased estimations. Nevertheless, results need to be interpreted with caution when it comes to the specific estimates. While our study revealed that shame in mathematics affected negatively pre-service primary teachers’ intention to teach mathematics later at school, replication studies are needed to investigate the true size of this effect.

Conclusions

Our studies have shown that it is possible to measure pre-service teachers’ shame in mathematics reliably and validly with respect to content, structure, and relations to other constructs. Thus, SHAME-Q offers an assessment tool for future studies to fill an important research gap in the field of achievement emotions in mathematics for pre-service primary school teachers. Previous studies about pre-service primary school teachers’ shame were mainly based on qualitative approaches. SHAME-Q allows to validly investigate pre-service teachers’ shame in mathematics based on quantitative approaches.

To further strengthen validity evidence of SHAME-Q, an investigation regarding convergent relations with the AEQ-M might be of interest for researchers (Pekrun et al., 2017). Such a validation study should address learners in mathematics at school as the AEQ-M was developed specifically for students at school. Furthermore, applications of SHAME-Q for other populations could be investigated in such a study. In contrast to other instruments that measure achievement emotions in mathematics, SHAME-Q does not name specific institutional contexts such as schools or university. However, whether SHAME-Q can be applied to other mathematics learning contexts than pre-service primary teachers was not part of the present validation study. This would be an important follow-up research question.

According to Frenzel (2014), shame might also be a relevant emotion for in-service teachers in mathematics. Since shame in mathematics can affect the development of pre-service teachers’ professional identity (Panagi, 2013), it can be assumed that shame when learning mathematics (SHAME-Q) and shame when teaching mathematics are also related. Thus, the prognostic validity of SHAME-Q in relation to a scale assessing shame when teaching mathematics might be of interest as future research. Studies that relate in-service teachers’ shame in mathematic to their shame experiences when they were pre-service teachers at university would increase our understanding of the development of teachers’ shame in mathematics.

The following aspects present ideas for follow-up questions besides psychometric properties of SHAME-Q: The level and development of shame in the educational context at university should be studied. The aim here may be to identify potential interventions concerned with, for instance, designing opportunities to learn or interventions to affect pre-service primary teachers’ shame in mathematics directly (e.g. Liljedahl et al., 2007, for beliefs), the social support through university teachers (e.g. Liu et al., 2018, for enjoyment), or the promotion of positive emotional learning opportunities at university (e.g. Finlayson, 2014, and Gresham & Burleigh, 2019, for anxiety).