Attenuation of THz Beams: A “How to” Tutorial

Abstract

Attenuation of ultrashort THz pulses poses a significant technological challenge due to the broadband nature of such light pulses. Several methods exist for this purpose, including crossed wire grid polarizers, high refractive index, high resistivity silicon wafers, and ultrathin metal films. In this review, we discuss the operational principles of these methods, and highlight some of the advantages and potential pitfalls of the methods. We describe the limits of high-frequency operation of wire grid polarizers, relevant for contemporary ultra-broadband THz sources in air photonics. We discuss the effects of multiple reflections and interference in sequences of silicon wafers for attenuation, and finally discuss the potential of using ultrathin metallic films for broadband attenuation.

1 Introduction

Technological developments in the past years has made it possible to use commercial table-top femtosecond laser systems to generate intense, ultrashort THz pulses in the 0.1–5-THz range with focused field strengths in the megavolt/centimeter range, and pulse energies from microjoules towards millijoules and beyond from inorganic and organic nonlinear crystals [1,2,3]. Such coherent THz pulses are used to investigate nonlinear interactions between strong, ultrafast THz fields and virtually all material types, including a few examples of studies of dielectrics [4,5,6], semiconductors, metals [7, 8], magnetic materials [9], 2D materials [10], liquids [11, 12], and gases [13].

With the availability of intense light sources comes naturally the need to attenuate the light in a controllable manner, for instance when investigating phenomena that depend on the peak field strength. In time-resolved measurements, it is important that the attenuation is uniform across a very broad bandwidth, so that all frequencies are attenuated by the same amount. In this manner, the temporal shape of the THz signal is preserved after attenuation. A pair of freestanding wire grid polarizers can perform this task as long as the THz signal has its spectral components within the high extinction range of the wire grids, when wavelength is much larger than the wire spacing. As a few examples, wire grid-based attenuation has been used in a range of nonlinear THz studies, using pulses generated by femtosecond tilted pulse front excitation of lithium niobate covering the spectral range up to approximately 2 THz [5, 14,15,16] and femtosecond pumping of organic nonlinear crystals with frequencies up to 5 THz [17]. The main advantage of using a pair of crossed freestanding wire grid polarizers for attenuation is the absence of a substrate, and thus there are no unwanted internal substrate reflections that disturb the signal. However, as we will demonstrate in the following, attenuating very broadband THz pulses with pairs of wire grid polarizers can lead to unexpected and detrimental performance. An alternative method for broadband, high-fidelity attenuation of THz signals is to make use of reflection losses from a sequence of high-index dielectrics such as high-resistivity silicon (HR Si) [18, 19]. In this case, internal substrate reflections will play a major role in the transmission properties. Therefore, this method is difficult to apply for instance for attenuation of continuous-wave or narrow-band THz sources. Narrow-band attenuation can for instance be realized by metamaterial-based surfaces designed for high absorption in the vicinity of a specific resonance frequency (see, e.g., [20,21,22]). Although the field of metamaterial absorbers is very active, we will not cover this in the current tutorial as we will concentrate on broadband attenuation.

This tutorial is organized as follows. First we offer a theoretical analysis of broadband attenuation of ultrafast THz signals with crossed wire grids, and in particular, we investigate the effect of the wire grids on the polarization state of an ultra-broadband THz signal. We then proceed with a theoretical and experimental analysis of broadband attenuation with sequences of HR Si wafers. Here, we focus on the effect of multiple reflections in and between the wafers in different configurations of such sequences, and we show experimentally that a sequence of HR Si wafers offers precise and uniform attenuation across the 0.1–17-THz range. Finally, we discuss, from a theoretical point of view, the performance of partially transparent thin metal films for attenuation of THz signals. We show that for frequencies well below the inverse scattering time of the free electrons in the metal, films with thicknesses in the nanometer range offer broadband and relatively uniform attenuation of broadband THz beams.

2 Broadband Attenuation with a Pair of Wire Grid Polarizers

The perfect wire grid polarizer transmits the polarization of the THz field perpendicular to the wires with an efficiency of 100%, and completely blocks the component of polarization parallel to the wires. However, the frequency range of the wire grid polarizer is limited by the spacing p and to some extent the diameter d of the wires. The wire grid polarizer works as expected for wire spacings d ≪ λ, with gradual performance loss as the wavelength approaches d, or the frequency approaches c/d. This means that in practice, there will always be some transmission of the parallel polarization (here labeled t_∥), and the perpendicular transmission (here labeled t_⊥) is never exactly unity. In order to show the influence of the imperfect wire grid polarizer, we will use the Jones polarization matrix formalism to describe the transmission properties.

We consider the transmission through the two polarizers shown in Fig. 1. Here, the first polarizer is rotated an angle θ with respect to the linearly polarized input field (here chosen to be in the x direction), and the second polarizer is fixed with wires perpendicular to the x direction. The transmission through the two wire grids can then be described as:

$$ {\mathbf{E}}_{out}=\mathbf{P}\;\mathbf{R}\left(\theta \right)\mathbf{P}\kern0.22em \mathbf{R}\left(-\theta \right){\mathbf{E}}_{in}, $$

(1)

where E_in and E_out are the input and output field vectors, respectively, and P and R(θ)are the Jones matrix for the wire grid, and the rotation matrix, respectively,

$$ \mathbf{P}=\left(\begin{array}{cc}{t}_{\perp }& 0\\ {}0& {t}_{\parallel}\end{array}\right),\kern1em \mathbf{R}\left(\theta \right)=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ {}\sin \theta & \cos \theta \end{array}\right). $$

(2)

Fig. 1

Wire grid (WG) pair for attenuation of THz beams. Red arrows and ellipses represent the electric field vector before, between, and after the wire grids

In the special case of x-polarized input field, the output electric field vector is thus:

$$ {E}_{out}={E}_{in}\left(\begin{array}{c}{t}_{\perp}\left({t}_{\perp }{\cos}^2\theta +{t}_{\parallel }{\sin}^2\theta \right)\\ {}{t}_{\parallel}\left({t}_{\perp }-{t}_{\parallel}\right)\sin \theta \cos \theta \end{array}\right). $$

(3)

This shows that, for an imperfect wire grid, the output polarization will be slightly rotated (in the case of real-valued transmission coefficients), or even elliptically polarized in the more general case of complex-valued transmission coefficients. This possible change of the polarization state of the THz field is indicated by the red ellipses in Fig. 1.

The parallel and perpendicular transmission coefficients can only be evaluated precisely by full-wave calculations [23, 24]. However, a transmission line analogy can be used to derive approximate analytical expressions for the transmission coefficients [25]. The perpendicular and parallel transmission coefficients are derived for model circuit systems were the wires of the wire grid form a capacitive or inductive obstacle to the field, respectively. For completeness, we reproduce the analytical expressions from [25] for the perpendicular and parallel transmission coefficients:

$$ {t}_{\perp }=\frac{Z_1{Z}_2/{Z}_0^2}{\left(1+{Z}_1/{Z}_0\right)\left({Z}_b/{Z}_0+{Z}_2/{Z}_0\right)}, $$

(4)

with the following list of definitions of the various quantities:

$$ {\displaystyle \begin{array}{l}{Z}_1/{Z}_0=\frac{Z_a^2/{Z}_0^2+{Z}_a{Z}_b/{Z}_0^2+{Z}_a^2{Z}_b/{Z}_0^3}{2{Z}_a/{Z}_0+{Z}_a^2/{Z}_0^2+{Z}_b/{Z}_0+{Z}_a{Z}_b/{Z}_0^2},\\ {}{Z}_2/{Z}_0=\frac{Z_a/{Z}_0}{1+{Z}_a/{Z}_0},\\ {}{Z}_0/{Z}_a=i{f}_a\left(p,d,\lambda \right),\\ {}{Z}_0/{Z}_b=i{f}_b\left(p,d,\lambda \right),\\ {}{f}_a\left(p,d,\lambda \right)=\frac{p}{2\lambda }{\left(\frac{\pi d}{p}\right)}^2\frac{1}{A_2},\\ {}{f}_b\left(p,d,\lambda \right)=\frac{2\lambda }{p}{\left(\frac{p}{\pi d}\right)}^2{A}_1-\frac{p}{4\lambda }{\left(\frac{\pi d}{p}\right)}^2\frac{1}{A_2},\\ {}{A}_1=1+\frac{1}{2}{\left(\frac{\pi d}{\lambda}\right)}^2\left(\ln \frac{p}{\pi d}+\frac{3}{4}\right)+\frac{1}{2}{\left(\frac{\pi d}{\lambda}\right)}^2\sum \limits_{m=1}^{\infty}\left(\frac{1}{C_m}-\frac{1}{m}\right),\\ {}{A}_2=1+\frac{1}{2}{\left(\frac{\pi d}{\lambda}\right)}^2\left(\frac{11}{4}-\ln \frac{p}{\pi d}\right)+\frac{1}{24}{\left(\frac{\pi d}{p}\right)}^2-{\left(\frac{\pi d}{p}\right)}^2\sum \limits_{m=1}^{\infty}\left[m-\frac{1}{2m}{\left(\frac{p}{\lambda}\right)}^2-{C}_m\right],\\ {}{C}_m={\left[{m}^2-{\left(\frac{p}{\lambda}\right)}^2\right]}^{1/2}.\\ {}{t}_{\parallel }=\frac{2{Z}_3{Z}_4/{Z}_0^2}{\left(1+{Z}_3/{Z}_0\right)\left({Z}_d/{Z}_0+{Z}_4/{Z}_0\right)\left(1+{Z}_d/{Z}_0\right)},\end{array}} $$

(5)

again with the following list of definitions of the various quantities:

$$ {\displaystyle \begin{array}{l}{Z}_3/{Z}_0=\frac{Z_d/{Z}_0+2{Z}_c{Z}_d/{Z}_0^2+{Z}_d^2/{Z}_0^2+{Z}_c/{Z}_0}{1+{Z}_c/{Z}_0+{Z}_d/{Z}_0},\\ {}{Z}_4/{Z}_0=\frac{Z_c/{Z}_0+{Z}_c{Z}_d/{Z}_0^2}{1+{Z}_c/{Z}_0+{Z}_d/{Z}_0},\\ {}{Z}_c/{Z}_0=i{f}_c\left(p,d,\lambda \right),\\ {}{Z}_d/{Z}_0=-i{f}_d\left(p,d,\lambda \right),\\ {}{f}_c\left(p,d,\lambda \right)=\frac{p}{\lambda}\left[\ln \frac{p}{\pi d}+\sum \limits_{m=1}^{\infty}\left(\frac{1}{C_m}-\frac{1}{m}\right)\right],\\ {}{f}_d\left(p,d,\lambda \right)=\frac{p}{\lambda }{\left(\frac{\pi d}{p}\right)}^2.\end{array}} $$

These equations are derived under the assumption of constant current in the wires, which is a valid approximation for d ≪ λ and d ≪ p, where d is the diameter of the individual wires and p is the period of the wire grid (i.e., distance between two wires). These conditions are not always met in a THz wire grid polarizer. State-of-the-art freestanding wire grid polarizers have wire diameter of 5 μm and wire spacing of 12.5 μm,¹ leading to d/p = 0.4. However, reasonable agreement with experimental results over a larger range of parameters is claimed in [25] and in a follow-up experimental study of a variety of wire grids [26].

To give a practical example of the implications of the frequency-dependent perpendicular and parallel transmission functions of the wire grid polarizer, we consider three different types of THz pulses, with different bandwidths. Figure 2a shows the temporal profiles of THz pulses, generated and detected with photoconductive antennas (blue curve), generated by difference-frequency generation of femtosecond laser pulses in the organic nonlinear crystal DAST, and detected by free-space electro-optics sampling in gallium phosphide (red trace). The orange trace represents a THz pulse generated by a two-color femtosecond air plasma and detected by air biased coherent detection (ABCD). The traces have all been normalized to unity peak strength (and offset for clarity). Figure 2b shows the corresponding spectral amplitudes, with the same color coding, on a logarithmic frequency scale. The spectral range covered by each pulse spans the 0.1–2-THz range, the 0.3–4-THz range, and the 1–30-THz range, respectively.

Fig. 2

a Three types of THz pulses, generated by photoconductive antennas (blue curve, low bandwidth), the organic crystal DAST (red curve, medium bandwidth), and two-color femtosecond air plasma (orange curve, high bandwidth). b The corresponding spectral amplitudes of the three signals

In the following, we will show the effect of a wire grid attenuator as shown in Fig. 1 on each of these signals. As a representative example of high-quality freestanding wire grids, we will use d = 5 μm as wire diameter and p = 12.5 μm for wire spacing. With this, we use Eq. ((4) and Eq. (5) to calculate the transmission coefficients of the wire grid. Figure 3a shows the perpendicular and parallel transmission coefficients as function of frequency, across the relevant spectral range 0.1–70 THz, covering the full spectral window for all representative signals considered here. Figure 3b shows the phase of the two transmission coefficients across the same spectral range. Notice again the logarithmic representation of the frequency axis. At low frequencies, the perpendicular transmission is as expected close to unity, and the parallel transmission coefficient is close to zero. However, as the frequency increases, the perpendicular and parallel transmission starts to deviate significantly from unity and zero, respectively, due to the shorter and shorter wavelength. At approximately 24 THz (corresponding to λ = p), there is a strong anomaly in the transmission coefficients, originating simply from the first diffracted order in the wire grid array, that now works like a diffraction grating. Similarly, the next two resonances at yet higher frequencies correspond to higher-order diffraction peaks. At first glance, it may be surprising that the theory based on a transmission line analogy that we apply here can reproduce diffractive effects. However, according to Blanco et al. [25], in the transmission line analogy, the resonance effects are due to the onset of coupling to evanescent higher-order modes of the transmission line.

Fig. 3

a Perpendicular and parallel transmission amplitudes for a wire grid with d = 5 μm wire diameter and p = 12.5 μm wire spacing. b Frequency-dependent phase shift of the two transmission coefficients

From this general overview of the behavior of the wire grid, from polarizing element at low frequencies to a diffractive element at higher frequencies, it is now possible to show the effect of attenuation of the exemplary THz pulses with a wire grid attenuator. The procedure is to multiply the spectrum of the THz signal (Fig. 2b) by the wire grid attenuator transmission function (Eq. ((3)), and then perform an inverse Fourier transform of the resulting two polarization components. This is shown in Fig. 4, for each of the three pulse types, transmitted through a configuration where the first polarizer is rotated θ = 45°, corresponding to a theoretical field transmission of 50% through ideal wire grids. The central red curve shows a three-dimensional view of the electric field vector as function of time, and the projections onto the x-t plane and y-t plane shows the x component and y component of the electric field, respectively. The projection onto the x-y plane gives an impression of the linearity of the polarization.

Fig. 4

Time-dependent polarization state of the three THz pulse types, after transmission through a wire grid pair with θ = 45°, d = 5 μm, and p = 12.5 μm. a Low bandwidth. b Medium bandwidth. c High bandwidth. The red curves show the time-dependent vectorial electric field, and the blue curves are the projections onto the x, y, and z planes, respectively

For the low-bandwidth THz pulse, the wire grid attenuator works exactly as expected—the x-component of the field is attenuated to 50% of the original field strength, and there are virtually no signs of cross-polarization. For the medium-bandwidth THz signal, the transmitted signal now has a small but significant y-component, and, importantly, a small amount of ellipticity due to the phase difference between the two orthogonal transmission coefficients of the wire grids. In the extreme case of the high-bandwidth signal, the polarization of the transmitted signal is highly disturbed, with a strong time-dependent ellipticity and rotation of the polarization.

Figure 5 shows the transmission in terms of the pulse energy U, temporally integrated over the duration of the pulse (U ∝  ∫ E²(t)dt), through the wire grid attenuator as function of rotation angle θ, for the three different THz signals considered here. The open symbols represents the ideal behavior (t_⊥ = 1, t_∥ = 0) that results in E_out = E_incos²θ or U_out = U_incos⁴θ (see Eq. ((3)). In line with the observations above, the wire grid attenuator works very well for the low-bandwidth signal, reasonably well for medium-bandwidth signal, and rather poorly for the high-bandwidth signal.

Fig. 5

Angle-dependent power transmission through the wire grid attenuator (d = 5 μm, p = 12.5 μm), for the three different THz pulses considered. The open circles indicate the expected behavior of ideal wire grids

Thus, the wire grid attenuator is useful for THz signals in the lower end of the THz spectral range, up to approximately 4 THz for the best freestanding wire grids available today. Although substrate-based wire grids can offer a finer line spacing, the substrate will in practice limit the operational frequency range, e.g., to a window in the mid-infrared, induce multiple reflections, and introduce frequency-dependent losses. For THz signals of extreme bandwidth, such as the plasma-generated signals discussed here, alternative methods for broadband attenuation are required.

3 Broadband Attenuation with Silicon Wafers

The refractive index of high-resistivity float-zone silicon is n = 3.4175 with a variation of less than 0.0001 across the THz range (up to 4.5 THz), and the loss is exceedingly low (below 0.025 cm⁻¹ up to 4.5 THz) [27, 28]. Ignoring multiple reflections, the transmission coefficient at normal incidence through a silicon wafer is thus t = 4n/(n+1)² = 0.700, corresponding to a power transmission coefficient of 0.491, which corresponds closely to an attenuation of 3 dB. Virtually all other materials that have been characterized in the THz range display much larger dispersion and significant frequency-dependent absorption across the THz frequency range and are thus less than ideal to use for attenuation of broadband THz signals. High-purity HR Si is commercially available in the form of wafers used as substrates and devices in the semiconductor industry.² Thus, it could perhaps be tempting to use a sequence of HR Si wafers as a universal method for attenuation of THz beams, with field and power transmission through a sequence of N wafers of t_N = 0.7^N and T_N = 0.5^N, respectively. Figure 6 shows an example of a THz pulse transmitted through a 525-μm-thick HR Si wafer. The transmitted signal is composed of a directly transmitted part (which we will call the direct pass) followed by a sequence of echoes due to the multiple reflections of the THz pulse inside the wafer.

Fig. 6

Time-domain trace of a reference THz pulse (blue curve, vertically offset by − 0.3 units) and the same pulse transmitted through a HR Si wafer (red curve). The direct transmission is seen at t = 0 ps, and subsequent echoes from multiple reflections in the wafer are seen at 12, 24, and 36 ps. The time window T_win is available for distortion-free spectroscopic measurements

Whereas the relative transmission of the direct pass is 0.7 and its relative pulse shape is left unmodified by the pass through the HR Si, the subsequent echoes influence the applicability of the THz signal for spectroscopy. It can be seen that there is a useful time window (labeled T_win in Fig. 6) before the arrival of the first echo. Since the available time window is a central part of THz-TDS analysis [29], these echoes are important to consider when planning a given experiment. The available temporal window is 2nd/c, which for the 525-μm wafers used here equals 12 ps. The basic frequency resolution of the spectrum of the THz signal recorded with this temporal window is Δf = 1/T_win = c/2nd, equal to 0.084 THz in this example. Although methods exist for inclusion of the echoes in THz-TDS analysis [30,31,32,33], the limited time window of the undisturbed waveform is still an important side effect of attenuation with HR Si wafers.

Figure 7 shows the two general configurations that will be discussed here.

Fig. 7

a Dielectric wafers of thickness d and refractive index n, spaced by L. Arrows indicate some of the infinitely many reflections occurring within the wafers and between them. b Matrix model of propagation in a multilayered structure. c Angled array of wafers that minimizes on-axis reflections between the wafers

The configuration in Fig. 7a shows a sequence of N silicon wafers positioned perpendicular to the propagation direction of the THz beam, and (ideally) evenly spaced by a distance L. As indicated in the figure, the high index of refraction of silicon leads to substantial reflections at all the interfaces in the structure, and hence the transmission is best formally described by standard transfer-matrix formalism, as indicated in Fig. 7b.

In general, the effect of any linear optical element in the path of a collimated optical beam can be described in the frequency domain by a transfer function:

$$ {E}_{out}\left(\omega \right)=T\left(\omega \right){E}_{in}\left(\omega \right), $$

(6)

where E_in(ω) and E_out(ω) represent the complex-valued (amplitude and phase) of the input and output electric field, respectively, and T(ω) is the complex-valued transfer function (transmission or reflection). Propagation in free space over a distance d is represented by T(ω) = exp(iωd/c), and transmission over interfaces is described by the standard Fresnel coefficients (see, e.g., [34]). The description of the transmission through the sequence of wafers is best described by the theory of stratified media. Here, we limit the theoretical description to normal incidence of the THz field, and follow the derivation by Saleh and Teich [35], who uses a combination of transfer matrices and scattering matrices. Stratified media are also treated in other standard textbooks, including Born and Wolf [34] and Pedrotti and Pedrotti [36].

The transfer function of a stack of silicon wafers is modeled by N transfer matrices, that each is the product of transmission and propagation matrices that describe the interface transmissions in and out of the silicon and propagation through silicon and air, respectively:

$$ {\mathbf{M}}_{tot}={\left({\mathbf{M}}_{12}{\mathbf{M}}_{Si}{\mathbf{M}}_{21}{\mathbf{M}}_{air}\right)}^N\equiv \left(\begin{array}{cc}A& B\\ {}C& D\end{array}\right), $$

(7)

where the individual matrices are:

$$ {\displaystyle \begin{array}{l}{\mathbf{M}}_{12}=\frac{1}{2n}\left(\begin{array}{cc}n+1& n-1\\ {}n-1& n+1\end{array}\right),\\ {}{\mathbf{M}}_{21}=\frac{1}{2}\left(\begin{array}{cc}n+1& 1-n\\ {}1-n& n+1\end{array}\right),\\ {}{\mathbf{M}}_{Si}=\left(\begin{array}{cc}\exp \left( i n\omega d/c\right)& 0\\ {}0& \exp \left(- i n\omega d/c\right)\end{array}\right),\\ {}{\mathbf{M}}_{air}=\left(\begin{array}{cc}\exp \left( i\omega L/c\right)& 0\\ {}0& \exp \left(- i\omega L/c\right)\end{array}\right).\end{array}} $$

(8)

The matrix element S₁₁ of the scattering matrix S then determines the frequency-dependent transmission through the stack:

$$ \mathbf{S}\left(\omega \right)=\left(\begin{array}{cc}{S}_{11}\left(\omega \right)& {S}_{12}\left(\omega \right)\\ {}{S}_{21}\left(\omega \right)& {S}_{22}\left(\omega \right)\end{array}\right)=\frac{1}{D}\left(\begin{array}{cc} AD- BC& B\\ {}-C& 1\end{array}\right). $$

(9)

The S₁₁ element is the transmission coefficient, so finally, for a given input signal E(t), the temporal shape of the signal transmitted through the stack is calculated as:

$$ {E}_N(t)={\mathcal{F}}^{-1}\left({S}_{11}\mathcal{F}\left({E}_0(t)\right)\right). $$

(10)

where ℱand ℱ⁻¹denote the Fourier transform and the inverse Fourier transform, respectively.

In practice, the distance between the individual wafers needs to be controlled to within a small fraction of the wavelength in order for the matrix formalism described above to give a precise representation of the transmission properties. Small random variations in the spacer distance L can be accommodated in a statistical manner by introducing a normal distribution of dithering to the lengths used in M_air in Eq. ((7).

The multiple reflections between the individual wafers can be avoided by placing the wafers at alternating small angles, as shown in Fig. 7c. In this way, the reflected parts of the beams are diverted away from the propagation axis, and the transmission through the stack can be described by the transmission through the individual wafer, decoupled from the propagation in air between the wafers:

$$ {\displaystyle \begin{array}{c}{T}_N\left(\omega \right)={\left(\exp \left( i\omega L/c\right)\frac{t_{12}{t}_{23}\exp \left( i n\omega d/c\right)}{1-{r}_{21}{r}_{23}\exp \left(2 in\omega d/c\right)}\right)}^N\\ {}\approx {\left(\exp \left( i\omega L/c\right)\frac{4n\exp \left( i n\omega d/c\right)}{{\left(1+n\right)}^2-{\left(1-n\right)}^2\exp \left(2 in\omega d/c\right)}\right)}^N,\end{array}} $$

(11)

where the approximation in the second line of Eq. ((11) is that the field is normally incident on the wafer sequence. It is straightforward to include the additional path length inside the wafers due to the angle of incidence, and to use the full angle-dependent transmission and reflection coefficients; however, for small angles, the approximation is good. Specifically, the additional path length inside each wafer at incidence angle θ is:

$$ \varDelta d\left(\theta \right)=d\left(\frac{1}{\cos \theta \hbox{'}}-1\right)=d\left(\frac{1}{\arcsin \left(\sin \left(\theta \right)/n\right)}-1\right)\approx \frac{d}{2}{\left(\frac{\theta }{n}\right)}^2, $$

(12)

where θ' is the angle of propagation inside the wafer, determined from Snell’s law. For an incidence angle of 5.5°, the additional optical path is Δd = 0.2 µm for a 525-μm HR-Si wafer.

The transmitted signal through a sequence of wafers can be detected either by time-resolved methods in THz-TDS, such as photoconductive sampling, electro-optic sampling, or air biased coherent detection (ABCD)—here the waveform of the transmitted signal E(t) is detected, ideally over a time interval sufficiently large to capture the full waveform of the complete sequence of echoes from the wafer sequence. Alternatively, the power or pulse energy of the transmitted signal can be detected by an incoherent detector, such as a bolometer, pyroelectric detector, or Golay detector. In this case, the detected signal is the temporally integrated power, proportional to:

$$ P\propto \underset{0}{\overset{\tau }{\int }}{E}^2(t) dt, $$

(13)

where τ is the repetition rate of the signal. For a continuous-wave THz source, τ equals the oscillation period of the THz field, and for a pulsed source, τ equals the repetition rate of the system.

4 Experiments and Comparison with Theory

We investigated the transmission function of sequences of up to 7 HR-Si wafers, each with a diameter of 101.6 mm (4″) and nominal thickness of 525 μm. We tested two configurations. Firstly, wafers were placed at nominal normal incidence angle with distances L = 5, 10, and 15 mm (configuration in Fig. 7a), and secondly, wafers were placed at alternating angles of 5.5° with respect to the propagation axis. In both series of experiments, the wafers were placed in a wafer tray, which due to the width of the wafer slots allowed a small variation of the wafer distance L of the order of ± 0.2 mm, as well as small variations of the incidence angle, of the order of ± 0.3°. Care was taken to minimize these deviations by consistent placements of the wafers during the experiments.

The majority of the experiments were performed in the 0.1–1.5-THz range. In these experiments, time-resolved detection of the transmission of ultrashort THz pulses was performed with a commercial fiber-coupled THz-TDS system (Picometrix T-Ray 4000), using a temporal scan window of 320 ps, and a temporal resolution of 78.13 fs. This time window captures the full sequence of sequential echoes from the wafers detectable above the noise floor of the system. The incident THz pulses covered a frequency range 0.05–2 THz. In another set of experiments, we performed transmission measurements over a much broader frequency range (1–17 THz). The THz pulses were generated by two-color femtosecond plasma [37,38,39,40] and detected by air biased coherent detection [41, 42]. For experimental details of the setup used here, we refer to [43]. In the experiments discussed here, we used a temporal resolution of 13.33 and 6.67 fs for the long scans (150 ps time window) in Fig. 16 and short scans (5 ps temporal window) in Fig. 18, respectively.

Measurements of the time-integrated power transmission through the wafer sequences were performed with a high-power THz system source. We used difference-frequency generation of intense THz pulses (initial pulse energy 4 μJ) in the organic crystal DAST with 100-fs laser pulses at a wavelength of 1450 nm from an OPA system (HE-TOPAS, Light Conversion/SpectraPhysics), driven by 6-mJ, 100-fs pulses at 800 nm from a Ti/sapphire-based laser amplifier (SpectraPhysics Solstice Ace). The high-power THz pulses covered a frequency range 1–5 THz, with peak spectral intensity at 2 THz. The power of the transmitted THz pulses was measured with a calibrated pyroelectric detector (Gentec model THZ9B-BL-DZ).

Figure 8 shows measurements of the transmission through N = 0–7 silicon wafers, spaced by L = 5, 10 and 15 mm. The time-domain traces show that the input signal, consisting mainly of a single cycle of the THz field, separates into a complex pattern of echoes. The leading part of the echo sequence is delayed corresponding to the increased amount of silicon in the beam path (Δt = N(n − 1)d/c or 4.23 ps per wafer). The echo sequence is most complex for the 5-mm spacing, and for the 10- and 15-mm spacings, the temporal transmission signal is seen to settle at a characteristic pattern with echoes separated by the round-trip time in the silicon wafer Δt_Si = 2nd/c = 11.96 ps, where the strongest part of the transmission signal is not the leading part.

Fig. 8

Measurement of the time-domain signals transmitted through N = 0–7 silicon wafers, spaced by aL = 5 mm, bL = 10 mm, and cL = 15 mm. Traces are vertically offset by N/2 for clarity

Figure 9 shows the amplitude of the measured transmission function of the N = 1–7 wafer sequence, based on the time traces shown in Fig. 8, and calculated as T_N(ω) =  ∣ E_N(ω)/E₀(ω)∣. The transmission spectra are most complex for the 5-mm spacing, and the spectra for the 10- and 15-mm spacings evolve into a rather regular Fabry-Perot-like transmission behavior, with frequency spacing Δf = 1/Δt_Si = c/(2nd) = 0.0836 THz and deeper modulation of the transmission minima with increasing number of wafers. We also see that there is a tendency of overall decreased transmission towards higher frequencies.

Fig. 9

Experimental spectra of the transmitted time-domain signals shown in Fig. 8, vertically offset by N-1 for clarity. aL = 5 mm. bL = 10 mm. cL = 15 mm

As a direct comparison with experiment, Fig. 10 shows the simulated time-domain transmission of the input signal (lower, blue trace) for N = 1–7 wafers, using the transfer matrix formalism described by Eqs. (7)–(10). Again, the distance between the wafers is 5, 10, and 15 mm.

Fig. 10

Numerical propagation of a THz signal (lowest trace in each panel) through a sequence (N = 1–7) silicon wafers at normal incidence, corresponding to the configuration shown in Fig. 8. aL = 5 mm. (b) L = 10 mm. cL = 15 mm. Traces are vertically offset by N/2 for clarity

The general agreement between the theoretical transmission in Fig. 10 and the corresponding experimental data in Fig. 8 is good. We observe the largest complexity of the transmitted signal for the smallest spacing (Fig. 10a vs. Fig. 8a), and the emergence of a stable transmission pattern with increasing number of wafers, especially for the larger spacings. Especially for the 15-mm spacing (Fig. 10c) the transmitted signal is composed of distinct groups of echo sequences, separated by the round-trip time between the wafers, Δt_air = 2L/c. This temporal grouping of the transmission signal is also observed in the experimental data (Fig. 8c), although with a significantly smaller amplitude of the signal group, delayed by the round-trip between the wafers. The reason for this discrepancy is mainly the non-perfect alignment of the angle and distance between the wafers in the experimental setup. Small angular deviations of the wafers will divert the reflected parts of the signal from the propagation axis, and small differences in distance will diminish the constructive interference between the reflected signals from the different air sections of the wafer sequence.

The combination of standing waves within the individual wafers and between the wafers can be observed in the frequency domain, as shown in Fig. 11. The calculated transmission spectra show a superposition of the slowly varying interference pattern from within the wafers and the more rapidly varying interference from the air spacing layers. Compared to the experimental transmission spectra in Fig. 9, the rapid modulation is much more pronounced in the ideal, calculated results. This is a direct consequence of the small misalignment of the wafers with respect to each other in the experiment. Such misalignment will severely diminish the standing waves between the wafers.

Fig. 11

Calculated transmission spectra through N = 1–7 wafers, equally spaced by L = 15 mm at normal incidence. Traces are vertically offset by N-1 for clarity

The effect of random variations of the air distance in a wafer sequence can be observed directly if the THz-TDS system is capable of displaying a live trace of the detected signal. In that case, small distance variations can be induced mechanically, and it can be observed how parts of the echo sequence that belong to the standing-wave pattern between the wafers slightly shifts temporally. In the transfer matrix numerical propagation, this effect can be mimicked by dithering the distance between the wafers and averaging the transmission function over a large number of configurations. This procedure washes out the interference between the wafers and simplifies the transfer function significantly. Figure 12 shows an example of such a calculation. Here, the nominal air distance L = 15 mm has been dithered by a normally distributed random distance of 100 μm, and the transmission of 100 such configurations has been averaged.

Fig. 12

a Time-domain and b frequency-domain average transmission spectra through N = 1–7 wafers, where the nominal spacing L = 15 mm has been randomly dithered with a normally distributed random variation of 0.1 mm in a series of 100 calculations. The corresponding experimental data are shown in Fig. 9c

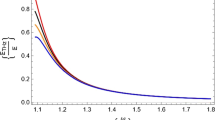
Based on the above results, Fig. 13 summarizes the predicted and measured attenuation properties of the wafer sequence at nominally normal incidence. The open-circle symbols represent the measurements with THz-TDS (L = 5, 10, and 15 mm) using Eq. (13) and results from measurements with the pulsed, high-power THz source and the pyroelectric detector. For the pyroelectric detector measurements, the wafers were placed at normal incidence with a spacing of approximately 5 mm. The green curve shows the average value and standard deviations of the measurements.

Fig. 13

Temporally integrated power transmission coefficient through N = 1–7 Si wafers placed at normal incidence in the beam path at spacings L = 5, 10, and 15 mm, and measured with a pyroelectric detector (open circle symbols), the average and standard deviation of the measurements (green curve). The dark red and blue curves show the predictions from ideal and dithered transfer matrix formalism, respectively. The light gray traces show the results of 100 individual transfer matrix calculations with spacings randomly dithered by 0.1 mm. The dashed, light blue curve shows T(N) = [4n/(n+1)²]^2N

For comparison, the light blue, dashed curve shows the relation for attenuation that could be expected if only the directly transmitted signal is considered (electric field transmission t(N) = [4n/(n + 1)²]^N), and the dark, red curve shows the expected result from ideal transfer matrix theory, where L is kept constant through the wafer sequence. If the distance is dithered by a small amount, here a normal distribution with a standard deviation of 0.1 mm, the resulting transmission, averaged over 100 independent calculations (blue curve shows the average and standard deviation and the light gray curves show the individual calculations), is smaller than the ideal transmission, and approaches our measured values.

Figure 14 shows results of the calculated and measured transmitted signals through N = 0–7 wafers arranged at a small angle (alternating ± 5.5^o with respect to the propagation direction, as shown in Fig. 7c). The calculations are performed with the independent slab model (last, approximative part of Eq. ((11)). The temporal and spectral transmission pattern is now only determined by the standing waves within the wafers, without the rapid oscillations in the transmission spectrum originating from standing waves between the wafers (Fig. 14c). As was the case for nominally normal incidence on the wafers, we observe a degradation of the transmission amplitude at high frequencies in the experimental data.

Fig. 14

a Time-domain calculation and b corresponding measurement of transmission through N = 0–7 wafers, slightly angled with respect to the propagation axis. c Comparison of the calculated (blue) and measured (red) field transmission coefficient through N = 7 wafers

Figure 15a shows the temporally averaged power transmission through the angled wafers measured by THz-TDS (orange curves) and pyroelectric detection (purple, open circles, same data as shown in Fig. 13). The predicted transmission, calculated by the independent slab model (Eq. ((11)) is represented by the blue curve, and the red, dashed curve again shows the prediction based on t(N) = [4n/(n + 1)²]^N. It is observed that our experimental results are close to, but lower than, the predicted values from the independent slab model. Figure 15b shows the measured field and power transmission coefficients through the angled wafer sequence if only the first part of the temporal signal, the directly transmitted pulse, is considered. The red, open circles show the transmission coefficient of the peak of this part of the signal. The blue, open circles show the temporally integrated (in a ± 5 ps window around the first peak) power transmission coefficient. The dashed curves are corresponding power-law fits, based on the measured transmission values after the first wafer. Only in this case, the simple behavior t(N) = [4n/(n + 1)²]^N is recovered experimentally.

Fig. 15

a Temporally integrated power transmission coefficient through N = 0–7 wafers at angled incidence (orange, open circles). For comparison, we show the results of the pyroelectric detection (purple, open circles, same data as in Fig. 13). The Blue curve shows the prediction from the independent slab model (Eq. ((11)), and the red, dashed curve shows the prediction T(N) = [4n/(n+1)²]^2N. b Transmission coefficient through the wafers, based on the directly transmitted part of the temporal signal. Red and blue open circles show the peak electric field transmission and blue, open circles show the temporally integrated power transmission, respectively. Dashed lines are power-law curves based on the field and power transmission values after a single wafer

5 Ultra-Broadband Performance of HR Si Sequences

Until now, we have only considered the low-frequency (< 1.5 THz) performance of HR Si sequences. As mentioned earlier, the refractive index of silicon is constant across a very large frequency range in the far infrared, and the absorption is very low, apart from a narrow region near 18 THz, where a phonon overtone [44, 45] leads to a weak absorption band. Thus, it can be expected that the discussion in the previous section is valid across a much wider frequency range.

Figure 16 shows a measurement of ultra-broadband THz pulse transmission through the same sequence of Si wafers as used in the previous section. The single-cycle pulses now cover the frequency range from 1 THz to beyond 20 THz, and thus, the pulses are much shorter than in the previous section. Figure 16a shows the time traces of the pulse propagating through the spectrometer without attenuation (blue trace), with 1 Si wafer inserted (red trace), and with 7 wafers inserted (orange trace). As expected, we observe attenuation of the signals. However, in this experiment, the 7-wafer temporal transmission pattern does not follow the same pattern as observed in the low-bandwidth experiment (see Fig. 8 and Fig. 14), where the direct transmission is weaker than the subsequent echoes. The reason for this observation is indicated in Fig. 16b, where we show a zoomed-in view of the direct pass and subsequent echoes after transmission through 7 wafers (boxed regions in Fig. 16a). The direct transmission (blue trace) consists of a single pulse, whereas the subsequent echoes consist of two peaks (first echo, red trace), three peaks (second echo, orange trace), and four peaks (third echo, purple trace).

Fig. 16

a Temporal traces of ultra-broadband THz pulses. Blue trace is the reference signal (with system echo at 55 ps), red trace (vertical offset + 0.005) is after transmission through 1 HR Si wafer, and orange trace (vertical offset + 0.01) is after transmission through 7 HR Si wafers. The dashed boxes indicate zoom regions on the direct pass and the first, second, and third echoes of the 7-wafer transmission shown in b. In b, each signal is horizontally shifted to t = 0 and vertically offset for clarity

This behavior is due to a small but systematic variation of the thicknesses of the 7 wafers, leading to two possible path lengths for the internally reflected parts of the signal within the wafer sequence. In Fig. 17, we show the result of a transfer matrix simulation of the experiment, following the same procedure as in the previous sections. In the simulation, the wafer thicknesses were chosen randomly to be either 525 or 528 μm. The origin of this variation is not precisely known, but we suspect that the wafers are from different production batches, leading to the binary thickness variation. The 3-μm variation is well within the tolerances for typical thickness specifications of commercial wafers.³

Fig. 17

Simulation of ultra-broadband transmission through HR Si wafers, using the experimental waveform as the input signal, and with a binary thickness variation of 3 μm of the wafers. a Reference signal (blue trace) compared to transmitted signal through 1 wafer (red trace, vertical offset + 0.2) and 7 wafers (orange trace, vertical offset + 0.4). The dashed boxes indicate zoom regions on the direct pass and the first, second and third echoes of the simulated 7-wafer transmission shown in b. In b, each signal is shifted horizontally to t = 0 and vertically offset and scaled by a factor of 5 for clarity

Figure 17b shows, in the same manner as Fig. 16b, a zoom-in on the simulated direct transmission and subsequent echoes. A splitting of the echo signals is observed in the simulation, in close agreement with the experimentally observed splitting. The detailed shape of the echo sequence, e.g., for the third echo, is determined by the distribution of the thicknesses of the 7 wafers, and we did not attempt to find the distribution that matches the experiment the best. Thus, the exact patterns are not the same in the experiment and in the simulation. The very small spacing of the peaks in the echoes (less than 100 fs) also show why this effect was not observed clearly in the low-bandwidth experiments in the previous section, using the same wafers. With a much longer THz pulse, the splitting is simply buried within the width of the THz pulse.

Figure 18 shows an analysis of the direct pass through N = 1 and N = 7 wafers, using the ultra-broadband THz pulses. Figure 18a shows the time traces of the reference (no wafers, blue trace), after 1 wafer (red trace) and after 7 wafers (orange trace). The traces have been scaled by the expected attenuation of 0.7^N. In the ideal case, this would result in pulses with identical height. However, there is a slight reduction of the N = 7 signal. Figure 18b shows the spectra (not scaled) of each of the signals in Fig. 18a. The Si phonon overtone absorption band is clearly visible in all traces, including the reference. This is due to another thicker Si wafer used in the experimental setup for blocking of residual pump light from the two-color femtosecond plasma generation of the THz pulse. This residual absorption and the general roll-off of the signal towards high frequencies results in a useful spectroscopic range of 1–17 THz in this particular experiment.

Fig. 18

Experimental determination of broadband attenuation of the directly transmitted ultra-broadband signal. a Time-domain traces of the reference signal (blue trace), direct pass through 1 and 7 wafers (red and orange trace, respectively). Pulses have been arbitrarily offset horizontally for clarity. b Spectral amplitude of the signals in a, on a semi-logarithmic scale. c Broadband transmission through 1 wafer (blue trace) and 7 wafers (red trace). The orange trace is the 1-wafer transmission to the 7th power, and the dashed and dotted lines are the theoretical transmission coefficients through 1 and 7 wafers, respectively, based on a constant refractive index of n = 3.4175

Figure 18c shows the calculated transmission coefficient of 1 wafer (blue curve) and 7 wafers (red curve). It can be seen that the attenuation is indeed broadband and approximately constant across the 1–17 THz range. However, there is a slight tendency for reduced transmission towards higher frequencies. The orange curve is the single-wafer experimental transmission raised to the 7th power, and the dashed and dotted horizontal lines in the plot shows the expected attenuation (0.7 and 0.7⁷ = 0.082) based on the single-wafer transmission 4n/(n + 1). The measurements are in good agreement with these estimates.

6 Alternative Methods for Controllable Broadband THz Attenuation

As we have discussed here, attenuation of THz beams by reflection from high-index dielectrics such as high-resistivity silicon is more complicated than could perhaps be expected from on simple estimates of the transmission coefficient through a single wafer at normal incidence. A more complex picture emerges when the full, frequency-dependent transfer function through the wafer sequence is calculated. Multiple reflections, partly within the wafers, and partly between the wafers, lead to strong modulations in the transfer function, corresponding to the free spectral range of the wafers and the cavities between the wafers, respectively. However, these standing-wave effects lead to echoes in the time domain, transmitted through the wafer sequence at later times compared to the directly transmitted signal. Hence, if only the directly transmitted signal is considered, the simple estimate of the total field transmission coefficient t(N) = [4n/(n + 1)²]^N is accurate.

The main reasons for the use of silicon wafers for attenuation of pulsed THz signals is the spectrally flat response of silicon and the high refractive index, leading to substantial reflection losses. In principle, a thin film with variable, but spectrally flat transmission would be preferable, as the majority of the effects related to standing waves in the dielectric substrate would vanish. Thin metallic films may be able to fulfill the requirements of flat spectral response and controllable transmission. Very thin films of high conductivity are required for such operation, and for instance gold, when deposited in few nanometer thickness, are known to form isolated islands that lead to a frequency-dependent transmission in the low THz range [46]. Thin metallic films on high-index substrates can form an antireflection coating for the internal reflection due to impedance matching with air, as demonstrated with chromium that form continuous films already from a few nm thickness [47], and with gold films below the percolation threshold [48]. Hence, careful design of such structures, possibly involving reproducible deposition on ultrathin, low-index membranes, will be required.

As two design examples, we consider deposition of a thin film of chromium on a thin polymer substrate and on a thicker HR Si substrate. Chromium is chosen for this design study due to the favorable coating properties, where thin, continuous films down to 2 nm thickness can be deposited on silicon [47]. The dielectric properties of the thin metal film are modeled by the Drude model for the effective conductivity at film thickness a:

$$ \sigma \left(\omega \right)=\frac{\sigma_{dc}(a)}{1- i\omega \tau (a)}, $$

(14)

where a is the film thickness, σ_dc = Ne²τ/mis the effective DC conductivity, and τ is the effective scattering time, dependent on the thickness of the film. We use a bulk resistivity of 100 μΩ-cm [49], corresponding to a bulk DC conductivity of σ_{dc, bulk} = 10⁶ S/m and a bulk scattering time τ_bulk = 10 fs, representative for metals with intermediate conductivity [50]. With a Fermi velocity in the range of 10⁶ m/s [50], the mean free path of electrons in bulk chromium is approximately l_mfp = v_Fτ ≈ 10 nm, comparable to the desired film thicknesses. Interface scattering reduces the effective scattering time, and thus the conductivity of the thin film. Under the assumption of diffusive scattering at the film interfaces, the reduced DC conductivity and scattering time can be modeled by [51]:

$$ \frac{\sigma_{dc, bulk}}{\sigma_{dc}(a)}=\frac{\tau_{bulk}}{\tau (a)}=\frac{\varPhi \left(\kappa \right)}{\kappa }, $$

(15)

$$ \frac{1}{\varPhi \left(\kappa \right)}=\frac{1}{\kappa }-\frac{3}{4}\left(1-\frac{1}{12}{\kappa}^2\right) Ei\left(-\kappa \right)-\frac{3}{8{\kappa}^2}\left(1-{e}^{-\kappa}\right)-\left(\frac{5}{8\kappa }+\frac{1-\kappa }{16}\right){e}^{-\kappa }, $$

(16)

where κ = a/l_mfp is the ratio of film thickness and mean free path and Ei(−κ) is the standard elliptical integral. The reduction of the bulk conductivity (right-hand side of Eq. ((15)) is plotted as function of film thickness in Fig. 19. It is clear that for film thicknesses comparable to the mean free path, the reduction from the bulk conductivity is significant.

Fig. 19

Reduction of bulk conductivity in thin films of chromium, as function of film thickness. Notice the logarithmic vertical axis

The effective conductivity for a specific film thickness can then be converted into an effective, complex-valued index of refraction of the film ($\varepsilon ={\varepsilon}_{\infty }+ i\sigma (a)/{\varepsilon}_0\omega, n=\sqrt{\varepsilon }$), and the frequency-dependent transmission through the full stack, consisting of the metal film and the substrate, can be calculated using the same transfer matrix formalism as discussed above (Eqs. (7)–(10)).

Figure 20 shows the result of such a simulation for a thin chromium film on a lossless 50-μm-thick polymer substrate with refractive index 1.5 (Fig. 20a–c) and on a 525-μm-thick HR-Si substrate (Fig. 20d–f). The film thickness was varied from 0 to 25 nm in the simulation. For the calculation, we used the same input signal as in the previous simulations, e.g., the N = 0 trace in Fig. 8a.

Fig. 20

Design of metallic thin-film attenuator for THz beams. a Temporally integrated power transmission, reflection, and absorption through a chromium film on a 50-μm polymer substrate (n = 1.5), as function of film thickness. b Spectrally resolved field transmission coefficient in the 0–2-THz range. c Temporal trace of transmitted THz pulse, as function of chromium film thickness. d–f Same as a–c, for a thin chromium film on a 525-μm HR-Si substrate

The temporally integrated power transmission, reflection, and absorption coefficients (T, R, and A = 1 − T − R, respectively) are shown in Fig. 20a, d for the thin polymer and thick HR-Si substrate, respectively. For the polymer film, the power transmission varies from 93 to 5% when the Cr film thickness is increased from 0 to 25 nm. The reflection increases generally with Cr film thickness, and the absorption in the Cr film peaks at approximately 10 nm film thickness. The frequency-dependent field transmission coefficient (Fig. 20b) shows a rather uniform spectral response that decreases monotonically with film thickness. This leads to a constant temporal shape of the transmitted THz signal without subsequent echo structure, as shown in Fig. 20c, and therefore a controllable, broadband attenuation determined by the metal film thickness.

If the same Cr film is placed on a 525-μm HR-Si substrate, the general behavior of the attenuator changes in some important respects. Most importantly, the frequency-dependent field transmission coefficient (Fig. 20e) is now heavily modulated due to the same standing wave pattern in the substrate as discussed in the first part of the paper. However, at a Cr film thickness of approximately 9 nm, this modulation is suppressed. The effect of this suppression is seen in the transmitted temporal waveform (Fig. 20f), where the general appearance of the transmitted signal is that of a main pulse followed by a weaker signal, coming from the first round-trip in the substrate. However, at 9 nm Cr thickness, this echo disappears, due to perfect impedance matching for transmission from the substrate through the Cr film into air. Thus, the transmitted signal is a single pulse, attenuated by the field transmission coefficient of 45% (power transmission 20%). This reduction of the internal reflection is identical to the observation in ref. [47], and therefore not unexpected. However, in the context of broadband attenuation of THz signals, the simulation illustrates the design of an easily manufactured structure (9 nm Cr on a standard HR-Si wafer) that offers 45% field transmission and virtually no temporal reshaping of the transmitted signal.

Crucially, the operational bandwidth of an attenuator based on thin metal films will be determined by the electron scattering rate of the metal. More specifically, Eq. ((14) shows that when ωτ = 1, the real part of the conductivity is reduced by a factor of two relative to its DC value. For chromium with a 10-fs bulk scattering time, the condition ωτ = 1 corresponds to a frequency of 15.9 THz. Thus, we could expect that the thin-film attenuator optical properties would be comparable to those shown in Fig. 20 up to much higher frequencies. We will demonstrate this by the following simulation, very similar to the previous discussion with the exception that we now use an ultra-broadband input pulse, identical to the input pulse used in the preceding section.

Figure 21a shows the time-domain simulation results of the transmission of the ultra-broadband input pulse (the blue curve) through the 50-μm polymer film covered with various thicknesses of Cr film (3.2, 9.5, and 25 nm, respectively, for the three red curves). The transmitted signals have been vertically shifted and horizontally shifted by the indicated values for clarity. The vertical arrows indicate the position of the first echo from the substrate, visible especially for the a = 9.5 and 25 nm Cr films.

Fig. 21

Ultra-broadband transmission through thin metal films. a Simulated time-domain traces through 3.2, 9.5, and 25 nm chromium on 50-μm thick polymer film (n = 1.5). Traces are offset vertically and horizontally for clarity. Arrows indicate the echo of the first reflection in the polymer substrate. b Transmission coefficient in the 0–20-THz range of the 3.2, 9.5, and 25 nm film thicknesses. c Same as a, with the thin metal film in a 525-μm HR Si substrate. d Transmission coefficient in the 0–20-THz range of the 3.2, 9.5, and 25 nm film thicknesses. Blue curves are the full transmission, taking all echoes in the Si substrate into account; red curves are considering the direct transmission only

Figure 21b shows the transmission coefficient through the different film thicknesses, calculated as the amplitude ratio of the spectra of the transmitted pulses and that of the reference pulse. As expected, the transmission reduces with increasing film thickness. The oscillatory behavior of the transmission is due to the interference between the direct pass and the first echo of the input signal. For the smallest thickness used here (3.2 nm), these etalon oscillations are significantly reduced, due to the vanishing reflection at this film thickness. The oscillations seen in the transmission coefficient in Fig. 21b are also observed in the low-bandwidth simulation in Fig. 20b, where the thickness of minimum reflection was also identified.

Figure 21c shows the simulation results using the 525-μm HR Si substrate. Due to the substrate thickness, the directly transmitted part of the THz pulses are delayed by approximately 6 ps (Δt = nd/c), so we have horizontally shifted the transmitted signal by the indicated amount in order to show the detailed waveform in the same short time window as the reference signal. In addition to the direct pass, we also observe subsequent echoes at later times, here delayed by additional multiples of 12 ps. Except for the thinnest metal films, only the first echo contributes significantly to the full transmitted signal. Figure 21d shows the frequency-resolved transmission coefficient for the three film thicknesses. The curves in blue color show the transmission calculated from the full transmitted time trace, i.e., including all echoes, and the red traces show the transmission coefficient, based on the direct pass (the part of the signals shown in Fig. 21c).

Again, we observe that there is an optimal thickness of the metal film for suppression of the etalon effect in the substrate. However, the antireflection properties are not perfect across this large bandwidth. This is simply due to the variation of the complex-valued conductivity as frequencies increase and approach the ωτ = 1 condition. Still, considering the direct-pass transmission, which is most relevant in THz-TDS measurements, the transmission is rather constant (t = 0.45–0.52 for the 9.5-nm film) across the 0–20-THz range, only marginally larger variation than observed experimentally for one Si wafer (t = 0.7–0.65 across the 1–17-THz range, Fig. 18).

7 Conclusions

In this review, we have discussed several methods for attenuation of broadband THz signals. The crossed wire grid attenuator was shown to be an excellent choice in the low-frequency region below approximately 4 THz for the best freestanding wire grids commercially available today, whereas signals at higher frequencies experience significant and frequency-dependent modifications of the polarization state.

For more broadband operation, we discussed how to attenuate broadband THz signals with a sequence of high-resistivity silicon wafers up to a frequency of 17 THz. Due to the exceedingly low dispersion and absorption loss, the temporal shape as well as the spectral amplitude and phase of the transmitted THz signals are maintained after transmission—when only the directly transmitted signal is considered as will be the case in most applications based on terahertz time-domain spectroscopy. If only the first transmitted signal is considered, the transmission through a sequence of N wafers follows a simple power law, based on the transmission through a single wafer. However, including the full temporal sequence of multiple reflections in each wafer, the power transmission deviates strongly from the simple power law, and the transmission settles at a constant value for large numbers of wafers, specifically a power transmission of 15–20%, depending on the accuracy of the alignment of the wafers with respect to each other and the THz beam. This scenario is relevant for continuous-wave applications. The multiple reflections lead spectrally to very strong oscillations in the transmission coefficient, thus limiting the value of this approach in narrow-band or continuous-wave applications. However, for both linear, low-power and nonlinear, high power THz-TDS applications, the direct pass is typically used, and the main drawback of subsequent echoes in the time-domain signal is the limitation of the available time window for undisturbed spectroscopic measurements.

As an alternative route to reproducible, broadband attenuation, we suggested and analyzed the use of thin metallic films, such as chromium, with favorable coating properties to a suitable substrate such as high-resistivity silicon. With metal film thicknesses in the range of 10 nm, it is possible to obtain controllable and approximately constant attenuation across a wide frequency range, here demonstrated up to 20 THz. The upper limit of constant attenuation is determined by the electron inverse scattering time in the metal.

As has become clear, the main technical challenge with attenuation based on either wafer sequences or metal-coated wafers is the presence of internal multiple reflections that lead to oscillatory behavior of the transmission spectrum of the attenuator. With an optimized thickness of the thin metal film attenuator, it is possible to suppress these internal reflections, but since this optimal thickness is directly linked to the attenuation, it is not possible to independently optimize the antireflective properties and the level of attenuation. Thus, a perfect antireflective layer on the back side of the wafer would be highly beneficial. Already some work in the literature addresses the construction of antireflective coatings in the THz range, based on deep plasma etching of silicon surfaces show promise in this direction [52, 53], and a further increase in performance bandwidth of such surfaces would be a great technological benefit for the THz community.

Having the right optical components is a prerequisite for advanced optical applications. With the increasing use of ultra-broadband light sources in the THz range, now approaching the mid-infrared, we believe that this tutorial has provided useful insights into the selection of appropriate methods for uniform attenuation of such signals.