Abstract
A vegetation-resolving CH3D-SWAN surge–wave modeling system is used to examine the role of mangroves and salt marshes along the shore of Biscayne Bay in buffering surge, wave, and inundation in Southeast Florida during Hurricane Andrew (1992). First, the 3D vegetation-resolving model is validated by comparing the simulated and measured high water marks from post-hurricane field survey, debris lines, and time series of water level at the Haulover Pier. The simulated water levels and magnitude and extent of maximum inundation agree well with the observed data, whereas the removal of vegetation from the model leads to massive flooding with increased total inundation volume and total inundation area in the highly populated low-lying area behind the Biscayne Bay. Additional simulations show that the surge–wave–inundation buffering capacity of the mangrove forest depends on the vertical structure of the wetted leaf area index, \(A_{\text{w}}\) and the frontal leaf area index, \(A_{\text{f}}\). The study demonstrates the capability of CH3D-SWAN in quantifying the role of mangroves in buffering storm surge, wave, and inundation, and demonstrates its potential application for assessing the effectiveness of coastal wetland restoration projects. Meanwhile, the accurate representation of vegetation’s vertical structure can enhance the numerical modeling of flow–vegetation interaction processes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Mangrove forests grow along the coast in tidal zones with fine and salty sediments across the tropics and sub-tropics, and along with salt marshes, can sequester carbon much more effectively than terrestrial forests, offering an important means to mitigate global climate change and sea level rise (SLR). Meanwhile, mangroves provide habitat for fisheries and are green infrastructures that can protect coastal communities from flooding due to tropical cyclones (e.g., Krauss et al., 2009; Mcivor et al., 2012; Sheng et al., 2012) and tsunamis (Alongi, 2008). Nowadays, the creation and restoration of coastal ecosystems, including mangrove forests, coral reefs, and salt marshes, are being considered by many as a more sustainable, cost-effective and ecologically sound alternative instead of hard infrastructure for the mitigation of future coastal hazards (Feagin, 2008; Gedan et al., 2011; Duarte et al., 2013; Temmerman et al., 2013; Spalding et al., 2014). Examples include the restoration of 80 km2 tidal marshes in San Francisco Bay, California, large marshlands restored in the Mississippi delta, Louisiana, and mangrove forest plantation in Soc Trang Province, Vietnam (Schmitt et al., 2013).
Krauss et al. (2009) found that the coastal vegetation in Southwest Florida buffered the peak water level during several hurricanes including Charley in 2004. The reduction in the peak water level ranged from 4.2 to 9.4 cm/km, depending on the wetland types, local geographic features, and storm characteristics. They also pointed out that it is difficult to rely on field observation alone to estimate the relative contribution of mangroves versus other wetland types, open water or microtopographic relief in buffering the peak water level over similar distances. Recent studies have shown that numerical surge–wave models which incorporate flow–wave–vegetation interactions can be used to assess the contribution of various factors, such as local coastal geographic features as well as storm and vegetation characteristics, to the reduction of surge, wave, and inundation by vegetation (e.g., Sheng et al., 2012).
Numerous storm surge models represent the effect of vegetation present in the water column by locally adjusting the Manning’s n coefficient in the bottom friction term of two-dimensional vertically integrated storm surge models (Wamsley et al., 2010; Zhang et al., 2012) and using the local land cover class data provided by the National Land Cover Dataset (NLCD) (Homer et al., 2004) from the U.S. Geological Survey (USGS). However, Lapetina & Sheng (2014) showed that Manning’s n is a function of vegetation and flow, making it a time-dependent and spatially varying coefficient and very difficult to tune. Indeed, ADCIRC (ADvanced CIRCulation, a circulation model developed by Luettich et al., 1992) simulations of Katrina (Bunya et al., 2010) and Ike (Hope et al., 2013) used Manning’s n that differ by a factor of two (0.02 vs. 0.01) in Louisiana shelf. The failure to capture the physical flow–vegetation processes and the necessity of excessive tuning for different flow situations to fit observed data make the 2D modeling approach unsuitable for accurate assessment of the buffering effects of vegetation under varying flow conditions during storms.
Unlike the traditional 2D approach, three-dimension (3D) vegetation-resolving numerical models (Temmerman et al., 2005; Sheng et al., 2012) explicitly represent the vegetation effects in 3D momentum equations and turbulence equations, which aim to model the vegetation-related physical processes without excessive tuning. In this study, 3D vegetation-resolving surge–wave modeling system CH3D-SWAN (Sheng et al., 2012; Lapetina & Sheng, 2014, 2015) is used to assess the role of vegetation, including mangroves and marshes, in buffering surge, wave, and inundation. The vegetation-resolving CH3D-SWAN is able to incorporate the horizontal distribution and vertical structure of coastal wetlands, including species, stem height, stem density, and vertical distribution of wetted and profile leaf area indices.
This study focuses on the southeastern coast of Florida where future 100-year inundation is expected to increase by up to 3 m by 2100 due to more intense storms and 2 m SLR (Sheng et al., Ongoing study to incorporate climate change effects into coastal inundation decision support tool). We simulate the impact that Hurricane Andrew had on this coastline in 1992. Along 30 km of the western shoreline of Biscayne Bay, there exists a mangrove forest with some marshes. By learning the flood protection value of these mangroves and marshes during a major hurricane, coastal community decision makers can start to develop wetland restoration plans to enhance coastal resiliency. This information is particularly useful for decision makers in highly urbanized centers such as Miami, New York City, and San Francisco where very limited space is available for creation and restoration of coastal wetlands to enhance coastal resiliency.
A brief description of the vegetation-resolving CH3D-SWAN is given in the next section, followed by a description of the model setup including the model domain and grid and the mangrove forest along the western shore of Biscayne Bay. Simulated surge, wave, and inundation during Hurricane Andrew (1992) are then given. Based on the simulation results obtained with and without the mangrove forest, the role of the coastal wetland in reducing storm surge and coastal inundation is assessed and discussed.
Vegetation-resolving CH3D-SWAN
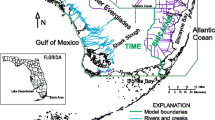
The vegetation-resolving CH3D-SWAN modeling system used in this study is based on a vegetation-resolving 3D baroclinic hydrodynamic model CH3D (Sheng, 1989; Sheng et al., 2012) coupled to SWAN (Suzuki et al., 2012), a vegetation-resolving wave model. CH3D uses a curvilinear boundary-fitted grid in horizontal and sigma grid in vertical direction. While CH3D-SWAN is used for the coastal domain, the modeled results from large-scale circulation model (CH3D or ADCIRC) and wave model WaveWatch III (Tolman, 2009) provide the storm surge and wave conditions, respectively, along the open boundaries of the coastal domain. Meanwhile, CH3D-SWAN can use the hurricane track data from NOAA to generate synthetic wind fields (e.g., Holland, 1980) or directly read the wind fields from an atmospheric model (e.g., the North Atlantic Mesoscale model of NOAA based on the Weather Research and Forecast model by Janjic et al. (2001)). CH3D-SWAN has been used to forecast water level and coastal circulation along Florida coast (Fig. 1) and to generate probabilistic coastal inundation maps in current and future climates throughout Florida, including the effects of SLR and future storms.
In contrast to status quo 2D storm surge models (e.g., Zhang et al., 2012) that parameterize the effect of vegetation on flow by empirical tuning of Manning’s n, CH3D-SWAN resolves the vertical and horizontal structures of mangroves and marshes (Sheng et al., 2012). The vegetation module has been validated by comparison with various laboratory experiments (Sheng et al., 2012; Lapetina & Sheng, 2014) and observed data in Galveston Bay during Hurricane Ike (Lapetina & Sheng, 2015).
The vegetation–flow–turbulence interaction in CH3D is simulated by a turbulent kinetic energy (TKE) model, which includes two drag terms in the \(u\)- and \(v\)- momentum equations: a profile drag term which is proportional to the frontal area of the vegetation and quadratic power of the flow, a skin-friction drag term which is proportional to the total wetted vegetation area and quadratic power of the flow. The drag terms in the \(u\)- and \(v\)- momentum equations of CH3D are listed below:
with \(C_{\text{f}}\) defined as
where \(D_{{{\text{P}}_{i} }}\) and \(D_{{{\text{S}}_{i} }}\) are the profile drag and skin friction drag, respectively; \(u_{i}\) and \(u_{j}\) are mean flow velocity components; \(C_{\text{P}}\) is the profile drag coefficient with typical values ranging from 0.1 to 1.0; \(C_{\text{f}}\) is the skin friction coefficient; \(A_{\text{w}}\) is the wetted area per unit volume; \(A_{\text{f}}\) is the frontal area per unit volume; q is the square root of twice the turbulence kinetic energy k; \({{\varLambda }}\) is turbulent length scale; \(c_{1}\) is an empirical constant; and \(\nu\) is the kinematic viscosity.
Two common vegetation types, i.e., salt marshes and mangroves, are included in the model simulations of Hurricane Andrew to accurately represent the wetland. Salt marshes have less vertical variation in frontal area and wetted area, while mangroves have much larger wetted area near the top and much larger profile area along at the bottom if they have the prop roots or pneumatophores.
The vegetation-laden turbulent transport model incorporates the creation of wake turbulence by the profile drag, dissipation of the turbulent fluctuations of velocity caused by the skin friction, and breaking of large eddies into smaller eddies due to the increased dissipation. The details of the mathematical model are given in the paper of Lapetina & Sheng (2014). A brief description of the vegetation-resolving TKE model is given in the Online Appendix.
Model domain and grid
The newly developed CH3D-SWAN domain with high-resolution grid, as shown in Fig. 2, covers most of the Miami metropolitan area, the eighth-largest metropolitan area in the U.S. Most of these areas are low-lying lands which are more vulnerable to the threat of storm and associated coastal inundation. The shoreline within the model domain extends from Key Largo in the south to West Palm Beach in the north with nearly 200 km distance. The grid resolution is around 220 m on average, and the minimum resolution reaches 20 m. The topography and bathymetry of the grid have been updated using the latest 1/3 arc-sec NGDC Coastal DEMs developed by NOAA Tsunami Inundation Project (Friday et al., 2012; Carignan et al., 2015). In the area where the Coastal DEMs are not available, the light detection and ranging data (LiDAR), collected by Florida Division of Emergency Management in 2007, are used for the topography part, and the NOAA’s 3 arc-second U.S. Coastal Relief Model (CRM; http://www.ngdc.noaa.gov/mgg/coastal/) is used for the bathymetry part. Due to the high resolution of grid cells and the accuracy of topographic and bathymetric data, small-scale geographic features such as a series of barrier islands on the south of Biscayne Bay entrance, the inlets and channels near Miami, are well resolved. These contribute to the accurate simulation of storm surge propagation and wave transformation inside the Bay. In order to incorporate the remote meteorological effect on the open boundary of the model domain, a coarser grid CH3D domain which covers the western North Atlantic and Gulf of Mexico is used for large-scale model runs to provide open conditions. Figure 3 shows the large-scale domain, and the location of the high-resolution nested Southeast Florida grid.
Incorporating mangrove forest and marshes into the modeling system
As one of Florida’s true natives, there are 469,000 acres of mangrove forest in Florida, mainly located in the state’s southern coastal zone (http://www.dep.state.fl.us/coastal/habitats/mangroves.htm). In Biscayne Bay coastal area, there is a rich resource of mangroves covering 30 km length of coastline with three dominant species: Red Mangrove (Rhizophora mangle), Black Mangrove (Avicennia germinans), and White Mangrove (Laguncularia racemosa), very similar to the mangroves in southwest Florida, but the width of these mangrove swamps varies from less than 30 m to 1.6 km (Teas, 1974), much narrower than the mangrove forests along southwestern coast, where Zhang et al. (2012) investigated the role of massive mangrove forests in attenuating the storm surge using 2D approach and an adjustable Manning’s n coefficient.
Based on the study of Teas (1974), the Biscayne Bay coastal area was characterized with five main communities distinguished as (1) Coastal Band, (2) Dense Scrub, (3) Sparse Scrub, (4) White & Mixed, and (5) Black Marsh, running parallel to the coastline in a landward direction, based on the salinity, water depth, and other extra environmental conditions. The detailed current vegetation communities along Biscayne Bay is available in GIS format (Fig. 4), and based on the digital map and the typical vegetation attributes summarized by Teas (1974), vegetation type, stem height, and stem density are assigned to each vegetation cell of CH3D grid. In order to isolate the effects of vegetation from complicated environments, two 3D simulations with and without vegetation are carried out. R1 refers to a model run with vegetation, and R2 refers to a run without vegetation.
For R1, both mangroves and marshes are modeled in the vegetation module. Due to the flexibility of marshes, \(C_{\text{P}}\) is set to 0.1 for salt marshes, smaller than \(C_{\text{P}} = 0.2\) for mangrove. These \(C_{\text{P}}\) values are comparable to those used by den Hartog & Shaw (1975), Uchijima & Wright (1964), as well as the value determined experimentally by Nepf (1999) for dense vegetation in a laboratory hydraulic flume. Doubling the \(C_{\text{P}}\) values resulted in negligible changes in the simulated inundation, hence no attempt was made to implement more complex forms of \(C_{\text{P}}\) which vary with stem density and Reynolds number based on vegetation length scale (see, e.g., Mazda et al., 1997; Nepf & Vivoni, 2000; Hu et al. 2015; Nepf 2012). Meanwhile, the values of \(c_{1}\) are set to 0.125 and 0.2 for marshes and mangroves, respectively, following the empirical correlations in Schlichting (1968); \(\alpha\) is set to 0.1 for both vegetation types, consistent with previous studies (Lewellen & Sheng, 1980; Lapetina & Sheng, 2014). To determine the more precise values of the drag coefficients, field data of flow and turbulence in the vegetation zone will be needed in future study which is beyond the scope of the present paper. For R2, all vegetations were removed from the model run and the bottom roughness was assumed to be the same as the surrounding land.
Due to the lack of detailed data for the spatially varying vegetation density, here we employ constant values for \(A_{\text{f}}\) in bottom layer based on the vegetation species. Based on the qualitative description of the mangroves and marshes in Teas (1974), the bottom frontal area per volume \(A_{{{\text{f}}_{\text{b}} }}\) is set to 1.2 and 0.6 m−1 for mangroves and marshes, respectively. For mangrove, \(A_{\text{f}}\) and \(A_{\text{w}}\) are kept the same as \(A_{{{\text{f}}_{\text{b}} }}\) and \(A_{{{\text{w}}_{\text{b}} }}\) in the bottom 75% part where the cylinder-like trunk is the main structure. In the top 25% part of mangroves, an enhanced \(A_{\text{f}} = 3.0 \times A_{{{\text{f}}_{\text{b}} }}\) s used to represent the appearance of leaves and branches, meanwhile, \(A_{\text{w}}\) is increased to ten times of \(A_{\text{f}}\) due to the large amount of leaves. In summary, \(A_{\text{f}}\) and \(A_{\text{w}}\) for mangroves can be expressed as
where h is the vertical position where \(A_{\text{f}}\) and \(A_{\text{w}}\) is calculated; \(A_{{{\text{f}}_{\text{b}} }}\) is bottom vegetation frontal area per volume; and H is total vegetation height. The computation of \(A_{\text{f}}\) and \(A_{\text{w}}\) for marshes is the same as the study of Lapetina & Sheng (2014). The above \(A_{\text{f}}\) and \(A_{\text{w}}\) for mangroves are good approximations for the black and white mangroves which are more dominant in areas outside the coastal band and dense scrub as shown in Fig. 4 where red mangrove is dominant (Teas, 1974). The selected values for \(A_{\text{f}}\) are within the range of 1.0 to 6.0 m−1 reported by Mazda et al. (1997) and Nepf (2012).
Different mangrove species have different morphological characteristics. Compared to the previous 2D approach, the 3D approach has the potential to reflect the vertical and spatial varying canopy structures, given the accurate data from the local field survey by ecological researcher. In the model run R1, only tree trunks are considered in the form of \(A_{\text{f}}\) and \(A_{\text{w}}\) for the bottom part of mangroves. However, red mangrove is well known by its tangle, reddish roots called “prop root”; for black mangrove, finger-shaped pneumatophores cluster around the trunk. Furthermore, in the mangrove forests, these complex root structures, when combined with tree stem characteristics and woody debris, produce a 3D tangle of woody structures that suppress wave and the bottom flow. To account for the influence of enhanced obstructions in the root layer, we conduct two additional model simulations to assess their effect on the buffering of storm surge. The experiment consists of two model simulations, with enhanced frontal and wetted area \(A_{\text{f}}\) and \(A_{\text{w}}\), respectively, under the lower 25% layer with the capping height set to 50 cm. \(A_{\text{f}}\) is enhanced to \(1.5 \times A_{{{\text{f}}_{ 0} }}\) and \(2.0 \times A_{{{\text{f}}_{ 0} }}\), respectively, where \(A_{{{\text{f}}_{ 0} }}\) is the frontal area of mangrove root in R1, the wetted area \(A_{\text{w}}\) keeps the same relation with \(A_{\text{f}}\), which is 3.14 in this study. We use R3 and R4 to name these two extra simulations with 1.5 and 2.0 of the original \(A_{\text{f}}\) and \(A_{\text{w}}\). The original and revised vertical profiles are shown in Fig. 5.
The vertical profiles of \(A_{\text{f}}\) and \(A_{\text{w}}\) (normalized by the bottom \(A_{{{\text{f}}_{\text{b}} }}\) and \(A_{{{\text{w}}_{\text{b}} }}\) in R1) along the normalized height for the three simulations with the original case (R1), and enhanced by 1.5 (R2) and 2.0 (R2) times under the bottom
Model simulations of surge, wave, and inundation during Hurricane Andrew (1992)
All four model runs R1, R2, R3, and R4 are obtained with the coupled surge–wave model (see Sheng et al. 2010 for the detailed surge–wave coupling) and driven by the same meteorological forcing and open boundary conditions. A continuous series of wind snapshots with 20 min interval are Lagrangian-interpolated from Hurricane Research Division (HRD)’s H*Wind snapshots (Powell & Houston, 1996), which are available at 1992/08/24 04:00 GMT, 09:00 GMT, 11:00 GMT, and 15:02 GMT, by the Wind Modeling System (WMS) (Paramygin, 2009). For time periods where H*Wind data are not available, 3-hourly NCEP North American Regional Reanalysis (NARR) wind fields are used for the interpolation. The open boundaries are prescribed with tides and remote surges from large-scale domain. Seven tidal constituents, including M2, N2, K1, S2, O1, K2, and Q1, are extracted from the ADCIRC tidal database (ADCIRC Tidal Database, version ed_95d; see http://www.unc.edu/ims/ccats/tides/tides.htm) to compose tides on the open boundaries. The simulations use a 5-s time step and 6 vertical layers. The only difference between these four runs is the vegetation: R1 resolves the coastal vegetation (primarily mangroves) as described in the previous section, whereas, in R2, the vegetation area is replaced with bare earth (with a bottom roughness \(z_{0} = 0.1 {\text{cm}}\)). For R3 and R4, \(A_{\text{f}}\) and \(A_{\text{w}}\) in the bottom layer are enhanced from R1 in the way described in the previous section.
Model results and comparison with observed data
Water level time series
Three types of data are commonly used to evaluate the performance of storm surge simulation; one is the time series of water level from tidal gauges, and the other two types, i.e., high-water-mark elevation and debris line collected in post-hurricane field survey, are mainly for the estimate of overland flooding. During Hurricane Andrew, only one NOS tide station, Haulover Pier, in North Miami Beach, resides within our computational domain. Since the station directly fronts the Atlantic Ocean, with no mangrove forests in front, its water levels were not affected by the mangrove forests along Biscayne Bay, and the modeled results among the four runs do not show any noticeable differences. So Fig. 6 only gives the comparison of modeled water levels from R1 with the hourly measured data (Breaker et al., 1994). The modeled results agree well with observed data, except for the underestimate of the peak value by 12.5% (12 cm) around landfall time. According to the preliminary report of Hurricane Andrew (Rappaport, 1992), the total rainfall during Hurricane Andrew for two stations in Dade County were 13.18 and 19.79 cm. Thus, the lack of rainfall in our simulations might have contributed to this discrepancy.
The comparison of time series of between water level obtained by simulation R1 (3D-VEG, with wave) and hourly measured data (Breaker et al., 1994) at Haulover Pier
High water marks
In contrast to the sparse hourly water level data, abundant high water marks along the southeastern coast from Miami to Key Largo, as well in some areas along southwestern part, were identified, described and surveyed by the USGS in the weeks following the storm (Murray, 1994). In total, 336 high water marks were collected to document the extent of flooding during Hurricane Andrew. Both high water marks and debris lines from paper quadrangle maps were digitized and geo-referenced into ArcGIS shape-files (Zhang et al., 2008). There are 279 out of 336 surveyed high water marks residing within the computational domain, and Fig. 7 shows the locations of these high water marks and the debris line estimated by USGS. All the elevation data have been converted and referred to vertical datum, NAVD88.
The spatial distribution of High Water Marks (in NAVD88) and the position of debris line collected by USGS in the post-hurricane survey (base map source: Esri, HERE, Delome, TomTom, Intermap, increment P Crop., GEBCO, USGS, FAO, NPS, NRCAN, GeoBase, IGN, Kadaster NL, Ordnance Survery, Esri Japan, METI, Esri China (Hong Kong), swisstopo, MapmyIndia, © OpenStreetMap contributors, and the GIS User Community)
The highest peak storm tide occurred in the vicinity of the street, S.W. 180th Terrace, east of Old Cutler Road in Perrine, due to the high onshore wind at the outer northern eye wall edge and the lack of protection by barrier islands. The peak storm tides gradually lowered to 1.2-1.8 m in both the northern and southern direction along the western shoreline of Biscayne Bay. The modeled HWMs from R1 show good agreements with the observed ones, as shown in Fig. 8, with \(R^{2} = 0.795\) and root mean square error (rmse) = 48.98 cm, whereas \(R^{2} = 0.597\) and rmse = 83.94 cm for R2.
The inundation maps obtained by R1 and R2 are shown in Fig. 9. For R2, large areas in the south of Miami are inundated due to the southeasterly hurricane wind blowing onshore during landfall period and no protection from coastal mangrove forests. In contrast, with the wetland, the inundation is limited in the coastal zone area, instead of sweeping the neighborhoods far inland. Moreover, the inundation pattern from R1 agrees well with the debris line measured from USGS, especially in the center-to-north coastal areas where peak water levels are much higher than in the south.
Maximum inundation maps during Hurricane Andrew (1992) simulated by CH3D-SWAN with vegetation R1 (left) and without vegetation R2 (Right). The vegetation, which consists of mangroves (primarily) and salt marshes, significantly reduced the surge, wave, and coastal inundation and protected communities behind the mangroves and marshes (base map source: Esri, DigitalGlobe, GeoEye, i-cubed, USDA FSA, USGS, AEX, Getmapping, Aerogrid, IGN, IGP, swisstopo, and the GIS User Community)
When incorporating prop roots in the bottom layer, the model simulated HWMs change only slightly for R1, R3, R4, and the error statistics of model simulated HWMs do not show an obvious trend. One possible reason is that many HWMs are located near the coastline, and some are even in vegetation free zones. The changes of flow pattern due to the increase of bottom obstructions might cause the acceleration of flow in some vegetation free areas, as well as deceleration of flow in vegetation-laden areas. The effects of enhanced obstructions in the bottom layer will be assessed quantitatively in the discussion section.
Maximum water level and maximum wave height
In Figs. 10 and 11, the snapshots of water level and significant wave height from R1 are shown at 1-h interval during the landfall period. At 08:00 GMT, 1 h before landfall, the coastline experienced a setdown due to the strong offshore (northwesterly) wind inside Biscayne Bay. The wind blew the water into the barrier islands in the southern part of the bay. Due to the presence of the barrier islands extending from north Miami, the water from Atlantic ocean could only be pushed into Biscayne Bay through the Biscayne Bay inlet area, when the wind switched from offshore to onshore in the later hours. The snapshots in Fig. 10 clearly show how the barrier islands protect the main inland area from the direct flooding impact of Atlantic Ocean under extreme natural conditions. By analyzing the wave fields computed by SWAN and bathymetry contour shown in Fig. 11, there is a transition zone from deep to shallow water, where waves started to break and dissipate with significant wave heights quickly decreasing from 7 to 3 m. Because of the shallow water depth inside Biscayne Bay and the barrier islands, the wave heights were commonly less than the offshore area, which attenuated the damages caused by the topping waves over surge, and acted as a buffer space for the wave energy before propagating to land.
Discussion
Assessing the effect of mangrove forest on coastal inundation
The abundance of surveyed HWM data over the domain enabled depiction of the spatial variation of surge and inundation over the coastal area, as well as demonstration of the model skill. To quantitatively assess the effect of the mangrove forest on coastal inundation, we follow Sheng et al. (2012) by calculating the total inundation volume (TIV) and total inundation area (TIA) with and without vegetation presence. The TIV and TIA (Sheng et al., 2012) are defined as follows:
where \(H_{ \hbox{max} } \left( {x,y} \right)\) and \(H_{0} \left( {x,y} \right)\) are the maximum water elevation and the land elevation at initial land cells \(\left( {x,y} \right)\), respectively.
Besides the previous mentioned quantities, a spatially average non-dimensional quantity, vegetation dissipation potential (VDP), defined by Sheng et al. (2012), is used to estimate the overall reduction of inundation due to vegetation:
where \(\left( {\text{TIV}} \right)_{v}\) represents the total inundation volume with the presence of vegetation canopy, and \(\left( {\text{TIV}} \right)_{0}\) is the total inundation volume with the absence of vegetation canopy.
Table 1 shows the computed values for the four runs. From R2 to R1, TIV decreases from 4.79 × 10 to 1.65 × 108 m2, and TIA drops from 5.28 × 108 to 1.79 × 108 m2, owing to the presence of vegetation in the coastal area. The reductions of TIV and TIA are resulted from the buffering of wind, wave, and surge by the coastal wetlands. If the coastal wetlands were replaced with bare-earth, large area of residential neighborhoods in the South of Miami and Dade would have been flooded due to Category 5 hurricane wind blowing from the Southeast and water from Biscayne Bay pushed directly onshore, as shown in Fig. 9. Nearly 66% (VDP = 0.66) of surge and inundation from the ocean was buffered by the vegetation from flooding the inland residents.
By incorporating the enhanced obstructions in root layer, TIV decreased from 1.65 for R1 to 1.53 and 1.50 × 108 m2, for R3 and R4, respectively, meanwhile, TIA reduced from 1.79 to 1.72 and 1.70 × 108 m2. The results imply that the increase of bottom obstructions initially had a greater effect on attenuating the water level, but the effect became less noticeable with further increase in bottom obstructions. To examine the buffering of wind-driven current and storm surge by the coastal mangrove forest, we select a 1.35-km long transect T1 located at the right side of the track, parallel to the track, as shown in Fig. 12. It experienced intense onshore winds (40–50 m/s) near landfall according to data from H*Wind. The East–West currents along the transect simulated by R1 to R4 at 1992/08/24 10:00 GMT are shown in Fig. 13. The mangroves greatly reduced the current magnitude from ~140 to ~20 cm/s. Meanwhile, the modeled vertical profiles of current within the emergent mangroves are more uniformly distributed compared to those within submerged plants, consistent with the experimental observations from Nepf & Vivoni (2000). Additionally, the existence of root systems and debris further obstructs the bottom flow, which can promote the deposition and accretion of sediment.
The above results demonstrate the ability of 3D approach in capturing the effect of vegetation (both horizontal distribution and vertical structure) on local flow and turbulence as well as surge, wave, and inundation. Status quo 2D approach, e.g., Zhang et al., 2012, however, cannot represent the vertical structure of vegetation on local flow and surge, but resorts to an enhanced empirical bottom friction coefficient to represent the vegetation induced drag which varies vertically. By increasing the bottom friction, however, 2D approach may lead to artificial sediment erosion. Lapetina and Sheng (2014 and 2015) showed detailed comparison between 2D (using Manning’s n) and 3D (using vegetation-resolving surge model) approaches for modeling the effect of vegetation on surge and flow. Their studies showed that the Manning coefficient is a function of the vegetation and the flow, hence cannot be accurately modeled. The 2D modeling approach requires extensive filed data of water level to allow excessive tuning of the Manning coefficient, which is actually a function of space and time. Therefore, while the 2D model could be used for hindcasting vegetated-flow when extensive water level data exist, it is not suitable for prediction when little water level data are available. The 3D vegetation-resolving modeling allows direct incorporation of the vegetation structure in the surge and wave model, hence is much more robust and can be used for prediction of flow over vegetation. Effort is underway to accurately measure the vertical profiles of profile and wetted leaf area indices.
Ecosystem service value of mangroves and marshes
It is known that mangroves have significant ecosystem service value by providing nursery ground for a variety of fishery species, due to flow retardation and deposition of sediments and nutrients. However, ecosystem service value of mangroves and marshes for flood protection is not well understood. Barbier and Enchelmeyer (2014) claimed that shoreline protection is one of the most undervalued mangrove ecosystem services because these woody wetlands can provide vital protection to inland coastal communities. While evidence suggests that mangroves provide an effective natural buffer against storms (e.g., Haiyan in 2014) and tsunamis (e.g., Indonesia tsunami in 2004), the extent to which mangroves reduce damage to coastal infrastructure is still debated (e.g., Mcivor et al., 2012). UNEP (2011) estimated the global economic value that can be extracted from mangrove habitat to be at least billions of U.S. dollars per year. Although some empirical studies provided rough estimation of shore protection value of mangroves, no one has estimated shoreline protective value of mangroves using robust predictive science.
This study showed that the vegetation-resolving CH3D-SWAN is capable of simulating the buffering of storm surge and coastal inundation by mangroves and marshes. By adding an economic analysis, CH3D-SWAN is suitable for predicting the ecosystem service value of mangroves and marshes for protecting coastal communities from future inundation due to SLR and future storms. Research to incorporate the effect of extreme wind on coastal wetlands (see, e.g., Doyle et al. 1995) is also underway.
Conclusion
Through a comprehensive comparison with continuous water levels at coastal station and surveyed HWMs, the vegetation-resolving CH3D-SWAN demonstrates good confidence in modeling not only surge propagation in the nearshore area but also the complicated vegetation-surge process overland. CH3D-SWAN is suitable for predicting the ecosystem service value of mangroves and marshes for protecting coastal communities from future inundation due to SLR and future storms.
The Miami, Florida area suffered several billions of U.S. Dollars in damage from the severe Category 5 winds of Hurricane Andrew in 1992, but flooding was not severe due to the protection of mangroves and marshes along Biscayne Bay. By comparing the simulated inundation maps with and without coastal vegetation, the attenuation effects of vegetation on storm surge are very obvious. Without the buffering of storm surge by coastal vegetation, it would have been a catastrophic disaster for the neighborhoods in south Miami-Dade County, since the southeasterly Category 5 hurricane wind would have blown a tremendous amount of water from the bay inland.
Different mangrove species have different morphological characteristics. Compared to the previous 2D approach, the 3D approach has the capability to accurately incorporate the vertical structure and horizontal distribution of vegetation, given the accurate field data from ecologists. Results show that the vegetation dissipation potential of the mangrove forest is on the order of 66% which is significantly higher than the 40% estimated for marshes (Sheng et al., 2012). By comparing the results of R1 with R3 and R4, the incorporation of enhanced obstructions in the bottom layer demonstrate influence on TIV and TIA. This research suggests the importance of accurate measurement of vertical structures in modeling the interaction between flow and vegetation. An accurate description of vegetation can advance the accuracy of numerical models, since the results depend on the estimates of \(A_{\text{f}}\) and \(A_{\text{w}}\). However, unlike the empirical tuning of Manning’s n in a 2D model, both \(A_{\text{f}}\) and \(A_{\text{w}}\) in the 3D models are measurable variables that describe the morphology of vegetation. With the aid of laser technologies, it is now possible to obtain high-precision vegetation data in the field to accurately estimate the values of wetted and profile leaf area index (LAI) required by the model. Therefore, vegetation-resolving surge–wave model can be used to assess the effectiveness of wetland restoration projects.
To further improve the modeling study, field experiments should be conducted inside the vegetation zone during future storms to gather data of water level, flow, and turbulence, to enable precise determination of the drag coefficients. Accurate measurement of the wetted area and frontal area throughout the vegetation zone should be conducted using modern terrestrial laser systems.
References
Alongi, D. M., 2008. Mangrove forests: resilience, protection from tsunamis, and responses to global climate change. Estuarine, Coastal and Shelf Science 76: 1–13.
Barbier, E. B., & B. S. Enchelmeyer, 2014. Valuing the storm surge protection service of US Gulf Coast wetlands. Journal of Environmental Economics and Policy 3(2): 167–185.
Breaker, L. C., L. D. Burroughs, Y. Y. Chao, J. F. Culp, N. L. Guinasso, R. L. Teboulle & C. R. Wong, 1994. The impact of Hurricane Andrew on the near-surface marine environment in the Bahamas and the Gulf of Mexico. Weather and Forecasting. doi:10.1175/1520-0434(1994)009%3C0542:TIOHAO%3E2.0.CO;2.
Bunya, S., J. C. Dietrich, J. J. Westerink, B. A. Ebersole, J. M. Smith, J. H. Atkinson, R. Jensen, D. T. Resio, R. A. Luettich, C. Dawson, V. J. Cardone, A. T. Cox, M. D. Powell, H. J. Westerink & H. J. Roberts, 2010. A high-resolution coupled riverine flow, tide, wind, wind wave, and storm surge model for Southern Louisiana and Mississippi. Part I: model development and validation. Monthly Weather Review 138: 345–377.
Carignan, K., S. J. McLean, B. W. Eakins, L. Beasley, M. R. Love & M. Sutherland, 2015. Digital elevation model of Miami, Florida: procedures, data sources, and analysis. Boulder, Colorado.
den Hartog, G., & R. H. Shaw, 1975. A field study of atmospheric exchange processes within a vegetative canopy. Heat and Mass Transfer in the Biosphere 299–309.
Doyle, T. W., T. J. Smith III & M. B. Robblee, 1995. Wind damage effects of Hurricane Andrew on mangrove communities along the southwest coast of Florida, USA. Journal of Coastal Research 21: 159–168.
Duarte, C. M., I. J. Losada, I. E. Hendriks, I. Mazarrasa & N. Marba, 2013. The role of coastal plant communities for climate change mitigation and adaptation. Nature Climate Change. doi:10.1038/NCLIMATE1970.
Feagin, R. A., 2008. Vegetation’s role in coastal protection. Science Translational Medicine 320: 176–177.
Friday, D. Z., L. A. Taylor, B. W. Eakins, R. R. Warnken, K. S. Carignan, R. J. Caldwell, E. Lim & P. R. Grothe, 2012. Digital elevation models of Palm Beach, Florida: procedures. Data Sources and Analysis, Boulder, Colorado.
Gedan, K. B., M. L. Kirwin, E. Wolanski, E. B. Barbier & B. R. Silliman, 2011. The present and future role of coastal wetland vegetation in protecting shorelines: answering recent challenges to the paradigm. Climatic Change 106: 7–29.
Holland, G. J., 1980. An analytical model of the wind and pressure profiles in hurricanes. Monthly Weather Review 108: 1212–1218.
Homer, C., C. Huang, L. Yang, B. Wylie & M. Coan, 2004. Development of a 2001 national land-cover database for the United States. Photogrammetric Engineering & Remote Sensing 70: 829–840.
Hope, M. E., J. J. Westerink, A. B. Kennedy, P. C. Kerr, J. C. Dietrich, C. Dawson, C. J. Bender, J. M. Smith, R. E. Jensen, M. Zijlema, L. H. Holthuijsen, R. A. Luettich, M. D. Powell, V. J. Cardone, A. T. Cox, H. Pourtaheri, H. J. Roberts, J. H. Atkinson, S. Tanaka, H. J. Westerink & L. G. Westerink, 2013. Hindcast and validation of Hurricane Ike (2008) waves, forerunner, and storm surge. Journal of Geophysical Research 118: 4424–4460.
Hu, K., Q. Chen & H. Wang, 2015. A numerical study of vegetation impact on reducing storm surge by wetlands in a semi-enclosed estuary. Coastal Engineering 95: 66–76.
Janjic, Z. I., J. P. Gerrity & S. Nickovic, 2001. An alternative approach to nonhydrostatic modeling. Monthly Weather Review 129: 1164–1178.
Krauss, K. W., T. J. Doyle, T. W. Doyle, C. M. Swarzenski, A. S. From, R. H. Day & W. H. Conner, 2009. Water level observations in mangrove swamps during two hurricanes in Florida. Wetlands 29: 142–149.
Lapetina, A. & Y. P. Sheng, 2014. Three-dimensional modeling of storm surge and inundation including the effects of coastal vegetation. Estuaries and Coasts 37: 1028–1040.
Lapetina, A. & Y. P. Sheng, 2015. Simulating complex storm surge dynamics: Three-dimensionality, vegetation effect, and onshore sediment transport. Journal of Geophysical Research: Oceans 120: 7363–7380.
Lewellen, W. S., & Y. P. Sheng, 1980. Modeling of dry deposition of SO2 and sulfate aerosols. Aeronautical Research Associates of Princeton, Princeton, NJ.
Luettich, R. A., J. J. Westerink, & N. W. Scheffner, 1992. ADCIRC: An advanced three-dimensional circulation model for shelves, coasts, and estuaries. Report 1. Theory and Methodology of ADCIRC-2DDI and ADCIRC-3DL. Vicksburg, http://www.dtic.mil/docs/citations/ADA261608%0.http://www.dtic.mil/cgi-bin/GetTRDoc?AD=ADA261608&Location=U2&doc=GetTRDoc.pdf
Mazda, Y., E. Wolanski, B. King, A. Sase, D. Ohtsuka & M. Magi, 1997. Drag force due to vegetation in mangrove swamps. Mangroves and Salt Marshes 1: 193–199.
Mcivor, A., T. Spencer, & I. Möller, 2012. Storm Surge Reduction by Mangroves. Natural Coastal Protection Series 35.
Murray, M. H., 1994. Storm-Tide Elevations Produced by Hurricane Andrew along the Southern Florida Coasts, August 24 1992. Tallahassee, Fl.
Nepf, H. M., 1999. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resources Research 35: 479–489.
Nepf, H. M., 2012. Flow and transport in regions with aquatic vegetation. Annual Review of Fluid Mechanics 44: 123–142.
Nepf, H. M. & E. R. Vivoni, 2000. Flow structure in depth-limited, vegetated flow. Journal of Geophysical Research 105: 28547–28557.
Paramygin, V. A., 2009. Towards a real-time 24/7 storm surge, inundation and 3-D baroclinic circulation forecasting system for the state of Florida. Ph.D. Dissertation, University of Florida.
Powell, M. D. & S. H. Houston, 1996. Hurricane Andrew’s Landfall in South Florida. Part II: surface wind fields and potential real-time applications. Weather and Forecasting 11: 329–349.
Rappaport, E., 1992. Preliminary Report, Hurricane Andrew, 16–28 August 1992. Coral Gables, Florida.
Schlichting, H., 1968. Boundary layer theory. McGraw-Hill Book Company, New York.
Schmitt, K., T. Albers, T. T. Pham & S. C. Dinh, 2013. Site-specific and integrated adaptation to climate change in the coastal mangrove zone of Soc Trang Province, Viet Nam. Journal of Coastal Conservation 17: 545–558.
Sheng, Y. P., 1989. Evolution of a three-dimensional curvilinear-grid hydrodynamic model for estuaries, lakes and coastal waters: CH3D. Estuarine and Coastal Modeling 40–49.
Sheng, Y. P., V. Alymov & V. A. Paramygin, 2010. Simulation of storm surge, wave, currents, and inundation in the outer banks and Chesapeake bay during Hurricane Isabel in 2003: the importance of waves. Journal of Geophysical Research. doi:10.1029/2009JC005402
Sheng, Y. P., A. Lapetina & G. Ma, 2012. The reduction of storm surge by vegetation canopies: three-dimensional simulations. Geophysical Research Letters 39: 1–5.
Spalding, M. D., S. Ruffo, C. Lacambra, I. Meliane, L. Zeitlin, C. C. Shepard & M. W. Beck, 2014. Ocean & Coastal Management The role of ecosystems in coastal protection: adapting to climate change and coastal hazards. Ocean and Coastal 90: 50–57.
Suzuki, T., M. Zijlema, B. Burger, M. C. Meijer & S. Narayan, 2012. Wave dissipation by vegetation with layer schematization in SWAN. Coastal Engineering 59: 64–71.
Teas, H. J., 1974. Mangroves of Biscayne Bay a study of the mangrove communities along the mainland in Coral Gables and south to U.S. Highway 1 in Dade County, Florida
Temmerman, S., T. J. Bouma, G. Govers, Z. B. Wang, M. B. De Vries & P. M. J. Herman, 2005. Impact of vegetation on flow routing and sedimentation patterns: three-dimensional modeling for a tidal marsh. Journal of Geophysical Research: Earth Surface 110: 1–18.
Temmerman, S., P. Meire, T. J. Bouma, P. M. J. Herman, T. Ysebaert, H. J. De Vriend, C. Nargis & N. Orleans, 2013. Ecosystem-based coastal defence in the face of global change. Nature 504: 79–83.
Tolman, H. L., 2009. User manual and system documentation of WAVEWATCH-IIITM version 3.14. Technical note
Uchijima, Z. & J. L. Wright, 1964. An experimental study of air flow in a corn plant-air layer. Bulletin of the National Institute of Agricultural Sciences 11: 19–66.
Wamsley, T. V., M. A. Cialone, J. M. Smith, J. H. Atkinson & J. D. Rosati, 2010. The potential of wetlands in reducing storm surge. Ocean Engineering 37: 59–68.
Zhang, K., C. Xiao & J. Shen, 2008. Comparison of the CEST and SLOSH models for storm surge flooding. Journal of Coastal Research 242: 489–499.
Zhang, K., H. Liu, Y. Li, H. Xu, J. Shen, J. Rhome & T. J. Smith, 2012. The role of mangroves in attenuating storm surges. Estuarine, Coastal and Shelf Science 102–103: 11–23.
Acknowledgements
This work is supported by NOAA Climate Program Office Grant NA11OAR4310105, SECOORA (NOAA/NOPP) (IOOS.11(033)UF.PS.MOD.1), and Florida Sea Grant (R/C-S-59). Miami-Dade County provided the vegetation map. We appreciate the insightful review of an anonymous reviewer.
Author information
Authors and Affiliations
Corresponding author
Additional information
Guest editors: K. W. Krauss, I. C. Feller, D. A. Friess & R. R. Lewis III / Causes and Consequences of Mangrove Ecosystem Responses to an Ever-Changing Climate
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sheng, Y.P., Zou, R. Assessing the role of mangrove forest in reducing coastal inundation during major hurricanes. Hydrobiologia 803, 87–103 (2017). https://doi.org/10.1007/s10750-017-3201-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10750-017-3201-8