Algorithmic strategies for a fast exploration of the TSP $4$-OPT neighborhood

Abstract

We describe an effective algorithm for exploring the $4$-OPT neighborhood for the Traveling Salesman Problem. $4$-OPT moves change a tour into another by replacing four of its edges. The best move can be found by a $\Theta (n^4)$ algorithm by complete enumeration, but a $\Theta (n^3)$ dynamic programming algorithm exists in the literature. Furthermore a $\Theta (n^2)$ algorithm also exists for a particular subset of symmetric $4$-OPT moves. In this work we describe a new procedure which behaves, on average, slightly worse than a quadratic algorithm over all moves (estimated at $O(n^{2.5})$) and like a quadratic algorithm on the symmetric moves. Computational results are reported which show the effectiveness of our strategy compared to other algorithms for finding the best $4$-OPT move, and discuss the strength of the $4$-OPT neighborhood compared to 2- and $3$-OPT.

1 Introduction

The Traveling Salesman Problem (TSP) consists in finding the shortest Hamiltonian cycle in a complete graph $G=(V,E)$ of n nodes, weighted on the edges (Applegate et al. 2007). In this paper we consider its symmetric version, i.e., the graph is undirected and the distance between two nodes is the same, irrespective of the direction in which an edge is traversed. Let us denote by $c(i,j)=c(j,i)$ the distance between any two nodes i and j. Each solution of the problem, called a tour, is identified by a permutation $(v_1,\ldots ,v_n)$ of the vertices. We call $\{v_i, v_{i+1}\}$, for $i=1,\ldots ,n-1$, and $\{v_n,v_1\}$ the edges of the tour. The length of a tour T, denoted by c(T), is the sum of the lengths of the edges of the tour. More generally, for any set F of edges, we denote by c(F) the value $\sum _{e\in F} c(e)$.

A large number of applications over the years have shown that local search is often a very effective way to tackle hard combinatorial optimization problems. The idea of local search has been around for a very long time and it is difficult to attribute it to any particular author. Examples of its use are reported in standard textbooks on combinatorial optimization, such as Papadimitriou and Steiglitz (1982), or devoted surveys, such as Aarts and Lenstra (1997). Suppose we seek to minimize an objective function f(x) over a set X of feasible solutions. Given a map $N:X\mapsto 2^X$ which associates to every solution $x\in X$ a set N(x) called its neighborhood, the basic idea is the following: start at any solution $x^0$, set $s:=x^0$, and look for a solution $x^1\in N(s)$ better than s. If one is found, replace s with $x^1$ and iterate the same search, looking for $x^2$. Continue this way until a local optimum is reached, i.e., a solution s such that $f(s)=\min \{f(x) | x\in N(s)\}$. Replacing $x^i$ with $x^{i+1}$ is called performing a move of the search, and $N(x^i)$ is the set of all solutions reachable with a move from $x^i$. The total number of moves performed to get from $x^0$ to the final local optimum is called the length of the convergence. If x is a solution reachable with a move from $x^i$, and $f(x)<f(x^i)$, we say that the move is an improving move and x is an improving solution. When searching in the neighborhood of $x^i$ we can adopt two main strategies, namely first-improvement and best-improvement. In the first-improvement strategy, we set $x^{i+1}$ to be the first solution that we find in $N(x^i)$ such that $f(x^{i+1})< f(x^i)$. In best-improvement, we set $x^{i+1}:=\text {argmin}_{N(x^i)} f(x)$. Generally speaking, an iteration of first-improvement is easier (faster) than one of best-improvement, but the difference in the time requested by the two types of moves tends to become smaller and smaller the closer one gets to the local optimum. Furthermore, the length of the convergence with first-improvement is generally larger than with best-improvement, so that the overall time required for convergence in the two cases is comparable.

Over time, many local search variants have been proposed, to make it more effective by avoiding to get stuck in local optima. Namely, some times a non-improving move must be performed to keep the search going. Examples of these techniques are tabu search (Glover and Laguna 1997) and simulated annealing (Kirkpatrick et al. 1983).

1.1 The $k$-OPT neighborhood for the TSP

Let $k\ge 2$ be an integer constant. A $k$-OPT move on a tour T consists in first removing a set R of k edges and then inserting a set I of k edges so as $(T\setminus R) \cup I$ is still a tour. A tour locally optimal for the $k$-OPT neighborhood will be called k-optimal. A $k$-OPT move is improving if $c((T\setminus R) \cup I) < c(T)$, i.e., $c(I) < c(R)$. An improving move is best-improving if $c(R)- c(I)$ is the maximum over all possible choices of R, I. For $k\ge 3$ we include in the definition the case that $R\cap I\ne \emptyset$. This implies that the $k'$-OPT moves are a subset of the $k$-OPT moves for each $k'< k$.

The first use of $k$-OPT dates back to 1958 with the introduction of $2$-OPT in Croes (1958). In 1965 Lin (1965) described the $3$-OPT neighborhood, and experimented with a complete enumeration algorithm, of complexity $\Theta (n^3)$, which finds the best $3$-OPT move by trying all possibilities. He also introduced a heuristic step fixing some edges of the solution (at risk of being wrong) with the goal of increasing the size of the instances that could be tackled (which, at the time, were fairly small, like a few dozen nodes). Later in 1968, Steiglitz and Weiner (1968) described an improvement over Lin’s method which made it 2 or 3 times faster (although still cubic).

The exploration of the $k$-OPT neighborhood, in search of its best move, might be considered ”fast” from a theoretical point of view, since the most obvious algorithm (complete enumeration) is $\Theta (n^k)$, i.e., polynomial for fixed k. However, despite being polynomial, the complete enumeration algorithm cannot be used in practice already for $k=3$ (if n is large enough, like 3, 000 or more). For instance, for a given tour of $n=6,000$ nodes, the time required to evaluate all $3$-OPT moves, on a reasonably fast desktop computer as of 2023, is more than one hour, let alone converging to a local optimum.

In a previous work (Lancia and Dalpasso 2020), we have described some algorithmic ideas to speed-up the exploration of the $3$-OPT neighborhood in order to lower its complexity and make it practical. The result is a procedure which appears to take a subcubic time to find the best $3$-OPT move. Similar ideas were successfully applied to the problem of finding the largest triangle in an edge-weighted undirected graph (Lancia and Vidoni 2020), where it is in fact mathematically proved that the procedure finds the optimal solution by looking, on average, only at $O(n^2)$ triangles out of $\Theta (n^3)$.

In the current paper, we are going to describe a similar strategy for the $4$-OPT neighborhood, in order to make it practical for graphs on which it could have never been applied before. Our goal is to beat the best approaches in the literature, which already provided faster solutions to this problem than the standard $\Theta (n^4)$ enumeration algorithm. In particular, de Berg et al. (2020) have described a dynamic programming procedure to find the best $4$-OPT move in time $\Theta (n^3)$. While this is already a huge improvement over the $\Theta (n^4)$ complete enumeration, still the cubic complexity is not practical for large values of n. In another paper, Glover (1996) has described a $\Theta (n^2)$ algorithm for finding the best $4$-OPT move, but valid only for three particular types of $4$-OPT moves (notice that, as we will describe later on, there are 25 possible types of $4$-OPT moves overall, determined by how we reattach the tour segments once four edges have been removed).

In the computational results section we will show how our procedure consistently behaves better than the cubic dynamic programming procedure, on all possible moves. Furthermore, we obtain a better performance than Glover’s procedure, on the only three types of $4$-OPT moves on which the latter can be applied, for graphs of up to 1,000 nodes. For larger graphs, we show how to combine our approach with Glover’s algorithm to obtain an improvement also in this case.

Notice that our paper is focused on making the optimization of the $4$-OPT neighborhood practical, but it does not try to assess the performance of such neighborhood in finding good-quality tours. Indeed, the TSP problem is today very effectively solved, even to optimality, by using sophisticated mathematical programming based approaches, such as Concorde (Applegate et al. 2007). No matter how ingenious, heuristics can hardly be competitive with these approaches when the latter are given enough running time. It is clear that simple heuristics, such as $3$-OPT and $4$-OPT local search, are even less effective than some more involved heuristics such as, e.g., Lin and Kernighan’s procedure (Lin and Kernighan 1973). For a very good chapter comparing various heuristics for the TSP, see Johnson and The traveling salesman problem (1997). At any rate, there are reasons which justify the utility of a fast procedure for finding the best $4$-OPT move also with respect to existing heuristics. For instance, it could provide a test of 4-optimality for any solution found by a solver. Indeed, current heuristic solvers from the literature only look for $4$-OPT moves in a greedy, limited, way, and are not guaranteed to end at a 4-optimal solution. By making sure that if an improving $4$-OPT move exists we do not miss it, we can unblock from the impasse a heuristic which could not find a way to improve its current solution (this is the case, e.g., of a particular step of Lin and Kernighan’s procedure that we will discuss at the end of Sect. 5.3). Another good reason for using 4-OPT in place, e.g., of simple heuristics which limit their search to 2- or 3-optimal solutions, is that there are 4-optimal solutions which have a much better objective value, and could be obtained, given the effectiveness of our $4$-OPT procedure, in the same amount of time (see Sect. 5.4 in which we have run a series of tests to compare the strength of the $4$-OPT neighborhood to that of $3$-OPT and $2$-OPT). As a final advantage of looking for the best $4$-OPT move by using our approach, we point out that the method becomes faster in finding the best-improving move, or just an improving move, the closer the tour gets to a local optimum. Both brute force and dynamic programming, on the other hand, take roughly constant time (for a fixed n) at each iteration. This fact can be exploited by using our procedure within an iterated local search strategy which, instead of starting each time from a random tour, starts from a random small perturbation of the last local optimum (Lourenço et al. 2019).

1.2 Paper organization

The remainder of the paper is organized as follows. In Sect. 2 we introduce the basic notation and define selections and reinsertion schemes. We also discuss some symmetries which allow us to group similar moves into classes called orbits. In Sect. 3 we describe, at a top level, the main ideas underlying our strategy. Section 4 illustrates the procedures in more detail, also providing pseudo-code for most of them. Section 5 is devoted to computational experiments and comparisons. Some conclusions are drawn in Sect. 6.

2 Selections, schemes and moves

Let $G=(V,E)$ be a complete graph on n nodes, and $c:E\mapsto \mathbb {R}^+$ be a cost function for the edges. Without loss of generality, we assume $V=\{0,1,\ldots ,{\bar{n}}\}$, where $\bar{n}:=n-1$. Furthermore, we always assume the current tour to be the tour $0\rightarrow 1 \rightarrow \cdots \rightarrow \bar{n}\rightarrow 0$.

We will be using modular arithmetic frequently. For convenience, for each $x\in V$ and $t\in \mathbb {N}$ we define

$$\begin{aligned} x \oplus t:= (x + t) \mod n, \qquad \text {} \qquad x \ominus t:= (x - t) \mod n. \end{aligned}$$

When moving from x to $x\oplus 1, x\oplus 2$ etc. we say that we are moving clockwise, or forward. In going from x to $x\ominus 1,x\ominus 2,\ldots$ we say that we are moving counter-clockwise, or backward.

A $4$-OPT move is fully specified by two sets, i.e., the set of removed and the set of inserted edges. We call a removal set any set of four tour edges, i.e., four edges of type $\{i,i\oplus 1\}$. A removal set is identified by a quadruple $S=(i_1,i_2,i_3,i_4)$ with $0 \le i_1< i_2< i_3 < i_4 \le {\bar{n}}$, where the edges removed are $R(S):=\{\{i_j,i_j \oplus 1\}: j=1,\ldots ,4\}$. We call any such quadruple S a selection. A selection is complete if $i_{h}\oplus 1\notin \{i_1,\ldots ,i_4\}$ for each $h=1,\ldots ,4$ (i.e., if the move never removes two consecutive edges of the tour), otherwise we say that S is a partial selection. We denote the set of all complete selections by $\mathcal{S}$.

Complete selections should be distinguished from partial $4$-OPT selections, since the number of choices required to determine a partial selection is actually lower than four. For instance, there is only a cubic number of selections in which $i_4=i_3\oplus 1$ since we can choose $i_1$, $i_2$ and $i_3$ but the value of $i_4$ is forced. Clearly, if we do not impose any special requirements on the selection then there are ${n\atopwithdelims ()4}$ selections. The exact number of complete $4$-OPT selections will be given in Sect. 2.1.

Let S be a selection and $I\subset E$ with $|I|=4$. If $(T {\setminus } R(S)) \cup I$ is still a tour then I is called a reinsertion set. Given a selection S, a reinsertion set I is pure if $I\cap R(S) = \emptyset$, and degenerate otherwise. Finding the best $4$-OPT move when the reinsertions are constrained to be degenerate is $O(n^3)$ (in fact, $4$-OPT degenerates to either $2$-OPT or $3$-OPT in this case). Therefore, the most computationally expensive task is to determine the best move when the selection is complete and the reinsertion is pure. We refer to this kind of moves as true $4$-OPT. Thus, in the remainder of the paper we will focus on true $4$-OPT moves.

2.1 Reinsertion schemes

Let S be a complete $4$-OPT selection. When the edges R(S) are removed from a tour, the tour gets broken into four segments which we label by $\{1,\ldots ,4\}$. For $l=1,\ldots ,4$, the segment labeled l is the path that has $i_l$ as its last vertex. In particular, the segments are $(i_4\oplus 1,\ldots , i_1)$, $(i_1\oplus 1,\ldots , i_2)$, $(i_2\oplus 1,\ldots , i_3)$ and $(i_3\oplus 1,\ldots , i_4)$. Since the selection is pure, each segment contains at least one edge. A reinsertion set patches back these segments into a new tour. If we adopt the convention to start always a tour with segment 1 traversed clockwise, the reinsertion set: (i) determines a new ordering in which the segments are visited along the tour and (ii) may cause some segments to be traversed counterclockwise. In order to represent this fact, instead of listing the edges of a reinsertion set we can use an alternative notation called a reinsertion scheme. A reinsertion scheme is a signed permutation of $\{2,3,4\}$. The permutation specifies the order in which the segments 2, 3, 4 are visited after the move. The signing $-s$ tells that segment s is traversed counterclockwise, while $+s$ tells that it is traversed clockwise. For example, the reinsertion set depicted in Fig. 1(left) is also represented by the reinsertion scheme $<+4,-2,-3>$ since from the end of segment 1 we jump to the beginning of segment 4 and traverse the segment forward. We then move to the last element of segment 2 and proceed backward to its first element. We then jump to the end of segment 3 and proceed backward to its beginning. Finally, we close the cycle by going back to the first element of segment 1.

Fig. 1

Three $4$-OPT moves and the corresponding reinsertion schemes

Clearly, there is a bijection between reinsertion schemes and reinsertion sets. If r is a reinsertion scheme, we denote by I(r) the corresponding reinsertion set, while if I is a reinsertion set, we denote by r(I) the corresponding reinsertion scheme.

Because of the equivalence between reinsertion sets and reinsertion schemes, in the following we will be using either of them, at our convenience, for the sake of simplicity.

There are potentially $2^{3}\times 3!$ reinsertion schemes for $4$-OPT, but for many of these the corresponding reinsertion sets are degenerate. A scheme for a pure reinsertion must not start with $+2$, nor end with “$+4$”, nor contain consecutive elements “$+t,+(t+1)$” or “$-t,-(t-1)$” for any t in $1,\ldots ,4$.

Proposition 1

There are 25 pure reinsertion schemes for $4$-OPT.

Proof

We prove the claim by listing the schemes, since we will be needing them when we discuss how to find the best true $4$-OPT move. The pure schemes, classified by a permutation $\pi$ of $\{2,3,4\}$ first and then the signing, are the following:

• $\pi =(2,3,4)$: Signing $+2$ is forbidden, and also $+4$ is forbidden.

  This leaves only two possibilities

  • $r_{1}=<-2,-3,-4>$      $r_{2}=<-2,+3,-4>$

• $\pi =(2,4,3)$: Signing $+2$ is forbidden. Also the sequence $-4,-3$ is forbidden.

  This leaves three possibilities

  • $r_{3}=<-2,-4,+3>$       $r_{4} = <-2,+4,-3>$       $r_{5} = <-2,+4,+3>$

• $\pi =(3,2,4)$: Signing $+4$ is forbidden. Also the sequence $-3,-2$ is forbidden.

  This leaves three possibilities

  • $r_{6} = <-3,+2,-4>$       $r_{7} = <+3,-2,-4>$       $r_{8} = <+3,+2,-4>$

• $\pi =(3,4,2)$: The sequence $+3,+4$ is forbidden.

  This leaves six possibilities

  • $r_{9} = <-3,-4,-2>$       $r_{10} = <-3,-4,+2>$       $r_{11} = <-3,+4,-2>$

  • $r_{12} = <-3,+4,+2>$       $r_{13} = <+3,-4,-2>$       $r_{14} = <+3,-4,+2>$

• $\pi =(4,2,3)$: The sequence $+2,+3$ is forbidden.

  This leaves six possibilities

  • $r_{15} = <-4,-2,-3>$       $r_{16} = <+4,-2,-3>$       $r_{17} = <-4,-2,+3>$

  • $r_{18} = <+4,-2,+3>$       $r_{19} = <-4,+2,-3>$      $r_{20} = <+4,+2,-3>$

• $\pi =(4,3,2)$: The sequence $-4,-3$ is forbidden as well as the sequence $-3,-2$.

  This leaves five possibilities

  • $r_{21} = <-4,+3,-2>$       $r_{22} = <-4,+3,+2>$       $r_{23} = <+4,-3,+2>$

  • $r_{24} = <+4,+3,-2>$       $r_{25} = <+4,+3,+2>$

$\square$

By looking at a graphical representation of $4$-OPT moves such as the one used in Fig. 1, we can see that there are different reinsertion schemes (i.e., different moves) that in fact, loosely speaking, “have the same shape”. We can then define an equivalence relation between moves. Namely, two moves are equivalent if the (unlabeled) drawing of one of them can be turned into the one of the other by some rotations of $\pi /2$ radians, and/or by flipping it vertically, horizontally or with respect to the diagonals $x=y$ or $x=-y$. For instance, in Fig. 1 we can see that $<+4,-2,-3>$ and $<-3,-4,+2>$ are equivalent, since we can turn one drawing into the other by a rotation of $\pi /2$ radians.

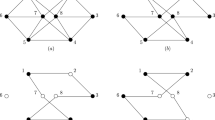
The relation that we have informally just described can be made formal by using the algebra of rotations and reflections in the plane (the so called optic group of operators). We think that this discussion, whose substance is quite simple, would be distracting here, and we refer the reader to Lancia and Dalpasso (2023) for all technical details. The important thing to remark here is that the relation is indeed an equivalence, and we can use it to partition the set of all $4$-OPT moves into orbits (i.e., classes of equivalent moves). Note that, after we have partitioned the reinsertion schemes into orbits, then it is enough to explain our method for one reinsertion scheme of each orbit, called the orbit’s representative. In fact, then the explanation applies to each reinsertion scheme r in the orbit, once we change the selection indices according to the transformation that turns the drawing of the representative into that of r. With a case analysis, we have then determined all orbits for the pure reinsertion schemes. By convention, we have chosen as the representative the smallest (in lexicographic order) scheme of the orbit. In Fig. 2 we illustrate the representatives of the 7 orbits.

Proposition 2

The pure reinsertion schemes for $4$-OPT are partitioned in 7 orbits $\mathcal{O}_1,\ldots ,\mathcal{O}_7$.

Proof

We have

• $\mathcal{O}_1=\mathcal{O}(r_{1})=\{r_{1},r_{24},r_{23},r_{22}\}$.

• $\mathcal{O}_2=\mathcal{O}(r_{2})=\{r_{2},r_{21}\}$.

• $\mathcal{O}_3=\mathcal{O}(r_{3})=\{r_{3},r_{7},r_{13},r_{17}\}$.

• $\mathcal{O}_4=\mathcal{O}(r_{4})=\{r_{4},r_{19},r_{11},r_{6}\}$.

• $\mathcal{O}_5=\mathcal{O}(r_{5})=\{r_{5},r_{20},r_{14},r_{15},r_{12},r_{18},r_{9},r_{8}\}$

• $\mathcal{O}_6=\mathcal{O}(r_{10})=\{r_{10},r_{16}\}$.

• $\mathcal{O}_7=\mathcal{O}(r_{25})=\{r_{25}\}$.

$\square$

Fig. 2

Orbits of $4$-OPT

Let $\mathcal{S}$ be the set of all complete selections. For $S\in \mathcal{S}$, let us denote by $\mathcal{I}(S)$ the set of all pure reinsertion sets for S. Then, the set of all true $4$-OPT moves is

$$\begin{aligned} \big \{\big (R(S),I\big ) : S\in \mathcal{S}, I\in \mathcal{I}(S)\big \} \end{aligned}$$

(1)

and the total number of true $4$-OPT moves is $\sum _{S\in \mathcal{S}} |\mathcal{I}(S)| = 25 \,|\mathcal{S}|$. An exact count can be obtained by first recalling a theorem that we proved in Lancia and Dalpasso (2020).

Theorem 1

For each $k=2,\ldots ,\lfloor n/2\rfloor$ the number $P_k$ of complete $k$-OPT selections in an n-nodes graph is

$$\begin{aligned} P_k={n-k+1 \atopwithdelims ()k} - {n-k-1 \atopwithdelims ()k-2}. \end{aligned}$$

From the theorem, we derive the following

Corollary 1

The number of true $4$-OPT moves in an n-nodes graph is

$$\begin{aligned} 25\, P_4 = 25\left( {n-3 \atopwithdelims ()4} - {n-5 \atopwithdelims ()2}\right) = 25\left( \frac{n^4-18 n^3 + 107 n^2 - 210 n}{24}\right) \end{aligned}$$

(2)

In Table 1 we report the number of moves for various values of n, giving a striking example of why the exploration of the $3$-OPT and $4$-OPT neighborhoods would be totally impractical unless some effective strategies were adopted.

Table 1 The number of true $k$-OPT moves for $k=2,3,4$ and various n

3 Speeding-up the search: the basic idea

Our method can be used to find either the best-improving selection (i.e., for a Best-Improvement local search) or any improving selection (i.e., for a First-Improvement local search). In the rest of the paper we will focus on the best-improvement case, since it is the harder of the two. The changes needed in order to adopt the method for a First-Improvement local search are trivial, and they are left to the reader.

The seven $4$-OPT orbits partition the set of all reinsertion schemes. Denote by $r^j$ the representative of the j-th orbit. Then, for each selection S the set $\mathcal{I}(S)$ of all the reinsertion sets for S is $\mathcal{I}(S)= \bigcup _{j=1}^{7} \{I(r): r\in \mathcal{O}(r^j) \}$ and $R(S)\times \mathcal{I}(S)$ is the set of all true $4$-OPT moves for S. If we denote by $\mu ^*$ the best among all true $4$-OPT moves (initially set to ”undefined”), the overall strategy to determine $\mu ^*$ could be as follows:

• 1. Consider, in turn, each orbit $j=1,\ldots ,7$.

• 2. Consider each element $r \in \mathcal{O}(r^j)$ (where each such r is obtained by $r^j$ by means of rotations and/or reflections).

• 3. Given r, consider (implicitly or explicitly) all complete selections $S=(i_1, \ldots ,i_4)$, obtaining the moves defined by $\mu :=(R(S),I(r))$. Each time $\mu$ is better than $\mu ^*$ update $\mu ^*:=\mu$.

The cost of step 3 by complete enumeration of all selections is $\Theta (n^4)$, where the code is a nested-for procedure such as

(where the expression $[A\text {?}]$, given a predicate A, returns 1 if A is true and 0 otherwise).

In the remainder of the paper we will focus on a method for significantly lowering the complexity of step 3, not only with respect to its $\Theta (n^4)$ enumerative implementation, but also with respect to the $\Theta (n^3)$ implementation of the dynamic programming procedure presented in de Berg et al. (2020).

Our idea for speeding-up the search is based on the following consideration. Suppose there exists an oracle which has access to all the optimal selections, but can look at only two indices at a time. We can inquire the oracle by specifying two indices $i_a$, $i_b$ (e.g., $a=2$ and $b=4$, etc.) and the oracle, in time O(1) returns us a pair of values $v_a, v_b\in V$ such that there exists at least one best-improving $4$-OPT move in which the two specified indices have those particular values. We call such a pair a pivot for a move. Let’s say that we make a first call with the pair of labels $i_1$ and $i_2$, and obtain the pivot $(v_1,v_2)$. Now we would keep calling the oracle with labels $i_3$ and $i_4$, asking for each pivot $(v_3,v_4)$ (we assume the oracle never repeats the same answer to the same question, so, after at most $\Theta (n^2)$ calls, it might tell us “no more pivots"). We would then determine the best solution among all the quadruples $\{v_1, v_2, v_3, v_4\}$ which do in fact represent feasible selections (i.e., $v_1< v_2< v_3 < v_4$ and $(v_1,v_2,v_3,v_4)\in \mathcal{S}$). If the number of best-improving selections is considerably smaller than $n^2$, this procedure would take less than $\Theta (n^2)$ time. As a matter of fact, the number of best selections is in general much smaller than $n^2$ (many times the best selection is unique, in which case we would determine it in time O(1) with two calls). Let us say that there are B best selections overall. Then the above approach would take time O(B). It is safe to say that B is in general a very small number (it can almost be considered a constant), as we will show in our computational experiments. This is particularly true if we are close to the end of the convergence to a local optimum, so that there are very few ways to improve the current tour.

The bulk of our work has then been to simulate, heuristically, a similar oracle, i.e., a data structure that can be queried to return two out of the four indices of a best-improving selection much in a similar way as described above. In our heuristic version, the oracle, rather than returning a pair of indices that are certainly in a best-improving solution, returns a pair of indices that are likely to be in a best-improving solution. As we will see, this can already greatly reduce the number of possible selections candidate to be best-improving. In order to assess the likelihood of two specific indices to be in a best solution, we will use suitable two-argument functions.

The fundamental quantities $\tau ^+$ and $\tau ^-$.

We define two functions of $V\times V$ into $\mathbb {R}$ fundamental for our work. Loosely speaking, these functions will be used to determine, for each pair of indices of a selection, the contribution of that pair to the value of a move. The rationale is that, the higher the contribution, the higher the probability that a particular pair is in a best selection.

For each $a, b\in \{0,\ldots ,{\bar{n}}\}$, we define $\tau ^+(a,b)$ to be the difference between the cost from a to its successor and the cost from a to the successor of b, i.e.,

$$\begin{aligned} \tau ^+(a,b) = c(a, a\oplus 1) - c(a,b\oplus 1) \end{aligned}$$

and we define $\tau ^-(a,b)$ to be the difference between the cost from a to its predecessor and the cost from a to the predecessor of b, i.e.,

$$\begin{aligned} \tau ^-(a,b) = c(a, a\ominus 1) - c(a,b\ominus 1). \end{aligned}$$

Clearly, each of these quantities can be computed in time O(1), and computing their values for a subset of possible pairs can never exceed time $O(n^2)$.

4 Searching the $4$-OPT neighborhood

Let r be a reinsertion scheme (we can assume that r is the representative of an orbit, since each scheme can always be reduced to a representative by a proper change of indices). For each selection $S=(i_1,i_2,i_3,i_4)$, we denote by $\Delta _r(i_1,i_2,i_3,i_4)$ the value of the move (R(S), I(r)), i.e., the difference between the cost of the removed edges $R(S)=\{\{i_1,i_1\oplus 1\},\{i_2,i_2\oplus 1\},\{i_3,i_3\oplus 1\},\{i_4,i_4\oplus 1\}\}$ and the cost of the reinsertion set I(r).

We will use an approach analogous to the one we introduced in Lancia and Dalpasso (2020) for the $3$-OPT case, starting by showing how to break up the function $\Delta _r()$, that has 4 parameters (and hence $\Theta (n^4)$ possible arguments), into a sum of functions of two parameters each. In particular, we have

$$\begin{aligned} \Delta _r(i_1,i_2,i_3,i_4) = f_r^1(i_{\pi (1)},i_{\pi (2)}) + f_r^2(i_{\pi (3)},i_{\pi (4)}) + f_r^3(i_{\sigma (1)},i_{\sigma (2)}) + f_r^4(i_{\sigma (3)},i_{\sigma (4)}) \end{aligned}$$

(3)

for suitable functions $f_r^1(), f_r^2(), f_r^3()$, $f_r^4()$, each representing the contribution of two specific indices to the value of the move, and permutations $\pi ,\sigma$ of the set $\{1,2,3,4\}$. The domains of these functions are, respectively, $\mathcal{S}_{\pi (1)\pi (2)}$, $\mathcal{S}_{\pi (3)\pi (4)}$, $\mathcal{S}_{\sigma (1)\sigma (2)}$ and $\mathcal{S}_{\sigma (3)\sigma (4)}$, which are subsets of $\{0,\ldots ,{\bar{n}}\}\times \{0,\ldots ,{\bar{n}}\}$ that limit the valid input pairs to values obtained from two specific elements of a selection. In particular, for $a,b\in \{1,2,3,4\}$, we define

$$\begin{aligned} \mathcal{S}_{ab} := \{(x,y) : \exists (v_1,v_2,v_3,v_4)\in \mathcal{S}\text { with } v_a=x \text { and } v_b=y\}. \end{aligned}$$

(4)

Theorem 2

For every $4$-OPT reinsertion scheme r there exist functions $f_r^1(), f_r^2(), f_r^3(), f_r^4():\mathbb {Z}\times \mathbb {Z}\mapsto \mathbb {R}$, and permutations $\pi$ and $\sigma$ of the set $\{1,2,3,4\}$ such that for each selection $(i_1,i_2,i_3,i_4)$ it is

$$\begin{aligned} \Delta _r(i_1,i_2,i_3,i_4) \\ = f_r^1(i_{\pi (1)},i_{\pi (2)}) + f_r^2(i_{\pi (3)},i_{\pi (4)}) + f_r^3(i_{\sigma (1)},i_{\sigma (2)}) + f_r^4(i_{\sigma (3)},i_{\sigma (4)}). \end{aligned}$$

Proof

Let us consider a bipartite graph B with 4 vertices on top and 4 on bottom. The top vertices are the tour edges $R=\{e_1, e_2, e_3, e_4\}$ removed by the selection, where $e_t=\{i_t,i_t\oplus 1\}$ for $t=1,2,3,4$. The bottom edges are the edges $I=\{e'_1,e'_2,e'_3,e'_4\}$ inserted by the reinsertion scheme. In B there is an edge $e e'$ between every two pair of vertices $e\in R$ and $e'\in I$ such that $e \cap e' \ne \emptyset$. It is immediate to see that every node has degree 2, and, in fact, B consists of a length-8 cycle. As an example, in the figure below we depict B for the reinsertion scheme $r_{11}=<-3,+4,-2>$.

The cycle is the disjoint union of two perfect matchings. From each one of them we can obtain the functions $f_r^1()$, $f_r^2()$, $f_r^3()$, $f_r^4()$. We adopt the convention to use the matching that contains the edge $e_1 e'_1$, where, w.l.o.g., $i_1\in e'_1$. In the example above, the matching is

$$\begin{aligned} e_1 \leftrightarrow \{i_1,i_3\}, \quad e_2 \leftrightarrow \{i_2,i_4\}, \quad e_3 \leftrightarrow \{i_2\oplus 1,i_3\oplus 1\}, \quad e_4 \leftrightarrow \{i_1\oplus 1,i_4\oplus 1\} \end{aligned}$$

From each edge of the matching we derive either a $\tau ^+$ or a $\tau ^-$ expression as follows. Assume the edge is $e_x e'$, with $x\in \{1,2,3,4\}$. If $e' = \{i_x,i_y\}$ then

$$\begin{aligned} c(e_x) - c(e') = c(i_x, i_x\oplus 1) - c(i_x,i_y)\\ = c(i_x, i_x\oplus 1) - c(i_x,(i_y\ominus 1)\oplus 1) = \tau ^{+}(i_x,i_y\ominus 1). \end{aligned}$$

Otherwise, it is $e' = \{i_x\oplus 1,i_y\}$ and

$$\begin{aligned} c(e_x) - c(e') = c(i_x, i_x\oplus 1) - c(i_x\oplus 1,i_y)\\ = c(i_x\oplus 1, i_x) - c(i_x\oplus 1,(i_y\oplus 1)\ominus 1) = \tau ^{-}(i_x\oplus 1,i_y\oplus 1). \end{aligned}$$

The sum of these values, for $x=1,2,3,4$, is then the cost of the move. For instance, in the move above it is

$$\begin{aligned} \Delta _r(i_1,i_2,i_3,i_4) \\ = \tau ^{+}(i_1,i_3\ominus 1) + \tau ^{+}(i_2,i_4\ominus 1)+\tau ^{-}(i_3\oplus 1,i_2\oplus 2)+\tau ^{-}(i_4\oplus 1,i_1\oplus 2). \end{aligned}$$

Let us call $A_1,\ldots ,A_4$ the four addends of the sum thus obtained (e.g., $A_1=\tau ^{+}(i_1,i_3\ominus 1)$, etc.) It remains to show that $A_1,\ldots ,A_4$ can always be rearranged so as all four type of indices appear in the first two (which implies that they also appear in the second two).

For $x\in \{1,2,3,4\}$ let us call a “type-x addend” an addend in which one of the two arguments is either $i_x$, $i_x\ominus 1$, $i_x\oplus 1$ or $i_x\oplus 2$. Notice that each addend is type-x and type-y for some $x\ne y$ and that there are exactly two type-x addends for each $x\in \{1,2,3,4\}$. Assume $A_1$ is type-a and type-b. There remain three addends, and two of them are not type-a or a would be overrepresented. Furthermore, these two cannot both be type-b or b would be overrepresented. So there is an addend which is neither type-a nor type-b. Swap that addend with $A_2$. Then the first two addends now range over all four indices. By reading the order in which the various types of indices appear in $A_1$ and $A_2$ we get the permutation $\pi$ of the theorem statement. Similarly, we get $\sigma$ from $A_3$ and $A_4$. $\square$

In the above example, $A_1$ is type-1 and type-3, while $A_2$ is type-2 and type-4. The permutations $\pi$ and $\sigma$ are $\pi =(1,3,2,4)$ and $\sigma =(3,2,4,1)$. Furthermore,

• 1. $f_r^1(x,y):=\tau ^{+}(x,y\ominus 1)$, with domain $\mathcal{S}_{13}$

• 2. $f_r^2(x,y):=\tau ^{+}(x,y\ominus 1)$, with domain $\mathcal{S}_{24}$

• 3. $f_r^3(x,y):=\tau ^{-}(x\oplus 1,y\oplus 2)$, with domain $\mathcal{S}_{32}$

• 4. $f_r^4(x,y):=\tau ^{-}(x\oplus 1,y\oplus 2)$, with domain $\mathcal{S}_{41}$

Notice how the theorem implies that each function $f^i(x,y)$ is either a $\tau ^+$ or a $\tau ^-$ in which each argument is offset by a constant in $\{-1,0,1,2\}$. By using Theorem 2, we can give the functions

$$\begin{aligned} f_r^1,\ldots ,f_r^4\end{aligned}$$

and the permutations $\pi$ and $\sigma$ such that $\Delta _r(i_1,i_2,i_3,i_4) = f_r^1(i_{\pi (1)},i_{\pi (2)}) + f_r^2(i_{\pi (3)},i_{\pi (4)}) + f_r^3(i_{\sigma (1)},i_{\sigma (2)}) + f_r^4(i_{\sigma (3)},i_{\sigma (4)})$ for the representatives of all orbits, as reported in Table 2. We recall that the permutations define also the domains of the functions $f_r^1,\ldots ,f_r^4$, which are, respectively, $\mathcal{S}_{\pi (1)\pi (2)}$, $\mathcal{S}_{\pi (3)\pi (4)}$, $\mathcal{S}_{\sigma (1)\sigma (2)}$ and $\mathcal{S}_{\sigma (3)\sigma (4)}$. (For a list of the inserted edges of each scheme, look at Fig. 2. For simplicity in checking the table vs the figure, we have called i, j, k, h the elements that will occupy, respectively, positions 1, 2, 3, 4 in the selection. That is $S_{13}=\{(i,k): \exists i_2,i_4 \text { with } (i,i_2,k,i_4)\in \mathcal{S}\}$, $S_{42}=\{(h,j): \exists i_1,i_3 \text { with } (i_1,j,i_3,h)\in \mathcal{S}\}$, etc.).

Table 2 Expressing $\Delta _r(i,j,k,h)$ as a sum $f_r^1()+f_r^2()+f_r^3()+f_r^4()$

The procedure to find the best selection

Given a reinsertion scheme r, assume we want to find the best selection and the current “champion” (the best selection found so far) is $S^*=({\bar{v}}_1,{\bar{v}}_2, {\bar{v}}_3,{\bar{v}}_4)$ of value $V:=\Delta _r(S^*)$ (in the beginning, we may assume $S^*$ is undefined and its value is $V:=0$). We make the trivial observation that for a selection $(i_1,i_2,i_3,i_4)$ to beat $S^*$ it must be

$$\begin{aligned} \left( f_r^1(i_{\pi (1)},i_{\pi (2)}) + f_r^2(i_{\pi (3)},i_{\pi (4)})> \frac{V}{2} \right) \nonumber \\ \vee \left( f_r^3(i_{\sigma (1)},i_{\sigma (2)}) + f_r^4(i_{\sigma (3)},i_{\sigma (4)}) > \frac{V}{2} \right) \end{aligned}$$

(5)

These are not exclusive, but possibly overlapping conditions.

We set up a two-phase algorithm, which we call SmartForce. In the first (second) phase, we restrict our search to the selections $(i_1,i_2,i_3,i_4)$ which satisfy the first (respectively, second) half of (5). Just for the sake of example, assume $\pi =(1,3,2,4)$ and $\sigma =(1,4,2,3)$. To find the optimal selection, we go through two phases. In the first phase we look for all selections (i, j, k, h) such that $f_r^1(i,k) + f_r^2(j,h)> \frac{V}{2}$ and then check if indeed $\Delta _r(i,j,k,h)>V$. In second phase, we look for all selections such that $f_r^3(i,h) + f_r^4(j,k)> \frac{V}{2}$ and then check if indeed $\Delta _r(i,j,k,h)>V$. Whenever we improve the champion, we immediately update V, thus making the condition more difficult to satisfy and, consequently, reducing the search space for the remaining selections.

In order to sample only selections that can satisfy the above conditions, we make use of two max-heaps. A heap is perfect for taking the highest-valued elements from a set, in decreasing order. It can be built in linear time with respect to the number of its elements and has the property that the largest element can be extracted in logarithmic time, while still leaving a heap. The heap is implemented by an array H with three fields; $\texttt {x}$ and $\texttt {y}$, which represent two indices of a selection (i.e., a pivot) and $\texttt {val}$ which is a numerical value, i.e., the key to sort the heap. By using the standard implementation of a heap (Cormen et al. 2022), the array corresponds to a binary tree, whose nodes are stored in consecutive entries from 1 to H.SIZE. The left son of node H[t] is H[2t], while the right son is $H[2t+1]$. The father of node H[t] is $H[t.\text {div}.2]$. A max-heap is such that the key of each node H[t] is the largest among all the keys of the subtree rooted at H[t].

The procedure for each phase, given in Procedure CombineHeaps (Procedure 1), has in input two heaps $H'$ and $H''$ and a permutation $\phi$ of $\{1,2,3,4\}$ (for code-reuse, we added an input coefficient $\alpha$ to represent the fraction of V that the sum of the heaps needs to achieve. In general it is $\alpha = 1/2$ but in the next paragraph we will describe a special case where it is convenient to set $\alpha = 1$). The heap $H'$ contains pivots in the domain $\mathcal{S}_{\phi (1)\phi (2)}$ while $H''$ contains pivots in the domain $\mathcal{S}_{\phi (3)\phi (2)}$. Each heap, built as in Procedure 4BuildHeap, corresponds to one of the addends of (3) and is sorted according to the value $f_H(x,y)$ of its pivots (x, y) (where $f_H()$ is one of $f_r^1,\ldots ,f_r^4$). The goal of the phase is to form all quadruples of value $>\alpha V$, where $\alpha =1/2$, by picking one element from each heap. This is achieved by running a loop which identifies all pairs (x, y), (z, w) of pivots, taken from $H'$ and $H''$ respectively, such that $f_{H'}(x,y) + f_{H''}(z,w) > \alpha V$. The loop terminates as soon as the sum of the maxima of the two heaps is $\le \alpha V$. To perform this search effectively, given that the maximum of $H'$ is $(x_1,y_1)$ of value $f_{H'}(x_1,y_1)$, we first extract from $H''$ all elements $(z_c,w_c)$ such that $f_{H'}(x_1,y_1) + f_{H''}(z_c,w_c) > \alpha V$. Note that this way we have in fact created a sorted array of those elements from $H''$, i.e., $H''$ now can be replaced by an array $A''=[(z_1,w_1),\ldots ,(z_Q,w_Q)]$ such that

$$\begin{aligned} f_{H''}(z_1,w_1) \ge \cdots \ge f_{H''}(z_Q,w_Q) > \alpha V - f_{H'}(x_1,y_1). \end{aligned}$$

Creating this array has cost $O(Q\log n)$. In a similar way, in time $O(P\log n)$ we create a sorted array $A'=[(x_1,y_1),\ldots ,(x_P,y_P)]$ containing all the elements of $H'$ such that

$$\begin{aligned} f_{H'}(x_1,y_1) \ge \cdots \ge f_{H'}(x_P,y_P) > \alpha V - f_{H''}(z_1,w_1). \end{aligned}$$

Now we combine elements from the first array and the second array to form all quadruples of value $>\alpha V$. For doing so we keep two pointers a and b, one per array. Initially $a=b=1$. If $f_{H'}(x_a,y_a) \ge f_{H''}(z_b,w_b)$ we say that a is the master and b is the slave, otherwise b is the master and a the slave. We then run a double loop which ends as soon as $f_{H'}(x_a,y_a) + f_{H''}(z_b,w_b) \le \alpha V$. At each iteration, a pointer runs through all the elements from the slave down, as long as the sum of their values and the master’s value is still $>\alpha V$. For example, if the master is a, then we would consider all elements $c=b, b+1, b+2, \ldots$ such that $f_{H'}(x_a,y_a) + f_{H''}(z_c,w_c) > \alpha V$. For each quadruple $(x_a,y_a,z_c,w_c)$ thus obtained we would, in time O(1) sort the indices so as to obtain values i, j, k, h with $i\le j \le k \le h$ (this is done by calling a subroutine decodeIndices$(x_a,y_a,z_c,w_c,\phi )$, in line 13.). Then we would check if indeed (i, j, k, h) is a valid pure selection and $\Delta _r(i,j,k,h) > V$. In that case, we would update the current champion and its value V.

Notice that once a quadruple is formed there is nothing more to do than compute its value, in time O(1). If the total number of quadruples evaluated is L, the complexity of the loop 8.–18. is O(L) so that, overall, the procedure takes time $O((P+Q)\log n + L)$ where $P=\texttt {size}(A^0)$ and $Q=\texttt {size}(A^1)$. As we will discuss in the section on experimental results, this procedure behaves, in practice, like $O(n^{2.5})$

Perfect splits

If we look at Table 2 we see that there are three cases in which $\{\pi (1),\pi (2)\} = \{\sigma (1),\sigma (2)\}$ (so that, also, $\{\pi (3),\pi (4)\} = \{\sigma (3),\sigma (4)\}$). We call such a situation a perfect split of the indices, and it occurs for the orbits $\mathcal{O}_2$, $\mathcal{O}_6$ and $\mathcal{O}_7$ which, altogether, contain five reinsertion schemes out of 25. The reinsertion schemes with perfect split can be treated differently than the other cases, with a method that, as shown in the computational experiments section, allows us to get a further 10% speedup over the general procedure described so far.

The key observation is that if r has a perfect split we can define two functions $g_r^1()$ and $g_r^2()$ as $g_r^1=f_r^1+f_r^3$ and $g_r^2=f_r^2+f_r^4$, so that (3) becomes

$$\begin{aligned} \Delta _r(i_1,i_2,i_3,i_4) = g_r^1(i_{\pi (1)}, i_{\pi (2)}) + g_r^2(i_{\pi (3)}, i_{\pi (4)}). \end{aligned}$$

The domain of $g_r^1$ is $\mathcal{S}_{\pi (1)\pi (2)}$ while the domain of $g_r^2$ is $\mathcal{S}_{\pi (3)\pi (4)}$. In particular, for the representatives of the above three orbits we have

r	$\pi$	$g_r^1()$	$g_r^2()$
$r_{2}$	(1, 2, 3, 4)	$\tau ^+(i,j\ominus 1) + \tau ^-(j\oplus 1,i\oplus 2)$	$\tau ^+(k,h\ominus 1) + \tau ^-(h\oplus 1,k\oplus 2)$
$r_{10}$	(1, 3, 2, 4)	$\tau ^+(i,k\ominus 1)+\tau ^-(k\oplus 1,i\oplus 2)$	$\tau ^+(j,h) + \tau ^+(h,j)$
$r_{25}$	(1, 3, 2, 4)	$\tau ^+(i,k)+ \tau ^+(k,i)$	$\tau ^+(j,h) + \tau ^+(h,j)$

In order to find the best selection for a scheme with perfect split, we prepare two heaps, one sorted by the values $g_r^1()$ with pivots over $\mathcal{S}_{\pi (1)\pi (2)}$ and the other by the values $g_r^2()$ with pivots over $\mathcal{S}_{\pi (3)\pi (4)}$. We then run a unique phase of search, analogous to the procedure CombineHeaps (Procedure 1) but with the difference that instead of computing quadruples of value $>V/2$, we compute quadruples of value $>V$ and stop at the first of such quadruples which turns out to be a feasible selection (since, because of the ordering of the values, it is necessarily the best selection). This is obtained by calling CombineHeaps with $\alpha =1$.

Overall procedure

The final procedure to find the best move is Find4-OPTmove (Procedure 2), which calls the subroutine SmartForce (Procedure 3) to find the best selection for a given reinsertion scheme.

Notice that we are considering the reinsertion schemes in a precise order. This is somewhat arbitrary, since any other ordering would have been valid as well. In the computational experiments we have tested also other orders and found out that the running times are pretty much independent on the ordering chosen. In practice, we suggest to randomize the order in which the reinsertion schemes are considered, since there is no real reason to prefer an ordering over another. We also note that if one would choose to optimize over only some of the reinsertion schemes but not on all, it is enough to remove from the procedure the calls relative to the reinsertion schemes that one does not want to use.

For completeness, we give also the code for the heap procedures, including $\textsc {Heapify}$ and $\textsc {ExtractMax}$ (Procedures 5 and 6), although they are the standard procedures for implementing heaps and can be found on any textbook on data structures. To simplify the code, we allow $H[t].\texttt {val}$ to be defined also for $t>$H.SIZE, with value $-\infty$. The procedure $\textsc {Heapify}(H,t)$ assumes that the subtree rooted at t respects the heap structure at all nodes, except, perhaps, at the root. The procedure then adjusts the keys so that the subtree rooted at t becomes indeed a heap. The cost of heapify is linear in the height of the subtree. The loop of lines 11–13 in procedure $\textsc {BuildHeap}$ turns an unsorted array H into a heap, working its way bottom-up, in time O (H.SIZE). The procedure ExtractMax returns the element of maximum value of the heap (which must be in the root node, i.e., H[1]). It then replaces the root with a leaf and, by calling $\texttt {heapify}(H,1)$, it moves it down along the tree until the heap property is again fulfilled. The cost of this procedure is $O(\log$ (H.SIZE)).

5 Computational results

All programs were coded in C, and run on an Intel(R) Core(TM) i7-7700 CPU at 3.60GHz with 16GB RAM, with operating system Ubuntu 16.04 and compiled under gcc version 5.4.0 with optimization option -O2.

We have run extensive tests to assess the effectiveness of our method. First, we have determined the best version of our procedure, and then we have compared it to the algorithms in the literature. The experiments were run on randomly generated data as well as on instances from public repositories. Randomly generated data are of two types, called UNI and GEO. UNI instances are complete graphs in which the edge costs are drawn uniformly at random in the interval (0, 1). GEO instances are complete graphs whose nodes are random points in the unit square and whose edge lengths are the Euclidean distances between the nodes. Finally, we used instances from the public repository TSPLIB for further experiments.

5.1 Determining the best version of our code

In this section we compare our smart-force algorithm without (ISF0) and with (ISF1) perfect split. Our tests consist in running local search up to conclusion starting from random tours. We considered graphs of size $n=50m$, with $m=2,\ldots ,10$. At each step, we find the best $4$-OPT-move over all the 7 orbits. For each value of n we generated 10 instances (the same 10 for each algorithm). In these, as well as in the similar tests described in the next sections, all runs with different algorithms were double-checked to make sure that they took the same number of steps and ended at the same local optima. Indeed, although extremely rare, there is the possibility that more than one move are optimal at a certain step, and therefore that two algorithms may make a different choice and become incomparable after such a move. We intended to remove these runs from the comparisons, but, as a matter of fact, they never happened.

The results, reported in Table 3, are averages over all 10 runs. We report the total running time to reach a local optimum (“Time per search”), the time required to determine each move (“Time per step”), the number of moves evaluated to find each best (“Move evals per step”) and the length of the convergence (“# steps”). Some results are rounded and shown with 4 significant figures. We use the suffix K for $10^3$. From the table it appears that ISF1 grants an extra saving of about 12% over ISF0, and therefore hereafter we will be using ISF1 in comparing our algorithm to other approaches in the literature.

Another interesting information that we can derive from the table is that GEO instances appear to require less work than UNI instances, both in finding the best move at each step than in the number of steps overall required for convergence. With respect to the length of the convergence, we notice that it grows, approximately, like $\Theta (n \log n)$. In Sect. 5.3 we will be using this estimate to improve over Glover’s algorithm for the orbits 6 and 7.

Table 3 Comparing ISF0 and ISF1 in finding a 4-optimal tour starting from a random tour. Values are averages over 10 instances for each n. Times in seconds

In a second experiment, we looked at the growth of the running time of ISF1 for a single step, in order to infer, empirically, a reasonable time complexity function for our algorithm. In particular, we considered the first step, i.e., finding the best move on a random tour. Notice that a random tour is just a special case of the tour to which a local search must be applied, and, indeed, the vast majority of tours on which a move is determined will be quite non-random, since they are the result of all the improving moves applied in the steps before the current one. We will be addressing again this aspect in Sect. 5.3. Here we choose to study the time to find the best move on a random tour since it is the simplest case to assess, given that random tours are very easy to generate, while tours of medium- or high- quality would be much more difficult to generate in a quantity large enough for statistical purposes.

In Table 4 we report the running times, in seconds, to find the best move on a graph of $n=100, 200, \ldots , 2000$ nodes, both for UNI and for GEO instances. Values are averages over 10 instances for each n. The values from the table are also shown as dots in Fig. 3. From the plots we can see a very good fit with an interpolating function $\Theta (n^{2.5})$ in both cases.

Table 4 Times (secs) to find the best move on a random tour for uniform and geometric instances. Values are averages over 10 trials

Fig. 3

Plots of the average time to find best move on a random tour. Left: UNI instances, fit=$\alpha \, n^{2.5}$, with $\alpha =5\times {10^{-8}}$. Right: GEO instances, fit= $\beta \, n^{2.5}$, with $\beta =4.5\times 10^{-8}$

5.2 Comparing our code with other algorithms

In this and in the next section we compare our algorithm to the best procedures in the literature for $4$-OPT local search. In particular, the most important comparison will be versus de Berg’s et al. $\Theta (n^3)$ procedure (de Berg et al. 2020), which can find the best $4$-OPT move over all the possible orbits. Of secondary importance, but still interesting, is the comparison versus Glover’s $\Theta (n^2)$ procedure (Glover 1996), which can find the best $4$-OPT move for only two very peculiar orbits. Indeed, the $4$-OPT moves considered by Glover are, in a sense, special combinations of $2$-OPT moves, which is the reason why it is possible to optimize them in quadratic time. As a matter of fact, de Berg’s at al have proven in their paper that, if an important conjecture in graph theory holds, it is impossible that a worst-case better than cubic algorithm exists for finding the best $k$-OPT move (over all orbits) for $k\ge 3$ (de Berg et al. 2020).

Our comparisons were made mostly for the time required by a convergence to a local optimum, from which we can derive the average time required to find the best move at each step. Notice that, given the particular logic behind our procedure, we might expect that finding the best move on a uniformly random tour, or on a tour obtained after a few improving moves have already been made, or on a tour close to a local optimum might take a quite different time. We will see that this behavior is particularly clear for the special moves to which Glover’s algorithm can be applied. By averaging over all tours of the local search we then have a much better estimate of the time required to find a $4$-OPT move than if we were to consider only random tours.

Vs De Berg et al.’s algorithm

In a first test, we compared the time of a local search convergence for our algorithm and De Berg et al.’s dynamic program (DYP), when the best move is determined over all seven orbits. For a description of DYP implementation refer to de Berg et al. (2020); Lancia and Dalpasso (2023). We considered random uniform and geometric instances of size n going from 100 to 500 with increments of 25. The results are reported in Table 5. From the table we can see that ISF1 outperforms DYP on all instances, with speed-ups going from about $4\times$ up to about $20\times$. We should expect even bigger speed-ups for $n>500$, but these comparisons were not done since DYP would have required too much time to run all experiments. In Fig. 4, the average times for finding the best $4$-OPT move with the two algorithms, taken from Table 5, are plotted and fitted with, repectively, a $\Theta (n^3)$ for DYN and a $\Theta (n^{2.5})$ function for ISF1.

Table 5 Comparing De Berg’s et al. Dynamic Programming and ISF1 in finding a 4-optimal tour starting from a random tour. Values are averages over 10 instances for each n

Fig. 4

Avg time to find best move on a random tour. Left UNI instances, right GEO instances. Fitting (DYN, UNI/GEO): $4.6\times 10^{-8}\, n^3 -9\times 10^{-5}\, n^2 + 10^{-3}\,n$. Fitting (ISF1, UNI): $4.1\times 10^{-8} \, n^{2.5}$, (ISF1, GEO): $3.3\times 10^{-8} \, n^{2.5}$

In a final test, we selected at random thirty TSPLIB instances with $100< n < 1000$, i.e., sizes neither too small to be instantly solved by both algorithms, nor too big to require unsuitably large times for our experiments. For each instance we ran a full local search, starting from three random tours, and computed the average of: (i) the time for the whole search; (ii) the time for finding the best move; (iii) the convergence length. The results are reported in Table 6. Even in this case, we can see that ISF1 outperforms DYP on all instances, with speed-ups between $20\times$ and $30\times$ for the largest instances considered.

Table 6 Comparing De Berg et al’s DYP with ISF1 for TSPLIB instances with $100< n < 1000$. Times in seconds, averaged over three runs for each instance

5.3 Comparison with Glover’s algorithm

In a final experiment, we compared our procedure with Glover’s $\Theta (n^2)$ algorithm (named GLO hereafter). For a description of GLO implementation, refer to Glover (1996); Lancia and Dalpasso (2023). As we already remarked, the scope of GLO is restricted to two very symmetric orbits (covering just 3 out of 25 reinsertion schemes) which, for convenience, we report in Fig. 5. This implies that, even if GLO would have turned out to be better than ISF1 on these three schemes, we could still have an improvement over the state-of-the-art algorithms for the entire $4$-OPT neighborhood by a hybrid algorithm which uses GLO for 3 schemes and ISF1 on the remaining 22 schemes.

Fig. 5

Orbits for Glover’s algorithm

Indeed, it is impossible to beat GLO from a worst-case complexity point of view, since it determines the best move for these special $4$-OPT orbits in time $\Theta (n^2)$, which is in fact the time needed to just read the input (i.e., the cost matrix c[i, j]). We still ran a comparison to see if at least we were not too worse, considering that our algorithm might behave differently for these peculiar type of orbits than for the other orbits.

We therefore generated random uniform and geometric instances of size n going from 200 to 1500 with increments of 100. The results are reported in Table 7 (left-half part, labeled “FULL CONVERGENCE”), in which we can see the average time for a convergence, the average time to find the best move and the average length of the convergence (over 10 instances for each value of n). From the table we can see that ISF1 is actually better than GLO for $n<1000$, while GLO becomes increasingly better than ISF1 for $n\ge 1000$. For these values, however the time differences are not big, in particular considering that these are fairly large instances for $4$-OPT.

Table 7 Comparing GLO and ISF1 in finding a 4-optimal tour for orbits 6 and 7, starting from a random tour. Values are averages over 10 instances for each n. Times in seconds

Another interesting observation that we can make by looking at the table is that, for these special schemes, finding the best move for GEO instances and UNI instances requires pretty much the same time, and the only difference is that the convergence length is slightly longer for GEO instances (which is the opposite of what happens when we search over all reinsertion schemes).

By a closer inspection of the time needed to find the best move at each step, we observed that our algorithm is sensitive to the quality of the tour it is applied to, and finding the best move on a random tour is different than finding it on tours closer to a local optimum. In particular, we noticed that while our algorithm is quite slower than Glover’s algorithm on the starting random tour, it becomes progressively faster as the search proceeds, and, at some point it becomes definitely faster than GLO. In Fig. 6 we can see an example of this phenomenon on a random medium-size instance from our experiments, but this behavior was observed over all instances. In this case, $n=800$, the convergence takes between 450 and 500 steps and, around step 140, ISF1 starts to become faster than GLO in finding the best move, and it stays such until the end.

Having made this observation, we suggest a hybrid approach which indeed behaves better than both GLO and ISF1 on all instances of our experiments. In particular, given n, we set a step s(n) and run GLO for the first s(n) steps, then we switch to ISF1 and use ISF1 until we reach the local optimum. In order to fix a value for s(n), we looked at plots such as that of Fig. 6 and observed that, more or less, the point when ISF1 starts to be faster than GLO is around 1/3rd of the convergence. We then gave a rough estimate of the convergence length as $l(n):=0.06\, n\log n$ and set $s(n):=l(n)/3$.

In the right half of Table 7 (labeled “FINAL PART OF CONVERGENCE”) we report the averages of total time and time per move for GLO and ISF1 in the second part of the convergence, i.e., over steps $s(n), s(n)+1, \ldots$. By looking at the time needed to find the best move, we can see that ISF1 on this part is much smaller than it was on the whole convergence, and it is always smaller than GLO’s time. In the last column (labeled HYB) we report the average time of the hybrid algorithm over the whole convergence. It can be seen, by comparison with the two corresponding columns from the left half of the table, that HYB is better than both GLO and ISF1 over all instances in the experiment.

A final remark can be made about the use of the orbit $\mathcal{O}_7$ (the “double bridge” move) within Lin and Kernighan’s heuristic (Lin and Kernighan 1973). Indeed, as also pointed out in Glover and Pesch (1997), this move cannot be constructed by the LK procedure, but it becomes useful to keep the search going when no other good moves can be found. This opens up to the possibility of using our approach (or the hybrid approach) for finding the double bridge moves within LK procedure.

Fig. 6

Plot of time to find best move along the convergence, orbits 6 and 7, $n=800$, GLO vs ISF1

5.4 Comparing $4$-OPT with $3$-OPT (and $2$-OPT)

Since we did not find in the literature any clear assessment of the effectiveness of the $4$-OPT neighborhood, in comparison with $3$-OPT and $2$-OPT, in standard best-improvement local search algorithms, we made some experiments with randomly-generated graphs, already described as UNI in this paper. The results are reported in Table 8.

Table 8 Comparing 2-optimal, 3-optimal and 4-optimal solutions

For various values of n (column 1), we have generated 5 instances, corresponding to which we report three main results, labeled “most” (the instance on which the gain of $4$-OPT over $3$-OPT was the highest) “least” (the instance on which the gain was the smallest) and “avg” (the average gain over the 5 instances). The gain is given by the percentage reduction in the value of the solution found by $4$-OPT with respect to the value of the best solution found by $3$-OPT. On each instance, a sequence of best-improvement $4$-OPT (inclusive of 3- and 2-OPT moves) convergences, from a random tour to a local optimum, was run, until the cumulative time t (checked at the end of the each convergence) exceeded a limit of 1 s. Note that for n large enough, this small time limit results in only one convergence of $4$-OPT. Then, a set of best-improvement convergences from random tours, of either $2$-OPT alone or $3$-OPT (inclusive of $2$-OPT) was run for a time t. This way we are ensured that 2- and $3$-OPT have as much time as $4$-OPT, and indeed they can run many convergences to beat the single one (or very few) allowed to $4$-OPT. In columns 3, 4 and 7, we report how many convergences of $2$-OPT, $3$-OPT and $4$-OPT were run in the time t. In columns 5 and 8 we report the percentage value (with respect to the best value found by $2$-OPT) of the best solution found by $3$-OPT and $4$-OPT, respectively. Furthermore, in column 6 we report the percentage gain of the $3$-OPT solution versus the $2$-OPT solution, and in column 9 the percentage gain of the $4$-OPT solution versus the $3$-OPT solution. In column 10 we report how many of the 3-optimal solutions generated over all convergences and all instances were in fact also 4-optimal. Finally, in column 11, we report how many times the best 3-optimal solution of each instance was also 4-optimal.

The table is full of interesting data, confirming and extending some of the results observed by Lin (1965) (e.g., that $3$-OPT is much better than $2$-OPT, and that it finds very good solutions for small n). The most important value reported is the average improvement that can be gained by using $4$-OPT in place of $3$-OPT, which has been written in bold (see column 9). It is clear how $4$-OPT does not add anything (or very little) to the power of $3$-OPT for small graphs (i.e., $n\le 100$), consistently with Lin’s observations. However, by increasing n the advantage in using $4$-OPT vs $3$-OPT becomes evident and substantial. This value grows with n and it soons becomes quite large (e.g., for $n=2000$ it is around 30%).

While for $n\le 50$ many 3-optimal solutions are also 4-optimal, and the best 3-optimal solution of the selected instances is always 4-optimal, this property ceases to hold pretty soon. Indeed, out of the 601 3-optimal solutions found overall for $n\ge 100$, only 6 were 4-optimal, and this statistics worsens to none for $n\ge 200$.

Finally, with respect to the running times, as we said there was no increase since we allowed the same time to both $4$-OPT and $3$-OPT (even if, for $n\ge 200$, this meant that we only allowed one convergence for $4$-OPT). In running the $3$-OPT optimization, we used our procedure (Lancia and Dalpasso 2020) which is better than the standard cubic enumeration. It can be seen that the ratio between $3$-OPT convergences and $4$-OPT convergences (see columns 4 and 7) is not too high, thereby showing that the increase of time from $3$-OPT to $4$-OPT with our method is not as bad as the one observed by Lin (1965).

In addition to the above tests, we did some more experiments with some medium-to-large instances from the public repository TSPLIB, that are very far from being random and are often taken from real-life problems. For each considered problem, we (i) found local optimal tours using the $3$-OPT neighborhood (from five different random starting tours); (ii) for each such 3-optimal tour, we looked for the best $4$-OPT move trying to get an even better tour. The goal was to show that these 3-optimal solutions are almost certainly not 4-optimal, and it proved to hold in all the cases we considered, namely for the following problems: gr666, u724, rat783, dsj1000, d2103, pcb3038, rl5934 and pla7397 (note that the number of nodes can be deduced from each instance name. E.g., d2103 has 2103 nodes).

6 Conclusions

In this paper we have described a new algorithm for finding the best $4$-OPT move within a local search strategy for the TSP. Since not only the $\Theta (n^4)$ enumerative algorithm, but also the $\Theta (n^3)$ algorithm DYP of de Berg et al. (2020) are too slow even for relatively small values of n, the application of $4$-OPT best-improvement local search to the TSP has never been really possible before. Furthermore, the fastest algorithm in the literature, i.e., GLO (Glover 1996), could only be applied to three type of moves out of the 25 possible.

Building on our previous works (Lancia and Dalpasso 2020; Lancia and Vidoni 2020), we have proposed a strategy based on picking halves of the selection starting from the most promising, and combining them into forming full selections. In order for this process to be fast, we employed sorted heaps to store the half selections, and described an effective master-servant cycle to combine them. The results is a procedure which can be used over all $4$-OPT moves, and whose average complexity to find the best move on a random tour is fitted well by a $\Theta (n^{2.5})$ function. Extensive experiments have shown how our procedure outperforms DYP on all instances considered, which included both random instances (uniform and geometric) and instances from the public repository TSPLIB. Furthermore, our procedure is also better than GLO on graphs of size $n< 1000$, while a hybrid combination of our procedure with GLO is better than GLO alone over all instances considered in our experiments.

Among the future developments of our work, we can list: (i) experimenting the effect of the addition of best-improving $4$-OPT moves to existing local search algorithms which were not using them. Also, experimenting with first-improvement other than best-improvement, since our algorithm can be easily adapted to stop as soon as it finds any improving move; (ii) applying these or similar ideas to other optimization problems, besides the TSP, in which local search is based on a $k$-OPT scheme, i.e., swapping k elements of the solution with some other k; (iii) studying the computational complexity of our algorithm from a theoretical point of view, and proving that it takes $\Theta (n^{2.5})$ expected time to find the best move on a random tour. Of these, point (iii) appears, by far, to be the most challenging.