1 Introduction

Adverse weather conditions pose a significant danger to ships, their crews, passengers, and cargo and represents one of the main causes of delays in the shipping industry (Notteboom 2006). Since over 90% of the world trade is carried by ships (Hoffmann and Sirimanne 2017), considering the weather when finding safe and efficient routes for ships is of utmost importance. Furthermore, finding good routes for ships lowers fuel consumption, leading to lower \(\hbox {CO}_2\) emissions. Finding routes that are not only safe and efficient, but also ensure that the ship arrives on time is a complex task that is difficult to do by hand, especially when considering the weather.

In this paper, we present an approach for finding routes between two points on the globe considering the current weather along the route. For this, we use a real-coded genetic algorithm (GA) with specialized mutation and crossover operators for the weather routing of ships. Our goal is to minimize the fuel consumption of the vessel while respecting a constraint on the latest arrival time at the vessel’s destination. Our GA finds realistic, smooth routes that are not restricted to an arbitrary grid and avoid adverse weather conditions, such as strong storms, considering spatial and temporal aspects of the weather.

Our approach contains the following novel components:

  1. 1.

    We provide a general routing algorithm that does not have preset values for the longitudes/latitudes of the waypoints along the path.

  2. 2.

    The speed of the vessel is variable, allowing for, e.g., slow-steaming.

  3. 3.

    The generated routes avoid sharp changes in direction to ensure they can be sailed by even large vessels.

We test our algorithm with instances based on many different geographies and weather conditions. Our results show that the minimization of fuel consumption leads to routes avoiding areas with adverse weather conditions, as weather and sea conditions largely effect the different factors travel time, safety and fuel consumption simultaneously. Due to the high bunker consumption of container vessels, even small percentage improvements lead to high cost savings. However, it is also possible to sail through areas with favorable weather conditions to increase the speed of the vessel. The weather data we use in our algorithm is provided by an industrial partner so that we have reliable, real-life information. Overall, the different instances show a wide range of possible savings potentials of up to 13.9% over ignoring the weather. Furthermore, our results also show that the consideration of weather conditions can have a high impact on the route depending on the weather intensity. Our algorithm is also faster than existing approaches, requiring only a single minute of CPU time even for large instances. For smaller instances, the runtime falls to under 30 s.

This paper is organized as follows. The weather routing problem is described in detail in Sect. 2. In Sect. 3, the main algorithms for weather-dependent routing of vessels are summarized. Our genetic algorithm is presented in Sect. 4. In Sect. 5, we show computational results for the algorithm for different instances. Section 6 summarizes the paper.

2 Weather routing of ships

Consider a decision maker who wants to determine a route for a vessel over the ocean between two ports. The route clearly must avoid landmasses, shallows, and any other undesirable area as specified by a planner [e.g., pirate zones, or Sulphur Emission Control Areas (SECA)]. SECA zones are areas in which the emission of sulphur and sulphur oxides by ships is restricted by law. Planners may also specify a maximum time duration (due date) for the voyage.

We allow vessels to vary their speed along their voyage, thus parameters related to the fuel consumption and impact of weather on the speed of the vessel (draft, displaced volume, waterline length, block coefficient and design speed; the design speed is a speed of the vessel for which the fuel consumption is known.) must be determined. The vessel also has a minimum and a maximum speed between which the speed can be chosen throughout the route. Typically, the problem of weather routing is modeled as a minimum time problem or a minimum fuel consumption problem subject to some constraints (avoiding unfavorable weather, etc.). We solve the problem as a minimum fuel consumption problem, since in the variable speed setting, minimizing only the time leads to expensive solutions with high \(\hbox {CO}_2\) outputs. In this work, we use a model of speed consumption that takes into account wind and waves. It is possible to use a more sophisticated model for the calculation of the fuel consumption, but we note that this has no impact on the algorithmic aspects of our approach.

2.1 Computation of the fuel consumption

Accurately representing the fuel consumption of vessels is critical for making realistic weather-dependent routes. We use the formula

$$\begin{aligned} F(v) = (v/v^*)^3\cdot f^* \end{aligned}$$
(1)

from Brouer et al. (2013) to compute the fuel consumption (subsequently referred to as the bunker consumption), where v is the speed of the vessel in knots, \(v^*\) is the design speed and \(f^*\) is the fuel consumption at the design speed. We split the route into n segments each with a fixed speed \(v_i\). The bunker consumption of the whole route is then calculated by summing the consumption of each segments.

The weather has a strong influence on the realized speed of the vessel. We calculate a speed loss coefficient that accepts the parameters of the vessel and the current weather to determine the actual speed. This speed is determined by the direction and speed of the wind and the direction and height of the waves. We use the approach from Larsson and Simonsen (2014) to calculate the speed loss that takes into account both waves and wind simultaneously. The percentage of speed loss is calculated with the following formula (Kwon 2008):

$$\begin{aligned} v_ loss = \alpha _ corr \cdot \mu _ red \cdot \frac{\varDelta v}{v}100\%, \end{aligned}$$
(2)

where \(v_{loss}\) is the speed loss in percent, \(\alpha _{corr}\) is the correction factor for the block coefficient of the vessel and \(\mu _{red}\) is the weather direction reduction factor. The block coefficient of a vessel is the ratio of the underwater volume of the ship to the volume of a rectangular block having the same length, breadth and depth. The factor \(\alpha _{corr}\) depends on the block coefficient of the vessel and its loading condition. A full list of formulas for the calculation of \(\alpha _{corr}\) for all different combinations of block coefficients and loading conditions can be found in Larsson and Simonsen (2014). The parameter \(\mu _{red}\) changes with the intensity of the weather and the angle of the wind/waves with respect to the ship. The speed loss in head weather is given as \(\frac{\varDelta v}{v}100\%\). The speed loss is represented with \(\varDelta v\) and the planned speed with v. The ratio is calculated by one of

$$\begin{aligned} \frac{\varDelta v}{v}100 \%&= 0.5BN+\frac{BN^{6.5}}{2.7\triangledown ^\frac{2}{3}}, \end{aligned}$$
(3)
$$\begin{aligned} \frac{\varDelta v}{v}100 \%&= 0.7BN+\frac{BN^{6.5}}{2.7\triangledown ^\frac{2}{3}}, \text { or } \end{aligned}$$
(4)
$$\begin{aligned} \frac{\varDelta v}{v}100 \%&= 0.5BN+\frac{BN^{6.5}}{22\triangledown ^\frac{2}{3}} \end{aligned}$$
(5)

depending on the loading condition of the vessel. The parameter BN is the Beaufort number and \(\triangledown \) is the displaced volume of the vessel. Equation 3 is used for vessels in laden condition and Eq. 4 for vessels in ballast condition. We use Eq. 5 for our experiments as this is the one for container ships and vessels in normal condition. The Beaufort number characterizes the strength of the waves and the wind.

3 Related work

Existing approaches in the literature for ship weather routing can be divided into three groups: exact approaches, single objective heuristic approaches, and multiobjective evolutionary approaches. Exact approaches to solve the problem are especially found in early works, whereas recent approaches are mainly heuristics. The following overview is divided into the three groups of approaches and summarizes the most important ones. We further identify differing objective functions for the approaches. Touati and Jost (2012) partitions the objective functions found in the ship routing literature into three groups: economic, climate/sustainability and regional fairness/health. The most frequent objective functions are the minimization of fuel consumption and distance traveled. The optimization of fuel consumption is also often combined with the minimization of risk related to a route, resulting in a multiobjective optimization problem. In the last part of this section, we present some papers related to the problem of weather routing.

3.1 Exact approaches

One of the first approaches for ship weather routing is the isochrone method (James 1957). It minimizes the travel time of the ship and allows the manual construction of a route. This method is improved by Hagiwara and Spaans (1987), who make it suitable for a computer and include fuel consumption in addition to travel time in the objective function. Another approach for the problem is the calculus of variations method proposed by Haltiner et al. (1962). It is an analytic approach to weather routing that determines the path and the engine power of the ship. There are also many approaches using dynamic programming such as De Wit (1990) and Motte and Calvert (1990) or based on shortest path algorithms such as Montes (2005), Panigrahi et al. (2012), Sen and Padhy (2015) and Mannarini et al. (2016).

3.2 Single objective heuristic approaches

Evolutionary approaches are well suited algorithms for solving path finding problems because they allow the inclusion of a wide range of constraints and objectives into problems that are hard to solve with exact algorithms. The optimization of only one objective makes these approaches additionally fast compared to the multiobjective ones. Walther et al. (2018) propose a genetic algorithm (GA) that supports variable ship speed and minimizes fuel costs. They compare a graph algorithm for a ship weather routing problem with a GA. The exact details of the GA are not clear, however to the best of our knowledge, our GA differs in its domain specific heuristics and variable length encoding.

Wang et al. (2018) propose a real-coded GA with fixed longitudes for the waypoints that make up the solution representation. This approach therefore has a problem finding paths around vertical obstacles, meaning circumnavigating landmasses can be very difficult or even impossible if the path must traverse a high range of latitude in only a small range of longitude. They integrate further constraints in their optimization including a restriction of the sailing area, avoidance of land obstacles and shallow waters, an interval for the ship’s speed and weather alarm zones that are caused by severe weather conditions and wave heights exceeding a certain value. Furthermore, they introduce a general mathematical model for the problem. Yuankui et al. (2014) introduce a simulated annealing algorithm minimizing the travel time of the vessel.

3.3 Multiobjective evolutionary approaches

Multiobjective evolutionary approaches allow for the simultaneous optimization of several objectives. Evolutionary algorithms (EA) are the most common multiobjective solution procedures for weather routing, such as the work of Tsou (2010) and Azariadis (2017) who combine an EA with a modified A* algorithm. The A* algorithm is used to compute one-third of the initial population, and the remaining two-thirds are computed randomly. Tsou (2010) calculates routes avoiding obstacles that are given to the evolutionary algorithm as the first population. The EA then tries to find the optimal route incorporating the safety and economy of routes.

Li and Zhang (2017) propose a GA that minimizes the turning variation and fuel consumption of vessels while considering fixed orientations of the vessel at the start and end position for the vessel as their approach is used to find the optimal trajectory in close-range maneuvering. The real-coded GA presented by Maki et al. (2011) supports variable ship speed by varying the propeller revolutions for each segment of the route. However, the longitudes of the route points are fixed and only the latitudes can be changed, severely limiting the possibilities of the algorithm. This leads to the same problems as the algorithm from Wang et al. (2018). Furthermore, the authors do not mention how to avoid obstacles (land masses, etc.) in the algorithm. Tsou and Cheng (2013) implement an ant colony algorithm that is combined with the crossover and mutation concept of GAs for finding routes while considering weather conditions. If ants pass the same waypoint, a crossover of both routes is conducted.

Krata and Szlapczynska (2012), Szlapczynska and Smierzchalski (2009), Szlapczynska (2013) and Szlapczynska (2015) use a multicriteria weather routing algorithm based on the concept of the Multi-objective Evolutionary Weather Routing Algorithm proposed by Szlapczynska (2007) to solve the problem of finding routes taking into account changeable weather conditions. All these approaches focus on minimizing the passage time, fuel consumption and the risk factor of routes. The constraints in Szlapczynska (2015) include regions to avoid and the variables of the algorithm are the coordinates of the waypoints and the settings of the ship’s engine. There is no information given about how the mutation and crossover in this algorithm are performed and therefore the quality of the algorithm cannot be evaluated.

Li et al. (2017), Veneti et al. (2015,2018) apply the NSGA II approach. Veneti et al. (2018) compare it to an implementation of the SPEA (Zitzler and Thiele 1999). Veneti et al. (2015) define a non linear integer programming problem and present a modified version of the NSGA II (Deb et al. 2002). The algorithm uses nodes in a grid to find an optimal path from the origin to the destination. The velocity of the ship is fixed, meaning adverse weather can only be avoided through route changes. Vettor and Guedes Soares (2016) perform their search only with the Strength Pareto Evolutionary Algorithm 2 from Zitzler et al. (2001) to minimize the the fuel consumption, time of arrival and risk related to rough weather. The optimization of the initial routes is done with a version of the grid-based Dijkstra’s algorithm and the speed may differ between two waypoints. Within the evolutionary algorithm the mutation only changes one waypoint at once strongly restricting the changes within one iteration. To select the most favorable route the hyperplane strategy distance method also presented by Vettor and Guedes Soares (2016) is used. It is used to select a solution out of a Pareto set according to user preferences specifying the importance of the different objectives.

3.4 Related problems

Several problems exist that are similar to the vessel weather routing problem. One of them is the routing of planes instead of vessels. The basis of the Flight Planning Problem (FPP) as presented by Knudsen et al. (2018) is a directed graph with nodes representing waypoints at different altitudes. The arcs are associated with a resource consumption and costs. These costs depend on the fuel consumed so far and on the weather conditions that depend on the time when the arc is traversed. Therefore, in contrast to our approach, the problem is solved with the help of a graph structure. The variant of the problem presented by Knudsen et al. (2017) assume a fixed altitude for the flight making the problem similar to ours. Normally, there are different flight levels and therefore a third dimension for each waypoint. Furthermore, variations in speed are often not considered in the FPP.

Shortest path problems over roads are also related to our problem [see Madkour et al. (2017) for a survey]. The key difference comes in the freedom of movement at sea as well as the varying speed of the ship. Although cars and trucks can vary their speed while driving, considering this in the planning phase is difficult since crowded roads and tight deadlines prevent speed variation in practice. Furthermore, the weather has much less impact on the quality of solutions and is therefore not included in approaches found in literature. One approach to solve these shortest path problems is the use of contraction hierarchies as presented by Geisberger et al. (2008) and extended in Geisberger et al. (2012). This approach is designed for road network specific structures where the visited points are directly linked, in contrast to the situation on oceans where the connections of the ports are flexible.

Another area of related problems is the path planning of Unmanned Aerial Vehicles (UAVs). Arantes et al. (2016), for example, use a genetic algorithm (GA) to plan the paths of drones and mention no-fly zones and obstacles that are similar to the land masses in the weather routing problem. They include position uncertainty of the aircraft due to turbulence, which does not occur in the weather routing problem. The multi-population genetic algorithm is combined with a visibility graph maintaining all feasible paths for the drone, which would not be possible for the weather routing problem because of the much larger solution space. Hasircioglu et al. (2008) also use a GA to plan paths offline for UAVs. The GA uses three different mutation operators that update, insert and delete control points visited by the UAV. Hence, there are no operators that are specific to the case of UAV path planning. In contrast to this, we are using customized operators involving the weather and the speed of the vessel when changing a solution to achieve better improvements than with general operators. Ragusa et al. (2017) also investigate a GA for “micro aerial vehicles”. The algorithm is similar to the approach presented by this paper for finding routes for an initial population for our GA. However, for the problem of weather routing, intersections are infeasible, which is different than in the approach of Ragusa et al. (2017). In their approach, intersections are allowed and the algorithm focuses on minimizing the degree of intersection with obstacles. Furthermore, the routes used by Ragusa et al. (2017) have fewer waypoints than in the case of ship routing, because the routes are much shorter and need fewer waypoints.

4 A genetic algorithm for realistic weather-dependent routes

We use a genetic algorithm (GA) to find weather-dependent routes for vessels. GAs provide an ideal framework for weather routing for a couple of reasons. First, GAs allow us to combine parts of routes in a natural way in the hopes of forming a high quality solution. Second, the population of a GA offers diversity that is important for avoiding local optima that can be induced by large storms or weather systems. Our GA uses a variable length, real-valued solution representation in which each individual is composed of waypoints, each characterized by a longitude, latitude and the planned speed of the vessel on the segment preceding the waypoint. The set A defines the arcs between the waypoints.

We fill the initial population with feasible routes that have random waypoints added to ensure diversity (Sect. 4.1). The crossover and mutation operators used within our algorithm are adapted to the weather routing problem and we use multiple operators, unlike in standard GA implementations (Sects. 4.2 and 4.3). The fitness function used for evaluating each individual of the population is the bunker fuel required to sail the route under the given weather conditions, and the computations for this are given in Sect. 2. We further add penalty costs to the fitness function for sailing through undesirable areas (e.g., areas with pirates) or not meeting temporal constraints. The GA terminates when the improvement between two iterations falls below a threshold value or after a given number of iterations. The objective function used to evaluate a solution is represented as

$$\begin{aligned} minimize&\sum _{a \in A } \left( c^a \cdot F^{arc}(a) \right) + p^{ pirate } \cdot y^{ pirate } + p^{ delay } \cdot t^{ delay } \end{aligned}$$
(6)

where \(F^{arc}(a)= \left\{ \begin{array}{ll} \infty , &{} \quad \text {if the wave height on arc } \textit{a} \text { exceeds } \textit{h} \\ \frac{F(v^{ plan }_a)}{24} \cdot \frac{d_a}{v^{ real }_a}, &{} \quad \text {otherwise.} \end{array} \right. \)

The set of all arcs used to construct the route from the start to the destination is denoted as A. The binary variable \(y^{ pirate }\) is set to 1 if the route has at least one arc intersecting a pirate zone and the vessel sails slower than 18 knots. Furthermore, \(t^{ delay }\) specifies the delay of the vessel in days if a time limit for the travel time exists. The penalty for additional safety costs is given by \(p^{ pirate }\) and the parameter \(p^{ delay }\) specifies the penalty for not meeting the arrival deadline, if one is specified. The function \(F^{arc}(a)\) calculates the fuel consumption for a single arc between two way points of a complete route, where \(v^{ plan }_a\) is the planned speed, \(d_a\) is the length and \(v^{ real }_a\) specifies the real speed calculated with the loss factor \(v^{ loss }_a\) for arc a. When the maximum acceptable wave height h is exceeded for an arc, the fuel consumption is set to \(\infty \), because solutions containing such arcs are infeasible and must therefore be ignored. For feasible solutions, the fuel consumption is multiplied by the cost of fuel per ton \(c^a\) to determine its cost for the objective function.

We define two types of high cost zones: areas with increased risk of pirate attacks, and the SECA zone in the North Sea. We specify four different pirate zones based on public information about pirate encounters: the Caribbean Sea, the Gulf of Guinea, around Somalia/the Horn of Africa/the Gulf of Bengal, and the South China Sea. In these zones, it is necessary to sail at a speed of at least 18 knots as recommended by The Baltic and International Maritime Council (2011) or to pay additional safety costs of 50,000 USD, as for example suggested by Wrede (2013). Therefore, \(p^{ pirate }\) is set to this value for our calculations. In the SECA zone, we assume more expensive fuel is used and adjust the bunker consumption function of the vessel accordingly.Footnote 1 The cost factor \(c^a\) is set to 450 USD except in the SECA zone where it is 850 USD. The penalty \(p^{ delay }\) for arriving too late is set to 25,000 USD and is calculated by multiplying a penalty of 100 USD per container per day, as suggested by Li et al. (2015), with an assumed number of transported containers of 2500, which is the half of the capacity of the vessel we use. The parameter h is set to 9 m corresponding to a Beaufort number of 10 for our calculations.

4.1 Initial route generation

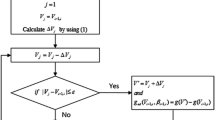
Our initial solution algorithm creates a route by first directly connecting the origin and destination and iteratively moving the midpoint of the line segments over land orthogonally into the water until no segments intersect with the land anymore. Note that a buffer zone could also be specified around land to ensure that ships travel further offshore. More specifically, a segment is divided into two parts by inserting and moving its midpoint. This is done until the distance between the start and end of a new segment falls below a set threshold, and therefore does not need be divided anymore. This process is visualized in Fig. 1. The left half of the route is arbitrarily chosen to be moved into the water before the right half (note that the order does not matter), leading to the evolution of a route as shown. To generate individuals for the initial population, this algorithm is used to find a route that has to visit one random point between the starting and the target point. The pseudocode for this algorithm is given in Algorithm 1. The algorithm accepts a start node s, an end node e, a threshold t for the length of segments and a distance d for the movement of middle points. The algorithm returns the node sequence from the start node to the end node, with the end node missing, which therefore still needs to be added. We use this algorithm to generate some initial solutions and then use the crossover and mutation procedures to expand the initial population so that the first generation has the full population size. Start and end points of connections generated with this algorithm can be chosen arbitrarily, however, we only use ports for our computational experiments.

Fig. 1
figure 1

Visualization of the generation of an initial route from Perth, Australia to Brisbane, Australia in 12 steps

Full size image
figure a

4.2 Crossover operators

In this step of the GA, the routes of two random individuals from the current population are combined into a single, new route. The selection of the individuals is based on a roulette wheel selection with quadratic fitness scaling. We use two different crossover methods. The first combines the routes by choosing a point to join the routes somewhere near the middle of each route, preferably at a position in which both routes are near each other. This operator is similar to the one from Vettor and Guedes Soares (2016) who combine the first k waypoints of a route with the waypoints of a second route from \(k+1\) to the end, but do not search for a waypoint in the middle of the route first. The second combines the routes using a random position from the first half of one route and a random position from the second half of the other route. Veneti et al. (2015,2018) also use a crossover operator combining routes at random points, but it requires the same node to be contained in both parent routes to perform a recombination, meaning it is rarely applicable. Furthermore, for both of our operators we post-process the route to ensure that it is completely located in the water using the same procedure as for the initial routes. The result of one of our crossovers is visualized in Fig. 2 by means of the website geojson.io, in which the two black routes are combined to obtain the red one. We use the great circle distanceFootnote 2 for the length of all routes presented in this paper, but in the visualizations the way points are connected with straight lines for ease of visualization.

Fig. 2
figure 2

Visualization of the crossover operator

Full size image

4.3 Mutation operators

The mutation operators are used to make different changes to random individuals of the population. These operators delete or move waypoints or change the speed at waypoints and allow the GA to search for new solutions that are not just combinations of existing individuals. We use several different operators to introduce a domain-specific heuristic for dealing with weather conditions and obtain realizable routes. The operator applied to an individual is selected uniformly at random from the list of nine operators.

Deleting a single point/deleting multiple points We first introduce two simple mutation operators that delete a single point or multiple points within a given interval, respectively. The now disconnected parts of the route are reconnected with the initial route algorithm to avoid any landmasses.

Moving a single point/moving multiple points Our second set of operators tries to move one point or an interval of a route by a random distance limited by a parameter in a random direction. Should any part of the route now intersect with land we use the same procedure as in the initial route algorithm to repair the route.

Moving a point with the maximum wind This operator takes the current weather on the route into account. In the first step the position along the route with the maximum influence of the wind on the vessel is determined. In the second step this waypoint is then moved in a randomly determined direction. Afterwards, the route points around the moved one are recalculated with the initial route algorithm to smoothen the route.

Moving a point with the maximum angle/Moving multiple points with the maximum angle Routes with sharp angles are difficult to realize in practice, as the turning radius of large vessels is limited. This operator thus tries to remove points or multiple points with large angles from the route. We select the point with the maximum angle and remove a given percentage defined by a parameter of all nodes in each direction. Afterwards, the initial route algorithm is used to adjust the route should it end up over land. This process can be repeated for multiple points with large angles. This leads to the second operator of this group that moves the points around the several largest angles with one application.

Mutating the speed of the vessel Our final operator adjusts the speed of the vessel for a segment of the route. The new speed is randomly determined in the interval between 80 and 120% of the current speed in the segment.

4.4 Stochastic optimization

We adjust the objective function to allow the GA to handle stochastic weather. Thus, instead of optimizing the fuel consumption for only a single weather scenario, we evaluate a route given multiple scenarios, giving us an expected fuel consumption. The multiple weather scenarios are forecasts for the true weather and are generated by modifying the historical weather data. The generation of scenarios is discussed in detail in Sect. 5.5. We note that this could be adjusted by risk averse users to use, e.g., conditional value at risk or other functions.

5 Computational results

In this section, we present computational results for our approach tested on 15 instances that we have constructed. The scenarios model various times of departure, starting/ending locations and travel times. We present two different weather routing settings: one with perfect information about the weather data and one where we plan under uncertainty. The first setting shows the performance of our approach under perfect information. In the second case, we show how the algorithm performs in a more realistic situation. We are able to conclude from both settings that including weather is critical for generating realistic routes. We implement the GA in C# and run it on a computer with an Intel Core i7-7700K 4.2 GHz processor and 32GB of RAM. The computation time for the solutions for all instances is less than 1 min. Every instance has been run 5 times and we report the average of these runs. Furthermore, we provide the standard deviation of the values for the fuel consumption of the five solutions. We cut the algorithm off at 60 CPU seconds or when the improvements within a single iteration become too small after a minimum number of iterations have been completed. We note that letting the GA run longer than 60 s can sometimes lead to slightly improved results on long routes.

5.1 Parameters for the GA

Our GA includes a number of parameters that influence the quality of the solutions found. Table 1 lists these parameters and the values used. The values have been determined using the GGA algorithm configurator (Ansótegui et al. 2009, 2015). We tune our GA with GGA for 5 days using 45 instances in our training set covering different departure times and locations. We use a Panamax vessel for all of our experiments, but it is also possible to run our algorithm with other vessel types having different vessel-specific parameters.

Table 1 Parameters for the GA
Full size table

5.2 Weather data

The weather data used in our experiments is provided by an industrial collaborator. It includes three months of weather information in a \(0.5^\circ \times 0.5^\circ \) grid with a 3 h interval for the time from August to October 2017. For each latitude, longitude, and timestamp, we are provided the wind direction and the wave height.

5.3 Experimental results for weather data with perfect information

We create 15 problem instances and try to include coverage of routes in a variety of locations around the world. Our instances also have a number of different weather conditions, ranging from “normal” inclement weather to Hurricane Irma in the instance from USNYC (New York, USA) to SRPBM (Paramaribo, Suriname). The computational results for all 15 instances using perfect information about the weather (one weather scenario) are listed in Table 2. The average of the five runs ignoring the weather is compared to the runs including the weather in terms of route length in nautical miles (nm), duration in days (d) and fuel consumption (FC) in tons (t) of fuel. The results of the tests with and without weather optimization (WO) can be found in the two rows for each instance and the difference of the values is given below each pair of values. The duration and fuel consumption were calculated both with and without the influence of weather to evaluate the quality of the routes leading to the two columns for each of the two key figures. The instances with more extreme weather (Beaufort scale 9 or higher) are marked with a star (*). The solutions for all instances are visualized in Fig. 5. Weather-optimized routes are colored black and non-weather-optimized routes gray. The map is shaded based on the influence of the weather (dark red is worse weather, meaning stronger winds and higher waves) over the entire time period. The weather is visualized for the points in time when the ship following the weather-optimized route traverses the area or is near the visualized area.

In general, considering the weather leads to less costly routes with shorter travel times. In only one case, the instance from ZACPT (Cape Town, South Africa) to INBOM (Mumbai, India), including the weather leads to a route with less fuel consumption even when evaluating it without weather because the combination of the shorter route west of Madagascar and the strong wind and high waves along that path make it hard for the GA to move its path to the east of Madagascar when generating a route without considering the weather.

For some scenarios there is only a small change in the vessel routing when weather is considered, usually when regions with adverse weather can be easily avoided. However, there are also instances where the weather has a decisive influence on the routing. The instances from USNYC (New York, USA) to SRPBM (Paramaribo, Suriname) and from AUPER (Perth, Australia) to AUBNE (Brisbane, Australia) show that a path without the influence of weather would lead to routes that are not feasible in reality due to very strong wind and high waves, leading to an infinite value for the fuel consumption and the duration. On the route from New York to Paramaribo we have the strongest weather conditions of all instances (11 on the Beaufort scale). Therefore, the longer routes are necessary here to guarantee safety for the vessel and lead to huge improvements. The instances located in the Mediterranean region (ITTRS to EGALY, ESALG to EGALY, and NLRTM to FRMRS.) show that taking the weather into consideration also makes sense for short/medium distance routes. Our three instances in this region show reductions of the fuel consumption of up to about 3%. The SECA-zone in the North Sea does not have a high impact on the routing in the affected instances because it is not possible to leave it to save costs.

In the instance from DEHAM (Hamburg, Germany) to ISREY (Reykjavík, Iceland) it is not efficient to leave the SECA-zone on a route other than the generated one because the zone reaches far north. The route and the zone are visualized in Fig. 3. One instance with a relatively small difference between the weather-optimized and the non-weather-optimized path is the connection from USDUT (Dutch Harbor, USA) to USLAX (Los Angeles, USA). Despite this small deviation in the routing, it leads to an improvement in travel time and fuel consumption of approximately 1.6% when comparing the weather-optimized route with the non-weather-optimized route. The weather-optimized route is visualized in Fig. 5a in black.

Fig. 3
figure 3

Route from Hamburg to Reykjavík and the SECA-zone

Full size image

The routes running from ZACPT (Cape Town, South Africa) to INBOM (Mumbai, India) show one of the biggest differences as the weather-optimized routes run east of Madagascar while routes ignoring the weather run west of it. This is the case because the western routes are shorter, but the weather to the west is worse than to the east. This is visualized in Fig. 5d. This leads to an average improvement of fuel consumption by almost 7% considering the weather during optimization. The routes from USNYC (New York, USA) to DEHAM (Hamburg, Germany) show a similar observation with routes running north and south of the United Kingdom depending on the use of weather data. The weather-optimized routes run south of the United Kingdom although this path is longer because the weather conditions in the north are worse than in the south. Another important aspect for the routing in the Arabian Sea is the pirate zone that covers a large part of it. The weather-optimized routes, which already run east of Madagascar, take a right turn to bypass the zone as far as possible, while the routes running west of Madagascar run directly through it. This can be seen in Fig. 4, which shows the pirate zone. The routes from AEDXB (Dubai, UAE) to AUPER (Perth, Australia) and the routes from MYTPP (Tanjung Pelepas, Malaysia) to OMSLL (Salalah, Oman) are not visibly affected by the zone because the pirate zone covers the complete coast and cannot be avoided. The greatest savings potential can be found for the last instance from JPTYO (Tokyo, Japan) to GUGUM (Guam), in which an approximately 4.3% longer distance leads to savings savings of fuel and travel time of nearly 14%.

Overall, the results for the instances using perfect information about the weather show that there is a huge savings potential when including weather conditions into the optimization of routes for vessels. The improvements range from about 1% to almost 14% excluding the instances for which infeasible routes were generated when not considering weather.

5.4 Pirate zones and travel time limitations

In addition to higher speeds in pirate zones, the objective function can be penalized to account for security services (e.g., armed mercenaries). Increasing the costs within pirate zones by 10%, as well as requiring a higher speed leads to routes similar to the one in Fig. 4. This route has been generated without considering the influence of weather conditions to show the effect of the increased costs for a higher level of security. Our approach generates a solution that completely avoids the pirate zone marked in orange, and requires no modifications to our heuristics to identify such zones.

Fig. 4
figure 4

Route optimized with additional costs for security

Full size image

Another aspect that can be included into the routing problem is the addition of penalty costs for a delayed arrival at the destination port. Very high penalty costs can be used to force the algorithm to meet the deadline at any cost (if it is at all possible). Therefore, the course of the routes are changed for some instances and the speed on the routes must be increased in most cases.

Table 2 Comparison of routes computed considering weather to ones computed ignoring the weather regarding length in nautical miles duration in days and fuel consumption in tons, averages over five runs
Full size table
Fig. 5
figure 5

Visualization of the solutions for the instances

Full size image

5.5 Experimental results for stochastic weather data

In reality, reliable weather forecasts are only available for the beginning of a route. Thus, we must plan a route under uncertainty and replan whenever a new weather forecast is available. Table 3 shows the results for the previously given instances using multiple stochastic weather scenarios instead of planning under certainty for a single scenario as shown previously. The route length, duration and fuel usage are computed using the “true” weather, averaging over five different executions of our approach. The route planning uses either perfect information (“PI”), the expected value over five scenarios with replanning (“Stochastic”), the expected value over five scenarios without replanning (“Stoch. NR”), or plans without considering the weather (“No WO”). Percentage differences to the plan with perfect information are given for each value. Furthermore, the standard deviation for the calculated values for the fuel consumption of the five different solutions is given. Figure 6 shows an example for the four different routes for the second instance from USNYC (New York, USA) to SRPBM (Paramaribo, Suriname). The weather is left out for this figure as it differs too much for the different solutions and would be misleading regarding the quality of the routes.

We perform stochastic routing by first generating five potential forecasts of the weather from the “true” weather. This is done by modifying the components (direction, wind speed, wave height) by a random factor between \(-\) 50% and + 50%. We plan a route from the starting location using these five forecasts and minimize the expected value over the scenarios. As the ship moves closer to a given location, the better the forecast becomes. Perfect information is provided for the exact location of the vessel and for all locations within seven days, a forecast is provided for other locations as an average of the “true” weather and randomized forecast weighted by the time needed to arrive at this point.Footnote 3 We therefore replan the route in regular intervals. These scenarios are then used to provide the algorithm with information about the possible weather on the route.

Fig. 6
figure 6

The four different routes from USNYC (New York, USA) to SRPBM (Paramaribo, Suriname). “PI” in black, “Stochastic” in orange, “Stoch. NR” in green and “No WO” in blue (Color figure online)

Full size image

Overall, the results presented in Table 3 show that the use of stochastic weather data and replanning the route when new data becomes available leads to lower total fuel consumption than only planning with stochastic data at the start of the route, or planning using no weather data at all. Our approach is generally only a few percent worse than the solution found planning with perfect information. Replanning the routes during the journey leads to shorter travel times for all instances. For two cases, not replanning the route even leads to infeasible routes (ZACPT to INBOM and AUPER to AUBNE) meaning replanning is essential in these cases. The fuel consumption is also improved and the second instance (USNYC to SRPBM) shows the biggest difference with a deviation of 21.2% (without replanning) compared to a deviation of 9.8% (with replanning). We observe that the best route found is often not much longer or shorter than the best route without replanning.

Comparing the results without the usage of weather data to the results with the usage of stochastic weather shows that there are two special cases. For the instance from ZACPT (Cape Town, South Africa) to INBOM (Mumbai, India), the route has a longer travel time caused by the fact that the fuel consumption is the optimization goal and a longer travel time leads to a lower fuel consumption in this case. The only case where the the stochastic results are worse than the results generated without weather is the instance from ESALG (Algeciras, Spain) to EGALY (Alexandria, Egypt), which is due to unstable weather in front of the coast of Egypt.

Using stochastic data leads to longer travel times and higher fuel consumption than using perfect information, but not necessarily to longer routes. For 10 of the 15 instances the routes are longer when using stochastic scenarios instead of the perfect information about the weather. The travel times increase by 0.6–9.3% and the fuel consumption increases by 0.6–9.8%, respectively. Uncertainties regarding the weather conditions on the remaining route make it difficult for the algorithm to find a route that is good for all weather scenarios.

Table 3 Comp. results for stochastic optimization with replanning along the route under perfect information (“PI”), stochastic optimization with replanning (“Stochastic”), stochastic optimization with no replanning (“Stoch. NR”), and without weather routing (“No WO”)
Full size table

The best example of difficulty in planning the speed and the route of the ship to avoid strong weather with very high waves is the instance from USNYC (New York, USA) to SRPBM (Paramaribo, Suriname). For this instance, the largest deviation of the stochastic results from the results using perfect information is observed. The uncertain forecasts result in the route partly passing through unfavourable areas. Nevertheless, areas that are impassable due to strong waves and wind are avoided. Furthermore, the replanning of the route has a very high impact on the fuel consumption, showing the importance of the adaption to current weather data.

It is essential to adapt the route during the journey, as is exemplified by the instance from ZACPT (Cape Town, South Africa) to INBOM (Mumbai, India). Here, the route runs east of Madagascar because of the strong weather conditions west of it, which we also observed when using perfect information. The same observation can be made for the instance from AUPER (Perth, Australia) to AUBNE (Brisbane, Australia). However, there are many instances where the replanning does not have a large impact, we note that since replanning is computationally cheap, there is no reason not to do it. Usually, replanning has little impact when there are no large storms or extreme weather along the planned route.

It can be concluded that our approach provides high quality solutions when provided stochastic data and can effectively replan the route in the face of adverse weather conditions. We are further able to show that the routes we find are not much worse than those generated with perfect information, meaning our algorithm could be used in a real system.

6 Conclusion

In this paper, we presented a GA for the weather-dependent optimization of routes for vessels. We introduced an algorithm for generating initial routes as a useful supplement for the GA and listed a variety of domain-specific mutation operators for the GA to find good routes adapted to the present weather. The combination of this algorithm and the GA is highly effective at finding weather-dependent routes. Overall, the solutions for the different instances indicate that there is a need for the consideration of weather when generating routes for vessels. Weather-optimized routes lead to lower costs, and in some cases these routes are the only feasible routes. The experimental results showed that the proposed GA is able to find high quality solutions in a short amount of time. We have shown that the algorithm can handle stochastic weather data and generate reasonable routes that are not much worse than routes generated with perfect information. Furthermore, it makes sense to recalculate the route when new weather data becomes available. For future work, we plan to include more external factors, for example tides. The function for the bunker consumption will have to be extended then as well to include the new factors.