1 Introduction

One of the major successes of Einstein’s theory of general relativity is the diffeomorphism covariance of its construction which yields a generalised equivalence principle. However, general relativity is an incomplete gravity theory. For example, it does not anticipate the acceleration of the expansion of the universe due to dark energy, nor does it explain the black hole information paradox which deals with the emission of radiation from an isolated black hole. It is also noted that the solutions yielding wormholes and white holes have yet to be accepted since these objects have not been observed. It is for these reasons, among others, that modifications to general relativity have become commonplace. One such modification is an imposition of a polynomial form for the higher dimensional Lagrangian action

$$\begin{aligned} S=\int d^{N}x\sqrt{-g}\sum _{r=0}^{k}\alpha _{r}\mathcal {R}^r+S_{\small {\text{ matter }}}, \end{aligned}$$
(1)

which gives rise to Lovelock gravity [1,2,3] where k is the order of the theory and N is the dimension of spacetime. The topological Lovelock term is given as

$$\begin{aligned} \mathcal {R}^k=\frac{1}{2^k}\delta _{a_{1}b_{1}...a_{k}b_{k}}^{c_{1}d_{1}...c_{k}d_{k}}\prod _{r=1}^{k}R^{a_{r}b_{r}}{}_{{}c_{r}d_{r}}, \end{aligned}$$

which consists of the generalised Kronecker delta, given as the antisymmetric product \(\delta _{a_{1}b_{1}...a_{k}b_{k}}^{c_{1}d_{1}...c_{k}d_{k}}=(2k)!\delta ^{c_{1}}_{[a_{1}}\delta ^{d_{1}}_{b_{1}}\cdots \delta ^{c_{k}}_{a_{k}}\delta ^{d_{k}}_{b_{k]}}\) and the Riemann curvature tensor \(R^{ab}{}_{cd}\). The coupling constants \(\alpha _{r}\) in the action (1) have dimensions of \((\text{ length})^{2r-N}\). This is the most general higher order and higher dimensional metric extension of general relativity which preserves energy conservation, the above-mentioned diffeomorphism covariance and beautifully, second order quasilinear equations of motion. Of these higher order corrections indicative of Lovelock gravity, the quadratic corrections \(\mathcal {R}^2\) are of particular importance. It is well known that classical general relativity, or first order Lovelock gravity, is the low-frequency limit of quantum gravity. It was shown by Zwiebach [4] that a quadratic correction of the Gauss–Bonnet form \(\mathcal {R}^2=L_{GB}=R^2+R_{abcd}R^{abcd}-4R_{cd}R^{cd}\) must appear in lower energy limit of the heterotic superstring \(E_{8}\times E_{8}\). Hence, second order Lovelock gravity, or Einstein–Gauss–Bonnet (EGB) gravity, appears in the lower energy limit of string theory. It is for this reason, among others, that the EGB corrected postulate is a physically important modified gravity theory to study.

In the EGB theory, the analogues of the Schwarzschild and Reissner-Nordström solutions in higher dimensions were found and analysed in [5,6,7] and a thorough study of the radiating versions of these radiating solutions can be found in [8,9,10]. It was shown that the behaviour of these solutions was similar to the general relativistic Vaidya solution counterparts. This notion, however, is not the case when analysing the gravitational collapse of null radiating matter. The collapse dynamics of the Boulware–Deser solution, whether charged or neutral, was studied in detail by [10,11,12,13,14]. It was shown that for neutral matter in five dimensions, the minimum dimension of EGB gravity, collapse ceases with the formation of an initially naked and weaker conical singularity, before eventually succumbing to an event horizon at a later time depending on the Gauss–Bonnet coupling constant \(\alpha \). This is a behaviour unique only to the five dimensional case. With an increase in spatial dimension, this central singularity is no longer necessarily nude initially, nor is it conical.Footnote 1 The situation with charge is, again, very different. The end state of gravitational collapse for charged null radiation is a singularity which acts as a branch separating the physical spacetime from a complex metric [10]. This singularity is covered by two horizons, a Cauchy (inner) horizon and the outer event horizon. Remarkably, unlike the neutral scenario, collapse proceeds in a similar fashion for all dimensions \(N\ge 5\). The minimum dimensional case is no different to higher dimensions. Both charged and uncharged collapse in EGB gravity differ in a significant manner to the limiting case of Einstein, i.e. charged or neutral Vaidya collapse [15,16,17,18,19,20,21].

Another aspect of collapse to consider is the nature of singularity formation. It is well known that the existence of trapped surfaces as well as the preservation of causality are two circumstances which, along with the theorems of singularity formation, guarantee spacetime singularities post collapse [22, 23]. The nature of these singularities, however, are not accounted for in the above-mentioned theorems. The cosmic censorship conjecture (CCC), divided into both the weak (WCCC) and strong (SCCC) categories, was founded by Penrose [24] to prevent naked singularities from forming. The WCCC states that for any initial generic data, a complete future null infinity is held by the maximal Cauchy development. The SCCC states that for any initial generic data which is asymptotically flat or compact, the maximal Cauchy development is inextendible, locally, as a regular Lorentzian manifold, i.e. singularities are not timelike, but generically null or spacelike.Footnote 2 As it stands, there is no proof of the conjecture in the literature. Moreover, there exist several treatments presenting different physical models that oppose the CCC, see for example [19,20,21, 25,26,27,28,29,30,31]. A comprehensive reviewFootnote 3 of spacetime singularities and the various consequences with regards to geodesic incompleteness/completeness and cosmic censorship can be found in a recent expository article by Landsman [32].

In any physical theory, including gravity and its various modifications (which preserve energy conservation), the notion of dimension is a crucial one. The dimension of spacetime indeed affects its own geometry and due to the invariance properties of general relativity and, for this article, Lovelock gravity, the implication is that the underlying physics will also be affected; this idea is embedded in the field equations. The classical spacetimes of general relativity were studied in higher dimensions by [33,34,35,36]; the dimension affects not only the form of the metric functions, but the resulting field equations. The stability of compact astrophysical objects is also affected by the spacetime dimension, for example see [37,38,39]. With regards to higher dimensional radiating stars, the Santos [40] matching conditions were extended to arbitrary dimensions by [41,42,43] where it was shown that the presence of these higher dimensions drastically alters the gravitational dynamics of these objects as well as their evolution. The notion of positive energy is also a fundamental one in classical field theories of gravity and the energy conditions generalise this idea. These conditions were thoroughly studied in the context higher dimensions by [44, 45]. The energy conditions turn out to have a different analytical structure in higher dimensions which is not seen in the conventional four dimensional spacetime. This becomes very important not only in general relativity, but specifically higher dimensional modified gravity theories where these effects will then become obviously apparent. In conventional Einstein gravity, it has been shown that an increase in spacetime dimension may prevent naked singularity formation as demonstrated in [20]. Various families of mass functions under certain conditions yielded collapse scenarios where horizon formation did indeed take place and a black hole formed; this was not prevalent in four dimensions. It must be emphasised that increasing the spacetime dimension need not prevent naked singularities. Some treatments of naked singularities in higher dimensions were analysed by [46,47,48], and this will be the basis of this paper.

In this article we study the full gravitational collapse of a higher dimensional geometry in EGB gravity in the presence of an electromagnetic field. We discuss branch singularity formation in neutral and charged collapse, and the physical constraints of their existence. It turns out the branch singularities are inherent in Lovelock gravity for all orders equal to and above two. We then consider the nature of singularity formation for the higher dimensional charged Boulware–Deser solution. We will prove an existence result; for a particular choice of the mass function and charge benefaction, a naked singularity is inevitable in Einstein-Gauss–Bonnet-Maxwell (EGBM) gravity for all arbitrary higher dimensions. This will extend the results obtained in [14]. The effects of both the electric charge and the dimension of spacetime prove crucial in this analysis.

2 EGBM gravity in higher dimensions

In this treatment we will assume a geometry which is spherically symmetric and that the Lorentzian signature of spacetime is \((-,+,+,\ldots ,+)\). In higher dimensions, Einstein’s coupling constant and the surface area of the unit \((N-2)\)-sphere are written in terms of the gamma function respectively as

$$\begin{aligned} \kappa _{N}= & {} \frac{2(N-2)\pi ^{\frac{N-1}{2}}}{(N-3)\Gamma \left( \frac{N-1}{2}\right) }, \end{aligned}$$
(2a)
$$\begin{aligned} \mathcal {A}_{N-2}= & {} \frac{2\pi ^{\frac{N-1}{2}}}{\Gamma \left( \frac{N-1}{2}\right) }. \end{aligned}$$
(2b)

The values of these quantities for various dimensions are presented in Table  1. In fact, from (2) it can be observed that Einstein’s coupling constant and the surface area are related by

$$\begin{aligned} \kappa _{N}=\left( \frac{N-2}{N-3}\right) \mathcal {A}_{N-2}. \end{aligned}$$

This is to say that the value of Einstein’s coupling constant \(\kappa _{N}\), as it appears in the field equations, is affected not only by the form of the energy momentum tensor but by the geometry of the \((N-2)\)-sphere. The Gauss–Bonnet action can be obtained from (1) and is written in arbitrary dimensions as

$$\begin{aligned} S=\int d^{N}x\sqrt{-g}(\alpha _{0}+\alpha _{1}\mathcal {R}+\alpha _{2}\mathcal {R}^2)+S_{\small {\text{ matter }}}, \end{aligned}$$
(3)

where \(\alpha _{0}\) is the cosmological constant, \(\alpha _{1}\) (equal to unity) is the constant attached to the action (\(\mathcal {R}=R\)) of Einstein gravity, and \(\alpha _{2}=\alpha >0\) is the EGB coupling constant. The EGB Lagrangian (or second order Lovelock term) is given by

$$\begin{aligned} \mathcal {R}^2=L_{GB}=R^2+R_{abcd}R^{abcd}-4R_{cd}R^{cd}, \end{aligned}$$
(4)

which is in terms of the curvature tensors of Riemann and Ricci, as well as the Ricci scalar. In four dimensions this term (4) is merely a quadratic surface term. When \(N<4\), by the Chern–Gauss–Bonnet theorem [49, 50], the quantity (4) identically vanishes. We have that is the action for the matter content.

Table 1 Gravitational constant and unit surface area values
Full size table

The EGBM field equations can be obtained by use of the variational principle on (3) and are written as

$$\begin{aligned} G_{ab}-\frac{1}{2}\alpha H_{ab}= & {} \kappa _{N}(T_{ab}+E_{ab}), \end{aligned}$$
(5a)
$$\begin{aligned} F_{[ab;c]}= & {} 0, \end{aligned}$$
(5b)
$$\begin{aligned} F^{ab}{}_{;b}= & {} \mathcal {A}_{N-2}J^a. \end{aligned}$$
(5c)

The tensor \(G_{ab}\) is that of Einstein, \(T_{ab}\) is the energy momentum tensor and \(E_{ab}\) is the electromagnetic energy tensor, defined in general as

$$\begin{aligned} E_{ab}=\frac{1}{\mathcal {A}_{N-2}}\left( F_{a}{}^{c}F_{bc}-\frac{1}{4}F^{cd}F_{cd}g_{ab}\right) , \end{aligned}$$
(6)

which is in terms of the Faraday tensor \(F_{ab}=\Phi _{b;a}-\Phi _{a;b}\), the N-dimensional electric gauge potential \(\Phi _{a}\) and the surface area \(\mathcal {A}_{N-2}\) of the unit \((N-2)\)-sphere.Footnote 4 We have that \(J^a\) is the current. The new higher order curvature contribution in the form of the Gauss–Bonnet tensor \(H_{ab}\) is written as

$$\begin{aligned} H_{ab}= & {} g_{ab}L_{GB}-4RR_{ab}+8R_{ac}R^c{}_{{}b}+8R_{acbd}R^{cd}-4R_{acde}R_{b}{}^{{}cde}. \end{aligned}$$
(7)

We now make the following points:

  • The critical dimensions of EGB gravity are \(N=5\) and \(N>5\).

  • The Gauss–Bonnet tensor has zero divergence, i.e. \(H^{ab}{}_{;b}=0\). This is such that \(\left( G^{ab}-\frac{1}{2}\alpha H^{ab}\right) {}_{;b}=0=T^{ab}{}_{;b}\).

  • If \(N<5\), the Lovelock tensor \(H_{ab}=0\) will vanish identically; general relativity is attained in four dimensions.

  • When \(\alpha \rightarrow 0\), general relativity will be regained in N dimensions.

It is also interesting to note that via a complete gauge invariance by Noether’s theorem, linearised EGB gravity can be shown to be connected to classical electrodynamics [51].

3 Boulware–Deser–Wiltshire solution

The N-dimensional generalised Boulware–Deser solution [5] is given by

$$\begin{aligned} ds^2=-f(v,r)dv^2+2dvdr+r^2d\Omega ^2_{N-2}, \end{aligned}$$
(8)

which is written in terms of ingoing Eddington-Finkelstein coordinates \((v,r,\theta _{1},\ldots ,\theta _{N-2})\). The metric for the unit \((N-2)\)-sphere is of the form

$$\begin{aligned} d\Omega _{N-2}^2=\sum _{i=1}^{N-2}\left( \left[ \prod _{j=1}^{i-1}\sin ^2(\theta _{j})\right] (d\theta _{i})^2\right) , \end{aligned}$$

which accounts for the spherical symmetry. The function is given by

$$\begin{aligned} f(v,r)=1+\frac{r^2}{2{\hat{\alpha }}}\left( 1-\sqrt{1+\frac{4{\hat{\alpha }}}{N-3}\left( \frac{2M(v,r)}{r^{N-1}}\right) }\right) , \end{aligned}$$
(9)

which contains the generalised mass function M(v, r) [8] and where we have set \({\hat{\alpha }}=\alpha (N-3)(N-4)\) for brevity. The energy momentum tensor for a two-component fluid distribution of type II is given by

$$\begin{aligned} T_{ab}=\mu l_{a}l_{b}+(\rho +P)(l_{a}n_{b}+l_{b}n_{a})+Pg_{ab}, \end{aligned}$$
(10)

which is a combination of a null dust with energy density \(\mu \) which moves along the null hypersurfaces \(v=\text{ const. }\) and a null string fluid with energy density and pressure \(\rho \) and P, respectively which moves along trajectories which are timelike in nature. The null vectors take the forms

$$\begin{aligned} l_{a}=\delta ^{0}{}_{a},\hspace{0.5cm} n_{a}=\frac{1}{2}f(v,r)\delta ^{0}{}_{a}+\delta ^{1}{}_{a}, \end{aligned}$$
(11)

with the restrictions \(l_{c}l^c=n_{c}n^c=0,l_{c}n^c=-1\). The higher dimensional generalised EGB field equations are then

$$\begin{aligned} \kappa _{N}\mu= & {} \frac{(N-2)M_{v}}{(N-3)r^{N-2}}, \end{aligned}$$
(12a)
$$\begin{aligned} \kappa _{N}\rho= & {} \frac{(N-2)M_{r}}{(N-3)r^{N-2}}, \end{aligned}$$
(12b)
$$\begin{aligned} \kappa _{N}P= & {} -\frac{M_{rr}}{(N-3)r^{N-3}}, \end{aligned}$$
(12c)

after lengthy calculationsFootnote 5 and where we have that

$$\begin{aligned} M_{v}=\frac{\partial M}{\partial v},\hspace{0.5cm}M_{r}=\frac{\partial M}{\partial r},\hspace{0.5cm}M_{rr}=\frac{\partial ^2M}{\partial r^2}. \end{aligned}$$

In five dimensions, the above system reduces to that studied in [10, 14]. We now make the selection for the generalised mass function

$$\begin{aligned} M(v,r)= & {} M(v)-\frac{\kappa _{N}Q(v)^2}{2(N-2)\mathcal {A}_{N-2}r^{N-3}}\nonumber \\= & {} M(v)-\frac{Q(v)^2}{2(N-3)r^{N-3}}, \end{aligned}$$
(13)

where we have used the system (2). The electromagnetic energy contribution (6) is then engrained into this above selection (13) for the mass. The tensor \(F_{ab}\) is analogous to the result in [52] and is given by,

$$\begin{aligned} F_{ab}=\frac{Q(v)}{r^{N-2}}(\delta ^{0}{}_{a}\delta ^{1}{}_{b}-\delta ^{1}{}_{a}\delta ^{0}{}_{b}), \end{aligned}$$
(14)

which depends on dimension. The function \(Q=Q(v)\) is the charge contribution for EGBM gravity. The function (9) along with the selection (13) then gives the higher dimensional charged radiating solution

$$\begin{aligned} ds^2= & {} -f(v,r)dv^2+2dvdr+r^2d\Omega ^2_{N-2}, \end{aligned}$$
(15a)
$$\begin{aligned} f(v,r)= & {} 1+\frac{r^2}{2{\hat{\alpha }}}\left( 1-\sqrt{1+\frac{4{\hat{\alpha }}}{N-3}\left[ \frac{2M(v)}{r^{N-1}}-\frac{Q(v)^2}{(N-3)r^{2N-4}}\right] }\right) . \end{aligned}$$
(15b)

The vacuum form of the above solution was found by Wiltshire [6, 7]. The above system (15) reduces to the higher dimensional charged Vaidya (or Vaidya-Bonner) solution [53, 54]

$$\begin{aligned} ds^2=-\left( 1-\frac{2M(v)}{(N-3)r^{N-3}}+\frac{Q(v)^2}{(N-3)^2r^{2N-6}}\right) dv^2+2dvdr+r^2d\Omega ^2_{N-2}, \qquad \end{aligned}$$
(16)

in the general relativity limit. Using the system (12) along with (13) we can write the EGBM field equations as

$$\begin{aligned} \kappa _{N}\mu= & {} \frac{N-2}{N-3}\left( \frac{M_{v}}{r^{N-2}}-\frac{QQ_{v}}{(N-3)r^{2N-5}}\right) , \end{aligned}$$
(17a)
$$\begin{aligned} \kappa _{N}\rho= & {} \kappa _{N}P=\frac{(N-2)Q(v)^2}{2(N-3)r^{2N-4}}. \end{aligned}$$
(17b)

In the four dimensional general relativity limit, these equations reduce to those found in [52]. The null, weak, strong and dominant energy conditions [44, 45, 55] for a null and string fluid combination imply that the energy density \(\mu \ge 0\) and so the following two conditions must hold:

$$\begin{aligned} M_{v}\ge & {} \frac{QQ_{v}}{(N-3)r^{N-3}}, \end{aligned}$$
(18a)
$$\begin{aligned} Q(v)\ge & {} 0. \end{aligned}$$
(18b)

It can be seen that the condition (18a) is undefined at \(r=0\) and hence is violated in this region. This is due to the singular nature of the metric function (15b) as well as an unavoidable branch singularity in the spacetime manifold, which we discuss in the following section. We can also see from equation (18a) that there exists a critical radius \(r_{c}>0\) for which \(\mu \ge 0\). This is given by

$$\begin{aligned} r_{c}=\frac{QQ_{v}}{(N-3)M_{v}}. \end{aligned}$$
(19)

When \(r<r_{c}\) we have that \(\mu <0\) and the energy conditions are violated. For the case of a collapsing distribution, the N-momenta of particles vanish on the hypersurface \(r=r_{c}\) due to the repulsive Lorentz force as indicated in four dimensions in [52, 56]. Therefore the region \(r<r_{c}\) is realistically unattainable to any particles, resulting in the preservation of the energy conditions.

4 Branch singularities in EGB gravity

We begin by noting that branch singularities are generic for neutral and charged collapse in EGB gravity [57, 58]. A branch singularity can be described as an interface separating a physical spacetime region from a complex (or non-real) region defined by a particular metric function in the line element. For example, metric functions containing surds yield such scenarios for negative values under the radicals. Branch singularities of this kind are inherent in all orders (above one) of Lovelock gravity; this notion can be seen in the EGB solutions [10, 14] as well as the radiating solution of third order Lovelock gravity found by [59]. For our purposes we will consider both the neutral and charged EGB cases separately.

4.1 Uncharged metric

If the charge \(Q(v)=0\) in (15) we have that the metric function is

$$\begin{aligned} f(v,r)=1+\frac{r^2}{2{\hat{\alpha }}}\left( 1-\sqrt{1+\frac{8{\hat{\alpha }}M(v)}{(N-3)r^{N-1}}}\right) . \end{aligned}$$
(20)

The dynamics of the uncharged collapsing solution were analysed in detail by [11,12,13]. We note that the above metric function is regular at \(r=0\) when the dimension of spacetime is \(N=5\). Due to this and the fact that the Kretschmann invariant diverges (in fact \(K=R_{abcd}R^{abcd}\sim r^{-16}\)), the spacetime has a singularity which is weaker and conical in nature. In principle, spacetime can be extended through it. The spacetime manifold with metric (20) is in a sense quasi-regular when \(N=5\). This is, however, only the case in five dimensions. We illustrate this graphically in Fig. 1 where we have used \(\alpha =1/2\) and a positive value for the mass function.

Fig. 1
figure 1

Plot indicating the behaviour of the uncharged metric function (20) for various dimensions. We note that when \(N=5\), the function is well behaved at \(r=0\), however for all \(N>5\), the metric functions are singular

Full size image

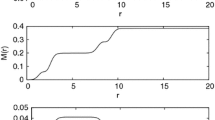
If we consider (20), the mass function at the horizon \(f(v,r)=0,r=r_{H}\) can be calculated as

$$\begin{aligned} M_{H}(r_{H}):=\frac{N-3}{2}r_{H}^{N-5}(r_{H}^2+{\hat{\alpha }}). \end{aligned}$$
(21)

In five dimensions this reduces to \(M_{H}(r_{H})=r_{H}^2+2\alpha \) (since \({\hat{\alpha }}=2\alpha \) when \(N=5\)), therefore there is a mass gap; the mass function does not vanish for a radius of zero and is instead a function of the EGB coupling constant, i.e. \(M_{H}(0)=2\alpha \). So the conical singularity at the centre of the collapsing distribution remains naked post collapse for a time depending on \(\alpha \); the coupling constant \(\alpha \) halts horizon formation [12]. This situation is only prevalent in five dimensions. For all \(N>5\), we have that \(M_{H}(0)=0\) identically at the singularity \(r=v=0\), and the Kretschmann invariant \(K\sim r^{-4(N-1)}\). We note now that in expression (20), a zero within the square root also implies a singularity; this is a branch singularity. Solving for the mass function in this scenario yields

$$\begin{aligned} M_{b}(r_{b}):=-\frac{(N-3)}{8{\hat{\alpha }}}r_{b}^{N-1}, \end{aligned}$$
(22)

where the subscript b is merely a label indicating the value at the branch. We observe that in this situation, i.e. neutral collapse, a branch singularity is only possible for a negative mass. The domain of r is \(0<r_{b}<r<\infty \) if we have that \(r_{b}\) is positive. We illustrate these notions graphically in Fig 2 and  3.

Fig. 2
figure 2

Plot indicating the mass functions \(M=M_{H}\) and \(M=M_{b}\) in five dimensions, with \(Q(v)=0\). It can be seen that \(M=M_{H}\) does not vanish when \(r=0\). A branch singularity appears for a negative mass \(M_{b}\) and so does not hold on physical grounds

Full size image
Fig. 3
figure 3

Plot indicating the mass functions \(M=M_{H}\) and \(M=M_{b}\) for dimensions \(N=6,7\). We note that \(M=M_{H}=0\), when \(r=0\). We again note that branch singularities appear for a negative mass \(M_{b}\) for all \(N>5\) and so are unphysical. This behaviour is similar for all \(N>5\)

Full size image
Fig. 4
figure 4

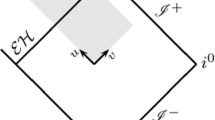
Spacetime diagram demonstrating possible uncharged null radiation collapse in five dimensions, for a positive mass. There exists a weak and initially naked conical singularity which forms in the region \(0\le v\le V_{0}\), with families of trajectories \(\gamma _{1}\) and \(\gamma _{2}\) escaping to infinity in the future. The EGB coupling constant \(\alpha \) delays the formation of the apparent horizon which only forms in the region \(V_{0}\le v\le V_{1}\). Nonspacelike trajectories \(\gamma _{3}\) emitted after the formation of the horizon can no longer escape now, falling into the singularity. Null radiation collapses into the singularity and once this process has terminated, a quasi-regular black hole results containing the conical singularity, covered by an event horizon separating it from the external universe

Full size image
Fig. 5
figure 5

Spacetime diagram showing possible neutral null radiation collapse in higher dimensions, for a positive mass function. The EGB coupling constant \(\alpha \) no longer hinders the formation of the apparent horizon which forms immediately in the region \(0\le v\le V_{0}\). Nonspacelike families of trajectories \(\gamma _{1}\) and \(\gamma _{2}\) emitted after the formation of the horizon cascade into the singularity. A higher dimensional null dust collapses into the curvature singularity and a black hole results once this process has ceased, with an event horizon covering the central singularity

Full size image

We have again used the value of \(\alpha =1/2\). In Fig. 2 we highlight the mass functions at the horizon and branch respectively for \(N=5\). We note that the \(M_{H}(v)\) does not vanish at \(v=r=0\) by (21). This is due to the fact that when \(N=5\), the metric function (20) is regular at \(r=0\) and the mass function \(M=M_{H}\) depends on \(\alpha \). A branch singularity appears when \(M(v)<0\) by equation (22) and so has no effect on the \(M(v)>0\) case. The situation is different for \(N>5\) as shown in Fig. 3, where we have illustrated the six and seven dimensional cases. The metric functions (20) are no longer regular in the vicinity of the singularity \(r=0\) in higher dimensions and we have that \(M_{r=0}=0\) as emphasised earlier. Again, we observe that a branch singularity appears for \(M(v)<0\) but it has no affect on the positive M(v) situations. In Fig. 4 a null radiating distribution of matter cascades into a five dimensional quasi-regular black hole of growing positive mass. Within the region \(0\le v\le V_{0}\) there exists a conical singularity which is naked due to the EGB coupling constant \(\alpha \) delaying the formation of the apparent horizon. The horizon eventually forms at \(v=V_{0}\) enclosing the trapped surfaces into a compact region \(V_{0}\le v\le V_{1}\). At \(v=V_{1}\) the apparent and event horizons smoothly match as a single trapping horizon, separating the five dimensional Boulware–Deser vacuum from the trapped surfaces and singularity. Figure 5 depicts radiating null matter falling into a higher dimensional singular black hole. The formation of the apparent horizon takes place at \(v=r=0\) containing all the trapped surfaces in a highly compact region \(0\le v\le V_{0}\). This is unlike the situation in five dimensions, and will be the case for all \(N>5\) [13]. The apparent and event horizons match smoothly at \(v=V_{0}\) to form one single trapping horizon separating the higher dimensional Boulware–Deser vacuum exterior from the trapped surfaces. Beneath this horizon of the black hole lies the central curvature singularity.

4.2 Charged metric

We will now look at the situation of the electrically charged solution. We recall from (15) that the higher dimensional metric function is of the form

$$\begin{aligned} f(v,r)=1+\frac{r^2}{2{\hat{\alpha }}}\left( 1-\sqrt{1+\frac{4{\hat{\alpha }}}{N-3}\left[ \frac{2M(v)}{r^{N-1}}-\frac{Q(v)^2}{(N-3)r^{2N-4}}\right] }\right) . \end{aligned}$$
(23)

The collapse dynamics of the above metric for \(N=5\) were studied in [12, 14]. Unlike the uncharged scenario, the metric functions are singular for all dimensions \(N\ge 5\), resulting from the additional charge term in (23). Hence the behaviour of this function is similar for all dimensions in EGB gravity; a fundamental difference to the uncharged case. We present this graphically in Fig. 6 for the same value of \(\alpha \).

Fig. 6
figure 6

The behaviour of the charged metric function (23) for dimensions \(N\ge 5\). We can see that for all \(N\ge 5\), the metric functions are singular unlike the uncharged case in Fig. 1

Full size image
Fig. 7
figure 7

Plot showcasing \(M=M_{H}\) and \(M=M_{b}\) for the charged metric function (23) in five dimensions. It can be seen that both \(M_{H}\) and \(M_{b}\) coincide for values of r nearing the branch singularity \(r=r_{b}>0\), showing that this branch singularity is the curvature singularity of the spacetime. For all values below \(M_{b}\), the spacetime is complex

Full size image
Fig. 8
figure 8

Plot showing \(M=M_{H}\) and \(M=M_{b}\) for the charged metric function (23) when \(N=6,7\). It can be seen that the behaviour is similar to the \(N=5\) case, highlighting that charged collapse is similar for all EGB dimensions \(N\ge 5\). Again, for all values below \(M_{b}\), the spacetime is complex

Full size image

Further to this notion, there is in fact no spacetime at \(r=0\). The electric charge contribution Q(v) fundamentally changes the singularity type manifesting once collapse has terminated. If we consider the term \(\frac{Q(v)^2}{(N-3)r^{2N-4}}\) in (23), we note that it has a minus sign, indicating that there exists a maximum charge for which the metric function will remain real. There is a fundamental branch singularity, which is independent of the sign for the mass function, which separates the real and physical spacetime from a complex metric. This branch singularity is indeed the curvature singularity of the spacetime. If we consider the metric function (23), the horizon radius, i.e. \(f(v,r)=0\) yields

$$\begin{aligned} M_{H}(r_{H}):=\frac{N-3}{2}r_{H}^{N-5}(r_{H}^2+{\hat{\alpha }})+\frac{Q(v)^2}{2(N-3)r_{H}^{N-3}}, \end{aligned}$$
(24)

where we note the presence of the charge Q(v). When \(Q(v)=0\) we regain (21) from earlier. We can clearly see that this function is undefined when \(r=0\) for the above-mentioned reasons, and that the situation remains the same for all \(N\ge 5\), unlike in the neutral scenario. If we consider the square root in the charged metric function (23), equating this to zero yields

$$\begin{aligned} M_{b}(r_{b}):=-\frac{N-3}{8{\hat{\alpha }}}r_{b}^{N-1}+\frac{Q(v)^2}{2(N-3)r_{b}^{N-3}}. \end{aligned}$$
(25)

We observe here that the mass function can be either positive or negative, so regardless of the physical situation, this branch singularity \(r=r_{b}\) is inherent in the collapse; it exists for all M. We illustrate, for the same values of the parameters, expressions (24) and (25) graphically in Figs 7 and  8 for different dimensions. The domain of r is \(0<r_{b}<r_{1}\le r_{0}<\infty \). There is no spacetime in the region \(0<r_{b}\). The inner and outer horizons \(r_{1}\) and \(r_{0}\) form at \(r_{b}>0,v=0\). These notions as well as spacetime diagrams depicting charged radiation collapse were discussed and provided in [10]. Consider the square root term in (23). If we have

$$\begin{aligned} \sqrt{1+\frac{4{\hat{\alpha }}}{N-3}\left[ \frac{2M(v)}{r_{b}^{N-1}}-\frac{Q(v)^2}{(N-3)r_{b}^{2N-4}}\right] }\ge 0, \end{aligned}$$
(26)

we can also write the following in terms of \(r_{b}\):

$$\begin{aligned} r_{b}^{2N-4}+8\alpha (N-4)M(v)r_{b}^{N-3}-4\alpha \left( \frac{N-4}{N-3}\right) Q(v)^2\ge 0, \end{aligned}$$
(27)

which is analogous to (25) and where we have utilised the fact that \({\hat{\alpha }}=\alpha (N-3)(N-4)\). This inequality admits \((2N-4)\) solutions, two of which are real and one of which is positive; the rest are complex. If \(Q(v)\ne 0\), there exists a branch singularity \(r=r_{b}(v)\) which then separates the physical spacetime metric from the complex region. The above equation (27) will become important for the analysis in the next section.

5 Higher dimensional gravitational collapse model

In this section we analyse the higher dimensional and charged gravitational collapse of a shell of null radiation (15). If we consider an asymptotically flat and empty N-dimensional EGB universe at infinitely large distances, a thick radiation shell of electrically charged matter collapses at the centre of symmetry.

5.1 Euler–Lagrange equations

Suppose that the tangent to nonspacelike geodesics is given by \(K^a\), where \(K^a=\frac{dx^a}{dk}\). We then have that for the affine parameter k that

$$\begin{aligned} K^a{}_{;b}K^b= & {} 0, \end{aligned}$$
(28a)
$$\begin{aligned} g_{ab}K^aK^b= & {} \mathcal {B}, \end{aligned}$$
(28b)

where \(\mathcal {B}\) is a constant which describes classes of geodesics. If \(\mathcal {B}\) is negative, this implies timelike geodesics and if \(\mathcal {B}\) vanishes, we then have null geodesics. The derivatives \(\frac{dK^v}{dk}\) and \(\frac{dK^r}{dk}\) can be calculated by use of the Euler–Lagrange equations

$$\begin{aligned} \frac{\partial L}{\partial x^a}-\frac{d}{dk}\left( \frac{\partial L}{\partial {\dot{x}}^a}\right) =0. \end{aligned}$$
(29)

The Lagrangian \(L=\frac{1}{2}g_{ab}{\dot{x}}^a{\dot{x}}^b\) for the higher dimensional line element (15) is given by

$$\begin{aligned} L=-\frac{1}{2}f(v,r){\dot{v}}^2+{\dot{v}}{\dot{r}}+\frac{1}{2}r^2\sum _{i=1}^{N-2}\left( \left[ \prod _{j=1}^{i-1}\sin ^2(\theta _{j})\right] {\dot{\theta }}_{i}^2\right) , \end{aligned}$$
(30)

where f(v, r) is the metric function (23). Therefore the relevant equations are calculated as

v-component:

$$\begin{aligned} \frac{dK^v}{dk}+\frac{1}{2}(K^v)^2f_{v}-r\sum _{i=1}^{N-2}\left( \left[ \prod _{j=1}^{i-1}\sin ^2(\theta _{j})\right] \left( K^{\theta _{i}}\right) ^2\right) =0. \end{aligned}$$
(31)

r-component:

$$\begin{aligned}&\frac{dK^r}{dk}+\left[ \frac{1}{2}f(v,r)(K^v)^2-K^vK^r\right] f_{r}+(K^v)^2f_{v}\nonumber \\&\quad -rf(v,r)\sum \limits _{i=1}^{N-2}\left( \left[ \prod \limits _{j=1}^{i-1}\sin ^2(\theta _{j})\right] \left( K^{\theta _{i}}\right) ^2\right) =0. \end{aligned}$$
(32)

\(\theta _{i}\)-components:

$$\begin{aligned}&\sum \limits _{i=1}^{N-2}\left( \left[ \prod \limits _{j=1}^{i-1}\sin ^2(\theta _{j})\right] \frac{dK^{\theta _{i}}}{dk}\right) +2rK^r\sum \limits _{i=1}^{N-2}\left( \left[ \prod \limits _{j=1}^{i-1}\sin ^2(\theta _{j})\right] \left( K^{\theta _{i}}\right) \right) \nonumber \\&\quad +r^2\sum \limits _{i=1}^{N-2}\left( \left[ \prod _{j=1}^{i-1}\sin (\theta _{j})\cos (\theta _{j})\right] \left( K^{\theta _{i}}\right) ^2\right) =0. \end{aligned}$$
(33)

Analogous to [26], we can define

$$\begin{aligned} K^v=\frac{P}{r}, \end{aligned}$$
(34)

for some arbitrary function P(v, r). Making use of (28b) as well as equations (31) and (32), a tedious calculation then gives

$$\begin{aligned} K^v= & {} \frac{dv}{dk}=\frac{P}{r}, \end{aligned}$$
(35a)
$$\begin{aligned} K^r= & {} \frac{dr}{dk}=f(v,r)\frac{P}{2r}+\frac{\mathcal {B}r}{2P}-\frac{l^2}{2rP}, \end{aligned}$$
(35b)

where l is referred to as the impact parameter.

6 Conditions for a locally naked singularity

We reiterate that for the charged solution (15) the branch singularity \(r=r_{b}\) is the curvature singularity of the spacetime; there is no metric spacetime in the vicinity \(0<r_{b}\). We will now determine whether the final fate of higher dimensional charged radiation collapse is a black hole or a naked singularity. It was shown by Brassel et al [14] that there indeed exists functional forms for the mass and electric charge, which guarantees naked singularity existence. The basis of this section is to reveal whether a similar notion is possible in higher dimensions. The motivation for this also lies in the fact that in dimensions \(N>5\) the geometry of the spacetime with metric (23) is wholly different. Given an electrically charged radiation shell of matter in higher dimensions with a mass which is large enough, this singularity branch forms at \(r_{b}=v=0\) and extends into the future. If future directed families of trajectories exist, reaching some observer at infinity in the higher dimensional spacetime, the branch singularity under question is then naked. If such families of trajectories do not exist, the result is a black hole covered by two horizons concealing the branch singularity inside [10].

6.1 Outgoing nonspacelike geodesics: existence

If we allow \(X_{0}\in (0,\infty )\) to be the tangent to the radial geodesic, id est the limiting value at \(r_{b}=v=0\) on any geodesic which is singular, this limiting value’s nature is written as

$$\begin{aligned} X_{0}=\lim _{r_{b}=v\rightarrow 0}X=\lim _{r_{b}=v\rightarrow 0}\frac{v}{r_{b}}. \end{aligned}$$
(36)

Making use of this above equation (36), a form for \(X_{0}\) can be calculated which will vividly describe null geodesic behaviour in the vicinity of the singularity \(r_{b}\). We recall expression (27) which is given by

$$\begin{aligned} r_{b}^{2N-4}+8\alpha (N-4)M(v)r_{b}^{N-3}-4\alpha \left( \frac{N-4}{N-3}\right) Q(v)^2\ge 0. \end{aligned}$$

Differentiating this expression and simplifying yields

$$\begin{aligned}&\frac{dr_{b}}{dv}+\left[ \frac{8\alpha M_{v}}{2N-4}\right] \frac{1}{r_{b}^{N-2}}+\left[ \frac{8\alpha (N-3)(N-4)M}{2N-4}\right] \frac{1}{r_{b}^{N-1}}\frac{dr_{b}}{dv}\nonumber \\&\quad -\left[ \frac{8\alpha (N-4)QQ_{v}}{(N-3)(2N-4)}\right] \frac{1}{r_{b}^{2N-5}}\ge 0. \end{aligned}$$
(37)

For the existence of a well defined tangent at the singularity \(r_{b}\), the mass and charge functions must take the forms

$$\begin{aligned} M(v)=\lambda v^{N-1},\hspace{0.6cm}Q(v)=\beta v^{N-2}, \end{aligned}$$
(38)

where the constants \(\lambda \) and \(\beta \) must be positive. We make these specific choicesFootnote 6 in order to employ (36) in equation (37). Expression (37) then becomes

$$\begin{aligned}{} & {} \frac{dr_{b}}{dv}+\frac{4\alpha \lambda (N-1)(N-4)}{N-2}\left( \frac{v}{r_{b}}\right) ^{N-2}+\left[ \frac{4\alpha \lambda (N-3)(N-4)}{N-2}\right] \left( \frac{v}{r_{b}}\right) ^{N-1}\frac{dr_{b}}{dv}\\{} & {} \quad -\frac{4\alpha \beta ^2(N-4)}{(N-3)}\left( \frac{v}{r_{b}}\right) ^{2N-5}\ge 0. \end{aligned}$$

The above expression then reduces to

$$\begin{aligned} X_{0}^{2N-4}-\frac{2(N-3)\lambda }{\beta ^2}X_{0}^{N-1}-\frac{N-3}{4(N-4)\alpha \beta ^2}\ge 0. \end{aligned}$$
(39)

We make note of the presence of the dimension N in the above expression. When \(N=5\), this reduces to the result obtained in [14]. In order to surmise the nature of the branch singularity, the expression (39) needs to be solved. The occurrence of a black hole or a naked singularity depends on the causal behaviour of the trapped surfaces which develop within the collapsing spacetime. The apparent horizon is the boundary of the region containing these trapped surfaces. Utilising the system (35), for the metric (23), the equation for null geodesics is

$$\begin{aligned} X_{N}= & {} \frac{K^v}{K^r}=\frac{dv}{dr}=\frac{2}{f(v,r)}. \end{aligned}$$
(40)

This is also known as the equation for the slope of the apparent horizon. This simplifies to the trivial result

$$\begin{aligned} X_{N}=2, \end{aligned}$$
(41)

in the vicinity of the region \(r_{b}=v=0\).

6.2 Sufficient conditions

We are now in a position to state the sufficient conditions which determine whether the branch singularity is naked locally for a higher dimensional and electrically charged collapsing Boulware–Deser spacetime.

Proposition 6.1

Consider an electrically charged Boulware–Deser spacetime of differentiability class \(C^2\) from a regular epoch, with mass and charge functions \(M(v)=\lambda v^{N-1}\) and \(Q(v)=\beta v^{N-2}\) respectively. If the following conditions hold at the branch singularity:

  1. 1.

    The derivatives \(\frac{\partial M}{\partial v}\) and \(\frac{\partial Q}{\partial v}\) exist and are continuous at the singularity,

  2. 2.

    There must exist at least one positive and real root \(X_{0}\) to the expression

    $$\begin{aligned} X_{0}^{2N-4}-\frac{2(N-3)\lambda }{\beta ^2}X_{0}^{N-1}-\frac{N-3}{4(N-4)\alpha \beta ^2}\ge 0, \end{aligned}$$
  3. 3.

    This positive and real root must be less than the slope

    $$\begin{aligned} X_{N}=2, \end{aligned}$$

then the singularity is locally naked and there exist outgoing \(C^1\) radial null geodesics escaping to infinity in the future.

7 Cosmic censorship violation

We now demonstrate that naked singularities are indeed possible for higher dimensional charged collapse. Consider the expression (39). It can be shown via mathematical induction that for positive values of \(\alpha \), \(\beta \) and \(\lambda \), this expression always admits two real roots and \((2N-6)\) complex roots. As it stands we cannot explicitly present all the roots without specifying the dimension N as well as the above-mentioned parameters \(\alpha \), \(\beta \) and \(\lambda \), due to the complicated nature of this polynomial. If we chooseFootnote 7\(\alpha =1/2\) and \(\beta =\lambda =2\) the expression (39) can be written as

$$\begin{aligned} X_{0}^{2N-4}-(N-3)X_{0}^{N-1}-\frac{N-3}{8(N-4)}\ge 0. \end{aligned}$$
(42)

For a specified N, if the positive roots to this equation are less than \(X_{N}=2\), the branch singularity \(r=r_{b}\) will be naked.

Table 2 Equations for tangents \(X_{0}\) to singularity curve and cosmic nudity for the parameters \(\alpha =1/2\) and \(\beta =\lambda =2\)
Full size table

In Table  2 we present the above equation for the parameters \(\alpha =1/2\) and \(\beta =\lambda =2\) for several dimensions. It can clearly be seen that the positive real roots are always less than \(X_{N}\), guaranteeing naked singularity formation. Therefore, Proposition 6.1 is always satisfied. We also notice that as the dimension increases, the value of \(X_{0}\) decreases, tending to unity. We can now state the following existence results.

Lemma 7.1

For the positive values of \(\alpha =1/2\), \(\beta =\lambda =2\), the real and positive root \(X_{0}\) of the expression (39) is always less than that of the null geodesic equation (41), i.e.

$$\begin{aligned} X_{0}<X_{N}=2,\hspace{0.6cm} \forall N\ge 5. \end{aligned}$$

This is to say that, for a positive and real \(C^2\) mass function \(M(v)=\lambda v^{N-1}\) and electric charge \(Q(v)=\beta v^{N-2}\), naked singularity formation is inevitable.

Lemma 7.2

If \(\alpha =1/2\) and \(\beta =\lambda =2\), the positive and real root \(X_{0}\) tends to one as the dimension becomes infinitely and countably large, i.e.

$$\begin{aligned} \lim _{N\rightarrow \infty }X_{0}=1,\hspace{0.6cm}\forall N\ge 5. \end{aligned}$$

The main result of this paper can now be stated in full.

Theorem 7.1

Consider a gravitationally collapsing and electrically charged Boulware–Deser spacetime in N dimensions given by (15) from a regular epoch. If there exists a positive and real \(C^2\) mass function \(M(v)=\lambda v^{N-1}\) and charge contribution \(Q(v)=\beta v^{N-2}\), satisfying the energy conditions in the entire spacetime, then for all \(\alpha =1/2\), \(\beta =\lambda =2\), the final outcome of collapse is a branch singularity which is locally naked for all time.

Fig. 9
figure 9

Spacetime diagram showcasing possible higher dimensional null radiation collapse in the presence of an electromagnetic field. There is a naked branch singularity \(r=r_{b}\) which begins to form at \(v=r_{b}(0)=0\) and then extends into the future separating the complex metric from the physical collapsing spacetime. An injected flow of charged and radiating null matter with \(M=M(v)\) and \(Q=Q(v)\), beginning with the first null ray at \(v=0\), is focused into the singularity of increasing mass. Families of geodesic \(C^1\) null trajectories are able to escape to infinity. Post collapse the naked branch singularity \(r_{b}\) is visible to external observers in the higher dimensional background

Full size image

Figure  9 depicts the gravitational collapse scenario for a charged radiation shell of matter, which begins from an initially flat space (that of Minkowski). The electric charge addition to the metric function (23) implies a splitting of the spacetime into two distinct regions, a complex and unphysical space and the real collapsing geometry. The branch singularity \(r=r_{b}\) acts as the boundary of this interface; there is no physical spacetime for \(0<r_{b}\). By Theorem  7.1 the naked singularity forms at \(v=r_{b}(0)=0\) and stretches into infinity. At some later time \(v=V_{0}\) the process of collapse will terminate and what is left is the naked singularity which will remain visible to all external observers residing in the charged background exterior spacetime.

8 Strength of the singularity

The strength of a curvature singularity is a measure of its destructive capacity. In essence, no object falling into a strong singularity can arrive at this point fully intact [60]; it is ripped apart by the strong gravitational effects in the region of the singularity and then crushed to a zero volume at the singularity itself [61]. One way to understand the strength of a singularity is by considering an affine parameter \({\hat{k}}\) which is null. We can calculate the singularity strength by considering null geodesics parametrised by \({\hat{k}}\), ending at the near central branch singularity \(r_{b}=v={\hat{k}}=0\). Following the approach of Tipler, Clarke and Królak [61,62,63], if the expression holds true

$$\begin{aligned} \lim _{{\hat{k}}\rightarrow 0}{\hat{k}}^2\eta =\lim _{{\hat{k}}\rightarrow 0}{\hat{k}}^2R_{ab}K^aK^b>0, \end{aligned}$$
(43)

where \(R_{ab}\) is the Ricci curvature tensor, then the singularity is strong. If the above condition does not hold, then we cannot say anything about singularity strength from this alone. In the EGB theory, five dimensional neutral collapse yields a conical singularity which is indeed weaker, for any mass, than what occurs in the \(N\ge 6\) cases [12]. However, whether such singularities for \(N\ge 6\) in EGB gravity are weaker/stronger than the general relativity counterparts, for other mass functions has not yet been analysed in detail; it is likely that this will need to be done on a case by case basis. For the charged solution (15) and the choices of the mass and charge functions (38), the scalar \(\eta =R_{ab}K^aK^b\) can be written as

$$\begin{aligned} \eta =\left( \frac{N-2}{3-N}\right) \left[ \frac{\left( \frac{N-2}{N-3}\right) \beta ^2\left( \frac{v}{r}\right) ^{2N-5}-(N-1)\lambda \left( \frac{v}{r}\right) ^{N-2}}{\sqrt{1+8(N-4)\alpha \lambda \left( \frac{v}{r}\right) ^{N-1}-\frac{4(N-4)}{N-3}\alpha \beta ^2\left( \frac{v}{r}\right) ^{2N-4}}}\right] \left( \frac{P}{r}\right) ^2,\nonumber \\ \end{aligned}$$
(44)

after a lengthy calculation. Therefore,

$$\begin{aligned} {\hat{k}}^2\eta =\left( \frac{N-2}{3-N}\right) \left[ \frac{\left( \frac{N-2}{N-3}\right) \beta ^2\left( \frac{v}{r}\right) ^{2N-5}-(N-1)\lambda \left( \frac{v}{r}\right) ^{N-2}}{\sqrt{1+8(N-4)\alpha \lambda \left( \frac{v}{r}\right) ^{N-1}-\frac{4(N-4)}{N-3}\alpha \beta ^2\left( \frac{v}{r}\right) ^{2N-4}}}\right] \left( \frac{P{\hat{k}}}{r}\right) ^2,\nonumber \\ \end{aligned}$$
(45)

and evaluating the limit as the null affine parameter \({\hat{k}}\rightarrow 0\) gives

$$\begin{aligned} \lim _{{\hat{k}}\rightarrow 0}{\hat{k}}^2\eta =\left( \frac{N-2}{3-N}\right) \left[ \frac{\left( \frac{N-2}{N-3}\right) \beta ^2X_{0}^{2N-3}-(N-1)\lambda X_{0}^{N}}{\sqrt{1+8(N-4)\alpha \lambda X_{0}^{N-1}-\frac{4(N-4)}{N-3}\alpha \beta ^2X_{0}^{2N-4}}}\right] ,\qquad \end{aligned}$$
(46)

which depends on the dimension N, the Gauss–Bonnet constant \(\alpha \), the real root \(X_{0}\) and the positive parameters \(\beta \) and \(\lambda \). Thus, we must have for a positive and real root \(X_{0}\) that the condition

$$\begin{aligned} \lim _{{\hat{k}}\rightarrow 0}{\hat{k}}^2\eta =\left( \frac{N-2}{3-N}\right) \left[ \frac{\left( \frac{N-2}{N-3}\right) \beta ^2X_{0}^{2N-3}-(N-1)\lambda X_{0}^{N}}{\sqrt{1+8(N-4)\alpha \lambda X_{0}^{N-1}-\frac{4(N-4)}{N-3}\alpha \beta ^2X_{0}^{2N-4}}}\right] >0,\nonumber \\ \end{aligned}$$
(47)

holds, in order for the singularity to be considered strong. In Table 3 we present the values for the condition (47) using the positive and real roots calculated in Table 2. It can clearly be seen that the values are all positive therefore indicating that the singularities are strong. In fact, as the dimension increases, the value of (47) increases as well indicating that strong singularities are guaranteed for all dimensions \(N\ge 5\) for our values of the parameters.

Table 3 Singularity strength
Full size table

We now consider the diffeomorphism (or curvature) invariants which are important quantities used to classify spacetime manifolds. For a metric of the form (15a) all diffeomorphism invariants are calculated for various increasing dimensions and then via use of mathematical induction on the dimension N giving

$$\begin{aligned} R_{abcd}R^{abcd}= & {} f_{rr}^2+\frac{2(N-2)}{r^2}f_{r}^2+\frac{2(N-2)(N-3)}{r^4}\bigg (f(v,r)-1\bigg )^2, \end{aligned}$$
(48a)
$$\begin{aligned} R_{ab}R^{ab}= & {} \frac{1}{2r^2}\bigg (rf_{rr}+(N-2)f_{r}\bigg )^2+\frac{N-2}{r^4}\bigg ((N-3)\left( 1-f(v,r)\right) -rf_{r}\bigg )^2,\nonumber \\ \end{aligned}$$
(48b)
$$\begin{aligned} C_{abcd}C^{abcd}= & {} \frac{N-3}{(N-1)r^4}\bigg (r^2f_{rr}-2(rf_{r}+f(v,r)-1)\bigg )^2, \end{aligned}$$
(48c)

where it can clearly be seen that these scalars will divergeFootnote 8 as \(r\rightarrow 0\) in (48). The rate of divergence can be determined when f(v, r) is known. Let’s now consider the Kretschmann scalar \(K=R_{abcd}R^{abcd}\) from (48a). If this diffeomorphism invariant diverges at the origin, the spacetime manifold intrinsically has a curvature singularity. Another means of understanding the strength of a singularity is by observing how K diverges. It is well known that in general relativity the gravitational collapse of the generalised Vaidya spacetime (and hence the pure and charged subcases) yields strong curvature singularities [19,20,21, 64]. For the higher dimensional pure Vaidya spacetime, the Kretschmann scalar diverges as \(K\sim r^{-2(N-1)}\) and for the charged Vaidya solution, \(K\sim r^{-4(N-2)}\). We will now demonstrate that in EGB gravity, the divergences of the scalar K are more profound, showcasing that these singularities are indeed strong, not only by condition (47), but in the purely geometric sense.

For the metric function (23), we have that K diverges as

$$\begin{aligned} K\sim \frac{1}{\alpha ^2r^{2N-4}\left( r^{2N-4}+8\alpha (N-4)M(v)r^{N-3}-4\alpha \left( \frac{N-4}{N-3}\right) Q(v)^2\right) ^3}, \end{aligned}$$
(49)

after some calculation. From the above expression we can determine that \(K\sim r^{-8(N-2)}\) which is a rapid divergence for any \(N\ge 5\), indicating the singularity is inherently destructive. This is consistent with the five dimensional case studied in [10]. For neutral collapse we have that \(K\sim r^{-4(N-1)}\). We also emphasise in the above expression, that the term in the bracket is identical to (27) further showing that the bracketed term is the branch singularity of the spacetime; the scalar K will diverge as this term vanishes. We note that if the energy conditions are satisfied, and a naked singularity forms as an end point of collapse, this naked singularity is always strong [19]. In Table  4 we present the divergence properties of the Kretschmann invariant for various dimensions in both the general relativity and EGB gravity cases. It can be seen that for all \(N\ge 5\), the divergences in the EGB cases are more profound than their general relativity counterparts. In the presence of an electromagnetic field, we note that in both cases, the divergences of K are more severe. We make the point that these more rapid divergences in EGB gravity do not imply that the singularities are necessarily stronger than those occurring in general relativity, we are merely remarking that the singularities appearing in EGB gravity are indeed strong, specifically for the charged scenario, in both the Tipler sense and the curvature invariance sense.

Table 4 Kretschmann scalar divergences for various dimensions in both general relativity (GR) and EGB gravity
Full size table

Figure  10 depicts the behaviour of the Kretschmann scalars for \(N=5,6\) in EGB gravity. We note that the divergences are more profound for the cases where \(Q\ne 0\) which is again due to the form of the metric function (23). We again mention that five dimensional EGB gravity is, remarkably, the only dimensional case where the uncharged metric functions are regular and so, along with the diverging K, the resulting singularity is conical in nature; spacetime can, in principle, be extended through it. For dimensions \(N\ge 6\), this is no longer the case; strong curvature singularities occur. Unlike the uncharged scenario, in the presence of the electromagnetic field, there is no difference between the \(N=5\) and \(N>5\) cases; collapse proceeds similarly for all \(N\ge 5\). This emphasises, again, that the effect of the electric charge and the Gauss–Bonnet corrections on gravitational collapse cannot be understated, in any dimension.

Fig. 10
figure 10

Log-log plot showing the behaviour of the Kretschmann invariants for neutral and charged matter in EGB gravity, in five and six dimensions. The charged cases (dashed lines) have a more severe divergence than their neutral counterparts. This behaviour is consistent for all \(N\ge 5\)

Full size image

9 Conclusion

In this paper we have analysed the gravitational contraction of a higher dimensional radiation shell of matter surrounded by an electromagnetic field in EGB gravity. The charged analogue of the Boulware–Deser metric is studied in higher dimensions and it is shown that the collapse dynamics are similar for all dimensions \(N\ge 5\), unlike in the neutral scenario where the \(N=5\) case yields significantly different physics to the higher dimensional cases, and is thus special. The notions of branch singularity formation were discussed in detail. In EGB gravity and more generally in higher order Lovelock gravity, branch singularities are generic. In our case, for neutral collapse the branch singularity only forms for a negative mass, and thus has no effect on the process. Collapse proceeds in the conventional sense yielding a singularity which is conical in nature, due to the regularity of the spacetime metric, coupled with a diverging Kretschmann invariant. The charged situation is different however; the branch singularity is unavoidable and is indeed the curvature singularity of the spacetime. The implication is that there exists a section of this spacetime which will be complex, separated from the real and physical spacetime, by this branch singularity \(r=r_{b}\); there is no real spacetime at \(r=0\). We then considered the nature of this branch singularity for the higher dimensional charged Boulware–Deser solution. We considered the sufficient conditions for locally naked singularity formation and have shown that for a particular choice of the mass and charge functions, a naked singularity is inevitable in EGBM gravity for all arbitrary higher dimensions; cosmic censorship is violated in EGBM gravity for all dimensions \(N\ge 5\). We also proved that the naked branch singularities are strong. The effects of the electric charge, the dimension of spacetime and the Gauss–Bonnet corrections crucially affect the dynamics of collapse and the nature of these branch singularities, and the nature of spacetime in the vicinity of these singularities.