1 Introduction

Traversable wormholes are spacetime structures that connect two otherwise distinct domains. In theories of gravitation, traversable wormhole solutions are ubiquitous. In these wormhole solutions, it is imperative that within a neck that opens up to the two antipodal mouths of each distinct domain, there is a narrow throat without horizons. This widening of the neck at the two sides of the throat gives rise, in geometrical terms, to the flaring out condition, essential to give the nontrivial topology of the spacetime that characterizes wormholes. In general relativity, to hold the throat and the mouths of the wormhole against collapse, one needs matter fields that have a tension much greater than their own energy density. Usual matter fields do not possess these energy features, nevertheless it might happen that exotic material made of appropriate quantum fields or some other suitable kind of fields might provide these prerequisite elements necessary for securing the whole wormhole structure. To understand the need for such exotic matter, one can resort to light spheres moving in a wormhole background. Ingoing light spheres starting in one of the two distinct domains enter the neck and will pass through the throat emerging then as outgoing light spheres in the other distinct domain of the wormhole spacetime. Thus, gravity, ordinarily an attractive field, in the neighborhood of the throat has to be repulsive in order to provide the necessary flaring out condition converting converging light spheres into diverging ones. More specifically, in general relativity the flaring out condition entails the violation of the null energy condition, or NEC for short, for the matter fields. The NEC states that the matter stress–energy tensor \(T_{ab}\) satisfies the inequality \(T_{ab}k^ak^b\ge 0\), where \(k^a\) is an arbitrary null vector of the spacetime, which in turn means that, in some specific frames of reference, the sum of the energy density and the pressure of the matter has a nonnegative value. When the NEC is violated, as it is the case at the wormhole throat in general relativity, the matter is called exotic matter. Since all the other energy conditions, namely, the weak, the strong, and the dominant energy conditions, can only be satisfied if the NEC is satisfied, the NEC operates as the basis to test the exoticity of matter. The NEC and the other energy conditions on the matter fields are a safeguard for classical general relativity, in that their violation raises deep questions concerning the structure and the validity of the theory itself. Be as it may, in general relativity the throats of wormhole solutions are allowed to exist only in neighborhoods where the NEC is violated. Theories of gravity beyond general relativity, commonly called modified theories of gravity, are generically motivated from quantum gravity low energy phenomena or from corrections that can show up at a cosmological scale. When applied to wormholes, these theories have also provided mechanisms to keep the wormhole throat open. In general, modified theories have, in their gravitational equation, the usual curvature term of general relativity epitomized in the Einstein tensor which depends on the metric and its first two derivatives, plus terms that contain higher order metric curvature tensors, together with terms for the other plausible fundamental fields, as well as a term for the stress–energy tensor of the matter fields, in addition to comprising all the other equations related to the new fields. The new terms in the modified theories of gravity can work for or against the NEC and the other energy conditions, i.e., they can provide smaller energy condition violations or higher ones. Since exotic matter is hard to find, one way out is to try to construct traversable wormhole solutions with new fundamental terms, gravitational or otherwise, that alleviate the NEC violation of the matter fields at the throat. Normally, although the condition violations can be reduced, they remain at some degree or another in the solution. Moreover, even if one manages to have the NEC satisfied at the throat neighborhood this does not imply that the condition cannot be violated elsewhere, and thus other places of the wormhole spacetime may contain some form of exotic matter. Rarely the NEC is satisfied for the entire traversable wormhole spacetime, from the throat to the the infinity of the two domains.

Let us mention some traversable wormhole solutions that underline the subtleties of their construction and in addition put some emphasis on the energy condition violation features. Traversable wormholes appeared in general relativity first as solutions connecting two different asymptotic flat spacetime domains [1,2,3]. Their possible use for interstellar travel was put forward in [4], and a firm theoretical basis for their construction was given in [5, 6]. Traversable wormholes with interesting features connecting two distinct asymptotically de Sitter or anti-de Sitter regions were explored in [7]. Wormholes supported by phantom matter were found in [8], in a cosmological context were discussed in [9], in braneworld scenarios together with their ringing properties were analyzed in [10], supported by Casimir type effects were introduced in [11], made of electrically charged shells in a Gauss-Bonnet theory appeared in [12], and built out of shells and cosmic strings were proposed in [13]. In nonminimal theories of gravity, a Wu-Yang wormhole was constructed in [14], state-of-the-art cylindrical wormhole solutions were searched for in [15], a class of traversable wormholes in f(R) theories of gravity, where R is the Ricci scalar of the spacetime and f some function of it, was displayed in [16], traversable wormholes as trapped ghosts were exhibit in [17], wormholes in nonminimally coupled gravitational and electromagnetic fields were carefully built in [18], thin shell traversable wormhole solutions in d-dimensional general relativity were disclosed and classified in [19], wormholes in the Brans-Dicke theory were established in [20], the structure of wormhole throats in f(R) theories was systematized in [21], wormholes in a hybrid metric-Palatini gravity were produced in [22], rotating wormholes with cylindrical symmetry were developed in [23], empty wormhole solutions in f(R) gravity theories were attempted in [24], traversable wormholes that minimally violate the NEC were proposed in [25], wormhole collisions with thin shells were featured in [26], thin shell wormholes with double layers in a quadratic f(R) gravity were considered in [27], wormholes with anisotropic fluid matter were built in [28], relativistic Bose-Einstein condensates thin shell wormholes were examined in [29], wormholes in generalized hybrid metric-Palatini gravity, characterized by the function \(f\left( R,{{\mathcal {R}}}\right) \), where \(\mathcal{R}\) is the Ricci scalar of an additional Palatini connection field, satisfying the matter NEC at the throat, were designed in [30], a traversable wormhole and its relation to a black bounce was treated in [31], traversable wormholes in five-dimensional Lovelock theory were advanced in [32], spherically symmetric wormholes in a specific hybrid metric-Palatini gravity were realized in [33], a phase space analysis for static wormholes sustained by an exotic isotropic perfect fluid was performed in [34], quantum features in wormholes were investigated in [35], the transition from a black hole to a wormhole in braneworld scenarios was inspected in [36], magnetic wormholes resembling Melvin’s universe were reported in [37], Morris-Thorne wormholes in a modified f(R, T) gravity, where T is the trace of the matter stress–energy tensor, were found in [38], the extension of Ellis wormholes into an anti-de Sitter background was described in [39], the existence of a wormhole in Rastall and k-essence theories was advocated in [40], self colliding wormholes were obtained in [41], a class of wormholes with double layers in hybrid metric-Palatini gravity was uncovered in [42], wormholes in f(R) gravity with a phantom scalar field were identified in [43], traversable wormholes in general relativity were contrasted to bubble universes in [44], a generic analysis of traversable wormholes was accomplished in [45], traversable wormholes violating energy conditions only near the Planck scale were revealed in [46], wormhole solutions in an f(R) gravity were further analyzed in [47], traversable wormholes in higher dimensions with warps were envisaged in [48], wormholes with partly phantom scalar fields were implemented in [49], and traversable wormhole solutions in f(R, T) gravity were further examined in [50].

In the investigation of traversable wormhole solutions of a given chosen theory, a tool that is often employed is the set of junction conditions that matches correctly one spacetime region, solution of the theory, into another region, also solution of the theory. Each theory has its own set of junction conditions. In general relativity the full set of junction conditions was given in [51], where smooth matching through a boundary surface or a nonsmooth matching through a boundary layer, i.e., a single layer thin shell, were accomplished. In f(R) theories of gravity the set of junction conditions were given in [52, 53]. In quadratic theories of gravity, where f(R) contains the usual Ricci scalar term R plus further terms quadratic in the curvature invariants, the set of junction conditions was found in [54], with the appearance, besides the smooth matching and the single layer thin shell, of a double layer thin shell. Moreover, junction conditions in \(f\left( R,T\right) \) theories have been worked out in [55], junction conditions in the generalized hybrid metric-Palatini gravity of the form \(f\left( R,\mathcal{R}\right) \) were inspected and displayed with applications in [56], and the junction conditions of Palatini \(f\left( R,T\right) \) gravity were scrutinized in [57].

Our aim here is to find traversable wormhole solutions in a quadratic theory of gravity making use of the double layer thin shells that consistently occur in the theory and analyze the behavior of the NEC throughout the whole spacetime. Double layers appear naturally from dipole layers in theories with two opposite charges, such as electromagnetic theories, but are rare in theories of gravitation that have only a single charge. The quadratic theory of gravity we use has as Lagrangian the function \(f\left( R\right) =R+\alpha R^2\), with R being the Ricci scalar of a spacetime endowed with a metric and \(\alpha \) being a free constant of the theory. Then, from the set of junction conditions of generic quadratic gravity theories, we pick up the set that fits our quadratic theory, and establish new solutions for traversable wormholes with double layer thin shells. The NEC is tested and it is found that it is satisfied at the throat and for the whole wormhole interior, and at the thin shell some stress–energy tensor components satisfy it, while others, for instance, the double layer distribution component, do not. We also study a class of traversable thin shell wormholes with a single layer that satisfies the NEC.

This paper is organized as follows. In Sec. 2, we introduce the quadratic theory of gravity we are going to study. In Sec. 3, we display the full set of junction conditions of the theory, show the particular condition that yields a double layer thin shell, indicate how this full set simplifies to the set of single layer thin shell junction conditions and to the set of smooth boundary surface junction conditions, and we give the full form of the stress–energy tensor for the whole spacetime. In Sec. 4, we derive a solution for a traversable wormhole with matter in the two domains, the upper and the lower, of the interior region that includes the throat, two double layer thin shells at the two junction mouths, the upper and lower, and two Schwarzschild asymptotically flat domains, the upper and lower, of the exterior region, and test the NEC for the whole solution. In Sec. 5, we derive a solution for an asymmetric single layer thin shell traversable wormhole for which the NEC is satisfied. In Sec. 6, we draw some conclusions. In Appendix B, we give some generalized formulas used in the text, and in Appendix C we make a plot to complement the main text.

2 Quadratic \(R+\alpha R^2\) gravity: action and field equation

Gravitational theories with the Hilbert–Einstein term R in the action, where R is the Ricci scalar, plus a quadratic term \(\alpha R^2\), with \(\alpha \) a coupling constant parameter, are an instance of quadratic theories of gravity. The general action S for such quadratic theories is

$$\begin{aligned} S=\frac{1}{16\pi }\int _{{\mathcal {V}}}\, \Big ( f\left( R\right) +\mathcal{L}_{\textrm{m}}\Big ) \, d{{\mathcal {V}}}, \end{aligned}$$
(1)

in units where the constant of gravitation G and the speed of light c are set to one, \({\mathcal {V}}\) is the spacetime manifold region on which a set of coordinates \(x^a\) is defined, \(d{\mathcal V}\) is the volume element defined by \(d{{\mathcal {V}}}=\sqrt{-g}\, d^4x\), g represents the determinant of the metric \(g_{ab}\), f(R) is given by

$$\begin{aligned} f\left( R\right) =R+\alpha R^2, \end{aligned}$$
(2)

and \({\mathcal {L}}_{\textrm{m}}\) is the matter Lagrangian which is assumed to be minimally coupled to the metric \(g_{ab}\). The sign of the quadratic term can be positive, zero, or negative, an interesting situation being the cosmological inflationary Starobinski model for which \(\alpha \) is positive, proportional to the square of the inverse of the inflaton mass. We stick to \(\alpha >0\), and put \(\alpha \) proportional the square of the inverse of the Planck mass, \(M_{\textrm{pl}}\), where here we set Planck’s constant to one \(\hbar =1\), and so \(M_{\textrm{pl}}=\sqrt{\frac{\hbar c}{G}}=1\). Equations (1) and (2) provide a particular case of f(R) theories, namely quadratic theories of gravity in the Ricci scalar. One can, if wished, include a cosmological constant \(\Lambda \) term to the function f(R) in Eq. (2). This is of greater interest in a cosmological context, where \(f\left( R\right) \) theories have given a number of insights but, in treating wormholes generated by matter confined to a compact region, discarding this term is a well justified choice.

The field equations for the \(f\left( R\right) \) gravity given by the generic form of Eq. (1) can be obtained by taking its variation with respect to the metric \(g_{ab}\). Denoting the stress–energy tensor by \(T_{ab}\) defined through \( T_{ab}=-\frac{2}{\sqrt{-g}}\frac{\delta (\sqrt{-g} \,\mathcal{L}_\textrm{m})}{\delta (g^{ab})} \), and defining \(f_R\equiv \frac{d f}{d R}\), the variation yields \( f_R R_{ab}-\frac{1}{2}g_{ab}f \left( R\right) - \left( \nabla _a\nabla _b-g_{ab} \Box \right) f_R=8\pi T_{ab} \), where \(\nabla _a\) is the covariant derivative and \(\Box =\nabla ^a\nabla _a\) is the d’Alembert operator, both written in terms of the Levi-Civita connection \(\Gamma ^c_{ab}\) of the metric \(g_{ab}\). For the specific quadratic \(f\left( R\right) \) gravity theory given in Eq. (2) one has \(f_R=1+2\alpha R\), and so one obtains the following equation of motion

$$\begin{aligned} \left( 1+2\alpha R\right) R_{ab}-\frac{1}{2} g_{ab}\left( R+\alpha R^2\right) - 2\alpha \left( \nabla _a\nabla _b-g_{ab} \Box \right) R =8\pi T_{ab}, \end{aligned}$$
(3)

which is the equation that interests us here.

We could look for other actions more generic than the ones with a quadratic f(R) Lagrangian, but the appearance of a double layer thin shell requires that \(f_{RRR}=0\). Moreover, for our purposes of finding interesting wormhole solutions with double layer thin shells it is appropriate to work with the specific f(R) given in Eq. (2). Of course, single layer thin shells and smooth boundaries traversable wormholes are also well defined in this quadratic theory.

3 Junction conditions for double layers, single layers, and smooth boundary surfaces in quadratic \(R+\alpha R^2\) gravity and the stress–energy tensor \(T_{ab}\)

3.1 Generic matching conditions for double layer thin shells and the particular cases of single layer thin shells and smooth boundary surfaces

The junction conditions are a set of conditions that two spacetime regions must satisfy in order to guarantee that they can be matched at a given separation hypersurface, and thus altogether form a whole spacetime, solution of the field equations.

A four-dimensional spacetime region is denoted by \({\mathcal {V}}\), which in turn is assumed to be composed of two regions, \(\mathcal V^-\) and \({\mathcal {V}}^+\) that match at a hypersurface \(\Sigma \). The metric in the region \({\mathcal {V}}^-\) with coordinates \(x^a_-\) is denoted by \(g_{ab}^-\), and the metric in the region \({\mathcal {V}}^+\) with coordinates \(x^a_+\) is denoted by \(g_{ab}^+\), with latin indices running from 0 to 3, 0 being in general a time index. In each side of \(\Sigma \), it is defined a set of coordinates \(y^\alpha \), with Greek indices running from some combination of three of the four latin indices, where the index excluded corresponds to the direction perpendicular to the hypersurface. Projection vectors from the four-dimensional regions \({\mathcal {V}}^-\) and \({\mathcal {V}}^+\) into the three-dimensional hypersurface \(\Sigma \) are defined by \(e^a_\alpha =\frac{\partial x^a}{\partial y^\alpha }\), where \(x^a\) can be either \(x^a_-\) or \(x^a_+\) depending which region one is considering. At \(\Sigma \) there is a unit normal vector \(n^a\) which is defined to point from \({\mathcal {V}}^-\) to \({\mathcal {V}}^+\). The affine parameter along the geodesics perpendicular to \(\Sigma \) is denoted by l, it can be a proper time if \(\Sigma \) is spacelike or a proper length if \(\Sigma \) is timelike. The parameter l is chosen to be negative in the region \({\mathcal {V}}^-\), zero at \(\Sigma \), and positive in the region \({\mathcal {V}}^+\). Along these geodesics perpendicular to \(\Sigma \), the infinitesimal coordinate displacement is \(dx^a=n^adl\), and the normal \(n_a\) can be written as \(n_a=\epsilon \partial _a l\), with \(\epsilon =\mp 1\), \(-1\) for \(n^a\) a timelike vector and \(+1\) for \(n^a\) a spacelike vector, so that \(n_a\) satisfies the normalization condition \(n^an_a=\epsilon \). In the matching process one uses the distribution function formalism. For that one defines two distribution functions, namely, the Heaviside step function \(\Theta \left( l\right) \) and the Dirac delta function \(\delta \left( l\right) \), with \(\delta \left( l\right) =\partial _l\Theta \left( l\right) \). For a given quantity A, it is possible to write \(A=A^-\Theta \left( -l\right) +A^+\Theta \left( l\right) \), where the index − indicates that the quantity \(A^-\) is the value of the quantity A in the region \({\mathcal {V}}^-\), and the index \(+\) indicates that the quantity \(A^+\) is the value of the quantity A in the region \({\mathcal {V}}^+\). The jump of the quantity A across \(\Sigma \) is denoted by \(\left[ A\right] =A^+|_\Sigma -A^-|_\Sigma \). The tangent vector \(e^a_\alpha \) and the normal \(n^a\) to \(\Sigma \) have zero jump by definition, so that \(\left[ n^a\right] =0\) and \(\left[ e^a_\alpha \right] =0\). The junction conditions for quadratic \(f\left( R\right) \) gravity have been derived in [53]. Here, we adapt these for the quadratic gravity defined in Eq. (2), i.e., \(f\left( R\right) =R+\alpha R^2\). There is a total of six junction conditions for this theory.

The first junction condition of the theory is related to the induced metric at the matching hypersurface. The induced metric \(h_{\alpha \beta }\) at \(\Sigma \) is defined generically by \(h_{\alpha \beta }=g_{ab}e^a_\alpha e^b_\beta \), with \(h_{\alpha \beta }^-\) corresponding to the induced metric from \(g_{ab}^-\), and \(h_{\alpha \beta }^+\) corresponding to the induced metric from \(g_{ab}^+\). The first junction condition is \(\left[ h_{\alpha \beta }\right] =0\), i.e., the induced metric at \(\Sigma \) is continuous. Defining the induced metric with full spacetime indices as \(h_{ab}= e_a^\alpha e_b^\beta h_{\alpha \beta }\), the first junction condition of the theory can be written as

$$\begin{aligned} \left[ h_{ab}\right] =0. \end{aligned}$$
(4)

The second junction condition of the theory is related to the trace of the extrinsic curvature at the matching hypersurface from the ambient spacetime regions. The extrinsic curvature \(K_{\alpha \beta }\) at \(\Sigma \) is defined by \(K_{\alpha \beta }=e^a_\alpha e^b_\beta \nabla _a n_b\), with \(K_{\alpha \beta }^-\) corresponding to the extrinsic curvature from the \({\mathcal {V}}^-\) region, and \(K_{\alpha \beta }^+\) corresponding to the extrinsic curvature from the \({\mathcal {V}}^+\) region. The trace K of the extrinsic curvature is \(K^-={K^{-\alpha }}_{\alpha }\) for \({\mathcal {V}}^-\) and \(K^+={K^{+\alpha }}_{\alpha }\) for \({\mathcal {V}}^+\). Defining the extrinsic curvature with full spacetime indices as \(K_{ab}= e_a^\alpha e_b^\beta K_{\alpha \beta }\) and \(K={K^a}_a\), the second junction condition of the theory can be writen as

$$\begin{aligned} \left[ K\right] =0, \end{aligned}$$
(5)

i.e., the jump in the trace of the extrinsic curvature vanishes at the thin shell.

The third junction condition of the theory is

$$\begin{aligned} -\epsilon \left[ K_{ab}\right] + 2\epsilon \alpha \left( h_{ab}n^c\left[ \nabla _cR\right] - R^\Sigma \left[ K_{ab}\right] -K_{ab}^\Sigma \left[ R\right] \right) =8\pi S_{ab}, \end{aligned}$$
(6)

where \(R^\Sigma \) is an average Ricci scalar at the hypersurface \(\Sigma \), defined as \(R^\Sigma =\frac{1}{2}\left( R^++R^-\right) \), \(K_{ab}^\Sigma \) is an average extrinsic curvature at the hypersurface \(\Sigma \), defined as \(K^\Sigma _{ab}=\frac{1}{2}\left( K^+_{ab}+K^-_{ab}\right) \), and \(S_{ab}\) is the four-dimensional surface stress–energy tensor of the matter thin shell, defined from the surface stress–energy tensor \(S_{\alpha \beta }\) of the matter thin shell that lives in \(\Sigma \) as \(S_{ab}= e_a^\alpha e_b^\beta S_{\alpha \beta }\).

The fourth junction condition of the theory is

$$\begin{aligned} 2\epsilon \alpha K^\Sigma \left[ R\right] =8\pi P, \end{aligned}$$
(7)

where \(K^\Sigma ={K^{\Sigma \,a}}_a\), and P is a quantity that measures the external normal pressure or tension supported on \(\Sigma \). In general relativity, thin shell spacetimes with nonzero [R] exist, but Eq. (7) does not manifest itself, since \(\alpha = 0\) for general relativity.

The fifth junction condition of the theory is

$$\begin{aligned} -2\epsilon \alpha h^c_a\nabla _c\left[ R\right] =8\pi F_a, \end{aligned}$$
(8)

where \(F_a\) is defined as the external flux momentum. The normal component of it measures the normal energy flux across \(\Sigma \) and its tangential spatial components measure the corresponding tangential stresses. In general relativity, thin shell spacetimes with nonzero \(\nabla _c\left[ R\right] \) exist, but Eq. (8) does not manifest itself, since \(\alpha = 0\) for general relativity.

The sixth junction condition of the theory can be written quite generically as \(2\epsilon \alpha \, \Omega _{ab}\left( l\right) = 8\pi s_{ab}\left( l\right) \), where \(\Omega _{ab}(l)\) is a distributional geometric quantity that is defined implicitly in terms of geometrical spacetime quantities and quantities on the layer, namely, \( \int _{{\mathcal {V}}} \Omega _{ab}(l) Y^{ab} d{{\mathcal {V}}}=- \int _\Sigma h_{ab}\left[ R\right] n^c\nabla _cY^{ab}d\Sigma \), with \(Y^{ab}\) being some arbitrary spacetime test tensor function, l being the proper distance perpendicular to the shell defined above, and \(s_{ab}(l)\) being the stress–energy tensor distribution of the double layer that naturally arises in this junction condition. Note that the geometric quantity distribution \(\Omega _{ab}(l)\) and, by inheritance, the stress–energy tensor distribution \(s_{ab}(l)\), are defined through the spacetime test tensorial function \(Y^{ab}\) and, although this function is quite arbitrary, having the sole constraint of being defined in a region of compact support, the distributional double layer quantity \(\Omega _{ab}(l)\), and so \(s_{ab}(l)\), is unique. One can show that the the double layer stress–energy tensor distribution \(s_{ab}\left( l\right) \) given by the sixth junction condition of the theory can also be written in the form, see Appendix A,

$$\begin{aligned} \epsilon \alpha h_{ab}\left[ R\right] n^c\nabla _c\delta \left( l\right) =4\pi s_{ab}\left( l\right) . \end{aligned}$$
(9)

The double layer stress–energy tensor distribution \(s_{ab}(l)\) in Eq. (9) has resemblances to classical electric dipole distributions. Here, this dipole term arises due to the existence of the coupling \(\alpha \) and a nonzero jump in the curvature R. The dipole distribution term in Eq. (9) is originated uniquely from the quadratic term of f(R) theories, here from the term \(\alpha R^2\). Since gravitation in general does not have different types of charge, apparently there is still no intuitive physical interpretation for why dipole double layer distributions should arise in such gravity theories. In general relativity, thin shell spacetimes with nonzero [R] exist, but Eq. (9) does not manifest itself, since \(\alpha = 0\) for general relativity.

The system of equations given in Eqs. (4)–(9) reduce to a single layer thin shell matching when the contribution of the double layer for the thin shell vanishes. In such a case, \(S_{ab}\) remains nonzero, while the quantities P, \(F_a\) and \(s_{ab}\left( l\right) \) vanish. So, the first junction condition, Eq. (4), continues to hold, \(\left[ h_{ab}\right] =0\). The second junction condition, Eq. (5), continues to hold, \(\left[ K\right] =0\). Equation (7) gives \([R]=0\), which implies that the third junction condition, Eq. (6), is \(-\epsilon \left[ K_{ab}\right] + 2\epsilon \alpha \left( h_{ab}n^c\left[ \nabla _c R\right] - R^\Sigma \left[ K_{ab}\right] \right) =8\pi S_{ab}\), and the fourth junction condition, Eq. (7), is \([R]=0\) itself. The fifth junction condition, Eq. (8) is trivial, since \([R]=0\) implies \(h^c_a\nabla _c\left[ R\right] =0\). The sixth junction condition, Eq. (9), is also trivial. Then the junction conditions of the quadratic theory of gravity given in Eq. (3) for a matching with a single layer thin shell are four, namely, \(\left[ h_{ab}\right] =0\), \(\left[ K\right] =0\), \(-\epsilon \left[ K_{ab}\right] + 2\epsilon \alpha \left( h_{ab}n^c\left[ \nabla _c R\right] - R^\Sigma \left[ K_{ab}\right] \right) =8\pi S_{ab}\), and \([R]=0\).

The system of equations given in Eqs. (4)–(9) reduce to a smooth matching, i.e., to a boundary surface, when both the contributions from the double layer and the single layer thin shell vanish. In such a case, all the quantities \(S_{ab}\), P, \(F_a\), and \(s_{ab}\left( l\right) \) vanish. The first junction condition, Eq. (4), continues to hold, \(\left[ h_{ab}\right] =0\). The second junction condition, Eq. (5), still holds, but it is not an independent condition anymore since it is implied by the third junction condition. This can be seen by noting that Eq. (7) yields \([R]=0\), which then implies \(h^c_a\nabla _c\left[ R\right] =0\), and then taking the trace of the third junction condition, Eq. (6), and using Eq. (5), one gets \(n^c\left[ \nabla _cR\right] =0\), which replacing back into Eq. (6) yields \([K_{ab}]=0\). Finally, tracing this result one obtains Eq. (5). So, now instead of Eqs. (5) and (6), one has simply \([K_{ab}]=0\). The fourth junction condition, Eq. (7), is now \([R]=0\), as mentioned above. The fifth and sixth junction conditions, Eqs. (8) and (9), are again trivial. Then, the junction conditions of the quadratic theory of gravity given in Eq. (3) for a smooth matching, i.e., for a boundary surface, are three, namely, \([h_{ab}]=0\), \([K_{ab}]=0\), and \([R]=0\).

3.2 The stress–energy tensor \(T_{ab}\)

The stress–energy tensor \(T_{ab}\), that appears in the field equation, Eq. (3), can be now given explicitly. The quantities that appear in it are \(T_{ab}^-\) which is the stress–energy tensor in the region \({\mathcal {V}}^-\), \(T_{ab}^+\) which is the stress–energy tensor in the region \({\mathcal {V}}^+\), and the quantities at the thin shell, specifically, \(S_{ab}\) which is the stress–energy tensor of the matter at the thin shell, P which measures the external normal pressure or tension supported at the thin shell, \(F_a\) which is the external flux momentum at the thin shell, and \(s_{ab}(l)\) which is the stress–energy tensor distribution of the double layer thin shell. Then, \(T_{ab}\) assumes the form

$$\begin{aligned} T_{ab}=T_{ab}^- \Theta \left( -l\right) + T_{ab}^+\Theta \left( l\right) + \delta \left( l\right) \left( S_{ab}+ Pn_an_b+ F_{(a}n_{b)}\right) + s_{ab}\left( l\right) . \end{aligned}$$
(10)

Note that the dipole tensor distribution \(s_{ab}(l)\) of Eq. (9) is an essential piece in making sure that the stress–energy tensor distribution is divergence free, i.e., \(\nabla ^a T_{ab}=0\).

4 Traversable wormholes with a double layer thin shell in quadratic \(R+\alpha R^2\) gravity

4.1 General considerations

Let us start by describing the geometric sector of a class of traversable wormholes with a double layer thin shell in quadratic \(R+\alpha R^2\) gravity. The generic line element for the four-dimensional spacetime is \(ds^2=g_{ab}dx^adx^b\), where \(g_{ab}\) is the metric in the coordinate system \(x^a\). Assuming a static spacetime and spherical coordinates \(\left( t,r,\theta ,\phi \right) \), the line element can be written as \(ds^2=g_{tt}dt^2+g_{rr} dr^2+g_{\theta \theta }d\theta ^2 +g_{\phi \phi }d\phi ^2\), where \(g_{tt}\), \(g_{rr}\), \(g_{\theta \theta }\), and \(g_{\phi \phi }\) are the time, radial, polar, and azimuthal metric potentials, respectively. In spherical coordinates \(g_{\theta \theta }=r^2\) and \(g_{\phi \phi }=r^2\sin ^2\theta \), and so one has \(ds^2=g_{tt}dt^2+g_{rr} dr^2+r^2d\Omega ^2\), where \(d\theta ^2+\sin ^2\theta d\phi ^2\) has been abbreviated to \(d\Omega ^2\), i.e., \(d\Omega ^2=d\theta ^2+\sin ^2\theta d\phi ^2\) is the line element on the unit sphere. For traversable wormhole spacetimes it is convenient to write \(g_{tt}=-e^{\zeta \left( r\right) }\) and \(g_{rr}= \frac{1}{1- \frac{b\left( r\right) }{r}} \), where \(\zeta \left( r\right) \) is defined as the redshift function and \(b\left( r\right) \) is defined as the shape function, so that the line element is

$$\begin{aligned} ds^2=-e^{\zeta \left( r\right) }dt^2+ \frac{dr^2}{1- \frac{b\left( r\right) }{r}}+r^2d\Omega ^2. \end{aligned}$$
(11)

A traversable wormhole spacetime connects two distinct spacetime domains through a throat situated at some radius \(r_0\). This implies that for traversable wormhole spacetimes the two metric functions of Eq. (11), \(\zeta \left( r\right) \) and \(b\left( r\right) \), near the throat are not arbitrary as two conditions must be fulfilled. First, the wormhole spacetime must have no horizons or singularities, such that motion in the neighborhood of the wormhole throat at \(r=r_0\) is allowed, and escape to the distinct spacetime domains is possible. To accomplish these conditions, it is sufficient in static spacetimes to impose that the redshift function must be finite everywhere, or at least in some sufficiently large region containing the throat, i.e., \(|\zeta \left( r\right) |<\infty \) within some sufficiently large r. Second, the wormhole spacetime has to satisfy the flaring out condition. This is a geometric condition that must be imposed at the wormhole throat guaranteeing that it is traversable. This condition implies that the shape function b(r) must satisfy \(b\left( r_0\right) =r_0\) and \(b'\left( r_0\right) <1\), where here a prime denotes derivatives with respect to r. The two metric functions of Eq. (11), \(\zeta \left( r\right) \) and \(b\left( r\right) \), also assume special forms compatible with the asympotics of the wormhole spacetime, for instance they can have forms that asymptotically approach the vacuum Schwarzchild line element.

Let us now describe the matter sector generically. The stress–energy tensor can be written as

$$\begin{aligned} T_{ab}=T_{ab}(r), \end{aligned}$$
(12)

where the dependence in the radius r is made explicit so that Eqs. (11) and (12) are compatible when one makes use of the field equation, i.e., Eq. (3). We can further specify the stress–energy tensor by establishing which type of fluid inhabits certain given regions of the spacetime.

In searching for traversable wormhole solutions, one is also interested in verifying whether and where the matter satisfies the NEC, specifically, in which regions the NEC is satisfied and which pieces of the stress–energy tensor \(T_{ab}\) satisfy the NEC. For instance, it can be shown that for a fluid with a stress–energy tensor of the form of an anisotropic perfect fluid, \({T_a}^b(r)=\text {diag}\left( -\rho (r),p_r(r),p_t(r),p_t(r)\right) \), with \(\rho \left( r\right) \) being the energy density, \(p_r\left( r\right) \) being the radial pressure, and \(p_t\left( r\right) \) being the transverse pressure, the NEC, i.e., \(T_{ab}k^ak^b\ge 0\), where \(k^a\) is a null vector, implies that the energy density \(\rho \), the radial pressure \(p_r\), and the tangential pressure \(p_t\), must satisfy the inequalities, \( \rho +p_r\ge 0\) and \(\rho +p_t\ge 0\). Within general relativity, the flaring out condition, i.e., \(b\left( r_0\right) =r_0\) and \(b'\left( r_0\right) <1\), and the NEC for anisotropic perfect fluids, i.e., \(\rho +p_r\ge 0\) and \(\rho +p_t\ge 0\), are incompatible. This comes from the fact that the flaring out condition, is a requirement on the geometry of the spacetime and thus on the the Einstein tensor \(G_{ab}\), which is in turn connected to the stress–energy tensor \(T_{ab}\) through the Einstein field equation \(G_{ab}= 8\pi T_{ab}\). For static and spherically symmetric spacetimes one can show that the flaring out condition implies \(\rho +p_r<0\), and since the NEC obliges that \(\rho +p_r\ge 0\), we see that the two conditions are irreconcilable, and thus traversable wormhole solutions violate the NEC in general relativity. However, in modified theories of gravity, the field equations can be envisaged in the form \(G_{ab}=8\pi T_{ab}^{\text {eff}}\), where \(T_{ab}^{\text {eff}}\) is an effective stress–energy tensor that contains not only the matter stress–energy tensor \(T_{ab}\), but also the higher order curvature terms that come from the field equations, in particular this holds for the quadratic gravity we are considering given in Eq. (3). In this way of setting the problem, it is the effective stress–energy tensor that must follow the flaring out condition \(\rho ^{\text {eff}}+p_r^{\text {eff}}<0\), and thus it is possible, in principle, that the matter stress–energy tensor \(T_{ab}\) satisfies \(T_{ab}k^ak^b\ge 0\), i.e., \(\rho +p_r\ge 0\) and \(\rho +p_t\ge 0\), and so satisfies the NEC, with the flaring out condition being simultaneously satisfied, as long as the extra higher order curvature terms provide a sufficient negative contribution to compensate the positive matter contributions. At the very least modified theories, if not having traversable wormhole solutions that satisfy the NEC, should mitigate the violations of the NEC for the matter.

Our wormhole spacetime \({\mathcal {V}}\) is composed of three regions. These three regions are the wormhole interior \({\mathcal {V}}^-\) which contains two domains at each side of the throat, two boundaries \(\Sigma \), one at each mouth, and the wormhole exterior \(\mathcal V^+\) which contains two domains each one starting at each mouth \(\Sigma \). The two domains belonging to the exterior region are thus connected to each other through the mouths, the two domains of the interior region, and the throat. The interior region is described by a line element of the form given in Eq. (11) and some specific stress–energy tensor for Eq. (12) which are valid for the two domains that come out of each side of the throat. The two domains of the exterior region, which in general can be different, can also be described by a specific form of the line element of Eq. (11). If one considers that the domains of the exterior region are vacuum regions, the stress–energy tensor of Eq. (12) is zero. The two boundaries from the interior to the exterior are dictated by the junction conditions previously found. At these boundaries one may have double layer thin shells, single layer thin shells, or boundary surfaces, i.e., a smooth matching without any thin shells. Here, we find a traversable wormhole with a double layer thin shell. To study the situation of the NEC for the matter, one must analyze it in the three regions, in the interior region, at the shell, and in the exterior region.

4.2 Traversable wormhole solutions with a double layer thin shell satisfying the NEC at the throat

4.2.1 The interior made of two symmetric domains

To find an interior solution with a throat we have to specify the redshift and shape functions, \(\zeta \left( r\right) \) and b(r), respectively, that appear in Eq. (11). A specific form for these functions is \(\zeta \left( r\right) =\zeta _0\left( \frac{r_0}{r}\right) \) and \(b\left( r\right) =r_0\left( \frac{r_0}{r}\right) \), so that the model has redshift and shape functions proportional to the inverse of the radius r. With this choice, the line element of Eq. (11) suitable for the interior region is

$$\begin{aligned} ds^2=-\textrm{e}^{\zeta _0\left( \frac{r_0}{r}\right) } dt^2+ \frac{dr^2}{1- {\left( \frac{r_0}{r}\right) ^{2}}} +r^2d\Omega ^2\,,\quad \quad \quad \quad r_0\le r<r_\Sigma \,, \end{aligned}$$
(13)

where we avoided to put a − in all quantities, as it should be for quantities in the \({\mathcal {V}}^-\) region, in order to not overload the formulas with symbols. The radial coordinate in Eq. (13) ranges from the throat radius \(r_0\) to \(r_\Sigma \), \(r_0\le r< r_\Sigma \), the upper domain of the interior region starting at \(r_0\) and extending to the upper separation boundary at \(r_\Sigma \), the upper mouth, and the lower domain of the interior region starting at \(r_0\) and extending to the lower separation boundary at \(r_\Sigma \), the lower mouth. One could have defined, instead, two broad families for the redshift and shape functions that are in line with the requirements for a traversable wormhole, as \(\zeta \left( r\right) =\zeta _0\left( \frac{r_0}{r}\right) ^\gamma \) and \(b\left( r\right) =r_0\left( \frac{r_0}{r}\right) ^\beta \) with \(\gamma \) and \(\beta \) being constant exponents. We choose to specify \(\gamma =1\) and \(\beta =1\), since it is sufficient to find an interesting double layer thin shell wormhole solution. In the Appendix B we deal with arbitrary \(\gamma \) and \(\beta \).

The stress–energy tensor considered for the interior \({\mathcal {V}}^-\) is that of an anisotropic perfect fluid, which can be written as

$$\begin{aligned} {T_a}^b(r)=\text {diag}\left( -\rho (r),p_r(r),p_t(r),p_t(r)\right) ,\quad \quad \quad \quad r_0\le r<r_\Sigma , \end{aligned}$$
(14)

where again we avoided to put a − in all quantities, as it should be for quantities in the \({\mathcal {V}}^-\) region, in order to not overload the formulas with symbols, \(\rho =\rho \left( r\right) \) is defined as the energy density, \(p_r=p_r\left( r\right) \) is defined as the radial pressure, and \(p_t=p_t\left( r\right) \) is defined as the transverse pressure of the matter. The three quantities \(\rho (r)\), \(p_r(r)\), and \(p_t(r)\), depend on the radial coordinate alone, so that the matter distribution is static and spherically symmetric. The radial coordinate in Eq. (14) ranges from the throat radius \(r_0\) to \(r_\Sigma \), \(r_0\le r< r_\Sigma \), the upper domain of the interior region starting at \(r_0\) and extending to the upper separation boundary at \(r_\Sigma \), the upper mouth, and the lower domain of the interior region starting at \(r_0\) and extending to the lower separation boundary at \(r_\Sigma \), the lower mouth.

Upon using the ansatz for redshift and shape function that yield the line element of Eq. (13) and the stress–energy tensor in the form of Eq. (14) in the field equation of the quadratic gravity theory we are considering, Eq. (3), one obtains three equations, for \(\rho =\rho (r)\), \(p_r=p_r(r)\), and \(p_t=p_t(r)\) in terms of the functions \(\zeta \left( r\right) \), \(b\left( r\right) \), and their first and second derivatives. These equations in general are long and not particularly useful, and thus we do not present them here. As an interesting specific case, we consider the throat to be at the radius \(r_0=2\,M\), where M is a constant with mass units yet to be specified. We obtain

$$\begin{aligned} \begin{aligned} \rho (r)=&-\frac{M^2}{4\pi r^{12}} \left[ 2r^8+160Mr^5\alpha \zeta _0+32M^5r\alpha \zeta _0^3+ +16M^6\alpha \zeta _0^4-24r^6\alpha \left( 4+\zeta _0^2\right) \right. \\&\left. -8M^3r^3\alpha \zeta _0 \left( 100+\zeta _0^2\right) -8M^4r^2\alpha \zeta _0^2 \left( 142+\zeta _0^2\right) + M^2r^4\alpha \left( 496+368\zeta _0^2+\zeta _0^4\right) \right] ,\\ {}&\quad r_0\le r<r_\Sigma , \\ p_r(r)=&\frac{M}{4\pi r^{12}}\left\{ -r^9\zeta _0-96M^6r\alpha \zeta _0^3+ 16M^7\alpha \zeta _0^4 -8M^5r^2\alpha \zeta _0^2\left( \zeta _0^2-30\right) \right. \\&+40M^4r^3\alpha \zeta _0\left( 8+\zeta _0^2\right) +M^3r^4\alpha \left( \zeta _0^4-120\zeta _0^2-208\right) -2Mr^6\left[ r^2-8\alpha \left( 4+\zeta _ 0^2\right) \right] \\&+\left. 4M^2r^5\zeta _0\left[ r^2-\alpha \left( 24+\zeta _0^2\right) \right] \right\} ,\quad r_0\le r<r_\Sigma , \\ p_t(r)=&\frac{M}{8\pi r^{12}}\left\{ r^9\zeta _0-512M^6r \alpha \zeta _0^3-32M^7\alpha \zeta _0^4 +16M^5r^2\alpha \zeta _0^2\left( \zeta _0^2-190\right) \right. \\&+ Mr^6\left( r^2-64\alpha \right) \left( 4+\zeta _0^2\right) +16M^4r^3\alpha \zeta _0\left( 13\zeta _0^2-96\right) \\&\left. -4M^2r^5\zeta _0\left[ 2r^2+5\alpha \left( \zeta _0^2-16\right) \right] -2M^3r^4\left[ 2r^2\zeta _0^2+\alpha \left( \zeta _0^4 -488\zeta _0^2-624\right) \right] \right\} ,\\ {}&\quad \quad r_0\le r<r_\Sigma , \end{aligned}\nonumber \\ \end{aligned}$$
(15)

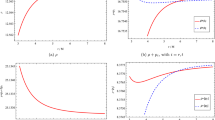
where the equations are valid for \(r_0\le r\le r_\Sigma \) in the upper and lower domains of the interior regions, i.e., for the two sides of the throat in the two domains of the interior region up to the two mouths. Different wormhole interior region solutions can be analyzed by varying the parameter \(\alpha \), which in turn yield different quadratic theories, as well as by varying the constants \(\zeta _0\) and \(r_0\), which here we fixed to \(r_0=2M\). In Fig. 1 we provide plots of the energy density \(\rho \), the radial pressure \(p_r\), and the tangential pressure \(p_t\) as functions of r, for some specific combination of values of the parameters of the solution, namely, \(\alpha =0.013\) in Planck units, \(\zeta _0=-60\), and \(r_0=2\,M\), for some parameter M.

Fig. 1
figure 1

Plots of the matter fields \(\rho \), \(p_r\), and \(p_t\) as functions of the radius r for \(\alpha =0.013\) in Planck units, \(\zeta _0=-60\), and \(r_0=2\,M\), where here M is some mass constant. The quantities plotted are normalized to M

Full size image

Having obtained the solutions for the matter fields, one computes \(\rho +p_r\) and \(\rho +p_t\) to verify whether the NEC is satisfied at the throat \(r_0\), which here is \(r_0=2M\), or not. In Fig. 2 we provide plots of \(\rho +p_r\) and \(\rho +p_t\) as functions of r for some specific combination of values of the parameters of the solution, namely, the same as in Fig. 1, i.e., \(\alpha =0.013\) in Planck units, \(\zeta _0=-60\), and \(r_0=2\,M\), for some parameter M.

Fig. 2
figure 2

Plots of \(\rho +p_r\) and \(\rho +p_t\) as functions of the radius r for \(\alpha =0.013\) in Planck units, \(\zeta _0=-60\), and \(r_0=2M\), where here M is some mass constant. Clearly the NEC is satisfied at the throat \(r=r_0\) but violated elsewhere. The quantities plotted are normalized to M

Full size image

One confirms that the NEC is satisfied at the wormhole throat \(r=r_0=2M\), but it is ultimately violated at larger values of r. To have an interior solution that satisfies the NEC throughout the entire interior region one must truncate the solution before the NEC starts to be violated. From Fig. 2 the NEC starts to be violated for radii \(\frac{r}{M}\) outside the throat, although close to it, so that for this set of parameters one should put an end to the interior solution at about \(r_\Sigma =2.024M\). We recall that to have the matter NEC and the flaring out condition both satisfied at the throat is only possible because we are dealing with a modified gravity theory, here a quadratic theory of gravity with an \(\alpha R^2\) term. In this case, it is possible to find a combination of parameters that fulfills the NEC at the throat as we showed, noting also that there are many other combinations of parameters for which the NEC is violated there. On the other hand, in general relativity, in which case \(\alpha =0\), the NEC is always violated at the throat. To see this, in the Appendix C we show that for \(\alpha =0\), the quantity \(\rho +p_r\) of the solution presented, is negative, violating thus the NEC, as expected.

4.2.2 The exterior made of two symmetric domains

We have now to provide an exterior solution to be matched with the interior solution presented above, in order to form the whole wormhole spacetime solution. To find an exterior solution we have to specify the redshift and shape functions, \(\zeta \left( r\right) \) and b(r), respectively, that appear in Eq. (11). A specific form for these functions is \(\zeta \left( r\right) =\ln \left( 1-\frac{2\,M}{r}\right) +\zeta _e\) and \(b\left( r\right) =2\,M\), where \(\zeta _e\), a constant to be determined later, and M is a parameter that represents the exterior spacetime mass. With this choice the line element of Eq. (11) suitable for the exterior region made of two domains, the upper and lower, is

$$\begin{aligned} ds^2=-\left( 1-\frac{2M}{r}\right) e^{\zeta _e}dt^2+\left( 1- \frac{2M}{r}\right) ^{-1}dr^2 + r^2d\Omega ^2 \,,\quad \quad \quad \quad r_\Sigma<r<\infty \,, \end{aligned}$$
(16)

where we avoided to put a \(+\) in all quantities, as it should be for quantities in the \({\mathcal {V}}^+\) region, in order to not overload the formulas with symbols. Note that \(\zeta _e\) ensures that the time coordinate of both regions, the interior wormhole and the exterior regions, is the same upon matching. The radial coordinate in Eq. (16) ranges from \(r_\Sigma \) to infinity, \(r_\Sigma< r <\infty \), the upper domain of the exterior region starting at the upper boundary \(r_\Sigma \), the upper mouth, and extending to infinite radial coordinate, and the lower domain of the exterior region starting at the lower boundary \(r_\Sigma \), the lower mouth, and extending to infinite radial coordinate. Having the same form of line element on both sides of the exterior region, the wormhole spacetime has thus two symmetric domains in the exterior region.

The stress–energy tensor considered for the exterior \({\mathcal {V}}^+\), constituted of the upper and lower domains, is that of an anisotropic perfect fluid, which can be written as

$$\begin{aligned} {T_a}^b(r)=\text {diag}\left( -\rho (r),p_r(r),p_t(r),p_t(r)\right) ,\quad \quad \quad \quad r_\Sigma<r<\infty , \end{aligned}$$
(17)

where again we avoided to put a \(+\) in all quantities, as it should be for quantities in the two domains of the exterior region \({\mathcal {V}}^+\), in order to not overload the formulas. The energy density \(\rho (r)\), the radial pressure \(p_r(r)\), and the transverse pressure \(p_t(r)\), depend on the radial coordinate alone, so that the matter distribution is static and spherically symmetric.

Upon using the ansatz for redshift and shape function that yield the line element of Eq. (16) and the stress–energy tensor in the form of Eq. (17) in the field equation of the quadratic gravity theory we are considering, Eq. (3), one obtains three equations, which in this case are simply

$$\begin{aligned} \rho (r)=0\,,\quad p_r(r)=0\,,\quad p_t(r)=0\,, \quad \quad \quad \quad r_\Sigma<r<\infty \,, \end{aligned}$$
(18)

where the equations are valid for \(r_\Sigma<r<\infty \) in the upper and lower domains, i.e., for the two sides of the mouths in the exterior up to infinity. Thus, the two domains of the exterior region are vacua, i.e., with \(T_{ab}=0\), and so the solution for them is the Schwarzschild solution, an asymptotically flat solution. Indeed, inserting the vacuum assumption into Eq. (3), one finds that the modified field equations are satisfied for any metric with \(R_{ab}=0\), and consequently with \(R=0\).

Since the two domains of the exterior solution are vacuum solutions, \(T_{ab}=0\), they satisfy the NEC, \(T_{ab}k^ak^b\ge 0\), automatically. We have now provided an exterior spacetime valid for the two symmetric domains of the exterior region. This exterior solution is to be matched with the interior spacetime solution presented above. In order to form the whole wormhole spacetime solution, we need to apply the junction conditions at the two junction boundaries which we assume both to have radii \(r_\Sigma \).

4.2.3 Matching the wormhole interior to the vacuum exterior

Before we apply the junction conditions, Eqs. (4)–(9), we need to compute the relevant quantities on which they depend, namely, \(h_{00}^-\), \(h_{00}^+\), \(n^{-c}\), \(n^{+c}\), \({{K^-}_{0}}^0\), \({{K^-}_{\theta }}^\theta \), \({K^-}\), \({{K^+}_{0}}^0\), \({{K^+}_{\theta }}^\theta \), \({K^+}\), \(R^{-\Sigma }\), \(R^{+\Sigma }\), \((\nabla _cR)^{-\Sigma }\), and \((\nabla _cR)^{+\Sigma }\), for the wormhole spacetime regions we are considering. These expressions, which have to be computed from the interior line element of Eq. (13) with its redshift and shape functions, and from exterior vacuum solution described by the line element of Eq. (16), are given in the Appendix B, where the exponents \(\gamma \) and \(\beta \) for the interior metric functions are put as generic, whereas here we adapt those expressions to \(\gamma =1\) and \(\beta =1\). In the junction conditions, Eqs. (4)-(9), we set \(\epsilon =1\) which is the value appropriate for a timelike thin shell, the case we are considering.

The first junction condition, i.e., Eq. (4), dictates the continuity of the metric through each of the two boundaries \(\Sigma \). For the two line elements in Eqs. (13) and (16) the junction condition \(\left[ h_{ab}\right] =0\) yields

$$\begin{aligned} e^{\zeta _0\left( \frac{r_0}{r_\Sigma }\right) }= \left( 1-\frac{2M}{r_\Sigma }\right) e^{\zeta _e}, \quad \quad \quad \quad \quad r=r_\Sigma , \end{aligned}$$
(19)

and thus, given \(\zeta _0\) from the model chosen, one finds a relation between \(r_\Sigma \) and \(\zeta _e\). Now, \(r_\Sigma \) is defined as the radius at which the matching is performed, and there is one \(r_\Sigma \) for the matching of the upper domain and another \(r_\Sigma \) for the matching of the lower domain.

The second junction condition, i.e., Eq. (5), yields a constraint on the radius \(r_\Sigma \). For the two line elements in Eqs. (13) and (16), the junction condition \(\left[ K\right] =0\) yields

$$\begin{aligned} \frac{2r_\Sigma -3M}{r_\Sigma ^2\sqrt{1-\frac{2M}{r_\Sigma }}}= \frac{1}{2r_\Sigma }\sqrt{1- \left( \frac{r_0}{r_\Sigma }\right) ^{2}} \left[ 4-\zeta _0\left( \frac{r_0}{r_\Sigma }\right) \right] , \quad \quad \quad \quad \quad r=r_\Sigma . \end{aligned}$$
(20)

For each chosen \(\zeta _0\), one can find \(r_\Sigma \) from Eq. (20). The matching between the two metrics must then be performed at the \(r_\Sigma \) found, one \(r_\Sigma \) for the upper domain and another for the lower domain. One can then insert into Eq. (19) the value of \(r_\Sigma \) found, and obtain the corresponding value of \(\zeta _e\).

The third junction condition, i.e., Eq. (6), is now used. We assume that each thin shell, one in the upper domain, the other in the lower domain, is made of an isotropic perfect fluid. For a perfect fluid, the surface energy density \(\sigma \) and the tangential pressure p of each thin shell are found from the surface stress–energy tensor \({S_{\alpha }}^\beta =S_{ac}e_\alpha ^ae^c_\gamma h^{\beta \gamma }\), where, as defined before, \(e^a_\alpha \) represent the projection vectors that project from the four-dimensional spacetime region to the hypersurface \(\Sigma \). The tensor \({S_\alpha }^\beta \) takes a diagonal form, and we can write \( {S_\alpha }^\beta =\text {diag}\left( -\sigma ,p,p\right) \). Defining the surface stress–energy tensor with full spacetime indices as \(S_{ab}= e_a^\alpha e_b^\beta S_{\alpha \beta }\), the third junction condition of the theory, namely, \(\left[ K_{ab}\right] + 2\alpha \left( h_{ab}n^c\left[ \nabla _cR\right] - R^\Sigma \left[ K_{ab}\right] -K_{ab}^\Sigma \left[ R\right] \right) =8\pi S_{ab}\), yields the surface energy density \(\sigma \) and the transverse pressure p of each thin shell as having the expressions \(\sigma = \frac{1}{8\pi } \Big [ \left[ K_0^0\right] \left( 1+2\alpha R_\Sigma \right) + 2\alpha \left( K^{0(\Sigma )}_{0}\left[ R\right] -n^c \left[ \nabla _c R\right] \right) \Big ]\), and \(p=\frac{1}{8\pi } \Big [ \frac{1}{2} \left[ K_0^0\right] \left( 1+2\alpha R_\Sigma \right) + \alpha \left( K^{0(\Sigma )}_{0} \left[ R\right] + 2n^c\left[ \nabla _c R\right] \right) \Big ] \), where we used the fact that, since \(\left[ K\right] =0\) holds, then in spherically symmetric spacetimes and spherical coordinates we have \(\left[ K_0^0\right] =- 2\left[ K_\theta ^\theta \right] =-2\left[ K_\phi ^\phi \right] \). One can thus write \(\sigma \) and p for each of the two thin shells, one in the upper domain and the other in the lower domain, as

$$\begin{aligned} \begin{aligned} \sigma =&\frac{1}{8\pi } \Bigg [ \,\,a(r_\Sigma )\, \Big (1\,+\,2\alpha f(r_\Sigma )\Big )+ 2\alpha \Big ( b(r_\Sigma )g(r_\Sigma )-h(r_\Sigma )\Big ) \Bigg ],\quad \quad \quad \quad \quad r=r_\Sigma , \\ p =&\frac{1}{8\pi } \Bigg [ \frac{1}{2} a(r_\Sigma ) \Big (1+2\alpha f(r_\Sigma )\Big )+ \alpha \Big ( b(r_\Sigma )g(r_\Sigma )+2h(r_\Sigma )\Big ) \Bigg ], \quad \quad \quad \quad \quad r=r_\Sigma , \end{aligned}\nonumber \\ \end{aligned}$$
(21)

where \(a(r_\Sigma )\), \(b(r_\Sigma )\), \(f(r_\Sigma )\), \(g(r_\Sigma )\), and \(h(r_\Sigma )\), are functions of \(r_\Sigma \) and depend also on the remaining free parameters that characterize the interior and exteriors regions, see the Appendix B for the explicit expressions. For the surface stress–energy tensor \(S_{ab}\), part of the full stress–energy tensor \(T_{ab}\) of Eq. (10), one has to verify whether the NEC is satisfied or not. Since one can write \(S_{ab}\) as \(S_{ab}= e_a^\alpha e_b^\beta S_{\alpha \beta }\), and \({S_\alpha }^\beta =\text {diag}\left( -\sigma ,p,p\right) \), one has in an orthonormal tetrad that \(S_{ab}=(\sigma ,0, p, p)\). For a null vector at \(\Sigma \) of the form \(k^a=(1,0,1,0)\) or of the form \(k^a=(1,0,0,1)\), i.e., null vectors on the shell, one has \(S_{ab}k^ak^b= \sigma + p\), so that for vectors on the shell \(\Sigma \), the NEC is satisfied if \(\sigma +p\ge 0\). For a null vector at \(\Sigma \) of the form \(k^a=(1,1,0,0)\) one has \(S_{ab}k^ak^b=\sigma \) and for this type of vectors, i.e., null vectors off the shell, the NEC implies \(\sigma \ge 0\). The three types of null vectors are representative of all null vectors at \(\Sigma \), so to satisfy the NEC, the fluid quantities must satisfy \(\sigma +p\ge 0\) and \(\sigma \ge 0\), which from Eq. (21) are conditions that depend on the functions \(a(r_\Sigma )\), \(b(r_\Sigma )\), \(f(r_\Sigma )\), \(g(r_\Sigma )\), and \(h(r_\Sigma )\).

The fourth junction condition, given in Eq. (7), i.e., \(2\alpha K^\Sigma \left[ R\right] =8\pi P\), yields for each of the two thin shells, one in the upper domain and the other in the lower domain, the following result

$$\begin{aligned} P=\frac{\alpha }{4\pi } c(r_\Sigma ) g(r_\Sigma ), \quad \quad \quad \quad \quad r=r_\Sigma , \end{aligned}$$
(22)

where \(c(r_\Sigma )\) and \(g(r_\Sigma )\) are functions of \(r_\Sigma \) and also depend on the remaining free parameters that characterize the interior and exteriors regions, see the Appendix B for the explicit expressions. P measures the external normal pressure supported on each thin shell, the upper and the lower ones. In the stress–energy tensor given in Eq. (10) the term that corresponds to this junction condition is \(Pn_an_b\), with the normal being \(n_{-a}=(0, \left( 1-\left( \frac{r_0}{r_\Sigma } \right) ^{2} \right) ^{-\frac{1}{2}},0,0)\) and \(n_{+a}=(0, \left( 1-\frac{2\,M}{r_\Sigma } \right) ^{-\frac{1}{2}},0,0)\), see the Appendix B. The normals \(n_{-a}\) and \(n_{+a}\) are the same at \(r_\Sigma \), only written in different coordinate systems, indeed \(n_{\mp a} n^{\mp a}=1\) and they are applied at the same point. Since this part of the stress–energy tensor at the thin shell has the form \(P\,n_an_b\), the NEC for it can be written as \(P\,n_an_bk^ak^b=P\,|n_ak^a|^2\ge 0\), which is equivalent to \(P\ge 0\), which in turn depends on the functions \(c(r_\Sigma )\) and \(g(r_\Sigma )\).

The fifth junction condition, given in Eq. (8), i.e., \(-2 \alpha h^c_a\nabla _c\left[ R\right] =8\pi F_a\), involves \(F_a\), which is the external flux momentum, the time component of which determines the energy flux across \(\Sigma \), while the spatial components determine the corresponding tangential stresses. Since the solution is spherically symmetric, one has that \(\nabla _c\left[ R\right] \) is a function of r only, and since the induced metric projects tensors into a hypersurface of constant radius, the contraction \(h_a^c\nabla _c\left[ R\right] \) in Eq. (8) vanishes, \(F_a=0\). More specifically, although \(\nabla _c\left[ R\right] \) is nonzero, the only nonvanishing component of this tensor is along the radial direction and so its projection with \(h^c_a\) into the hypersurface vanishes. So,

$$\begin{aligned} F_\alpha =0, \quad \quad \quad \quad \quad r=r_\Sigma . \end{aligned}$$
(23)

Thus, each of the two thin shells, the upper and the lower, support zero external flux momentum. In the stress–energy tensor given in Eq. (10), the term that corresponds to this junction condition is \(F_{(a}n_{b)}\). It satisfies the NEC if \(F_{(a}n_{b)}k^ak^b\ge 0\), which, since \(F_a=0\), is the case without further specification.

The sixth junction condition, given in Eq. (9), i.e., \(\frac{\alpha }{4\pi } h_{ab}[R]n^c\nabla _c\delta \left( l\right) =s_{ab}\left( l\right) \), has to be worked out with care. Since \(h_{ab}\) is a diagonal tensor, we can write the double layer thin shell stress–energy tensor \(s_{ab}\left( l\right) \) as \({s_a}^b\left( l\right) =\text {diag} \left( -{\bar{\sigma }}\left( l\right) ,0,{\bar{p}}\left( l\right) ,\bar{p}\left( l\right) \right) \), where \({\bar{\sigma }}\left( l\right) \) and \(\bar{p}\left( l\right) \) are defined to be the double layer surface density and tangential pressure distributions, respectively. Then, for this wormhole Eq. (9) gives

$$\begin{aligned} {\bar{\sigma }}=-\frac{\alpha }{4\pi }g(r_\Sigma )\,,\quad \quad \bar{p}=\frac{\alpha }{4\pi }g(r_\Sigma ) \,, \quad \quad \quad \quad \quad r=r_\Sigma \,, \end{aligned}$$
(24)

where we have defined \({\bar{\sigma }}\) and \({\bar{p}}\) as the corresponding quantities without \(n^c\nabla _c\delta \left( l\right) \), i.e., \(\bar{\sigma }\left( l\right) ={\bar{\sigma }}\, n^c\nabla _c\delta \left( l\right) \) and \({\bar{p}}\left( l\right) ={\bar{p}} \,n^c\nabla _c\delta \left( l\right) \), and where \(g(r_\Sigma )\) is a function of \(r_\Sigma \) and also depends on the remaining free parameters that characterize the interior and exteriors regions, see the Appendix B for the explicit expression. These are the expressions for the double layer surface energy density and surface pressure that each thin shell, one in the upper domain, another in the lower domain, must satisfy. We have now to check the NEC for this double layer part of the stress–energy tensor, \(s_{ab}(l)\). Since \(s_{ab}(l)\) is proportional to a derivative of a delta function, namely, \(n^c\nabla _c\delta \left( l\right) \), it is not enough to verify whether \(s_{ab}(l)k^ak^b\ge 0\) is satisfied at the thin shell. One has to verify the inequality in the neighborhood of the thin shell, i.e., whether \(\int s_{ab}(l)k^a k^b dl\ge 0\) holds, for \(k^a\) any null vector. A null vector \(k^a\) satisfies \(g_{ab}k^ak^b=0\), and so it can be written, apart some conformal factor, as \(k^a=\left( \frac{-1}{\sqrt{g_{tt}}},\frac{a}{\sqrt{g_{rr}}}, \frac{b}{\sqrt{g_{\theta \theta }}}, \frac{c}{\sqrt{g_{\phi \phi }}}\right) \), where the parameters a, b and c satisfy the condition \(a^2+b^2+c^2=1\). One can now compute \(\int s_{ab}(l)k^a k^b dl\). Putting \(s\equiv \frac{\alpha }{4\pi }g(r_\Sigma )\) to shorten the notation, one has \(s_{ab}\left( l\right) = s \,h_{ab}n^c\nabla _c\delta \left( l\right) \). Thus, \(\int s_{ab}(l)k^a k^b dl =\int s \,h_{ab}k^a k^b n^c\nabla _c\delta \left( l\right) dl\). One can perform this integral by parts to obtain \( \int s \,h_{ab}k^a k^b n^c\nabla _c\delta \left( l\right) dl = \int n^c\partial _c\left[ s \,h_{ab}k^a k^b \delta \left( l\right) \right] dl -\int n^c\nabla _c \left( s \,h_{ab} k^a k^b \right) \delta \left( l\right) dl \). The first term, \(\int n^c\partial _c\left[ s \,h_{ab}k^a k^b \delta \left( l\right) \right] dl\), can be integrated directly and can be seen to vanish because at the limits of integration in l the function \(\delta (l)\) is zero, i.e., \(\left[ s \,h_{ab}k^a k^b \delta \left( l\right) \right] _{l_{\textrm{min}}}^{l_{\textrm{max}}}=0\). The second term, \(-\int n^c\nabla _c \left( s \,h_{ab} k^a k^b \right) \delta \left( l\right) dl\), however, does not vanish. Indeed, since s is a constant one can write \(-n^c\nabla _c \left( s \,h_{ab} k^a k^b \right) =-s n^c\nabla _c \left( h_{ab} k^a k^b \right) \). Now, on any neighborhood of \(\Sigma \), the null vector \(k^a\) can be any, and so the term \(h_{ab}k^ak^b\) can be different along any radial path in several manners, in certain radial paths it is negative, in others it is zero, and yet in some others is positive, and thus the integral can have negative values for arbitrary \(k^a\). So, the NEC condition on the stress–energy component \(s_{ab}(l)\) is not satisfied. Moreover, even at \(\Sigma \), the NEC may not be satisfied. In this case one needs to check that \(s_{ab}k^ak^b\ge 0\) at \(\Sigma \). As we have seen above for \(S_{ab}\), now repeated for \(s_{ab}\), this means \({\bar{\sigma }}\ge 0\) and \({\bar{\sigma }}+{\bar{p}}\ge 0\). Here, from Eq. (24) one has \({\bar{\sigma }}+{\bar{p}}=0\) and the sign of \({\bar{\sigma }}\) depends on the function \(g(r_\Sigma )\).

4.3 Full solution for a traversable wormhole with matter and double layer thin shell

We now provide specific values for the parameters appearing in this wormhole solution in order to find an explicit solution.

Let us choose a quadratic theory of gravity for which the coupling constant \(\alpha \) has the value

$$\begin{aligned} \alpha =0.013, \end{aligned}$$
(25)

in Planck units. In fact, one should write \(\alpha =0.013 \left( \frac{1}{M_{\textrm{pl}}}\right) ^2\) where \(M_{\textrm{pl}}\) is the Planck mass, but in the natural system of units considered here, the Planck mass is one, and thus \(\alpha =0.013\). We take the exterior mass M as the scale for the whole solution. We can now describe a full solution composed of the two symmetric domains of the interior region, the two double layer thin shells at the mouths \(\Sigma \), and the two symmetric asymptotically flat domains of the exterior region.

For the two symmetric domains of the interior, we have the line element Eq. (13), and choose for redshift constant \(\zeta _0\) the value

$$\begin{aligned} \zeta _0=-60, \end{aligned}$$
(26)

and for the throat radius \(r_0\) the value

$$\begin{aligned} r_0=2M. \end{aligned}$$
(27)

These are the same numbers as chosen for the solution plotted in Figs. 1 and 2. We have seen that for these parameters the NEC is satisfied at the throat of the wormhole \(r_0=2M\), and is indeed satisfied up to the radius \(r_\Sigma \). We can also note in passing that, for these parameters, the WEC is also satisfied at the throat since \(\rho >0\), although this feature per se is not of major physical importance, since the WEC is violated elsewhere.

For the two thin shells, one at each mouth, the results are the following. The first junction condition, Eq. (19), gives

$$\begin{aligned} \zeta _e=-54.847. \end{aligned}$$
(28)

The second junction condition, Eq. (20), gives

$$\begin{aligned} r_\Sigma =2.024M. \end{aligned}$$
(29)

The third junction condition, Eq. (21), gives

$$\begin{aligned} \sigma =-\frac{1}{8\pi } \frac{58.642}{M},\quad \quad p=\frac{1}{8\pi }\frac{62.964}{M}, \end{aligned}$$
(30)

which are the values of the energy density and the pressure at each of the thin shells, the upper one and the lower one. From Eq. (30) we have \((\sigma +p)=\frac{1}{8\pi } \frac{4.322}{M}\). Thus, although \(\sigma +p>0\) and thus the NEC is satisfied for null vectors on the shell, one has \(\sigma <0\), meaning that the NEC is not satisfied for null vectors out of the shell, and so this piece of the thin shell stress–energy tensor does not satisfy the NEC. The fourth junction condition, Eq. (22), gives the external normal pressure at each thin shell,

$$\begin{aligned} P=\frac{1}{8\pi }\dfrac{1.515}{M}. \end{aligned}$$
(31)

Since \(P>0\), it implies that this piece of the thin shell stress–energy tensor satisfies the NEC. The fifth junction condition, Eq. (23), gives the external flux momentum at each thin shell, which vanishes,

$$\begin{aligned} F_\alpha =0. \end{aligned}$$
(32)

Since \(F_\alpha =0\), it implies that this piece of the thin shell stress–energy tensor satisfies the NEC. The sixth junction condition, Eq. (24), gives the stress–energy tensor distribution of the corresponding double layer at each of the two thin shells, which for our particular choice of parameters yields

$$\begin{aligned} {\bar{\sigma }}=-\frac{1}{4\pi } \frac{ 0.319}{M^2}\,,\quad \quad \bar{p}=\frac{1}{4\pi } \frac{ 0.319}{M^2} \,. \end{aligned}$$
(33)

Thus, \({\bar{\sigma }}+ {\bar{p}}=0\) and \({\bar{\sigma }}<0\). It implies that this piece of the thin shell stress–energy tensor does not satisfy the NEC.

In summary, this traversable wormhole is a symmetric wormhole solution. It presents combinations of \(\rho +p_r\) and \(\rho +p_t\) for the two domains of the interior region that are positive in the range of r between the wormhole throat radius \(r_0\) and the shell radius \(r_\Sigma \). At the the two shell radii, \(r_\Sigma \), the solution yields \(\sigma +p>0\) with \(\sigma <0\), \(P>0\), \(F_\alpha =0\), and \({\bar{\sigma }}+ {\bar{p}}=0\) with \({\bar{\sigma }}<0\). For the exterior region, \(r>r_\Sigma \), the stress–energy tensor vanishes and so the NEC is satisfied. Thus, we see that the stress–energy tensor has two components that do not satisfy the NEC. Although we have not proved, in practical terms we found it impossible to have this type of traversable wormholes with thin shell double layers in quadratic gravity having the NEC satisfied for all pieces of the wormhole matter stress–energy tensor.

5 Thin shell traversable wormholes with a single layer in quadratic \(R+\alpha R^2\) gravity

5.1 General considerations

A thin shell traversable wormhole is defined as a traversable wormhole with no interior and with the thin shell located precisely at the throat. Here, we construct a thin shell traversable wormhole with a single layer. For the construction of a thin shell traversable wormhole with a double layer see [27].

In a thin shell traversable wormhole, the two domains of the exterior region are matched directly to each other at a given throat radius \(r_0\), which in turn coincides with the matching boundary radius \(r_\Sigma \), i.e., the throat and the two mouths coincide. Since we are interested in a wormhole solution for which the matching is done with a single layer thin shell at the separation boundary, the double layer junction conditions, Eqs. (4)–(9), can be used noting that they reduce by a careful examination to a single layer thin shell matching, as shown in Sec. 3. The wormhole to be constructed is asymmetric, i.e., the two domains of the exterior region, situated at each side of the throat, are different. \({{\mathcal {V}}}^+\) is now the upper domain, say, and \({{\mathcal {V}}}^-\) is now the lower domain, the whole wormhole spacetime \({{\mathcal {V}}}\) is composed of \({{\mathcal {V}}}^+\) and \({{\mathcal {V}}}^-\) plus the thin shell at the throat \(\Sigma \).

5.2 Asymmetric single layer thin shell traversable wormhole solutions satisfying the NEC and all the energy conditions at the throat

5.2.1 The interior

By definition, the interior of a thin shell traversable wormhole is an empty set, i.e., it has no line element and no stress–energy tensor, so it is degenerated.

5.2.2 The exterior made of two asymmetric domains

For the exterior region made of two domains, the upper and the lower, one possibility would be to consider two vacuum Schwarzschild spacetimes with the same mass M. However, this is not feasible, since the third junction condition \(\left[ K\right] =0\) would not be satisfied at any radius \(r_\Sigma \). We thus consider instead two Schwarzschild spacetimes, the upper exterior domain with positive mass, M, and the lower exterior domain with negative mass, \(-M\), thus it is a domain of gravitational repulsion. In this case the line elements for the two spacetime domains of the exterior region, the upper and lower domains, are

$$\begin{aligned} \begin{aligned} ds^2=&-\left( 1-\frac{2M}{r}\right) e^{\zeta _u}dt^2+ \left( 1-\frac{2M}{r}\right) ^ {-1}dr^2+r^2d\Omega ^2\,\,\\ r_0=&r_\Sigma \le r<\infty \quad \mathrm{upper \; domain}, \\ ds^2=&-\left( 1+\frac{2M}{r}\right) \;\;dt^2\;+\, \left( 1+\frac{2M}{r}\right) ^ {-1}dr^2+r^2d\Omega ^2,\,\\ r_0=&r_\Sigma \le r<\infty \quad \mathrm{lower \; domain}, \end{aligned} \end{aligned}$$
(34)

where the radial coordinate ranges from \(r_0=r_\Sigma \) to infinity, i.e., \(r_0=r_\Sigma \le r<\infty \), for both spacetime domains of the exterior region, the throat radius \(r_0\) and the two mouths at \(r_\Sigma \) coincide in this case, and \(\zeta _u\) is a constant introduced in the upper domain line element for later convenience. Since the two line elements of Eq. (34) have \(R_{ab}=0\), and are vacuum regions, i.e., \(T_{ab}=0\), they are solutions of the quadratic gravity field equation given in Eq. (3). These two exterior spacetimes are to be matched at the radius \(r_\Sigma \) with a single layer thin shell.

5.2.3 Matching the two domains of the wormhole exterior: A single layer thin shell

Let us now apply the junction conditions provided in Eqs. (4)–(9) in the single layer matching situation, see Sec. 3, to the two domains of the wormhole exterior, Eq. (34). In the junction conditions we set \(\epsilon =1\) which is the value appropriate for a timelike thin shell, the case we are considering.

The first junction condition, i.e., Eq. (4), \(\left[ h_{ab}\right] =0\) provides a constraint on the constant \(\zeta _u\) of the form

$$\begin{aligned} r_\Sigma +2M=\left( r_\Sigma -2M\right) e^{\zeta _u}, \end{aligned}$$
(35)

where the radius \(r_\Sigma \) at which the matching is performed will be set by the second junction condition.

The second junction condition, i.e., Eq. (5), \(\left[ K\right] =0\), can be written as

$$\begin{aligned} \frac{2r_\Sigma -3M}{\sqrt{1- \frac{2M}{r_\Sigma }}}=\frac{2r_\Sigma +3M}{\sqrt{1+\ \frac{2M}{r_\Sigma }}}. \end{aligned}$$
(36)

This equation can now be solved for \(r_\Sigma \). Then, the value found for \(r_\Sigma \) can be inserted into Eq. (35) to obtain the value of \(\zeta _u\).

The third junction condition, i.e., Eq. (6), for a single layer matching is reduced to the following form \(-\left[ K_{ab}\right] + 2\alpha \left( h_{ab}n^c\left[ \nabla _c R\right] - R^\Sigma \left[ K_{ab}\right] \right) =8\pi S_{ab}\). We assume that the thin shell is made of an isotropic perfect fluid. For a perfect fluid, the tensor \({S_\alpha }^\beta \) takes a diagonal form, and we can write \( {S_\alpha }^\beta =\text {diag}\left( -\sigma ,p,p\right) \). Defining the four-dimensional surface stress–energy tensor as \(S_{ab}= e_a^\alpha e_b^\beta S_{\alpha \beta }\), the third junction condition for a single layer thin shell yields the surface energy density \(\sigma \) and the transverse pressure p of the thin shell as having the expressions \(\sigma = \frac{\left[ K_0^0\right] }{8\pi }\) and \(p=\frac{\left[ K_0^0\right] }{16\pi }\). Since \(\left[ K_0^0\right] = \frac{M}{r_\Sigma ^2}\left( \sqrt{\frac{r_\Sigma }{r_\Sigma -2\,M}}+ \sqrt{\frac{r_\Sigma }{r_\Sigma +2\,M}} \right) \), the full expressions are

$$\begin{aligned} \sigma =&\frac{1}{8\pi } \frac{M}{r_\Sigma ^2}\left( \sqrt{\frac{r_\Sigma }{r_\Sigma -2M}}+ \sqrt{\frac{r_\Sigma }{r_\Sigma +2M}} \right) \,,\nonumber \\ p =&\frac{1}{8\pi } \frac{M}{2r_\Sigma ^2}\left( \sqrt{\frac{r_\Sigma }{r_\Sigma -2M}}+ \sqrt{\frac{r_\Sigma }{r_\Sigma +2M}} \right) \,. \end{aligned}$$
(37)

Then, the value found for \(r_\Sigma \) in Eq. (36) can be inserted into Eq. (37) to obtain the values of \(\sigma \) and p. The NEC for \(S_{ab}\) is satisfied if \(S_{ab}k^ak^b\ge 0\) for any null vector \(k^a\). In an orthonormal tetrad one has \(S_{ab}=(\sigma ,0, p, p)\), null vectors on the shell have the form \(k^a=(1,0,1,0)\) or \(k^a=(1,0,0,1)\), and null vectors out of the shell have the form \(k^a=(1,1,0,0)\). This implies that the NEC is satisfied if \(\sigma +p\ge 0\) and \(\sigma \ge 0\).

The fourth junction condition, Eq. (7), which is now reduced to \([R]=0\), is automatically satisfied for any matching radius \(r_\Sigma \) since the two spacetimes given in Eq. (34) have \(R_{ab}=0\) and so \(R=0\).

The fifth and sixth junction conditions, Eqs. (8) and (9), respectively, are trivially satisfied, as both sides of the equations vanish.

5.3 Full solution for the single layer thin shell traversable wormhole

For the thin shell traversable wormhole solution considered there are no free parameters. The two line elements given in Eq. (34) depend solely on the mass M which is used as a scale in the problem, and the coupling constant \(\alpha \) does not play a role since both domains of the exterior region have \(R=0\). Thus, these thin shell wormholes with a single layer and vacuum domains in the exterior region are solutions of quadratic gravity for any value of \(\alpha \), including \(\alpha =0\), i.e., general relativity. Note that the reverse is not true, wormhole solutions in general relativity are not by rule wormholes in quadratic theories of gravitation, as the case we mentioned in the passing above is an example of, i.e., two Schwarzschild solutions with the same positive mass M matched at the throat are solutions in general relativity but not solutions in the quadratic theory presented here. Let us describe in full the wormhole.

The interior is an empty set, indeed there is no interior per se.

The matching thin shell is at a radius \(r_\Sigma \) which coincides with the radius \(r_0\) of the throat, \(r_0=r_\Sigma \). The thin shell properties are determined from the junction conditions. The first junction condition, i.e., Eq. (35), provides a constraint on the constant \(\zeta _u\), where the radius \(r_\Sigma \) at which the matching is performed is set by the second junction condition, i.e., Eq. (36), which yields \(r_\Sigma =\frac{3}{\sqrt{2}}\,M\). This value can be inserted into Eq. (35) to obtain \(\zeta _u=\ln \left( 17+12\sqrt{2}\right) \). Thus, we have

$$\begin{aligned} e^{\zeta _u}=17+12\sqrt{2}, \end{aligned}$$
(38)

which is approximately \(e^{\zeta _u}=33.981\), and

$$\begin{aligned} r_\Sigma =\frac{3}{\sqrt{2}}\,M, \end{aligned}$$
(39)

which is approximately \(r_\Sigma =2.121\). The third junction condition, i.e., Eq. (37), then gives

$$\begin{aligned} \sigma = \frac{1}{8\pi }\frac{1.089}{M}\,,\quad \quad p = \frac{1}{8\pi }\frac{0.544}{M}\,. \end{aligned}$$
(40)

Then, \(\sigma +p=\frac{1}{8\pi }\frac{1.633}{M}\). Since \(\sigma +p\) and \(\sigma \) are positive, the NEC for the matter at the thin shell is satisfied. Furthermore, since also \(p>0\), and \(\sigma =2p\), one can show that this actually implies that all energy conditions are satisfied by the matter at the thin shell, as \(\sigma \ge 0\), \(\sigma +p\ge 0\), \(\sigma +2p\ge 0\), and \(\sigma \ge |p|\). Given that both the upper and lower spacetime domains are vacuum solutions, which automatically satisfy all energy conditions, the single layer thin shell traversable wormhole solution obtained satisfies all energy conditions for the entire spacetime. The fourth junction condition is automatically satisfied. Note also that since \(r_\Sigma =\frac{3}{\sqrt{2}}\,M\) is approximately \(r_\Sigma =2.121M\) one has that \(r_\Sigma \) satisfies \(r_\Sigma >2M\). Since the upper spacetime domain solution given in Eq. (34) has positive mass M with \(r_\Sigma >2M\), there is no horizon on this side of the solution, and since the lower domain spacetime solution given in Eq. (34) has negative mass \(-M\), there is no horizon from that side also, thus guaranteeing the traversability of the solution.

In summary, this solution represents an asymmetric traversable wormhole with a single layer thin shell that satisfies all the energy conditions. More specifically, the wormhole has no interior and possesses a single layer thin shell at the throat that joins an upper domain, belonging to the exterior region, described by a Schwarzschild spacetime with positive mass to a lower domain, also belonging to the exterior region, described by a Schwarzschild spacetime with negative mass. In this wormhole, whatever matter is attracted from the upper region into the throat is expelled repulsively from the throat into the lower region.

6 Conclusions

We have found asymptotically flat traversable wormhole solutions in the quadratic theory of gravity given by the following \(f\left( R\right) \) function, \(f\left( R\right) =R+\alpha R^2\). One set of wormhole solutions has double layer thin shells at the interfaces between an interior with two domains made of nonexotic perfect fluid material and a symmetric exterior with two Schwarzschild spacetime domains. These double layers are characteristic of quadratic theories of gravity, and although there are no two different types of charge in gravitation they are analogous to dipole double layers in electrodynamics. The NEC for these double layer traversable wormholes has been tested and it was found that at the throat and for the whole wormhole interior it is satisfied, and at the two thin shells some stress–energy tensor components satisfy it, while others, for instance, the double layer distribution component, do not. Another set of wormhole solutions found has a single layer thin shell at the the throat, characteristic of thin shell traversable wormhole solutions, and two asymmetric exterior Schwarzschild spacetimes, one with positive mass, the other with negative mass. The matter at the thin shell satisfies the NEC.

The set of six junction conditions in quadratic gravity for a double layer matching implies fewer restrictions to the solutions, and thus the method outlined to obtain traversable wormhole spacetimes with double layer thin shells allows to find numerous solutions for a great variety of combinations of parameters, although it seems that the NEC is basically impossible, or at least very hard, to be satisfied when double layer thin shells are present, at least in this quadratic theory of gravity. The set of four junction conditions for a single layer matching, which can be found directly from the double layer set of junction conditions, is more constrained, and thus hampers the construction of traversable wormhole spacetimes, although traversable thin shell wormholes, asymmetric ones, that satisfy the NEC at the throat were possible to construct. The set of three junction conditions for a boundary surface matching, which can be found directly from the previous sets of junction conditions, restricts even further the constructions of this type of wormholes, and we have not been able to find a solution with a smooth boundary surface matching.