Abstract
The weakest known criterion for local rotational symmetry (LRS) in spacetimes of Petrov type D is due to Goode and Wainwright (Gen Rel Grav 18:315, 1986). Here it is shown, using methods related to the Cartan-Karlhede procedure, to be equivalent to local spatial rotation invariance of the Riemann tensor and its first derivatives. Conformally flat spacetimes are similarly studied and it is shown that for almost all cases the same criterion ensures LRS. Only for conformally flat accelerated perfect fluids are three curvature derivatives required to ensure LRS, showing that Ellis’s original condition for that case is necessary as well as sufficient.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Ellis [12] introduced the concept of local rotational symmetry of spacetime (LRS). He set out three definitions for which he then proved equivalence in the case of spatial rotations in dust spacetimes in general relativity. His definition (B) reads “At each point P in an open neighbourhood V of a point \(P_o\), there exists a nondiscrete isotropy group.” Because only dust matter content was considered, this isotropy had to be a spatial rotation group. Assuming that the dust was not both shear-free and nonrotating, Ellis proved the equivalence of (B) with the definitions:
“(A\({}_m\)) At each point P in an open neighbourhood U of a point \(P_o\), there exists a nondiscrete subgroup g of the Lorentz group in the tangent space \(T_P\) which leaves invariant the curvature tensor and all its covariant derivatives to the m-th order” (Ellis took \(m=3\))Footnote 1 and “(C) There exists a local group of motions \(G_r\) in an open neighbourhood W of a point \(P_o\) which is multiply transitive on some q[-dimensional] surface through each point P of W”. (This implies \(r > q\)).
Stewart and Ellis [50] then generalized the dust result to spacetimes containing perfect fluid and/or an electromagnetic field.
This is the first of a set of papers finding the minimal m in (A\({}_m\)) which guarantees (C) [and (B)] for the three cases where the group g contains respectively a spatial rotation, a boost and a null rotation. For clarity g will be referred to as a local invariance, or a linear isotropy as defined below, ‘isotropy’ without a preceding qualifier being reserved for the spacetime isometry at each point \(P \in W\) which leaves P fixed. When there is an isotropy, it induces a local invariance: these papers address the converse, with the aim of facilitating identification of such solutions (via the methods discussed in Sect. 2) if rediscovered in unusual coordinates or from other assumptions.
Where there is isotropy, the spacetimes, following Ellis, will be called locally rotationally symmetric (LRS). Analogously, ‘locally boost symmetric’ (LBS) and ‘locally null rotation symmetric’ (LNRS) may be used. LRSI, LBI and LNRI may similarly be used for the local invariances imposed by (A\({}_m\)).
In the definition (A\({}_m\)), it is implicit that g is the same at all P in U, i.e. that \(g_P \cong g_{P_o}\) and \(g_P\) at P and \(g_{P_o}\) at \(P_o\) have the same action on the curvature and its derivatives at those points. The spacetime metric is also assumed to be of class \(C^{n},~n\ge m+2\), so that the m-th covariant derivatives of the curvature are well defined and continuous. (C) \(\Rightarrow \) (A\({}_m\)) for all \(m \le n\). For brevity, (A\({}_\infty \)) will mean that (A\({}_m\)) is true for all m for which the derivatives are continuous, but that notation does not mean that the metric is assumed to be \(C^\infty \).
The elements of g form the linear isotropy group at P: here ‘linear’ distinguishes a group of transformations of the tangent plane at P from a group of motions in the spacetime, or a neighbourhood thereof, leaving P fixed (isotropies). The linear isotropies could also be called local isotropies but to avoid confusion that term will not be used in this paper: ‘local’ here will mean that the same condition holds throughout a neighbourhood.
‘Spacetime’ here simply means a four-dimensional Lorentzian manifold. The field equations of general relativity will not be used, but cases where the Ricci tensor takes the form that would be implied by specific matter content in general relativity will be referred to.
In [46], §1.9, it is stated that any spacetime can be characterized by second and third order invariants of the metric (the Riemann tensor and its first derivatives): while this result, and hence the proof claimed by Siklos [46], are now known to be false, as shown by Karlhede and Åman [23] and by the series of examples [24, 32, 47, 48] needing higher derivatives, culminating in the proof [38] that for a particular metric one needs the 7-th derivative of the Riemann tensor (a 9-th order invariant of the metric), it provided the initial conjecture that (A\({}_1\)) would be sufficient to imply isotropy, which will be proved for LRSI or LBI Petrov type D spacetimes and almost all of the conformally flat cases. This will be referred to as Siklos’ conjecture.
Only Petrov type D and conformally flat spacetimes have a Weyl tensor that can satisfy (A\({}_0\)) (or (A\({}_m\)) for larger m) with a linear isotropy group g containing spatial rotations and/or boosts. Similarly, only Petrov type N or conformally flat spacetimes can satisfy (A\({}_m\)) with null rotations in g. The boost and null rotation cases are studied in the later papers of this series. The spatial rotation and boost cases are related by the asterisk operation of the GHP formalism [14].Footnote 2 Note that both rotational and boost isotropies lead to calculations, in an appropriate null tetrad \((\varvec{k},\, \varvec{l},\,\varvec{m},\,\varvec{\overline{m}})\), with a natural interchange symmetry between \(\varvec{k}\) and \(\varvec{l}\).
There are rather more Ricci tensor types than Weyl tensor types that can satisfy (A\({}_0\)) for spatial rotations (or boosts or null rotations). For (A\({}_0\)) to apply to the whole Riemann tensor, the Weyl and Ricci tensors must of course be appropriately aligned, and there may be a nonzero Ricci scalar R. The tracefree part of the Ricci tensor can be characterized by its Segre type. The possible isotropy groups of the Ricci tensor were listed by Segre type in Table 5.2 of Stephani et al. [49]. Table 1 here lists those with nontrivial invariance groupsFootnote 3\(\hat{I}_0\) which include a spatial rotation. The possible \(\hat{I}_0\) appear in the list of subgroups of the Lorentz group in Table 6.1 of Hall [18], which follows work of Shaw and Schell.
Cahen and Defrise [7] showed that for all LRSI or LBI Petrov type D spacetimes (A\({}_2\)) was a sufficient criterion for the spacetime to be LRS or LBS. Subsequently Goode and Wainwright [15] gave criteria for the LRS Petrov type D case in terms of properties of the values of the spin coefficients and curvature expressed in a Newman–Penrose (NP) null tetrad.
The methods used in this paper are introduced in Sect. 2. They are based on the Cartan-Karlhede procedure for characterizing spacetimes and testing their equivalence, and the software CLASSI embodying it using the Newman–Penrose formalism. (Where CLASSI is mentioned below, hand calculation, or suitable alternative software, could of course be used.) The Cartan-Karlhede procedure provides a natural context for the investigation of (A\({}_m\)). With these methods it is shown that Ellis’s original characterization for LRS can be sharpened in almost all cases, and the characterization of Goode and Wainwright re-formulated.
In Sect. 3, the Goode and Wainwright criteria are shown to be equivalent to (A\({}_1\)), and to imply (A\({}_m),~m\le 4\), with a spatial rotation as the local invariance. From the Cartan-Karlhede procedure as outlined in Sect. 2, this implies that the spacetime is LRS and there is a local isometry group \(G_r~(r\ge 3)\). Thus the Siklos conjecture is proved for the type D LRS case.
Many of the steps in Sect. 3 are not original, but simply echo those of Goode and Wainwright. They are set out here because they prompted and illustrate the strategy used in the rest of this paper and its companion papers. Having imposed conditions on curvature consistent with the invariance being studied, one uses the Bianchi identities and the conditions implied by (A\({}_1\)) in order to obtain conditions on the spin coefficients, and then uses the Ricci identities (“NP” equations), any additional conditions implied by (A\({}_m),~m > 1\), and in some cases the commutator relations, to complete the arguments.
Section 4 considers the (A\({}_m\)) required for LRS in LRSI conformally flat spacetimes, including the cases studied by Ellis [12] and Stewart and Ellis [50] not included in Sect. 3. Here a three-dimensional group of spatial rotations is possible, not just the one-dimensional group allowed by Petrov type D, provided the Ricci tensor has Segre type [(111), 1] or [(111, 1)].
A somewhat different approach to the LRS perfect fluid cases (Segre type [(111), 1]), using a \(1+3\) “threading” description of spacetime, was given by Van Elst and Ellis [51]. In other related work, Marklund [33] and Marklund and Bradley [34] considered the construction of the metrics for LRS perfect fluid solutions starting from data on the curvature, some of the rotation coefficients and expressions involving invariantly defined coordinates. A large number of papers have considered solving the field equations of general relativity for the LRS cases with various matter contents: see for example sections 13.4 and 14.3, and Chapters 15 and 16, in [49], and sections 2.6, 2.11 and 7.5 and Chapter 4 of Krasiński [25].
A complementary problem of finding the possible metrics and their curvatures assuming a multiply-transitive group acting on nonnull hypersurfaces (i.e. assuming at least a \(G_4\) rather than a \(G_3\)) was addressed in [27], using a method due to Schmidt [42, 44].
Whenever there is a local isometry group \(G_r\) in a neighbourhood, the result of Hall [17] implies that the neighbourhood is isometric to a region of a spacetime with a global isometry group \(G_r\) or larger, provided that one has a simply-connected connected smooth Hausdorff manifold with smooth Lorentz metric. The smoothness is essential since, for example, junction conditions allow one to match Schwarzschild and Szekeres spacetimes at a spherical boundary [5].
One can also consider analogous results for discrete rather than continuous linear isotropy groups: a first result for such isotropies was proved by Schmidt [43], and another by Debever et al. [10]. In collaboration with Filipe Mena I have worked further on Schmidt’s and related cases [35,36,37]. It was in updating and completing that work that the issues covered in this paper arose. There has also been consideration of spacetimes where there are homotheties, rather than isometries, with fixed points [16].
2 The Cartan-Karlhede procedure
2.1 The procedure and spacetime characterization
The Cartan-Karlhede procedure for characterizing spacetimes relies on Theorem 9.1 in [49], which is Cartan’s result as stated by Sternberg and Ehlers. The current way to apply this result was introduced by Karlhede [2, 19,20,21] and is set out in Chapter 9 of Stephani et al. [49] and elsewhere. It consists of the following iteration, where \(\mathcal{R}^q\) denotes the set \(\{R_{abcd},\,R_{abcd;f} ,\,\ldots ,R_{abcd;f_1f_2\cdots f_q}\}\) of the components of the Riemann tensor and its derivatives up to the qth.
-
1.
Set the order of differentiation q to 0.
-
2.
If \(q >0\), calculate the qth derivatives of the Riemann tensor.
-
3.
Find the canonical form of \(\mathcal{R}^q\).
-
4.
Fix the frame as far as possible by this canonical form, and note the residual frame freedom. The group of allowed transformations is a linear isotropy group \(\hat{I}_q\).Footnote 4 Let us denote \(\dim \hat{I}_q\) by \(s_q\). Necessarily \(s_q \le s_{(q-1)}, \forall q>0\).
-
5.
Find the number \(t_q\) of independent functions of space-time position in \(\mathcal{R}^q\) in the canonically chosen frame. Necessarily \(t_q \ge t_{(q-1)}, \forall q>0\).
-
6.
If the isotropy group and number of independent functions are the same as at the previous step, let \(p+1 = q\) and stop; if they differ (or if q = 0) increment q by 1 and go to stage 2.
The iteration of 2–5 above for a given q will be referred to as step q of the Cartan-Karlhede procedure. The quantities computed, i.e. the components in \(\mathcal{R}^p\) in a canonically chosen frame, are scalar invariants defined by the curvature and its derivatives: they are called Cartan invariants. One may also use functions of these invariants, e.g. their ratios, which are also scalar invariants. In particular these may be spin coefficients or Ricci rotation coefficients evaluated in the canonically chosen frame, as mentioned below. Such quantities can be called extended or derived Cartan invariants, and for brevity here will just be called invariants.
The space-time is then characterized locally by the canonical form chosen, the successive linear isotropy groups and independent function counts, and the values of the non-zero invariants. It is sometimes convenient to use the term “s sequence” for \((s_0,\,s_1,\,s_2,\ldots )\) and similarly for t. The isotropy group of the space-time will have dimension \(s = s_p =\mathrm{dim}{ }\hat{I}_p\). Since there are \(t_p\) essential space-time coordinates, clearly the remaining \(4-t_p\) are ignorable so the isometry group has dimension \(\displaystyle {r = s + 4 - t_p}\) (see e.g. [19]). Note that if \(s \ge 1\), (A\({}_{(p+1)}\)) is true, and vice versa.
Considering stage 4 of the above iteration, one may note that linear isotropies imply that the basis vectors in the subspaces invariant under their action can be determined only up to those transformations. Spatial rotations about an axis and boosts act respectively in spacelike or timelike two-planes; a position-dependent boost or rotation (respectively) can be used in the orthogonal two-planes to determine the frame as far as possible. This cannot determine the frame uniquely, but at best up to the linear isotropies. Similar remarks apply to the null rotation case.
In the calculations that follow, particular canonical choices of frame are used, but the outcomes are not frame dependent, being statements about geometric properties of the curvature and its derivatives. Those properties would merely be harder to recognize in a randomly chosen frame.
When a quantity Q is invariant under the remaining allowed transformations of a canonical frame determined by the curvature and its derivatives, then its derivatives will share the relevant (A\({}_m\)) isotropy and it can be included in the count of the \(t_i\). In what follows this will often be true of specific spin coefficients. Note that if the invariance applies only after a frame choice at step i then the derivatives of Q have to obey the isotropy only at steps \(j\ge (i+1)\). In practice the restrictions on derivatives of Q often follow from (e.g.) the NP equations, without invoking (A\({}_{i+1}\)), but this has not been systematically checked for all instances.
A (pseudo-)Riemannian manifold is said to be curvature-homogeneous of order k, denoted CH\({}_k\), if \(t_i=0,~\forall ~ 0\le i \le k\), and proper CH\({}_k\) if \(t_{k+1}>0\). Spacetimes which are CH\({}_k\) for all k are homogeneous. Milson and Pelavas [38] studied CH\({}_k\) spacetimes when finding the unique spacetime whose characterization requires the 7th derivative of the Riemann tensor: it is a proper CH\({}_2\) manifold. In the process they found that there are no CH\({}_3\) spacetimes and only a few possible CH\({}_1\) and CH\({}_2\) cases. Potential CH\({}_1\) and CH\({}_2\) cases have to be eliminated at some points in the following arguments.
2.2 Possible \((s_i,\,t_i)\) pairs in the Cartan-Karlhede procedure
There is an interplay between the \(t_i\) and \(s_{(i+1)}\) in the Cartan-Karlhede procedure. At step \((i+1)\), the \(t_i\) independent functions from step i will define \(t_i\) linearly independent vectors, their gradients. \(\hat{I}_{(i+1)}\) must preserve those vectors. If \(\hat{I}_{(i+1)}\) is a one-parameter local invariance group of spatial rotations or boosts, it acts in a two-dimensional non-null subspace, and the orthogonal subspace W in which the \(t_i\) gradients lie is also two-dimensional and non-null. Thus \(t_i\le 2\) in this case.
If \(\hat{I}_{(i+1)}\) is a one-parameter local invariance group of null rotations preserving a null vector \(\varvec{k}\), \(t_i\le 2\) is again true. This follows because \(\hat{I}_{(i+1)}\) also preserves a spatial vector orthogonal to \(\varvec{k}\), so there is only a two-dimensional space in which the \(t_i\) gradients can lie, although that space is not orthogonal to the two-space in which the null rotation invariance acts. Thus if (A\({}_\infty \)) holds with \(s=1\) there is at least a \(G_3\) acting on the spacetime.
If \(\mathrm{dim}{ } \hat{I}_{(i+1)}=2\), the linear invariance group consists either of boosts and rotations in orthogonal two-planes, so \(t_i=0\), or of null rotations preserving a null vector \(\varvec{k}\) in which case \(t_i\le 1\). If \(\mathrm{dim}{ } \hat{I}_{(i+1)}=3\), \(t_i\le 1\) again follows. (The group \(\hat{I}_{(i+1)}\) will be one of SO(3), SO(2,1), or the group generated by two null rotations preserving different null vectors and a spatial rotation. See Table 5.2 of Stephani et al. [49] and Table 6.1 of Hall [18].)
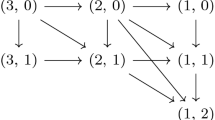
Possible pairs \((s,\,t)\) for spacetimes with local linear isotropies, and their evolution in successive steps of the Cartan-Karlhede procedure. For the full description see the text of Sect. 2.2
Figure 1 shows the resulting possible successive pairs \((s,\,t)\) with \(s_i\ne 0\) in the Cartan-Karlhede procedure, assuming one starts with \(s_0\le 3\) and ends with \(s\ge 1\) (thus omitting the possibility \(s_0=6\) which leads only to the well-known conformally flat Einstein spaces). The arrows join possible pairs at steps i and \(i+1\) if the procedure does not terminate at step i. The arrows showing termination at step i, which are loops back to the same values, have been omitted. Note that termination must happen at the pair \((1,\,2)\) if \(s=1\). Pairs \((s_i,\,t_i)\) and \((s_{(i+1)},\, t_{(i+1)})\) may be joined by two or more arrows e.g. one could have \((3,\,0)\rightarrow (1,\,2)\) in one step. There are of course spacetimes for which \(s=0\) but which have \(s_i\ge 0\) for some \(i<p\). An example is given by the metric of Koutras [24] that requires 4 derivatives (\(p=3\)) for its characterizationFootnote 5: there the \((s,\,t)\) sequence is \((3,\,0)\rightarrow (1,\,1) \rightarrow (0,\,3)\rightarrow (0,\,4)\).
2.3 Implementation
The Cartan-Karlhede procedure is embodied in the software CLASSI which is used below. A more extended description of the Cartan-Karlhede procedure was given by Pollney et al. [39,40,41], who provided modified, corrected and extended details, as compared with CLASSI’s version, which were used in their Maple implementation. Note that the details for the null rotation case are further corrected by the results of MacCallum [29].
CLASSI was developed by Jan Åman and collaborators, using and extending Inge Frick’s SHEEP software, and is described in [31] and more briefly in [28] (see also the manual [1] supplied with the software). To carry out the Cartan-Karlhede procedure CLASSI uses the Newman–Penrose formalism as set out in Chapter 7 of Stephani et al. [49].Footnote 6 The “Newman–Penrose equations” (the Ricci equations) and Bianchi identities [(7.21a)–(7.21r) and (7.32a)–(7.32k) in [49]] will be referred to below as (NPa)–(NPr) and (Ba)–(Bk). For any scalar Q, the vector defined by \(Q_{,a}\) is
As implemented in CLASSI, the Cartan-Karlhede procedure uses totally symmetrized multi-index spinors. A shorthand notation for those will be used here: it first appeared in print in [22]. It is an extension of the Newman–Penrose notation, in which, for example, the completely symmetric Weyl spinor \(\varPsi _{ABCD}=\varPsi _{(ABCD)}\) is represented by 5 componentsFootnote 7\(\varPsi _{A},~A=0\ldots 4\), formed by contractions with the basis spinors \((o^B,\,\iota ^B)\). The index A on \(\varPsi _{A}\) counts the number of contractions with \(\iota ^B\): thus, for example, \(\varPsi _{3}=\varPsi _{(BCDE)}o^B\iota ^C\iota ^D\iota ^E\).
This notation is extended as follows. Suppose that \(Q^{BCD\ldots }{}_{E'F'\ldots }\) is a completely symmetric multi-index spinor, so that \(Q^{BCD\ldots }{}_{E'F'\ldots }=Q^{(BCD\ldots )}{}_{(E'F'\ldots )}\). (Here the unprimed indices have been raised to enable clarity in the use of the standard notation for symmetrization, but the shorthand notation actually assumes all are covariant, i.e. lowered, in order to avoid the sign issues arising because for any spinors \(S^AT_A=-S_AT^A\).) Such a spinor is said to have valence \((m,\,n)\) if it has m unprimed and n primed indices. Then \(Q_{AB'}\) denotes the component in which A of the unprimed indices and B of the primed indices are contracted with the basis spinors \(\iota ^A\) and \(\bar{\iota }^{W'}\) respectively (and the other indices with \(o^A\) and \(\bar{o}^{X'}\)). As an example, consider the totally symmetrized part of the second covariant derivative of the Weyl spinor, \(\nabla _{AA'}\nabla _{BB'}\varPsi _{CDEF}\). It has valence \((6,\,2)\). The component \(\nabla ^2\varPsi _{41'}={\nabla ^{\left( A \right. }}_{\left( X'\right. }{\nabla ^B}_{\left. W'\right) }\varPsi ^{\left. CDEF\right) } o_Ao_B\iota _C\iota _D\iota _E\iota _F\bar{o}^{X'}\bar{\iota }^{W'}\).
A minimal set of Cartan invariants in the form of totally symmetrized spinors, taking into account their interrelations, and sufficient for the above procedure, was defined by MacCallum and Åman [30]. The set defined there contains the totally symmetrized derivatives of \(\varPsi \), \(\varPhi \) and \(\varLambda \), together with, at order 1, \(\Xi _{DEFW'}={\nabla ^C}_{W'}\varPsi _{CDEF}\) and at order \(q+2 \ge 2\), the d’Alembertians of quantities at order q. Although in principle unnecessary, it may be convenient at step q to consider in addition the gradients of quantities at step \((q-1)\).
For an LRSI totally symmetric spinor Q of valence \((m,\,n)\) only the components \(Q_{AB'}\) with \(2(A-B)=m-n\) are invariant under spatial rotation in the \((\varvec{m},\,\varvec{\overline{m}})\) plane; thus all other components must be zero. If the spacetime is LRSI, a canonically chosen frame will be one in which this is true.
3 Criteria for LRS Petrov type D spacetimes
It is known that in general Petrov type D vacua need at most 3 steps for classification [9]: in the non-vacuum case an upper bound of 6 steps was found [8]. Here it is shown that the smaller bound \(p=1\) applies when LRSI is assumed.
Petrov type D Weyl tensors are invariant under both boost and spatial rotation isotropies. If the Ricci tensor shares those symmetries, \(s_0=2\) and the only possible non-zero component of \(\varPhi _{AB'}\) in a canonical null tetrad is \(\varPhi _{11'}\). If \(s_1=2\), so that \(\hat{I}_1\) consists of both boosts and rotations, it has no fixed vectors so invariance of first derivatives of the curvature implies \(t_0=0\). None of the first derivative symmetrized spinor quantities defined by MacCallum and Åman [30] is invariant under both boosts and rotations, so they must all be zero; hence \(t_1=0\) and the Cartan-Karlhede procedure terminates at the first step. The resulting homogeneous spacetimes, (12.8) in [49], consist of two orthogonal two-dimensional spaces of constant curvature and admit an isometry group \(G_6\), like the well-known Bertotti-Robinson solutionFootnote 8.
The remaining Petrov type D cases with \(s>0\) must have \(s_1=1=s\), so \(\hat{I}_1\) consists of either rotations or boosts but not both. Here the case with rotations is studied, and in a companion paper the case with boosts. By the argument in Sect. 2, \(t_i \le 2\) at all \(i\ge 0\) in either case. Thus the Cartan-Karlhede procedure must terminate at \(p\le 3\), the worst case sequence being \((2,\,0)\rightarrow (1,\,0)\rightarrow (1,\,1)\rightarrow (1,\,2)\rightarrow (1,\,2)\): in this case the spacetime is proper CH\({}_1\). Thus showing that (A\({}_4\)) holds will always suffice to imply LRS for Petrov D spacetimes with LRSI.
Since the Petrov type is assumed to be D, a Newman-Penrose null tetrad can be chosen which is invariant under the group of spatial rotations in the \((\varvec{m},\,\varvec{\overline{m}})\) plane and in which the only nonzero \(\varPsi _A\) is \(\varPsi _2\). For LRSI the Ricci tensor and the first derivatives of curvature must also be invariant under those rotations. The rotational invariance of \(\nabla \varLambda \) implies
Of the \(\varPhi _{AB'}\) only \(\varPhi _{00'}\), \(\varPhi _{11'}\) and \(\varPhi _{22'}\) can be nonzero. Rotational invariance implies that the gradient of the scalar \(\varPsi _2\) in the symmetry plane is zero so \(\delta \varPsi _2=0 =\bar{\delta }\varPsi _2\). Rotational invariance of the Cartan invariants \(\nabla {\varPsi _{AB'}}\) requires that
which give respectively
The possibly non-zero components are \(\nabla \varPsi _{20'}\) and \(\nabla \varPsi _{31'}\). (The components not mentioned above are identically zero.) One may note that the results for \(\kappa \), \(\sigma \), \(\lambda \) and \(\nu \) show that condition (c) of the Kundt–Thompson theorem (Theorem 7.5 in [49]) is satisfied, and that (3.2) implies rotational invariance of \(\varPsi \).
Thus in Petrov type D invariance of the Riemann tensor and its first derivatives under spatial rotation implies that there is a Newman-Penrose tetrad (a canonical one for Petrov type D, unique up to a spatial rotation and boost) in which the following criteria hold
Goode and Wainwright [15] proved:
Theorem 1
(Theorem 2.1 of Goode and Wainwright [15]) A space-time (assumed conformally curved) is LRS if and only if there exists a null tetrad \((\varvec{k},\, \varvec{l},\,\varvec{m},\,\varvec{\overline{m}})\) in which (C1)-(C3) hold.
Conversely, (C1)–(C3) imply local rotational invariance of the curvature and its first derivatives. For the curvature this requires that \(\varPhi _{02'}=0\), which follows immediately from (C1) and (NPg). For the first derivatives \(\nabla \varLambda \) and \(\nabla \varPsi \) it has already been shown that LRSI follows from (C1) and (C3). The components of \(\nabla \varPhi \) that must vanish for LRSI are given in full as (4.1)–(4.5) in Sect. 4, and the relations between those components of \(\nabla \varPhi \) and the Bianchi identities are discussed there. Given (C1), those components all vanish, due to (Ba) and (Bd).
From (Bj) with (C1)–(C3) \(\delta \varPhi _{11'}=0\). The LRSI of the gradients of the other admissible components of the Ricci curvature (\(\varPhi _{00'}\) and \(\varPhi _{22'}\)) is equivalent to \((\bar{\alpha }+\beta )=0\), from (Ba) and (Bd). To prove from (C1)–(C3) that this holds requires some calculation. The detailed arguments of Goode and Wainwright [15] will be repeated here because they illustrate the strategy to be used in other cases and because variants of them also work for the conformally flat cases to be considered later (and for the local boost invariance to be considered in a companion paper).
Goode and Wainwright [15] begin their proof by substituting (C1) in (NPb, c, g, i and p) and using (C2) to show that
Therefore the spacetime must have Petrov type D or 0 and its Riemann tensor is invariant under the rotations. (Bg) and (Bh) now give \(\delta \varPsi _2=\bar{\delta }\varPsi _2=0\).
At this point the frame is only fixed up to a position-dependent boost (and an arbitrary spatial rotation). Under a boost with parameter A and a spatial rotation through \(\theta \), (C1)–(C3) are preserved and \((\bar{\alpha }+\beta )^\star = [(\bar{\alpha }+\beta )+\delta A]e^{i\theta }\), where \(\star \) denotes the transformed value. Goode and Wainwright [15] use the NP equations, Bianchi identities and the commutator expressions to show that one can choose a boost to obtain a frame in whichFootnote 9
This will complete the equivalence of (C1)–(C3) with an assumption of rotational invariance of the Riemann tensor and its first derivative in a Petrov type D spacetime. (The rotational invariance of \(\Xi _{AB'}\) is readily checked.) So all first derivatives of curvature including \(\nabla \varPhi \) will then be LRSI.
To prove that (C1)–(C3) imply (3.6) and the further equations which will eventually imply that (A\({}_4\)) is manifestly true, one first notes that (Bk) minus (Bf) gives
The commutator \([\delta ,\,\varDelta ]\) is applied to this. (Bd, h and j) yield \(\delta (\varPhi _{11'}+\varLambda -\varPsi _2)=0\), and (NPk and m) give
Using these, the commutator gives
if \(\varPsi _2\ne 0\). Thus if \(\mu \ne 0\), boosting the frame by \(A=\sqrt{\mu \bar{\mu }}\) will give (3.6). Similarly applying \([\bar{\delta },\,D]\) to the difference of (Bg) and (Bi), which gives
one obtains \(\delta \bar{\rho }=\bar{\rho }(\bar{\alpha }+\beta )\) if \(\varPsi _2\ne 0\). This calculation analogously uses (Ba, g and j) and (NPk and m) and shows that if \(\mu =0\) one can boost by \(A=\sqrt{\rho \bar{\rho }}\) to obtain (3.6).
If both \(\mu \) and \(\rho \) are 0, calculating \([\delta ,\,\bar{\delta }]A\) shows that the equations \(\delta A = -A(\bar{\alpha }+\beta )\) and its complex conjugate are compatible and thus have a solution, again giving (3.6).
To show the spacetime must be LRS, first substitute from (3.6) into (NPd) and (NPe) to show \(\delta (\varepsilon +\bar{\varepsilon })=0\) and similarly, from (NPo) and (NPr), \(\delta (\gamma +\bar{\gamma })= 0.\) (One may note that \(\rho \), \(\mu \), \((\varepsilon +\bar{\varepsilon })\) and \((\gamma +\bar{\gamma })\) are invariant under the spatial rotations.)
Summarizing, (3.2) implies that in a frame with boost chosen to ensure (3.6) the following hold.
In both Cahen and Defrise [7] and Goode and Wainwright [15] the proof that the spacetime is LRS is completed by introducing coordinates and finding the possible metrics. However, one can obtain that result in a coordinate-free manner using Cartan invariants. Inserting the Eqs. (3.2), (3.6) and (3.9) into the spinor k-th derivative quantities of MacCallum and Åman [30] for \(k=1\ldots 4\), one finds (A\({}_4\)) holds. (The further equations between spin coefficients etc found by Goode and Wainwright [15] are not needed in obtaining this result, though they may simplify the final expressions obtained.) Thus the Cartan-Karlhede procedure must terminate at \(p=3\) or earlier, with \(s\ge 1\) and \(t_p\le 2\). This gives:
Theorem 2
If a neighbourhood of a spacetime of Petrov type D is such that the Riemann tensor and its first derivative are invariant under a local spatial rotation isotropy, then the spacetime is locally rotationally symmetric and admits a multiply-transitive \(G_r ~(r\ge 3)\).
The converse is of course trivial.
One can show that in fact (A\({}_3\)) is sufficient to prove Theorem 2, i.e. that the spacetime cannot be proper CH\({}_1\), as follows.Footnote 10
If \(t_0=0\), \(\varPsi _2\) must be constant and constancy of \(\nabla \varPsi _{AB}\) then implies that \(\rho \) and \(\mu \) are constant. Any non-zero \(\varPhi _{AB'}\) are also constant. If at least one of \(\rho \) or \(\mu \) is non-zero then, from (NPa and q), or (NPh and n), \(\varepsilon +\bar{\varepsilon }\) and \(\gamma +\bar{\gamma }\) are constant (possibly zero). Calculation (using CLASSI) then shows that \(t_2=0\) i.e. all terms in the second derivatives would also be constant, so the Cartan-Karlhede procedure would terminate at step 1 or 2. If both \(\rho \) and \(\mu \) are zero, (NPa) and (NPn) imply \(\varPhi _{00'}=\varPhi _{22'}=0\), and then inspection (using CLASSI) shows that all first derivatives of the Riemann tensor, and hence all higher derivatives, are zero, and the Cartan-Karlhede procedure would terminate at step 1.
In showing that (A\({}_4\)) [a fortiori, (A\({}_3\))] is true, in order to prove Theorem 2, the rotational invariance of the Ricci tensor and its derivatives up to the fourth was checked but no assumption on invariance of these quantities other than (C2)–(C3) was made. In the conformally flat case one usually has to assume, rather than being able to derive, \(\varPhi _{02'}=0\). The nonvanishing of \(\varPsi _2\) in Petrov type D was used in deriving (3.2) and (3.6) but was not otherwise required in proving (A\({}_4\)). (3.2) and (3.6) imply (3.9) due to the NP equations. Thus if one can obtain (3.2) and (3.6) in a conformally flat spacetime whose Ricci tensor is rotationally invariant, (A\({}_4\)) will hold and the spacetime will be LRS. The arguments in the Petrov D case suggest that to achieve this one must exploit the information in Ricci and Bianchi identities as much as possible.
4 Criteria for conformally flat spacetimes
The conformally flat cases to be considered have a Ricci tensor of one of the Segre types appearing in Table 1. (A\({}_m\)) is assumed to hold with a group g which contains spatial rotations about at least one axis.
For Ricci tensors of Segre type [(111, 1)], the linear isotropy \(\hat{I}_0\) is the whole Lorentz group. Only \(\varLambda \) can be a non-zero curvature component. The Bianchi identities show that \(\varLambda \) is constant, giving (locally) the well-known spacetimes of constant curvature: Minkowski spacetime and the de Sitter and anti de Sitter spacetimes. The subgroup g in (A\({}_m\)) is the trivial one comprising the whole Lorentz group. So \(s=6\), \(t_p=0=t_0\), and there is a group \(G_{10}\) transitive on the whole spacetime. In these cases the Cartan-Karlhede procedure terminates at the first step and (A\({}_0\)) suffices because it will imply (A\({}_1\)).
The rest of this section studies the (A\({}_m\)) required for LRS in conformally flat spacetimes with Ricci tensors of the Segre types in Table 1 which are less special than [(111, 1)]. Obviously \(m\ge 1\) is needed.
4.1 The first derivatives of the Ricci tensor
The first step is to impose LRSI on the first derivatives of \(\varPhi \) and \(\varLambda \). Then one can try first to derive (3.2), which was obtained in Petrov type D from invariance of \(\nabla \varPsi \), and then (3.6) and (3.9).
In the Segre types that admit a spatial rotation (which is again assumed to be in the \((\varvec{m},\,\varvec{\overline{m}})\) plane) only the components of \(\varPhi _{AB'}\) for which \(A=B\) can be nonzero. So (C2) and \(\varPhi _{02'}=0\) are assumed. For (A\({}_1\)) to hold with LRSI also implies (C3). When the frame has been fixed sufficiently that components of \(\varPhi \) become invariants, the \(\delta \) derivatives of those components must vanish.
The components of \(\nabla \varPhi \) that must vanish for LRSI are
Note that \(\nabla \varPhi _{03'}\equiv 0\). Inspecting the Bianchi identities, one finds that (Bb) implies (4.2), (Bh) and the conjugate of (Bg) imply (4.3), and the conjugate of (Bc) implies (4.4). Subtracting (Ba) from (4.1), and subtracting the conjugate of (Bd) from (4.5) leaves
as the only possible information from rotational invariance of \(\nabla \varPhi \) not already contained in the Bianchi identities. Hence if (4.6) are satisfied \(\nabla \varPhi \) will be rotationally invariant. [In Segre type [(111), 1] (“perfect fluid”) (4.6) gives no new information, being equivalent to (Bg) and (Bh) in the canonical frame in which \(\varPhi _{00'}=\varPhi _{22'}=2\varPhi _{11'}\)]. If (C1) holds, (4.6) is identically satisfied, but in some conformally flat cases (4.6) is needed in order to infer (C1).
4.2 Conformally flat spacetimes with Ricci tensors of Segre types for which \(s_0=1\)
These Segre types appear in the first line of Table 1: they are types [(11)1, 1], [(11)\(,Z\bar{Z}\)], and [(11), 2]. Taking the spatial rotation to act in the \((\varvec{m},\,\varvec{\overline{m}})\) plane, these have canonical forms with \(\varPhi _{22'}\ne 0\ne \varPhi _{11'}\) (and \(\varPhi _{01'}=\varPhi _{02'}=\varPhi _{12'}=0\)). The three different cases, [(11)1,1], [(11),\(Z\bar{Z}\)], and [(11),2], are characterized by \(\varPhi _{00'}\varPhi _{22'}>0\), \(\varPhi _{00'}\varPhi _{22'}<0\) and \(\varPhi _{00'}=0\) respectively. None have a generally accepted physical interpretation: however, the combined perfect fluid and electromagnetic field solutions of Stewart and Ellis [50] have type [(11)1, 1]. Avoiding the more special type [(111), 1] requires that \(\varPhi _{00'}\varPhi _{22'}\ne 4\varPhi _{11'}^2\), which is assumed for the rest of this section. Since \(\varPhi _{11'}\) is invariant under the remaining frame freedom (a position-dependent boost), (A\({}_1\)) implies \(\delta \varPhi _{11'}=0\).
If these spacetimes obey (A\({}_\infty \)) the Cartan-Karlhede procedure must terminate after at most 3 steps (\(p=2\)) since \(s=1\) at every step and \(t_2\) is at most 2 (since \(t_0 \ge 0\)) which is the maximum possible \(t_p\). So (A\({}_3\)) would suffice. All the resulting spacetimes would again admit a \(G_r,~r\ge 3\) acting on submanifolds of dimension at least 2.
Assuming (A\({}_1\)) and using the Bianchi identities, one can now obtain (3.2). (Bb) and (Bc), or equivalently (4.2) and (4.4), imply that \(\sigma =\lambda =0\) (provided \(\varPhi _{00'}\varPhi _{22'}\ne 4\varPhi _{11'}^2\)). Similarly (4.6), (Bg) and (Bh), which read
give \(\kappa =\pi =0\) and \(\tau =\nu =0\), completing the derivation of (3.2).
If the remaining boost freedom is used in the cases [(11)1, 1] and [(11), \(Z\bar{Z}\)] to set \(\varPhi _{00'}=\pm \varPhi _{22'}\ne 0\) then (Ba) and (Bd) imply (3.6). As in Sect. 3 this implies \(\delta (\varepsilon +\bar{\varepsilon })=0=\delta (\gamma +\bar{\gamma })= 0.\) From (NPi) and (NPm) one has \(\delta \rho =\delta \bar{\mu }=0\). To obtain the remaining equations in (3.9), one can either argue that since \(\rho \) and \(\mu \) are invariants under the allowed changes of frame, \(\bar{\delta }\rho =\delta \rho =\delta {\mu }=\bar{\delta }\mu =0\) or consider applying \([\delta , D]\) to \(\varPhi _{11'}+\varLambda \) using (3.7) and \([\bar{\delta }, \varDelta ]\) to it using (3.8) to obtain a pair of linear equations for \(\bar{\delta }\rho \) and \(\delta \mu \) leading to the same conclusion. Then as in Sect. 3 this ensures (A\({}_4\)) and the spacetimes are LRS.
For Segre type [(11), 2] one can use the allowed boost to make \(\varPhi _{22'}=\varPhi _{11'}\ne 0\) so that \(\delta \varPhi _{22'}=0\) and hence, from (Bd), (3.6) again holds. Then the rest of (3.9) and the conclusion that the spacetime is LRS follow as before.
Thus for these cases of rotational invariance, Theorem 2 holds with ‘spacetime of Petrov type D’ replaced by ‘conformally flat spacetime’.
4.3 Conformally flat spacetimes with Ricci tensors of Segre type [(11)(1,1)]
Here \(s_0=2\). Only \(\varPhi _{11'}\) and \(\varLambda \) can be non-zero Ricci tensor components, and both are invariant under rotations and thus obey \(\delta Q = \bar{\delta } Q=0\). Assuming \(\varPhi _{11'}\ne 0\), (Ba) to (Bd) give
If \(s=2\) one must have \(t_1=0\) (as the boost and rotations together have no invariant vectors) and so the Cartan-Karlhede procedure terminates at step 1 since \(s_1=s_0\) and \(t_1=t_0\). Hence as in Sect. 3 one has the Bertotti-Robinson type spacetimes with a \(G_6\) transitive on the whole spacetime, and (A\({}_1\)) suffices.
If \(s=1\) and \(\hat{I}_1\) is a group of spatial rotations then from (Bg) and (Bh) \(\pi =\tau =0\) so (3.2) holds. To obtain (3.6), note that (NPk) gives \(\delta \rho = \rho (\bar{\alpha }+\beta )\) and (Be) and (Bi) give \(D\varPhi _{11'}=(-\rho +2\bar{\rho })\varPhi _{11'}\). Applying the commutator \([\delta ,\,D]\) to \(\varPhi _{11'}\), gives \(\delta \bar{\rho } = \bar{\rho }(\bar{\alpha }+\beta )\). Similarly the conjugate of (NPm) gives \(\delta \bar{\mu }=-\bar{\mu }(\bar{\alpha }+\beta )\), (Bf) and (Bk) give \(\varDelta \varPhi _{11'}=(\mu -2\bar{\mu })\varPhi _{11'}\), and applying \([\delta ,\,\varDelta ]\) to \(\varPhi _{11'}\) gives \(\delta \mu = -\mu (\bar{\alpha }+\beta )\). Then as in Sect. 3 there is a boost such that (3.6) holds, and hence the spacetime is LRS.
Thus for a conformally flat spacetime with a Ricci tensor of Segre type [(11)(1, 1)], (A\({}_1\)) with a one-dimensional group of spatial rotations implies LRS.
4.4 Conformally flat spacetimes with Ricci tensors of Segre type [(11,2)]
Here \(s_0=3\), \(\hat{I}_0\) being generated by a two-parameter group of null rotations about \(\varvec{k}\), say, and spatial rotations in a plane orthogonal to \(\varvec{k}\). Only \(\varPhi _{22'}\) and \(\varLambda \) can be non-zero in a frame adapted to the null rotation isotropies. Such a Ricci tensor can represent a null electromagnetic field or other forms of “pure radiation”. The conformally flat pure radiation solutions with \(\varLambda =0\) are completely known (Theorem 37.19 in [49]). One set are plane waves, with an obvious rotational symmetry, as well as null rotation symmetry [(37.104) in [49]], and the other set [(37.106) in [49]], the Edgar-Ludwig metrics, cannot have local rotational symmetry [47].
Note first that an \(\hat{I}_i, ~i\ge 1\) with \(s_i=2\) cannot include both a spatial rotation (by an angle \(\theta \) say) and a one-parameter group of null rotations, with parameter \(B=|B|e^{i\psi }\) say, because the spatial rotation would transform those null rotations to a different one-parameter null rotation invariance group with parameter \(B'=Be^{i\theta }=|B|e^{i(\theta +\psi )}\). Thus if \(s_i=2,~i\ge 1\) the remaining isotropies are the two null rotations, a case treated in a companion paper, and if \(\hat{I}_p\) contains the spatial rotation but \(s_p\ne 3\), \(s_1=1\). By the same logic as in Sect. 4.2, (A\({}_3\)) will suffice to imply LRS, the Cartan-Karlhede procedure then terminates at step 3 or earlier and there is a \(G_r\), \(r\ge 3\) (which will act in a spacelike surface).
To obtain the minimal m by the methods of this paper, a boost is used to set \(\varPhi _{22'}=1\). The remaining frame freedoms are position-dependent rotations. One has \(\delta \varLambda =0\) and the Bianchi identities (Bc), (Bf) and (Bk) give \(\kappa =\sigma =D\varLambda =0\), \(\bar{\tau }=2(\alpha +\bar{\beta })\), \(\varDelta \varLambda =\rho \), and \(\rho =-2(\varepsilon +\bar{\varepsilon })\). Imposing (A\({}_1\)) implies, from \(\nabla \varPhi _{23'}=0\), that \(\tau +\bar{\alpha }+\beta =0\) so \(\tau =\alpha +\bar{\beta }=0\). Then (NPc), (NPk) and (NPp) give \(\rho \bar{\pi }=\delta \rho ~[=\delta (\varepsilon +\bar{\varepsilon })] =\rho \bar{\lambda }=0\). Subtracting (NPo) from the conjugate of (NPr) gives \(\delta (\gamma +\bar{\gamma })=-\rho \bar{\nu }/2.\) The two cases \(\rho =0\) and \(\rho \ne 0\) will now be considered.
If \(\rho =0=\varepsilon +\bar{\varepsilon }\), then \(\varLambda \) is constant. (NPq) gives \(\varLambda =0\) and (NPf) then yields \(D(\gamma +\bar{\gamma })=0\). Then by direct calculation (A\({}_3\)) holds and the spacetime is LRS. So (A\({}_1\)) suffices to prove LRS in the case. The metric this leads to is (37.104) in [49], in which the Ricci tensor is interpretable as that of an electromagnetic field.
If \(\rho \ne 0\), \(\varLambda \) cannot be constant (in particular not zero). (NPq) implies \(\mu \) is real; it is invariant under spatial rotations so \(\delta \mu =0\). \((\gamma +\bar{\gamma })\) is also a spatial rotation invariant so \(\delta (\gamma +\bar{\gamma })=0=\nu \). Thus all the Eqs. (3.2), (3.6) and (3.9) are satisfied, (A\({}_1\)) implies (A\({}_3\)), and the spacetime is LRS. A manifestly LRS example of such a spacetime is given by
here \(\varPsi _2=1\) and \(\varLambda =-2u/3\). Such metrics are unlikely to be of physical interest.
4.5 Conformally flat spacetimes with Ricci tensors of Segre type [(111),1] (perfect fluid)
In general relativity, a Ricci tensor of Segre type [(111), 1] is usually referred to as a perfect fluid whether or not it obeys any standard equation of state. Conformally flat perfect fluids have been rather fully investigated (see Section 37.4.2 of Stephani et al. [49] and references therein). They are all known (see Theorem 37.17 of Stephani et al. [49] and the paragraph following it). They are more naturally treated in a \(3+1\) or orthonormal tetrad formalism than the null tetrad used so far here. The correspondence between the NP spin coefficients and the Ricci rotation coefficients in the orthonormal tetrad (ONT) formalism (as set out in [26]), some of which coincide with components of the kinematic quantities as defined by Ehlers [11], is given in the appendix to Goode and Wainwright [15]. In this section the ONT variables will appear where they enable briefer exposition.
Bradley [6] showed that the third covariant derivative was needed to complete the classification of one subset of the solutions, those with a non-expanding fluid, implying that \(p=2\) in the Cartan-Karlhede procedure. He also constructed the solutions by a method that in effect inverts the Cartan-Karlhede procedure. Barnes [4] studied the possible isometry groups admitted by these cases, and their results were later re-obtained using the Cartan-Karlhede procedure (computed in an orthonormal rather than null tetrad) by Seixas [45]. Barnes [3] studied the isometry groups of the expanding metrics (Stephani metrics). This section studies the m required in (A\({}_m\)) for the subset of the solutions which admit LRSI to be LRS.
Note that this will complete the re-investigation of the original arguments that (A\({}_3\)) implies LRS [12, 50]: the Petrov type D cases are covered in Sect. 3 and the conformally flat perfect fluid plus electromagnetic field cases in Sect. 4.2. Both those cases needed only (A\({}_1\)).
To avoid confusion with the spin coefficients \(\mu \) and \(\rho \), \(\xi \) is used here for the fluid energy density (and p for pressure despite its different use in the Cartan-Karlhede procedure). Then \(R=\xi -3p\) and in a frame such that the fluid flow vector \({\varvec{u}} = (\varvec{k}+\varvec{l})/\sqrt{2}\) (fixing the frame up to swaps of axes and spatial rotations), \(\varPhi _{00'}=\varPhi _{22'}=2\varPhi _{11'}=(\xi +p)/4\). This is nonzero as otherwise the Segre type is [(111, 1)], considered above.
The invariance group of the Riemann tensor is SO(3). Because that has no two-dimensional subgroup, either \(s_p=3\) or \(s_p=1\). Consider first the case \(s_1=3\), i.e. assume (A\({}_1\)) with SO(3) as g. This leads only to the well-known Robertson-Walker geometries,Footnote 11 a result stated in this form by Ellis [12] for dust (and repeated for a more general perfect fluid in [50]).
For these geometries \(t_p=1\) or 0, \(s=3\) and there is a \(G_6\) (or in the special case of the Einstein static universe, where \(t_0=0\), a \(G_7\)). This result is easy to rederive. The kinematic quantities \(\dot{u}^a,\,\omega _{ab}\) and \(\sigma _{ab}\) must all be zero, and that conversely characterizes these geometries (see (5.1a) and the subsequent argument in [13]). The first derivatives of the Riemann tensor will then involve only the expansion \(\Theta \) and the partial derivatives of \(\xi \) and p. From the Ricci equations, \(\Theta \) is not independent of \(\xi \) (this can also be obtained from (A\({}_2\)), as stated in [50]). Therefore \(t_1=t_0\) and either \(t_0=0\) or \(t_0=1\), \(p=1\), and (A\({}_1\)) is sufficient.
The remaining spacetimes to consider are those where \(s_1=1=s\). The frame can as before be chosen so that the rotation that remains acts in the \((\varvec{m},\,\varvec{\overline{m}})\) plane. Then \(\delta \varLambda =0=\delta \varPhi _{11'}\). With that constraint, the Bianchi identities (Ba–d, g and h), or equivalently (A\({}_1\)), give (4.1)–(4.5) and (4.6) (see Sect. 4.1). Thus
In the orthonormal frame used by Ellis [12], (4.7) implies \(\dot{u}^2=\dot{u}^3=\omega _2=\omega _3 =\sigma _{12}=\sigma _{13}=\sigma _{23}=0\), and \(\Theta _2=\Theta _3\) (so \(\sigma _{22'}=\sigma _{33'}\)), as obtained by Ellis from (A\({}_1\)) (which is used here just to give \(\delta \varLambda =0=\delta \varPhi _{11'}\)).
Moreover the imaginary part of (Be) [or (Bf)] implies
which shows that \(\omega _1=0\). Thus the conformally flat perfect fluids have no vorticity (as was already known, see e.g. [6]), and therefore belong to case II or case III of Ellis [12] and Stewart and Ellis [50].
The 4 equations (Be, f, i and k) contain combinations of the D and \(\varDelta \) derivatives of \(\varPhi _{11'}\) and \(\varLambda \) of which only 3 are linearly independent. From (Bi)–(Be) and (Bk)–(Bf) one finds
showing that \(\xi \) has a zero derivative perpendicular to the fluid velocity. The linear combination with no derivative terms [obtainable from (Be) + (Bf) using (4.9)] is
which shows that the ONT variable \(\sigma _{11}=0\), whence also \(\sigma _{22}=0\), completing \(\sigma _{ab}=0\) in agreement with Bradley [6].
Using that information and (4.9), one obtains the usual equation for \(\partial _0\xi \) in the ONT frame. From (Bi)–(Bk), using (4.9), the remaining independent combination of the Bianchi identities (Be, f, i and k) yields
which is the usual equation relating \(\partial _1p\) and \(\dot{u}^1 = [(\varepsilon +\bar{\varepsilon })+(\gamma +\bar{\gamma })]/\sqrt{2}\) in the ONT frame. Note that if \(\dot{u}^1 = 0\) the conditions for Robertson-Walker geometry are satisfied, and \(s=3\) rather than 1, so one must assume \(\dot{u}^1 \ne 0\).
From (4.9) and (4.11) one can now compute \((\varDelta -D)\varPhi _{11'}\) and \((\varDelta -D)\varLambda \), which are useful in simplifying the second derivatives.
Using (4.7), (4.8) and (4.10) in (NPe) plus the conjugate of (NPd), and in (NPo) minus the conjugate of (NPr), one obtains
so the ONT variables \(\Theta _1\) and \(\dot{u}^1\) obey \(\delta \Theta _1=0=\delta \dot{u}^1\). Since \(\sigma _{\alpha \beta }=0\), this implies \(\delta \Theta =\delta \Theta _{22}~[= \delta \Theta _{33}] =0\) also, whence \(\delta (\rho +\bar{\rho })=\delta (\mu +\bar{\mu })\). Ellis [12] used (A\({}_2\)) to derive the corresponding statement, his equation (4.3e), for \(\Theta _{\alpha \alpha }\) (no sum), which is more general because in Petrov type D \(\sigma _{11'}\) need not be zero. Here (4.12) was obtained from the consequence \(\delta \varLambda =0=\delta \varPhi _{11'}\) of (A\({}_1\)) and the Bianchi and Ricci identities.
Using the information obtained so far, those second derivative terms \(\nabla ^2\varPhi _{AB'}\) which must vanish for (A\({}_2\)) give \(\sigma \dot{u}^1=\kappa \dot{u}^1=\tau \dot{u}^1=0\). Since for \(s=1\) one must have \(\dot{u}^1\ne 0\), one obtains (3.2).Footnote 12 (NPk) gives \(\delta \rho =0\) and (NPm) \(\bar{\delta }\mu =0\). To complete the set of Eqs. (3.2), (3.6) and (3.9), which as before imply LRS (see Sect. 3), one needs to prove that \(\delta \mu ~[=\delta \bar{\rho }]=0\). One finds \(\nabla ^3\varPhi _{23'}\propto \dot{u}^1\varPhi _{11'}\delta (\rho +\bar{\rho })=0\), so (A\({}_3\)) gives \(\delta \bar{\rho }=0\) as required. This agrees with (4.3f) in [12]. Hence in this case (A\({}_3\)) is required.
5 Conclusion
Summarizing the work in Sects. 3 and 4 gives the following theorem
Theorem 3
In spacetimes with a Ricci tensor of Segre type [(111), 1] whose timelike eigenvector is not geodesic, local spatial rotational invariance of the curvature and its derivatives up to the third holds if and only if the spacetime is locally rotationally symmetric. In all other cases, local spatial rotational invariance of the curvature and its first derivatives holds if and only if the spacetime is locally rotationally symmetric.
Notes
The notation has been altered here to avoid the same letter being used for different quantities.
The calculations for type D spacetimes with boost invariance, and for conformally flat spacetimes with spatial rotation invariance, were guided by this correspondence, using prior calculations for type D spacetimes with rotational invariance and conformally flat spacetimes with boost invariance.
The notation here follows that in [49].
The notation \(\hat{I}\) is adopted to distinguish between the linear isotropy group at P and, if it exists, the isotropy group I, the subgroup of the full isometry group leaving P fixed.
I am grateful to Jan Åman for drawing this example to my attention.
Except that here the prime on the second index of \(\varPhi _{AB'}\) is retained and the NP scalar \(\varLambda =R/24\) is used in preference to R. Note that in an Einstein space this is a multiple of the cosmological constant, usually also denoted by \(\varLambda \). Calling this L for clarity, \(L=R/4\).
This use of upper case Latin indices for two distinct but related purposes does not lead to confusion in practice.
This form was actually first studied by Levi–Civita in 1917: see [49], Section 12.3.
It is this possibility that Cahen and Defrise [7] overlooked, instead using invariance of second derivatives to obtain their equivalent result: for some details see the Appendix. Note that use of the commutators implies the existence but not the invariance of second derivatives.
Milson and Pelavas [38] have shown there are no such spacetimes for type D. This is also implied by the simple proof which follows and shows that for a t sequence with \(t_2=1\), \(t_1=t_0=0\) the Cartan-Karlhede procedure terminates with \(p\le 2\).
In general relativity, called Friedman–Lemaître-Robertson–Walker spacetimes in recognition of the pioneering work on their dynamics.
Hence the ONT variables obey \(n_{12}+a_3= n_{13}+a_2= n_{23}= \Omega _2=\Omega _3\) agreeing with results in [12] obtained from (A\({}_2\)).
References
Åman, J.E.: Manual for CLASSI: Classification Programs for Geometries in General Relativity (3rd provisional edition), Report, University of Stockholm Institute of Theoretical Physics (1987)
Åman, J.E., Karlhede, A.: A computer-aided complete classification of geometries in general relativity. First results. Phys. Lett. A 80(4), 229–31 (1980)
Barnes, A.: Symmetries of the Stephani universes. Class. Quant. Grav. 15, 3061–3070 (1998)
Barnes, A., Rowlingson, R.R.: Killing vectors in conformally flat perfect fluid spacetimes. Class. Quant. Grav. 7(10), 1721–31 (1990)
Bonnor, W.B.: Non-radiative solutions of Einstein’s equations for dust. Commun. Math. Phys. 51, 191 (1976)
Bradley, M.: Construction and invariant classification of perfect fluids in general relativity. Class. Quant. Grav. 3(3), 317–34 (1986)
Cahen, M., Defrise, L.: Lorentzian 4-dimensional manifolds with “local isotropy”. Commun. Math. Phys. 11, 56 (1968)
Collins, J.M., d’Inverno, R.A.: The Karlhede classification of type-D nonvacuum spacetimes. Class. Quant. Grav. 10(2), 343–51 (1993)
Collins, J.M., d’Inverno, R.A., Vickers, J.A.: The Karlhede classification of type D vacuum spacetimes. Class. Quant. Grav. 7, 2005–2015 (1990)
Debever, R., McLenaghan, R.G., Tariq, N.: Riemannian–Maxwellian invertible structures in general relativity. Gen. Relativ. Gravit. 10(10), 853–79 (1979)
Ehlers, J.: Beiträge zur relativistischen Mechanik kontinuerlicher Medien. Akad. Wiss. Lit. Mainz, Abh. Math.-Nat. Kl. 1), 792–837 (1961). (English translation by G.F.R. Ellis and P.K.S. Dunsby, ’Contributions to the relativistic mechanics of continuous media’ in Gen. Rel. Grav. 25 1225-1266 (1993)) with editorial note by A. Held. Also reprinted as no. 9 in Golden Oldies in General Relativity: Hidden Gems, ed. A. Krasinski, G.F.R. Ellis and M.A.H. MacCallum, Springer, Heidelberg (2013)
Ellis, G.F.R.: Dynamics of pressure-free matter in general relativity. J. Math. Phys. 8, 1171 (1967)
Ellis, G.F.R.: Relativistic cosmology. In: Schatzman, E. (ed.) Cargese Lectures in Physics, vol. 6, pp. 1–60. Gordon and Breach, New York (1973)
Geroch, R., Held, A., Penrose, R.: A space-time calculus based on pairs of null directions. J. Math. Phys. 14, 874 (1973)
Goode, S.W., Wainwright, J.: Characterization of locally rotationally symmetric space-times. Gen. Relativ. Gravit. 18, 315 (1986)
Hall, G.S.: Homothetic transformations with fixed points in spacetime. Gen. Relativ. Gravit. 20, 671–681 (1988)
Hall, G.S.: The global extension of local symmetries in general relativity. Class. Quant. Grav. 6(2), 157–61 (1989)
Hall, G.S.: Symmetries and Curvature Structure in General Relativity. Lecture Notes in Physics, vol. 46. World Scientific, Singapore (2004)
Karlhede, A.: On a coordinate-invariant description of Riemannian manifolds. Gen. Relativ. Gravit. 12, 963 (1980a)
Karlhede, A.: A review of the geometrical equivalence of metrics in general relativity. Gen. Relativ. Gravit. 12(9), 693–707 (1980b)
Karlhede, A., Åman, J.E.: Progress towards a solution of the equivalence problem in general relativity. In: Ng, E. (ed.) EUROSAM ’79: Symbolic and Algebraic Computation. Lecture notes in Computer Science, vol. 72, pp. 42–44. Springer, Berlin (1979)
Karlhede, A., Åman, J.E.: Classifying geometries in general relativity. In: 9th International Conference on General Relativity and Gravitation, Abstracts of Contributed Papers, Jena, GDR, vol. 1, pp. 104–105. Friedrich Schiller Universität Jena (1980)
Karlhede, A., Åman, J.E.: Inequivalent metrics with equal spin coefficients. Gen. Relativ. Gravit. 14(1), 49–52 (1982)
Koutras, A.: A spacetime for which the Karlhede invariant classification requires the fourth covariant derivative of the Riemann tensor. Class. Quant. Grav. 9, L143–145 (1992)
Krasiński, A.: Inhomogeneous Cosmological Models. Cambridge University Press, Cambridge (1997)
MacCallum, M.A.H.: Cosmological models from the geometric point of view. In: Schatzman, E. (ed.) Cargese Lectures in Physics, vol. 6, pp. 61–174. Gordon and Breach, New York (1973)
MacCallum, M.A.H.: Locally isotropic spacetimes with non-null homogeneous hypersurfaces. In: Tipler, F. (ed.) Essays in General Relativity (A Festschrift for A.H. Taub), pp. 121–138. Academic Press, New York (1980)
MacCallum, M.A.H.: Computer algebra in gravity research. Living Rev. Relat. 21, 6 (2018)
MacCallum, M.A.H.: Totally symmetrized spinors and null rotation invariance. Class. Quant. Grav. 37, (2020)
MacCallum, M.A.H., Åman, J.E.: Algebraically independent \(n\)-th derivatives of the Riemannian curvature spinor in a general spacetime. Class. Quant. Grav. 3(6), 1133–41 (1986)
MacCallum, M.A.H., Skea, J.E.F.: SHEEP: a computer algebra system for general relativity. In: M.J. Rebouças, W.L. Roque (eds.) Algebraic computing in general relativity (Proceedings of the first Brazilian school on computer algebra, vol 2). Oxford University Press, Oxford, pp. 1–172 and index pp. 361–9 (1994)
Machado Ramos, M.P.: Invariant differential operators and the Karlhede classification of type \(N\) non-vacuum solutions. Class. Quant. Grav. 15, 435–43 (1998)
Marklund, M.: Invariant construction of solutions to Einstein’s field equations: LRS perfect fluids I. Class. Quant. Grav. 14, 1267–1284 (1997)
Marklund, M., Bradley, M.: Invariant construction of solutions to Einstein’s field equations: LRS perfect fluids II. Class. Quant. Grav. 16, 1577–1597 (1999)
Mena, F.C.: Discrete symmetries and Bianchi metrics. In: Ibañez, J. (ed.) Recent Developments in Gravitation—Proceedings of the Spanish Relativity Meeting ’99’, pp. 271–275. Servicio Editorial de la Universidade del Pais Vasco (2000)
Mena, F. C. (2001), Inhomogeneous and anisotropic spacetimes in general relativity. Ph.D. thesis, Queen Mary University of London
Mena, F.C., MacCallum, M.A.H.: Locally discretely isotropic space-times. In: V. Gurzadyan, R. Jantzen, R. Ruffini (eds.) Proceedings of the Ninth Marcel Grossmann Meeting on General Relativity. World Scientific, Singapore, p. 1976 (2002)
Milson, R., Pelavas, N.: The curvature homogeneity bound for Lorentzian metrics. Int. J. Geom. Methods Mod. Phys. 06, 99 (2009)
Pollney, D., Skea, J.E.F., d’Inverno, R.A.: Classifying geometries in general relativity: I. Standard forms for symmetric spinors. Class. Quant. Grav. 17, 643–663 (2000a)
Pollney, D., Skea, J.E.F., d’Inverno, R.A.: Classifying geometries in general relativity: II. Spinor tools. Class. Quant. Grav. 17, 2267–2280 (2000b)
Pollney, D., Skea, J.E.F., d’Inverno, R.A.: Classifying geometries in general relativity: III. Classification in practice. Class. Quant. Grav. 17, 2885–2902 (2000c)
Schmidt, B.G.: Riemannsche räume mit mehrfach transitiver isometriegruppe, Ph.D. thesis, Hamburg (1968)
Schmidt, B.G.: Discrete isotropies in a class of cosmological models. Commun. Math. Phys. 15, 329–336 (1969)
Schmidt, B.G.: Homogeneous Riemannian spaces and Lie algebras of Killing fields. Gen. Relativ. Gravit. 2, 105 (1971)
Seixas, W.: Killing vectors in conformally flat perfect fluids via invariant classification. Class. Quant. Grav. 9, 225–238 (1992)
Siklos, S.T.C.: Singularities, invariants and cosmology. Ph.D. thesis, Cambridge (1976)
Skea, J.E.F.: Type \(N\) spacetimes whose invariant classification requires the fourth covariant derivative of the Riemann tensor. Class. Quant. Grav. 14, 2947–50 (1997)
Skea, J.E.F.: A spacetime whose invariant classification requires the fifth covariant derivative of the Riemann tensor. Class. Quant. Grav. 17, L69–L74 (2000)
Stephani, H., Kramer, D., MacCallum, M.A.H., Hoenselaers, C.A., Herlt, E.: (2003), Exact Solutions of Einstein’s Field Equations, Corrected Paperback edition, 2nd edn. Cambridge University Press, Cambridge (2009)
Stewart, J., Ellis, G.: On solutions of Einstein’s equations for a fluid which exhibit local rotational symmetry. J. Math. Phys. 9, 1072 (1968)
Van Elst, H., Ellis, G.: The covariant approach to LRS perfect fluid spacetime geometries. Class. Quant. Grav. 13, 1099–1127 (1996)
Acknowledgements
I am grateful to Jan Åman for his work in developing the software CLASSI, used above at several points where ‘calculation’ appears without details, and for preliminary calculations for the LRS cases, and to Filipe Mena, working with whom on discrete isotropies prompted this paper, and who was kind enough to check some calculations. I am also retrospectively grateful to the late John Stewart, who first prompted my interest in this area in 1967, leading to me joining him as one of George Ellis’s students, and to George himself.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author is an Editorial Board member of the journal General Relativity and Gravitation.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: The Cahen and Defrise paper
Appendix: The Cahen and Defrise paper
This appendix explains where Cahen and Defrise [7] used (A\({}_2\)). Reference to their equations is in the form (e.g.) CD(3.16). They focused on the imaginary parts of \(\mu \) and \(\rho \) and took three cases. Note that in the following, factors of 2 or sign in the comparisons between their formalism and the NP formalism have been neglected for brevity.
Cahen and Defrise consider 3 cases:
-
1.
\(\mu -\bar{\mu }= 0 = \rho -\bar{\rho }\) which means \(\varvec{k}\) and \(\varvec{l}\) are parallel to gradients. In this case they integrated the remaining equations to obtain the metric CD(3.20).
-
2.
\(\mu -\bar{\mu } \ne 0 = \rho -\bar{\rho }\) (or the same with \(\mu \) and \(\rho \) swapped) Applying \([\delta ,\,\bar{\delta }]\) to \(Q = \varLambda \), \(\varPsi _2\), and \(\varPhi _{11'}\) one obtains \((\mu -\bar{\mu })DQ=0\) giving CD(3.21). If \(\mu =\bar{\mu }\) one is back at case 1, and if \(DQ=0\) for the three Q then from (Be) and (Bi) one has
$$\begin{aligned} D\varPsi _2-D\varPhi _{11'}-D\varLambda /24= 3\rho \varPsi _2-2\bar{\rho }\varPhi _{11'}+\mu \varPhi _{00'}=0. \end{aligned}$$Since \(\rho \) is real the imaginary part of this is
$$\begin{aligned} \rho (\varPsi _2-\bar{\varPsi }_2)=-(\mu -\bar{\mu })\varPhi _{00'} \end{aligned}$$[their (3.22)]. Then the imaginary part of (NPq) gives \(\varPsi _2-\bar{\varPsi }_2=-\rho (\mu -\bar{\mu })\) so \(\varPhi _{00'}=2\rho ^2\) giving CD(3.23). Now (NPa) gives \(D\rho =3\rho ^2\) [CD(3.24)] in a frame such that \(\varepsilon +\bar{\epsilon }=0\) and then \([\delta ,\,\bar{\delta }]\) applied to \(\rho \) gives \(\mu =\bar{\mu }\) or \(D\rho =0\). Since one assumes \(\rho \ne 0\) this gives case 1 again.
-
3.
\(\mu -\bar{\mu } \ne 0 \ne \rho -\bar{\rho }.\) Here Cahen and Defrise apply a (position-dependent) boost to make
$$\begin{aligned} (\mu -\bar{\mu })=\pm (\rho -\bar{\rho }), \end{aligned}$$(A.1)then used \([\delta ,\,\bar{\delta }]\) again to get CD(3.26). The imaginary part of (NPa) is CD(3.27) and CD(3.28) is the imaginary part of (NPh). They then find another expression for the imaginary part of \(\varPsi _2\), which follows from (NPn) and (NPq), and compare using the equality (A.1). CD(3.29) relates \(\gamma +\bar{\gamma }\) and \(\varepsilon +\bar{\varepsilon }\). Invariance of the second derivatives of \(\varPsi _2\) is used at this point to obtain \(\delta \rho \) and \(\bar{\delta }\mu \) (CD(3.30)), and (NPm) and (NPk) (with vanishing \(\varPsi _A\) other than \(\varPsi _2\)) to obtain the other derivatives (CD(3.31)) and then \([\delta ,\,\bar{\delta }]\) is used again to get CD(3.32)–CD(3.34). Thus one finally arrives at CD(3.36), the equivalent of (3.6). As shown above a different choice of boost enables one to show that only (A\({}_1\)) is actually necessary.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
MacCallum, M.A.H. Spacetimes with continuous linear isotropies I: spatial rotations. Gen Relativ Gravit 53, 57 (2021). https://doi.org/10.1007/s10714-021-02829-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10714-021-02829-9