Newtonian wormholes

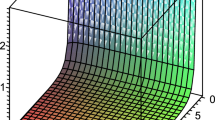
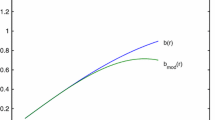
Abstract

A wormhole solution in Newtonian gravitation, enhanced through an equation relating the Ricci scalar to the mass density, is presented. The wormhole inhabits a spherically symmetric curved space, with one throat and two asymptotically flat regions. Particle dynamics in this geometry is studied, and the three distinct dynamical radii, namely, the geodesic, circumferential, and curvature radii, appear naturally in the study of circular motion. Generic motion is also analyzed. A limiting case, although inconclusive, suggests the possibility of having a Newtonian black hole in a region of finite (nonzero) size.

Appendix 1: Spatial geodesics

Here we display the spatial geodesics of the wormhole space.

1.1 Spatial geodesic equations

To complete the analysis of the Newtonian wormhole geometry, we find the expressions for the geodesics in this space. To start we consider a spatial curve $c$ on the Newtonian wormhole parametrized by a parameter $\lambda$. A point on $c$ is given by the parametric equation $c^{i}\left( \lambda \right) =\left( l\left( \lambda \right) , \theta \left( \lambda \right) ,\varphi \left( \lambda \right) \right)$ and the tangent vector to the curve at a given point by $c^{i\prime }\left( \lambda \right) =\left( l'\left( \lambda \right) , \theta '\left( \lambda \right) ,\varphi '\left( \lambda \right) \right)$, where a dash means derivative with respect to the affine parameter $\lambda$. The curve $c^{i}$ is said to be a geodesic if it parallel transports its tangent vector along itself, i.e., its tangent vector must be such that the equation

$$\begin{aligned} c^{i\prime }\nabla _{i}\, c\,^{j\prime }=0, \end{aligned}$$

(53)

is verified, and where $\nabla _i$ is the covariant derivative. Before we write the geodesic equations explicitly for this space, we can simplify the calculations by noticing that due to the spherical symmetry of the space we can always choose a coordinate system in such a way that the polar angle, represented by the coordinate $\theta$, is constant along the curve and equal to $\pi /2$. In other words, since the $2$-sphere, $S^{2}$, is a submanifold of the space and it is a well known fact that part of great circles are geodesics in $S^{2}$, then any geodesic on the space, under isometries, is part of a great circle. Thus, the geodesic equations for the wormhole space are

$$\begin{aligned} \left\{ \begin{aligned}&l''+\left[ \frac{b\, e^{\frac{l^{2}}{b^{2}}}\left( 2b^{2}+l^{2}\right) \left( e+ \beta \right) -2\sqrt{b^{2}+l^{2}}\left[ \beta \, l^{2} \left( 1+l^{2}/b^{2}\right) +b^{2}\left( e^{1+ \frac{l^{2}}{b^{2}}}+\beta \right) \right] }{2l\left( b^{2}+ l^{2}\right) \left[ b\, e^{\frac{l^{2}}{b^{2}}}\left( e +\beta \right) -\sqrt{b^{2}+l^{2}}\left( e^{1+ \frac{l^{2}}{b^{2}}}+\beta \right) \right] }\right] \,\, l'^{2}\\&\qquad \quad +\left[ \frac{b\sqrt{b^{2}+l^{2}} \left( e+\beta \right) -\left( b^{2}+l^{2}\right) \left( e+\beta \, e^{-\frac{l^{2}}{b^{2}}}\right) }{ e\, l}\right] \,\,\varphi '^{2}=0\,;\\&\varphi ''+2\frac{l}{b^{2}+l^{2}}\, l'\varphi '=0\,;\\&\theta '=0,\\&\theta =\pi /2. \end{aligned} \right. \nonumber \\ \end{aligned}$$

(54)

The geodesic equations in their general form are quite complicated to solve and find an analytical solution. We can however consider simpler cases than the general one.

1.2 Spatial azimuthal geodesics

Let us first consider the case of purely azimuthal geodesics, i.e., consider geodesics of the form $c^{i}\left( \lambda \right) =\left( l_{0}, \pi /2,\varphi \left( \lambda \right) \right)$. In this case, the geodesic equations simplify to $\varphi ''=0$. If we take the initial and final position of the geodesic to be, respectively, $c^{i}\left( 0\right) =\left( l_{0},\pi /2,\varphi _{0}\right)$ and $c^{i}\left( \lambda _{f}\right) =\left( l_{0},\pi /2,\varphi _{f}\right)$ we conclude that

$$\begin{aligned} \varphi \left( \lambda \right) =\frac{\varphi _{f}- \varphi _{0}}{\lambda _{f}}\,\lambda +\varphi _{0}. \end{aligned}$$

(55)

1.3 Spatial radial geodesics

Let us now consider the case of purely radial geodesics. In this case the geodesics are of the form $c^{i}\left( \lambda \right) = \left( l\left( \lambda \right) ,\pi /2,\varphi _{0}\right)$, such that the geodesic equations simplify to

$$\begin{aligned} l''\!+\!\left[ \frac{b\, e^{\frac{l^{2}}{b^{2}}}\left( 2b^{2}\!+\! l^{2}\right) \left( e\!+\!\beta \right) \!-\!2\sqrt{b^{2}\!+\! l^{2}}\left[ \beta \, l^{2}\left( 1\!+\!l^{2}/b^{2}\right) \!+\!b^{2}\left( e^{1 \!+\!\frac{l^{2}}{b^{2}}}\!+\!\beta \right) \right] }{2l \left( b^{2}\!+\!l^{2}\right) \left[ b\, e^{\frac{l^{2}}{b^{2}}}\left( e\!+\!\beta \right) \!-\! \sqrt{b^{2}\!+\!l^{2}}\left( e^{1+\frac{l^{2}}{b^{2}}}\!+\! \beta \right) \right] }\right] \,\, l'^{2}\!=\!0.\nonumber \\ \end{aligned}$$

(56)

This equation is still too complicated and it does not seem to be possible to find an analytical solution to it. We can, however, consider a further simplification, namely, we consider that the initial and final radial coordinate, $l_0$ and $l_f$, respectively, are very close to the wormhole’s throat. This allow us to Taylor expand the expression in parenthesis in Eq. (56) such that

$$\begin{aligned} l''+\left[ \frac{l\left( e-3\beta \right) }{4b^{2} \left( \beta -e\right) }\right] \,\, l'^{2}=0. \end{aligned}$$

(57)

This expression can be analytically integrated. If we then consider the initial and final points to be $c^{i}\left( 0\right) =\left( l_{0},\pi /2,\varphi _{0}\right)$ and $c^{i}\left( \lambda _{f}\right) =\left( l_{f},\pi /2,\varphi _{0}\right)$, respectively, we find that

$$\begin{aligned} \begin{aligned} l\left( \lambda \right)&= -i\sqrt{\frac{8b^{2}\left( \beta -e\right) }{e- 3\beta }}\text {erf}^{-1}\\&\quad \times \left( i\,\frac{\lambda _{f}-\lambda }{\lambda _{f}}\text {erfi} \left( \sqrt{\frac{e-3\beta }{8b^{2}\left( \beta -e\right) }}\, l_{0}\right) +\frac{i\,\lambda }{ \lambda _{f}}\text {erfi}\left( \sqrt{\frac{e- 3\beta }{8b^{2}\left( \beta -e\right) }}\, l_{f}\right) \right) \end{aligned} \qquad \end{aligned}$$

(58)

where $\text {erf}^{-1}$ represents the inverse Gauss error function and $\text {erfi}$ the imaginary Gauss error function. Equation (58) gives the expression for the radial coordinate of purely radial geodesics when the two considered points are very close to the wormhole’s throat.

1.4 Spatial general geodesics

The simplifications adopted in the previous subsections greatly simplified the geodesic equations and allowed us to find closed form solutions for those simplified cases. Let us, however, tackle the general problem of studying geodesics of the form $c^{i}\left( \lambda \right) =\left( l\left( \lambda \right) , \pi /2,\varphi \left( \lambda \right) \right)$, with initial and final points $c^{i}\left( 0\right) =\left( l_{0},\pi /2,\varphi _{0}\right)$ and $c^{i}\left( \lambda _{f}\right) =\left( l_{f},\pi /2,\varphi _{f}\right)$, respectively. Notice that we imposed the angular coordinate $\theta =\pi /2$. This reflects the argument that we presented in the beginning of this section, i.e., given any two points on the spherically symmetric Newtonian wormhole we can always find an isometry such that the geodesic that connects those two points is part of a great circle.

To start, we introduce a new equation:

$$\begin{aligned} l'^{2}\left( \frac{e\, l^{2}}{\left( b^{2}+l^{2}\right) \left( e+\beta \, e^{-\frac{l^{2}}{b^{2}}}\right) -b\sqrt{b^{2}+l^{2}} \left( e+\beta \right) }\right) +\varphi '^{2} \left( b^{2}+l^{2}\right) =1.\qquad \end{aligned}$$

(59)

This equation represents the restriction that the norm of the tangent vector to the curve $c^{i}$ is constant, which we normalized and set to $1$. Next, we integrate the azimuthal equation in Eq. (54), obtaining

$$\begin{aligned} \varphi '=\frac{C}{b^{2}+l^{2}}, \end{aligned}$$

(60)

where $C$ is a constant of integration. Substituting Eq. (60) in Eq. (59) we find that

$$\begin{aligned} l'=\sqrt{\left[ \frac{e+\beta \, e^{-\frac{l^{2}}{b^{2}}}}{e\, l^{2}}-\frac{b\left( e+\beta \right) }{e\, l^{2}\sqrt{b^{2}+l^{2}}}\right] \left( l^{2}+b^{2}- C^{2}\right) }. \end{aligned}$$

(61)

Dividing Eq. (60) by Eq. (61) we finally find that

$$\begin{aligned} \frac{d\varphi }{dl}=C\sqrt{\frac{e\, l^{2}}{\left[ \left( b^{2}+l^{2}\right) ^{2}\left( e+\beta \, e^{-\frac{l^{2}}{b^{2}}}\right) -b\sqrt{\left( b^{2}+ l^{2}\right) ^{3}}\left( e+\beta \right) \right] \left( l^{2}+b^{2}-C^{2}\right) }},\nonumber \\ \end{aligned}$$

(62)

or

$$\begin{aligned}&\varphi \left( l_{f}\right) \nonumber \\&\quad \!=\!{\displaystyle C\int _{l_{i}}^{l_{f}}\sqrt{\frac{e\, l^{2}}{\left[ \left( b^{2}+l^{2}\right) ^{2}\left( e+\beta \, e^{-\frac{l^{2}}{b^{2}}}\right) -b\sqrt{\left( b^{2}+ l^{2}\right) ^{3}}\left( e+\beta \right) \right] \left( l^{2}+b^{2}-C^{2}\right) }}}\,\, dl\!+\!\varphi _{0},\nonumber \\ \end{aligned}$$

(63)

which can be numerical integrated, provided the value of the constant $C$ is given, such that the geodesic’s path is described by $c(l)=\left( l,\pi /2,\varphi (l)\right)$.

We can further define the constant of integration $C$. Let’s consider the unit vector

$$\begin{aligned} X_{\varphi }^{i}=\frac{1}{\sqrt{b^{2}+l^{2}}}\delta _{\varphi }^{i}, \end{aligned}$$

(64)

defined has the tangent unit vector to curves with constant $l$ and $\theta$ coordinates.Taking the dot product of $X_{\varphi }^{i}$ and the tangent vector of the geodesic $c^{i\prime }$, we have, using Eq. (27), that

$$\begin{aligned} X_{\varphi }^{i}\, c_{i}^{\prime }=\sqrt{\left( b^{2}+ l^{2}\right) }\varphi '=\frac{C}{\sqrt{b^{2}+ l^{2}}}, \end{aligned}$$

(65)

where in the last step we used Eq. (60). On the other hand, defining the smaller angle between $X_{\varphi }^{i}$ and $c^{i\prime }$ as $\xi$, the definition of the dot product implies that

$$\begin{aligned} X_{\varphi }^{i}\, c_{i}^{\prime }=\cos \left( \xi \right) , \end{aligned}$$

(66)

where we used the fact that the vectors $X_{\varphi }^{i}$ and $c^{i\prime }$ are unitary vectors. Comparing Eqs. (65) and (66) we find that the integration constant $C$ is related to the angle $\xi$ by:

$$\begin{aligned} C=\sqrt{b^{2}+l^{2}}\cos \left( \xi \right) . \end{aligned}$$

(67)

Incidentally, Eqs. (63) and (67) allow us to further describe the purely radial geodesics, studied in the previous subsection where a closed form solution for such geodesics was only possible if the beginning and ending points were very close to the wormhole’s throat. If we consider that the angle $\xi =\pi /2$ in Eq. (67), using Eq. (63) we find that the coordinate $\varphi \left( l\right)$ is constant along the geodesic. This is exactly as we expected since for $\xi =\pi /2$ the geodesic $c^{i}$ is orthogonal to the geodesics with constant $l$-coordinate, i,e., $c^{i}$ is a radial geodesic. This result allow us to describe all the radial geodesics on the wormhole space, such that, $c^{i}\left( l\right) =\left( l,\pi /2,\varphi _{0}\right)$, supplanting Eq. (58) which was valid only when the initial and final points were very close to the wormhole’s throat.