Static spherically symmetric black holes with scalar field

Abstract

Static spherically symmetric black holes and particle like solutions with self interacting minimally coupled scalar field $\varphi$ are analyzed. They are asymptotically flat or anti-de Sitter (AdS). We express them in terms of a single function $\rho$ which undergoes simple conditions. If $\varphi$ is nontrivial the ADM mass $M$ has to be positive. No-hair theorems are generalized to the AdS asymptotic. For both asymptotics the Killing horizon is nondegenerate and its radius cannot be bigger than $2M$. Derivatives of $\rho$ at singularity determine properties of admissible potentials $V(\varphi )$ as regularity, boundedness and behavior for maximal values of $\varphi$. Several classes of solutions with singular or nonsingular potentials are obtained. Their examples are presented in a form of plots.

1 Introduction

The first solution of the Einstein equations with scalar field $\varphi$ was found by Fisher [1]. Then it was rediscovered by several authors [2–5]. Fisher’s solution is static, spherically symmetric and $\varphi$ is massless. It generalizes the Schwarzschild solution, but its global structure is completely different. If $\varphi$ is nontrivial singularity and the event horizon are at the same place [5].

Later studies on the Einstein-scalar equations led to a number of no-hair theorems on static spherically symmetric solutions representing black holes or particle like solutions which are asymptotically flat [6–16]. They show that in the case of black holes potential $V$ of the scalar field cannot be positive definite simultaneously at all points outside the event horizon. If there is no horizon and $V$ is positive definite everywhere a naked singularity must be present. The global structure of the maximally extended metric is that of the Schwarzschild or Minkowski spacetime. Some of these results were generalized to asymptotically anti-de Sitter or de Sitter solutions [15, 16] and more involved models of gravity interacting with scalar field, also in higher dimensions (see [17] for a review). On the other hand examples of black holes and particle like solutions, which do not undergo the no-hair theorems, were constructed (see e.g. [16, 18–21]). Since the standard energy conditions are often not respected in modern relativity, these solutions can still be valuable.

In this paper we study exclusively static spherically symmetric solutions of the Einstein equations with minimally coupled scalar field. They are assumed to be asymptotically flat or anti-de Sitter (AdS). We consider two classes of fields: black holes with the regular Killing horizon and no naked singularities and particle like solutions with no singularities at all. In the latter case it follows from the Einstein equations that there is no horizon. In order to avoid numerical analysis we assume that function $V(\varphi )$ is not a’priori prescribed. In this case the Einstein equations form an underdetermined system of three equations for four unknowns: $\varphi , V$ and two metric coefficients (other two can be fixed by means of a coordinate transformation), all depending on a radial coordinate $r$. We solve these equations (Sect. 2) and express all fields in terms of a free function $\rho$ which is monotonically growing, convex, has a zero point and approximates $r-3M$ when $r$ is large. Given $\rho (r)$ a dependence of the potential $V$ on $\varphi$ is defined in a parametric way.

This description allows to obtain new results and refine old ones. We generalize the no-hair theorems to the AdS asymptotic. As in the asymptotically flat case potential $V$ cannot be positive definite outside the Killing horizon, or everywhere in the case of particle like solutions, if scalar field is nontrivial in this domain (Sects. 5 and 6). Other results refer to both asymptotics. Despite of violation of standard energy conditions (dominant, strong and weak) except the null one, for any potential $V(\varphi )$ the total ADM mass $M$ has to be positive or $\varphi$ is trivial and metric is flat or AdS (Sect. 6). Singularity is unavoidable in the case of black holes [15] (see Sect. 4 for a proof). It occurs at $r_0>0$ if necessary properties of the function $\rho$ break down at $r_0$, otherwise it is at $r=0$. There is only one horizon [15]. Its radius $r_h$ obeys the Penrose inequality $r_h\le 2M$ and the surface gravity is never zero (Sects. 3 and 5).

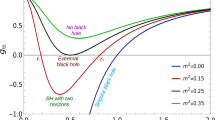
The representation of solutions in terms of $\rho$ allows also to obtain general properties of admissible potentials (Sects. 4 and 5). Potential $V$ and its derivative $V_{,\varphi }$ have to vanish at $\varphi =0$. In generic case $\varphi$ is finite at singularity and $V$ is infinite. Regular potentials $V(\varphi )$ are possible, bounded or unbounded, if singularity is at $r=0$ and derivatives of $\rho$ at this point are properly chosen. Examples of solutions are easy to construct thanks to the description of necessary and sufficient conditions on the function $\rho (r)$. They are plotted in Fig. 1.

Fig. 1

Solutions corresponding to (42)–(44) with parameters (n,a,b,c) and $\Lambda =0$: 1 solid line (0,3,1,.45) BH with singular $V(\varphi )$, 2 dotted line (0,1,1,.6) BH with nonsingular $V(\varphi )$ bounded from below, 3 solid line with space (5,1,2.5,.5) BH with nonsingular $V(\varphi )$ bounded from both sides, 4 dashed line (3,3,1,.006) particle like solution with nonsingular $V(\varphi )$ bounded from both sides, 5 solid line with dot the Schwarzschild metric

In Sect. 2 asymptotically flat solutions of the Einstein-scalar equations are represented in terms of the free function $\rho$. In Sect. 3 we study maximal extensions of solutions admitting the nonsingular Killing horizon. Section 4 is mainly devoted to properties of potentials $V(\varphi )$ as functions of scalar field $\varphi$. Section 5 contains generalizations to solutions with the AdS asymptotic. Section 6 deals with particle like solutions with any of the two asymptotics. Main results are collected in Theorems 1–7 and Remarks 1–4.

2 Solutions with undefined $V(\varphi )$

The Einstein equations with scalar field $\varphi$, potential $V(\varphi )$ and the cosmological constant $\Lambda$ take the form

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}Rg_{\mu \nu }=\varphi _{,\mu } \varphi _{,\nu }+\left( \Lambda +V-\frac{1}{2}\varphi ^{,\alpha } \varphi _{,\alpha }\right) g_{\mu \nu }, \end{aligned}$$

(1)

where $R_{\mu \nu }$ is the Ricci tensor of metric $g_{\mu \nu }$ and units $c=1, 8\pi G=1$ are chosen. If $\varphi _{,\mu }\ne 0$ it follows from (1) that the scalar field equation

$$\begin{aligned} \varphi ^{|\mu }_{\ |\mu }=-V_{,\varphi } \end{aligned}$$

(2)

is satisfied. In Sects. 2–4 we will study black hole solutions of equations (1) and (2) with $\Lambda =0$ and in Sects. 5, 6 we will admit $\Lambda <0$.

Definition 1

We say that a $C^2$ solution of (1) and (2) with $\Lambda =0$ is a static spherically symmetric black hole with scalar field if the following conditions are satisfied:

• 1. Metric $g$ and scalar field $\varphi$ are spherically symmetric and invariant under an additional complete Killing vector $k$.

• 2. Metric is asymptotically flat [22] and $\varphi$ vanishes at infinity.

• 3. Vector $k$ is timelike in the asymptotic region and becomes null on the Killing horizon. Metric and scalar field can be continued through the horizon.

Outside the Killing horizon metric tensor can be written in the form

$$\begin{aligned} g=g_{00}dt^2+g_{11}d\rho ^2-r^2\left( d\theta ^2+sin^2\theta d\phi ^2\right) , \end{aligned}$$

(3)

where $k=\partial _t$ is the timelike Killing field. Functions $g_{00}, g_{11}, r$ and $\varphi$ depend only on the coordinate $\rho$. Coordinates $t,\rho$ break down on the Killing horizon where $g_{00}=0$. Metric can be continued through it if the Eddington–Finkelstein type coordinates exist. To this end functions $g_{00}$ and $g_{00}g_{11}$ should have $C^2$ continuations through the horizon and condition

$$\begin{aligned} g_{00}g_{11}<0 \end{aligned}$$

(4)

should be preserved. Thus, under the assumptions of Definition 1 functions $g_{00}, g_{00}g_{11}$ and $\varphi$ are globally defined and condition (4) has to be everywhere satisfied.

We use a notion of the asymptotical flatness based on the conformal compactification of spacetime [22]. For our purposes it is sufficient to require that fields have the following expansions for large values of $\rho$

$$\begin{aligned}&g_{00}=1-\frac{2M}{\rho }+0\left( \rho ^{-2}\right) \!,\quad g_{00}g_{11}=-1+0\left( \rho ^{-1}\right) \!,\nonumber \\&r=\rho +3M+0\left( \rho ^{-1}\right) \!,\ \ \ \ \ \ \ \ \varphi =0\left( \rho ^{-1}\right) \!. \end{aligned}$$

(5)

The k-derivative of a term $0(\rho ^{-n}), k,n=1,2$, is assumed to behave like $0(\rho ^{-n-k})$. The constant $M$ is the total mass and the component $3M$ in the relation between $r$ and $\rho$ is introduced for a later convenience.

Thanks to (4) one can choose the coordinate $\rho$ in such a way that outside the horizon metric reads

$$\begin{aligned} g=Fdt^2-F^{-1}d\rho ^2-r^2\left( d\theta ^2+sin^2\theta d\phi ^2\right) \!. \end{aligned}$$

(6)

In this gauge one of the Einstein equations can be easily solved. After doing this we will pass to coordinates $t,r,\theta ,\varphi$ which seem more suitable for analyzing solutions.

If $\Lambda =0$ Eq. (1) for metric (6) and scalar field $\varphi$ yields

$$\begin{aligned}&r^2F_{,\rho \rho }-F(r^2)_{,\rho \rho }+2=0 \end{aligned}$$

(7)

$$\begin{aligned}&\varphi '^2=-\frac{2r_{,\rho \rho }}{r} \end{aligned}$$

(8)

$$\begin{aligned}&V=\frac{1}{r^2}-\frac{1}{r^2}(rr_{,\rho }F)_{,\rho }. \end{aligned}$$

(9)

Above equations are equivalent to Eqs. (9)–(11) in [16] for $d=2$ [note that Eq. (12) in [16] contains an error]. By virtue of (5) an integration of (7) leads to

$$\begin{aligned} r^2F_{,\rho }-F(r^2)_{,\rho }+2\rho =0 \end{aligned}$$

(10)

(see Eq. (13) in [16]). The second integration allows to represent $F$ in terms of the function $r$

$$\begin{aligned} F=2r^2\int \limits _{\rho }^{\infty }{\frac{\tilde{\rho }}{r^4}d\tilde{\rho }}. \end{aligned}$$

(11)

It follows from (8) that $r_{,\rho \rho }\le 0$ and from (5) that $r_{,\rho }\rightarrow 1$ if $\rho \rightarrow \infty$. Hence $r_{,\rho }\ge 1$ everywhere and we can interchange roles of $\rho$ and $r$. In coordinates $t,r,\theta ,\varphi$ metric tensor reads

$$\begin{aligned} g=Fdt^2-F^{-1}\rho '^2dr^2-r^2\left( d\theta ^2+sin^2\theta d\phi ^2\right) \!, \end{aligned}$$

(12)

where the prime denotes the derivative with respect to $r$. Now, formulas (8), (9) and (11) take the following form

$$\begin{aligned} F&= 2r^2\int \limits _r^{\infty }{\frac{\rho \rho '}{\tilde{r}^4}d\tilde{r}} \end{aligned}$$

(13)

$$\begin{aligned} \varphi '^2&= \frac{2 \rho ''}{r\rho '} \end{aligned}$$

(14)

$$\begin{aligned} V&= \frac{1}{r^2}-\frac{1}{r^2\rho '}\left( \frac{rF}{\rho '}\right) '. \end{aligned}$$

(15)

By virtue of (13) the last equation can be also written as

$$\begin{aligned} V=\frac{1}{r^2}+\frac{2\rho }{r^3\rho '}+\frac{F}{r\rho '^2}\left( \frac{\rho ''}{\rho '}-\frac{3}{r}\right) \!. \end{aligned}$$

(16)

Condition (8) and (14) impose the following simple constraints on function $\rho$

$$\begin{aligned} 1\ge \rho '>0,\ \ \rho ''\ge 0. \end{aligned}$$

(17)

In order to guarantee that $F$ and $\varphi$ are $C^2$ differentiable we have to assume that $\rho \in C^3$ and

$$\begin{aligned} (\sqrt{\rho ''})'\in C^0 \end{aligned}$$

(18)

at points where $\rho ''=0$. Asymptotic conditions (5) reduce to

$$\begin{aligned} \rho = r-3M+0(r^{-1})\quad {\text{ i }f}\ \ r\rightarrow \infty . \end{aligned}$$

(19)

Note that (17) and (19) yield

$$\begin{aligned} \rho (r)\ge r-3M. \end{aligned}$$

(20)

In addition to (13)–(15) the scalar field equation (2) has to be taken into account at points where $\rho ''=0$ since then $\varphi '=0$ at these points. Let us assume that $\rho ''=0$ at $r=r_0$ which is a limit of a sequence of points in which $\rho ''\ne 0$. Equation (2) will be satisfied at $r_0$ if values of $V_{,\varphi }=V'/\varphi '$ at these points have a limit at $r_0$. Here $V'$ is given by differentiation of (16)

$$\begin{aligned} V'=-\frac{4\rho \rho ''}{r^3\rho '^2}+\frac{F}{r^2\rho '^4} \left( r\rho '\rho '''+7\rho '\rho ''-3r\rho ''^2\right) \!. \end{aligned}$$

(21)

Let $S$ be a set of all other points in which $\rho ''=0$. Each of them possesses a neighborhood where $\varphi =\hbox {const}$. It follows from (21) that also $V=$const in this neighborhood. Equation (2) reduces to $V_{,\varphi }=0$. It is satisfied provided $V'/\varphi '\rightarrow 0$ when one approaches boundary of $S$ from its exterior. Thus, again the continuity of $V_{,\varphi }$ is required. It follows from (14) and (21) that this property is assured by the already assumed condition (18). Concluding, Eq. (2) does not generate a new constraint.

Given $V$ as a function of $\varphi$ relations (13)–(15) yield an equation for $\rho (r)$ which is hard to study in an analytic way. For this reason we will treat $V$ as an unknown variable. Then formulas (13)–(15) define $F, \varphi$ and $V$ in terms of a free function $\rho (r)$. We admit only such functions $\rho (r)$ for which $\varphi (r)$ and $V(r)$ correspond to some potential $V(\varphi )$.

Remark 1

In principle function $\varphi '$ may change sign at points where $\rho ''=0$ or, more generally, when $r$ passes an interval on which $\rho ''=0$. If it happens potential $V$ is a function of $\varphi$ if and only if $\rho (r)$ satisfies in a neighborhood of the interval an involved equation containing $\rho ', \rho ''$ and an inverse function to $\rho ''/\rho '$. If there is no interval on which $\rho$ satisfy this equation we refer to $\rho$ as a generic function.

If $\rho$ is generic in the above sense it follows from (14) that scalar field is given by the monotonic function

$$\begin{aligned} \varphi (r)=\int \limits _{r}^{\infty }\sqrt{\frac{2 \rho ''}{r\rho '}} \end{aligned}$$

(22)

up to the factor $\pm 1$. Formulas (16) and (22) define a differentiable potential $V(\varphi )$ in a parametric way.

3 Maximal extension

Let $r_h$ be a position of the Killing horizon, $F(r_h)=0$. Since $\rho '>0$ everywhere it follows from (13) that $\rho$ cannot have an uniform sign for $r>r_h$. Thus, there is a unique point $r_c$ such that $r_c>r_h$ and

$$\begin{aligned} \rho (r_c)=0,\ \ r_c\le 3M. \end{aligned}$$

(23)

Since $\rho <0$ if $r<r_c$ it is clear from (13) that $(r^{-2}F)'>0$ for $r<r_c$. Hence, there are no more Killing horizons [15].

Using (13) one can calculate the surface gravity of the Killing horizon at $r_h$

$$\begin{aligned} \kappa =\frac{|\rho (r_h)|}{r_h^2}. \end{aligned}$$

(24)

Thus, the horizon is nondegenerate. Moreover, its radius satisfies the Penrose inequality

$$\begin{aligned} r_h\le 2M. \end{aligned}$$

(25)

In order to prove (25) let us consider the function

$$\begin{aligned} f=\int \limits _r^{\infty }{\frac{\rho \rho '}{\tilde{r}^4}d\tilde{r}} \end{aligned}$$

(26)

which is proportional to $F$ and vanishes at $r_h$. From (17) and (20) one obtains $\rho \rho '\ge r-3M$ if $r\le r_c$, hence

$$\begin{aligned} f\ge \int \limits _r^{r_c}{\frac{\tilde{r}-3M}{\tilde{r}^4}d\tilde{r}}+f(r_c). \end{aligned}$$

(27)

Integrating (26) by parts yields

$$\begin{aligned} f=-\frac{\rho ^2}{2r^4}+2\int \limits _r^{\infty }{\frac{\rho ^2}{\tilde{r}^5}d\tilde{r}}. \end{aligned}$$

(28)

Since $\rho (r_c)=0$ it follows from (28) and (20) that

$$\begin{aligned} f(r_c)=2\int \limits _{r_c}^{\infty }{\frac{\rho ^2}{\tilde{r}^5}d\tilde{r}}\ge 2\int \limits _{3}^{\infty }{\frac{\rho ^2}{\tilde{r}^5}d\tilde{r}} \ge 2\int \limits _{3}^{\infty }{\frac{(\tilde{r}-3M)^2}{\tilde{r}^5}d\tilde{r}} =\int \limits _{3}^{\infty }{\frac{\tilde{r}-3M}{\tilde{r}^4}d\tilde{r}}. \end{aligned}$$

Substituting the last relation into (27) and using (13) leads to the inequality

$$\begin{aligned} F(r)\ge 1-\frac{2M}{r}\ \ \mathtt{if}\ \ r\le r_c. \end{aligned}$$

(29)

Since $r_h<r_c$, condition (25) follows.

If one of properties (17)–(19) breaks down at $r_0$ such that $0<r_0<r_h$ the corresponding field configuration is singular at $r_0$. If not, and $M\ne 0$ a singularity of the Riemann tensor appears at $r=0$ (see the next section). Assume for a moment that $M\le 0$. It follows from (20) that there is no zero point $r_c$ of $\rho$. Hence, there is no room for the horizon radius $r_h$. Either $M=0$ and $\rho =r$ (flat space with $\varphi =0$) or there is naked singularity at $r=0$ or at $r_0>0$.

Remark 2

Black hole solutions can exist only for $M>0$.

A question arises what are sufficient conditions for $\rho$ to define black hole. Of course, conditions (17)–(19) and (23) should be satisfied but they do not assure vanishing of $F$ at some value $r_h>0$. Assume that these conditions are satisfied for all $r>0$. In this case, since $\rho (r)$ is increasing and convex, functions $\rho$ and $\rho '$ are finite at $r=0$ and $\rho (0)<0$. If $\rho '(0)>0$ then it follows from (13) that function $r^{-2}F$ tends to $-\infty$ if $r\rightarrow 0$. Moreover $F(r_c)>0$ and $(r^{-2}F)'>0$ for $r<r_c$. Hence, there is exactly one value $r_h$ such that $F(r_h)=0$. The same result follows for a more general condition on $\rho (r)$ near singularity

$$\begin{aligned} \rho '\approx cr^n,\ \ c={\text {const}}>0,\ \ 0\le n\le 3. \end{aligned}$$

(30)

Let us consider global structure of the maximally extended black hole solutions. It is convenient to come back to the form (6) of metric tensor. All extensions of metrics of this type were given by Walker [23] (see also [24]). They can be composed from standard building blocks. Since (13) admits only one horizon and it has the first order zero at $r=r_h$ the corresponding maximal extension is obtained by gluing the same blocks as in the case of the Schwarzschild solution.

We summarize results of this section in the following theorem.

Theorem 1

• A static spherically symmetric black hole with scalar field corresponds to a function $\rho \in C^3$ with properties (17)–(19) and (23). Metric is given by (12) and (13). Scalar field $\varphi$ and its potential $V$ are given by (22) [or (14), see Remark 1] and (16).

• The global structure of the maximally extended metric is the same as that of the Schwarzschild solution, possibly with the singularity shifted to $r_0> 0$. The radius $r_h$ of the horizon satisfies $r_h\le 2M$ and $r_h<r_c\le 3M$. The surface gravity is nonzero.

• Any $C^3$ function $\rho$ satisfying (17)–(19), (23) and (30) for all $r>0$ defines a black hole solution via relations (12), (13), (16) and (22).

4 Properties of $\varphi$ and $V$ and examples

First, let us consider $\varphi$ and $V$ in the region outside the horizon. From (19), (14) and (16) it follows that

$$\begin{aligned} \varphi =0(r^{-1}),\ \ V=0(r^{-3}) \end{aligned}$$

(31)

for large values of $r$. By virtue of (2) and (31) one obtains that potential, as a function of $\varphi$, satisfies

$$\begin{aligned} V\rightarrow 0,\ \ \ V_{,\varphi }\rightarrow 0\ \ \ {\text{ i }f}\ \ \varphi \rightarrow 0. \end{aligned}$$

(32)

Somewhere between the horizon and infinity potential $V$ should take negative values. This is the content of the no-hair theorem of Bekenstein [8] (with later generalization).

No-hair Theorem. Static spherically symmetric black hole with nontrivial scalar field outside the regular horizon cannot have potential $V$ which is positive definite outside the horizon.

Following [16] we show below how this theorem can be proved in our approach. One can easily verify that Eqs. (13) and (16) imply the following identity

$$\begin{aligned} 2r\rho 'V+\rho ''\left( 1+\frac{F}{\rho '^2}\right) =\left( r^2\rho 'V -\frac{r\rho ''F}{\rho '^2}\right) '. \end{aligned}$$

(33)

Since $F(r_h)=0$ and (31) implies $r^2V\rightarrow 0$ if $r\rightarrow \infty$ integration of (33) between $r_h$ and $\infty$ yields

$$\begin{aligned} \int \limits _{r_h}^{\infty }{\left[ 2r\rho 'V+\rho ''\left( 1+\frac{F}{\rho '^2}\right) \right] }= -r_h^2\rho '(r_h)V(r_h). \end{aligned}$$

(34)

If $V\ge 0$ outside the horizon Eq. (34) is satisfied only if $V=0$ and $\rho ''=0$ for every $r\ge r_h$. By virtue of the asymptotic condition (19) it follows that $\rho =r-3M$ for $r\ge r_h$. Hence, $r_h=2M$ and one obtains the Schwarzschild metric and trivial scalar field outside the horizon. This solution may be different under the horizon since function $\rho =r-3M$ can be continued to $r<2M$ in many different ways respecting conditions (17) and (18).

The remaining part of this section is mainly devoted to behavior of solutions near singularity. In order to simplify conclusions we will assume that $\varphi$ is given by formula (22). Let singularity be at $r_0>0$. Since $\rho$ and $\rho '$ are monotonic and bounded for $r<r_c$ they are finite at $r_0$. Conditions (17), (18) can break down at $r_0$ because $\rho ''$ is not well defined at $r_0$ (generic case) or $\rho '(r_0)=0$ or $\rho ''(r_0)=0$ but $\sqrt{\rho ''}$ is not differentiable at $r_0$. In the first case with $\rho '(r_0)>0$ the scalar field $\varphi$ is finite at $r_0$ and a singular part of $V$ is proportional to $-\rho ''$. In the case $\rho ''(r_0)=\infty$ potential tends to $-\infty$ at $r_0$. Potential of this type is also obtained if $\rho '(r_0)=0$ and $0<\rho ''(r_0)<\infty$. In all other cases a dependence of $V$ on $r$ or $\varphi$ is rather not acceptable, e.g. $\varphi$ and $V$ are finite at $r_0$ but the derivative $V_{,\varphi }$ is not defined at $\varphi _0$. We conclude this analysis in the following remark.

Remark 3

In generic case black hole singularity at $r_0>0$ corresponds to a singular potential $V(\varphi )$. If $\rho '>0$ and $\rho ''=\infty$ or $\rho '=0$ and $\rho ''>0$ at $r_0$ the scalar field is finite and $V=-\infty$ at $r_0$.

Let conditions (17)–(18) and (23) be satisfied for all $r>0$. Values of $\rho$ and $\rho '$ at $r=0$ will be denoted by the subscript 0. They are finite and they satisfy

$$\begin{aligned} {-}3M\le \rho _0<0,\ \ 0\le \rho '_0\le 1. \end{aligned}$$

(35)

From (12) and (13) one obtains

$$\begin{aligned} F\approx \frac{2\rho _0\rho '_0}{3r}\ \ \text {if}\ \ r\rightarrow 0 \end{aligned}$$

(36)

and

$$\begin{aligned} g_{11}(0)=0. \end{aligned}$$

(37)

It follows from (37) that the Kretschmann invariant diverges at $r=0$, hence the Riemann tensor is singular. In most cases the function $V(\varphi )$ is also singular. For instance, let us assume that $\rho '_0>0$ and $\rho ''_0>0$ (generic case). Then $\varphi$ takes a finite value $\varphi _0$ at $r=0$ but $F$ and $V$ tend to infinity. Hence, potential $V(\varphi )$ must be singular

$$\begin{aligned} V\rightarrow \infty \quad {\text{ i }f}\ \ \varphi \rightarrow \varphi _0. \end{aligned}$$

(38)

An example of this kind is presented in Fig. 1 (case 1).

If $\rho '_0>0$ the function $\varphi$ is finite at $r=0$. Otherwise $\rho ''$ would diverge at least as $r^{-1}$, but this is incompatible with the existence of $\rho '_0$. In order to avoid singularity of $V(\varphi )$ at $\varphi _0$ functions $V(r)$ and $V'/\varphi '$ should have limits at $r=0$. This implies condition $r^2V\rightarrow 0$. By virtue of (16) it yields

$$\begin{aligned} \left( \rho ''-3r^2\int \limits _r^{\infty }{\tilde{r}^{-3}\rho ''d\tilde{r}}\right) \rightarrow 0. \end{aligned}$$

(39)

It follows from (39) that $\rho _0''=0$ or $\rho ''\sim r^{-1}$. Since the latter condition leads to divergent $\rho '$ we require $\rho _0''=0$. Still this condition does not guarantee finiteness of $V$. For instance, if $\rho '''\rightarrow \rho '''_0\ne 0$ one obtains $V\rightarrow \epsilon \infty$, where $\epsilon =\pm 1$ is the sign of $\rho '''_0$. To avoid this situation we should assume condition $rV\rightarrow 0$ in addition to $\rho _0''=0$. Using (16) yields $\rho '''\sim r^2$. Now $V$ is finite at $r=0$ but to obtain nonsingular $V'/\varphi '$ we still need stronger conditions near singularity

$$\begin{aligned} \rho ''\approx c_1 r^5,\ \ \left( \sqrt{\rho ''}\right) '\approx c_2 r^{\frac{3}{2}}, \end{aligned}$$

(40)

where $c_1, c_2$ are nonnegative constants. Note that condition with $c_2$ can be postponed if $c_1>0$. An example of solution satisfying (40) is presented in Fig. 1 (case 3).

Now, we assume that $\rho _0'=0$. Then $\phi \rightarrow \infty$ if $r\rightarrow 0$ and potential $V(\varphi )$ is nonsingular. Generically $V(r)\rightarrow \pm \infty$ and $V(\varphi )$ behaves like $\pm \exp {(c\varphi )}$ if $\varphi \rightarrow \infty$, where $c=$const$>0$. An example of this kind with $\rho _0''>0$ and $\rho _0'''>0$ is presented in Fig. 1 (case 2). In this example function $V(\varphi )$ is positive and proportional to $\exp {(3\varphi /\sqrt{2})}$ for large values of $\varphi$.

If $\rho _0'=0$ it may happen that function $V(\varphi )$ is bounded. It is the case if $\rho$ admits up to six derivatives at $r=0$ and they satisfy the following conditions

$$\begin{aligned}&-3M<\rho _0<0,\ \ \rho ''_0>0,\ \ \rho ^{(k)}_0=0,\ \ k=1,3,5 \nonumber \\&\rho _0^{(4)}=-\frac{3\rho _0''^2}{\rho _0} ,\ \ \ \ \ \rho _0''^2=4\int \limits _0^\infty {\frac{r\rho _0\rho _0''-\rho \rho '}{r^4}}. \end{aligned}$$

(41)

We summarize results of this section in the following theorem.

Theorem 2

If the only singularity is at $r=0$ then $g_{11}(0)=0$ and the Riemann tensor is singular at $r=0$. Potential $V(\varphi )$ and its derivative $V_{,\varphi }$ vanish at $\varphi =0$. Generically $\varphi$ takes a finite value $\varphi _0$ at $r=0$ and $V(\varphi )$ becomes infinite at $\varphi _0$. A nonsingular potential $V(\varphi )$ can be obtained if either $\rho _0'>0$ and conditions (40) are satisfied or $\rho _0'=0$. In the latter case $\varphi$ is unbounded and either $|V(\varphi )|$ grows exponentially or conditions (41) are satisfied and $V$ is bounded.

Examples of black holes (BH) considered in this section are given in Fig. 1 (cases 1–3). In all of them $M=1$ and $\rho ''$ takes the form

$$\begin{aligned} \rho ''=cr^ne^{-b^2(r-a)^2}, \end{aligned}$$

(42)

where n, a, b and c are parameters. Functions $\rho '$ and $\rho$ are defined by

$$\begin{aligned} \rho '&= 1-\int \limits _r^{\infty }\rho ''(r')dr', \end{aligned}$$

(43)

$$\begin{aligned} \rho&= r-3+\int \limits _r^{\infty }dr'\int \limits _{r'}^{\infty }\rho ''(\hat{r})d\hat{r}. \end{aligned}$$

(44)

They can be also expressed without integrals in terms of functions exp, Erfc and powers of $r$. Figure 1 contains graphs of functions $\rho , g_{00}=F, -g_{00}g_{11}=\rho '^2, \varphi , V$ as functions of $r$ and potential $V(\varphi )$ as a function of $\varphi$. A zero point of $F$ defines the radius $r_h$ of the black hole horizon. Potentials $V$ are negative on some intervals in agreement with the no-hair theorems.

Case 1 represents the generic class of functions $\rho$ for which $\rho '_0>0, \rho ''_0>0, \varphi _0$ is finite and potential $V$ is infinite at $r=0$. In the case 2 there is $\rho '_0=0$ and $\varphi$ is infinite at $r=0$. Function $V(r)$ is singular at $r=0$ but $V(\varphi )$ is nonsingular and it grows exponentially if $\varphi \rightarrow \infty$. In the case 3 conditions (40) are realized. Both $\varphi$ and $V$ are bounded and function $V(\varphi )$ is nonsingular. Case 4 represents a particle-like solution (to be considered in the next section). Case 5 includes graphs which can be plotted for the Schwarzschild metric.

5 Asymptotically AdS black holes

Up to now we considered metrics which are asymptotically flat. Not much changes if they are asymptotically anti-de Sitter with the cosmological constant $\Lambda <0$. We will use the term ’AdS black hole with scalar field’ if solution is asymptotically AdS and satisfies assumptions of Definition 1 except that about $\Lambda =0$ and asymptotical flatness. All equations and results of the preceding sections are still true up to the following modifications. Now, instead of (13) one has

$$\begin{aligned} F=2r^2\int \limits _r^{\infty }{\frac{\rho \rho '}{\tilde{r}^4}d\tilde{r}}-\frac{1}{3}\Lambda r^2. \end{aligned}$$

(45)

The asymptotic condition (19) is unchanged since $\rho =r-3M$ is still true for the Schwarzschild–anti-de Sitter solution. Potential $V$ in Eqs. (9), (15) and (16) should be replaced by $V+\Lambda$. Now, Eq. (15) takes the form

$$\begin{aligned} V=\frac{1}{r^2}-\frac{1}{r^2\rho '}\left( \frac{rF}{\rho '}\right) '-\Lambda \end{aligned}$$

(46)

and Eq. (29) transforms into

$$\begin{aligned} F(r)\ge F_{AdS}=1-\frac{2M}{r}-\frac{1}{3}\Lambda r^2\ \ \ \mathtt{if}\ \ r\le r_c. \end{aligned}$$

(47)

Hence

$$\begin{aligned} r_h\le r_{AdS}\le 2M, \end{aligned}$$

(48)

where $r_{AdS}$ is the horizon radius of the AdS metric (zero point of $F_{AdS}$). Theorem 1 is replaced by the following one.

Theorem 3

• A static spherically symmetric AdS black hole with scalar field corresponds to a function $\rho$ with properties (17)–(19) and (23). Metric is given by (12) and (45). Scalar field $\varphi$ and its potential $V$ are given by (22) [or (14), see Remark 1] and (16).

• The global structure of the maximally extended metric is the same as that of the Schwarzschild–anti-de Sitter metric, possibly with a singularity shifted to $r_0> 0$. A position $r_h$ of the horizon is defined by $F(r_h)=0$ and it satisfies $r_h\le r_{AdS}\le 2M$ and $r_h<r_c\le 3M$. The surface gravity is nonzero.

• Any $C^3$ function $\rho$ satisfying (17)–(19), (23) and (30) for all $r>0$ defines AdS black hole solution via relations (12), (45), (16) and (22).

For $\Lambda <0$ estimation (31) changes since potential $V$ vanishes as $0(r^{-2})$ at infinity. Instead of (33) one obtains

$$\begin{aligned} 2r\rho 'V+\rho ''\left( 1+\frac{F}{\rho '^2}-\Lambda r^2\right) =\left( r^2\rho 'V -\frac{r\rho ''F}{\rho '^2}\right) '. \end{aligned}$$

(49)

Integrating (49) between $r_h$ and $\infty$ yields

$$\begin{aligned} \int \limits _0^{\infty }{\left[ 2r\rho 'V+\rho ''\left( 1+\frac{F}{\rho '^2}-\Lambda r^2\right) \right] }&= \lim _{r\rightarrow \infty }\left( r^2\rho 'V -\frac{r\rho ''F}{\rho '^2}\right) -r_h^2\rho '_hV_h \nonumber \\&= \Lambda \lim _{r\rightarrow \infty }\left( \frac{r^2}{\rho '}-r^2\rho '\right) -r_h^2\rho '_hV_h. \end{aligned}$$

(50)

If $V\ge 0$ outside the horizon then, because of (17), the r.h.s. of (50) is never positive and its l.h.s. cannot be negative. Hence, $V=\rho ''=0$ and $\rho '=1$. It follows that $\rho =r-3M$ if $r\ge r_h$. Thus, $r_h=r_{AdS}$ and for $r\ge r_{AdS}$ scalar field is trivial and metric coincides with the Schwarzschild–AdS solution. This proves an analog of Bekenstein’s no-hair theorem for a negative cosmological constant.

Theorem 4

Static spherically symmetric AdS black hole with nontrivial scalar field outside the regular horizon cannot have potential $V$ which is positive definite outside the horizon.

The analysis of solutions near singularity in Sect. 4 applies to the present case in an unchanged form with the exception of conditions (41) which need modifications.

Remark 4

Theorem 2 is true for $\Lambda <0$ provided conditions (41) are appropriately changed.

Like for $\Lambda =0$ one can construct examples of solutions for $\rho$ given by (42)–(44). Corresponding plots are similar to those in Fig. 1 except that now $F$ is dominated by the term proportional to $\Lambda$ for large values of $r$.

6 Particle like solutions

Finally, let us consider particle like solutions which are asymptotically flat or AdS and everywhere regular. In this case the Killing horizon is not admitted since otherwise singularity would be present. Properties (17)–(19) and $F>0$ have to be satisfied for all $r>0$. Inspection of the Kretschmann invariant at $r=0$ shows that metric should flatten at $r=0$. It follows that

$$\begin{aligned} 0<F_0<\infty ,\ \ \frac{\rho _0'^2}{F_0}=-1. \end{aligned}$$

(51)

This together with (36) yields

$$\begin{aligned} \rho _0=0,\ \ \rho _0'>0. \end{aligned}$$

(52)

In order to avoid singularities of the first and second derivatives of metric with respect to the Cartesian coordinates related in the standard way to $r, \theta$ and $\phi$ we should also assume that

$$\begin{aligned} \rho _0''=\rho _0'''=0. \end{aligned}$$

(53)

To obtain $\varphi \in C^2$ and a nonsingular function $V(\varphi )$ we still have to strengthen (53) by assuming

$$\begin{aligned} \rho ''\approx 4cr^3,\ (\sqrt{\rho ''})'\approx 3c\sqrt{r},\ c=\mathtt{const}>0\ \ \text {if}\ \ r\rightarrow 0. \end{aligned}$$

(54)

Theorem 5

• A static spherically symmetric, asymptotically flat or AdS, everywhere regular solution with scalar field corresponds to some function $\rho$ with properties (17)–(19), (52) and (54). Metric is given by (12) and either (13) or (45). There is no horizon. Scalar field and its potential $V$ satisfy (22) [or (14), see Conclusion 2] and (16).

• Any $C^3$ function $\rho$ satisfying (17)–(19), (52) and (54) for all $r> 0$ defines a particle like solution via relations (12), (16), (22) and either (13) or (45).

If $\rho \in C^5$ conditions (52) and (54) are satisfied by

$$\begin{aligned} \rho =c_1r+c_2r^5f, \end{aligned}$$

(55)

where $c_1$ and $c_2$ are positive constants and $f$ is a function such that $f\rightarrow 1$ if $r\rightarrow 0$. An asymptotically flat example of this kind is represented by the case 4 in Fig. 1. The corresponding function $V(\varphi )$ is defined only on an interval and it can be prolongated in any differentiable way.

Following [16], where the flat asymptotic was considered, we can show for any $\Lambda \le 0$ that potential $V$ has to be somewhere negative if $\varphi$ is nontrivial. Indeed, integrating of (46) from zero to infinity yields

$$\begin{aligned} \int \limits _0^{\infty }{r^2\rho 'Vdr}&= \lim _{r\rightarrow \infty }\left( \rho -\frac{rF}{\rho '}-\Lambda \int \limits _r^{\infty }{\tilde{r}^2\rho 'd\tilde{r}}\right) \nonumber \\&= -M+\frac{1}{3}\Lambda \lim _{r\rightarrow \infty }\left( \frac{r^3}{\rho '}-r^3\rho '+\int \limits _r^{\infty }{\tilde{r}^3\rho ''d\tilde{r}}\right) \!. \end{aligned}$$

(56)

Because of (17) the r.h.s. of (56) is never positive. If $V\ge 0$ then it follows from this equation that $V=M=0$ and $\rho =r$. Hence, scalar field is trivial and metric is flat or AdS. In this way we obtain the following generalization of Theorem 5 in [16].

Theorem 6

Static spherically symmetric, asymptotically flat or AdS, everywhere regular solution with nontrivial scalar field cannot have positive definite potential $V$.

If $M<0$ it follows from (20) that condition (52) cannot be satisfied. For $M=0$ the only nonsingular configuration (flat or AdS metric with $\varphi =V=0$) is given by $\rho =r$. As in the case of black holes nontrivial particle like solutions exist only if $M>0$. This observation together with Remark 1 leads to the following statement.

Theorem 7

For $M\le 0$ there are no static spherically symmetric, asymptotically flat or AdS, black holes or particle like solutions with nontrivial scalar field.

Thus, in case of these solutions one can assume $M>0$ without loss of generality.

7 Summary

We have been studying static spherically symmetric solutions of the Einstein-scalar equations which are asymptotically flat or AdS and have no naked singularities. Our approach is based on a representation of these solutions in terms of a function $\rho (r)$ which is monotonically growing, convex and tends to $r-3M$ if $r\rightarrow \infty$. Moreover it should have a zero point in the case of black holes or to satisfy conditions (52) and (54) in the case of particle like solutions. Necessary and sufficient conditions for the function $\rho$ are given in Theorems 1, 3 and 5.

Theorem 7 shows that the total mass of field configurations with nontrivial scalar field has to be positive. This particular version of the positive energy theorem is satisfied for any shape of potential $V(\varphi )$. Note that general $V(\varphi )$ does not assure any reasonable energy condition except the null one.

Theorems 4 and 6 generalize to the AdS asymptotic the no-go theorems for asymptotically flat black holes and particle like solutions. They show that potential $V$ has to be somewhere negative or $V=\varphi =0$ everywhere. In agreement with [15] the global structure of solutions is that of the Schwarzschild or Minkowski metric or their AdS partners (Theorems 1 and 3). We also show that in the case of black holes horizons are not degenerate (the surface gravity is nonzero) and the Penrose inequality $r_h\le 2M$ or stronger $r_h\le r_{AdS}$ is satisfied (Theorems 1 and 3).

In our approach an exact form of the function $V(\varphi )$ is not a’priori assumed. It follows implicitly when function $\rho (r)$ is chosen. Some properties of $V(\varphi )$, like regularity or boundedness, can be easily related to behavior of $\rho$ near singularity. For generic $\rho$ potential $V(\varphi )$ becomes infinite at a finite value of $\varphi$. The simplest way to make it regular in the case of black holes is to assume that the first derivative of $\rho$ at $r=0$ vanishes. Then $V$ is bounded from below or above and $|V|$ grows exponentially when $\varphi \rightarrow \infty$. To get potential bounded from both sides one has to assume stronger conditions (40) or (41) (modified in the case of the AdS asymptotic). In the first case the function $\varphi (r)$ is also bounded. Hence, potential $V(\varphi )$ is given only on an interval and it can be prolongated in any way. Similar situation takes place in the case of particle like solutions. Properties of $V(\varphi )$ for black holes are summarized in Theorem 2 and Remark 3.

Thanks to sufficient conditions on $\rho$ given in Theorems 1, 3 and 5 it is easy to construct examples of different classes of solutions. Some of them, with a singular or nonsingular potential $V(\varphi )$, are presented in Fig. 1. Plots were done by means of Mathematica 9.