Highlights

  • Holt-Winters additive algorithm is introduced into polar motion forecast for the first time

  • Chandler Wobble variability is considered in polar motion forecast via variable Chandler period

  • Our new method can improve polar motion forecast notably with enhanced geophysical significance

1 Introduction

The rotational variations of the solid Earth, relative to the international celestial reference frame (ICRF) and the international terrestrial reference frame (ITRF), are defined by five Earth Orientation Parameters (EOPs), namely nutation, polar motion (PM) and changes in universal time ΔUT1, which can be accurately measured by advanced geodetic observation (e.g., Petit and Luzum 2010; Ratcliff and Gross 2010; Gross 2015; Ray 2016; Ray et al. 2017) and routinely released by the International Earth Rotation and Reference System Service (IERS) (Bizouard et al. 2019). While real-time EOPs are not available mainly due to delays in collecting and processing global data sets, they are of great significance for a number of practical applications, such as precise positioning, satellite navigation and satellite orbit determination (e.g., Ray et al. 2017; Wang et al. 2017). Therefore, accurate and efficient forecast of EOPs is urgently needed but a challenging task since PM, part of EOPs, contains not only the components excited by quasi-periodic mass redistributions and relative motions within the Earth system (Lambeck 1980; Jochmann 2009; Chen et al. 2013a, b; Gross 2015; Bizouard, 2020; Harker et al. 2021) but also the freely damping Chandler Wobble (CW) (Gross 2000, 2015; Schuh et al. 2001; Wang et al. 2016). These complexities can significantly degrade the accuracy of PM forecast.

For over three decades, PM has usually been predicted with harmonic analyses, least squares (LS), autoregressive (AR) and Kalman filter, etc., applied to accurate observations of recent past PM variations. (e.g., Javanović 1988; Freedman et al. 1994; Kosek et al. 1998; Gross et al. 1998; Akulenko et al. 2002a, b, c). By combining LS and AR, Kosek et al. (2008) put forward the LS + AR method. Xu et al. (2012) applied a Kalman filter prior to LS + AR, while Wu et al. (2018) used weighted LS + AR, both of which were proved to be effective, reducing mean absolute errors (MAE) of 1-day X- and Y-pole polar motion (PMX and PMY) forecasts to less than 0.3 mas (milli-arcsecond). Dobslaw and Dill (2018) and Dill et al. (2019) forecasted PM using effective angular momentum (EAM) and then adopted LS + AR to model unexplained residuals (named as EAM + LS + AR). The root-mean-square errors (RMSE) of their 1-day and 6-day PM forecasts are, respectively, within 0.2–0.4 mas and 0.9–1.5 mas, reduced, respectively, to 85.4% and 57.8% compared with the IERS bulletin A forecasts, validating the reliability of utilizing EAM products in PM prediction. Besides the widely adopted (revised) LS + AR method, Malkin and Miller (2010) and Modiri et al. (2018) proposed the use of singular spectrum analysis (SSA), Kosek et al. (2006) and Su et al. (2014) tried wavelet or normal time–frequency analysis, Schuh et al. (2002), Liao et al. (2012) and Wang et al. (2018) also used artificial neural networks. Zotov et al. (2018) predicted 90-day PM by combining LS, AR, LS collocation and artificial neural networks, in which weights are negatively correlated to respective PM prediction errors. Jin et al. (2021) used the multi-channel singular spectrum analysis (MSSA) method combining linear PM trend and autoregressive moving average to improve long-term PM forecast. Most of these PM forecast methods require either long PM timeseries or priori values of CW period Tcw and quality factor Qcw, and thus predict long-time PM better rather than short-term PM.

Although the numerical value of Qcw is poorly determined and varies significantly from study to study [for example, 63 of Jeffreys (1972); 88.4 of Mathews et al. (2002); 96 of Ooe (1978); 100 of Wilson and Haubrich (1976); 100.2 of Chen and Shen (2010); 127 of Nastula and Gross (2015); 179 of Wilson and Vicente (1990)], Qcw is in fact dominated by mantle anelasticity (e.g., Lambeck 1980; Smith and Dahlen 1981; Chen et al. 2013a) which is determined by properties of mantle minerals and thus unlikely to change within a relatively short time scale. On the contrary, many studies indicated that the “well-determined” Tcw may be variable (see Conclusions and Discussions for detailed discussions) (Chandler 1891; Iijima 1965; Proverbio et al. 1971; Carter 1981; Gao 1997; Höpfner 2003; Chen et al. 2009).

In this research, we propose a short-term PM forecast method based on the Holt-Winters (HW) additive algorithm to combine contributions from both the EAM and variable CW. This new method, termed as the HW-VCW for short, can determine Tcw (we assume Qcw being stable as it is dominated by mantle anelasticity) from PM timeseries using an eight-year sliding window and then use them to model the short-time CW, and thus can model the non-excited part of PM better.

This study is arranged as follows. Data and method are introduced in Sects. 2 to 4, respectively. PM forecast results, including secular stability test during 1998–2020 and forecast test in 2021, are shown in Sect. 5. Conclusions and Discussions are given in Sect. 6.

2 Data

2.1 IERS Polar Motion Observation Data

The daily-sampled PM of IERS Earth orientation parameter product EOP 14 C04 (C04 for short) is obtained by combining measurements from independent space geodetic observation systems and released by the IERS with 30-day latency. The pole coordinates of EOP 14 C04 products are consistent with the International Terrestrial Reference Frame 2014 (ITRF2014). The IERS 14 C04 PM data are used as the truth reference to test our HW-VCW method.

IERS also provides the continuously updated product called Bulletin A, which contains not only quick-look daily EOP estimates by smoothing the observed data, but also EOP forecasts up to 365 days following the last day of data (see https://www.iers.org/IERS/EN/DataProducts/EarthOrientationData/eop.html for more details). The Bulletin A forecasts are to be compared with our PM forecasts in Sect. 5.

2.2 ESMGFZ Angular Momentum Products

The Earth System Modeling group at the Deutsches GeoForschungsZentrum (ESMGFZ) releases non-tidal effective angular momentum (EAM) products, including atmospheric, oceanic, hydrological and sea level angular momentum (AAM, OAM, HAM, SLAM), based on their global grid solutions of general circulation models (GCM) (Dobslaw et al. 2010). The ESMGFZ AAM is based on the European Centre for Medium-Range Weather Forecasts (ECMWF) operational analysis with inverted barometer correction applied and surface pressure tides subtracted. The ESMGFZ OAM is based on the Max-Planck-Institute for Meteorology Ocean Model (MPIOM) ocean model (Jungclaus et al. 2013) and forced by the ECMWF atmospheric pressure. The ESMGFZ HAM is based on the Land Surface Discharge Model (LSDM) hydrological model (Dill 2008), in which soil moisture, snow, surface water, and water in rivers and lakes are all considered. High-resolution geographic-information-system-based river networks are used in this model for higher accuracy of the spatial mass distribution. The ESMGFZ SLAM is derived to conserve the global mass based on a global mean sea-level. In recent updates, loading, self-attraction and rotation deformation correction of the ocean are included. Therefore, the sum of the four EAM products presents the total excitation of polar motion caused by changes in geophysical fluids. The AAM and OAM are 3-h sampled, while the HAM and SLAM are 24-h sampled. All ESMGFZ EAM operational products (ESMGFZ EAM Op) are in radian and can be converted into polar motion excitations in arc-second (e.g., Gross 2015).

ESMGFZ also provides 6-day forecasts (Dobslaw and Dill 2018) and 90-day forecasts (Dill et al. 2019) of EAM products (ESMGFZ EAM F06 and ESMGFZ EAM F90), both of which are based on the same meteorological models of EAM products and routinely published every day. All ESMGFZ EAM datasets can be downloaded at https://rz-vm115.gfz-potsdam.de:8080/repository.

3 Formulas

3.1 Relationship Between PM and EAM

Time-dependent pole coordinates \(p\left( t \right)\) consist of damping free PM \(p_{free} \left( t \right)\) and excited PM \(p_{exci} \left( t \right)\) caused by geophysical fluids. According to Lambeck (1980) (also see Chen et al. 2013b), the observed PM \(p\left( t \right)\) can be divided into the free damping CW and the excited PM due to the total excitation \(\chi \left( t \right)\):

$$\left\{ \begin{gathered} p\left( t \right) = p_{{{\text{free}}}} \left( t \right) + p_{{{\text{exci}}}} \left( t \right) \hfill \\ p_{{{\text{free}}}} \left( t \right) = A_{0} e^{{i\phi_{0} }} e^{{i\sigma_{cw} t}} \hfill \\ p_{{{\text{exci}}}} \left( t \right) = - i\sigma_{cw} e^{{i\sigma_{cw} t}} \int\limits_{ - \infty }^{t} {\chi \left( \tau \right)} e^{{ - i\sigma_{cw} \tau }} {\text{d}}\tau \hfill \\ \end{gathered} \right.$$
(1)

where \(A_{0}\) and \(\phi_{0}\) are, respectively, the initial amplitude and phase angle of \(p_{free} \left( t \right)\), and \(\sigma_{cw}\) is the angular frequency of Chandler wobble defined by its period \(T_{cw}\) and quality factor \(Q_{cw}\):

$$\sigma_{cw} = 2\pi \frac{1}{{T_{cw} }}\left[ {1 + \frac{i}{{2Q_{cw} }}} \right]$$
(2)

Using the EAMs described in Sect. 2.2, the excited PM can be obtained according to the last equation of Eq. (1). According to the frequency-domain Liouville’s equation for polar motion (Chen et al. 2017), one can derive the geodetic (or observed) excitation by

$$\chi_{FFT} \left( f \right) = \frac{{\sigma_{cw} - 2\pi f}}{{\sigma_{cw} }}p_{FFT} \left( f \right)$$
(3)

where \(p_{FFT} \left( f \right) = FFT\left( {p\left( t \right)} \right)\) and \(\chi_{FFT} \left( f \right) = FFT\left( {\chi \left( t \right)} \right)\), and \(FFT\left( {p\left( t \right)} \right)\) means applying the Fast Fourier Transfer (FFT) to \(p\left( t \right)\). In fact, Eq. (3) also illustrates that excitations and excited PM can be easily converted to each other in the frequency domain.

3.2 Holt-Winters Additive Method

The Holt-Winters (HW) additive method (Holt 2004; Winters 1960) is capable of modeling and predicting timeseries containing trend and roughly constant seasonality through exponential weighted moving averages. It is a series of algorithms proposed for industrial situation where mechanized inventory control and production scheduling require massive forecasts of sales and usage of individual products and materials (Winters 1960). In an exponential system based on sufficient data, new variables are derived by weighted-combining values from both last and current periods, leading to easy and flexible derivation of model and prediction. Besides, it responds more rapidly to sudden variations and depends less on the older data, which makes an exponential system suitable for short-term forecast based on recent information (Holt 2004). Detailed descriptions of the HW additive method can be found in some textbooks (e.g., Brockwell and Davis 2002; Hyndman and Athanasopoulos 2021).

In the HW additive algorithm, a discrete signal Yt with rounded period T and length N can be modeled by the recursion formula:

$$\left\{ \begin{gathered} \tilde{Y}_{t} = a_{t - 1} + b_{t - 1} + c_{t - T} ,t \in \left[ {T + 2,N} \right] \hfill \\ \tilde{Y}_{t} = Y_{t} ,t \in \left[ {1,T + 1} \right] \hfill \\ \end{gathered} \right.$$
(4)

where \(\tilde{Y}_{t}\) is the HW model of Yt. at, bt and ct are variable intercept, slope and seasonal factor determined by weighted combination of present and previous variables. The recursions and initial values of them are expressed as

$$\left\{ \begin{gathered} a_{T + 1} = Y_{T + 1} \hfill \\ a_{t} = \alpha \left( {Y_{t} - c_{t - T} } \right) + \left( {1 - \alpha } \right)\left( {a_{t - 1} + b_{t - 1} } \right),t \in \left[ {T + 2,N} \right] \hfill \\ b_{T + 1} = \left( {Y_{T + 1} - Y_{1} } \right)/T \hfill \\ b_{t} = \beta \left( {a_{t} - a_{t - 1} } \right) + \left( {1 - \beta } \right)b_{t - 1} ,t \in \left[ {T + 2,N} \right] \hfill \\ c_{t} = Y_{t} - Y_{1} - \left( {t - 1} \right)b_{T + 1} ,t \in \left[ {1,T + 1} \right] \hfill \\ c_{t} = \gamma \left( {Y_{t} - a_{t} } \right) + \left( {1 - \gamma } \right)c_{t - T} ,t \in \left[ {T + 2,N} \right] \hfill \\ \end{gathered} \right.$$
(5)

where α, β and γ are damping factors with values within the interval [0,1] and are estimated to minimize the difference between \(\tilde{Y}_{t}\) and \(Y_{t}\). By using Eq. (4) and (5), \(\tilde{Y}_{t}\) modeled by Holt-Winters additive method can be iterated. Therefore, h-step forecast of Yt can be expressed as

$$\tilde{Y}_{N + h} = a_{N} + hb_{N} + c_{{N + h - \left( {k + 1} \right)T}}$$
(6)

where k is the integer part of \({{\left( {h - 1} \right)} \mathord{\left/ {\vphantom {{\left( {h - 1} \right)} T}} \right. \kern-\nulldelimiterspace} T}\). More details about the HW additive method can be found in Sect. 9.3 of Brockwell and Davis (2002).

4 Algorithm of the HW-VCW Method

By using formulas mentioned in Sect. 3, we can make PM forecast by using the HW-VCW method proposed by this study. The HW-VCW method consists of two major procedures: One is the determination of Tcw, and the other is modeling the residuals unexplained by the ESMGFZ EAMs (see Fig. 1 for the flowchart). The two steps are explained in detail below.

Fig. 1
figure 1

Flowchart of PM forecast with the HW-VCW method. The procedure can be divided into two major parts: 1, determination of the Tcw that minimize the difference between C04 PM observation and ESMGFZ EAM-derived PM (denoted as ESMGFZ PM for short); 2, modeling of the residuals unexplained by ESMGFZ PM with the HW-VCW method. The two parts are marked with boxes with red and blue dashed lines, respectively

Full size image

4.1 Determination of CW Period

To minimize the errors of PM forecast in the HW-VCW method, period and quality factor of Chandler Wobble (Tcw and Qcw) corresponding to the eight-year-long PM timeseries for modeling should be determined first with the following steps (also see the box with red dashed line in Fig. 1).

STEP 1: We derive the observed polar motion excitation \(\chi_{C04}\) PM in IERS EOP14C04 \(p_{C04}\) by using Eq. (3). Please notice that appropriate data extensions at both ends of \(p_{C04}\) are necessary to overcome the edge effects brought by frequency domain computation.

STEP 2: We derive C04 excited PM \(p_{exci,C04}\) from \(\chi_{C04}\) by using Eq. (1). Then, C04 free PM is determined by \(p_{free,C04} = p_{C04} - p_{exci,C04}\).

STEP 3: Similar to STEP2, we derive ESMGFZ excited PM \(p_{exci,ESMGFZ}\) from \(\chi_{ESMGFZ}\). Total ESMGFZ polar motion \(p_{ESMGFZ}\) can be expressed as \(p_{ESMGFZ} = p_{free,C04} + p_{exci,ESMGFZ}\) since the free PM \(p_{free,C04}\) should be independent from excitations within the modeling timespan.

STEP 4: We calculate the X- and Y-component standard deviation (SD) \(\delta_{PMX}\) and \(\delta_{PMY}\) of \(p_{C04} - p_{ESMGFZ}\), respectively. According to Eq. (1) to (3), \(\delta_{PMX}\) and \(\delta_{PMY}\) are determined by the \(T_{cw}\) and \(Q_{cw}\). Therefore, the objective function is defined as

$$\delta_{PM} \left( {T_{cw} ,Q_{cw} } \right) = \sqrt {\delta_{PMX} \left( {T_{cw} ,Q_{cw} } \right)^{2} + \delta_{PMY} \left( {T_{cw} ,Q_{cw} } \right)^{2} }$$
(7)

\(\delta_{PM} \left( {T_{cw} ,Q_{cw} } \right)\) represents the difference between observation \(p_{IERS} \left( t \right)\) and model \(p_{ESMGFZ} \left( t \right)\). Therefore, smaller \(\delta_{PM} \left( {T_{cw} ,Q_{cw} } \right)\) means that \(T_{cw}\) and \(Q_{cw}\) used in STEP1–STEP3 are more reliable for the timespan.

STEP5: With initial CW period T0 = 433 days, we use derivative-free fluctuated optimization in MATLAB to find the \(T_{cw}\) that minimizes \(\delta_{PM} \left( {T_{cw} ,Q_{cw} } \right)\). This determined \(T_{cw}\) is regarded as the period of CW involved in the corresponding 8-year PM timeseries since it minimizes deviation between observed geodetic and modeled geophysical PM excitation function (Nastula and Gross 2015). However, we choose to adopt the constant value Qcw = 179 obtained by Wilson and Vicente (1990) and recommended by Gross (2015) in this research. That is because (1) Qcw is mostly determined by properties of mantle minerals and unlikely to change within a relatively short time scale, as discussed in the Introduction; (2) our numerical tests indicate that while small Qcw (e.g., Qcw < 50) will affect the EAM-derived PM significantly, the choice of Qcw value hardly changes our PM forecast results for Qcw > 100.

4.2 Modeling the PM Residuals Unexplained by EAMs

By using the \(T_{cw}\) and \(Q_{cw}\) determined/adopted in Sect. 4.1, we can get the EAM-derived PM \(p_{exci,ESMGFZ}\)(this holds for both the ESMGFZ operational and forecast products). There is usually some difference between \(p_{C04}\) and \(p_{exci,ESMGFZ}\), denoted as the residual unexplained by \(p_{exci,ESMGFZ}\):

$$p_{res} = p_{C04} - p_{exci,ESMGFZ}$$
(8)

which can be separated into a linear trend \(p_{res,l}\) and a nonlinear part \(p_{res,v}\), which is dominated by the free damping CW according to Eq. (1), and can be predicted by the Holt-Winters algorithm.

The high-frequency components in \(p_{res,v}\), such as daily fluctuations, will cause notable errors in short-term forecast using the Holt-Winters algorithm. Therefore, we model \(\Delta p_{res,v}\), the 60-sample-smoothed first-order difference of \(p_{res,v}\), instead of \(p_{res,v}\) to reduce errors in PM forecast. The HW model of \(\Delta p_{res,v}\) is established according to Eqs. (4) and (5). However, its h-step forecast \(\Delta \tilde{p}_{{res,v,\left\{ {N + h} \right\}}}\) is empirically modified from Eq. (6) to weaken the edge effect of parameters caused by numerical smoothing:

$$\Delta \tilde{p}_{{res,v,\left\{ {N + h} \right\}}} = \left\{ \begin{gathered} \frac{{a_{N - 1} + a_{N} }}{2} + \frac{{b_{N - 1} + b_{N} }}{2}h + c_{{N + h - \left( {k + 1} \right)T}} ,\,h = 1 \hfill \\ \frac{{\sum\limits_{i}^{h} {a_{N - i + 1} } }}{h} + \frac{{\sum\limits_{i}^{h} {b_{N - i + 1} } }}{h}h + c_{{N + h - \left( {k + 1} \right)T}} ,\,h > 1 \hfill \\ \end{gathered} \right.$$
(9)

where \(T\) is the nearest integer value of \(T_{cw}\), while other parameters are defined the same as those in Eqs. (4) to (6). Therefore, the forecast of \(p_{res,v}\) (represent by \(\tilde{p}_{res,v}\)) is restored as

$$\left\{ \begin{gathered} \tilde{p}_{{res,v,\left\{ {N + 1} \right\}}} = \Delta \tilde{p}_{{res,v,\left\{ {N + 1} \right\}}} + p_{{res,v,\left\{ N \right\}}} \hfill \\ \tilde{p}_{{res,v,\left\{ {N + h} \right\}}} = \Delta \tilde{p}_{{res,v,\left\{ {N + h} \right\}}} + \tilde{p}_{{res,v,\left\{ {N + h - 1} \right\}}} ,\,h > 1 \hfill \\ \end{gathered} \right.$$
(10)

(see the box with blue dashed line in Fig. 1).

With all relevant components obtained, the h-step (or h-day) PM forecast can be expressed as

$$\tilde{p}_{{HW - VCW,\left\{ {N + h} \right\}}} = \tilde{p}_{{res,l,\left\{ {N + h} \right\}}} + \tilde{p}_{{res,v,\left\{ {N + h} \right\}}} + \tilde{p}_{{exci,ESMGFZ,\left\{ {N + h} \right\}}}$$
(11)

according to Eq. (8). Here, \(\tilde{p}_{{res,l,\left\{ {N + h} \right\}}}\) is the predicted linear trend (namely the forecast of \(p_{res,l}\)), \(\tilde{p}_{{res,v,\left\{ {N + h} \right\}}}\) is calculated by Eq. (10), and \(\tilde{p}_{{exci,ESMGFZ,\left\{ {N + h} \right\}}}\) is derived from ESMGFZ forecast products using Eq. (1).

5 Results and Validations

The 30-day polar motion forecasts based on the HW-VCW method are illustrated and compared with the IERS EOP products and forecasts from some previous studies in this section.

In this study, 8-year-long IERS EOP14C04 and ESMGFZ EAM products before each forecast timespan are adopted to establish corresponding forecast models. However, the access to previous forecast products is unavailable since ESMGFZ online product repository preserves only the latest forecast products. Therefore, we separate the validation of the HW-VCW method into 2 parts: (1) Secular stability test, HW-VCW Op: January 1998 to December 2020: monthly and weekly 30-day forecast, in which ESMGFZ EAM Op are used to replace the inaccessible ESMGFZ EAM forecast products in forecast timespan. (2) Forecast test, HW-VCW F06: 22 September 2021 to 29 October 2021: daily 6-day forecast, in which ESMGFZ 6-day forecast products are used in forecast timespan.

5.1 Secular Stability Test

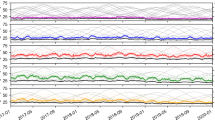
To test the stability of the HW-VCW method, we make 276 monthly 30-day polar motion forecasts starting from 2nd of each month during 1998–2020. Figure 2 shows the time-variable Tcw determined according to Sect. 3.2 for PM forecast. One can see that Tcw fluctuates within 426–436 days with an average 431.06 days, in accord with most previous studies (e.g., Jeffreys 1972; Wilson and Haubrich 1976; Ooe 1978; Wilson and Vicente 1990; Vicente and Wilson 1997; Guo et al. 2005).

Fig. 2
figure 2

Time-variable CW period (Tcw) for 30-day polar motion forecasts spanning January 1998 to December 2020 (276 monthly forecasts in total). Tcw are determined for every 8-year sliding timespan according to the method described in Sect. 3.2 with Qcw = 179. These Tcw values may not be very reliable (as they are determined using only 8-year data) but are efficient in improving PM forecasts

Full size image

Figure 3 shows monthly 30-day PM forecast error of HW-VCW Op relative to IERS EOP14C04 observation \(\left( {\Delta PM = \tilde{p}_{VC + HW} - p_{C04} } \right)\) during Jan., 1998–Dec., 2020. In general, closer forecasts are more likely to be accurate and errors of Y-pole are significantly smaller than that of PMX. For the most important case 1-day forecast, 73.19% ΔPMX and 87.32% ΔPMY are smaller than 0.3 mas. When PMX and PMY are both considered, 59.42% ΔPM are smaller than 0.3 mas, and the root mean square errors (RMSE) is 0.34 mas for 1-day forecast, comparable to those of Dobslaw and Dill (2018) (0.35 mas), Dill et al. (2019) (0.40 mas), Schuh et al. (2002) (0.29 mas) and Chin et al. (2004) (0.29 mas).

Fig. 3
figure 3

Deviations between PM forecast derived by the HW-VCW method and IERS EOP14C04 polar motion observation during January 1998 to December 2020. a PMX and PMY forecast errors (ΔPMX and ΔPMX) up to 30 days, and b similar to a but for details up to 7-day forecast. Please notice that EAM operational products instead of forecast products are used for forecast in this figure

Full size image

Specifically, in Fig. 4, we compare absolute errors (AEs) and mean absolute errors (MAEs) of 1-, 5-, 10-, 20- and 30-day PM forecasts derived by HW-VCW Op with recent researches (Xu et al. 2012; Wu et al. 2018, 2021; Yao et al. 2013; Wang et al. 2018; Jin et al. 2021). Most AEs for the HW-VCW forecasts are smaller than MAEs of other researches in relative timespans. On day-1, MAEs of HW-VCW Op are 0.214 mas and 0.154 mas for PMX and PMY, while the best published results are 0.223 mas and 0.183 mas derived by weighted LS + AR (WLS + AR) (Wu et al. 2018). In forecasts up to day-30, our MAEs are still smaller than others, indicating that forecasts made by HW-VCW are reliable and stable within 30-day PM forecasts.

Fig. 4
figure 4

Absolute errors (AEs) and mean absolute errors (MAEs) of 1-, 5-, 10-, 20- and 30-day PM forecasts spanning January 1998 to December 2020. Left: AE of PMX; Right: AE of PMY. Grey dots: AE of HW-VCW Op; Dashed black line: MAE of HW-VCW Op spanning January 1998 to December 2020; colored lines and texts: MAEs of other researches in their timespans given for comparison

Full size image

To further verify the HW-VCW method, we also make 828 weekly forecasts corresponding with IERS bulletin A products spanning 7 January 2005 to 20 November 2020. According to MAE listed in Table 1, by using the HW-VCW method, MAE of PMX forecast decreases by 20.00% while that of PMY forecasts decrease by 33.33% on day-1, reaching 0.24 and 0.16 mas, respectively. The HW-VCW method also improves 22.95–38.41% MAEs of PMX and 26.46–34.33% MAEs of PMY compared with Bulletin A within day-2–day-10. On day-20 and day-30, the HW-VCW method is still much better than Bulletin A in PMX forecasts with > 23% improvements achieved. However, PMY forecasts of Bulletin A perform much better than that of PMX during the same period, leading to decreasing MAE improvements of the HW-VCW method. In addition, please notice that Bulletin PM predition products have MAEs on day-0 (0.06 mas and 0.09 mas) caused by their combined EOP solution (slightly different from C04 EOP) spanning 6–8 days before the prediction horizon, which may enlarge the MAEs of Bulletin A PM prediction.

Table 1 Mean absolute error (MAE) of deviations between polar motion forecasts and IERS EOP14C04 EOP observation
Full size table

5.2 Forecast Test

To test the HW-VCW method in real forecast and simulate the influences of the delay in C04 release, we also compare the AEs of PM forecasts made by the HW-VCW F06 (using ESMGFZ EAM F06) with that of the HW-VCW Op (using ESMGFZ EAM Op) during 22 September 2021 to 29 October 2021 (their AE differences are determined as ΔAE = AEF06 – AEOp).

Assuming we have real-time access of PM observation data (namely, C04 release delay = 0 day), according to Fig. 5, PM predicted by the HW-VCW F06 is similar to that of ESMGFZ EAM F06 on day-1 and day-2 with most ΔAE < 0.1 mas, while larger ΔAE appears on day-3 to day-6. However, it can be seen from the MAE curves in Fig. 5 and L0 vs. E0 in Table 2 that, for PMX and PMY, MAEsF06 are almost the same as MAEsOp on day-1 to day-3 while 0.02–0.06 mas smaller than MAEsOp on day-4 to day-6, indicating that the HW-VCW F06 is even slightly better than the HW-VCW OP in this duration. Therefore, we infer that utilizing ESMGFZ EAM F06 instead of ESMGFZ EAM Op in the HW-VCW method will not significantly affect the accuracy of ultra-short PM forecast.

Fig. 5
figure 5

Differences between 6-day PM absolute errors predicted by the HW-VCW Op and the HW-VCW F06 (ΔAE = AEF06–AEOp) spanning 22 September 2021 to 29 October 2021 (36 forecasts in total). (left): ΔAEs of PMX and PMY, sharing the same color bar. Each rectangle presents the ΔAE on that day; (right): corresponding MAEs on each forecast days within 6-day forecast horizon (y-axis). (ESMGFZ EAM F06 on 26 September 2021 to 21 October 2021 were not available for download.)

Full size image
Table 2 MAE of polar motion predicted by the HW-VCW F06 and the HW-VCW Op relative to IERS EOP14C04 EOP observation (MAEF06 and MAEOP)
Full size table

For the actual case that there is C04 release delay, most PM prediction methods are forced to make traditional multiple-day PM prediction (similar to L0 in Table 2). However, HW-VCW method has another option (L1–L6 in Table 2) by involving the latest EAM operational products if the daily released ESMGFZ EAM operational products are published on time. In this situation, excited PM of the delay days can be estimated from the available ESMGFZ EAM operational instead of forecast products. Delays of PM observation not only introduce deviations on day-0 but also enlarge MAEs of HW-VCW method on the same prediction day due to the extended prediction of free PM. Compared with non-delay conditions by calculating L6–L0 in Table 2, 6-day delay of C04 increases MAEs of PMX and PMY by 1.30–0.95 mas and 0.79–1.25 mas separately on prediction day-1 to day-6. Besides, we find that MAEs in Table 2 are generally descending from bottom-right to top-left, corresponding to PM prediction results with longer delays but shorter prediction distances in L0–L6. For example, MAE of 1-day PMX prediction in L5 (1.47 mas) is smaller than other MAEs along its diagonal and significantly better than 1.68 mas of 6-day PMX prediction in L0. When the sums of delay and prediction steps are the same, L0–L6 have to predict free PM from the same distance. However, in L1–L6, parts of excited PM are calculated from EAM operational products, which is totally predicted by EAM forecast products in L0. Similar features of RMSE variations can also be found in Dobslaw and Dill (2018). Therefore, we infer that accuracy of HW-VCW method can be further improved by involving the latest ESMGFZ EAM operational products when PM observation is delayed in real PM forecast.

6 Discussion and Conclusions

Based on the Holt-Winters (HW) additive algorithm, we have proposed a new short-term PM forecast method HW-VCW, which can handle the variability of CW and take advantage of GCM-derived angular momentum products, and thus improve the accuracy of PM forecasts. The HW-VCW method is tested with both the IERS EOP C04 PM observation and Bulletin A PM forecast for its secular stability and then applied to real PM forecasts using ESMGFZ EAM 6-day forecast products. Our results show that the HW-VCW method is stable and reliable in different timespans and can bring 20.00–38.41% improvements in ΔPMX and 1.05–34.33% improvements in ΔPMY from 1 to 30 days into the future compared with PM forecasts in IERS bulletin A, from the aspect of MAE. Besides, we also proved that HW-VCW method is effective in real PM forecasts, in which case there is certain C04 release delay. Especially, the day-0 ESMGFZ EAM operational products contribute significantly in reducing the forecast MAE. Thus, the ESMGFZ EAM operational and forecast products are very beneficial for PM forecasts.

In the development of the HW-VCW PM forecast method, we have used the integration as expressed by Eq. (1) rather than the frequency-domain conversion as expressed by Eq. (3), since the possible noises and errors within the CW frequency band of excitations caused by observation or modelling (e.g., Zotov 2020) may be amplified.

In addition, we have assumed Tcw being variable since long-time observations show that Tcw may be time dependent. Chandler (1891) first suggested Tcw might be not only variable but also positively correlated with the CW amplitude. Iijima (1965) analyzed the International Latitude Service (ILS) data for the period 1900.0–1963.2 with a 0.1-year sampling and found that the Tcw varies from about 1.1 to 1.2 years and the smaller period happens when the CW has a smaller amplitude, and vice versa. Later, Proverbio et al. (1971) confirmed the correlation between the amplitudes and periods of the CW. Carter (1981) proposed a frequency modulation model to explain variations of both the amplitude and frequency of the CW and suggested that the nonequilibrium ocean pole tide can vary with time and lead to the frequency modulation of CW. Gao (1997) concluded that Tcw might have a 10-day fluctuation in correlation with CW amplitude during the last several decades. Höpfner (2003) found that the Chandler wobble has a period variation between 422 and 438 days with an estimated standard deviation of only 0.48 days, while its amplitude varies from 150 to 200 mas with a temporal dependence similar to the period. Based on the Jacobian elliptic functions, Chen et al. (2009) derived a theoretical model for the frequency-amplitude modulation of the CW, which indicates Tcw is time dependent and can be affected by the CW amplitude.

Physically speaking, if the Earth is a body with fixed size, figure and density distribution, the CW frequency, as a normal mode or eigenfrequency of the Earth, would be a constant. However, as is well known, the Earth is undergoing continuous deformations (namely changing figure and density distribution) due to loading and tidal attractions, etc. Therefore, the normal mode CW frequency must be changing correspondingly, and the traditionally referred “observed CW frequency (or period)” should be understood as the mean value over a certain period. To conclude, Tcw can change with time though the amplitude of fluctuation is still uncertain.

Finally, the HW-VCW method developed in this study is most suitable for short-term PM forecast, as its forecast errors increase notably beyond 30 days in the future. However, one may extend the HW-VCW method to middle-term or even long-term PM forecast by improving the algorithms involved.