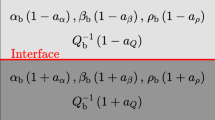Abstract
The problem of frequency-dependent seismic inversion for estimating attenuation and anisotropy based on rock physics effective model is reviewed and analyzed. Based on an extended periodically layered medium model, frequency-dependent stiffness parameters of anisotropic anelastic media as a function of attenuation factor and weaknesses are presented. For the case of an interface separating two anisotropic anelastic media, a new parameterized P-to-P reflection coefficient and anisotropic anelastic impedance \({\mathcal {A}}_\mathrm{EI}\) are proposed. Based on the anisotropic \({\mathcal {A}}_\mathrm{EI}\), an inversion workflow of employing frequency components of seismic amplitudes to estimate attenuation factor and weaknesses for anisotropic anelastic media is presented. In the first stage inversion, the anisotropic \({\mathcal {A}}_\mathrm{EI}\) is calculated using frequency components of partially incidence-angle-stacked seismic data; and the second-stage inversion for unknown attenuation factor and weaknesses is implemented combining a Newton method and Bayesian Markov chain Monte Carlo algorithm by calculating first- and second-order derivatives of anisotropic \({\mathcal {A}}_\mathrm{EI}\) with respect to unknown parameters. Tests on synthetic seismic gathers confirm the accuracy of new parameterized reflection coefficient, and the unknown parameters are estimated reliably even in the case of seismic data of signal-to-noise ratio of 2 being employed. Applying the inversion approach and workflow to a field data set acquired over a shale reservoir, reliable attenuation factors and weaknesses that match well log curves are obtained, which are preserved as indicators for identifying potential hydrocarbon-bearing cracked reservoirs.
Article Highlights
-
A new parameterized PP-wave reflection coefficient and anisotropic anelastic impedance are derived in terms of attenuation factor and weaknesses
-
A two-stage inversion workflow of employing frequency components of seismic data to estimate attenuation factor and weaknesses combining Newton method and Bayesian Markov chain MonteCarlo algorithm
-
Reliably estimated attenuation factor and weakness that match well log curves appear to be indicators or identification of potential cracked reservoirs














Similar content being viewed by others
References
Agersborg R, Johansen TA, Jakobsen M, Sothcott J, Best A (2008) Effects of fluids and dual-pore systems on pressure-dependent velocities and attenuations in carbonates. Geophysics 73(5):N35–N47
Aki K, Richards PG (2002) Quantitative seismology. University science books
Alkhalifah T, Tsvankin I (1995) Velocity analysis for transversely isotropic media. Geophysics 60(5):1550–1566
Bachrach R, Sengupta M, Salama A, Miller P (2009) Reconstruction of the layer anisotropic elastic parameters and high-resolution fracture characterization from P-wave data: a case study using seismic inversion and Bayesian rock physics parameter estimation. Geophys Prospect 57(2):253–262
Backus GE (1962) Long-wave elastic anisotropy produced by horizontal layering. J Geophys Res 67(11):4427–4440
Bakulin A, Grechka V, Tsvankin I (2000) Estimation of fracture parameters from reflection seismic data-Part I: HTI model due to a single fracture set. Geophysics 65(6):1788–1802
Behura J, Tsvankin I (2009) Reflection coefficients in attenuative anisotropic media. Geophysics 74(5):WB193–WB202
Bird C (2012) Amplitude-variation-with frequency (AVF) analysis of seismic data over anelastic targets. Master’s thesis, University of Calgary
Borcherdt RD (2009) Viscoelastic waves in layered media. Cambridge University Press
Brajanovski M, Gurevich B, Schoenberg M (2005) A model for P-wave attenuation and dispersion in a porous medium permeated by aligned fractures. Geophys J Int 163(1):372–384
Brajanovski M, Müller TM, Gurevich B (2006) Characteristic frequencies of seismic attenuation due to wave-induced fluid flow in fractured porous media. Geophys J Int 166(2):574–578
Brajanovski M, Müller TM, Parra JO (2010) A model for strong attenuation and dispersion of seismic P-waves in a partially saturated fractured reservoir. Sci China Phys Mech Astron 53(8):1383–1387
Carcione JM (2015) Wave fields in real media: wave propagation in anisotropic, anelastic, porous and electromagnetic media, vol 38. Elsevier
Carcione JM, Gurevich B, Santos JE, Picotti S (2013) Angular and frequency-dependent wave velocity and attenuation in fractured porous media. Pure Appl Geophys 170(11):1673–1683
Chapman M (2003) Frequency-dependent anisotropy due to meso-scale fractures in the presence of equant porosity. Geophys Prospect 51(5):369–379
Chapman M, Liu E, Li XY (2006) The influence of fluid sensitive dispersion and attenuation on AVO analysis. Geophys J Int 167(1):89–105
Chen H, Innanen KA (2018) Estimation of fracture weaknesses and integrated attenuation factors from azimuthal variations in seismic amplitudes. Geophysics 83(6):R711–R723
Chen H, Zhang G (2017) Estimation of dry fracture weakness, porosity, and fluid modulus using observable seismic reflection data in a gas-bearing reservoir. Surv Geophys 38(3):651–678
Chen H, Pan X, Ji Y, Zhang G (2017) Bayesian Markov Chain Monte Carlo inversion for weak anisotropy parameters and fracture weaknesses using azimuthal elastic impedance. Geophys J Int 210(2):801–818
Chen H, Innanen KA, Chen T (2018) Estimating P-and S-wave inverse quality factors from observed seismic data using an attenuative elastic impedance. Geophysics 83(2):R173–R187
Chen H, Ji Y, Innanen KA (2018) Estimation of modified fluid factor and dry fracture weaknesses using azimuthal elastic impedance. Geophysics 83(1):WA73–WA88
Chen H, Zhang G, Chen T, Yin X (2018) Joint PP-and PSV-wave amplitudes versus offset and azimuth inversion for fracture compliances in horizontal transversely isotropic media. Geophys Prospect 66(3):561–578
Downton J, Roure B (2010) Azimuthal simultaneous elastic inversion for fracture detection. In: SEG technical program expanded abstracts 2010, Society of Exploration Geophysicists, pp 263–267
Downton JE, Roure B (2015) Interpreting azimuthal Fourier coefficients for anisotropic and fracture parameters. Interpretation 3(3):ST9–ST27
Dupuy B, Stovas A (2016) Effect of anelastic patchy saturated sand layers on the reflection and transmission responses of a periodically layered medium. Geophys prospect 64(2):299–319
Dvorkin JP, Mavko G (2006) Modeling attenuation in reservoir and nonreservoir rock. Lead Edge 25(2):194–197
Galvin RJ, Gurevich B (2015) Frequency-dependent anisotropy of porous rocks with aligned fractures. Geophys Prospect 63(1):141–150
Grechka V, Tsvankin I, Bakulin A, Hansen JO, Signer C (2002) Joint inversion of PP and PS reflection data for VTI media: A North Sea case study
Guo J, Germán Rubino J, Barbosa ND, Glubokovskikh S, Gurevich B (2018) Seismic dispersion and attenuation in saturated porous rocks with aligned fractures of finite thickness: theory and numerical simulations-part 1: P-wave perpendicular to the fracture plane. Geophysics 83(1):WA49–WA62
Guo J, Han T, Fu LY, Xu D, Fang X (2019) Effective elastic properties of rocks with transversely isotropic background permeated by aligned penny-shaped cracks. J Geophys Res Solid Earth 124(1):400–424
Gurevich B, Brajanovski M, Galvin RJ, Müller TM, Toms-Stewart J (2009) P-wave dispersion and attenuation in fractured and porous reservoirs-poroelasticity approach. Geophys Prospect 57(2):225–237
Hsu CJ, Schoenberg M (1993) Elastic waves through a simulated fractured medium. Geophysics 58(7):964–977
Innanen KA (2011) Inversion of the seismic AVF/AVA signatures of highly attenuative targets. Geophysics 76(1):R1–R14
Köhn D (2011) Time domain 2D elastic full waveform tomography. PhD thesis, Christian-Albrechts Universität Kiel
Kong L, Gurevich B, Müller TM, Wang Y, Yang H (2013) Effect of fracture fill on seismic attenuation and dispersion in fractured porous rocks. Geophys J Int 195(3):1679–1688
Li Y (2006) An empirical method for estimation of anisotropic parameters in clastic rocks. Lead Edge 25(6):706–711
Lines L, Wong J, Innanen K, Vasheghani F, Sondergeld C, Treitel S, Ulrych T (2014) Research note: experimental measurements of q-contrast reflections. Geophys Prospect 62(1):190–195
Margrave GF (2013) Q tools: summary of CREWES software for Q modelling and analysis. The 25th annual report of the CREWES project
Mavko G, Jizba D (1991) Estimating grain-scale fluid effects on velocity dispersion in rocks. Geophysics 56(12):1940–1949
Moradi S, Innanen KA (2015) Scattering of homogeneous and inhomogeneous seismic waves in low-loss viscoelastic media. Geophys J Int 202(3):1722–1732
Moradi S, Innanen KA (2016) Viscoelastic amplitude variation with offset equations with account taken of jumps in attenuation angle. Geophysics 81(3):N17–N29
Müller TM, Gurevich B, Lebedev M (2010) Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks-a review. Geophysics 75(5):75A147-75A164
Pan W, Innanen KA, Margrave GF, Fehler MC, Fang X, Li J (2016) Estimation of elastic constants for HTI media using Gauss-Newton and full-Newton multiparameter full-waveform inversion. Geophysics 81(5):R275–R291
Pan X, Zhang G, Yin X (2017) Azimuthally anisotropic elastic impedance inversion for fluid indicator driven by rock physics. Geophysics 82(6):C211–C227
Pšenčík I, Gajewski D (1998) Polarization, phase velocity, and NMO velocity of qP-waves in arbitrary weakly anisotropic media. Geophysics 63(5):1754–1766
Pšenčík I, Vavryčuk V (1998) Weak contrast PP wave displacement R/T coefficients in weakly anisotropic elastic media. Pure Appl Geophys 151(2):699–718
Quintal B, Jänicke R, Rubino JG, Steeb H, Holliger K (2014) Sensitivity of S-wave attenuation to the connectivity of fractures in fluid-saturated rocks. Geophysics 79(5):WB15–WB24
Rowbotham P, Marion D, Eden R, Williamson P, Lamy P, Swaby P (2003) The implications of anisotropy for seismic impedance inversion. First Break, 21(5)
Rüger A (1998) Reflection coefficients and azimuthal AVO analysis in anisotropic media. PhD thesis, Colorado School of Mines
Rüger A, Tsvankin I (1997) Using AVO for fracture detection: analytic basis and practical solutions. Lead Edge 16(10):1429–1434
Schoenberg M, Protazio J (1990) \(^{\prime }\)Zoeppritz\(^{\prime }\) rationalized, and generalized to anisotropic media. J Acoust Soc Am 88(S1):S46–S46
Schoenberg M, Sayers CM (1995) Seismic anisotropy of fractured rock. Geophysics 60(1):204–211
Shaw RK, Sen MK (2004) Born integral, stationary phase and linearized reflection coefficients in weak anisotropic media. Geophys J Int 158(1):225–238
Shaw RK, Sen MK (2006) Use of AVOA data to estimate fluid indicator in a vertically fractured medium. Geophysics 71(3):C15–C24
Shuai D, Stovas A, Wei J, Di B, Zhao Y (2021) Effective elastic properties of rocks with transversely isotropic background permeated by a set of vertical fracture cluster. Geophysics 86(3):C75–C87
Thomsen L (1986) Weak elastic anisotropy. Geophysics 51(10):1954–1966
Tsvankin I (1996) P-wave signatures and notation for transversely isotropic media: an overview. Geophysics 61(2):467–483
Tsvankin I (1997) Reflection moveout and parameter estimation for horizontal transverse isotropy. Geophysics 62(2):614–629
Vogelaar B, Smeulders D (2007) Extension of White’s layered model to the full frequency range. Geophys Prospect 55(5):685–695
Whitcombe DN (2002) Elastic impedance normalization. Geophysics 67(1):60–62
Zhang F, Zhang T, Li XY (2019) Seismic amplitude inversion for the transversely isotropic media with vertical axis of symmetry. Geophys Prospect 67(9-Advances in Seismic Anisotropy):2368–2385
Zhang G, Li L, Pan X, Li H, Liu J, Han L (2020) Azimuthal fourier coefficient inversion for horizontal and vertical fracture characterization in weakly orthorhombic media. Geophysics 85(6):C199–C214
Zeng J, Stovas A, Huang H (2020) Anisotropic attenuation of stratified viscoelastic media. Geophys Prospect 69:180–203
Acknowledgements
This work was funded by The National Natural Science Foundation of China (42104109). This work was also supported by the Natural Science Foundation of Shanghai (21ZR1464700), the Shanghai Sailing Project, and the Fundamental Research Funds for the Central Universities. We thank the sponsors of CREWES for continued support. We acknowledge Hampson-Russell software package for processing seismic data and extracting wavelets.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Derivation and simplification of stiffness parameters and perturbations across the interface
In Eq. 2, we present stiffness parameters of the PLM, and under the assumptions that \(\frac{h_\mathrm{c}}{H}{\rightarrow }0\) and \(\frac{h_\mathrm{b}}{H}{\approx }1\), we simplify the stiffness parameters in terms of weaknesses. Taking \(C_{11}\) as an example, we obtain
where \({{Z}_{\text{N}}}{\approx }\lim \limits _{h_\mathrm{c}\rightarrow 0}\frac{{{h}_{\text {c}}}}{H{{{\mathcal {M}}}_{\text {c}}}}\). In the case of fluid filled compliant layers (fractures or cracks), we assume \(\frac{{\mathcal {M}}_\mathrm{c}}{{\mathcal {M}}_\mathrm{b}}{\approx }0\) and \(\frac{{\mathcal {U}}_\mathrm{c}}{{\mathcal {M}}_\mathrm{b}}{\approx }0\), and we further simplify \(C_{11}\) as
where \({\kappa }_\mathrm{b}={{\mathcal {U}}_\mathrm{b}}/{{\mathcal {M}}_\mathrm{b}}\).
Using relationship \(\delta _{\text{N}}=\frac{{\mathcal {M}}_\mathrm{b}Z_{\text{N}}}{1+{\mathcal {M}}_\mathrm{b}Z_{\text{N}}}\), we rewrite equation A.2 as
Other stiffness parameters are simplified as
Similar to the simplification of \(C_{11}\), we express \(C_{55}\) and \(C_{66}\) as
under the assumption that \(\frac{h_\mathrm{c}}{H}{\approx }0\).
In Eq. 5, we show the frequency-dependent stiffness parameters of the extended PLM model, and using the frequency-dependent stiffness parameters, we next show perturbations in stiffness parameters in the case of an interface separating two anisotropic anelastic media. Again taking \(C_{11}\) as an example, we obtain the perturbation \({\varDelta }C_{11}\) as
where \(M_{0}\), \({{{\mathcal {Q}}}_{\text{P}0}}\) and \(\delta _{\text{N}0}\) represent P-wave modulus, attenuation factor and weakness of background, and \({\varDelta }M\), \({\varDelta }{{{\mathcal {Q}}}_{\text{P}}}\) and \({\varDelta }\delta _{\text{N}}\) represent changes in P-wave modulus, attenuation factor and weakness. Under the assumption of isotropic elastic background (\({{\mathcal {Q}}}_\text{P0}=0\) and \(\delta _\text{N0}=0\)), we further derive \(\varDelta {C}_{11}(f)\) as
and under the assumption that \({\varDelta }M\), \({\varDelta }{{{\mathcal {Q}}}_{\text{P}}}\) and \({\varDelta }{\delta _{\text{N}}}\) are not too large, we neglect the term proportional to \({\varDelta }M{\varDelta }{{{\mathcal {Q}}}_{\text{P}}}\) and \({\varDelta }M{\varDelta }{\delta _{\text{N}}}\) to further simplify \(\varDelta {C}_{11}\) as
where we approximately replace \(M_{0}\) with M. Perturbations in other stiffness parameters, \(\varDelta {C}_{12}\), \(\varDelta {C}_{13}\) and \(\varDelta {C}_{33}\), are simplified as
The perturbation in stiffness parameter \(C_{55}\) expressed as
and again under the assumption of isotropic elastic background and small perturbations in S-wave modulus, attenuation and anisotropy, we further simplify \({\varDelta }C_{55}\) as
where we approximately replace \(\mu _{0}\) with \(\mu\).
The perturbation in stiffness parameter \(C_{66}\) simplifies as
Appendix B: PP-wave reflection coefficient in anisotropic anelastic media
Shaw and Sen (2004, 2006) propose an approach of employing the scattering function that is related to perturbations in stiffness parameters to calculate reflection coefficients in anisotropic media. Following Shaw and Sen (2004, 2006), we use simplified perturbations in frequency-dependent stiffness parameters shown in Appendix A to derive P-to-P reflection coefficient in anisotropic anelastic media. The scattering function in anisotropic anelastic media is calculated as
where \(\varDelta \rho\) represents perturbation in density across the reflection interface, \(\theta\) is the angle of P wave, and \(\chi _{ij}\) is a function of \(\theta\) and azimuth \(\phi\), which is given by
where \(\alpha\) is P-wave velocity of background. The P-to-P reflection coefficient is derived as
Substituting perturbations in stiffness parameters to equation A.15, we derive \(R_\mathrm{PP}(\theta ,f)\) as
Appendix C: Algorithm of Bayesian Markov chain Monte Carlo (MCMC)
Following Chen et al. (2017), we express the posterior probability distribution function (PDF), \(P\left( \mathbf {m}|\mathbf {d}\right)\), as
where \(P\left( \mathbf {d}|\mathbf {m}\right)\) is the likelihood function, and \(P\left( \mathbf {m}\right)\) is the prior probability function. In the present study, we assume both the likelihood function and the prior probability are consistent with Gaussian distribution; hence the posterior PDF is expressed as
where \(\psi _\mathbf{{M}}\), \(\psi _{\varvec{\mu }}\), \(\psi _{{\varvec{\rho }}}\), \(\psi _\mathbf{{Q}_{\text{n}}}\), \(\psi _{{{\varvec{\delta }}_{\text{N}}}}\), and \(\psi _{{{\varvec{\delta }}_{\text{T}}}}\) represent average values of corresponding vectors respectively, \(\sigma ^2_\mathbf{{M}}\), \(\sigma ^2_{\varvec{\mu }}\), \(\sigma ^2_{{\varvec{\rho }}}\), \(\sigma ^2_\mathbf{{Q}_{\text{n}}}\), \(\sigma ^2_{{{\varvec{\delta }}_{\text{N}}}}\), and \(\sigma ^2_{{{\varvec{\delta }}_{\text{T}}}}\) represent variance values of corresponding vectors respectively, and \(\sigma ^2_\mathbf{{e}}\) represents the variance of errors/noises between input and modeled data.
In the Bayesian MCMC algorithm, we determine whether the generated candidate \(\mathbf{{m}}^{'}\) should be accepted or not based on the calculation of a acceptance probability
where \(P\left( \mathbf{{m}}^{'}|{\textbf {d}}\right)\) and \(P\left( \mathbf{{m}}_{0}|\mathbf {d}\right)\) are posterior probabilities that are computed using equation A.18 for the generated candidate and the initial guess, respectively.
Given a generated candidate \({\textbf {m}}^{'}\), we compute the acceptance probability \(P_\mathrm{ac}\left( {\textbf {m}}^{'}\right)\) using equation A.19 and compare \(P_\mathrm{ac}(\mathbf{{m}}^{'})\) with a random value \(\beta\) generated in the range of \(\left[ 0,1\right]\). We only accept the candidate that makes \(P_\mathrm{ac}\left( {\textbf {m}}^{'}\right)\) be larger than \(\beta\).
Rights and permissions
About this article
Cite this article
Chen, H., Han, J., Geng, J. et al. Anisotropic Anelastic Impedance Inversion for Attenuation Factor and Weaknesses Combining Newton and Bayesian Markov Chain Monte Carlo Algorithms. Surv Geophys 43, 1845–1872 (2022). https://doi.org/10.1007/s10712-022-09727-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10712-022-09727-y