Abstract
The Earth-like planets and moons in our solar system have iron-rich cores, silicate mantles, and a basaltic crust. Differentiated icy moons can have a core and a mantle and an outer water–ice layer. Indirect evidence for several icy moons suggests that this ice is underlain by or includes a water-rich ocean. Similar processes are at work in the interiors of these planets and moons, including heat transport by conduction and convection, melting and volcanism, and magnetic field generation. There are significant differences in detail, though, in both bulk chemical compositions and relative volume of metal, rock and ice reservoirs. For example, the Moon has a small core [~ 0.2 planetary radii (RP)], whereas Mercury’s is large (~ 0.8 RP). Planetary heat engines can operate in somewhat different ways affecting the evolution of the planetary bodies. Mercury and Ganymede have a present-day magnetic field while the core dynamo ceased to operate billions of years ago in the Moon and Mars. Planets and moons differ in tectonic style, from plate-tectonics on Earth to bodies having a stagnant outer lid and possibly solid-state convection underneath, with implications for their magmatic and atmosphere evolution. Knowledge about their deep interiors has improved considerably thanks to a multitude of planetary space missions but, in comparison with Earth, the data base is still limited. We describe methods (including experimental approaches and numerical modeling) and data (e.g., gravity field, rotational state, seismic signals, magnetic field, heat flux, and chemical compositions) used from missions and ground-based observations to explore the deep interiors, their dynamics and evolution and describe as examples Mercury, Venus, Moon, Mars, Ganymede and Enceladus.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
-
Methods to explore the interiors of terrestrial planets and satellites using space missions are described and compared
-
All planets and most satellites are differentiated into iron-rich cores, rocky mantles and crusts and—for the satellites—ice-water layers
-
Mercury, Venus, Moon, Mars, Ganymede and Enceladus are discussed in some detail as examples
1 Introduction
Since the days of Copernicus (1473–1543), Brahe (1546–1601) and Kepler (1571–1630), we know that the Earth is the third planet out from the sun, orbiting the latter at a distance that is—as we learned to understand—within the sun’s habitable zone. While the Earth is the main focus of our interest as our home planet and of this particular collection of articles (Cazenave et al. 2022), we consider some of the other planets out of curiosity and because comparing similar and not so similar objects is a trusted way in science of deepening our understanding and testing hypotheses.
Of particular interest for scientists studying the interior of the Earth are the interiors of other rocky planets and moons of comparable size (Fig. 1). While the Earth is the biggest and most massive of these bodies in our solar system, other planetary systems host what has been termed super-Earths, planets with radii of up to twice the Earth’s and masses of up to ten times the latter. The pressure in super-Earths ranges up to terapascals and is far beyond what is accessible to date in high pressure experiments, at least in static experiments.
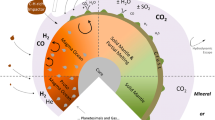
Schematic view of the interior structure and magnetic field evolution of Mercury, Venus, Earth, Moon, Mars and Ganymede. Upper panel: The white surface shows the silicate mantle, the light grey surface the fluid core and the dark grey surface the solid inner core and the white dotted area shows a water/ice mantle. Furthermore, the percentages of the crust/mantle volume ratio are shown. Apart from the Earth, the sizes of the different layers (core, solid inner core, silicate mantle, basaltic crust, or ice mantle) are determined with different precision for the bodies; for more detail, see text. Lower panel: The dark grey surface shows remnant magnetized crust. In case of the Moon dark grey shows a strong field and light grey a weaker field indicating the strong decrease of the magnetic field strength with time. The small hatched regions at the right hand side of the diagram for Earth, Mercury and Ganymede indicate the magnetic fields today. It is important to note that the lack of observed remnant magnetized crust is no clear sign that also an internally generated magnetic field was lacking at that time. This applies in particular to the early evolution of the planets and Venus and Ganymede. It is difficult for crustal rock on Venus to get remnant magnetization due to the high surface temperature close to or above the Curie temperature of magnetic minerals, and the silicate crust of the Ganymede is located under a thick layer of ice and water
Amongst the bodies of interest in the solar system is Venus as the most similar to the Earth in terms of radius and mass, the former being just a few percent smaller, Mars about half the size and roughly 10 per cent in mass but with a climate that resembles that of Earth’s more than that of the other terrestrial planets, and Mercury, the smallest and least massive but the one with the highest density if evaluated at standard conditions of pressure and density (105 Pa and 273 K) and a present-day intrinsic magnetic field (Fig. 1). Geophysical data are comparatively scarce for these planets, but missions have allowed measurements of the gravity and magnetic fields, and imaging and spectroscopy have allowed geological mapping and analysis of the compositions of surface rock and of the atmospheres. Information on planetary composition comes in addition from samples from Mars that we have in our meteorite collection, but also from in-situ measurements from lander and rover missions on Mars (e.g., Abbey et al. 2019) and Venus (e.g., Surkov et al.1984). Most recently, Mars has been the target of a dedicated geophysical observatory mission, InSight (Banerdt et al. 2020), that placed an extremely sensitive seismometer with broadband and short period sensors on the surface of the planet. It also enabled highly accurate measurements of the rotation axis, of the local—small scale—magnetic field and its time variation and of atmosphere pressure, temperature and wind speed (Banfield et al. 2019; Folkner et al. 2018; Lognonne et al. 2019) and of the thermal and mechanical properties of the Martian soil (Grott et al 2021; Spohn et al. 2021a) and interior (Lognonne et al. 2020; Giardini et al. 2020; Knappmeyer-Endrun et al. 2021; Khan et al. 2021; Stähler et al. 2021. Unfortunately, attempts to emplace thermal sensors at the required depth of 3–5 m were not successful and the goal of measuring for the first time the heat flow from another terrestrial planet had to be abandoned. However, the measurements of the other instruments were not affected by this and operated nominally.
Of the planetary satellites, the Moon is of particular interest not the least because it has been explored by humans during the Apollo program (1969–1972), when not only were the gravity and magnetic fields mapped, but seismic data was also recorded and the heat flow was measured (e.g., Taylor 2016; Jolliff et al. 2006 for lunar mission research reviews). In addition, the lunar rotation axis has been accurately measured over extended periods of time, the composition of surface rocks has been mapped and roughly 400 kg of lunar rock have been collected and brought to Earth. The origin of the Moon is closely linked to the early history of Earth (e.g., Canup et al. 2021) and the surface of the Moon, being devoid of traces of erosion apart from the effects of impacts is recording data pertinent to the long-eroded record of the early history of our own planet.
Other planetary satellites of particular interest to geophysics and covered in this article include Ganymede, the biggest of the Galilean satellites, covered with a thick ice mantle, with traces of lateral tectonic movements and a self-sustained magnetic field, and Enceladus, measuring only 500 km in diameter with geysers emanating from the surface near the south pole. Enceladus has been speculated to potentially harbor primitive life and together with Mars, Titan, and Europa belongs to the bodies in the solar system that are regarded as those with the greatest potential for detecting extraterrestrial life.
The evolution of these bodies depends essentially on the functioning of their heat engines. The latter are mostly driven by heat deposited during planet formation and generated by the decay of radioactive elements and, in some cases, by tidal dissipation. In the early evolution large catastrophic impacts likely played an important role as has been discussed for example for the Moon (compare Sect. 3.2). Convection is expected to take place in their rocky mantles, iron-rich cores, and outer ice layers, as has been recognized early on by, e.g., Schubert (1979). In the core, dynamo mechanisms can generate magnetic fields as we will discuss further below in Sect. 2.3. In the rock and ice mantle, convection and the dominant tectonic style are significantly influenced by their composition, the internal structure, and the surface conditions. Among the tectonic styles, a distinction is made between the plate tectonic regime of the Earth and the stagnant lid regime of the other planetary bodies like Mercury, Mars and the Moon as we will discuss in Sect. 3. Mixed tectonic styles may have existed, such as episodes of plate tectonics and stagnant lid convection, that are being discussed for Venus (Sect. 3.2). In the case of icy moons, the thermal evolution is additionally shaped by the outer ice layer, which may have a water ocean either trapped between ice layers (Ganymede, Sect. 3.5) or in direct contact with the silicate mantle (Enceladus, Sect. 3.6).
This article reviews the current state of knowledge about the interior of rocky planetary bodies, including constraints on their interior composition, internal structure, magnetic field generation and their thermo-chemical evolution. We describe the data obtained from planetary missions and ground-based observations and the methods used to analyze these data. We conclude with what understanding we have gained so far of Mercury, Venus, Mars, Ganymede and Enceladus with the help of mission data, modeling and laboratory experiments, and put these results in context with what we know about Earth.
2 Exploring the Deep Interior of Planets
2.1 Composition
Exploring the deep interior of planets commonly relies on the use of indirect methods, because direct access is severely limited. Even on Earth, the deepest hole ever drilled (the Kola Superdeep Borehole, e.g., Pavlenkova 1992) reached a depth of only ~ 12 km before the temperature at the bottom of the borehole exceeded the technical limits of the drilling equipment. This depth corresponds to less than 0.2 per cent of the distance to the center of our planet. Drilling holes in other planets and moons has been even more limited to date: the deepest hole in the Moon (drilled during the Apollo 17 mission in 1972) reached less than 3 m (e.g., Alton and Waltz 1980) and the deepest hole in Mars (dug during the InSight mission) reached ~ 40 cm depth (Grott et al. 2021)–both representing almost negligible distances compared to the bodies overall sizes. No samples of the iron-rich metal cores of the Earth or planets and moons have ever been obtained, and are unlikely to ever be obtainable in the foreseeable future. Core fragments of smaller bodies have been retrieved in the form of iron meteorites, but these represent remnants of planetesimals that were much smaller than the terrestrial planets, and that were broken up and destroyed by violent impacts early in the history of the solar system. NASA plans to fly the Psyche mission to M-type asteroid 16 Psyche, possibly an exposed core of a proto-planet (Elkins-Tanton et al. 2014).
In the absence of deep drilling, surface samples can provide clues about the interior composition and internal structure of rocky planets and moons. Volcanic samples that can be found at the surface form by partial melting of source rocks in the interior. Their chemical compositions reflect, albeit in a non-linear and often non-unique fashion, the composition of the source and pressure/temperature conditions of melting. In addition, volcanic deposits can contain xenoliths, solid rock samples incorporated into magma during magma transport from interior source to the surface. These provide a valuable window into the composition and mineralogy of the interior underneath a volcano. On Earth, some volcanism-related samples retrieved at Earth’s surface originated at up to several 100 km depth (far exceeding the bottom of the deepest drill hole), with some geochemical evidence as reviewed by Dehant et al. (2022), suggesting that a small part of some volcanic rocks may have originated near the core-mantle boundary (~ 2900 km depth).
Tectonic processes including subduction and orogenesis can lead to substantial vertical transport of rock masses, and if accompanied by significant erosion can exhume rocks initially formed tens of kilometers deep all the way to the surface. For example, some of the deepest-formed rocks presently found at the surface in Europe are located in the Swiss Alps, brought to the surface during the Alpine orogeny (e.g., Dobrzhinetskaya et al. 1996). Tectonic emplacement of interior rocks onto the surface is limited in the solar system, as plate tectonics appears to be limited to Earth at present. Strong vertical movements bringing deep interior rocks to the surface can also be induced by impacts–a process that has left clear marks on the surfaces of almost all rocky bodies in the solar system. Large impacts can directly expose subsurface material by evaporating and ejecting overlying rocks or ice. Rebounding of the subsurface after larger impacts leads to the formation of a central peak in the crater, with the material exposed in this peak originating from deep below the crater floor (e.g., Flahaut et al. 2012). The precise depth from which central peak material originated depends, amongst other factors, on the size of the impact (and hence on the size of the crater).
Surface rock samples have been collected, and returned to Earth, only from the Moon (thanks to the Apollo, Luna and Chang’e missions), and asteroids Itokawa and Ryugu (thanks to the two Hayabusa missions) (Kawaguchi et al. 2008), with samples from the surface of asteroid Bennu currently on their way back to our planet (OSIRIS-Rex mission) (Lauretta et al. 2017). Sample return from Mars is being planned for this decade. The NASA Perserverance and the ESA Pasteur rovers will be collecting samples that are planned to be returned to Earth by a dedicated mission (e.g., Kminek et al. 2021). An extensive review of past and outlook to future sample return missions is provided in Anand et al. (2021). On Venus, Mars, and the Moon, lander missions have obtained additional compositional data in situ on the surface. The accuracy and precision of these data is necessarily limited compared to that achievable for returned samples.
For Mercury, the Moon, Mars and outer planetary bodies, surface compositional data is available from remote sensing missions (again with limitations on accuracy, precision, and spatial resolution). A major advantage of remote sensing and lander missions without a sample return component is that they provide more complete global coverage of surface mineralogy and composition compared to the very limited surface areas from which samples have currently been obtained. On top of this, remote sensing missions can provide mineralogical and compositional information for areas that cannot be reached by lander or rover missions, such as steep mountain slopes. As an example, the mineralogy and chemical composition of the central peaks of lunar craters can be mapped from space, and remote sensing analyses of the composition of central peaks in lunar craters of different sizes has been used to map the vertical structure of the lunar crust, as well as its lateral homogeneity (e.g., Martinot et al. 2018, 2020)–something that cannot be done on the basis of sample return or in situ data.
Naturally, combinations of remote sensing, landing/roving, and sample return missions provide most information. In this case, accuracy and precision of space-based remote sensing and/or lander/rover in situ observations can be improved by the data from returned samples, as they enable so-called ground truthing. At the moment this integrated approach is limited to the Moon. A combination of remote sensing and sample return missions is especially important for bodies with a significant atmosphere such as Mars, as the atmosphere complicates remote sensing observations of the surface.
Surface samples from some bodies across the solar system are available on Earth in the form of meteorites. Some of these are remnants of primitive bodies formed very soon after the formation of the solar system (iron meteorites, stony iron meteorites, chondrites); others (the achondrites) were ejected from larger, differentiated bodies including the Moon, Mars, and asteroids. The former provide a cross-section of the nature of potential building blocks of rocky planets and form the basis for the development of models for the bulk chemical composition of Mercury, Venus, Earth, and Mars. The latter provide further insight into the composition of the outer crust and mantle of the Moon, Mars and large asteroids such as Vesta, even though it is often impossible to link these meteorites to a specific location on the surface of the parent body.
Tiny aliquots of returned samples as well as meteorites can be dissected in laboratories on Earth and analyzed for their mineralogy, major and trace elements, stable isotopic, and radiogenic isotopic compositions. These analyses provide constraints on the composition of the silicate reservoirs of planets (planetary crusts and mantles). Sample age information is important as it can yield constraints on models of the dynamics of a planetary interior as a function of time. To link such compositional and age information with geodetic and geophysical data on a planet’s interior structure, experiments in which the high-pressure, high-temperature interior conditions in planets are reproduced are required. Such experiments are important for two reasons. First, they can be used to constrain the chemical composition as well as the formation conditions of planetary mantles and cores, providing boundary conditions for thermochemical models of the evolution of planetary interiors from their origin until the present day. Second, they can help determine the mineralogy and physical state (solid versus molten), as well as the physical properties, of planetary crusts, mantles, and cores as a function of depth, providing independent tests of geophysical models of the present-day geodetic and geophysical properties (such as physical state, density and seismic wave propagation speeds) of planetary interiors.
An overview of the techniques used to recreate the high-pressure and high-temperature conditions in planetary interiors in the laboratory is provided in Dehant et al. (2022). In short, small (on the order of cubic millimeter-sized) synthetic or natural samples consisting of powdered silicate glass and/or iron rich metal of the appropriate composition can be compressed and simultaneously heated in a high-pressure apparatus. Figure 2 shows some examples of the types of experiments that can be performed to assist planetary interior studies. Experiments can be focused on determining the temperatures required to melt a planet’s or moon’s mantle at different depths (Fig. 2a). This information is required to constrain the source depth and temperature at which volcanic rocks found on the surface were formed. Other experiments focus on chemical equilibration between model cores and mantles of planets and moons (Fig. 2b). In such experiments, molten iron-rich metal is chemically equilibrated with molten rock to mimic the conditions of core formation early in a body’s history, and to determine how different elements distribute themselves between metal and silicate during this process. Such information is vital to ascertain under which conditions core formation occurred, and can help constrain the chemical composition of the core of a body on the basis of the chemical composition of its silicate shell. A third type of experiment is focused on determining which minerals are stable at different depths within a planetary mantle or core, and on determining key physical properties of these minerals such as their density or rheological behavior (e.g., Fig. 2c). Complementing and extending such laboratory techniques are computer simulations. Ab initio molecular dynamics approaches are increasingly used to calculate physical and chemical properties of minerals and melts at conditions that cannot be reached in the laboratory, with the added advantage of providing atomic-scale views of processes taking place at these conditions.
a Back-scatter electron (BSE) microscope image of a polished section through the run product of a high-pressure experiment mimicking the interior of the Moon (after Lin et al. 2020). This experiment illustrates conditions at which the lunar mantle would be partially molten and partially solidified. 1: Magma (light grey), solidified to a glass at the end of the experiment; 2: Clinopyroxene crystals (dark grey, large); 3: Plagioclase crystals (dark grey, long needles); 4: Graphite capsule surrounding the sample. b BSE image of a polished section through the run product of a high-pressure experiment mimicking the conditions of core formation in small planets (after Steenstra et al. 2017b). 5: Ball of iron-rich metal (molten during the experiment); 6: Silicate magma (quenched to a combination of lighter grey glass and darker quench crystals of olivine); 7: MgO capsule surrounding the sample. c X-ray radiography image looking through a high-pressure assembly aimed at measuring the density of ferropericlase (an oxide mineral present in planetary interiors) at high pressure and high temperature (after Van Westrenen et al. 2005). 8: Powdered ferropericlase material (light grey); 9: Rhenium disk separating sample powder from rest of the assembly; 10: Thin layer of mixture of gold and MgO powder serving as pressure calibrants; 11: Thermocouple wires for temperature measurements
Although initially focused exclusively on elucidating the properties of the interior of the Earth, in recent years high-pressure experimental as well as computational techniques are increasingly applied to constrain processes and evolution in other solar system bodies, as well as rocky exoplanets. A few recent examples are given in Sect. 3. Together with the geophysical techniques discussed in the following section, they form a powerful method to elucidate planetary interiors, even in the case of planets and moons for which we will never be able to obtain direct deep subsurface samples.
2.2 Interior Structure
Spacecraft data are essential for unravelling the internal structure of planets and satellites (Tables 1, 2). Since gravitational and electromagnetic fields decrease with distance (squared), close proximity to planetary objects is required for an accurate characterization of the fields. Observations from close distance also allow determination of topographic maps from laser ranging, imaging and radar observations, and complement the capacity of field observations to probe the interior. The orbital and rotational motions of planetary objects provide further information on their deep interiors, in particular on internal dissipation processes and on the existence of global liquid layers beneath the surface. For the most detailed view on the interior of a planet or natural satellite, equivalent to our knowledge about the Earth’s interior, equipment on the surface is needed. In this section, we describe the different methods to study the internal structure, with the exception of electromagnetism that is discussed in Sect. 2.3. Applications and results to planets and satellites are given in Sect. 3.
From close flybys, the mass and the low-degree components of the gravitational field can be determined. In practice, at most a few to some tens of close flybys have been performed of planetary satellites other than the Moon, and knowledge of their gravitational field is restricted to degree two or three (Anderson et al. 1996, 1998; Schubert et al. 2004; Iess et al. 2012, 2014). Since most flybys were approximately in the equatorial plane of the satellites, the best-known component of the gravitational field for satellites is the sectorial component of degree 2 (C22). Rotation is known to flatten the satellites at the poles and to create an equatorial bulge, but that only induces a zonal degree-two component (C20), not a sectorial component. The sectorial component results from the static tide raised by the central planet, which stretches the satellite in the direction to the planet. This static tide is a consequence of the fact that most large and mid-sized satellites of the solar system are in a 1:1 spin–orbit resonance–the equilibrium rotation state in which spin and orbit periods are equal–as a result of rotational evolution due to tidal dissipation. The large-scale shape of satellites is thus expected to be mainly described by an ellipsoidal shape of the planet with the long axis along the rotation axis due to rotation and an additional ellipsoid with long axis in the direction to the central planet resulting from the static tides (Murray and Dermott 1999). If we assume that a satellite behaves as a body in hydrostatic equilibrium with respect to rotational and tidal forces, the resulting polar flattening (the relative difference of mean equatorial and polar radii) is 5/6 of the equatorial flattening (the relative difference of longest and shortest equatorial axes) and the ratio of C20 to C22 is -10/3 (e.g., Van Hoolst et al. 2008). These ratios are therefore an important indicator of hydrostatic equilibrium, but have up to now only been determined for a few satellites.
Important insight into the mass distribution along the radial direction can be obtained if a satellite is in hydrostatic equilibrium, or if hydrostatic and non-hydrostatic components of the gravity field can be separated. The Radau-Darwin equation (e.g., Hubbard 1984) shows that, for hydrostatic equilibrium, the mean moment of inertia I can be determined from \(C_{22}\) (e.g., Sohl and Schubert 2015). For a satellite with homogeneous density \(I = 0.4MR^{2}\), with \(M\) the mass and \(R\) the radius of the satellite, which is an upper limit for the mean moment of inertia. Lower values provide information on the degree of differentiation of the satellite and set bounds on the sizes of the different layers. For example, for Io, which has a \(C_{22} /C_{20}\) consistent with hydrostatic equilibrium, the mean moment of inertia is equal to \(0.378MR^{2}\) (Schubert et al. 2004). This indicates that Io has a core denser than its mantle and that the core radius is between about 650 and 950 km (Schubert et al. 2004; Baland and Van Hoolst 2010).
For the terrestrial planets and the Moon, the gravitational field is much better known than for other satellites. The spatial resolution varies from a degree of about 50 on average for Mercury’s northern hemisphere (Genova et al. 2019; Konopliv et al. 2020a, b), determined from radio tracking the NASA MESSENGER spacecraft, to more than 900 for the Moon, derived from NASA's twin spacecraft GRAIL mission (Lemoine et al. 2014, Konopliv et al. 2014). The joint analysis of these data together with topography data, which are known with a higher resolution than the gravity field, gives information on the crustal thickness and density, and on the elastic thickness of the lithosphere, and provides insight into the mechanism of support of topography, and into the planet’s thermal evolution and magmatic processes (e.g., Wieczorek 2015). It has also been used to infer the presence of a global subsurface ocean in satellites (e.g., Beuthe et al. 2016; Cadek et al. 2016). Some examples are discussed in Sect. 3.
Besides the static gravity field, terrestrial planets and satellites also have a time-variable degree-two component of the gravity field due to periodic tides. For the terrestrial planets, the main tide has a period equal to half a solar day–except the Earth, for which the main tide is the lunar one. For satellites rotating synchronously with their orbital motion, the main period is equal to the orbital (or spin) period. Tides are excellent probes of global internal layers, such as a liquid iron core, a subsurface ocean or a magma ocean, since shear stresses balancing the tidal force require much less deformation than pressure gradients in a liquid. Therefore, tides of a planetary object with a global internal liquid layer are significantly larger than for the same object lacking such a liquid layer. The difference is more pronounced the closer the liquid layer is to the surface. Tidal observations can therefore be used to determine the size of the core or the depth to a subsurface water or magma ocean (Moore and Schubert 2000, 2003; Van Hoolst and Jacobs 2003; Rivoldini et al. 2011; Iess et al. 2012; Bierson and Nimmo 2016; Van Hoolst et al. 2020). Ideally, different physical manifestations of tides should be used to allow distinguishing between the effects of the liquid layer and the rigidity of the solid layers above the liquid. Besides the tidally induced time-variable gravity field (described by the so-called Love number \(k_{2}\)), the tidal surface displacement (described by the Love number \(h_{2}\)) can also be determined from orbit, and their joint analysis strongly improves the constraints that can be put on the internal structure beyond what can be obtained from a single tidal quantity (Wahr et al. 2006; Hussmann et al. 2011).
A further approach to deduce the internal structure of planetary bodies is to observe their rotation. Planets and satellites undergo small variations in their rotation due to various reasons. A main cause of rotation variations is the gravitational torque exerted by the central object on the planetary object. As is well known for the Earth, the torque slowly changes the planet’s orientation (precession and nutation, see Dehant and Mathews 2015). Since the rate of precession depends on the polar moment of inertia, an accurate determination of it combined with the degree-two gravity field allows determination of the mean moment of inertia—even if the body is not in hydrostatic equilibrium. Nutations are periodic orientation variations superposed on the precessional motion. They can be resonant with a rotational normal mode related to an internal global fluid layer and therefore their observation can be used to infer the existence and properties of such a fluid layer. This is particularly relevant for Mars, for which nutation observations by the InSight and ExoMars 2022 missions will constrain the core radius and density and inform on the existence of an inner core (e.g., Dehant et al. 2000, 2020; Smrekar et al. 2019). For bodies in a spin–orbit resonance, dissipation drives the spin axis to an equilibrium orientation in which the angle between the spin pole and the orbit normal, the obliquity, is nearly constant and determined by a balance between the precession of the orbit and precessional reaction of the planet or satellite (Williams et al. 2001; Bills 2005). In this configuration called Cassini state, the spin axis precesses together with the orbit normal around the normal to the mean orbital plane in such a way that the three axes remain coplanar. Like the precession rate, the obliquity depends on the polar moment of inertia and observation of it can therefore be used to determine the mean moment of inertia. In addition, measurements of deviation to this Cassini state bring information on tidal dissipation and friction at core-mantle boundary. Such approach has been used to deduce the existence of fluid lunar core (Williams et al. 2001) and estimation of its size (Viswanathan et al. 2019) from the lunar laser ranging measurements.
In addition to changes in orientation, the rotation rate can also change. For bodies in a spin–orbit resonance, the central object exerts a periodic gravitational torque that leads to departures from the mean rotation with a period equal to the orbital period (Comstock and Bills 2003). The amplitude of these forced librations depends on the internal structure of the object and in particular on the existence of global internal liquid layers and the tidal deformations of the object (e.g., Van Hoolst et al. 2013). We will show in Sect. 3 that librations have, for example, been essential in constraining the size of Mercury’s core and in establishing the presence of the global subsurface ocean in Enceladus. Angular momentum exchange between an atmosphere and the solid surface also induces variations in the rotation and can also be used to study the interior (e.g., Rambaux 2014; Van Hoolst 2015). That rotational forcing is, however, not always well known, in contrast to gravitationally forced rotation variations, making it more difficult to infer properties of the planetary interior from those variations.
Seismology is the method used on Earth for a detailed mapping of the interior [see e.g., Romanowicz et al. (2015) and chapters therein]. Seismology uses the propagation of seismic or acoustic waves generated mostly by quakes through the interior of the Earth and other rocky planetary bodies. The velocities, polarizations and amplitudes as well as the direction of these waves depend on the elastic properties of the interior, in particular on its mineralogy and composition as well as on temperature and pressure. By comparing observed propagation properties with laboratory measurements at high pressure and high temperature conditions (Sect. 2.1), seismological data can provide strong constraints on possible interior layering, composition and mineralogy. Seismic waves travel as compressional and shear waves and are reflected and refracted at discontinuities. They are subject to dispersion and attenuation and compressional waves may induce shear waves and vice versa. In addition to body waves traveling through the interior, seismic energy may propagate as surface waves. Because the velocities of these waves differ, with compressional waves being the fastest followed by shear and surface waves, differences in arrival times of phases can be used. On Earth, strong seismic events are monitored by seismic observatories all over the world while smaller events are recorded by local arrays of stations, sometimes arranged as antennas. Because the origin of the seismic event is usually not known a priori at least three recording stations are necessary to uniquely determine the location of the source from one single phase, e.g., compressional waves.
Seismology is an iterative method that improves prior knowledge with every additional event recorded and evaluated. Seismology started in the late nineteenth century to explore the variation of the seismic velocities with depth leading to the discovery of the major zones such as the core, the upper and lower mantles and the crust and then to 1-D reference models such as the much used IASPEI-91-model (Kennet and Engdahl 1991) or the older PREM model (Dziewonski and Anderson 1981). The huge amount of data that has been accumulated through more than a century of seismic observation has led to detailed knowledge of the Earth’s interior with seismic tomography (e.g., Thurber and Ritsema 2015) allowing exploration of the lateral variation of the velocities and the mapping of undulations of interfaces as well as of tectonic features such as subducting slabs.
The Apollo 11 mission in July 1969 not only landed the first human being on the Moon but the Apollo astronauts succeeded in installing the first seismometer on the surface of an extraterrestrial body, followed by three more successful installations by Apollo missions (e.g., Lognonne and Johnson 2015). Two seismometers were aboard flown on Viking 1 and 2 sent to Mars. The Viking seismometers were less successful than expected, largely because they could not be installed properly on the surface of the planet and protected against the Martian winds but remained mounted on the lander platform, whereas the Apollo seismometers yielded a wealth of data on the interior of the Moon. During December 1972 to September 1977, more than twelve thousand events were recorded on the Moon and catalogued with the long-period sensors, including shallow and deep lunar quakes as well as meteorite and man-made impacts (e.g., Toksöz et al. 1974; Nakamura 1983). The moonquakes are typically very small-magnitude events with the largest shallow moonquake having a body-wave magnitude of about 5, whereas the deep moonquakes have magnitudes less than 3 (Goins et al. 1981 Although the seismic signals from the Moon have a high degree of scatter, the seismological surveys allowed the crustal thickness to be determined at the landing site and provided clues to the mantle structure (e.g., Tokzöz et al. 1974; Goins et al. 1981; Nakamura 1983; Khan and Mosegaard 2002; Lognonné et al. 2003; Gagnepain-Beyneix et al. 2006; Khan et al. 2013) and to the core size (Weber et al. 2011; Garcia et al. 2011). See also Garcia et al. (2019a, b) and Nunn et al. (2020) for recent reviews on Apollo lunar seismic data and the interior structure models.
Most recently, in January 2019, the InSight mission (Banerdt et al. 2020) installed a highly sophisticated seismometer on Mars with ultra-sensitive short period and broad band three component sensors (Lognonne et al. 2019; Lognonne et al. 2020). As a single station, the InSight seismometer cannot uniquely locate seismic events. Instead, the team has developed a method that will allow the location of sufficiently strong and not too distant quakes from the delays between body wave phases and surface waves (Panning et al. 2015). Unfortunately, to date surface waves of a Martian quake have not been observed. Instead, the team has used the differences between body wave phases and their polarizations of three sufficiently strong events (magnitude 3.5) together with a mapping of tectonic features to locate these events in an area on Mars known as Cerberus Fossae (Giardini et al. 2020). These signals have been inverted to determine the crust thickness (Knappmeyer-Endrun et al. 2021), mantle properties (Lognonné et al 2020; Khan et al. 2021) and core radius (Stähler et al. 2021). Three new magnitude 4.1 and 4.2 quakes were recently reported (https://www.jpl.nasa.gov/news/nasas-insight-finds-three-big-marsquakes-thanks-to-solar-panel-dusting) and await interpretation.
In addition, the seismometer has recorded the hammering of the Heat Flow and Physical Properties Package (HP3) mole (Spohn et al. 2021a) and used it to constrain the elastic properties of the top decimeters of the Martian soil (Brinkmann et al 2019). Moreover, the noise generated by winds and its propagation in the soil is a subject of intense study.
2.3 Magnetic Fields
Spacecraft and ground-based observations have demonstrated that the terrestrial bodies in our solar system display a large range of magnetic field behaviors. Internally generated fields are observed at Mercury, Earth, and Ganymede. Remanent crustal fields, demonstrating that dynamo action occurred sometime in the past, have been detected at Mercury, Earth, Moon and Mars. Magnetized meteorites also constrain the dynamos of Mars, the asteroid Vesta, and other asteroids and planetesimals early in the solar system. An obvious missing body in the list above is Venus, where no crustal or internal magnetic fields have (yet) been detected (O’Rourke et al. 2018). For a recent review of planetary magnetic fields, see Christensen (2019).
The properties of Earth’s magnetic field have been elucidated through a combination of ground-based observatory data, satellite magnetometer data, ship logs of compass readings, and paleo- and archeo- magnetic records. The Earth’s magnetic field data set is plentiful compared to other planetary magnetic data. In particular, its combination of ground-based and satellite observations at the same time and location as well as the long temporal record of observations has allowed for detailed study of the dynamics and structure of Earth’s core.
Data from spacecraft magnetometers typically consist of vector magnetic field measurements along the track of a spacecraft orbiting a planetary body. For the terrestrial bodies and satellites in the solar system (other than Earth), missions that provided orbital magnetic data from intrinsic magnetic fields include Mariner 10 and MESSENGER at Mercury (Ness et al. 1976; Anderson et al. 2012), Lunar Prospector at the Moon (Richmond and Hood 2008), Mars Global Surveyor and Maven at Mars (Acuna et al. 1999; Langlais et al. 2019, Fig. 3), and Galileo at Ganymede (Kivelson et al. 1996). These missions provided spatial coverage that can constrain the field to a maximum length scale based on the orbit coverage and altitude of the spacecraft. Electron reflectometry has also been used to indirectly measure planetary magnetic field intensity at the Moon and Mars (Mitchell et al. 2007; Mitchell et al. 2008) and this data set complements magnetometer data for global coverage of a planetary field. On the local scale, paleomagnetic fields observed in collected Apollo samples from the Moon (Tikoo et al. 2014; Weiss and Tikoo 2014) and meteorites from other parent bodies (Weiss et al. 2010) adds information regarding the intensity and timing of the parent bodies’ magnetizing fields. For Mars, the InSight mission also provided data on the local magnetic field (Johnson et al. 2020).
Maps of the Martian magnetic field at the surface, as predicted by the spherical harmonic model up to n, m = 134. a B, b Br, c Bθ, d Bϕ, Figure from Langlais et al. (2019)
Furthermore, the time-varying field resulting from the interaction between the solar wind and the planet's environment can be measured. This transient magnetic field induces electric currents in the planet's crust and mantle, which in turn are responsible for an internally induced magnetic field superimposed on the former. Electromagnetic induction is thus a process that provides access to the electrical properties of the planet by observing the transient magnetic field. These depend on the composition, especially the water content and/or the abundance of hydrated minerals, and the temperature. For the Moon, electromagnetic sounding, largely performed during the Apollo program, provided constraints on core size, mantle composition, and interior temperature (Hood et al 1999; Khan et al. 2006). For Mars, the InSight magnetometer, including joint observations with MAVEN, offers the opportunity to study the thermal structure and volatile content of the planet's interior (Johnson et al. 2020). Magnetic induction has also been used to identify subsurface liquid saltwater oceans on the Galilean satellites Europa, Ganymede and Callisto (e.g., Kivelson et al. 2004) and a subsurface magma ocean on Io (Khurana et al. 2011).
Vector magnetic data can be used to create spherical harmonic observational models of the planetary magnetic field. After correction for spacecraft magnetic fields and other known external sources not attributed to the planet’s crustal or internal fields, the magnetic fields are assumed to be measured in an insulating region and hence can be represented as the gradient of a scalar potential: \(\vec{B} = - \nabla V \) where the potential is expanded in spherical harmonics:
where \(R_{P}\) is the planetary radius, \(\left( {l,m} \right)\) are spherical harmonic degree and order, respectively, \(\left( {r, \theta ,\varphi } \right)\) are spherical coordinates, and \(P_{l}^{m} \left( {\cos \theta } \right)\) are associated Legendre polynomials. The Gauss coefficients, \(\left( {g_{l}^{m} ,h_{l}^{m} } \right)\) describe the contributions to the field at different spatial wavelengths. Typically, inverse problem methodology is used to determine the best-fit Gauss coefficients for the magnetic field data. Once the Gauss coefficients are determined, the potential, and hence the magnetic field, can be characterized at any radius in an insulating region. Because downward continuation of the field from satellite altitude to the surface or interior of a planet is particularly sensitive to small-scale noise in the data, inversion methods typically employ various regularization techniques to ensure the field is not dominated by unresolved or noisy data when downward continued.
Equation (1) demonstrates that small scale fields (represented by higher l and m Gauss coefficients) are more challenging to observe from spacecraft altitude and there is a minimum wavelength at which a field can be resolved depending on the altitude of the spacecraft. This makes it challenging to determine the total intensity of the field at either the surface or core-mantle boundary of the planet if small-scale fields have significant contributions. This was recently demonstrated at Mars when the InSight mission magnetometer data determined that the surface field strength at the InSight landing site was ten times stronger than expected from downward continuation of spacecraft field models (Johnson et al. 2020). This can be somewhat alleviated if there is an expected distribution of field intensity with scale. For example, arguments based on the idea that a dynamo-generated field should produce a white spectrum in the core have been used to extrapolate the field intensity at larger wavelengths to smaller wavelengths to determine the field strength in the Earth’s core.
If spacecraft data are available at different altitudes at the same latitude and longitude, then the depth of magnetization can also be constrained based on Eq. (1). This can be useful to determine the source of magnetic fields (e.g., whether from a core dynamo or crustal remanence) and the depth of magnetized crustal layers. Crustal magnetic fields are used to constrain properties of previously-active dynamos. For example, if the magnetic mineralogy, thickness, and depth of crustal units are known, then the intensity of the magnetizing dynamo-generated field can be determined. In addition, if the age of the magnetized rocks is known, then the timing of the dynamo can be constrained.
Finer details of dynamo-generated fields may also be related to properties of planetary cores. For example, dynamo simulations demonstrate that the presence of stably-stratified layers, thermal perturbations at the core-mantle boundary, and the geometry of the convective shell provide possible explanations for observed features in planetary magnetic fields, as described for the Earth in Dehant et al. (2022).
Information about a present-day and especially an early magnetic field can be used to constrain the structure and thermal evolution of a planet. Dynamos are usually generated in convecting, electrically conducting liquid cores—there are, however, exceptions, such as magnetic field generation in the oceans of icy moons or possibly even in early basal magma oceans. In the dynamo process, mechanical energy is converted into electromagnetic energy by induction. Necessary conditions are not only that the electrically conducting fluid convects, but the convection must have a certain strength, which is measured by the magnetic Reynolds number, the ratio of the characteristic velocity times a length scale to the magnetic diffusivity. An active planetary dynamo needs to have a Reynolds number larger than ~ 10.
The fluid motions required for dynamo action must have a power source. An important mechanism for dynamo generation in the iron-rich cores of terrestrial bodies is compositional convection that can occur when a buoyant chemical component is released during the freezing of a fluid core with a non-eutectic composition (Braginsky 1964). In the case of Earth, core crystallization started in the center of the core and compositional convection due to inner core growth drives the dynamo. In the small planets, iron may start crystallizing at the core–mantle boundary (CMB) rather than in the center, and iron snow may form (e.g., Hauck et al. 2006). As a consequence, a dynamo that is tied to crystallization may work differently in these planets than it would in Earth. In the iron-snow regime, Fe-rich crystals crystallize, sink and re-melt deeper in the core. The crystallization layer (iron-snow) grows with time until it encompasses the entire core. At the time it reaches the center, an inner solid core begins to grow. A magnetic field is generated under the iron-snow layer (Christensen 2015), which is stable against large-scale convection except for the sinking crystals. As a consequence, the dynamo is less long-lived than in the case of the Earth-like crystallization scenario. Such a process of dynamo generation has been suggested for the magnetic fields of Ganymede and Mercury (e.g., Breuer et al. 2015).
There are not only chemical or compositional dynamos but also those which are only driven by thermal buoyancy, i.e. a thermal dynamo for an entirely fluid core, if a sufficiently large super-adiabatic temperature difference exists between core and mantle. The mantle must remove heat from the core at a rate exceeding the heat flux conducted along the adiabat of the core to become convective. If the mantle removes heat at a rate below this critical heat flux, the core becomes thermally stably stratified and cools conductively, and dynamo action driven by thermal convection is not possible. To study the magnetic field evolution of a planet, therefore, coupling with the mantle is necessary. On the one hand to determine the core-mantle heat flux but also the change of the core temperature with time. The latter determines when the core starts to freeze out and a chemical dynamo can exist. Thermal dynamos are to be expected in the early evolution of the planetary bodies, when the core is still completely liquid and can be cooled effectively. An early thermal dynamo is assumed for the Earth, but also for Mars, Mercury and the Moon. Today's magnetic fields are likely to be generated by chemical dynamos.
Mechanical driving has also been suggested as a potential source for motions in certain planetary cores that could create dynamo action. As examples, libration, precession and impact torques have all been proposed to create dynamo-capable flows due to coupling between the solid mantle and fluid core in the Moon (Dwyer et al. 2011; Le Bars et al. 2011; Stys and Dumberry 2020).
2.4 Thermochemical Evolution and Heat Flow
Modeling dynamical processes in terrestrial planetary mantles on local/regional or global scales is a common approach to learn about the interior evolution of terrestrial planets or, in turn, to study how the interior influences planetary evolution. In particular, modeling on global scales allows us to study the thermochemical evolution and heat transport mechanism of a planet or satellite since its formation.
Mantle dynamics in 2D or 3D domains is calculated by solving a set of differential equations for the conservation of mass, momentum, and energy including an appropriate constitutive equation. Typically, a fluid with Newtonian rheology and infinite Prandtl number is assumed with either the Boussinesq approximation (BA), extended Boussinesq approximation (EBA) (e.g., King et al. 2010) or the anelastic approach for a compressible fluid (e.g., Steinbach et al. (1989) for a comparison of these approaches). As for the Boussinesq approximation, the EBA assumes the density to be constant everywhere except in the buoyancy term of the momentum equation but considers additionally the thermal effects of viscous dissipation and adiabatic compression/decompression. In compressible models an equation of state is solved to consider density variations with pressure. Models can be expanded to further consider the influence of mantle phase transitions on the mantle dynamics. This is particularly important for terrestrial planets as large or larger than Mars but also for icy satellites, in which various exothermal and endothermal phase transitions can occur in the ice mantle. The convection models can further include compositional buoyancy and an equation for conservation of composition to account for compositional changes due to mantle melting and crust formation (e.g., Plesa and Breuer 2014) or for compositional layers formed as a consequence of magma ocean crystallization or of crustal recycling.
Two- or even three-dimensional thermal evolution calculations are very time-consuming on present-day computers, in particular if a large parameter range needs to be investigated. Because of the complexity of these models a semi-empirical approach is often used for which the convective heat transfer rate is parameterized. Parameterizations can be derived using simple theories, e.g., boundary layer theory, that give the heat transport rate as a function of the convective strength, the latter usually parameterized by the Rayleigh number,
where \(\alpha\) is the thermal expansion coefficient, \(g\) is gravity, \(\Delta T\) the superadiabatic temperature difference across the mantle, \(D\) its thickness, \(\kappa\) the thermal diffusivity, and \(\upsilon\) the kinematic viscosity (e.g., Breuer and Moore 2015). With the parameterized models, the evolution of the average mantle and core temperatures, heat fluxes and crust production rates are calculated.
Two main types of heat transport mechanisms and tectonic regimes can be distinguished: the plate tectonics or mobile lid regime and the stagnant lid regime. Plate tectonics is known from the Earth and efficiently cools the interior through the subduction of cold surface plates. In the stagnant lid regime, convection takes place below a rigid lid and results in a less efficient cooling of the planet interior by conduction through this outer lid. The stagnant lid regime is the natural regime because of the large viscosity contrast between the surface and the mantle caused by the strong temperature dependence of the viscosity of mantle rock, and is observed for all terrestrial planets, except Earth. To explain the occurrence of plate tectonics, complex rheologies must be considered, such as those that allow for brittle deformation (e.g., Moresi and Solomatov 1998) or even the memory of failure (Bercovici and Ricard 2014). Of course, such deformation mechanisms must plausibly be inoperative or ineffective on the other terrestrial planets where plate tectonics is absent.
The difference in heat transfer rate between plate tectonics and stagnant lid convection is reflected in the scaling laws for the heat flow (Breuer and Moore 2015). The parametrization of stagnant lid convection has been improved in recent years and was tested against fully dynamic evolution models in 3D (Thiriet et al. 2019). It should be noted here that due to the complex rheology of silicates, other tectonic regimes can occur. This includes the so-called transitional regime, when the viscosity contrast between mantle and surface is not too large (for instance in case of high surface temperatures), but also the episodic regime and the so-called slushy lid regime. The latter becomes active when the intrusion rate is very large and is characterized by local resurfacing events: Magma is not entirely transported to the surface, but a large part intrudes into the crust and weakens the material there. In these regions, the crust can become locally destabilized, detaches and sinks with the convection. Especially for Venus and also the early Earth these mechanisms are discussed (Gerya et al. 2015).
The models (parameterized or full 2D or 3D convection) can be extended to include important physical processes, such as the growth of a solid inner core that is important for magnetic field generation (Stevenson et al. 1983), crust formation and associated redistribution of radioactive elements, as well as outgassing of volatile elements (Morschhauser et al. 2011). The latter may have a strong influence on the mantle viscosity, the higher the volatile content the lower the viscosity and the stronger the mantle convection and more effective cooling of the planet.
The outgassing of the mantle also has an influence on the atmospheric composition and pressure, which in turn can influence the surface temperature and thus also the internal dynamics. The interior-atmosphere coupling has proven important for Venus (Gillmann and Tackley 2014), for example, but also for the early evolution of other terrestrial planets—in the phase where strong outgassing is expected. Even more advanced models couple both accretion and core formation and the subsequent thermochemical convection (e.g., Golabek et al. 2018 for Mars) or the influence of impacts on the thermochemical evolution (e.g., Padovan et al. 2017 for Mercury). For planets and moons for which tidal effects in the interior play a major role as a heat source, coupled models of the interior with orbital dynamics are needed [e.g., Husmann and Spohn (2004) for Io and Europa, Bland et al. (2009) for Ganymede].
To model the thermochemical evolution of a planet, model parameters and initial and boundary conditions must be defined and observations are then used as constraints for successful models. An important input is the internal structure and composition. Each body has its own peculiarities here, which are partly due to the fact that they have different sizes (Moon versus Venus), a different core to mantle ratio (Moon versus Mercury) and a different composition (e.g., Mg number, water content in the mantle, abundances of light elements in the core or radioactive elements in the silicate shell).
Here, the observational and laboratory-based knowledge about the interiors of the respective planets, as described in Sects. 2.1 and 2.2, serve as input for the models. Whereas knowledge about the present and past magnetic field, as described in Sect. 2.3, can serve as a constraint for successful models. Via planetary missions we obtain further important constraints that have to be fulfilled. Indeed, several quantities, which can be inferred from remote or in-situ observations, are tightly related to the thermochemical evolution of the interior. Measurements of topography, gravity, magnetic and seismic fields, surface spectra and surface images can all be employed to infer a series of fundamental constraints for the evolution of the interior in addition to those describe in Sects. 2.1 and 2.2 (see Tosi and Padovan 2021, for a review).
The heat flow from the deep interior of a planetary body is an important quantity to constrain its thermal evolution, interior dynamics and composition (e.g., Breuer and Moore, 2015; Spohn et al., 2018). The heat flow can be used as a boundary condition for thermal evolution models that would be required to satisfy the present-day value. Because a significant part—measured by the Urey ratio—of the heat flow is due to radiogenic heat from the mantle and the crust, the concentration of radiogenic elements in the interior can be constrained if the Urey ratio and the surface heat flow are known (Plesa et al. 2015 for Mars).
The surface heat flow varies over the surface of a planet, having relative maxima where the temperature at depth is high as in volcanic provinces and relative minima where the latter is low, such as in regions of anomalously thick lithosphere. The heat flow data base for Earth (https://ihfc-iugg.org/products/global-heat-flow-database/data) contains almost 75,000 data points covering most of the oceanic and continental areas. The heat flow map (e.g., Lucazeau 2019) mirrors the elements of plate tectonics such as mid-ocean ridges with the highest heat flow values, subduction zones, volcanic arcs and continents.
To measure the heat flow one usually measures the thermal conductivity and the temperature gradient, the product of the two giving the heat flow. The difficulty with the measurement comes from two sources: First, the temperature gradient and the conductivity are mostly small values of order 1 K/m and 10–2 W/mK. But more severe is the disturbance of the near-surface temperature gradient by heat transferred from the surface to depth. The depth of penetration depends on the period of the disturbance with daily variations penetrating to centimeters depth while annual perturbations can be measured even at the depth of several meters. On Earth even climatic changes are taken into consideration and the heat flow is measured in boreholes extending to 10 s of meters depth or deeper.
Heat flow has been measured at two locations on the Moon on which the Apollo astronauts drilled to 1.4 m (Apollo 15) and 2.4 m (Apollo 17) depth. The heat flow values measured were 21 mW/m2 at the Apollo 15 and 16 mW/m2 at the Apollo 17 site (Langseth et al. 1976). The difference between the two reflects differences in subsurface radiogenic Thorium content (Wieczorek and Phillips 2000). The Apollo 15 site is closer to the center of the Procellarum KREEP terrain with its high Th content than the Apollo 15 site. The InSight mission has a Heat Flow and Physical Properties Package (Spohn et al. 2018) that was planned to measure the heat flow at Homestead Hollow in Elysium Planitia at a depth of 3–5 m, targeted to avoid the daily and annual temperature disturbances. The package deployed a small penetrator with thermal conductivity and temperature sensors. Unfortunately, the attempts to penetrate sufficiently deep had to be given up in January 2021. The penetrator reached only a depth of about 40 cm being inclined to the vertical at about 30° (it is 40 cm long) and serves as a thermal probe to study surface atmosphere interactions and the properties of the Martian soil (Spohn et al. 2021a,b).
In the absence of direct heat flux measurements, the thickness of the elastic lithosphere can be used to constrain the surface heat flow. The evolution of the elastic thickness is considered an important quantity to reconstruct the thermal history of a planet (e.g., Grott and Breuer 2008). The elastic thickness can be estimated by analyzing the response of the lithosphere to loading stresses such as volcanoes or by analyzing fault structures. The mechanical thickness of the lithosphere can then be inferred from the elastic thickness using a rheological model and the mechanical thickness can, in turn, be identified with an isotherm (McNutt 1984). Assuming a crustal thermal conductivity, an estimate of the surface heat flow can be made. Most elastic thickness estimates have been derived from gravity and topography data (e.g., McGovern et al. 2004), but some geological features allow more direct approaches such as studies of lithosphere deflection due to volcanic or polar cap loading. The heat flow thus obtained, however, is not the present-day value but is related to the time when the surface loading took place. This requires dating of the age of the structure mostly by crater counting.
Other constraints that can be gained with the help of planetary missions include crustal thickness, duration and timing of volcanism, amount of accumulated radial contraction, surface concentration of radioactive elements, or evolution of the mantle potential temperature. Knowledge of input parameters and observations for determining the themo-chemical evolution of terrestrial bodies is available in varying degrees of accuracy and depends on the particular body considered and the missions performed. Examples are given in the following section.
3 Selected Planets and Moons
3.1 Mercury
Our knowledge of Mercury’s interior has greatly improved due to recent analyses of Mercury’s rotational dynamics, gravity field, magnetic field, and surface properties, mostly from MESSENGER data. This complements recent high-pressure experiments on relevant core compositions and theoretical modeling of the planet’s thermal evolution, mantle dynamics and core dynamo. Detailed reviews of results from the MESSENGER mission and the implications for the planet’s interior can be found in Margot et al. (2018), Johnson et al. (2018), and Hauck et al. (2018), see also Genova et al. (2021).
Geodetic data for Mercury (e.g., obliquity, libration amplitude, gravity coefficients) have constrained the interior structure of the planet. Earth–based radar observations (Margot et al. 2012) and MESSENGER radio science, imaging, and laser altimeter data (Mazarico et al. 2014, Stark et al. 2015, Verma and Margot 2016, Genova et al. 2019, Konopliv et al. 2020a, b) have accurately determined Mercury’s orientation in space and indicate that Mercury closely occupies the equilibrium Cassini state. The normalized polar moment of inertia can then be determined from the orientation and is between 0.32 and 0.35. These geodetic data also show that Mercury’s librations have an amplitude between about 37 arcsec and 40 arcsec. The librations, periodic variations in Mercury’s rotation, strongly depend on the size of the core and also can contain a signature of an inner core (Rambaux et al. 2007; Van Hoolst et al. 2012). Together with the orientation of Mercury, they provide an estimate of the polar moment of inertia of the silicate shell of Mercury. Both polar moments of inertia can be used as constraints for interior structure models to determine allowable layer thicknesses and densities for Mercury’s crust, mantle, and core.
Mercury has long been known to contain a large core-mass fraction (e.g., Siegfried and Solomon 1974). By using the geodetic data as constraints on interior structure models based on likely compositions of Mercury’s core, mantle and crust, the core’s radius is shown to be around 2000 km, i.e. ~ 80% of the planet’s radius (e.g., Hauck et al. 2013; Rivoldini and Van Hoolst 2013; Margot et al. 2018; Knibbe et al. 2021). Combined with estimates for Mercury’s crustal thickness of ~ 35 km (James et al. 2015; Padovan et al. 2015; Margot et al. 2018) this implies a very thin mantle layer in Mercury of ~ 400 km (Fig. 1). Such a thin mantle suggests that mantle convection is challenging, and it is currently debated whether the planet undergoes very sluggish convection under a stagnant lid or, rather, is purely conductive (e.g., Hauck et al. 2018). If convection is occurring, then the planform is likely to be small-scale, i.e. length scales of convection are likely on the order of the mantle thickness (Tosi et al. 2013). This suggests that there may be significant heterogeneity in Mercury’s mantle due to lack of mixing over large lateral distances.
Mercury has a liquid layer in its core, as revealed by the presence of an intrinsic magnetic field (Anderson et al. 2012) and observations of its 88‐day longitudinal libration forced by the periodically reversing solar torque (Peale 1976; Margot et al. 2007). Independent evidence in support of a liquid core is provided by the measurement of the tidal Love number k2 (e.g., Genova et al. 2019) since it is significantly larger than that expected for a fully solid Mercury (Rivoldini et al. 2009; Padovan et al. 2014). There is no direct observational data on the existence or size of Mercury’s solid inner core. Inferring the presence and size of an inner core based on geodetic and geochemical data is strongly dependent on the knowledge of the core’s composition and thermal state, which are not well-constrained. However, some constraints come from implications of inner core sizes on the thermal contraction Mercury should have experienced from core solidification, from compensating densities required in other regions of Mercury if the planet has a solid iron core in order to match the polar moments of inertia, as well as from dynamo models. A range of inner core sizes is consistent with the data. Monte Carlo solutions using the lowest estimate of the polar moment of inertia suggest that the solid inner core most likely occupies between 30 and 70% of Mercury’s total core radius (Genova et al. 2019). Steinbrügge et al. (2021) studied the implications of the lower polar moment of inertia value from Genova et al. (2019) on the size of the inner core using interior structure models. Models with a larger normalized moment of inertia (0.346) favor a small inner core whereas models with the smaller value (0.333) require an inner core > 600 km. Furthermore, the smaller MoI suggests a smaller core radius by about 75 km and a smaller mantle density than previous estimates (Fig. 4).
Core‐mantle boundary (CMB) radius and temperature, sulfur content, and mantle density as a function of inner core boundary (ICB) radius, for Mercury models with a Fe‐S core composition and constrained to match C/MR2 = 0.346 (red) or C/MR2 = 0.333 (blue). The blue dashed lines bracket the range of models matching C/MR2 = 0.333 + 0.005, the 1σ error bar given in Genova et al. (2019). The red dashed line corresponds to C/MR2 = 0.346–0.014 = 0.332, the lower 1σ error bar given in Margot et al. (2012). Figure from Steinbrügge et al. (2021)
Studies of Mercury’s surface composition demonstrate that the interior is chemically reduced (Nittler et al. 2011). This implies that silicon would have been more soluble in iron during planet differentiation and hence that there may be significant silicon in Mercury’s core. Although sulfur has long been considered a potential light element for Mercury’s core, the observed high sulfur to silicon ratios on Mercury’s surface suggest that sulfur may be much less abundant in Mercury’s core than previously thought. This suggests that the Fe-S-Si system may be an important composition to understand at Mercury’s core pressures and temperatures. Interestingly, there are hints that the Fe-S-Si system might have unusual melting properties and experience immiscibility at certain pressures and temperatures relevant for Mercury’s core, both of which may have important implications for Mercury’s dynamo (e.g., Chabot et al. 2014). Other light elements may also be present in the core and hence further high-pressure studies of iron mixed with light elements such as carbon and phosphorus are also needed (e.g., Knibbe et al. 2021). An inner core size less than about 1200 km likely requires the presence of another light element than Si, such as S or C, at the wt% level in the core (Knibbe et al. 2021).
MESSENGER data confirmed the Mariner 10 results that Mercury has an internally generated magnetic field (Anderson et al. 2012). The mission also discovered crustal magnetization in the north polar region implying that Mercury’s dynamo was also active around 3.9–3.7 Ga (Johnson et al. 2015). This provides constraints on the thermal evolution of Mercury since the planet must have been sufficiently convective to produce a dynamo at both of these times. Whether the field has been active in the interim time, or earlier than 3.9–3.7 Ga, is currently unknown.
The morphology and intensity of Mercury’s magnetic field seem to require some special circumstances in Mercury’s core. In particular, the low field strength is a challenge for dynamo scaling laws and the ability for the field to maintain a large dipole offset (equivalent to a significant axial quadrupole moment) while also appearing quite axisymmetric is a challenge for dynamo generation theory. Studies of dynamo models for Mercury have appealed to the presence of stably stratified layers at the top of the core (Christensen 2006; Christensen and Wicht 2008), as well as thermal perturbations at the core-mantle boundary (Cao et al. 2014; Tian et al. 2015) or double diffusive convection (Takahashi et al. 2019) to explain these field characteristics. However, discerning between these possibilities will likely require better understanding of the composition of Mercury’s core (i.e. to constrain the stability profile) and the role of the mantle in linking surface features to thermal signatures at the core-mantle boundary (e.g., Beuthe et al. 2020). Magnetic induction studies have also provided an estimate of the radius of Mercury’s core, independent from that determined from geodetic studies which is consistent with the value based on Mercury’s geodetic data (Wardinski et al. 2019; Katsura et al. 2021).
Resolving smaller scales in Mercury’s internally generated field from spacecraft data is made particularly challenging because of the prevalence of external fields in the data. External fields are particularly impactful at Mercury because of the small magnetosphere and relatively strong solar wind at Mercury. Future work to model and understand these external fields may therefore lead to further insights on the morphology and generation of Mercury’s field. More details about the magnetic field but also the internal structure are expected from the upcoming BepiColombo mission, a joint mission of ESA and JAXA launched in 2018 (Benkhoff et al. 2010). BepiColombo consists of two individual orbiters: the Mercury Planetary Orbiter (MPO) to map the planet, and the Mercury Magnetospheric Orbiter (MMO) to study its magnetosphere.
3.2 Venus
Venus is the closest analog to Earth in the solar system in terms of mass, radius, and density (Table 1) but differs significantly in surface tectonics and atmosphere composition. However, of all terrestrial planets we know the least about Venus, in particular about its interior. Firstly, the conditions for investigation are more difficult due to Venus’ dense atmosphere, that is opaque to visible light, and the high surface temperatures, which poses a particular challenge for lander science. Secondly, there have been comparatively few missions that have studied the deep interior and surface of Venus such as the Russian Venera landers (1970–1981) (Keldysh 1977), Pioneer Venus (1977–1992) (Colin 1980), Magellan (1990–1994) (Saunders et al 1992) and Venus Express (2006–2014) (Svedhem et al. 2009). In this subsection, we summarize what we have learned so far about the internal structure and dynamics with a focus on the knowledge we have gained through the analysis of gravity and topography data.
The diameter of Venus is 5% smaller than that of Earth and for the same mantle and core composition the Venusian core radius would be 0.51 of the planetary radius as compared with Earth, for which the core radius is 0.55 of the planetary radius. However, the composition of Venus is not well known and previous models based on cosmochemical constraints vary strongly with the amount of FeO in the mantle between almost no iron and FeO of 18.7% (Earth value corresponds to 8.4 wt%) (see Fegley 2014 for a review). To fit the observed mass and radius of Venus, models show then a 500 km uncertainty in the core size with values between 2940 and 3425 km (Dumoulin et al. 2017). As the observed gravity coefficient J2 is 25 times larger than the hydrostatic one, the estimation of the mean moment of inertia from gravity field measurements alone is prevented and measurement of the precession rate are required. Recently, Margot et al. (2021) used Earth based observations of radar speckles tied to the rotation of Venus obtained in 2006–2020 to measure its spin axis orientation and precession rate. They obtained a mean moment of inertia normalization factor of 0.337 ± 0.024, but the large uncertainty does not allow better constraint of the core size. Similarly, the tidal Love number k2 derived from Doppler tracking of the Magellan and Pioneer Venus spacecraft of k2 = 0.295 ± 066 (Konopliv and Yoder 1996) shows a large uncertainty which implies that even the state of the core, i.e. whether Venus’ present core is solid or fluid, cannot be constrained (Dumoulin et al. 2017, Fig. 5). The absence of an observation of a planetary magnetic field is consistent with both implied extreme core states but does not help to place further constraints on interior structure. Knowing the present-day state of the core is essential because it would provide constraints on the efficiency of heat extraction from the core by mantle convection through Venus’ history, in particular, on the possible cessation of a core dynamo. It should also be noted that no magnetization has yet been measured on the surface of Venus either, so it is not clear whether Venus once had an early magnetic field. A scenario that can certainly not be excluded at present (Stevenson et al. 1983).
Potential Love number, k2, as a function of the dissipation factor Q. The case of a solid core of pure iron is illustrated using hexagons, and the case of a 2500 km radius solid core and a liquid outer core with diamonds. The black triangle stands for the case with an entirely liquid core. Colors of hexagons depict the chosen viscosity of the solid core. The star on the right side shows the result obtained for the elastic solid core case. The long-dashed line represents the lowest estimate of k2 from Konopliv and Yoder (1996), the upper one being too large to be drawn on the figure due to the chosen scale. This figure illustrates that the state of the core, i.e. whether Venus present core is solid or fluid, cannot be constrained with the measured k2 value. Figure from Dumoulin et al (2017)
The present convective regime seems to be consistent with convection underneath a stagnant lid–no clear present-day plate tectonic features have been observed. However, in some locations, this lid does not seem to be entirely “stable”, but a so-called sluggish lid is formed in some places, which may be an instability of the lower crust like a delamination or even the beginning of subduction similar to plate tectonics, possibly connected to upwelling mantle plumes (Davaille et al. 2017). In fact, the analysis of gravity and topographic data indicates that Venus has a comparable number of active large mantle plumes to Earth, as well as many hundreds of smaller plumes that may also be active (Smrekar and Phillips 1991). Active volcanism has also possibly been detected by Venus Express via a thermal signature (Shalygin et al. 2012) and recent volcanism from surface emissivity near 1 micron that distinguishes fresh from weathered basalt (Smrekar et al. 2010).
The strong correlation of the long-wavelength global gravity with the global topography spectrum is a particularity of Venus and is probably caused by mantle convection. The analysis of the long-wavelength spectra thus allows conclusions to be drawn about internal dynamic processes. It has been used, for example, to constrain the viscosity structure of the Venusian mantle (Rolf et al. 2018). General features of the viscosity structure, which are similar for various models, show that there is no pronounced asthenosphere and viscosity jump between upper and lower mantle—in contrast to Earth. Global estimates of elastic thickness from the gravity and topography data find a wide range of values, from 0 to 100 km (Anderson and Smrekar 2006; Jiménez-Díaz et al. 2015), with more than half of the planet having best-fit values of 20 km (or less, indistinguishable from isostatic compensation). Thus, these regions might have a quite high heat flux and exclude models of a cold Venus.
In general, Venus shows a relatively young surface with a mean crustal thickness of less than 50 km (e.g., James et al. 2013) and an average age younger than 1 Ga (McKinnon et al. 1997). Venus’ geologically young surface requires extensive volcanic resurfacing, but it is not clear whether this happens in a global-scale resurfacing event (e.g., Strom et al. 1994) or whether a more continuous resurfacing occurs (e.g., Bjonnes et al. 2012). Currently discussed evolution scenarios include episodic catastrophic resurfacing (e.g., Armann and Tackley 2012), gradual decay of volcanism over time in a stagnant lid regime, but also mixed forms and transitions between the different tectonic regimes, i.e. stagnant lid regime, mobile lid regime, episodic regime and transitional regime (e.g., Gillmann and Tackley 2014; Weller and Kiefer 2020). A key parameter controlling the tectonic regime may be surface temperature, which is influenced by the atmosphere evolution and thus by the coupling between interior and the atmosphere (Gillmann and Tackley 2014).
Distinguishing these various evolution scenarios is not possible with today's data and will be a task of upcoming missions such as DAVINCI + and VERITAS (NASA Discovery Missions) or EnVision (ESA M5 Mission). VERITAS and EnVision are specifically dedicated to studying the surface and deep interior of Venus with radio science, radar and infrared spectroscopy. Among other things, the combined processing of Earth Doppler tracking and radar data will allow accurate determination of the planet's rotational state and moment of inertia factor in addition to the much more accurate determination of the Love number k2 from tracking alone (Rosenblatt et al. 2021; Cascioli et al. 2021). VERITAS will provide accuracies (\(3\sigma )\) in the estimates of the tidal Love number \(k_{2}\) to \(4.6 \times 10^{ - 4}\), its tidal phase lag to \(0.05^\circ\), and the moment of inertia factor to \({9}.{8} \times 10^{ - 4}\) (0.3% of the expected value) (Cascioli et al. 2021).Those results will place much tighter constraints on the state and size of the core and the viscous response of the planet than is currently the case as shown in the analysis by Dumoulin et al. (2017).
3.3 Moon
More than fifty years after the first crewed mission to the lunar surface, the Moon remains a cornerstone in planetary science. The amount and quality of data that is available from returned samples, remote sensing observations from Earth and from space, instruments placed on the lunar surface, high-pressure experiments, and thermochemical modeling is still unrivaled. Almost 400 kg of lunar rock and soil samples were returned by American, Soviet, and Chinese robotic and manned missions over the past 5 decades, dozens of remote missions have orbited the Moon (and continue to do so), and its proximity to Earth means the Moon is a favorite target for new space-faring nations. It is likely that the coming decades will see a further resurgence of lunar exploration, with advanced plans for the return of humans to the lunar surface as well as a plethora of robotic and sample return missions, including many that intend to explore areas of the surface not covered previously. In this short overview, three first order aspects of the lunar interior and its evolution are discussed: (1) Moon formation; (2) the lunar core and lunar magnetic field generation, and (3) the hypothesis of an initial global lunar magma ocean (LMO), that can tie together many of the geochemical and geophysical constraints on the interior of the Moon.
The scientific goal of the Apollo missions was to figure out how the Moon formed. Although the giant impact model, in which the Moon formed from the debris of a giant collision between Earth and another planet, is almost universally accepted, many unresolved issues, some of them fundamental, remain (e.g., review by Canup et al. 2021). Even with the vast amount of geochemical and geophysical data obtained during and since these missions, the origin of the Moon therefore remains hotly debated. The core of the problem with the giant impact model lies in the observation that, on the one hand, the Moon’s chemical composition, for all elements except the volatile elements, very closely resembles the composition of the bulk silicate Earth, whereas on the other hand physical models of classic versions of the giant impact show that the Moon should mainly consist of material originating from the planet that hit Earth (e.g., De Meijer et al. 2013). The only ways out of this conundrum seem to require significant loss of angular momentum after the giant impact (e.g., Cuk and Stewart 2012), complete equilibration of both light and very heavy isotopic systems between silicate Earth and Moon after the giant impact (e.g., Pahlevan and Stevenson 2007) or a similarity between Earth and giant impactor of a level currently not seen anywhere in the solar system.
In view of models for the interior evolution of the Moon, this makes it difficult to accurately quantify the thermal state of the Moon just after formation. One way of estimating the initial interior conditions in the Moon is to study the conditions under which the small lunar iron-rich core formed. There are several lines of evidence to suggest the Moon has a small core. An ancient lunar magnetic field generated by dynamo action in the metallic molten core has been identified in lunar rock samples (e.g., Tikoo et al. 2017); siderophile (iron-metal loving) elements are depleted in lunar samples relative to realistic lunar bulk composition models, suggesting they have been sequestered into a core (e.g., Steenstra et al. 2016; Righter 2019); and lunar seismic data (e.g., Weber et al. 2011; Garcia et al. 2011, 2012) and lunar laser ranging observations (e.g., Williams et al. 2001, 2014; Viswanathan et al. 2019) also require the presence of a small core. Recent analyses of Apollo-era seismic data suggest a core radius of 330 ± 20 km radius, possibly with a solid inner core with a radius of 240 ± 10 km covered by a molten outer core (Weber et al. 2011) or 380 ± 40 km (Garcia et al 2011, 2012). Based on results from the GRAIL gravity field mission and lunar laser ranging results, Williams et al. (2014) suggested that the moment of inertia, k2 Love number, and density of the core are consistent with the presence of 0–280 km solid inner core and/or a 200–380 km molten core. Based on a combination of high-pressure experimental measurements and seismic travel times from Apollo seismometers, Antonangeli et al. (2015) derive core radii close to ~ 240 km for the inner core and ~ 325 km for the outer core, close to the GRAIL-based estimates. Recent analysis of Lunar laser ranging observations combined with the lunar gravity field of the Moon derived from GRAIL mission provided a lunar core radius of 380 ± 12 km (Viswanathan et al. 2019). Overall these results suggest that the core makes up less than 1.5 wt. % of the Moon (Fig. 1a). Some of the geophysical models of the deep lunar interior argued in favor of the presence of a partially molten rock layer on top of the core-mantle boundary (e.g., Weber et al. 2011; Harada et al. 2014, 2016) but its geophysical signature is still debated (Matsuyama et al. 2016). The melt percentages in this layer could exceed 10 per cent, requiring special circumstances to prevent transport of this magma towards the surface (Van Kan Parker et al. 2012).
The chemical composition of the lunar core strongly affects its physical properties and magnetic field evolution. The current fluid state of the outer core requires the presence of one or more light elements along with iron to reduce the solidus (temperature above which molten metal is presence). Sulfur and carbon are the likeliest candidates, but there is currently no agreement on their core concentrations. One way to estimate the light element content comes indirectly from observing the remanent magnetization of the lunar crust. The Moon does not have an internally generated global magnetic field today, but the remanent magnetization in the crust and in returned Apollo samples (e.g., Weiss and Tikoo 2014) suggests that a core dynamo probably existed in the Moon at least 4.25 billion to 3.56 billion years ago, with an intensity of ~ 100 \(\mu T\), similar to that at the surface of the Earth today. The field then decreased by at least an order of magnitude until 3.3 billion years ago, possibly remaining until 2.25–1 Ga b.p. (Tikoo et al. 2014; Tikoo et al. 2017) persisting at a low level of a few \(\mu T\) (Fig. 1b). The early strong field, and later rapid decay, is not well understood so far and may require two different mechanisms (Wieczorek et al. 2021). To explain the strong early magnetic field, mechanisms such as the precession driven dynamo (e.g., Dwyer et al. 2011; Cebron et al. 2019) or impact induced dynamos (LeBars et al. 2011) are proposed. The long duration, however, seems to require that the core had a chemical dynamo. For example, Zhang et al. (2013) and Laneuville et al. (2014) suggested, on the basis of thermochemical evolution models, that > 5 wt.% S should be present in the lunar core to fit the magnetic field evolution, whereas Steenstra et al. (2017a) and Righter et al. (2017) suggested on the basis of experimental work on the partitioning of sulfur between metal and silicate melt that the amount of S in the lunar core is < 0.5 wt.%.
Measurements of the abundances of siderophile element abundances in lunar returned samples and meteorites can be combined with high-pressure, high-temperature experiments (Sect. 2.1) to estimate the pressures and temperatures at which core and mantle last equilibrated. Results of this exercise are non-unique, but one consistent recent result appears to be that molten iron-rich metal and molten lunar mantle have equilibrated at a pressure of approximately 5 GPa (Rai and van Westrenen 2012, Steenstra et al. 2016, 2020). This pressure is equivalent to the pressure at the present-day core-mantle boundary of the Moon as derived from seismological data (e.g., Garcia et al. 2011). This result implies that the Moon was fully molten at the time the core formed, consistent with high-energy formation scenarios for the Moon. Some core formation models suggest that the Moon formed super-hot, at temperatures above 3000 K–temperatures that far exceed what is needed to fully form the Moon. On the other hand, high-pressure experiments have been used to suggest the Moon never melted completely, using the average thickness of the lunar anothositic crust as constraint (e.g., Charlier et al. 2018). Its thickness is between 34 and 43 km and was derived from seismic data near the Apollo landing sites (Lognonné et al. 2003, Khan and Mosegaard 2002) in combination with the inversion of gravity topography data from Gravity Recovery and Interior Laboratory (GRAIL) mission (Wieczorek et al. 2013). According to this line of thought, the lower part of the mantle of the Moon can be still primitive (i.e., essentially the same as when the Moon formed), with perhaps the top ~ 600 km formerly fully molten early in lunar history, forming a global magma ocean. This is also consistent with a discontinuity in seismic velocities at depths of about 500–550 km (e.g., Nakamura 1983; Khan et al. 2000, 2006; Lognonné 2005). However, a wide range of acceptable models have been proposed and care should be taken in interpreting this seismic discontinuity (e.g., Gagnepain-Beyneix et al. 2006; Wieczorek et al. 2006). It should also be noted that these mantle reservoirs may have been mixed by convection after their formation (e.g., Laneuville et al. 2014) and may not exist in their original structure today.
Although opinions vary as to its initial depth (e.g., Gaffney et al. 2021), a global lunar magma ocean (LMO) is thought to have played a crucial role in the interior evolution of the Moon. Several recent experimental studies have focused on the cooling history of such an ocean (e.g., Lin et al. 2017a, b, 2020; Charlier et al. 2018; Rapp and Draper 2018), and thermodynamic modeling has also been used to constrain magma ocean crystallization (e.g., Maurice et al. 2020; Johnson et al. 2021). LMO crystallization led to the formation of a series of cumulate layers on the bottom of the ocean. Early cumulates were dominated by olivine and pyroxene, but the later cumulates are more important for the evolution of the lunar interior. After ~ 70 per cent crystallization, the white mineral plagioclase starts forming. In contrast to earlier-formed minerals plagioclase is lighter than the lunar magma it formed in, leading to floatation. The highlands crust still covering the majority of the lunar surface is therefore considered by many to be the roof of a giant magma chamber. After > 90 per cent crystallization, the dense mineral ilmenite (an iron–titanium oxide) starts forming. At this point, the remainder of the LMO is very shallow, leading to the gravitationally unstable situation that the densest lunar mineral is formed just below the plagioclase-rich crust. This special situation sets the scene for a large-scale mantle overturn, during which ilmenite-bearing cumulates sink towards the core-mantle boundary, balanced by olivine-pyroxene bearing cumulates rising towards the surface (e.g., De Vries et al. 2010; Zhao et al. 2019; Yu et al. 2019; Maurice et al. 2020). The latter can lead to decompression melting and the formation of large volcanic deposits found on the surface of the Moon, whereas the former can lead to the formation of a stable titanium-rich ilmenite-bearing layer on top of the core, that is relatively easy to remelt. The Ti–rich magma that is formed here is neutrally buoyant, providing a possible explanation for the observed stable partially molten rock layer on top of the core (Van Kan Parker et al. 2012).
The interplay between magma ocean crystallization, vertical buoyancy-driven transport of denser and lighter cumulates, core evolution and corresponding scope for the generation of a magnetic field, is an area of active research in lunar science, and a great illustration of the necessity of combining information from geochemistry and geophysics in thermochemical evolution models.
3.4 Mars
Mars is arguably the best explored planet in the solar system next to Earth. The Nasa Space Science Data Coordinated Archive NSDCC counts 50 missions up to Mars 2020 but not all of them have been successful. Nevertheless, Mars has been visited by an international fleet of orbiters, four rovers and eight landers, including the InSight geophysical observatory. Most recently, as of this writing, the landing of the Chinese Tianwen1 lander and rover on May 15th 2021 has been reported by the Chinese space administration CNSA (Zou et al. 2021). Given that Mars’ surface temperature varies through the day near the equator from 180 to 295 K, as recently measured by the HP3 radiometer on InSight (Piqueux et al. 2021; Müller et al. 2021), Mars is marginally habitable, in particular at some depth were liquid brines may be present and temperatures more benign. Although life may have originated on the planet, no biosignatures have been detected to date. Moreover, the planet is well within the reach of present-day space travel technology. The interest in Mars by the space faring nations and agencies is a consequence of Mars’ habitability and reachability.
The InSight mission (e.g., Banerdt et al. 2020) has significantly improved the data available for constraining Mars interior structure and evolution. Previous models have used the gravity field, rotation data and the chemistry of the SNC meteorites, the latter complemented by in-situ measurements from rover missions (e.g., Morrison et al. 2018 for the Curiosity mission; Yoshizaki and McDonough 2020). InSight brought a suite of geophysical instruments to Mars, including foremost a very broadband seismometer, transponders for accurately measuring rotation data, a magnetometer and a heat flow probe and radiometer, the latter for measuring the surface brightness temperature, albedo and thermal inertia.
Even before spacecraft went to Mars, the moment of inertia factor MoI—C/MR2, where C is the moment of inertia about the rotation axis, M the mass of the planet and R its mean radius—was estimated from the orbital periods of its satellites Phobos and Deimos and from Mars’ rotation rate (see review by Spohn et al. 1998). The orbital periods of the satellites constrain the J2 coefficient of the spherical harmonic representation of the gravity field. Assuming that Mars was in hydrostatic equilibrium and using the Radau-Darwin relation a value of 0.377 for the MoI was found from the measured value of J2. But already Wells (1979) showed that the assumption of a hydrostatic planet was inconsistent with the dynamical flattening of the planet as revealed by the satellite data. Early spacecraft images and gravity data suggested that the MoI value should be corrected in particular for contributions from the isostatically uncompensated Tharsis bulge (Reasenberg 1977; Kaula 1979). The corrected value of 0.366 has been used by a number of models including Sohl and Spohn (1997). These authors showed that there was a discrepancy with geochemical models of the planet. While the models based on the MoI factor could not reproduce the Fe/Si value constrained from SNC meteorite data (Dreibus and Wänke 1985), the chemical models of the planet suggested an MoI factor of only 0.357. Sohl et al. (2005) argued that the MoI should be calculated from the mean moment of inertia rather than from the moment of inertia about the rotation axis because the models would use the former rather than the latter. They corrected the MoI to arrive at a value of 0.3635 ± 0.0012. With the help of improved gravity data (Genova et al. 2016; Goosen et al. 2017) and of the Pathfinder and later landing missions it was possible to estimate the value of the precession constant and thereby removing the problems associated with the use of the Radau-Darwin relation to arrive at a value of 0.3637 \(\pm\) 0.0001 (Konopliv et al. 2016; Kahan et al. 2021). Constraints from measurements of the tidal Love number due to solar tides k2 = 0.163 ± 0.008 (Konopliv et al., 2016; Genova et al., 2016) and the detection of the Chandler Wobble (Konopliv et al. 2020a, b) further help to refine the interior structure models (see Rivoldini et al 2011 for a model using the MoI and the Love number data).
Smrekar et al. (2018) reviewed the knowledge about the interior of Mars prior to the InSight mission. Accordingly, Mars’ core is at least partly fluid—an inner core not to be definitely ruled out albeit less likely—with a radius of 1788 ± 73 km (Fig. 6). This large core has the consequence that the core density must be relatively low and thus the core must have a significant amount of light alloying elements such as S and O. Recent estimates are ~ 13.5% S and ~ 4% O (Steenstra and van Westrenen 2018), which are consistent with older geochemical models of Wänke and Dreibus (1985).
a Mars core size and b core sulfur fraction as function of k2 for a hot and cold mantle temperature for models that satisfy the MOI. Contours delimit domains corresponding to 0.997, 0.954, and 0.682 probability of occurrence. The blue dotted lines delineate the 0.997 domains of the cold models. The gray shaded areas represent the k2 values of Marty et al. (2009), Konopliv et al. (2011), Smith et al. (2009) (from left to right). The insets correspond to the individual 0.997 contours of the models with an inner core and without an inner core for cold and hot mantle models. Figure from Rivoldini et al. (2011)
Furthermore, due to the relatively large core, the presence of a perovskite layer is rather unlikely. The mantle is divided into an upper mantle where olivine is stable and a lower mantle dominated by wadsleyite and ringwoodite; the layers are separated by a transition zone, about 300 km thick. On top of the mantle, there is a basalt-rich crust that is the product of mantle melting and differentiation. Upon differentiation, radiogenic elements are enriched in the crust estimated to vary by a factor between 13 and 20 (Knapmeyer-Endrun et al. 2021). The thickness of the crust varies across the planet but its thickness is uncertain, estimates ranging between—on average—38 km (Wieczorek and Zuber 2004) and 115 km (Nimmo and Stevenson 2001). Plesa et al. (2016) used the gravity and crustal thickness model of Neumann et al. (2004) but varied the average crustal density for which Neumann et al. had assumed 2900 kg/m3. Plesa et al (2016) find the crust is thickest underneath Tharsis where it may be up to 100 km thick, while the thinnest part of the crust is found underneath the Isidis impact basins with 1–5 km thickness. The average thickness is 45 km for the Neumann et al (2004) model but varies between 27 and 89 km depending on the assumed average density between 2700 kg/m3 and 3200 kg/m3.
Plesa et al. (2016) used their crustal thickness model together with the compositional model of Dreibus and Wänke (1985) and a model of convective mantle heat transfer to estimate the heat flow from the interior and its variation across the surface. They found the heat flow to vary with the crust thickness with values between 17.2 and 49.9 mW/m2. The predicted average value is 23.2 to 27.3 mW/m2. Furthermore, they show that the low thermal conductivity crust insulates the mantle which has important effects on the volcanic evolution of the planet. The long-lasting activity of Tharsis and Elysium can thus be understood—especially when the viscosity in the mantle increases by two orders of magnitude with depth. The models are consistent with the inferred variation of the elastic lithosphere thickness over time (compare Sect. 2.4). A thickness of less than 20 km was derived for the Noachian and a value greater than 300 km below the South Pole at present (e.g., Grott et al. 2013). The latter probably does not represent a present-day mean value, however. It is possible that upwelling mantle currents still exist underneath the Tharsis region and that the elastic lithosphere thickness varies across the planet (e.g., Grott et al. 2010).
The InSight seismic and rotational data have already resulted in refined values of the interior structure. Knapmeyer-Endrun et al. (2021) found that the crust underneath the InSight lander is either two-layered and 25–30 km thick or three layered and 40–45 km thick, the quality of the data not yet allowing to distinguish between the models. Yet, as the authors write, their data suggests that the average crust thickness cannot be more than 70 km. Note that the properties of a layer comprising the first 10 km (Lognonné et al. 2020; Knapmeyer-Endrun et al. 2021) is a feature of both models which will provide important constraints on models of the evolution of the upper crust. Khan et al (2021) used data from the three Cerberus Fossae events described by Giardini et al (2020) and identified multiple phases from which they constructed seismic velocity and temperature vs depth models for the mantle down to 700 km depth. They find the lithosphere to be likely 400–500 km thick and underlain by an about 200 km thick low velocity zone. Stähler et al. (2021) using the model of Khan et al. (2021) found core phases that suggest a core radius of 1830 ± 40 km consistent with the constraints from MoI and k2 (Rivoldini et al. 2011; Kahan et al. 2021) (Fig. 7). Plesa et al. (2021) checked a large variety of thermal models of the interior of Mars for cases that would exclude a shadow zone for the three events. They find that the absence of seismic shadow zones between Cerberus Fossae and the InSight landing site suggests that the mantle contains not more than 80% of the heat producing elements of bulk Mars and that the crust must thus provide more than 20% of the total heat production rate at present.
Schematic diagram of Mars’ interior structure. The cross section depicts the core-induced shadow zone for seismic waves. The surface topography is a cut through the Mars Orbiter Laser Altimeter (MOLA) map (Smith et al. 2001) on a great circle arc from InSight through the Mars Orbiter Laser Altimeter (MOLA) map. The S-wave shadow zone is minimal and probably filled by diffracted S waves, whereas the P-wave shadow zone is large and contains specifically the Tharsis region. The existence of an inner core cannot be determined by current data, and the seismic ray paths shown assume no inner core. Topography and InSight lander are exaggerated in scale. Figure from Stähler et al. (2021)
The presence of magnetized rocks (Fig. 3) suggests the existence of an early dynamo in the Martian core. Most models for the timing of the Martian dynamo are based on the presence of magnetic fields over the heavily cratered southern hemisphere and their absence over the interiors of the major basins: Hellas, Argyre, and Isidis. An early dynamo, extinct at the time of basin excavation about 4.1 Ga ago, is the most widely accepted scenario. Most models of the Martian evolution with an early dynamo generated magnetic field and the lack thereof at present suggest that the Martian core is entirely fluid with no solid inner core. An early thermally driven dynamo would have stopped operating after several hundred million years (e.g., Stevenson et al. 1983; Spohn et al. 1998; Hauck and Phillips 2002; Breuer and Spohn 2003, 2006). The absence of an inner core is supported by recent geochemical evidence as discussed in Stähler et al. (2021) and by the interior structure models of Rivoldini et al. (2011).
Recent analysis of Mars Atmosphere and Volatile EvolutioN (MAVEN) magnetic field data, however, detected a magnetization above the 3.7 Ga old Lucus Planum suggesting a longer lasting (or rejunavated) dynamo activity (Mittelholz et al. 2020). This observation has significant implications for the thermal evolution of Mars because a purely thermal dynamo and the absence of an inner core is difficult to reconcile with this observation (e.g., Stevenson et al. 1983). However, a thermal dynamo could be active longer if the thermal conductivity of the Martian core is lower than the typically assumed value of 40 W/mK (Greenwood et al. 2021). Recent electrical resistivity experiments on Fe-Ni and Fe-Ni-S alloys suggest that values for the thermal conductivity as low as 5 W/mK to ~ 30 W/mK, depending on the composition (Pommier 2018, 2020). A chemical dynamo, which would be an alternative for generating a younger magnetic field, is not compatible with present thermal models due to the inferred low melting temperatures in the core (e.g., Plesa et al. 2016).
A particular feature of the observed magnetization on the surface of Mars is the strong dichotomy, with the southern hemisphere being more magnetized than the northern hemisphere (e.g., Langlais et al. 2019). Two general types of models have been proposed to explain this striking feature. Homogeneous magnetization could have been destroyed in the northern hemisphere, e.g., by hydrothermal alteration (Solomon et al. 2005) or impacts (Rochette et al. 2003). An alternative explanation proposes that the dynamo itself generates a hemispherical field due to lateral heat flow variations at the CMB (Stanley et al. 2008, Amit et al. 2011). However, it has been suggested (Dietrich and Wicht 2013) that these hemispheric dynamos reverse polarity on time scales of about 10 kyr and may not be capable of unidirectionally magnetizing a thick crustal layer. This would be required to explain the strong magnetization in the southern hemisphere.
3.5 Ganymede
Ganymede is the largest of the Galilean satellites discovered in 1610 by Galileo Galilei (1564–1642). The orbits of Io, Europa and Ganymede exhibit a 4:2:1 mean motion resonance, the Laplace resonance (Laplace 1805) that is unique in the solar system. This resonance implies a Ganymede non-zero eccentricity which brings orbital energy to this oversized satellite as large as a planet. Indeed, its radius is 2631 ± 1.7 km (Anderson et al. 1996; Schubert et al. 2004), which is larger than that of Mercury. The Galileo mission flew over Ganymede seven times during its mission (1995–2003) (Johnson et al. 1992) and determined a mass equal to 1.482 1020 kg, i.e. about one-third less than that of Mercury. The main geophysical quantity is the average density equal to 1942 ± 4.8 kg m−3 (Anderson et al. 1996; Schubert et al. 2004) implying that Ganymede is an icy body with up to 50% of its mass made of ice/water (Hussmann et al. 2015).
The second important geophysical quantity, after density, is the moment of inertia. The value deduced from radio-science measurements of the Galileo probe under hydrostatic equilibrium hypothesis and using the Radau-Darwin equation is C/MR2 = 0.3115 ± 0.00028 (Anderson et al. 1996; Schubert et al. 2004). This value is the smallest in the solar system. This implies a large concentration of mass towards the center of Ganymede and argues in favor of a completely differentiated three-layered body. Ganymede would be composed of a 400–1200 km metallic core, a silicate mantle of 700–1400 km thick and an up to 700 km thick layer of water (Anderson et al. 1996; Baland and Van Hoolst 2010; De Marchi et al. 2021) (Fig. 1). Interestingly, Jupiter's moon Callisto, which has a similar size and composition as Ganymede, has a very different structure. Callisto's measured MoI of 0.3549 ± 0.0042 (Anderson et al 2001) indicates that it is not fully differentiated, i.e. it does not have an iron core and possibly silicate mantle and water are not fully separated either (e.g., Kuskov et al. 2005). This difference suggests a completely different thermal evolution of the two bodies, which is not yet well understood.
Galileo brought to light a third important geophysical characteristic rarely observed for a celestial body: an intrinsic magnetic field and an induced magnetic field (Kivelson et al. 1996; Kivelson et al. 2002). The intrinsic magnetic field demonstrates that the metallic core, whose presence has been inferred in the gravity field data, must be partially liquid (Schubert et al. 1996; Anderson et al. 1996). For Ganymede core pressures, core crystallization occurs by iron-snow freezing under the assumption that the sulfur content is less than eutectic (Hauck et al. 2012). It has been shown that the iron-snow scenario can explain the observed magnetic field of Ganymede (Christensen 2015). Core crystallization models coupled with thermal evolution models further suggest that this Fe-snow dynamo must be very young with an age of less than a billion years (Rückriemen et al. 2018). This would further imply that Ganymede has no present solid inner core.
The induced magnetic field may originate from a liquid ocean in the ice layer as suggested by Kivelson et al. (2002). Due to the depth-dependent melting temperature of water, the ocean is likely located at a depth below 150 km (Vance et al. 2014, Fig. 8). This hypothesis is strengthened by the observation of oscillations in auroral ovals by the Hubble Space Telescope suggesting the presence of an electrically conductive ocean (Saur et al. 2015). The ocean would be sandwiched between two icy layers, the bottom one made of high-pressure ices (Sohl et al. 2002). It was suggested that Ganymede could maintain several liquid layers between high-pressure ice (Vance et al. 2014).
Illustration of the melting curve (liquidus) of pure water ice and the boundaries between different ice forms as a function of depth below the surface of Ganymede (after Schubert et al.1986). Superimposed is a temperature profile as a function of depth below the surface (dashed line). Due to the minimum in the melting curve of ice, the melting range is at a depth of 170 km
Currently, Ganymede’s deformation expressed through the Love numbers k2 and h2 and their phase lags are not known (e.g., Rambaux and Castillo-Rogez 2013). Measurements of the Love numbers by the JUICE mission (Grasset et al. 2013) will constrain the thickness and elastic behavior of the ice shell and the phase lags will reveal the presence of a global ocean and could inform on the thermal state of the deeper interior (Kamata et al. 2016; Hussmann et al. 2016). Although the tidal heating input is currently low in Ganymede this would not always have been the case (e.g., Hussmann et al. 2010). In the past, this moon could have passed through resonances which increase tidal heating and may sustain the development of a subsurface ocean (Showman and Malhotra 1997). Fundamental geodetic quantities, the libration and the obliquity, have not yet been measured but they can bring information on the internal structure, in particular the thickness and rigidity of the ice layer (Rambaux et al. 2011; Van Hoolst et al. 2013; Baland et al. 2012).
In conclusion, by combining the few geophysical measurements accessible thanks to to Galileo space mission, Ganymede is classified among the ocean worlds. It is therefore essential for exobiology studies and, it is the main target of the first L-class ESA mission, JUpiter Icy Moons Explorer (JUICE) (Grasset et al. 2013; Witasse et al. 2020). The payload is composed of several geophysical instruments, such as the laser altimeter GALA (GAnymede Laser Altimeter) to determine its topography and rotation (e.g., Steinbrügge et al. 2021), a radio-science experiment (Geodesy and Geophysics of Jupiter and the Galilean Moons, 3GM) to measure its gravity field, tides and rotation (e.g., Capuccio et al. 2020), and the radar sounder RIME (Radar for Icy Moon Exploration) to probe the ice shell. In addition, several in situ and remote sensing instruments including the JUICE MAGnetometer (J-MAG, Dougherty et al. 2013) and the visible camera JANUS (Jovis instrument, Amorum ac Natorum Undique Scrutator) JANUS) (e.g., Della Corte et al. 2019), will contribute to the geophysical investigation of Ganymede. The science payload of JUICE is the most powerful and versatile of any spacecraft that has visited the outer solar system before. It will largely improve and extend the Galileo measurements and the combination of the data would characterize Ganymede as a planetary object in unprecedented detail (Grasset et al. 2013). Unraveling the interior of this satellite, which is as big as a planet, will also contribute to future research and missions on the conditions of habitability and astrobiology.
3.6 Enceladus
Measurements by the Cassini mission (2004–2017) (Matson et al. 2003) showed that the small satellite Enceladus (radius of 252 km), which is in a close orbit around Saturn (semi-major axis of 238 × 103 km), is one of the most dynamic satellites of the Solar System. Enceladus has active geysers venting water vapor and ice particles (Porco et al. 2006), which are associated with large fractures in its south polar terrain. It moreover cools fast as shown by the large heat flow it emits, and yet has a warm interior with a global subsurface ocean. Here, we focus on planetary geodesy, and in particular rotation, gravity and topography data, which provided the most complete picture of Enceladus’s interior structure, including proof of the existence of the global subsurface ocean, an estimate of its size, and constraints on the thickness of the ice shell (Fig. 9).
The mass of Enceladus (M = 1.0794 × 1020 kg, Iess et al. 2014) together with its radius, leads to a mean density of 1607 kg/m3, which indicates that Enceladus has a significant rock fraction. The ratio of the second-degree zonal and sectorial gravity field coefficients differs about 10% from the hydrostatic value (Beuthe et al. 2016, note that the hydrostatic value differs from the classically used ratio of -10/3 by a few percent because of the fast rotation of Enceladus). Further evidence of the non-hydrostatic nature of Enceladus is given by the degree-two shape ratio, which differs from the hydrostatic value by 30%, and the significant zonal degree-three gravity coefficient. The larger deviation of the shape ratio from the hydrostatic value with respect to that for the gravity ratio is indicative of isostasy, in which topography is to a large degree gravitationally compensated by subsurface mass anomalies. The most plausible compensation for Enceladus is that of Airy compensation in which topography highs are associated with a thicker local shell above a water ocean that is denser than the shell, like an iceberg floating on water (Iess et al. 2014). The observation of librations convincingly showed that such a subsurface ocean must be global (Thomas et al. 2016; Van Hoolst et al. 2016). The observed amplitude of libration is about 4 times larger than the amplitude predicted for an interior structure without a global liquid layer. Since libration sensitively increases with decreasing shell thickness, a mean thickness of the shell of about 20 km could be determined from the libration amplitude (Thomas et al. 2016; Van Hoolst et al. 2016; Beuthe et al. 2016; Cadek et al. 2016).
By separating hydrostatic from nonhydrostatic, isostatically compensated degree-two components of the gravity and topography field, the mean moment of inertia has been estimated to be about 0.33 MR2, which implies a water/ice shell about 60 km thick above a rocky core with a density of 2375–2500 kg/m3 (McKinnon 2015). By adopting a physically consistent model of isostasy in which the shell is assumed to have reached a state of minimum deviatoric stress for the observed topography, the gravity-topography data confirm that Enceladus has a global ocean beneath a 20 km thick ice shell (Beuthe et al. 2016; Trinh 2019). It is important to note that this topography/gravity method is independent of libration, thereby strengthening the result. Different formulations of isostasy, such as dynamic isostasy in which the visco-elastic evolution of the shell to the isostatic end-state is considered (Cadek et al. 2019a), or the physically unsatisfying classical idea of isostasy in which equal pressures are required at the depth of compensation (Hemingway and Matsuyama 2017) lead to the same result.
These models in addition show that the ice shell must be about 30 km thick at equatorial regions and decrease to about 15 km at the south and about 7 km at the north pole (Beuthe et al. 2016) (Fig. 9). Due to the large thickness variations, hydrostatic pressure varies laterally, leading to viscous flow of ice that can remove basal topography on a timescale of some Myr to hundreds of Myr (Kamata and Nimmo 2017; Cadek et al. 2019b). In order to maintain the ice shell in a steady state, the viscous flow at the base of the ice shell must be balanced by changes in ice due to melting and freezing. This requires large heat fluxes and variations in the flux at the top of the ocean, which could be due to high tidal heating in the core or in the shell. The latter is likely only relevant for the thin ice shell in the south polar region. High tidal heating in the core may be due to a hydrated porous core, indicated by the low core density (Choblet et al. 2017).
4 Synthesis: Understanding the Differences Between the Earth’s and Other Planet’s Interiors
This ISSI Special Issue and book and Space Science Reviews Topical Collection discusses the synergistic use of gravity and magnetic field data and of the planet’s rotation to explore the deep interior of the Earth. Historically, these data have been provided by networks of observatories on the Earth’s surface. But in recent years observations from spacecraft in orbit around the Earth have significantly augmented the data set.
Planetary scientists use the same techniques to explore the interiors of planets, satellites and small bodies in the solar system although a comparable coverage in space and time has been achieved only for a couple of objects, Moon and Mars. But why would anyone interested in the Earth’s interior care about the interior of other planets? It is the differences and the commonalities in the interior structures and the workings of the planets that require explanation and offer opportunities for a better understanding of the “Bowels of the Earth” (Elder 1978). Although we are far from having a detailed knowledge of the gravity and magnetic fields of exoplanets, even research on such distant bodies can offer more insight into the physics of the Earth’s interior. Estimates of their rotation rates are often based on the hypothesis of them orbiting close to their primaries in 1:1 resonances between their rotation and orbital revolution. The apparent dominance of super-Earths in the observational statistics over Earth and smaller sized rocky planets (e.g., Youdin 2011; Batalha 2014) is interesting as are theories of the state and the dynamics of interiors at TPa pressures (e.g., Valencia et al. 2007; Stamenkovic et al. 2011; Karato 2011). What is more, even the overall structure of the solar system with small rocky planets orbiting close to the sun and giant planets at considerable distance appears to be unusual (e.g., Zhu and Dong 2021), although it must be admitted that there is an observational bias favoring the detection of close-in large planets. Only 30% of all known planetary systems around sun-like stars have rocky planets at distances \(\le 1AU\) (Raymond and Morbidelli 2020; Zhu and Dong 2021) and only 1% have a giant Jupiter-like planet at an orbital distance of around \(5AU\). A Jupiter like planet at that distance would be guarding the inner region of the system against disturbances from inward migrating planets (Batygin and Laughlin 2015).
We have discussed a small subset of rocky solar system bodies, the three Earth-like planets, the Moon and two icy satellites of Jupiter and Saturn, Ganymede and Enceladus. The latter two are of interest as they show that ice can have features similar to those observed for rock, e.g., lateral plate-like movement of surface units of differing age (although the similarity to plate tectonics may not reach deeply into the interior) and ice volcanism. Of the terrestrial planets, Venus is the closest to Earth in terms of mass and radius but is very different in terms of its atmosphere. It is generally accepted that Venus’ atmosphere—more massive than of Earth with a surface pressure higher by almost two orders of magnitude—has experienced a runaway greenhouse effect leading to surface temperatures exceeding 700 K. It has been speculated that early Venus may have been habitable, though (e.g., Way et al. 2016). Mars is about half the size of Earth and Venus but resembles Earth’s climate much more than Venus’. Mercury and the Moon resemble each other by the absence of an atmosphere and in their cratered surfaces (shared with some surface units of Ganymede), but Mercury surprises by having an unusually large core and a self-sustained magnetic field.
As we have shown in the preceding sections, all rocky planets in the solar system share the same first-order internal structure with an iron-rich core, a silicate mantle, and a crust that is generated by partial melting of the mantle. But the relative sizes and masses of these major reservoirs differ. Take the cores for example, with the Moon’s comprising only 0.5 percent of its volume or about 1% of its mass while Mercury’s core comprises 55% of the planet’s volume and about 80% of its mass. More Earth-like are the values of 13% and 25%, respectively that are approximately valid for Mars and Venus. The reasons for the Moon and Mercury being so extraordinary is generally associated with their origins, with that of the Moon being closely related to the early history of the Earth (see Canup et al. 2021 for a recent collection of papers) and with Mercury’s related to the early history of the inner solar system (e.g., Benz et al. 2008; Ebel and Stewart 2018). Models of the growth of the Earth’s inner core and its relation to the evolution of the dynamo and magnetic field generation can also be improved by looking at other planets. A model that explains the Earth magnetic field must also be able to explain the present-day lack of fields of Venus and Mars. While it is unclear whether Venus ever had a dynamo, for Mars it is the strength of the magnetization that puzzles along with evidence for late magnetizations, suggesting that dynamos may switch off and restart. The strength of the present field of Mercury, believed to be powered by a chemical dynamo (as we have discussed above), is not easily explained with otherwise widely accepted scaling laws currently in use in Earth science (Christensen and Aubert 2006). The origin of Mars’ early field and the lack of a present field is debated. It is possible that Mars lacks a (growing) inner core and the chemical buoyancy to drive a dynamo as has been speculated by Schubert and Spohn (1990). This view is supported by the recent data suggesting a core size of around 1800 km with a significant volatile content that would suppress the melting temperature as we have discussed above. This then leaves the evidence for late remnant magnetizations unexplained, however.
The second major reservoir—as we move out from the center—is divided into the rock mantle and the crust. And as far as we understand, the latter originates by partial melting of the former. Although their compositions differ slightly, all terrestrial planets have basaltic crusts. However, their volumetric shares are typically larger than on Earth, as the crusts are substantially thicker. The reason for this lies with the crustal recycling mechanism through plate tectonics that is unique to the Earth. There may be crustal recycling by delamination on other bodies, but not to an extent that rivals plate tectonics’ crustal subduction. Partial melting of basaltic crust together with mantle rock and sediments in subduction zones is the mechanism to generate Si-rich continental crust, a type of crust that is—as far as we know—unique to the Earth and is related to plate tectonics.
Plate tectonics has farther reaching effects on the evolution of the Earth that go beyond the scope of the present article and this book. The composition and the long-term climatic stability of the atmosphere are associated with the mechanisms and it has been claimed that it is essential for the Earth’s habitability. But just why plate tectonics occurs on Earth and not on any other of the terrestrial planets remains an open question. A recent paper by Höning and Spohn (2016) suggested that a planet with an approximately equal share of surface covered by oceans and by continental land masses may be a rather unlikely outcome of the evolution of a plate tectonics planet. In their study, the most likely outcome would be a planet mostly covered by continental crust with an ocean planet as the second most likely. Together with the notion that the solar system is likely not to be typical, this lends an interesting twist to the discussion of the likelihood of a second Earth.
In the early days of spacecraft exploration of the Earth-like planets it was held that they should have evolved similarly. Attempts at finding remnants of earlier phases of plate tectonics on Mars and Venus were made. For Mars, the almost linear line-up of the three Tharsis volcanoes were speculated to be remnants of an island arc (Sleep 1994). Attempts at finding ridges and subduction zones on Venus were many (e.g., Kaula and Philipps 1981). And Kaula (1975) has speculated that there were seven phases of an evolution that all rocky planets went through. Plate tectonics would have been a relatively early phase of tectonics accompanied by rapid cooling. Earth as the largest and therefore most slowly evolving planet was the one still in the plate tectonics regime but would at one time turn Mars-like. Today, we appreciate that the rocky planets and moons are rather individual manifestations of the many degrees of freedom of the formation of complex structures from chemically versatile silicates and planetary formation and evolution processes where chaos is a factor. We further appreciate the differences that minor chemical components may cause for melting relations and rheology and therefore for volcanism and tectonics. Still, since the physics is the same, there is a lot to be learned from solid Earth-like bodies—in a very general sense—for our home planet Earth.
Change history
06 January 2022
A Correction to this paper has been published: https://doi.org/10.1007/s10712-021-09687-9
References
Abbey W, Anderson R, Beegle L et al (2019) A look back: the drilling campaign of the Curiosity Rover during the Mars science laboratory’s prime mission. Icarus. https://doi.org/10.1016/j.icarus.2018.09.004
Allton JH, Waltz SR (1980) Depth scales for Apollo 15, 16 and 17 drill cores. In: Proceedings Apollo 11 lunar science conference. pp 1463–1477
Anand M, Russel C, Lin Y et al (2021) Role of sample return in adressing major questions in planetary sciences, Space Science Series of ISSI, vol 74. Springer, Heidelberg
Anderson JD, Lau EL, Sjogren WL, Schubert G, Moore WB (1996) Gravitational constraints on the internal structure of Ganymede. Nature 384:541–543
Anderson JD, Schubert G, Jacobson RA, Lau EL, Moore WB, Sjogren WL (1998) Europa’s differentiated internal structure: inferences from four Galileo encounters. Science 281:2019–2022
Anderson JD, Jacobson RA, McElrath TP, Moore WB, Schubert G, Thomas PC (2001) Shape, mean radius, gravity field, and interior structure of Callisto. Icarus 153(1):157–161
Anderson BJ, Johnson CL, Korth H, Winslow RM, Borovsky JE, Purucker ME, Slavin JA, Solomon SC, Zuber MT, McNutt RL Jr (2012) Low-degree structure in Mercury’s planetary magnetic field. J. Geophys. Res. 117:E00L12. https://doi.org/10.1029/2012JE004159
Anderson FS, Smrekar SE (2006) Global mapping of crustal and lithospheric thickness on Venus. J Geophys Res Planet 111:E08006. https://doi.org/10.1029/2004JE002395
Antonangeli D, Morard G, Schmerr NC, Komabayashi T, Krisch M, Fiquet G, Fei Y (2015) Towards a mineral physics reference model for the Moon’s core. Proc Natl Acad Sci 112:3916–3919
Armann M, Tackley PJ (2012) Simulating the thermochemical magmatic and tectonic evolution of Venus's mantle and lithosphere: two‐dimensional models. J Geophys Res Planets 117:E12003. https://doi.org/10.1029/2012JE004231
Baland RM, Van Hoolst T (2010) Librations of the Galilean satellites: the influence of global internal liquid layers. Icarus 209:651–664
Baland RM, Yseboodt M, Van Hoolst T (2012) Obliquity of the Galilean satellites: the influence of a global internal liquid layer. Icarus 220:435–448
Banerdt WB, Smrekar SE, Banfield D et al (2020) Initial results from the InSight mission on Mars. Nat Geosci. https://doi.org/10.1038/s41561-020-0544-y
Banfield D, Rodriguez-Manfredi JA, Russell CT et al (2019) InSight auxiliary payload sensor suite (APSS). Space Sci Rev 215(1):1–33
Batalha NM (2014) Exploring exoplanet populations with Nasa’s Kepler mission. PNAS 111:12647–12654. https://doi.org/10.1073/pnas.1304196111
Batygin K, Laughlin G (2015) Jupiter’s decisive role in the inner solar systems early evolution. PNAS. https://doi.org/10.1073/pnas.1423252112
Benkhoff J, Van Casteren J, Hayakawa H, Fujimoto M, Laakso H et al (2010) BepiColombo—comprehensive exploration of mercury: mission overview and science goals. Planet Space Sci 58(1–2):2–20
Benz W, Anic A, Horner J, Whitby JA (2008) The origin of Mercury. In: Balogh A, Ksanfomality L, von Steiger R (eds) Mercury, Space Science Series of ISSI Vol 26, pp 7–20.
Bercovici D, Ricard Y (2014) Plate tectonics, damage and inheritance. Nature 508(7497):513–516
Beuthe M, Rivoldini A, Trinh A (2016) Enceladus’s and Dione’s floating ice shells supported by minimum stress isostasy. Geophys Res Lett 43:10,088-10,096
Beuthe M, Charlier B, Namur O, Rivoldini A, Van Hoolst T (2020) Mercury’s crustal thickness correlates with lateral variations in mantle melt production. Geophys Res Lett. 47:e2020GL087261
Bierson CJ, Nimmo F (2016) A test for Io’s magma ocean: Modeling tidal dissipation with a partially molten mantle. J Geophys Res Planets 121:2211–2224. https://doi.org/10.1002/2016JE005005
Bills BG (2005) Free and forced obliquities of the Galilean satellites of Jupiter. Icarus 175:233
Bjonnes EE, Hansen VL, James B, Swenson JB (2012) Equilibrium resurfacing of Venus: results from new monte Carlo modeling and implications for Venus surface histories. Icarus 217(2):451–461
Bland MT, Showman AP, Tobie G (2009) The orbital–thermal evolution and global expansion of Ganymede. Icarus 200(1):207–221
Braginsky SI (1964) Magnetohydrodynamics of the Earth’s core. Geomag Aeron 4:698–712
Breuer D, Moore B (2015) Dynamics and thermal history of the terrestrial planets, the moon, and Io. In: Schubert G, Spohn T (eds) Physics of terrestrial planets and moons treatise on geophysics, 2nd edn. Elsevier, New York, pp 255–305
Breuer D, Spohn T (2003) Early plate tectonics versus single-plate tectonics on Mars: evidence from magnetic field history and crust evolution. J Geophys Res Planets. https://doi.org/10.1029/2002JE001999
Breuer D, Spohn T (2006) Viscosity of the Martian mantle and its initial temperature: constraints from crust formation history and the evolution of the magnetic field. Planet Space Sci 54(2):153–169
Breuer D, Rueckriemen T, Spohn T (2015) Iron snow, crystal floats, and inner-core growth: modes of core solidification and implications for dynamos in terrestrial planets and moons. PEPS 2(1):1–26
Brinkmann N, Schmelzbach S, Solberger D et al (2019) The first active seismic experiment on Mars to characterize the shallow subsurface structure at the InSight landing site. SEG. https://doi.org/10.1190/segam2019-3215661.1
Čadek O, Tobie G, Van Hoolst T, Massé M, Choblet G, Lefèvre A, Mitri G, Baland RM, Běhounková M, Bourgeois O, Trinh A (2016) Enceladus’s internal ocean and ice shell constrained from Cassini gravity, shape and libration data. Geophys Res Lett 43:5653–5660
Čadek O, Soucek O, Behounkova M (2019) Is Airy isostasy applicable to icy moons? Geophys Res Lett. 46:14,299-14,306
Čadek O, Souček O, Běhounková M, Choblet G, Tobie G, Hron J (2019b) Long-term stability of Enceladus’ uneven ice shell. Icarus 319:476–484
Canup RM, Righter K, Dauphas N, Pahlevan K, Ćuk M, Lock SJ, Stewart ST, Salmon J, Rufu R, Nakajima M, Magna T (2021) Origin of the moon. New views of the moon II, Mineralogical Society of America
Cao H, Aurnou JM, Wicht J, Dietrich W, Soderlund KM, Russell CT (2014) A dynamo explanation for Mercury’s anomalous magnetic field. Geophys Res Lett 41:4127–4134
Cappuccio P, Hickey A, Durante D, Di Benedetto M, Iess L, De Marchi F, Plainaki C, Milillo A, Mura A (2020) Ganymede’s gravity, tides and rotational state from JUICE’s 3GM experiment simulation. Planet Space Sci 187:104902
Cascioli G, Hensley S, De Marchi F, Breuer D, Durante D, Racioppa P, Iess L, Mazarico E, Smrekar SE (2021) The determination of the rotational state and interior structure of Venus with VERITAS. Planet Sci J 2(6):220–232
Cébron D, Laguerre R, Noir J, Schaeffer N (2019) Precessing spherical shells: flows, dissipation, dynamo and the lunar core. Geophy J Int 219:34-S57
Chabot NL, Wollack EA, Klima RL, Minitti ME (2014) Experimental constraints on Mercury’s core composition. Earth Planet Sci Lett 390:199–208. https://doi.org/10.1016/j.epsl.2014.01.004
Charlier B, Grove TL, Namur O, Holtz F (2018) Crystallization of the lunar magma ocean and the primordial mantle-crust differentiation of the Moon. Geochim Cosmochim Acta 234:50–69
Choblet G, Tobie G, Sotin C, Běhounková M, Čadek O, Postberg F, Souček O (2017) Powering prolonged hydrothermal activity inside Enceladus. Nat Astron. https://doi.org/10.1038/s41550-017-0289-8
Christensen UR (2006) A deep dynamo generating Mercury’s magnetic field. Nature 444:1056–1058
Christensen UR (2015) Iron snow dynamo models for Ganymede. Icarus 247:248–259
Christensen UR, Aubert J (2006) Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields. Geophys J Int 166(1):97–114
Christensen UR, Wicht J (2008) Models of magnetic field generation in partly stable planetary cores: Applications to Mercury and Saturn. Icarus 196:16–34. https://doi.org/10.1016/j.icarus.2008.02.013
Christensen UR (2019) Planetary magnetic fields and dynamos. In Oxford research encyclopedia of planetary science.
Colin L (1980) The pioneer Venus program. J Geophys Res Space Physics 85(A13):7575–7598
Comstock RL, Bills BG (2003) A solar system survey of forced librations in longitude. J. Geophys. Res. 108(E9):5100. https://doi.org/10.1029/2003JE00210
Cuk M, Stewart ST (2012) Making the Moon from a fast spinning Earth: a giant impact followed by resonant despinning. Science 338:1047–1052
Davaille A, Smrekar SE, Tomlinson S (2017) Experimental and observational evidence for plume-induced subduction on Venus. Nat Geosci 10(5):349–355
De Marchi F, Di Achille G, Mitri G, Cappuccio P, Di Stefano I, Di Benedetto M, Iess L (2021) Observability of Ganymede’s gravity anomalies related to surface features by the 3GM experiment onboard ESA’s JUpiter ICy moons Explorer (JUICE) mission. Icarus 354:114003
de Meijer R, Anisichkin VF, van Westrenen W (2013) Forming the Moon from terrestrial silicate-rich material. Chem Geol 345:40–49
de Vries J, van den Berg A, van Westrenen W (2010) The formation and evolution of a lunar core from ilmenite-rich magma ocean cumulates. Earth Planet Sci Lett 292:139–147
Dehant V, Mathews PM (2015) Precession, nutation, and wobble of the Earth. Cambridge University Press, Cambridge
Dehant V, Defraigne P, Van Hoolst T (2000) Computation of Mars’ transfer functions for nutations, tides and surface loading. Phys. Earth Planet. Int. 117:385–395
Dehant V, Le Maistre S, Baland RM, Karatekin O, Péters MJ, Rivoldini A, Van Hoolst T, Yseboodt M, Mitrovic M and the LaRa team (2020) The radio-science LaRa instrument onboard ExoMars 2020 to investigate the rotation and interior of Mars, Space Sci Rev 180: 104776https://doi.org/10.1016/j.pss.2019.104776
Dehant V, Compuzano SA, De Santis A, van Westrenen W (2022) Structure, materials and processes in the Earth’s core and mantle. Surv Geophys (in press)
Della Corte V, Noci G, Turella A, Paolinetti R, Zusi M, Michaelis H, Soman M, Debei S, Castro JM, Herranz M, Amoroso M, Castronuovo M, Holland A, Lara LM, Jaumann R, Palumbo P (2019) Scientific objectives of JANUS Instrument onboard JUICE mission and key technical solutions for its Optical Head, In: 2019 IEEE 5th International workshop on metrology for aerospace (MetroAeroSpace), 2019, pp. 324–329, doi: https://doi.org/10.1109/MetroAeroSpace.2019.8869584.
Dietrich W, Wicht J (2013) A hemispherical dynamo model: Implications for the Martian crustal magnetization. Phys Earth Planet Int 217:10–21
Dobrzhinetskaya LF, Green HW II, Wang S (1996) Alpe Arami: a peridotite massif from depths of more than 300 kilometers. Science 271:1841–1845
Dougherty MK (2013) JUICE: a European mission to Jupiter and its icy moons. In: AGU fall meeting abstracts, vol 2013, pp SM13D-03
Dreibus G, Wanke H (1985) Mars, a volatile-rich planet. Meteoritics 2:367–381
Dumberry M, Rivoldini A (2015) Mercury’s inner core size and core-crystallization regime. Icarus 248:254–268
Dumoulin C, Tobie G, Verhoeven O, Rosenblatt P, Rambaux N (2017) Tidal constraints on the interior of Venus. J Geophys Res Planets 122(6):1338–1352
Dwyer CA, Stevenson DJ, Nimmo F (2011) A long-lived lunar dynamo driven by continuous mechanical stirring. Nature 479:212–214
Dziewonski AM, Anderson DL (1981) Preliminary reference Earth model. Phys Earth Planet Int. https://doi.org/10.1016/0031-9201(81)90046-7
Ebel DS, Stewart ST (2018) The elusive origin of Mercury. In: Solomon S, Nittler L, Anderson B (eds) Mercury: The View after MESSENGER. Cambridge University Press, Cambridge, pp 497–515. https://doi.org/10.1017/9781316650684.019
Elder J (1978) The bowels of the Earth. Oxford University Press, Oxford
Elkins-Tanton LT, Asphaug E, Bell J et al (2014) Journey to a metal world: concept for a discovery mission to Psyche. Lunar Planet Sci Conf 45:1253
Fegley B Jr (2014) Venus. Planets, Asteriods, Comets Solar Syst 2:127–148
Flahaut J, Blanchette-Guertin JF, Jilly C, Sharma P, Souchon A, van Westrenen W, Kring DA (2012) Identification and characterization of science-rich landing sites for lunar lander missions using integrated remote sensing observations. Adv Space Res 50:1647–1665
Folkner WM, Dehant V, Le Maistre S, Yseboodt M, Rivoldini A, Van Hoolst T et al (2018) The rotation and interior structure experiment on the InSight mission to Mars. Space Sci Rev 214(5):1–16
Gaffney AM, Gross J, Borg LE, Donaldson Hanna KL, Draper DS, Dygert N, Elkins-Tanton LT, Prissel KB, Prissel TC, Steenstra ES, Warren PH, van Westrenen W (2021) Magmatic evolution I - initial differentiation of the Moon. New views of the Moon II, Mineralogical Society of America
Gagnepain-Beyneix J, Lognonné P, Chenet H, Lombardi D, Spohn T (2006) A seismic model of the lunar mantle and constraints on temperature and mineralogy. Phys Earth Planet Inter 159(3–4):140–166
Garcia RF, Gagnepain-Beyneix J, Chevrot S, Lognonné P (2011) Very preliminary reference Moon model. Phys Earth Planet Inter 188(1–2):96–113
Garcia RF, Gagnepain-Beyneix J, Chevrot S et al (2012) Erratum to “Very preliminary reference Moon model.” Phys Earth Planet Int 202–203:89–91
Garcia RF, Khan A, Drilleau M, Margerin L, Kawamura T, Sun D et al (2019a) Lunar seismology: an update on interior structure models. Space Sci Rev 215(8):1–47
Garcia RF, Khan A, Drilleau M, Margerin L, Kawamura T, Sun D, Wieczorek MA, Rivoldini A, Nunn C, Weber RC, Marusiak AG (2019) Lunar seismology: An update on interior structure models. Space Sci Rev. 215(8):1–47
Genova A, Goossens S, Lemoine FG, Mazarico E, Neumann GA, Smith DE, Zuber MT (2016) Seasonal and static gravity field of Mars from MGS, Mars Odyssey and MRO radio science. Icarus 272:228–245
Genova A, Goossens S, Mazarico E, Lemoine FG, Neumann GA, Kuang W et al (2019) Geodetic evidence that Mercury has a solid inner core. Geophys Res Lett 46:3625–3633
Genova A, Hussmann H, Van Hoolst T, Heyner D, Iess L, Santoli F, Thomas N, Kolhey P, Langlais B, Mieth JZD, Oliveira JS, Stark A, Tosi N, Wicht J, Benkhoff J (2021) Geodesy, geophysics and fundamental physics investigations of the BepiColombo mission. Space Sci Rev 217:31. https://doi.org/10.1007/s11214-021-00808-9
Giardini D, Lognonné P, Banerdt WB et al (2020) The seismicity of Mars. Nat Geosci. https://doi.org/10.1038/s41561-020-0539-8
Gillmann C, Tackley P (2014) Atmosphere/mantle coupling and feedbacks on Venus. J Geophys Res Planets 119(6):1189–1217
Goins NR, Dainty AM, Toksöz MN (1981) Lunar seismology: the internal structure of the Moon. J Geophys Res Solid Earth 86(B6):5061–5074
Golabek GJ, Emsenhuber A, Jutzi M, Asphaug EI, Gerya TV (2018) Coupling SPH and thermochemical models of planets: Methodology and example of a Mars-sized body. Icarus 301:235–246
Goossens S, Sabaka TJ, Genova A et al (2017) Evidence for a low bulk crustal density for Mars from gravity and topography. Geophys Res Lett 44(15):7686–7694
Grasset O, Dougherty MK, Coustenis A, Bunce EJ, Erd C, Titov D, Blanc M, Coates A, Drossart P, Fletcher LN, Hussmann H, Jaumann R, Krupp N, Lebreton JP, Prieto-Ballesteros O, Tortora P, Tosi F, Van Hoolst T (2013) JUpiter ICy moons explorer (JUICE): an ESA mission to orbit Ganymede and to characterise the Jupiter system. Planet Space Sci 78:1–21
Greenwood S, Davies CJ, Pommier A (2021) Influence of thermal stratification on the structure and evolution of the Martian core. Geophys Res Lett 48(22):e2021GL095198. https://doi.org/10.1029/2021GL095198
Grott M, Breuer D (2008) The evolution of the Martian elastic lithosphere and implications for crustal and mantle rheology. Icarus 193(2):503–515
Grott M, Baratoux D, Hauber E, Sautter V, Mustard J, Gasnault O et al (2013) Long-term evolution of the Martian crust-mantle system. Space Sci Rev 174(1):49–111
Grott M, Spohn T, Knollenberg J et al (2021) Thermal conductivity of the Martian regolith at the InSight landing site from HP3 active heating experiments. Lunar Planet Sci Conf 52:2548
Grott M, Breuer D (2010). On the spatial variability of the Martian elastic lithosphere thickness: evidence for mantle plumes? J Geophys Res Planets 115:E03005. https://doi.org/10.1029/2009JE003456
Harada Y, Goossens S, Matsumoto K, Yan J, Ping J, Noda H, Haruyama J (2014) Strong tidal heating in an ultralow-viscosity zone at the core-mantle boundary of the Moon. Nat Geosci 7(8):569–572
Harada Y, Goossens S, Matsumoto K, Yan J, Ping J, Noda H, Haruyama J (2016) The deep lunar interior with a low-viscosity zone: Revised constraints from recent geodetic parameters on the tidal response of the Moon. Icarus 276:96–101
Hauck SA, Phillips RJ (2002) Thermal and crustal evolution of Mars. J Geophys Res 107:6–1
Hauck SA II et al (2013) The curious case of Mercury’s internal structure. J Geophys Res Planets 118:1204–1220
Hauck SA II, Grott M, Byrne PK, Denevi BW, Stanley S, McCoy TJ (2018) Mercury’s global evolution. In: Solomon SC, Anderson BJ, Nittler LR (eds) Mercury: The view After MESSENGER. Cambridge University Press, Cambridge, pp 516–543
Hauck SA II, Aurnou JM, Dombard AJ (2006) Sulfur's impact on core evolution and magnetic field generation on Ganymede. J Geophys Res Planet 111:E09008. https://doi.org/10.1029/2005JE002557
Hemingway DJ, Matsuyama I (2017) Isostatic equilibrium in spherical coordinates and implications for crustal thickness on the Moon, Mars, Enceladus, and elsewhere. Geophys Res Lett. https://doi.org/10.1002/2017GL073334
Höning D, Spohn T (2016) Continental growth and mantle hydration as intertwined feedback cycles in the thermal evolution of Earth. Phys Earth Planet Inter 255:27–49
Hood LL, Mitchell DL, Lin RP, Acuna MH, Binder AB (1999) Initial measurements of the lunar induced magnetic dipole moment using Lunar Prospector magnetometer data. Geophy Res Lett 26(15):2327–2330
Hubbard WB (1984) Planetary interiors, vol 334. Van Nostrand Reinhold, New York
Hussmann H, Spohn T (2004) Coupled thermal and orbital evolution of Europa and Io. Icarus. https://doi.org/10.1016/j.icarus.2004.05.020
Hussmann H, Choblet G, Lainey V, Matson DL, Sotin C, Tobie G, Van Hoolst T (2010) Implications of rotation, orbital states, energy sources, and heat transport for internal processes in icy satellites. Space Sci Rev 153(1):317–348
Hussmann H, Sohl F, Oberst J (2011) Measuring tidal deformations at Europa’s surface. Adv Space Res 48:718–724
Hussmann H, Shoji D, Steinbrügge G, Stark A, Sohl F (2016) Constraints on dissipation in the deep interiors of Ganymede and Europa from tidal phase-lags. Celest Mech Dyn Astr 126:131–144
Hussmann H, Sotin C, Lunine J. (2015) Interiors and evolution of Icy satellites. Treatise on geophysics. Second Edition, pp 605–635.
Iess L, Jacobson RA, Ducci M, Stevenson DJ, Lunine JI, Armstrong JW, Asmar SW, Racioppa P, Rappaport NJ, Tortora P (2012) The tides of Titan. Science 337:457–459
Iess L, Stevenson DJ, Parisi M et al (2014) The gravity field and interior structure of Enceladus. Science 344:78–80
James PB, Zuber MT, Phillips RJ (2013) Crustal thickness and support of topography on Venus. J Geophys Res Planet 118(4):859–875
James PB, Zuber MT, Phillips RJ, Solomon SC (2015) Support of long-wavelength topography on Mercury inferred from MESSENGER measurements of gravity and topography. J Geophys Res Planet. 120:287–310
Jiménez-Díaz A, Ruiz J, Kirby JF, Romeo I, Tejero R, Capote R (2015) Lithospheric structure of Venus from gravity and topography. Icarus 260:215–231
Johnson CL, Phillips RJ, Purucker ME, Anderson BJ, Byrne PK, Denevi BW, Feinberg JM, Hauck SA II, Head JW III, Korth H, James PB, Mazarico E, Neumann GA, Philpott LC, Siegler MA, Tsyganenko NA, Solomon SC (2015) Low-altitude magnetic field measurements by MESSENGER reveal Mercury’s ancient crustal field. Science 348:892–895. https://doi.org/10.1126/science.aaa8720
Johnson CL et al (2018) Mercury’s internal magnetic field. In: Solomon SC, Anderson BJ, Nittler LR (eds) Mercury: the view after MESSENGER. Cambridge University Press, Cambridge, pp 114–143
Johnson CL et al (2020) Crustal and time-varying magnetic fields at the InSight landing site on Mars. Nat Geosci 13:199–204
Johnson TE, Morrissey LJ, Nemchin AA, Gardiner NJ, Snape JF (2021) The phases of the Moon: Modelling crystallisation of the lunar magma ocean through equilibrium thermodynamics. Earth Planet Sci Lett 556:116721
Johnson TV, Yeates CM, Young R (1992) The Galileo Mission overview. Space Sci Rev 60:3–21
Jolliff BL, Wieczorek MA, Shearer CK, Neal CR (2006) New views of the Moon, vol 60. Mineralogical Society of America, Chantilly, VA
Kahan D, Folkner WM, Buccino DR, Dehant V, Le Maistre S, Rivoldini A, Van Hoolst T, Yseboodt M, Marty JC (2021) Mars precession rate determined from radiometric tracking of the insight lander. Planet Space Sci 199:105208. https://doi.org/10.1016/j.pss.2021.105208
Kamata S, Nimmo F (2017) Interior thermal state of Enceladus inferred from the viscoelastic state of the ice shell. Icarus 284:387–393
Kamata S, Kimura J, Matsumoto K, Nimmo F, Kuramoto K, Namiki N (2016) Tidal deformation of Ganymede: sensitivity of love numbers on the interior structure. J Geophys Res (planets) 121:1362–1375
Karato SI (2011) Rheological structure of the mantle of a super-Earth: Some insights from mineral physics. Icarus 212:14–23
Katsura T, Shimizu H, Momki N, Toh H (2021) Electromagnetic induction revealed by MESSENGER’s vector magnetic data: The size of Mercury’s core. Icarus 354:114112
Kaula WM (1975) The seven ages of a planet. Icarus. https://doi.org/10.1016/0019-1035(75)90138-4
Kaula WM (1979) The moment of inertia of Mars. Geophys Res Lett 6(3):194–196
Kaula WM, Philipps RJ (1981) Quantitative test for plate tectoncs on Venus. J Geophys Res. https://doi.org/10.1029/GL008i012p01187
Kawaguchi JI, Fujiwara A, Uesugi T (2008) Hayabusa—Its technology and science accomplishment summary and Hayabusa-2. Acta Astronaut 62(10–11):639–647
Keldysh MV (1977) Venus exploration with the Venera 9 and 10 spacecraft. Icarus 30:605–625
Kennet BLN, Engdahl ER (1991) Traveltimes for global earthquake location and phase identification. Geophys J Int. https://doi.org/10.1111/j.1365-246X.1991.tb06724.x
Khan A, Mosegaard K (2002) An inquiry into the lunar interior: a nonlinear inversion of the Apollo lunar seismic data. J Geophys Res Planets 107(E6):3–1
Khan A, Mosegaard K, Rasmussen KL (2000) A new seismic velocity model for the Moon from a Monte Carlo inversion of the Apollo lunar seismic data. Geophys Res Lett 27(11):1591–1594
Khan A, Pommier A, Neumann GA, Moosegaard K (2013) The lunar Moho and the internal structure of the Moon: a geophysical perspective. Tectonophysics 609:331–352
Khan A, Ceylan S, van Driel M et al (2021) Upper mantle structure of Mars from InSight seismic data. Science 373(6553):434–438
Khan A, Maclennan J, Taylor SR, Connolly JAD (2006) Are the Earth and the Moon compositionally alike? Inferences on lunar composition and implications for lunar origin and evolution from geophysical modeling. J Geophys Res Planet 111:E05005. https://doi.org/10.1029/2005JE002608
Khurana KK, Jia X, Kivelson MG, Nimmo F, Schubert G, Russell CT (2011) Evidence of a global magma ocean in Io’s interior. Science 332(6034):1186–1189
King SD, Lee C, Van Keken PE, Leng W, Zhong S, Tan E et al (2010) A community benchmark for 2-D Cartesian compressible convection in the Earth’s mantle. Geophys J Int 180(1):73–87
Kivelson M et al (1996) Discovery of Ganymede’s magnetic field by the Galileo spacecraft. Nature 384:537–541
Kivelson MG, Khurana KK, Volwerk M (2002) The permanent and inductive magnetic moments of Ganymede. Icarus 157:507–522
Kivelson MG, Bagenal F, Kurth WS, Neubauer FM, Paranicas C, Saur J (2004) Magnetospheric interactions with satellites. In: Bagenal F, Dowling TE, McKinnon WB (eds) Jupiter. The planet, satellites and magnetosphere, vol 1. Cambridge planetary science, Cambridge University Press, pp 513–536
Kminek G, Meyer MA, Haltigin T et al (2021) Mars Sample Return Science Planning Group phase 2 (MSPG2): overview and interim report. Lunar Planet Sci Conf 52:2548
Knapmeyer-Endrun B, Panning MP, Bissig F, Joshi R, Khan A, Kim D et al (2021) Thickness and structure of the martian crust from InSight seismic data. Science 373(6553):438–443
Knibbe JS, Rivoldini A, Luginbuhl SM, Namur O, Charlier B, Mezouar M et al (2021) Mercury’s interior structure constrained by density and P-wave velocity measurements of liquid Fe-Si-C alloys. J Geophys Res Planets. 126:e2020JE006651
Konopliv AS, Yoder C (1996) Venusian k2 tidal Love number from Magellan and PVO tracking data. Geophys Res Lett 23:1857–1860
Konopliv AS, Park RS, Yuan D-N, Asmar SW, Watkins MM, Williams JG, Fahnestock E et al (2014) High-resolution lunar gravity fields from the GRAIL primary and extended missions. Geophys Res Lett 41:1452. https://doi.org/10.1002/2013GL059066
Konopliv AS, Park RS, Folkner WM (2016) An improved JPL Mars gravity field and orientation from Mars orbiter and lander tracking data. Icarus 274:253–260
Konopliv AS, Park R, Ermakov A (2020) The Mercury gravity field, orientation, love number, and ephemeris from the messenger radiometric tracking data. Icarus 335:113386
Konopliv AS, Park RS, Rivoldini A, Baland R-M, Le Maistre S, Van Hoolst T et al (2020) Detection of the Chandler wobble of Mars from orbiting spacecraft. Geophys Res Lett 47:e2020GL090568. https://doi.org/10.1029/2020GL090568
Kuskov OL, Kronrod VA (2005) Internal structure of Europa and Callisto. Icarus 177(2):550–569
Laneuville M, Wieczorek MA, Breuer D, Aubert J, Morard G, Rückriemen T (2014) A long–lived lunar dynamo powered by core crystallization. Earth Planet Sci Lett 401:251–260
Langlais B et al (2019) A new model of the crustal magnetic field of Mars using MGS and MAVEN. J Geophys Res 124:1542–1569
Langseth MG, Keim SJ, Peters K (1976) Revised lunar heat flow values. In: Proceedings of the Lunar and Planetary Science Conference /:3143–3171.Laplace, P. S. 1805, Mécanique Cé́leste, Vol. 4
Lauretta DS, Balram-Knutson SS, Beshore E, Boynton WV, d’Aubigny CD, DellaGiustina DN et al (2017) OSIRIS-REx: sample return from asteroid (101955) Bennu. Space Sci Rev 212(1):925–984
Le Bars M, Wieczorek MA, Karatekin Ö, Cébron D, Laneuville M (2011) An impact-driven dynamo for the early Moon. Nature 479(7372):215–218
Lin YH, Tronche EJ, Steenstra ES, van Westrenen W (2017a) Evidence for an early wet Moon from experimental crystallisation of the lunar magma ocean. Nat Geosci 10:14–18
Lin Y, Tronche EJ, Steenstra ES, van Westrenen W (2017b) Experimental constraints on the solidification of a nominally dry lunar magma ocean. Earth Planet Sci Lett 471:104–116
Lin Y, Hui H, Xia X, Shang S, van Westrenen W (2020) Experimental constraints on the solidification of a hydrous lunar magma ocean. Meteor Planet Sci 55:207–230
Lognonné P (2005) Planetary seismology. Annu Rev Earth Planet Sci 33:571–604
Lognonné P, Johnson C (2015) Planetary seismology. In: Schubert G, Spohn T (eds) Treatise in geophysics, vol 10, 2nd edn. Elsevier, Amsterdam. https://doi.org/10.1016/B978-0-444-53802-4.00167-6
Lognonné P, Banerdt WB, Giardini D et al (2019) SEIS: InSight’s seismic experiment for internal structure of Mars. Space Sci Rev. https://doi.org/10.1007/s11214-018-0574-6
Lognonné P, Banerdt WB, Pike WT, Giardini D, Christensen U, Garcia RF et al (2020) Constraints on the shallow elastic and anelastic structure of Mars from InSight seismic data. Nat Geosci 13(3):213–220
Lucazeau F (2019) Analysis and mapping of an Updated Terrestrial Heat Flow Data Set. Geochem Geophys Geosys 20:4001–4024. https://doi.org/10.1029/2019gc008389
Margot JL, Peale SJ, Jurgens RF, Slade MA, Holin I~V, (2007) Large longitude libration of Mercury reveals a molten core. Science 316(5825):710–714
Margot JL et al (2018) Mercury’s internal structure. In: Solomon SC, Anderson BJ, Nittler LR (eds) Mercury: the view after MESSENGER. Cambridge University Press, Cambridge, pp 85–113
Margot JL, Campbell DB, Giogini JD, Jao JS, Snedeker LG, Ghigo FD, Bonsall A (2021) Spin state and moment of inertia of Venus. Nat Astron 5:676–683
Martinot M, Flahaut J, Besse S, Quantin-Nataf C, van Westrenen W (2018) Compositional variations in the vicinity of the lunar crust-mantle interface from Moon Mineralogy Mapper data. J Geophys Res-Planets 123:3220–3237
Martinot M, Flahaut J, Besse S, Quantin-Nataf C, van Westrenen W (2020) Mineralogical survey of the Anorthositic Feldspathic Highlands Terrane crust using Moon Mineralogy Mapper data. Icarus 345:113747
Matson DL, Spilker LJ, Lebreton JP (2003) The Cassini/Huygens mission to the Saturnian system. The Cassini-Huygens Mission. pp 1–58.
Matsuyama I, Nimmo F, Keane JT, Chan NH, Taylor GJ, Wieczorek MA, Kiefer WS, Williams JG (2016) GRAIL, LLR, and LOLA constraints on the interior structure of the Moon. Geophys Res Lett 43:8365–8375
Maurice M, Tosi N, Schwinger S, Breuer D, Kleine T (2020) A long-lived magma ocean on a young Moon. Sci Adv 6:eaba8949. https://doi.org/10.1126/sciadv.aba8949
Mazarico E, Genova A, Goossens S, Lemoine FG, Neumann GA, Zuber MT, Smith DE, Solomon SC (2014) The gravity field, orientation, and ephemeris of Mercury from MESSENGER observa- tions after three years in orbit. J Geophys Res Planets. 119(12):2417–2436. https://doi.org/10.1002/2014JE004675
McGovern PJ, Solomon SC, Smith DE, Zuber MT, Simons M, Wieczorek MA et al (2004) Correction to Localized gravity/topography admittance and correlation spectra on Mars: implications for regional and global evolution. J Geophys Res Planets 109(E7). https://doi.org/10.1029/2004JE002286
McKinnon WB (2015) Effect of Enceladus’s rapid synchronous spin on interpretation of Cassini gravity. Geophys Res Lett 42:2137–2143
McKinnon WB, Zahnle KJ, Ivanov BA, Melosh HJ (1997) Cratering on Venus: Models and observations. In: Bougher SW, Hunten DM, Philips RJ (eds) Venus II: geology, geophysics, atmosphere, and solar wind environment. University of Arizona Press, pp 969
Mcnutt MK (1984) Lithospheric flexure and thermal anomalies. J Geophys Res Solid Earth. 89(13):11180–11194
Mitchell DL et al (2007) A global map of Mars’ crustal magnetic field based on electron reflectometry. J Geophys Res 112:E01002
Mittelholz A, Johnson CL, Feinberg JM, Langlais B, Phillips RJ (2020) Timing of the martian dynamo: new constraints for a core field 4.5 and 3.7 Ga ago. Sci Adv 6(18). https://doi.org/10.1126/sciadv.aba0513
Mitchell DL et al (2008) Global mapping of lunar crustal magnetic fields by Lunar Prospector. Icarus 194:401–409
Moore WB, Schubert G (2000) The tidal response of Europa. Icarus 147:317–319
Moore WB, Schubert G (2003) The tidal response of Ganymede and Callisto with and without liquid water oceans. Icarus 123:223–226
Moresi L, Solomatov V (1998) Mantle convection with a brittle lithosphere: thoughts on the global tectonic styles of the Earth and Venus. Geophys J Inter 133(3):669–682
Morrison SM, Downs RT, Blake DF et al (2018) Crystal chemistry of Martian minerals from Bradbury Landing through Naukluft Plateau, Gale crater, Mars. American Mineralogist. https://doi.org/10.2138/am-2018-6124
Morschhauser A, Grott M, Breuer D (2011) Crustal recycling, mantle dehydration, and the thermal evolution of Mars. Icarus 212(2):541–558
Mueller N, Piqueux S, Lemmon M et al (2021) Near surface properties of Martian regolith derived from InSight HP3-RAD temperature observations during Phobos transits. Geophys. Res. Lett. 48(15):e2021GL093542
Murray CD, Dermott SF (1999) Solar System Dynamics. Cambridge University Press, Cambridge
Nakamura Y (1983) Seismic velocity structure of the lunar mantle. J Geophys Res Solid Earth 88(B1):677–686
Ness NF, Behannon KW, Lepping RP, Whang YC (1976) Observations of Mercury’s magnetic field. Icarus 28:479–488
Neumann GA, Zuber MT, Wieczorek MA et al. (2004). Crustal structure of Mars from gravity and topography. J Geophys Res Planets 109:E08002. https://doi.org/10.1029/2004JE002262
Nimmo F, Stevenson DJ (2001) Estimates of Martian crustal thickness from viscous relaxation of topography. J Geophys Res 106:5085–5098
Nittler LR et al (2011) The major-element composition of Mercury’s surface from MESSENGER X-ray spectrometry. Science 333:1847–1850
Nunn C, Garcia RF, Nakamura Y, Marusiak AG, Kawamura T, Sun D et al (2020) Lunar seismology: a data and instrumentation review. Space Sci Rev 216(5):1–39
O’Rourke JG, Gillmann C, Tackley P (2018) Prospects for an ancient dynamo and modern crustal remanent magnetism on Venus. Earth Planet Sci Lett 502:46–56
Padovan S, Margot J-L, Hauck SA II, Moore WB, Solomon SC (2014) The tides of Mercury and possible implications for its interior structure. J Geophys Res Planets 119:850–866. https://doi.org/10.1002/2013JE004459
Padovan S, Wieczorek MA, Margot J-L, Tosi N, Solomon SC (2015) Thickness of the crust of Mercury from geoid-totopography ratios. Geophys Res Lett 42:1029–1038
Padovan S, Tosi N, Plesa AC, Ruedas T (2017) Impact-induced changes in source depth and volume of magmatism on Mercury and their observational signatures. Nat Commun 8(1):1–10
Pahlevan K, Stevenson DJ (2007) Equilibration in the aftermath of the lunar-forming giant impact. Earth Planet Sci Lett 262:438–449
Panning MP, Beucler É, Drilleau M, Mocquet A, Lognonné P, Banerdt WB (2015) Verifying single-station seismic approaches using Earth-based data: Preparation for data return from the InSight mission to Mars. Icarus 248:230–242
Pavlenkova EI (1992) The Kola Superdeep drillhole and the nature of seismic boundaries. Terra Nova 4:117–123
Peale SJ (1976) Does Mercury have a molten core? Nature 262(5571):765–766
Piqueux S, Müller N, Grott M et al (2021) Soil Thermophysical properties near the InSight lander derived from 50 Sols of radiometer measurements. J. Geophys. Res. Planets 126(8):e2021JE006859
Plesa AC, Breuer D (2014) Partial melting in one-plate planets: Implications for thermo-chemical and atmospheric evolution. Planet Space Sci 98:50–65
Plesa AC, Tosi N, Grott M, Breuer D (2015) Thermal evolution and Urey ratio of Mars. J Geophys Res Planets. 120(5):995–1010
Plesa AC, Grott M, Tosi N et al (2016) How large are present-day heat flux variations across the surface of Mars? J Geophys Res Planets 121:2386–2403
Plesa AC, Bozdag E, Rivoldini A et al (2021) Seismic velocity variations in a 3D Martian mantle: implications for the InSight measurements. J Geophys Res. https://doi.org/10.1029/2020JE006755
Pommier A (2018) Influence of sulfur on the electrical resistivity of a crystallizing core in small terrestrial bodies. Earth Planet Sci Lett 496:37–46
Pommier A (2020) Experimental investigation of the effect of nickel on the electrical resistivity of Fe-Ni and Fe-Ni-S alloys under pressure. Am Miner 105(7):1069–1077
Porco CC, Helfenstein P, Thomas PC et al (2006) Cassini observes the active south pole of Enceladus. Science 311:1393–1401
Rambaux N, Van Hoolst T, Dehant V, Bois E (2007) Inertial core-mantle couplings and libration of Mercury. Astron Astrophys 468:711–719
Rambaux N, Van Hoolst T, Karatekin O (2011) Librational response of Europa, Ganymede, and Callisto with an ocean for a non-Keplerian orbit. Astron Astrophys 527:A118
Rambaux N, Castillo-Rogez J (2013) Tides on satellites of giant planets, Lecture Notes in Physics, Springer Verlag, Berlin, Vol 861, 167
Rambaux N (2014) Rotational and librational motion of solar system bodies. Proceedings of the Journées 2013 "Systèmes de référence spatio-temporels": Scientific developments from highly accurate space-time reference systems, Observatoire de Paris, 16–18 September 2013, Edited by Nicole Capitaine, ISBN 978-2-901057-69-7, pp 235–240
Rapp JF, Draper DS (2018) Fractional crystallization of the lunar magma ocean: updating the dominant paradigm. Meteor Planet Sci 53:1432–1455
Raymond SN, Morbidelli A (2020) Planet formation: Key mechanisms and global models. http://arxiv.org/abs/2002.05756v1
Reasenberg RD (1977) The moment of inertia and isostasy of Mars. J Geophys Res 82:369–375
Richmond NC, Hood LL (2008) A preliminary global map of the vector lunar crustal magnetic field based on Lunar Prospector magnetometer data. J Geophys Res 113:E02010
Righter K (2019) Volatile element depletion of the Moon—The roles of precursors, post-impact disk dynamics, and core formation. Sci Adv 5:eaau7658
Rivoldini A, Van Hoolst T (2013) The interior structure of Mercury constrained by the low-degree gravity field and the rotation of Mercury. Earth Planet Sci Lett 377–378:62–72
Rivoldini A, Van Hoolst T, Verhoeven O (2009) The interior structure of Mercury and its core sulfur content. Icarus 201(1):12–30
Rivoldini A, Van Hoolst T, Verhoeven O, Mocquet A, Dehant V (2011) Geodesy constraints on the interior structure and composition of Mars. Icarus 213(2):451–472
Rolf T, Steinberger B, Sruthi U, Werner SC (2018) Inferences on the mantle viscosity structure and the post-overturn evolutionary state of Venus. Icarus 313:107–123
Romanowicz, BA, Dziewonski, AM, G. Schubert, eds (2015) Treatise on Geophysics, Vol. 1. Deep Earth Seismology, Elsevier, Amsterdam
Rosenblatt P, Dumoulin C, Marty JC, Genova A (2021) Determination of Venus’ interior structure with EnVision. Remote Sens 13:1624. https://doi.org/10.3390/rs13091624
Rückriemen T, Breuer D, Spohn T (2018) Top-down freezing in a Fe–FeS core and Ganymede’s present-day magnetic field. Icarus 307:172–196
Saunders RS, Spear AJ, Allin PC, Austin RS, Berman AL, Chandlee RC et al (1992) Magellan mission summary. J Geophys Res Planets 97(E8):13067–13090
Saur J et al (2015) The search for a subsurface ocean in Ganymede with hubble space telescope observations of its auroral ovals. J Geophys Res Space Physics 120:1715–1737. https://doi.org/10.1002/2014JA020778
Schubert G (1979) Subsolidus convection in the mantles of the terrestrial planets. Annu Rev Earth Planet Sci 7:289–342
Schubert G, Spohn T (1990) Thermal history of Mars and the sulfur content of its core. J Geophys Res. https://doi.org/10.1029/JB095iB09p14095
Schubert G, Spohn T, Reynolds RT (1986) Thermal histories, compositions, and internal structures of the moons of the solar system. In: Burns JA, Matthews M (eds) Satellites. University of Arizona Press, Tucson, pp 224–292
Schubert G, Zhang K, Kivelson MG, Anderson JD (1996) The magnetic field and internal structure of Ganymede. Nature 384:544–545
Schubert G, Anderson JD, Spohn T, McKinnon WB (2004) Interior composition, structure, and dynamics of the Galilean Satellites. In: Bagenal F, Dowling TE, McKinnon WB (eds) Jupiter: the planet, satellites, and magnetosphere. Cambridge University Press, Cambridge, pp 281–306
Shalygin EV, Basilevsky AT, Markiewicz WJ, Titov DV, Kreslavsky MA, Roatsch T (2012) Search for ongoing volcanic activity on Venus: case study of Maat Mons, Sapas Mons and Ozza Mons volcanoes. Planet Space Sci 73(1):294–301
Showman AP, Malhotra R (1997) Tidal evolution into the Laplace resonance and the resurfacing of Ganymede. Icarus 127:93–111
Siegfried RW II, Solomon SC (1974) Mercury: Internal structure and thermal evolution. Icarus 23: 192-205
Sleep NM (1994) Martian plate tectonics. J Geophys Res. https://doi.org/10.1029/94JE00216
Smith DE, Zuber MT, Frey HV, Garvin JB, Head JW, Muhleman DO et al (2001) Mars orbiter laser altimeter: experiment summary after the first year of global mapping of Mars. J Geophys Res Planets 106(E10):23689–23722
Smrekar SE, Phillips RJ (1991) Venusian highlands: Geoid to topography ratios and their implications. Earth Planet Sci Lett 107(3–4):582–597
Smrekar SE, Stofan ER, Mueller N et al (2010) Recent hotspot volcanism on Venus from VIRTIS emissivity data. Science 328(5978):605–608
Smrekar SE, Lognonne P, Spohn T et al (2019) Pre mission InSights on the interior of Mars. Space Sci Rev. https://doi.org/10.1007/s11214-018-0563-9
Sohl F, Schubert G (2015) Interior structure, composition and mineralogy of the terrestrial planets. In: Schubert G, Spohn T (eds) Treatise on Geophysics, vol 10, 2nd edn. Planets and Moons. Oxford, Elsevier, pp 23–64
Sohl F, Spohn T (1997) The interior structure of Mars: Implications from SNC meteorites. J Geophys Res Planets 102(E1):1613–1635
Sohl F, Spohn T, Breuer D, Nagel K (2002) Implications from Galileo observations on the interior structure and chemistry of the Galilean satellites. Icarus 157:104–119
Sohl F, Schubert G, Spohn T (2005) Geophysical constraints on the composition and structure of the Martian interior. J Geophys Res Planets 110(E12).
Spohn T, Sohl F, Breuer D (1998) Mars. Astrophys Rev 8:181–235
Spohn T, Grott M, Smrekar SE et al (2018) The heat flow and physical properties package for the InSight mission. Space Sci Rev. https://doi.org/10.1007/s11214-018-0531-4
Spohn T, Hudson TH, Marteau E et al. (2021a) The InSight HP3 penetrator (Mole) on Mars: Soil properties derived from the penetration attempts and related activities. Submitted to Space Sci Rev.
Spohn T, Hudson TH, Wiite L et al. (2021) The InSight-HP3 Mole on Mars: Lessons learned from attempts to penetrate to depth in the Martian soil. Submitted to Adv Space Res
Stähler SC, Khan A, Banerdt WB, Lognonné P, Giardini D, Ceylan S et al (2021) Seismic detection of the Martian core. Science 373(6553):443–448
Stamenkovic V, Breuer D, Spohn T (2011) Thermal and transport properties of mantle rock at high pressure: applications to super-Earth. Icarus. https://doi.org/10.1016/j.icarus.2011.09.030
Stark A, Oberst J, Preusker F, Peale SJ, Margot SJ, Phillips RJ, Neumann GA, Smith DE, Zuber MT, Solomon SC (2015) First MESSENGER orbital observations of Mercury’s librations. Geophys Res Lett 42(19):7881–7889. https://doi.org/10.1002/2015gl065152.ISSN00948276
Steenstra ES, van Westrenen W (2018) A synthesis of geochemical constraints on the inventory of light elements in the core of Mars. Icarus 315:69–78
Steenstra ES, Rai N, Knibbe JS, Lin YH, van Westrenen W (2016) New geochemical models of core formation in the Moon from metal–silicate partitioning of 15 siderophile elements. Earth Planet Sci Lett 441:1–9
Steenstra ES, Lin Y, Dankers D, Rai N, Berndt J, Matveev S, van Westrenen W (2017a) The lunar core can be a major reservoir for volatile elements S, Se Te and Sb. Nat Sci Rep 7:14552
Steenstra ES, Lin YH, Rai N, Jansen M, van Westrenen W (2017b) Carbon as the dominant light element in the lunar core. Am Mineral 102:92–97
Steenstra ES, Berndt J, Klemme S, Fei Y, van Westrenen W (2020) A possible high-temperature origin of the Moon and its geochemical consequences. Earth Planet Sci Lett 538:116222
Steinbach V, Hansen U, Ebel A (1989) Compressible convection in the earth’s mantle: a comparison of different approaches. Geophys Res Lett 16(7):633–636
Steinbrügge G, Dumberry M, Rivoldini A, Schubert G, Cao H, Schroeder DM, Soderlund KM (2021) Challenges on Mercury’s inteiror structure posed by the new measurements of its obliquity and tides. Geophys. Res. Lett. 48:e2020GL089895
Stevenson DJ, Spohn T, Schubert G (1983) Magnetism and thermal evolution of the terrestrial planets. Icarus 54(3):466–489
Strom RG, Schaber GG, Dawson DD (1994) The global resurfacing of Venus. J Geophys Res Planet. 99(E5):10899–10926
Stys S, Dumberry M (2020) A past lunar dynamo thermally driven by the precession of its inner core. J. Geophys. Res. Planets 125:e2020JE006396
Surkov YuA, Barsukov VL, Moskalyeva LP et al (1984) New data on the composition, structure, and properties of Venus rock obtained by Venera 13 and Venera 14. J Geophys Res Suppl 89:B393–B402
Svedhem H, Titov D, Taylor F, Witasse O (2009) Venus Express mission. J Geophys Res Planets 114:E00B33. https://doi.org/10.1029/2008JE003290
Takahashi F, Shimizu H, Tsunakawa H (2019) Mercury’s anomalous magnetic field caused by a symmetry-breaking self-regulating dynamo. Nat Comm 10:208
Taylor SR (2016) Lunar science: A post-Apollo view: Scientific results and insights from the lunar samples. Elsevier, Amsterdam
Thiriet M, Breuer D, Michaut C, Plesa AC (2019) Scaling laws of convection for cooling planets in a stagnant lid regime. Phys Earth Planet Int 286:138–153
Thomas PC, Tajeddine R, Tiscareno MS et al (2016) Enceladus’s measured physical libration requires a global subsurface ocean. Icarus 264:37–47
Thurber C, Ritsema J (2015) Theory and observations: Seismic tomography and inverse methods. In: Schubert G, Dziewonski AM, Romanowicz BA (eds) Treatise in Geophysics, vol 1, 2nd edn. Elsevier, Amsterdam
Tian Z, Zuber MT, Stanley S (2015) Magnetic field modeling for Mercury using dynamo models with a stable layer and laterally variable heat flux. Icarus 260:263–268
Tikoo et al (2014) Decline of the lunar core dynamo. Earth Planet Sci Lett 404:89–97
Tikoo SM, Weiss BP, Shuster DL, Suavet C, Wang H, Grove TL (2017) A two-billion-year history for the lunar dynamo. Sci Adv 3:e1700207
Toksöz MN, Dainty AM, Solomon SC, Anderson KR (1974) Structure of the Moon. Rev Geophys 12(4):539–567
Tosi N, Grott M, Plesa AC, Breuer D (2013) Thermochemical evolution of Mercury’s interior. J Geophys Res Planets. 118(12):2474–2487
Tosi N, Padovan S (2021) Mercury, Moon, Mars: surface expressions of mantle convection and interior evolution of stagnant-lid bodies. In: Marquardt H, Ballmer M, Cottar S, Konter J (eds) Mantle convection and surface expressions, AGU monograph series. https://doi.org/10.1002/9781119528609.ch17
Trinh A (2019), Modelling the interior of Enceladus: A combined view from gravity, topography, and libration, Ph.D. thesis, Université catholique de Louvain, Louvain-la-Neuve, Belgium, http://hdl.handle.net/2078.1/216772.
Valencia D, Sasselov DD, O’Connel RJ (2006) Radius and structure models of the first super-Earth Planet. Astrophys J 656:545–551
Van Hoolst T, Jacobs C (2003) Mercury’s tides and interior structure. J Geophys Res 108(E11):5121. https://doi.org/10.1029/2003JE002126
Van Hoolst T, Rambaux N, Karatekin Ö, Dehant V, Rivoldini A (2008) The librations, shape, and icy shell of Europa. Icarus 195(1):386–399
Van Hoolst T, Rivoldini A, Baland RM, Yseboodt M (2012) The effect of tides and an inner core on the forced longitudinal libration of Mercury. Earth Planet Sci Lett 333:83–90. https://doi.org/10.1016/j.epsl.2012.04.014
Van Hoolst T, Baland R-M, Trinh A (2013) On the librations and tides of large icy satellites. Icarus 226:299–315. https://doi.org/10.1016/j.icarus.2013.05.036
Van Hoolst T, Baland RM, Trinh A (2016) The diurnal libration and interior structure of Enceladus. Icarus 277:311–318
Van Hoolst T, Baland R-M, Trinh A, Yseboodt M, Nimmo F (2020) The librations, tides, and interior structure of Io. J Geophys Res Planets 125:e2020JE006473. https://doi.org/10.1029/2020JE006473
Van Kan PM, Sanloup C, Sator N, Guillot B, Tronche EJ, Perrillat J-P, Mezouar M, Rai N, van Westrenen W (2012) Neutral buoyancy of titanium-rich melts in the deep lunar interior. Nat Geosci 5:186–189
van Westrenen W, Li J, Fei Y, Frank MR, Funakoshi K, Hellwig H, Komabayashi T, Mibe K, Minarik WG, Van Orman JA, Watson HC, Schmidt MW (2005) Thermoelastic properties of (Mg0.64Fe0.36)O ferropericlase based on in situ X-ray diffraction to 26.7 GPa and 2173 K. Phys Earth Planet Int 151:163–176
Vance S, Bouffard M, Choukroun M, Sotin C (2014) Ganymede’s internal structure including thermodynamic of magnesium sulfate oceans in contact with ice. Planet Space Sci 96:62–70
Verma AK, Margot JL (2016) Mercury’s gravity, tides, and spin from MESSENGER radio science data. J Geophys Res Planets. 121(9):1627–1640. https://doi.org/10.1002/2016JE005037
Viswanathan V, Rambaux N, Fienga A, Laskar J, Gastineau M (2019) Observational constraint on the radius and oblateness of the lunar core-mantle boundary. Geophys Res Lett 46(13):7295–7303
Wahr JM, Zuber MT, Smith DE, Lunine JI (2006) Tides on Europa, and the thickness of Europa’s icy shell. J Geophys Res 111:E12005. https://doi.org/10.1029/2006JE002729
Way M, Del Genio AD, Kliang NL et al (2016) Was Venus the first habitable world of our solar system? Geophys Res Lett. https://doi.org/10.1002/2016GL069790
Weber RC, Lin PY, Garnero EJ, Williams Q, Lognonne P (2011) Seismic detection of the lunar core. Science 331:309–312
Weiss BP, Tikoo SM (2014) The lunar dynamo. Science 346:1246753
Weiss BP et al (2010) Paleomagnetic records of meteorites and early planetesimal differentiation. Space Sci Rev 152:341–390
Weller MB, Kiefer WS (2020) The physics of changing tectonic regimes: Implications for the temporal evolution of mantle convection and the thermal history of Venus. J Geophys Res Planet. 125(1):e2019JE005960
Wells RA (1979) Geophysics of Mars. Elsevier, Amsterdam
Wieczorek M, Phillips R (2000) The Procellarum KREEP Terrane: implications for mare volcanism and lunar evolution. J Geophys Res 105:20417–20430
Wieczorek MA, Jolliff BL, Khan A, Pritchard ME, Weiss BP, Williams JG et al (2006) The constitution and structure of the lunar interior. Rev Mineral Geochem 60(1):221–364
Wieczorek MA, Zuber MT (2004). Thickness of the Martian crust: improved constraints from geoid‐to‐topography ratios. J Geophys Res Planets 109:E01009. https://doi.org/10.1029/2003JE002153
Williams JG, Boggs DH, Yoder CF, Ratcliff JT, Dickey JO (2001) Lunar rotational dissipation in solid body and molten core. J Geophys Res Planets 106(E11):27933–27968
Williams JG, Konopliv AS, Boggs DH, Park RS, Yuan DN, Lemoine FG et al (2014) Lunar interior properties from the GRAIL mission. J Geophys Res Planets 119(7):1546–1578
Witasse O (2020) JUICE (Jupiter Icy Moon Explorer): a European mission to explore the emergence of habitable worlds around gas giants. (No. EPSC2020-76). Copernicus Meetings
Yoshizaki T, McDonough WF (2020) The composition of Mars. Geochim Cosmochim Acta 273:137–162
Youdin AN (2011) The exoplanet census: a general method, applied to Kepler. Astrophys J. https://doi.org/10.1088/0004-637X/742/1/38
Yu S, Tosi N, Schwinger S, Maurice M, Breuer D, Xiao L (2019) Overturn of ilmenite-bearing cumulates in a rheologically weak lunar mantle. J Geophys Res Planets 124:418–436
Zhang N, Parmentier EM, Liang Y (2013) A 3-D numerical study of the thermal evolution of the Moon after cumulate mantle overturn: the importance of rheology and core solidification. J Geophys Res Planets 118:1789–1804
Zhao Y, de Vries J, van den Berg AP, Jacobs MHG, van Westrenen W (2019) The participation of ilmenite-bearing cumulates in lunar mantle overturn. Earth Planet Sci Lett 511:1–11
Zhu W, Dong S (2021) Exoplanet statistics and theoretical implications. http://arxiv.org/abs/2103.02127v1
Zou Y, Zhu Y, Bai Y, Wang L, Jia Y, Shen W et al (2021) Scientific objectives and payloads of Tianwen-1, China’s first Mars exploration mission. Adv Space Res 67(2):812–823
Acknowledgements
We thank Philippe Lognonné and an anonymous reviewer for their careful and constructive criticism, which contributed significantly to the improvement of this manuscript.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Breuer, D., Spohn, T., Van Hoolst, T. et al. Interiors of Earth-Like Planets and Satellites of the Solar System. Surv Geophys 43, 177–226 (2022). https://doi.org/10.1007/s10712-021-09677-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10712-021-09677-x