Abstract
Geomagnetic observations from satellites have highlighted interannual variations in the rate of change of the magnetic field originating from Earth’s core. Downward continued to the core surface, these variations primarily show up in the equatorial belt. First, we recall the main characteristics of these patterns, addressing their spatio-temporal resolution, as seen from field models. We then review the several dynamical frameworks proposed so far to understand and model these observations, which populate the frequency spectrum on time scales close to the Alfvén time \(\tau _A\approx 2\) yr, much shorter than the vortex turnover time \(\tau _U\approx 150\) yr in Earth’s core. Magnetic–Archimedes–Coriolis (MAC) waves in a stratified layer below the core surface constitute a first possibility in the case of a sub-adiabatic heat flux at the top of the core. Their period may reach the interannual range for a layer thickness less than \(\approx 30\) km, for a buoyancy frequency of the order of the Earth’s rotation rate. An alternative has been proposed in a context where the Coriolis force dominates the momentum balance, rendering transient motions almost invariant along the rotation axis (quasi-geostrophy, QG). Torsional Alfvén waves, consisting of axisymmetric QG motions, operate at periods similar to the Alfvén time, but are not sufficient to explain the interannual field changes, which require non-axisymmetric motions. QG Alfvén waves (involving the Coriolis and magnetic forces) constitute another possibility, with inertia playing an important role. They have been detected in the latest generation of geodynamo simulations, propagating in a ubiquitous manner at a speed slightly less than the Alfvén velocity. They are localized in longitude and as a result their description requires high azimuthal wavenumber. But the branch of QG waves with large extent in azimuth is also worth considering, as it reaches interannual periods as their radial wavenumber is increased. The excitation of such high-frequency dynamics is discussed with respect to the temporal spectrum of the core field, which presents a slope \(\sim f^{-4}\) for periods approximately between \(\tau _A\) and \(\tau _U\). We finally summarize the main geophysical implications of the existence of this interannual dynamics on core and lower mantle structure, properties, and dynamics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Article Highlights
-
The geomagnetic field originating from Earth's core, recorded from ground-based observatories and satellites, show interannual changes, generally stronger towards the core equator
-
Major dynamical interpretations of these are based on magneto-hydro-dynamics waves, either involving a stratified layer at the top of the core, or within a quasi-geostrophic framework via Alfvén and Magneto-Coriolis modes
-
The observed and modeled interannual dynamics in the core brings geophysical constraints on the evolution of the Earth, and on the mechanisms that sustain the geodynamo
1 Observational Constraint on Rapid Magnetic Field Changes
The Earth’s magnetic field \(\mathbf{B}(t)\) evolves on long time scales compared to human lifetimes. In order to reveal changes of the field on faster time scales, it is common to examine the first time derivative of the field, \(\partial \mathbf{B}(t)/\partial t\). We will refer to this quantity as the secular variation (SV) of the geomagnetic field. Rapid changes in the observed geomagnetic field originating from the core were first highlighted in ground-based records. They were presented as isolated events called geomagnetic jerks, characterized by abrupt changes in the rate of change of the SV (see Mandea et al. 2010, for a review). With improvements in the data quality, such events have been isolated more and more frequently (e.g., Brown et al. 2013), thus questioning the pertinence of a search for features localized in time.
The past two decades of magnetic observations from space, thanks to their global coverage, have highlighted interannual fluctuations of the geomagnetic field (for a review, see Lesur et al. 2021). These were put to the fore via the secular acceleration (SA) \(\partial ^2\mathbf{B}/\partial t^2\) (Lesur et al. 2008). The SA intensity averaged over the core–mantle boundary (CMB) presents pulses with an apparent periodicity of \(\approx 3\) years (Chulliat and Maus 2014; Finlay et al. 2016). In between two SA pulses, jerks seem more frequent, and a periodicity of \(\approx 6\) yr in the abundance of jerk events recorded from the ground is indeed advocated by Soloviev et al. (2017).
But the characterization of SA/jerk events is biased in several ways. First, their initial detection in ground stations was concentrated towards continental areas, and in particular over Europe. This region is not necessarily representative of the general SA behaviour when observed all over the globe from satellites (Hammer et al. 2021a). Second, the description of SA events via a global norm may average events localized in distinct areas at the core surface, and which might be dynamically independent. This effect is illustrated in Fig. 1: over the satellite era, the equatorial belt and regions centred around the meridian at 100\(^{\circ }\)E carry most of the subdecadal SV changes once downward continued at the CMB. Our difficulty to interpret the observed SA is magnified by the ill-posedness of the geomagnetic inverse problem: as the signal is recorded away from the source (the CMB), rapid variations in small length scales patterns are sacrificed. This effect, associated with the dominance of external signals towards high frequencies, limits the space-time resolution of the SA in core field models (Gillet 2019).
Mollweide projection of the r.m.s. radial SV at subdecadal periods (filtered at periods shorter than 9 yr), at the Earth’s surface (top) and at the CMB (bottom), for the CHAOS-7 field model over 2000–2020 (Finlay et al. 2020)
In order to illustrate the limits of resolution of the field models, we superimpose in Fig. 2 SV Gauss coefficients for several models (quantities that are often used as ‘observations’ for the recovery of core dynamics). We consider here three models built using different philosophies, all considering both ground-based and satellite data:
-
CHAOS-7 (Finlay et al. 2020) is a field model focalized on the satellite era (1998–2021, including data from Oersted, SAC-C, CHAMP, CryoSat-2 and Swarm missions). Its core field model, projected onto splines, is co-estimated together with models of the static lithospheric field and of the low-degree magnetospheric field (plus the associated induced response in the mantle, subject to a model of mantle conductivity). The ionospheric field contribution is not co-estimated. Being constructed upon adjusted regularizations, CHAOS-7 is not provided with uncertainties.
-
COV-OBS-x2 (Huder et al. 2020) covers the entire observatory era since 1840. Satellite data are considered by means of virtual observatories (Hammer et al. 2021a). The core evolution is co-estimated with the magnetospheric external dipole in dipole coordinates. It is also projected onto splines, but with a longer (2-yr) knot spacing. This compromise, chosen so as to accommodate periods with much different data coverage, renders impossible the description of fluctuations at periods shorter than 3 years or so (Pick et al. 2019). The a priori information added to reduce the non-uniqueness of the inverse problem is based on stochastic processes compatible with the temporal spectrum of the field. Realistic model uncertainties can thus be extracted from the posterior covariance matrix.
-
MCM (Ropp et al. 2020) covers the satellite era. Based on a Kalman filter and a correlation-based method (Holschneider et al. 2016), it considers data by bins of 3 months, co-estimating sequentially the core field and its rate of change, the static lithospheric field, as well as the magnetospheric fields. An extra source internal to the satellites and external to the core (and a priori independent from other sources) is also incorporated, possibly corresponding to the induced and/or ionospheric fields. The correlation-based methods come with uncertainty estimations.
Although for many coefficients (e.g. \({\dot{g}}_1^1\), \({\dot{g}}_3^1\) and \({\dot{g}}_7^7\) in Fig. 2, where the dot stands for the time derivative) the overall variations are coherent within the different models, one can notice significant discrepancies on interannual time scales for Gauss coefficients of order \(m=0\) and \(m=1\) (see, for instance, \({\dot{g}}_7^0\) and \({\dot{h}}_5^1\)). This likely results from the ambiguity between rapid variations originating from the core and the ionosphere, two sources that are internal to the satellites. (So they cannot be dissociated only by a projection onto spherical harmonics.) The ionosphere dynamics is associated with a system of coordinates controlled by both the Sun–Earth direction and the magnetic field (contrary to the core field that rotates with the Earth), which results in ambiguities in near-zonal Gauss coefficients. For these coefficients, some significant fluctuations appear in the MCM core field model that are damped in CHAOS-7 and filtered in COV-OBS-x2. They lie within the uncertainty level estimated from a realistic stochastic prior for periods shorter than \(\approx 3\) years (light orange shaded area in Fig. 2). As such, they present at least a plausible reconstruction, obtained from magnetic data. Towards high spherical harmonic degrees, the solution of the geomagnetic inverse problem is not constrained enough to isolate interannual changes (see \({\dot{h}}_{12}^8\)).
SV Gauss coefficient time series for the CHAOS-7 (black, Finlay et al. 2020) MCM (cyan, Ropp et al. 2020) and COV-OBS-x2 (orange, Huder et al. 2020) field models, in nT/yr. For the MCM model the shaded area represents \(\pm 1\sigma\) errorbars. For the COV-OBS-x2 model the dark shaded area represents \(\pm 1\sigma\) error bars on the spline model (with 2-yr knot spacing), while the light shaded area incorporates modelling errors due to unmodelled rapid changes—see text for details and Huder et al. (2020)
To partly reduce these drawbacks, local methods have been developed to map regressions of the magnetic records either at satellite altitude (through geomagnetic virtual observatories or GVO, see Hammer et al. 2021a), or at the CMB (Hammer and Finlay 2019). These confirm that intense SA features occur all over the globe above the Earth’s surface (see Fig. 1), in particular also in the Pacific region, where the SV is less intense and the observational constraint from ground observations sparser. Downward continued at the CMB, SA events appear more frequent in the equatorial belt, although mid- to high-latitude signals also show up.
Time-longitude diagrams of the subdecadal SV (filtered at periods shorter than 9 yr) at the CMB at the equator (left) and at 70\(^{\circ }\)N (right), for the CHAOS-7 field model over 2000–2020 (Finlay et al. 2020)
Time-latitude diagrams of the subdecadal SV (filtered at periods shorter than 9 yr) at the CMB at 90\(^{\circ }\)E (left) and 110\(^{\circ }\)E (right), for the CHAOS-7 field model over 2000–2020 (Finlay et al. 2020)
Characterizing rapid SV changes at the CMB remains difficult today. It seems that their interpretation in terms of dynamics at the surface of the core requires a non-axisymmetric flow contribution (Chulliat and Maus 2014), which dominates over the axisymmetric part by a factor 3 to 5 in magnitude (Gillet et al. 2015; Kloss and Finlay 2019). Because of the nonlinear nature of the electromotive force at the origin of the SV, subgrid processes involving small length scales of the flow and of the magnetic field likely influence the recorded signal (Pais and Jault 2008; Gillet et al. 2019). To which extent remains debated. Should we expect drifting patterns (see Chulliat et al. 2015; Chi-Durán et al. 2020)? This seems natural as the direction of propagation distinguishes, for instance, in a quasi-geostrophic framework (see below), eastward Rossby modes from westward slow Magneto-Coriolis (MC) modes (Hide 1966; Malkus 1967). Throughout the paper, we use both waves and modes terminologies, as they appear in the literature; the latter refers to a free oscillatory response affected by the boundaries of the domain, while the former carries the meaning of propagation through the medium without care of the boundaries.
Example of time-longitude and time-latitude diagrams of the subdecadal, radial SV at the CMB are proposed in Figs. 3, 4 for the satellite era. Standing oscillations seem to show up in some places, around, for instance, 60\(^{\circ }\)W at the equator, or at 100\(^{\circ }\)E, 70\(^{\circ }\)N. They may be associated with some Eastward and/or Westward drifting (see Chi-Durán et al. 2020), although the nodes are severely affected by the spatial resolution. Oscillations spanning over almost 90 degrees in latitude (in the Northern hemisphere) also show up around 110\(^{\circ }\)E, with a clear node close to \(60^{\circ }\)N. Interestingly, the picture is rather different just 20\(^{\circ }\) away to the East, where instead a latitudinal equatorward drift seems to occur at a speed of \(\approx 10^{\circ }\)/yr (or 600 km/yr) at the CMB (see Fig. 4). This is orders of magnitudes larger than the fluid flow velocity within the core (some 10 km/yr) and may require wave propagation.
However, the recovered periods might be biased when performing analyses on SV series filtered in time (or on the SA, which implicitly contains a high-pass filter). Biases may also show up due to spatial filtering, because the SV and SA spatial spectra are blue at the CMB (their power increases with increasing wavenumber), and the interannual small length scale SA is not well constrained by data. This is further enhanced by the reduced time resolution (see for instance the analysis of GVO data by Domingos et al. 2019).
The aim of this paper is not to replicate the thorough reviews by Finlay et al. (2010); Jault and Finlay (2015), on which we will lean on concerning the physics at work in the presence in particular of both global rotation and magnetic field. Instead we propose an updated discussion that integrates the latest physical analyses pertinent to help us understand the recorded magnetic signals.
Several possible interpretations have been proposed so far. Waves in the presence of stratification, rotation and a magnetic field, the MAC waves (for Magneto–Archimedes–Coriolis, e.g., Knezek and Buffett 2018), are a natural candidate in the case of a sub-adiabatic heat flux below the CMB – an issue that is currently debated, as we shall see. Alternatively, Aubert and Finlay (2019) have detected a particular set of transient Alfvén waves (carried by the ambient magnetic field and localized in longitude) in numerical geodynamo simulations at parameters approaching Earth-like conditions. These are quasi-geostrophic (QG), i.e. almost invariant along the rotation axis due to the dominance of the Coriolis force. Finally, the dispersion relation of the QG magneto-Coriolis (MC) modes has been revisited recently. These modes, which have long been characterized by centennial and longer periods, appear to present interannual time scales as their radial complexity is increased (Gerick et al. 2021). Despite their short radial length scale, they can have large latitudinal extent in the equatorial region. They may thus constitute the elementary bricks needed to understand the searched interannual dynamics.
The present paper is organized as follows. In Sect. 2 we review several dynamical models candidate to explain the rapid SV signal originating from the core, starting from the primitive equations (Sect. 2.1). This includes MAC waves in a stratified layer (Sect. 2.2), interannual MC modes and QG Alfvén waves (Sect. 2.3), as well as a discussion of the geomagnetic temporal spectrum (Sect. 2.4). A geophysical outlook is then provided in Sect. 3.
2 Dynamical Models Suited to Explain Rapid Magnetic Field Changes
2.1 Primitive Equations and Dimensionless Numbers
We first recall the main lines of the rotating magnetohydrodynamic (MHD) equations, applied to planetary cores. We refer, for instance, to Jones (2011) for a review. From now on we will consider both the spherical \((r,\theta ,\phi )\) and the cylindrical \((s,\phi ,z)\) coordinates systems. We use as length unit the gap D between the inner and outer cores (of radii \(r_i=1220\) km and \(r_c=3485\) km). We choose as the time unit the Alfvén time \(\tau _A=D/U_A\), with \(U_A=B_0/\sqrt{\rho \mu }\) the Alfvén speed and \(B_0\) a magnetic field intensity within the core. \(\mu\) is the magnetic permeability of Earth’s core, and \(\rho\) its density. Then, the dimensionless momentum and induction equations for a rotating shell are
where \(\mathbf{F}_L=\left( \nabla \times \mathbf{B}\right) \times \mathbf{B}\) is the Lorentz force, \(\mathbf{F}_V\) stands for extra volumetric forces (such as buoyancy), \(\Pi\) is a modified dimensionless pressure, and \(\mathbf{1}_z\) is the unit vector along the rotation axis. \(Ek = \nu / \Omega D^2\) is the Ekman number, with \(\Omega \simeq 7.3\times 10^{-5}\) s\(^{-1}\) the Earth’s rotation rate and \(\nu \simeq 10^{-6}\) m\(^2\)/s the kinematic viscosity of the fluid core (e.g., de Wijs et al. 1998). For the Earth’s core, one then obtains \(Ek\sim 10^{-15}\), meaning that viscous forces will be negligible. Two other output dimensionless numbers are: the Lehnert number \(Le=\tau _{\Omega }/\tau _A\), ratio of the time scale \(\tau _{\Omega }=1/\Omega\) associated with Earth’s rotation to the Alfvén time, and the Lundquist number \(Lu=\tau _{\eta }/\tau _A\), or the number of Alfvén times per magnetic diffusion time \(\tau _{\eta }=D^2/\eta\), with \(\eta \simeq 1\) m\(^2\)/s the magnetic diffusivity of the liquid core (e.g., Pozzo et al. 2012). The kinematic and magnetic diffusivities define the (dimensionless) magnetic Prandtl number \(P_m=\nu /\eta\). This quantity is much less than unity in liquid metals where momentum diffuses much more slowly than the magnetic field. In the Earth’s core \(P_m\approx 10^{-6}\).
Another time scale of interest is the vortex turnover time \(\tau _U=D/U\), with U the magnitude of the fluid velocity. Its comparison with \(\tau _A\) gives the Alfvén number \(Al=\tau _A/\tau _U\), and with \(\tau _{\eta }\) the magnetic Reynolds number \(R_m=\tau _{\eta }/\tau _U\). The above dimensionless numbers are recalled in Table 1. In the Earth’s core, for a field intensity deep in the fluid \(B\approx 4\) mT (Gillet et al. 2010), and a fluid flow velocity \(U\approx 15\) km/yr (e.g. Finlay et al. 2010), one gets \(\tau _A\approx 2\) yr and \(\tau _U\approx 150\) yr, so that
-
\(Lu\sim 10^5\): large length scale Alfvén waves can travel throughout the core with little effect of magnetic dissipation (with the exception of possible thin magnetic boundary layers, and in the absence of an electromagnetic coupling with the mantle).
-
\(Le\sim 10^{-4}\): inertial waves travel much faster than Alfvén waves, giving a tendency for transient flows to be organized in columns aligned with the rotation axis (or quasi-geostrophic), even in the presence of a magnetic field (Jault 2008; Gillet et al. 2011).
-
\(Al\sim 10^{-2}\): Alfvén waves travel 100 times faster than the flow, so that at large length scales the kinetic energy is \(10^4\) times less than the magnetic energy.
-
\(R_m\sim 10^3\): diffusion is subdominant in the SV budget at large length scales.
In order to close the system, the above two equations must be completed with an evolution equation for the forcing (such as an entropy equation for buoyancy) that we do not detail here. Whether or not the fluid outer core is fully convective or not is today an open question. There are indeed some evidences in favour of a sub-adiabatic heat flux within a layer below the CMB. This corresponds to a re-evaluation to higher values of the thermal conductivity of iron alloys from high pressure, high temperature experiments and ab initio calculations (Pozzo et al. 2012; Ohta et al. 2017; Li et al. 2021). These high values have been, however, disputed (see Konôpkovà et al. 2016). There is also some evidence for radial inhomogeneity in composition of the top of the core from the analysis of SmKS waves travelling in the top 200–400 km below the CMB (Helffrich and Kaneshima 2010). Kaneshima and Helffrich (2013) found than the P-wave speed is about 0.5% slower than the speed calculated for homogeneous adiabatic models close to the PREM model (Dziewonski and Anderson 1981) in this topmost layer. However, Brodholt and Badro (2017) remarked that it is difficult to construct a low velocity layer that is also gravitationally stable. They found that increasing the concentration of light elements in the iron alloy always makes the seismic velocity greater. The presence of a low velocity layer can be reconciled with ab initio calculations of the elastic parameters of iron alloys at core pressures if there is exchange of light elements across the layer. They also note that such a phenomenon may result from the history of the Earth’s evolution. Irving et al. (2018) have recently calculated the elastic parameters of a new isentropic well-mixed model of the outer core. Their model presents lower velocity and steeper velocity gradient at the top of the core than the PREM model, and it may be more easily reconciled with SmKS records. According to this work, there is no need for a compositionally distinct layer at the top of the core. The difficulty to detect seismologically a stable layer does not mean it is not present. We discuss some geodynamical implications of a possible stably stratified layer at the top of the core in Sect. 3.6.
2.2 MAC Waves in a Stratified Layer
Time changes of the Earth’s magnetic field have been interpreted as the result of wave motion within the Earth’s fluid core. Early on, the models investigated global waves for which the restoring forces are the Magnetic, Archimedes and Coriolis forces. These waves have been termed MAC waves (Braginsky 1976). The early studies dealt with models including a large-scale background magnetic field (possibly much stronger than the magnetic field at the core surface) and a large-scale density gradient. With these assumptions, MAC waves of large spatial extent in the fluid interior are found to have periods either much shorter or much larger than the typical time scale of observed SV changes. There was thus a need to close this frequency gap. It turns out that waves with periods 10–100 years can be obtained in models where the density gradient is localized in a layer adjacent to the core–mantle boundary with thickness \(H \sim 10-300\) km and buoyancy (or Brunt-Väisälä) frequency
comparable to the rotation frequency (Braginsky 1984). g(r) is the gravity acceleration, and \(\rho '(r)\) the profile of the density anomaly, with respect to a profile of stable density \(\rho (r)\). This hypothetical region at the top of the core has been termed the stratified or hidden ocean of the core (Braginsky 1993, 1998). Interestingly, this configuration is amenable to local studies in Cartesian geometry where the core–mantle boundary is approximated as a plane and only the component of the rotation vector perpendicular to the boundary is considered (Braginsky 1993). It is then possible to calculate the frequency and the damping rate of these waves without heavy computations. Analytical models are now complemented by numerical models to study MHD waves in a layer of stratified fluid decoupled from the dynamics in the core interior (Knezek and Buffett 2018). The wave properties can be computed for any configuration of the background magnetic field.
Theories of the stratified ocean of the core have paid special attention to the equatorial region where the waves can be trapped as the result of the vanishing radial component of the rotation vector at the equator (Bergman 1993). Buffett and Matsui (2019) found equatorially trapped waves with periods less than 10 years when the layer thickness H is less than 30 km. They calculated the quality factor of these waves, \(Q \sim 1\), and found them to be strongly damped. It is noteworthy that equatorially trapped boundary waves can also occur in the absence of stratification. Zhang (1992) showed that the equatorial region can act as a waveguide tube for inertial waves. He also anticipated that magnetic disturbances can similarly be concentrated in the equatorial region in the presence of a background magnetic field. More specifically, in the case of the current-free Malkus (1967) field \(\mathbf{B}_{M67}\propto s \mathbf{1}_{\phi }\), MHD and hydrodynamic solutions share the same waveforms, but with different frequencies, typically \(T<T_A\) and \(T>T_A\) for, respectively, inertial and MHD waves. The mechanism of equatorial trapping highlighted by Zhang (1992) might thus be relevant over a broad range of periods. For a given azimuthal wavenumber, Zhang (1992) focused his study on the waves with the largest length scale in the meridional plane. To some extent, Gerick et al. (2021) complemented his study and considered waves with length scales in the cylindrical radial direction smaller than in the azimuthal direction. They also found enhanced (but not focalized) energy of the waves in the equatorial region (see Sect. 2.3.3). This respect, observation of rapid changes of the Earth’s magnetic field mainly in the equatorial region of the Earth’s core surface does not necessarily point to the existence of a stratified layer at the top of the core.
Other features of the Earth’s magnetic field that can be considered as a signature of the stratified ocean have been searched for. A stably stratified layer at the top of the core would smooth out the rapidly varying and small-scale features of the Earth’s magnetic field. Gastine et al. (2020) introduced a variety of stratified layers in their dynamo model and found an upper bound on the layer thickness to reproduce the morphology of the Earth’s magnetic field, \(H < {\mathcal {D}}_p= (N/\Omega )^{-1} d_c\), where \(d_c\) is the horizontal size of the convective flow below the layer. The length \({\mathcal {D}}_p\) was obtained by Takehiro and Lister (2001) as the distance of penetration of thermal Rossby waves in the stratified layer. It holds also for general quasi-geostrophic modes (Vidal and Schaeffer 2015). Gastine et al. (2020) conclude from their analysis that the current geomagnetic field morphology is not in favour of a strong stratification below the CMB, unless a more complex physics (e.g., double diffusion) modifies their scenario. Although the morphology of the simulated geomagnetic fields seems, within some subspace, relatively insensitive to the input parameters (e.g., Christensen et al. 2010; Aubert et al. 2017), the above analysis performed at \(Ek\ge 3\times 10^{-6}\) still has to be extrapolated over several orders of magnitude in \(E_k\) towards Earth-like value.
Waves in the Earth’s core are more easily detected when their energy is predominantly magnetic as the only direct information is magnetic. The distribution of the energy of MAC waves in stratified layers among their kinetic and magnetic components is also an important property of the waves in addition to their period and their dissipation. Knezek (2019) shows an example (see his figure 3.1) where the magnetic energy is \(10^3\) times larger than the kinetic energy. However, our observations bear on the radial component of the magnetic field at the CMB. The radial field carried by the waves in the stratified layer is much weaker than the field parallel to the boundary to the point that their modelling has often used a ’pseudo-vacuum’ boundary condition on the horizontal field only (Braginsky 1998; Knezek and Buffett 2018).
Most models of MAC waves in a stratified layer next to the core–mantle boundary do not predict directly modes in the radial magnetic field but instead modes in the tangential velocity field. In this framework, the calculated velocity modes interact with the observed radial magnetic field only in a second step of the modelling to produce modes in the secular variation and in the secular acceleration (Buffett 2014; Knezek and Buffett 2018).
Excitation of MAC waves in a stably stratified layer at the top of the core remains largely an open question. Buffett and Knezek (2018) investigated linear excitation and found that Maxwell stresses yield an efficient generation mechanism with most power in the period range 30 to 100 years, long compared to the timescales discussed here. We may learn also from other fluid systems where a stratified layer is adjacent to a turbulent layer such as the Earth’s stratosphere or the Sun’s tachocline (Le Bars et al. 2020). The quasi-biennial oscillation of the Earth’s atmosphere has been much studied. It results from the vertical propagation of internal gravity waves in the stratified atmosphere where it interacts nonlinearly with the mean zonal flow. It gives us an example of a wave motion in a stratified layer with period independent of the forcing.
2.3 Quasi-Geostrophic Magnetohydrodynamics
2.3.1 Various Quasi-Geostrophic Models
Quasi-geostrophic (QG) models adopt their name from the dominant geostrophic balance between Coriolis and pressure forces of flows under rapid rotation. Flows in this balance show an alignment of the fluid columns along the axis of rotation. The reduction to a two-dimensional problem allows the investigation of flows closer to the extreme physical parameters found in Earth’s core (e.g., Guervilly et al. 2019). Originating in the atmospheric community, QG models have traditionally been developed for shallow layers, assuming that the slope of the boundary varies only slightly. Hide (1966) was the first to adapt this approach to investigate hydromagnetic modes in planetary cores and Busse (1975) first formulated a set of QG MHD equations, making use of the small-slope approximation in a rotating annulus.
A QG model usually refers to an evolution equation for a stream function \(\psi (s\,\phi ,t)\) that depends only on two spatial variables in the equatorial plane that is to be derived. There have been different approaches to arrive at such a scalar equation. The various evolution equations for \(\psi\) obtained for the different QG assumptions mentioned below are provided in Table 2. In a first family of QG models the flow is described by the evolution of the axial vorticity \(\zeta _z=\mathbf{1}_z\cdot \nabla \times {\mathbf {u}}\), averaged over the fluid column. The choice of the z-component of the vorticity equation is somewhat arbitrary yet reasonable, as the horizontal components of the vorticity are much smaller for strongly columnar flows. The evolution equation for the axial vorticity is obtained by taking the curl of the momentum equation, thus eliminating the pressure term, and averaging the z-component over the fluid column. This vorticity approach has been used widely in the literature with several small modifications, most notably the treatment of the Lorentz force, as well as the choice for the relation between the flow and the stream function, as discussed below.
In the original small-slope approximation (e.g., Busse 1975), the flow is defined as
where \(\displaystyle \beta (s) =\frac{1}{H}\frac{\mathrm {d}H}{\mathrm {d}s}\), with \(H(s)=\sqrt{r_c^2-s^2}\) the half-height of a fluid column. The equatorial part of the flow is z-invariant, while the vertical component \(u_z(s,\phi ,z,t)\) is present to satisfy the non-penetrating condition \({\mathbf {u}}\cdot {\mathbf {n}}=0\) on the top and bottom boundaries, with \({\mathbf {n}}\) the unit vector normal to the CMB. The presence of a nonzero \(u_z\) at the core surface (i.e. a nonzero boundary slope) is at the origin of the second term in the evolution equation for \(\psi\). It is the key restoring ingredient for slow (barotropic, or z-invariant) Rossby waves, also called the \(\beta\)-effect.
QG vorticity models involving (4) are by design inapplicable at the equator and a rigorous derivation for a spherical core is not at hand. Albeit the apparent invalidity of these QG models near the equator, flows within a rapidly rotating spherical core seem to remain aligned along the axis of rotation, even in the presence of a magnetic field (Jault 2008; Gillet et al. 2011). Schaeffer and Cardin (2005) derived an expression for QG velocities that takes into account the slope of the boundary in a spherical shell. (A similar formulation can be found in Becker and Salmon 1997, in an oceanographic context.) The flow is taken to be incompressible and does not penetrate the boundary. Then, with the a priori assumption that the flow is columnar (that is the horizontal components of the flow are independent of z), the velocity takes the form (Schaeffer and Cardin 2005; Bardsley 2018)
Canet et al. (2009) rewrote the signature of the magnetic force \(\mathbf{F}_L\) onto the evolution equation for \(\psi\) using z-averaged quantities for squared products of the 3-D magnetic field (e.g., \(\lbrace B_sB_\phi \rbrace (s,\phi ,t)\), see also, Jault and Finlay 2015). They were, however, unable to close the system without neglecting surface terms (because the curl and axial average do not commute, extra terms involving surface expressions of the magnetic field show up). Another route has been followed by Canet et al. (2014): using a scalar magnetic potential (in analogy to the stream function of the velocity) a closed system of equations in the equatorial plane is found (see also, Busse 1976), which makes it possible to account for magnetic diffusion. However, the description of the magnetic field by the scalar potential implies that the mantle is perfectly conducting (or \({\mathbf {B}}\cdot {\mathbf {n}} = 0\) at the CMB), forbidding any association of the core interior dynamics with magnetic field changes recorded outside the core. To address this issue, another model has been proposed by Jackson and Maffei (2020), under the formulation of Equation (5), where the z-averaging is done before taking the curl, and eliminating the pressure by using asymmetric integrals over z. With this approach, called ‘plesio-geostrophy’, they are able to derive a closed system of equations fully reduced to the equatorial plane, with the unknowns being the stream function \(\psi\) and a collection of squared products for the magnetic field. In that, they do not rely on the magnetic potential form of the magnetic field and the magnetic perturbations are continuous through the CMB.
Instead of z-averaging the axial vorticity equation, Labbé et al. (2015) found a set of equations by projecting the momentum equation on the subset of QG velocities of the form (5). With this operation the pressure term also vanishes, leading to an alternative evolution equation for \(\psi\) that is more sensitive to the slope of the spherical boundary (see Table 2). As illustrated in Fig. 5, this latter model improved upon the approximation of the slow (or columnar) 3-D inertial modes (i.e. \(\mathbf{F}_L=\mathbf{0}\)), relative to the vorticity (Maffei et al. 2017) or plesio-geostrophic (Jackson and Maffei 2020) approaches. 3D eigen solutions calculated analytically by Zhang et al. (2001) are better approximated by QG solutions for larger radial complexities. On the contrary, all QG approximations perform less well towards larger azimuthal wavenumbers, because these involve relatively larger cylindrical radial velocity.
Period of the slow inertial modes as a function of the azimuthal wavenumber m, for several radial wavenumbers N from 1 to 10. Comparison between exact 3D solutions (black) together with their analytical approximation (blue) from Zhang et al. (2001), and solutions from various derivations of the QG model: the projection method (Labbé et al. 2015, orange), the axial vorticity equation (Maffei et al. 2017, green), and plesio-geostrophy (Jackson and Maffei 2020, red). See text for details
In their study, Labbé et al. (2015) also made use of the scalar magnetic potential, to investigate magnetic modes in an annulus. More recently it has been shown that the projection method can be combined with a 3-D magnetic field that is governed by the unaltered 3-D induction equation (Gerick et al. 2021). For a spherical core this 3-D magnetic field can be matched to a potential field at the CMB using a spherical harmonic basis, linking magnetic field variations at the CMB to dynamics deep within the core. An inter-comparison of the projection-based model by Gerick et al. (2021) with the plesio-geostrophic model of Jackson and Maffei (2020), in the presence of a 3-D magnetic field, will be interesting and is expected in the near future.
The motivation for deriving such QG models in order to investigate Earth’s core dynamics is apparent in terms of reducing computational complexity. On top of this, there are several physical motivations. Among them, let us mention the possibility for QG motions to naturally produce a westward propagation, as witnessed in core flow models with the eccentric gyre (Pais and Jault 2008): it is the case for the phase velocity of slow QG MC waves (Hide 1966), with potential application to centennial field changes (Finlay and Jackson 2003), as well as for the group velocity of Rossby waves, when these present a structure elongated in the cylindrical radial direction (Bardsley 2018). More importantly when focusing on interannual changes, core-flow inversions already reveal that a large part of the flow at the core’s surface is well approximated by QG motions (e.g., Kloss and Finlay 2019). The solutions to the linearized QG equations could be used as a basis for core-flow inversions. These modes are directly coupled to the magnetic field at the core’s surface, allowing a determination of the flows and magnetic field structure deep within the core. The types of magnetic modes captured by QG models are discussed in the following.
2.3.2 Torsional Alfvén Waves
One specific family of motions, which enters the QG equations, consists of axially invariant zonal (or geostrophic) flows \(u_G(s)\). Their geometry is organized on the geostrophic cylinders \(\Sigma _G(s)\) whose axis is aligned with the Earth’s rotation vector. It appears that the projections onto such cylinders of the pressure, Coriolis and buoyancy forces vanish. Then in the absence of inertia and viscosity, it is found from Equation (1) that the Lorentz force integrated over \(\Sigma _G(s)\) must be zero. This sets Taylor (1963)’s constraint, from which a condition on the flow, knowing the three-dimensional magnetic field, can be deduced (e.g., Roberts and Wu 2014; Hardy et al. 2018).
If the core state is moved away from such a Taylor’s state, inertia will tend to drive back the cylinders to their initial position. The field induced by the perturbation generates a restoring Lorentz force, at the origin of the specific family of torsional Alfvén waves (Braginsky 1970). Their structure is organized on time-dependent geostrophic flows \(u_G(s,t)\). Their phase velocity is
so that their detection amounts to measuring an average of the background field deep in the core. For a more detailed theoretical description, we refer to Roberts and Aurnou (2012); Jault and Finlay (2015). Torsional Alfvén waves are the only large length scales Alfvén waves in the core, because any other kind of motions will be affected by the Coriolis force, giving birth instead to inertial and magneto-Coriolis modes (see below).
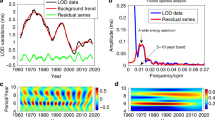
Quasi-periodic zonal motions have been detected from geomagnetic observatory records at a period close to 6 yrs. They propagate mainly outward, from the inner core to the core equator in about 4 yrs. Interpreted as torsional Alfvén waves, they led to the first indirect measure of the magnetic field within the core. A field of several mT is required (Gillet et al. 2010, 2015), a value \(\approx 10\) times larger than the strength of the field downward continued at the CMB. This value is in agreement with the ratio between the exterior and interior magnetic field strengths found in geodynamo simulations. Torsional waves have now been recovered in these computations (Wicht and Christensen 2010; Teed et al. 2014), and as the parameters are pushed towards Earth’s core conditions, they become ubiquitous (Schaeffer et al. 2017; Aubert et al. 2017; Aubert and Gillet 2021). Similarly to torsional waves reconstructed from magnetic data, in simulations they show a preference for an outward propagation, which may be explained by the moderate reflexion coefficient at the core equator, as this latter depends on \(P_m\)—or on the mantle conductance (Schaeffer et al. 2012; Schaeffer and Jault 2016).
Torsional waves in geodynamo simulations are mainly found outside the cylindrical surface tangent to the small and solid inner core (called the “tangent cylinder”). Above and below the solid inner core, one can define two potentially different velocities for the torsional waves, \(V_A^{+}(s)\) and \(V_A^{-}(s)\), depending whether the vertical average in equation (6) is performed above or below the inner core. Transmission and reflection of the torsional waves at the tangent cylinder may depend on how much \(V_A^{+}\) and \(V_A^{-}\) are different. In addition to this effect arising from the discrepancy between the squared amplitude of the magnetic field below and above the equatorial plane, there might be a geometrical effect. Torsional waves with wavelength large compared to the typical distance along which the height of the geostrophic cylinders changes may be partly reflected as the sound waves in a tube of variable section. Apart from its geometrical effect, we do not expect this boundary to have much influence on the wave propagation if \(V_A^{+}\) and \(V_A^{-}\) are similar (i.e. full transmission if \(V_A^{+}=V_A^-\)). However, the spherical cap enclosed by the tangent cylinder amounts to a small fraction of the core surface. This explains why investigations of core surface flows from geomagnetic data have often ignored this region (but see the attempts by Livermore et al. (2017, 2020), to address specifically the dynamics at the origin of high-latitude SV variations). Inference of torsional waves in this region, where wave-like patterns have been isolated in the SA (Chi-Durán et al. 2020), is a challenge.
Torsional waves detected from magnetic data are only responsible for a tiny part of SV signal (of the order of 2 nT/yr), although presenting some spatial coherence over the globe. The confidence in their recovery relies on their convincing prediction of a 6-yr signal first detected in the length-of-day (LOD) by Abarca del Rio et al. (2000), an entirely independent geophysical observable. This is the signature of the angular momentum carried by the waves. The modulation (or not) of the 6-yr signal (Chao et al. 2014; Holme and De Viron 2013), as well as the presence of several spectral lines around 6 yrs in the LOD spectrum (Duan and Huang 2020), remain open questions. This last point raises a possible need for two distinct periods at 6 and 8.5 years in core flow models deduced from magnetic data. What is clear is that (i) outward propagating modulated waves can naturally arise in the presence of an electromagnetic torque at the core surface, with a forcing either in the bulk or on the ICB, and (ii) the frequency of these waves is not necessarily a multiple of the gravest frequency, allowing for several peaks around 6 yrs (Gillet et al. 2017). However, in terms of LOD signature, not much power is expected towards shorter periods, as short-period harmonics will likely project little energy onto the angular momentum function (Jault and Finlay 2015).
2.3.3 Quasi-Geostrophic Magneto-Coriolis Modes
Besides torsional Alfvén modes, that evolve on periods close to the Alfvén wave period, Magneto-Coriolis (MC) modes can be found in the rotating MHD system. These modes take their name from a dominant balance of magnetic and Coriolis forces. As such, they are strongly affected by the magnetic field properties and inertia has typically been said to play a minor role, i.e. they evolve on periods much longer than the Alfvén period (Hide 1966; Malkus 1967). For Earth’s core they are usually associated with centennial to millennial time scales. This is certainly the case for the very largest scale MC modes, as first calculated for the idealized magnetic field \(\mathbf{B}_{M67}\) by Malkus (1967). However, when considering smaller-scale modes, inertia becomes increasingly important and the mode frequencies approach the Alfvén wave frequencies. Similarly, QG inertial (or Rossby) modes of small scale have frequencies closer to the Alfvén wave frequencies. This is evident from the analytical results obtained with the magnetic field studied by Malkus (1967) and remains valid for non-idealized magnetic fields (see Labbé et al. 2015). However, these small-scale modes have been assumed to be irrelevant for changes in the geomagnetic field observations, being below the spatial resolution of observations or because they would be strongly affected by magnetic diffusion.
By projecting the fields onto a polynomial basis, Gerick et al. (2021) investigated QG modes in an inviscid core without stratification permeated by a 3-D poloidal background magnetic field that is continuous at the CMB. The background magnetic field was chosen so that the mean radial component at the equator is nonzero, a quantity known to be relevant for torsional Alfvén modes. The spectrum of modes calculated at \(\text {Le}= 10^{-4}\) and with truncation at polynomial degree 29 is shown in Fig. 6. Three families of modes are identified as Rossby, torsional Alfvén and QG MC modes and are characterized by the ratio of kinetic to magnetic energy. For a truncation at a polynomial degrees as high as about 30, some QG MC modes show frequencies equivalent to that of torsional modes, but with a slightly stronger magnetic than kinetic energy. One of these QG MC modes is illustrated in Fig. 7. Despite the small scale along the cylindrical radius, the azimuthal wavenumber is relatively low, resulting in spatially large features in the radial magnetic field perturbation and the surface velocity, with a strong amplitude near the equatorial region. This localization of energy in the equatorial region shares some similarity with the ‘equatorial trapping’ that has been observed for Rossby waves (Zhang 1993) and MAC waves (Bergman 1993; Buffett and Matsui 2019). Unlike previously thought, there does not seem to be the necessity of stratification at the core’s surface (Braginsky 1993; Buffett and Matsui 2019), or a strong azimuthal magnetic field component (Hori et al. 2015, 2018), to find MC modes at interannual periods.
A concern that is justified when investigating modes of smaller scale is the influence of diffusion. For MAC waves in a stratified layer it has been shown that magnetic diffusion has a strong impact (Bergman 1993; Buffett and Matsui 2019). Similarly, the transient QG Alfvén waves, which travel along strongly heterogeneous magnetic fields in numerical dynamo simulations, seem to be strongly influenced by diffusion (Aubert and Gillet 2021). The preliminary results (Gerick 2020) have shown that this does not seem to be the case in the unstratified and large-scale mean magnetic field case studied by Gerick et al. (2021), but a thorough investigation is needed. It is possible that a much more spatially complex background magnetic field increases diffusion of the modes. The latter may also be significantly affected by the presence of an electrically conducting mantle.
Finally, one may wonder if the westward moving perturbations associated with QG MC modes near the equator can be observed in geomagnetic field changes at the interannual time scale (see Sect. 1). Eastward moving Rossby modes also approach the interannual periods as shorter length scales are considered. But these latter are less likely to have a large imprint in the radial magnetic field perturbations, due to their large kinetic-to-magnetic energy ratio.
2.3.4 Quasi-Geostrophic Alfvén Waves
Another type of linear motion that results from a balance of Coriolis, Lorentz and inertial acceleration at short length scales has been proposed to operate at time scales close to the Alfvén period and thus has been associated with interannual magnetic field variations. These QG Alfvén waves have been isolated in numerical simulations of the geodynamo as low values of Al are achieved. This requires lowering Ek and \(P_m\) below the level achievable with direct numerical simulations – currently \(Ek=10^{-7}\) and \(P_m=10^{-1}\), see Schaeffer et al. (2017). To do so, large eddy simulations (LES) have been developed, where high spatial wavenumbers of the fluid velocity and the co-density fields are damped with hyper-diffusivity (Aubert et al. 2017). A one-dimensional path in the input parameters space (Ek, \(P_m\), Ra) has been designed, where Ra is the dimensionless Rayleigh number that measures the strength of the volumic forcing \(\mathbf{F}_V\) (buoyancy, through a co-density formalism) in equation (1). It sets a line in the parameter space from \(Ek=3\times 10^{-5}, P_m=2.5\) where \(Al=O(1)\), towards Earth’s core conditions where \(Al\sim 10^{-2}\). Lowering Al comes to a large numerical cost even for LES simulations, as these show a slow decrease \(Al\propto Ek^{1/4}\) (Aubert et al. 2017; Aubert and Gillet 2021). In this framework, by advancing along the path the time scales \(\tau _U\) and \(\tau _A\) get more and more separated. Earth-like separation (by a factor \(\approx 100\)) should be achieved at 100%-path (\(Ek\approx 3\times 10^{-12}, P_m\approx 8\times 10^{-4}\)). Note that these values of Ek and \(P_m\) differ from those mentioned above for the Earth, because what is targeted is the parameter space where an Earth-like force balance is achieved (where effects of thermal and viscous diffusivities are negligible), which actually depends on the ratio \(Ek/P_m\) (for a complete description of the path theory, see Aubert et al. 2017).
QG Alfvén waves propagating away from the inner core have been first isolated in the 50%-path dynamo (i.e. \(Ek=10^{-8}\), \(P_m=4.5\times 10^{-2}\)), where they have been found to be the source of computed geomagnetic jerks and SA pulses (Aubert and Finlay 2019). Such events occur mainly (but not only) in the equatorial region (Aubert 2018). Advancing along the path, QG Alfvén waves become ubiquitous and SA events more numerous, as witnessed for the 71%-path simulation at \(Ek=3\times 10^{-10},P_m=7.9\times 10^{-3}\) (Aubert and Gillet 2021). The computed waves are spatially segregated by regions of sharp field gradients (Aubert 2019), and because of geometrical arguments they primarily show an outward propagation (i.e. along the cylindrical radial direction), once triggered by buoyancy releases. In contrast to the global QG MC modes, these transient QG Alfvén waves are thus confined to a restricted region, with a relatively large azimuthal wavenumber, showing only a minimal azimuthal propagation compared to the latitudinal (or outward) motion along the locally amplified magnetic field. These small-scale magnetic field variations can project onto larger scales at the core surface, in agreement with the observations of geomagnetic jerks. It is yet unclear, whether or not QG MC modes and QG Alfvén waves share a common phenomenological origin, having similar force balances and time scales, but very different spatial geometries and propagation.
By extrapolating amplitudes of the wave patterns to Earth-like values, simulations performed at parameters following the path theory suggest a ratio of zonal to non-zonal flow acceleration \(\approx 1/3\) to 1/5, comparable with what is obtained with core flow reconstructions from magnetic observations (see Gillet et al. 2015). We retrieve here that the majority of the SA pulses is associated with non-axisymmetric motions. The magnitude of interannual motions, once scaled to geophysical units, is nevertheless a little too weak in comparison with core flow models (by a factor of 2 to 3). This may suggest a need to explore across path simulations (inflating the heat flux, or considering a super-adiabatic heat flux at the CMB). In this framework, the observation of SA pulses, signature of waves reaching the CMB equator, might be seen as an evidence against a strongly stratified layer (see also Gastine et al. 2020).
Finally, it is worth highlighting a non-direct link between the above interannual waves and LOD changes, suggested by Aubert and Finlay (2019). Non axisymmetric QG Alfvén waves can indeed be associated with a nonzero magnetic torque along the rotation axis (because the background magnetic field is also non-zonal). They are thus a natural source of excitation for torsional waves close to the period of their gravest modes. As a consequence, one can foresee here a possible indirect relation between geomagnetic jerks and LOD variations (see Holme and De Viron 2013; Duan and Huang 2020), QG Alfvén waves being a potential source for both signals.
2.4 Temporal Spectrum and Waves in Geodynamo Simulations
The quest for localized jerk events is at odds with the temporal spectrum of the geomagnetic field records, which behaves approximately as
for periods \(T=1/f\) spanning a few years to almost a century (De Santis et al. 2003; Lesur et al. 2018). Indeed, these kind of spectra are characteristic of processes presenting jerks potentially at any epoch with occurrences depending on the sampling rate (Gillet et al. 2013), as suggested by Brown et al. (2013). Such a steep spectrum reflects the overall slow evolution of the magnetic field and consequently the need to consider its time-derivatives.
However, some regional variability in \(S_B(f)\) is observed at the Earth’s surface, with generally higher spectral content at interannual periods for sites closer to the equator (Lesur et al. 2021), in agreement with Fig. 1. This questions the existence of spectral lines in \(S_B(f)\) at interannual time scales, presenting moderate quality factors. The presence of such spectral lines may sign waves that could be mapped through the SA. At the core surface the SA can be interpreted by considering the time derivative of the induction Eq. (2) ,
Under the assumption of a potential field above the core surface, its radial component is enough to describe entirely the observed field evolution (e.g., Lesur et al. 2010):
SA events can thus sign either a flow acceleration, the advection of SV by the flow, or diffusion of SV patterns. In the 71%-path dynamo, rapid changes in the SV signal are primarily associated with the former, though in some cases the advection of SV plays an important role (Aubert and Gillet 2021). In all cases diffusion plays a minor role.
The modes described in the previous sections do not operate over a static core state. On the one hand, they might be excited by the nonlinear rapidly rotating MHD dynamics. On the other hand, they could as well participate into the saturation of this dynamics. The former scenario is, for instance, suggested for torsional waves with magneto-convection (Teed et al. 2015) and geodynamo (Schaeffer et al. 2017; Aubert et al. 2017) numerical simulations. In this case the nonlinear nature of the Lorentz torque is likely important, as Reynolds stresses play a secondary role in Earth’s core (Aubert 2019; Schwaiger et al. 2019). Another example concerns the triggering of non-axisymmetric QG Alfvén waves that has been associated with the release of deep convective plumes (Aubert and Finlay 2019).
But the saturation of the nonlinear dynamics is also enslaved to the wave propagation, as put to the fore by Aubert and Gillet (2021) with their 71%-path simulation. They show that the cut-off frequency of the temporal spectrum evolves as \(f_c\sim \sqrt{Lu}\). This frequency separates the period range characterized by Equation (7) from the dissipative range and its steeper decay. \(f_c\) seems thus controlled by the number of free Alfvén oscillations within a magnetic diffusion time. We present in Fig. 8 the spectrum of magnetic field series at the Earth’s surface from 71%-path. It illustrates the two ranges, with spectral indices close to respectively \(-4\) and \(-6\), separated around a frequency \(f_c\) slightly less than \(1/\tau _A\). Extrapolations to Earth-like values from LES simulations give \(f_c\approx 1/10\) yr\(^{-1}\). This value is somewhat longer than what is witnessed with ground-based magnetic data, with an upper bound at \(\approx 1\) yr \(<\tau _A\). It is difficult to access shorter periods (see Finlay et al. 2017), because of the difficulty to separate internal from external signals at shorter time scales (but see Hammer and Finlay 2019; Hammer et al. 2021b). The insufficient power in the dynamo simulation on short time scales resonates with the slightly too weak intensity of interannual flow acceleration highlighted in Sect. 2.3.4, suggesting a need for a parameter sensitivity study across the path (i.e. increasing the Rayleigh number or \(P_m\)).
Power spectral density (PSD) of the radial magnetic field at the Earth’s surface, from the 71%-path dynamo (Aubert and Gillet 2021). The PSD have been obtained with a multi-taper method, from \(\approx 10\) kyr of simulated series, using 20 tapers and applying a Hanning window on each of the tapers. In black the average of PSD obtained all over the globe. In red the average of PSD obtained at the equator. The grey dashed line indicates the −4 and −6 slopes. The dash–dotted line indicates the Alfvén frequency of the simulation (5.8 years).
Nevertheless, the 71%-path dynamo interestingly reveals a stronger power in the equatorial belt, which resonates with the observation by Lesur et al. (2021). Spectral lines with moderate quality factor indeed show up at periods several times \(\tau _A\) (for instance around 20 years \(\approx 3.5\tau _A\) in Fig. 8, which would correspond to \(\sim 7\) years if scaled to the Earth’s Alfvén time). The larger power in the equatorial region is further documented with the latitude–frequency diagrams for the radial magnetic field in Fig. 9a, b. It appears more obvious once downward continued at the core surface. To a lesser extent, we also witness some more power within the tangent cylinder. This picture is coherent with the higher SA found in these places by Aubert (2018); Aubert and Finlay (2019) from the 50%-path dynamo, although here we show that this particularity is found over a broad range of periods that span a fraction of \(\tau _A\) to some tenths of \(\tau _A\) (by focusing on the SA, Aubert (2018) implicitly focuses on short periods).
A similar diagram for the azimuthal fluid velocity is much more contrasted, both in frequency and in latitude (Fig. 9c). The apparent better resolution in frequency results not only from the less steep temporal spectrum of the flow in comparison with the magnetic field (Gillet et al. 2015), but also likely from the mixing of frequencies from the nonlinear electro-motive term in the induction equation (2). We associate the stronger focalization of the energy with latitude to the QG constraint that, in particular, favours azimuthal flows near the equator. This diagram highlights numerous spectral lines in f that occupy a broad range of \(\theta\). It also shows bands of latitudes with stronger power. We witness resonances and zero-crossings in latitude that seem to reveal the triggering of eigen modes. For \(T<\tau _A\), these have been associated with Rossby modes, as documented by Aubert and Gillet (2021). For \(T\approx \tau _A\) the resonances may correspond to the propagating QG-Alfvén waves put forward by Aubert and Finlay (2019). Spectral lines found at \(T>\tau _A\) have not yet been documented. We envision that these could sign the presence of QG MC modes as those found by Gerick et al. (2021). In this scenario, such modes would populate the flow and magnetic spectra at periods from a few \(\tau _A\) to centuries. All the QG modes mentioned above share the property to present small radial length scales, while they are distinguished upon their magnetic-to-kinetic energy ratio (that increases from Rossby to QG Alfvén and then to MC waves). We conclude from this analysis that the isolation of such modes from geophysical data should be easier from core flow models than from magnetic field models.
Power spectral density as a function of the colatitude \(\theta\) (averaged in longitude), for the radial component of the magnetic field at the Earth’s surface (top) and at the core surface (middle), and for the azimuthal component of the velocity at the core surface (bottom), from the 71%-path dynamo (Aubert and Gillet 2021). The horizontal dashed lines indicate the position of the tangent cylinder and of the equator. The vertical dotted line indicates the Alfvén time of the simulation (5.8 years). The magnetic field (resp. flow) is truncated at spherical harmonic degree 13 (resp. 18)
Interestingly, the period range where \(S_B(f)\propto f^{-4}\) has been observed before its discussion in terms of a flat SA spectral range (Aubert 2018). This was actually first highlighted for series of the axial dipole at \(Ek\ge 6\times 10^{-5}\) (Olson et al. 2012; Buffett and Matsui 2015), in simulations where the Alfvén time is close to the turnover time (or \(Al\sim 1\)), before it was verified for non-dipole Gauss coefficients at \(Ek\ge 2\times 10^{-6}\) (Bouligand et al. 2016). There, the \(f^{-4}\) slope is followed only from \(O(\tau _U)\) down to decadal time scales, because of the reduced separation of the Alfvén and turnover time scales.
The separation of \(S_B(f)\) into several spectral ranges has been interpreted in terms of stochastic processes, either in order to constrain temporal cross-covariance functions in the purpose of field modelling (Gillet et al. 2013; Hellio and Gillet 2018; Ropp et al. 2020), or to estimate advection/diffusion characteristics of the dynamo runs (e.g., Buffett et al. 2014; Buffett and Matsui 2015; Meduri and Wicht 2016). Based on geodynamo simulations at relatively high Ekman numbers, such analyses are restricted to time scales longer than a few decades – they under-estimate the power in short period changes due to the shrinking of the rapid changes at \(Al\sim 1\) (Bouligand et al. 2016). This is the case even though such simulations produce values of the SA time scales
relatively close to that obtained from satellite observations, with \(g_n^m,h_n^m\) the geomagnetic Gauss coefficients. Christensen et al. (2012) propose for instance an approximately constant \(\tau _{SA}(n)\simeq 12\) yr whatever the degree for \(n\le 10\). Aubert and Gillet (2021) show that \(\tau _{SA}\) only slowly decreases with Ek, to reach interannual time scales when extrapolated towards Earth-like values, as is observed from satellite field models such as CHAOS-7 (Finlay et al. 2020) or MCM (Ropp et al. 2020).
3 Geophysical Outlook from Dynamical Re-analyses of Rapid Secular Variation Changes
3.1 Geophysical Overview
The advent of a network of space- and ground-based geomagnetic observatories, together with various data analysis approaches (as summarized in Lesur et al. 2021), has allowed to identify the frequent identification of the occurrence of rapid variations in the geomagnetic field. These carefully curated observations contain abundant information on the structure, properties, dynamics and evolution of the deep interior. However, the inherent non-uniqueness and complexity of the system presents a challenge in interpreting the observations of rapid changes in the geomagnetic field and obfuscates these insights.
In dealing with this complexity, it is insightful to start with a simpler case. Therefore, let us first consider an inviscid and perfectly conducting fluid core (\(\eta =\nu =0\)). Then, any perturbation which contributes to the first two terms in the r.h.s. of equation (9) gives rise to secular acceleration of the geomagnetic field. In the case of a perfectly insulating mantle, these variations with a spatial structure of spherical harmonic degree n are then observed at a radius r above the surface of the Earth, with an energy damped by a factor proportional to \((r_c/r)^{2n+4}\) (resp. \((r_c/r)^{2n+2}\)) for the radial (resp. horizontal) component of the field. Additionally, in this simplified hypothetical scenario, the interplay between the perturbation and restoring forces present in the system will give rise to continuous oscillations that manifest as waves and modes (given the lack of a dissipation mechanism).
However, in reality, not all contributions to the terms in Equation (9) will produce observable geomagnetic variations at Earth’s surface and satellite altitude. Even the perturbations that do produce a geomagnetic signature will not yield endless oscillations and will be damped away completely unless a continuous or periodic forcing is present, as evidenced in other geophysical systems. Therefore, with this outlook in mind, we attempt to link the observations of rapid geomagnetic field changes from Sect. 1 and the waves from which they manifest, as discussed in Sect. 2.2-2.3, to gain insight into Earth’s deep interior.
A (non-exhaustive) list of key geophysical insights to be gained from magnetic observations includes:
-
the leading force balances for rapid magnetic variations;
-
understanding the energy power spectra (e.g., influence of small-scale flows and field onto larger scale geomagnetic field variation);
-
the magnetic field strength and spatial heterogeneity in the core – including the partitioning between toroidal and poloidal fields;
-
the excitation mechanisms for oscillations (e.g., triggering by buoyancy or Lorentz torque);
-
the dissipation mechanisms and quality factor (connected to viscosity, electrical conductivity, mantle conductance, turbulent mixing, etc.);
-
the existence of a stable layer at the top of the core (in link with the CMB heat flux, and the stratification level at the top of the core);
-
spatial patterns of the mantle thermal and electrical conductivities.
The above points are further addressed in the following sections.
3.2 Rapid Secular Variation in Context
The methods by which we choose to interrogate geomagnetic observations shape the insights we are able to obtain. Thus, it is prudent to understand the commonly used analysis techniques and identify aspects that lack a specific definition, thereby being highly study and dataset or model dependent. The first challenge then is to determine what constitutes a rapid SV change, especially when looking at time series of SV from observatories (both ground based and virtual). This can vary from study to study as the definition of what feature constitutes a rapid variation highly depends on the time resolution of the observations and on the smoothing that is applied to reduce the noise in the data or model. With a working definition, rapid SV variations can then for instance be analysed via time-longitude and time-latitude plots as shown in Figs. 3, 4, to provide insight into the spatial and temporal characteristics of the variations. Further spatio-temporal insight can be gained by analysing the frequency–wavenumber spectra of the time-longitude/latitude plots (Finlay and Jackson 2003; Chulliat et al. 2015), which may help reveal the different waves present in the dataset.
Subsequently, to characterize the difference between the distinct rapid variation occurrences, it is useful to define the amplitude of the rapid variation. In geomagnetic field models, this can simply be defined based on the SA. Meanwhile, studies based on SV time series data from observatories have used the difference in the gradient of the linear SV segments before and after sudden accidents (e.g., Brown et al. 2013). However, searching for such segments around events localized in time relies on a strong a priori assumption, as processes characterized by power spectra such as (7) possibly present abrupt changes at any epoch (Gillet et al. 2013), so that the occurrence and amplitude of a jerk shall depend on the sampling rate. Another subtlety in analysing observations is the difference in variation in the three magnetic field components both regionally and globally. In observatory data, the radial component of the field has been shown to have the largest amplitudes of rapid variation (Sabaka et al. 2004; Olsen and Mandea 2007), though it has been noted by Olsen and Mandea (2007) that most observatory studies use the \(\phi\)-component of the field as it is least influenced by external fields (and historically stronger over Europe that is the best covered area on ground).
As discussed in Sect. 2, rapid SV observations have to be understood in terms of the core dynamics, specifically the occurrence of waves and oscillatory modes. Table 3 lists the possible waves/modes that could be present in Earth’s outer core (see Finlay 2008, for a comprehensive review). From the aforementioned list, the efficiency of inertial waves (including Rossby modes, see Zhang et al. 2001) in producing observable rapid SV variations is low, because they carry little magnetic energy (Rossby modes in the presence of an imposed field are only weakly influenced by the magnetic field in the limit \(Le\ll 1\), see Hide 1966). In the same vein, it was also recently noted by Aubert and Gillet (2021) that Rossby waves may not be readily detectable with geomagnetic signals due to the low magnetic to kinetic energy partitioning in the waves, and given current spatio-temporal coverage limitations in geomagnetic observations. Under the influence of potential vorticity conservation within the spherical core, general ‘slow’ MC modes (Malkus 1967) may in fact manifest as QG-MC modes (Canet et al. 2014; Labbé et al. 2015; Hori et al. 2015, 2018; Gerick et al. 2021). The interplay between all these different waves, their dispersion relationships for an idealized geometry and the influence of the boundaries present in Earth’s core that may change the observed waveform and frequency are important considerations when trying to gain geophysical insight about Earth’s deep interior.
3.3 Insights into Core Flow and Dynamics
Perhaps the most pertinent of geophysical insights to be gained from rapid SV observations are regarding the core flows and dynamics that allow the variations to occur. Core surface flows have been inferred from geomagnetic observations using inversions based on the radial magnetic induction equation with additional constraints such as tangential geostrophy, quasi-geostrophy, purely toroidal flow, dynamo norms, etc., allowing a unique solution to be determined (for reviews see, e.g., Holme 2015; Finlay et al. 2010). The assumptions that go into constraining the under-determined inversion impacts the resulting core flows and may obscure the small-scale flows and very rapid dynamics. However, inverse geodynamo modelling as described in Aubert (2020) and advances in geodynamo simulations operating at as close to Earth-like parameters as possible (e.g., Aubert and Gillet 2021) enable us to probe the force balance in Earth’s core across various spatial scales (Schwaiger et al. 2019).
For rapid SV observations that occupy a spatial extent of spherical harmonic degree \(n<{{{\mathcal {O}}}}(10)\), the dynamics are governed to first order by QG, followed by a MAC balance, in what has come to be known as a QG-MAC balance (Aubert 2020). With this hindsight, we are able to scrutinize the spatial pattern of rapid SV observations, identify the corresponding force balance as a function of the spatial wavenumber and subsequently understand the waves that may be associated with the rapid SV. As an example, it is useful to consider the axisymmetry and equatorial symmetry of observed rapid SV signals, which may point not only to the dynamical mechanism at hand, but as well to some properties of the background state (such as the intensity or some heterogeneity of the field morphology within the core, the height of the stratified layer, etc.). The search for rapid SV structures unambiguously associated with some specific physics is, however, obscured due to the complexity of the background field, which mixes wavelengths and symmetries via the nonlinear processes at work (namely the electro-motive force in the induction equation, and the Lorentz force in the momentum equation). Furthermore, heterogenities in the local properties of the medium in which the original transient signal is propagating through has been invoked to explain the absence of systematic equatorial symmetry or of a uniform time lag between the signals observed in the two hemispheres (Alexandrescu et al. 1996; De Michelis et al. 1998).
Another nuance that needs to be reconciled is the ability of small-scale fields to produce large-scale SV. This effect was first considered by Eymin and Hulot (2005); Pais and Jault (2008) in the context of core flow inversions. For a more general discussion of the effects of the MHD turbulence in dynamos, we refer to Nataf and Schaeffer (2015) and Tobias (2021). Small-scale flows can be defined based on the length scale at which the Lorentz force dominates the Coriolis force, typically observed for \(n \ge 13\) (Aubert 2019; Aubert and Gillet 2021). Note that the shortest associated length scale is somewhat comparable to the actual spatial resolution of observed SV and inferred flow changes. It is possible then for the energy from the Lorentz force to cascade to larger scales (Nataf and Schaeffer 2015), with impacts on the large-scale dynamics. The influence of small-scale fields therefore depends on how diffusive the dynamics is, and on the slopes of the magnetic field and flow power spectra. This is an important consideration when inferring the core dynamics by simply analysing the information from the observed SV. More studies focused on understanding the interactions between the various scales (e.g. Huguet et al. 2016) are needed in order to better elucidate the dynamics underlying rapid SV, thereby allowing better predictions of the geomagnetic field evolution.
3.4 Magnetic Field Strength in the Core
The temporal pattern or frequency with which the rapid SV signals appear in observations, considered in tandem with the possible wave mechanism in the core, provides insight into the magnetic field strength in the core that is not directly probable otherwise. First, the dispersion relation for the waves discussed above has a dependence on the magnetic field strength. This provides an opportunity to tune the magnetic field strength in the core to best fit rapid SV observations, and subsequently refine our understanding of the generation of the field in the core.
Over the years, core magnetic field estimates have varied from fractions of a mT (Zatman and Bloxham 1997; Buffett et al. 2009) up to \(\sim 10\) mT, depending on which component of the magnetic field is being analysed. By analysing the outward propagation of geostrophic motions across the outer core, interpreted as torsional oscillations, Gillet et al. (2010) estimated a lower bound of \(\sim 2\) mT in the cylindrical radial component of the magnetic field yielding a magnetic field strength of \(\sim 4\) mT in the core. Taking the westward drift to be the signal of magnetic Rossby waves, Hori et al. (2015) estimated the toroidal magnetic field strength in the core to be around or greater than 3 mT, in some cases reaching values as high as 12 mT.
If it is indeed the case that the toroidal field in the core is much stronger, then the partitioning between the toroidal field and observed poloidal fields need to be reconciled. This may bear important insights into the dynamo mechanism at play, such as an enhanced \(\omega\)-effect capable of producing strong toroidal fields from radial shear through differential rotation, as suggested by a thin shell dynamo model developed for Mercury (Stanley et al. 2005). However, geodynamo simulations the closest to Earth’s core conditions seem not to favour such a strong toroidal field in comparison with the poloidal one, at least outside the tangent cylinder (Aubert 2019; Schaeffer et al. 2017). Therefore with future data assimilation analysis tools involving rapid SV observations, there remains an opportunity to further constrain the magnetic field strength and distribution throughout the core and thus to improve our understanding of the inner workings of the geodynamo.
Some preliminary steps in this direction have been made, first with inference of magnetic, velocity and co-density fields for a snapshot in time using dynamo statistics (Aubert 2014), then by re-analysing magnetic Gauss coefficient data with the application of Kalman filter assimilation tools embedding geodynamo simulations (Sanchez et al. 2020). These simulations still lack the rapid physics at work on interannual periods; hence, they have been supplemented with some stochastic forcing (anchored to spatio-temporal geodynamo cross-covariances to mimic their decadal and slower dynamics) by Gillet et al. (2019).
3.5 Excitation and Dissipation of Waves/Modes
Next, we turn our attention to the sources of perturbation and diffusion needed to, respectively, initiate and damp the wave motions associated with rapid SV. Waves and modes in the core may be excited through a variety of mechanisms and it remains a challenge to determine the exact trigger leading to specific oscillatory modes. We have already seen that vigorous buoyancy releases in the core were capable of triggering QG-Alfvén waves that produce geomagnetic jerks in geodynamo simulations (Aubert and Finlay 2019). Convective flows can also trigger torsional waves (Teed et al. 2018). Instabilities in the flow (e.g Roberts and Stewartson 1974; Fearn 1989, 1994) and topographic torques (Hide 1969) are alternative natural excitation mechanisms.
Analysing the temporal pattern of specific rapid SV observations may help discern the excitation mechanism, as well as the way transient motions are dissipated. The forcing may be from periodic (for instance external periodic forcing from Earth’s nutations or tidal forces, see Kerswell 1994) or stochastic (such as the buoyancy release, or through Lorentz forces) drivers. The efficiency of dissipation can be measured by the quality factor (Q), i.e. the ratio of the maximum energy stored in the wave to the energy dissipated over a wave cycle: if the wave has a time dependence of \(e^{( \sigma + i\omega ) t}\), then the quality factor is \(Q = \omega /2\sigma\). A wave with a higher quality factor will propagate further before being dissipated away. In the frequency range of interest for interannual to decadal SV changes, studies of MAC waves in a stably stratified layer atop Earth’s core reveal values of \(Q=O(1)\) (Buffett et al. 2016; Buffett and Matsui 2019). Similarly torsional waves are likely associated with moderate Q-factors if coupled electromagnetically to the mantle (Schaeffer and Jault 2016; Gillet et al. 2017), as they show faint evidence of reflection at the equator. On the contrary QG MC modes calculated over non-axisymmetric imposed field (but still characterized by a relatively low spatial complexity) show a rather low impact of magnetic dissipation in the bulk. For Earth-like values of the Lundquist numbers, Q could indeed increase from O(10) to O(100) for centennial to interannual periods (Gerick 2020). These values though are only valid in the case of an electrically insulating mantle. Q-factors for QG MC modes may be significantly revised downward for finite conductance of the lowermost mantle, as it is the case for torsional modes (Schaeffer and Jault 2016).
The different Q-factors for the various waves not only give us insight into the energy available for the waves but also on how and where the dissipation takes place. Dissipation in the core, on large scales, is assumed to be predominantly ohmic as magnetic fields diffuse much faster than momentum in metallic fluids, as measured by the low value of \(P_m\). However, for short length scales, where the viscous forces start to exceed inertial forces, and especially in the boundary layers, the effect of viscous dissipation may become important (Schaeffer et al. 2017). Further analysis of waves associated with rapid SV observations can help determine where the energy of the wave is dissipated, whether it be within a boundary layer (Triana et al. 2021) or in the internal shear layers as claimed by Buffett (2010). This latter mechanism was found to be inefficient by Lin and Ogilvie (2020), who observe in numerical simulations (for values of Ek as low as \(10^{-11}\)) a too weak dissipation in conical shear layers, in order to explain the damping of the free inner core nutation. Understanding how transient SV patterns are generated and damped could help isolate the dominant source of dissipation (either viscous or ohmic). Ultimately then, the observed spatio-temporal patterns of rapid SV has the potential to further constrain the viscosity and electrical conductivity in the core and the lower mantle.
3.6 Probing the Stable Layer and the Lower Mantle
In addition to the insight on various dynamics and properties of Earth’s outer core, rapid SV observations also allow us to probe the properties of a possible stably stratified layer atop Earth’s core and regions of varying electrical conductivity in Earth’s mantle. MAC waves (discussed in Sect. 2.2) require a form of stratification to propagate through. Though the presence of stably stratified layer is highly debated (see Gastine et al. 2020), observations of rapid SV could be used to infer properties of a layer capable of yielding the observations. This subsequently provides an additional diagnostic to assess its existence. MAC wave periods depend on the magnetic field strength, the thickness of the stable layer and its degree of stratification, through the Brunt-Väisälä frequency given by Equation (3). Current estimates for MAC wave periods obtained by solving for wave perturbations given a background magnetic field and stable layer are between several years to multi-decadal periods (Buffett 2014; Buffett et al. 2016; Buffett and Matsui 2019; Chi-Durán et al. 2020), shorter periods demanding stronger stratifications. More years of continuous, high-precision, global geomagnetic SV data from satellites and ground observatories combined with the ability to solve for MAC modes at Earth-like parameters with eigenvalue solvers provide the prospect of better constraining the presence and properties of the stable layer, the geophysical implications of which are significant.
The presence of a stable layer or lack thereof provides insight into the evolution and dynamics of Earth’s core. In its presence, a point of intrigue is the formation mechanism of the stable layer. Current theories include a primordial stable layer from merging the core with an impactor (Landeau et al. 2016), sub-adiabatic temperature gradient at the top of the core (Lister and Buffett 1998; Gubbins et al. 2015), expulsion of light elements as a result of inner core crystallization (Helffrich and Kaneshima 2013; Bouffard et al. 2019), and barodiffusion (Gubbins and Davies 2013). The presence of the stable layer will also affect the heat flux at the CMB, which is currently not well known (Lay et al. 2008). Observationally, apart from harbouring waves, the stable layer may also affect the large-scale morphology of the geomagnetic field (Yan and Stanley 2018). This may help contextualize archeo- and paleomagnetic data. The absence of a discernible stable layer on the other hand will provide insight into the convective dynamics. In the regime of accessible numerical geodynamos, the observation of Earth-like SV patterns do not favour the existence of a stable layer (Gastine et al. 2020). However, this result might still be contradicted in the future with simulations run at parameters closer to Earth-like (reaching higher values of Lu, and lower Al), and including a possibly efficient magnetic coupling between the dynamics within the stable layer and the convective dynamics below.
Rapid SV observations also yield information on the mantle conductivity based on differential arrival times of a rapid SV signal (Mandea et al. 2010). Alternatively, the lack of evidence for a cut-off frequency in the spectrum of the observed magnetic field may allow us to probe the deep mantle conductance with the core as the source (see Jault 2015), complementing the electromagnetic sounding of the mantle from above with the magnetosphere as the main inductor (e.g., Velímskỳ 2010; Püthe et al. 2015). More indirectly, the absence of significant lag between observed LOD variations and LOD changes predicted by core flow models inverted from magnetic data favours weak conductance of the mantle (Gillet et al. 2015).
With the various wave discussed above, there is also an opportunity to use the amplitude of flow motions in specific regions to identify heterogeneities in Earth’s mantle conductivity. Consistent damping of SV signals in specific regions could be a result of higher conductivity of the mantle locally. For instance, Dumberry and More (2020) show that the weaker SV observed over the Pacific at the core surface may be coherent with higher conductance in this area of the lowermost mantle. Alternatively, it could also be a result of natural variations in the local background magnetic field and flow governed by the primitive equations (Schaeffer et al. 2017), or of an asymmetric gravitational coupling between the inner core and the mantle (Aubert et al. 2013). One possibility to distinguish between the several scenarios would be to correlate regions where transient magnetic signals are damped to known heterogeneous seismic features in the mantle, such as the Large Low Shear Velocity Provinces (LLSVPs), Ultra Low Velocity Zones (ULVZs) (as described in McNamara 2019) and/or hotspots and mantle plumes.
3.7 Corroborating Rapid Secular Variation Observations
The discussion above detailed the various aspects in which rapid SV observations provides insight into Earth’s deep interior. Main observational issues may be summarized as follows:
-
Are there singular events in the observed rapid magnetic variations? Or does the observed SV evolution fit with stationary stochastic representations?
-
Are there oscillatory signals and, if, so, on which periods?
-
Are magnetic patterns localized or global?
-
What shall we expect in terms of symmetry (equatorial, or zonal)?
-
How does it imprint the several components of the measurements recorded above the Earth’s surface?
-
Is there any geographical dependence in the amplitude of rapid variations? If so, can we relate it to regional boundary constraints (in link with the mantle conductivity or heat flux)?
However, in an effort to go beyond plausible scenarios and verify these insights, it is important that rapid SV observations are complemented and corroborated through various methods. In understanding the rapid dynamics and the excitation mechanisms for the various waves, an ultimate validation comes from numerical geodynamo models operating close to Earth-like parameters (Aubert and Gillet 2021) and eigenmode analyses (e.g., Triana et al. 2019; Gerick et al. 2021). Assimilation of geomagnetic observations (Fournier et al. 2010; Sanchez et al. 2020) will help constrain flows in the core and also provide estimates for the magnetic field strength. Convergence of core magnetic field strength from several avenues such as rapid SV observations, data assimilation and tidal/Earth’s nutational studies will subsequently allow us to better understand the dynamo mechanism at work and compare it to our knowledge of other planetary dynamos. To get a handle on 1) viscous and ohmic dissipation in the core, 2) constrain the CMB heat flux, and 3) verify mantle conductivity estimates, ratification of viscosity, and electrical and thermal conductivity estimates from high-pressure experimental mineral physics and ab initio simulations will be key. Advances and insight from seismology and numerical models will also hopefully help provide a clearer picture on how these rapid SV observations relate to the possible stable layer and overlying mantle.
Change history
28 June 2022
A Correction to this paper has been published: https://doi.org/10.1007/s10712-022-09714-3
References
Abarca del Rio R, Gambis D, Salstein DA (2000) Interannual signals in length of day and atmospheric angular momentum. Annales Geophysicae 18(3), 347–364, DOI: https://doi.org/10.1007/s00585-000-0347-9
Alexandrescu M, Gibert D, Hulot G, Le Mouël JL, Saracco G (1996) Worldwide wavelet analysis of geomagnetic jerks. J Geophys Res Solid Earth 101(B10):21975–21994. https://doi.org/10.1029/96JB01648
Aubert J (2014) Earth’s core internal dynamics 1840–2010 imaged by inverse geodynamo modelling. Geophys J Int 197(3):1321–1334
Aubert J (2018) Geomagnetic acceleration and rapid hydromagnetic wave dynamics in advanced numerical simulations of the geodynamo. Geophys J Int 214:531–547, DOI: 10.1093/gji/ggy161
Aubert J (2019) Approaching Earth’s core conditions in high-resolution geodynamo simulations. Geophys J Int 219(Supplement\_1):S137–S151, https://doi.org/10.1093/gji/ggz232
Aubert J (2020) Recent geomagnetic variations and the force balance in Earth’s core. Geophys J Int 221(1):378–393. https://doi.org/10.1093/gji/ggaa007
Aubert J, Finlay CC (2019) Geomagnetic jerks and rapid hydromagnetic waves focusing at Earth’s core surface. Nature Geosci 12(5):393–398
Aubert J, Gillet N (2021) The interplay of fast waves and slow convection in geodynamo simulations nearing Earth’s core conditions. Geophys J Int 225(3):1854–1873
Aubert J, Finlay CC, Fournier A (2013) Bottom-up control of geomagnetic secular variation by the Earth’s inner core. Nature 502(7470):219–223
Aubert J, Gastine T, Fournier A (2017) Spherical convective dynamos in the rapidly rotating asymptotic regime. J Fluid Mech 813:558–593
Bardsley OP (2018) Could hydrodynamic Rossby waves explain the westward drift? Proc R Soc A Math Phys Eng Sci 474(2213). https://doi.org/10.1098/rspa.2018.0119
Becker JM, Salmon R (1997) Eddy formation on a continental slope. Journal of marine research 55(2):181–200
Bergman MI (1993) Magnetic Rossby waves in a stably stratified layer near the surface of the Earth’s outer core. Geophys Astrophys Fluid Dyn 68(1–4):151–176. https://doi.org/10.1080/03091929308203566
Bouffard M, Choblet G, Labrosse S, Wicht J (2019) Chemical convection and stratification in the Earth’s outer core. Front Earth Sci 7:99. https://doi.org/10.3389/feart.2019.00099
Bouligand C, Gillet N, Jault D, Schaeffer N, Fournier A, Aubert J (2016) Frequency spectrum of the geomagnetic field harmonic coefficients from dynamo simulations. Geophys J Int 207(2), 1142–1157
Braginsky SI (1967) Magnetic waves in the Earth’s core. Geomag Aeron 7:851–859
Braginsky SI (1970) Torsional magnetohydrodynamic vibrations in the Earth’s core and variations in day length. Geomag Aeron 10:1–8
Braginsky SI (1984) Short-period geomagnetic secular variation. Geophys Astrophys Fluid Dyn 30:1–78
Braginsky SI (1993) MAC-oscillations of the hidden ocean of the core. J geomag geoelec 45(11–12):1517–1538
Braginsky SI (1998) Magnetic Rossby waves in the stratified ocean of the core, and topographic core-mantle coupling. Earth, planets and space 50:641–649
Brodholt J, Badro J (2017) Composition of the low seismic velocity E’ layer at the top of Earth’s core. Geophys Res Lett 44:8303–8310
Brown W, Mound J, Livermore P (2013) Jerks abound: An analysis of geomagnetic observatory data from 1957 to 2008. Phys Earth Planet Int 223:62–76, DOI: https://doi.org/10.1016/j.pepi.2013.06.001
Buffett B (2014) Geomagnetic fluctuations reveal stable stratification at the top of the Earth’s core. Nature 507:484–487. https://doi.org/10.1038/nature13122
Buffett B, Matsui H (2015) A power spectrum for the geomagnetic dipole moment. Earth Planet Sc Lett 411:20–26
Buffett B, Matsui H (2019) Equatorially trapped waves in Earth’s core. Geophys J Int 218(2):1210–1225
Buffett B, Knezek N, Holme R (2016) Evidence for MAC waves at the top of Earth’s core and implications for variations in length of day. Geophys J Int 204(3), 1789–1800
Buffett BA (2010) Tidal dissipation and the strength of the Earth’s internal magnetic field. Nature 468(7326):952–954. https://doi.org/10.1038/nature09643
Buffett BA, Knezek N (2018) Stochastic generation of MAC waves and implications for convection in Earth’s core. Geophys J Int 212:1523–1535
Buffett BA, Mound J, Jackson A (2009) Inversion of torsional oscillations for the structure and dynamics of Earth’s core. Geophys J Int 177(3):878–890. https://doi.org/10.1111/j.1365-246X.2009.04129.x
Buffett BA, King EM, Matsui H (2014) A physical interpretation of stochastic models for fluctuations in the Earth’s dipole field. Geophys J Int 198(1), 597–608
Busse FH (1975) A model of the geodynamo. Geophys J Int 42(2), 437–459, DOI: https://doi.org/10.1111/j.1365-246X.1975.tb05871.x
Busse FH (1976) Generation of planetary magnetism by convection. Phys Earth Planet Int 12(4), 350–358, DOI: 10.1016/0031-9201(76)90030-3
Canet E, Fournier A, Jault D (2009) Forward and adjoint quasi-geostrophic models of the geomagnetic secular variation. J Geophys Res 114:B11,101, DOI: 10.1029/2008JB006189
Canet E, Finlay CC, Fournier A (2014) Hydromagnetic quasi-geostrophic modes in rapidly rotating planetary cores. Phys Earth Planet Int 229(Supplement C):1–15. https://doi.org/10.1016/j.pepi.2013.12.006
Chao BF, Chung W, Shih Z, Hsieh Y (2014) Earth’s rotation variations: a wavelet analysis. Terra Nova 26(4), 260–264
Chi-Durán R, Avery MS, Knezek N, Buffett BA (2020) Decomposition of geomagnetic secular acceleration into traveling waves using complex empirical orthogonal functions. Geophys Res Lett, p e2020GL087940
Christensen U, Wardinski I, Lesur V (2012) Timescales of geomagnetic secular acceleration in satellite field models and geodynamo models. Geophys J Int 190(1), 243–254
Christensen UR, Aubert J, Hulot G (2010) Conditions for earth-like geodynamo models. Earth Planet Sc Lett 296(3–4), 487–496
Chulliat A, Maus S (2014) Geomagnetic secular acceleration, jerks, and a localized standing wave at the core surface from 2000 to 2010. J Geophys Res: Solid Earth 119(3), 1531–1543
Chulliat A, Alken P, Maus S (2015) Fast equatorial waves propagating at the top of the Earth’s core. Geophys Res Lett 42(9):3321–3329
De Michelis P, Cafarella L, Meloni A (1998) Worldwide character of the 1991 geomagnetic jerk. Geophys Res Lett 25(3), 377–380, doi: 10.1029/98GL00001
De Santis A, Barraclough D, Tozzi R (2003) Spatial and temporal spectra of the geomagnetic field and their scaling properties. Phys Earth Planet Int 135(2), 125–134
Domingos J, Pais MA, Jault D, Mandea M (2019) Temporal resolution of internal magnetic field modes from satellite data. Earth, Planets and Space 71(1), 1–17
Duan P, Huang C (2020) Intradecadal variations in length of day and their correspondence with geomagnetic jerks. Nature communications 11(1):1–8
Dumberry M, More C (2020) Weak magnetic field changes over the pacific due to high conductance in lowermost mantle. Nature Geoscience 13(7), 516–520
Dziewonski AM, Anderson DL (1981) Preliminary reference Earth model. Phys Earth Planet Int 25(4), 297–356
Eymin C, Hulot G (2005) On core surface flows inferred from satellite magnetic data. Phys Earth Planet Int 152(3), 200–220, doi: 10.1016/j.pepi.2005.06.009
Fearn D (1994) Magnetic instabilities in rapidly rotating systems. In: Proctor MRE, Matthews PC, Rucklidge AM (eds) Solar and planetary dynamos. Publications of the Newton Institute, Cambridge University Press, pp 59–68. https://doi.org/10.1017/CBO9780511662874.009
Fearn DR (1989) Differential rotation and thermal convection in a rapidly rotating hydromagnetic system. Geophys Astrophys Fluid Dyn 49(1–4), 173–193, DOI: 10.1080/03091928908243471
Finlay C, Dumberry M, Chulliat A, Pais M (2010) Short timescale core dynamics: theory and observations. Space science reviews 155(1–4):177–218
Finlay C, Lesur V, Thébault E, Vervelidou F, Morschhauser A, Shore R (2017) Challenges handling magnetospheric and ionospheric signals in internal geomagnetic field modelling. Space Science Reviews 206(1–4), 157–189
Finlay C, Kloss C, Olsen N, Hammer M, Tøffner-Clausen L, Grayver A, Kuvshinov A (2020) The CHAOS-7 geomagnetic field model and observed changes in the South Atlantic Anomaly. Earth Planets Space 72(156)
Finlay CC (2008) Course 8 – Waves in the presence of magnetic fields, rotation and convection. In: Cardin P, Cugliandolo L (eds) Dynamos, Les Houches, vol 88, Elsevier, pp 403–450.https://doi.org/10.1016/S0924-8099(08)80012-1
Finlay CC, Jackson A (2003) Equatorially dominated magnetic field change at the surface of Earth’s core. Science 300(5628):2084–2086. https://doi.org/10.1126/science.1083324
Finlay CC, Olsen N, Kotsiaros S, Gillet N, Tøffner-Clausen L (2016) Recent geomagnetic secular variation from Swarm and ground observatories as estimated in the CHAOS-6 geomagnetic field model. Earth, Planets and Space 68(1), 1–18
Fournier A, Hulot G, Jault D, Kuang W, Tangborn A, Gillet N, Canet E, Aubert J, Lhuillier F (2010) An introduction to data assimilation and predictability in geomagnetism. Space science reviews 155(1–4):247–291
Gastine T, Aubert J, Fournier A (2020) Dynamo-based limit to the extent of a stable layer atop Earth’s core. Geophys J Int 222(2):1433–1448
Gerick F (2020) Modes magnéto-coriolis rapides et couples de pression résultant des modes de torsion d’alfvén dans les noyaux planétaires. PhD thesis, Université GrenobleAlpes, France
Gerick F, Jault D, Noir J (2021) Fast quasi-geostrophic magneto-coriolis modes in the Earth’s Core. Geophys Res Lett 48(4):e2020GL090,803. https://doi.org/10.1029/2020GL090803
Gillet N (2019) Spatial and temporal changes of the geomagnetic field: Insights from forward and inverse core field models. In: Mandea M, Korte M, Yau A, Petrovsky E (eds) Geomagnetism, aeronomy and space weather: a journey from the Earth’s Core to the Sun. Special Publications of the International Union of Geodesy and Geophysics, Cambridge University Press, pp 115–132. https://doi.org/10.1017/9781108290135.010
Gillet N, Jault D, Canet E, Fournier A (2010) Fast torsional waves and strong magnetic field within the Earth’s core. Nature 465(7294):74–77
Gillet N, Schaeffer N, Jault D (2011) Rationale and geophysical evidence for quasi-geostrophic rapid dynamics within the Earth’s outer core. Phys Earth Planet Int 187(3):380–390
Gillet N, Jault D, Finlay C, Olsen N (2013) Stochastic modelling of the Earth’s magnetic field: inversion for covariances over the observatory era. Geochem Geophys Geosyst 14(4):766–786. https://doi.org/10.1002/ggge.2004441
Gillet N, Jault D, Finlay C (2015) Planetary gyre, time-dependent eddies, torsional waves, and equatorial jets at the Earth’s core surface. J Geophys Res Solid Earth 120(6):3991–4013
Gillet N, Jault D, Canet E (2017) Excitation of travelling torsional normal modes in an Earth’s core model. Geophys J Int 210(3):1503–1516
Gillet N, Huder L, Aubert J (2019) A reduced stochastic model of core surface dynamics based on geodynamo simulations. Geophys J Int 219(1), 522–539
Gubbins D, Davies C (2013) The stratified layer at the core-mantle boundary caused by barodiffusion of oxygen, sulphur and silicon. Phys Earth Planet Int 215:21–28, doi: 10.1016/j.pepi.2012.11.001
Gubbins D, Alfè D, Davies C, Pozzo M (2015) On core convection and the geodynamo: effects of high electrical and thermal conductivity, transport properties of the Earth’s Core. Phys Earth Planet Int 247:56–64. https://doi.org/10.1016/j.pepi.2015.04.002
Guervilly C, Cardin P, Schaeffer N (2019) Turbulent convective length scale in planetary cores. Nature 570(7761), 368–371
Hammer MD, Finlay CC (2019) Local averages of the core-mantle boundary magnetic field from satellite observations. Geophys J Int 216(3), 1901–1918
Hammer MD, Cox GA, Brown WJ, Beggan CD, Finlay CC (2021a) Geomagnetic Virtual Observatories: monitoring geomagnetic secular variation with the Swarm satellites. Earth, Planets and Space 73(1), 1–22
Hammer MD, Finlay CC, Olsen N (2021b) Applications for cryosat-2 satellite magnetic data in studies of earth’s core field variations. Earth Planets Space 73(1):1–22
Hardy CM, Livermore PW, Niesen J, Luo J, Li K (2018) Determination of the instantaneous geostrophic flow within the three-dimensional magnetostrophic regime. Proc R Soc A Math Phys Eng Sci 474(2218):20180412
Helffrich G, Kaneshima S (2010) Outer-core compositional stratification from observed core wave speed profiles. Nature 468(7325), 807–810
Helffrich G, Kaneshima S (2013) Causes and consequences of outer core stratification. Phys Earth Planet Int 223:2–7. https://doi.org/10.1016/j.pepi.2013.07.005, sI:13th SEDI conference
Hellio G, Gillet N (2018) Time-correlation-based regression of the geomagnetic field from archeological and sediment records. Geophys J Int 214(3), 1585–1607, DOI: 10.1093/gji/ggy214
Hide R (1966) Free hydromagnetic oscillations of the Earth’s core and the theory of the geomagnetic secular variation. Phil Trans R Soc London A Math Phys Eng Sci 259(1107):615–647. https://doi.org/10.1098/rsta.1966.0026
Hide R (1969) Interaction between the Earth’s liquid core and solid mantle. Nature 222(5198):1055–1056
Holme R (2015) Large scale flow in the core. In: Olson P, Schubert G (eds) Treatise in geophysics, core dynamics, vol 8, chap 4, pp 91–113. Elsevier
Holme R, De Viron O (2013) Characterization and implications of intradecadal variations in length of day. Nature 499(7457), 202–204
Holschneider M, Lesur V, Mauerberger S, Baerenzung J (2016) Correlation-based modeling and separation of geomagnetic field components. J Geophys Res: Solid Earth 121(5), 3142–3160
Hori K, Jones CA, Teed RJ (2015) Slow magnetic rossby waves in the Earth’s core. Geophys Res Lett 42(16):6622–6629. https://doi.org/10.1002/2015GL064733
Hori K, Teed RJ, Jones CA (2018) The dynamics of magnetic Rossby waves in spherical dynamo simulations: A signature of strong-field dynamos? Phys Earth Planet Int 276:68–85. https://doi.org/10.1016/j.pepi.2017.07.008
Huder L, Gillet N, Finlay CC, Hammer MD, Tchoungui H (2020) COV-OBS.x2: 180 years of geomagnetic field evolution from ground-based and satellite observations. Earth Planets Space 72:160. https://doi.org/10.1186/s40623-020-01194-2
Huguet L, Amit H, Alboussiere T (2016) Magnetic to magnetic and kinetic to magnetic energy transfers at the top of the Earth’s core. Geophys J Int 207(2):934–948
Irving JC, Cottaar S, Lekić V (2018) Seismically determined elastic parameters for Earth‘s outer core. Sci Adv 4:eaar2538
Jackson A, Maffei S (2020) Plesio-geostrophy for Earth’s core: I. basic equations, inertial modes and induction. Proc R Soc A 476(2243):20200,513
Jault D (2008) Axial invariance of rapidly varying diffusionless motions in the Earth’s core interior. Phys Earth Planet Int 166(1–2):67–76
Jault D (2015) Illuminating the electrical conductivity of the lowermost mantle from below. Geophys J Int 202(1), 482–496
Jault D, Finlay CC (2015) Waves in the core and mechanical core-mantle interactions. In: Schubert G, Olson P (eds) Treatise on geophysics, core dynamics, 2nd edition, vol 8, Oxford, chap 8.09, pp 225–244. Elsevier
Jones CA (2011) Planetary magnetic fields and fluid dynamos. Annual Review of Fluid Mechanics 43:583–614
Kaneshima S, Helffrich G (2013) Vp structure of the outermost core derived from analysing large-scale array data of SmKS waves. Geophys J Int 193:1537–1555
Kerswell RR (1994) Tidal excitation of hydromagnetic waves and their damping in the Earth. J Fluid Mech 274:219–241, DOI: 10.1017/S0022112094002107
Kloss C, Finlay CC (2019) Time-dependent low-latitude core flow and geomagnetic field acceleration pulses. Geophys J Int 217(1), 140–168
Knezek N, Buffett B (2018) Influence of magnetic field configuration on magnetohydrodynamic waves in Earth’s core. Phys Earth Planet Int 277:1–9
Knezek NR (2019) Equatorial magnetic waves in the stratified ocean of Earth’s core. PhD thesis, University of California, Berkeley
Konôpkovà Z, McWilliams RS, Gómez-Pérez N, Goncharov AF (2016) Direct measurement of thermal conductivity in solid iron at planetary core conditions. Nature 534:99–101
Labbé F, Jault D, Gillet N (2015) On magnetostrophic inertia-less waves in quasi-geostrophic models of planetary cores. Geophys Astrophys Fluid Dyn 109(6), 587–610
Landeau M, Olson P, Deguen R, Hirsh BH (2016) Core merging and stratification following giant impact. Nature Geoscience 9(10), 786–789, DOI: https://doi.org/10.1038/ngeo2808
Lay T, Hernlund J, Buffett BA (2008) Core-mantle boundary heat flow. Nature Geoscience 1(1), 25–32, DOI: https://doi.org/10.1038/ngeo.2007.44
Le Bars M, Couston LA, Favier B, Léard P, Lecoanet D, Le Gal P (2020) Fluid dynamics of a mixed convective/stably stratified system - A review of some recent works. Comptes Rendus Physique 21:151–164
Lesur V, Wardinski I, Rother M, Mandea M (2008) GRIMM: the GFZ reference internal magnetic model based on vector satellite and observatory data. Geophys J Int 173(2), 382–394
Lesur V, Wardinski I, Asari S, Minchev B, Mandea M (2010) Modelling the Earth’s core magnetic field under flow constraints. Earth Planets Space 62(6):503–516
Lesur V, Wardinski I, Baerenzung J, Holschneider M (2018) On the frequency spectra of the core magnetic field gauss coefficients. Phys Earth Planet Int 276:145–158
Lesur V, Gillet N, Hammer M, Mandea M (2021) Rapid variations of Earth’s core magnetic field. Surv Geophys
Li WJ, Li Z, He XT, Wang C, Zhang P (2021) Constraints on the thermal evolution of Earth’s core from ab initio calculated transport properties of FeNi liquids. Earth Planet Sci Lett 562(116):852. https://doi.org/10.1016/j.epsl.2021.116852
Lin Y, Ogilvie GI (2020) Ohmic dissipation in the Earth’s outer core resulting from the free inner core nutation. Earth Planet Sci Lett 530(115):888
Lister JR, Buffett BA (1998) Stratification of the outer core at the core-mantle boundary. Phys Earth Planet Int 105(1), 5–19, doi: 10.1016/S0031-9201(97)00082-4
Livermore PW, Hollerbach R, Finlay CC (2017) An accelerating high-latitude jet in Earth’s core. Nature Geoscience 10(1):62–68
Livermore PW, Finlay CC, Bayliff M (2020) Recent north magnetic pole acceleration towards Siberia caused by flux lobe elongation. Nature Geoscience 13:387–391
Maffei S, Jackson A, Livermore PW (2017) Characterization of columnar inertial modes in rapidly rotating spheres and spheroids. Proc R Soc A Math Phys Eng Sci 473(2204):20170181
Malkus WVR (1967) Hydromagnetic planetary waves. J Fluid Mech 28:792–802
Mandea M, Holme R, Pais A, Pinheiro K, Jackson A, Verbanac G (2010) Geomagnetic jerks: rapid core field variations and core dynamics. Space science reviews 155(1–4):147–175
McNamara AK (2019) A review of large low shear velocity provinces and ultra low velocity zones, linking plate tectonics and volcanism to deep earth dynamics—a tribute to Trond H. Torsvik. Tectonophysics 760:199–220. https://doi.org/10.1016/j.tecto.2018.04.015
Meduri DG, Wicht J (2016) A simple stochastic model for dipole moment fluctuations in numerical dynamo simulations. Frontiers in Earth Science 4:38
Nataf HC, Schaeffer N (2015) Turbulence in the core. In: Schubert G, Olson P (eds) Treatise on Geophysics, Core Dynamics, 2nd edition, vol 8, Elsevier, Oxford, pp 161–181
Ohta K, Yagi T, Hirose K, Ohishi Y (2017) Thermal conductivity of ferropericlase in the Earth’s lower mantle. Earth Planet Sci Lett 465:29–37
Olsen N, Mandea M (2007) Investigation of a secular variation impulse using satellite data: The 2003 geomagnetic jerk. Earth Planet Sci Lett 255(1), 94–105, doi: https://doi.org/10.1016/j.epsl.2006.12.008
Olson PL, Christensen UR, Driscoll PE (2012) From superchrons to secular variation: a broadband dynamo frequency spectrum for the geomagnetic dipole. Earth Planet Sc Lett 319:75–82
Pais M, Jault D (2008) Quasi-geostrophic flows responsible for the secular variation of the Earth’s magnetic field. Geophys J Int 173(2):421–443
Pick L, Korte M, Thomas Y, Krivova N, Wu CJ (2019) Evolution of large-scale magnetic fields from near-Earth space during the last 11 solar cycles. J Geophys Res: Space Physics 124(4), 2527–2540
Pozzo M, Davies C, Gubbins D, Alfe D (2012) Thermal and electrical conductivity of iron at Earth’s core conditions. Nature 485(7398):355–358
Püthe C, Kuvshinov A, Khan A, Olsen N (2015) A new model of Earth’s radial conductivity structure derived from over 10 yr of satellite and observatory magnetic data. Geophys J Int 203(3):1864–1872
Roberts PH, Aurnou JM (2012) On the theory of core-mantle coupling. Geophys Astrophys Fluid Dyn 106(2), 157–230
Roberts PH, Stewartson K (1974) On finite amplitude convection in a rotating magnetic system. Phil Trans R Soc London Series A, Mathematical and Physical Sciences 277(1269), 287–315, DOI: https://doi.org/10.1098/rsta.1974.0052
Roberts PH, Wu CC (2014) On the modified taylor constraint. Geophys Astrophys Fluid Dyn 108(6), 696–715
Ropp G, Lesur V, Baerenzung J, Holschneider M (2020) Sequential modelling of the Earth’s core magnetic field. Earth Planets Space 72(1):1–15
Sabaka TJ, Olsen N, Purucker ME (2004) Extending comprehensive models of the Earth’s magnetic field with Ørsted and CHAMP data. Geophys J Int 159(2):521–547. https://doi.org/10.1111/j.1365-246X.2004.02421.x
Sanchez S, Wicht J, Bärenzung J (2020) Predictions of the geomagnetic secular variation based on the ensemble sequential assimilation of geomagnetic field models by dynamo simulations. Earth, Planets, and Space 72(1):157, DOI: https://doi.org/10.1186/s40623-020-01279-y
Schaeffer N, Cardin P (2005) Quasigeostrophic model of the instabilities of the Stewartson layer in flat and depth-varying containers. Phys Fluids 17(10):104111. https://doi.org/10.1063/1.2073547
Schaeffer N, Jault D (2016) Electrical conductivity of the lowermost mantle explains absorption of core torsional waves at the equator. Geophys Res Lett 43(10), 4922–4928
Schaeffer N, Jault D, Cardin P, Drouard M (2012) On the reflection of alfvén waves and its implication for Earth’s core modelling. Geophys J Int 191(2):508–516
Schaeffer N, Jault D, Nataf HC, Fournier A (2017) Turbulent geodynamo simulations: a leap towards Earth’s core. Geophys J Int 211(1):1–29
Schwaiger T, Gastine T, Aubert J (2019) Force balance in numerical geodynamo simulations: a systematic study. Geophys J Int 219(Supplement\_1):S101–S114
Soloviev A, Chulliat A, Bogoutdinov S (2017) Detection of secular acceleration pulses from magnetic observatory data. Phys Earth Planet Int 270:128–142
Stanley S, Bloxham J, Hutchison WE, Zuber MT (2005) Thin shell dynamo models consistent with Mercury’s weak observed magnetic field. Earth Planet Sci Lett 234(1):27–38. https://doi.org/10.1016/j.epsl.2005.02.040
Takehiro S, Lister JR (2001) Penetration of columnar convection into an outer stably stratified layer in rapidly rotating spherical fluid shells. Earth Planet Sci Lett 187:357–366
Taylor JB (1963) The magnetohydrodynamics of a rotating fluid and the Earth’s dynamo problem. Proc R Soc London A 274:274–283
Teed RJ, Jones CA, Tobias SM (2014) The dynamics and excitation of torsional waves in geodynamo simulations. Geophys J Int 196(2), 724–735
Teed RJ, Jones CA, Tobias SM (2015) The transition to Earth-like torsional oscillations in magnetoconvection simulations. Earth Planet Sci Lett 419:22–31
Teed RJ, Jones CA, Tobias SM (2018) Torsional waves driven by convection and jets in Earth’s liquid core. Geophys J Int 216(1):123–129. https://doi.org/10.1093/gji/ggy416
Tobias S (2021) The turbulent dynamo. J Fluid Mech 912(P1). https://doi.org/10.1017/jfm.2020.1055
Triana SA, Rekier J, Trinh A, Dehant V (2019) The coupling between inertial and rotational eigenmodes in planets with liquid cores. Geophys J Int 218(2), 1071–1086, DOI: 10.1093/gji/ggz212
Triana SA, Trinh A, Rekier J, Zhu P, Dehant V (2021) The viscous and ohmic damping of the Earth’s free core nutation. J Geophys Res: Solid Earth 126(4):e2020JB021042. https://doi.org/10.1029/2020JB021042
Velímskỳ J (2010) Electrical conductivity in the lower mantle: Constraints from CHAMP satellite data by time-domain EM induction modelling. Phys Earth Planet Int 180(3–4), 111–117
Vidal J, Schaeffer N (2015) Quasi-geostrophic modes in the Earth’s fluid core with an outer stably stratified layer. Geophys J Int 202:2182–2193
Wicht J, Christensen UR (2010) Torsional oscillations in dynamo simulations. Geophys J Int 181:1367–1380
de Wijs GA, Kresse G, Vočadlo L, Dobson D, Alfe D, Gillan MJ, Price GD (1998) The viscosity of liquid iron at the physical conditions of the Earth’s core. Nature 392(6678):805–807
Yan C, Stanley S (2018) Sensitivity of the geomagnetic octupole to a stably stratified layer in the Earth’s core. Geophys Res Lett 45(20):11005–11011. https://doi.org/10.1029/2018GL078975
Zatman S, Bloxham J (1997) Torsional oscillations and the magnetic field within the Earth’s core. Nature 388(6644):760–763
Zhang K (1992) On inertial waves in the Earth’s fluid core. Geophys Res Lett 19:737–740
Zhang K (1993) On equatorially trapped boundary inertial waves. J Fluid Mech 248:203–217, DOI: 10.1017/S0022112093000746
Zhang K, Earnshaw P, Liao X, Busse F (2001) On inertial waves in a rotating fluid sphere. J Fluid Mech 437:103
Acknowledgements
NG and DJ were partially supported by the French Centre National d’Etudes Spatiales (CNES) for the study of Earth’s core dynamics in the context of the Swarm mission of ESA. NG and DJ contributions have been also funded by ESA in the framework of EO Science for Society, through contract 4000127193/19/NL/IA (SWARM + 4D Deep Earth: Core). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (GRACEFUL Synergy Grant agreement No. 855677). RA would like to thank Sabine Stanley and Ankit Barik for fruitful discussions and comments pertaining to Sect. 3. We thank two anonymous referees for their comments that helped improve the quality of the manuscript. We thank J. Aubert for making available the data from the 71%-path dynamo.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised on June 6, 2022
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gillet, N., Gerick, F., Angappan, R. et al. A Dynamical Prospective on Interannual Geomagnetic Field Changes. Surv Geophys 43, 71–105 (2022). https://doi.org/10.1007/s10712-021-09664-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10712-021-09664-2