Abstract
Detailed observations of the solar system planets reveal a wide variety of local atmospheric conditions. Astronomical observations have revealed a variety of extrasolar planets none of which resembles any of the solar system planets in full. Instead, the most massive amongst the extrasolar planets, the gas giants, appear very similar to the class of (young) brown dwarfs which are amongst the oldest objects in the Universe. Despite this diversity, solar system planets, extrasolar planets and brown dwarfs have broadly similar global temperatures between 300 and 2500 K. In consequence, clouds of different chemical species form in their atmospheres. While the details of these clouds differ, the fundamental physical processes are the same. Further to this, all these objects were observed to produce radio and X-ray emissions. While both kinds of radiation are well studied on Earth and to a lesser extent on the solar system planets, the occurrence of emissions that potentially originate from accelerated electrons on brown dwarfs, extrasolar planets and protoplanetary disks is not well understood yet. This paper offers an interdisciplinary view on electrification processes and their feedback on their hosting environment in meteorology, volcanology, planetology and research on extrasolar planets and planet formation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Earth and the solar system planets were the only planetary objects known until the discovery of the first brown dwarf GD165B (Becklin and Zuckerman 1988) and the first extrasolar planet in 1992 (orbiting the pulsar PSR1257+12, Wolszczan and Frail (1992)). Earth, Jupiter and Saturn are cloudy solar system planets for which atmospheric discharges in the form of lightning are confirmed observationally in radio and in optical wavelengths. Space exploration and ground-based observations have shown that lightning is a process universal in the solar system, but also that charge and discharge processes occur in a large diversity on solar system planets. Charging and discharging processes are essential for our understanding of the origin of our planet and maybe even for the origin of life: It is believed that charged dust is required to form planets and that lightning opens chemical paths to the formation of biomolecules. The purpose of this paper is to point out overlapping interests in electrifying media that contain liquid and solid particles in meteorology, volcanology, solar system objects, extrasolar planets, brown dwarfs and protoplanetary disks. We therefore provide a selective overview of atmospheric electrification processes and related electrical phenomena based on knowledge from solar system and Earth observations, and on laboratory-based research in combination with relevant findings and development in research on extrasolar planets, brown dwarfs and protoplanetary disks. We hope to stimulate a closer interaction between these communities.
The last few decades have taken us from a Universe with only a single planetary system known, to one with thousands, and maybe millions, of such systems. We are now entering the time when we explore theories and results derived for the solar system and for Earth in application to unknown worlds. Figure 1 places Jupiter, one of the solar system giant gas planets, into the astrophysical context: Jupiter (right) is compared to the coolest stellar objects (M-dwarfs and brown dwarfs). Brown dwarfs bridge the stellar (represented by the Sun in Fig. 1) and the planetary regime as their atmospheres can be as cold as those of planets, but they form like stars. The Sun (left) is surrounded by hot plasma (corona), while planets are enveloped in a cold cloud-forming atmosphere some of which exhibit electrical phenomena as part of a global electric circuit. The Sun is intensively studied by satellites like SOHOFootnote 1 and HINODEFootnote 2 leading to efforts like SWIFF for space weather forecasting (Lapenta et al. 2013). Comparable high-resolution monitoring is neither feasible for solar system planets, moons or comets nor for extrasolar objects. Instead, experimental work on Earth, Earth observation, modelling and comparative studies for the solar system and as an extrasolar objects need to be combined; examples for Earth studied as extrasolar planet are, e.g., given in Kitzmann et al. (2010), Bétrémieux and Kaltenegger (2013) and Hodosán et al. (2016).
The large context: Planets are the coldest and smallest objects in the Universe known to possess a cloud-forming and potential life-protecting atmosphere. Brown dwarfs are as cool as planets, but they form like stars (like the Sun) through the collapse of a gravitationally unstable interstellar cloud. Planets (like Jupiter and Earth) form as by-product of star formation in protoplanetary disks. Note that the lower temperature boundary is not yet well determined
Figure 2 compares images, spectra (disk-integrated radiation flux), atmospheric (\(T_{\mathrm{gas}}\), \(p_{\mathrm{gas}}\))-structures and the local degrees of gas ionisation for Earth, Saturn and two types of brown dwarfs (L-type (pink)–hotter, and T-type (purple)–cooler). All data for Earth are from observations, the Saturn data are derived from CassiniFootnote 3 spacecraft observation, the brown dwarf spectra are observed with SpeX on IRTFFootnote 4 (Cushing et al. 2005), and the (\(T_{\mathrm{gas}}\), \(p_{\mathrm{gas}}\))—and the \(f_e\)-structure are results from atmosphere simulations. \(f_e\) refers to the local degree of ionisation and is defined as \(f_{\mathrm{e}}=p_{\mathrm{e}}/p_{\mathrm{gas}}\) with \(p_{\mathrm{e}}\) and \(p_{\mathrm{gas}}\) the local electron and the local gas pressure, respectively. The Earth image is a photograph taken from the International Space Station. The Saturn image is a visible light image taken by the Cassini spacecraft, and the brown dwarf image is an artist’s impression based on atmosphere simulations. No direct image exists for any brown dwarf because the nearest brown dwarfs (the binary system Luhman 16) are 6.59 light years away from Earth. All three classes of objects have chemically and dynamically active atmospheres that form clouds and that may be undergoing local charge and discharge events. Their local atmospheric conditions differ, including the chemical composition, as result of their formation history and the irradiation received from a host star. Interdisciplinary research combining plasma physics, meteorology, volcanology, solar system exploration and astrophysics as suggested in Füllekrug et al. (2013) is required to study weather phenomena on Earth, solar system planets and on extrasolar planetary objects also in view of upcoming space missions like CHEOPSFootnote 5, PLATOFootnote 6 and JWSTFootnote 7.
This figure shows the spectrum of emitted radiation, \(F(\lambda )\), the temperature-pressure profile in the atmosphere, (\(T_{{\mathrm{gas}}}\), \(p_{{\mathrm{gas}}}\)) and the degree of ionisation, \(f_{\mathrm{e}}\), as a function of pressure for planet Earth, for Saturn and for two brown dwarfs. The Saturn thermodynamical data from Moses et al. (2000), Moore et al. (2004) (solid line) and Galand et al. (2009) (dashed line) were used to derive the degree of ionisation [courtesy: Alejandro Luque]. Saturn’s disk-integrated spectrum is based on the latest profiles of atmospheric temperature and gaseous composition derived from retrieval analysis of Cassini Composite Infrared Spectrometer spectra (Irwin et al. 2008; Fletcher et al. 2012; courtesy: Leigh Fletcher). The brown dwarf spectra are from Cushing et al. (2005) [courtesy: Sarah Casewell], the atmosphere models from Witte et al. (2011) [courtesy: Isabel Rodrigues-Barrera].
Plasma and discharge experiments are essential in providing a controlled environment in contrast to observation of atmospheric phenomena. Such experiments can involve the three different mass components constituting an atmospheric gas: electrons, ions and dust particles with their masses \(m_{\mathrm{e}-}<m_{\mathrm{ion}}<m_{\mathrm{d}}\). The mass differences result in different spatial effects like ion acoustic waves and plasma crystals. An atmospheric environment that is only partially ionised may show plasma character on only local scales compared to the global scale of the comet, moon, planet, brown dwarfs or protoplanetary disk. One potentially far-reaching example for the origin of life on Earth is volcanoes (Johnson et al. 2008) which can produce significant electrostatic charging and subsequent lightning during eruption (Sect. 3.4), maybe also on Jupiter’s moon Io, for example. In volcanoes but also in terrestrial clouds, particles of similar mass govern the charge and discharge processes and plasmas form during violent discharges only. Understanding dust charging processes is important for space exploration because the local ionisation changes as a result of the variability of the solar wind hitting the moon’s or an asteroid’s surface. A spacecraft landing, like Philae, the Rosetta lander, has a very similar effect (Sect. 4). In situ measurements from the chemically active Earth’s atmosphere offer insight into charge and discharge processes, their local properties and their global changes (Sect. 3.1). While plasma experiments are conducted in a controlled laboratory environment, measurements inside the uncontrollable Earth’s natural atmospheric environment lead to an understanding of the vertical and horizontal ionisation where the relative importance of electrons, ions and dust, hence their total mass relation, changes with atmospheric height. For example, the fair weather current is carried by ions only due to the lack of free electrons between 0 and 60 km. Understanding the Wilson Global circuit (Sect. 3.3) helps the understanding of the Earth’s weather and climate. Such observations allow an understanding of atmospheric processes on Earth that can only be gained for solar system and extrasolar bodies by intensive modelling efforts guided by observations and experiments.
Section 2 provides a short background summary on charge processes of discrete solid or liquid surfaces in atmospheric gases, the link to laboratory works and an example of related plasma technology development. Section 2 further sets the stage for this interdisciplinary paper by defining terms used in later sections.
Section 3 summarises charging and discharging processes in the terrestrial atmosphere, including processes in the atmospheres of other solar system planets. Section 4 reviews charging processes on the Moon and asteroids in the presence of solar wind and space plasmas, but without substantial neutral atmospheres. Section 5 provides insight into astronomical observations that suggest that mineral-cloud forming atmospheres of brown dwarfs and extrasolar planets are also electrically active, that different ionisation processes will electrically activate different parts of such atmospheres, and that similar processes are expected to act in protoplanetary disks. Section 6 concludes this paper. Each section ends with a list of future works/ open questions where suitable.
2 Setting the Stage for Interdisciplinary Exchange
This section outlines the key concept of this interdisciplinary paper, and it provides definitions of terms used in Sects. 3–5. This section links to laboratory experiments which have driven the understanding of ionised atmosphere gases that contain or form dust particles or liquid droplets. One example of plasma technology development is included to demonstrate the impact of this paper’s theme also beyond academic research. This section deals with the smallest scales where charge processes act, and later sections will address topics related to successively larger-scale charge processes in the terrestrial atmosphere, on the Moon and asteroids, and also outside the solar system in extrasolar planets, brown dwarfs and protoplanetary disks.
2.1 Fundamental Charging Processes
The key concepts in this paper depend on the accumulation and dissipation of electrical charge on discrete solid or liquid surfaces suspended in atmospheric gases. The free charge on the surfaces can arise from two primary mechanisms (in the planetary atmosphere context): processes involving (1) friction (triboelectric charging); and (2) the transport of free charge (plasma processes). More details on processes specific to various environments like Earth’s atmosphere, volcanoes or extrasolar planets are provided in the respective subsections (e.g., Sects. 3.1, 3.2 and 3.4).
2.1.1 Classical Frictional Charging
Transiently contacting surfaces can lead to charge accumulation, by producing either a surplus or a deficit of electrons compared to the neutral case. Indeed, there is evidence that fragments of polymer chains can be exchanged by colliding particles (Saunders 2008), leaving net charges on the surfaces. This process is termed triboelectric charging and has a very long history of practical application (Galembeck et al. 2014), even if the underlying processes are still not entirely resolved. Originally, contact electrification was used to refer to electrostatic charge transfer resulting from contact, including contact modes such as detachment, sliding, rolling, impact. The specific charge processes related to rubbing were only later termed as triboelectrification. Such charging is an inevitable consequence of the frictional interaction between hard surfaces: electrons transfer (by some process) from one surface to the other, leading to charged surfaces. For example, dust entrained in strong, collisional flows (such as volcanic eruptions or mineral clouds in extrasolar planets, Sects. 3.4 and 5) will acquire charges of different polarity (negative and positive) directly from the intergrain collisions themselves. Such macroscopic particles can include ice crystals in atmospheric clouds, where the diversity of growth rates (and consequent dynamics) of crystals influences the polarity of charge transfer and leads to such clouds becoming charge separated by the relative drift of the charged particles (Saunders 2008). Charge accumulation and separation can lead to energetic relaxation, in the form of lightning.
2.1.2 Plasma Charging
There is an additional mechanism for forcing charge onto a surface, in possibly much larger quantities than can be acquired by triboelectric or contact processes: plasma charging. A plasma is a gas in which a fraction of the molecules are ionised, leading to an abundance of free charge existing as an additional “gas” component. Though neutral overall, there is a natural scale-length over which the plasma can create large potential differences caused by charge population fluctuations: this is because free electrons are light and mobile compared to the heavier positive ions, and therefore the electrons can temporarily escape their charged counterparts, leading to charge densities appearing for short intervals, and over restricted distances (this is explained in detail in subsequent sections below). Should an isolated solid (dust or crystal) or liquid (aerosol) surface be introduced into this plasma, these natural fluctuations in the charge distribution will cause such surfaces to acquire surplus free charge, forced onto it by the action of the plasma itself. Isolated surfaces exposed to plasma will quickly (typically on a microsecond timescale or less) charge up to reach the plasma or floating potential (Khrapak et al. 2012; Khrapak and Morfill 2008; Hutchinson and Patacchini 2007), by the action of a continuous electron current to the surface from the ambient plasma, which rapidly establishes a negative charge before the compensating positive ion current can respond. Ultimately, there is a balance reached, but one that reflects the relative electron mobility over the ions. Since there is so much more free charge available in a plasma compared to triboelectric processes, there is an enhanced capacity for dust exposed to plasma discharges to store considerable surface charge in comparison with purely collisional interactions between grains: since the plasma surface charge reflects the plasma conditions, and not just the grain chemistry and collisionality, then the plasma is an independent and effective agent for creating charged particles.
2.1.3 Defining General Terms
After a summary of the principal mechanisms for charging surfaces in gases in Sects. 2.1.1 and 2.1.2, the most important vocabulary used throughout the paper is defined below to allow a better understanding of the links between the interdisciplinary topics in Sects. 3–5. The Appendix provides an glossary.
Dust particles, aerosols, droplets. An important feature of many charging processes is the presence of macroscopic particles such as dust, aerosols or droplets. These are macroscopic particles large enough to move under the influence of gravity. The particle sizes can vary by orders of magnitude. They can be liquid or solid. They can be composed of a mix of different materials that changes with temperature. Aerosols are suspended particles of either phase. Dust is predominant on the Moon and asteroids, in volcanic lightning and mineral clouds of extrasolar planets and brown dwarfs, and as building blocks for planets in protoplanetary disks. Also hydrometeors (droplets, graupel and ice particles, snowflakes \(\ldots\)) could fall into this category, but are considered aerosols in geoscience. Macroscopic particles such as dust and aerosols can be electrically charged which de-mobilises the charge that previously resided in the gas in the form of electrons or ions. Dust, for example, will acquire a negative total charge in the absence of external influence like stellar UV radiation.
Ionisation is the process of dissociating neutrals into charged species, due to a variety of mechanisms: electron impact ionisation, Penning ionisation (ionisation through chemical reactions), direct dissociation by strong electric fields, UV-photoionisation. The total electric charge is conserved during ionisation, but once the charges are free they can move independently. In air (the atmospheric gas on Earth with its electronegative oxygen component) free electrons are very short lived in the absence of strong electric fields. Ionised air in the Earth’s troposphere and stratosphere consists of positive and negative ions. The fair weather currents on Earth are ion currents (see Sect. 3.3).
Plasma is a gas consisting of charged particles. It is often restricted to charged particle gases where collective phenomena, like plasma oscillations, are more important than collisional phenomena. A plasma is created if there is sufficient ionisation of neutrals that the charged particle density becomes significant. A plasma is characterised by the capacity to produce a collective self-field that is significant when compared to any imposed field (such as that produced by external electrodes, or induced by collapsing magnetic fields, or by impinging electromagnetic radiation). An electrically neutral medium is created that can respond to an external electromagnetic field, but there is no spontaneous charge separation in equilibrium on scale-lengths greater than the Debye length.Footnote 8 There is a significant distinction between plasmas which are collisionless, and those which are collisionalFootnote 9: (1) Collisionless plasmas consist mainly of positively charged ions and of electrons or negatively charged ions, depending on the electronegativity of the ionised gas. They interact through electromagnetic fields rather than through mechanical collisions. Examples are the magnetosphere and the interplanetary plasma (Sect. 4) where the assumption of ideal magnetohydrodynamics (MHD) holds. (2) In a collision dominated plasma, the motion of charged particles is dominated by collisions with neutral atoms and molecules, rather than by the direct electromagnetic interaction with other charged particles. The transiently existing plasmas in the terrestrial tropo-, strato- and mesosphere up to the E layer of the ionosphere are mostly collision dominated plasmas, except for the highly ionised and hot lightning return stroke channel.
Charging or Charge Separation will be used for the process where macroscopic particles like dust or aerosols are charged. This can occur in particle collisions (in thundercloud electrification, dust devils in deserts, volcanic lightning) in non-ionised atmospheres or in vacuum or by attaining charge from a plasma (e.g., in dusty plasmas) spontaneously due to the different mobility of the charged species, in ambipolar diffusion, for example.
If mechanical forces (gravity, convection) that act on the charged dust particles are stronger than the electric forces, charges can be separated over a certain distance. An electric potential builds up that can discharge by lightning and the related transient luminous events.
Electrification is understood as the processes leading to charging of dust or other macroscopic particles obeying both polarity and charge conservation. As a result, a macroscopic electric field can build up. Electrification is sometimes used synonymously with Charging or Charge separation.
Discharging is the process where the electric potential is released by electric currents. This can happen continuously or through a rapid transition like the rapid growth of discharge channels in lightning discharges. Emission of high-energy radiation can be associated with the rapid channel growth.
2.2 Charged Dust in Experimental Work
Dust in plasmas has a long history—one which is even more relevant in contemporary planetary exploration. This section explores the phenomena associated with dust interacting with ionisation in the ambient atmosphere to ensure non-equilibrium processes (both physics and chemistry) have a significant and enduring influence on the evolution of the atmosphere in general, including the dust itself. The discussion here ranges over the impact of charged dust imposing a long-range order in confined plasmas, through to microdischarges arising from binary encounters between freely floating charged aerosols, releasing low-energy free electrons into the ambient atmosphere, with all the possibilities that this entails for molecular activation by dissociative attachment and radical formation. The common theme throughout is the capacity—literally— for dust to retain the electrostatic memory of ambient discharges via free-charge acquisition and for that discharge legacy to be reshaped and realised in potent form by harnessing hydrodynamical forces on fluid timescales, rather than plasma ones. In this way, transient plasma effects can be stored, reconfigured and released on meaningful scales in such a way as to have a tangible influence on large-scale evolution of planetary atmospheres. The following sections discuss dust–plasma interactions in Sect. 2.2.1. laboratory plasma dust, where floating particulates can be a help or a hazard in plasma applications, including plasma crystals, and in Sect. 2.2.2. the dynamic evolution of charged aerosols, where fluid deformation and evaporation can moderate the evolution of encapsulated targets.
2.2.1 The Plasma Laboratory: Dusty Plasmas and Plasma Crystals
Dusty plasmas have been studied in laboratory experiments for several decades. Langmuir et al. (1924) reported the observation of minute solid particles and aggregates in a laboratory streamer discharge and suggested the dust could play a role in ball lightning (see also Rakov and Uman 2003 for a review). “Dusty plasmas” are sometimes referred to as “complex plasmas” although the latter description is more wide-ranging and can include other types of constituents and features such as sheaths (Phelps and Allen 1976), quantum effects and dust. Dusty plasma is referred to in cases when collective behaviour of dust becomes important resulting in new types of waves and instabilities. This occurs when the Debye length and interparticle distance are of the same order and the effects of neighbouring particles cannot be neglected, as opposed to the case when the Debye length is much less than the typical interparticle distance (isolated charged dust).
The experimental research on dusty plasmas in laboratories has (1) been aimed at increasing fundamental understanding and (2) also been strongly motivated by the need to control the behaviour of dust in plasmas that are used in industrial applications. Dust deposited from within the plasmas that are involved in the semiconductor component fabrication and materials processing industries can damage the components and significantly affect the productivity of these industries. In contrast to the need to mitigate the potentially harmful effects of dust in industrial plasma etching and deposition, the capability to form and control dust in plasmas is being exploited in the production of nanoparticles for the expanding nanoscience industry.
Fundamental research programmes have explored phenomena such as dust crystallisation and wave propagation within dusty laboratory plasmas where a stationary and fully ionised gas is considered. In laboratory experiments, the Earth’s gravitational field influences the dusty plasma behaviour and, while the vast majority of experiments have been carried out in laboratories on the surface of the Earth, there have been some experiments on dusty plasmas carried out in the near-weightless conditions within the International Space Station. Whereas at sea level 2D dust crystals can be produced, the low-gravity conditions are usually needed to produce 3D dust crystals.
Several types of waves, including longitudinal electron plasma waves and ion acoustic waves (Allen and Phelps 1977), can propagate in dust-free plasmas formed from ionised gas and containing electrons and ions as well as some neutral atoms and molecules. Additional wave propagation modes appear if a magnetic field is applied to the plasma. While all of these waves are usually damped as they propagate, it is also possible for them to become growing waves, or instabilities (Allen and Phelps 1977; Kuhn et al. 1981), when appropriately excited. For example, ion acoustic waves (Allen and Phelps 1977) can be driven unstable by passing a current through the plasma, i.e. they are triggered by a drift motion of the electrons relative to the ions. In a dusty plasma, the charged, massive dust particles can produce new types of wave motion: The dust-ion acoustic wave (DIAW) is a modified ion acoustic wave, where the ions continue to provide the inertia and the presence of the quasi-stationary charged dust particles modifies the normal ion acoustic wave dispersion. In contrast to the DIAW, in the dust acoustic wave (DAW) the dust particles move and provide the inertia rather than the ions. Both the DIAW and the DAW can be observed because their frequencies are low enough for camera systems to resolve the images of the wave propagation.
Measurement of dusty plasmas in the laboratory and comparison with simulations using particle in cell (PIC) codes allows these codes to be benchmarked against the laboratory experimental observations. PIC code simulation of laboratory plasma experiments and comparison with space measurements has proven successful in the case of auroral kilometric radiation (Speirs et al. 2008; McConville et al. 2008) because of their capability to simulate the onset and dynamics of microinstabilities in dusty plasmas. The use of PIC codes to simulate the behaviour of dusty plasmas in space should prove equally fruitful in obtaining detailed explanations of the formation, properties and consequences in astrophysics (Shukla and Mamun 2002; Fortov and Morfill 2010).
2.2.2 Delivering Charges to Microscopic Particles
The evolutionary processes governing the dynamics and stability of charged macroscopic water droplets in a discharge plasma are part of an innovative collaborative project on bacteria detection (Rutherford et al. 2014; Maguire et al. 2015). The technique of using droplet evaporation as a moderator for charge deposition provides a method to precisely deliver a known amount of charge to microscopic particles such as bacteria cells or (cloud) condensation seeds. For that, aerosolised bacteria samples will be passed through a discharge plasma to acquire significant electrical charge which can be measured in the laboratory. If the charge-carrying aerosol evaporates, its surface area decreases, but the aerosol retains the charge. Ultimately, if the Coulomb force overcomes the surface tension, then the droplet expels charge to bring the retained charge back into the stability limit (the Rayleigh limit \(Q_{\mathrm{r}}(t)\)), which is a function of its radius. Hence the droplet continues to track the Rayleigh limitFootnote 10 as it evaporates. Once all the fluid has gone and the interior seed particle (bacterium or grain) is revealed, the charge placed on it is known. This is the charge consistent with the Rayleigh limit at the radius of the grain.
The charging mechanism can be described as follows (Maguire et al. 2015). Water droplets entering a plasma will form a sheath between the droplet surface and the plasma, as a simple consequence of the disparity in mobility between electrons and ions. Electrons will collide more frequently with the drop surface and remain there, causing it to acquire a negative surface charge. The charged droplet will then attract positive ions from the plasma until the electron and ion currents to the surface of the droplet reach equilibrium; at this point, the droplet is at the plasma potential.
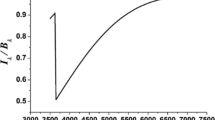
The figures show the evolution of a liquid droplet that acquires a surface charge as a result of travelling through a plasma discharge. The horizontal axis is time, normalised to the characteristic time required to reduce (by evaporation) the droplet radius to one-tenth of its initial value. The droplet spends 50 % of its evolution inside the plasma; the green dotted line shows the time at which the droplet leaves the discharge environment. Top: The radius evolution as the droplet evaporates. Bottom: The charge (red line) and Rayleigh limit (blue line) of an evaporating water droplet containing a bacteria cell that is one-tenth of the initial droplet radius. Outside the plasma, the charge on the droplet remains relatively constant until the stability limit is reached, at which point the droplet emits enough charge to remain stable and enters a feedback cycle of emission and evaporation. The final charge deposited on the bacterium is closely linked to the Rayleigh limit of the minimally encapsulating droplet (Maguire et al. 2015)
Suppose an initially stable water droplet has acquired charge by passing through a plasma (or indeed by an alternative charging mechanism; green vertical line in Fig. 3) and is now floating freely in air, having left the plasma behind. If the initial droplet charge is less than the initial Rayleigh limit, \(Q_{{\mathrm{r}}_0}\), of the droplet, then the droplet is stable. As evaporation proceeds outside the plasma, the droplet charge stays roughly constant, while the Rayleigh limit, \(Q_{\mathrm{r}}(t)\), evolves according to
with \(Q (t=0) = \alpha \, Q_{{\mathrm{r}}_0}, \,\alpha <1\) being the initial charge on the droplet, and \(\beta (t) < 1\) for all \(t>0\). The initial values for the results in Fig. 3 are: \(\alpha (t=0)=0.0025\), \(r_0=r(t=0)=10\,\upmu\)m, \(Q(t=0)=10^4\) electronic charges (e) because Rayleigh limit is \(4\times 10^6\) e. \(\beta =1\) at \(t=0\); \(\beta\) is not shown in Fig 3. If \(Q_r(t)\) decreases far enough that \(Q_r(t) \approx Q(t)\), then the droplet will become unstable and emit sufficient charge to restore the stability condition of \(Q_{\mathrm{r}}(t) > Q(t)\). Evaporation continues until once again the stability condition is broken and more charge is emitted back into the ambient gas. This feedback loop continues until the entire droplet has evaporated.
As the droplet evaporates, both the droplet radius r(t) and the Rayleigh limit for the charges on the droplet, \(Q_{\mathrm{r}}(t)\), decrease. If the droplet encapsulates a bacteria or dust grain, the evaporation cannot proceed beyond a minimum radius \(r_{{\mathrm{m}}}\). The final charge on the droplet of size \(r_{{\mathrm{m}}}\) at a final time, \(t_{\mathrm{f}}\), is then
The upper limit of final droplet charge depends only on the minimum radius of the particle, γ surface tension of the droplet, \(r_{{\mathrm{m}}}\), left behind once the droplet has evaporated, irrespective of the starting charge. This is assuming that the Rayleigh limit is encountered at some intermediate point in the evaporative evolution of the water mantle that forms the drop encapsulating a bacteria or dust grain.
This is a valuable process, since grains processed in this way carry the electrostatic legacy of the plasma environment encountered earlier in their history. Such charged particles can either act as a source of low-energy free charge injected into the atmosphere to produce non-equilibrium electron-moderated chemical evolution of the latter (for example, dissociative attachment producing radicals) or indeed a constraining electrostatic environment stable over fluid length and time scales.
3 Electrification and Discharging in Terrestrial and Planetary Atmospheres
When we aim to understand electrification and electric phenomena in weakly ionised atmospheres of extrasolar planets, a characterisation of the phenomena on Earth and in the atmospheres of solar system planets can provide guidelines and inspiration. This section therefore starts with an overview of the main electrical processes in the terrestrial atmosphere up to the ionosphere, the fair weather currents and the thunderstorms with transient luminous events and terrestrial gamma-ray flashes. Then we continue with lightning phenomena in volcanic ash plumes and review a few processes in the atmospheres of other solar system planets. For more details see Rakov and Uman (2003), Leblanc et al. (2008), Dwyer and Uman (2014), Betz et al. (2009), Füllekrug et al. (2006), Ebert and Sentman (2008).
Ionisation and electric currents in the terrestrial atmosphere are driven by two main mechanisms: (a) The atmosphere is very weakly ionised by external sources like Cosmic Rays and radioactivity (Sect. 3.1). The resulting conductivity supports the fair weather currents that relax electric potentials in atmospheric regions far from thunderstorms. (b) Thunderclouds play a particular role in separating electric charges and in building up large electric potentials (Sect. 3.2). Cloud particles first exchange charge during collisions and are then separated due to mechanical forces (such as gravity and convection) larger than the attractive electric forces between particles of opposite polarity. For this reason, meteorologists use lightning flashes as indicators for strong turbulent convection in the atmosphere. When these electric potentials suddenly discharge, a variety of ionised and conducting channels is formed through localised ionisation processes (collisional, thermally driven or photon impact). In the first stage of a discharge, these ionisation reactions are driven by strong electric fields and local field enhancements and are dominated by the impact of fast electrons on neutral atoms or molecules, while at later stages Ohmic heating and thermal equilibration create temperature driven ionisation reactions.
3.1 Ionisation of the Terrestrial Atmosphere Outside Thunderstorm Regions
In common with other solar system atmospheres (Harrison et al. 2008), the Earth’s lower atmosphere outside thunderstorm regions is made electrically conductive by the ionising action of high-energy charged particles generated within the heliosphere (e.g., solar energetic particles, SEPs) and beyond (e.g., galactic cosmic rays, GCRs). A consequence of the terrestrial atmosphere’s small but finite conductivity (\(\approx 10^{-14}\hbox { S}\,\hbox {m}^{-1}\) in surface air, see also Fig. 6) is that current flows can occur through the atmosphere, between disturbed weather and fair weather regions. Similar circumstances occur in other atmospheres, depending on the existence of charge separation processes and the atmospheric conductivity.
Ion production in the Earth’s lower atmosphere (i.e. the troposphere and stratosphere) results from a combination of terrestrial and extraterrestrial sources. Near the planet’s continental surfaces, the effects of natural radioactivity contained within the soil and rocks, or released in the form of radioactive gases such as radon, provide the dominant source of ion production. At heights from 3 to 5 km above, the continents (i.e. above the boundary layer where eddy diffusion of radon isotopes occurs which depend on orography), or over the oceans, extraterrestrial sources, principally GCRs dominate the ion production, while SEPs and UV irradiation dominate the ionisation in the ionosphere, but typically do not have sufficient energy to reach the troposphere.
Balloon-borne Measurements Vertical soundings of the ion production rate in the troposphere and stratosphere (i.e. to about 35 km) can be made using balloon-carried instrumentsFootnote 11. Historically, this was the original airborne platform through which the existence of the cosmic source of ionisation was confirmed, in a manned balloon flight made by Victor Hess on 7 August 1912 (Hess 1912). This flight carried ionisation chambers and fibre electrometers, in which the rate of decay of the charged fibre was recorded visually and the ion production rate inferred (Pfotzer 1972). Hess found that the ion production rate initially diminished with height, but then began to increase (Fig. 4A). This subsequent increase indicated that ionisation was originating from above. Figure 4B shows a profile of the ion production rate per unit volume at standard temperature and pressure, \(q_{\mathrm{STP}}\), made using a modern balloon-carried Geiger counter (or Geigersonde) launched from a midlatitude site (details are given in Harrison et al. 2014). This shows the same increase in ionisation observed by Hess at the lower altitudes, but the modern balloons extend the measurements to greater altitudes. A characteristic feature is the maximum in ionisation at about 20km, first observed by Regener and Pfotzer (1935). The presence of the Regener–Pfotzer maximum results from a balance between the energy of the incoming particles, and the density of the atmosphere.
Vertical profile of the ionisation rate in the terrestrial atmosphere, as (A) originally obtained by Hess (7th August 1912), with ionisation at each height shown relative to the measured surface ionisation and, (B) from a series of balloon flights (colours used to identify individual flights) made from Reading, UK, during 2013. \(q_{\mathrm{STP}}\ [{\text{cm}}^{-3}\,{\text{s}}^{-1}]\) the ion production rate per unit volume, for air at standard temperature and pressure (STP)
A long series of regular Geigersonde measurements has been made by the Lebedev Institute in Moscow, using a variety of sites including Moscow, Murmansk and Mirny (Antarctica). The value of this stable long-term measurement series is considerable, as, by taking advantage of the different geomagnetic latitudes of the sites concerned, it allows features of the cosmic ray ionisation to be established. Cosmic rays follow the geomagnetic field lines, and the lower energy particles are able to enter at higher latitudes (which is expressed as a lower geomagnetic rigidity). The high-energy CR particles survive for longer in the Earth’s atmosphere, while the low-energy CR particles are completely absorbed soon after they enter the atmosphere. Figure 5 shows a long times series of Geigersonde measurements made at the Regener–Pfotzer maximum, from sites with different rigidity (Stozhkov et al. 2013). The 11-year (Schwabe) cycle in solar activity is clearly present through the inverse response in GCRs, and, at the high-latitude sites, the exceptional nature of the cosmic ray maximum in 2010/11 associated with the deep solar minimum is particularly apparent.
Time series of monthly averages of cosmic ray fluxes, \(N_{\mathrm{m}}\) [\(\hbox {cm}^{-2}\hbox {s}^{-1}\)], measured at the height of the Regener–Pfotzer maximum. Curves show measurements made at northern polar latitude (geomagnetic rigidity \(R_{\mathrm{c}} = 0.6\hbox { GV}\), green curve), southern polar latitude in Antarctica (\(R_{\mathrm{c}} = 0.04\hbox { GV}\), blue curve) and at the midlatitude location of Moscow (\(R_{\mathrm{c}} =2.4\hbox { GV}\), red curve). The CR flux increase since 2010 can be seen from the comparison provided by the dashed lines, which mark the cosmic ray levels in1965 (from Stozhkov et al. 2013)
Atmospheric Conductivity Cosmic ray ionisation in the terrestrial atmosphere sustains a steady source of cluster ions, which provide the finite conductivity of air. The total conductivity, \(\sigma _{\mathrm{t}}\), is given by
where \(\mu _{\pm }\) represents the mean mobility of positive or negative ions present, \(n_{\pm }\) the associated bipolar ion number concentrations and e is the elementary charge. Ions are removed by attachment to aerosol particles and water droplets, reducing the conductivity in these regions. Both the mobility and concentration vary with atmospheric properties and composition. The mobility of ions depends on the environmental temperature and pressure, and the ion concentration is strongly affected by attachment to aerosol particles and water droplets, reducing the conductivity accordingly where the aerosols are abundant. This means that, in the Earth’s environment, where aerosols are generated both naturally and through human activities, the local air conductivity can show an anthropogenic influence (Harrison 2006; Silva et al. 2014), allowing early indirect conductivity measurements to provide an insight into historical air pollution (Harrison 2006; Aplin 2012). Together with variations in the source rate, \(q_{\mathrm{STP}}\), these lead to a variation in the conductivity with height (e.g., Harrison and Carslaw 2003). At the heights of the lower ionosphere, where photoionisation also contributes appreciably, the conductivity becomes substantially larger than in the lower atmosphere. Figure 6 shows a vertical profile of the air’s conductivity, and a calculation of the relaxation timescale, defined by \(\epsilon _0 / \sigma _{\mathrm{t}}\). This is the e-folding timescale for the discharge of an isolated particle in a conductive medium. This provides an indication of how active (in terms of the rate of charge separation) a charging process needs to be at different heights in the atmosphere. In comparison with lower troposphere air with a typical conductivity of \(\approx 10^{-14}\hbox { S}\,\hbox {m}^{-1}\) as reviewed by Rycroft et al. (2008), the planetary surface has a greater electrical conductivity, of at least \(10^{-8}\,\hbox { S}\,\hbox {m}^{-1}\). This means the air represents a low-conductivity region sandwiched between upper and lower boundaries having much greater conductivity.
Vertical variation in electrical conductivity, \(\sigma _{\mathrm{t}}\) [S/m], of the terrestrial atmosphere, as represented in the model of Rycroft et al. (2007). The dashed line indicates the change of conductivity due to thunderclouds. The equivalent electrical relaxation time is found from \(\epsilon _0/\sigma _{\mathrm{t}}\), where \(\epsilon _0\) is the permittivity of free space
3.2 Thundercloud Electrification, Lightning and Transient Luminous Events
Ionic Conductivity and Ionic Plasmas in the Terrestrial Atmosphere Most electric phenomena in the terrestrial atmosphere are carried by ions and aerosols; only in the strong transient electric fields of an evolving discharge or in the ionosphere are more electrons free and not attached to electronegative atoms, molecules or larger compounds consisting, e.g., of water molecules clustering around ions, other aerosols, up to droplets from micro- to millimetre size. Cosmic rays and radioactivity are external sources of ionisation (Sect. 3.1); they first create electron ion pairs, and then the electrons rapidly attach to electronegative molecules (mostly to oxygen) leaving the positive and negative ions in the atmosphere behind which carry the fair weather currents (Sect. 3.3).
The Electric Field in Thunderclouds builds up in two stages. In the first stage, macroscopic particles are electrically charged, and in the second stage particles of different polarity are separated by gravitation or other (mechanical) forces; in order to separate particles with different polarities, these forces need to be stronger than the electric attraction between charges of different polarity, since otherwise the electric forces would counteract the growth of the electric field. The possible charging mechanisms at work within normal terrestrial thunderclouds are reviewed, e.g., by Jayaratne et al. (1983) and Saunders (2008). An important conclusion of these reviews is that charge is efficiently separated between particles only in direct collisions.
Liquid droplets cannot experience collisions or fracture as a charging process as they would typically merge on contact, and hence they do not charge easily. However, frozen particles can collide and exchange charge. Therefore, terrestrial water clouds get electrified mostly in regions below the freezing temperature (Mason 1953), more precisely at temperatures between 0 and 40 °C. The dominant charging mechanism is thought to occur when graupel and ice particles collide. Saunders (2008) reviews the evidence from Krehbiel’s (1986) cloud measurements in 1986 “that ice crystals rebounding from riming graupelFootnote 12 in the presence of super-cooled water is a requirement of the charge transfer process”. This observation is consistent with laboratory measurements of Saunders (2008) that during collision essentially “fast growing ice surfaces charge positively, and conversely, sublimating (graupel) surfaces charge negatively”. However, further dependencies on growth velocities, etc. need to be taken into account. The particle collisions are mediated by gravity acting on large particles and by turbulent convection within the cloud. Gravity will also move the heavy positively charged graupel particles downward, while the light positive ice crystals move upward with the convective flow of the cloud air, creating charge centres and electric fields within the cloud. This particular charging mechanism is based on the intrinsic polarisation of water molecules. Macroscopic particles of different material can charge quite efficiently, too, and create electric fields and discharges. Both volcanic ash plumes, so-called dust devils in terrestrial deserts and various granular media in the laboratory, support discharges, as is discussed further in Sect. 3.4. The understanding of charging processes in volcanic ash plumes might inspire further progress on the long-standing question of charging normal thunderclouds (Yair 2008). Such normal water clouds mixed with dust have recently been observed to exhibit particularly strong and exceptional discharges (Füllekrug et al. 2013).
Due to the attachment of ions to water droplets, electric charges in clouds are particularly immobile. The conductivity in the remaining gas phase is therefore low before lightning activity starts. This low conductivity (hence low degree of ionisation, see also Fig. 2) supports a high electric field up to the moment of discharging.
The Stages of Lightning Lightning is the sudden release of the electric potential energy through the fast growth of a disperse network of ionised channels. On average, \(44\pm 5\) lightning flashes (intracloud and cloud-to-ground combined) occur around the globe every second (Christian et al. 2003). Moreover, according to OTD (Optical Transient Detector) measurements, lightning occurs mainly over land areas with an average land/ocean ratio of approximately 10:1 (Christian et al. 2003). The visible growing channels are called lightning leaders; their path is prepared by streamer coronae. While streamers are space-charge-driven ionisation fronts, leaders maintain their internal conductivity by increased temperature, molecular excitations and ionszation reactions in the discharge channel. If a conducting channel connects cloud and ground, the return stroke carries the largest current and is visible and audible as the lightning stroke; but intra- and intercloud lightning are much more likely. The stages of lightning have been described in many articles, with varying emphasis on phenomena or physical mechanisms. A few recent ones are by Bazelyan et al. (2009), Cooray (2003), Rakov and Uman (2003), Betz et al. (2009), Dwyer and Uman (2014) and Cooray (2015).
A long-standing question is how lightning can be initiated because the observed electric fields are below the classical breakdown field (where electron impact ionisation overcomes electron attachment to oxygen in the Earth’s atmosphere; e.g., Treumann et al. 2008; Helling et al. 2013), and free electrons are not available anywhere in the atmosphere. Gurevich et al. (1992) suggested that cosmic particle showers could supply free electrons and that relativistic run-away electron avalanches could develop in an electric field below the classical breakdown value. Gurevich and Karashtin (2013) recently suggested that the interplay of a cloud particle with Cosmic Rays could start the discharge. A quantitative analysis confirming this scenario is presented by Dubinova et al. (2015).
Lightning occurs not only between cloud and ground, but also within and between clouds. Also the “bolt from the blue” is a phenomenon where a lightning strike seems to appear out of a blue sky next to a thundercloud. These strikes are an indication that lightning leaders can leave the cloud also at its upper edge or in the sideward direction and then turn downwards.
Transient Luminous Events The full-scale discharge activity associated with terrestrial water clouds became known in the scientific literature only after 1989 when the first Transient Luminous Events were described (for article collections, see Füllekrug et al. (2006), Ebert and Sentman (2008)). Basically, electric potential stored in a cloud can also discharge in the upward direction as a jet up into the stratosphere or as a gigantic jet that extends into the mesosphere. The primary lightning can drive secondary discharges, namely elves, halos and sprites in the E layer of the ionosphere and in the night-time mesosphere (where the D layer of the ionosphere is located during day time)Footnote 13. Elves and halos are responses of the lower edge of the ionospheric E layer to the electromagnetic pulse and the quasi-static potential of the parent lightning stroke, while sprites propagate downward from the ionosphere into the mesosphere (so-called column sprites) and sometimes back up again (carrot sprites; Stenbaek-Nielsen and McHarg 2008, Luque and Ebert 2009). Due to similarity relations between discharges at different atmospheric densities (Pasko 2007; Ebert et al. 2010), tens of kilometres-long sprite discharge channels in the tenuous upper atmosphere are physically similar to cm-size streamer discharges at normal temperature and pressure up to corrections due to different electron attachment and detachment reactions that can explain long-delayed sprites (Luque and Gordillo-Vázquez 2012). Sprites are pure streamer discharges (Liu and Pasko 2004b, a) and therefore are less complex than lightning strokes with their streamer, leader and return stroke stages, evolving on very different scales of space, time and energy. Due to the efforts of many authors in the past 20 years, the models for streamer discharges are now becoming more quantitative, so that we now approach the quantitative understanding of sprite discharges through detailed modelling and experimental efforts (Nijdam et al. 2014).
Gamma-Ray Flashes and Other High-Energy Emissions from Thunderstorms In 1994, the BATSEFootnote 14 satellite detected gamma radiation from Earth, and it was recognised that this radiation came from thunderstorms (Fishman et al. 1994; Fishman and Meegan 1995). Later also beams of electrons (Dwyer et al. 2008) and even positrons (Briggs et al. 2011) were discovered by satellites. The Fermi Gamma-Ray Space Telescope detected a clear positron annihilation signal over Egypt from a thunderstorm over Zambia where the two events were connected in space and time through a geomagnetic field line (that electrons and positrons follow sufficiently high in the ionosphere where collisions with air molecules are negligible; Briggs et al. 2011). High-energy X-rays were also detected from lightning leaders approaching ground and from long sparks in the laboratory, see, e.g., Kochkin et al. (2012). We refer to the review by Dwyer and Uman (2014). It is clear that electrons are accelerated into the run-away regime within the electric fields inside and above the thunderstorm, where they continuously gain more energy from the field than they can lose in collisions with neutral air molecules. These collisions with molecules result in X- or gamma-ray emission (Bremsstrahlung). The gamma rays are ionising radiation and generate electron positron pairs or liberate neutrons or protons in photonuclear reactions (Babich et al. 2014).
There are two basic mechanisms discussed in the literature for the primary electron acceleration: either galactic cosmic rays with sufficient energy to penetrate deep into the atmosphere and to generate relativistic run-away electrons avalanches (RREAs) in the electric fields inside the thundercloud, or the acceleration of low-energy free electrons into the high-energy run-away regime at the tip of a lightning leader where electric fields are very high. The review by Dwyer and Uman (2014) favours the RREA mechanism, in agreement with the previous model development by the first author. The alternative is the runaway of thermal electrons at the leader tip suggested by Xu et al. (2012). Such detailed models depend on the model parameters for the background cloud field and its geometry, on the altitude of the lightning leader, but also on the collision cross-sections at the required energies that are not reliably available.
Füllekrug et al. (2013) reported on the observation of two consecutive positive lightning discharges where the first positive lightning discharge initiates sprite streamers which discharge the lightning electromagnetic field above the thundercloud. This was seen as a pulsed discharge event followed by a high-energy electron beam. A small number of stratospheric, charged aerosols were probably present as result of a Sahara dust storm and forest fires in Spain, providing a collimating electric field geometry that accelerated the electrons. This is the first simultaneous detection of radio signatures from electrons accelerated to thermal and relativistic energies above thunderclouds.
3.3 The Wilson Global Circuit
The vertical structure of conductivity in the atmosphere, with the upper and lower conducting regions each able to sustain a local potential, allows a vertical potential difference to exist between the two regions. Investigations using balloon measurements from the late 1800s showed a variation in potential with atmospheric height (Nicoll 2012), with the upper conducting region being about 250kV positive with respect to the lower conducting region. The finite conductivity of the intermediate atmosphere between these charged regions allows a vertical current to flow. This current was observed directly by CTR Wilson (Wilson 1906) in fair weather conditions with no local charge separation. CTR Wilson concluded that the current flow was likely to be sustained by charge separation in distant disturbed weather regions. Evidence supporting this is that the diurnal variation in Universal Time (UT) near-surface electric field, measured under fair weather conditions, is independent of where it is measured globally and shows strong similarities with the diurnal variation in active global thunderstorm area (Whipple and Scrase 1936). This diurnal variation in surface atmospheric electric field is known as the Carnegie curve, after the sailing vessel on which the original defining measurements were made (Harrison 2013).
The conceptual model that described the electrical transport across the planet between disturbed weather and fair weather zones—the global atmospheric electric circuit (Wilson 1921, 1929)—has provided a fruitful description for investigation of terrestrial atmospheric electrification, which may offer useful insights for other atmospheres (Aplin et al. 2008). Although the original reasoning used to identify the global circuit was based on current flow considerations, the wide range of timescales of the contributing processes leads to a distinction being made conventionally between the AC and DC global circuit (Rycroft and Harrison 2012).
The AC Global Circuit The upper and lower conducting regions of the terrestrial atmosphere form a simple waveguide, in which electromagnetic waves can propagate, as originally predicted by Schumann (Schumann 1952). Lightning provides a source of such electromagnetic radiation to excite waves in this cavity oscillator, and natural resonances with a fundamental mode at about 8 Hz as predicted were first observed at the Earth’s surface in the 1960s (Balser and Wagner 1960; Rycroft 1965). These natural resonances in the Earth-ionosphere cavity (Q resonator) constitute the AC global electric circuit. Somewhat surprisingly, resonances at 8, 14, 20 Hz are also observed on satellites at altitudes of several hundred km, above the ionosphere (Simões et al. 2011; Dudkin et al. 2014). Although the electric field measured is much smaller at a satellite platform compared with ground-based measurements (three orders of magnitude smaller for the first Schumann peak), the fact that it is detectable at all offers the possibility for fly-by measurements at other planetary bodies.
The DC Global Circuit Figure 7 summarises the DC current flow in the Wilson global circuit. Charge separation in disturbed weather regions leads to current flow within the ionosphere, fair weather regions and the planetary surface. The vertical conduction current density, \(J_{\mathrm{c}}\), in fair weather regions is \(\sim 2\hbox {pA m}^{-2}\), where the resistance of a unit area column of atmosphere, \(R_{\mathrm{c}}\), is about 100 to \(300\hbox { P}\Omega \hbox {m}^2\) (Rycroft et al. 2000). If horizontal layers of cloud or particles are present, the electrical conductivity is reduced because of the removal of the ions providing the conductivity by the particles. Hence, for a passive particle layer, this means that the layer also defines a region of reduced conductivity. If a current passes vertically through the passive particle layer (PPL), charging will result at the step change in conductivity at the upper and lower layer boundaries. The charging can be derived by assuming no horizontal divergence of the current (as is observed, Gringel et al. 1986) and assuming Ohm’s Law and Gauss’ Law in one dimension. For a conductivity \(\sigma _{\mathrm{t}}(z)\) varying with height z, the charge per unit volume \(\rho _{\mathrm{e}}\) is given by
where \(J_{\mathrm{c}}\) is the vertical current density and \(\epsilon _0\) is the permittivity of free space. Figure 8 shows calculations of the charging for a PPL of prescribed concentration and size. This leads to a reduction in the concentration of positive and negative ions in the same region. The gradients in conductivity at the PPL boundaries allow the charge density to be derived, either in terms of the mean charge calculated across the particles or as a particle charge distribution (Fig. 8). The charging expected at the PPL edges is clearly evident, and similar charging effects have been observed at the boundaries of layer clouds in the terrestrial atmosphere (Nicoll and Harrison 2010).
Schematic depiction of the role of ionisation from solar energetic particles (SEP), relativistic electron precipitation (REP) and galactic cosmic rays (GCR), in facilitating the current flow within the global atmospheric electric circuit. Natural sources of radioactivity include isotopes within the soil and the release of radon (from Nicoll (2014))
Simulated effect of a horizontal layer of particles through which a current flows. The panel shows profile of: (upper left) prescribed particle size and concentrations, (upper right) number concentrations of positive (\(n_+\), dashed red line) and negative (\(n_-\), solid blue line) small ions, (lower left) mean charge on particles and (lower right) particle charge distribution evaluated at the three positions marked on the lower left panel with dashed lines (assumptions: ion production rate 10 ions \(\hbox {cm}^{-3}\hbox {s}^{-1}\), vertical conduction current density \(2\hbox { pA m}^{-2}\).)
Conditions for Global Circuits The existence of global circuits in planetary atmospheres has been suggested through possible analogies with the Earth system, in which current flows between charge-separating and non-charge-separating (or “fair weather”) regions, through the enhanced conductivity zones provided by the planetary surface and the upper atmosphere (Aplin 2006, 2013). Entirely different electrical processes may be involved, such as in the global circuit suggested for Mars (Fillingim 1986; Farrell and Desch 2001) which is driven by dust, or be associated with volcanic dust electrification (Houghton et al. 2013). The basic electrical requirements for a planetary global circuit have been discussed by Aplin et al. (2008), which are
-
upper and lower conductive regions
-
charge-separating processes
-
current flow
Implied necessary conditions are (1) a sufficiently strong gravitational field to retain a gaseous atmosphere, and (2) proximity to energetic sources of radiation (e.g., a host star or a binary companion) which can form ionised layers in the atmosphere; ultraviolet and X-ray regions of the spectrum can create an ionosphere. Table 1 summarises the possible approaches which might be used to detect these necessary requirements.
Of these requirements, providing evidence in a planetary atmosphere of current flow is a particularly key aspect. In the terrestrial atmosphere, current flow was originally established using a surface electrode with an appreciable collecting area (Wilson 1906). Use of similar surface mounted electrodes is unlikely to be practical in space missions, and hence other approaches suitable to the single burst of measurements made by descent probes entering an atmosphere need consideration. If horizontal layers of cloud or particles are present in an atmosphere, which are passive electrically (i.e. not able to generate electrification internally), Eq. 4 indicates that seeking charging at the edges of particle layers provides an opportunity for the existence of vertical current flow. PPL edge charging can, in principle, be determined using a descent probe able to measure charge and detect the presence of particles, for example using the combination of electrical (Nicoll 2013) and optical (Harrison and Nicoll 2014) detectors used in the terrestrial atmosphere. Through deploying such sensing technology on a suitable platform, vertical current flow in a planetary atmosphere in the solar system may be inferred without the need for surface measurements.
In summary, the bigger picture here concerns the relationship between physical processes external to an atmosphere and active processes within it. Future work in this area therefore needs to consider:
-
The range of charge separation processes which can occur in different planetary environments and the controlling influences on current flow, which may be internal or external in origin. Charge separation occurs between the same materials (e.g., the dust electrification on Mars), different phases of the same substance (e.g., water-ice-hail interactions on Earth) or between different substances and phases.
-
In the last set of circumstances, account of the local atmospheric chemistry and its influence on charging will be needed. Some consideration should be given to the nature of the charge separation and whether simple electrical analogies in terms of constant current or voltage sources are appropriate.
-
In terms of the current flow, there may be significant external influences, including the triggering of lightning-like discharges by external variations (e.g., Owens et al. 2014). For some planetary body configurations, there may also be direct tidal effects on the conductive regions in the atmosphere or other coupled interactions such as those between Saturn’s magnetosphere and Titan.
3.4 Electrical Charging in Volcanic Plumes and Volcanic Lightning Experiments
Electrical Charging in Volcanic Plumes Volcanoes generate some of the most violent forces in nature and are not only present on Earth but on several of the planets and moons in our solar system, e.g., on Venus and Io (Shalygin et al. 2015) or, more generally volcanism can occur on rocky planetary objects with a hot core. The set of presently known extrasolar planets contains also planets (e.g., 55 Cancri e, Demory et al. 2011) that may be classified as volcanic due to their proximity to their host star and their high bulk density that indicates a rocky bulk composition. On Earth, volcanic lightning is often present during eruptions (see Harrison and Mather 2006; McNutt and Williams 2010 for reviews), providing strong evidence for the electrical charging of volcanic ash as well as demonstrating that charge separation sufficiently large to initiate breakdown within the volcanic plume environment. Numerous mechanisms have been suggested by which volcanic ash in Earth-based volcanoes can become electrified including fractoemission (James et al. 2000), contact or triboelectrification (Houghton et al. 2013) and thunderstorm-style ice-contact charging (’dirty thunderstorm’ mechanism; Williams and McNutt 2005), each of which may occur at different altitudes throughout the plume (Fig. 9). Understanding the relative importance of these mechanisms in generating volcanic lightning during an eruption is required in order to explain observations of volcanic lightning and why some eruptions produce lightning and not others. On Earth, volcanic lightning provides the ability to detect explosive volcanic plumes remotely, as well as estimates of the minimum plume height to be made in the absence of other observational methods such as radar and lidar (Bennett et al. 2010). Electrostatic forces may also play an important role in modulating the dry fallout of ash from volcanic plumes, potentially important for modelling of ash transport downwind of volcanic eruptions (Harrison et al. 2010), although much future research is required in this area.
Sketch of volcanic charge generation mechanisms thought to be active in volcanoes on Earth. Fractoemission, caused by the fragmentation of magma, is thought to occur close to the vent, whereas triboelectric charging (frictional contact charging) can occur throughout the plume, wherever particles are present. The dirty thunderstorm mechanism requires ice particles in the plume and is only likely to be important for plumes which reach altitudes with temperatures that allow freezing to occur
Away from Earth, active volcanism exists on several bodies in our solar system. Volcanic eruptions on Venus are typically associated with fluid lava flows—there is no evidence of the explosive ash eruptions that occur frequently on Earth which are often associated with active volcanic lightning. Conversely, Io, one of the Jupiter’s moons, often exhibits signs of explosive eruptions. Io’s eruptive columns reach to hundreds of km altitude in contrast to Earth-based plumes which may reach up to 40 km in rare circumstances (Oppenheimer 2003). The existence of volcanoes on other bodies in the solar system (e.g., Venus, Airey et al. 2015) suggests the possibility of charging mechanisms associated with such volcanic activity, which may or may not be similar to those on Earth (Fig. 10). This leads to the possibility that studying volcanic lightning on Earth may provide insight into dust charging processes in environments where mineral dust is common such as in the atmospheres of brown dwarfs or extrasolar planets as detailed in Sect. 5.
Results of a rapid decompression experiment with volcanic ash (\(250\,\upmu \hbox {m}\)). Panel A Electric potential recorded by the antennas, pressure at the nozzle and angle of the core of the flow (\(\beta\)) and the surrounding turbulent shell (\(\alpha\)) with respect to the vertical. Shaded area indicates the time window of lightning occurrence. Panel B Rest-frame of the high-speed videos showing the particle-laden jet is well-constrained and surrounded by the turbulent sheath of finer ash and lightning flashes are recorded. Panel C Schematic section of the jet showing the main flow core (coarser particles; dark grey shadow), the turbulent shell (finer particles; light grey shadow) and the respective opening angles (\(\beta\) and \(\alpha\)) to the vertical. Panel D Number of discharges \(> 0.2\hbox { V}\) recorded at the lower antenna in experiments with bimodal glass beads (500 and 50 μm) as a function of the wt% of finer particles
Volcanic Lightning Experiments Explosive volcanic eruptions are commonly associated with intense electrical activity and lightning. A number of techniques have been used to study the electrical activity of volcanic plumes including close-range VHF lightning mapping arrays (e.g., Thomas et al. 2007; Behnke et al. 2013), long-range VLF lightning observations (e.g., Bennett et al. 2010) and optical lightning detection using high-speed cameras (Cimarelli et al. 2015). Direct measurement of the electric field near the vent, where the electrical activity in the volcanic plume is first observed, is difficult, but a handful of studies exist including those by Anderson et al. (1965), Gilbert et al. (1991), James et al. (1998), Miura et al. (2002). Laboratory-based experiments are also essential to studying volcanic charge generation mechanisms in a controlled environment and can allow different charge mechanisms to be examined individually. Laboratory experiments by Büttner et al. (2000) and James et al. (2000) have studied the fractoemission mechanism, whereby James et al. generated silicate particles by fracture during collisions between pumice samples. During the experiments, there was evidence of ion release during the fracture process. Triboelectrification processes have also been studied in the laboratory using both silica beads (Forward et al. 2009) and volcanic ash (Houghton et al. 2013), where it has been demonstrated that the particle size distribution has important effect on the magnitude of the charge generated.
Cimarelli et al. (2015) have achieved an analogue of volcanic lightning in the laboratory during rapid decompression (shock tube) experiments of gas–particle (both natural volcanic ash and glass beads) mixtures under controlled conditions. Experiments show that more discharges are generated for finer starting material and that there is no correlation between the number of discharges and the sample chemistry (Taddeucci et al. 2011). The experiments highlight that clustering of particles trapped in the turbulent eddies of the jet provides an efficient mechanism for both charge generation (tribocharging) and lightning discharge as observed in volcanic plumes. Clusters form and break-up by densification and rarefaction of the particle-laden jet. A cluster’s lifetime is regulated by the turbulence time scale and its modification during the evolution of the jet flow. Cluster generation and disruption provide the necessary conditions for electrification of particles by collision, local condensation of electrical charges and its consequent separation, thus creating the electric potential gradient necessary to generate lightning discharges. Clustering can be particularly effective in the presence of prevalently fine ash-laden jets exiting volcanic conduitsFootnote 15 thus facilitating ash aggregation in the plume (Taddeucci et al. 2011). Further charging by the formation of hydrometeors (i.e. water droplets or ice particles) in the upper regions of the plume (Eaton et al. 2012) could provide additional mechanisms of plume electrification, although the presence of ice particles in the plume (from low-latitude volcanoes where surface temperatures are high and plume heights low (Aizawa et al. 2010)) can be ruled out in many monitored eruptions that produced electrical discharges, thus confirming the primary role of particle self-charging in the generation of volcanic lightning. The experiments show the direct relation between the number of lightning discharges and the abundance of fine particles in the plume as observed in the case of 2010 Eyjafjallajökull eruption in Iceland, as well as in many other ash-rich eruptions or explosive episodes, independently from their eruption magnitude and magmatic composition. Improved lightning monitoring at active volcanoes may provide first-hand information not only on the location of the eruption but more importantly on the presence and amount of fine ash ejected during an eruption, which is a fundamental input in ash-dispersion forecast models. Multi-parametric observations of volcanic plumes are therefore needed to fully understand the favourable conditions for volcanic lightning generation and to correctly interpret electrification and discharge phenomena to understand plume properties. Newly designed shock-tube experiments open new perspectives in the investigation of self-charging mechanism of particles that are relevant for atmospheric phenomena on Earth (such as dust storms and mesocyclones) and other planetary bodies, as well as industrial processes involving granular materials.
3.5 Kinetic Gas-Chemistry During Discharges in Solar System Planet Atmospheres
Atmospheric discharges have been detected on all gaseous giants of our solar system (Yair 2012) and are therefore likely to be present on extrasolar planets (Helling et al. 2011; Aplin 2013; Helling et al. 2013; Bailey et al. 2014). Transient Luminous Events (TLEs) occur in the Earth’s atmosphere (see Sect. 3.2) where they influence the local gas composition and with that potential observational features.
A number of models to study in detail the non-equilibrium kinetic chemistry of TLEs have been developed (Gordillo-Vázquez 2008; Gordillo-Vázquez and Donkó 2009; Gordillo-Vázquez and Luque 2010; Parra-Rojas et al. 2013; Parra-Rojas et al. 2015). These studies have allowed the optical signatures and spectra of TLE optical emissions (from the UV to the NIR) to be quantified as should be seen from ground, balloons, planes and from space (e.g., Gordillo-Vázquez et al. 2012), illustrating good agreement with available observed spectra.
Kinetic gas-chemistry models have been developed to calculate the TLE-induced changes in the electrical conductivity (Gordillo-Vázquez and Luque 2010) of the Earth’s upper atmosphere showing good agreement with available measurements. The importance of some key kinetic mechanisms (electron detachment from \(\hbox {O}^-\)) has been shown to explain the inception of delayed sprites (Luque and Gordillo-Vázquez 2012). The impact of lightning on the lower ionosphere of Saturn and the possible generation of halos and sprites has been modelled by Dubrovin et al. (2014). This allowed us to study the coupling between atmospheric layers in Saturn and Jupiter due to lightning-generated electromagnetic pulses and to predict different possible optical emissions from elve-like events triggered by lightning in the giant planets (Luque et al. 2014). The extension of such an approach to extrasolar atmospheres requires a dedicated kinetic gas-chemistry network which is able to handle a considerably wider range of chemical compositions and temperatures than for the solar system planets (see, e.g., the STAND2015 network from Rimmer and Helling 2015).
3.6 Future Studies
On Earth, the quasi-static and the radiation components of the lightning electric field have comparable effects on the secondary TLE-discharges in the upper atmosphere. However, in planets with larger typical distances, the radiation field can be stronger than the quasi-static field (Luque et al. 2014). The radiation field is responsible for ring-shaped expanding emissions of light at the lower edge of the ionosphere. It is therefore speculated that giant TLEs may exist in giant planets. This new area of research has introduced many open questions, such as:
-
Can lightning-related TLEs occur on Saturn and Jupiter? What kind of TLE could be observable, what would be the required sensitivity and appropriate wavelength range? Could the optical flash emission on Saturn and Jupiter originate from other discharge processes than conventional lightning discharges?
-
Can lightning-related TLEs take place in the upper layer of the Venusian atmosphere? How would lightning influence the chemical composition and electrical properties of the Venusian upper atmosphere?
-
No direct optical lightning observation is available for the atmospheres of Neptune and Uranus, only indirect radio detection possibly associated with electric discharge events. What could be the lightning mechanisms on Neptune and Uranus?
-
What would be the possible atmospheric optical and chemical signatures in the case that lightning activity exists in the atmospheres of extrasolar planets and brown dwarfs?
4 Electrification on the Moon and on Asteroids
Charged dust grains and dusty plasmas are known to constitute the near-surface environment of airless bodies such as the Moon, asteroids, comets, Saturn’s rings and many planetary moons. Our solar system, being exposed to a variety of plasma conditions and solar activity, provides a natural laboratory to study dust charging and dynamics. Charging of neutral dust particles occurs when dust grains are exposed to space plasma, for example, through interactions with the solar wind. These plasma interactions are believed to be the reason for many of the observations reported in the literature (e.g., spokes in Saturn’s B ring and dust streams ejected from Jupiter (Horányi et al. 2004)).
In dusty plasmas, dust particles have the ability to alter the properties of various plasma waves and instabilities (e.g., D’Angelo 1993; Kopnin et al. 2009; Rao 1993, 1995). In some cases, the presence of dust can affect the instability (e.g., Sen et al. 2010), whereas in other cases the presence of dust can drive new unstable modes (Rao and Shukla 1990). Both high- and low-frequency modes can be excited. High-frequency modes are excited because the dust can modify the relative drift between the plasma species (electrons and ions) or simply reduce the electron density. Low-frequency modes (both electrostatic and electromagnetic) occur when the dust dynamics are considered. One of the interesting modes is the dust-ion acoustic instability which is driven by the relative drift between the dust and the plasma (Rao 1993). An example of such a scenario exists in Saturn’s E-ring where the plasma co-rotates with the planet, while the dust follows Keplerian orbits. Rosenberg (1993) has shown that the relative speed between the dust and the plasma to drive the instability is of the order of the ion thermal speed. By introducing the magnetic field new modes called dust-magneto-acoustic waves are excited according to the theory (e.g., Rao 1995) which is the generalisation of the electrostatic dust-ion acoustic wave, first reported by Shukla and Silin (1992).
Beyond the macroscopic behaviour of dusty plasmas, understanding dust charging in the space environment is important for several reasons. The variable exposure of the Moon to solar wind, UV radiation, terrestrial magnetospheric plasmas and meteoroid impacts results in a time-dependent, complex plasma environment. The charging, possible subsequent mobilisation and transport of fine lunar dust have remained a controversial issue since the Apollo era and have been suggested to lead to the formation of a dusty exosphere, extending tens to hundreds of kilometres above the surface. Recent international interest and potential return to the Moon in the near future has been declared by major space agencies around the world (NASA, ESA, JAXA, Russia, China). The success of these missions depends largely on the ability to understand and predict the effects of dust on the lunar environment in order to prepare crews and equipment to withstand such a harsh environment. While NASA’s Lunar Atmosphere and Dust Environment Explorer (LADEE) (launched on 6th September 2013) is the first dedicated mission to make measurements of lunar dust composition, other missions are planned. For example, there are dust detectors on the Russian lander mission to the Moon’s South pole (Luna Glob, 2016) and a joint Russian-Indian (Lunar-Resurs) mission in 2017/18.
Asteroids and comets are similarly complex environments, of interest because they are formed from material originating from the time when the solar system was formed. Precise isotope ratio measurements give insights into the formation of our planetary system. Carbonaceous compounds from some primitive asteroid, that have not been affected by weathering other than in interplanetary space, could have contributed to the origins of life through delivery of organic compounds to Earth. There is therefore substantial scientific interest in measuring the surface material of asteroids and comets. Examples of successful missions include NASA’s Deep Impact and Stardust (see review by Ververka 2013) and the European Rosetta mission’s Philae lander which touched down on the comet 67P/Churyumov-Gerasimenko in November 2014 (e.g., Todd et al. 2007). The mass spectrometry needed to understand the rocky particles on the surface of asteroids (regolith: dust, soil, broken rock, and other related materials and is present on Earth, the Moon, Mars, some asteroids, and other terrestrial planets and moons) is too sophisticated for comparatively simple spacecraft-borne instrumentation, and this has motivated several sample return missions aiming to return regolith to Earth for more detailed analysis. The Japanese Hayabusa mission collected a sample from asteroid Itokawa in 2005, NASA’s Osiris-Rex mission visits asteroid Bennu in 2016, and a European mission, Marco Polo-R, was also recently studied in detail (Michel et al. 2014).
4.1 Charge Effects on the Moon
In its orbit, the Moon is exposed to the incoming solar wind when it is not in the Earth’s magnetosheath where most of the plasma interacts with the Moon’s surface, forming a wake region behind the lunar obstacle. The exposed (sunlit) surface is charged positively to about +5V due to high photoelectron current, but on the shadow side, the inability of ions to fill in the plasma void results in regions with energetic electrons, which will subsequently charge the surface negatively to a few hundred volts in normal conditions or up to a few thousand volts in extreme cases. The charging from galactic cosmic rays is negligible in comparison with the effects of the solar wind. Like the Moon, asteroids have dusty plasma environments, with similar charging mechanisms such as from space plasmas or the solar UV flux (Lee 1996).
At midpoint between the sunlit and the night side of the Moon, the solar wind passes through almost parallel to the surface. At much lower negative potential compared to the night side, this lunar terminator region has been found to be the source of “streamers” or “horizon glow” as observed by astronauts during the Apollo mission. It is found that the glow is produced by the scattering of sunlight by dust particles originating from the surface, a result to be confirmed by LADEE. It is thought that the dust on the lunar surface is charged by the Sun’s UV radiation and that other processes can contribute, such as solar wind plasma, secondary electron emission and triboelectric charging. The repulsive electric field between the dust and the surface causes the dust to levitate from the surface. Similar mechanisms are expected to act on asteroids. Although dust charging and levitation have been extensively discussed (e.g., Whipple 1981; Goertz 1989), these processes are not yet fully understood for the complex lunar surface where both the topology and orbital configurations of the Moon add to the complexity. Recent development of 3D dusty plasma code based on Space Plasma Interaction Software (SPIS) (Anuar et al. 2013; Hess et al. 2015) has provided a useful tool to simulate many possible scenarios on lunar surface such as lunar surface charging, shadowing phenomena and dust levitation. Figure 11 presents time-sequence simulations of the release of dust outside the rim of a lunar crater. At the terminator (top panels), the presence of strong negative electric fields repels dust particles, preventing them from reaching the basin of the crater. On the dayside (bottom panels) dust is attracted towards the middle of the crater basin due to the basin having a lower surface potential than the rim surface.
In the lunar environment, a controversial and an open question is the high-altitude component of the lunar dust: what is the maximum height that dust can be observed? The topology and the orbit of the Moon itself pose interesting questions such as:
-
What is the charge density distribution on the surface as a function of local time and how does it change along the orbit as the Moon enters the Earth’s magnetosphere?
-
What is the plasma density distribution above the lunar surface, and how does it change with height and time as a result of interaction with dust particles?
-
What is the configuration of the local small-scale electric fields? How do the vertical and horizontal components of the surface electric fields evolve during the passage of the sunlit–dark boundary, and along the lunar orbit?
-
How do magnetic anomalies on the Moon alter the surface electric fields and plasma?
Time-sequence simulations of the release of dust outside the rim of a lunar crater for two regions: terminator (top panels) and dayside (bottom panels). The crater of 5 m diameter is modelled as a opening in the bottom of the panels which represents the surface of the Moon. The x and y axes represent the lunar surface and the height of the simulation, which are 45 and 60 m, respectively
4.2 Charge Effects on Asteroids
In the case of an asteroid, there are possible electrostatic effects on, firstly, surface material and, secondly, through the electrostatic effects of a spacecraft visiting an asteroid, which could influence the outcomes of sample return missions. Asteroids become charged by cosmic rays, the solar wind and photoelectron emission. For asteroids in the solar system, the charging effects of cosmic rays are negligible in comparison with the solar wind’s effect on the nightside and photoelectron charging on the dayside. The most direct mechanism for charging effects on asteroids views electrostatic processes as one type of “space weathering” which is a broad term for surface modification of these bodies. Space weathering is relevant for asteroid sample return missions since it refers to processes that could physically and chemically modify the sample from its “pristine” state, thought to be representative of the early solar system. As photoelectric levitation of dust particles on the surfaces of asteroids is expected to occur, charging effects could modulate the size distribution, by redistribution of regolith, for example, through “ponding” in craters. Modification of the size distribution could also have more complex effects for the asteroid’s density and orbital evolution (Aplin et al. 2014).
Recent models (Aplin et al. 2014) considered the electrostatic implications of a spacecraft visiting an asteroid and found that photoelectric shadowing from the spacecraft itself was substantial. This shadowing will generate electric fields in the sampling region, a hitherto neglected process that could modify the sample to be collected. Aplin et al. (2014) demonstrated that simple isolated electrodes mounted on a spacecraft could measure the screening from the spacecraft, and, with careful choice of position, these electrodes could also measure the minimally disturbed electrical environment. Figure 12 shows modelled electric fields at the surface of the asteroid Itokawa. The dayside is assumed to be at +5V, and the nightside at \(-\)1000 V (Aplin et al. 2011), resulting in high electric fields at the terminator. Further work is needed to consider other electrostatic effects of a sample return mission, for example the mechanical lofting of particles from spacecraft touchdown, which would become charged. Triboelectric (frictional charging) effects could also be significant. Although both Martian analogue and lunar material tribocharge efficiently (e.g., Aplin et al. 2012; Forward et al. 2009), triboelectric effects have not been considered in the asteroidal (as in Fig. 12) or lunar environment. Triboelectric charging could occur both from collisional processes between lofted regolith, and potentially more significantly for human exploration and sample return, from interactions between spacecraft and the environment, such as sampling mechanisms or rovers.
Four viewing angles of 3D electrostatic modelling of the surface electric field for the asteroid Itokawa (after Aplin et al. 2011). The highest electric fields exist at the terminator region. Effects of surface topography on the electric field can also be seen
There is clearly much work to be done in understanding the mechanisms involved in dust charging and their effects. For the asteroid case, dust needs to be included in the simulations as well as more realistic representations of the spacecraft geometry, so that shadowing effects can be studied more carefully.
5 Charge Processes in Extrasolar Atmospheric Environments
Charge processes and their effects occur in many astrophysical environments. This section focuses on extrasolar objects where charge and discharge processes introduce feedback cycles similar to those discussed previously. This section summarises a field of research on cool extrasolar objects which starts to emerge as the result of recent progress in X-ray and radio observations of brown dwarfs. Brown dwarfs are objects with mass intermediate between stars and planets (Fig. 1; for a review see Helling and Casewell 2014). Since they are not sufficiently massive for hydrogen burning in their core, they cool during their entire life time. Brown dwarf atmospheres therefore evolve from the state of a warm stellar atmosphere into an atmosphere as cool as the atmospheres of solar system planets. The oldest brown dwarfs are amongst the oldest objects in our Universe. Very-low mass stars and brown dwarfs are collectively known as ultracool dwarfs.
Charge processes are important also in star and during planet formation in protoplanetary disks. Ionisation processes are suggested to help the first steps of planet formation as demonstrated by microgravity coagulation experiments at the International Space Station (Konopka et al. 2005; see also Sect. 3.4) and to allow the star to continue to accrete mass through the propolanetary disk.
Planets and stars do have magnetic fields. The magnetic field strength and geometry differ for different stars (Donati and Landstreet 2009) which has implications, e.g., the size of a planetary magnetopause or the high-energy radiation impact into a planetary atmospheres (Vidotto et al. 2014; See et al. 2014). Stellar magnetism changes with mass and rotation (as an indicator of the age of some stars) of the objects (Donati et al. 2008; Morin et al. 2008, 2010; Vidotto et al. 2014) introducing an additional complexity in the astrophysical context of atmospheric electrification. Brown dwarfs can have magnetic field strengths of \(1000{\hbox {G}}\ (= 0.1{\hbox { T}})\).
This section first summarises recent multi-wavelength observation of brown dwarfs as the best detectable ultracool and planet-like objects (Sect. 5.1). Section 5.2 addresses ionisation mechanisms in ultracool atmospheres, and Sect. 5.3 summarises recent ideas for ionising protoplanetary disks through which stars grow and planets form.
5.1 Multi-Wavelength Observations of Activity on Ultracool Dwarfs
Below the mid-M spectral type stars (\(T_{\mathrm{eff}}<3200\,\hbox {K}\); for definitions see the Appendix), a strongly declining H\(\alpha\) emission indicates a weakening of chromospheric activityFootnote 16 (Gizis et al. 2000; Kirkpatrick et al. 2000; Liebert et al. 2003; Reiners and Basri 2008; Williams et al. 2014). X-ray observations support this finding: While X-ray detections are common for late-M spectral types (\(T_{\mathrm{eff}}>3400\,\hbox {K}\)), the X-ray luminosity declines steeply for L-type brown dwarfs (\(T_{\mathrm{eff}}<2000\,\hbox {K}\); Williams et al. 2014). By contrast, brown dwarfs are very bright radio emitters, but no correlation between X-ray and radio emission exists as is established for stars and solar events (Güdel-Benz relation, Benz and Güdel 1994). Since the discovery of the first radio emitting brown dwarf by Berger et al. (2001), numerous surveys have detected radio emission at GHz frequencies in nearly 200 objects (Berger 2002, 2006; Berger et al. 2010; Hallinan et al. 2006, 2007, 2008; McLean et al. 2012), including emission in the coolest brown dwarfs with spectral types as late as T6.5 (Route and Wolszczan 2012). In twelve of these objects, the radio emission is highly polarised, coherent and pulses on the rotation period of the dwarf. These properties suggest that the source of the radio emission is the electron cyclotron maser instability (CMI; Wu and Lee 1979). The electron cyclotron maser mechanism has been shown to be responsible for the auroral kilometric radiation on Earth (see, Trakhtengerts and Rycroft 2008; Speirs et al. 2008; Vorgul et al. 2011). Figure 13 shows a light curve of a M-dwarf (TVLM 513-46546) of spectral type M9.5 which shows clear and periodically repeating emission peaks at 8.44 GHz.
Light curves of the total intensity (Stokes I) and the circularly polarised (Stokes V) radio emission detected at 8.44 GHz from TVLM 513-46546, an M9.5 dwarf, taken from Hallinan et al. (2007). Right circular polarisation is represented by positive values, and left circular polarisation is represented by negative values in the Stokes V light curve. Bursts of both 100 % right circularly polarised emission (an example is highlighted as “RCP”) and 100 % left circularly polarised emission (an example is highlighted as LCP) are detected with a periodicity of 1.96 h
In the solar system, planets have been extensively shown to be closely associated with auroral emission, caused when electrons moving along the magnetic field lines impact the atmosphere. Nichols et al. (2012) show that a model designed to explain Jupiter’s aurora (Cowley and Bunce 2001) is able to explain the observed radio fluxes in the ultracool dwarf “pulsars”Footnote 17 of order \(\hbox {MW Hz}^{-1}\). It could therefore be possible that the radio emissions of some ultracool dwarfs are powered by auroral currents. If this is true, there are profound implications for the importance of ionisation processes on ultracool dwarfs. The current system described by Nichols et al. (2012) requires, however, both a seed ionisation in the atmosphere and a plasma in the magnetosphere to operate. In turn, the impact of auroral electrons on the atmospheres is likely to be dramatic; while Jupiter’s aurora increase the atmospheric conductivity by a factor of 1000 (e.g., Strobel and Atreya 1983; Millward et al. 2002), the radio power of ultracool pulsars is 10,000 times that of Jupiter. Jupiter’s seed plasma is largely driven by the solar wind and the volcanically active Jupiter moon Io. Brown dwarfs will not have such external plasma sources, unless they are part of a binary system with mass transfer.
It is likely that these aurorae are linked to optical variability seen in the ultracool dwarf pulsars. This association is suggested by the fact that five of the six ultracool dwarf pulsars that have been observed at optical wavelengths show periodic variability on the same period as the radio emission. For comparison, \(\sim 5\,\%\) of randomly chosen ultracool dwarfs show periodic variability. While the exact mechanism producing this optical variability is not yet clear, multi-colour observations of one ultracool dwarf pulsar have ruled out starspots as the cause (Littlefair et al. 2008).
Near-IR Signature of Chromospheric Activity in Brown Dwarfs Recent near-IR observations with the AKARI satellite can only be explained under the assumption that a chromosphere comparable to the solar chromosphere is present. Theoretical studies of brown dwarf atmospheres predict that such low-temperature atmospheres are dominated by molecules and dust and that they can be well modelled by simple radiative equilibrium assuming thermodynamic equilibrium. However, AKARI observations in the near-infrared wavelength range suggest that also chromospheric activity plays an important role for the atmospheric structure, in particular for early-type brown dwarfs (Sorahana et al. 2014). Deviations between theoretical model spectra and observed spectra around 3.0 and \(4.5\,\upmu \hbox {m}\), sensitive to the upper atmospheric structure of brown dwarfs, suggest an additional heating source in the upper atmosphere. The comparison of the model spectrum with the observed spectrum for a L4.5-type brown dwarf with moderate \(\hbox {H}\alpha\) emission, 2MASS J2224-0158, is shown in Fig. 14 as an example. Sorahana et al. (2014) construct a simple model that includes heating due to chromospheric activity which results in a dramatic change of the chemical structure of the atmosphere. The resulting model spectra of early-type brown dwarfs with chromospheric heating considerably improve the match with the observed spectra. This result suggests that chromospheric activity is essential to understanding the near-infrared spectra of brown dwarfs and that MHD processes can heat the upper atmosphere. A similar conclusion was reached by Schmidt et al. (2015) who photometrically examined a sample of 11820 M7-L8 dwarfs. Rodriguez-Barrera et al. (2015) have used a grid of model atmosphere simulations to demonstrate that it is reasonable to expect the formation of an ionosphere and, therefore, also a chromosphere in ultracool atmospheres such as on brown dwarfs.
Irradiated Brown Dwarf Atmospheres Only a handful of systems are known where a brown dwarf is heated by a hot companion. These brown dwarfs have close orbits of a few days, and they transit their host star, giving a measure of the brown dwarf’s radius, which is inflated by the energy input from its star. White dwarf—brown dwarf binaries provide a case where the brown dwarfs are not outshone by their companions, and therefore an opportunity to study irradiated brown dwarfs. In five of these systems, WD0137-349B (Maxted et al. 2006), NLTT5306 (Steele et al. 2013), SDSS141126\(+\)200911 (Beuermann et al. 2013), WD0837\(+\)185 (Casewell et al. 2012) and GD1400B (Farihi and Christopher 2004), the brown dwarf is known to have survived a phase of common envelope evolution.Footnote 18 WD0137-349 is the best studied system. It is photometrically variable at all wavelengths from the V band though to \(8.0\,\upmu \hbox {m}\). These variations are at the orbital period of the system and peak at \(4.5\,\upmu \hbox {m}\). Converting the dayside and nightside flux to brightness temperature (peak blackbody temperature with that flux at that wavelength) shows a temperature difference between the two hemispheres of \(\sim 500\hbox { K}\), and a possible temperature inversion in the atmosphere. Casewell et al. (2015) compare the observed photometry fluxes (i.e. radiative fluxes measured in a certain wavelength interval) to models of irradiated brown dwarfs and show that the data are best fit by models that incorporate full-energy circulation around the brown dwarf, but do not contain a temperature inversion. However, at \(2\,\upmu \hbox {m}\) (K band) and at \(4.5\,\upmu \hbox {m}\), the flux of the brown dwarf is still much brighter than the model predicts. Casewell et al. (2015) suggest that UV irradiation can cause photochemical reactions in the upper brown dwarf’s atmosphere that produce large hydrocarbon molecules causing the brown dwarf to be brighter at 2 and \(4.5\,\upmu \hbox {m}\) as were demonstrated for cosmic ray impact by Rimmer et al. (2014).
Brightness temperatures for WD0137-349 on the irradiated (circles) and unirradiated (open boxes) sides of the brown dwarf. The error bars on the X scale represent the widths of the filters used. Solid lines are models that use full circulation and energy transport from the heated to non-heated side of the brown dwarf. Dotted lines show the zero circulation models. The grey lines are models containing TiO and black lines for the non-TiO model. The models represent the flux on the dayside only. The H and \([5.8]\,\upmu \hbox {m}\) temperatures for the unirradiated side are upper limits only (diamonds), derived from the white dwarf’s flux (Casewell et al. 2015)
5.2 Ionisation Processes in Ultracool Atmospheres
Brown dwarf and planetary atmospheres are spectroscopically characterised by a rich ensemble of molecules (e.g., SiO, TiO, VO, CO, \(\hbox {H}_2\hbox {O}\), FeH) which led to the conclusion that such atmospheres are too cool for thermal ionisation to significantly influence the local chemistry or energy content. But brown dwarfs and extrasolar planets exist in a larger diversity and, hence, are exposed to very different environments: The cosmic ray flux will be different in an interstellar environment than in the solar system (compare Sect. 3). The chemical composition of the gas in atmospheres outside the solar system causes the formation of mineral clouds where the cloud particles are composed of a mix of silicates, iron and metal oxides (Helling 2003, 2009; Helling and Rietmeijer 2009), very similar to volcanic ash. Extrasolar mineral clouds are much larger than terrestrial clouds due to the larger extension of the atmospheres of brown dwarfs and giant gas planets. Also such clouds are susceptible to charge and discharge processes through cosmic rays (Rimmer and Helling 2013) and turbulence-enhanced dust-dust collisions (Helling et al. 2011). The study of the breakdown condition in non-solar system atmospheres suggests that different intracloud discharge processes dominate at different heights inside mineral clouds: local coronal (point discharges) and small-scale sparks at the bottom region of the cloud where the gas density is high, and flow discharges and large-scale sparks near, and maybe above, the cloud top (Helling et al. 2013). Bailey et al. (2014) apply scaling laws to demonstrate that discharges will propagate farther in brown dwarf atmospheres than in atmospheres of giant gas planets.
Brown dwarfs can be irradiated by a binary companion (Maxted et al. 2006; Casewell et al. 2013, Sect. 5.1) resulting in similar global circulation patterns as demonstrated for irradiated giant gas planets (e.g., Knutson et al. 2007; Dobbs-Dixon and Agol 2013). If such a wind of sufficient high speed hits a sufficiently pre-ionised gas, Alfvén ionisation can produce bubbles of gas with a degree of ionisation of \(\sim 1\) (Stark et al. 2013). The surrounding atmosphere remains in its low degree of ionisation leading to an atmosphere with a time-dependent and spatially intermittent degree of ionisation. A sufficient degree of ionisation is the precondition to understand the magnetic coupled atmospheric gas responsible for radio emission in brown dwarfs (Sect. 5.1), and from magnetically driven mass loss of extrasolar planetary atmospheres (Tanaka et al. 2014). Other mechanisms for planets to lose mass are related to their host star’s radiation field (Murray-Clay et al. 2009).
An important input for understanding ionisation processes is the global atmospheric structure, and results from radiative-hydrodynamic simulations are therefore discussed in more detail below.
Large-Scale Modelling of Globally Circulating Extrasolar Atmospheres A prominent sub-class of extrasolar planets are the short-period gaseous planets. They are (and due to observational constraints will remain) the best characterised of all extrasolar planets. The short periods (\(\sim 3\hbox { days}\)), gaseous nature and largely circular orbits suggest that the rotation rate of these planets is tidally locked to their orbital period. The result is a stationary day–night heating pattern across the surface. The proximity to their host stars means that the hot daysides will be highly irradiated, reaching temperatures of several thousand degrees.
The large longitudinal temperature gradient between the day and night hemispheres drives atmospheric dynamics that transports heat from day to night sides. The efficiency of this advective transport is a subject of extensive multi-dimensional radiative hydrodynamical modelling. Phase-curve observations, consisting of infrared measurements of the planetary flux throughout the entire orbit, do suggest that the night side of the planet is somewhat cooler than the day side (e.g., Knutson et al. 2007). However, the night-side temperatures are still on the order of a thousand degrees, much larger then one would expect simply from the internal cooling of the planet. This suggests that the atmosphere is actually fairly good at transporting energy across the entire planetary surface.
The winds driven by the extreme temperatures on short-period planets are unlike any seen in any solar systems. The coupling between the (slow) planetary rotation and the temperature differential results in the development of a broad, supersonic, super-rotating equatorial jets (Tsai et al. 2014). Gas velocities at pressure levels of 0.1 bars in the well-known HD189733b can reach 5 km/s (e.g., Dobbs-Dixon and Agol 2013).
Thus, longitudinal transport and mixing, in contrast to vertical convection/turbulence as is important in Jupiter, plays a much larger role. The complexity of the atmospheric dynamics requires coupling together a dynamical model (solving the fluid equations) to a radiative model (involving the detailed opacities). Currently, models utilise molecular opacities, primarily due to species such as CO, \(\hbox {H}_2\hbox {O}\), and \(\hbox {CH}_4\). However, transit observations (Pont et al. 2013; Sing et al. 2014) taken for different wavelength bands suggest a cloud coverage throughout the atmosphere. While in hindsight based on observations of brown dwarfs or our gas giant planets this is not surprising, it makes the coupled problem significantly more complex. As the efficiency of energy transport by the gas flow depends on both the fluid velocity and the cooling timescale, the growth of cloud layers and the associated change in opacity will modify the radiative timescale and may have important consequences for energy redistribution. Conversely, the changes in the dynamics will alter the growth efficiency of clouds. Unfortunately, as with clouds on Earth, it is not at all clear if this will result in a net cooling or heating of various regions. The precision with which the local atmospheric properties, like gas temperature, cloud properties, gas composition, are modelled is crucial, and efforts are ongoing in the community by, for example, improving the treatment of the equation of state that covers a temperature range of \(250\hbox {K}\,\ldots \,6000\hbox {K}\) and a gas pressure range of \(10\mu \hbox {bar}\) to 10Mbar. The equation of state provides the abundances of opacity species (ions, atoms, molecules, cloud particles) that influence the local temperature through radiative transfer effects. Theoretical calculations now suggest that clouds should be very prevalent throughout these atmospheres (Lee et al. 2015).
MHD simulations allow first insights into magnetic coupling effects despite containing much less information about atmospheric processes than radiative-hydrodynamic circulation models. Such MHD simulations have also been inspired by studies of protoplanetary disks (site of planet formation) and solar physics (e.g., Rogers and Showman 2014). Tanaka et al. (2014), for example, have used an open magnetic flux-tube model in their ideal MHD simulation to demonstrate that under this conditions the planet could form a wind driven by Alfvén waves. Murray-Clay et al. (2009) present an extensive study of UV and X-ray driven mass loss from irradiated extrasolar giant gas planets.
5.3 Discharges in Protoplanetary Disks
Discharge in Magneto-Hydrodynamically Turbulent Gases Magneto-hydrodynamical turbulence is suggested as a mechanism to sustain the ionisation in a cool atmospheric gas. The energy dissipated from MHD turbulence is to ionise the gas. If this energy is large enough, a positive feedback loop develops where this local ionisation serves as driving mechanisms for magneto-hydrodynamical turbulence. Magneto-hydrodynamical turbulent motion in weakly ionised media continuously creates local electric fields even in the co-moving frame of the media. If the electric field is larger than the critical electric field for electron avalanche, discharge occurs in such a weakly ionised media. This idea has been proposed for the turbulence driven by magneto-rotational instability in protoplanetary disks by Si and Sano (2005) who found that energetic electrons in a Druyvesteyn distribution may produce impact ionisation in particular conditions of the dusty gaseous disks.
The atmospheres of gaseous planets and brown dwarfs are non-uniform in chemical composition for various reasons (formation of dust grains and their sedimentation, temperature stratification, occasional accretion of planetesimals, etc., see Sect. 5.2). The convection of those objects can be “double-diffusive convection” where the structure is destabilised by the diffusion of an elemental abundance gradient.
Recent numerical simulations show that the double-diffusive convection evolves into a multi-layer structure where double-diffusive convection is confined into thin layers and usual convection occupies most of the volumes, which results in very small energy flux in the radial direction (e.g., Rosenblum et al. 2011a, b). The effect of magnetic field can be important in the thin layers, since the magnetic tension force is inversely proportional to the length scale of the eddy. If the ionisation degree is kept high enough in the thin layers, the magnetic field possibly lowers the convective energy flux even further and hence slows down the gravitational contraction of those objects. Therefore, any processes that may increase the ionisation degree is important in the theory of long-term evolution of very cool brown dwarfs and gaseous planets. A simple energetics argument based on the order of magnitude calculations shows that the energy required for keeping the ionisation degree sufficiently high (magnetic Reynolds number >1) is substantially small (<10−4) compared to the available energy as a turbulent convective motion. The critical electric field for impact ionisation in the astrophysical dusty plasma is calculated in detail as a function of gas density in Okuzumi and Inutsuka (2014) who also show that the resultant Ohm’s law is highly nonlinear and requires a new method to handle the magneto-hydrodynamics in particular regime. To determine the viability of the proposed process theoretically, magneto-hydrodynamics numerical simulations incorporating the microphysics of electron impact ionisation are required (e.g., Muranushi et al. 2012, 2013).
Observation of Lightning in Protoplanetary Disks by Ion Lines Lightning, a large-scale discharge process in analogy to Earth-lightning, in protoplanetary disks has been studied as a candidate mechanism for chondrule formation, and it provides a unique window to probe the electromagnetic state of the protoplanetary disks. Evidence for strong (500–1000 G = 0.05-0.1T; Wasilewski and Dickinson 2000), transient magnetic fields is found in meteorites. As a consequence, multiple lightning models have been proposed for protoplanetary disks (Gibbard et al. 1997; Weidenschilling 1997; Desch and Cuzzi 2000; Muranushi 2010). Muranushi (2010) calculate the charge distribution of dust in a protoplanetary disk where a magneto-resonance instability produces an electromagnetic field. If the electric field potential is large enough for an ensemble of insulated but charged dust particles, a field breakdown will occur similar to the field breakdown in dust clouds of brown dwarfs and extrasolar planets (Helling et al. 2013). Different breakdown models (Townsend, Druyversteyn-Penning, Runaway) can be tested which lead to different values for the breakdown field influencing the shape of the line profile (Fig. 16, N—no field).
\(\hbox {HCO}^+\) (3-2) line profiles [Jy] at 267.56 GHz (1.1205 mm) without (left) and with (right) lightning. Lightning is here understood in analogy to Earth lightning as a large-scale discharge process. Different line styles (N, T, DP, R) indicate different breakdown models. The disk inclination of 7deg at a distance of 56 pc is similar to TW Hya. A minimum-mass solar nebula was applied, and a lightning region \(25\hbox {AU }\ldots 50\hbox { AU}\) was considered. The line flux considerably increases if lightning occurs. The ALMA sensitivity limit is 0.01 Jy for this line
Simulated integrated emissions maps [\(\hbox {Jy beam}^{-1}\hbox { km s}^{-1}\)] for the \(\hbox {HCO}^+\) line at 267.56 GHz (1.1205 mm) without (top) and with (middle and bottom row, classic Townsend breakdown model) lightning. The lightning is considered to occur in a region of \(25\hbox {AU}\ldots 50\hbox {AU}\) for the middle row, and of \(50\hbox {AU}\ldots 100\hbox {AU}\) for the bottom row. These ALMA channel maps were simulated for 10 mJy per beam of 0”.65x0”.44. \(\hbox {HCO}^+\) appears in a larger fraction of a protoplanetary disk through the effect of lightning
The electric field accelerates the free electrons that ionise the surrounding gas but also the positively charged ion species to the energy comparable to the electrons. Because the ionisation energy is a universal constant for each individual species, each ion will move with a characteristic, constant velocity in the lightning zone that is larger than the thermal gas velocity. This will be unique observational feature to detect and distinguish breakdown models in protoplanetary disks.
In this model, it is assumed that the fractional abundances of \(\hbox {HCO}^+\) relative to \(\hbox {H}_2\) is \(9 \times 10^{-9}\). The value is taken from r = 100 au, z = 2H (z is the height about the midplane, H is the pressure scale height), from the X-ray and ultraviolet disk chemistry model of Walsh et al. (2012). The underlying assumption is that \({\mathrm{HCO}}^+\) has been gradually produced and, although the \({\mathrm{HCO}}^+\) molecules may experience a sudden accelerated by the lightning electric fields, this does not contribute to the change of the number density of \({\mathrm{HCO}}^+\) in the present model.
The velocity distribution of the ion species (e.g., \({\mathrm{HCO}}^+\), \(\hbox {DCO}^+\) and \(\hbox {N}{_2}\hbox {H}^+\)) can now be derived and the line profiles simulated (Fig. 16 for \({\mathrm{HCO}}^+\)). The two-dimensional position-velocity images with lightning assumed to occur in a certain disk region (middle, bottom) is shown as simulated ALMAFootnote 19 channel maps in Fig. 17. The change in the line profiles depending on the presence of a large-scale discharge is demonstrated in Fig. 16. We found that lightning features of 10–100 mJy appear in the line profile. Using ALMA, full-disk lightning will produce \(100\sigma\) signals at 56 pc (TW Hya, Fig. 17) and \(20\sigma\) signals at 140 pc (Orion nebula; see Muranushi et al. 2015).
5.4 Future Studies
Combining the expertise available on solar system and terrestrial atmosphere research and electrical phenomena therein will help in answering some of the following questions, but might also be inspired by these questions:
-
How far can terrestrial and solar system lightning statistics guide our expectation for extrasolar environments like on extrasolar planets, brown dwarfs and in protoplanetary disks?
-
How are brown dwarf (and extrasolar planet) atmospheres affected by the irradiation of their companion (or host star)?
-
Going beyond the solar system, clouds are present in brown dwarf and exoplanetary atmospheres. What kind or which combination of atmospheric electricity phenomena could explain the required levels of ionised atmosphere to provide an explanation for the continuous radio emissions, the 656 nm and X-ray emissions?
-
What would be the possible atmospheric optical and chemical signatures in the case that lightning activity exists in exoplanetary and brown dwarfs atmospheres?
6 Conclusions
Electrification processes and electrical phenomena are ubiquitous: dust charging and discharging are linked to the electrical breakdown of gas in planetary atmospheres inside and beyond the solar system where it is involved in global circuits and the occurrence of plasma processes. Charge processes play a major role in modifying the ambient chemical composition and the transport properties of neutral gas also in protoplanetary disks where planets form. Charged relativistic grains are suggested as potential primary particles for ultrahigh-energy Cosmic Rays (Hoang et al. 2015). The following set of challenges has emerged as common for the themes of this paper which have been guided by the Workshop “Electrification in dusty atmospheres inside and outside the solar system” held in September 2014Footnote 20:
-
(a)
An increased population of ions, free electrons and radicals, lowers the chemical potential for gas-species reactions, leading to potentially observable spectroscopic fingerprints, and
-
(b)
also increases the thermal and electrical conductivity of the gas to a certain threshold, enabling more energetic phenomena such as lightning to take place or accretion to proceed during star and planet formation.
-
(c)
The presence of free charge may be transient (as in lightning), but the electrostatic influence can endure: Charging of dust and aerosols can influence the electrostatic character of the ambient atmosphere on longer length and time scales to produce small non-thermal populations of energetic particles.
-
(d)
Finite enhanced electrical conductivity can allow magnetic relaxation, and access to stored magnetic energy as a general source of excitation which in unavailable to neutral gases.
-
(e)
Non-thermal electrons may facilitate chemical reactions in ways that are classically (i.e. gas-thermodynamically) unlikely: for example, dissociative electron attachment can produce oxygen radicals at little energetic cost, leading to oxidative reactions proceeding at a rate inconsistent with ambient temperatures, or the formation of complex carbohydrates.
-
(f)
Charged dust may evolve differently from neutral dust: Long-range organisation produced by electrostatic effects could produce coherent dust dynamics that would not be possible if only fluid mechanics dominates—surface charging, leading to elongated growth (nonzero eccentricity: polarisation of light is observable), or destruction of part of the grain population by Coulomb explosion.
These themes lead to the need for:
-
Further research on dust charging mechanisms in the context of volcanic lightning, the atmospheres of brown dwarfs and exoplanets, and protoplanetary disks.
-
New instruments for future space missions to test new findings about electrical activity on solar system planets. The results might provide models that could mimic electrical activity on brown dwarfs and exoplanets.
-
Further research about the role of dust in electrical discharges in the upper atmosphere of the Earth.
-
New key insights into charging mechanisms of the Moon and asteroid fine dust grains by interacting with the solar wind and UV flux. This contributes to the fundamental knowledge of the Moon’s electric environment and will be very useful for further human missions to the Moon and unmanned missions to the asteroids.
-
3D simulations of extrasolar atmospheres including chemical and electrical feedbacks of clouds in a magnetised gas.
Notes
The Debye length is the length beyond which the Coulomb force of a charge cannot affect other charges. Strictly, the Debye length is the e-folding distance within which charge neutrality is not guaranteed, because thermal fluctuations can displace electrons relative to positive ions, leaving a small net charge.
These terms refer to approximations made in the plasma kinetic gas theory where the Boltzmann equation describes the evolution of the particle distribution function \(f({\mathbf {x}}, {\mathbf {v}}, t)\). Neglecting the collisional source term of the Boltzmann equation leads to the collisionless Boltzmann equation (Vlasov equation) from which then the MHD equations are derived, and the electric and magnetic field strengths are derived as macroscopic quantities. In a collisional plasma, the full Boltzman equation is to be solved.
The Rayleigh limit, \(Q_{\mathrm{r}}(t)\), gives the limiting size of the surface electric field that balances the surface tension: the latter provides the restoring force to return the droplet to its equilibrium spherical shape and so causes the perturbed droplet to oscillate. If the distorted outer surface of the droplet carries sufficient electric charge, then the local surface field may oppose the effect of surface tension and thus prolong the restoration to equilibrium profile, i.e. reduce the oscillation frequency. If there is sufficient surface charge, then the deformation persists, and the oscillation frequency is formally zero which defines the Rayleigh limit. Exceeding the Rayleigh limit means that the droplet is unstable to perturbation and is forced to eject charge and mass.
The atmosphere above this altitude is sometimes called ignorosphere, because above balloon and below satellite altitudes it is very difficult to explore. In particular, the density of free electrons in the lower ionosphere can now be measured only indirectly through the pattern of electromagnetic radiation that is emitted by lightning strokes and reflected by the ionosphere (Lay et al. 2010; Shao et al. 2013).
Riming graupel is a graupel particle coated with water droplets that froze immediately when they collided with the ice surface of the graupel. The surface structure of graupel deviates from a perfect crystalline structure (e.g., Blohn et al. 2009).
The volcano conduit is the pipe that carries magma from the magma chamber, up through the crust and through the volcano itself until it reaches the surface.
Chromospheric activity in the form of H\(\alpha\), X-ray or Ca II K&K line emission results from the interaction of the stellar radiation field with a hot plasma above the atmosphere of a stellar object. The hot plasma that forms the chromosphere is the result of magnetic wave dissipation into thin gases and/or the deposition of excess radiation energy.
Classically, a pulsar (a pulsating radio star) is a neutron star that is highly magnetised and rapidly rotating. The emitted radiation can only be observed when the beam is pointing towards Earth. The term “ultracool dwarf pulsar” borrows this idea of beamed, lighthouse-like radiation.
The phase of common envelope evolution in the binary star evolution involves the brown dwarf being engulfed by, and immersed in, the expanding atmosphere of the white dwarf progenitor as it evolves away from the main sequence (Fig. 15). These systems are very close and tidally locked resulting in one side of the brown dwarf continually being heated by its companion.
Atacama Large Millimetre Array, www.almaobservatory.org.
References
Airey MW, Mather TA, Pyle DM, Glaze LS, Ghail RC, Wilson CF (2015) Explosive volcanic activity on Venus: the roles of volatile contribution, degassing, and external environment. Planet Space Sci 113:33–48. doi:10.1016/j.pss.2015.01.009
Aizawa K, Yokoo A, Kanda W, Ogawa Y, Iguchi M (2010) Magnetotelluric pulses generated by volcanic lightning at Sakurajima volcano, Japan. Geophys Res Lett 37:L17301. doi:10.1029/2010GL044208
Allen JE, Phelps ADR (1977) Waves and microinstabilities in plasmas-linear effects. Rep Prog Phys 40:1305–1368. doi:10.1088/0034-4885/40/11/002
Anderson R, Bjornsson S, Blanchard DC, Gathman S, Hughes J, Jonasson S, Moore CB, Survilas HJ, Vonnegut B (1965) Electricity in volcanic clouds. Science 148:1179–1189. doi:10.1126/science.148.3674.1179
Anuar AK, Honary F, Hapgood M, Roussel JF (2013) Three-dimensional simulation of dust charging and dusty plasma using SPIS. J Geophys Res Space Phys 118:6723–6735. doi:10.1002/jgra.50599
Aplin KL (2006) Atmospheric electrification in the solar system. Surv Geophys 27:63–108. doi:10.1007/s10712-005-0642-9
Aplin KL (2012) Smoke emissions from industrial western Scotland in 1859 inferred from Lord Kelvin’s atmospheric electricity measurements. Atmos Environ 50:373–376. doi:10.1016/j.atmosenv.2011.12.053
Aplin KL (2013) Electrifying atmospheres: charging, ionisation and lightning in the solar system and beyond. SpringerBriefs in Astronomy. Springer. doi:10.1007/978-94-007-6633-4
Aplin KL, Harrison RG, Rycroft MJ (2008) Investigating Earth’s atmospheric electricity: a role model for planetary studies. Space Sci Rev 137:11–27. doi:10.1007/s11214-008-9372-x
Aplin KL, Bowles NE, Urbak E, Keane D, Sawyer EC (2011) Asteroid electrostatic instrumentation and modelling. J Phys Conf Ser 301(1):012008. doi:10.1088/1742-6596/301/1/012008
Aplin KL, Goodman T, Herpoldt KL, Davis CJ (2012) Laboratory analogues of Martian electrostatic discharges. Planet Space Sci 69:100–104. doi:10.1016/j.pss.2012.04.002
Aplin KL, Macfaden AJ, Bowles NE (2014) Modelling of an asteroid photoelectron sheath and implications for a sample return mission. Planet Space Sci 99:103–111. doi:10.1016/j.pss.2014.04.018
Babich LP, Bochkov EI, Kutsyk IM, Rassoul HK (2014) Analysis of fundamental interactions capable of producing neutrons in thunderstorms. Phys Rev D. doi:10.1103/PhysRevD.89.093010
Bailey RL, Helling Ch, Hodosán G, Bilger C, Stark CR (2014) Ionization in atmospheres of brown dwarfs and extrasolar planets VI: properties of large-scale discharge events. Astrophys. J. Lett. 784:43. doi:10.1088/0004-637X/784/1/43
Balser M, Wagner CA (1960) Observations of Earth-ionosphere cavity resonances. Nature 188:638–641. doi:10.1038/188638a0
Bazelyan EM, Raizer YuP, Aleksandrov NL, D’Alessandro F (2009) Corona processes and lightning attachment: the effect of wind during thunderstorms. Atmos Res 94(3):436–447. doi:10.1016/j.atmosres.2009.07.002
Becklin EE, Zuckerman B (1988) A low-temperature companion to a white dwarf star. Nature 336:656–658. doi:10.1038/336656a0
Behnke SA, Thomas RJ, McNutt SR, Schneider DJ, Krehbiel PR, Rison W, Edens HE (2013) Observations of volcanic lightning during the 2009 eruption of Redoubt Volcano. J Volcanol Geotherm Res 259:214–234. doi:10.1016/j.jvolgeores.2011.12.010
Bennett AJ, Odams P, Edwards D, Arason P (2010) Monitoring of lightning from the April–May 2010 Eyjafjallajökull volcanic eruption using a very low frequency lightning location network. Environ Res Lett 5(4):044013. doi:10.1088/1748-9326/5/4/044013
Benz AO, Güdel M (1994) X-ray/microwave ratio of flares and coronae. Astron Astrophys 285:621–630
Berger E (2002) Flaring up all over-radio activity in rapidly rotating late M and L dwarfs. Astrophys J 572:503–513. doi:10.1086/340301
Berger E (2006) Radio observations of a large sample of late M, L, and T dwarfs: the distribution of magnetic field strengths. Astrophys J 648:629–636. doi:10.1086/505787
Berger E, Ball S, Becker KM, Clarke M, Frail DA, Fukuda TA, Hoffman IM, Mellon R, Momjian E, Murphy NW, Teng SH, Woodruff T, Zauderer BA, Zavala RT (2001) Discovery of radio emission from the brown dwarf LP944-20. Nature 410:338–340
Berger E, Basri G, Fleming TA, Giampapa MS, Gizis JE, Liebert J, Martín E, Phan-Bao N, Rutledge RE (2010) Simultaneous multi-wavelength observations of magnetic activity in ultracool dwarfs. III. X-ray, radio, and H\(\alpha\) activity trends in M and L dwarfs. Astrophys J 709:332–341. doi:10.1088/0004-637X/709/1/332
Beuermann K, Dreizler S, Hessman FV, Backhaus U, Boesch A, Husser T-O, Nortmann L, Schmelev A, Springer R (2013) The eclipsing post-common envelope binary CSS21055: a white dwarf with a probable brown-dwarf companion. Astron Astrophys 558, A96. doi:10.1051/0004-6361/201322241
Bétrémieux Y, Kaltenegger L (2013) Transmission spectrum of Earth as a transiting exoplanet from the ultraviolet to the near-infrared. Astrophys J Lett 772:L31. doi:10.1088/2041-8205/772/2/L31
Betz HD, Schumann U, Laroche P (eds) (2009) Lightning: principles, instruments and applications. In: Lightning: principles, instruments and applications. Review of modern lightning research. Springer, Berlin
Briggs MS, Connaughton V, Wilson-Hodge C, Preece RD, Fishman GJ, Kippen RM, Bhat PN, Paciesas WS, Chaplin VL, Meegan CA, von Kienlin A, Greiner J, Dwyer JR, Smith DM (2011) Electron-positron beams from terrestrial lightning observed with Fermi GBM. Geophys Res Lett. doi:10.1029/2010GL046259
Büttner R, Zimanowski B, Röder H (2000) Short-time electrical effects during volcanic eruption: experiments and field measurements. J Geophys Res 105:2819–2827. doi:10.1029/1999JB900370
Casewell SL, Burleigh MR, Lawrie KA, Maxted PFL, Dobbie PD, Napiwotzki R (2013) Irradiated brown dwarfs. Mem Societa Astronomica Italiana 84:1022
Casewell SL, Lawrie KA, Maxted PFL, Marley MS, Fortney JJ, Rimmer PB, Littlefair SP, Wynn G, Burleigh MR, Helling Ch (2015) Multiwaveband photometry of the irradiated brown dwarf WD0137-349B. Mon Not R Astron Soc 447:3218
Christian HJ, Blakeslee RJ, Boccippio DJ, Boeck WL, Buechler DE, Driscoll KT, Goodman SJ, Hall JM, Koshak WJ, Mach DM, Stewart MF (2003) Global frequency and distribution of lightning as observed from space by the optical transient detector. J Geophys Res Atmos 108:4005. doi:10.1029/2002JD002347
Cimarelli C, Alatorre-Ibargüengoitia MA, Aizawa K, Díaz Marina AI, Yokoo A, Kueppers U, Mueller S, Scheu B, Dingwell DB (2015) Volcanic lightning: in nature and in the lab, vol 17. In: EGU General Assembly conference abstracts, p 7194
Cooray V (2003) The lightning flash. IEE, London
Cooray V (2015) An introduction to lightning. Springer, Dordrecht
Cowley SWH, Bunce EJ (2001) Origin of the main auroral oval in Jupiter’s coupled magnetosphere–ionosphere system. Planet Space Sci 49:1067–1088. doi:10.1016/S0032-0633(00)00167-7
Cushing MC, Rayner JT, Vacca WD (2005) An infrared spectroscopic sequence of M, L, and T dwarfs. Astrophys J 623:1115–1140. doi:10.1086/428040
D’Angelo N (1993) The Rayleigh–Taylor instability in dusty plasmas. Planet Space Sci 41:469–474. doi:10.1016/0032-0633(93)90007-O
Demory BO, Gillon M, Deming D, Valencia D, Seager S, Benneke B, Lovis C, Cubillos P, Harrington J, Stevenson KB, Mayor M, Pepe F, Queloz D, Ségransan D, Udry S (2011) Detection of a transit of the super-Earth 55 Cancri e with warm Spitzer. Astron Astrophys 533:A114. doi:10.1051/0004-6361/201117178
Desch S, Cuzzi J (2000) The generation of lightning in the solar nebula. Icarus 143(1):87–105
Dobbs-Dixon I, Agol E (2013) Three-dimensional radiative-hydrodynamical simulations of the highly irradiated short-period exoplanet HD 189733b. Mon Not R Astron Soc 435:3159–3168. doi:10.1093/mnras/stt1509
Donati JF, Landstreet JD (2009) Magnetic fields of nondegenerate stars. Annu Rev Astron Astrophys 47:333–370. doi:10.1146/annurev-astro-082708-101833
Donati JF, Morin J, Petit P, Delfosse X, Forveille T, Aurière M, Cabanac R, Dintrans B, Fares R, Gastine T, Jardine MM, Lignières F, Paletou F, Ramirez Velez JC, Théado S (2008) Large-scale magnetic topologies of early M dwarfs. Mon Not R Astron Soc 390:545–560. doi:10.1111/j.1365-2966.2008.13799.x
Dubinova A, Rutjes C, Ebert U, Buitink S, Scholten O, Trinh GTN (2015) Prediction of lightning inception by large ice particles and extensive air showers. Phys Rev Lett 115(1):015002. doi:10.1103/PhysRevLett.115.015002
Dubrovin D, Luque A, Gordillo-Vazquez FJ, Yair Y, Parra-Rojas FC, Ebert U, Price C (2014) Impact of lightning on the lower ionosphere of Saturn and possible generation of halos and sprites. Icarus 241:313–328. doi:10.1016/j.icarus.2014.06.025
Dudkin D, Pilipenko V, Korepanov V, Klimov S, Holzworth R (2014) Electric field signatures of the IAR and Schumann resonance in the upper ionosphere detected by Chibis-M microsatellite. J Atmos Solar Terr Phys 117:81–87. doi:10.1016/j.jastp.2014.05.013
Dwyer JR, Uman MA (2014) The physics of lightning. Phys Rep 534(4):147–241. doi:10.1016/j.physrep.2013.09.004. http://www.sciencedirect.com/science/article/pii/S037015731300375X
Dwyer JR, Grefenstette BW, Smith DM (2008) High-energy electron beams launched into space by thunderstorms. Geophys Res Lett 35:L02815. doi:10.1029/2007GL032430
Ebert U, Sentman DD (2008) Editorial Review: Streamers, sprites, leaders, lightning: from micro- to macroscales. J Phys D Appl Phys 41(23):230301. doi:10.1088/0022-3727/41/23/230301
Ebert U, Nijdam S, Li C, Luque A, Briels T, van Veldhuizen E (2010) Review of recent results on streamer discharges and discussion of their relevance for sprites and lightning. J Geophys Res Space Phys. doi:10.1029/2009JA014867
Farihi J, Christopher M (2004) A possible brown dwarf companion to the white dwarf GD 1400. Astron J 128:1868–1871. doi:10.1086/423919
Farrell WM, Desch MD (2001) Is there a Martian atmospheric electric circuit? J Geophys Res Planets 106:7591–7596. doi:10.1029/2000JE001271
Fillingim M (1986) Global electric circuit of Mars. In: Florida institute of technology (unpublished report)
Fishman GJ, Meegan CA (1995) Gamma-ray bursts. Annu Rev Astron Astrophys 33:415–458. doi:10.1146/annurev.aa.33.090195.002215
Fishman GJ, Bhat PN, Mallozzi R, Horack JM, Koshut T, Kouveliotou C, Pendleton GN, Meegan CA, Wilson RB, Paciesas WS, Goodman SJ, Christian HJ (1994) Discovery of intense gamma-ray flashes of atmospheric origin. Science 264:1313–1316. doi:10.1126/science.264.5163.1313
Fletcher LN, Hesman BE, Achterberg RK, Irwin PGJ, Bjoraker G, Gorius N, Hurley J, Sinclair J, Orton GS, Legarreta J, García-Melendo E, Sánchez-Lavega A, Read PL, Simon-Miller AA, Flasar FM (2012) The origin and evolution of Saturn’s 2011–2012 stratospheric vortex. Icarus 221:560–586. doi:10.1016/j.icarus.2012.08.024
Fortov VE, Morfill GE (2010) Complex and dusty plasmas: from laboratory to space. CRC Press/Taylor & Francis, Boca Raton
Forward KM, Lacks DJ, Sankaran RM (2009a) Charge segregation depends on particle size in triboelectrically charged granular materials. Phys Rev Lett 102(2):028001. doi:10.1103/PhysRevLett.102.028001
Forward KM, Lacks DJ, Sankaran RM (2009b) Triboelectric charging of lunar regolith simulant. J Geophys Res Space Phys 114(13):A10109. doi:10.1029/2009JA014559
Füllekrug M, Mareev EA, Rycroft MJ (2006) Sprites, elves and intense lightning discharges. Springer, Berlin
Füllekrug M, Diver D, Pinçon JL, Phelps ADR, Bourdon A, Helling Ch, Blanc E, Honary F, Harrison RG, Sauvaud JA, Renard JB, Lester M, Rycroft M, Kosch M, Horne RB, Soula S, Gaffet S (2013a) Energetic charged particles above thunderclouds. Surv Geophys 34:1–41. doi:10.1007/s10712-012-9205-z
Füllekrug M, Kolmasova I, Santolik O, Farges T, Bór J, Bennett A, Parrot M, Rison W, Zanotti F et al (2013b) Electron acceleration above thunderclouds. Environ Res Lett 8(3):035027. doi:10.1088/1748-9326/8/3/035027
Galand M, Moore L, Charnay B, Mueller-Wodarg I, Mendillo M (2009) Solar primary and secondary ionization at Saturn. J Geophys Res Space Phys 114:A06313. doi:10.1029/2008JA013981
Galembeck F, Burgo TAL, Balestrin LBS, Gouveia RF, Silva CA, Galembeck A (2014) Friction, tribochemistry and triboelectricity: recent progress and perspectives. RSC Adv 4:64280–64298. doi:10.1039/C4RA09604E
Gibbard S, Levy E, Morfill G (1997) On the possibility of lightning in the protosolar nebula. Icarus 130(2):517–533
Gilbert JS, Lane SJ, Sparks RSJ, Koyaguchi T (1991) Charge measurements on particle fallout from a volcanic plume. Nature 349:598–600. doi:10.1038/349598a0
Gizis JE, Monet DG, Reid IN, Kirkpatrick JD, Liebert J, Williams RJ (2000) New neighbors from 2MASS: activity and kinematics at the bottom of the main sequence. Astron J 120:1085–1099. doi:10.1086/301456
Goertz CK (1989) Dusty plasmas in the solar system. Rev Geophys 27:271–292. doi:10.1029/RG027i002p00271
Gordillo-Vázquez FJ (2008) Air plasma kinetics under the influence of sprites. J Phys D Appl Phys 41(23):234016. doi:10.1088/0022-3727/41/23/234016
Gordillo-Vázquez FJ, Donkó Z (2009) Electron energy distribution functions and transport coefficients relevant for air plasmas in the troposphere: impact of humidity and gas temperature. Plasma Sources Sci Technol 18(3):034021. doi:10.1088/0963-0252/18/3/034021
Gordillo-Vázquez FJ, Luque A (2010) Electrical conductivity in sprite streamer channels. Geophys Res Lett 37:L16809. doi:10.1029/2010GL044349
Gordillo-Vázquez FJ, Luque A, Simek M (2012) Near infrared and ultraviolet spectra of TLEs. J Geophys Res Space Phys 117:A05329. doi:10.1029/2012JA017516
Gringel W, Rosen JM, Hoffman DJ (1986) Electrical structure from 0 to 30 km. In: Krider EP (ed) The Earth’s electrical environment. National Academic Press
Gurevich A, Milikh G, Roussel-Dupre R (1992) Runaway electron mechanism of air breakdown and preconditioning during a thunderstorm. Phys Lett A 165(5–6):463–468. doi:10.1016/0375-9601(92)90348-P
Gurevich AV, Karashtin AN (2013) Runaway breakdown and hydrometeors in lightning initiation. Phys Rev Lett. doi:10.1103/PhysRevLett.110.185005
Hallinan G, Antonova A, Doyle JG, Bourke S, Brisken WF, Golden A (2006) Rotational modulation of the radio emission from the M9 dwarf TVLM 513–46546: broadband coherent emission at the substellar boundary? Astrophys J 653:690–699. doi:10.1086/508678
Hallinan G, Bourke S, Lane C, Antonova A, Zavala RT, Brisken WF, Boyle RP, Vrba FJ, Doyle JG, Golden A (2007) Periodic bursts of coherent radio emission from an ultracool dwarf. Astrophys J Lett 663:L25–L28. doi:10.1086/519790
Hallinan G, Antonova A, Doyle JG, Bourke S, Lane C, Golden A (2008) Confirmation of the electron cyclotron maser instability as the dominant source of radio emission from very low mass stars and brown dwarfs. Astrophys J 684:644–653. doi:10.1086/590360
Harrison RG (2006) Urban smoke concentrations at Kew, London, 1898–2004. Atmos Environ 40:3327–3332. doi:10.1016/j.atmosenv.2006.01.042
Harrison RG (2013) The Carnegie curve. Surv Geophys 34:209–232. doi:10.1007/s10712-012-9210-2
Harrison RG, Carslaw KS (2003) Ion-aerosol-cloud processes in the lower atmosphere. Rev Geophys 41:1012. doi:10.1029/2002RG000114
Harrison RG, Mather TA (2006) The electrification of volcanic plumes and volcanic lightning. In: AGU fall meeting abstracts, p A286
Harrison RG, Nicoll KA (2014) Note: active optical detection of cloud from a balloon platform. Rev Sci Instrum 85(6):066104. doi:10.1063/1.4882318
Harrison RG, Aplin KL, Leblanc F, Yair Y (2008) Planetary atmospheric electricity. Space Sci Rev 137:5–10. doi:10.1007/s11214-008-9419-z
Harrison RG, Nicoll KA, Ulanowski Z, Mather TA (2010) Self-charging of the Eyjafjallajökull volcanic ash plume. Environ Res Lett 5(2):024004. doi:10.1088/1748-9326/5/2/024004
Harrison RG, Nicoll KA, Aplin KL (2014) Vertical profile measurements of lower troposphere ionisation. J Atmos Sol Terr Phys 119:203–210. doi:10.1016/j.jastp.2014.08.006
Helling Ch (2003) Circuit of dust in substellar objects (with 10 figures). In: Schielicke RE (ed) Reviews in modern astronomy, vol 16, p 115
Helling Ch (2009) Cloud formation in substellar atmospheres. In: Stempels E (ed) 15th Cambridge workshop on cool stars, stellar systems, and the sun, American Institute of Physics Conference Series, vol 1094, pp 162–171. doi:10.1063/1.3099087
Helling Ch, Casewell S (2014) Atmospheres of brown dwarfs. Astron Astrophys Rev 22:80. doi:10.1007/s00159-014-0080-0
Helling C, Rietmeijer FJM (2009) Glittery clouds in exoplanetary atmospheres? Int J Astrobiol 8:3–8. doi:10.1017/S1473550408004382
Helling Ch, Jardine M, Mokler F (2011) Ionization in atmospheres of brown dwarfs and extrasolar planets. II. Dust-induced collisional ionization. Astrophys J 737:38. doi:10.1088/0004-637X/737/1/38
Helling Ch, Jardine M, Stark C, Diver D (2013) Ionization in atmospheres of brown dwarfs and extrasolar planets. III. Breakdown conditions for mineral clouds. Astrophys J 767:136. doi:10.1088/0004-637X/767/2/136
Hess VF (1912) Über Beobachtungen der durchdringenden Strahlung bei sieben Freiballonfahrten. Phys Z 13:1084
Hess SLG, Sarrailh P, Matéo-Vélez JC, Forest J, Jeanty-Ruard B, Cipriani F (2015) Simulation of the electrostatic charging of Philae on 67P/Churyumov-Gerasimenko and of its interaction with the dusts. In: Martins F, Boissier S, Buat V, Cambrésy L, Petit P (eds) SF2A-2015: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, pp 57–61
Hoang T, Lazarian A, Schlickeiser R (2015) On origin and destruction of relativistic dust and its implication for ultrahigh energy cosmic rays. Astrophys J 806:255. doi:10.1088/0004-637X/806/2/255
Hodosán G, Helling Ch, Asensio-Torres R, Vorgul I, Rimmer PB (2016) Lightning climatology of exoplanets and brown dwarfs guided by solar system data. Mon Not R Astron Soc (submitted)
Horányi M, Hartquist TW, Havnes O, Mendis DA, Morfill GE (2004) Dusty plasma effects in Saturn’s magnetosphere. Rev Geophys 42:RG4002. doi:10.1029/2004RG000151
Houghton IMP, Aplin KL, Nicoll KA (2013) Triboelectric charging of volcanic ash from the 2011 Grímsvötn eruption. Phys Rev Lett 111(11):118501. doi:10.1103/PhysRevLett.111.118501
Hutchinson IH, Patacchini L (2007) Computation of the effect of neutral collisions on ion current to a floating sphere in a stationary plasma. Phys Plasmas. doi:10.1063/1.2431584
Inutsuka S, Sano T (2005) Self-sustained ionization and vanishing dead zones in protoplanetary disks. Astrophys J Lett 628:L155–L158. doi:10.1086/432796
Irwin PGJ, Teanby NA, de Kok R, Fletcher LN, Howett CJA, Tsang CCC, Wilson CF, Calcutt SB, Nixon CA, Parrish PD (2008) The NEMESIS planetary atmosphere radiative transfer and retrieval tool. J Quant Spectrosc Radiat Transf 109:1136–1150. doi:10.1016/j.jqsrt.2007.11.006
James MR, Lane SJ, Gilbert JS (1998) Volcanic plume monitoring using atmospheric electric potential gradients. Geol Soc Lond J 155:587–590. doi:10.1144/gsjgs.155.4.0587
James MR, Lane SJ, Gilbert JS (2000) Volcanic plume electrification: experimental investigation of a fracture-charging mechanism. J Geophys Res 105(16):641. doi:10.1029/2000JB900068
Jayaratne ER, Saunders CPR, Hallett J (1983) Laboratory studies of the charging of soft-hail during ice crystal interactions. Q J R Meteorol Soc 109:609–630. doi:10.1002/qj.49710946111
Johnson AP, Cleaves HJ, Dworkin JP, Glavin DP, Lazcano A, Bada JL (2008) The Miller volcanic spark discharge experiment. Science 322:404
Khrapak SA, Morfill GE (2008) An interpolation formula for the ion flux to a small particle in collisional plasmas. Phys Plasmas 15(11):114503. doi:10.1063/1.3035913
Khrapak SA, Tolias P, Ratynskaia S, Chaudhuri M, Zobnin A, Usachev A, Rau C, Thoma MH, Petrov OF, Fortov VE, Morfill GE (2012) Grain charging in an intermediately collisional plasma. Europhys Lett. doi:10.1209/0295-5075/97/35001
Kirkpatrick JD, Reid IN, Liebert J, Gizis JE, Burgasser AJ, Monet DG, Dahn CC, Nelson B, Williams RJ (2000) 67 Additional L dwarfs discovered by the two micron all sky survey. Astron J 120:447–472. doi:10.1086/301427
Kitzmann D, Patzer ABC, von Paris P, Godolt M, Stracke B, Gebauer S, Grenfell JL, Rauer H (2010) Clouds in the atmospheres of extrasolar planets. I. Climatic effects of multi-layered clouds for Earth-like planets and implications for habitable zones. Astron Astrophys 511:A66. doi:10.1051/0004-6361/200913491
Knutson HA, Charbonneau D, Allen LE, Fortney JJ, Agol E, Cowan NB, Showman AP, Cooper CS, Megeath ST (2007) A map of the day-night contrast of the extrasolar planet HD 189733b. Nature 447:183–186. doi:10.1038/nature05782
Kochkin PO, Nguyen CV, van Deursen APJ, Ebert U (2012) Experimental study of hard X-rays emitted from metre-scale positive discharges in air. J Phys D Appl Phys. doi:10.1088/0022-3727/45/42/425202
Konopka U, Mokler F, Ivlev AV, Kretschmer M, Morfill GE, Thomas HM, Rothermel H, Fortov VE, Lipaev AM, Molotkov VI, Nefedov AP, Baturin YM, Budarin Y, Ivanov AI, Roth M (2005) Charge-induced gelation of microparticles. New J Phys 7:227. doi:10.1088/1367-2630/7/1/227
Kopnin SI, Popel SI, Yu MY (2009) Phenomena associated with complex (dusty) plasmas in the ionosphere during high-speed meteor showers. Phys Plasmas 16(6):063705. doi:10.1063/1.3147931
Krehbiel P (1986) The electrical structure of thunderstorms. In: The earth’s electrical environment. Nat'l. Academy Press, Washington, DC, pp 90–113
Kuhn S, Phelps ADR, Fang MTC (1981) Low-frequency longitudinal instability in collisionless single-ended Q machines. Phys Fluids 24:1586. doi:10.1063/1.863548
Langmuir I, Found CG, Dittmer AF (1924) A new type of electric discharge: the streamer discharge. Science 60:392–394. doi:10.1126/science.60.1557.392
Lapenta G, Pierrard V, Keppens R, Markidis S, Poedts S, Šebek O, Trávníček PM, Henri P, Califano F, Pegoraro F et al (2013) SWIFF: space weather integrated forecasting framework. J Space Weather Space Clim 3(27):A05
Lay EH, Rodger CJ, Holzworth RH, Cho M, Thomas JN (2010) Temporal-spatial modeling of electron density enhancement due to successive lightning strokes. J Geophys Res Space Phys 115:A00E59. doi:10.1029/2009JA014756
Leblanc F, Aplin K, Yair Y, Harrison R, Lebreton J, Blanc M (eds) (2008) Planetary atmospheric electricity. Springer, Berlin
Lee G, Helling Ch, Dobbs-Dixon I, Juncher D (2015) Modelling the local and global cloud formation on HD 189733b. Astron Astrophys 580:A12. doi:10.1051/0004-6361/201525982
Lee P (1996) Dust levitation on asteroids. Icarus 124:181–194. doi:10.1006/icar.1996.0197
Liebert J, Kirkpatrick JD, Cruz KL, Reid IN, Burgasser A, Tinney CG, Gizis JE (2003) A flaring L5 dwarf: the nature of H\(\alpha\) emission in very low mass (Sub)stellar objects. Astron J 125:343–347. doi:10.1086/345514
Littlefair SP, Dhillon VS, Marsh TR, Shahbaz T, Martín EL, Copperwheat C (2008) Optical variability of the ultracool dwarf TVLM 513–46546: evidence for inhomogeneous dust clouds. Mon Not R Astron Soc 391:L88–L92. doi:10.1111/j.1745-3933.2008.00562.x
Liu N, Pasko VP (2004a) Correction to “Effects of photoionization on propagation and branching of positive and negative streamers in sprites”. J Geophys Res Space Phys 109:A09306. doi:10.1029/2004JA010692
Liu N, Pasko VP (2004b) Effects of photoionization on propagation and branching of positive and negative streamers in sprites. J Geophys Res Space Phys 109:A04301. doi:10.1029/2003JA010064
Luque A, Ebert U (2009) Emergence of sprite streamers from screening–ionization waves in the lower ionosphere. Nat Geosci 2:757–760. doi:10.1038/ngeo662
Luque A, Gordillo-Vázquez FJ (2012) Mesospheric electric breakdown and delayed sprite ignition caused by electron detachment. Nat Geosci 5:22–25. doi:10.1038/ngeo1314
Luque A, Dubrovin D, Gordillo-Vázquez FJ, Yair Y, Parra-Rojas FC, Ebert U, Price C (2014) Coupling between atmospheric layers in gaseous giant planets due to lightning-generated electromagnetic pulses. J Geophys Res Space Phys 119(10):8705–8720
Maguire PD, Mahony CMO, Kelsey CP, Bingham AJ, Montgomery EP, Bennet ED, Potts HE, Rutherford DCE, McDowell DA, Diver DA, Mariotti D (2015) Controlled microdroplet transport in an atmospheric pressure microplasma. Appl Phys Lett 106(22):224101. doi:10.1063/1.4922034
Mason BJ (1953) On the generation of charge associated with graupel formation in thunderstorms. Q J R Meteorol Soc 79:501–509. doi:10.1002/qj.49707934206
Maxted PFL, Napiwotzki R, Dobbie PD, Burleigh MR (2006) Survival of a brown dwarf after engulfment by a red giant star. Nature 442:543–545. doi:10.1038/nature04987
McConville SL, Speirs DC, Ronald K, Phelps ADR, Cross AW, Bingham R, Robertson CW, Whyte CG, He W, Gillespie KM, Vorgul I, Cairns RA, Kellett BJ (2008) Demonstration of auroral radio emission mechanisms by laboratory experiment. Plasma Phys Controll Fusion 50(7):074010. doi:10.1088/0741-3335/50/7/074010
McLean M, Berger E, Reiners A (2012) The radio activity-rotation relation of ultracool dwarfs. Astrophys J 746:23. doi:10.1088/0004-637X/746/1/23
McNutt SR, Williams ER (2010) Volcanic lightning: global observations and constraints on source mechanisms. Bull Volcanol 72:1153–1167. doi:10.1007/s00445-010-0393-4
Michel P, Barucci MA, Cheng AF, Böhnhardt H, Brucato JR, Dotto E, Ehrenfreund P, Franchi IA, Green SF, Lara LM, Marty B, Koschny D, Agnolon D (2014) MarcoPolo-R: near-Earth asteroid sample return mission selected for the assessment study phase of the ESA program cosmic vision. Acta Astronaut 93:530–538. doi:10.1016/j.actaastro.2012.05.030
Millward G, Miller S, Stallard T, Aylward AD, Achilleos N (2002) On the dynamics of the Jovian ionosphere and thermosphere: III. The modelling of auroral conductivity. Icarus 160:95–107. doi:10.1006/icar.2002.6951
Miura T, Koyaguchi T, Tanaka Y (2002) Measurements of electric charge distribution in volcanic plumes at Sakurajima Volcano, Japan. Bull Volcanol 64:75–93. doi:10.1007/s00445-001-0182-1
Moore LE, Mendillo M, Müller-Wodarg ICF, Murr DL (2004) Modeling of global variations and ring shadowing in Saturn’s ionosphere. Icarus 172:503–520. doi:10.1016/j.icarus.2004.07.007
Morin J, Donati JF, Petit P, Delfosse X, Forveille T, Albert L, Aurière M, Cabanac R, Dintrans B, Fares R, Gastine T, Jardine MM, Lignières F, Paletou F, Ramirez Velez JC, Théado S (2008) Large-scale magnetic topologies of mid M dwarfs. Mon Not R Astron Soc 390:567–581. doi:10.1111/j.1365-2966.2008.13809.x
Morin J, Donati JF, Petit P, Delfosse X, Forveille T, Jardine MM (2010) Large-scale magnetic topologies of late M dwarfs. Mon Not R Astron Soc 407:2269–2286. doi:10.1111/j.1365-2966.2010.17101.x
Moses JI, Bézard B, Lellouch E, Gladstone GR, Feuchtgruber H, Allen M (2000) Photochemistry of Saturn’s atmosphere. I. Hydrocarbon chemistry and comparisons with ISO observations. Icarus 143:244–298. doi:10.1006/icar.1999.6270
Muranushi T (2010) Dust–dust collisional charging and lightning in protoplanetary discs. Mon Not R Astron Soc 401(4):2641–2664
Muranushi T, Okuzumi S, Inutsuka S (2012) Interdependence of electric discharge and magnetorotational instability in protoplanetary disks. Astrophys J 760:56. doi:10.1088/0004-637X/760/1/56
Muranushi T, Okuzumi S, Inutsuka S (2013) Erratum: “Interdependence of electric discharge and the magnetorotational instability in protoplanetary disks” /abs/2012ApJ...760...56M (2012, ApJ, 760, 56). Astrophys J 771:138. doi:10.1088/0004-637X/771/2/138
Muranushi T, Akiyama E, Inutsuka SI, Nomura H, Okuzumi S (2015) Development of a method for the observation of lightning in protoplanetary disks using ion lines. Astrophys J 815:84. doi:10.1088/0004-637X/815/2/84
Murray-Clay RA, Chiang EI, Murray N (2009) Atmospheric escape from hot Jupiters. Astrophys J 693:23–42. doi:10.1088/0004-637X/693/1/23
Nichols JD, Burleigh MR, Casewell SL, Cowley SWH, Wynn GA, Clarke JT, West AA (2012) Origin of electron cyclotron maser induced radio emissions at ultracool dwarfs: magnetosphere–ionosphere coupling currents. Astrophys J 760:59. doi:10.1088/0004-637X/760/1/59
Nicoll KA (2012) Measurements of atmospheric electricity aloft. Surv Geophys 33:991–1057. doi:10.1007/s10712-012-9188-9
Nicoll KA (2013) Note: A self-calibrating electrometer for atmospheric charge measurements from a balloon platform. Rev Sci Instrum 84(9):096107. doi:10.1063/1.4821500
Nicoll KA (2014) Space weather influences on atmospheric electricity. Weather 69:238–241. doi:10.1002/wea.2323
Nicoll KA, Harrison RG (2010) Experimental determination of layer cloud edge charging from cosmic ray ionisation. Geophys Res Lett 37:L13802. doi:10.1029/2010GL043605
Nijdam S, Takahashi E, Markosyan AH, Ebert U (2014) Investigation of positive streamers by double-pulse experiments, effects of repetition rate and gas mixture. Plasma Sources Sci Technol 23(2):025008. doi:10.1088/0963-0252/23/2/025008
Okuzumi S, Inutsuka S (2014) The nonlinear Ohm’s Law: plasma heating by strong electric fields and its effects on the ionization balance in protoplanetary disks. Astrophys J 800(1):47
Oppenheimer C (2003) Climatic, environmental and human consequences of the largest known historic eruption: Tambora volcano (Indonesia) 1815. Prog Phys Geogr 27:230–259. doi:10.1191/0309133303pp379r
Owens MJ, Scott CJ, Lockwood M, Barnard L, Harrison RG, Nicoll K, Watt C, Bennett AJ (2014) Modulation of UK lightning by heliospheric magnetic field polarity. Environ Res Lett 9, 115009. doi:10.1088/1748-9326/9/11/115009
Parra-Rojas FC, Luque A, Gordillo-Vázquez FJ (2013) Chemical and electrical impact of lightning on the Earth’s mesosphere: the case of sprite halos. J Geophys Res Space Phys 118:5190–5214. doi:10.1002/jgra.50449
Parra-Rojas FC, Luque A, Gordillo-Vázquez FJ (2015) Chemical and thermal impacts of sprite streamers in the Earth’s mesosphere. J Geophys Res Space Phys 120:8899–8933. doi:10.1002/2014JA020933
Pasko VP (2007) TOPICAL REVIEW: Red sprite discharges in the atmosphere at high altitude: the molecular physics and the similarity with laboratory discharges. Plasma Sources Sci Technol 16:13. doi:10.1088/0963-0252/16/1/S02
Pfotzer G (1972) History of the use of balloons in scientific experiments. Space Sci Rev 13:199–242. doi:10.1007/BF00175313
Phelps ADR, Allen JE (1976) A floating electrostatic sheath in a thermally produced plasma. R Soc Lond Proc Ser A 348:221–233. doi:10.1098/rspa.1976.0034
Pont F, Sing DK, Gibson NP, Aigrain S, Henry G, Husnoo N (2013) The prevalence of dust on the exoplanet HD 189733b from Hubble and Spitzer observations. Mon Not R Astron Soc 432:2917–2944. doi:10.1093/mnras/stt651
Rakov VA, Uman MA (2003) Lightning: physics and effects. Cambridge University Press, Cambridge
Rao NN (1993) Dust-magnetoacoustic waves in magnetized dusty plasmas. Phys Scr 48:363–366. doi:10.1088/0031-8949/48/3/015
Rao NN (1995) Magnetoacoustic modes in a magnetized dusty plasma. J Plasma Phys 53:317. doi:10.1017/S0022377800018237
Rao NN, Shukla PK (1990) Dust-acoustic waves in dusty plasmas. Planet Space Sci 38:543–546
Regener E, Pfotzer G (1935) Vertical intensity of cosmic rays by threefold coincidences in the stratosphere. Nature 136:718–719. doi:10.1038/136718a0
Reiners A, Basri G (2008) Chromospheric activity, rotation, and rotational braking in M and L dwarfs. Astrophys J 684:1390–1403. doi:10.1086/590073
Rimmer PB, Helling Ch (2013) Ionization in atmospheres of brown dwarfs and extrasolar planets. IV. The effect of cosmic rays. Astrophys J 774:108. doi:10.1088/0004-637X/774/2/108
Rimmer PB, Helling Ch (2015) A chemical kinetics network for lightning and life in planetary atmospheres. ArXiv e-prints
Rimmer PB, Walsh C, Helling Ch (2014) Cosmic rays, UV photons, and haze formation in the upper atmospheres of hot Jupiters. In: Booth M, Matthews BC, Graham JR (eds) IAU symposium, vol 299, pp 303–304. doi:10.1017/S1743921313008703
Rodriguez-Barrera MI, Helling C, Stark CR, Rice AM (2015) Reference study to characterise plasma and magnetic properties of ultra-cool atmospheres. Mon Not R Astron Soc 454:3977–3995. doi:10.1093/mnras/stv2090
Rogers TM, Showman AP (2014) Magnetohydrodynamic simulations of the atmosphere of HD 209458b. Astrophys J Lett 782:L4. doi:10.1088/2041-8205/782/1/L4
Rosenberg M (1993) Ion- and dust-acoustic instabilities in dusty plasmas. Planet Space Sci 41:229–233. doi:10.1016/0032-0633(93)90062-7
Rosenblum E, Garaud P, Traxler A, Stellmach S (2011a) Erratum: “Turbulent mixing and layer formation in double-diffusive convection: three-dimensional numerical simulations and theory” /abs/2011ApJ...731...66R (2011, ApJ, 731, 66). Astrophys J 742:132. doi:10.1088/0004-637X/742/2/132
Rosenblum E, Garaud P, Traxler A, Stellmach S (2011b) Turbulent mixing and layer formation in double-diffusive convection: three-dimensional numerical simulations and theory. Astrophys J 731:66. doi:10.1088/0004-637X/731/1/66
Route M, Wolszczan A (2012) The arecibo detection of the coolest radio-flaring brown dwarf. Astrophys J Lett 747:L22. doi:10.1088/2041-8205/747/2/L22
Rutherford D, McDowell D, Mariotti D, Mahony C, Diver D, Potts H, Bennet E, Maguire P (2014) Impact of plasma induced liquid chemistry and charge on bacteria loaded aerosol droplets. In: APS meeting abstracts
Rycroft MJ (1965) Resonances of the Earth–ionosphere cavity observed at Cambridge, England. Radio Sci J Res Natl Bur Stand D 69:1071–1081
Rycroft MJ, Harrison RG (2012) Electromagnetic atmosphere-plasma coupling: the global atmospheric electric circuit. Space Sci Rev 168:363–384. doi:10.1007/s11214-011-9830-8
Rycroft MJ, Israelsson S, Price C (2000) The global atmospheric electric circuit, solar activity and climate change. J Atmos Solar Terr Phys 62:1563–1576. doi:10.1016/S1364-6826(00)00112-7
Rycroft MJ, Odzimek A, Arnold NF, Füllekrug M, Kułak A, Neubert T (2007) New model simulations of the global atmospheric electric circuit driven by thunderstorms and electrified shower clouds: the roles of lightning and sprites. J Atmos Sol Terr Phys 69:2485–2509. doi:10.1016/j.jastp.2007.09.004
Rycroft MJ, Harrison RG, Nicoll KA, Mareev EA (2008) An overview of Earth’s global electric circuit and atmospheric conductivity. Space Sci Rev 137:83–105. doi:10.1007/s11214-008-9368-6
Saunders C (2008) Charge separation mechanisms in clouds. Springer, New York, pp 335–353. doi:10.1007/978-0-387-87664-1_22
Schmidt SJ, Hawley SL, West AA, Bochanski JJ, Davenport JRA, Ge J, Schneider DP (2015) BOSS ultracool dwarfs. I. Colors and magnetic activity of M and L dwarfs. Astron J 149:158. doi:10.1088/0004-6256/149/5/158
Schumann WO (1952) Über die strahlungslosen Eigenschwingungen einer leitenden Kugel die von einer Luftschicht und einer Ionosphärenhülle umgeben ist. Z Naturforsch Teil A 7:149
See V, Jardine M, Vidotto AA, Petit P, Marsden SC, Jeffers SV, do Nascimento JD (2014) The effects of stellar winds on the magnetospheres and potential habitability of exoplanets. Astron Astrophys 570:A99. doi:10.1051/0004-6361/201424323
Sen S, Fukuyama A, Honary F (2010) Rayleigh Taylor instability in a dusty plasma. J Atmos Sol Terr Phys 72:938–942. doi:10.1016/j.jastp.2010.05.001
Shalygin EV, Markiewicz WJ, Basilevsky AT, Titov DV, Ignatiev NI, Head JW (2015) Active volcanism on Venus in the Ganiki Chasma rift zone. Geophys Res Lett 42:4762–4769. doi:10.1002/2015GL064088
Shao XM, Lay EH, Jacobson AR (2013) Reduction of electron density in the night-time lower ionosphere in response to a thunderstorm. Nat Geosci 6(1):29–33. doi:10.1038/NGEO1668
Shukla PK, Mamun AA (2002) Introduction to dusty plasma physics. Institute of Physics Publishing, Philadelphia
Shukla PK, Silin VP (1992) Dust ion-acoustic wave. Phys Scr 45:508. doi:10.1088/0031-8949/45/5/015
Silva HG, Conceicão R, Melgõa M, Nicoll K, Tlemcani M, Reis AH, Harrison RG (2014) Atmospheric electric field measurements in urban environment and the pollutant aerosol weekly dependence. Environ Res Lett 9(114):025
Simões F, Pfaff R, Freudenreich H (2011) Satellite observations of Schumann resonances in the Earth’s ionosphere. Geophys Res Lett 38:L22101. doi:10.1029/2011GL049668
Sing DK, Wakeford HR, Showman AP, Nikolov N, Fortney JJ, Burrows AS, Ballester GE, Deming De (2014) HST hot-Jupiter transmission spectral survey: detection of potassium in WASP-31b along with a cloud deck and Rayleigh scattering. ArXiv e-prints
Sorahana S, Suzuki TK, Yamamura I (2014) A signature of chromospheric activity in brown dwarfs revealed by 2.5–5.0 μm AKARI spectra. Mon Not R Astron Soc 440:3675–3684. doi:10.1093/mnras/stu479
Speirs DC, McConville SL, Gillespie KM, Ronald K, Phelps ADR, Cross AW, Bingham R, Robertson CW, Whyte CG, Vorgul I, Cairns RA, Kellett BJ (2008) Numerical simulation of auroral cyclotron maser processes. Plasma Phys Control Fusion 50(7):074011. doi:10.1088/0741-3335/50/7/074011
Stark CR, Helling Ch, Diver DA, Rimmer PB (2013) Ionization in atmospheres of brown dwarfs and extrasolar planets. V. Alfvén Ionization. Astrophys J 776:11. doi:10.1088/0004-637X/776/1/11
Steele PR, Saglia RP, Burleigh MR, Marsh TR, Gänsicke BT, Lawrie K, Cappetta M, Girven J, Napiwotzki R (2013) NLTT 5306: the shortest period detached white dwarf+brown dwarf binary. Mon Not R Astron Soc 429:3492–3500. doi:10.1093/mnras/sts620
Stenbaek-Nielsen HC, McHarg MG (2008) High time-resolution sprite imaging: observations and implications. J Phys D Appl Phys. doi:10.1088/0022-3727/41/23/234009
Stozhkov YV, Okhlopkov V, Makhmutov V, Logachev A (2013) Solar activity, cosmic rays, and global climate changes. In: Proceedings of 33rd international cosmic ray conference (ICRC)
Strobel DF, Atreya SK (1983) Ionosphere. In: Dessler A (ed) Physics of the Jovian Magnetosphere, vol 1. Cambridge University Press, Cambridge, pp 51–67
Taddeucci J, Scarlato P, Montanaro C, Cimarelli C, Del Bello E, Freda C, Andronico D, Gudmundsson MT, Dingwell DB (2011) Aggregation-dominated ash settling from the Eyjafjallajokull volcanic cloud illuminated by field and laboratory high-speed imaging. Geology 39:891–894. doi:10.1130/G32016.1
Tanaka YA, Suzuki TK, Inutsuka S (2014) Atmospheric escape by magnetically driven wind from gaseous planets. Astrophys J 792:18. doi:10.1088/0004-637X/792/1/18
Thomas RJ, Krehbiel PR, Rison W, Edens HE, Aulich GD, Winn WP, McNutt SR, Tytgat G, Clark E (2007) Electrical activity during the 2006 Mount St. Augustine volcanic eruptions. Science 315:1097. doi:10.1126/science.1136091
Todd JF, Barber SJ, Wright IP, Morgan GH, Morse AD, Sheridan S, Leese MR, Maynard J, Evans ST, Pillinger CT, Drummond DL, Heys SC, Huq SE, Kent BJ, Sawyer EC, Whalley MS, Waltham NR (2007) Ion trap mass spectrometry on a comet nucleus: the Ptolemy instrument and the Rosetta space mission. J Mass Spectrom 42:1–10
Trakhtengerts VY, Rycroft MJ (2008) Whistler and Alfvén mode cyclotron masers in space. Cambridge University Press, Cambridge
Treumann RA, Zbigniew K, Parrot M (2008) Physics of elelctric discharges in atmospheric gases: an informal introduction. In: Leblanc F, Aplin KL, Yair Y, Harrison RG, Lebreton JP, Blanc M (eds) Planetary atmospheric electricity, Space Science Series of ISSI, vol 137, p 133
Tsai SM, Dobbs-Dixon I, Gu PG (2014) Three-dimensional structures of equatorial waves and the resulting super-rotation in the atmosphere of a tidally locked hot Jupiter. Astrophys J 793:141. doi:10.1088/0004-637X/793/2/141
Van Eaton AR, Muirhead JD, Wilson CJN, Cimarelli C (2012) Growth of volcanic ash aggregates in the presence of liquid water and ice: an experimental approach. Bull Volcanol 74:1963–1984. doi:10.1007/s00445-012-0634-9
Ververka J et al (2013) Return to Comet Tempel 1: overview of Stardust-NExT results. Icarus 222:424–435
Vidotto AA, Gregory SG, Jardine M, Donati JF, Petit P, Morin J, Folsom CP, Bouvier J, Cameron AC, Hussain G, Marsden S, Waite IA, Fares R, Jeffers S, do Nascimento JD (2014a) Stellar magnetism: empirical trends with age and rotation. Mon Not R Astron Soc 441:2361–2374. doi:10.1093/mnras/stu728
Vidotto AA, Jardine M, Morin J, Donati JF, Opher M, Gombosi TI (2014b) M-dwarf stellar winds: the effects of realistic magnetic geometry on rotational evolution and planets. Mon Not R Astron Soc 438:1162–1175. doi:10.1093/mnras/stt2265
von Blohn N, Diehl K, Mitra SK, Borrmann S (2009) Riming of graupel: wind tunnel investigations of collection kernels and growth regimes. J Atmos Sci 66:2359. doi:10.1175/2009JAS2969.1
Vorgul I, Kellett BJ, Cairns RA, Bingham R, Ronald K, Speirs DC, McConville SL, Gillespie KM, Phelps ADR (2011) Cyclotron maser emission: stars, planets, and laboratory. Phys Plasmas 18(5):056501. doi:10.1063/1.3567420
Walsh C, Nomura H, Millar TJ, Aikawa Y (2012) Chemical processes in protoplanetary disks. II. On the importance of photochemistry and X-ray ionization. Astrophys J 747:114. doi:10.1088/0004-637X/747/2/114
Wasilewski P, Dickinson T (2000) Aspects of the validation of magnetic remanence in meteorites. Meteorit Planet Sci 35:537–544. doi:10.1111/j.1945-5100.2000.tb01434.x
Weidenschilling S (1997) Production of chondrules by lightning in the solar nebula? Not so easy! In: Lunar and Planetary Science Conference, vol 28, p 1515
Whipple EC (1981) Potentials of surfaces in space. Rep Prog Phys 44:1197–1250. doi:10.1088/0034-4885/44/11/002
Whipple FJW, Scrase FJ (1936) Point discharge in the electric field of the Earth. Geophys Mem Met Off Lond 38:1
Williams ER, McNutt SR (2005) Total water contents in volcanic eruption clouds and implications for electrification and lightning. In: Pontikis C (ed) Recent progress in lightning physics. Research Signpost, Kerala, pp 81–94
Williams PKG, Cook BA, Berger E (2014) Trends in ultracool dwarf magnetism. I. X-ray suppression and radio enhancement. Astrophys J 785:9. doi:10.1088/0004-637X/785/1/9
Wilson CTR (1906) On the measurement of the Earth–air current and on the origin of atmospheric electricity. Proc Camb Philos Soc 13:363–382
Wilson CTR (1921) Investigations on lightning discharges and on the electric field of thunderstorms. R Soc Lond Philos Trans Ser A 221:73–115. doi:10.1098/rsta.1921.0003
Wilson CTR (1929) Some thundercloud problems. J Frankl Inst 208:1–12
Witte S, Helling Ch, Barman T, Heidrich N, Hauschildt PH (2011) Dust in brown dwarfs and extra-solar planets. III. Testing synthetic spectra on observations. Astron Astrophys 529:A44. doi:10.1051/0004-6361/201014105
Wolszczan A, Frail DA (1992) A planetary system around the millisecond pulsar PSR 1257 + 12. Nature 355:145–147. doi:10.1038/355145a0
Wu CS, Lee LC (1979) A theory of the terrestrial kilometric radiation. Astrophys J 230:621–626. doi:10.1086/157120
Xu W, Celestin S, Pasko VP (2012) Source altitudes of terrestrial gamma-ray flashes produced by lightning leaders. Geophys Res Lett. doi:10.1029/2012GL051351
Yair Y (2008) Charge generation and separation processes. In: Leblanc F, Aplin KL, Yair Y, Harrison RG, Lebreton JP, Blanc M (eds) Planetary atmospheric electricity. Space Science Series of ISSI, vol 137, p 119
Yair Y (2012) New results on planetary lightning. Adv Space Res 50:293–310. doi:10.1016/j.asr.2012.04.013
Acknowledgments
Christian Helling highlights the financial support of the European Community under the FP7 by an ERC starting Grant 25473. Declan Diver gratefully acknowledges support from EPSRC via Grant Numbers EP/K006142/1 and EP/K006088/1. Francisco Gordillo-Vasquez thanks the Spanish Ministry of Economy and Competitiveness (MINECO) under projects FIS2014-61774-EXP and ESP2013-48032-C5-5-R and the EU through the FEDER programme. We thank all the participants at the Workshop Electrification in dusty atmospheres inside and outside the solar system held in September 2014 in the Scottish Highlands for their input and inspiration. We thank the Royal Astronomical Society, the European Research Council and the Institute of Physics Electrostatics Group for financial support. We thanks Sarah Casewell and Isabel Rodrigues-Barrera for their help in preparing Table 1. Gabriella Hodosán is thanked for helping with the literature collection. Keri Nicoll is thanked for her inspiring feedback on Sect. 3.4. Most of the literature search has been performed using ADS.
Author information
Authors and Affiliations
Corresponding author
Appendix: Glossary
Appendix: Glossary
-
AC: alternating current.
-
Asteroid: small rocky bodies of the inner solar system, ranging in size from 10 to 900 m in diameter.
-
Aurora: large diffuse light-emitting structures in the lower ionosphere (>90 km) generated when energetic charged particles precipitating from the magnetosphere collide with ground state neutral species and excite them. The excited species (oxygen atoms and nitrogen molecules) emit light when returning to their ground state.
-
Carbonaceous Compound: material rich in carbon; in an astrophysical context, such compounds usually are associated with primitive solar system remnants.
-
Conduit, Volcano Conduit: the pipe that carries magma from the magma chamber, up through the crust and through the volcano itself until it reaches the surface.
-
Chondrule: molten or partially molten droplets that appear as spherical, solid inclusions of different chemical composition from the the matrix of their parent asteroid. They represent one of the oldest solid materials within the solar system.
-
Cosmic Rays: ionised nuclei and electrons that are distinguished by their high energies. The ionised nuclei have energies ranging from \(10^6\hbox { eV}\) to greater than \(10^{20}\hbox { eV}\) and comprise 99 % of cosmic rays. They originate from either the Sun or outside the solar system, probably from Super Novae or Gamma Ray Bursts.
-
Cyclotron Maser Instability: the mechanism whereby a population of relativistic electrons move in ambient magnetic fields, producing coherent radiation that reflects depends upon the magnetic field strength.
-
DC: direct current.
-
Debye Length: the scale-length associated with the violation of charge neutrality in a plasma, due to thermal fluctuations causing charge separation.
-
Double-Diffusive Convection: a form of convection (i.e. hydrodynamic bulk motion) that is driven by two distinct gradients in fluid composition arising from two different species abundances.
-
Druyvesteyn Distribution: a driven-equilibrium distribution function that takes into account the presence of large-scale electric fields in a plasma, as well as interactions with neutrals.
-
Effective Temperature: \(T_{\mathrm{eff}}\) [K] is a measure of the total radiation flux emitted at all wavelengths \(\lambda\) [Å] (\(T_{\mathrm{eff}}=F_{\mathrm{tot}}/\sigma\) with \(F_{\mathrm{tot}}=\int F_\lambda d\lambda\); \(F_\lambda\) [\({\hbox {erg/s/cm}}^2/\AA\)]—radiative flux; \(\sigma\) [\(\hbox {erg cm}^{-2}\hbox {s}^{-1}\hbox {K}^{-4}\)]—Stefan–Bolzmann constant).
-
Electrical Conductivity: a material property that characterises the ease with which electricity can be passed through it.
-
Extrasolar: outside or beyond the solar system.
-
Fair Weather Current: atmospheric current of ions present during undisturbed weather condition.
-
Floating Potential: the electric potential (or voltage) that spontaneously arises on a surface immersed in a plasma, due to the difference in mobility between electrons and heavier ions.
-
Fractoemission: the emission of particles (charged, neutral and photons) during and after fracturing of surfaces.
-
Geiger Counter: an instrument for measuring ionising radiation that detects alpha particles, beta particles and gamma rays using the ionisation produced in a Geiger–Müller tube.
-
Hydrometeors: water droplets or ice particles.
-
Ion Acoustic Wave: a sound wave carried by the motion of plasma ions, as opposed to the electrons.
-
Isotope Ratio: means of quantifying the relative abundance of isotopes (which are elements which have nuclei that differ in the number of neutrons, but which are otherwise chemically identical).
-
Jet: directed and confined stream of fluid or gas.
-
Jy: Janskys (symbol: Jy) are the unit for the spectral flux density of radio waves: \(1\hbox { Jy} = 10^{-26}\hbox { W m} ^{2}\hbox { Hz}^{1}\). The unit is named after Karl G. Jansky, an US radio astronomer. His discovery of the radio waves emitted by the Milky Way initiated radio astronomy as a new research field.
-
M-Dwarfs: the lowest mass (\(0.075\hbox {-}0.5\hbox {M} _{\mathrm{Sun}}\)), main sequence stars; most common type of stars in the Milky Way.
-
Magma: fluid mixture of molten and semi-molten rock and volatiles produced by volcanism.
-
Magnetic Reynolds Number: a dimensionless number equal to the ratio of advective to diffusive effects, where the latter are characteristic of the magnetic field. Hence a large magnetic Reynolds number (\(\gg 1\)) means that the magnetic field plays a dominant role in the fluid evolution as diffusion is unimportant and the magnetic field is advected with the fluid flow.
-
M (Spectral Type): stars are grouped into spectral classes which link to their effective temperature, luminosity, evolutionary state. The spectral class M indicates the coolest stars on the main sequence where hydrogen burning assures the most stable phase in a star’s life. Brown dwarfs are cooler than M-dwarfs and were classified as L, T and Y with Y being the coolest and most planet like.
-
Mesocyclone: a rapidly rotating column of air, typically a few miles in diameter, readily identified by its characteristic radar signal and consistent with storm conditions.
-
Mobility: the drift speed of a charged particle produced when subjected to a steady electric field.
-
Near-IR: electromagnetic radiation in the near infrared, with wavelengths between 800 nm and 5 microns.
-
Ohm’s Law: relates the electrical current flowing between two points to the potential difference between those same points.
-
Plasma Void: a finite region in a dusty plasma which is dust free.
-
Protoplanetary Disk: a region of dust and rocks orbiting a young star from which planets could be formed.
-
Regolith: layer of unconsolidated dust and fragmented rock that covers a terrestrial planet.
-
Shock Tube: a device designed to create shocks (i.e. sharp density and pressure discontinuities) in gases, usually in order to produce ionisation fronts.
-
Sounding: a method to measure local temperature, humidity, wind, etc., in the Earth’s atmosphere by means of radio sondes, laser beams (optical) or sound waves.
-
Sprite: a large (50 km high and 10–20 km wide) electrical discharge that occurs above thunderclouds at altitudes around 50–85 km with a diffuse region (above 70–75 km) and a filamentary (streamer-like) region (below 70–75 km) [values are given for Earth].
-
Stratosphere: major layer of the Earth’s atmosphere, lying above the troposphere (0–11 km) and below the mesosphere (50–90 km).
-
Thunderstorm: storm characterised by the presence of lightning.
-
Triboelectrification: the process whereby two surfaces can acquire or lose charges by mutual collision.
-
Troposphere: lowest layer of the Earth’s atmosphere, lying between 0 and 11km, in which most of the weather phenomena occur.
-
Turbulence: chaotic flow in which the pressure and gas velocity change rapidly in space and time.
-
Volcanic Ash: fragments of rock created during a volcanic eruption, usually 2 mm or less in diameter.
-
Volcanic Conduit: passage or tube created by the flow of magma in a volcano.
-
Volcanic Plume: the gas and ash cloud ejected into the atmosphere by a volcanic eruption.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Helling, C., Harrison, R.G., Honary, F. et al. Atmospheric Electrification in Dusty, Reactive Gases in the Solar System and Beyond. Surv Geophys 37, 705–756 (2016). https://doi.org/10.1007/s10712-016-9361-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10712-016-9361-7