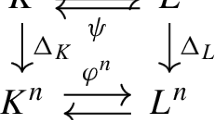A Lefschetz duality for intersection homology

Abstract

We prove a Lefschetz duality theorem for intersection homology. Usually, this result applies to pseudomanifolds with boundary which are assumed to have a “collared neighborhood of their boundary”. Our duality does not need this assumption and is a generalization of the classical one.

1 Introduction

The main feature of intersection homology is that it satisfies Poincaré duality for a large class of singular sets, called pseudomanifolds. This duality is particularly nice when the considered singular set may be stratified by a stratification having only even dimensional strata, like for instance the complex analytic sets.

In their fundamental papers Goresky and MacPherson [6, 7] introduced intersection homology, showed that it is finitely generated and independent of the stratification and established their generalized Poincaré duality. They also introduced the notion of pseudomanifold with boundary to which a generalized Lefschetz duality applies.

A pseudomanifold is a set $X$ whose singular locus is of codimension at least 2 in $X$ (and is nowhere dense in $X$). Pseudomanifolds with boundary are couples $(X,\partial X)$ such that $X\setminus \partial X$ and $\partial X$ are pseudomanifolds and such that $\partial X$ has a neighborhood in $X$ which is homeomorphic to a product $\partial X \times (0,1]$. In this paper, we show how the last requirement can be left out without affecting Lefschetz duality. We introduce the notion of stratified $\partial$-pseudomanifold (see Definitions 4.1 and 4.3) and establish Lefschetz duality for this class of sets.

The intersection homology groups as defined in [6] depend on the choice of a perversity (see definitions below). In this article we will work not with one but two perversities: one for the considered set $X$ and one for its boundary. We explain that, if the difference between the chosen perversities of $X$ and $\partial X$ is constant then Lefschetz duality holds on $X$ (if $X$ is a $\partial$-pseudomanifold). We shall consider what is called general perversities which provide a more general framework. These perversities were studied by Friedman [3, 5] who extended Goresky and MacPherson’s theory to them (see Sect. 3).

Our approach is different from the one developed by Friedman in [1–3, 5] where the author obtained several very interesting results on pseudomanifolds with possibly one co-dimensional strata with general perversities. The novelty of the present paper is that the allowable chains of $\partial X$ are allowable in $X$.

In [13], the author proves that the cohomology of $L^\infty$ forms on a compact subanalytic pseudomanifold is isomorphic to intersection cohomology in the maximal perversity. In [14], we give a Lefschetz duality theorem, relating the $L^\infty$ cohomology to the so-called Dirichlet $L^1$-cohomology. As a corollary of these two results, on compact subanalytic pseudomanifolds, we got that the Dirichlet $L^1$ cohomology is isomorphic to intersection cohomology in the zero perversity. The Lefschetz duality of [14] is true for any bounded subanalytic manifold (i.e. we do not assume that the closure is a pseudomanifold) while Lefschetz duality for intersection homology is usually stated on pseudomanifolds with boundary. This lead the author to the conclusion that there must be a Lefschetz duality in a slightly more general setting than the framework of pseudomanifolds with boundary in the way that they are usually defined. The Lefschetz duality for $\partial$-pseudomanifolds that we carry out in this paper is indeed the exact geometric counterpart of the duality observed in [14] (on $\partial$-pseudomanifolds).

As in [6], we will work in the PL framework. Although the arguments presented in [6, 7] (for proving Poincaré duality) seem to apply for proving our theorem, we shall present a different argument. Our proof actually bears some resemblance with the proof of Lefschetz duality for general perversities on pseudomanifolds with boundary given in [5] (and makes use of this result). Even the proof of Lefschetz duality in the case of perversities as defined in [6] will require to investigate general perversities.

Content of the paper   In the first section we recall the definitions of intersection homology and stratified pseudomanifold. In the second section we recall the notion of general perversity and show that intersection homology with general perversities is preserved under refinement for suitable general perversities (Proposition 3.4). In Sect. 4 we introduce our notion of stratified $\partial$-pseudomanifold and extend the basic notions to this setting. We finish Sect. 4 by stating the three main theorems: one formulating our Lefschetz duality for $\partial$-pseudomanifolds (Theorem 4.7), one stating independence with respect to the stratification (in the case of GM-perversities, Theorem 4.10) and one establishing that the groups are finitely generated (Theorem 4.9). These theorems are all proved in Sect. 5.

Some notations and conventions   We denote by $cL$ the open cone on the space $L\subset \mathbb{R }^n$ (for simplicity we will assume that its vertex is the origin), $c\emptyset$ being a point. Open balls in $\mathbb{R }^n$ are denoted $B^{n}(x_0,\varepsilon )$ and are considered for the norm $\sup _{1\le i\le n} |x_i|$. We write $\dim S$ for the dimension of a piecewise linear set $S$ (PL for short, meaning that it is endowed with a compatible family of triangulations) and $\text{ cod }_X S$ for the codimension of $S$ in $X$ (if $S \subset X$) i.e. the integer $\dim X-\dim S$. All the considered sets will be PL spaces.

A triangulation of a set $X\subset \mathbb{R }^n$ is a homeomorphism $T:K \rightarrow X$, with $K$ union of open simplices of a finite simplicial complex $L$ (an open simplex being a simplex $\sigma$ where the faces of dimension less than $\dim \sigma$ have been deleted). Given a piecewise linear space $X$ and a compatible triangulation $T:K\rightarrow X, K\subset L$, let $C^T_\bullet (X)$ denote the chain complex generated by the simplices of $L$ (not the open simplices considered just above but the full simplices with no face deleted) that belong to $K$. The PL chain complex $C_\bullet (X)$ is defined to be $\lim _{\rightarrow T} C_\bullet ^T(X)$, where the limit is taken with respect to the directed set of compatible triangulations (as in [3, 6]). Our coefficient ring will always be $\mathbb{R }$.

We denote by $X_{reg}$ the regular locus of $X$, i.e. the set of points at which $X$ is a $C^0$ manifold (without boundary) of dimension $\dim X$. We denote by $X_{sing}$ its complement in $X$. A PL subspace of $X$ is a union of images of open simplices of a compatible triangulation. In particular $X_{reg}$ and $X_{sing}$ are subspaces of $X$. We write $cl(S)$ for the topological closure of a PL subspace $S$ of $X$.

2 Intersection homology

We recall the definition of intersection homology as it was introduced by Goresky and MacPherson [6].

Definition 2.1

Let $X$ be a PL space. A stratification of $X$ is a finite partition $\Sigma$ of $X$ into connected $C^0$ manifolds which are PL subspaces. An element of $\Sigma$ is called a stratum of $X$. The depth of $\Sigma$ is the integer $\max _{S \in \Sigma } \text{ cod }_X S$.

A stratum of codimension at least 2 in $X$ is called a singular stratum of $\Sigma$. We denote by $\Sigma _s$ the collection of all the singular strata of $\Sigma$.

A stratification is compatible with a subset $Y$ of $X$ if this subset is a union of strata.

Observe that if $L$ is stratified by $\Sigma$ then $cL$ is stratified by $cS\setminus \{0\}, S \in \Sigma$, and $\{0\}$. We now define inductively on the dimension the locally topologically trivial stratifications. For $\dim X\,=\,0$, every stratification is locally topologically trivial.

A stratification $\Sigma$ of $X$ is said to be locally topologically trivial if for every $x \in S, S \in \Sigma$, there is a PL homeomorphism

$$\begin{aligned} h:U_x \rightarrow B^i(0,1) \times \textit{cL}, \end{aligned}$$

(where $i\,=\,\dim S$) with $U_x$ neighborhood of $x$ in $X$ and $L\subset X$ compact PL subspace having a locally topologically trivial stratification such that $h$ maps the strata of $U_x$ (induced stratification) onto the strata of $B^i(0,1) \times cL$ (product stratification).

Definition 2.2

A locally closed PL subset $X\subset \mathbb{R }^n$ is an $l$-dimensional pseudomanifold (without boundary) if $X_{ reg}$ is an $l$-dimensional manifold which is dense in $X$ and $\dim X_{ sing}<l-1$.

A stratified pseudomanifold (of dimension $l$) is the data of an $l$-dimensional pseudomanifold $X$ together with a locally topologically trivial stratification $\Sigma$ of $X$ having no stratum of dimension $(l-1)$.

Definition 2.3

A stratified pseudomanifold with boundary is a couple $(X,\partial X)$ of PL spaces together with a partition $\Sigma$ of $X$ into PL subspaces such that:

• (1) $X{\setminus } \partial X$ is a stratified pseudomanifold (with the stratification $\{S {\setminus } \partial X :S \in \Sigma \}$),

• (2) $\partial X$ is a stratified pseudomanifold (with the stratification $\{S \cap \partial X: S \in \Sigma \}$),

• (3) $\partial X$ has a stratified collared neighborhood: there exist a neighborhood $U$ of $\partial X$ in $X$ and a PL homeomorphism $h: \partial X \times (0,1]\rightarrow U$ such that $h((S\cap \partial X)\times (0,1])=U \cap S$, for every $S\in \Sigma$, as well as $h(\partial X \times \{1\})=\partial X$.

The above partition $\Sigma$ is not a stratification for its elements are not manifolds. They are nevertheless manifolds with boundary. We will however sometimes abusively consider it below as a stratification as no confusion may arise. Let $(X,\partial X, \Sigma )$ be a stratified pseudomanifold with boundary.

Definition 2.4

A perversity (or $l$-perversity) is a sequence of integers $p = (p_2, p_3, \ldots , p_l)$ such that $p_2 = 0$ and $p_{k+1} = p_k$ or $p_k + 1$. A PL subspace $Y \subset X$ is called $(p,i)$-allowable if for every singular stratum $S \in \Sigma _s$, we have:

$$\begin{aligned} \dim Y \cap S \le i-k+p_k, \end{aligned}$$

where $k=\text{ cod }_X S$. Define $I^{p}C_i (X)$ as the subgroup of $C_i(X)$ consisting of the PL chains $\sigma$ such that $|\sigma |$ is $(p, i)$-allowable and $|\partial \sigma |$ is $(p, i - 1)$-allowable.

The $i\mathrm{th}$ intersection homology group of perversity $p$, denoted $I^{p}H_i (X)$, is the $i\mathrm{th}$ homology group of the chain complex $I^{p}C_\bullet (X).$

Given a PL subspace $A$, denote by $I^pC_j(A)$ the chain complex constituted by the chains of $I^p C_j(X)$ which have support in $A$. Relative intersection homology $I^pH_j(X,A)$ is then defined in the obvious way.

2.1 Lefschetz-Poincaré duality for pseudomanifolds with boundary

We denote by $t$ the maximal perversity, i.e. $t=(0,1,\ldots ,l-2)$. Two perversities $p$ and $q$ are said to be complementary if $p+q=t$.

Theorem 2.5

(Generalized Lefschetz-Poincaré duality [3, 5–7, 10])  Let $X$ be a PL compact oriented stratified pseudomanifold with boundary $\partial X$. For any complementary perversities $p$ and $q$:

$$\begin{aligned} I^p H_j(X)\simeq I^q H_{l-j}(X, \partial X). \end{aligned}$$

3 General perversities

We are going to introduce a bigger category of perversities, called general perversities. They were considered by Saralegi in [11] and studied in detail by Friedman [5] who fully described the theory by means of a sheaf theoretic approach.

Definition 3.1

Let $X$ be a stratified set and denote by $\Sigma$ its stratification. A general perversity is a function $p:\Sigma _s \rightarrow \mathbb{N }$ satisfying for any singular stratum $S \in \Sigma _s$:

$$\begin{aligned} p(S)\le \text{ cod }_X S-2. \end{aligned}$$

In order to avoid any confusion, perversities as introduced in Definition 2.4 are sometimes called GM-perversities. Any GM-perversity $(p_2,\ldots ,p_l)$ gives rise to a general perversity defined by $p(S):=p_k$, where $k:=\text{ cod }_X S$, for each $S\in \Sigma _s$.

Two general perversities $p$ and $q$ are complementary if $p(S)+q(S)=\text{ cod }_X S-2$, for every singular stratum $S$.

3.1 Intersection homology with general perversities

Fix for this section a PL stratified pseudomanifold with boundary $(X,\partial X,\Sigma )$. As we pointed out right after Definition 2.3, we shall consider $\Sigma$ as a stratification of $X$.

We now recall the definition of intersection homology with general perversity. Fix a general perversity $p:\Sigma _s \rightarrow X$. A PL subspace $Y \subset X$ is called $(p,i)$-allowable (w.r.t. $\Sigma$) if for every $S\in \Sigma _s$:

$$\begin{aligned} \dim Y \cap S \le i-\text{ cod }_X S+p(S). \end{aligned}$$

Define $I^{p}C_i (X)$ as the subgroup of $C_i(X)$ consisting of the PL chains $\sigma$ such that $|\sigma |$ is $(p, i)$-allowable and $|\partial \sigma |$ is $(p, i-1)$-allowable.

The $j\mathrm{th}$ intersection homology group of perversity $p$, denoted $I^{p}H_j (X)$, is the $j\mathrm{th}$ homology group of the chain complex $I^{p}C_\bullet (X).$ Relative intersection homology is then defined in the same way as in the case of GM-perversities.

Friedman established in [5] that Poincaré duality is true for general perversities ([5], Corollary 4.4). Lefschetz duality also holds for pseudomanifolds with boundary (i.e. Theorem 2.5 applies to these general perversities). Indeed, in [5], Friedman gave a nice proof of Lefschetz duality, which is derived from Poincaré duality for intersection homology with general perversities (considering even more general perversities). Thus, although general perversities provide a much wider setting, we see that most of the theory still works.

The Mayer-Vietoris exact sequence also holds for intersection homology with general perversities. Indeed, if a PL pseudomanifold with boundary $X$ may be covered by two open sets $U$ and $V$, it is shown in [2] (Sect. 2.5, by means of barycentric subdivisions) that $I^{p}C_j(X)$ gives rise to the same homology theory as $I^{p} C_j(U)\oplus I^{p}C_j(V)$ (the latter article deals with singular chains but King showed [9] that singular chains give rise to the same homology theory as PL-chains). This is enough to ensure the exactness of the Mayer-Vietoris sequence.

3.2 $IH$ and refinements

The inconvenient of working with general perversities is that we lose stratification independence. It is a very important feature of intersection homology for it entails that $IH$ is a topological invariant. We nevertheless can prove a statement which will be useful for proving Theorem 4.10 (although this theorem only deals with GM-perversities!): we will show that the intersection homology with respect to a general perversity is preserved by refinements (Proposition 3.4). To the best knowledge of the author, this result seems to be new. Before stating the proposition, we define precisely what we mean.

Throughout this section $X$ is a compact $l$-dimensional PL stratified pseudomanifold with boundary.

Definition 3.2

Let $\Sigma$ denote a stratification of $X$. A refinement of $\Sigma$ is a stratification $\Sigma ^{\prime }$ of $X$ such that every stratum of $\Sigma$ is a union of strata of $\Sigma ^{\prime }$. We write in this case $\Sigma ^{\prime } \prec \Sigma$.

Of course, we implicitly assume below in this section that all the considered stratifications make X into a stratified pseudomanifold with boundary.

Given some general perversities $p:\Sigma _s\rightarrow \mathbb{N }$ and $p^{\prime }:\Sigma ^{\prime }_s\rightarrow \mathbb{N }$, where $\Sigma ^{\prime }\prec \Sigma$ are stratifications of $X$, we write $p^{\prime }\prec p$ if

$$\begin{aligned} p(S)\le p^{\prime }(S^{\prime })\le p(S)+\text{ cod }_S S^{\prime }, \end{aligned}$$

for any couple $(S^{\prime },S)\in \Sigma ^{\prime } _s\times \Sigma _s$ with $S^{\prime }\subset S$.

In the situation where $p^{\prime }\prec p$ and $\Sigma ^{\prime } \prec \Sigma$ then it directly follows from the definitions that $I^{p^{\prime }} C_j (X)\subset I^p C_j(X)$.

Remark 3.3

In the case where $p$ and $p^{\prime }$ are induced by the same GM-perversity $r$, then the condition $r_{k+1} \in \{r_k, r_k+1\}$ forces $p^{\prime }\prec p$.

Proposition 3.4

Let $\Sigma ^{\prime }\prec \Sigma$ be stratifications of $X$ and let $p^{\prime } \prec p$ be respectively two general perversities on these stratifications. The map $I^{p^{\prime }} H_j(X)\rightarrow I^pH_j (X)$ induced by the inclusion of the two chain complexes is an isomorphism.

The following Lemma will be needed to prove Proposition 3.4. In this lemma and in the sequel we use the symbol 0 to denote the origin in $\mathbb{R }^n$ for all $n \in \mathbb{N }$, as no confusion may arise. For instance, in the lemma below $U\setminus 0$ denotes the set $U$ from which we have removed the origin of $\mathbb{R }^n$, if $U \subset \mathbb{R }^n$.

Lemma 3.5

Let $L$ be a compact PL stratified pseudomanifold and let $U:= cL \times B^i(0,1)$. Endow $U$ with the product stratification $\mathcal{S }$ and let $p:\mathcal{S }_s\rightarrow \mathbb{N }$ denote a general perversity. If $j<\dim U-p( 0 \times B^i(0,1))-1$ then the mapping

$$\begin{aligned} \beta :I^{p} H_{j} (U \setminus 0)\rightarrow I^{p} H_{j} (U), \end{aligned}$$

induced by inclusion, is an isomorphism.

Proof

Set $W_\alpha := 0 \times B^i(0,\alpha ), \alpha >0$. Remark that, due to the conic structure and topological triviality, for $\alpha$ small enough the mapping $v_y:I^{p} C_j(U \setminus cl(W_\alpha )) \rightarrow I^{p} C_j(U \setminus y)$ induces an isomorphism in homology for any $j$ and any $y\in W_\alpha$.

We first show that $\beta$ is one-to-one. Take $\sigma \in \ker \beta$, i.e. assume that there is $\tau \in I^{p} C_{j+1}(U)$ with $\sigma =\partial \tau$. For $\alpha >0$ small enough, $|\sigma |$ does not meet $W_\alpha$. Then, as $|\tau |$ is $(j+1,p)$-allowable, we have for $S:= 0 \times B^i(0,1)$:

$$\begin{aligned} \dim |\tau | \cap S\le j+1-\text{ cod }_U S+p( S)<i. \end{aligned}$$

(3.1)

Consequently, there must be $y \in W_\alpha \setminus |\tau |$. Therefore, $\sigma$ bounds a chain of $I^p C_{j+1} (U \setminus y)$ and is thus zero in $I^p H_j (U \setminus 0)$ (since $v_yv_{0}^{-1}$ is an isomorphism), as required.

We turn to show ontoness. Let $c$ be a nontrivial cycle of $I^p H_j (U)$. If $j=0$ then, due to the allowability conditions, $|c|$ cannot contain the origin. If $j>0$ then $|c|$ cannot contain the origin either since otherwise it could be retracted to the origin. Consequently, it is a cycle of $U\setminus 0$. $\square$

Proof of Proposition 3.4

We will argue by induction on $\dim X$.

Given a PL open subspace $V\subset X$, let $\Theta _V:I^{p^{\prime }} H_j(V)\rightarrow I^p H_j(V)$ denote the mapping induced by the inclusion between the two chain complexes. We shall show that $\Theta _V$ is an isomorphism for each PL open subspace $V\subset X$. We will argue by induction on the depth of the stratification induced on $V$ by $\Sigma ^{\prime }$, the case of depth $0$ being vacuous.

Choose $x_0 \in X \setminus \partial X$. As $\Sigma$ (resp. $\Sigma ^{\prime }$) is a locally topologically trivial stratification, there exists a neighborhood of $x_0$, say $U_{x_0}$ (resp. $V_{x_0}$), which is stratified homeomorphic to a product $cL \times B^i(0,1)$ (resp. $cL^{\prime } \times B^k(0,1)$) where $L$ (resp. $L^{\prime }$) is a PL compact stratified pseudomanifold. We will identify $x_0$ with $0$ and $V_{x_0}$ with $cL^{\prime } \times B^k(0,1)\subset \mathbb{R }^{n+k}$. Let

$$\begin{aligned} V_0 ^\varepsilon := (cL^{\prime }\cap B^{n}(0, \varepsilon )) \times B^k(0, \varepsilon ). \end{aligned}$$

Define in the same way, replacing $L^{\prime }$ with $L$ and $k$ with $i$, a fundamental system of neighborhoods of the origin $U_0^\varepsilon$. $\square$

Claim 1

$\Theta _{V_{0}^\varepsilon }$ is an isomorphism for any real $\varepsilon >0$ small enough.

For suitable $0<\varepsilon ^{\prime }<\varepsilon$, we have $V_0 ^{\varepsilon ^{\prime }}\subset U_0 ^{\varepsilon }$. We first check that in this case the map

$$\begin{aligned} \nu :I^{p}H_j(V_0 ^{\varepsilon ^{\prime }}) \rightarrow I^{p} H_j(U_0^{\varepsilon }), \end{aligned}$$

induced by inclusion, is an isomorphism. Indeed, for suitable $0<\varepsilon _1<\varepsilon _2<\varepsilon _3< \varepsilon _4$ we have the following inclusions:

$$\begin{aligned} V_0 ^{\varepsilon _1}\subset U_0 ^{\varepsilon _2} \subset V_0 ^{\varepsilon _3}\subset U_0 ^{\varepsilon _4}. \end{aligned}$$

Due to the conic structure, the inclusions $V_0 ^{\varepsilon _1} \subset V_0 ^{\varepsilon _3}$ and $U_0 ^{\varepsilon _2} \subset U_0^{\varepsilon _4}$ induce isomorphisms in intersection homology with perversity $p$. Consequently, $\nu$ must be an isomorphism, as claimed. For the same reason, the mapping $\nu ^{\prime }:I^{p}H_j(V_0 ^{\varepsilon ^{\prime }}\setminus 0) \rightarrow I^{p} H_j(U_0^{\varepsilon }\setminus 0),$ also induced by inclusion, is an isomorphism.

Let $S$ (resp. $S^{\prime }$) be the stratum of $\Sigma$ (resp. $\Sigma ^{\prime }$) which contains the origin.

If $j < l-p^{\prime } (S^{\prime })-1$ then since $p^{\prime } \prec p$ a fortiori $j< l-p(S)-1$. Let $star(0)\subset X$ be constituted by all the closed geometric simplices which contain the origin (for some subdivision of the triangulation compatible with all the strata). This set covers a neighborhood of the origin. Let $M$ be the subspace constituted by all the faces of the simplices of $star(0)$ which do not contain the origin (this set is sometimes called the link at the origin). After a homothetic transformation, it fits in $V_0^{\varepsilon ^{\prime }} \subset U_0 ^\varepsilon$. The stratifications $\Sigma$ and $\Sigma ^{\prime }$ induce two stratifications of $M$, one refining the other, and the perversities $p$ and $p^{\prime }$ induce two general perversities of these stratifications (assigning the value at $Z$ to $Z \cap M, Z$ singular stratum). This gives rise to a refinement map $\Theta _M$. By the induction on dimension, $\Theta _M$ is an isomorphism. Furthermore, by the Künneth formula [4, 5] (these articles deal with singular chains but King showed [9] that singular chains give rise to the same homology theory as PL-chains) and the conic structure, the inclusions $M \hookrightarrow U_0^\varepsilon \setminus 0$ and $M \hookrightarrow V_0^{\varepsilon ^{\prime }}\setminus 0$ induce isomorphisms in intersection homology, for both perversities. We thus have the following commutative diagram (all the arrows being induced by inclusion):

We see that $\Theta _{V_{0}^{\varepsilon ^{\prime }}\setminus 0}$ is an isomorphism, for $\varepsilon ^{\prime }>0$ small enough. We therefore have the following commutative diagram:

where $\beta :I^p H_{j} (U_0^\varepsilon \setminus 0)\rightarrow I^p H_{j} (U_0 ^\varepsilon )$ and $\beta ^{\prime } :I^{p^{\prime }} H_{j} (V_0^{\varepsilon ^{\prime }} \setminus 0)\rightarrow I^{p^{\prime }} H_{j} (V_0^{\varepsilon ^{\prime }})$ are induced by inclusion. Since, by Lemma 3.5, $\beta$ and $\beta ^{\prime }$ are both isomorphisms, the result follows.

If $j\ge l-p^{\prime }(S^{\prime })-1$ then, since $p^{\prime }(S^{\prime })\le p(S)+(i-k)$, a fortiori $j\ge l-p(S)-i-1$. Hence, by Proposition 2.1 of [5] and the Künneth formula [4, 5], we have in this case $I^{p^{\prime }} H_j (V_0^{\varepsilon ^{\prime }} )\simeq I^p H_j (U_0^\varepsilon ) \simeq 0$. As $\nu$ is an isomorphism, we immediately derive $I^{p} H_j (V_0^{\varepsilon ^{\prime }} ) \simeq 0$. This yields that $\Theta _{V_0^{\varepsilon ^{\prime }}}$ is an isomorphism, establishing Claim 1.

Claim 2

$\Theta _V$ is an isomorphism for every PL open set $V=cL^{\prime } \times W$, with $W$ PL open subset of $B^k(0,1)$.

To see this, first write $W$ as the union of the star-shaped open sets $W_i:=int(star(v_i))$ ($int$ stands for interior), $v_i$ vertex of $W$ (of some suitable subdivision), and let $N_i := \cup _{k<i} W_k$ as well as $U_i:=cL^{\prime }\times N_i$ and $V_i:=cL^{\prime }\times W_i$. Consider the Mayer-Vietoris exact sequences of the pair ($V_i, U_i$) for both perversities $p$ and $p^{\prime }$. These two long exact sequences, together with the mappings $\Theta _{U_{i}\cup V_i},\,\Theta _{U_i},\,\Theta _{V_i}$, and $\Theta _{U_i\cap V_i}$, constitute a commutative diagram. Both $N_i$ and $N_i \cap W_i$ are unions of $(i- 1)$ star-shaped open sets, so by induction on the number of such sets in a cover we may assume that $\Theta _{U_i}$ and $\Theta _{U_i\cap V_i}$ are isomorphisms. Moreover, by Claim 1, $\Theta _{V_i}$ is an isomorphism (Claim 1 actually establishes that $\Theta _V$ is an isomorphism if $V$ is PL homeomorphic to $cL^{\prime } \times B^k(0,1)$ since so is $V_{x_0} ^\varepsilon$). Hence, thanks to the five Lemma, $\Theta _{U_{i}\cup V_i}$ is an isomorphism, which shows that $\Theta _{U_k}$ is an isomorphism for all $k$.

Claim 3

$\Theta _V$ is an isomorphism for every PL open set $V\subset V_{x_0}$.

Set $V_1:=\{(y,x)\in cL^{\prime } \times W: |y| < \varepsilon _x\}$, where $W:=\{x \in B^k(0,1): (0,x) \in V\}$ and $\varepsilon _x:=d((0,x),X\setminus V)$, and let $V_2$ be the complement of $0 \times W$ in $V$. Since $cL^{\prime }$ is a cone, $V_1$ is homeomorphic to the product $cL^{\prime } \times W$. By Claim 2, $\Theta _{V_1}$ is an isomorphism.

By induction on depth, $\Theta _{V_2}$ and $\Theta _{V_1\cap V_2}$ are both isomorphisms. By the five Lemma and the Mayer-Vietoris exact sequences of the pairs ($V_1, V_2$) (for perversities $p$ and $p^{\prime }$, as in Claim 2), this yields Claim 3.

Observe that, thanks to the stratified collared neighborhood, every point $y$ of $\partial X$ in a stratum of dimension $i$ has a neighborhood PL homeomorphic to $cL \times B^{i-1}(0,1) \times (0,1]$, which has the same intersection homology as $cL \times B^{i}(0,1)$. Hence, the above argument shows that Claim 3 holds true at boundary points as well.

We are now ready to conclude that $\Theta _V$ is an isomorphism for any PL open subspace $V\subset X$. Indeed, again thanks to the Mayer-Vietoris exact sequence and the five Lemma, Claim 3 yields that $\Theta _V$ is an isomorphism for any set $V$ which is contained in the union of finitely many $V_{x_1},\ldots , V_{x_k}$, with $x_1,\ldots , x_k$ elements of $X$. As $X$ is compact, we are done. $\square$

4 $\partial$-Pseudomanifolds

We first introduce the notion of $\partial$-pseudomanifold and then naturally extend intersection homology to these spaces. Basically, we drop the assumption (3) of having a collared neighborhood (see Definition 2.3). Let $X\subset \mathbb{R }^n$ be a locally closed PL space of dimension $l$.

Definition 4.1

The $\partial$-regular locus of $X$ is the set of points of $X$ at which $X$ is a manifold with nonempty boundary of dimension $l$ (i.e. there are arbitrarily small neighborhoods homeomorphic to the subset $\{x \in \mathbb{R }^l: x_l\ge 0\}$). We will denote it by $X_{\partial ,{ reg}}$. The closure of $X_{\partial ,{ reg}}$ in $X$ will be called the boundary of $X$ and will be denoted $\partial X$. The PL space $X$ is said to be a $\partial$-pseudomanifold if $X\setminus \partial X$ is a pseudomanifold and if $\dim \partial X\setminus X_{\partial ,{ reg}}<l-2$.

Example 4.2

It follows from the above definition that if $X$ is a pseudomanifold then it is a $\partial$-pseudomanifold (with empty boundary).

Let us give a more interesting example. Let $f:\mathbb{R }^n \rightarrow \mathbb{R }$ be a subanalytic $C^1$ function such that $\dim {\textit{Sing}}(f)\cap \{ f=0 \}<n-2$ (${\textit{Sing}}(f)$ denoting the critical locus of $f$). Then, since we can triangulate it [12], the set $\{x \in \mathbb{R }^n: f(x) \ge 0\}$ is a $\partial$-pseudomanifold.

It comes down from the definitions that $\partial X \subset X_{\textit{sing}}$. It makes a difference with [1–3, 5, 6] where the boundary is not considered as a subset of the singular locus. This is due to the fact that regular points of the boundary are for us elements of $X_{\partial , {\textit{reg}}}$.

4.1 Stratified $\partial$-pseudomanifolds

Definition 4.3

A stratified $\partial$-pseudomanifold is a PL set $X$ together with a locally topologically trivial stratification $\Sigma$ compatible with $\partial X$ and such that:

• (1) $X{\setminus } \partial X$ is a stratified pseudomanifold (with the stratification $\{S {\setminus } \partial X :S \in \Sigma \}$).

• (2) $\partial X$ is a stratified pseudomanifold (with the stratification $\{S \cap \partial X :S \in \Sigma \}$).

Remark 4.4

In the definition of stratified pseudomanifolds with boundary, the elements of $\Sigma$ are manifolds with boundary. The boundary of a stratum $S$ is $S\cap \partial X$. In the definition of stratified $\partial$-pseudomanifolds, the elements of $\Sigma$ are manifolds without boundary, $\partial X\cap S$ being either empty or $S$ for every $S$ in $\Sigma$. Hence, in Definition 4.3, $S\cap \partial X$ has dimension $\dim S$ (if nonempty) while in Definition 2.3, $S \cap \partial X$ had dimension $(\dim S-1)$. This difference is no loss of generality since any partition like Definition 2.3 may be refined to fulfill the above definition (see Sect. 6 Remark 3). Example 4.2 nevertheless shows that a $\partial$-pseudomanifold does not always admit a structure of pseudomanifold with boundary.

We are now going to define the intersection homology of a $\partial$-pseudomanifold, extending naturally Goresky and MacPherson’s definition. We will show that Lefschetz duality holds for $\partial$-pseudomanifolds. We give an explicit example (a double pinched torus in $S^3$) in the last section.

4.2 Intersection homology of a $\partial$-pseudomanifold

Denote by $\Sigma$ the stratification of a PL stratified $\partial$-pseudomanifold $X$ and by $\tilde{\Sigma }$ the induced stratification of $\partial X$ (see Definition 4.3 (2)).

We shall work not with one general perversity but two: one for the boundary and one for $X$ itself.

Definition 4.5

A pair of general perversities on $X$ is a couple $\bar{p}=(p,\tilde{p})$ where $p:\Sigma _s\rightarrow \mathbb{N }$ and $\tilde{p}:\tilde{\Sigma }_s\rightarrow \mathbb{N }$ are general perversities satisfying either $p(S)- \tilde{p}(S)\equiv 0$ or $p(S)-\tilde{p}(S)\equiv 1$, for $S \in \tilde{\Sigma }_s$ (i.e. $(p(S)-\tilde{p}(S))$ is constant on the singular strata of $\partial X$, taking either $0$ or $1$ as constant value).

Two pairs of perversities $\bar{p}$ and $\overline{q}$ are complementary if so are $p$ and $q$ on the one hand and $\tilde{p}$ and $\tilde{q}$ on the other hand.

Example 4.6

Given a GM-$l$-perversity $p$, define a GM-$(l-1)$-perversity by $\check{p}_j:=p_{j+1}-p_3,$ for $j\ge 2$. It is easily checked from the definition that $\check{p}$ is an $(l-1)$-perversity. Then, $\bar{p}:=(p,\check{p})$ is a pair of perversities. Note that if $p$ and $q$ are complementary $l$-perversities then $\check{p}$ and $\check{q}$ are complementary $(l-1)$-perversities. In this case, by definition, so are the couples $(p,\check{p})$ and $(q,\check{q})$.

The intersection homology groups   Fix a pair of general perversities $\bar{p}=(p,\tilde{p})$ on $X$.

We say that a PL subspace $Y\subset X$ is $(j,\bar{p})$-allowable (with respect to $\Sigma$) if for every $S \in \Sigma _s$

$$\begin{aligned} \dim cl(Y\setminus \partial X)\cap S\le j-\text{ cod }_X S+p(S), \end{aligned}$$

(4.1)

and if $Y \cap \partial X$ is $(j ,\tilde{p})$-allowable (w.r.t. $\tilde{\Sigma }$).

Let $I^{\bar{p}} C_j(X)$ be the vector subspace of $C_j(X)$ constituted by the PL $j$-chains $\sigma$ for which $|\sigma |$ is $(j,\bar{p})$-allowable and $|\partial \sigma |$ is $(j-1,\bar{p})$-allowable. If $X$ is a pseudomanifold and $p$ stems from a GM-perversity then of course this chain complex coincides with the chain complex $I^p C_j(X)$ introduced in [6].

We denote by $I^{\bar{p}}H_j(X)$ the homology groups of this chain complex. Similarly as in the latter article, it will turn out that, if $p$ and $\tilde{p}$ are GM-perversities then the homology groups are independent of the chosen stratification (Theorem 4.10).

Relative intersection homology of $\partial$ -pseudomanifolds   Observe that it follows from the definitions that $I^{\tilde{p}} C_j(\partial X) \subset I^{\bar{p}} C_j( X)$ and hence we may set:

$$\begin{aligned} I^{\bar{p}} C_j (X,\partial X):=\frac{I^{\bar{p}} C_j(X)}{I^{\tilde{p}} C_j(\partial X)}. \end{aligned}$$

As usual, we have the following long exact sequence:

$$\begin{aligned} \cdots \rightarrow I^{\tilde{p}} H_j(\partial X) \rightarrow I^{\bar{p}} H_j (X)\rightarrow I^{\bar{p}} H_j (X, \partial X) \rightarrow I^{\tilde{p}} H_{j-1} (\partial X) \rightarrow \cdots \end{aligned}$$

(4.2)

4.3 The main results

The first result we provide is Lefschetz duality which generalizes Theorem 2.5 to $\partial$-pseudomanifolds. Let $X\subset \mathbb{R }^n$ be a compact $l$-dimensional PL stratified $\partial$-pseudomanifold.

Theorem 4.7

Assume that $X$ is oriented. For any complementary pairs of general perversities $\bar{p}$ and $\overline{q}$, we have:

$$\begin{aligned} I^{\overline{q}} H_{l-j} (X)\simeq I^{\bar{p}} H_{j} (X,\partial X). \end{aligned}$$

This theorem is proved in Sect. 5. In particular, in the case of GM-perversities, we get:

Corollary 4.8

Let $p$ and $q$ be two complementary GM-$l$-perversities and let $\check{p}$ and $\check{q}$ be the GM-$(l-1)$-perversities defined in Example 4.6. If $X$ is orientable then we have for any $j$:

$$\begin{aligned} I^{(q,\check{q})} H_{l-j}(X)\simeq I^{(p,\check{p})} H_{j} (X,\partial X). \end{aligned}$$

In Sect. 5, we will also prove:

Theorem 4.9

The intersection homology groups of a compact PL stratified $\partial$-pseudomanifold are finitely generated.

One of the main features of intersection homology theory is that, when the perversity is a GM-perversity, the resulting groups are independent of the stratification. This was proved by Goresky and MacPherson in their fundamental papers [6, 7] (see also [1, 9]). This is still true for $\partial$-pseudomanifolds.

Theorem 4.10

Let $\bar{p}=(p,\tilde{p})$ be a pair of perversities. If $p$ and $\tilde{p}$ are $GM$-perversities then the intersection homology groups $I^{\bar{p}} H_j(X)$ are independent of the stratification.

This theorem is also proved in Sect. 5.

5 Proofs of the main theorems

Proof of Theorem 4.7

Denote by $\Sigma$ the stratification of $X$ and by $\tilde{\Sigma }$ the induced stratification of $\partial X$. Let $\hat{X}$ be the pseudomanifold with boundary obtained by attaching a collared neighborhood of $\partial X$ along $\partial X$. More precisely, let:

$$\begin{aligned} \hat{X}:=\left( X \times \{0\}\right) \cup \left( \partial X \times [0,1]\right) . \end{aligned}$$

(5.1)

Let $\widehat{\Sigma }$ be the partition of $\widehat{X}$ constituted by the reunion $\Sigma _1\cup \Sigma _2$, where $\Sigma _1:=\{ S \times 0: S\in \Sigma _s \}$, and $\Sigma _2 :=\{ S \times (0,1] :S\in \tilde{\Sigma }_s\}$. Complete this partition by adding the nonsingular strata of $\widehat{X}$, i.e. the connected components of set $\widehat{X}\setminus \cup _{S\in \Sigma _1\cup \Sigma _2} S$, which is nothing but the top strata of $X$ to which we have attached a collar along the points of $X_{\partial ,reg}$ lying in their closure. Since $\Sigma$ and $\tilde{\Sigma }$ are locally topologically trivial stratifications, so is $\widehat{\Sigma }$.

This partition makes $\widehat{X}$ into a stratified pseudomanifold with boundary in the sense of Definition 2.3. In what follows, we implicitly identify $X$ and $X \times \{0\}$, considering $X$ as a subset of $\widehat{X}$.

Let us define a general perversity $\hat{p}$ on $\widehat{X}$ by setting $\hat{p}(S\times \{0\}):=p (S)$ for any $S \in \Sigma _s$ and $\hat{p}(S \times (0,1]):=\tilde{p}(S)$ for all $S \in \tilde{\Sigma }_s$ (if $\bar{p}=(p,\tilde{p})$).

There is a natural mapping $\pi :\widehat{X}\rightarrow X$, assigning to every $(x,t) \in \widehat{X}$, the element $x \in X$. We claim that $\pi$ induces an isomorphism $\pi _{*}: I^{\hat{p}} H_j (\widehat{X}) \rightarrow I^{\bar{p}} H_j (X)$ for every $j$.

We start by proving that if a chain $c$ belongs to $I^{\hat{p}} C_j (\widehat{X})$ then $|\pi _{*}(c)|$ is a $(j,\bar{p})$-allowable subset of $X$. Indeed, as the mapping $\pi$ induces a homeomorphism above $X \setminus \partial X$, condition (4.1) is clearly fulfilled by $|\pi _*(c)|$. We therefore only have to show that $|\pi _*(c)| \cap \partial X$ is $(j,\tilde{p})$-allowable. As $|c|$ is $(j,\hat{p})$-allowable, we have for any singular stratum $S \in \tilde{\Sigma }_s$:

$$\begin{aligned} \quad \dim |c|\cap \left( S \times (0,1]\right) \le j-\text{ cod }_{\widehat{X}} \left( S\times (0,1]\right) +\hat{p}\left( S\times (0,1]\right) = j-\text{ cod }_{\partial X} S +\tilde{p}(S). \end{aligned}$$

Moreover, as $\hat{p}(S\times 0)=p (S) \in \{\tilde{p}(S),\tilde{p}(S)+1\}$ we have:

$$\begin{aligned} \dim |c| \cap (S\times 0) \le j-\text{ cod }_{\widehat{X}}(S\times 0)+\hat{p}(S\times 0) \le j-\text{ cod }_{\partial X}S+\tilde{p}(S). \end{aligned}$$

Together with the preceding inequality, this implies that for any stratum $S \in \tilde{\Sigma }_s$:

$$\begin{aligned} \dim \pi (|c|)\cap S\le \dim |c|\cap \left( S \times [0,1]\right) \le j-\text{ cod }_{\partial X} S+\tilde{p}(S), \end{aligned}$$

showing that $|\pi _*(c)| \cap \partial X$ is $(j,\tilde{p})$-allowable in $\partial X$.

Consequently, $\pi$ induces a map $\pi _*:I^{\hat{p}} H_j (\widehat{X}) \rightarrow I^{\bar{p}} H_j (X)$.

We now are going to establish that this map is an isomorphism of every $j$. By definition of pairs of perversities we have either $p(S)-\tilde{p}(S)=1$ for all strata $S$ of $\tilde{\Sigma }_s$ or $p(S)-\tilde{p}(S)=0$ for every such stratum. We address below these two cases separately.

First case: $p(S)-\tilde{p}(S)=0$, for all $S\in \tilde{\Sigma }_s$. We shall define a mapping $\theta :I^{\bar{p}} H_j (X) \rightarrow I^{\hat{p}} H_j (\widehat{X})$ and show that it is the inverse of $\pi _*$. In order to define this mapping, let us introduce some notations.

Define two linear mappings $\rho _1: C_j(X) \rightarrow C_j(\partial X)$ and $\rho _2: C_j(X) \rightarrow C_j( X)$ as follows. Given a simplex $\sigma$, we set $\rho _1(\sigma ):=\sigma$ if $\sigma$ is a simplex of $\partial X$ and $\rho _1(\sigma ):=0$ otherwise. We then set $\rho _2(\sigma ):=\sigma -\rho _1(\sigma )$.

Observe first that if $c$ is a PL chain then $|c| \cap \partial X$ is a union of image of simplices (since the triangulation is compatible with $\partial X$). In particular, $|\rho _2(\sigma )|\setminus \partial X$ is dense in $|\rho _2(\sigma )|$.

Let now $r:\partial X \times [0,1] \rightarrow \widehat{X}$ denote the natural inclusion. We can consider this map as a deformation of $\partial X$ in $\widehat{X}$. Such a mapping induces a chain homotopy, i.e. linear mappings $r_*: C_j (\partial X ) \rightarrow C_{j+1}(\widehat{X})$ satisfying:

$$\begin{aligned} r_*\partial +\partial r_*=r_{1*}-I_*, \end{aligned}$$

(5.2)

where $r_1:\partial X\rightarrow \widehat{X}$ is the mapping defined by $r_1(x):=(x,1)$ and $I:\partial X \rightarrow \widehat{X}$ is the natural inclusion (see [8] Chap. 2 for more details on chain homotopies). Now, we can define the desired mapping $\theta$ by (below we often write $\rho _1\sigma$ instead of $\rho _1(\sigma )$, omitting parentheses for simplicity):

$$\begin{aligned} \theta (\sigma ):=\rho _2\sigma +r_* \rho _1 \partial \rho _2 \sigma +r_{1*}\rho _1 \sigma , \end{aligned}$$

for any chain $\sigma \in C_j (X)$. We first check that $\theta$ carries the allowable chains of $X$ onto those of $\widehat{X}$.

Fix $\sigma \in I^{\bar{p}} C_j(X)$. As $|\sigma |$ is a $(j,\bar{p})$-allowable subset of $X$, by (4.1) we have for every stratum $S\in \Sigma _s$ since $|\rho _2\sigma |\setminus \partial X$ is dense in $|\rho _2\sigma |$:

$$\begin{aligned} \dim | \rho _2\sigma | \cap S\le \dim cl(|\sigma | \setminus \partial X)\cap S \le j-\text{ cod }_X S +p(S). \end{aligned}$$

This already shows that $|\rho _2\sigma |$ is a $(j,\hat{p})$-allowable subset of $\widehat{X}$.

Moreover, as the set $|r_*\rho _1\partial \rho _2\sigma |$ cuts $X$ along a smaller set, it fulfills the allowability condition with respect to the strata of $X$. We have to check that it satisfies the allowability condition with respect to the strata of $\partial X \times (0,1]$ as well. By definition of $r$, the preceding inequality entails for all $S \in \tilde{\Sigma }_s$:

$$\begin{aligned} \dim |r_*\rho _1\partial \rho _2\sigma |\cap \left( S\times (0,1]\right) \le j-\text{ cod }_X S+p(S)+1 =j-\text{ cod }_{\widehat{X}} \left( S\times (0,1]\right) +\tilde{p}(S), \end{aligned}$$

as required.

Finally, we have to check that $|r_{1*}\rho _1\sigma |$ is $(j,\hat{p})$-allowable as well. But, as $|\rho _1\sigma |$ is $(j,\tilde{p})$-allowable and $r_1$ is a homeomorphism, it directly follows from the definitions that $r_{1*}\rho _1 \sigma$ is $(j,\hat{p})$-allowable in $\widehat{X}$.

This implies that $|\theta (\sigma )|$ is $(j,\hat{p})$-allowable if $|\sigma |$ is ($j,\bar{p}$)-allowable. We now claim that $\theta$ is a chain map, i.e. that it satisfies $\partial \theta =\theta \partial$.

To see this, fix a chain $\sigma$ and compute:

$$\begin{aligned} \theta (\partial \sigma )=\rho _2\partial \sigma +r_*\rho _1\partial \rho _2 \partial \sigma +r_{1*} \rho _1 \partial \sigma . \end{aligned}$$

(5.3)

On the other hand, we can write:

$$\begin{aligned} \partial \theta (\sigma )=\partial \rho _2 \sigma +\partial r_* \rho _1 \partial \rho _2 \sigma +\partial r_{1*} \rho _1 \sigma . \end{aligned}$$

(5.4)

Observe that, since $\sigma =\rho _1\sigma +\rho _2\sigma$, we have $\partial \sigma =\partial \rho _1 \sigma +\partial \rho _2\sigma$, so that applying $\rho _1$:

$$\begin{aligned} \rho _1\partial \sigma =\partial \rho _1 \sigma + \rho _1\partial \rho _2\sigma . \end{aligned}$$

(5.5)

Applying $\partial$ to this identity we get:

$$\begin{aligned} \partial \rho _1\partial \sigma =\partial \rho _1\partial \rho _2\sigma . \end{aligned}$$

(5.6)

Write now:

$$\begin{aligned} \partial r_* \rho _1 \partial \rho _2\sigma \overset{(4.5)}{=}&- r_*\partial \rho _1\partial \rho _2\sigma -\rho _1\partial \rho _2\sigma +r_{1*}\rho _1 \partial \rho _2 \nonumber \sigma \\ \overset{(4.8)}{=}&-r_*\partial \rho _1\partial \rho _2\sigma -\rho _1\partial \rho _2\sigma +r_{1*} \rho _1\partial \sigma -r_{1*}\partial \rho _1 \sigma . \end{aligned}$$

(5.7)

By definition of $\rho _1$ and $\rho _2$ (of the element $\partial \rho _2\sigma$),

$$\begin{aligned} -\rho _1 \partial \rho _2 \sigma =\rho _2\partial \rho _2 \sigma -\partial \rho _2 \sigma . \end{aligned}$$

Putting it into (5.7) and then substituting the result in (5.4) we get (since $r_{1*}\partial =\partial r_{1*}$):

$$\begin{aligned} \partial \theta (\sigma )=\rho _2\partial \rho _2 \sigma - r_*\partial \rho _1\partial \rho _2 \sigma +r_{1*}\rho _1 \partial \sigma . \end{aligned}$$

(5.8)

As $\partial \rho _1\sigma$ has support in $\partial X$, we have $\rho _2\partial \rho _1 \sigma =0$. Recall that $\partial \sigma =\partial \rho _1\sigma +\partial \rho _2 \sigma$, so that applying $\rho _2$ we get:

$$\begin{aligned} \rho _2 \partial \rho _2 \sigma =\rho _2\partial \sigma . \end{aligned}$$

(5.9)

Furthermore, applying (5.5) to $\partial \sigma$ we see:

$$\begin{aligned} \rho _1\partial \rho _2\partial \sigma = -\partial \rho _1 \partial \sigma \overset{(4.9)}{=} -\partial \rho _1\partial \rho _2\sigma . \end{aligned}$$

(5.10)

We can see that (5.3), (5.8), (5.9), and (5.10) imply the desired equality. As a matter of fact, $\theta$ is a chain map and thus induces a mapping $\theta :I^{\bar{p}} H_j (X)\rightarrow I^{\hat{p}} H_j (\widehat{X})$. We first are going to prove that $\pi _* \circ \theta (\sigma )=\sigma$, for any cycle $\sigma \in I^{\bar{p}} H_j (X)$.

For this purpose, observe that if $\sigma$ is a cycle of $X$ then by (5.5) we have $\rho _1\partial \rho _2 \sigma =-\partial \rho _1 \sigma$ so that $\theta (\sigma )$ may be rewritten as:

$$\begin{aligned} \theta (\sigma )= \rho _2(\sigma )-r_*\partial \rho _1 \sigma +r_{1*}\rho _1 \sigma \overset{(4.5)}{=}\sigma +\partial r_*\rho _1 \sigma . \end{aligned}$$

(5.11)

Consequently, it is enough to show that $\pi _*(\partial r_*\rho _1 \sigma )$ is zero in $I^{\bar{p}}H_j(X)$ (since $\pi _*(\sigma )=\sigma$, as chains). As this cycle bounds the $(j+1)$-chain $\pi _*(r_*\rho _1 \sigma )$, it suffices to prove that this chain is $(j+1,\bar{p})$-allowable. But since:

$$\begin{aligned} |\pi _*(r_*\rho _1 \sigma )|\subset |\sigma |, \end{aligned}$$

this follows from the fact that $|\sigma |$ is $(j,\bar{p})$-allowable. This establishes that $\pi _* \,{\circ }\, \theta =Id$.

It remains to prove that $\theta \circ \pi _*$ is the identity map as well. Define a map $u:\widehat{X}\times [0,1]\rightarrow \widehat{X}$ by setting $u(x,t,\tau ):=(x, \tau t)$. We claim that if $c$ is a cycle of $I^{\hat{p}}C_j(\widehat{X})$ then $|u_*c|$ is $(j+1,\hat{p})$-allowable where $u_*$ is the chain homotopy induced by $u$ (again see [8] Chap. 2). Indeed, for any stratum $S \in \tilde{\Sigma }_s$:

$$\begin{aligned} \dim |u_*c| \cap (S\times (0,1])&\le 1+ \dim |c|\cap (S \times (0,1])\nonumber \\&\le 1+j-\text{ cod }_{\widehat{X}} S\times (0,1]+\tilde{p}(S). \end{aligned}$$

(5.12)

Furthermore,

$$\begin{aligned} \dim |u_*c|\cap (S\times 0)\!\le \! \dim |c|\cap (S \times [0,1])\!\le \! j\!-\!\text{ cod }_{\widehat{X}} S\times (0,1]\!+\!\tilde{p}(S), \end{aligned}$$

(5.13)

which is equal to $(j+1-\text{ cod }_{\widehat{X}} S +p(S))$. Together with (5.12), this implies that $|u_*c|$ is $(j+1,\hat{p})$-allowable (since $|u_*c|\cap (X\setminus \partial X) \subset |c|\cap (X \setminus \partial X)$, the other conditions are obviously fulfilled).

Since $u(x,0)=\pi (x)$ we have for any cycle $c$ of $I^{\hat{p}} C_j(\widehat{X})$:

$$\begin{aligned} c -\pi _*(c)=\partial u_* (c). \end{aligned}$$

(5.14)

But, by (5.11), we have:

$$\begin{aligned} \theta (\pi _*(c))-\pi _*(c)=\partial r_*\rho _1\pi _*(c). \end{aligned}$$

Subtracting these two equalities we get:

$$\begin{aligned} c-\theta (\pi _*(c))=\partial u_* c-\partial r_* \rho _1 \left( \pi _*(c)\right) . \end{aligned}$$

We have seen that $|u_* c|$ is $(j+1,\hat{p})$-allowable in $\widehat{X}$. Moreover, as $|\rho _1 (\pi _*(c))|$ is $(j,\tilde{p})$-allowable, $|r_*\rho _1 (\pi _*(c))|$ is $(j+1,\hat{p})$-allowable. We thus can conclude that $\theta (\pi _*(c))=c$ in $I^{\hat{p}} H_j(\widehat{X})$. This yields that the mapping $\pi _*: I^{\hat{p}} H_j(\widehat{X})\rightarrow I^{\bar{p}} H_j (X)$ is an isomorphism.

Since $\pi (\partial \widehat{X})=\partial X$, the mapping $\pi$ also induces a morphism between the relative homology groups $\overline{\pi }: I^{\hat{p}} H_j(\widehat{X},\partial \widehat{X})\rightarrow I^{\bar{p}} H_j (X,\partial X)$. We are going to see that this mapping is also an isomorphism.

Let $p^{\prime }$ be the general perversity on $\partial \widehat{X}$ defined by $p^{\prime }(S\cap \partial \widehat{X}):=\hat{p}(S)$, for $S \in \widehat{\Sigma }_s$.

We have the long exact sequence:

$$\begin{aligned} \cdots \!\rightarrow \! I^{\hat{p}}H_{j+1}\left( \widehat{X},\partial \widehat{X}\right) \!\rightarrow \! I^{p^{\prime }}H_j(\partial \widehat{X}) \rightarrow I^{\hat{p}}H_j(\widehat{X})\rightarrow I^{\hat{p}}H_j\left( \widehat{X},\partial \widehat{X}\right) \rightarrow \cdots \end{aligned}$$

(5.15)

For every stratum $S \in \tilde{\Sigma }_s$ we have:

$$\begin{aligned} p^{\prime }(S\times \{1\})=\hat{p}(S\times (0,1])= \tilde{p}(S)=\tilde{p}\left( \pi \left( S\times \{1\}\right) \right) . \end{aligned}$$

As a matter of fact, since $\pi$ induces a stratified homeomorphism from $\partial \widehat{X}$ to $\partial X$ preserving the value of the perversity, it gives rise to an isomorphism $\tilde{\pi }:I^{p^{\prime }}H_j(\partial \widehat{X})\rightarrow I^{\tilde{p}}H_j(\partial X)$. Now, the exact sequences (4.2) and (5.15), together with the mappings $\pi _{*},\,\overline{\pi }$ and $\tilde{\pi }$, constitute a diagram which is commutative (all the vertical arrows are induced by $\pi$). By the five Lemma, $\overline{\pi }$ must be an isomorphism.

Second case: $p(S)-\tilde{p}(S)=1$, for all $S \in \tilde{\Sigma }_s$. We first prove that in this case $I^{\bar{p}}C_j(X)\subset I^{\hat{p}} C_j(\hat{X})$. Take $\sigma \in I^{\bar{p}} C_j(X)$ and note that since $|\sigma |$ is $(j,\bar{p})$-allowable in $X$ we have for every stratum $S\in \tilde{\Sigma }_s$:

$$\begin{aligned} \dim |\sigma |\cap S \le j-\text{ cod }_{\partial X}S+\tilde{p}(S)=j-\text{ cod }_{X}S+p(S)=j-\text{ cod }_{\widehat{X}}S+\hat{p}(S), \end{aligned}$$

which implies that the allowability condition with respect to every stratum of $\partial X$ holds. The allowability condition with respect to the other strata obviously also holds because $\hat{p}(S)=p(S)$, for every stratum of $X$. This yields that $I^{\bar{p}}C_j(X)\subset I^{\hat{p}} C_j(\hat{X})$.

First, notice that $|u_*c|$ is $(j+1,\hat{p})$-allowable whenever $c$ is a cycle of $I^{\hat{p}} C_j(\widehat{X})$. Indeed, as in the first case, this follows from (5.12) and (5.13).

Let $\iota :I^{\bar{p}}H_j(X)\rightarrow I^{\hat{p}} H_j (\widehat{X})$ be induced by inclusion and note that $\pi _*\circ \iota$ is the identity map. We are going to show that $\iota \circ \pi _*$ is the identity map as well. Indeed, as chains we have:

$$\begin{aligned} \iota (\pi _*(c))-c=\pi _*(c)-c\overset{(4.17)}{=}-\partial u_* c, \end{aligned}$$

which, since $|u_*c|$ is $(j+1,\hat{p})$-allowable, establishes that $\iota \circ \pi _*$ is the identity map. Thus, $\pi _*$ is an isomorphism.

Applying the five Lemma in the same way as in the case where $p(S)=\tilde{p}(S)$ for all $S\in \tilde{\Sigma }_s$, we see that the induced map $\overline{\pi }:I^{\hat{p}}H_j(\widehat{X},\partial \widehat{X})\rightarrow I^{\bar{p}} H_j (X,\partial X)$ is also an isomorphism. This completes the second case.

Let now $\hat{q}$ be the perversity derived from $\bar{q}=(q,\tilde{q})$ in the same way as $\hat{p}$. Observe that, since $\bar{q}$ and $\bar{p}$ are complementary pairs of perversities, we have for any $S \in \Sigma _s$:

$$\begin{aligned} p(S)+q(S)=\text{ cod }_X S-2=\text{ cod }_{\widehat{X}} (S\times 0)-2, \end{aligned}$$

and for any $S\in \tilde{\Sigma }_s$:

$$\begin{aligned} \tilde{p}(S)+\tilde{q}(S)=\text{ cod }_{\partial X} S-2=\text{ cod }_{\widehat{X}} S\times (0,1]-2. \end{aligned}$$

Therefore, $\hat{q}$ and $\hat{p}$ are complementary general perversities of ($\widehat{X},\widehat{\Sigma }$).

We thus conclude that the composite of the following sequence of isomorphisms

$$\begin{aligned} I^{\bar{p}} H_j(X)\overset{\pi ^{-1}_*}{\longrightarrow } I^{\hat{p}} H_j(\widehat{X}) \overset{\psi _{\widehat{X}}}{\longrightarrow } I^{\hat{q}} H_{l-j}(\widehat{X},\partial \widehat{X}) \overset{\overline{\pi }}{\longrightarrow } I^{\overline{q}} H_{l-j} (X,\partial X), \end{aligned}$$

where $\psi _{\widehat{X}}$ stands for the Lefschetz duality isomorphism of the pseudomanifold with boundary $\widehat{X}$, constitutes the desired Lefschetz duality isomorphism. $\square$

Proof of Theorems 4.9 and 4.10

We start by proving Theorem 4.9. Let $(X,\partial X,\Sigma )$ be a stratified $\partial$-pseudomanifold and let $\bar{p}:=(p,\tilde{p})$ be a pair of general perversities. The proof of Theorem 4.7 just above established that $I^{\bar{p}} H_j (X)$ and $I^{\hat{p}}H_j(\widehat{X})$ are isomorphic, where $\widehat{X}$ is the pseudomanifold with boundary obtained by attaching a collar to $X$ and $\hat{p}:\widehat{\Sigma }_s \rightarrow \mathbb{N }$ is a general perversity ($\widehat{\Sigma }$ being a stratification of $\widehat{X}$). Namely, we have set $\hat{p}(S \times (0,1]):=\tilde{p}(S)$, whenever $S \in \tilde{\Sigma }_s$, and $\hat{p}(S\times 0):=p(S)$, for every $S \in \Sigma _s$.

As $\widehat{X}$ is a compact PL pseudomanifold with boundary, its homology groups are finitely generated [6] (the latter article proves it for pseudomanifolds without boundary for GM-perversities but the proof applies to our setting as well, the arguments of [3] also show it). This yields Theorem 4.9.

We turn to show Theorem 4.10. Assume now that $\bar{p}$ is a pair of GM-perversities. Since two given stratifications have a common refinement, in order to establish Theorem 4.10, it is enough to show that intersection homology remains unchanged under refinements.

Take two stratifications $\Sigma ^{\prime } \prec \Sigma$. The refinement $\Sigma ^{\prime }$ induces a refinement $\widehat{\Sigma }^{\prime }$ of the stratification $\widehat{\Sigma }$ of $\widehat{X}$ constructed in the same way as $\widehat{\Sigma }$. The pair of GM-perversities $\bar{p}$ induces a general perversity $\hat{p}^{\prime }:\widehat{\Sigma }^{\prime }_s \rightarrow \mathbb{Z }$ defined in the same way as $\hat{p}$. We wish to deduce the desired statement from Proposition 3.4. This requires to show that $\hat{p}^{\prime }\prec \hat{p}$.

On the strata of $\Sigma _s$, as $\hat{p}$ and $\hat{p}^{\prime }$ are induced by the GM-perversity $p$, the required property must hold for these strata (see Remark 3.3). On the strata of $\widehat{X}\setminus X,\,p$ and $\hat{p}$ are induced by the GM-$(l-1)$-perversity $\tilde{p}$ (considered as an $l$-perversity, there is no stratum of codimension $l$ in $\widehat{X}\setminus X$). We thus clearly have $\hat{p}^{\prime }\prec \hat{p}$. By Proposition 3.4, the groups are independent of the stratification.

6 Some concluding remarks and an example

• 1. For simplicity, we restricted ourselves to compact pseudomanifolds but Lefschetz duality for $\partial$-pseudomanifolds continues to hold in the noncompact case. Of course, one has then to adapt the statement and to involve the intersection cohomology with compact support. If $X$ is subanalytic, we can also use the Borel-Moore homology, defined in the usual way by considering the locally finite allowable chains. Stratification independence also holds for noncompact PL $\partial$-pseudomanifolds.

• 2. It seems that the results of this paper could be generalized to stratified sets $(X,\Sigma )$ which are not stratified pseudomanifolds but which have a one co-dimensional stratum whose closure is a stratified pseudomanifold. However, the statement of duality needs to be adapted. Nevertheless, the groups seem to be an invariant of $(X,|\Sigma |)$, where $|\Sigma |$ is the union of all the elements of $\Sigma$ that have positive codimension. It would be interesting to compare this with the results obtained by Friedman in [2], where the author studied pseudomanifolds with possibly one co-dimensional strata and established theorems of this type.

• 3. Theorem 4.7 generalizes Lefschetz duality for general perversities on pseudomanifolds with boundary [5]. This can be seen as follows. Let $(X,\partial X, \Sigma )$ be a stratified pseudomanifold with boundary and let $p:\Sigma _s\rightarrow \mathbb{N }$ be a general perversity.

Let $\Sigma _1$ be the family constituted by the elements of $\Sigma$ which are manifolds with nonempty boundary (those which intersect $\partial X$). Let

$$\begin{aligned} \Sigma ^{\prime }:=\left\{ \partial S:S \in \Sigma _1\right\} \cup \left\{ S\setminus \partial S:S \in \Sigma \right\} . \end{aligned}$$

This constitutes a stratification making of $(X,\partial X)$ a stratified $\partial$-pseudomanifold.

Define now a general perversity $p^{\prime }:\Sigma ^{\prime }_s\rightarrow \mathbb{N }$ as follows. Set $p^{\prime }(S \setminus \partial S):=p(S)$, for any $S\in \Sigma$, and $p^{\prime }(\partial S):=p(S)+1$ for any $S \in \Sigma _1$.

Define another one $p^{\prime \prime }:\Sigma ^{\prime }_s\rightarrow \mathbb{N }$ by $p^{\prime \prime }(S \setminus \partial S):=p(S)$, for any $S\in \Sigma$, and $p^{\prime \prime }( \partial S):=p(S)$ for any $S \in \Sigma _1$.

Define then a perversity $\tilde{p}:\tilde{\Sigma }_s \rightarrow \mathbb{N }$ (a “boundary perversity”), $\tilde{\Sigma }$ being the stratification of $\partial X$ induced by $\Sigma ^{\prime }$, by $\tilde{p}(\partial S):=p(S)$ for every $S \in \Sigma _1$.

Observe that both $\bar{p}:=(p^{\prime },\tilde{p})$ and $\bar{\bar{p}}:=(p^{\prime \prime },\tilde{p})$ are pairs of perversities. Furthermore, if $p$ and $q$ are complementary perversities then $(p^{\prime },\tilde{p})$ and $(q^{\prime \prime },\tilde{q})$ are complementary pairs of perversities (here $q^{\prime \prime }$ and $\tilde{q}$ are derived in the same way as $p^{\prime \prime }$ and $\tilde{p}$). Thus, Theorem 4.7 applies. In order to deduce the Lefschetz duality result of [5] we have to show that for any general perversity $p$:

$$\begin{aligned} I^{\bar{p}} H_j(X)\simeq I^{\bar{\bar{p}}} H_j(X)\simeq I^p H_j(X), \end{aligned}$$

and that the same holds true for the relative homology.

It is actually straightforward from the definitions of the perversities that $I^{\bar{p}} C_j(X)=I^p C_j(X),\,I^p C_j(\partial X)=I^{\tilde{p}}C_j(\partial X),$ and $I^{\bar{p}} C_j(X,\partial X)=I^p C_j(X,\partial X)$ so that the two theories provide the same homology groups. The result is thus clear for $\bar{p}$.

One may also see that $I^{\bar{\bar{p}}} H_j(X)\simeq I^{p} H_j(X)$. This can be deduced from Proposition 3.4 and the proof of Theorem 4.7, since $X$ is homeomorphic to the pseudomanifold $\widehat{X}$ constructed in the latter proof. This can also be seen directly as follows.

The allowability conditions imply that $I^{\bar{\bar{p}}} C_j(X)\subset I^{p} C_j(X)$. Let $\iota : I^{\bar{\bar{p}}} H_j(X)\rightarrow I^{p} H_j(X)$ be induced by inclusion. Every chain of $X$ may be retracted by deformation into $X\setminus \partial X$ by means of the collared neighborhood. The retraction of every chain of $I^{\bar{\bar{p}}} C_j(X)$ (resp. $I^{p} C_j(X)$) provides a chain of $I^{\bar{\bar{p}}} C_{j}(X\setminus \partial X)$ (resp. $I^{p} C_{j}(X\setminus \partial X)$). This shows that the inclusion $X\setminus \partial X\hookrightarrow X$ induces isomorphisms for both perversities $\bar{\bar{p}}$ and $p$, yielding that $\iota$ is an isomorphism (since $I^{\bar{\bar{p}}} C_j(X\setminus \partial X)= I^{p} C_j(X\setminus \partial X)$). That $I^{\bar{\bar{p}}} H_j(X,\partial X)\simeq I^{p} H_j(X, \partial X)$ follows from the five Lemma.

• 4. Let $X$ be a compact subanalytic pseudomanifold. It may be endowed with a PL structure [12]. In [13], it is proved that the $L^\infty$ cohomology of $X_{ reg}$ is isomorphic to intersection cohomology in the maximal perversity. This theorem is still true if $X$ is a $\partial$-pseudomanifold if one takes the maximal perversity for both $X$ and $\partial X$ (the Poincaré Lemma proved in [13] does not assume that $X$ is a pseudomanifold). In [14], we prove that the Dirichlet $L^1$ cohomology is always dual to $L^\infty$ cohomology. Therefore, the Lefschetz duality proved in the present paper implies that, if $X$ is a $\partial$-pseudomanifold, the Dirichlet $L^1$ cohomology of $X_{ reg}$ is isomorphic to the intersection cohomology of $(X,\partial X)$ in the $(0,\check{0})$ perversity (compare with [14] Corollary 1.6).

Example 6.1

Consider a double pinched torus embedded in $S^3=\mathbb{R }^3 \cup \infty$ (see picture below) Fig. 1.

Fig. 1

A double pinched torus embedded in $S^{3}=\mathbb R ^3\cup \infty$

Consider the $\partial$-pseudomanifold $X$ constituted by this pinched torus together with the connected component of its complement which is not simply connected (the unbounded one on the picture). The boundary of this $\partial$-pseudomanifold is this double pinched torus.

We first examine the intersection homology groups for the pair of top GM-perversities $\overline{t}=(t,\check{t})$ near a singular point $x_0$ of the singular torus. Let $X^\varepsilon :=B^3(x_0,\varepsilon )\cap X$. Since the allowability conditions make it possible to retract any cycle $\sigma$ of dimension at least $1$ onto $x_0$ we have: $I^{\overline{t}} H_2(X^\varepsilon ,\partial X^\varepsilon )\simeq I^{\overline{t}}H_2(X^\varepsilon )\simeq I^{\bar{t}}H_1(X^\varepsilon )\simeq 0$.

Using the exact sequence of the pair $(X^\varepsilon ,\partial X^\varepsilon )$, it is easily derived

$$\begin{aligned} I^{\overline{t}} H_1\left( X^\varepsilon ,\partial X^\varepsilon \right) \simeq \mathbb{R }. \end{aligned}$$

A representative of the generator of $I^{\overline{t}} H_1(X^\varepsilon ,\partial X^\varepsilon )$ is provided by any PL arc joining the two connected components of the regular locus of the torus.

The groups $I^{\overline{t}} H_j (X,\partial X)$ may now be determined as follows. Consider the set $W:=X{\setminus } \cup _{i=1,2} B(x_i,\frac{\varepsilon }{2})$, where $x_1$ and $x_2$ are the two singularities. Since $W$ is a manifold with boundary, its intersection homology coincides with its homology. By the Mayer-Vietoris exact sequence, it is then easily seen that $I^{\overline{t}} H_1(X,\partial X) \simeq \mathbb{R }$.

By duality, we must have if $\overline{0}=(0,\check{0})$:

$$\begin{aligned} I^{\overline{0}} H_2(X)\simeq \mathbb{R }. \end{aligned}$$

A generator of $I^{\overline{0}} H_2(X)$ is given by either of the two irreducible cycles of the pinched torus (the intersection with the generator of $I^{\overline{t}}H_1(X,\partial X)$ has nontrivial class). We see in particular that this class does not have a 0-allowable representative in $X\setminus \partial X$. The 0-allowability condition of chains in $\partial X$ (since $\check{0}=0$) is thus essential to ensure Lefschetz duality.