Laboratory Investigations on the Mode of Failure in Frictional and Low-Cohesive Materials Under the Load of a Ground Anchor

Abstract

Ground anchors are widely used in many types of construction works, such as stabilization of rock slopes, wind turbines, concrete dams and bridge towers. Some of the modes of failure for these anchors still have an insufficient scientific basis, and that applies especially to what happens in the ground when overloaded. This paper presents investigations on the failure development in frictional and low-cohesive materials which are subjected to loading by an embedded anchor with a free length towards the surface. The failure development is demonstrated through a series of small-scale physical model tests performed in the laboratory. The physical model setup consists of a transparent PVC test chamber, a rigid «anchor block», and a hydraulic jack. The model is instrumented with a camera, an extensometer and a load cell to continuously record the failure development and resistance from the material as the anchor block is pushed through the sample material. The main question investigated is how the failure appears, as a failure along the whole pull-out body at once or as an advancing fracture along the plane, where in the first case the shear capacity of the material will be the main input in calculations, and for the second case, one also needs to take failure propagation into account.

1 Introduction

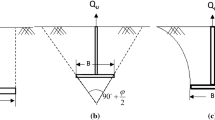
Rock or ground anchors are structural members that transmit an applied tensile load to the soil or rock mass at a certain ground depth. High-capacity anchors are commonly used for stabilizing slopes, retaining walls and large-scale infrastructure, such as building foundations, wind turbines, concrete dams and bridge towers. It is of great importance to ensure that the anchors are correctly dimensioned, as a failure of the anchor may lead to structural damage, and potentially great economic or social consequences. The principles behind anchoring dimensioning are primarily based the following four failure mechanisms (Littlejohn and Bruce 1977) (see Fig. 1):

• (A) Rupture of the steel tendon,

• (B) Failure of the tendon-grout interface/bond,

• (C) Failure of the grout-rock bond, and

• (D) Failure and uplift of a conical body of rock/soil mass.

Fig. 1

Failure mode: A rupture of the steel tendon; B grout-tendon bond failure; C rock-grout bond failure; and D conical failure to surface in the rock mass

Failure mechanisms (A) and (B) have been thoroughly studied and well known (Pease and Kulhawy 1984). There are, on the other hand, great uncertainties regarding mechanisms (C) and (D), as there currently exists limited knowledge on how failure initiates and progresses within the rock/soil (Ilamparuthi and Muthukrishnaiah 1999; García-Wolfrum et al. 2007) and in the rock-grout interface following over-stressing of the anchor. This paper will focus on failure mechanism (D) and investigate the mode of failure in the conical surface for frictional and low-cohesive materials under the load of a ground anchor.

Assuming the interface between the grout and rock remains intact, several methods exist for calculating the rock mass' resistance against uplift in an isotropic rock. All the methods assume that a defined body of rock mass, with a simple geometric shape of an inverted cone, is separated and pulled up from the ground by the axial force applied to the anchor. The main approaches for analysing the uplift resistance of the conical body are through: (1) the weight of the conical body of rock mass or (2) the shear strength of the conical body (Ongstad and Bergh-Christensen 2010).

The first approach, assuming that uplift is resisted solely by the weight of conical body of rock/soil mass, is the most conservative method of estimating the resistance to rock mass uplift. Thus, the conical body is expected to be completely loosened from the surrounding material, and no bridges or interlocking elements exist, such that the surfaces have no shear strength, and thereby generate no joint surface friction. These assumptions ignore the fact that the material likely has shear and/or tensile strength which must be exceeded for uplift to occur.

The second approach also presumes failure of a conical body of the rock mass, but assumes that the shear or tensile strength or cohesion of the rock mass alone provides the resistance against uplift of the conical body (Coates 1970; Hobst and Zajíc 1983; American society of civil engineers 1966; Brown 2015; Kim and Cho 2012).

The strength and cohesion are constants that depend on the quality of the rock mass. For cases where the in-situ stresses are zero or very low, and no other stresses are imposed from structures on the rock mass, the shear strength may be conservatively assumed as equal to the rock mass cohesion (U.S. Army Corps of Engineers 1994). Some choose to apply both the weight of the cone and the estimated resistance from cohesion, shear or tensile strength to the total uplift resistance (Brown 2015).

The angle of the cone may vary according to the assumed rock mass properties. The most common angles used are 60° for weak, tightly jointed or weathered rock mass, and 90° for strong, low jointed rocks. One may also use 80° for rock mass of moderate quality, or 120° for high quality rock mass (Pedersen and Knutson 2004; Wyllie 2009; Statens vegvesen 2018). The location of the apex will typically be at the center or end of the socket length and relies to some extent on the rock mass quality. Usually, the apex is assumed to be at the center of the socket when dealing with low quality rock mass (either weak or tightly jointed) or for cases in which the properties are unknown due to lack of pull-out test data. The apex is placed at the end when the rock mass is known to be of good quality with few joints confirmed by pull-out-tests, or when the loads from the anchor are transferred to rock mass by use of an end plate or wedges (Littlejohn and Bruce 1977).

Brown (2015) also states that the 90° uplift cone assumption may not always be as valid for cases of deep anchors, as the controlling surface mechanisms differ from those of shallow, fully grouted anchors, which display this phenomenon more commonly. “The deeper the anchor, or the greater the ratio of the anchor depth, D, to the embedment length, L, the less likely the conical rock mass uplift mechanism is to control the behaviour of the post-tensioned anchor” (Brown 2015).

Weak rocks, meaning both hard soils and soft rocks, are often encountered in the shallow stratums around the world, thus forming the foundation ground for many construction projects (Nickmann et al. 2006). Determining whether a material is a hard soil or soft rock may be difficult, though also crucial, as it determines whether applying soil mechanics or rock mechanics is the most appropriate approach. One way to distinguish rocks from soils—that is, from frictional soils—is by the Mohr–Coulomb strength parameter cohesion, c. Cohesion represents the pure shear strength of the material, and is independent of the material's angle of internal friction, ' (Li 2017). A material is often considered a soil or loose material if its shear strength is a result of purely frictional resistance, that is, c = 0. Some soils, such as clays, do possess true cohesion, though it is due to inter-particle bonding rather than crystallization as it is in rocks.

The International Society for Rock Mechanics (1978), classifies a material with uniaxial compressive strength, UCS,  ≤ 0.25 MPa as a soil, regardless of its texture, structure, jointing or cohesion. Cohesive soils, such as clays, are not within the scope of this thesis, however when anchored in, they are assumed to fail in the cone-shaped failure wedge described earlier, with an apex angle twice the angle of internal friction, ' (Hobst and Zajíc, 1983).

An anchor in frictional, non-cohesive soil is considered loaded in its neutral state by the pressure of the overlying soil. If a tension is applied to the anchor less than and equal to the downward acting force arising from this pressure, the anchor will not move. However, using this limit as the governing design criterion leads to borehole depths and anchor cross-sections that are over safe and uneconomic. Therefore, this condition is not applied in practice. By allowing some deformation of the ground above the anchor and some degree of pull-out, greater anchor loads may be considered than if no movement is allowed. However, the exact stress state in the soil as a result of the anchor tension is difficult to express theoretically. This is mostly because the soils cannot be considered elastic materials while they are undergoing plastic deformation, as tensile stresses cannot occur within the soil. Shear failure is expected to occur as a conical shape in the soil, when the ultimate shear strength is reached at its surface, the cone angle being equal to twice the angle of internal friction, φ (Hobst and Zajíc 1983).

The anchor capacity is dependent on the soil's degree of compaction. Increasing compaction increases the frictional force of the potential plane of shear failure and coefficients of transverse expansion. Stresses from the anchor are introduced to a wedge of mass surrounding the socket, creating radial stresses. These radial stresses are larger in more compacted soils, and contribute to an increased shear strength of the soil and resistance to pull-out. Such soils often show dilatancy at the point of shear failure, which increases pressure in the soil, thus further impeding anchor pull-out. In less compacted soils, shear failure may cause increased compaction, which in turn reduces the soil volume. This makes it difficult to ensure sufficiently high resistance from pull-out in uncompacted soils. Anchor pull-out does not cause shearing above the anchor, in fact, in most cases the soil flows around the anchor (Hobst and Zajíc 1983).

Even with previous extensive research on the behaviour of anchors, there is still a lack of understanding of the anchor's interaction with the surrounding soil during uplifting. Most studies have focused on measuring the final shape of the pull-out body (Liu et al. 2012), thus disregarding how the failure develops in the soil.

Two main questions are (1) whether the failure appears on the whole surface of the cone instantly or (2) if the fracture develops from the bottom of the anchor and develops in a conical shape. In the case of (1) a calculation using the shear capacity of the material is appropriate, or in the case of (2) one should use an approach taking the fracture initiation and propagation into account.

The objective of the study is therefore to investigate the mode of failure in the ground of frictional soils and materials of low cohesion due to an overload of an embedded anchor with a free length towards the surface. This also includes looking into the failure and load development found, and its possible implications on anchor capacity calculations.

2 Preparation of Physical Model Testing

2.1 Rig Design

A mini test-rig (see Fig. 2) was designed and built at the Department of Geoscience and Petroleum (DGP) at the Norwegian University of Science and Technology, where the testing was performed. It consists of a rigid steel loading frame with removable, 10 mm thick, transparent PVC glass sheets installed on both sides of the frame. The PVC sheets and steel frame form an open test chamber with internal dimensions 600 mm (width) × 400 mm (height) × 100 mm (depth), which will contain the material samples. A 40 mm thick, 100 mm wide, 410 mm high engineering thermoplastic (Polyoxymethylene POM) block is fitted into a guide slot in the bottom center of the test chamber. The POM block is designed to transfer the load from the jack to simulate the anchor force. To create a socket that mobilizes the material under loading, a 200 mm long section on each of the anchor’s surfaces facing the testing materials in the chamber are furrowed with horizontal, semi-circular grooves (radius 3.5 mm, spacing 5.5 mm). The top 200 mm section of the block is left smooth to represent the free anchor length above the socket, as the smooth surface causes minimal mobilization.

Fig. 2

Test-rig setup: 1) Manual hydraulic jack; 2) load cell and extensometer; 3) steel frame; 4) soil chamber/PVC test chamber; 5) anchor block; 6) camera; 7) computer and monitor

In reality, the load is applied to the anchor on the top of the bond length. The bond length is fully mobilized and more or less rigidly moves when conical failure is created in the material around the anchor. It is believed that the conical failure would not be affected whether the load is applied on the top or bottom of the bond length. The load is applied on the bottom of the anchor on the mini test-rig. The anchor is placed in the slot, atop a manual hydraulic jack which rests on the rig's steel footing. In this position, the socket section protrudes 160 mm into the test chamber. Pumping the jack pushes the anchor vertically into the test chamber. The jack is equipped with a vertical extensometer and load cell. A digital camera on a tripod is positioned to fully capture one of the transparent fronts, linked to a computer which also logs data from the load cell and extensometer during tests. The video recording is automatically synchronized to the displacement and load recordings for easy post-analysis.

2.2 Sample Materials

In this study, six tests were performed with different configurations as listed in Table 1. The materials in the A and B tests were frictional with different grain sizes, while C were low-cohesive materials. For the A and B tests one used dry material and one used moist material. The C tests used only one grain size which was added small amounts of cement at two different w/c-ratios. To avoid organic substances and have a uniform base material it was used an eclogite which had been crushed and sieved. The chosen amount of cement and curing time was balanced between the how little cement that could be used and the wanted strength on the material. For more details regarding the materials see Tables 2 and 3.

Table 1 Test configurations

Table 2 Properties of the materials used in the A and B tests

Table 3 Properties of the materials used in the C tests

2.3 Sample Preparation

For preparation of the samples in the rig, two different methods were used for the frictional materials and one for the low-cohesive.

For tests A and B the material was added in layers into the test rig. Each layer consisted of approximately 3 L of material and was compacted by striking it 60 times by hand using a fitted compactor. After each compacting a contrasting white mineral was lined against the PVC glass surface for visual reference during the test. To limit outward bulging of the PVC glass, a clamp was applied before filling and compaction process started. The height of the sample material was approximately 300 mm. An example can be seen in Fig. 3.

Fig. 3

Example of frictional test ready to be run

For the C-tests the sample preparation procedure was slightly changed. To prevent the cement from adhering to the PVC sheets, they were greased with form oil. The wet material mixture was added in the test chamber and moderately compacted by hand to reduce presence of large air pockets and was left to cure for 3 days, theoretically reaching about 80% of maximum strength. On day 2, the screws holding the PVC sheets were loosened slightly and the panels carefully detached from the material to allow excess moisture to evaporate from the panels to ensure a clear view and to avid material/panel grip. Before testing, on day 3, the PVC sheets were reassembled.

Starting the C.1 test it was discovered that the friction between the rig sides and the material was too low as the sample started to slide. For C.1 this was solved by adding blocks on top of the sample on each side (see Fig. 4) and for sample C.2 it was solved by increasing the friction in the sample/rig-interface.

Fig. 4

Setup of the low-cohesive material test, C.1

2.4 Test Procedure

The test procedure was identical for all tests. Testing began by pumping the hydraulic jack, thus loading the anchor. Vertical displacement and load were registered while the developing failure in the test material was recorded by the video camera. The anchor had a displacement rate of 40 mm/min and was loaded until it slipped through the material or until the jack reached its maximum extension (50 mm).

2.5 Apparatus Calibration

To estimate the internal friction of the anchor block due to its tight fit between the PVC plates a calibration without any material in the chamber was performed. The empty-chamber-test was performed before testing started and repeated after the final material test to control whether this value has changed during use. The internal friction prior to the tests ranges within approximately 0.35–4.0 kN after 1 mm displacement, and 0.26–0.33 kN after all the tests. The reduction is likely caused by paint on the steel wearing off and slight bulging of the PVC plate.

2.6 Pull-Out Resistance Estimation

As mentioned in the introduction the pull-out resistance has two components: weight of the pull-out body (F_W) and the resistance to failure of the material (F_M) in which the anchor is embedded. For the case of these tests the different components can be separated from each other by taking into account the force from the test rig’s internal friction (F_sys). The volume of the conical pull-out body is first calculated:

$$V=\mathit{tan}{\theta }_{c}\times {\left(h-x\right)}^{2}\times w$$

(1)

where h is the material height before the test (see Fig. 5). The height from the test chamber bottom to where the failure plain hits the anchor block (apex point) is x and w is the width of the test chamber (100 mm) (see). The weight of the pull-out body is then found by:

$${F}_{W}={\rho }_{\text{c}}\times V\times g$$

(2)

where ɡ is the acceleration of gravity, 9.8 m/s².

Fig. 5

Dimensions of the calculation of pull-out body volume

One can then find an estimated corrected peak resistant load (P_c) by subtracting the system's average internal friction from the peak resistant load (P), P_c = P − F_sys. It is then also possible to calculate the ratio between them by dividing F_M on P_c, P_c/F_M. See Sect. 3.4 for results.

3 Results of Physical Model Testing

3.1 Frictional Material Behaviour

The load–displacement curves from the frictional material tests are shown in Figs. 6 and 7. Based on the curves, it is hard to identify any significant characteristic differences due to the variation in particle size and gradation. However, it seems that there is a difference between the dry and moist samples, where the dry samples display slower failure development with respect to the anchor displacement than the moist ones. Despite the difference in deformation behaviour, all the tests produced load–displacement curves with a typical development, which may be described by four characteristic phases: (1) elastic/linear development (2) pre-peak yielding, (3) post-peak softening, (4) lifting/slipping phase, which are shown in Fig. 8.

Fig. 6

Load–displacement relationship of the dry frictional material testing. Data from B.1 – Test 2 is missing due to problems with the recording equipment

Fig. 7

Load–displacement relationship of the frictional material with added water

Fig. 8

Characteristic load–displacement based on the frictional material tests

Phase 1, the elastic/linear development, is characterized by a steep load increase during the first 1.0–1.5 mm of anchor displacement. Then, in Phase 2 at the point of first visible deformation, the curve’s slope gradually decreases with further displacement until the anchor’s peak load value is reached, at an average about 5 mm displacement. The failure starts to form during this phase, and it starts as a small separation of the material near the bottom of the anchor block and propagates in the shape of a V towards the sample surface (see Fig. 9). The failure body is typically narrower than the total mobilized part of material. It continues to propagate as the anchor reaches and passes the peak load value, thus entering the post-peak softening phase. However, it seems that there is a small difference between the dry and moist eclogite where the transition from Phase 1 to Phase 2 is more gradual and starts earlier for the eclogite with added water. One can also see that the average peak load is higher for the dry than for the moist samples.

Fig. 9

Start of the formation of a V-shaped failure in the A.2—1, marked as a circle in Fig. 6

The post-peak phase is characterized by the further development of the failure propagation, as the anchor load gradually decreases with displacement. In most cases, the failure appears to have fully developed to the surface (see Fig. 10) after 2–4 mm displacement beyond the peak. Note that the exact time when the failure has reached the surface is difficult to determine in some of the tests, as it was observed that the fracture trace could be covered by loose material falling from the failure of the pull-out body as the fracture apex progressing upwards. After the failure planes appear to have reached the surface, the anchor load decreases with displacement at a rate between linear and exponential decay, during which the pull-out body becomes more defined/separated from the underlying material (see Fig. 11). For video of test A.2—2 see Online Resource 1.

Fig. 10

Failure developed to surface for A.2—2

Fig. 11

Failure after further development for A.2—2

3.2 Low-Cohesive Material Behaviour

Results from the low-cohesive samples display some similarity to the frictional materials described above (see Fig. 12), namely the nearly linear, abrupt load increase in the pre-peak phase, followed by the initiation of a failure plane. However, failure, in the form of an inclined fracture, occurs at the center of each half side of the low-cohesive samples, as seen in Figs. 13 and 14. Also, the fracture forms at the peak load for sample C.2, the 2% cement sample, while before the peak load for C.1, the 4% cement sample. After the initial fracture occurs, it grows in both directions—toward the socket and toward the surface, developing into a V-shaped failure form.

Fig. 12

Load–displacement relationship of the low-cohesive testing

Fig. 13

Failure initiation of test C.1

Fig. 14

Failure initiation of test C.2

In the case of C.1, the fracture halts at a point located beneath the blocks on the surface before reaching the peak load. From here multiple fractures appear in a zone located beneath the corners of the blocks. This zone develops to the surface as the resistance reduces in the post-peak phase, see Fig. 15.

Fig. 15

Failure pattern of test C.1 Fracture zone progressing upwards surface, with an array of sub-horizontal fine cracks beneath the block

In the case of C.2, when the fracture has reached the surface/sides after 5 mm displacement, only small bridges of intact material contribute to the anchor's resistance, as seen Fig. 16. As these are gradually broken off, the load reduces with displacement, and finally approaches a load which should equal the system's internal friction plus the weight of the final failure body.

Fig. 16

Failure pattern of test C.2

3.3 Failure Body Measurements

The failure body measurements are presented in Table 4 and include the location of the failure cones’ apex points, measured vertically on the socket from the base of the test chamber (see example from test A.2—2, Fig. 17a); the angle of the initial failure planes to the socket (see Fig. 17b), as well as the angle of the final failure shape (that is, when the failure has reached the surface), which is measured at the center of the sample (Fig. 17c). In cases where the final angle at the socket differs greatly from the initial angle, the final angle is also listed. Otherwise, the angle remains roughly the same as the “Initial”.

Table 4 Measured values of failure bodies. Angles are listed as left- and right-hand side measurements, respectively

Fig. 17

Example of failure measurements on A.2 – 2. a Point of failure initiation b Initial angle of failure surfaces c Shape of final failure body

3.4 Pull-Out Resistance Estimation

Following the method described in Sect. 2.6 the pullout resistance caused by weight of the pull-out body and the material resistance to failure is shown in Table 5. In the calculations an F_sys of 0.355 kN and the widest pull-out body angle observed in the tests were used. As seen in the lowest row, showing the ratio between the load from the frictional component and the corrected peak load, up to 85% of the total load is frictional force for the loose material and up to 98% for the low-cohesive. The friction between the test material and PVC panels are not accounted for in F_sys as this value is hard to obtain. However, during testing it is observed that the triangles which were pulled up quick and easy fell down, indicating low friction as it is easily overcome by the weight (see Online Resource 1). In addition, the weight is as described above is only a small part of the total resistance it is therefore believed that the material/PVC panel friction is not of large significance on the results.

Table 5 Calculation of resistance from weight of pull-out body, W, by the widest angles observed in each frictional material test

4 Discussion

This study was designed to investigate the mode of failure in frictional and low-cohesive materials due to overload of an embedded anchor. A series of physical tests were performed in the laboratory to study the development of the failure behaviour.

In all the tests with the frictional materials the failure propagates upward at an inclination from an apex point on the socket. The location of this point varies among the different materials but remains roughly consistent within the same material and is generally within the bottom one fourth of the socket. Besides this, there has not been found any correlation between the moisture content or grain size with respect to the apex point's location. The literature cited in the introduction regarding the location of the apex point states either a placement of the apex at the bottom of the anchor, for solid rock or with the use of an endplate, or at the middle for weaker rock. The scale difference between the tests and an in-situ anchor makes it hard to transfer the results as one does not know if an upscale of the test would cause the apex form at the same place (10 s of mm above) or at the same percentage above the socket. However, it may seem that for a frictional material a lower placement than the middle of the socket may be used.

The inclinations of the final failure surfaces typically vary with a few degrees from the peak friction angle and creates a delimited straight or curved cone-shaped failure. In the literature the values vary from 60° for weak, tightly jointed or weathered rock mass to 90° for strong, low jointed rocks by some and 80° for rock mass of moderate quality to 120° for high quality rock mass by others. In the tests reported in this article the values ranged from approximately 60° to 80° for the frictional materials and 100° and 110° for the low-cohesive materials. As the frictional and low-cohesive material is assumed to have a lower strength than, respectively, the “low” and “high” descriptions above, the literature recommendations, based on the results from these tests, may be considered conservative. The width/height ratio of the tested material is believed to have influenced the results to some degree and a larger ratio would be preferable for later tests. The influence of the side boundaries is expected to increase as the failure develops.

In test C.1 the fracture begins to initiate before the peak resistant load is reached, however in C.2, the fracture initiates at or immediately after the peak value and the failure planes created a much wider angle than observed in the frictional materials. The peak values of the cohesive materials are higher than for the frictional materials, and considerably higher in C.1, which had clamped-on blocks holding down the surface near the rig sides. The failure propagates well beneath the clamped-on blocks, which may have served as an external load on the surface, and above the failure line forms a series of fine cracks (see Fig. 15). This causes mobilization of a larger part of the material that may explain some of the larger peak failure value for this test. Interestingly, for the low-cohesive samples the fractures appear to initiate at the center of each half and propagate in both directions at an angle, as shown in Figs. 13, 14, 15, and 16. Despite these differences to the frictional material tests, the trends of both load–displacement plots have similar phases, except for the values at which the incidents occur.

The load–displacement relationship as well as the failure development, presented in Fig. 7, may provide us new knowledge on the interaction between the ground anchor and frictional materials. In Phase 1, the load–displacement behaviour is linearly elastic. The transition between Phase 1 and 2 is more gradual for the moist eclogite than the dry eclogite, which may be owing to the change in the surface condition of the eclogite grains by the added water.

In Phase 2 several processes may be going on at the same time at different places in the material. As shown in Figs. 6 and 7 the first visible movement can be seen in the transition to Phase 2, while the first visible failure is in the middle of the phase. So, at the beginning of this phase, two processes may be happening; some residual elastic deformation, but gradually more and more plastic deformation and failure until the fracture initiation starts. The videos taken during the tests show that plastic deformation is occurring all along the cone well before fracture initiation, hence, no elastic load contribution at this point. As one must assume that the residual strength of the fractured material is far lower than that which has only undergone plastic failure, one still can see that the load increases for a short while after fracture initiation. One can assume that the load absorbed by the failed material increases from the surface down to the beginning of the fracture, where the material’s load absorption rapidly decreases.

After the appearance of the first visible failure, the load continued to increase but the increase rate became reduced due to the fracturing. After the peak load, the fracturing was so extensive that the load-bearing capacity of the material dropped with the displacement. As these tests are deformation controlled, one also gets the load behaviour after the peak load. If controlled by load, as an overloaded in-situ anchor would be, a sudden pull-out of the anchor block would occur at peak load as it would not have enough force to hold it back.

Similar analyses have not been done for the low-cohesive materials since only two tests were carried out. It would be unwise to make conclusive comments based on such a small number of tests. However, similar failure processes may also exist in cohesive materials.

Using small scale testing equipment always raises questions on the applicability of the results to large-scale, real problems. In addition, in laboratory investigations only a limited selection, compared to natural materials and conditions, is possible to test. It is often also necessary with simplifications and modifications to suit the objective of the tests and practical issues. One should therefore be careful of applying test results of such tests directly to practical problems. Large scale testing of such problems is difficult and resource-demanding, and small-scale testing is therefore an important tool to widen the current knowledge of the issue.

In the tests conducted in this study a limited amount of test materials and conditions were tested on a small-scale rig. Possibly, both the same material in a larger scale, and other materials in the same scale, may fail differently than observed in this study. To know more about this, further testing with other parameters should be conducted. As mentioned above it is expected that the side boundaries have an increasing influence as the failure develops, and one should consider a larger width/height-ratio for further testing.

5 Conclusions

In the study, failure in homogeneous, frictional and low-cohesive materials under the load of a ground anchor was tested on a small-scale test apparatus. As described above a limited number of tests was performed and one should consider the results as suiting conditions as tested, and not necessarily as a general behavior.

The main findings regarding failure were that failure starts within the body of the material, propagates, and eventually reaches the surface. Failure takes the form of an inverted cone with a downward-curved failure surface. The location of the cone's apex point on the anchor depends on the material but is generally within the bottom 1/4 of the socket’s length. The inclination angle of the failure surface is smallest at the position of the anchor and becomes larger towards the ground surface. The apex angle of the failure body generally varies within a few degrees from the material’s peak friction angle and is wider for cohesive materials than frictional. It is in the range from approximately 60° to 80° for the frictional materials and 100° and 110° for the low-cohesive materials.

The peak resistant load is higher in the cohesive materials than in the frictional materials. The test results showed that the weight force of the failure body is only 15% of the peak load in the frictional materials and 2% in the low-cohesive materials. In other words, the material strength contributes up to 85% of the peak load in the frictional materials and 98% in the low-cohesive materials. This strongly suggests that one should take into account the strength of the rock mass in estimation of the anchor capacity.

Two important loading stages are identified in the tests to characterize the anchor-ground interaction. The first is the transition from the elastic behavior in Phase 1 to the plastic behavior in Phase 2. This transition marks the limit beyond which plastic and large deformations will occur. The second is the transition from Phase 2 to 3, that is, the peak load, which is mainly determined by the frictional coefficient and cohesion of the material.