1 Introduction

Rock anchors are used as load carrying elements for large-scale infrastructure by transferring large loads to the stable rock ground (Xanthakos 1991; Brown 2015). Anchors have been used for dam reinforcement (Xu and Benmokrane 1996; Cavill 1997), stabilisation of large structures (Jordan 2007; Koca et al. 2011), bridges (Schlotfeldt et al. 2013), reducing wind turbine foundation size (Yan et al. 2013; Shabanimashcool et al. 2018), reinforcement of underground caverns (Aoki 2007; Ma et al. 2021) and slopes (Choi et al. 2013; Wang et al. 2018), anchorage of submerged structures (Mothersille and Littlejohn 2012; Roesen and Trankjær 2021), and reinforcement of structures in seismic regions (Takemura et al. 2007).

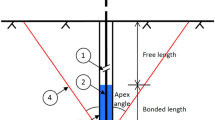
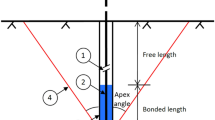
A typical rock anchor is shown in Fig. 1. It consists of a steel tendon, which is stressed to transfer the loads from or fasten the structure to the ground. The ground around the anchor is stressed through shear loads from the anchor (Hanna 1982; Hobst and Zajíc 1983; Xanthakos 1991). Anchor loads are transferred to structures or rock surfaces through the anchor head. The end of the tendon is fastened to the ground through a bonded length. Between the anchor head and the bond length is the free length, which elongates freely during the tensioning (stressing) of the anchor.

Fig. 1
figure 1

Rock anchor components

Full size image

There are four principal ways a rock anchor could fail. They are failure within the rock mass (Mode 1), failure of the grout-rock bond (Mode 2), failure of the tendon-grout bond (Mode 3), and failure of the steel tendon or anchor head (Mode 4) (Littlejohn and Bruce 1977). These failure modes are shown in Fig. 2. The ultimate tensile capacity of an anchor is the lowest load among the four failure modes (Kim and Cho 2012). When the failure modes are considered, they are usually calculated for individual anchors except for failure mode 1. Rock anchors are often installed in close proximity to each other, then it is important to account for the interaction between adjacent anchors when considering failure mode 1 (Brown 2015).

Fig. 2
figure 2

The four principal failure modes of a grouted rock anchor under tension. (1) Rock mass uplift failure; (2) grout-rock bond or interface failure; (3) tendon-grout bond or interface failure; and (4) steel tendon tensile failure

Full size image

Earlier research has investigated rock anchors to some extent in the laboratory. The most common laboratory tests are anchor pullout tests. Failure mode 3, grout-tendon interface failure, has been tested, for example, by Barley (1997); Jarred and Haberfield (1997); Kim and Lee (2005); Ivanovic and Neilson (2008) and Akisanya and Ivanovic (2014). Barley (1997) also tested failure mode 2, grout-rock interface failure, when investigating the behaviour of grout in a confined state. García-Wolfrum et al. (2007) conducted pullout tests on intact rock samples to investigate conical failure (mode 1). Farmer (1975) and Benmokrane et al. (1995a) monitored the stresses along the tendon during pullout tests. Kaiser et al. (1992) investigated the effect stress changes had on the tendon-grout pullout/bond strength by changing the confining pressure around the bond length. Benmokrane et al. (1995b) studied the effect of grout on the pullout strength, while Jia et al. (2019) tried to optimise the grouting mixture and Park et al. (2013) tested different grouting methods. Zheng et al. (2016) developed a lab-model to investigate the performance of a rock anchor in a rock slope in a seismically active area, where the anchor was cyclically loaded.

The most similar tests to those reported in this paper was run by Dados (1984), who tested the pullout of an anchor in a block model. The blocks were made up of aluminium cubes and a confinement was set on the sides of the model. The test showed that the blocks bulged upward during the pullout test, and the vertical joints tended to open.

The design of rock anchors requires understanding of the mechanisms and interaction between the anchor and the surrounding rock (Showkati et al. 2015). A thorough review has been carried out by Brown (2015) on the design of post-tensioned anchors. The review concluded that the design is based on simplified assumptions about the stress distribution, shape and volume of the rock influenced, and the failure mechanisms. The design was also considered to be excessively conservative and represents poor engineering practice. There is thus a clear need to increase knowledge about the stress distribution and how failure develops in the rock mass around a rock anchor.

In Norway, the ground rock mass is in general hard and massive, but contains fractures, geological discontinuities and foliation that sometimes function as weakness planes. These geological structures cut the rock to blocks in various sizes. Rock failure occurs often along the geological structures in such a blocky rock mass. Under the concentrated loading condition by a rock anchor, a load-arching effect may exist in the blocky rock mass, which would significantly enhance the load-bearing capacity of the rock mass. The current design practice only takes into account the dead weight or presumptive shear strength values of the potential failed rock body which results in underestimates of the load capacity of the rock mass. There are currently no specific guidelines for load estimation in blocky rock masses. It is therefore important to investigate how the load in transferred from an anchor to the blocky rock masses as well as the load capacity of the rock mass.

The objectives of this paper are to qualitatively demonstrate the deformation behaviour of rock blocks, the arching effect, and the failure mode of the blocky rock mass through laboratory pull tests on a specially designed mini test rig. Digital image correlation (DIC) was used to measure the displacements in the block models. UDEC modelling was also conducted after the model tests to verify the results of the physical testing. Tests similar to those in this study have, to the best knowledge of the authors, not previously been carried out and therefore seem to be novel.

2 Physical Testing

2.1 Experimental Program

2.1.1 Mini Test Rig

The constructed test setup is shown in Fig. 3. The mini test rig consisted of a steel frame made of rectangular tubes and a hydraulic jack. There is an opening 4 cm \(\times \) 10 cm in the middle of the bottom horizontal beam. A steel block representing the rock anchor goes through the opening and contacts the bottom layer of the blocks. The working area in the frame has dimensions 60 cm \(\times \) 40 cm \(\times \) 10 cm (width \(\times \) height \(\times \) depth). Concrete blocks are placed on the bottom frame in layers, to build up the blocky rock mass model. On each side of the frame there are two bolts which are tightened to provide lateral confinement to the model blocks. A steel plate is placed between the side blocks and the bolts to distribute the bolt load evenly (Fig. 4). A steel beam was fastened on top of the side frame pillars to enhance the horizontal stiffness of the frame. A manually operated hydraulic jack is used to apply the load to the anchor block. It is fastened to the bottom frame by two bolts and the load from the hydraulic jack is measured with a load cell. The movements of the blocks are measured by DIC technology with two cameras. It was a question how the anchor load would be applied in the model tests when the test setup was designed. As previously mentioned, the anchor load in reality is applied to the rock mass through the shear stress at the anchor-grout and grout-rock contacts. The purpose of this experimental study is the behaviour and failure mode of a blocky rock mass under a concentrated anchor load, but not the behaviour of the contacts. The effects will be the same regardless of whether the anchor load is applied by pull or compression, provided the directions of the loads on the rock anchor are the same. To simplify the loading procedure, therefore, it was decided to construct the setup so that the anchor load would be applied by pressing a rigid block upward in the bottom of the model.

Fig. 3
figure 3

The mini test rig composed of a steel frame and hydraulic jack, and equipped with DIC cameras

Full size image

Three models were run with increased stiffness, shown in Figs. 4 and 5. The stiffness was increased in two ways, with clamps on top of the steel plates in two models with two and three layers (Fig. 4), and with extra steel plates in the void between the frame and the steel plates in a model with five layers (Fig. 5).

Fig. 4
figure 4

Increased horizontal stiffness of steel plates with clamps

Full size image
Fig. 5
figure 5

Increased horizontal stiffness with extra steel plates in the void between the frame and steel plates

Full size image

2.1.2 Test Materials

The materials used in the test were 20 cm \(\times \) 5 cm \(\times \) 40 cm concrete pavement blocks. These were cut into small blocks with dimensions of 5 cm \(\times \) 5 cm \(\times \) 10 cm and 2.5 cm \(\times \) 5 cm \(\times \) 10 cm. Small errors occurred during cutting, which resulted in an uneven width of the block layers in the model. To ensure a satisfactory contact between each layer’s end blocks and the side steel plate a cement liner (Fischer cement express) was used to fill the gaps.

Five 40 mm cores were drilled out of the concrete pavement blocks and cylindrical samples prepared. The samples were tested under uniaxial compression as described in Bieniawski and Bernede (1979) to obtain the mechanical properties of the concrete material. The axial and radial strains were measured during the tests to calculate the Young’s modulus (E) and Poisson’s ratio (\(\nu \)). The uniaxial compressive strength (UCS/\(\sigma _c\)) was measured to 65.3 MPa, the Young’s modulus 27.7 GPa and Poisson’s ratio 0.25. The UCS was used to estimate the tensile strength (\(\sigma _t\)) and the cohesion (c) of the concrete using equations 1 (Indian Standard 2000) and 2 (Sivakugan et al. 2014):

$$\begin{aligned} \sigma _t = 0.7 \sqrt{\sigma _c} \end{aligned}$$
(1)
$$\begin{aligned} c = \frac{0.5 \sigma _c \sigma _t}{\sqrt{\sigma _t(\sigma _c - 3\sigma _t})} \end{aligned}$$
(2)

From the equations, the tensile strength was estimated to be 5.66 MPa and the cohesion 11.2 MPa. Tu et al. (2020) found in their tests on high strength concrete (UCS > 60 MPa) that the friction angle (\(\phi \)) of the concrete was 34\(^\circ \). This value was assumed to be representative for the concrete blocks. The basic friction angles of the blocks were also measured with tilt-tests (Fig. 6) as described in Alejano et al. (2018). Two basic friction angles were measured on the blocks, one on rough untreated surfaces and one on smoother cut surfaces: 41.2\(^\circ \) for the rough surfaces and 31.3\(^\circ \) for the cut surfaces.

Fig. 6
figure 6

Test apparatus used for the tilt-tests

Full size image

2.1.3 DIC Monitoring

The tests were monitored with DIC cameras from Correlated Solutions. The side of the concrete blocks facing the cameras had to be painted white before a speckle pattern was applied on the surface. The speckle pattern was non-repetitive and was 50/50 black and white with high contrast. The speckles should have a size of at least 3–4 pixels to avoid aliasing (Correlated Solutions 2020). The cameras were placed at a distance where the whole block model could be seen with both cameras, and they had an angle of 25\(^\circ \) between them. During the tests the loading was applied slowly with a load rate varying from 12–75 N/s, so the cameras were set to take two images per second (i.e., four images in total per second). The load rate was decided based on the operator trying applying loading in a steady and controlled manner but varied greatly due to the manual operation of the hydraulic jack. The software used to analyse the images post testing was Vic-3D (Correlated Solutions 2020). The strains were calculated from changes in the speckle pattern by taking reference in an image from before the tests started.

2.1.4 Estimation of Rock Mass Strength and Horizontal Confinement

In the design of rock anchors, the strength is commonly estimated based upon the weight of overlying rock and in some countries the shear or tensile strength of the rock mass is also included in the calculations, generally by applying assumed values of the tensile strength, shear strength and cohesion (Brown 2015). The strength of the block mass in the model was estimated with the design method based on the weight of overlying rock. This is a commonly applied method for estimating rock anchor strength against failure mode 1 in weak and heavily fractured rock masses (Brown 2015). The shape of the rock mass volume over the anchor is illustrated in Fig. 7. The anchor capacity was estimated using

$$\begin{aligned} Q_{cone}= & {} \left[ 2 \cdot \frac{1}{2} h \cdot ( h \cdot \tan \alpha ) + d \cdot h \right] \cdot z \cdot \gamma \nonumber \\= & {} (h^2 \cdot \tan \alpha + d \cdot h )z\cdot \gamma \end{aligned}$$
(3)

where h is the height of the mobilised cone, \(\alpha \) the angle of the potential failure cone, d the width of the loaded block, z the depth of the model and \(\gamma \) the unit weight of the block material. In the tests, h = 0.05 m \(\times \) number of layers, d = 0.05 m, z = 0.1 m, and \(\gamma \) = 22563 N/m\(^3\). Based on the staggered pattern, \(\alpha \approx \) 25\(^\circ \) (sect. 2.2.2). This results in an estimated capacity of 213 N for a model with 8 layers and 94 N for a model with 5 layers.

Fig. 7
figure 7

Illustration of the dimensions of a hypothetical uplifted cone of rock mass, z illustrates the depth of the uplifted material

Full size image

Confinement was applied to the model by applying torque to the bolts on the side of the model. The torque was applied with a torque wrench at 2.5–25 Nm. The numerical modelling of the tests required input of the confinement on the model, estimated based upon the applied torque with(USACE 1990):

$$\begin{aligned} T = P_B \cdot \left( \frac{L}{2\pi }+\frac{d_2\cdot \mu _1}{2 \cos \alpha }+\frac{(d+b)\cdot \mu _2}{4}\right) \end{aligned}$$
(4)

where T is the applied torque, P\(_B\) the resulting axial force in the bolt, L the lead of the thread helix, d\(_2\) the pitch diameter of the bolt, \(\mu _1\) the coefficient of friction of the bolt thread, \(\alpha \) the angle of the thread pitch, d the nominal bolt diameter (at the bolt head), and b the diameter of the washer face.

The equation was simplified since the bolt head did not interact with any other materials, and then both d and b could be set to zero. The bolt and the frame were made of steel and were lubricated with mineral oil which resulted in an approximate coefficient of friction \(\mu _1\) of 0.15 (USACE 1990). The bolt pitch diameter d\(_2\) was 16 mm and the lead L of the thread helix was 2.0 mm. The angle of the thread pitch \(\alpha \) was 60\(^\circ \). The calculated bolt force was then used to calculate the resulting stress on the side of the block mass with

$$\begin{aligned} S = \frac{2P_B}{A_{Bm}} \end{aligned}$$
(5)

where S is the resulting stress in the side of the block mass, P\(_B\) the force applied by the bolts, and A\(_{Bm}\) the area of the block mass on the side. The estimated confinements are shown in Table 1.

2.1.5 Test Procedure

Several tests were run with the block model. The number of layers and confinement were varied. All the tests followed the same procedure, which is shown step by step here:

  1. 1.

    The blocks were placed in the model with the number of layers wanted.

  2. 2.

    Confinement was applied to the blocks by tightening the bolts on the sides.

  3. 3.

    The DIC cameras were calibrated.

  4. 4.

    The DIC capturing software was started.

  5. 5.

    The block model was then loaded gradually by the anchor block at the middle bottom. The loading was stopped when a desired load was reached or failure occurred.

  6. 6.

    The system was then unloaded slowly.

  7. 7.

    The DIC capturing was stopped.

2.2 Physical Testing Results

2.2.1 Load-Deformation Behaviour

The loading of the block model showed that the displacement at the anchor block and the displacement in the top centre block were almost equal. At small displacements, they were slightly larger in the anchor block, while with large displacements the top centre block had the greatest displacement due to bulging of the layers, as demonstrated in Fig. 8. Figure 9 shows the load-vertical displacement curve when the block model was run to failure. The curves show a linear relationship between the load and the displacement at small loads (elastic behaviour) then the curve starts to bend until a peak load is reached before the load starts to drop while the displacements increase (plastic deformation) until the model failed abruptly. The total displacement in the block models was reduced with increasing confinement and increasing number of layers, as demonstrated in Figs. 10–12. It was also observed that the vertical displacement was reduced when the horizontal stiffness of the steel plates was increased with clamps or adding extra steel plates, shown in Figs. 4 and 5. The results from the block model tests are summarised in Table 1.

Fig. 8
figure 8

Plots of the load applied on the anchor block versus the vertical displacements of the anchor block (A) and the centre concrete block (TC) on the top layer in three typical model tests

Full size image
Fig. 9
figure 9

Plots of the load applied on the anchor block versus the vertical displacements of the anchor block (A) and the centre concrete block (TC) on the top layer in the model test run to failure (test no. 9)

Full size image
Fig. 10
figure 10

Vertical displacement in models with 8 layers at 2 kN and 5 kN anchor load with trend lines

Full size image
Fig. 11
figure 11

Vertical displacement at 2 kN anchor load and 2.5 Nm torque applied to side bolts

Full size image
Fig. 12
figure 12

Vertical displacement at 2 kN anchor load for all the tests under normal conditions with trend line and with increased stiffness of the steel plates

Full size image
Table 1 Test parameters and results from the small block model tests
Full size table

2.2.2 Load Transfer in Rock Mass During External Loading

The load of the anchor block was transferred to the blocks in the middle of the bottom of the model. The displacements of the blocks were largest in the centre of the model at the bottom at small loads. They decreased upwards and at the sides. As an example, Fig. 13 shows the displacement of the model in test 1 at four different loads.

Fig. 13
figure 13

Vertical displacement plots (mm) for test 1 at 4 different loads

Full size image

The horizontal strains in the material were processed with the DIC software Vic-3D. The blocks in the model rotated and bulged upwards during loading. Figure 14 shows the horizontal strains of the model in test 1 at Fig. 13 D with an applied load of 5.5 kN, and the potential failure cone (\(\alpha \)) based upon the fracture pattern. The vertical joints opened (red) at the top of the blocks in the middle of each layer and were pressed (purple) at the bottom. On the sides, the joints were pressed at the top and tended to open at the bottom. Apparently, a load arch, which is the trajectory of the most pressed portion of the joints, was formed in each layer. The load arches in each layer diverged the anchor load to the frame of the test rig. These arches were observed in all the tests.

Fig. 14
figure 14

Plot of the horizontal strain in test 1 with the locations of pressure-transmitting arches drawn in red and potential failure surface based upon the block pattern drawn in yellow

Full size image

2.2.3 Failure of the Block Model

The block model was run to complete failure in a model with five layers. The result is shown in Fig. 15. The confinement of the model material was enforced by applying a torque of 2.5 Nm to each bolt on the test frame, which resulted in an estimated confinement of 0.072 MPa. The highest load measured in the test was 9.71 kN with an anchor displacement of 14.1 mm. The load then started to drop gradually with continued displacement. At a displacement of 38.2 mm, the block model completely lost its load-bearing capacity and failed in the form of an inverted cone, as shown in Fig. 15.

Fig. 15
figure 15

The model run to failure with 5 layers. The block model failed as an inverted cone

Full size image

3 Numerical Modelling of the Block Model

The block model was re-created in a discontinuous numerical model with the UDEC program (Itasca 2011). The purpose of the numerical model was to verify the observed phenomena in the physical tests, and evaluate the suitability of UDEC for simulating the behaviour of a rock mass subjected to an anchor load. The results from the physical model tests and DIC analysis were used to calibrate the models.

UDEC (Universal Distinct Element Code) software was chosen for the analysis of the block model because of its capabilities to model discontinuous behaviour. The program can model large displacements caused by rigid motion of individual blocks, by finding the motion through a continuous detection and treatment of the contact between the blocks when solving the equations of motion (Jing 2003), which is ideal when considering the large displacements in the physical tests.

An important parameter in UDEC regarding simulating plastic deformations is computational rounding, as it indirectly simulates the crushing and shearing of block corners. The UDEC manual specifies that the corner rounding should be 1% of the total block length (Itasca 2011). For a 5 cm \(\times \) 5 cm block, this would result in a rounding radius of 0.5 mm. In the physical tests, it was observed that the crushing of the corners exceeded 0.5 mm and was in multiple locations up to 1–2 cm. The rounding radius had great influence on the displacements in the models, greater than both the joint strength and confinement. Therefore, it was challenging to decide the rounding radius. Based on observations in the physical tests, it was set to 1 mm, but 3 mm was also tested in some models as shown in Table 4.

The numerical block model included two types of materials. The concrete block was a Mohr-Coulomb material with properties determined by the laboratory tests described in Sect. 2.1.2. The frame and the anchor block in the model were made of an elastic steel material with properties of 18-8 grade steel as described by Budynas and Nisbett (2011). The material parameters are presented in Table 2.

Table 2 Material parameters used in the numerical models
Full size table

There are three types of joints in the UDEC model. The joints between the steel plates or the anchor block and the steel frame had no contact, and therefore the shear strength was set to zero. The cut surfaces of the concrete blocks were smoother than their original surfaces, and were implemented into the model using different friction angles for the original horizontal joints compared to the cut vertical joints. The friction angles of the two types of joint surfaces measured by the tilt tests were implemented as two types of joints in the model. The shear and normal stiffness of the joints are based on best fit from earlier physical tests with eight layers (i.e., tests 1–3 in table 1). The stiffness in the numerical models was found from iterative testing until a satisfactory match was found. The cohesion was set to zero, implying contact joints without infill material. All the joints were considered to be smooth, and therefore the dilation angle is zero (Barton et al. 1985; Kulatilake et al. 2001). The mechanical properties of the three types of joints are presented in Table 3.

Table 3 Joint material parameters used in the numerical models
Full size table

The geometry of the 2D UDEC models was like the physical models; Fig. 16 shows a UDEC model with 8 block layers. The concrete blocks were 5 cm \(\times \) 5 cm or 2.5 cm \(\times \) 5 cm in the models. The blocks were placed in a staggered pattern like the physical tests and the number of layers varied. A separate model was also created with 8 layers and continuous joints vertically and horizontally to evaluate the effect of the vertical joints on the arching. The width of the models were 60 cm with two vertical steel plates on the sides. Horizontal forces were applied to the model sides through the vertical steel plates. The anchor loads were applied in the UDEC models under both load and displacement controls. The models were under gravity loading.

Fig. 16
figure 16

Model geometry in UDEC with a staggered block pattern and 8 layers

Full size image

3.1 Numerical Modelling Procedure

Several models were set up by varying the number of layers, the corner rounding and the confinement. All simulations followed the following same procedure:

  1. 1.

    The geometry of the model was set up and the outer boundary of the frame was fixed in both x- and y-directions.

  2. 2.

    The model was cycled to equilibrium.

  3. 3.

    Horizontal confinement was applied to the steel plates which were set free to move in the x-direction.

  4. 4.

    It was then cycled to equilibrium again.

  5. 5.

    The steel plates were fixed.

  6. 6.

    The system was then cycled to equilibrium.

  7. 7.

    The anchor block was moved upward in the y-direction to apply the anchor load.

  8. 8.

    The model was then cycled to equilibrium under load control, or it was cycled for a desired time interval under displacement control.

3.2 Numerical Modelling Results

The numerical models gave similar results as the physical tests. The displacements in the rock mass decreased with higher confinements. The numerical models gave smaller displacements at low confinement than the physical models with the same load in the anchor block. Under displacement control, the load in the numerical models was higher than the physical models for a given displacement except for the models with two and three layers. In the models with two and three layers, the steel plates acted as levers with rotation around the top layer. The results of the numerical models are summarised in Table 4.

Table 4 Results of numerical simulations of the physical tests
Full size table

3.3 Load Transfer in the UDEC Block Models

The load transfer in the UDEC models started from the anchor block in the bottom of the model. The displacements were largest close to the anchor block in the centre of the model and attenuated to the sides, as shown in Fig. 17. There were similar displacement patterns in the models of both staggered and continuous vertical joints.

Fig. 17
figure 17

Vertical displacement plot for numerical simulation 1 at equilibrium for a load controlled model with 5.6 kN load of physical test 1

Full size image

The plots of the horizontal stresses in the numerical models showed that compressive load arches were established in the blocks in the same way as was observed in the physical models. Figures 18 and 19 show the horizontal stresses in numerical models with staggered and continuous vertical joints, respectively. In both models, load arches are formed in each layer and the anchor load is transferred to the abutment steel plates through the arches.

Fig. 18
figure 18

Horizontal stress plot for numerical simulation 1 with 5.6 kN anchor load for load controlled model of physical test 1

Full size image
Fig. 19
figure 19

Horizontal stress plot for numerical simulation 9 at 3.5 mm anchor displacement for a displacement controlled model with a non-staggered block pattern and continuous vertical and horizontal joints

Full size image

4 Discussion

The laboratory tests and discontinuous numerical modelling aimed to develop a better understanding on how the load from a rock anchor affects a layered and jointed rock mass and how such a rock mass would fail. The numerical modelling was used to verify the mechanisms observed and measured in the physical laboratory tests.

The physical tests and numerical models of a block model exposed to an anchor load in small-scale models had similar results. They showed that load bearing arches, voussoir arches, were developed in each layer of the laminated block mass owing to rotations of the blocks within the layer. The test results indicate that load arches may exist in each layer in laminated rock masses if the layer deforms under the anchor load. The load arches transferred the anchor load to the boundaries in the models. In a real rock mass, the load would be transferred to the rock at some distance from the anchor position. Because of the existence of the load arches, the load capacity of the block models was higher than the weight of the overlying material in the model. As an example, the model with 5-layers had a capacity of 9.71 kN while the estimated capacity with the weight of overlying material was 94 N. The induced horizontal stress from the arches might also have increased the rock mass strength more than what would have been calculated using the rock mass shear strength along the failure surface.

Under the anchor load, the horizontal block layers bulged upwards and separated from each other in a similar way as described by Dados (1984). The block model tests conducted in this paper failed through a combination of sliding, rotation and wedging between the blocks, and at the end in an inverted cone (as shown in Fig. 15). After failure, the blocks in the centre rotated and were lifted, while the blocks on the sides only experienced slight horizontal movement. The failure trajectory followed the joints in a staggered pattern and had a smaller failure angle, approximately 25\(^\circ \), rather than what is used in the design methods, 30–45\(^\circ \) (Littlejohn and Bruce 1977). Apparently, the failure shape was affected by the joint pattern in the test.

The total displacement of the anchor block depended on the number of layers and horizontal confinement for a given anchor load. The displacements of the anchor block decrease with increasing confinement for a given anchor load and a constant wall height in the block model, demonstrated in Fig. 10. The displacement of the anchor block with 2 kN loading increased when a constant torque was applied to the side bolts of the model while removing layers from the block model, as shown in Fig. 11. The block model capacity was reduced when the number of layers were reduced. This is demonstrated in Fig. 12, where the vertical displacements increase when the number of layers is reduced at an anchor load of 2 kN.

Figure 12 demonstrates the relationship between the vertical displacement and number of layers. In three of the models the horizontal stiffness was changed, which affected the displacements of the model directly, as can be seen with the orange plotted points. In the final physical test (5 layers) with the smaller steel plates placed in the void between the frame and the steel plates, the increased stiffness resulted in a higher capacity of the physical model compared to earlier tests. These tests indicate that the horizontal stiffness has an effect on the displacements and model capacity; when the stiffness is increased, the displacements decrease. Therefore, it is important to know the stiffness of the material to estimate the displacements and capacity.

These small-scale anchor tests are not direct replications of physical rock anchors. In the model tests, the blocks were loaded by pushing an anchor block upwards, while in reality the anchor is pulled and the load is transferred to the rock mass through the shear stresses along the anchor. The mechanism of the load application in the laboratory tests and the numerical modelling, that is, direct uplift of the blocks above the anchor block, is different from that of the rock anchor in the field, that is, shearing along the bond length of the anchor. This deviation results in different stress fields in a small immediate zone around the anchor. However, the stress distribution further away is not affected. In other words, the load-transferring pattern in the rock mass is not changed significantly by the loading means used in the tests. Therefore, the authors believe that the behaviour presented in this study is a good representative of the behaviour of the rock mass affected by actual rock anchors. Table 4 shows the results of the numerical modelling. The results from the numerical modelling had smaller displacements at the same loads or higher loads at the same displacements as the physical tests. The stiffness in the numerical models was found from iterative testing until a satisfactory match was found. There are several factors that might cause these differences. One likely reason is the difference in the stiffness of the steel plates on the sides of the rock mass in the physical model and the numerical models. The plates are stiffer in the numerical models which prevents the blocks rotating as much as in the physical tests, and the capacity of the block mass is increased. The cement liner used to make all the layers have the same width could be less stiff than the concrete blocks, which may have resulted in more rotation of the blocks in the physical model and a lower capacity than the numerical models.

There are several other factors that might be the cause of the discrepancies between the physical models and the numerical simulations. In the physical model, the contact between the blocks varied since they were cut down to the right size. In some places, it was possible to see through the joints between the blocks while in the numerical model the contact between the blocks was perfect. Therefore, the contact forces in the numerical models were higher and the block model capacity increased. At high loads in the physical tests, cracking sounds could be heard during testing and the corners of some blocks failed slightly, while in the numerical model the blocks remained intact. The horizontal stress level applied to the numerical models was estimated based on the torque applied to the side bolts on the frame; these estimations are uncertain, and the physical tests and the numerical models showed that the block model displacement was highly influenced by the applied confinement. The estimated confinement was calculated as an average based on the applied torque, while the load distribution possibly was more uneven when there were less than eight layers. In the models with few layers, the steel plates may act as a lever with rotation around the top layer which results in uneven confinement, which was especially evident in the numerical models with two and three layers.

Further research is needed to evaluate the load arches formed in the rock mass above rock anchors and the failure shape. The joint patterns in the block models should be varied: these tests have only considered continuous horizontal joints and discontinuous vertical joints. Therefore, it would be necessary to test with continuous joints in both directions, joint patterns set at an angle or interlocked joints. The horizontal stress should be measured to evaluate the capacity of the load arches. These results will be used in the development of a large test frame where the confinement can be controlled and measured, and the stresses in the block model determined.

5 Conclusion

A series of small-scale two-dimensional block model tests were carried out in the laboratory to investigate load transferring from rock anchor to rock mass. The test results showed that load transfer arches were formed in individual block layers, through which the anchor load was transferred to the side frames of the test apparatus. The load capacity of the model increased with increases both in the confining stress and in the number of block layers (corresponding to an increase in the depth). The trajectory of the inverted failure cone followed the joints in a staggered pattern. The tests also showed that the load capacity of the block model is significantly higher than the weight force of the potential failure cone, which is commonly used to estimate the load capacity of the rock mass in the current practice of rock anchoring. The observed phenomena like load arching were also captured in the discontinuous UDEC numerical modelling. The numerical modelling revealed that the voussoir arching was achieved owing to block rotations as well as the confinement. The load capacity of the voussoir arches increases with an increase in the confining stress. The displacements in the mass are approximately identical along a vertical line from the anchor to the ground surface, except in the immediate area surrounding the anchor. At a given depth, the displacement decreases with an increase in the distance to the centre line of the anchor.