1 Introduction

A safe and cost effective ground reinforcement design is an important aspect of any underground mining operation. These can prevent ground failure incidents which can lead to fatalities, injuries and loss of production. Among the different rock reinforcement methods in use currently, fully grouted rock bolts constitute the major form of reinforcement in underground mines. Rock bolts provide an easy, quick and efficient way of reinforcing the rock. Fully grouted rock bolts are a type of rock bolt in which a solid steel rebar is coupled to the rock using a grout. These types of rock bolts are used for their high stiffness and corrosion resistance. The rock bolt provides reinforcement to the rock by resisting the deformations in the rock. This transfer of load from rock to bolt occurs through a complex interaction between rock, grout and steel bar. In order to design a safe and efficient rock reinforcement, it is important to understand this behaviour.

Different analytical and empirical methods have been proposed for rock reinforcement design. Most of these methods rely on a simplified model of the rock bolt to reduce the complexity of the calculation (Obert and Duvall 1967, Potvin 1988; Mark 2000). Numerical modelling as a tool for designing rock reinforcement has the advantage of easily modelling complex mechanisms and therefore its use in rock reinforcement design has become common in recent years.

Numerical modelling uses the fundamental mechanics of the materials and therefore can be used to analyse specific systems without the need for significant simplification to approximate the problem. However, a numerical model needs to be calibrated and validated before its results can be useful (Esterhuizen 2014). This calibration of the numerical model is done using in-situ measurements and observations. Once a model is calibrated and produces verifiable results for a current in-situ excavation, it can be extrapolated and used for making reliable predictions for future excavations. The in-situ measurements used for calibrating numerical models are done using different types of instrumentation. The instrumentations used on rockbolts in underground mines have evolved from the use of resistive strain gauges to digital (inductive) gauges and now into the use of optical sensing (Kostecki 2019). Each improvement in instrumentation technology provided more accurate measurements with higher resolution along more of the rockbolt length. This increase in the quality of data available has made it possible for new and better methods for the calibration of numerical models. The focus of this paper is to present a procedure for using the data obtained from optical instrumented bolts to calibrate in-situ rock bolt models under shear, tensile and combined loads.

2 Background

2.1 Instrumented Bolts

The first type of instrumented rock bolts installed in underground mines used resistive strain gauges attached in several fixed positions along the length of the rock bolts to measure the strains. Freeman (1978) used instrumented fully grouted rock bolts in Kielder experimental tunnel to study the axial load transfer between rock and bolt. Similar studies were done by other researchers in the subsequent years using resistive strain gauge instrumented rock bolts to study the axial and bending loads on rock bolts installed in-situ (Serbousek and Signer 1987; Signer 1990; Signer et al. 1997; Johnson et al. 1999; Signer 2000). The shortcoming of these resistive strain gauges was their limited coverage of the rock bolt length. The measured strain depended on the positioning of the gauges on the rock bolt. The small resistive gauges were unable to reliably measure concentrated loads on the rock bolt. They were also only attached in 2 positions 180° apart so the results were not reliable.

The shortcoming of limited coverage of rock bolt length by small resistive strain gauges was overcome by the use of long base inductive sensors. Rock bolts instrumented with these long base inductive sensors were used by researchers to study the axial and bending loads on rock bolts (Spearing and Gadde 2011; Spearing and Gadde et al. 2011; Hyett et al. 2013). The longer sensor provided better coverage of the rock bolt length and was used in staggered and stacked configurations. The studies were able to measure bending loads on the rock bolts in-situ. However, the longer inductive sensors averaged the strain measured over their length. This resulted in a significant underestimation of the peak loads measured on the rock bolts. The shortcomings of the short resistive strain gauge and long inductive sensors were overcome by the use of optical sensors.

Distributed optical sensors (DOS) consists of an optical fibre attached to the whole length of the rock bolt. The optical fibre can measure strain typically every 5 mm along the length of the rock bolt. This provided a significant increase in the resolution and accuracy of the strain measured on the rock bolt. The use of optical fibres in instrumented rock bolts was first described by Hyett, Forbes et al. (2013). The rock bolts were instrumented with optical fibres running along with two diametrically opposite slots along the length of the rock bolt. The instrumented bolt was used to measure axial and bending strain in laboratory tests. Kostecki et al. (2015) used the DOS instrumented rock bolts with three slots along the rock bolt to demonstrate the need for a third slot to successfully capture the true strain of the rock bolt (axial and bending). It was concluded that instrumented bolts with two slots for measuring strain were not able to capture the bending of the rock bolt if the slots were not oriented parallel to the bending direction. Therefore, to capture the bending strain of a rock bolt in-situ a minimum of three slots are required. Figure 1 shows a comparison of the three types of instrumentation technology described above and the rock bolt strain profile they are capable of capturing. Optical instrumented rock bolts have been used by researchers to measure strain on the rock bolts in a laboratory and in-situ (Jessu et al. 2016; Forbes; Vlachopoulos et al. 2018; Vlachopoulos; Forbes et al. 2018; Kostecki 2019). Hoehn et al. (2020) improved the optical instrumented bolt technology using an All-Grating Fibre (AGF). Improvements were also made by increasing the number of sensing slots to four and better tooling of the slots. This improved instrumented rock bolt was used in this study for in-situ measurements.

Fig. 1
figure 1

Comparison of the three types of instrumentation technology

Full size image

2.2 Numerical Modelling

Numerical modelling can be used for rock bolt reinforcement design by creating a detailed mathematical model for the specific case of an excavation. The model can then be used to analyse the response of the rock bolts to the stresses and deformations produced in the rock. As the basis of a numerical model are mathematical equations based on the basic mechanics of the material. These equations define the response of each element such as rock or rock bolt in the model. In the case of rock bolt support models, there are two ways of modelling the rock bolt. The rock bolt can be modelled using grid elements like the surrounding rock whose behaviour is based on the basic mechanics of the material or using linear structural elements based on analytical models. Several different analytical models have been proposed to describe the axial, bending and shear behaviour of the fully grouted rock bolt (Spang and Egger 1990; Hyett et al. 1996; Pellet and Egger 1996; Li and Stillborg 1999; Cai et al. 2004; Jalalifar and Aziz 2010; Ren et al. 2010; Ma et al. 2013; Ghadimi et al. 2015; Zhang et al. 2020; Singh and Spearing 2021).

Although numerical models have great potential for use in rock bolt support design, the lack of a detailed geotechnical model of the rock mass presents a challenge in the wider adoption of numerical modelling. Uncertainty in the properties of the rock mass, the location, variation and properties of discontinuities create difficulties in creating a representative numerical model including rock bolt support. Therefore, once a model has been created it needs to be calibrated against in-situ measurements and observations; and the uncertain parameters adjusted (Esterhuizen 2014). Common sources of in-situ measurements for calibration of rock bolt numerical models are the instrumented rock bolts discussed in the previous section. Spearing and Gadde (2011), Spearing and Hyett (2014) used instrumented rock bolts to measure axial loads on the rock bolts during coal panel excavation. A numerical model of the excavation was created in FLAC3D and used structural elements to simulate rock bolts. The axial loads from in-situ measurements were used to calibrate the models. However, due to the unavailability of optical sensors, the instrumentation could not capture the true strain profile along the length of the rock bolt. This made it difficult to use the data to calibrate the rock bolt model for concentrated loads (axial and bending) such as caused by local discontinuities in the rock. Kostecki (2019) used DOS instrumented rock bolts with a three-slot configuration for in-situ rock bolt monitoring. Calibration of in-situ numerical models using the data from the instrumented rock bolts was discussed. It was found that the instrumentation was able to capture the strain on the rock bolt due to the local inhomogeneity of the rock mass such as the presence of discontinuities. This made it possible to create and calibrate rock bolt models to capture the localized rock strain.

In this study, the numerical modelling is done using the linear structural element as they are commonly used in most of the currently available geotechnical analysis software. The numerical modelling of in-situ rock bolt support is done using FLAC3D (2017) software with the inbuilt pile structural element. The pile element in FLAC3D simulates the behaviour of a fully grouted rock bolt using a linear two noded element. The linear element is connected to the surrounding rock grid with spring sliders which simulate the behaviour of rock-grout and grout-bolt interface (Fig. 2). The properties of the linear element can be derived from the structural properties of the rock bolt. However, the parameters controlling the behaviour of the spring-slider system cannot be directly derived from the bolt or grout properties. The she2012ar spring parameters which control the axial behaviour of the pile have been calibrated using data from in-situ pull tests (Bin et al. 2012; Nemcik et al. 2014). Calibration for normal spring parameters which control the bending and shear behaviour of piles has only been done using laboratory shear tests (Tulu et al. ). This is done by calibrating the shear-load vs displacement plot of the bolted interface in the model with the actual measured shear-load vs displacement from laboratory tests. No work has been done on calibrating the normal spring parameters using in-situ data as the shear-load vs displacement data is not available in an in-situ test. Also, the actual orientation of the discontinuity with the rock bolt in-situ is often not known. However, with the availability of new instrumentation technology which can provide a high-resolution plot of the in-situ strains on the rock bolt, it is possible to calibrate the rock bolt models to simulate the shear loading. In this work procedures for calculating the bolt-discontinuity angle and consequently calibrating the pile element in FLAC3D to simulate shear behaviour of rock bolt using in-situ data has been presented.

Fig. 2
figure 2

Pile structural element [modified from Tulu et al. (2012)]

Full size image

3 Discontinuity-Bolt Angle

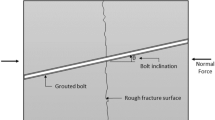
The effect of bolt inclination angle on the shear behaviour of rock joints has been studied by many researchers (Bjurstrom 1974; Haas 1981; Dight 1982; Pellet and Egger 1996; Grasselli 2005). Haas (1976) studied the effect of bolt inclination on shear behaviour using laboratory shear tests and found that the shear resistance of the joint increased with an increase in bolt inclination. Similar results were presented by Dight (1983) where the inclined bolts were found to be stiffer than perpendicular ones. Spang and Egger (1990) conducted laboratory and in-situ shear testing of fully grouted rock bolts and found that the inclination of the rock bolt affects the maximum shear resistance and shear displacement of the joint. The maximum shear resistance was found to increase with bolt inclination while the shear displacement reduced. Based on the laboratory and in-situ observations analytical models for shear behaviour of rock bolt also include the effect of bolt inclination. Pellet and Egger (1996) described an analytical model which showed a good correlation with laboratory tests for the effect of bolt inclination on shear resistance and displacement. Since then, a lot of research has been done in improving the analytical models for shear behaviour of rock bolts (Jalalifar and Aziz 2010; Lin et al. 2014; Li et al. 2015; Singh and Spearing 2021). Jessu, Kostecki et al. (2016) used optical instrumented rock bolts to compare the difference in strain profile of rock bolts at a different inclination to the discontinuity under shear loads. It was shown that the axial and bending strain profile of the rock bolt changes significantly with the inclination of the bolt. However, no method was proposed to calculate this inclination angle from the strain data. In this section, an analytical procedure is presented to determine the bolt-discontinuity angle from the instrumented rock bolt strain data based on the analytical model proposed by Singh and Spearing (2021).

3.1 Calculating the Discontinuity-Bolt Angle

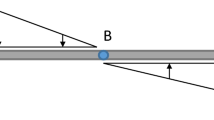
A rock bolt undergoes a combination of axial, shear and bending load as shear displacement takes place at the discontinuity. Axial load is induced in the rock bolt parallel to its axis due to change in its length. The bending load is caused by the curving of rock bolt as a result of the shear load acting perpendicular to the axis of the rock bolt. The rock bolt mechanical system described in the analytical model in Singh and Spearing (2021) is shown in Fig. 3. Q0 and N0 are the shear load and axial load at point O. A is the point of maximum bending strain and pu is the rock/grout reaction. According to the analytical model, the elastic axial strain in the rock bolt is dependent on the angle between the rock bolt and the discontinuity and the shear displacement of the bolt. The shear displacement of the bolt can be calculated from using the bending strain and La (active length) obtained from the instrumented rock bolt strain data. Once the shear displacement is known the angle between the rock bolt and the discontinuity can be back calculated from the axial strain obtained from the instrumented rock bolt strain data.

Fig. 3
figure 3

Rock bolt mechanical system (Singh and Spearing 2021)

Full size image

The shear load Qo can be calculated as:

$$ Q_{0} = \frac{{4\varepsilon_{b} EI_{z} }}{{D_{b} }} $$
(1)

where \(\varepsilon_{b}\) is the maximum bending strain at point A (measured from instrumented rock bolt), E is the young’s modulus of a bolt, Iz is the area moment of inertia along the z-axis of the bolt and Db is the bolt diameter.

The shear displacement uy is calculated as:

$$ u_{y} = \frac{1}{{EI_{z} }}\left( {\frac{{8Q_{0} l_{A}^{3} }}{3} - \frac{{133p_{u} l_{A}^{4} }}{360}} \right) $$
(2)

where lA is the length of section OA (measured from the instrumented rock bolt data), pu is the bearing capacity per unit length of the soil.

The value of pu before reaching maximum value is calculated as:

$$ p_{u} = \frac{{Q_{0} }}{{l_{A} }} $$
(3)

The maximum value for pu is given by:

$$ p_{u} = K\sigma_{c} D_{d} $$
(4)

where K is a load factor (K ≥ 1) and σcis the unconfined compressive strength (UCS) of rock.

The axial strain in the bolt at point O is given by (Ma, Zhao et al. 2019, Singh and Spearing 2021):

$$\varepsilon_{A} = \Delta_{ext} \frac{{\left( {1 + \frac{{\pi D_{b}K_{1} l_{A}^{2} }}{2EA}} \right)}}{{\left(2l_{A} + \frac{{\pi D_{b} K_{1}l_{A}^{3} }}{2EA}\right)}} $$
(5)
$$ \Delta_{ext} = \frac{{u_{y} \cos (\alpha - \theta )}}{\sin (\alpha )} $$
(6)
$$ \theta = \frac{1}{{EI_{z} }}\left( {\frac{{19p_{u} l_{A}^{3} }}{24} - 2Q_{o} l_{A}^{2} } \right) $$
(7)

where K1 is the stiffness of the bond-slip model in the elastic stage (Ma, Zhao et al. 2019), θ is the bolt deflection angle, A is the area of the bolt cross-section, α is the angle between bolt and discontinuity, and Δext is the axial extension in the bolt.

Using the Eqs. (5), (6) and (7) if the axial strain in the bolt is known α (angle between bolt and discontinuity) can be back calculated.

3.2 Validation of Discontinuity-Bolt Angle Calculation

Measurements from double shear lab tests and double shear numerical models are used to validate the method outlined in the above section. Results from two sets of double shear lab tests are used in the validation. The first set of results were taken from series of double shear tests done in this study with the rock bolt perpendicular to the discontinuity in two different strength concretes. The second set of lab test results were taken from the double shear tests presented in Jessu, Kostecki et al. (2016) and Kostecki (2019). These tests consist of two double shear tests, one with bolt perpendicular to discontinuity and the other with rock bolt at 80° to discontinuity. Due to the difficulty in testing rock bolt in double shear at a lower angle with discontinuity in a lab test, a numerical model of the double shear test is created and calibrated with the lab test results. The numerical model is then used to simulate the double shear tests at angles of 60° and 45°. The axial and bending strain profile of the rock bolt in each test is used to measure the parameters outlined in Sect. 3.1 and then the bolt-discontinuity angle is calculated for each case.

The analytical model for shear behaviour of rock bolt used in calculation of the discontinuity-bolt angle and rock bolt shear response does not consider the effect of normal displacement of grout-bolt interface due to rock bolt rib profile. The effect of gap in discontinuity is also not taken into account in the model. As the effect of these factors cannot be directly measured from the strain profile of the rock bolt, they are not considered in this work.

3.2.1 Double Shear Test

Six double shear tests were conducted on instrumented rock bolts embedded in concrete blocks with two different strength concrete. The concrete blocks were casted in wooden moulds of 30cmX30cmX30cm and a steel rod of 30 mm diameter was placed through the middle of the blocks to create the hole for grouting the bolt prior to pouring the concrete. The blocks were curing for 28 days before testing. After the concrete was completely set, the steel rod was removed, and the instrumented rock bolt was grouted in the hole through the middle of the blocks (Fig. 4). The ends of the rock bolt were kept unconstrained during the test. The grout was cured for 24 h, and the double shear test was conducted by applying a load on the middle block while the two side blocks were supported at their base. The instrumented bolt was connected to the interrogator and the strains on the rock bolt were recorded during the test (Fig. 5). The vertical displacement of the centre block and load applied on it was also recorded. An increasing load was applied until the concrete blocks failed. The properties of the concrete and rock bolt used in the test are given in Tables 1 and 2.

Fig. 4
figure 4

Double shear test schematic

Full size image
Fig. 5
figure 5

Double shear test—a Experiment setup b Instrumented bolt

Full size image
Table 1 Concrete and grout properties
Full size table
Table 2 Rock bolt properties
Full size table

The axial and bending strain plot for all the tests can be found in the Appendix Figs. 22, 23, 24, 25, 26, 27. The bending strain at point A, axial strain at point O and the length of the section OA can be measured from the strain plots.

3.2.2 Angled Shear Test

To increase the dataset for validation of bolt angle calculation, results from double shear tests conducted by Jessu, Kostecki et al. (2016) and Kostecki (2019) are also used. Jessu, Kostecki et al. (2016) and Kostecki (2019) conducted double shear tests on instrumented rock bolts installed at 90° and 80° to the discontinuity. The double shear tests were conducted in a similar manner to the test described in the previous section. The bolts were cast in concrete blocks and the centre block was loaded vertically keeping the side blocks fixed. The properties of concrete and rock-bolt used in the test are given in Table 3. The strain profiles of the bolt under double shear at 5 tonnes of load are shown in Fig. 6 and Fig. 7 for 90° and 80° bolt angles, respectively. A positive axial strain indicates extension and negative axial strain indicates compression. A positive bending strain indicates compression on the lower part of rock bolt and tension on top part and vice versa. From the strain plots it can be seen that the ratio of bending strain to the axial strain in the 90° bolt angle is higher than in the 80° bolt angle. This is consistent with the analytical model. The bending strain at point A, axial strain at point O and the length of the section OA are measured from the strain plots similar to the previous section.

Table 3 Concrete and rock bolt properties (Kostecki 2019)
Full size table
Fig. 6
figure 6

Strain profile 90° a Bending strain b Axial Strain

Full size image
Fig. 7
figure 7

Strain profile 80° a Bending strain b Axial Strain

Full size image

3.2.3 Numerical Modelling

As double shear tests with lower bolt-discontinuity angles are very difficult to conduct in a lab, numerical modelling is used to analyse the bolt strains under shear tests with bolt-discontinuity angles of 60° and 45°. A numerical model is created in Ansys (2019) with a bolt at 80° to the discontinuity (Fig. 8) and calibrated with the results of Jessu, Kostecki et al. (2016). The strain plots from the calibrated model compared with the lab results (at 2.5 tonnes load) are shown in Fig. 9. The calibrated material properties of the numerical model are shown in Table 4. Two new models were created with bolt-discontinuity angles of 60° and 45° using the calibrated material properties. The numerical models and the axial and bending strain plots for the two cases are shown in the Appendix Figs. 28, 29, 30, 31. The bending strain at point A, axial strain at point O and the length of the section OA are measured from the strain plots of the rock bolts.

Fig. 8
figure 8

Angled double shear model

Full size image
Fig. 9
figure 9

Calibration of angled double shear test a Bending strain b Axial Strain

Full size image
Table 4 Calibrated material properties for the angled shear test
Full size table

3.2.4 Validation with Laboratory and Numerical Modelling Results

Bolt-Discontinuity angles are calculated from the strain plots obtained from the laboratory and numerical models presented in the previous sections. The parameters calculated from the strain plots for each case are given in Table 5. Figure 10 compares the bolt-discontinuity angles calculated using Eqs. (1) to (7) for each case with the actual bolt-discontinuity angle. As can be seen from Fig. 10 the values of the angles calculated analytically, matches with the actual bolt-discontinuity angle.

Table 5 Parameters calculated from strain plots of shear tests and numerical models
Full size table
Fig. 10
figure 10

Validation of bolt angle calculation

Full size image

4 Calibration of Pile Element Parameters

The pile element used in FLAC3D to model rockbolts as discussed earlier uses springs to combine the interface interactions in a fully grouted rock bolt between bolt-grout and grout-rock. The parameters which define the behaviour of these springs need to be calibrated to simulate the real rock bolt behaviour. There are two springs—shear and normal which control the axial and shear behaviours of the pile element, respectively. The three parameters that define the spring properties are stiffness, cohesion and friction angle. The stiffness of the spring represents the deformability of the interface and the cohesion and friction angle control the strength of the interface. The parameters for the shear spring can be obtained using the load–displacement plot from in-situ pull testing of the rock bolt (Bin, Taiyue et al. 2012, Nemcik, Ma et al. 2014). Calibration of the normal spring parameters which control the shear behaviour of the pile element requires load–displacement data from an in-situ shear test of the rock bolt. However, no method is currently available to directly obtain the load–displacement data from in-situ testing. In this study, a method is proposed to derive the load–displacement plot for the shear loading of rock bolt from in-situ instrumented rock bolt data. The load–displacement plot can then be used to calibrate a rock bolt shear model in FLAC3D to obtain the pile’s normal spring parameters which can then be used in an in-situ model.

4.1 Load vs Displacement Plot

The load and displacement values can be calculated from the strain plots using the analytical model proposed by Singh and Spearing (2021). The analytical model gives a relationship between the bolt displacement, load and strains. The shear load on the rock bolt Q0 can be calculated using Eq. (1). The axial load N0 can be calculated as:

$$ N_{0} = \varepsilon_{A} EA $$
(8)

The displacement can be calculated using Eq. (2). The total displacement of the joint will be double the value obtained from Eq. (2). The total load can be calculated as:

$$ \begin{aligned} L &= (N_{0} \cos (\alpha - \theta ) + Q_{0} \sin (\alpha - \theta )) \\ & \quad + (N_{0} \sin (\alpha - \theta ) + Q_{0} \cos (\alpha - \theta ))\tan \phi \\ \end{aligned} $$
(9)

where φ is the joint friction angle.

4.2 Validation with Laboratory Double Shear Test

The above procedure is used to calculate the load–displacement plot from the strain plots of a double shear laboratory test with inclined bolt (Jessu, Kostecki et al. 2016) and compared with the actual load–displacement plot from the test. The test has been described in Sect. 3. The axial and bending strain plots at five different loads are shown in Fig. 11. The load and displacement are calculated using Eq. (2) and (9) as discussed in the previous section. The calculated load–displacement plot is compared with the measured load–displacement values in Fig. 12. As can be seen from the figure the calculated plot matches with the actual.

Fig. 11
figure 11

Strain plots 80° angled bolt a Bending strain b Axial strain

Full size image
Fig. 12
figure 12

Load—displacement: actual vs calculated

Full size image

5 In-Situ Modelling

In-situ rock bolt models need to be calibrated with actual in-situ observations before they can produce results useful for rock-bolt reinforcement design. In this study, optical instrumented rock bolts were installed in a hard rock mine and the recorded strain data from the instrumentation is used to calibrate an in-situ rock bolt model.

5.1 In-Situ Instrumented Rock Bolt Study

Six instrumented rock bolts were installed in a hard rock gold mine and the rock bolt strains were recorded over a period of 2 months. The instrumented rock bolts used a newly developed continuous Fibre Bragg grating (FBG) technology and the strain data from the bolts were recorded at a fixed interval of 30 min (Hoehn, Spearing et al. 2020). The location chosen for the installation of the instrumented rock bolt was a development heading in an inclined Room and Pillar mining area at a depth of approximately 627 m. The rock bolts were located adjacent to a pillar in an intersection as shown in Fig. 13. The instrumented rock bolts were installed as secondary supports. The specifications of the rock bolts used in the test are given in Table 6. The position of the rock bolts and their orientation is shown in Fig. 14.

Fig. 13
figure 13

Rock bolt installation location

Full size image
Table 6 Instrumented rock bolt properties
Full size table
Fig. 14
figure 14

Instrumented rock bolt installation a position and direction of inclination b orientation with roof

Full size image

As the instrumented rock bolts were un-tensioned it was expected that they will undergo an increasing load as the development proceeded in the adjacent headings. While the strain on the rock bolt was recorded continuously, the rock bolts only showed an increase in load when the excavation progressed. Therefore, in this study three mining stages have been identified where the rock bolts showed a significant change in strain magnitudes. The excavation stages are shown in Fig. 15.

Fig. 15
figure 15

Excavation stages with significant strain increases in instrumented rock bolts

Full size image

The strain data obtained from the rock bolts was processed to calculate the axial and bending strain plots at each of the three excavation stages. To calculate bending strain and directions on the rock bolt strain values from at least three of the four fibres are required. Due to installation errors and later due to mining activity some of the fibres were damaged on one of the rock bolts. Complete strain profiles from only five of the rock bolts were obtained at the end of the test. The axial and bending strain profile of the bolts at the three stages of excavation are given in Appendix Figs. 32, 33. The rock bolts do not show much increase in axial loading as the excavation progressed. This can be attributed to the fact that the bolts were installed as secondary supports and were un-tensioned. Also, the rock in the mine is very competent and has high strength and elastic modulus therefore the rock behaviour is mostly dominated by structures in the rock mass. Bolts 7 and 10 show a significant bending loading which increases with the mining progress Figs. 16 and 17. In the axial and bending profile of the rock bolts, a bending point can be seen about 0.75 m from the bolt head. This strain profile indicates the presence of a discontinuity that intersects the bolts. The axial strains on the rock bolts can also be attributed to the discontinuity as the load is concentrated at the bending point. As can be seen from the strain profiles in Figs. 16 and 17, the new instrumented rock bolt technology can provide a very high-resolution detail of the strains on the complete length of the rock bolt. This data can be used to calibrate the numerical models for in-situ rock bolt reinforcement design as shown in the section below. Since bending was observed only in bolt 7 and 10, these two bolts will be used to calibrate the rock bolt model for shear loading.

Fig. 16
figure 16

Strain profile bolt 7 a Bending strain b Axial strain

Full size image
Fig. 17
figure 17

Strain profile bolt 10 a Bending strain b Axial strain

Full size image

5.2 Calibration of the Numerical Model with In-Situ Data

Numerical modelling of the in-situ rock bolt reinforcement was done using FLAC3D. A three-dimensional model of the excavation was created with the excavation stages progressing according to the actual mining progress. The model boundaries dimensions are 60mX60mX40m. The development headings are 3mX2m and the Pillars are 3.5mX2m. The grid size is 0.5mX0.5mX0.5 m in the pillars and 0.5mX0.5mX0.2 m in the roof close to the excavation. The 3D model of the excavation is shown in Fig. 18. The model’s sides were constrained using roller boundary and the base was constrained using a fixed boundary. A load equivalent to the vertical stress was applied at the top boundary of the model. The rock properties, the prominent discontinuity data and the in-situ stress data obtained from the mine are given in Tables 7, 8, 9. The in-situ stresses were rotated to the direction of the coordinate system of the model and applied using the in-built stress initialization command of FLAC3D. The Mohr–Coulomb constitutive model was used for the rock because the rockmass in the area behaved basically elestically.

Fig. 18
figure 18

FLAC3D in-situ model

Full size image
Table 7 Rock properties
Full size table
Table 8 Major structures
Full size table
Table 9 In-situ stress state
Full size table
Table 10 In-situ discontinuity orientation calculation
Full size table

As seen from the in-situ data the major strain identified on the rock bolts was bending due to the presence of a shearing discontinuity. Therefore, the focus was to calibrate the model to the shear behaviour of the rock bolts observed in-situ. The calibration process can be divided into two parts—discontinuity and rock bolt properties. The location and orientation of the discontinuity are calculated using the method detailed in Sect. 3.1. The parameters calculated from the strain plots and angles calculated for Bolt 7 and 10 are given in Table 10. From the bolt-discontinuity angle calculated in Table 10, the orientation of the discontinuity can be derived by considering the orientation of the rock bolts with respect to excavation. From the prominent structure data in Table 8, the joint set with 51° dip and 259° strike matches closest with the calculated discontinuity orientation (Fig. 19). The discontinuity properties are estimated from joint data in Table 8 and joint properties for similar rock type from Bandis, Lumsden et al. (1983), Hoek, Kaiser et al. (1995), Sitharam, Maji et al. (2007). The joint was modelled as an interface and the location was adjusted to match the location of the bending point on the rock bolts. Joint properties used in the model are given in Table 11.

Fig. 19
figure 19

Model showing the instrumented rock bolts and the structure

Full size image
Table 11 Structure interface properties
Full size table

The model is first run without any excavations to initiate the in-situ stresses in the rocks. Then the excavation is made in stages as shown above in Fig. 15. The primary rock bolt reinforcement in the mine consisted of 1.8 m bolts installed at a 1m × 1.5 m spacing. These bolts are installed in the model as soon as the excavation stage is progressed. The instrumented bolts were installed as secondary supports. The strain developed on these bolts is measured at end of each excavation stage and the procedure outlined in Sect. 4 is used to calibrate the pile element’s parameters. The rock bolt properties and calibrated parameters are given in Table 12. The strain plots of bolts 7 and 10 in the numerical model are compared with the strain plots measured from in-situ instrumented bolts in Figs. 20 and 21. As can be seen from the plots the strain in the rock bolt numerical model matches closely with the in-situ measured strains.

Table 12 Calibrated Pile element parameter
Full size table
Fig. 20
figure 20

Calibrated bolt 7 model vs in-situ a Bending strain b Axial strain

Full size image
Fig. 21
figure 21

Calibrated bolt 10 model vs in-situ a Bending strain b Axial strain

Full size image

6 Conclusions

Optical instrumented rock bolts have been used to study rock bolt behaviour under shear loading in laboratory test and in in-situ. In this paper analytical methods have been proposed to process the strain data from instrumented rock bolts. Bolt-discontinuity angle has been calculated using strain data and the FLAC3D pile element parameters have been calibrated to model the shear behaviour of rock bolt. The results have been validated with laboratory tests and numerical modelling. To demonstrate the methods outlined in the work an in-situ rock bolt model is created in FLAC3D and calibrated with the data from in-situ instrumented rock bolts. The following conclusions can be made from the work done in this paper.

  1. 1.

    New optical instrumented rock bolts provide a very high-resolution strain profile of the rock bolt installed in-situ. This is especially important in the case of a localised loading of rock bolt such as produced by a discontinuity. The instrumentation is capable of capturing the bending strain of the rock bolt due to the shear loading from a discontinuity. The bending strain data can be used for identifying structures and determining their orientation in the rock mass.

  2. 2.

    The strain data from instrumented rock bolt can be used to calculate the load–displacement plot for a rock bolt undergoing shear loading in-situ. This plot can be used to calibrate the shear behaviour of an in-situ rock bolt model. This calibration process provides a better representation of rock bolt’s in-situ behaviour compared to the existing method of calibrating the rock bolt model with laboratory shear tests where it is difficult to reproduce the exact in-situ conditions. The calibrated rock bolt model can then be used for designing rock bolt reinforcement for underground excavations using numerical modelling.