State-of-the-art on the anchorage performance of rock bolts subjected to shear load

Abstract

Rock bolts are extensively utilized in underground engineering as a means of offering support and stability to rock masses in tunnels, mines, and other underground structures. In environments of high ground stress, faults or weak zones can frequently arise in rock formations, presenting a significant challenge for engineering and potentially leading to underground engineering collapse. Rock bolts serve as a crucial structural element for the transmission of tensile stress and are capable of withstanding shear loads to prevent sliding of weak zones within rock mass. Therefore, a complete understanding of the behavior of rock bolts subjected to shear loads is essential. This paper presents a state-of-the-art review of the research progress of rock bolts subjected to shear load in three categories: experiment, numerical simulation, and analytical model. The review focuses on the research studies and developments in this area since the 1970s, providing a comprehensive overview of numerous factors that influence the anchorage performance of rock bolts. These factors include the diameter and angle of the rock bolt installation, rock strength, grouting material, bolt material, borehole diameter, rock bolt preload, normal stress, joint surface roughness and joint expansion angle. The paper reviews the improvement of mechanical parameter setting in numerical simulation of rock bolt shear. Furthermore, it delves into the optimization of the analytical model concerning rock bolt shear theory, approached from the perspectives of both Elastic foundation beam theory coupled with Elastoplasticity theory and Structural mechanic methods. The significance of this review lies in its ability to provide insights into the mechanical behavior of rock bolts. The paper also highlights the limitations of current research and guidelines for further research of rock bolts.

1 Introduction

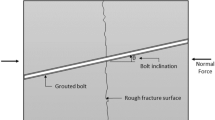
Modern engineering construction frequently necessitates some form of support, particularly for projects such as underground space development and foundation excavation where the role of support is crucial for ensuring project safety. The non-homogeneity and anisotropy of rock and soil materials often make evaluating project safety and quality a challenging task. In underground rock engineering, the extremely ground stress can cause the rock to appear weak at structural surfaces or joint fracture zones, leading to rock body sliding along these weakened areas, ultimately jeopardizing the safety of underground engineering, as shown in Fig. 1. Therefore, the construction of underground engineering often requires support, and rock bolts, being one of the primary cost-effective support methods, are extensively employed in underground space development projects and slope support projects.

Fig. 1

Application of rock bolt in underground construction. a Rock bolt support b Rock bolt subjected to shear load c Rock bolt failure under tensile and shear loading (Li 2010)

Although rock bolt support can significantly enhance the safety of structures, determining the specific contribution of rock bolts to the stability of rock masses is a challenging task. The mechanical properties and behavior of rock bolts are exceedingly complex due to their frequent exposure to multiple material media when acting on the rock structure, especially when resisting rock shear along a weak structural surface or jointed surface. When the rock mass exhibits shear or shear slip along such surfaces, lower-strength material can frequently suffer damage due to the strength differential between the materials, for example, rock-bolt grouting material appears as a broken segment due to rock bolt extrusion. It makes the analysis of the relationship between the broken media and the rock bolt more complicated.

Numerous scholars have investigated the mechanical properties and mechanism of rock bolts during rock shear to address these challenges. Since Bjurstrom first reported the shear test of rock bolts in 1974, scholars have focused on three primary aspects of rock bolt shear: rock bolt shear test, numerical simulation of rock bolt shear, and analytical models of rock bolt shear theory (Bjurstrom 1974). This paper will first present the progress and research findings of rock bolt shear tests, followed by a discussion of the role of numerical simulation in understanding the mechanical mechanism and properties of rock bolt shear. Finally, it will summarize the fundamental principles and assumptions of the analytical models of rock bolt shear proposed by scholars and analyze the unique features of each analytical model. In this paper, the limitations of the current research on rock bolt shear will be discussed in terms of experimental, numerical simulation and analytical models. Furthermore, the guidelines and the need for further reliable and accurate research will be discussed.

2 Overview of experiment in rock bolt shearing

In civil and mining engineering, tests are often the most direct and effective means to study the mechanical properties and mechanisms of materials or structures. Rock bolt shear tests are no exception and have been extensively used to investigate the shear mechanism and mechanical properties of rock bolts for engineering guidance. So far, a large number of rock bolt shear tests have been conducted under different conditions, leading to a clearer understanding of the mechanical mechanism and properties of rock bolts.

Based on the number of shear surfaces, rock bolt shear tests can be divided into two categories: single-shear test (involving a single shear surface, such as straight shear and single shear tests) and double-shear tests (with two shear surfaces). Typically, the single-shear test involves only two bolt-rock bolted blocks sliding relative to each other along the shear surface, as shown in Fig. 2, while the double-shear test involves three rock bolt-rock bolted blocks arranged side by side, with a load applied to the middle block to simulate the shear effect, as shown in Fig. 3.

Fig. 2

Schematic diagram of single shear test

Fig. 3

Schematic diagram of double shear test

In this section, the development of the rock bolt shear test since the 1970s is described, focusing on the progress of single-shear tests and double-shear tests. The pioneering elements and limitations of the representative studies are briefly analyzed.

2.1 Single shear test

Bjurstrom (1974) was the first to report that in rock bolt shear tests conducted on granite specimens reinforced with fully grouted steel rock bolts, the rock bolts failed in tension as shear developed when the angle was less than 35°. Moreover, he concluded that the shear effect of rock bolts is composed of three primary components: reinforcement effect, pin effect and friction effect of the rock bolting medium at the joints (Bjurstrom 1974). Based on Bjurstrom’s research conclusions, Hass (1976, 1981) conducted shear tests on limestone or schist blocks reinforced with resin grouted rock bolts as depicted in Fig. 4. The research findings indicated that rock bolts inclined to the shear plane were stiffer than those perpendicular to the shear plane and contributed significantly to the strength. Furthermore, the normal stress did not affect the rock bolt resistance in the shear plane.

Fig. 4

Arrangement for bolt shear testing (Haas 1981)

However, the expansion of nodal due to normal stress affects the stiffness of the rock mass rock bolted by the rock bolt. Additionally, rock bolts tilted at an acute angle to the shear plane have better performance than those tilted in the opposite direction. The overall shear strength of rock bolts for rock reinforcement is determined by adding the rock bolt contribution and the frictional strength along the shear plane. This was confirmed in Azurr’s study (Azuar 1977).In addition, dilatancy increases the bolted joint's resistance to shear displacement. In a study by Dight (1982), several different materials were used to construct rock bolts, including gypsum, basalt and steel. The effect of joint expansion was comparable to the effect of rock bolt tilting, and the rock bolts deformed due to shear. The length of deformation is related to the deformation capacity of the rock, and there is a difference in shear resistance of fully grouted rock bolts and the pin effect of point rock bolts.

Egger and Zabuski (1993) discovered that the optimal tilt angle of the rock bolt relative to the nodal surface was between 30° and 60°. Furthermore, the minimal shear displacement for rock bolt failure occurred when the rock bolt inclination angle is between 40° and 50° while providing shear resistance perpendicular to the shear surface. In a study on slope stability, Sharma and Pande (1989) found that the stress path method yields an optimal reinforcement angle in the direction normal to the joint direction for fully grouted passive reinforcement in a jointed rock mass. Meanwhile, Yoshinaka et al. (1987) suggested an angle of 35°–55° with respect to the joint plane as the most favorable. Schubert (1984) performed shear tests on concrete and limestone blocks attached to rock bolts, as illustrated in Fig. 5. The deformation capacity of the surrounding rock was found to have a significant impact on rock bolt response, and hard rock-embedded bolts required relatively less displacement to achieve a certain shear resistance compared to soft rock embedded rock bolts. and not only that, but soft steel also improves the deformation capacity of bolting system in soft rock.

Fig. 5

Shear test device (Schubert 1984)

In a series of laboratory and field tests on rock bolts with sandstone, concrete and granite grouting, Spang and Egger (1990) found that:

• (1) Increasing the cross-section of rock bolt results in a linear increase in the maximum shear force, while the shear displacement at maximum load is directly proportional to the diameter of the rock bolt. Additionally, larger-diameter rock bolts require less displacement to achieve a given shear force.

• (2) Friction angle of the shear surface is crucial in determining the behavior of the rock bolt connection, as it affects the shear strength and stiffness of the connection. In the case of frictionless joints, the maximum shear resistance amounts to 80% of the maximum tensile loads, and the friction angle has no impact on displacement.

• (3) Rock bolt joints have higher shear capacity in soft rocks, but may cut into the rock.

• (4) Tilted rock bolts exhibit greater strength compared to vertical rock bolts, with their maximum shear strength increasing alongside the tilt angle. Similarly, their shear displacement also rises with the tilt angle.

Egger and Zabuski (1993) conducted a shear test on small-diameter rock bolts and found that the rock bolts failed due to shear and axial forces. However, this test did not consider normal pressure and pre-stress, and its applicability was limited to low-strength steels since the load distribution in the shear plane was neither uniform nor balanced during the test.

Ferrero (1995) conducted tests to verify the effect of different reinforcement and rock properties, as shown in Fig. 6. The results showed that ductile reinforcement and soft rock produced the maximum shear strength, while harder rock produced greater shear stress in the shear plane of the reinforcement, resulting in a decrease in overall shear strength. The application of pre-stress to the rock bolt only affects the stress–strain behavior of the reinforcement near the shear surface and does not affect the overall shear strength. Ferrero also proposed two damage mechanisms for rock bolts: one resulting from shear and tensile stresses within the shear face, and the other arising from tensile stresses and bending moments.

Fig. 6

Laboratory test device (Ferrero 1995)

Afterward, Goris et al. (1996) conducted single shear tests on cable bolt and found that these tests produced higher shear resistance due to the uneven distribution of stresses on the shear surface and the concentrated loading through the block in front of the rock bolt cable, which pulled the two together. McHugh and Signer (1999) studied the behavior of 17 mine cavern top rock bolts under a range of axial rock bolt loads. The study found that axial load has little effect on rock bolt shear load resistance, as there is a weak correlation between yield strength and axial load. However, the ultimate shear strength remains unaffected. Both shear face separation and plastic failure of the grout material propagate the bending force along the rock bolt to a greater distance.

Over the past decade, researchers have delved deeper into the study of rock bolt shear to adapt to the development of engineering construction. Experiments were used to investigate the deformation and force characteristics of rock masses of varying strengths under shear force, as well as the shear deformation law of rock masses before and after bolted reinforcement. The effects of rock strength, prestressing, and anchoring method on shear capacity of joints were investigated.

The mechanism of axial force analysis and the deformation characteristics of the rock bolt during joint shear were investigated (Zhang and Liu 2014). Chen and Li (2015a, b) developed a novel rock bolt shear test method to evaluate the effect of different displacement angles, surrounding rock materials and joint gaps on rock bolt shear, which explains the shear mechanical properties of the D-Bolt and rebar rock bolts in the experimental results. The experimental setup is shown in Fig. 7.

Fig. 7

The NTNU/SINTEF bolt test rig used for the test (Chen and Li 2015a, 2015b)

Srivastava and Singh established the relationship between factors influencing the shear strength of rock bolts with different area ratios and spacing ratios by large-scale direct shear experiments and found that exceeding a certain threshold of installed rock bolts increased the ductility of the rock connection (Srivastava et al. 2019). Forbes et al. (2017) used a new optical strain sensing technique to monitor the strain curve of fully grouted rock bolts with a spatial resolution of 0.65 mm.

Chen et al. (2018) found that the peak shear strength (PSS) and residual shear strength (RSS) of rock bolt joint specimens had different degrees of increase compared with non-rock bolt joint specimens, and the equivalent cohesion increase rate increased with the roughness. Liu et al. (2018) proposed the concept of equivalent shear area of the joint surface with rock bolt, and verified that the shear strength of the joint surface considering the equivalent shear area is more consistent with reality by tests under different dip angles, surrounding rock strength, anchor diameter and normal stress of the joint surface.

Joint roughness can usually be measured in terms of JRC values and can effectively influence the shear behavior of the joint's surface, as demonstrated in a series of shear tests of rock-anchored rock masses with different JRC values by Wu et al. (2018b). Li and Liu (2019) found that the rock bolt contribution increased and then decreased with the increase of rock bolt installation angle, following a parabolic relationship. They suggested that to maximize the rock bolt contribution, the rock bolt installation angle should be 40°–50° relative to the joint surface angle.

Pinazzi et al. (2020, 2021) evaluated the effect of initial shear displacement on axial bearing capacity and displacement, as well as the effect of axial displacement on shear bearing capacity, to provide a reference for the design of anchor reinforcement in rock masses with and without gaps. Ding et al. (2017, 2021) found that the thickness of weak interlayer, uniaxial compressive strength and inclination angle have a significant weakening effect on the peak strength and elastic modulus of the samples with a single free face. Moreover, these factors greatly affected the crack distribution and damage mode of the specimens using an in-house developed experimental system. He et al. (2022a, b) investigated the shear performance of rock masses connected by quasi-NPR steel rock bolts under different normal stresses.

With the continuous advancement of test equipment, some researchers study the effect of interfacial shear during a shear from a microscopic perspective. Zhang et al. (2020a) investigated the effects of bolt profile and grout mixture on mechanical behavior and failure modes under constant normal load conditions in his research on the shearing behavior and failure mechanism of bolt-grout interfaces. The results demonstrated that it is possible to optimize bolt performance, with peak shear strength and deformation capacity being highly dependent on bolt profile and grout mixture. The “sheared-crush” failure mode was proposed, which is characterized by progressive crush failure of grout asperities between steel ribs during shearing. Zhang et al. (2020a) also investigated the effect of boundary conditions on the shear behavior of the bolt-grout interface, discovering that initial normal stress and stiffness have a significant influence on the shear behavior of the interface. The results of the tests also revealed a relationship between acoustic emission parameters and shear stress curves (Zhang et al. 2020b).

Zhang et al. (2022) investigated the bolt effect of rock bolts under trapezoidal fracture by straight shear test, focusing on and comparing two types of rock bolts: energy-absorbing (EA) rock bolts and conventional steel (CR) rock bolts. They explored in-depth the shear damage structure of en-echelon fracture and the deformation mechanism of rock bolts, discussing and evaluating the prediction of rock bolt fracture displacement and the rock bolt contribution values. Thus, the aforementioned studies provide valuable insights into the complex mechanics of rock bolt subjected to shear load in different geological settings. The conclusions are as follows, which are somewhat more informative.

• (1) The shearing process of trapezoidal fracture can be divided into two stages: the cracking stage (stage 1) and the shear-slip stage (stage 2).

• (2) Rock bolts have been shown to enhance the shear strength of trapezoidal fracture.

• (3) Both energy-absorbing rock bolts and conventional steel rock bolts exhibit significant expansion inhibition effect.

• (4) En-echelon fracture shows three different shear damage structures, which account for the varying rock bolt deformation mechanisms observed.

• (5) The deformation factor can be employed to characterize the deformation properties of the rock bolt and predict rock bolt fracture displacement.

With the development of deep ground engineering construction, the dynamic effects encountered in the engineering have become more and more significant, and some scholars began to focus on analyzing the process of rock bolt from the perspective of dynamic response. Wang et al. (2018) studied shear properties, damage, mechanism, and acoustic emission of bolted joints with varying roughness and anchorage. The findings of their study serve as a valuable reference for static shear damage investigations. Wu et al. (2018a, 2019a) investigated cyclic shear properties of energy-absorbing and encapsulated rock bolts. They introduced the shear energy loss rate (SELR) to evaluate energy-absorbing rock bolt behavior. Results show superior cyclic shear performance for energy-absorbing bolts compared to encapsulated ones. The Joint Roughness Coefficient (JRC) was identified as a significant factor affecting the performance of joints and bolts under cyclic shear, with higher JRC values providing greater resistance to shear deformation (Wu et al. 2023).

To adapt to the engineering environment under high ground stress, Wu invented a new yielding rock bolt that can accommodate large deformation and displacement of the rock mass (Wu et al. 2019b). Kang developed an experimental device to evaluate the mechanical behavior of rock bolts under complex loading conditions, including pre-tension, tension, torsion, bending, shear, and impact (Kang et al. 2020). Li analyzed the stress, deformation, acoustic emission and rock damage phenomena of rock bolts in direct shear tests. The study compared the shear damage characteristics of granite nodal surfaces for reinforcement and reinforced rock bolts to explain the effect of reinforced rock bolts on the dynamic damage of hard rock structural surfaces from the perspective of dynamic loading (Li et al. 2023).

2.2 Double-shear test

In addition to conducting single-shear tests, scholars led by Aziz have also carried out double-shear tests on rock bolts to gain a deeper understanding of the shear mechanism and the contribution of rock bolt support (Aziz et al. 2003, 2005; Jalalifar et al. 2004, 2005, 2006a, 2006b; Jalalifar and Aziz 2010a, b). This method provides an effective means of evaluating the effectiveness of multilevel reinforcement rock bolts in engineering applications. A series of tests were conducted on fully grouted rock bolts installed in two different types of three concrete blocks, as shown in Fig. 8, with and without preload applied to the rock bolts in shear. The aim was to evaluate the effect of the thickness of the grout resin on the shear strength of the rock bolts and the rock bolt-grout-concrete interaction. The strength of the surrounding concrete is more important than the strength of the grout thickness in terms of shear strength and shear displacement when the rock bolt is loaded laterally. When the resin thickness increases slightly, it was observed that (Aziz et al. 2003, 2005):

• (1) The rock bolt tensile and compressive strains decrease slightly.

• (2) The shear displacement decreases

• (3) The plastic strain within the grout perpendicular to the rock bolt axis decreases.

• (4) The concrete interface along the rock bolt axis has a slight decrease in compressive and tensile strains.

Fig. 8

Instron testing machine by Aziz et al. (2003)

Grasselli (2005) conducted a large-scale (1:1) double-shear test on concrete blocks reinforced with fully grouted rock bolts and Swellex rock bolts. The test demonstrated the difference in deformation of these two rock bolts and their different mechanical response to shear loading. Swellex rock bolts, due to their unique hollow design and lack of grouting, can be operated differently, unlike the fully grouted rock bolts that fail due to traction between the two plastic hinge points.

Based on these findings, Jalalifar et al. (2005, 2006b) performed double-shear tests on fully grouted rock bolts to assess load transfer capacity and failure mechanisms. Results showed that preload loads influenced shear displacements within the elastic range and post-yielding. The strength of the material affected the distances of hinge points, while preload exhibited minimal impact. Aziz and Jalalifar (2007) studied the shear behavior of vertically installed rock bolts under two shear surfaces. The results showed that the shape design of the rock bolt has a significant influence on the load transfer capacity between the rock bolt, resin and rock (Jalalifar et al. 2006a). Additionally, the strength of the concrete has a significant influence on the shear bearing capacity and shear deformation. In most cases, the higher the initial preload, the higher the shear load at the maximum frictional bond strength limit.

Further, in-depth studies by Jalalifar, the following results were found (Jalalifar and Aziz 2010a, b).

• (1) The location of the hinge point from the shear connection plane is influenced by the strength of the surrounding medium and the applied axial force. For rock bolts with higher axial loads, the location of the hinge point is smaller than for rock bolts with lower axial loads, and the distance of the hinge point increases in weaker media.

• (2) The distance of the hinge point from the shear plane increases with an increase in the rock bolt diameter, and this increase varies with the strength of the surrounding medium.

• (3) When the rock bolt is in a plastic state, the distance between the hinge point and the shear connection surface increases.

• (4) The deflection of the composite bolt concrete is higher in weaker media for a given vertical load.

• (5) In general, the shear load of rock bolt increases with an increase in the rock bolt shaft force.

• (6) The contribution of the rock bolt depends on the maximum tensile strength of the rock bolt and the concrete strength.

In recent years, numerous scholars have studied the shear performance of rock bolts with different materials and different structural combinations. Li et al. (2016b) developed a double-shear testing apparatus capable of evaluating the difference in behavior of rock support systems both individually and in combination. The system included rock bolts, shotcrete and thin shotcrete lining (TSL). The researchers discovered that shotcrete and TSL enhanced energy absorption, whilst the use of shotcrete increased the initial stiffness of the combined support system. Furthermore, TSL increased the cohesiveness of the shotcrete and improved the shear resistance. In another study, Li et al. (2016c) compared the shear behavior of glass fiber (FG), rock (reinforcement), and cable rock bolts via tests to determine their contribution to the shear strength of the rock bolt concrete surface and their damage modes.

Table 1 shows the comparison of rock bolt shear tests by different scholars.

Table 1 Comparison of the tests on the shear behavior

2.3 Bolt material

The mechanical properties of different material are distinctly different. Consequently, the shear performance of bolts is significantly influenced by their substance. This review discusses common threaded steel rock bolts that are widely used in engineering due to their cost-effectiveness and efficiency.Three kinds of steel rock bolts were used for testing reinforced joint resistance failure mechanism by Ferrero in order to compare experimental and theoretical analysis results (Ferrero 1995). Aziz conducted double shear tests on three types of bolts, namely AX, AXR, and JAB, which are commonly used in Australia, to assess their performance (Aziz et al. 2003). Additionally, the mechanical behavior of Swellex was investigated by Grasselli (Grasselli 2005). Jalarifar compared the mechanical behavior between high-strength steel (T1, T2, T3) and low-strength steel (T4, T5) rock bolts under different strength concrete by double shear test (Jalalifar and Aziz 2010b). Chen and Li evaluated the anchorage performance of the D-Bolt under pull-and-shear loads. The results reveal that the range of yielding of the D-Bolt is larger than that of rebar bolt when subjected to pure shear (Chen 2014; Chen and Li 2015a, b). Li assessed the contribution of different bolt types (fiber glass bolt, rock bolt/steel rebar bolt, and cable bolt) to the shear strength of bolted concrete surfaces, revealing that rock bolts contribute the most, followed by cable bolts, and fiber glass bolts contribute the least (Li et al. 2016c). In recent years, there has been a significant increase in the use of engineering components made of negative Poisson's materials due to their growing importance. Micro-Negative Poisson’s Ratio (NPR) steel, a novel bolt material with high strength, high toughness, and exceptional energy absorption capabilities, provides a well-balanced combination of strength and ductility. This allows for substantial deformation and superior energy absorption in the bolt material (He et al. 2022a, b).

3 Overview of numerical simulation in rock bolt shearing

Due to the limitation of physical coupling for multi-media involved in the shear behavior of rock bolt, numerical simulation is an effective way to study rock bolt shear performance. Numerical simulation can provide a reasonable explanation and visualize the reasons for the test results. Therefore, many scholars have combined numerical simulation to verify their test results when studying the mechanical behavior and effects of rock bolt reinforcement.

3.1 Numerical simulation of rock bolt shear

The application of numerical simulation technology in civil and mining engineering has not stopped with the development of computer performance. Hibino and Motojima (1981) applied the two-dimensional finite element method to calculate the stress changes in rock foundation, as shown in Fig. 9. The rock bolts were pre-stretched, and it was found that uniformly distributed compressive strain caused by pre-stress appeared at the joint surface of rock joints.

Fig. 9

Stress distribution due to prestress of the rock bolt, rock bolt ABC and fixing parts BC (Hibino and Motojima 1981)

In the 1990s, due to the improvement of computer arithmetic power, Spang and Egger (1990) used the three-dimensional finite element method to conduct a numerical simulation of rock bolt shear and quantitatively analyzed the shear test of rock masses reinforced by rock bolts, as shown in Fig. 10. The numerical simulation was based on the ADINA code implemented at the Swiss Federal Institute of Technology. The following observations were made based on the simulations:

• (1) Rock bolt bending becomes dominant as the shear force increases. Two hinges appear, but the increase in shear stress has little effect on the stress at the hinge points.

• (2) Rock bolt damage may occur at the point of plastic hinge bending or under the combined action of shear and tension near the shear plane.

• (3) The bending and yielding of rock bolts is the key to achieving shear resistance.

• (4) The increase in shear load leads to an increase in stress, especially near the shear surface.

• (5) Inclined rock bolts can mobilize considerable shear resistance without bending compared to vertical rock bolts, and the maximum deformation and plastic deformation degree is significantly less than that of vertical rock bolts.

Fig. 10

Three-dimensional representation of the model (Spang and Egger 1990)

In 1995, Ferrero (1995) developed a numerical model to evaluate the shear strength at rock joints reinforced by rock bolts. It was found that both plastic hinges in the rock and concrete specimens reached full plasticization, and the flexible loading of the concrete specimen was so pronounced that two symmetrical plastic hinges about the shear surface appeared even when very low shear loads were applied. At higher shear loads, the concrete stress state between the two hinges in the specimen remains almost constant while the shear stress in the rock specimen increases. Jalalifar et al. (2004) developed a three-dimensional numerical model based on ANSYS software was developed to simulate the nodal plane shear test for rock bolt reinforcement. The model was developed to better explain the role of rockbolt pre-tensioning in shear joints and bedding plane reinforcement. The following observations were made:

• (1) The increase in rock bolt preload leads to an increase in the axial tensile stress of the rock bolt.

• (2) An increase in restraint pressure decreases the deflection of the rock bolt.

• (3) An increase in shear force is accompanied by an increase in shear surface contact pressure. However, as the pretension increases, the contact pressure decreases.

• (4) Induced stresses are generated in the concrete block, leading to fracture and failure of the rock bolt.

On this basis, Jalalifar and Aziz et al. also studied the effect of resin thickness on rock bolt stress, strain and displacement under rock bolt reinforcement, as well as the mechanical response of the rock bolt and grout during shear (Aziz et al. 2005; Jalalifar et al. 2005). Jalalifar et al. set up a simulated loading under progressive vertical load with a series of rock bolt tensile loads and concrete strengths, and the results were analyzed for linear and nonlinear regions of load–deflection behavior (Jalalifar et al. 2006a, b; Jalalifar and Aziz 2010b). Grasselli (2005) conducted shear tests using a commercial three-dimensional finite element (FEM) code (ZSOIL_3D^®) to better understand the deformation mechanisms of grouted rock bolts and Swellex rock bolts, and to compare the two types of rock bolts. Besides, Aziz and Jalalifar (2007) simulated the induced stresses and strains along the rock bolt under shear.

Song et al. (2010) developed a rock bolt double-shear model to study the shear behavior of rock bolts and the effect of rock bolt diameter on deformation and strain. Based on the previous work, Li et al. (2016a) simulated the rock bolt double-shear test by FLAC3D, considering the effects of rock bolt strength, inclination and diameter on the ultimate shear capacity of the system, as shown in Fig. 11. Bahrani and Hadjigeorgiou (2017) investigated the mechanical properties of fully grouted anchors with universal distinct element code (UDEC) in a discontinuous stress analysis model for local and global reinforcement in pure tension and pure shear, focusing on the different loading phases of the calibration force–displacement curve, including initial elastic response, hardening behavior, and anchor fracture.

Fig. 11

A quarter section of DST model with block/grout/rock bolt. a Horizontal rockbolt installation b 45° inclined rockbolt installation (Li et al. 2016a)

With the continuous improvement of computer performance, numerical simulation studies of rock bolt shear modes are becoming refined. Singh et al. (2020) calibrate the ANSYS numerical model using the double-shear test data and studied the stress state of rock bolts at different concrete strengths, comparing it with the analytical model proposed by Pellet and Egger, as show in Fig. 12 (Pellet and Egger 1996; Kostecki 2019). The proposed analytical model found that the yielding and damage behavior of rock bolts in high-strength concrete is determined by shear stresses rather than the bending and tensile stresses predicted in the analytical model. Based on this finding, Singh et al. (2020) also used the FLAC3D code to modify the pile foundation structural units by considering the unit transverse shear strain to simulate the correct response of rock bolts under shear in order to further investigate the shear of rock bolts in high-strength concrete, as shown in Fig. 13. The modified model was compared with the experimental results from McHugh and Signer (1999) for verification.

Fig. 12

Rock bolt double shear numerical model by ANSYS (Singh et al. 2020)

Fig. 13

Rock bolt double shear numerical model by FLAC3D (Singh et al. 2020)

Saadat and Taheri (2020) conducted research on the mechanical performance of fully grouted rock bolts using a new cohesive contact model in distinct element codes (PFC2D). The study successfully predicted grout failure and the bolt-grout interface’s shear response, and developed a novel numerical stepwise pull-and-shear test scheme to analyze the mechanical behavior of bolted rock joints under simultaneous pull-shear loading. The research also assessed the influence of pretension stress, bolt profile rig angle, and constant normal stiffness condition on the shear strength of bolted rock joints, highlighting their sensitivity to various factors. Liu et al. (2022) used FLAC3D to simulate rock bolts reinforced with rock under compression-shear loading to test the elastic solution based on the Lame solution and the radial deformation characteristics of the elastic mechanics and the rock bolt. Ranjbarnia et al. (2022) analyzed the performance of rock bolts in the plastic state by modeling with ABAQUS software. The results showed that pre-tensioning and shear-surface roughness could improve the shear resistance and pre-tensioned rock bolts could play a greater role in high-strength rock slopes. Jiang et al. (2022) investigated accurate modeling of bolted rough joints subjected to tensile-shear loads for support design in complex geological conditions. The researchers modified the FLAC3D Pile element model and investigated bolted joint performance under shear load and normal stress. Besides, Sun et al. (2022) developed a mechanical criterion and constitutive model for yield and fracture of rock bolts under tension-shear coupling, and realized secondary development of the FLAC3D platform.

3.2 The mechanical parameter of bolts in numerical simulation

Most numerical simulation of rock bolt shear are based on finite element and discrete element implementations. Thus, this section primarily focuses on reviewing the investigation of the mechanical parameters in these two types of numerical simulations.

Spang’s numerical simulation model presents several innovative aspects in parameter setup. The Drucker-Prager and Mises failure criteria are used to describe elastic–plastic materials. The “penetration modulus EM” is utilized to described the relationship between the deformation of rock and the shear strength. Material characteristics such as cohesion, friction angle and compressive strength are obtained from laboratory tests. However, to reduce computing time, only the element in the vicinity of the expected plastic steel deformations are modeled with elasto-plastic materials (Spang and Egger 1990). In contrast, Ferrero’s numerical simulation model adopts the Drucker-Prager yielding criterion for rock and mortar, while the von Mises yielding criterion is used for bolts (Ferrero 1995). With the development of computer technology, computational power has been greatly improved. Consequently, model mechanics parameter settings have become more refined. Aziz and Jalalifar’s numerical simulation model utilizes 3D solid elements (Solid 65 and Solid 95) with irregularly shaped 8-nodes and 20-nodes to represent materials such as concrete, grout and reinforcement. 3D surface-to-surface contact elements (Contact 174) are utilized to represent the contact between 3D target surfaces. (Jalalifar et al. 2004, 2005, 2006a, b; Aziz et al. 2005; Aziz and Jalalifar 2007).

Different from Aziz and Jalaifar’s model settings, Grasselli (2005) apply incorporates elements to simulate the material structure, while elastic–plastic contact elements are used for vertical joints and surface contact. Additionally, many scholars have proposed a variety of methods for determining the mechanical parameters of numerical models. Song et al. (2010) used 3D bar element LINK8 to simulate the rock bolt, and a 3D 8-Node Surface-to-Surface Contact Pair TARGE170 and CONTACT174 were adopted to simulate the rock joint and contact surface between concrete and bolt (Song et al. 2010). Li et al. (2016a) modelled concrete and grouting materials as Mohr–Coulomb criterion elastoplasticity, while the rock was treated as an elastoplastic material. The strain–stress relationship of rock bolts was modified based on laboratory tensile tests and divided into four stages: elastic, yield, strain hardening, and strain softening (Li et al. 2016a). The pile structural element in FLAC3D is modified to take into account the transverse shear strain in the element (Singh et al. 2020). Based on ABAQUS, linear elasticity with perfect plasticity and elasticity are assumed to consider the bolt and grout behavior, respectively. The contact between the grout and bolt was simulated with no friction along the deflection length but with rough contact in the remaining length (Ranjbarnia et al. 2022). Jiang et al. (Jiang et al. 2022) modified the mechanical model of the pile element to incorporate a direct shear break model of the bolt and embed the bolt yielding criterion. Sun et al. (2022) also proposed a pile element tensile-shear yield and fracture modified model, dividing shear mechanical model into three stages: elastic stage, plastic stage and fracture stage. When the shear and axial force of the rock bolt meet the yield criteria, the rock bolt enters the yield stage and is subjected to tensile-shear stress. The rock bolt cracks when its elongation approaches the fracture condition.

4 Overview of theoretical derivation in rock bolt shearing

After extensive research by numerous scholars on the mechanical properties of rock bolt subjected to shear load, it has been discovered that the rock bolts provide the following three main effects on joints or weak structural surfaces: reinforcement effect, shear resistance provided by the dowel effect, and shear resistance provided by the friction effect. To investigate the effects of these different mechanisms on reinforcement, scholars initially derived empirical formulas for rock bolt contribution and shear slip based on a large amount of experimental data, reasonable assumptions, and the equilibrium theory of system internal forces. With further research, some scholars simplified the rock bolt shear process into an analytical model, using elastic foundation beam and elastic-plasticity theory methods to obtain analytical solutions for rock bolt shear contribution and rock bolt shear slip. In recent years, other scholars have employed the method of structural mechanics to simplify the rock bolt shear process and obtain the ultimate contribution of rock bolt to the shear surface based on the mechanical equations and displacement coordination conditions in the structural mechanics method.

4.1 Early theory of rockbolt shear analytical model

Dulacska (1972) introduced an expression for the shear bearing capacity of rock bolts, which was based on the development of a plastic hinge at the point of contact, using an idealized stress distribution and the point of maximum moment, given by (Dulacska 1972):

$$\begin{array}{*{20}c} {T = 0.2 d_{\text{b}}^{2} \sigma_{y} \left( {\sqrt {1 + \left( {\frac{{\sigma_{\text{c}} }}{{0.03\sigma_{y} \sin \beta }}} \right)} - 1} \right)} \\ \end{array}$$

(1)

where $T =$ Shear force carried by the bolt, $\sigma_{\text{c}} =$ Uniaxial compressive strength of rock, $d_{\text{b}} =$ Bolt diameter, $\sigma_{y} =$ Yield stress of bolt, $\beta =$ Angle between bolt and normal to the joint.

Bjurstrom (1974) developed an analytical solution for the total shear strength of a bolt-reinforced joint, which was dependent on three parameters. This solution was based on the equilibrium of forces acting on the system.

5 Shear resistance due to reinforcement effect

$$\begin{array}{*{20}c} {T_{\text{b}} = p\left( {\cos \beta + \sin \beta \tan \varphi } \right)} \\ \end{array}$$

(2)

where $T_{\text{b}} =$ The reinforcement effect in shear resistance due to bolting, $p =$ Axial load corresponding to the yield strength due to shear displacement, $\beta =$ Initial angle between bolt and joint direction, $\varphi =$ The friction angle of the joint.

6 Shear resistance due to the dowel effect

$$\begin{array}{*{20}c} {T_{\text{d}} = 0.67d_{\text{b}}^{2} \left( {\sigma_{y} \sigma_{\text{c}} } \right)^{0.5} } \\ \end{array}$$

(3)

where $d_{\text{b}} =$ Bolt diameter, $\sigma_{y} =$ Bolt yield strength, $\sigma_{\text{c}} =$ Uniaxial compression strength of the rock.

7 Shear resistance due to friction of the joint

$$\begin{array}{*{20}c} {T_{\text{f}} = A_{\text{j}} \sigma_{\text{n}} \tan \varphi_{\text{j}} } \\ \end{array}$$

(4)

where $A_{\text{j}}$ is Joint area, $\sigma_{\text{n}}$ is Normal stress on joint, $\varphi_{\text{j}}$ is Joint friction angle.

Therefore, the total contribution of the bolt to the shear strength of the joint was given as:

$$\begin{array}{*{20}c} {T_{\text{t}} = p\left( {\cos \beta + \sin \beta \tan \varphi } \right) + 0.67d_{\text{b}}^{2} \left( {\sigma_{y} \sigma_{\text{c}} } \right)^{0.5} + A_{\text{j}} \sigma_{\text{n}} \tan \varphi_{\text{j}} } \\ \end{array} .$$

(5)

Spang and Egger (1990) proposed a semi-empirical formula solution based on dimensionless expressions. This solution was derived from tests conducted on bolts with varying diameters, friction angle, inclination, joint dilatancy, and normal stress. The expressions for evaluation of the maximum shear force and shear displacement were provided.

8 The maximum shear resistance $T_{0}$ is defined by the following general expression

$$\begin{array}{*{20}c} {T_{0} = P_{\text{t}} \left( {1.0 + \Delta T_{\text{A} + \text{G}} } \right) \cdot m_{\text{F}} \cdot m_{\text{R}} } \\ \end{array}$$

(6)

where $P_{\text{t}}$ is The maximum tensile load of the bolt, $\Delta T_{\text{A} + \text{G}}$ is Coefficient of consideration of the bolt inclination and dilatancy, $m_{\text{F}}$ is Coefficient of consideration of the rock deformability, $m_{\text{R}}$ is Coefficient of consideration of the joint friction.

9 The maximum shear displacement $f\left( s \right)$ is defined by the following general expression

$$\begin{array}{*{20}c} {f\left( s \right) = \left( {15.2 - 55.2 \cdot \text{EM}^{ - 0.2} + 56.2 \cdot \text{EM}^{ - 0.4} } \right) \cdot \left( {1 - \tan \alpha \cdot \left( {\frac{20}{{\text{EM}^{ - 0.4} }}} \right)^{0.25} \cdot \left( {\cos \alpha } \right)^{ - 0.5} } \right)} \\ \end{array}$$

(7)

$$\begin{array}{*{20}c} {f\left( s \right) = \left( {15.2 - 55.2 \cdot \sigma_{\text{c}}^{ - 0.14} + 56.2 \cdot \sigma_{\text{c}}^{ - 0.28} } \right) \cdot \left( {1 - \tan \alpha \cdot \left( {\frac{20}{{\sigma_{\text{c}}^{ - 0.4} }}} \right)^{0.125} \cdot \left( {\cos \alpha } \right)^{ - 0.5} } \right)} \\ \end{array}$$

(8)

where $f\left( s \right) \, \text{is} \, \frac{s}{{d_{\text{b}} }}$, $d_{\text{b}}$ is bolt diameter, $\text{EM}$ is the stiffness of mortar and rock, $\sigma_{\text{c}}$ is uniaxial compression strength of the rock.

It should be noted that the empirical nature of the above expressions imposes limitations on their applicability. The conditions for their use must satisfy the rock bolt and grout materials, borehole diameter and loading conditions in the experiment.

9.1 Elastic foundation beam theory and elastoplasticity theory of rockbolt shear analytical model

When both rock and steel are in the elastic field, the dowel deformation is analyzed by the means of the classic equations of the classic foundation without considering the axial load that acts in the bar. This is expressed as followed, as shown in Fig. 14:

$$\begin{array}{*{20}c} {\frac{{{\text{d}}^{4} y}}{{{\text{d}}^{4} x}} + \frac{{K_{\text{s}} d_{\text{b}} }}{EI}y = 0} \\ \end{array}$$

(9)

where $E =$ The steel Young’s modulus, $I =$ The moment of inertia, $y =$ The transverse deformation of the bar, $K_{\text{s}} =$ The rock modulus.

Fig. 14

Sketch of elastic foundation beam model. a Elastic compressive buckling of foundation beam b Micro-segment force equilibrium analysis

Based on Eq. (9), Ferrero considered the failure of rock bolt as a result of the combined action of shear and tension forces, and proposed the existence of two yielding mechanisms (Ferrero 1995). The Tresca–von Mises law shown in Eq. (10) was used to determine the failure of rock bolts under tension and bending forces.

$$\begin{array}{*{20}c} {\left( {\frac{{T_{r} }}{{T_{y} }}} \right)^{2} + \frac{{M_{0} }}{{M_{y} }} = 1} \\ \end{array}$$

(10)

Considering the lateral reactions given by the rock in the elastic and plastic fields, the reactions can be expressed by Eqs. (11) and (12)

$$\begin{array}{*{20}c} {p_{\text{u}} = K_{\text{s}} u_{\text{s}} } \\ \end{array}$$

(11)

$$\begin{array}{*{20}c} {p_{\text{u}} = n\sigma_{\text{c}} } \\ \end{array}$$

(12)

where $p_{\text{u}}$ is the rock reaction perpendicular to the bar, $K_{\text{s}}$ is the rock modulus and $u_{\text{s}}$ is the bar displacement perpendicular to its axis in the elastic field; $\sigma_{\text{c}}$ is the rock uniaxial compressive strength, $n$ is a factor that depends on the rock internal friction angle and it varies between 2 and 5 in the plastic field (Holmberg 1991). By combing Eqs. (9)–(12), the limiting shear displacement can be evaluated. This involves determining formation of the two plastic hinges (1st yielding mechanism) and corresponding to the bar yielding under shear and tension at the joint intersection (2nd yielding mechanism). The expressions for these can be found in Eqs. (13) and (14):

$$\begin{array}{*{20}c} {u_{\text{s}} < \frac{{5.27\sigma_{y} l_{0}^{2} }}{{Ed_{\text{b}} }}} \\ \end{array}$$

(13)

$$\begin{array}{*{20}c} {u_{\text{s}} < \frac{{4\sigma_{y} l_{0}^{3} }}{{Ed_{\text{b}}^{2} }}} \\ \end{array}$$

(14)

where $l_{0}$ is defined as $\sqrt[4]{{\frac{4EI}{{K_{\text{s}} d_{\text{b}} }}}}$.

The axial tension in the rock bolt in both modes of yielding can be obtained by applying the equilibrium equation for the rock bolt, both parallel and perpendicular to the axial direction, under ultimate plasticity condition.

$$\begin{array}{*{20}c} {T_{r} = p_{\text{u}} d_{\text{b}} \frac{{x_{0}^{2} }}{{2y_{0} }}} \\ \end{array}$$

(15)

$$\begin{array}{*{20}c} {T_{r} = p_{\text{u}} d_{\text{b}} \frac{{x_{0}^{2} }}{{2y_{0} }} \left( {1 + \frac{{4y_{0}^{2} }}{{x_{0} }}} \right)^{\frac{3}{2}} } \\ \end{array}$$

(16)

In contrast to Ferrero’s approach (Ferrero 1995), which established the relationship between axial tension and bending yield using the equilibrium equation of forces, Pellet and Egger (1996) proposed a new analytical model that accounts for the interaction of axial and shear forces during the rock bolt action, as well as the plastic displacement of the rock bolt during the loading damage. They divided the rock bolt shear behavior into two phases: the elastic phase, which extends from the beginning of the loading process to the bolt yielding (as shown in Fig. 15), and the plastic phase, which extends from yielding to failure (as shown in Fig. 16). For the elastic phase, the rock bolt shaft force and shear force are linked via the minimum residual energy theorem, while for the plastic phase, the presence of the rock bolt plastic hinge causes the shear force to remain constant, while the shaft force continues to increase until the rock bolt fails.

Fig. 15

Displacements and rotations of the bolt for elastic conditions (Pellet and Egger 1996)

Fig. 16

Displacements and rotations of the bolt for plastic conditions (Pellet and Egger 1996)

The yield limit and the shear force in the plastic phase of the rock bolt can be obtained from Eqs. (17) and (18), respectively.

$$\begin{array}{*{20}c} {Q_{\text{oe}} = 0.5\sqrt {p_{\text{u}} D_{\text{b}} \left( {\frac{{\uppi D_{\text{b}} \sigma_{\text{el}} }}{4} - N_{\text{oe}} } \right)} } \\ \end{array}$$

(17)

$$\begin{array}{*{20}c} {Q_{\text{of}} = \frac{{\uppi D_{\text{b}}^{2} \sigma_{\text{ec}} }}{8}\sqrt {1 - 16\left( {\frac{{N_{\text{of}} }}{{\uppi D_{\text{b}}^{2} \sigma_{\text{ec}} }}} \right)} } \\ \end{array}$$

(18)

where $Q_{\text{oe}}$ is shear force acting at point O at the yield stress of the bolt material, $Q_{\text{of}}$ is shear force acting at point O at the failure of the bolt material, $N_{\text{oe}}$ is axial force acting at point O at the yield stress of the bolt material, $N_{\text{of}}$ is axial force acting at point O at the failure of the bolt material, $\sigma_{\text{el}}$ is yield stress of the bolt material, $\sigma_{\text{ec}}$ is failure stress of the bolt material.

The relations between shear force and axial load were presented in Fig. 17. The elastic limit (Eq. 17) was parabolic, while the failure criterion is elliptical (Eq. 18).

Fig. 17

Shear force versus axial force in the bolt (Pellet and Egger 1996)

The displacement of the bolt in the elastic stage and the plastic stage were obtained from Eqs. (19) and (20) respectively:

$$\begin{array}{*{20}c} {U_{\text{oe}} = \frac{{8192Q_{\text{oe}}^{4} b}}{{E\uppi^{4} D_{\text{b}}^{4} p_{\text{u}}^{3} \sin \beta }}} \\ \end{array}$$

(19)

$$\begin{array}{*{20}c} {\Delta U_{\text{op}} = \frac{{Q_{\text{oe}} \sin \Delta \omega_{\text{op}} }}{{p_{\text{u}} \sin \left( {\beta - \Delta \omega_{\text{op}} } \right)}}} \\ \end{array}$$

(20)

where

$$\Delta \omega_{\text{op}} = arcos\left[ {\frac{{l_{\text{e}} }}{{l_{\text{f}} }}\sin^{2} \beta \pm \sqrt {\cos \beta \left( {1 - \left( {\frac{{l_{\text{e}} }}{{l_{\text{f}} }}} \right)^{2} \sin^{2} \beta } \right)} } \right]$$

where, $l_{\text{e}}$ is distance between bolt extremity (point O) and the loacation of the maximum bending moment (point A) when the yield limit is reached, $l_{\text{f}}$ is length of the part O–A at failure.

The rotation of the bolt in the elastic stage was obtained from Eqs. (21):

$$\begin{array}{*{20}c} {\omega_{\text{oe}} = - \frac{{2048Q_{\text{oe}}^{3} b}}{{E\uppi^{3} D_{\text{b}}^{4} p_{\text{u}}^{2} }}} \\ \end{array}$$

(21)

where $b = 0.27$, $p_{\text{u}} =$ maximum bearing pressure pre unit of length (yielding pressure of the grout).

The total displacement and the total rotation of the bolt at failure were respectively computed by the following formulas:

$$\begin{array}{*{20}c} {\omega_{\text{of}} = \omega_{\text{oe}} + \Delta \omega_{\text{op}} } \\ \end{array}$$

(22)

$$\begin{array}{*{20}c} {U_{\text{of}} = U_{\text{oe}} + \Delta U_{\text{op}} } \\ \end{array}$$

(23)

Jalalifar and Aziz (2010a) developed an analytical method based on the analytical model proposed by Pellet and Egger (1996) that could provide a better understanding of the bolt shearing across joint planes under lateral confinement, particularly the hinge point position of the bolt-bending behavior under elastic and plastic conditions. The lateral reaction of the bolt is shown in Fig. 18. Based on experiments, it was observed that there was no significant change in the value of the axial load in the elastic region (Jalalifar et al. 2006a, b). Thus, the hinge point distance to the shear joint can be expressed as follows:

$$\begin{array}{*{20}c} {L_{\text{p}} = \frac{1}{4}\sqrt {\frac{{\sigma_{y} \uppi D_{\text{b}}^{3} }}{{P_{\text{u}} }}} } \\ \end{array}$$

(24)

where $L_{\text{p}}$ is reaction length (hinge length), $P_{\text{u}}$ is reaction force, which can be equal to $\sigma_{\text{c}} D_{\text{b}}$, $\sigma_{y} =$ Elastic yield stress, $D_{\text{b}}$ is bolt diameter.

Fig. 18

Reaction forces in a bolt loaded (Jalalifar and Aziz 2010a)

Based on the analytical model proposed by Pellet and Egger (1996), Chen and Li 2015a, b) proposed the loading angle and displacing angle of the bolt for its pull-and-shear performance calculation. The loading angle was defined as the angle between the lateral shear load and the axial pull load, while the displacing angle was defined as the angle between the pull displacement and the shear displacement. The displacing angle $\alpha$ and the loading angle $\theta$ are defined as followed:

$$\begin{array}{*{20}c} {\alpha = \arctan \frac{{D_{\text{s}} }}{{D_{\text{p}} }}} \\ \end{array}$$

(25)

$$\begin{array}{*{20}c} {\gamma_{0} = \arctan \frac{{Q_{0} }}{{N_{0} }}} \\ \end{array}$$

(26)

$$\begin{array}{*{20}c} {\theta = \omega_{o} + \gamma_{0} } \\ \end{array}$$

(27)

where $D_{\text{s}}$ is the shear displacement, $D_{\text{p}}$ is the pull displacement, $Q_{0}$ is the shear load of the point O, $N_{0}$ is the axial load of the point O, $\omega_{\text{o}} \, \text{is}\, \omega_{\text{oe}} + \omega_{\text{op}}$, which could be found in Pellet and Egger (1996).

Zhang and Liu (2014) proposed an analytical model taking into account the tangential and axial deformability of rock bolt bolts comprehensively, which divides the deformation of the bolt into two parts: the elastic deformation zone and the crushing failure zone. Relationships between tangential load and tangential displacement, and axial load and axial displacement were deduced respectively. Through the analysis of the yield failure model of the bolt, a method for calculating the length of the crushing failure zone was proposed (Liu et al. 2018).

In the elastic deformation zone, the lateral deformation of the bolt satisfied the Winkle assumption. In the crushing failure zone, the force on the rock bolt can be assumed to be linear based on Oreste's research conclusions (Oreste and Cravero 2008). Combined with boundary conditions, the shear displacement of the bolt in the elastic deformation zone and the crushing failure zone could be obtained from Eqs. (28) and (29):

$$\begin{array}{*{20}c} {y = \frac{1}{{2EI\beta^{3} }}e^{{ - \beta x\left[ {\left( {T_{0} + \beta M_{0} } \right)\cos \beta x - \beta M_{0} \sin \beta x} \right]}} } \\ \end{array}$$

(28)

$$\begin{array}{*{20}c} {y = \frac{1}{{2EI\beta^{3} }}\left\{ {T\left[ {\frac{1}{3} + \frac{2}{3}\left( {1 + \beta l_{\text{f}} } \right)^{3} } \right] - P_{\text{u}} \left[ {l_{\text{f}} \left( {1 + \frac{1}{2}\beta l_{\text{f}} } \right)\left( {1 + \beta l_{\text{f}} + \frac{1}{2}\beta^{2} l_{\text{f}}^{2} } \right)} \right]} \right\}} \\ \end{array}$$

(29)

where $T_{0} = T - p_{\text{u}} l_{\text{f}}$, The shear force in the point O, $M_{0} = Tl_{\text{f}} - \frac{1}{2}p_{\text{u}} l_{\text{f}}^{2}$, The moment in the point O, $\beta = \sqrt[4]{{\frac{kd}{{4EI}}}}$, $l_{f} =$ The length of the crushing failure zone.

The total deformation of the bolt in the elastic deformation zone and the crushing failure zone of the axial direction could be expressed in Eqs. (30) and (31):

$$\begin{array}{*{20}c} {u_{1} = \frac{{N_{0} }}{{E_{\text{b}} A\alpha }}\frac{1}{{\tanh \left( {\alpha L} \right)}}} \\ \end{array}$$

(30)

$$\begin{array}{*{20}c} {u_{2} = \frac{1}{{E_{\text{b}} A\alpha }}\left( {N_{0} l_{\text{f}} + p_{\text{u}} \frac{1}{2}\uppi d\tan \emptyset l_{f}^{2} } \right)} \\ \end{array}$$

(31)

where

$$\alpha = \sqrt {\frac{{k_{\text{s}} }}{{E_{\text{b}} A}}}$$

$A$ is the cross-sectional area of the bolt, $\emptyset$ is the internal friction angle.

The joint displacement, consisting of axial and transverse deformation, can be used to determine which stage the joint is in.

However, the aforementioned papers seldom focus on the coupled synergistic effects of different materials, such as rock bolts, grouting and surrounding rock, under fracture conditions. Therefore, the analytical models of rock bolts proposed by scholars in recent years have mainly focused on the reinforcement effect under the coordination between shear and axial forces. Ma et al. (2018, 2019) proposed an analytical model to overcome some limitations of the previous analytical model by taking into account the axial forces developed in the bolt, the interfacial bond stress between the bolt and grout, the pretension, and the dowel shear forces acting transversely to the bolt axis. The bolt was divided into three sections: OA, AB and BC as shown in Fig. 19. The point O was the intersection point, the point A was the hinge point where the moment had the maximum value and the shear force was zero, and the point B was located between points A and C with $L_{\text{AB}} = L_{\text{OA}} = L_{\text{A}}$. For the OA section, the interfacial shear stress was assumed to be zero.

Fig. 19

The strain distribution and the interfacial shear stress distribution along the length of the bolt. a Strain distribution b The interfacial shear stress distrbution (Ma et al. 2019)

Based on the assumption above, the axial force of the bolt at the intersection point O of the elastic stage can be deduced using Eq. (32):

$$\begin{array}{*{20}c} {N_{\text{o}} = \frac{{AE + k_{1} H}}{{L + \frac{{k_{1} L_{\text{A}} H}}{AE}}}u_{\text{o}} } \\ \end{array}$$

(32)

where $k_{1}$ is the stiffness of the bond-slip model in the first stage, $A$ is the cross-sectional area of the bolt, $E$ is the Young’s modulus of the bolt

$$\begin{aligned} & H = \left[ {\uppi d_{\text{b}} \left( {x_{\text{B}} - x_{\text{A}} } \right) + \frac{{\uppi d_{\text{b}}^{2} }}{2\alpha }} \right]\left( {x_{\text{B}}^{\prime } - x_{\text{C}}^{\prime } } \right) - \frac{{\uppi d_{\text{b}}^{3} }}{{4\alpha^{2} }}\left( {1 - e^{{ - 2\alpha \frac{{x_{\text{B}}^{\prime } - x_{\text{C}}^{\prime } }}{{d_{\text{b}} }} }} } \right)\;{\text{and}} \\ & \quad + \;\uppi d_{\text{b}} \left( {L - x^{\text{A}} } \right)\left( {x_{\text{A}}^{\prime } - x_{\text{B}}^{\prime } } \right) - \uppi d_{\text{b}} \frac{{x_{\text{A}}^{\prime } - x_{\text{B}}^{\prime } }}{2} \\ \end{aligned}$$

$$L = x_{\text{O}}^{\prime } - x_{\text{C}}^{\prime }$$

$$u_{\text{o}} = \Delta U_{\text{o}} \cos \left( {\beta - \omega_{\text{o}} } \right)$$

$\omega_{\text{o}}$ is the incremental rotation angle which could be derived by iterative calculation.

The elastic limit of the bolt at the hinge point A could be obtained from Eq. (33):

$$\begin{array}{*{20}c} {N_{\text{A}} = \sigma_{y} A - \frac{{AQ_{\text{o}}^{2} }}{{2p_{\text{u}} W_{\text{b}} }}} \\ \end{array}$$

(33)

where $\sigma_{y}$ is the yield strength of the bolt, $W_{\text{b}} = \frac{{\uppi d_{\text{b}}^{3} }}{32}$, the section modulus of the bolt, $I_{\text{b}} = \frac{{\uppi d_{\text{b}}^{4} }}{64}$, the moment of the inertia of the bolt. $d_{\text{b}}$ is the bole diameter, $v_{\text{o}} = \Delta U_{\text{o}} \cos \left( {\beta - \omega_{\text{o}} } \right)$, $k = \left\{ {\begin{array}{*{20}l} {a \cdot f_{c}^{\prime 0.85} ,} \hfill & {{\text{elastic}}\;{\text{stage}}} \hfill \\ {\frac{{a \cdot f_{c}^{\prime 0.85} }}{{\left[ {1 + 3\left( {DI\left( v \right) - b} \right)^{0.8} } \right]^{4} }},} \hfill & {{\text{ealsto - plastic}}\;{\text{stage}}} \hfill \\ {\frac{{a \cdot f_{c}^{\prime 0.85} }}{{\left[ {1 + 3\left( {c - b} \right)^{0.8} } \right]^{4} }},} \hfill & {{\text{plastic}}\;{\text{stage}}} \hfill \\ \end{array} } \right.$, the spring stiffness, $DI\left( v \right) = \frac{{v_{\text{o}} }}{{d_{\text{b}} }}$, the damage index DI, $b = \frac{{v_{\text{o1}} }}{{d_{\text{b}} }}$ and $c = \frac{{v_{\text{o2}} }}{{d_{\text{b}} }}$.

During the shearing process, Ma’s analytical model assumed that the bolt and the concrete would interact with each other, entering the elasto-plastic (Stage II) and plastic (Stage III) stages simultaneously, as shown in Figs. 20 and 21.

Fig. 20

Typical shear load–displacement curve of double shear tests

Fig. 21

The axial behavior of bolts under tension (Ma et al. 2019)

In contrast to the analytical model mentioned above, Chen et al. (2020) developed an analytical model that takes into account the bolt pullout model (Li and Stillborg 1999). The analytical model could predict the mechanical behavior of fully grouted rock bolts subjected to pull-and-shear load. The elastic theory of a semi-infinite length beam and the approximate differential equations of the deflection curve (elastic and elastoplastic) were used to analyze the lateral behavior of the bolts, as shown in Fig. 22. The axial behavior of the bolts was based on a realistic tri-linear bond-slip model with residual bond strength at the grout-bolt interface. In the pure elastic stage, bolt deformation was approximately the differential equation of the deflection curve as shown in Eq. (34). In the elastic-and-plastic stage, bolt deformation was consistent with the deflection curve from Eq. (35), which was simplified based on rectangular cross-section beams:

$$\begin{array}{*{20}c} {\frac{{{\text{d}}^{2} y}}{{{\text{d}}x^{2} }} = - \frac{M\left( x \right)}{{EI}} } \\ \end{array}$$

(34)

$$\begin{array}{*{20}c} {\frac{{{\text{d}}^{2} y}}{{{\text{d}}x^{2} }} = \frac{{\sqrt {2\sigma_{\text{s}} } }}{Ed}\frac{1}{{\sqrt {\frac{3}{2} - \frac{M\left( x \right)}{{M_{\text{e}} }}} }}} \\ \end{array}$$

(35)

where $EI$ is the flexural rigidity of the bolt, $d$ is the bolt diameter, $\sigma_{\text{s}}$ is the failure stress of the bolt, $M_{\text{e}}$ is the elastic limit bending moment.

Fig. 22

Force diagram showing the forces for bolt lateral behavior lateral force diagram (Chen et al. 2020)

The lateral deformation $y\left( x \right)$ of the point O could be deduced as Eq. (36):

$$\begin{array}{*{20}c} {y\left( x \right) = \left\{ {\begin{array}{*{20}l} {\frac{1}{EI}\left( {\frac{1}{6}Q_{0} x^{2} - \frac{1}{24}q_{\text{u}} x^{3} + C_{1} x + D_{1} } \right),} \hfill & {0 \le x \le U_{\text{e}} } \hfill \\ {n\left\{ {R\left( x \right)\ln \left[ {R\left( x \right)^{2} + m^{2} } \right] - \sqrt {R\left( x \right)^{2} + m^{2} } + C_{2} x + D_{2} } \right\},} \hfill & { U_{\text{e}} \le x \le U} \hfill \\ {Ae^{ - \beta x} \cos \left( {\beta x + B} \right),} \hfill & {U \le x \le L_{\text{q}} } \hfill \\ \end{array} } \right.} \\ \end{array}$$

(36)

where $Q_{0}$ is the shear force of the point O, $q_{u}$ is the expression for the bearing capacity, $m = \sqrt {\frac{{\left( {3q_{\text{u}} M_{\text{e}} - Q_{0}^{2} } \right)}}{{q_{\text{u}}^{2} }}}$, $n = \frac{{2\sigma_{\text{s}} }}{{ED_{\text{b}} }}\sqrt {\frac{{M_{\text{e}} }}{{q_{\text{u}} }}}$, $R\left( x \right) = \frac{{q_{\text{u}} x - Q_{0} }}{{q_{\text{u}} }}$, $U_{\text{e}} , U,A, B, C_{1} , C_{2} , D_{1}$ and $D_{2}$ are the constant values obtained by analyzing the boundary conditions of the bolt’s endpoint and the continuity conditions of the bolt deflection, rotation angle, bending moment, and shear force at $x = U$ and $x = U_{\text{e}}$.

The axial behavior of the bolt was analyzed using the shear stress model as shown in Fig. 23 (Li and Stillborg 1999). The shear action influence range length was simplified to U, representing the length of rock mass squeezed by the yielding bolt, plus the interface between the bolt and surrounding rock mass, as shown in Eq. (37). The shear stress along the bolt is expressed as Eq. (38):

$$\begin{array}{*{20}c} {f = \mu q\left( x \right)} \\ \end{array}$$

(37)

$$\begin{array}{*{20}c} {\tau_{\text{b}} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {0 \le x \le L_{0} } \hfill \\ {\mu q_{\text{U}} ,} \hfill & {L_{0} \le x \le U} \hfill \\ {{{S}}_{{\text{r}}} ,} \hfill & { U \le x \le L_{1} } \hfill \\ {\omega S_{\text{p}} + \frac{{x - L_{1} }}{\Delta }\left( {1 - \omega } \right)S_{\text{p}} ,} \hfill & {L_{1} \le x \le L_{2} } \hfill \\ {S_{\text{p}} e^{{ - 2\alpha \frac{{x - L_{2} }}{d}}} ,} \hfill & {L_{2} \le x \le L} \hfill \\ \end{array} } \right.} \\ \end{array}$$

(38)

where $\mu$ is the friction coefficient, ${{S}}_{{\text{r}}}$ is the residual shear strength at the bolt–rock interface, $S_{\text{p}}$ is the peak shear strength at the bolt–rock interface, $\omega = \frac{{{{S}}_{{\text{r}}} }}{{S_{\text{p}} }}$, the ratio of the residual shear strength to the peak shear strength, $\alpha^{2} = \frac{{2G_{\text{r}} }}{{E_{\text{b}} \ln \left( {\frac{{d_{0} }}{{d_{\text{b}} }}} \right)}}$.

Fig. 23

Distribution of shear stress along with the fully grouted rock bolt under pull load (Li and Stillborg 1999)

Three eigenvalues $N_{1}$, $N_{2}$, and $N_{3}$ are summarized in Eq. (39)–(41). $N_{1}$ is the maximum shear stress when the interface between the bolt and grout remains elastic; $N_{2}$ is the minimum shear stress when the interface undergoes decoupling; $N_{3}$ is the yield force of the bolt:

$$\begin{array}{*{20}c} {N_{1} = \frac{{\uppi d^{2} }}{4}\left[ {\frac{{2S_{\text{p}} }}{\alpha }\left( {1 - e^{{ - \frac{2\alpha L}{d}}} } \right) + \frac{{4\mu q_{\text{U}} U}}{d}} \right]} \\ \end{array}$$

(39)

$$\begin{array}{*{20}c} {N_{2} = \frac{{\uppi d^{2} }}{4}\left[ {\frac{{2S_{\text{p}} }}{\alpha }\left( {1 - e^{{ - \frac{2\alpha L}{d}}} } \right) + \frac{{4\mu q_{\text{U}} U + 2S_{\text{p}} \Delta \left( {1 + \omega } \right)}}{d}} \right]} \\ \end{array}$$

(40)

$$\begin{array}{*{20}c} {N_{3} = \frac{{\uppi d^{2} }}{4}\sigma_{\text{s}} } \\ \end{array}$$

(41)

Using the virtual working principle of the virtual force method, Singh and Spearing (2021) proposed an analytical model to derive the relationship between the lateral displacement at point O and the shear force of the bolt. Equation (42) depicts the method for considering the effect of post-elastic strain hardening on the bending stiffness of rock bolts when the bolts are in the plastic phase.

$$\begin{array}{*{20}c} {E_{\text{r}} = \frac{256}{{\uppi D_{\text{b}} \Delta^{3} }}\mathop \smallint \limits_{{\varepsilon_{2} }}^{{\varepsilon_{1} }} \sigma \varepsilon \sqrt {\frac{{D_{\text{b}}^{2} }}{4} - \frac{{D_{\text{b}}^{2} \varepsilon^{2} }}{{\Delta^{2} }}} \text{d}\varepsilon } \\ \end{array}$$

(42)

The rotation, axial extension, and axial load in the bolt could be expressed as:

$$\begin{array}{*{20}c} {\tan \theta = \frac{{u_{y} }}{{l_{\text{A}} + \frac{{u_{y} }}{\tan \alpha }}}} \\ \end{array}$$

(43)

$$\Delta_{\text{ext.p}} = \frac{{l_{\text{A}} }}{\cos \theta } + \frac{{u_{y} }}{\tan \alpha \cos \theta } - \left( {l_{\text{A}} + \Delta_{\text{ext.e}} } \right)$$

(44)

$$\begin{array}{*{20}c} {N_{0} = \frac{{\uppi D_{\text{b}}^{2} E_{\text{p}} \Delta_{\text{ext.p}} }}{{4l_{\text{P}} }} + N_{\text{oe}} } \\ \end{array}$$

(45)

where $l_{\text{P}}$ is the length of the plastic section (where the bending moment is greater than the plastic moment) of the bolt. $\Delta_{\text{ext.e}}$ is the axial extension at the yield point. $N_{\text{oe}}$ is the axial load at point O at the yield point. $E_{\text{p}} = \left( {\frac{{\sigma_{\text{f}} - \sigma_{y} }}{{\varepsilon_{\text{f}} - \varepsilon_{y} }}} \right)$. $\sigma_{\text{f}} ,\sigma_{y}$ is the yield and ultimate strength of the bolt. $\varepsilon_{\text{f}} ,\varepsilon_{y}$ is the yield and failure strain of the bolt. $\theta = \frac{1}{{EI_{z} }}\left( {\frac{{19p_{\text{u}} l_{\text{A}}^{3} }}{24} - 2Q_{\text{o}} l_{\text{A}}^{2} } \right)$.

To study the deformation of discontinuous rocks, Zou and Zhang (2021) built an analytical model to describe the opening displacement and shear displacement of the rock joints. A closed-form solution incorporating the nonlinear constitutive model of the interfaces between bolts and grout was proposed to formulate the full-range behavior of the bolts subjected to the opening displacements of rock joints. As the opening displacement of the rock joint shown in Fig. 24, the opening displacement $\delta$ of the joint was divided into two sections: the left section and the right section. The boundary conditions were expressed as Eq. (46). By substituting the opening displacement $\delta$ or applied load at the joint in the coupling equations, the distribution of axial load and displacement along the bolt can be solved.

$$\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}l} {U_{\text{b1}} \left( {L_{1} } \right) = \delta_{1} } \hfill \\ {U_{\text{b2}} \left( {L_{2} } \right) = \delta_{2} } \hfill \\ {\varepsilon_{1} \left( {L_{1} } \right) = \varepsilon_{2} \left( {L_{2} } \right)} \hfill \\ {\delta_{1} + \delta_{2} = \delta } \hfill \\ \end{array} } \right.} \\ \end{array}$$

(46)

Fig. 24

A simplified model of the bolt subject to a joint aperture increment $\delta$. (The upper part represents the initial state while lower part represents the loaded state) (Zou and Zhang 2021)

A novel numerical approach considering the nonlinear rock reaction force was developed to analyze stress and displacement conditions on each point along a bolt. Both decoupling between the bolt and grout, and the yield and failure patterns of two potential points along the bolt were emphasized. The dilatancy phenomenon at the rough joint surface of the total shear displacement was computed with a model proposed by Indraratna et al. (2015) under constant normal stiffness (CNS) conditions as shown in Eqs. (47):

$$\begin{array}{*{20}c} {U_{\text{d}} = \mathop \smallint \limits_{0}^{{U_{0} }} \left( {\dot{v}} \right){\text{d}}U_{0} } \\ \end{array}$$

(47)

where $\dot{v}$ is the dilation rate (${\text{d}}U_{\text{d}} /{\text{d}}U_{0} = \dot{v}$), which can be calculated as:

$$\begin{array}{*{20}c} {\dot{v} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {0 < \left( {U_{0} /U_{0 - \text{peak}} } \right) \le c_{0} } \hfill \\ {\dot{v}_{0 - \text{peak}} \left( {1 - \frac{1}{{\left( {c_{0} - 1} \right)^{2} }}\left( {\frac{{U_{0} }}{{U_{0 - \text{peak}} }} - 1} \right)^{2} } \right),} \hfill & { c_{0} < \left( {U_{0} /U_{0 - \text{peak}} } \right) \le 1.0} \hfill \\ {\dot{v}_{0 - \text{peak}} \exp \left( { - \left( {c_{1} \left( {\frac{{U_{0} }}{{U_{0 - \text{peak}} }} - 1} \right)} \right)^{{c_{2} }} } \right),} \hfill & {\left( {U_{0} /U_{0 - \text{peak}} } \right) > 1.0} \hfill \\ \end{array} } \right.} \\ \end{array}$$

(48)

where $U_{0 - \text{peak}}$ is the peak shear displacement, $\dot{v}_{0 - \text{peak}}$ is the peak dilation rate, $c_{0}$ is the ratio of $U_{0}$ and $U_{0 - \text{peak}}$ when the dilation begins, $c_{1}$ and $c_{2}$ are the decay constants obtained from the existing experimental data.

Under the boundary condition of constant normal stiffness, the normal stress $\sigma_{\text{n}}$ applied to the joint surface at each level of shear displacement could be calculated using CNS coefficient $k_{\text{n}}$:

$$\begin{array}{*{20}c} {\sigma_{\text{n}} = \sigma_{\text{n0}} + k_{\text{n}} U_{\text{d}} } \\ \end{array}$$

(49)

According to the shear displacement of the bolt shown in Fig. 25, the bolt body on one side of the joint face was discretized into n elements and n + 1 nodal points. Therefore, the Euler–Bernoulli beam theory was rewritten as a finite difference scheme:

$$\begin{array}{*{20}c} {y_{i - 2} - 4y_{i - 1} + \left( {6 + A_{i} } \right)y_{i} - 4y_{i + 1} + y_{i + 2} = 0} \\ \end{array}$$

(50)

where $A_{i} = \frac{{h^{4} }}{EI}k_{i}$, $k_{i}$ is the tangential stiffness and is calculated as $k_{i} = \frac{{p_{i} }}{{y_{i} }}$, $p_{i}$ and $y_{i}$ represents the transverse force and displacement of a specific node.

Fig. 25

Discretization of the bolt body (Zou and Zhang 2021)

9.2 Statically indeterminate beam theory on Structural Mechanic Methods of rockbolt shear analytical model

Structural Mechanic Methods was used to solve the statically indeterminate beam problem. The original problem was initially transformed into a statically determinate beam by eliminating all redundant reactions, as depicted in Fig. 26. Using the force method of statically indeterminate structures, three compatibility equations can be formulated as Eq. (51):

$$\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}l} {f_{11} R_{1} + f_{12} R_{2} + f_{13} R_{3} + \Delta_{{1{\text{q}}}} = \Delta_{1} } \hfill \\ {f_{21} R_{1} + f_{22} R_{2} + f_{23} R_{3} + \Delta_{{2{\text{q}}}} = \Delta_{2} } \hfill \\ {f_{31} R_{1} + f_{32} R_{2} + f_{33} R_{3} + \Delta_{{3{\text{q}}}} = \Delta_{3} } \hfill \\ \end{array} } \right.} \\ \end{array}$$

(51)

Fig. 26

A simplified model of nonstatically indeterminate beam mechanics based on structural mechanics approach. a Nonstatically indeterminate beam model simplified model b Statically indeterminate beam model Simplified model

Based on beam theory, the flexibility matrix and the deformation matrix induced by external loads could be obtained from Eqs. (52) and (53):

$${\varvec{f}} = \left[ {\begin{array}{*{20}c} \frac{L}{EA} & 0 & 0 \\ 0 & {\frac{{L^{3} }}{3EI} + \frac{kL}{{GA}}} & {\frac{{L^{2} }}{2EI}} \\ 0 & {\frac{{L^{2} }}{2EI}} & \frac{L}{EI} \\ \end{array} } \right]$$

(52)

$$\begin{array}{*{20}c} {\Delta_{{\text{q}}} = \left[ {\begin{array}{*{20}c} 0 \\ { - \left( {\frac{{q_{0} L^{4} }}{360EI} + \frac{{kq_{0} L^{2} }}{12GA}} \right)} \\ { - \frac{{q_{0} L^{3} }}{60EI}} \\ \end{array} } \right]} \\ \end{array}$$

(53)

where $L = \sqrt {\frac{{\uppi d^{3} \sigma_{\text{yield}} - 4N_{\text{A}} d}}{{16p_{\text{u}} }}}$ The plastic hinge distance from the joint to the hinges. ($p_{\text{u}}$ the maximum concrete reaction), $A$ is the area of the tendon cross section, $I$ is the inertia moment of the tendon cross section, $E$ is the tensile modulus of the tendon, $G$ is the shear modulus of the tendon, $q_{0}$ is the compression load density at point O, $k$ is a concentration coefficient of the shear stress distribution at the tendon cross section.

Li et al. (2015) proposed an analytical model that was based on the theory of statically indeterminate beams, incorporating fundamental research findings and conclusions of other scholars in predicting the joint shear strength and shear displacement of a fully grouted cable bolt. The bolt pretension, joint friction angle, concrete strength and bolt installation angle were considered. In Li’s analytical model, the deformation relationship between the axial and transverse shown in Fig. 27 could be expressed as Eq. (55):

$$\begin{array}{*{20}c} {\frac{{\Delta_{2} }}{{\Delta_{1} }} = \frac{\sin \alpha }{{\cos \left( {\alpha - \theta } \right)}} = \frac{\sin \alpha }{{\cos \alpha \cos \theta - \sin \alpha \sin \theta }}} \\ \end{array}$$

(54)

where $\alpha$ is the bolt installation angle to the joint, $\theta$ is the deflection angle (bending) of the bolt.

Fig. 27

Deformation compatibility condition at bolt joint intersection (Li et al. 2015)

In the elastic stage of the host material, the tensile load and the shear force at the point O could be expressed as Eqs. (55) and (56):

$$\begin{array}{*{20}c} {R_{1} = \frac{EA}{L}\Delta_{1} } \\ \end{array}$$

(55)

$$\begin{array}{*{20}c} {R_{2} = \frac{{240kGAE^{2} I^{2} - 40G^{2} A^{2} EIL^{2} }}{{\left( {6EIkL - GAL^{3} } \right)\left( {13GAL^{2} + 30kEI} \right)}}\Delta_{2} } \\ \end{array}$$

(56)

In the plastic stage of the host material, the tensile load at the point O was the same as the Eq. (48) and the shear load could be expressed as Eq. (57):

$$\begin{array}{*{20}c} {R_{2} = \frac{{\Delta_{2} + \frac{{p_{\text{u}} L^{4} }}{8EI} + \frac{{kp_{\text{u}} L^{2} }}{2GA}}}{{\frac{{L^{3} }}{3EI} + \frac{kL}{{GA}}}}\Delta_{2} } \\ \end{array}$$

(57)

The relationship between the tensile load and the plastic load in the plastic stage could be obtained from Eq. (58):

$$\begin{array}{*{20}c} {R_{2} = k_{2} \cdot R_{1} + k_{3} } \\ \end{array}$$

(58)

where $k_{1} = \frac{{\Delta_{2} }}{{\Delta_{1} }}$, $k_{2} = \frac{{\frac{{AL^{2} }}{3i} + \frac{kE}{G}}}{{k_{1} }}$, $k_{3} = - \frac{{\frac{{p_{\text{u}} AL^{2} }}{8I} + \frac{{kp_{\text{u}} EL}}{2G}}}{{k_{1} }}$.

The final deformation curve of a tendon at failure subjected to shearing consisted of two components: the host medium reaction and the tendon shear force. The corresponding contributions of shear force ($Q_{0}$) was derived from Eq. (59), while the host medium reaction strength ($p_{\text{u}}$) was derived from Eq. (60):

$$\begin{array}{*{20}c} {V_{{Q_{0} }} = \frac{{Q_{0} }}{6EI}\left( {3Lx^{2} - x^{3} } \right) + \frac{{kQ_{0} }}{GA}x} \\ \end{array}$$

(59)

$$V_{{p_{\text{u}} }} = \frac{{p_{\text{u}} }}{24EI}\left( {x^{4} - 4Lx^{3} - 4L^{2} x^{2} } \right) + \frac{{kp_{\text{u}} }}{2GA}x^{2} $$

(60)

The actual deformation curve at failure was given by:

$$\begin{array}{*{20}c} {V\left( x \right) = V_{{Q_{0} }} - V_{{p_{\text{u}} }} } \\ \end{array}$$

(61)

Liu and Li (2017) discussed the influence of the inclination of the bolt and analyzed the contribution of the axial and shear forces of the bolt. The relationship between the shear force and tensile load at the joint could be obtained from Eq. (62):

$$\begin{array}{*{20}c} {\frac{{{{R}}_{{\text{Q}}} }}{{{{R}}_{{\text{N}}} }} = K\tan \left( {\alpha - \beta } \right)\tan \left( {\alpha - \varphi } \right)} \\ \end{array}$$

(62)

where $K = \frac{1}{{\frac{kE}{{3G}} + \frac{{3l^{2} A}}{80I}}}$, $\alpha$ is the angle of the bolt with respect to the joint plane, $\beta$ is the dilation angle of the joint, $\varphi$ is the friction angle of the joint plane.

The axial force and shear force were expressed as Eqs. (63) and (64):

$$\begin{array}{*{20}c} {N_{0} = \frac{1}{{\sqrt {4K^{2} \tan^{2} \left( {\alpha - \beta } \right) + 1} }}Af_{y} } \\ \end{array}$$

(63)

$$\begin{array}{*{20}c} {Q_{0} = \frac{{K\tan \left( {\alpha - \beta } \right)}}{{\sqrt {4K^{2} \tan^{2} \left( {\alpha - \beta } \right) + 1} }}Af_{y} } \\ \end{array}$$

(64)

The contribution ($R$) of the axial force and shear force was expressed as Eq. (65):

$$\begin{array}{*{20}c} {R = \frac{{\left( {\cos \alpha + \sin \alpha \tan \varphi } \right) + K\tan \left( {\alpha - \beta } \right)\left( {\sin \alpha - \cos \alpha \tan \varphi } \right)}}{{\sqrt {4K^{2} \tan^{2} \left( {\alpha - \beta } \right) + 1} }}Af_{y} } \\ \end{array}$$

(65)

where $A$ is the cross-sectional area of the bolt, $f_{y}$ is the yield strength of the bolt.

Liu and Li (2020) developed an improved method that considers both axial and shear forces activated in the bolt and incorporates the minimum total potential energy principle to derive an algorithm for calculating the length of the transverse deformation section of a passive fully grouted bolt under shearing.

Based on the Structural Mechanic Methods, Li et al. (2021) studied the plastic strain-hardening of rockbolts subjected to large deformation. In the elastic stage, the implicit function of the transverse deformation length of the bolt when yielding initiates is obtained:

$$\begin{array}{*{20}c} {\frac{{10.56Q_{\text{o}} l}}{{\uppi d^{3} }} + \frac{{4N_{\text{o}} }}{{\uppi d^{2} }} - \sigma_{y} = 0} \\ \end{array}$$

(66)

where $Q_{\text{o}}$ is the shear force of the bolt at point O, $N_{\text{o}}$ is the axial force of the bolt at point O, d is the bolt diameters, $\sigma_{y}$ is the yield strength of the bolt.

The plastic strain in the bolt in the plastic deformation stage is obtained by the following expression:

$$\begin{array}{*{20}c} {\varepsilon_{\text{p}} = \mathop \smallint \limits_{{\frac{{N_{1} }}{A}}}^{{\frac{{N_{2} }}{A}}} \frac{1}{{H_{\text{p}} }}{\text{d}}\sigma } \\ \end{array}$$

(67)

where $N_{1}$ and $N_{2}$ are the axial force in the yield and ultimate rapture stages respectively, $A$ is the cross-section area of the bolt, $H_{\text{p}} = \frac{1}{{\frac{1}{D} - \frac{1}{E}}}$, $D$ is the strain hardening modulus of the bolt, $E$ is Young’s modulus of the bolt.

To investigate the effect of the pre-tension, the joint roughness and bolt inclination with respect to the joint plane and rock strength, Ranjbarnia et al. (2022) proposed a simple analytical approach to better understand the performance of pre-tensioned grouted rock bolts in bedding rock slopes. They utilized the force method approach and the deformation compatibility principles to model the contribution of developed axial and shear bolt forces at the intersection between the bolt and the joint plane, to evaluate the behavior of rock bolt in the elastic state. The design support force provided by a pre-tensioned bolt or the absence of pre-tension force against sliding for the yielding state could be expressed as follows:

$$\begin{array}{*{20}c} {R = T\left( {\sin \alpha \tan \left( {\emptyset_{r} + i} \right) + \cos \alpha } \right) + N_{\text{O}} \left[ {\begin{array}{*{20}c} {\left( {\cos \alpha + \sin \alpha \tan \left( {\emptyset_{r} + i} \right)} \right) + } \\ {K\tan \left( {\alpha - i} \right)\left( {\sin \alpha - \cos \alpha \tan \left( {\emptyset_{r} + i} \right)} \right)} \\ \end{array} } \right]} \\ \end{array}$$

(68)

where $T$ is the pre-tensioned force, $N_{\text{O}}$ is the axial force of the bolt, $\alpha$ is the angle between the bolt axis and joint plane, $i$ and $\emptyset_{r}$ is the roughness and friction angles of the rock joint, $\sigma_{\text{c}}$ is the uniaxial compressive strength of the rock or the grout, $K = \frac{1}{{\frac{5}{{24r^{2} }}\left( {\frac{{Af_{y} - \left( {T + N_{\text{o}} } \right)}}{{\sigma_{\text{c}} }}} \right) + \frac{5}{9}\frac{E}{G}}}$.

In the design support force, the roughness angle of joints depending on the effective normal stress is taken into account as shown in Eq. (69) (Barton 1973; Barton and Choubey 1977; Barton et al. 1985):

$$\begin{array}{*{20}c} {i = \left[ {JRC\log_{10} \left( {\frac{JCS}{{\sigma_{\text{n}} }}} \right)} \right]} \\ \end{array}$$

(69)

where $JRC$ is the joint roughness coefficient and $\sigma_{\text{n}}$ is the effective normal stress which is created by two factors: the sliding block weight ($\sigma_{\text{nW}}$) and the pre-tensioned load ($\sigma_{\text{nT}}$) thus:

$$\begin{array}{*{20}c} {\sigma_{\text{n}} = \sigma_{\text{nW}} + \sigma_{\text{nT}} } \\ \end{array}$$

(70)

where

$$\begin{array}{*{20}c} {\sigma_{\text{nT}} = \frac{T\sin \alpha }{{s_{\text{l}} s_{\text{t}} }}} \\ \end{array}$$

(71)

where $s_{\text{l}}$ and $s_{\text{t}}$ are the longitudinal and transverse bolt distances in a block if a systematic bolting pattern is used to stabilize a rock slope. By the combination of Eqs. (68) and (71), the design support force considering Barton–Bandis joint model could be obtained.

10 Limitations and recommendations for further research

After extensive research by scholars on the shear performance of rock bolt, the practice of using rock bolts to reinforce weak structures in engineering has gained wider acceptance. However, there are still limitations in current research on rock bolt shear. This paper analyzes and suggests the limitations of the current rock bolt research from experiments, numerical simulations, and analytical models.

• (1) In terms of testing, most of the rock bolt shear tests have been conducted on static rock bolts. Few shear tests have been conducted on the mechanism and mechanical properties of rock bolts under dynamic conditions. Most of the tensile tests under dynamic loads of rock bolts have only considered the results under elastic conditions. The tests are still based on static rock bolt shear tests and do not address the effects of dynamic effects, such as rock bursts, earthquakes and other stress wave effects, on the shear mechanical properties of rock bolts.

• (2) The current numerical simulation methods are mainly based on continuous medium numerical methods, such as finite element and finite difference methods. When dealing with interface problems, it is typically necessary to pre-set a well-defined interface coupling intrinsic structure relationship. However, due to the coupling of physical fields, such as material fragmentation, as well as thermal, soil and water effects that exist in the real world, the pre-set intrinsic structure model often fails to match the actual physical field environment. As a result, significant deviations can occur between simulation results and real field test results. In addition, there are few numerical simulations on the dynamic conditions of rock bolt, and most of them are simulated in an equivalent way to simulate the dynamic load effect, which usually ignores the weakening effect of the structure surface caused by the development of small cracks under the action of stress waves.

• (3) Regarding analytical models, there are limited analytical models available for rock bolt subjected to dynamic shear load, and several mechanical mechanisms unknown for rock bolt shear under dynamic conditions. Unlike the constant action experienced under static conditions, the dynamic response is frequently accompanied by microcracks and dynamic loads. Therefore, it is crucial to develop analytical models for dynamic rock bolts to advance rock bolt support into high-stress projects.

11 Conclusions

Based on the aforementioned review, the anchoring mechanism and anchorage contribution of rock bolts under shear loading are discussed in depth from three aspects: shear experiments, numerical simulations and theoretical derivation. The following will summarize each of these three aspects in turn:

11.1 Shear experiment

Regarding experimental research, significant progress has been made in understanding the mechanical mechanism and properties of rock bolt subjected to static shear load:

• (1) Factors affecting the shear contribution of rock bolts, such as the diameter and angle of rock bolt installation, rock strength, grouting material, bolt material, borehole diameter, rock bolt preload, normal stress, joint surface roughness, and joint expansion angle, have been studied extensively.

• (2) With the advancement of experimental technology, the study of rock bolt test has become more refined, and the development of measurement technology and loading technology has made the data reliable.

• (3) However, the majority of the current research on rock bolt shear test primarily focuses on static conditions. Further research is required to understand the shear behavior of rock bolts under dynamic conditions, particularly for high-stress deep ground conditions encountered in deep ground engineering.

11.2 Numerical simulation

Numerical simulations, based on finite element,finite difference methods and discrete methods, provide details that cannot be obtained from rock bolt shear tests in terms of visualization. They present changes in test parameters, such as stress, strain and displacement, during rock bolt loading in a dynamically varying manner and offer a reasonable explanation for the results of rock bolt shear tests

• (1) With advancements in computational capabilities, the mechanical parameters used in numerical models for rock bolt shear are becoming more refined and aligned with actual engineering scenarios.

• (2) Due to the limitations of the intrinsic model, numerical simulation results under complex physical field conditions inevitably show deviations.

• (3) There are relatively few studies focusing on numerical simulations under dynamic conditions, and the simulated dynamic loading does not accurately match realistic tests.

11.3 Theoretical derivation

In terms of analytical models, the conclusions obtained from a large number of rock bolt tests show that the contribution of rock bolts mainly features three aspects: (1) the reinforcement effect, (2) the shear resistance provided by the dowel effect action, (3) the shear resistance provided by the friction action:

• (1) Previously, models were usually obtained based on equilibrium of forces or empirical formulas, limiting their scope of application.

• (2) In recent years, the analytical models have expanded in scope and are based on elastic foundation beam theory, elasto-plasticity theory and structural mechanics methods. These models have a wide range of applications and are in good agreement with test results.

• (3) Furthermore, as the current analytical models mainly focus on static analytical models, there is a considerable gap in the study of analytical models of rock bolt subjected to shear dynamic loading.