Abstract
Poor and variable crop responses to fertilizer applications constitute a production risk and may pose a barrier to fertilizer adoption in sub-Saharan Africa (SSA). Attempts to measure response variability and quantify the prevalence of non-response empirically are complicated by the fact that data from on-farm fertilizer trials generally include diverse nutrients and do not include on-site replications. The first aspect limits the extent to which different studies can be combined and compared, while the second does not allow to distinguish actual field-level response variability from experimental error and other residual variations. In this study, we assembled datasets from 41 on-farm fertilizer response trials on cereals and legumes across 11 countries, representing different nutrient applications, to assess response variability and quantify the frequency of occurrence of non-response to fertilizers. Using two approaches to account for residual variation, we estimated non-response, defined here as a zero agronomic response to fertilizer in a given year, to be relatively rare, affecting 0–1 and 7–16% of fields on average for cereals and legumes respectively. The magnitude of response could not be explained by climatic and selected topsoil variables, suggesting that much of the observed variation may relate to unpredictable seasonal and/or local conditions. This implies that, despite demonstrable spatial bias in our sample of trials, the estimated proportion of non-response may be representative for other agro-ecologies across SSA. Under the latter assumption, we estimated that roughly 260,000 ha of cereals and 3,240,000 ha of legumes could be expected to be non-responsive in any particular year.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Low agricultural productivity, recurrent food shortages and high prevalence of food insecurity in sub-Saharan Africa (SSA) have led to repeated calls to intensify agriculture, with a particular focus on addressing the widespread soil fertility depletion in agricultural lands (UN Millennium project 2005; Sanchez 2010; Shapouri et al. 2010; Andriesse and Giller 2015; Binswanger-Mkhize and Savastano 2017). Sustainable agricultural intensification is viewed as a prerequisite for combatting food insecurity and reversing the trend of natural resource degradation (Tittonell and Giller 2013; Vanlauwe et al. 2014; Zurek et al. 2015), and an increased use of mineral fertilizers is considered to be an essential part of the solution (IFDC 2006; Sanchez 2010; Holden 2018). Despite efforts to enhance the use of fertilizers in the region (Druilhe and Barreiro-Hurle 2012; Jayne et al. 2018), average application rates remain very low, with recent studies reporting an average fertilizer use around 14 kg ha−1 (Bonilla Cedrez et al. 2020), though there is a wide variability between countries, with averages of some countries surpassing 50 kg ha−1 (Liverpool-Tasie et al. 2017; Sheahan and Barret 2017). While the accessibility to fertilizers remains a main constraint to the widespread use of fertilizers by smallholder farmers, the production risk associated with poor crop responses caused by variable weather conditions (Mafongoya et al 2007) and/ or by local edaphic constraints (e.g. limited soil rootable zone or water holding capacity and soil organic matter) i.e. the so-called non-responsive soils (Vanlauwe et al. 2010), could discourage farmers to invest in fertilizers (Holden 2018; Schut and Giller 2020). A lack of crop response to the application of fertilizers represents an obvious economic loss to farmers and, if enduring, may make fertilizer application unattractive to farmers and potentially harmful to the environment. Determining the rate of incidence of non-response to fertilizer is needed to understand the magnitude of the problem, and this requires on-farm observations on the variability in yield responses. While there is a diverse literature reporting on response variability observed in on-farm trials performed at different spatial scales across SSA (Tittonel et al. 2007; Kihara et al. 2016; Zingore et al. 2007; Ronner et al. 2016; Njoroge et al. 2017; Ichami et al. 2019; Roobroeck et al. 2021; Garba et al. 2018; Wortmann et al. 2017), few quantify the proportion of fields that fail to show an appreciable response in a given year. Two methodological issues make the quantification of non-response in on-farm data more challenging than it may seem. First, quantifying inadequate yield response in a dataset on fertilizer responses requires a measure against which observations can be compared. For single nutrient fertilizers, the agronomic efficiency (AE), the amount of extra produce per quantity of nutrient applied, which is commonly reported while assessing response to inputs (Olk et al. 1999; Ngome et al. 2013; Kaizzi et al. 2012; Vanlauwe et al. 2016; Kamanga et al. 2014; Xu et al. 2014; Adiele et al. 2020) provides such a measure. However, an equivalent metric does not exist for multi-nutrient fertilizers which are typically used in on-farm trials and by farmers in SSA, often with varying rates for the different nutrients, and which are expected to illicit different yield responses to the same total amount of fertilizer. One solution is to restrict comparisons to cases where the same fertilizer is applied, but this obviously limits the scope and applicability of such analyses, given that various types of fertilizers are used in SSA. Another option is to look at economic efficiencies only, since these can be calculated on any type of fertilizer (Jayne and Rashid 2013), but the variation in response is then determined to a large extent by differences in input prices (Bonilla Cedrez et al. 2020), which can vary over space and time, therefore requiring additional estimates of agronomic response for proper interpretation and translation to current conditions.
The second issue relates to the lack of on-site replication that tends to characterize on-farm trials (Bielders and Gérard 2015; Njoroge et al. 2017; Shehu et al. 2018). Regardless of how response is quantified, the observed variation in response not only reflects field-level variation due to rainfall, soil nutrient status or other biotic and abiotic factors, but is also determined by variation between experimental plots caused by random agronomic and experimental factors that are not repeatable at the field scale. The lack of on-field replicates implies that the random plot-level variation, which will be referred to as residual variation here, is confounded with the field-to-field variation, leading to an overestimation of the latter (Vanlauwe et al. 2016) and consequently, to inflated estimates of the proportion of non-response. Simply stated, even if all fields in a study have the same positive response to inputs, large residual variation will cause a proportion of control-treatment comparisons to yield negative observed responses by random chance. Only when the amount of residual variation is known or can be estimated from on-site replicates, then it is possible to determine what proportion of fields are truly non-responsive in a given season (Vanlauwe et al. 2016).
Together, the inability to account for residual variation and the lack of general measures of fertilizer response may thwart efforts to quantify the extent of non-response in SSA. Here we applied two simple approaches to address one or both limitations. The first uses published averages of residual variation to obtain corrected estimates of response variation from sets of non-replicated on-farm trials. The second aims at overcoming both limitations simultaneously by using a random regression approach that, under simplified assumptions, measures response from the yield increase as a linear function of a general measure of the fertilizer application intensity (Janssen 1998, 2011) while estimating the residual variation as the deviation from this linear relationship.
The main objective of this paper is to provide an estimate of the prevalence of non-response to fertilizers in trials performed across SSA using various types of fertilizers, accounting for residual variation. In addition, we performed spatial analyses of the results to evaluate if inferred effects of climatic and edaphic factors suggest the existence of repeatable patterns of non-response. The latter is of relevance since a lack of trial repetitions on the same field over different seasons does not allow effects of location-specific factors to be directly assessed.
Methods
Dataset
The on-farm fertilizer response data included in this study were obtained from on-going or completed projects at the time of acquisition. Within projects, on-farm trials performed in a single season on the same crop were grouped into separate collections of trials called studies here. The main criterion for selection of trials to include in the dataset was the presence of a control and a fertilizer treatment conducted side by side. There was no further selection made in regards to the type of fertilizer used, therefore the dataset included fertilizers of diverse nutrient compositions. Both published and non-published data were assembled per project, and generally included geographic coordinates. Crops evaluated in the studies were cereals (maize, sorghum) or legumes (soybean, bush bean, climbing bean, groundnut, cowpea). In total, 41 studies (14 for cereals and 27 for legumes) were included, from 11 countries including 6 for cereals and 10 for legumes, with data for specific countries and crops covering one to three separate seasons (Table S1). In total, 515 fields were included for cereals and 3930 for legumes, though one project conducted in Nigeria, in four States, accounted for more than half (2578) of the legume fields. In fertilizer treatments, the ranges of N and P rates were 100–140 kg N ha−1 and 30–50 kg P ha−1 for cereals, and 0–36 kg N ha−1 and 18–69 kg P ha−1 for legumes.
Measures of fertilizer response
Absolute response
As mentioned above, fertilizer response can be assessed using the agronomic efficiency (AE) (Hutton et al. 1956; Vanlauwe et al. 2010; Ichami et al. 2019), calculated as the yield increase per unit of nutrient applied in the fertilizer or: \(\frac{{{\Delta }Y}}{{F_{appl} }}\), with \({\Delta }Y = y_{f} - y_{c}\); where \({F}_{appl}\) is the quantity of specific nutrient applied (usually in kg ha−1) and \(y_{f}\) and \(y_{c}\) are the yields with and without the application of that nutrient (usually in kg ha−1). Since this measure does not extend to multi-nutrient fertilizers, we defined the absolute response as \({\Delta }Y = y_{f} - y_{c}\). Although useful for describing the response to any fertilizer, single or multi-nutrients, it has little comparative value, since its magnitude depends on the specifics of the fertilizer (amount and composition).
Relative response
One way to overcome the challenge of obtaining comparable values of response across different fertilizer formulations, is to define \(F_{appl}\) such that it accounts for differences in fertilizer nutrient composition to adequately express the total amount of applied nutrients simultaneously. Here, we refer to such a general measure as fertilizer application intensity, to express the fact that a single measure of the magnitude of application is used. We adopted an agronomic measure of application intensity that is available in the literature (Janssen 1998, 2011). Based on a popular framework for quantifying soil fertility (QUEFTS, Janssen et al. 1990), the so-called Crop Nutrient Equivalent (CNE) expresses the total nutrient input as the equivalent amount (kg) of nitrogen that would need to be applied to achieve an equivalent yield response if other nutrients and water were not limiting (i.e. available in balanced proportions). Using CNE as measure of fertilizer application intensity, it is possible to obtain a universal definition of fertilizer response as the additional yield (in kg) per unit of CNE (in kg N equivalent).
The calculation of CNE while simple, requires agreement on parameter values and its interpretation depends on several assumptions on crop nutrient responses implicit in the QUEFTS framework (Janssen et al. 1990, see supplement S1a for details). Within this framework, CNE is expected to have an approximately linear relation with yield for balanced fertilizer, which is convenient when using a regression approach to estimate the fertilizer response as described below. Although a strictly linear response to balanced fertilizer may not occur in practice, and alternative nutrient response functions do not share this property (e.g. Greenwood et al. 1971), we expect deviations of linearity to be moderate at the nutrient levels considered here. Alternatively, alternative measures derived from non-linear response functions could be proposed but would require additional agreement on efficiency of parameters and reference levels for soil nutrients.
Estimating field-specific response and its variability
To estimate the extent of non-response to fertilizers, it is imperative to estimate field-level response and its variability, and to separate this variation by accounting for plot-level residual variation as much as possible. Since individual fields are typically not replicated across years, it is important to emphasise that field-level variation represents response variation among fields in a given year, and provides no measure of variation in long-term responsiveness of specific fields or locations. Both statistical methods used here are based on the use of linear mixed models (Henderson 1982), which have the advantage over standard general linear models because, in addition to the residual error term, they can contain other normally distributed random effects. In our case, this offers the possibility of modelling field-level variation in fertilizer response separately from the residual variation. This means that response variation inferred from the data, represented by field-level random effects, can be larger or smaller depending on the magnitude of the plot-level residual variation. For the same amount of observed response variation, larger residual variation will cause the model to infer less variation at the field level. The inferred values of field-level response and their variation can therefore be corrected for plot-level residual variation. Such correction is missing when using standard linear models or observed differences between control and treated plots, leading to overestimation of field-level variation.
For the absolute response calculated per study, we applied a relatively crude method to adjust estimates of plot-level residual variation by using fixed values derived from existing studies that included some form of field-level replication. Based on average values in the literature, the plot-level residual variation (i.e. the residual error) was set to 697 kg ha−1 for cereals ( Njoroge et al. 2017; ten Berge et al. 2019; De Laune et al. under review; Kamanga et al. 2014) and 250 kg ha−1 for legumes (Ronner et al. 2016; van Heerwaarden et al. 2018). For comparison, we also used a model where the residual error was fixed at 0, which corresponds to the observed paired differences between control and fertilized plots, without correction for plot-level residual variation.
For the relative response (as a function of fertilizer application intensity as measured by CNE), a slightly more sophisticated approach was used in which the plot-level residual variation was estimated from the dataset itself (see van Heerwaarden et al (2018) for a description of a similar approach and the Supplement S1b for details). Briefly, since part of the trials in the dataset contain several blends or rates of fertilizer on the same field, it was possible to apply a regression approach to quantify the fertilizer response using CNE as a covariate. Conceptually, on each field a regression line was fit to model yield as a linear function of CNE. The inferred slope for each field was then taken as a general measure of response, equivalent to the agronomic efficiency. Under the assumption that the yield is indeed linear with respect to CNE, the field-level deviations from each regression line can be considered as the residual, and can be used to estimate the plot-level residual variation. By using a mixed linear model and incorporating the field-level slopes as a random effect, two things are achieved. First, these statistical models are robust to unbalanced data and an estimate of plot-level residual variation is obtained even if not all fields have more than two fertilizer treatments. Second, the variation in slopes inferred from such a model is automatically adjusted for the amount of residual variation, providing a more accurate assessment of the actual field-level response variability and non-response than would be obtained from standard regression models. Although attractive, it is important to point out two caveats of this approach. First, the assumption of a linear relation between yield and fertilizer application intensity is likely to be commonly violated to some extent, which means that plot-level residual variation may be overestimated and, consequently, field-level response variation may be underestimated. Second, we currently assume a single level of residual variation for the entire dataset, an assumption that if violated could lead to inaccurate estimates of field-level variation in some areas.
Spatial representativeness and geospatial patterns in responsiveness
Two types of spatial analysis were performed on the dataset: an evaluation of potential spatial bias in the selection of our trial sites and an analysis of the geospatial patterns of responsiveness. All georeferenced trial locations were linked to geospatial information consisting of freely available spatial raster layers, namely a set of 250 m resolution maps of predicted topsoil properties and soil nutrient levels (Hengl et al. 2015, 2017) and a crop mask produced by the African Soil Information Service project (AfSIS) and 30 s resolution maps representing bioclimatic variables (Fick and Hijmans 2017) (See Supplement Table S2 for details). For the crop mask, only pixels with a larger than 50% probability of being under crop cover were retained as cropped sites.
The evaluation of spatial representativeness was performed as follows: for both crop types, a training dataset was compiled by combining the trial locations, and associated geospatial data, with an equal number of non-trial locations sampled at random from the crop mask sites. A random forest model (Breiman and Random 2001) was then fit to this training data, resulting in a predictive model for the probability of a new location to be classified as a trial location. This model was then applied to all retained cropped sites, where the site-specific probability of being classified as a trial location was used as a probability weight determining the chance of a location to end up in a random sample subject to the same spatial and environmental biases as the current set of trial locations. Site selection bias is expected to cause a skewed distribution of these probabilities, since sites with high environmental similarity to the trial locations would have the highest selection probabilities, whereas in the absence of such bias the distribution of selection probabilities should be uniform.
We used this principle to quantify spatial and environmental sampling bias by resampling all cropped sites with replacement and quantifying the proportion of sites that ended up in the final sample. In the case of uniform selection probabilities, the expected proportion of sites that end up in a sample of size n is 63%. This follows from the fact that random site selection can be treated as a set of Bernoulli trials for which the probability of inclusion of each individual site is given by:
Spatial bias in the set of trial locations was therefore quantified by comparing the actual proportion of sites that ended up in the sample to this theoretical value. Proportions below 0.63 are evidence of spatial bias.
The second analysis aimed to establish if predictable geospatial patterns were present in the fertilizer responses. The estimated field-level relative fertilizer responses were first tested for spatial structure using Moran's test for spatial autocorrelation (implemented in the spdep package). Association with geospatial variables was evaluated by fitting a random forest model with all variables and comparing the predictive ability with that of a model with geographic coordinates as only explanatory variables. Predictive ability was thereby defined as the correlation between the out of bag (OOB) predictions with the observed fertilizer response vector.
Defining threshold for non-response
We define non-response simply as cases where the yield differences between fertilized and unfertilized treatments are not significantly different from 0 or significantly lower than 0. For the regression approach used here, this translates to a zero or negative slope with respect to the fertilizer application intensity (CNE).
Results
Mean response, response variability, and prevalence of non-response
Absolute response
Absolute responses to inputs in cereals averaged 1365 kg ha−1 (Table 1), ranging from 599 to 2279 kg ha−1 for sorghum in Mali in 2009 and maize in Malawi in 2011 respectively (Supplement Table S3a). In legumes, the average response to applied fertilizers was 252 kg ha−1 (Table 1) with a range from −27 kg ha−1 in groundnut in Zimbabwe to 671 kg ha−1 in climbing bean in Rwanda in 2012 (Supplement Table S4a).
Variations in the absolute response for different studies are shown for cereals and legumes in Fig. 1, and Supplement Figures S1 and S2. For cereals, the proportion of non-responsive fields was generally very low when taking into account the residual variation, with a mean of only 0.9% and an average 95% confidence interval from 0.4 to 6.5% (Table 1). In fact, for the majority of studies, the mean and the lower confidence limit for the percentage of non-response were zero (Table S3b). The largest proportion of non-response was observed in trials in Kenya in 2004, the only study in which the lower confidence boundary of non-response was above 0 (6.8%). Not surprisingly, ignoring the residual variation led to higher estimates of non-response, with a mean of 4.9% and a confidence interval from 2.2 to 16.1% (Table 1, Supplement Table S3a).
Cumulative distributions, with 95% confidence intervals, of predicted absolute fertilizer response for maize in Malawi (mz.mlw09) and Soybean in Ghana (Sy.gh11). Black represent the “empirical” distribution assuming zero residual error. Red represent the distribution under the assumption of a residual error of 697 kg ha−1 for cereals and 250 kg ha−1 for legumes. mz.mlw09 refers to maize grown in 2009 season in Malawi; Sy.gh11 to soybean grown in 2011 season in Ghana. Other studies are presented in Supplement Figure S1 for cereals and Figure S2 for legumes
For legumes, the mean proportion of absolute, residual-corrected non-response was relatively high (7.4%), with a confidence interval from 2.0 to 27.8% (Table 1). The highest proportion of non-response (50%) was found in the groundnut study in Zimbabwe, associated with a mean response close to 0 (Table S4b). Only 5 out of 27 studies had a proportion of non-response above 5% at the lower confidence limit, whereas 6 studies had a zero percent non-response at the upper confidence limit. Not correcting for residual error, again led to a substantially higher mean proportion of non-response of 17% with a confidence interval from 11.8 to 33.7% (Table 1, Supplement Table S4a).
Relative response
In terms of the relative response to the fertilizer application intensity defined by CNE, the mean response was 5.8 kg grain kg−1 CNE for cereals, ranging from 2.8 to 9.8 kg grain kg−1 CNE (Table 1, Supplement Table S5). The corresponding values for legumes were 4.9 kg grain kg−1 CNE with a range of −0.67 to 13.5 kg grain kg−1 CNE (Table 1, Supplement Table S6).
Variations in the relative response for different studies are shown in Fig. 2, and in Supplement Figure S3 for cereals and Figure S4 for legumes, and indicate that, for all cereal studies, the lower confidence boundary non-response was 0.
Cumulative distributions, with 95% confidence intervals, of predicted relative fertilizer response for maize in Malawi (mz.mlw09) and Soybean in Ghana (Sy.gh11). mz.mlw09 refers to maize grown in 2009 season in Malawi; Sy.gh11 to soybean grown in 2011 season in Ghana. Other studies are presented in Supplement Figure S3 for cereals and Figure S4 for legumes
The estimated proportions of non-response in cereals were very low, with a mean of 0% and a confidence interval of 0 to 7.5% (Table 1). This upper limit was similar to that of the absolute response corrected with fixed residual error. For legumes, the mean proportion of non-response was 15.9%, somewhat higher compared to that in residual error-corrected absolute response, but not significantly so considering the width of the 95% confidence interval.
Spatial representativeness and spatial patterns in response
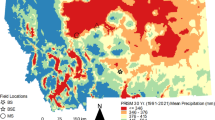
A spatial bias was evident in the selection of both cereal and legume trial locations but was more pronounced in the latter (Fig. 3). In both cases, the probability of being a trial site was highest around the actual trial locations, but for legumes, the large number of trial locations belonging to a single soybean study caused a clear bias towards Nigeria. This was reflected in a representativity measure of only 35 out of 63 percent for legumes, compared to 51 out of 63 percent for cereals, indicating that a spatial sampling bias was present. The extent to which this spatial bias is expected to affect the overall estimates of non-response would depend on the relation between response estimates and geospatial factors. After correcting for individual study, the response variation showed evidence of spatial auto-correlation in legumes (p < 0.0001) but not in cereals (p = 0.5249). In both cases, random forest predictions, using the full set of geospatial covariates, explained only a negligible amount of variation in relative response, 0.5 and 4% for cereals and legumes respectively, the same prediction accuracies as observed for a model with latitude and longitude only. This implies that there was no predictable spatial or environmental variation in the observed fertilizer responses in our data and suggests that there is no reason for estimates of non-response to be different if our study included trials located elsewhere. Hence, under the assumption of representativity, we attempted to provide a rough estimate of the total cropping area in sub-Saharan Africa that would be expected to be non-responsive to fertilizer application. Taking published estimates of total cropland areas planted to cereals as 52 million ha (van Ittersum et al. 2016) and to legumes as 27 million ha (Abate et al. 2012), and average levels of non-response (absolute with correction for residual error, and CNE relative response combined) of 0.5 and 12% found in the present study, respectively for cereals and legumes, the point estimate of the total area of non-response to fertilizers for the two crop types would be 260,000 ha for cereals and 3,240,000 ha for legumes.
When ignoring plot-level residual variation (absolute response without accounting for residual error or empirical response), the average non-response of 4.9% for cereals and 17% for legumes would lead to corresponding point estimates of total non-responsive area of 2,548,000 ha and 4,590,000 ha respectively.
Discussion
Prevalence of non-response to fertilizers
The present study used different statistical approaches to quantify the field-level variability in crop response to fertilizers from a collection of nonreplicated on-farm trials in SSA.
Our results show that while significant variations in response exist for both crops, actual agronomic non-response is relatively rare among on-farm trials and most probably below 1% and 15% of fields respectively for cereals and legumes. For cereals, accounting for plot-level residual error, either by fixing it to published values or by estimating it using our regression approach, produced low estimates of non-response compared to simple, empirical estimates of non-response, which do not consider the residual error. Studies have reported agronomic non-responses for maize in the range of 10–21% fields (Shehu et al. 2018; Ichami et al. 2019; Kihara et al. 2016). These proportions are higher than the mean in our study (Table 1) but mostly within the upper confidence limits in the option of non-consideration of residual error (Supplement Table S3a). Without residual error correction, only 3 studies had the mean proportion non-response within the reported range, whereas none of the studies was in that range when the residual error was considered (Supplement Table S3a&b). It seems therefore that although non-response exists, its magnitude may be lower than often reported, as long as residual variation is considered in the analysis.
The occurrence of agronomic non-response was more pronounced in legumes regardless of the approach used, and the wide confidence interval makes all approaches relatively similar. Studies reporting non-response to fertilizers in legumes are rare and information on that topic scanty. In on-farm fertilizer trials conducted in DR Congo, Kenya, Nigeria and Tanzania, Roobroeck et al (2021) reported 18–62% non-responsive fields for soybean, when non-response was defined as a failure to increase the yield of unfertilized control above 150 kg ha−1. Ronner et al (2016), using 10% yield increase as the increase needed for a treatment effect to be visible for farmers, reported 10–40% fields which did not reach that benchmark in Northern Nigeria. These ranges are probably not very different if a common threshold for non-response could be used. Defining a universal benchmark for response could improve the estimation of the occurrence of non-response in legumes.
Regardless of the crop, the range in the proportions of non-response estimated using the regression approach, with CNE as measure of general fertilizer application intensity, was similar to that when a fixed residual error was considered (Table 1). The regression-based approach solves two limitations to the quantification of fertilizer response variation. First, it implements a single measure of fertilizer application intensity that can be used for data on all types of fertilizers (single, multi-nutrient). Second, it avoids inflating variability by estimation plot-level residual variation from the regression model. Although attractive, there are obvious limitations to this approach. First, by using a single measure of application intensity the interpretation of response is not always straightforward, since a soil may be unresponsive for single nutrients only, requiring caution when interpreting results. Second, the use of CNE implies assumptions on crop nutrition, including a linear response at lower nutrient rates, that may not be entirely accurate and involve crop specific parameters that may be adjusted over time, potentially making published values of agronomic efficiency obsolete. Nonetheless, we consider this approach to have promise as a basis for diagnosing general problems that inhibit crop responses to nutrient applications using the type of nonreplicated data that is typically available in the African smallholder context.
Representativeness of trial locations and spatial patterns of non-response
One may question the extent to which our reported proportions of non-response is representative for sub-Saharan Africa, considering that our trial locations only cover a relatively small portion of the target region. Indeed, on one hand, we found a rather strong spatial bias in our sample of trials, particularly in the case of legumes. On the other hand, we could not predict any meaningful amount of response variation, after correcting for individual studies, based on climatic and environmental covariables. This lack of obvious dependence on environmental factors suggests that data from other parts of the region can be expected to yield similar outcomes, although results may vary considerably between individual studies, especially for legumes. Therefore, accepting the current average level of non-response as representative, we can provide a rough estimate of non-responsive cultivated area as 260,000 ha and 3,240,000 ha for cereals and legumes respectively, though there was a wide confidence interval for the proportion of non-response. Failing to account for plot-level residual variation (i.e. relying on simple empirical response data) would result in estimates that are tenfold higher for cereals and 1.4-fold higher for legumes.
The fact that variation in responses to fertilizers was not explained by any climatic or topsoil factors suggests that the variation primarily reflects transient weather or field-level soil effects, implying that the data used does not allow to identify and target specific areas of high or low fertilizer efficiency, something that has been reported in other studies (Ronner et al. 2016). In fact, studies trying to identify the biophysical properties (soil, rainfall) that cause non-response to fertilizers have generated inconsistent results, attributed to the interactions between factors (Roobroeck et al. 2021; Kihara et al. 2016). Zingore et al (2007) reported that low soil organic C was the main cause of the non-response in their study. In opposite, non-responsive fields in Kihara et al (2016), and Shehu et al (2018), had relatively higher soil organic C than the responsive fields, even though they did not show high yields in the unfertilized treatments. The two studies attributed non-response to imbalanced soil nutrients, including secondary and micronutrients, but other, not considered factors likely also play an important role.
Conclusions
The two approaches used here demonstrate that it is possible to account for plot-level residual variation in non-replicated on-farm trials, and that using a general measure of fertilizer application intensity allows for joint analysis and comparison of disparate datasets on nutrient responses. Our study also identifies some clear limitations that further research will hopefully help to overcome. First, the estimates of plot-level residual variation would improve by making specific adjustments to on-farm trial designs for this purpose. The need for sufficient coverage of geographic and farming systems heterogeneity thereby has to be balanced with that for estimates of residual variation. Options include the inclusion of duplicate plots for certain treatments or increasing the number of evaluated nutrient levels. Even applying a small number of on-site replications across the study region could be an option in this regard. Second, while our regression approach for estimating fertilizer response is attractive, it works best when the relation between the measure of application intensity and yield is expected to be linear. While this may be true for CNE under some assumptions, there is a clear need to look critically at what type of nutrient response functions might perform best in this regard and validate them empirically if possible. Third, the relatively strong spatial bias reported for our dataset is a reminder of the need for better sampling design when setting up on-farm nutrient response trials. Logistic and organization constraints very often lead to clustered and spatially unrepresentative trial sites. While it does not necessarily invalidate the outcomes, it is obvious that a systematic sampling approach that ensures proper representation of a pre-defined target area would hold many advantages in terms of analysis and extrapolation of results, an aspect that some recent initiatives are considering (e.g. African Cassava Agronomy initiative (https://acai-project.org) and which should be widely adopted.
Change history
10 November 2021
In the PDF version of the original publication, grey shades were missing for the “Mid” values for the Legume category in Table 1. Now this has been fixed.
References
Abate T, Alene AD, Bergvinson D, Shiferaw B, Silim S, Orr A, Asfaw S (2012) Tropical grain legumes in Africa and South Asia: knowledge and opportunities. PO Box 39063, Nairobi, Kenya: International Crops Research Institute for the Semi-Arid Tropics. 112 pp. ISBN: 978–92–9066–544–1. Order Code: BOE 056
Adiele JG, Schut AGT, van den Bueken RPM, Ezui KS, Pypers P, Ano AO, Egesi CN, Giller KE (2020) Towards closing cassava yield gap in West Africa: agronomic efficiency and storage root yield responses to NPK fertilizers. Field Crop Res. https://doi.org/10.1016/j.fcr.2020.107820
Adjei-Nsiah S, Alabi BU, Ahiakpa JK, Kanampiu F (2018) Response of grain legumes to phosphorus application in the Guinea Savanna Agro-Ecological zones of Ghana. Agron J 110:1089
Andriesse W, Giller K (2015) The state of soil fertility in sub-Saharan Africa. Agric Dev 24:32–36
Bielders CL, Gérard B (2015) Millet response to microdose fertilization in south-western Niger: effect of antecedent fertility management and environmental factors. Field Crops Res 171:165–175. https://doi.org/10.1016/j.fcr.2014.10.008
Binswanger-Mkhize HP, Savastano S (2017) Agricultural intensification: the status in six African countries. Food Policy 67:26–40
Bonilla Cedrez C, Chamberlin J, Guo Z, Hijmans RJ (2020) Spatial variation in fertilizer prices in Sub-Saharan Africa. PLoS ONE. https://doi.org/10.1371/journal.Pone.,0227764
Breiman L, Random F (2001) Machine learning 45: 5–32
CIALCA (2009) Technical progress report No 6 of the Consortium for Improving Agriculture-based Livelihoods in Central Africa (CIALCA). CIAT-TSBF, IITA, Bioversity
Druilhe Z, Barreiro-Hurlé J (2012) Fertilizer subsidies in sub-Saharan Africa. ESA Working paper No. 12–04. Rome, FAO
Fick SE, Hijmans RJ (2017) WorldClim 2: new 1km spatial resolution climate surfaces for global land areas. Int J Climatol 37:4302–4315
Garba M, Serme I, Wortmann CS (2018) Crop yield response to fertilizer relative to soil properties in sub-Saharan Africa. Soil Sci Soc Amer J 82:862–870
Greenwood DJ, Wood JT, Cleaver TJ, Hunt J (1971) A theory for fertilizer response. J Agric Sci 77:511–523. https://doi.org/10.1017/S0021859600064595
Henderson CR (1982) Analysis of covariance in the mixed model: higher-level, nonhomogeneous, and random regressions. Biometrics 38:623. https://doi.org/10.2307/2530044
Hengl T, Heuvelink GBM, Kempen B, Leenaars JGB, Walsh MG, Shepherd KD, Sila A, MacMillan RA, Mendes de Jesus J, Tamene L, Tondoh JE (2015) Mapping soil properties of Africa at 250 m resolution: random forests significantly improve current predictions. PLoS ONE 10:e0125814. https://doi.org/10.1371/journal.pone.0125814
Hengl T, Leenaars JGB, Shepherd KD, Walsh MG, Heuvelink GBM, Mamo T, Tilahun H, Berkhout E, Cooper M, Fegraus E, Wheeler I, Kwabena NA (2017) Soil nutrient maps of Sub-Saharan Africa: assessment of soil nutrient content at 250 m spatial resolution using machine learning. Nutr Cycl Agroecosyst 109:77–102. https://doi.org/10.1007/s10705-017-9870-x
Holden AT (2018) Fertilizer and sustainable intensification in Sub-Saharan Africa. Glob Food Secur 18:20–26
Hutton CE, Robertson WK, Hanson WD (1956) Crop response to different soil fertility levels in a 5 by 5 by 5 by 2 factorial experiment: I. Corn 1. Soil Sci Soc Am J 20:531–537
Ichami SM, Shepherd KD, Sila AM, Stoorvogel JJ, Hoffland E (2019) Fertilizer response and nitrogen use efficiency in African smallholder maize farms. Nutr Cycl Agroecosyst 113:1–19. https://doi.org/10.1007/s10705-018-9958-y
IFDC (2006) Africa Fertilizer Summit Proceedings, Abuja, Nigeria June 9–13 2006. Florence, Alabama, IFDC
Janssen BH (1998) Efficiency use of nutrients: an art of balancing. Field Crops Res 56:197–201
Janssen BH (2011) Simple models and concepts as tools for the study of sustained soil productivity in long term experiments II: crop nutrient equivalents, balanced supplies of available nutrients and NPK triangles. Plant Soil 339:17–33
Janssen BH, Guiking FCT, van der Eijk D, Smalling EMA, Wolf J, van Reuler H (1990) A system for quantitative evaluation of the fertility of tropical soils (QUEFTS). Geoderma 46:299–318
Jayne TS, Rachid S (2013) Input subsidy programs in sub-Saharan Africa: a synthesis of recent evidence. Agric Econ 44:547–562
Jayne TS, Mason NM, Burke WJ, Ariga J (2018) Review: taking stock of Africa’s second-generation agricultural input subsidy programs. Food Policy 75:1–14. https://doi.org/10.1016/j.foodpol.2018.01.003
Kaizzi KC, Byalebeka J, Semalulu O, Alou I, Zimwanguyizza W, Nansamba A, Musinguzi P, Ebanyat P, Hyuha T, Wortmann CS (2012) Maize response to fertilizer and nitrogen use efficiency in Uganda. Agron J 104:73–82
Kamanga BCG, Waddington SR, Whitbread AM, Almekinders CJM, Giller KE (2014) Improving the efficiency of use of small amounts of nitrogen and phosphorus fertiliser on smallholder maize in central Malawi. Exp Agr 50:229–249. https://doi.org/10.1017/S0014479713000513
Kihara J, Nziguheba G, Zingore S, Coulibaly A, Esilaba A, Kabambe V, Njoroge S, Palm C, Huising J (2016) Understanding variability in crop response to fertilizer and amendments in sub-Saharan Africa. Agric Ecosyst Environ 229:1–12. https://doi.org/10.1016/j.agee.2016.05.012
Liverpool-Tasie LSO, Omonona BT, Sanou A, Ogunleye WO (2017) Is increasing inorganic fertilizer use for maize production in sub-Saharan Africa a profitable proposition? Evidence from Nigeria. Food Policy 67:41–51
Mafongoya PL, Bationo A, Kihara J, Waswa BS (2007) Appropriate technologies to replenish soil fertility in southern Africa. Nutr Cycl Agroecosyst 76:137–151. https://doi.org/10.1007/s10705-006-9049-3
Ngome AF, Becker M, Mtei MK, Mussgnug F (2013) Maize productivity and nutrient use efficiency in Western Kenya as affected by soil type and crop management. Int J Plant Product 7:517–536
Njoroge S, Schut AGT, Giller KE, Zingore S (2017) Strong spatial-temporal patterns in maize yield response to nutrient additions in African smallholder farms. Field Crops Res 214:321–330
Notore (2016) Technical report Notore-IITA (Apr 2015-May 2016)_PJ 1535. Pg 12. Notore Chemical Industries Limited, Notore Industrial Complex Onne, Rivers State, Nigeria; PROMIS data-base, IITA, Ibadan, Nigeria
Olk DC, Cassman KG, Simbahan G, Cruz PCS, Abdulrachman S, Nagarajan R, Tan PS, Satawathananont S (1999) Interpreting fertilizer use efficiency in relation to soil nutrient supplying capacity, factor productivity and agronomic efficiency. Nutr Cycl Agroecosyt 53:35–41
Ronner E, Franke AC, Vanlauwe B, Dianda M, Edeh E, Ekem B, Bala A, van Heerwaarden J, Giller KE (2016) Understanding variability in soybean yield and response to P-fertilizer and rhizobium inoculants on farmers’ fields in northern Nigeria. Field Crops Res 186:133–145
Roobroeck D, Palm CA, Nziguheba G, Weil R, Vanlauwe B (2021) Assessing and understanding non-responsiveness of maize and soybean to fertilizer applications in African smallholder farms. Agric Ecosyst Environ 305:107165
Sanchez PA (2010) Tripling crop yields in tropical Africa. Nat Geosci 3:299–300
Schut AGT, Gillet KE (2020) Sustainable intensification of Agriculture in Africa. Front Agr Sci Ang 7:371–375
SFG (2006) Final technical report of the Valuing within-farm soil fertility gradients to enhance agricultural production and environmental service functions in smallholder farms in East Africa project (SFG). CIAT-TSBF
Shapouri S, Rosen S, Peters M, Baquedano F, Allen S (2010) Food Security Assessment, 2010–20: a Report from the Economic Research Service. United States Department of Agriculture (USDA)
Sheahan M, Barret CB (2017) Ten striking facts about agricultural input use in sub-Saharan Africa. Food Policy 67:12–25
Shehu BM, Merckx R, Jibrin JM, Kamara AY, Rurinda J (2018) Quantifying variability in maize yield response to nutrient applications in the northern Nigerian savanna. Agron 8:18. https://doi.org/10.3390/agronomy8020018
ten Berge HFM, Hijbeek R, van Loon MP, Rurinda J, Tesfaye K, Zingore S, van Ittersum MK (2019) Maize crop nutrient input requirements for food security in sub-Saharn Africa. Glob Food Secur 23:9–21
Tittonell P, Giller KE (2013) When yield gaps are poverty traps: the paradigm of ecological intensification in African smallholder agriculture. Field Crops Res 143:76–90
Tittonell P, Vanlauwe B, de Ridder N, Giller KE (2007) Heterogeneity of crop productivity and resource use efficiency within smallholder Kenyan farms: soil fertility gradients or management intensity gradients? Agric Syst 94:376–390
UN Millennium project (2005) Halving hunger: it can be done. Earthscan, London
van Heerwaarden J, Baijukya F, Kyei-Boahen S, Adjei-Nsiah S, Ebanyat P, Kamai N, Wolde-meskel E, Kanampiu F, Vanlauwe B, Giller KE (2018) Soyabean response to rhizobium inoculation across sub-Saharan Africa: patterns of variation and the role of promiscuity. Agric Ecosyst Environ 261:211–218
van Ittersum MK, van Bussel LGJ, Wolf J, Cassman KG (2016) Can sub-Saharan Africa feed itself? PNAS 113:1964–1469
Vanlauwe B, Bationo A, Chianu J, Giller KE, Merckx R, Mokwunye U, Ohiokpehai O, Pypers P, Tabo R, Shepherd KD, Smaling EMA, Woomer PL, Sanginga N (2010) Integrated soil fertility management: operational definition and consequences for implementation and dissemination. Outlook Agr 39:17–24
Vanlauwe B, Kihara J, Chivenge P, Pypers P, Coe R, Six J (2011) Agronomic use efficiency of N fertilizer in maize-based systems in Sub-Saharan Africa within the context of integrated soil fertility management. Plant Soil 339:35–50
Vanlauwe B, Coyne D, Gockowski J, Hauser S, Huising J, Masso C, Nziguheba G, Schut M, Van Asten P (2014) Sustainable intensification and the smallholder farmer. Curr Opin Environ Sustain 8:15–22
Vanlauwe B, Coe R, Giller KE (2016) Beyond averages: new approaches to understand heterogeneity and risk of technology success or failure in smallholder farming. Exp Agr. https://doi.org/10.1017/S0014479716000193
Wortmann CS, Milner M, Kaizzi KC, Nouri M, Cyamweshi AR, Dicko MK, Kibunja CN, Macharia M, Maria R, Nalivata PC, Demissie N, Nkonde D, Ouattara K, Senkoro CJ, Tarfa BD, Tetteh FM (2017) Maize-nutrient response information applied across Sub-Saharan Africa. Nutr Cycl Agroecosyst 107:175–186. https://doi.org/10.1007/s10705-017-9827-0
Xu X, He P, Pampolino MF, Johnston AM, Qiu S, Zhao S, Chuan L, Zhou W (2014) Fertilizer recommendation for maize in China based on yield response and agronomic efficiency. Field Crops Res 157:27–34
Zingore S, Murwira HK, Delve RJ, Giller KE (2007) Soil type, management history and current resource allocation: three dimensions regulating variability in crop productivity on African smallholder farms. Field Crops Res 101:296–305
Zingore S, Murwira HK, Delve RJ, Giller KE (2008) Variable grain legume yields, responses to Phosphorus and rotational effects on maize across soil fertility gradients on African smallholder farms. Nutr Cycl Agroecosyst 80:1–18
Zurek M, Keenlyside P, Brandt K (2015) Intensifying agricultural production sustainably: A framework for analysis and decision support. Amsterdam, The Netherlands: IFPRI. Climate focus
Acknowledgements
The authors are grateful to individuals who provided datasets used in the paper: Job Kihara, Cargele Masso, Ibrahim Mohammed, Pieter Pypers, Dries Roobroeck, Shamie Zingore. Although no funding was received to assist in the preparation of this manuscript, datasets used were generated from projects funded by various donors: Bill and Melinda Gates Foundation, Belgium Directorate General for Development Cooperation, National Science Foundation, Alliance for the Green Revolution in Africa, International Fund for Agricultural Development, UK Department for international Development, and Rockefeller Foundation.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nziguheba, G., van Heerwaarden, J. & Vanlauwe, B. Quantifying the prevalence of (non)-response to fertilizers in sub-Saharan Africa using on-farm trial data. Nutr Cycl Agroecosyst 121, 257–269 (2021). https://doi.org/10.1007/s10705-021-10174-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10705-021-10174-1