Introduction

Haber’s 1909 discovery of an industrial nitrogen (N) fixation process catalyzed a century of booming agricultural production and development, feeding the rapidly growing world population and fueling consumption of N fertilizer (Coleman and Dec 1989; Gliessman and Engles 2014; Paul and Robertson 1989). Between 1940 and 1980, the amount of N fertilizer applied in the United States increased from 9 to 47 million metric tons and reached 12 Tg N yr−1 as of 2015 (Gliessman 2016), furthering long-held concerns about the ecological and environmental implications of intensive fertilizer use (Gliessman and Engles 2014; Vitousek et al. 1997). Studies to date suggest that an amount of reactive N equal to at least half of fertilizer N applied is lost each year to N leaching and denitrification from soils (Bouwman et al. 2013). Overapplication of inorganic fertilizers in the quest for maximizing current productivity degrades soil through acidification, overloads water resources with nutrients, and contributes to eutrophication, biodiversity loss and greenhouse gas emissions (Allaire et al. 2018; Capel et al. 2008; DeLonge et al. 2016; Weiner 2017).

Increasing the efficiency of agricultural inputs, including N fertilizer, is a key step in transitioning modern agriculture towards sustainability (Foley et al. 2011; Gliessman 2016). Nitrogen use efficiency (NUE) is typically measured as the percentage of crop biomass N to soil available N (Ping and Dobermann 2003; Prey et al. 2019; Yin et al. 2020). The relationship between crop N and available N over time depends on how available N is assessed, and here we distinguish between NUE and fertilizer use efficiency (FUE). Fertilizer use efficiency is the ratio of crop N to fertilizer N, while NUE is the ratio of crop N to total available N in the soil, including available N produced from soil organic matter through mineralization. Using isotopically labeled N fertilizer FUE has been measured up to 0.65 using the ratio of crop N to fertilizer N (Sebilo et al. 2013). Typical NUE estimates are around 0.3, though in semiarid regions like Montana FUE is expected to be higher due to less leaching and denitrification when drier (Guttieri et al. 2017; Macnack et al. 2014).

Here we focus on dryland small-grain agroecosystems in Montana, where low NUE has been linked to elevated nitrate levels in drinking water, acidification of agricultural soils, and substantial loss to denitrification with associated production of the greenhouse gas N2O (Engel 2012; John et al. 2017; Sigler et al. 2018, 2022). Generally, the degree of NUE from conventionally managed fields in dryland Montana agroecosystems reflects soil character, weather, and agronomic management (Sigler et al. 2020). Efficiency is lowest when nitrogen loss is greatest, which occurs with deep percolation of water following substantial precipitation events and summer fallow, as well as with denitrification under related soil conditions of elevated water content in the absence of plant uptake (Sigler et al. 20202022). Not only does summer fallow increase the potential for deep percolation of soil water to an underlying aquifer, but it may also stimulate mineralization of soil organic matter, further increasing the risk of nitrate leaching (Sigler et al. 2020). Previous work showed that while heavy precipitation can cause “hot moments” of nitrate leaching, soil character can dictate “hot spots” of nitrate leaching within agricultural fields. These spatial and temporal trends in N loss provide insight about NUE dynamics as a function of management, weather and soils.

Farmers who understand the controls and drivers of NUE can alter decisions based on conditions and practices that expose them to potential economic loss due to low NUE. Understanding the variation in soil character within fields represents an opportunity to inform site-specific N fertilizer management that maximizes NUE within fields. While farmers cannot control the weather, advances in remote sensing and modeling have improved the accuracy and spatial scale of weather predictions, which provide farmers with better weather forecasts to inform N fertilizer management decisions. Moreover, the affordability of personal weather stations gives farmers direct access to their own weather data. Importantly, interactions between weather, soils, and management interact with each other to make N transport dynamics complex. However, at a simple level, crop rotations and weather influence N loss at the field scale and soil texture and structure, and the resulting WHC influence N loss at the sub-field scale. Therefore, linking subfield scale variation in crop response to variation in soil character is the starting point for making effective predictions about NUE to achieve greater sustainability in these systems.

The subfield variation in crop response to variable N fertilizer (Hegedus and Maxwell 2022a) suggests that NUE varies substantially within fields, at a resolution higher than most farmers’ soil sampling practices can reveal. Soil mapping and soil sampling provide information on the WHC of soils yet current soil maps may not provide the resolution needed for site-specific N fertilizer management (Kamilaris et al. 2017; Lokers et al. 2016; Wolfert et al. 2017). Additionally, soil sampling and analysis are expensive and typically conducted in a sparse manner across fields, making it difficult for farmers to acquire and analyze soil data at spatial resolutions adequate for site-specific N management decisions. In response to this challenge, statistical models of the relationships among NUE, spectral imagery and landscape characteristics have been developed (Oelofse et al. 2015; Pavuluri et al. 2015; Semenov et al. 2007). These estimates of NUE have typically involved simple linear models that require site-and-time-specific parameters, and represent a first step towards developing tools to estimate efficiency at subfield scales for informing N fertilizer management decisions (Arnall et al. 2009; Macnack et al. 2014; Van Sanford and MacKown 1986).

Precision agriculture has progressed over the last few decades into a management approach for inputs like N fertilizer that account for spatial variation at relatively high resolution across fields (Bullock et al. 2019). At the same time, the recent revolution in agricultural data acquisition has coincided with the introduction of data science approaches into agronomic research and development (Coble et al. 2018; Pham and Stack 2018; Vinila Kumari et al. 2016). The amount of farm data now available makes it possible for data science to aid in the management and analysis of agronomic data and inform local within-field decision making (Gibert et al. 2018; Provost and Fawcett 2013). Investigating the benefit of generalizable data science tools for modeling the relationship of NUE with soil parameters, N fertilizer rates, and other open-source data can inform precision agroecological approaches to N fertilizer management that are conscious of economic and ecological outcomes (Duff et al. 2022; Mittermayer et al. 2021). Identifying areas of a field at risk of N loss using freely available remotely sensed data benefits farmers by providing information on where NUE is potentially low, which can inform site-specific N fertilizer management decisions.

The goal of this study was to introduce protocols for utilizing empirical measurements to estimate NUE and develop analytical tools that can aid farmers in the application of N fertilizer that maximizes profit and reduces the risk of pollution from applied fertilizer N loss. The first objective of this study was to evaluate the relationships of NUE with causal variables derived from low-cost open-source and on-farm data sources in conventional dryland Montana agroecosystems cropped with winter wheat (Triticum aestivum L.). To consider these relationships in a hypothetical low-cost decision support system, the second objective was prediction of NUE in similar dryland winter-wheat systems without soil sampling, using a suite of potential generalizable models. The modelling objective was to estimate subfield NUE for a given year without requiring producers to take detailed soil samples or provide difficult to measure parameters for complex biogeochemical models. While developed in dryland winter-wheat systems of Montana, the methods outlined in this paper are applicable to other crops and systems when similar procedures are used to generate information for increasing agronomic input efficiency with simultaneous consideration for profitability.

Methods

Study sites

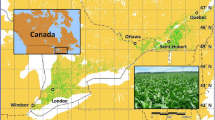
Four fields from farmers collaborating with the On-Farm Precision Experiments (OFPE) project (https://sites.google.com/site/ofpeframework/home) at Montana State University (MSU) were used. Four separate fields from two regions of Montana (Fig. 1) were sampled, two in 2020 and two in 2021 (Table 1) where average statewide yields were 3362 kg ha−1 in 2020 and 2084 kg ha−1 in 2021. All fields have been in a crop-fallow rotation since 2014. In the seasons since 2016 when winter wheat was grown, each field was subjected to spatially variable N experiments. These experimental rates that encompassed the whole field were designed based on stratified random sampling to ensure representation of experimental rates across previous yield, protein, and any prior N rate experimentation to account for legacy effects. An example experimental N rate design is shown in SI Fig. 1 of the Online Resource.

Fig. 1
figure 1

Map showing 30-year mean (1991–2021) precipitation at a 4 km resolution from the University of Orgeon PRISM Climate Group. Symbols indicate fields sampled during 2020 and 2021. Two fields were sampled from Farm B (BS and BSE), one in each year, with a corresponding field in Farm W (WH 2020) or M (MS, 2021)

Full size image
Table 1 Field and soil characteristics for each experimental field
Full size table

Fields were chosen based on data availability, data quality, and geographic location across Montana, in the interest of creating a general model for estimating NUE within the predominant dryland small-grain agroecosystems (Table 1). While in an ideal world, field specific measurements to generate field specific models would be available, offering a generalizable NUE model for use in dryland small-grain agroecosystems gives farmers access to NUE information at a low cost.

The fields observed in this study were similar in management and environment to the fields observed by Sigler et al. (2020) and John et al. (2017). All fields used in our study were cropped with winter wheat in alternate years with chemical fallow, a practice where no crop is grown to conserve water in the soil. While the detailed character of soils used in this study differed from those in Sigler et al. (2020) and John et al. (2017), these well-drained soils are on similar landforms with similar climate, suggesting that inference about the drivers of N loss from Sigler et al. (2020) and John et al. (2017) pertain to the fields used in this study.

Classification of water holding capacity

A high spatial density estimate of WHC was created based on remotely sensed Normalized Difference Vegetation Index (NDVI) data. Estimating WHC from remotely sensed information has been a subject of research for decades (Fuka and McBratney 2004; McBratney and Pratley 2000). Greater soil WHC was expected to result in productivity consistency over time at a specific point in a field, while more variable productivity may reflect moderate WHC and risk of N loss. While we are aware of no studies that have linked historical maps of sub-field-scale NDVI over time to the corresponding NUE or WHC, Sigler et al. (2020) used a single time point to estimate soil WHC and depth of fine textured soils, and Araya et al. (2016) used NDVI over time to estimate available water content, supporting the value of NDVI for estimating soil properties.

The fields used in this study were classified into WHC zones that were used to stratify soil and plant biomass sampling. NDVI was derived from satellite imagery from 2000 to 2021. Landsat imagery (https://developers.google.com/earth-engine/datasets/catalog/landsat) was collected on 30 × 30 m raster grids, a coarser resolution than satellites such as Sentinel-2 but with a longer history of data available. Depending on the year collected, Landsat images were from Landsat 5, 7, or 8.

Imagery was downloaded from Google Earth Engine (GEE), where image processing was performed to correct images for clouds and other atmospheric anomalies (Gorelick et al. 2017). The cloud computing platform of GEE was used to calculate NDVI as:

$$NDVI = \frac{NIR - Red}{{NIR + Red}}$$
(1)

where ‘NIR’ is reflectance at the near-infrared wavelength (~ 865 nm) and ‘Red’ corresponds to reflectance at a visible red wavelength (~ 665 nm). Landsat images for each field for 2000–2021 were composited via the greenest pixel across the calendar year to reflect maximum crop biomass. Although data were collected from 2000 to 2021, years in which average NDVI across each field fell below 0.3 were omitted because these represent fallow years in which no crops were grown, and any productivity was due to weeds growing in the fallow field. For each field, the rasterized NDVI for each year was stacked, and WHC was classified based on each pixel’s mean and coefficient of variation (CV) to produce a single map with classifications of high, medium, and low WHC. High, medium, and low categories for the mean and CV for each pixel were delineated via k-means classification in one dimension to maximize between class variance and minimizing within class variance. A matrix of the mean and CV groups for NDVI were then derived to estimate hypothesized WHC zones where; a low mean NDVI and medium or low CV were labeled as low WHC, a high mean NDVI and medium or low CV were labeled as high WHC, and all other combinations were labeled as medium WHC. High and low NDVI cells that also exhibit a high CV classification were considered medium WHC because the high CV classification indicates that NDVI is occasionally but not consistently high. An illustration of the classification matrix is shown in SI Table 1 of the Online Resource.

Soil and plant biomass sampling

Calibration soil samples were taken at 75 locations with a truck-mounted hydraulic probe in each field twice per year, in March and August, at positions randomly selected with stratification based on WHC category and N application rate (Fig. 2). Samples were taken in March and August for future research that measured inorganic N levels. Soil samples were taken at depths of 0–15, 15–30, 30–60, 60–90, and from 90 cm to as deep as possible. The depth of the deepest sample corresponded to either gravel content, rock layer or the limit of the probe (110 cm). The maximum depth at each location was recorded during sampling. Soil samples were taken within seven days prior to fertilizer application and within seven days post-harvest. Winter wheat biomass samples were hand harvested in June at plant maturity at each of the sampling locations. Samples were transported in coolers on ice from the fields back to MSU where soil and plant samples were weighed wet, oven dried at 50 °C for 7–14 days, and then weighed dry to determine water content. Plant samples were ground using an UDY Cyclone Sample Mill (UDY Corporation, Fort Collins, CO, USA). Soil samples were gently crushed to break up peds and aggregates, sieved (< 2 mm) to remove rocks and roots, and milled with a Dynacrush DC-5 soil crusher (Custom Laboratory, Hodlen, MO, USA). Aliquots were taken from each sample (plant and soil) and analyzed for total N with a combustion analyzer (Costech analytical technologies Inc., Valencia, CA, USA) in the Environmental Analytical Laboratory at Montana State University.

Fig. 2
figure 2

Water holding capacity classifications and sampling locations for each field. A BS 2020, B MS 2021, C BSE 2021, D WH 2020

Full size image

Derivation of nitrogen use efficiency

A mass balance approach was used to determine an estimate for efficiency for each sample location. Prior to assessing NUE, fertilizer use efficiency (FUE) was calculated:

$$FUE = \frac{{N_{crop} }}{{N_{fert} }}$$
(2)

where Ncrop was the N taken up by the crop in the grain, stubble, and roots (kg ha−1) and Nfert was the input of N fertilizer (kg ha−1) from the farmer, measured from the farmer’s fertilizer spraying equipment. Farmers B and M both use a 2002 John Deere 4710 sprayer and farmer W uses a 2015 Case 4440 sprayer. All farmers applied 32% UAN which was converted from gallons ac−1 to kg N ac−1. Montana wheat farmers typically apply one uniform N fertilizer application, typically around 75 lbs N ac−1 in spring (March–April). Grain N was estimated using on-combine protein concentration and yield measurements collected every 10 s and three seconds across the field, respectively. As the data gathered depends on the speed of travel, observations gathered where the speed of the combine was outside the bounds of two standard deviations from the mean speed were omitted. Protein (g protein g−1 grain) was divided by a conversion of 5.83 (g protein g N−1) to estimate g N g grain−1 (Mariotti et al. 2008). To generate an area normalized estimate of grain N uptake, the g N g grain−1 estimates were multiplied by grain yield measurements (g grain ha−1). Grain protein and grain yield measurements were georeferenced to corresponding sample point locations by calculating the distance of each metric to the sample point and selecting the closest measurement within 5 m. Stubble N was estimated as 30% of grain N (Woyema et al. 2012). Root N was estimated as 20% of aboveground biomass N (Andersson et al. 2005; John et al. 2017), calculated as the sum of grain N and stubble N. Crop N uptake was then calculated as the sum of grain N, stubble N, and root N in kg ha−1.

Crop N, as-applied N fertilizer, and estimates of mineralized N for each sample point were used to calculate subfield NUE as:

$$NUE = \frac{{N_{crop} }}{{N_{min} + N_{fert} }}$$
(3)

where Ncrop and Nfert where defined above and Nmin was estimated N mineralized in the top 15 cm of soil (kg ha−1). Due to the nature of the crop-fallow rotation, N fixation was likely negligible, so N fixation was assumed to be zero. Total N deposition was estimated to be 2.92 kg N ha−1 year−1 based on the mean total N deposition from 2000 to 2018 recorded at the closest EPA CASTNET station at Glacier National Park. Compared to other inputs, this rate is negligible and N deposition was omitted from further analysis.

Measured soil mass percent total N (TN) and bulk density (g cm−3) were multiplied to generate a bulk N concentration at each depth (g cm−3) and multiplied by the depth (cm) of each interval to generate an areal density of soil TN (kg ha−1). Bulk density was calculated by dividing the dry weight of the soil sample (g) by the volume of the soil sample (cm3). Measured at the same georeferenced locations in March and August with a 1-m resolution GPS, t-tests comparing TN measures from the two seasons indicated that the TN was equal within uncertainty for all fields. Soil TN includes inorganic and organic pools where the soil organic nitrogen (SON) is present at much greater magnitudes than inorganic N (Wang et al. 2009). Given the magnitude of TN compared to the potential for change in a short study, TN was not included in the calculation of NUE, and TN measurements were only used to calculate N mineralization.

Assessment of NUE requires knowledge of N mineralization from soil organic nitrogen (SON) within fields. Due to the decline of SON and hence mineralization with depth, as well as for consistency among locations with variable sampling depths, soil samples from the top 15 cm were used to calculate mineralization and model NUE (Cassman and Munns 1980). Mineralized N was estimated using a regression model derived from a review of multiple mineralization studies on the relationship between mineralization rate and percent total N from 0 to 15 cm (Vigil et al. 2002);

$$N_{min} = 10.8 + 304.6TN$$
(4)

where TN is the percent by mass total nitrogen in the soil and Nmin was in kg ha−1 for the top 15 cm of soil. Sample points that did not have corresponding TN measurements at each depth interval to 15 cm in both March and August were omitted to generate consistent estimates of mineralized N at each point, yielding observations at 67, 69, 60, and 75 out of 75 sample locations in BS 2020, BSE 2021, WH 2020, and MS 2021, respectively.

Nitrogen use efficiency modeling

A set of six potential generalizable models for estimating NUE at a subfield scale were compared to explore the potential for low-cost methods of developing fertilizer application prescriptions. Development of a general model for predicting subfield NUE relied on environmental covariates gathered from Google Earth Engine (GEE), which were assumed to influence NUE (Table 2). All environmental covariate data were gathered from public domain GEE data repositories (Gorelick et al. 2017) and aggregated with soil sample data. Soil characteristic data collected from OpenLandMap were derived from internal OpenLandMap developers that utilized open-source data from organizations such as the European Space Agency, Copernicus Program, National Aeronautics and Space Administration, United States Geologic Survey, Natural Resources Conservation Service, Food and Agriculture Organization, National Oceanic and Atmospheric Administration, and others (https://opengeohub.org/about-openlandmap/).

Table 2 Table of covariate data types gathered from Google Earth Engine to enrich the crop yield and protein datasets gathered from on-farms
Full size table

Information from each covariate was extracted to each soil sample location to form the analysis dataset (Hegedus et al. 2022; Hegedus and Maxwell 2022b). Temporal data were gathered, delineated by year, and constrained in a range to the point in time that a farmer needs to make decisions on N fertilizer management of dryland winter-wheat in Montana (Hegedus and Maxwell 2022b). The covariates selected for modeling were based on assumptions about environmental variables that influence the components of NUE and observed relationships from evaluation of observed NUE (Table 2). SI Fig. 2 in the Online Resource shows remotely sensed covariate data included in the model selection process and their relation to components of the NUE calculation in Eq. (3).

Candidate models were chosen based on their potential for predictive and not inferential modeling because our objective was not to test direct causality between predictors and NUE, rather to make a model useful for predicting NUE on a subfield scale. Model candidates were selected to represent simple to complex approaches with varying degrees of flexibility and assumptions. The models tested included (1) a baseline simple linear regression (SLR) model that only included as-applied nitrogen as a covariate, and (2) a non-linear regression model using an exponential decay function with as-applied N (NLR). The exponential decay function was selected based on exploratory analysis of the relationship between NUE and N sources, with the assumption that NUE could be predicted solely based on as-applied nitrogen, as in the SLR model. Other models tested were (3) a multiple linear regression model (MLR), (4) a generalized additive model (GAM), (5) a random forest regression machine-learning model (RF) and (6) a support vector regression machine-learning model (SVR). Models 3–6 included all spatially variable covariates from Table 2. Random forest regression is an ensemble tree approach where covariates are randomly sampled in each tree and used to classify observations (Breiman 2001). Support vector regression mapped observations to the feature space generated by the covariate data (Lau and Wu 2008; Smola and Schölkopf 2004).

Spatial covariance structures were incorporated into the models in varying ways to account for spatial autocorrelation of NUE observations. The SLR, MLR, and NLR models used a Gaussian process spatial correlation structure (De Bastiani et al. 2015; Diggle and Tawn 1998; Mardia and Marshall 1984; Xia et al. 2008). The spatial covariance structure for the GAM incorporated a Gaussian basis function on spatial coordinates (Gotway and Stroup 1997; Guisan et al. 2002; Holland et al. 2000; Zuur et al. 2012). The RF and SVR models used approaches commonly described for machine learning approaches which incorporate the spatial data in the model (Janatian et al. 2017; Langella et al. 2010; Walsh et al. 2017; Wang et al. 2017).

Fig. 3
figure 3

Crop N uptake (grain N + stubble N + root N) vs. as-applied nitrogen measured from the farmer’s fertilizer spraying equipment. Colors represent measurements in each field and the black line shows the trend smoothed across all fields

Full size image

All models except the SLR and NLR were subjected to features selection during the fitting process to optimize model performance. Top-down Akaike information criterion (AIC) based feature selection was performed for the MLR and GAM models, where a reduction of two AIC units with the removal of a covariate justified its omission. As AIC is not appropriate for machine learning methods, top-down root mean square error (RMSE) based feature selection was performed for the RF and SVR models. Feature selection was based on a reduction in RMSE to determine whether withholding a covariate improved model performance. All models, except the SLR and NLR, that only used as-applied N fertilizer, began feature selection with a full model that included the WHC classification, and the covariates illustrated in Fig. 4.

Fig. 4
figure 4

Fertilizer use efficiency (FUE) vs. as-applied nitrogen measured from the farmer’s fertilizer spraying equipment. Colors represent measurements in each field. Dashed line indicates FUE = 1. Note that at fertilizer rates of 0 kg ha−1fertilizer, FUE was calculated with a fertilizer rate of 1 to visualize FUE values approaching infinity at zero rates

Full size image

The initial candidate models were subjected to a hold-one out cross validation (HOOCV) approach using observed farm fields to initially assess the ability of the model to predict NUE. Each model was subjected to four cases of HOOCV across all four fields where they were independently trained on data from three fields with performance tested by calculating the RMSE between the predicted and observed NUE from the one field held out from training. The HOOCV scheme is visualized in SI Table 2 of the Online Reference. The RMSE across the four test datasets were averaged for each model and compared to identify the two candidate models that generated the lowest mean RMSE. The two models selected from the HOOCV approach were then empirically assessed using 5 × 2 cross validation (CV) (Dietterich 1998). All the data from the fields were pooled and randomly selected evenly into a training and test dataset. Both models were trained on the training dataset and RMSE was calculated based on predicted and observed NUE in the test dataset. Then the training and testing datasets were swapped (2 folds), and the process was repeated to generate four error metrics and calculate the variance of the difference in the predictions. Beginning with randomly splitting the data evenly, the process was repeated five times (5 folds), and the error estimates and variance from the five repetitions were used to calculate the 5 × 2 t-statistic (Dietterich 1998). Assuming a t-distribution with five degrees of freedom, evidence against the null hypothesis that there was no difference in RMSE between observations and predictions from the two models was evaluated with a two-tailed significance test with a 95% confidence threshold (α = 0.05).

Results

Nitrogen use efficiency evaluation

Based on raw numbers and not statistical differences, the field BSE 2021 had the highest average mineralization and the highest mean experimental N fertilizer rates (Table 3). The range of experimental fertilizer rates were selected for associated research on the development of crop response models but served the purpose of gathering NUE responses across a range of applied N fertilizer rates for this purpose. The lack of zero N fertilizer rates in BSE 2021 were due to a farmer B request made prior to 2021 to discontinue the use of zero N rate experimental plots (Table 3). Crop N uptake was highest on average in field BS 2020 (Table 3). However, NUE was highest on average in WH 2020 due to relatively high crop N uptake and low mineralization and fertilization (Table 3). Calculated NUE values greater than 1 were observed in all fields, ranging from 1.17 to 2.14, indicating that estimated crop N uptake in areas of these fields exceeded total N inputs or that N availability—likely from N mineralization—was underestimated (Table 3).

Table 3 Summary statistics for each component of nitrogen use efficiency (NUE) calculated in Eq. (3)
Full size table

Characterization of the relationship between crop N uptake and N fertilizer using a GAM with cubic shrinkage splines showed an asymptotic relationship (Fig. 3), indicating that crop N uptake does not increase past a threshold of N fertilization. Efficiency was expected to decline with increasing N fertilizer rates due to the asymptotic relationship of crop N uptake and fertilizer (Fig. 5). A negative exponential relationship between FUE and as-applied N fertilizer was observed, where low N rate locations had the largest calculated FUE before approaching a minimum, at higher N rates (Fig. 4). At zero N rates FUE was undefined, indicating that winter-wheat was taking up N contributed by other processes besides fertilization, such as mineralization of SON. When accounting for mineralization in calculations of efficiency, a negative relationship between NUE and as-applied N fertilizer was observed as seen in the black (observed) symbols of Fig. 5. Including mineralized N in the calculation for efficiency provides a more realistic estimate of N inputs to the system, and lowers efficiency values between FUE and NUE calculations, as mineralization compensates for a lack of N fertilizer at low or zero rates. An illustration of the contributions of mineralization and fertilizer to the total N inputs of the system can be referenced in SI Fig. 3 in the Online Reference.

Fig. 5
figure 5

Observed nitrogen use efficiency (NUE) (black points) across variable as-applied N rates, where shapes indicate each field. Predicted NUE values are RF and SVR predictions from the test sets performed in the 5 × 2 CV. Dashed line indicates NUE = 1

Full size image

Model evaluation

In each of the fields, the HOOCV analysis indicated different models reduced uncertainty in predictions of NUE (Table 4). The SLR had the lowest mean RMSE on average across hold-out cases, while the RF had the second lowest mean RMSE on average across hold-out cases, however there was little to no difference between the mean RMSE across fields for the SLR, MLR, RF and SVR models (Table 4). Due to the objective of creating a predictive model of subfield NUE that can be used across dryland winter-wheat agroecosystems in Montana, the SLR was compared to each of the MLR, RF, and SVR models by 5 × 2 CV to test for significant differences between RMSE.

Table 4 RMSE (kg N kg N−1) calculated from the observed and predicted NUE from each model during the hold-one field out cross validation
Full size table

There was little to no evidence against the null hypothesis that RMSE did not differ between the SLR and NLR models (t5 = − 0.25, p-val = 0.8143) indicating that there was no statistical difference in the uncertainty of NUE predictions between the two models. Due to the lack of a difference between the SLR and NLR, the SLR was retained as the best model based on the mean RMSE from the HOOCV and compared to the SVR model. There was strong evidence against the null hypothesis that RMSE did not differ between the RF and SVR models (t5 = 3.76, p-val = 0.0131) indicating that there was a statistical difference in the uncertainty of NUE predictions between the two models and leading to the conclusion that the SVR performed better than the SLR. The mean RMSE across the 5 folds for the SLR model was 0.3229 compared to 0.2608 from the SVR. Based on these results, the SVR overtook the SLR as the best model and was compared to the RF for a final round of 5 × 2 CV. There was little to no evidence against the null hypothesis that RMSE did not differ between the RF and SVR models (t5 = 0.32, p-val = 0.7624) indicating that there was no statistical difference in the uncertainty of NUE predictions between the two models.

Both models indicated similar relationships between NUE and as-applied fertilizer N (Fig. 5). Although both the SVR and RF produced similar predictions and there was no statistical difference between them, the RF was selected as the final model because it provided the lower mean RMSE based on the HOOCV analysis. The lowest mean RMSE from the HOOCV indicated that the RF performed better than the SVR when making predictions in fields unseen by the model during training. All the sampled data were compiled as a training dataset to fit a final RF model. After top-down features selection, the RF model that provided the best predictions of NUE using environmental and management (e.g., N fertilizer rates) covariate data was:

$$\begin{gathered} NUE \sim f(x, y, N, slope, aspect_{sin} , aspect_{cos} , prec_{cy} , prec_{py} , ndvi_{cy} , ndvi_{py} ,ndvi_{2py} , \hfill \\ ndwi_{cy} , ndwi_{py} ,ndwi_{2py} , bulkdensity, claycontent,watercontent phw, carboncontent) \hfill \\ \end{gathered}$$
(5)

where x and y were the spatial coordinates of each sample point, and all other terms are defined in Table 5 with descriptions of the data sources in Table 2. The importance of each variable retained in the final model was assessed by the difference in predictive accuracy, defined by mean square error, between permutations of the model that include and omit each variable. The N fertilizer rate was the most predictive variable, followed by the normalized difference water index (NDWI) from the previous year (Fig. 6).

Table 5 Parameter identifiers from final SVR NUE model with the corresponding data type and description
Full size table
Fig. 6
figure 6

Variable importance from the final RF model fit with all data, where importance is defined as the increase in predictive performance of the model between permutations that independently include and omit each variable of interest. Variables on the y axis are defined in Table 5

Full size image

Discussion

Nitrogen use efficiency declined with increasing nitrogen fertilizer inputs

This research demonstrates a novel methodology for utilizing low-cost data to characterize within-field variation in NUE to aid N fertilizer management decisions. The approach is adaptable to any system with any input that can be spatially varied and where detailed sampling of representative fields across an area of interest is conducted. Efficiency, defined as FUE or NUE both declined with increasing N fertilizer rates (Figs. 4, 5) and mirrors the relationship between crop uptake and N fertilizer (Fig. 3) where low crop uptake at low N fertilizer rates corresponds to the highest efficiency. These results corroborate many other studies that investigated the relationship between NUE and fertilizer rates (Öztürk et al. 2010; Song et al. 2009; Zhang et al. 2009b). While farmers are not expected to cease applying N fertilizer, and have little control over mineralization of N, the relationship of NUE and crop uptake with as-applied N fertilizer provides an opportunity to infer where TN is higher. Site-specific prescriptions can lower N fertilizer rates based on knowing the TN distribution within a field, which can save producers money on fertilizer and prevent the overapplication of N that can contribute to pollution. This inference agrees with other studies that show reducing N fertilizer rates in areas of high TN (due to greater N mineralization) is an economically viable management strategy (Paustian et al. 1997; Zhang et al. 2009a, 2009b).

A few key relationships illustrate general concepts that emerge from this NUE assessment. If the crop N is of a similar magnitude to the fertilizer N, one can assume that the total amount of available N is likely to exceed the crop nitrogen needs due to likely mineralization of organic N. When crop N is higher than fertilizer N, the crop has likely tapped into mineralized N sources to satisfy its N requirements, and greater efficiency is probable, depending on total mineralization and immobilization. Conversely, if crop N is lower than fertilizer N, one can assume the presence of N inefficiencies resulting from N loss, or that there were constraints on N uptake by the crop, such as drought, resulting in amplified inefficiency of N use. Montana is a semiarid region where water often limits growth and N uptake by the crop, increasing inefficiency of N use across all fields, and inducing variability in efficiency within fields in areas with different moisture conditions.

Need for methods on estimating nitrogen mineralization

In Montana agroecosystems, with adequate moisture and optimal temperatures, microbes mineralize organic N into plant available forms, which increases the amount of available N for crop uptake (Hart and Firestone 1990). Mineralization of SON to plant available forms is a function of organic matter, moisture, and temperature (Booth et al. 2005; Sigler et al. 2018); however, the estimate of mineralization in this study used only percent soil TN to estimate mineralized N, increasing uncertainty in the mass balance approach (Vigil et al. 2002). Uncertainty in the evaluation and modeling of NUE could be reduced by improving estimates of N mineralization and immobilization, or by using direct measures of N mineralization and immobilization. Mineralization is important to account for in calculations of NUE for these systems especially if low or zero N fertilizer rates are applied in areas of the field, as seen in SI Fig. 3 in the Online Reference. Possible avenues of improving N mineralization estimates include use of remotely sensed soil moisture interpolated for depth effects, and upscaled modeling of soil climate based on rainfall and temperature patterns, along with soil mapping, and calibrated using growing soil climate observation networks. Overall, methods of accurately measuring N mineralization and immobilization require additional research, a fact that has been long recognized (Bremner and Mulvaney 1982; Wang et al. 2009; Zhang et al. 2009a).

Inference from machine learning models reflects biophysical controls on nitrogen use efficiency

We demonstrated methods drawing on modern data science can contribute to developing NUE models by providing a suite of tools from which the most appropriate model for a given system can be selected. Recognized as imperfect, the model that was statistically shown to outperform the other candidate models was the RF. However, due to the lack of difference between SLR, MLR, NLR, RF, and SVR in the HOOCV there is an argument that for practical usage the RF model is more complex than needed. Despite significant differences between SLR, MLR, or NLR and either RF or SVR, the difference of 0.06 In NUE may not be significant in practice. Using the SLR, MLR, or NLR models that solely use as-applied N as a covariate would provide farmers a simple method for estimating NUE prior to making N fertilizer decisions without requiring satellite imagery to be gathered. Despite this, as the RF used spatially and temporally varying covariates, it provides insight into factors that were deemed predictive of NUE in these fields.

As the medium that supplies N to plants, soil plays a role in influencing N dynamics (Sigler et al. 20182020). The influence of fine textured soils on NUE was captured in the RF model through the incorporation, and retention after feature selection, of clay and soil organic carbon content estimates from OpenLandMap [Eq. (5)]. Additionally, because fine textured soils hold more water and N, but can limit oxygen, NUE further decreases when denitrification reduces nitrate to gaseous forms that are lost to the atmosphere (Sigler et al. 2022).

Due to the linkage of water and temperature with N mineralization, weather plays a significant role in NUE (Thilakarathna et al. 2020). Unsurprisingly, precipitation and water content estimated from OpenLandMap were retained in the RF model as a covariate that decreased variation between predicted and observed NUE [Eq. (5)]. The combination of temperature and precipitation also influence photosynthesis of the crop, which in turn influences the water retention and the N efficiency of crops (Michaletz et al. 2016; Pearcy et al. 2005). Information on the water status of the crop were derived from NDWI data, which generated more accurate NUE predictions when included in the RF model than when omitted [Eq. (5)].

Information on the productivity of the crop, measured by NDVI, was retained in the final RF model post-feature selection [Eq. (5)]. This indicates that the RF model utilized the measure of the crop greenness and indications of summer fallow to predict NUE. The greenness of a crop is related to crop productivity and biomass and can indicate when a field was in summer fallow and provide information on the amount of stubble post-harvest because a higher biomass of a crop correlates with an increased amount of stubble post-harvest after grain is harvested. Additional topographic parameters such as slope and aspect were included in the final RF model [Eq. (5)], likely due to the influence of site characteristics on fine scale water and N transport, nutrient availability, and microclimate conditions (Grant et al. 2016).

Future impacts of nitrogen use efficiency models

The models developed from NUE responses at sampling locations and corresponding open-source data from the four fields demonstrates potential for future methods that can provide farmers with predictions of NUE for identifying N rates that optimize crop N uptake and NUE. The NUE of fields varied spatially and in magnitude (Table 3), indicating that management of NUE would be suited for OFPE, where data from a field is used to make decisions on that field (Hegedus and Maxwell 2022a). Maps of predicted NUE that show the spatial variation of NUE across the fields are shown in SI Fig. 4 in the Online Reference. However, the cost and time expenditures to gather and analyze the data to develop field specific NUE models is not feasible for a farmer to accomplish in addition to their normal operations. Thus, there is a need for a generalized model of NUE. The fields in this work showed similar relationships between as-applied N fertilizer and crop N uptake, FUE, or NUE (Figs. 3, 4, 5) suggesting the potential for these models to be applied across fields with similar soils, weather, and management in MT.

Evaluating and modeling NUE not only informs spatial N fertilizer management but has potential for temporal N management as well. Mineralization or fertilizer applications early in the growing season contribute to lower NUE or FUE because the supply exceeds demand, leaving N vulnerable to leaching as nitrate or denitrification (Ravier et al. 2017; Yin et al. 2020). Applying N fertilizer early in the growing season thus further reduces NUE due to the lack of demand by the crop. When fertilizer is applied at a rate equivalent to plant needs, any mineralized N contributes to a lower NUE as N saturation in the crop leads to excess N available in the soil, thus systems with significant mineralization require less supplemental N from fertilizer.

Although technology will improve, the coarse resolution of open-source satellite imagery potentially hinders it’s use in precision agriculture. Developing site-specific farming approaches with the level of resolutions currently available provides farmers and crop managers initial tools that will improve with advancements in satellite imagery collection. Additionally, usage of open-source satellite imagery is an important avenue of research in precision agriculture to avoid burdening farmers with any extra costs associated with gaining information about their fields. Increased effort in the downscaling and ground truthing of remote sensing data can decrease uncertainty in NUE predictions. Knowledge of the spatial variation of NUE across fields can highlight areas of fields that require differing management strategies to maximize NUE. Thus, models that adequately predict the spatial variation of NUE are crucial to decision support systems. When applying NUE models in data-driven decision making, users must be willing to accept current uncertainties in N mineralization and remote sensing covariate data to begin shifting conventional N management towards greater sustainability in terms of both economic gains and efficiency. Improvements in these arenas warrant future research and updating of initial methods that incorporate efficiency into decision making, yet the pressing global need to increase production without detriment to the agricultural resource base requires increasing agronomic input efficiency with the tools and technology available now.

Conclusion

It is important to understand subfield scale N dynamics and NUE as the agricultural industry grapples with becoming more efficient with N fertilizer usage while advancing the ability for practicing site-specific N management. Agriculture’s technological revolution has led to an abundance of data available at a low cost on the subfield scale but translating that data into insights relevant to management requires data science, which is the nexus of computer science, statistics, and agronomic understanding. Applying machine learning approaches to open-source subfield scale data resulted in a NUE model that aligns with assumptions about biophysical processes that drive N dynamics. Subfield information on NUE informs farmers about where applying N fertilizer decreases NUE and does not improve crop N uptake, which results in an increased potential for N pollution. The development of a subfield scale model for predicting NUE demonstrates an avenue for including information about efficiency into a farmer’s decision matrix for variable N fertilizer rates. Future research will be required on how NUE models can coexist with crop models to develop N fertilizer management recommendations that balance the tradeoff between reducing potential N pollution and profit maximization. Additionally, due to the inherent spatial and temporal variability of field and crop conditions, a model acting as a “silver bullet” across space and time for predicting NUE is unlikely, and so efficient methods for developing NUE models that consider field and farm level specificity will need to be addressed by future research.