Abstract
Improving fertilizer recommendations for farmers is essential to increase food security in smallholder landscapes. Currently, blanket recommendations are provided across agro-ecological zones, although fertilizer response and nutrient use efficiency by maize crop are spatially variable. We aimed to identify factors that could help to refine fertilizer recommendation by analyzing the variability in fertilizer response (FR) and the agronomic nitrogen use efficiency (N-AE). A literature search for on-farm studies across Kenya and Sub-Sahara Africa (SSA), excluding Kenya, yielded 71 publications. The variability in FR was studied using a meta-analysis whereas key factors that influence FR and N-AE were studied with linear regression models. On average, the FR was 2, but it varied considerably from 1 to 28.5 (excluding outliers). In SSA, 18% of the plots were non-responsive plots with an FR < 1. The main factors affecting N-AE for Kenya were P-Olsen, silt content, soil pH, clay and rainfall, whereas only soil pH, exchangeable K and texture were important for SSA. However, our study indicates that available data on soil, climate and management factors could explain only a small part (< 33%) of the variation in FR and N-AE. Soil pH, P-Olsen, silt content, and rainfall had significant but low levels of power in explaining variation in FR and N-AE. Our findings indicate that strategies to refine fertilizer recommendation should include information on soil types and soil properties.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The population of Sub-Saharan Africa (SSA) is projected to increase up to 1.2 billion by 2050 (United Nations Population Division 2009; Ray et al. 2013). The increasing food demand of this growing population requires agricultural intensification with efficient fertilizer use. Current fertilizer recommendations in SSA are often only specified to the level of a region, for instance, an agro-ecological zone (AEZ) or administrative district (e.g., Mowo and Mlingano 1993; FURP 1994; Schnier et al. 1996). The fertilizer recommendations for these larger regions are commonly referred to as blanket fertilizer recommendations. However, environmental and management factors vary at short distances in the smallholder landscapes of SSA (Tittonell et al. 2005; Vanlauwe et al. 2011; Zingore et al. 2007; Stoorvogel and Smaling 1998; Tittonell et al. 2008). As a result, the blanket fertilizer recommendations are often considered to be of limited relevance to farmers (Tittonell et al. 2013).
The blanket fertilizer recommendations can only be refined if the factors that influence the variation in fertilizer response are known. This is increasingly urgent since an increasing number of farmers report a decreasing fertilizer response for staple food such as maize. Giller et al. (2006) introduced the concept of non-responsive soils: soils on which crops do not respond to mineral fertilizer application. However, the causes behind non-responsive soils are poorly understood. With a better understanding of factors that affect the variability in response to fertilizers, fertilizer recommendations can be improved. There is, however, a lack of studies that systematically identify key factors that affect the fertilizer response across smallholder farming systems of SSA. A recent meta-analysis pointed to the importance of secondary and micronutrient deficiencies in SSA in low fertilizer responses (Kihara et al. 2017). Multiple studies have shown that the fertilizer response varies across smallholder landscapes due to environmental (soil-related and climatic) and management factors. Zingore et al. (2007) demonstrate that the low level of soil organic carbon in maize fields of Zimbabwe led to a poor fertilizer response. Sileshi et al. (2008) attributed a high variability in rainfall amounts to low fertilizer response. Vanlauwe et al. (2016) observed that the poor fertilizer response in maize is a result of unbalanced soil fertilization. However, it remains unclear which are the key determinants (factors) of variability in fertilizer response.
Fertilizer recommendations (both type and amount of fertilizer) can be evaluated using indicators such as fertilizer response (FR) and agronomic nutrient use efficiency. The FR is defined as the incremental crop yield due to fertilization, independent of the quantity or the type of fertilizers applied. The FR is calculated as the ratio of fertilized crop yield and an unfertilized crop yield of a control plot. The FR is a useful concept for identifying, for example, “non-responsive soils”, i.e., soils in which no effect of fertilization is observed (Tittonell et al. 2007; Zingore et al. 2007; Njoroge et al. 2017). FR can also be used to evaluate the overall effect of fertilizer use across farms in a region. The agronomic nutrient use efficiency is a measure of the crop yield increase for a given amount of nutrient added (Dobermann et al. 2002) and can be used to evaluate the efficiency of a specific nutrient applied. For example, the agronomic nitrogen use efficiency (N-AE) is defined as the incremental crop yield per applied nitrogen (expressed in kg/kg).
Soil property maps of relevant variables to fertilizer management are increasingly becoming available (Hengl et al. 2015, 2017). These maps may help to get better insight in the spatial variability of nutrient concentrations (Antwi et al. 2016). However, these maps are generally at coarse spatial resolution and are only suitable for guiding recommendations at the regional scale but not at the farm level. Even though high throughput and cost-effective methods for soil analysis are also available (Shepherd and Walsh 2007; Shepherd 2010) most smallholder farmers do not have access to soil analyses services at the plot level. Knowledge of key factors that influence FR and N-AE is therefore critical for strategies aimed at improving nutrient management.
This paper aims to identify key factors that influence FR and N-AE to refine fertilizer recommendations for smallholder farmers. The specific objectives of this study were to: (1) quantify the variation in FR and N-AE, and (2) identify key environmental and management factors that influence variability in FR and N-AE. We employed a meta-analysis approach (Hedges et al. 1999; Borenstein et al. 2011) to analyze FR, and a regression analysis to understand the driving factors for FR and N-AE. This study focused on Nitrogen fertilization in maize across SSA with specific attention on Kenya. Maize is an important staple crop in the region and Nitrogen is found to be the most limiting nutrient in SSA (Nziguheba et al. 2009; Ma et al. 2016). A more detailed analysis was done for Kenya, because of the numerous agronomic studies conducted over a wide variation of environmental conditions.
Materials and methods
Literature search
A literature search on agronomic studies was conducted using Google Scholar, Mendeley, and Web of Science databases (1980–2016). All combination of the following terms were searched: ‘fertilizer application’, ‘maize yield’, ‘inorganic or mineral fertilizer’, ‘fertilizer response’, ‘smallholder’, ‘sub-Sahara Africa’, and ‘fertilizer treatment’ (e.g., ‘fertilizer response + maize yield + smallholder farm + sub-Sahara Africa’ or ‘fertilizer treatment + maize yield + smallholder farm’ or ‘fertilizer application + maize yield + smallholder farm’). Additional studies were searched in the reference lists of relevant publications. Publications consisted of peer-reviewed scientific articles, books, conference proceedings, and reports. Criteria used for obtaining a set of comparable studies for the analysis were: (1) maize was cultivated in monoculture, (2) the experiment was conducted on a smallholder farm in SSA, and (3) fertilizer treatments were randomly allocated to the plots. We selected treatments in which only inorganic N or combinations with inorganic P and or K were applied. Treatments in which additional organic fertilizers were applied were excluded. A systematic process for the selection of suitable fertilizer studies is presented in a flowchart in the Supplementary Material 2 (Fig. S1).
Data extraction and treatment
Data on fertilizer treatments, crop yields, soils, climatic (agro-ecological zones) and management factors were extracted from the selected publications. A database was established with each record representing a treatment plot (Table 1).
Typically, experiments included various fertilizer treatments and or multiple seasons and sites. The data obtained from the studies contained multiple fertilizer treatment from a single experiment. Formally, these observations cannot be considered independent. However, López-López et al. (2014) showed that multiple entries from a single experiment are valid and can help to increase the precision of the analysis when using literature data. Controls were considered as treatments with no application of fertilizers (organic or inorganic). The data variables were harmonized by: (1) converting units, and (2) reclassifying soil types as World Resource Base Reference Soil Groups (IUSS Working Group WRB 2014), and (3) converting soil test values to a common method. For example, P-Olsen and P-Bray were never both measured in the same experiment. Therefore, published conversion factors was used to estimate P-Olsen from P-Bray 1: P-Olsen = 0.44 P-Bray 1 (Kleinman et al. 2001) and from P-Bray 2 to P-Olsen = 0.79 P-Bray 2 (Wuenscher et al. 2015). The database still included many missing values because soil descriptions and analytical procedures differed. A flowchart deducing different steps of estimating the missing data is presented in Supplementary Material 2 (Fig. S2). To handle the rest of the missing data on soil properties, we used the following approaches:
-
1.
Pairwise correlation analysis was conducted to establish the correlation among paired soil properties. Paired soil properties with a Pearson correlation coefficient > 0.8 was selected. From this pair, the property with the highest number of missing values was dropped. Prior to dropping the property out, a linear equation was established and used to estimate the missing value of the retained property (with fewer missing values). But where the pair-wise points were both missing, the next approach was employed.
-
2.
We used a Predictive Mean Matching (PMM) approach to impute the remaining missing soil data using the “mice” R-package (Van Buuren and Groothuis-Oudshoorn 2011). The PMM approach is based on regression analysis and estimates missing values by means of the nearest neighbor (Di Zio and Guarnera 2009; Vink et al. 2014). We used this approach so that the originality of the soil data and the underlying distribution are maintained (Little and Rubin 2002; Vink et al. 2014). Remaining missing values (18%) for soil pH, total C, Exch. K, silt and clay were estimated using the PMM approach.
Lastly, to calculate sampling variance for meta-analysis, we included the standard deviation (sd) in our database. If only the standard errors or coefficient of variation were reported, they were used to estimate the sd. In studies where no measures of variance were presented, a value of 1.5 times of the mean of all reported sd’s was assigned (Ishak et al. 2008; Ros et al. 2011).
Database overview
The literature search on experiments conducted on smallholder farms yielded 503 publications on on-farm fertilizer maize experiments. We identified only 71 studies, which matched our criteria, with 202 observations for Kenya and 255 for other SSA countries (see Supplementary Materials 1, 2). The geographical distribution of the observations besides Kenya were; Togo 64, Uganda 49, Malawi 42, Tanzania 26, Zimbabwe 32, Nigeria 19, Ghana 12, Cameroon 8, Rwanda 2, and Benin 1. The experiments were limited from 1986 to 2016 and, include treatments with a single N application or a combined application of N with P and or K. Basal fertilizers were the commonly applied inorganic fertilizers (e.g., di-ammonium phosphate and urea). Nitrogen application rates varied between 15 and 150 kg N ha−1 (Supplementary Material 1, Table S2). Wide ranges in maize yield between the fertilized and control treatments plots was observed (see Supplementary Material 1, Table S3). In general, the database contained higher control yields with more variability in Kenya compared to the rest of SSA countries.
Excluded studies include studies with little information on environmental and management factors (see Supplementary Material 2, Fig. S1). Information on soil properties was missing in 25% of the excluded studies. For example, only 45% of the studies reported on soil texture, CEC, Ca and Mg concentrations. Studies that reported aggregate data from multiple field trials (constitute 54% of excluded studies) were culled from the database and further analysis, since they did not record data on each trial sites. Studies which reported fertilizer treatments without including a control were also culled from our analysis and constituted 5% of the excluded studies. Most studies described one experiment on a single location. Only 31% of the observations in the dataset were extracted from studies with experiments at multiple locations, which had information on each of the individual site.
Data analysis
First, dependent variables FR and N-AE were computed. The effect size (response ratio i.e. FR) estimator was used to quantify the magnitude of the effect of fertilizer application on yield (Hedges et al. 1999) and was considered a proxy index of soil responsiveness. Agronomic nitrogen use efficiency was taken to represent nutrient use efficiencies across the fertilizer studies. Secondly, a meta-analysis was conducted to: (1) quantify heterogeneity across fertilizer studies and, (2) to evaluate causes of variation in FR and effect size across categorical variables. Lastly, regression analysis was done to discern the continuous independent variables that explain variability in FR and N-AE.
Fertilizer response
Fertilizer response was taken as the ratio of the mean maize yield of the fertilized plot (\(\bar{x}_{t}\) in kg ha−1) and the mean maize yield of the control plot (\(\bar{x}_{c}\) in kg ha−1) (Hedges et al. 1999; Ros et al. 2011) and was computed as a natural log to normalize the data distribution (Johnson and Curtis 2001). A normalized FR is required to develop random effect meta-regression models. The ln FR was computed as:
Soils with FR > 1 were categorized as responsive. Within the non-responsive soils (FR ≤ 1) we distinguished poor and fertile soils (less responsive), based on the maize yields in the control plots, and as described by Vanlauwe et al. (2014). The fertile soils category were soils where no significant increase in maize yield was realized after N fertilization or a combination of N with inorganic P or K, (Vanlauwe et al. 2014), but would still have high maize yields (> 1125 kg ha−1 for smallholder farm in SSA) as displayed in the control plots. A FR ≤ 1 meant that fertilization had no effect or negatively affected yield.
The sampling variance of the fertilizer response (FRv) is required to compute the heterogeneity between fertilizer studies and evaluate factors affecting FR. FRv was calculated as:
where n is the sample size/number of replicates, sdt is the standard deviation for the yields within the treatment and sdc is the standard deviation for the yields within the control.
Agronomic nitrogen use efficiency
The agronomic nitrogen use efficiency was computed following Vanlauwe et al. (2011):
where \({\text{FN}}\; ( {\text{kg}}\;{\text{N}}\;{\text{ha}}^{ - 1} )\) is the amount of applied fertilizer N. The N-AE was reported as kg dry weight kg−1 N. The average N-AE was computed across the different groups of categorical factors (Table 1). We could not compute the sampling variance of N-AE, since N-AE is not an effect size as defined in the meta-analysis. Hence N-AE was not subjected to meta-analysis.
Meta-analysis of fertilizer response
We followed the methods used by Hedges et al. (1999) and Luo et al. (2006) to evaluate FR using a meta-analysis approach. The FR was used to evaluate soil responsiveness to N fertilization, or combinations with inorganic P and or K. To establish the different categories of soil responsiveness, we evaluated the relationship between FR and maize yield of the control plots. The dataset was split into three categories of soil responsiveness to fertilizer application, similar to Njoroge et al. (2017). To further evaluate these categories, we analyzed their corresponding soil properties.
To examine the heterogeneity (QT) of FR in fertilizer studies across Kenya and SSA, a random effects (RE) meta-regression model was developed (Viechtbauer 2010). The RE model was fitted using the Restricted Maximum Likelihood method (Brown and Kempton 1994). A test of QT was used to assess how comparable the studies were and to test the significance of QT of the FR (Hedges and Olkin 1985). Significant QT of the FR indicates that the variation cannot only be attributed to the sampling error and other explanatory factors are playing a role as well (Huedo-Medina et al. 2006). The latter situation would provide an option to identify explanatory factors of the heterogeneity across fertilizer studies.
We tested the potential effect of publication bias in the meta-analysis using a regression test for the overall dataset (71 studies) (Viechtbauer 2010). The test is a quantitative representation of the importance of publication bias in the meta-analysis (Thornton and Lee 2000). The publication bias was also evaluated through a “funnel” plot. We analyzed the distribution of ln FR in the “funnel” plot to check if indeed publication bias was likely to influence the meta-analysis results (Viechtbauer 2010). The trim and fill method was used to estimate the number of additional observations necessary to change the results of the analysis from significant to non-significant (Duval and Tweedie 2000; Viechtbauer 2010).
To examine the influence of soil, climatic and management factors on FR, we conducted an analysis for the categorical variables, as a further step in meta-analysis (Table 1). The categorical variables included; soil types, soil textural classes, agro-ecological zones, type of management (farmer or researcher managed), range of N application rates and nutrient types (N, P and K). To compare the effect of fertilization across the groups, the weighted means \((ln \;{\text{FR}}_{w} )\) of FR and their corresponding 95% confidence intervals (CIs) were computed for each group, following Luo et al. (2006):
where i is an observation, wi is the weight of i, defined by the reciprocal of the ln FRv (wi = \(1/ln \;{\text{FR}}^{v} )\), and m is the number of observations within a group of that categorical variable. The effect of fertilization for each group was considered significantly different from 1 if the CI did not overlap the line of no effect (ln FR = 0), and different from one another if their 95% CIs were non-overlapping (Hedges et al. 1999). A back-transformed \(ln \;{\text{FR}}_{w}\) was reported in text and figures. The “metafor” R-package was used to conduct the meta-analysis (similar to Barto and Rillig 2010). Back transformed values (FR) were reported in the figures.
Regression analyses
To further study how soil properties, management and climatic factors (the continuous factors) affect FR and N-AE, general linear regression models (GLM) were developed. In this analyses ln FR or N-AE was the dependent variable and independent variables were: N application rate (only for ln FR), total C, soil pH, P-Olsen, exchangeable K, clay, silt and rainfall. The variables soil pH, total C, N application rates, rainfall, and P-Olsen were skewed to the left and were log-transformed to approximate normal distribution. Variables were standardized by dividing each observation with the standard deviation of the variable, so that each factor had equal representation in the GLM. The relationship between dependent (ln FR or N-AE) and independent variables was assessed based on the level of significance (p) and coefficient of determination (adjusted R2).
Further evaluation of the GLMs were conducted by computing the variable importance projections (VIP) scores from each GLM (ln FR or N-AE), which primarily indicate the relative measure of the importance of each predictors in the model (Kuhn 2008a, b). These scores were considered robust, because they took into account the orthogonal variation between independent factors (Chong and Jun 2005; Farrés et al. 2015) and high variation in ln FR or N-AE. The VIP scores were used to discern the important (key) factors, which also explain the underlying variation in FR or N-AE (Kuhn 2008a, b; Mehmood et al. 2012; Farrés et al. 2015). The scores are computed independently for each other (predictors) using the t-statistic (Kuhn 2008a, b). A criterion of VIP scores > 1 was adopted for identifying the important factors, so that those with scores > 1 were taken as the important ones (Chong and Jun 2005). The “pls” R-package was used for regression analysis (Mevik and Wehrens 2007). The “caret” R-package was used to compute VIP scores (Kuhn et al. 2014).
In the regression analysis of N-AE, we excluded N application rates as an independent variable. Inclusion of N application rate could have led to redundancy in the predictor information as it was used to compute N-AE.
Results
Fertilizer response
The maize yield almost doubled with N fertilization: The median FR was 1.8 for Kenya and 1.7 for SSA (excluding Kenya). There was a significant non-linear, negative relationship between FR and the maize yields of control plots (Fig. 1a, b) with R2 value of 0.47 for Kenya (p = 0.003) and 0.49 for SSA (p = 0.002). There was no obvious relationship between FR and N application rate (Fig. 1c, d) although the maximum attainable FR in Kenya tended to decrease with N application rate (Fig. 1d).
Fertilizer response (FR) as a function of maize yield in the unfertilized control plots (a, b) or N application rate (c, d) for Sub-Saharan Africa (a, c) and Kenya (b, d). The dashed line is the line of no response to the fertilizer (FR = 1). The solid lines describe non-linear relationships function as: FR = 32,244 (control yield)−0.7 (P = 0.003; R2 = 0.47) for Kenya and FR = 83 (control yield)−0.5 (P = 0.002; R2 = 0.49) for Sub-Saharan Africa
Responsive soils (FR > 1) were common in Kenya (86%) and SSA (89%). The non-responsive soils (FR ≤ 1) constituted 14% for Kenya and 11% for SSA. The maize yields in control plots of these non-responsive soils varied from 100 to 7000 kg ha−1. Of these soils, 72% were considered fertile non-responsive soils (control plots with maize yields > 1125 kg ha−1). At this point, the quadratic curve started to level, which was an indication of no significant effect of fertilization, and most observation (> 20%) were close to or below the line of no effect to fertilization (FR = 1, Fig. 1).
The mean FR was 2.2 for the responsive soils, 0.68 for poor, non-responsive and 0.89 for fertile, non-responsive soils in SSA including Kenya. The number of non-responsive soils for Kenya (51) was too small for further analyses, so we pooled the data of the non-responsive plots for Kenya and the rest of SSA for further analysis.
Soil characteristics varied within the three soil responsive categories (Fig. 2). For example, average total C ranged from 2 to 27 g kg−1 for poor, non-responsive soils and from 1 to 56 g kg−1 for fertile, non-responsive soils. The average total C content for responsive plots was 63% higher than that of poor, non-responsive plots. Surprisingly, the mean concentration of P-Olsen for the poor, non-responsive plots was higher (8.7 mg kg−1) than that of responsive soils (5.7 mg kg−1) and fertile, non-responsive plots (4.1 mg kg−1). Soil C and exchangeable K seemed to be the main separators between poor, non-responsive soils and the other two categories (Fig. 2c, f). The mean N application rates were on average 22% lower for poor, non-responsive plots compared to the responsive soils.
Heterogeneity in fertilizer studies and test of publication bias
Random effect (RE) meta-regression model results indicate significant variation in FR among the observations of the fertilizer studies for Kenya (QT = 15,435, degree of freedom = 198, p < 0.001) and for SSA (QT = 1645, degrees of freedom = 245, p < 0.001). This implies independent variables explained a significant part of this variation other than the sampling error alone. Thus, evaluation of factors that attribute to the variability in FR was necessary.
The regression test results (z value = 0.75, p = 0.39) suggests absence of publication bias across the selected 71 fertilizer studies. Although the distribution of ln FR observations in the “funnel” plot was not symmetrical because of more relatively high values for ln FR, only 84 observation were missing and did not have any effect on the overall results of meta-analysis (Supplementary Material 1, Fig. S3). Additional observations would however have resulted in a more symmetrical “funnel” plot.
Variability in fertilizer response
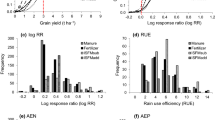
Weighted mean across categorical variables was used to assess variability between their sub-groups using CIs (Fig. 3). The meta-analysis showed that the CIs around the FR on of all soil orders except Cambisols (Kenya) and Areonsols (rest of SSA) overlapped with the line of no response. The FR was significantly higher than 1 for these two soil orders (Fig. 3a).
Means of the fertilizer response (FR) across categorical variables, a world reference soil groups, b nutrient types, c soil textural classes, d agro-ecological zones. The dashed line is the line of no response to the fertilizer (FR = 1). Error bars represent confidence intervals; numbers in brackets represent the number of observations
Combined application of N, P and K led to a doubling of the mean FR (p < 0.0001) both SSA and Kenya (Fig. 3b) compared to application of N alone. For plots in which only N was applied, the FR did not differ significantly from 1. Again, the variation in FR was large.
For Kenya, sandy soils in general tended to show a higher FR than non-sandy soils (Fig. 3c). This trend was, however, not confirmed for the rest of SSA. There, sandy loam soils were the only class of soils with a FR significantly higher than 1. For clay soils, the FR did not differ significantly from 1.
The FR was similar between the farmer and researcher-managed plots (Fig. 3d). The mean FR in SSA farmer-managed plots was significantly higher than 1.
The response to fertilization did not vary significantly among agro-ecological zones (Fig. 3e). In Kenya, the FR was highest in the lower humid zone (4.8) and > 1 also in the upper midlands and lowlands. There was no significant response to N fertilization in the lower midlands and lower highlands. For the rest of SSA, the mean FR for the sub-humid zone was 2.9. The FRw for sub-humid zone was significantly higher than 1.
The FR had wide CI range (0.8–1.5) across the N application rates < 30 kg N ha−1 for Kenya (Fig. 3f). The average FR for 30–60 kg N ha−1 application ranges was 1.61 and was not significantly different from 1. For SSA, FR was not significantly different from 1 for N application rates range of 30–60 kg N ha−1 since the CI overlapped with the line of no effect.
Agronomic nitrogen use efficiency
The average N-AE was 42 kg dw kg−1 N for Kenya and 18 kg dw kg−1 N for the rest of SSA. The N-AE varied from − 27 to 165 kg dw kg−1 N across all observations (Fig. 4a, b). We did not find any significant relations between maize yield of the control plot (Fig. 4a, b) or N application rate (Fig. 4c, d) and N-AE, though the maximum attainable N-AE seemed to decline with increasing maize yields in the control plots and N application rates. Mean N-AE varied across the soil, climate and management factors (Table 2).
Key factors affecting fertilizer response and agronomic nitrogen use efficiency
The regression (GLM) with the eight continuous predictors explained 29% of the variation in FR for Kenya and 13% for SSA (Table 2). Fertilizer response decreased significantly with increasing P-Olsen (p < 0.0001) in Kenya, but not in the rest of SSA. Here, soil pH, exchangeable K and average rainfall during a growing season were the significant predictors of variation in FR. They correlated positively with FR. Low values for soil pH and rainfall of a growing season displayed decreased FR (< 1). Fertilizer response increased marginally significantly with soil total C in Kenya (p = 0.10), but not in the rest of SSA. When we tested whether addition of maize yields of control plots as predictor could improve the predictive ability of the model, the adjusted R2 value increased from 29 to 63% for Kenya and 13 to 48% for SSA. In that case, P-Olsen no longer explained any variation in FR for Kenya, and for SSA rainfall and exchangeable K dropped out of the model. The FR decreased with increasing maize yield in the control plots (Fig. 1).
Eight continuous predictors were used to develop the regression model for N-AE. The best model explained 32% of variability in N-AE for Kenya and 3.5% for SSA (Table 2). Similar to FR, rainfall and total C positively influenced variability in N-AE and P-Olsen did so negatively in Kenya; for SSA variation in N-AE silt was the best predictor
We identified key explanatory factors explaining variation in FR using VIP scores (Fig. 5). Three factors relevant to FR in both Kenya and the rest of SSA were exchangeable K, soil pH and rainfall (Fig. 5a, b). In addition, P-Olsen, total C and silt were relevant in Kenya, and N application rate in SSA. Clay was the least important factor for both Kenya and SSA. Results from the GLM indicate rainfall, as the significant factor influencing FR in Kenya and SSA. P-Olsen, total C and silt were additional significant factors for Kenya while soil pH and exchangeable K were significant for SSA (Table 3). These factors had VIP scores > 1 (Fig. 5). Nitrogen application rates was not significant but were important based on the VIP score that was 2.18 for SSA (Fig. 5).
Relative importance of continuous management, soil and climate factors based on the variable importance projection (VIP) values computed from the general regression model explaining variation for in the fertilizer response (FR) (a, b) and agronomic nitrogen use efficiency (c, d). For Sub-Sahara Africa and Kenya. The dotted line represents the threshold value for the VIP value (VIP = 1) below which variables were considered not to be important predictors. N rate nitrogen application rate, pH soil pH, P-Olsen extractable phosphorus, Total C soil organic carbon and Exch. K exchangeable potassium
For N-AE, results of relative importance of key explanatory factors based on VIP indicate P-Olsen, clay, silt, soil pH, and rainfall as key determinates for Kenya (Fig. 5d). Only soil pH, exchangeable K and silt were the key factors explaining variation in N-AE for SSA: less silt meant higher N-AE (Fig. 5c).
Discussion
Factors affecting variability of FR and N-AE
Our results indicate that both FR and N-AE vary largely within Kenya, which supports the claim that fertilizer recommendations need to be refined to a higher spatial resolution. The FR response varied roughly from 1 to 12 (disregarding two extremes) and the N-AE from 0 to 160 kg dw kg−1 N. Fertilization, on average, almost doubled the maize yield in both Kenya and the rest of SSA. The average response was statistically significant only when N was applied in combination with P and/or K (Fig. 3b). The average N-AE we found (18 kg dw kg−1 N) for SSA is similar to that of Vanlauwe et al. (2011) who reported 19 kg dw kg−1 N for farmer-managed experiments. The average N-AE for Kenya (42 kg dw N kg−1) was substantially higher but not uncommon for East Africa (Vanlauwe et al. 2011).
Reoccurring variables significantly explaining variation in both FR and N-AE in Kenya and SSA are total C, pH, P-Olsen, exchangeable K, rainfall and silt (Figs. 2, 5, Tables 3). Soils with a lower pH (i.e. lower than the average of 5.2), less rainfall and less silt tended to have lower FRs and N-AEs. In line with earlier studies (Kihara et al. 2016), pH and FR and N-AE were positively related. This is probably because most soils in our study had a soil pH below the optimum of 5.5–6.5. At soil pH < 5.5 N mineralization rates decrease and P increasingly binds to the soil’s solid phase. Factors with a high VIP scores varied to some extent between Kenya and SSA, which must be related to differences in agro-ecological zones, soil orders and soil textural classes between these two regions. The results between factors that were significant from regression analysis and computed VIP scores also varied to some extent (Table 3, Fig. 5). For example, for SSA, silt was not significant based on the coefficient from the regression model (Table 3), but were important based on computed VIP scores (> 1, Fig. 5a). The variation in the results can be attributed to the difference in statistical computation. Grömping (2009) explained such computation differences, which is caused by the non-unique decomposition of model sum of squares in the regression model, due to correlated predictors. However, we used uncorrelated variables to develop the regression models, which is contrary to this observation. Unexpectedly, higher FR values (for N) were found in soils with higher P-Olsen concentrations (> 8.7 mg kg−1), but below the critical level of 15 mg kg−1. This may be attributed to the fact that in part of the entries, N fertilization was combined with P (and K) fertilization, and FR was > 1 particularly in those cases (Fig. 3b).
Nevertheless, it appeared difficult to capture a relevant amount of variation using parameters that are widely available. The meta-analysis of factors affecting FR provided few points of departure for spatial refinement of fertilizer recommendations. The wide CIs for soil orders and texture were all overlapping each other, although some orders and textural classes with FRs significantly > 1 were identified (the more fertile Cambisols and Arenosols for Kenya and SSA, respectively, and sandy (clay) loam soils consistently for Kenya and SSA). The regression analyses showed that the set of continuous environmental characteristics used, explained a very limited proportion of the variation in FR and N-AE (Table 3). The available continuous variables explained only 29% of the total variation in FR in Kenya and as little as 13% in SSA. For the N-AE the respective percentages of explained variation were even lower.
Units aggregating several factors determining FR or N-AE would intuitively be most suitable to refine fertilizer recommendations for spatially relevant units. The spatial mapping unit AEZ potentially captures a combination of factors (length of the growing season, climate, landform and soils) related to land use. As such, it aggregates some of the other individual variables tested and is currently used to refine fertilizer recommendations. However, the average FR in the AEZ distinguished for Kenya (not including soils but based on temperature, water supply and length of growing period; (Jätzold and Kutsch 2000) did not differ significantly (Fig. 4e), although the FR was significantly > 1 in three of the seven zones of Kenya. This renders AEZs an unsuitable unit for refining recommendations based on our results. Extending them with soil information (pH, P-Olsen, texture, order) could be a promising strategy.
The maize yield in the non-fertilized control seemed to be the best predictor for the FR (p = 0.0001; Fig. 1a, b). This variable can, similar to AEZ, be regarded an integral proxy for environmental (soil fertility, climate, weather), genetic (maize variety) and management factors (planting density, control of pests, weeds, diseases). Both for Kenya and for SSA the adjusted R2 increased substantially when these yields were added to the set of independent variables (from 29 to 63% for Kenya and from 13 to 48% for SSA). The FR was higher when the yield in the control plots was lower (Fig. 2a, b). However, this statistical relationship is probably a result of autocorrelation because the maize yield in the non-fertilized control (xc) is in the denominator of FR. This suggestion of autocorrelation is supported by the absence of any relationship between control yields and N-AE (Fig. 1a, b).
Soil responsiveness to fertilizer application
The FR when considered as index, can provide useful tool for diagnosing soil responsive to fertilizer application. The majority of sites (> 85%) were responsive to fertilization for SSA and Kenya. To prevent complete failure of fertilizers, prior identification of non-responsive soils is of utmost importance. Non-responsiveness of poor soils is often related to low soil organic matter content (Tittonell and Giller 2013), causing soil physical constraints (low water-holding capacity), low micronutrient availability (Kihara et al. 2017) and low microbial activity leading to increased soil disease risk (Lal 2016). Our results confirm this: although the variation was high, the average C content of poor, non-responsive soils (11 g kg−1) was significantly lower (p = 0.031) than in responsive, (18 g kg−1) and fertile non-responsive soils (19 g kg−1; Fig. 2c). The soil responsiveness categories were clearly distinguished by total C and exchangeable K (Fig. 2c, f). Thus, total C and exchangeable K could act as useful indicators for discerning the different categories of soil responsiveness to N fertilization, which may be useful for nutrient management. The high variation indicates that non-responsiveness is a complex feature that is not easily operationalized using easily available environmental data. This is probably the reason that soil total C is not a powerful predictor of the FR (Table 3).
Challenges for meta-analysis in agronomic studies
This study adhered to standards recommended for meta-analysis in agronomy studies (Philibert et al. 2012). However, exclusion of publications (only 71 studies out of the total of 503 found were acceptable) is a clear indication of the challenges for merging and comparing data from past literature for meta-analysis, which may be attributed to differences in reporting across fertilizer studies. For example, all studies reported on fertilizer treatments, which allowed us to quantify the FR and N-AE. Studies that did not report control treatments (5%; where no fertilization was done) were omitted from the analysis. Familiar environmental and management factors that influence FR were not reported. For example, there was variation on the different set of soil properties used in characterizing each study area. As a result, we imputed missing soil properties (18%), since different analytical methods were used for soil characterization.
There is therefore a need of promoting standards of reporting finding (results) in agronomy, specifically in fertilizer-related studies for future meta-analytical inferences. We recommend developing standard to provide enough information. For example, there should be a minimum list (set) of soil properties that should be included in future studies, and clear description of any other factors observed within the site that is under investigation. This may allow combination as well as comparability of datasets across agronomic studies. Supply of information describing the availed data (metadata) should be a requirement for all agronomic studies. However, developing guidelines, calls for detailed investigation that could avail a standard protocol of presenting additional information for agronomic studies similar to those developed for biochar and metabolic studies (Fiehn et al. 2007; Jeffery et al. 2011).
Conclusions
The basic premise of this study was to identify key soil, climate and management factors that can be used to refine fertilizer recommendation across smallholder farms of SSA. The findings in this study indicate that available data layers can explain only very small amounts (< 33%) of variation in FR and N-AE and there is need for more systematic studies at high spatial resolution to identify yield-limiting factors. Our data indicated that soil pH, P-Olsen, exchangeable K, silt content and rainfall had significant but low levels of power in explaining variation in FR and N-AE. This finding implies that strategies for refining the current blanket fertilizer recommendation should include information on soil type, soil properties (texture, P-Olsen and total carbon). Such information can be derived through soil testing, which should be accompanied by nutrient response trials and preferably plant nutrient testing to diagnose limiting factors.
Due to the limitation of our dataset, this study did not comprehensively unravel factors that lead to soil non-responsiveness across smallholder farms. The complexity of soil responsiveness to fertilizer application requires further studies to fully understand other factors that led to non-responsive soils, besides total C, soil pH, exchangeable K and P-Olsen as indicated in this study.
Abbreviations
- AEZ:
-
Agro-ecological zone
- CI:
-
Confidence interval
- CEC:
-
Cation exchange capacity
- dw:
-
Dry weight
- FR:
-
Fertilizer response
- FRw :
-
Weighted fertilizer response
- FURP:
-
Fertilizer use recommendation project
- GLM:
-
General linear model
- IUSS:
-
International union soil science
- N-AE:
-
Agronomic nitrogen use efficiency
- PMM:
-
Predictive mean matching
- QT :
-
Heterogeneity
- RE:
-
Regression model
- SSA:
-
Sub-Sahara Africa
- VIP:
-
Variable importance in projection
References
Antwi M, Duker AA, Fosu M, Abaidoo RC (2016) Geospatial approach to study the spatial distribution of major soil nutrients in the Northern region of Ghana. Cogent Geosci. https://doi.org/10.1080/23312041.2016.1201906
Barto EK, Rillig MC (2010) Does herbivory really suppress mycorrhiza? A meta-analysis. J Ecol 98:745–753. https://doi.org/10.1111/j.1365-2745.2010.01658.x
Borenstein M, Hedges LV, Higgins JP, Rothstein HR (2011) Introduction to meta-analysis. Wiley, New York
Brown HK, Kempton RA (1994) The application of REML in clinical trials. Stat Med 13:1601–1617
Chong IG, Jun CH (2005) Performance of some variable selection methods when multicollinearity is present. Chemom Intell Lab Syst 78:103–112. https://doi.org/10.1016/j.chemolab.2004.12.011
Di Zio M, Guarnera U (2009) Semiparametric predictive mean matching. AStA Adv Stat Anal 93:175–186. https://doi.org/10.1007/s10182-008-0081-2
Dobermann A, Witt C, Dawe D et al (2002) Site-specific nutrient management for intensive rice cropping systems in Asia. Field Crop Res 74:37–66
Dudal R (1980) Soil-related constraints to agricultural development in the tropics. In: Priorities for alleviating soil-related constraints to food production in the tropics. International Rice Research Institute, Los Banos, pp 23–37
Duval S, Tweedie R (2000) Trim and fill: a simple funnel-plot-based method of testing and adjusting for publication bias in meta-analysis. Biometrics 56:455–463. https://doi.org/10.1111/j.0006-341X.2000.00455.x
Farrés M, Platikanov S, Tsakovski S, Tauler R (2015) Comparison of the variable importance in projection (VIP) and of the selectivity ratio (SR) methods for variable selection and interpretation. J Chemom 29:528–536. https://doi.org/10.1002/cem.2736
Fiehn O, Sumner LW, Rhee SY et al (2007) Minimum reporting standards for plant biology context information in metabolomic studies. Metabolomics 3:195–201. https://doi.org/10.1007/s11306-007-0068-0
FURP (1994) The fertilizer use recommendation project, Kenya Agricultural Research Institute, National Agricultural Research Laboratories, Nairobi. Final Report Annex I Fertil trial Doc (FERDOC) Minist Agric Nairobi
Giller KE, Rowe EC, de Ridder N, van Keulen H (2006) Resource use dynamics and interactions in the tropics: scaling up in space and time. Agric Syst 88:8–27. https://doi.org/10.1016/j.agsy.2005.06.016
Grömping U (2009) Variable importance assessment in regression: linear regression versus random forest. Am Stat 63:308–319. https://doi.org/10.1198/tast.2009.08199
Hedges LV, Olkin I (1985) Statistical methods for meta-analysis. Academic Press, Orlando, FL
Hedges LV, Gurevitch J, Curtis PS (1999) The meta-analysis of response ratios in experimental ecology. Ecology 80:1150–1156
Hengl T, Heuvelink GBM, Kempen B et al (2015) Mapping soil properties of Africa at 250 m resolution: random forests significantly improve current predictions. PLoS ONE 10:e0125814. https://doi.org/10.1371/journal.pone.0125814
Hengl T, Leenaars JGB, Shepherd KD et al (2017) Soil nutrient maps of Sub-Saharan Africa: assessment of soil nutrient content at 250 m spatial resolution using machine learning. Nutr Cycl Agroecosyst 109:77–102. https://doi.org/10.1007/s10705-017-9870-x
Huedo-Medina TB, Sánchez-Meca J, Marín-Martínez F, Botella J (2006) Assessing heterogeneity in meta-analysis: Q statistic or I2 index? Psychol Methods 11:193–206. https://doi.org/10.1037/1082-989X.11.2.193
Ishak KJ, Platt RW, Joseph L, Hanley JA (2008) Impact of approximating or ignoring within-study covariances in multivariate meta-analyses. Stat Med 27:670–686. https://doi.org/10.1002/sim.2913
IUSS Working Group WRB (2014) World reference base for soil resources 2014. International soil classification system for naming soils and creating legends for soil maps
Jätzold R, Kutsch H (2000) Agro-ecological zones of the tropics, with a sample from Kenya, 15–32
Jeffery S, Verheijen FGA, van der Velde M, Bastos AC (2011) A quantitative review of the effects of biochar application to soils on crop productivity using meta-analysis. Agric Ecosyst Environ 144:175–187. https://doi.org/10.1016/j.agee.2011.08.015
Johnson DW, Curtis PS (2001) Effects of forest management on soil C and N storage: meta analysis. For Ecol Manag 140:227–238. https://doi.org/10.1016/S0378-1127(00)00282-6
Kihara J, Nziguheba G, Zingore S et al (2016) Understanding variability in crop response to fertilizer and amendments in sub-Saharan Africa. Agric Ecosyst Environ 229:1–12. https://doi.org/10.1016/j.agee.2016.05.012
Kihara J, Sileshi GW, Nziguheba G et al (2017) Application of secondary nutrients and micronutrients increases crop yields in sub-Saharan Africa. Agron Sustain Dev. https://doi.org/10.1007/s13593-017-0431-0
Kleinman PJA, Sharpley AN, Gartley K et al (2001) Interlaboratory comparison of soil phosphorus extracted by various soil test methods. Commun Soil Sci Plant Anal 32:2325–2345. https://doi.org/10.1081/CSS-120000376
Kuhn M (2008a) Caret package. J Stat Softw 28:1–26
Kuhn M (2008b) Building predictive models in R using the caret package. J Stat Softw 28:1–26. https://doi.org/10.1053/j.sodo.2009.03.002
Kuhn M, Wing J, Weston S et al (2014) caret: classification and regression training. R package version 6.0-21
Lal R (2016) Soil health and carbon management. Food Energy Secur 5:212–222
Little RJA, Rubin DB (2002) Statistical analysis with missing data, 2nd edn. Wiley, New York
López-López JA, Marín-Martínez F, Sánchez-Meca J et al (2014) Estimation of the predictive power of the model in mixed-effects meta-regression: a simulation study. Br J Math Stat Psychol 67:30–48. https://doi.org/10.1111/bmsp.12002
Luo Y, Hui D, Zhang D (2006) Elevated CO2 stimulates net accumulations of carbon and nitrogen in land ecosystems: a meta-analysis. Ecology 87:53–63. https://doi.org/10.1890/04-1724
Ma BL, Zheng ZM, Morrison MJ, Gregorich EG (2016) Nitrogen and phosphorus nutrition and stoichiometry in the response of maize to various N rates under different rotation systems. Nutr Cycl Agroecosyst 104:93–105. https://doi.org/10.1007/s10705-016-9761-6
Mehmood T, Liland KH, Snipen L, Sæbø S (2012) A review of variable selection methods in Partial Least Squares Regression. Chemom Intell Lab Syst 118:62–69
Mevik B-H, Wehrens R (2007) The pls Package: principal component and partial least squares regression in R. J Stat Softw 18:1–24. https://doi.org/10.18637/jss.v018.i02
Mowo JG, Mlingano ARI (1993) Review of fertilizer recommendations in Tanzania. National Soil Service, ARI Mlingano, Ministry of Agriculture
Njoroge R, Otinga AN, Okalebo JR et al (2017) Occurrence of poorly responsive soils in western Kenya and associated nutrient imbalances in maize (Zea mays L.). Field Crop Res 210:162–174. https://doi.org/10.1016/j.fcr.2017.05.015
Nziguheba G, Tossah BK, Diels J et al (2009) Assessment of nutrient deficiencies in maize in nutrient omission trials and long-term field experiments in the West African Savanna. Plant Soil 314:143–157. https://doi.org/10.1007/s11104-008-9714-1
Philibert A, Loyce C, Makowski D (2012) Assessment of the quality of meta-analysis in agronomy. Agric Ecosyst Environ 148:72–82. https://doi.org/10.1016/j.agee.2011.12.003
Ray DK, Mueller ND, West PC, Foley JA (2013) Yield trends are insufficient to double global crop production by 2050. PLoS ONE. https://doi.org/10.1371/journal.pone.0066428
Ros GH, Temminghoff EJM, Hoffland E (2011) Nitrogen mineralization: a review and meta-analysis of the predictive value of soil tests. Eur J Soil Sci 62:162–173. https://doi.org/10.1111/j.1365-2389.2010.01318.x
Schnier HF, Recke H, Muchena FN, Muriuki AW (1996) Towards a practical approach to fertilizer recommendations for food crop production in smallholder farms in Kenya. Nutr Cycl Agroecosyst 47:213–226. https://doi.org/10.1007/bf01986276
Shepherd KD (2010) Soil spectral diagnostics—infrared, X-ray and laser diffraction spectroscopy for rapid soil characterization in the Africa Soil Information Service. In: 19th world congress of soil science
Shepherd KD, Walsh MG (2007) Infrared spectroscopy-enabling an evidence-based diagnostic surveillance approach to agricultural and environmental management in developing countries. Journal of Near Infrared Spectroscopy. J Near Infrared Spectrosc 1:1–20
Sileshi G, Akinnifesi FK, Ajayi OC, Place F (2008) Meta-analysis of maize yield response to woody and herbaceous legumes in sub-Saharan Africa. Plant Soil 307:1–19. https://doi.org/10.1007/s11104-008-9547-y
Stoorvogel JJ, Smaling EMA (1998) Research on soil fertility decline in tropical environments: integration of spatial scales. Nutr Cycl Agroecosyst 50:151–158
Thornton A, Lee P (2000) Publication bias in meta-analysis: its causes and consequences. J Clin Epidemiol 53:207–216
Tittonell P, Giller KE (2013) When yield gaps are poverty traps: the paradigm of ecological intensification in African smallholder agriculture. Field Crop Res 143:76–90. https://doi.org/10.1016/j.fcr.2012.10.007
Tittonell P, Vanlauwe B, Leffelaar PA et al (2005) Exploring diversity in soil fertility management of smallholder farms in western Kenya: I. Heterogeneity at region and farm scale. Agric Ecosyst Environ 110:149–165. https://doi.org/10.1016/j.agee.2005.04.001
Tittonell P, Zingore S, van Wijk MT et al (2007) Nutrient use efficiencies and crop responses to N, P and manure applications in Zimbabwean soils: exploring management strategies across soil fertility gradients. F Crop Res 100:348–368. https://doi.org/10.1016/j.fcr.2006.09.003
Tittonell P, Vanlauwe B, Corbeels M, Giller KE (2008) Yield gaps, nutrient use efficiencies and response to fertilisers by maize across heterogeneous smallholder farms of western Kenya. Plant Soil 313:19–37. https://doi.org/10.1007/s11104-008-9676-3
Tittonell P, Muriuki A, Klapwijk CJ et al (2013) Soil heterogeneity and soil fertility gradients in smallholder farms of the East African Highlands. Soil Sci Soc Am J 77:525–538. https://doi.org/10.2136/sssaj2012.0250
United Nations Population Division (2017) World population to exceed 9 billion by 2050: developing countries to add 2.3 billion inhabitants with 1.1 billion aged over 60 and 1.2 billion of working agen. http://esa.un.org/unpd/wpp/index.htm. Accessed 24 Oct 2018
Van Buuren S, Groothuis-Oudshoorn K (2011) Multivariate imputation by chained equations. J Stat Softw 45:1–67. https://doi.org/10.1177/0962280206074463
Vanlauwe B, Kihara J, Chivenge P et al (2011) Agronomic use efficiency of N fertilizer in maize-based systems in sub-Saharan Africa within the context of integrated soil fertility management. Plant Soil 339:35–50. https://doi.org/10.1007/s11104-010-0462-7
Vanlauwe B, Descheemaeker K, Giller KE et al (2014) Integrated soil fertility management in sub-Saharan Africa: unravelling local adaptation. SOIL Discuss 1:1239–1286. https://doi.org/10.5194/soild-1-1239-2014
Vanlauwe B, Coe R, Giller KE (2016) Beyond averages: new approaches to understand heterogeneity and risk of technology success or failure in smallholder farming. Exp Agric. https://doi.org/10.1017/S0014479716000193
Viechtbauer W (2010) Conducting meta-analyses in R with the metafor package. J Stat Softw 36:1–48
Vink G, Frank LE, Pannekoek J, van Buuren S (2014) Predictive mean matching imputation of semicontinuous variables. Stat Neerl 68:61–90. https://doi.org/10.1111/stan.12023
Wuenscher R, Unterfrauner H, Peticzka R, Zehetner F (2015) A comparison of 14 soil phosphorus extraction methods applied to 50 agricultural soils from Central Europe. Plant Soil Environ. https://doi.org/10.17221/932/2014-pse
Zingore S, Murwira HK, Delve RJ, Giller KE (2007) Soil type, management history and current resource allocation: three dimensions regulating variability in crop productivity on African smallholder farms. Field Crop Res 101:296–305. https://doi.org/10.1016/j.fcr.2006.12.006
Acknowledgements
The Ph.D. project of the principal author is funded through co-operation of University of Nairobi, World Agroforestry Center (ICRAF) Fellowship Program, Wageningen University Sandwich Ph.D. fellowship program and International Center for Research in the Tropics (CIAT-Kenya). Funding was provided by Bill and Melinda Gates Foundation (Grant No. 52), Wageningen University (Grant No. 549).
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ichami, S.M., Shepherd, K.D., Sila, A.M. et al. Fertilizer response and nitrogen use efficiency in African smallholder maize farms. Nutr Cycl Agroecosyst 113, 1–19 (2019). https://doi.org/10.1007/s10705-018-9958-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10705-018-9958-y