The effect of crack orientation on the mode I fracture resistance of pinewood

Abstract

The fracture resistance of pinewood under mode I loading is investigated experimentally for different crack plane orientations and the crack propagation direction parallel to longitudinal cells. Experiments are conducted on double cantilever beams using a digital image correlation system to evaluate the crack tip opening displacement. The compliance based beam method is used to determine the energy release rate at various crack lengths. The decomposition of crack propagation into the pre-peak and post-peak propagations is proposed to find the fracture energy contributions from individual toughening mechanisms in pinewood. The cohesive strengths measured in the experiments are confirmed by comparison with the tensile strengths obtained from separate tests performed on pinewood. An analytical model for evaluating the fracture process zone is used to validate the experimental results. The difference between the fracture energy values in different crack propagation systems is explained by using X-ray microtomography images of the fracture surfaces.

1 Introduction

There is a need for better understanding of the propagation of cracks in wood, because of increased interest in using wood as a building material which can replace concrete and steel in sustainable and environmentally friendly constructions.

The cracking phenomenon in wood is controlled by two toughening mechanisms occurring in a zone ahead of the crack tip, namely microcracking and fiber bridging (Smith and Vasic 2003; Stanzl-Tschegg 2006). The non-linearity appearing in the load–displacement curve before the peak load is attributed to the microcracks formation in the fracture process zone (FPZ). The microcracks facilitate bridging of fibers in this zone, which, in turn, results in the load drop observed in the load–displacement curve and finally the crack propagation is visible to the unaided eye. It is assumed that the peak load during displacement control tests is achieved when microcracking transforms into fiber bridging (Yu et al. 2021; Romanowicz 2022). Although progress has been made, quantitative evaluation of these toughening mechanisms is still a challenge.

Because it is experimentally difficult to detect the real crack tip in a material that exhibits fiber bridging, several data reduction methods based on compliance calibration or beam theories were proposed in order to evaluate the energy release rate at various crack lengths (de Moura et al. 2008; Yoshihara and Kawamura 2006). The variation of energy release rate with crack length (R-curve) in a quasi-brittle material like wood follows an initially increasing trend before reaching a plateau, which defines a critical value of the resistance to crack growth. The appearance of a constant resistance means self-similar propagation of the main crack with its critical fracture process zone. Displacement-control fracture tests show that the peak load is reached for a resistance smaller than the critical resistance (Morel et al. 2005; Dourado et al. 2015). This finding implies that the R-curve and FPZ develop both in the pre-peak and in the post-peak regime, which causes difficulties in assessing the critical resistance because a clear plateau of the R-curve occurs rarely in practice due to FPZ confinement. Such a plateau is only observed for sufficiently large size specimens in which the FPZ can develop freely. The fractions of energy dissipated in wood by microcracking and fiber-bridging were calculated in papers de Moura et al. (2008), Dourado et al. (2008), Morel et al. (2010), Coureau et al. (2013) as softening law parameters by using iterative procedures in which the numerical load–displacement curve and the numerical R-curve were adjusted to give the best fit to the corresponding experimental curves.

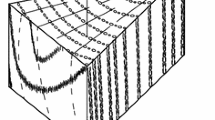
To investigate the mode I fracture properties of wood, different types of specimens are used i.e., double cantilever beam (DCB) (de Moura et al. 2008), single edge notched beam loaded in three point bending (SENB) (Dourado et al. 2015), wedge splitting test specimen (WST) (Stanzl-Tschegg 2006), compact tension test specimen (CT) (Biswal and Singh 2023). Based on these tests there is an inconsistency in results of existing studies on the fracture behavior of wood in different crack propagation systems. Within the same wood category i.e. softwood, some studies on specimens with short cracks find a higher fracture energy in the RL crack propagation system than in the TL crack propagation system (Reiterer et al. 2002; Vasic and Smith 2002) whereas some on specimens with long cracks find the opposite result (Wilson et al. 2013; Frühmann et al. 2002). In the first case, the obtained result is attributed to ray cells (Fig. 1a), which act as a reinforcement in the RL crack propagation system. In the second case, annual rings consisting of the earlywood and the latewood, are considered to have a toughening effect in TL crack propagation system. The inconsistency may be not only due to the different specimens used for fracture tests but also due to the method of estimation of the fracture energy. The mean fracture energy defined as the area under the load–displacement curve divided by the entire fracture area is often measured instead of the value of energy release rate obtained for self-similar propagation.

Fig. 1

Crack orientation within the tested material: microscopic structure of wood, where LRT is the coordinate system associated with the symmetry axes of wood (a), crack propagation systems considered in the analysis (b), modification of thicker TL specimens (c)

The findings of recent research (Xavier et al. 2014; Gómez-Royuela et al. 2022) indicate that the cohesive law of wood under mode I loading can be effectively evaluated from measurements of the crack tip opening displacement by using the digital image correlation technique. This new method provides the opportunity to explore again the effect of crack orientation on the fracture resistance. Taking the above into account, this paper presents a comparative analysis of the fracture process in pinewood for different crack plane orientations and the crack propagation direction parallel to longitudinal cells. The experimentally obtained relations between the cohesive traction and opening displacement in different crack propagation systems are here used to determine the fracture energies corresponding to different mechanisms of toughening and to point out which crack orientation provides better resistance to cracking. Additionally, the study involves an assessment of microtomography images of the fracture surfaces as well as an analysis of different specimen sizes to gain a deeper understanding of the fracture process. It discusses the role of the annual ring curvature in fracture tests on wood beam specimens and recommends strategies for addressing this issue.

2 Material and test method

2.1 Mode I fracture tests

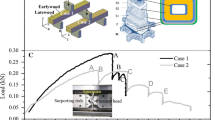
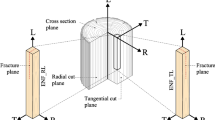
The mode I fracture tests were carried out on a electromechanical testing machine MTS Insight using a 1KN load cell under displacement control conditions with a constant crosshead rate of 5 mm/min. The experimental setup is shown in Fig. 2a. The mode I double cantilever beam (DCB) specimen shown in Fig. 2b was mounted in grips of the load frame using two steel pins of 3 mm diameter passed through loading holes of the specimen. The initial crack was first cut using a band saw with 1 mm thickness to form a notch and then prolonged a few millimeters with a razor blade to obtain required length. As shown in Fig. 1b, the initial cracks ran parallel to longitudinal cells in two ways: with the crack plane normal to the radial direction (RL cracks) or normal to the tangential direction (TL cracks).

Fig. 2

Experimental setup including MTS testing machine and Aramis digital image correlation system (a), the DCB specimen (b) and the dog-bone tensile specimen (c)

Three groups of the DCB specimens with an aspect ratio $h/a_{0}$ of $0.095,{ }0.143{\text{ and }}0.214$ were tested in this paper. The DCB specimen thickness 2 h and initial crack length $a_{0}$ measured from the center of the pins were 20 mm and 105 mm in the first group, 20 mm and 70 mm in the second group, 60 mm and 140 mm in the third group. The DCB specimen length measured from the center of the loading pins L and width B were the same in all the groups and equal to 280 mm and 20 mm, respectively.

The material under consideration was pinewood (Pinus Silvestris) commonly used for construction purposes in Europe and Asia. The DCB specimens were fabricated from straight grained boards, sawn both radially and tangentially from different pine trunks at different heights. Before tests, the specimens were conditioned at 20 °C and 65%RH until equilibrium, inducing 12% moisture content of wood. A total of 52 DCB specimens were tested, of which 13 (6 RL cracks and 7 TL cracks) had the aspect ratio of $0.095,{ }$ 18 (8RL cracks and 10TL cracks) had the aspect ratio of $0.143$ and 21 (12RL cracks and 9TL cracks) had the aspect ratio $0.214$. The region near the crack tip was covered by a speckle pattern and, as the crack propagated, the displacement field of specimen was monitored with a digital image correlation system Aramis 3D consisting of two 4 megapixel cameras. In the case of DCB specimens with aspect ratios of 0.095 and 0.143, the Aramis system was calibrated for a measurement region of 25 mm × 18 mm. In the case of DCB specimens with aspect ratio of 0.214, this region was increased to 65 mm × 48 mm. The resulting conversion factors of images were 0.010 mm/pixel in the first case and 0.028 mm/pixel in the second case. The crack tip opening displacement $\delta_{n}$ (CTOD) was found from the vertical displacement maps by selecting a pair of points equidistant from the crack tip and determining the relative displacement between them. The measurement points were identified before loads were applied as points lying on the vertical line passing through the crack tip. Based on the results of preliminary observations, the smallest vertical distance between the measurement points at which there is no discontinuity in CTOD data was fixed to 1 mm for $h/a_{0}$ = 0.095 and 0.143. In the case of $h/a_{0}$ = 0.214, this distance was increased to 1.5 mm. Load P, crosshead displacement $\delta$ and crack tip opening displacement $\delta_{n}$ were recorded throughout each test with a frequency of 4 Hz.

2.2 Microtomographic observations

After fracture tests, small blocks of size 20 mm × 20 mm × 10 mm (length × width × height), encompassing the fracture surface near the crack tip were resected from the DCB specimens to analyze the topography of fracture surface. High-resolution three-dimensional images of the fracture surfaces formed in specimens were obtained by using X-ray microtomography. Microtomographic measurements were made using Bruker X-ray microscope (SkyScan 1172). The spatial resolution was set to a pixel size of 12 μm. The images of fracture surfaces were obtained for a source voltage of 59 kV.

2.3 Transverse tensile tests

Using the same testing machine as applied to the fracture tests, transverse tensile tests of pinewood were carried out on dog-bone shaped specimens shown in Fig. 2c, composed of a gage section of 20 mm long and 8 mm thick that was glued to two grip sections of 20 mm wide. The dog-bone tensile specimens had a total length of 270 mm and were tested at the crosshead rate of 5 mm/min. The gage section of the specimen was cut out both in the LR and LT orthotropy plane from the same boards as those used for fracture tests and inserted into the specimen so that the length of the gage section was oriented either in the R or T direction. Using the two different types of gage section, transverse tension of pinewood was investigated both in the R and T direction. During these tests, only load P and crosshead displacement $\delta$ were monitored up to failure occurring within the gage section. The dog-bone tensile specimens with premature failure at the adhesive interface were excluded from the statistical analysis. A total of 16 dog-bone tensile specimens were correctly tested of which 9 in the R direction and 7 in the T direction.

2.4 Decomposition method

Two damage mechanisms occurring in the FPZ of wood under mode I loading can be described by using a constitutive relation between the normal cohesive traction $\sigma_{n}$ and opening displacement on the critical plane $\delta_{n}$. The total area under the curve $\sigma_{n} \left( {\delta_{n} } \right)$ represents the total fracture energy of wood $G_{{{\text{Ic}}}}$.

$$ G_{{{\text{Ic}}}} = \mathop \int \limits_{0}^{{{\delta_{n}{\text{c}}} }} \sigma_{n} {\text{d}}\delta_{n} $$

(1)

where $\delta_{n}^{{\text{c}}}$ is the opening displacement at the completion of damage development. This area can be divided into two sub-areas illustrating works consumed by microcracking and fiber bridging, which is formally written as $G_{{{\text{Ic}}}} = G_{{{\text{Ic}}}}^{{\text{m}}} + G_{{{\text{Ic}}}}^{{\text{b}}}$. The two sub-areas are calculated by following five steps.

First, the R-curve of wood is determined directly from the load deflection data using the compliance based beam method proposed by de Moura et al. (2008). The procedure for calculating the energy release rate $G_{{\text{I}}}$ is provided in Appendix. The calculations are performed using established values of elastic constants from the literature for pinewood (Pinus Silvestris), listed in Table 1 (Wilczynski and Gogolin 1990). Second, the total fracture energy $G_{{{\text{Ic}}}}$ is evaluated from the R-curve of wood as the plateau value. In the present paper, it is calculated by averaging all values of the energy release rate obtained beyond the peak load. Third, the relation between energy release rate and the crack tip opening displacement $G_{{\text{I}}} = f\left( {\delta_{n} } \right)$ is approximated by a logistic function, similarly to a study by Szekrenyes and Uj (2005)

$$ G_{{\text{I}}} = \frac{{A_{1} - A_{2} }}{{1 + \left( {\delta_{{\text{n}}} /\delta_{{\text{n}}}^{0} } \right)^{p} }} + A_{2} $$

(2)

where $A_{1} , A_{2} , \delta_{{\text{n}}}^{0} {\text{and}} p$ are constants determined by the regression method. Only data up to $G_{{{\text{Ic}}}}$ are included in the regression calculation. It should be noted that because the value of function (2) approaches $A_{2}$ as $\delta_{{\text{n}}}$ tends to infinity, the value of $A_{2}$ can be regarded as an estimate of $G_{{{\text{Ic}}}}$. Fourth, following Bao and Suo (1992), the cohesive law of wood $\sigma_{n} \left( {\delta_{n} } \right)$ is established by differentiating the energy release rate (2) with respect to $\delta_{{\text{n}}}$

$$ \sigma_{n} = \frac{{{\text{d}}G_{{\text{I}}} }}{{{\text{d}}\delta_{{\text{n}}} }} $$

(3)

Table 1 Elastic constants of pinewood (Pinus Silvestris) (Wilczyński and Gogolin 1990)

Fifth, the two sub-areas under the curve $\sigma_{n} \left( {\delta_{n} } \right)$ representing the fractions of energy dissipated by microcracking and fiber-bridging are calculated by integrating the curve $\sigma_{n} \left( {\delta_{n} } \right)$

$$ G_{{{\text{Ic}}}}^{{\text{m}}} = \mathop \int \limits_{0}^{{{\delta_{n}{\text{b}}} }} \sigma_{n} {\text{d}}\delta_{n} - 0.5\sigma_{n}^{{\text{b}}} \delta_{n}^{{\text{b}}} $$

(4)

$$ G_{{{\text{Ic}}}}^{{\text{b}}} = G_{{{\text{Ic}}}} - G_{{{\text{Ic}}}}^{{\text{m}}} $$

(5)

where $\sigma_{n}^{{\text{b}}} , \delta_{n}^{{\text{b}}}$ are the normal traction and opening displacement corresponding to the onset of fiber bridging. In the present paper, it is assumed that the onset of fiber bridging takes place at the peak load.

The proposed method of evaluating the fracture energies of wood $G_{{{\text{Ic}}}}^{{\text{m}}}$ and $G_{{{\text{Ic}}}}^{{\text{b}}}$ uses nonlinear relationships represented by 4 curves: (1) load P vs. deflection of specimen $\delta$, (2) energy release rate $G_{{\text{I}}}$ vs. crack length a, (3) energy release rate $G_{{\text{I}}}$ vs. opening displacement on the critical plane $\delta_{n}$, (4) cohesive traction $\sigma_{n}$ vs. opening displacement on the critical plane $\delta_{n}$, which are shown in Fig. 3a–d. In order to explain the method, three points corresponding to the completion of cracking (CRIT) and the onsets of microcracking (INIT) and fiber bridging (MAX) are visible in these figures. The onset of microcracking corresponds to the point on the cohesive traction–separation curve at which the maximum is reached. It can be seen from these figures that averaging the energy release rate values located beyond the peak load allows us to determine the plateau value with satisfactory accuracy, which, in turn, allows us to predict the critical load in the post-peak regime. Also, it can be seen that the fitting function (2) is able to reproduce correctly the experimental data.

Fig. 3

Schematic illustration of the decomposition method: a load P vs. deflection of specimen $\delta$, b energy release rate $G_{{\text{I}}}$ vs. crack length a, c energy release rate $G_{{\text{I}}}$ vs. opening displacement $\delta_{n}$, d cohesive traction $\sigma_{n}$ vs. opening displacement $\delta_{n}$

3 Results and discussion

3.1 Influence of the crack plane orientation

In order to determine the mode I fracture properties of pinewood in different crack propagation systems, DCB specimens with aspect ratio $h/a_{0}$ of 0.095 and cracks growing in the TL and RL systems have been tested. The obtained results in terms of the load P, the energy release rate $G_{{\text{I}}}$ and the cohesive traction on the critical plane $\sigma_{n}$ are shown for every specimen in Fig. 4a–d and summarized in Tables 2, 3 and 4.

Fig. 4

Comparison between the fracture behavior of pinewood in the RL and TL crack propagation system obtained for $h/a_{0} = 0.095$: a load P vs. deflection of specimen $\delta$, b energy release rate $G_{{\text{I}}}$ vs. crack length a, c energy release rate $G_{{\text{I}}}$ vs. opening displacement $\delta_{n}$, note: the pre-critical and post-critical results are plotted separately with solid and dashed lines, respectively. d cohesive traction $\sigma_{n}$ vs. opening displacement $\delta_{n}$

Table 2 Densities of specimens and characteristic values of loads $P$

Table 3 Fracture energies of pinewood corresponding to microcracking $G_{{{\text{Ic}}}}^{{\text{m}}}$ and fiber bridging $G_{{{\text{Ic}}}}^{{\text{b}}}$

Table 4 Parameters of the logistic function and characteristic values of cohesive tractions $\sigma_{n}$ and opening displacements $\delta_{n}$

From the load–displacement curves shown in Fig. 4a, it is evident that the change in orientation of the crack plane normal from R to T leads to increasing the peak load without modifying the initial stiffness of specimen. This is because the initial stiffness of specimen is mainly affected by the flexural properties and the initial crack length, which are the same for the RL and TL specimens. The average fracture initiation and maximum load were $P_{{\text{i}}}^{{{\text{RL}}}} = 48.12 {\text{N}}$ and $P_{{{\text{max}}}}^{{{\text{RL}}}} = 70.25 {\text{N}}$ in the RL system and $P_{{\text{i}}}^{{{\text{TL}}}} = 64.57 {\text{N}}$ and $P_{{{\text{max}}}}^{{{\text{TL}}}} = 100.93 {\text{N}}$ in the TL system (Table 2). It is seen from this data that the onset of microcracking determined from the cohesive strength data takes place when the load reaches 68 and 64% of the peak load in the RL and TL crack propagation system respectively.

Based on Fig. 4b and Table 3, it can be found that when the crack propagation system varies from RL to TL, the plateau of the R curve is raised so that the total fracture energy $G_{{{\text{Ic}}}}$ increases keeping the FPZ length constant. The average FPZ lengths, defined as $l_{{{\text{cz}}}} = a_{{\text{c}}} - a_{0}$, are 12.67 mm for RL cracks and 13.37 mm for TL cracks. This means that the FPZ develops in both the propagation systems along the length of five longitudinal cells (tracheids shown in Fig. 1a), assuming that the average length of longitudinal cell in pinewood is equal to 2.5 mm (Górska and Roszyk 2019). Based on the above, it can be concluded that the change in orientation of the crack plane normal from R to T leads to one-variable rescaling the R-curve along the energy release rate axis. Analyzing the average value of the critical load $P_{{\text{c}}}^{{{\text{RL}}}} = 67.45 {\text{N}}$, $P_{{\text{c}}}^{{{\text{TL}}}} = 95.84 {\text{N}}$ and the critical resistance $G_{{{\text{Ic}}}}^{{{\text{RL}}}} = 0.218 {\text{N/mm}}$, $G_{{{\text{Ic}}}}^{{{\text{TL}}}} = 0.476 {\text{N/mm}}$ in the two crack propagation systems it is clear from the data that, for pinewood, crack propagation in the RL system is easier than in the TL system. The average critical load $P_{{\text{c}}}$ and critical resistance $G_{{{\text{Ic}}}}$ in the TL crack propagation system increased, respectively, by 42 and 118% compared to the RL crack propagation system.

The variations in energy release rate with crack opening in both the crack propagation systems are shown in Fig. 4c. Steady-state crack propagation was observed in every specimen which made it possible to apply the decomposition method introduced in the previous section. Figure 4d shows the cohesive laws for every specimen obtained from the values of parameters of the logistic function given in Table 4. Based on the data, the values of energy dissipated in pinewood by microcracking $G_{{{\text{Ic}}}}^{{\text{m}}}$ and fiber-bridging $G_{{{\text{Ic}}}}^{{\text{b}}}$ are calculated and summarized in Table 3. It is interesting to note from this table that the contributions of energy consumed by microcracking and fiber bridging to the total fracture energy account for approximately 80 and 20% in the RL crack propagation system and 77 and 23% in the TL crack propagation system. Thus, the main toughening mechanism in pinewood is the formation of microcracks. This finding is in agreement with results obtained from de Moura et al. study (2008) for similar wood species (Pinus Pinaster) where the 74 and 26% contributions were estimated for RL cracks by using numerical simulations. The average values of energy dissipated in pinewood by microcracking $G_{{{\text{Ic}}}}^{{\text{m}}}$ and fiber-bridging $G_{{{\text{Ic}}}}^{{\text{b}}}$ increase in the TL crack propagation system compared to the RL crack propagation system by 110 and 153%, respectively.

Comparing the average value of the cohesive strength $\sigma_{{{\text{max}}}}^{{{\text{RL}}}} = 1.81 {\text{MPa}}$ with $\sigma_{{{\text{max}}}}^{{{\text{TL}}}} = 1.71 {\text{MPa}}$, it can be seen that, the difference in the cohesive strength between the two crack propagation systems is much less than the differences in the critical load and the critical fracture resistance. Furthermore, it is surprising that the trends seen in the critical load and the critical resistance are reversed here. The average ${\text{cohesive strength }}$ $\sigma_{{{\text{max}}}}$ in the TL crack propagation system decreased, by about 5%, compared to the RL crack propagation system. The higher cohesive strength of pinewood in the RL system than in the TL system can be attributed to acts of additional reinforcement in the form of ray cells (Fig. 1a). Thus it can be concluded that an initial crack in pinewood starts growing first in the RL system although this system offers a larger ${\text{cohesive strength}}$.

3.2 Influence of the specimen geometry

In order to determine the influence of the DCB specimen geometry on the mode I fracture properties of pinewood in different crack propagation systems, the fracture tests were repeated for three values of aspect ratios $h/a_{0}$ of $0.095,{ }0.143{\text{ and }}0.214$. The obtained R-curves of pinewood for RL and TL cracks with different aspect ratios are presented in Figs. 4b, 5b and 6b. For all the tested specimens, the plateau value on the R-curve was calculated by averaging the energy release rate that is beyond the maximum load in order to determine the fracture resistance $G_{{{\text{Ic}}}}$. Variations of the average $G_{{{\text{Ic}}}}$ values with the aspect ratio in the RL and TL crack propagation systems are shown in Fig. 7. It is interesting to note from this figure that the average $G_{{{\text{Ic}}}}$ values for RL cracks are nearly constant for all tested values of $h/a_{0}$ in comparison to the average $G_{{{\text{Ic}}}}$ values for TL cracks. In the case of TL cracks, the fracture resistance for $h/a_{0} = 0.214$ decreased significantly. On the one hand, the independence of the fracture resistance on the aspect ratio in the case of RL cracks indicates that all the considered specimen sizes are valid in the light of the assumptions of beam theory which is used to calculate the energy release rate $G_{{\text{I}}}$. On the other hand, the drop in the TL fracture resistance observed for $h/a_{0} = 0.214$ shows that another factor that is not connected with beam theory affects the $G_{{{\text{Ic}}}}$ results. This factor is a deviation of the annual ring orientation in the cross-section of the TL specimen with aspect ratio of 0.214 from the T direction. When the thickness of TL specimen 2 h is large, the orientation of the annual rings is not parallel to the T direction. This means that it is not possible to comply, even approximately, with the orthotropic symmetry conditions. In order to address this issue, the governing equations of compliance based beam method (Appendix) for thicker TL specimens need to be transformed from the material coordinate system to the problem coordinate system. The reason why the RL specimens tested in this paper are free from the effect of annual ring orientation is the fact that the width of specimens B was small enough to maintain the orthotropic symmetry.

Fig. 5

Comparison between the fracture behavior of pinewood in the RL and TL crack propagation system obtained for $h/a_{0} = { }0.143$: a load P vs. deflection of specimen $\delta$, b energy release rate $G_{{\text{I}}}$ vs. crack length a, c energy release rate $G_{{\text{I}}}$ vs. opening displacement $\delta_{n}$, note: the pre-critical and post-critical results are plotted separately with solid and dashed lines, respectively. d cohesive traction $\sigma_{n}$ vs. opening displacement $\delta_{n}$

Fig. 6

Comparison between the fracture behavior of pinewood in the RL and TL crack propagation system obtained for $h/a_{0} = { }0.214$: a load P vs. deflection of specimen $\delta$, b energy release rate $G_{{\text{I}}}$ vs. crack length a, c energy release rate $G_{{\text{I}}}$ vs. opening displacement $\delta_{n}$, note: the pre-critical and post-critical results are plotted separately with solid and dashed lines, respectively. d cohesive traction $\sigma_{n}$ vs. opening displacement $\delta_{n}$

Fig. 7

Variations of the average $G_{{{\text{Ic}}}}$ values with the aspect ratio $h/a_{0}$ in the RL and TL crack propagation systems. Error bars show standard deviation

The modification of CBB method is out of scope of this paper, but in order to provide a stronger argument for it, additional fracture tests for TL cracks and $h/a_{0} = 0.214$ were made using new specimens built with three TL specimens with aspect ratio of 0.095 glued together (see Fig. 1c). These tests were repeated twice. The obtained fracture characteristics for the two new TL specimens with aspect ratio of 0.214 and parallel orientation of the annual rings are plotted with dashed lines in Fig. 6a–d. It is clear from Fig. 6b that the plateau values of the new R-curves are located above the mean plateau of old R-curves for $h/a_{0} = 0.214$. Based on the results from tests on the glued TL specimens, it can be concluded that when the orientation of the annual rings within these specimens is close to parallel to the T direction, it is possible to obtain a similar value of $G_{{{\text{Ic}}}}$ for TL cracks independently on the aspect ratio.

In order to confirm that the higher cohesive strength of pinewood in the RL system than in the TL system is a rule, the cohesive law of pinewood was established for the two other values of $h/a_{0} = { }0.143{\text{ and }}0.214$. The obtained cohesive traction–separation curves of pinewood for RL and TL specimens with different aspect ratios are presented in Figs. 4d, 5d and 6d. It is interesting to note from these figures that the RL curves are arranged into two groups which represent narrow and broad forms of cohesive law in pinewood for RL cracks. The first group has its maximum above and the second group below the average ${\text{cohesive strength }}$ $\sigma_{{{\text{max}}}}^{{{\text{TL}}}}$ in the TL crack propagation system. Also, the initial stiffness of cohesive law in the first group is higher than in the second group. An explanation of the duality in the cohesive law for RL cracks is given in the next section. Variations of the average $\sigma_{{{\text{max}}}}$ values with the aspect ratio in the RL and TL crack propagation systems are shown in Fig. 8. It can be seen from this figure that values of the cohesive strength are higher in the RL system than in the TL system regardless the value of $h/a_{0}$.The observed increase in the cohesive strength of pinewood with increasing the aspect ratio is associated with the increase in the FPZ length $l_{{{\text{cz}}}}$ shown in Fig. 9. Such an increasing trend is consistent with the analytical model developed for orthotropic materials by Xie et al. (2016) who found that thinner DCB specimen or longer initial crack length results in a shorter process zone. It is important to note that the differences in values of $\sigma_{{{\text{max}}}}$ and $l_{{{\text{cz}}}}$ between the different crack propagation systems will not increase significantly with increasing the aspect ratio if the modified TL specimens are used. Thus, contrary to the fracture resistance, the cohesive strength and the FPZ length obtained from displacement-controlled tests cannot to be considered as material constants. The above conclusion is supported by the data of Suo et al. (1992) and Sorensen and Jacobsen (1998), which showed that the cohesive law is independent of specimen geometry only for DCB specimens loaded under pure moments.

Fig. 8

Variations of the average $\sigma_{{{\text{max}}}}$ values with the aspect ratio $h/a_{0}$ in the RL and TL crack propagation systems. Error bars show standard deviation

Fig. 9

Variations of the average $l_{{{\text{cz}}}}$ values with the aspect ratio $h/a_{0}$ in the RL and TL crack propagation systems. Error bars show standard deviation

3.3 Influence of the annual ring curvature

In order to provide a stronger argument for why crack propagation in the RL system is easier than in the TL system, images of fracture cross-sections were taken with an X-ray microscope. Figure 10 shows two typical images of fracture cross-sections for RL and TL specimens with aspect ratio of 0.095 acquired by the instrument for a crack length increment of about 10 mm. For comparison purposes, the analysis is made for specimens with a visible curvature of annual rings which is inevitable for wood. It is evident from this figure that TL cracks under mode I conditions consume more energy for propagation than RL cracks because their surfaces are not so smooth as those of the RL cracks. During crossing over the latewood rings, the TL crack front travels along the path of least resistance in a zigzag manner whereas the RL crack front always keeps a straight line. It is interesting to note that the TL zigzag crack front follows movement in the R direction. This is because the TL crack tends to grow along ray cells, which locally weaken the specimen. In the case of very small cross-sections with straight annual rings, it is reasonable to assume that the RL crack front will grow within the earlywood of one year and the zigzag pattern observed for TL cracks will be less pronounced.

Fig. 10

Typical images of fracture cross-sections in pinewood specimens for the RL (a) and TL (b) cracks

It was found that RL specimens with a small curvature of annual rings attain higher cohesive strength than RL specimens with a significant curvature. In the first case, ray cells, which appear in these images as thin radial lines, are perpendicular to the crack plane whereas in the second case they are oblique with respect to the crack plane. This means that the toughening effect of ray cells in the second case is not as strong as in the first case. The opposite effect was observed for TL specimens, namely that TL specimens with a small curvature reach lower cohesive strength than TL specimens with a significant curvature. This is because when ray cells within a TL specimen lie nearly parallel to the crack plane, they weaken the wood structure and when ray cells within a TL specimen are oblique with respect to the crack plane, they strengthen the wood structure.

A possible explanation of why crack propagation in the RL system is easier than in the TL system is that the crack plane in the TL system separates both weaker earlywood cells and stronger latewood cells whereas the crack plane in the RL system is oriented parallel to annual rings, which enables the crack to grow only through weaker earlywood cells. It is well known that latewood has thicker cell walls which results in higher resistance to microcrack formation. The results of the present study do not provide evidence for findings reported in the literature (Reiterer et al. 2002; Vasic and Smith 2002) that the RL crack propagation system offers higher fracture energy than the TL crack propagation system. This may be explained by the idea that the fracture energy also depends on the specimen size. In particular, it is easier to break ray cells in the RL system by pulling them with long lever arms (long cracks) than with short lever arms (short cracks). However, for sufficiently long initial cracks used in this study, their role in fracture resistance is negligible.

Based on the above it can be concluded that the fracture energy of wood is controlled by the density of longitudinal cells whereas the cohesive strength of wood depends on the orientation of ray cells.

3.4 Verification of the results

In order to validate the results of the present study, two additional analyses were performed. First, the cohesive strength of pinewood in the two crack propagation systems was compared to the transverse tensile strength in the R and T direction obtained from specimens extracted from the same boards as those previously used for fracture tests. The transverse strengths provided by the transverse tensile experiments are as follows: $\sigma_{{\text{c}}}^{{\text{R}}} = 3.26 {\text{MPa}}$ and $\sigma_{{\text{c}}}^{{\text{T}}} = 2.20 {\text{MPa}}$ with a COV of 39.93% and 34.11%, respectively. The values of the average transverse strength in the R and T direction are denoted by horizontal dotted lines in Figs. 4d–6d and 8. It should be noted that the results of transverse tensile tests are in agreement with the results of fracture tests and show that pinewood has the larger strength in the R direction than in the T direction.

Next, the FPZ length of pinewood in the two crack propagation systems was compared to an analytical prediction of Yang and Cox (2005) based on beam theory. According to this prediction, the FPZ length for orthotropic materials under mode I is as follows

$$ l_{cz} = M\left( {E_{{{\text{eff}}}} \frac{{G_{{{\text{Ic}}}} }}{{\left( {\sigma_{{{\text{max}}}} } \right)^{2} }}h^{3} } \right)^{1/4} $$

(6)

where M is a scaling factor, $E_{{{\text{eff}}}} = E_{L} /\left( {1 - \nu_{LR} \nu_{RL} } \right)$ is the effective Young’s modulus of a beam under plane-strain assumption, h is the half thickness of beam. It has been suggested by Harper and Hallett (2008) that a reasonable match is obtained for $M = 0.5.$ In this paper, the FPZ length is calculated separately for each ratio $h/a_{0}$ by using the experimental values of $G_{{{\text{Ic}}}}$ and $\sigma_{{{\text{max}}}}$ obtained from fracture tests. In the case of TL crack, the Poisson’s ratios $\nu_{LR}$ and $\nu_{RL}$ in the equation for the effective modulus need to be replaced by their analogues in the TL orthotropy plane $\nu_{LT}$ and $\nu_{TL}$. The predicted values of the FPZ length for different aspect ratios $h/a_{0}$ are connected by broken dotted lines in Fig. 9. It should be noted that they lie close to the experimental values obtained in the present study and follow the experimental trend.

4 Conclusions

A comparative analysis of the fracture resistance of pinewood under mode I loading in the RL and TL crack propagation systems was made. It was found that the critical load $P_{{\text{c}}}$ and critical resistance $G_{{{\text{Ic}}}}$ in the TL crack propagation system increase significantly compared to the RL crack propagation system whereas the differences in values of the cohesive strength $\sigma_{{{\text{max}}}}$ and FPZ length $l_{{{\text{cz}}}}$ between the two crack propagation systems are small. The small difference in $l_{{{\text{cz}}}}$ leads to a conclusion that the change in orientation of the crack plane normal causes one-variable rescaling the R-curve along the energy release rate axis. It was demonstrated that the difference in $\sigma_{{{\text{max}}}}$ between the RL and TL crack propagation system is much smaller than the difference in the transverse tensile strength $\sigma_{{\text{c}}}$ between the R and T direction. This finding suggests that the toughening effect of ray cells weakens in the presence of long cracks.

The higher fracture energy consumption in the TL crack propagation system was confirmed by using the X-ray microtomography images of the fracture surfaces. They showed that during crossing over the latewood rings, the RL crack front always keeps a straight line whereas the TL crack front travels along the path of least resistance in a zigzag manner. It was also observed that RL specimens with a small curvature of annual rings attain higher cohesive strength than RL specimens with a significant curvature. This finding indicates that the toughening effect of ray cells depends on the angle that these rays make with the crack plane. It was also found that a large curvature of annual rings is a limitation of the governing equations of compliance based beam method for thicker TL specimens. The way to overcome this limitation was to use glued specimens in which the orientation of the annual rings is close to parallel to the T direction. The experimental values of $G_{{{\text{Ic}}}}$, $\sigma_{{{\text{max}}}}$ and $l_{{{\text{cz}}}}$ obtained in this study were found to be in good agreement with the values predicted by Yang and Cox’s model. Furthermore, it was demonstrated that, within the range of specimen sizes tested, the cohesive strength and the FPZ length cannot to be considered as material constants because their values change significantly for different specimen sizes, contrary to the fracture resistance. The proposed method of the decomposition of crack propagation into the pre-peak and post-peak propagations was found to be effective in identifying the fracture energy contributions from individual toughening mechanisms in pinewood.

Appendix

Compliance based beam method proposed by de Moura et al. (2008) is an example of the data reduction method which allows us to determine the strain energy release rate based only on the specimen compliance without the need of measuring the crack length. According to the Timoshenko beam theory, the compliance of the DCB specimen with RL crack can be expressed as

$$ C = \frac{{8a_{eq}^{3} }}{{E_{L} Bh^{3} }} + \frac{{12a_{eq} }}{{5BhG_{LR} }} $$

(7)

where $a_{eq} = a + {\Delta } + {\Delta }_{FPZ}$ is an equivalent crack length which includes increments due to both rotation and FPZ effects that occur around the crack tip, h is the half-thickness of the specimen, $E_{L}$ is the Young’s modulus in the longitudinal direction, $G_{LR}$ is the shear modulus in the LR orthotropy plane. The equivalent crack length $a_{eq}$ can be estimated from the current specimen compliance $C$ replacing the Young’s modulus $E_{L}$ by the flexural modulus $E_{f}$ in Eq. (7). The flexural modulus $E_{f}$ is calculated substituting the initial compliance $C_{o}$ into (7) and considering only the initial crack length $a_{0}$ and the correction Δ (de Moura et al. 2008),

$$ E_{f} = \frac{{8\left( {a_{0} + \Delta } \right)^{3} }}{{Bh^{3} }}\left( {C_{0} - \frac{{12\left( {a_{0} + \Delta } \right)}}{{5BhG_{LR} }}} \right)^{ - 1} $$

(8)

where the correction $\Delta$ is given by the following equation proposed by Williams (1989)

$$ \Delta = h\sqrt {\frac{{E_{f} }}{{11G_{LR} }}\left[ {3 - 2\left( {\frac{{\Gamma }}{{1 + {\Gamma }}}} \right)^{2} } \right]} $$

(9)

where ${\Gamma } = 1.18\frac{{\sqrt {E_{f} E_{R} } }}{{G_{LR} }}$, $E_{R}$ is the Young’s modulus in the radial direction. Finally, differentiating the specimen compliance (7) with respect to the crack length $a_{eq}$, the mode I strain energy release rate in the RL crack propagation system can be expressed as

$$ G_{{\text{I}}} = \frac{{P^{2} }}{2B}\frac{{{\text{d}}C}}{{{\text{d}}a_{eq} }} = \frac{{6P^{2} }}{{B^{2} h}}\left( {\frac{{2a_{eq}^{2} }}{{E_{f} h^{2} }} + \frac{1}{{5G_{LR} }}} \right) $$

(10)

In the case of TL crack, the elastic constants $E_{R}$ and $G_{LR}$ in the above equations need to be replaced by their analogues in the TL orthotropy plane $E_{T}$ and $G_{LT}$.